Boosting Tree-Assisted Multitask Deep Learning for Small Scientific Datasets

Abstract

Machine learning approaches have had tremendous success in various disciplines. However, such success highly depends on the size and quality of datasets. Scientific datasets are often small and difficult to collect. Currently, improving machine learning performance for small scientific datasets remains a major challenge in many academic fields, such as bioinformatics or medical science. Gradient boosting decision tree (GBDT) is typically optimal for small datasets, while deep learning often performs better for large datasets. This work reports a boosting tree-assisted multitask deep learning (BTAMDL) architecture that integrates GBDT and multitask deep learning (MDL) to achieve near-optimal predictions for small datasets when there exists a large dataset that is well correlated to the small datasets. Two BTAMDL models are constructed, one utilizing purely MDL output as GBDT input while the other admitting additional features in GBDT input. The proposed BTAMDL models are validated on four categories of datasets, including toxicity, partition coefficient, solubility, and solvation. It is found that the proposed BTAMDL models outperform the current state-of-the-art methods in various applications involving small datasets.

Graphical Abstract

INTRODUCTION

In the past a few decades, substantial advances in machine learning (ML) algorithms have spanned data-driven approaches throughout essentially every field, including science, engineering, technology, medicine, and industry.^1–3 The essence behind these achievements is that the behavior in unknown domains can be accurately estimated by quantitatively learning the pattern from sufficient training samples. However, compared to the large dataset with billions or even trillions of data points in computer vision and image analysis, it is typically difficult to obtain large datasets in scientific experiments. For example, in biomedical research, the size of datasets is often constrained by the complexity, ethnicity, and high cost of large-scale experiments.^4–7 A similar problem is faced in the material study where the data size is typically smaller compared with that in other fields.^8,9 Moreover, in the domains of structural bioinformatics, it is also very difficult to construct a large-scale well-annotated dataset due to the high expense of data acquisition and costly annotation. When the number of training examples is very small, the ability for ML-based models to learn from the observed data sharply decreases, resulting in the poor performance of predictions. Therefore, improving the performance of ML for small scientific datasets is an important issue.

One possible way to solve this problem is transfer learning, which pretrains a model by using existing related datasets and then uses the trained model either as an initialization or a fixed feature extractor for a new task. This method reduces the need and effort to recollect a large training data, mitigating the limitation of small data sizes.^10–15 The original motivation of transfer learning is from the fact that one can cleverly apply the knowledge previously learned to solve new related problems. Note that the difference between the learning process of traditional ML and the transfer learning technique is that the former tries to learn each task from scratch, while the latter transfers the knowledge from some previous tasks to a current task when the current task has insufficient training data.

A unified definition of transfer learning is given as following.¹⁴ Given a specific domain, $\mathcal{D}=\{\mathcal{X},P(X)\}$, which has two parts, a feature space $\mathcal{X}$ and a marginal probability distribution P(X), where $X=\left\{x_1,\dots ,x_n\right\}\in \mathcal{X}$, a task $\mathcal{T}=\{\mathcal{Y},f(\cdot )\}$ also has two parts, a label space $\mathcal{Y}$ and a predictive function f(·) that is not observed and can be learned from the feature, and the label pairs {x_i, y_i} are formed, where x_i ∈ X and $y_i\in \mathcal{Y}$. Most of the literature in transfer learning only considers the case that there is one source domain ${\mathcal{D}}_S$ and one target domain ${\mathcal{D}}_T$, and thus the transfer learning is formally defined as that, given a source domain ${\mathcal{D}}_S$ with a corresponding source task ${\mathcal{T}}_S$, and a target domain ${\mathcal{D}}_T$ with a corresponding target task ${\mathcal{T}}_T$, it is the process of improving the target predictive function f_T(·) by using the knowledge from ${\mathcal{D}}_S$ and ${\mathcal{D}}_T$, where ${\mathcal{D}}_S\ne {\mathcal{D}}_T$ or ${\mathcal{T}}_S\ne {\mathcal{T}}_T$. There are many successful applications of transfer learning applied to different fields, including text sentiment classification,¹⁶ image classification,^17,18 human activity classification,¹⁹ software defect classification,²⁰ multilanguage text classification,²¹ and so on.

The problem of limited sample sizes also occurs in other important fields of ML, such as deep learning, which recently has received increasing attention. Deep learning has been successfully applied to numerous real-world applications. The algorithm of deep learning attempts to learn high-level features from massive datasets, which makes it different from traditional ML. In other words, deep learning is a representation learning algorithm based on large-scale datasets in ML. Unfortunately, deep learning with conventional methods on small datasets commonly shows worse performance than traditional ML methods, such as gradient boosting decision tree (GBDT);⁸ hence, data size dependence becomes one of the most challenging aspects for deep learning since it needs to take massive training dataset to learn the latent patterns behind the data. Therefore, the combination of deep learning and transfer learning, i.e., deep transfer learning (DTL) is a good choice to resolve the problem of insufficient training data when there is a large related dataset available. Recently, based on the techniques used in DTL, Tan et al. classified the deep transfer learning into four categories: instance-based DTL, mapping-based DTL, network-based DTL, and adversarial-based DTL.¹² Feng et al. attempted to predict solidification defects by deep neural network regression with a small dataset and found that a pretrained and fine-tuned deep neural network shows a better generalization performance over traditional ML methods, like shallow neural network and support vector machine.⁸ Liu et al. designed an ensemble transfer learning framework to improve classification accuracy when the training data are insufficient.²² George et al. applied DTL to transfer the knowledge from real-world object recognition tasks to glitch classifier for the detector of multiple gravitational wave signals.²³ In addition, there are many successful applications of DTL on image classification,^24,25 language learning,²⁶ domain adaption,^27,28 and gene regulation.^29,30 From the literature, one may notice that the previous studies of ML with small dataset paid more attention to deep learning or transfer learning and less attention to multitask deep learning, which is similar to the inductive transfer learning when labeled datasets in the source domain are available. The target and source tasks can be learned simultaneously in multitask deep learning.

In the present work, we introduce a boosting tree-assisted multitask deep learning (BTAMDL) to improve the performance of GBDT and/or DTL on predictions of small training dataset. In this framework, transfer learning is implemented by the method of multitask deep learning. We emphasize that different from the traditional multitask learning, where all relevant tasks may be benefited together simultaneously by leveraging the task relatedness and the shared information across different tasks, in the proposed framework, we aim at achieving better performance for the task with a small number of training samples. This is achieved by transferring knowledge from other tasks and we only care about whether the task with a small dataset is benefited or not from the transfer learning. Since our goal is to enhance performance of the task with small datasets, we do not care whether the task with large dataset become better or worse. Under the framework of the deep neural network, the task with a large number of training samples can usually achieve a good performance, which consequently assists the task with a small number of training samples to boost its predictive power.

The GBDT method is a widely used ML algorithm for handling problems with low feature dimensions and small data size, although it becomes very time-consuming when dealing with large datasets.^31–34 Based on the advantage of GBDT over small datasets, we develop two BTAMDL methods to combine GBDT with multitask deep neural networks. In the first BTAMDL method, we utilize the output of the last hidden layer of multitask deep neural networks as the input of the GBDT. In the second BTAMDL method, the GBDT input also includes additional features. Furthermore, consensus strategy,^35,36 and feature selection from importance ranking,^37–40 are implemented in the present work. The proposed methods are validated on various datasets, and the results of our numerical experiments confirm that the present models indeed achieve better performance on tasks with small data and outperform other state-of-the-art ML methods.

METHODS

Multitask Deep Learning (MDL).

The multitask learning technique learns multiple tasks simultaneously with the aim of mutual benefit and has been widely applied in various implementations, including image processing,⁴¹ speech recognition and classification,^42,43 identification of handwritten digits,⁴⁴ natural language processing,⁴⁵ computer vision,⁴⁶ microarray data integration,⁴⁷ and drug discovery.^48–51 Most formulations of multitask learning extract hand-crafted features during the learning process and are based on the assumption that there is a linear relationship between the data and target labels. However, this assumption is not true in many practical applications where a complex nonlinear data-to-target relationship may exist, which limits the predictive performance of the model.⁵² Recently, due to the capability in learning a latent representation of the data without significant hand-crafted feature formulation, deep learning with neural networks has been adopted for multitask learning with an end-to-end fashion.⁵³ There are two commonly used approaches to perform multitask learning in deep neural networks. One is called hard parameter sharing of hidden layers, which shares the hidden layers between all tasks. The other is called soft parameter sharing of hidden layers, which contains individual hidden layers for each task. In the present study, we adopt the first approach in our multitask deep learning, which is shown in Figure 1 as a simple illustration of a typical four-layer MDL for training four different tasks simultaneously.

Figure 1.

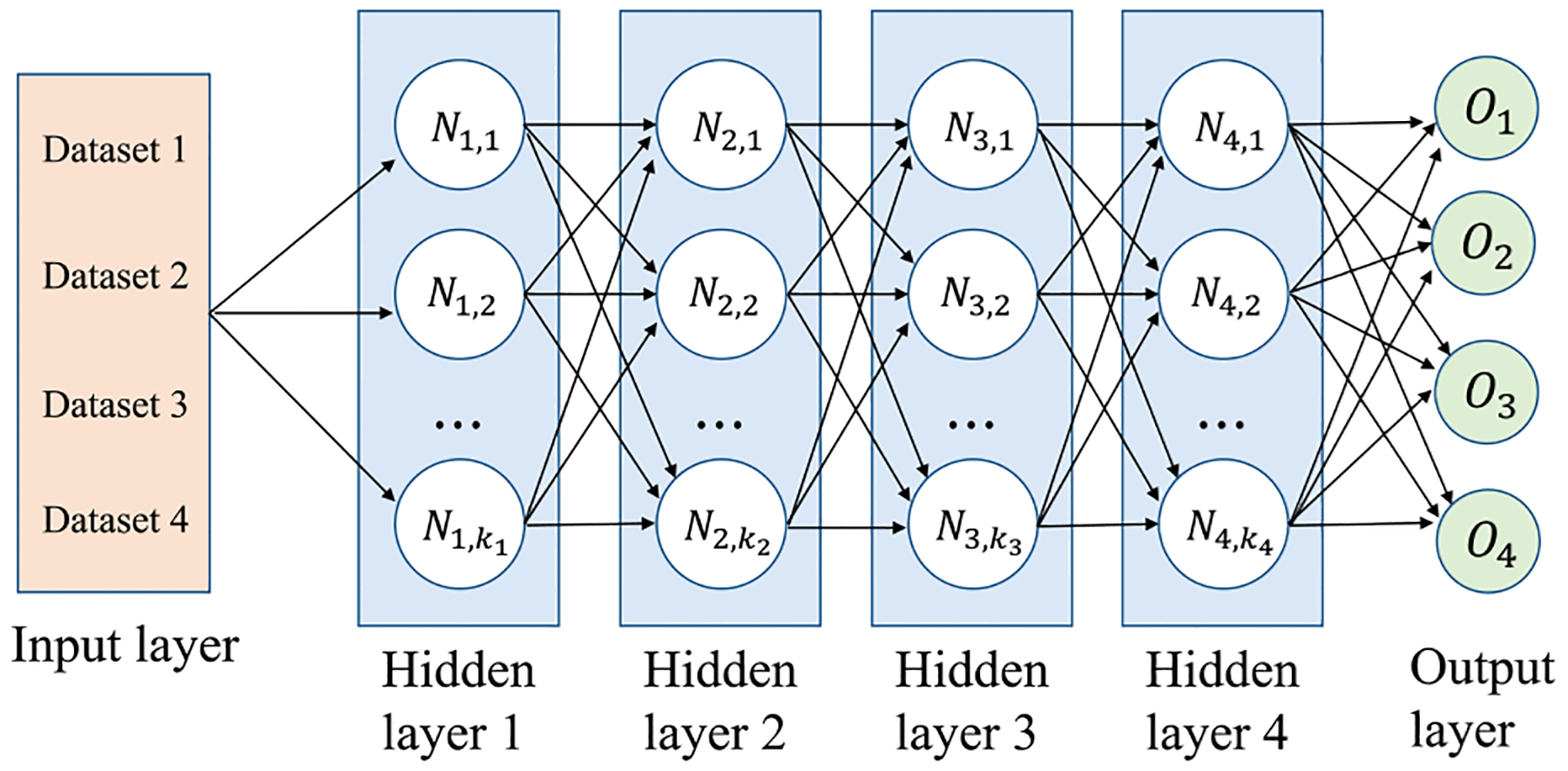
Simple illustration of a typical MDL training four tasks (datasets) simultaneously, including four hidden layers. k_i (i = 1, 2, 3,4) denotes the neuron number in the ith hidden layer, and N_i,j is the jth neuron in the ith hidden layer. O_i (i = 1, 2, 3, 4) represents the output of the ith task.

Suppose that there are T tasks during the learning, the training data for the tth task is ${\left({\mathit{X}}_i^t,y_i^t\right)}_i^{N_t}$, where ${\mathit{X}}_i^t\in {ℝ}^{N_t\times D}$ is a feature vector of the tth task, $y_i^t\in {ℝ}^{N_t\times 1}$ a target vector with the ith sample in the tth task, t = 1, …, T, with T being the total number of tasks, i = 1, …, N_t, with N_t being the number of samples in the tth task, and D the number of features in each task. If ${\mathit{W}}^t=\left\{w_j^t\in {ℝ}^D\right\}$ denotes the weight vector in the tth task, there would be a relationship between ${\mathit{X}}_i^t$ and $y_i^t,y_i^t={\sum }_j^D{X}_{ij}^t{w}_j^t+{\epsilon }_i\approx {\sum }_j^D{X}_{ij}^t{w}_j^t$ for a linear regression problem, where ε_i is random noise and can be neglected. A typical formulation for a MDL algorithm is given in the following form:

$$\text{arg\hspace{0.17em}min}\sum _{t=1}^{T}L\left({\mathit{y}}^t,{\mathit{f}}^t\left({\mathit{X}}^t,{\theta }^t\right)\right)+\lambda \text{Reg}(\mathit{W})$$ (1)

where the first term is the loss function (L) and the second term is a regularizer. ${\mathit{f}}^t\left({\mathit{X}}^t,{\theta }^t\right)=\left\{f^t\left(X_i^t,{\theta }^t\right)\right\}$ is a predictor vector and its ith sample in the tth task is a function of the feature vector X^t and θ^t. Here, θ^t is the collective set of machine learning hyper-parameters for the tth task. Note that, for a given fingerprint, the feature vector of all the tasks has the same dimensionality of features D but each task can have a different number N_t of samples. Here, W = [W¹, …, W^T] is a weight vector of all the tasks and can be obtained by concatenating all the weight vectors {w^t} of each task together and the features in each row of W for each task. Reg(W) denotes the regularizer of W and gives the constraint of weight vectors. Here λ is the regularization parameter balancing the loss function and the regularizer.

The mean square loss function for regression is given as following:

$$L(\mathit{y},\mathit{f}(\mathit{X},\theta ))=\sum _{t=1}^T\frac{{\mathcal{W}}^t}{N_t}\sum _{i=1}^{N_t}{\left(y_i^t-f^t\left(X_i^t,{\theta }^t\right)\right)}^2$$ (2)

where ${\mathcal{W}}^t\in [0,1]$ is a weight factor for balancing different tasks. Note that, in the present study, we can change the value of this factor to emphasize the task with a small dataset. When ${\mathcal{W}}^t$ is equal to $\frac{1}{T}$, eq 2 recovers the conventional mean square loss function.^54,55 For the constraint on weight vector W, there are several different commonly used regularizations for various conditions, including l₁-norm regularization,⁵⁶ l_2,1-norm regularization,⁵⁷ l_p,q-norm regularization,^58,59 capped l_p,1-norm regularization,⁶⁰ multilevel Lasso constraint,^61,62 and low-rank constraint.⁶³

Gradient boOsting Decision Tree (GBDT).

Due to its high efficiency, accuracy, and interpretability, GBDT is a widely used ensemble model of decision trees. It has already achieved good performances in many different applications, such as multiclass classification,⁶⁴ learning to rank,⁶⁵ and click prediction.⁶⁶ In this method, individual decision trees are trained sequentially and are assembled in a stagewise fashion to boost their capability of learning complex feature−target relationships. In general, based on N consecutive decision trees, the prediction of the model with data ${\left\{{\mathit{x}}^{(i)},y^{(i)}\right\}}_{i=1}^M$ (M is the number of samples) is as follows:

$${\widehat{y}}_N(\mathit{x})={\sum }_{n=1}^N{p}_n(\mathit{x})$$ (3)

where p_n(x) is the predicted labels of the nth tree. At each step, a new decision tree is trained to fit the residual between ground truth and current prediction. Taking regression as an example, a general loss function is given by

$$L_n=\sum _i{l}_i\left(y^{(i)},{\widehat{y}}_n^{(i)}\right)$$ (4)

where $l_i={\left(y^{(i)}-{\widehat{y}}^{(i)}\right)}^2/2$ with a square loss is taken into consideration. In each iteration, GBDT learns the decision trees by fitting the negative gradients. The total loss function L can be minimized along the following gradient direction:

$$-\frac{\partial L_n}{\partial p_n\left({\mathit{x}}^{(i)}\right)}=y^{(i)}-{\widehat{y}}_n^{(i)}$$ (5)

The main procedure of GBDT is the learning of decision trees, which costs most of the time to find the best split spot. Compared to deep neural networks (DNN), GBDT is robust, relatively insensitive to hyper-parameters, more suitable for dealing with small datasets, and easy to implement. Additionally, it is faster to train than DNN, which is a major advantage of GBDT. A challenge of GBDT is how to balance the trade-off between the accuracy and efficiency under the emergence of big datasets, which makes the GBDT implementation very time-consuming.

Boosting Tree-Assisted Multitask Deep Learning (BTAMDL).

In order to take the advantages of both GBDT and MDL, we introduce two two-step approaches to integrate MDL and GBDT. In the first step, MDL networks are constructed and trained to achieve better performance for the tasks with small datasets. After the training, outputs from the last hidden layer are put forward to the GBDT as its inputs. We call this method boosting tree-assisted multitask deep learning (BTAMDL). BTAMDL 1 denotes the case there are no additional features in GBDT rather than the features from MDL. In BTAMDL 2, additionally, inputs of nondeep learning features, in terms of the features of fingerprint, are applied to the GBDT as well.

Note that, the present BTAMDL proposes to further improve the generalization of GBDT on small datasets. These approaches may be or may not be suitable for relatively larger datasets.

Figure 2 illustrates our BTAMDL 1 with a four-task system. In the figure, ∑ denotes the sum of all weighted inputs from the previous hidden layer at a neuron, and AO denotes the activated output at a hidden layer neuron. For example, on the first hidden layer, for the tth task, summing the weighted inputs of the jth neuron is ${\sum }_i{w}_{ij}^{1t}{X}_i^t$, where $w_{ij}^{1t}$ is the weight between the input layer and the first hidden layer of the jth neuron in the tth task, and then the activated output (AO) of the jth neuron on the first hidden layer is $\sigma \left({\sum }_i{w}_{ij}^{1t}{X}_i^t\right)$, where σ(·) is an activation function. Training on different tasks is carried out iteratively. The AOs of the last hidden layer in each task are put forward as the inputs to train the GBDT model for the tasks with small datasets in step two.

Figure 2.

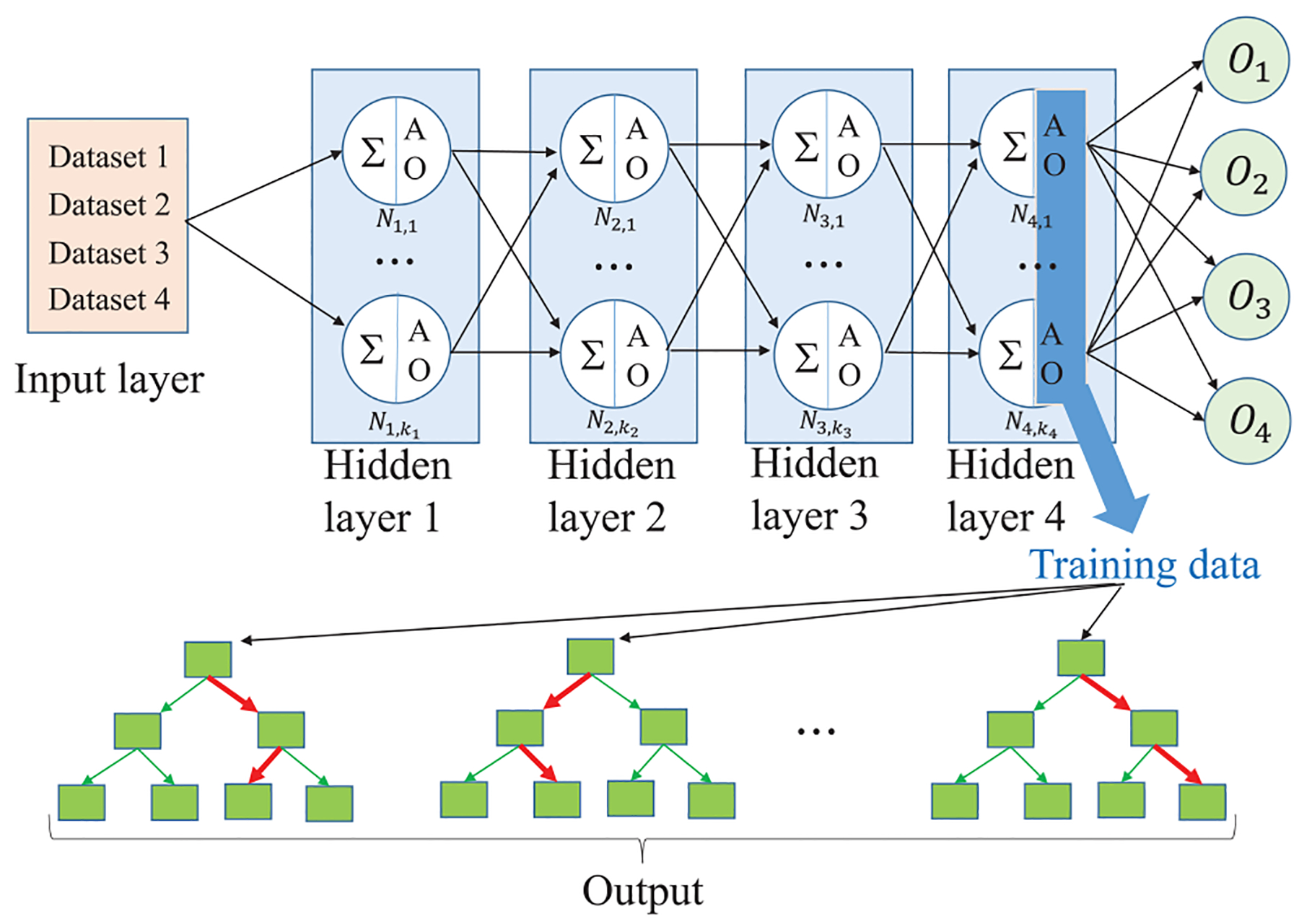
Simple illustration of BTAMDL 1 where the input vector of the training data of GBDT is from the activated outputs (AO) on the last hidden layer of BTAMDL, marked by the blue rectangle.

2D Fingerprint.

Compared to the traditional experiments conducted in vivo or in vitro, quantitative structure−activity/ property relationship (QSAR/QSPR) analysis is one of the most popular computer-aided or in-silico methods in the measurement of drug properties nowadays, based on the assumption that similar molecules have similar bioactivities or physicochemical properties. Currently, this method becomes more and more attractive since it can quickly generate highly accurate results.⁶⁷ As the property profile of a molecule, molecular fingerprint plays a fundamental role in QSAR/QSPR analysis and can be used to represent the molecules in the datasets due to the ability of encoding the structure of a molecule. The common type of fingerprint is a series of binary digits (bits) that indicate the presence or absence of particular substructures in the molecule. Additionally, for a SMARTS pattern, if a substructure was present in the given molecule, the corresponding bit was set to 1 and otherwise set to 0.⁶⁸ One can determine the similarity between two molecules by comparing the fingerprints. There are four major 2D molecular fingerprints, in terms of keys-based fingerprints, pharmacophore fingerprints, topological or path-based fingerprints, and circular fingerprints.^69,70 In present work, we select four popular 2D fingerprints, namely Daylight fingerprint,⁷¹ molecular access system (MACCS) fingerprint,⁷² Estate 1 (electro-topological state) fingerprint, and Estate 2 fingerprint,⁷³ which are generated by RDKit (version 2018.09.3)⁷⁴ and were tested with good performance in toxicity prediction in our other work.⁷⁵ Table S1 (see Supporting Information) summarizes the essential information related to these fingerprints.

RESULTS

In this section, we will show how to improve the performance of machine learning on small datasets in different fields, including toxicity prediction and small molecule property prediction, based on the aforementioned methods, such as GBDT, MDL, and two BTAMDL models. We use Pearson correlation coefficient (R), root mean squared error (RMSE), mean absolute error (MAE), and Tanimoto coefficient (S_A,B) to evaluate the performances of these models. The details of these evaluation metrics can be found in section S1 of the Supporting Information. The toxicity prediction contains four quantitative datasets, including LD₅₀, IGC₅₀, LC₅₀, and LC₅₀- DM. The description and origin of these datasets are in section S2 of the Supporting Information.

Performance of GBDT.

For all experiments in the present study, GBDT is implemented by the Scikit-learn package (version 0.20.1).⁷⁶ Since the size of four datasets is not the same, we choose different hyper-parameters in respective GBDT models, which can be found in Table S3 in the Supporting Information. We measure the model accuracy via the squared Pearson correlation coefficient (R²). Table 1 shows the values of R² with three fingerprints, Estate 2, Estate 1, and Daylight for four datasets, as well as the consensus results of these three models, which produces the average predicted values of three fingerprints. The method of consensus is to train different models on the same set of descriptors and average across all predicted values.

Table 1.

Comparison of Prediction Results of GBDT for Four Datasets in Quantitative Toxicity Prediction

	LD50			IGC50			LC50			LC50-DM
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
Estate 2	0.589	0.455	0.629	0.742	0.341	0.503	0.662	0.597	0.830	0.502	0.871	1.117
Estate 1	0.590	0.456	0.627	0.720	0.360	0.525	0.634	0.612	0.847	0.532	0.850	1.105
Daylight	0.620	0.434	0.607	0.687	0.383	0.554	0.599	0.637	0.862	0.313	0.973	1.294
consensus	0.662	0.406	0.557	0.777	0.334	0.481	0.692	0.570	0.811	0.472	0.899	1.120

From Table 1, one can find the following:

1. The LD₅₀ test set is the largest set having as many as 7413 compounds, compared to the other three sets studied. Since this set has a relatively high experimental uncertainty of the values or high diversity of molecules;⁷⁷ that is, the large difference between the maximum value and the minimum value (shown in Table S2 in the Supporting Information), it is relatively difficult to do the prediction with high accuracy. From results, the Daylight fingerprint gets the largest R² of 0.620 for a single fingerprint, while the consensus of three fingerprints can further improve the performance by 6.8% up to R² = 0.662.

2. The IGC₅₀ test set is the second largest set investigated with 1792 compounds and has the lowest diversity of molecules as indicated in Table S2 in the Supporting Information, resulting in the best prediction among four sets. The results show that Estate 2 fingerprint achieves the best performance with R² = 0.742 for a single fingerprint, and the consensus method using all three fingerprints can improve the result by 4.7% with R² = 0.777.

3. LC₅₀ is a small set with 823 compounds. By comparison, the Estate 2 fingerprint gets a good result with R² = 0.662 and a better result is obtained by the consensus method with R² = 0.692, increased by 4.5%.

4. LC₅₀-DM has the smallest size with only 353 compounds, which gives rise to a difficulty to build a robust model. As a result, the best single fingerprint Estate 1 gets a low accuracy with R² = 0.532, compared to other datasets. Unexpectedly, the consensus model even gets a worse result with R² as low as 0.472, which decreased by 11.3%. The possible reason is that the Daylight fingerprint with a poor performance of R² = 0.313 hinders the consensus method. In addition, due to the same difficulty of the small dataset, using a 3D-topology fingerprint, the accuracy R² of the GBDT model can only be improved to 0.505.⁷⁸ Hence, with respect to the small dataset, multitask deep learning method is needed and will be introduced in the next subsection.

Performance of Multitask Deep Learning (MDL).

As Estate 2, Estate 1, and Daylight fingerprints have different feature numbers (See Table S1 in Supporting Information), we adopt different neural network architectures. For example, for Estate 2 and Estate 1 fingerprints with a small number of features, a six-layer neural network is built with four hidden layers, 500, 1000, 1500, and 500 neurons, respectively, while, for Daylight fingerprint with a large number of features, a six-layer neural network with more neurons is built. The number of neurons for four hidden layers are 3000, 2000, 1000, and 500, respectively. The other network parameters used in multitask deep learning are as follows: (1) the optimizer is SGD (stochastic gradient descent) with a momentum value of 0.5; (2) 2000 epochs for all networks; (3) the mini-batch is 4; (4) the learning rate is 0.01 for the first 1000 epochs and 0.001 for the remaining 1000 epochs. Besides these parameters, we tried the technique of dropout or L₂ regularization to avoid the overfitting and to increase the prediction accuracy. Unfortunately, they do not seem to work well. Therefore, these two tricks are omitted in our experiments. In addition, all the multitask deep learning were performed by Pytorch (version 1.0).⁷⁹

In Table 2, we show the performance of MDL on four datasets with three different fingerprints, which is significantly promoted by the multitask strategy. Compared to the results of GBDT in Table 1, the relatively small set, especially, LC₅₀-DM, benefits a lot from the large sets, improved as high as 52.8% of R² that is increased from 0.472 to 0.721 with consensus, and for Estate 2, Estate 1, and Daylight fingerprints, the values of R² are significantly increased by 24.1%, 31.6%, and 114.7%, respectively. For other relatively small datasets, such as LC₅₀ and IGC₅₀, with the method of consensus, the accuracies of R² are increased by 11.6% and 1.9%, respectively. However, for the largest set LD₅₀, it is even decreased by 5.3% from 0.662 to 0.627 with consensus. Therefore, multitask deep learning could be a good choice for small datasets, which better learned from other large datasets by sharing representations between datasets. Additionally, the Daylight fingerprint performs the best with MDL among three fingerprints in the LD₅₀ dataset.

Table 2.

Comparison of Prediction Results of MDL for Four Datasets in Toxicity Prediction

	LD50			IGC50			LC50			LC50-DM
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
Estate 2	0.489	0.511	0.701	0.696	0.373	0.541	0.660	0.587	0.834	0.623	0.770	1.028
Estate 1	0.560	0.473	0.652	0.725	0.357	0.519	0.733	0.586	0.747	0.700	0.718	0.946
Daylight	0.606	0.446	0.616	0.711	0.395	0.541	0.713	0.561	0.803	0.672	0.731	0.992
consensus	0.627	0.439	0.594	0.792	0.323	0.446	0.772	0.483	0.701	0.721	0.667	0.927

Performance of Two BTAMDL Models.

From the above performances of four datasets with different models of GBDT and MDL, the framework of MDL can indeed dramatically improve the prediction accuracy of the task with a small dataset, like LC₅₀-DM. Since GBDT is well-known for its superb performance for small datasets, we are particularly interested to know whether the combination of GBDT and MDL can further improve the predictions on small datasets,i.e., LC₅₀-DM. To this end, we test our BTAMDL models. Meanwhile, we also concern how BTAMDL models perform on other datasets.

As the input matrix of GBDT in BTAMDL 1 is the activated output obtained from trained MDL on the last hidden layer, the feature numbers of training data of four datasets become the same and are equal to the neuron number on the last hidden layer of the neural network. Table 3 shows the prediction performance under this new framework. The consensus results of the four sets are improved slightly by 1.9%, 0.4%, 0.5%, and 1.7% of R², respectively, compared to those of MDL in Table 2. In particular, for the smallest dataset, LC₅₀-DM, there is the largest improvement from 0.472 to 0.733 of R², increased as high as 55.3% for that of GBDT in Table 1. Moreover, for Estate 2, Estate 1, and Daylight fingerprints, their results are improved by 30.5%, 31.6%, and 118.2%, respectively. These results indicate the usefulness of the proposed BTAMDL method.

Table 3.

Comparison of Prediction Results of BTAMDL 1 in Toxicity Prediction

	LD50			IGC50			LC50			LC50-DM
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
Estate 2	0.478	0.519	0.711	0.686	0.383	0.555	0.684	0.578	0.825	0.655	0.744	1.011
Estate 1	0.565	0.469	0.649	0.724	0.358	0.520	0.749	0.577	0.736	0.700	0.718	0.945
Daylight	0.605	0.447	0.616	0.713	0.393	0.539	0.704	0.579	0.820	0.683	0.726	0.980
consensus	0.639	0.426	0.579	0.795	0.322	0.445	0.776	0.480	0.697	0.733	0.655	0.905

We further analyze the performance of BTAMDL 2. Table 4 confirms the following. (1) Compared with those of MDL in Table 2, in terms of consensus methods, the accuracies of four datasets are improved by 1.8%, 0.1%, 0.8%, and 2.8%, respectively. The highest improvement is from the smallest dataset, LC₅₀-DM as expected. (2) Compared with the results of BTAMDL 1 in Table 3, in terms of consensus methods, there is a minor decrease −0.2% for datasets LD₅₀ and IGC₅₀. In contrast, there are slight improvements of 0.3% and 1.1% for tasks with small datasets, LC₅₀, and LC₅₀-DM, respectively. From these findings, we can conclude that using the activated output of MDL and additional features or the features of fingerprint as the new features in training data in BTAMDL approaches can bring a better performance on small datasets.

Table 4.

Comparison of Prediction Results of BTAMDL 2 in Toxicity Prediction

	LD50			IGC50			LC50			LC50-DM
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
Estate 2	0.479	0.525	0.716	0.685	0.382	0.556	0.686	0.578	0.823	0.668	0.850	1.124
Estate 1	0.564	0.472	0.652	0.716	0.363	0.531	0.750	0.514	0.735	0.698	0.710	0.946
Daylight	0.605	0.448	0.617	0.710	0.395	0.541	0.706	0.583	0.823	0.675	0.723	0.993
consensus	0.638	0.428	0.580	0.793	0.321	0.447	0.778	0.477	0.694	0.741	0.682	0.934

Feature Importance Analysis.

Since different features should play different roles in machine learning predictions, redundant and noisy features may play a negative role in the training process. Hence, it is often necessary to rank the importance of all features to understand the relationship between predictive accuracy and feature importance. During the feature importance analysis, we construct a family of models using top N% features obtained from feature importance ranking, where N goes from 0 to 100. The optimized number of features is reached when the maximum accuracy is obtained.

Figure 3 shows the influence of the number of features on the accuracy R² of four datasets with BTAMDL 2 in toxicity prediction, where the feature numbers of Estate 2, Estate 1, and Daylight are 579, 579, and 2548, respectively. In Figure 3a, for the LD₅₀ set, R² increases sharply with the increase of feature number for all three fingerprints. Specifically, for Daylight fingerprint marked by the red line, when the number of features increases up to around 15 (0.6% of 2548 features), the value of R² is saturated and reaches the maximum value 0.604, which is almost the same as that in Table 4. This result suggests that for Daylight fingerprint, choosing only 0.6% most important features could optimize the prediction performance and the method of rank feature importance is a more efficient and less time-consuming way for machine learning. Similarly, for Estate 1 and Estate 2 fingerprints marked by the blue and black lines, the maximum R² values of 0.569 and 0.479 are reached with feature numbers being around 21 and 60, respectively, which are about 3.6% and 10.3% of their respective features. Similar to Figure 3a, Figure 3 parts b–d have a similar relation between accuracy R² and number of features. More precisely, in Figure 3b, for the IGC₅₀ set, 7, 35, and 37 top features can yield the maximal R² values, i.e., 0.707, 0.717, and 0.681 for Daylight, Estate 1, and Estate 2 fingerprints, respectively. In Figure 3c, for the LC₅₀ set, the maximal values 0.755, 0.690, and 0.704 are achieved with 20, 40, and 67 top features for Daylight, Estate 1, and Estate 2 fingerprints, respectively. In Figure 3d, for the LC₅₀-DM set, the 21, 45, and 61 top features could sharply increase the R² values to 0.666, 0.697, and 0.656, for three fingerprints, respectively.

Figure 3.

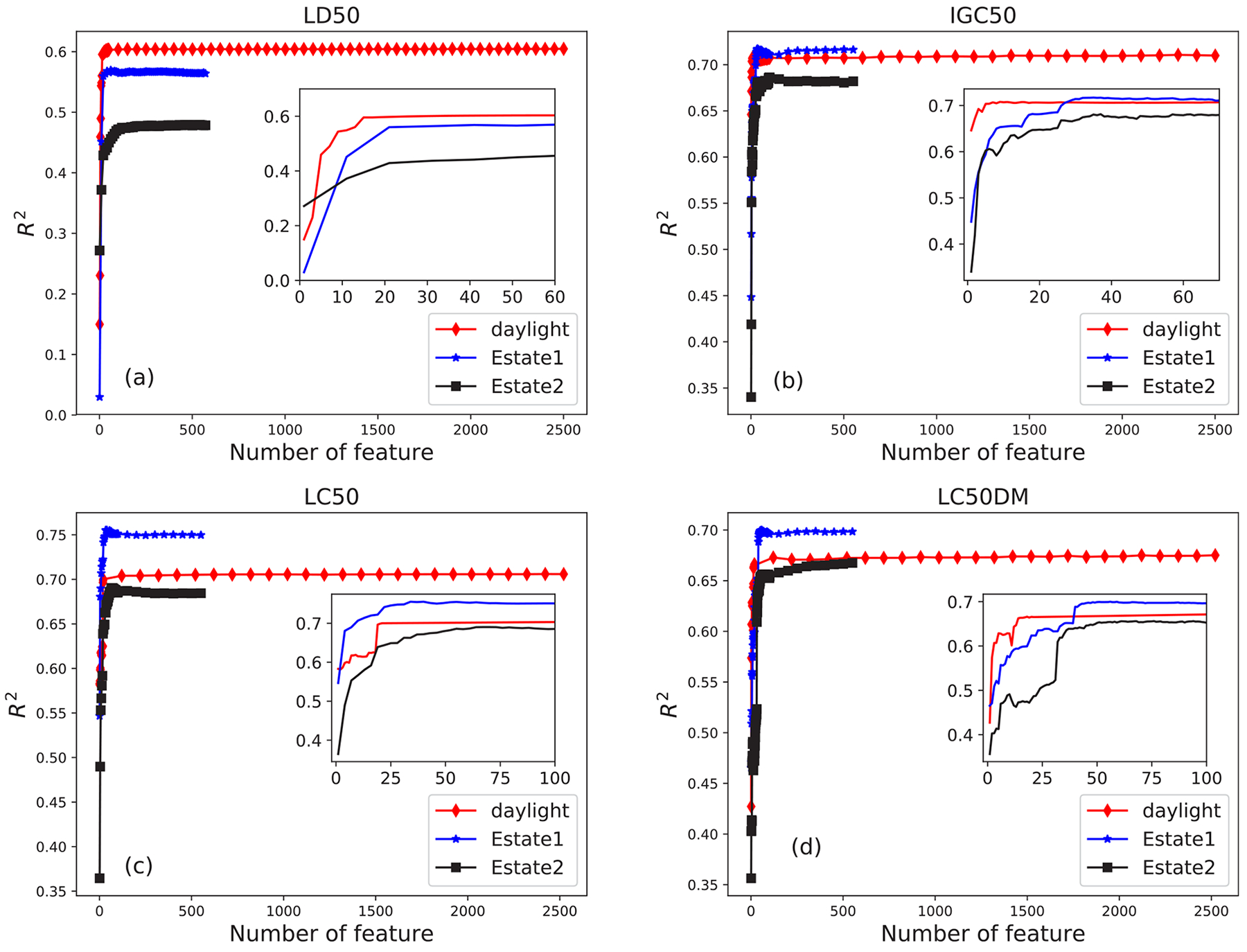
Relationship between R² value and the number of top features for three different fingerprints, Daylight, Estate 2, and Estate 1 in four datasets obtained by BTAMDL 2 in toxicity predictions.

Comparison with Other Methods.

The toxicity estimation software tool (TEST) is a useful program that allows a user to easily estimate the quantitative toxicity of chemicals using QSAR methodologies. Results for the hierarchical method, single-model method, FDA method, group contribution method, nearest neighbor method, and consensus method are made available for all of four datasets studied above.⁸⁰ Therefore, a comparison between the results from our models and those from TEST is meaningful and helps in understanding the predictive power of our models.

Table 5 shows this comparison of three relatively small datasets, i.e., IGC₅₀, LC₅₀, and LC₅₀-DM, using GBDT, MDL, and two BTAMDL approaches. As shown in Table 5, the values of R² with BTAMDL 2 are higher than those of all TEST methods on three datasets. Especially, compared to the best method of TEST, TEST consensus, the increments of R² are 3.8%, 6.9%, and 0.3%, respectively, for three datasets.

Table 5.

Comparison Results of Accuracy R² between Our Models (green) and Other Methods (pink) of Toxicity Prediction^a

Method	IGC50	LC50	LC50-DM	Average
BTAMDL 2	0.793	0.778	0.741	0.771
BTAMDL 1	0.795	0.776	0.733	0.768
MDL consensus	0.792	0.772	0.721	0.762
GBDT consensus	0.777	0.692	0.472	0.647
Hierarchical [79]	0.719	0.710	0.695	0.708
Single-model [79]	NA	0.704	0.697	0.701
FDA [79]	0.747	0.626	0.565	0.646
Group contribution [79]	0.682	0.686	0.671	0.680
Nearest neighbor [79]	0.600	0.667	0.733	0.667
TEST consensus [79]	0.764	0.728	0.739	0.744
3D MDL consensus [78]	0.802	0.789	0.678	0.756

^aThe results in pink are available in ref 4 of the Supporting Information.

Additionally, the average R² for BTAMDL 2 is 0.771 for three datasets, while that for TEST consensus is 0.744. The result of the recent 3D structure-based topological consensus is 0.756.⁷⁸ These results confirm that the proposed BTAMDL method outperforms previous 2D and recent 3D models.

Dataset Similarity Analysis.

The above results indicate that the performance of the task with a small dataset, like LC₅₀-DM, can be dramatically improved by tasks with large datasets in BTAMDL. To better understand our results, we analyze the similarity between the largest dataset (LD₅₀ (7413)) and other datasets through eq 4 in the Supporting Information. Our similarity analysis is shown in Table 6 with three fingerprints. The improvement in accuracy R² is also given through the comparison between the results with consensus in Tables 1 and 4. First, we found that LC₅₀-DM dataset has the highest similarity with LD₅₀ by every fingerprint, which explains why its prediction gets the largest improvement in BTAMDL approaches. Data set IGC₅₀ (1792) has the lowest similarity and thus its prediction benefits the smallest amount in BTAMDL. Based on this similarity analysis, one can anticipate the potential improvement before carrying out the actual BTAMDL calculation.

Table 6.

Similarity between the Largest Dataset LD₅₀ (7413) with the Other Three Datasets with Three Different Fingerprints in Toxicity Prediction^a

fingerprint	IGC50 (1792)	LC50 (823)	LC50-DM (353)
Estate 2	0.968	0.980	0.989
Estate 1	0.950	0.973	0.985
Daylight	0.778	0.869	0.914
increment of R2	2.1%	12.4%	57.0%

^aThe number in the bracket is the total size of the dataset. The percentage in the last row is the increment of accuracy for three datasets.

It is interesting to note that Estate 2 reports the highest similarity scores while Daylight reports the lowest similarity scores as shown in Table 6. As shown in Figure 3, the Estate 2 fingerprint has the lowest prediction accuracy for every dataset, which indicates that the Estate 2 fingerprint has the lowest ability to discriminate these compounds.

More Validation.

We did more tests of BTAMDL model in small molecule property predictions, including the datasets of partition coefficient (logP), solubility (logS), and solvation in section S3 and S4 of the Supporting Information, respectively. These two parts additionally validate that BTAMDL model can boost the performance of small datasets and suggest that more similarity between large and small datasets, higher increment of prediction power for small datasets. Table 7 summarizes the improvement by the BTAMDL model upon MDL and GBDT including the applications of toxicity prediction.

Table 7.

Summary of the Improvement by BTAMDL Models upon MDL and GBDT for Four Toxicity Datasets^a

	LD50 (7413)		IGC50 (1792)		LC50 (823)		LC50-DM (353)
model	MDL	GBDT	MDL	GBDT	MDL	GBDT	MDL	GBDT
BTAMDL 1	−3.5%	1.9%	2.3%	0.4%	12.1%	0.5%	55.3%	1.7%
BTAMDL 2	−3.6%	1.8%	2.1%	0.1%	12.4%	0.8%	57.0%	2.8%

^aThe number in the bracket is the total size of the dataset.

DISCUSSION AND CONCLUSION

The combination of machine learning and big data has had great success in image analysis, computer vision, and language processing, which has lead to substantial impact on a wide variety of fields, including social media, banking, insurance, etc. However, in science, one often faces an obstacle with limited data size. The collection of scientific data can be very difficult, time-consuming, and expensive. Therefore, enhancing the performance of machine learning with small scientific datasets is an important issue.

Gradient boosting decision trees (GBDT) are known for their advantage in handling small datasets, while deep learning algorithms typically perform better for large datasets. Transfer learning is an excellent approach for enhancing the prediction of small datasets when they have shared statistics with a large dataset; therefore, multitask deep learning (MDL) based on transfer learning techniques becomes a good choice for aiding the prediction of small datasets where there is a large dataset involved. In this work, we propose boosting tree-assisted multitask deep learning (BTAMDL) to take the advantages of GBDT, deep learning, and transfer learning. In BTAMDL, MDL is used to generate a set of input features for GBDT. These features are the outputs of the last hidden layer of the MDL network. The BTAMDL is realized in two ways. In BTAMDL 1, MDL outputs are used for GBDT inputs. Whereas in BTAMDL 2, GBDT admits the features of fingerprint as the additional nondeep learning features.

To validate the proposed methods and understand their limitations, we select four types of benchmark datasets, namely toxicity, partition coefficient (logP), solubility (logS), and solvation. Among them, toxicity includes four subsets, i.e., LD₅₀, IGC₅₀, LC₅₀, and LC₅₀-DM. Additionally, each dataset has nonoverlapping training set and test set. The aforementioned molecular datasets are the so-called complex data for which each data entry has its internal structure. As a result, their predictions involve not only datasets and learning models, but also descriptors or features to represent the internal structure. We select four popular 2D fingerprints, i.e., Daylight fingerprint,⁷¹ molecular access system (MACCS) fingerprint,⁷² Estate 1 (electro-topological state) fingerprint, and Estate 2 fingerprint⁷³ to represent the above molecular datasets.

To understand the performance of various methods, we first compare the results of MDL and GBDT using various datasets. It is found that relatively small datasets, namely IGC₅₀, LC₅₀, and LC₅₀-DM, can be efficiently boosted by 1.9%, 11.6%, and 52.8% respectively from their GBDT predictions by the MDL model. Additionally, the GBDT performance of another relatively small dataset, the solvation dataset, is also enhanced by 0.2% and 3.9% with two large datasets, logP, and logS, respectively, by using MDL. All these results suggest that compared to GBDT, MDL could be a useful strategy to improve the prediction accuracy of relatively small datasets.

It is also interesting to know whether the proposed BTAMDL methods can further improve the predictions of small datasets. To this end, we compare the performance of BTAMDL and MDL methods. It is found that with BTAMDL 1 model, the prediction accuracies of four toxicity datasets were further improved by 1.9%, 0.4%, 0.5%, and 1.7% from their MDL predictions, respectively. For logP and solvation datasets, the increments are very small, i.e., 0.1% and 0.3%, respectively. Last, the results of BTAMDL 2 are also compared with those of MDL. It is found that BTAMDL 2 model can further improve MDL predictions by 1.8%, 0.1%, 0.8%, and 2.8%, respectively, for four toxicity datasets, and 0.5% for the solvation dataset. Hence, we confirm that BTAMDL models are able to boost the performance of small datasets.

It is noted that none of the aforementioned transfer learning methods can guarantee a performance enhancement to a small dataset from a large dataset. The amount of enhancement depends on the similarity between datasets and the quality of the large datasets. To illustrate this point, we have carried out systematic similarity analysis between small and large datasets. We show that for a given large dataset and many small datasets, those small datasets that have higher similarity with the large dataset could obtain more benefits from multitask learning methods. Similarly, for a given small dataset and many large datasets, the large dataset that has a higher similarity with small dataset will be able to provide a higher enhancement in the transfer learning. This explains why the prediction accuracy of a small solvation dataset gets a higher improvement from logS than from logP, although the size of logS is smaller than that of logP. In this work, we assume that all datasets have the same level of quality, which may not be true in practice.

Finally, we would like to mention that compared with the literature, the performances of the proposed methods are some of the best for all datasets tested in the present work. Therefore, we recommend transfer learning methods, including BTAMDL methods proposed in this work, as the state-of-theart approaches for small scientific datasets. Nonetheless, for a given pair of small and large datasets, the amount of enhancement to the small dataset from the large dataset depends crucially on the similarity between them, the quality of the large datasets, and the transfer learning algorithm selected.