Significance
There are various scenarios for the formation of the Moon and subsequent dynamical evolution of the Earth–Moon system, all of which are subject to a constraint that has not previously been fully exploited. Using this constraint, we demonstrate that the recently proposed high-obliquity scenario is not consistent with the present Earth–Moon system. This constraint will have to be taken into account in all future investigations of the formation and evolution of the Moon.
Keywords: moon formation, orbital evolution, angular momentum
Abstract
The Moon likely formed in a giant impact that left behind a fast-rotating Earth, but the details are still uncertain. Here, we examine the implications of a constraint that has not been fully exploited: The component of the Earth–Moon system’s angular momentum that is perpendicular to the Earth’s orbital plane is nearly conserved in Earth–Moon history, except for possible intervals when the lunar orbit is in resonance with the Earth’s motion about the Sun. This condition sharply constrains the postimpact Earth orientation and the subsequent lunar orbital history. In particular, the scenario involving an initial high-obliquity Earth cannot produce the present Earth–Moon system. A low-obliquity postimpact Earth followed by the evection limit cycle in orbital evolution remains a possible pathway for producing the present angular momentum and observed lunar composition.
Recent giant-impact simulations (1–3) aimed at producing a Moon with an Earth-like isotopic composition (4–8) would leave the postimpact Earth rotating too fast. Some subsequent process must be responsible for draining the excess angular momentum (AM).
Ćuk and Stewart (1) proposed that the excess AM could be drained by the lunar orbit’s temporary capture into the evection resonance (9). Wisdom and Tian (10) found that the evection limit cycle can also do the job. While ref. 10 used the Darwin–Kaula constant tidal model (SI Appendix, Model Comparison), Rufu and Canup (11) found similar phenomena using the constant tidal model. Tian et al. (12) studied the consequences of tidal heating in these resonance and near-resonance mechanisms and found that the evection resonance is unstable and therefore unable to drain enough AM, whereas the evection limit cycle is stable and continues to drain AM.
Instead of starting the postimpact fast-spinning Earth with a small obliquity (), C̀uk et al. (13) proposed that the giant impact left the Earth in a high-obliquity (Ie = 65 to 80°), fast-spinning state. They suggested that the subsequent evolution could not only drain the excess AM through an instability associated with the Laplace plane transition (LPT), but also solve the long-standing puzzle of the present-day lunar inclination (, where is the lunar inclination, and the superscript denotes the present-day value) (9, 14, 15). When the Moon is close to the Earth, the lunar precessional motion is strongly affected by the oblateness of the Earth, but when the Moon is far from the Earth, the precessional motion is more strongly affected by solar perturbations. The LPT occurs when these two effects are comparable. The LPT instability occurs only when reaches large values during the LPT (16, 17). The high leads to nonzero orbital eccentricities via Lidov–Kozai-like oscillations and temporary contraction of the lunar orbit, during which substantial AM is removed from the Earth–Moon.
However, there exists a nearly conserved quantity, which has so far not been taken into account, that significantly constrains the possible evolutionary histories of the Earth–Moon system.
A New Constraint: Vertical AM
For a test particle around a central mass with large eccentricity () and inclination (), nonresonant perturbation from a massive exterior body moving in a circular orbit induces oscillations in and , the Lidov–Kozai oscillations (18, 19). In the nontidal Lidov–Kozai problem, the Hamiltonian governing the system evolution is averaged over the orbital periods of both the test particle and the perturber. This leads to a conservation of the semimajor axis () of the test particle, and the component of the orbital AM of the test particle that is perpendicular to the orbital plane of the massive perturber, which we refer to as . Taking the orbital plane of the massive perturber as the reference plane for inclination, then . The conservation of and implies that as and oscillate, the quantity is conserved (the Lidov–Kozai constant).
The motion of the Earth–Moon system has much richer dynamics than the three-body problem. Perturbations to the system come from not only the Moon–Sun interaction, but also the Earth’s oblateness, which leads to precession of the Earth’s spin axis and contributes to lunar-orbit precession; the Moon’s permanent triaxial figure, which allows the Moon to maintain synchronous rotation; and the Moon’s oblateness and triaxiality, which dictates the equilibrium obliquity of the Moon (the Cassini states)—not to mention the tides on the Earth and Moon. These processes modify the orbital AM of the Moon and the rotational AM of the Earth. Nevertheless, there is a quantity analogous to the Lidov–Kozai constant, the vertical component of the AM of the Earth–Moon system (), that is conserved if resonances between the Sun and the Earth or Moon are not encountered. For instance, the evection resonance and the evection limit cycle (1, 10–12) can modify . Such resonances or near-resonances are absent in scenarios like the LPT instability, which we term as nonresonant scenarios. The demonstration of the conservation of for nonresonant scenarios exactly follows the derivation for the Lidov–Kozai problem (SI Appendix, SI Text). The Hamiltonian is averaged over the orbital period of the Moon and the orbital period of the motion of the Earth about the Sun. The average over the lunar period leads to the conservation of the semimajor axis of the Moon. The average over the motion of the Earth about the Sun leads to the conservation of . Tides between the Earth and Moon conserve , but induce long-term changes in and the other system parameters.
The AM of the Earth–Moon system is approximately , where is the rotational AM of the Earth and is the orbital AM of the Moon. Here, we are neglecting the small rotational AM of the Moon. Taking the ecliptic as the reference plane, the component of AM perpendicular to this plane is
| [1] |
where is the magnitude of , and is the magnitude of . We denote the scalar sum by .
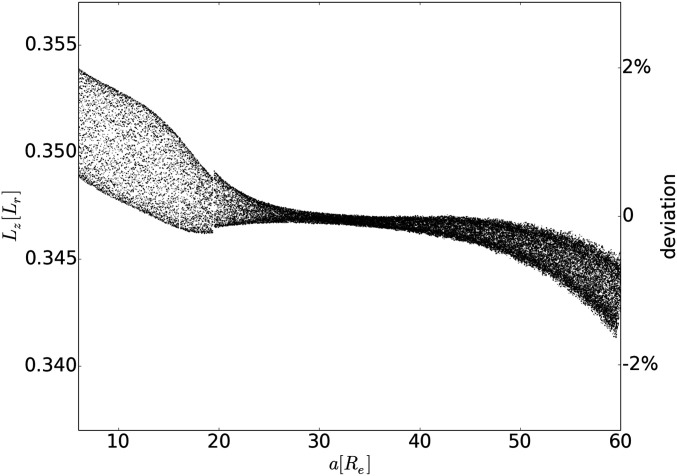
In our model, which includes the full rotational and orbital dynamics of the Moon, interacting with an oblate, precessing Earth on a near circular orbit about the Sun, with tidal interactions between the Moon and Earth, we find that is conserved to a part in a thousand, as the Moon evolves from 5 to 50 (where we terminate the integrations; Re = 6,371 km). This is the case, even though the system passes through the instability associated with the LPT and the Cassini state (lunar spin) transitions. Touma and Wisdom (20) investigated the evolution in a model that was, in a number of ways, more complete than that used here. That model included a fully evolving eccentric and inclined Earth orbit, perturbed by all of the chaotically evolving planets, with not only tidal interactions between the Earth and Moon, but also direct tides from the Sun on the Earth, and cross-tidal interactions from tides raised on the Earth by the Sun that affect the Moon. (But it did not include tides raised on the Moon and the rotational dynamics of the Moon, which are included here.) A reexamination of those results shows that, even with all these additional effects, was still conserved to about (Fig. 1). (Note that refs. 16, 20, and 21 already recognized that is conserved in the averaged nontidal case, and refs. 16 and 20, in addition, stated that is conserved if only tides between the Earth and Moon are considered. Our derivation is more general.) We show in SI Appendix, SI Text that even without averaging, when solar tides are ignored, the amplitude of oscillation of is at most of order in Earth–Moon history (SI Appendix, Eq. S11 and Fig. S2) ( is the reference AM, where is Earth’s largest principal moment, is the present-day value, is Earth’s mass; and ).
Fig. 1.
versus for a simulation in ref. 20, which evolves the Earth–Moon system with solar tides, Earth–Moon mutual tides, and Sun–Earth–Moon cross tides, in the full chaotically evolving planetary system, using the constant tidal model. The system begins with a conventional initial state, instead of a high-AM state. declines by only 3.5% throughout the evolution.
Apart from the dynamical evolution, is also susceptible to small changes due to collisional processes after the Moon-forming giant impact, e.g., the stochastic late-accretional impacts on Earth that are proposed to explain the presence of highly siderophile elements in the terrestrial mantle (22–26). These impacts can change the Earth’s rotational AM by up to 4%, with the Earth rotating with a period between 6 and 8 h (22). Taking , the change in is , i.e., 2.3% of . The late impacts on the Moon are much smaller in volume, and their effects on the system AM can be ignored. Even if the change in is perfectly aligned to the vertical direction, this will only cause changes to by up to (either increase or decrease). So we ignore these possible late stochastic variations in .
Therefore, we can take conservation as a strong constraint on the evolution of the Earth–Moon system. For nonresonant scenarios of Earth–Moon formation and evolution (e.g., ref. 13), the postimpact value should be near (at most a few percent different). For models of Earth–Moon history that involve resonances related to Earth’s motion about the Sun (e.g., refs. 1 and 10–12), the postresonance should be near in the same way.
Constraint on the High-Obliquity Scenario
C̀uk et al. (13) argued that following a high-AM, high-obliquity postimpact Earth, the present-day AM, and can be produced through nonresonant orbital evolution. However, the values of for their initial conditions were much lower than (SI Appendix, Table S1 and Figs. S1 and S4) and therefore inconsistent with the present Earth–Moon system.* We investigate the high-obliquity Moon-forming scenario with the constraint taken into account. Our numerical model is exactly the same as used in ref. 10. It is based on the N-body symplectic mapping algorithm (27) and the conventional Darwin–Kaula constant model (28). We provide a detailed comparison of our algorithm to that of ref. 13 in the SI Appendix, Model Comparison. As a check, we did calculations with the same initial conditions as used in ref. 13. The main features of ref. 13 are reproduced, but some differences are found. We find smaller final , with larger final and (SI Appendix, Figs. S1, S3, and S4).
We sample the -consistent (i.e., ) initial conditions (postimpact states) in the whole range of successful high-AM giant impact simulations; , , and are of key interest. We assume that the Moon accreted on the Earth’s equatorial plane, i.e., initially . We take the initial , just outside the Earth’s Roche limit. So (, ) adequately represents an initial state. In ref. 1, for successful impacts, ranges in 1.94 to 2.84 or 0.67 to 0.98. Candidate impacts in ref. 2 produce from 1.77 to 2.71 or 0.61 to 0.94. With the constraint of , we take four sampling points: (, 0.63), (, 0.7), (, 0.8), and (, 0.98). A larger initial corresponds to a larger initial . We take and , the values used in ref. 13, where is the potential Love number, and is the tidal quality factor.
In the case (, 0.63), does not get large enough for the instability during the LPT (17), so the AM is not decreased.
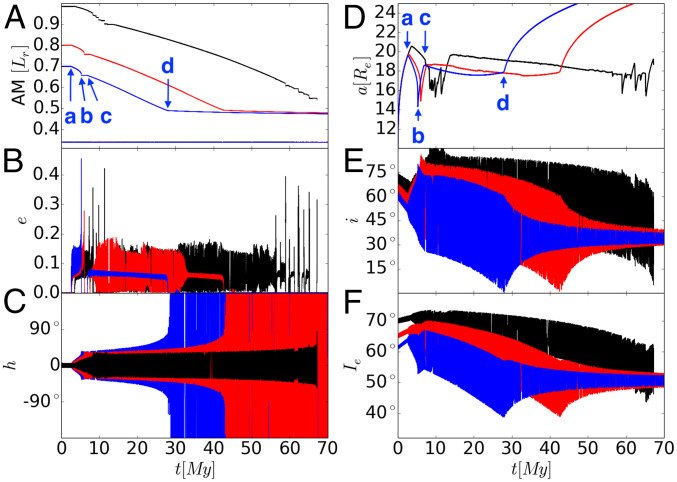
Results for the (), (), and () cases are shown in Fig. 2. In the () case, there are a lot of sudden, large excursions in eccentricity, and it ends with an unbound orbit. All of the cases end with a high , 45% larger than the present value of 0.345. The Earth’s obliquity after the LPT, around , is too large to produce the present of in the later evolution (SI Appendix, Low-e Phases of Evolution). The post-LPT inclination being high () may not be a problem, since it can be damped during the subsequent Cassini-state transition, provided that the lunar magma ocean has not solidified by that point (29). However, conservation of implies that if the inclination is damped, then the obliquity must increase, making it even more difficult to produce the present .
Fig. 2.
Details of LPT [(A) angular momentum, (B) lunar eccentricity, (C) the angle between the ascending node of the lunar orbit and the ascending node of the Earth’s equator, (D) lunar semimajor axis, (E) lunar inclination, and (F) Earth’s obliquity], with -consistent initial conditions (in [, ]): (, 0.7 [blue]), (, 0.8 [red]), (, 0.98 [black]). Parameters are as follows: , . In A, the top lines are (), and the horizontal line is (). The fact that the line is horizontal indicates that it is conserved by the evolution. Most of the decline in occurs when both is nonzero and oscillates. For the blue curves, a and d mark the beginning and end of the LPT.
Since these initial conditions are representative of all possible combinations of post-giant-impact and , these results show that, with , the high-obliquity scenario does not work to produce the present-day AM and Earth’s obliquity, at least for the tidal parameters used ( and ). Next, we show that this is the case regardless of the tidal model and tidal parameters.
Characteristics of the High- Scenario
The decrease in (AM scalar sum) occurs predominantly during the LPT instability, during which the lunar eccentricity is nonzero and the semimajor axis, , stalls. The rate of change of () is a competition between tides on Earth (which tend to increase ) and tides on the Moon (which tend to decrease ). At zero , is positive. But decreases as is increased (e.g., ref. 10). There is an at which is zero. The value of at this point depends on a ratio of the tidal parameters of the Earth and Moon and the tidal model. Though the expressions in ref. 10 need to be generalized, they give a rough estimate of the value of for that is consistent with our simulations and tidal parameters.
During the phase in which , declines. We can calculate the rate of decline if we assume . In this case, the changing part of is predominantly the rotational AM of the Earth. The rate of change of AM is the component of the tidal torque on the spin axis of the Earth. Though the tidal torque depends on many factors, the leading term, , sets the timescale and depends only on parameters and the semimajor axis. This term is the same for the constant tidal model and the constant tidal model (20):
| [2] |
where is the mass of the Moon. Using the expression for the reference AM , we find
| [3] |
where is the present moment of inertia of the Earth divided by , and is the mean motion of the lunar orbit. Evaluating this expression for , we find, independent of tidal models, a decline of about per million years (My). The decline found in the simulations is comparable to this, about per My. The agreement is excellent. This success allows us to generalize our simulation results to other tidal parameters. The rate of decline of is simply proportional to . With a larger , we can expect that it would take longer to leave the LPT, but that the ending value of would be roughly the same (see below).
Termination of the LPT is marked by a change in the behavior of the angle between the ascending node of the lunar orbit on the ecliptic () and the ascending node of the Earth’s equator on the ecliptic (); we denote this angle by (). During the LPT, oscillates about 0; after exit from the LPT, circulates through all angles (Fig. 2). The point of transition from oscillation to circulation of is well defined. At this point, the semimajor axis resumes its outward evolution. Though there is a brief interval in which is still nonzero after this point, the decline of is small. Once decays to zero, changes very little.
We can determine the lowest value of that can be obtained during the LPT instability by systematically exploring the behavior of the averaged, nontidal Earth–Moon system. For to be nonzero, the circular orbit must be unstable; otherwise, the orbit will stay circular () and not get elliptical (). To be in the LPT instability, must oscillate. So we can determine the minimum that can be obtained by systematically finding all -consistent states that satisfy two conditions: 1) is unstable, and 2) oscillates. If the minimum determined in this way is much larger than , then the high- scenario is not consistent with the present Earth–Moon system. The conclusion is independent of tidal models and tidal parameters.
The Hamiltonian describing the evolution of the nontidal Earth–Moon system, averaged over the orbital timescales of the Earth and Moon, denoted as , is shown in SI Appendix, SI Text. is very similar to the Hamiltonian derived in Touma and Wisdom (20), but is generalized to arbitrary nonzero eccentricity. For the averaged system, three quantities are conserved: , , and Earth’s rotation rate. Then, has two degrees of freedom (or a four-dimensional phase space).
Since the Hamiltonian has two degrees of freedom, it is natural to study the evolution with surfaces of section, which reveal the phase-space structure and determine the stability of fixed points (30). The values of the three conserved quantities must be specified for each section. We set for all sections. We make a stability diagram for each . On this stability diagram, initial values of and are chosen, for and . From these, we determine the Earth’s rotation rate and the value of the Hamiltonian. Since has no time dependence, it is conserved. All points on a section share the same value.
We take the axes of the surface of section to be and , where is the argument of pericenter of the lunar orbit. The section condition is (restricted to the case). The value of the momentum conjugate to is determined by requiring that has the chosen value. The return map is obtained by integrating the evolution until the section condition () is again satisfied. The map from the pair to the next defines the return map .
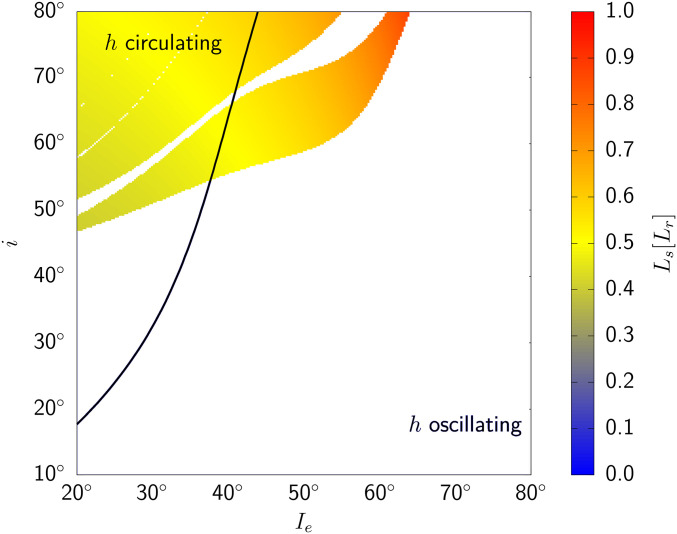
Linear stability analysis of the map determines the stability of the fixed point (at ) (30). We make a stability diagram for a specified (e.g., Fig. 3). For the initial values of and , if the fixed point is unstable, then a color corresponding to the value of is plotted. A black line marks the boundary between oscillating and circulating. For to decline substantially, must be unstable, and must be oscillating.
Fig. 3.
The stability diagram for plots the color corresponding to the value of if the circular orbit is linearly unstable. The black line marks the boundary between oscillating and circulating . can only decrease if the system is in the unstable region with oscillating. There is a small “disconnected” arc-like unstable region with smaller and that is not shown, because it cannot be reached by tidal evolution.
The stability diagram for is shown in Fig. 3. The minimum value of satisfying both conditions is 0.47, which is significantly larger than the present value of 0.34. The minimum Earth obliquity reached is about , much larger than the post-LPT obliquity that is required for subsequent evolution to reach the present (SI Appendix, , Low-e Phases of Evolution). The results for other values of are shown in Table 1. and are the minimum and obliquity in the unstable , oscillating regions, such as the colored region in Fig. 3. Notice that the predicted agrees well with the minimum obtained in our simulations (Fig. 2). We see that with set at , the high- scenario is not able to produce the present Earth–Moon system, regardless of tidal parameters and tidal models. The present-day lunar inclination remains a puzzle.
Table 1.
Minimum obtained while the system is undergoing the LPT instability, at different semimajor axis values
| 16 | 0.437 | |
| 17 | 0.452 | |
| 18 | 0.472 | |
| 19 | 0.498 | |
| 20 | 0.496 |
Even though the stability diagrams are for the nontidal averaged system, they suggest what the tidal evolution through the LPT instability would look like on the – plane. The system begins with large and . As it evolves into the region of the LPT instability, the system enters the colored tongues of instability and develops nonzero eccentricity. At this point, the system begins to undergo large variations in and , while maintaining roughly constant (the system roughly stays on the stability diagram). These large oscillations in and are reminiscent of those found by Atobe and Ida (16) in the case. Tidal torques reduce , and the system proceeds down the tongue of instability (diagonally toward the lower left). But once the boundary between oscillation and circulation is reached, the system changes course and soon leaves the LPT instability. There is no further significant reduction in .
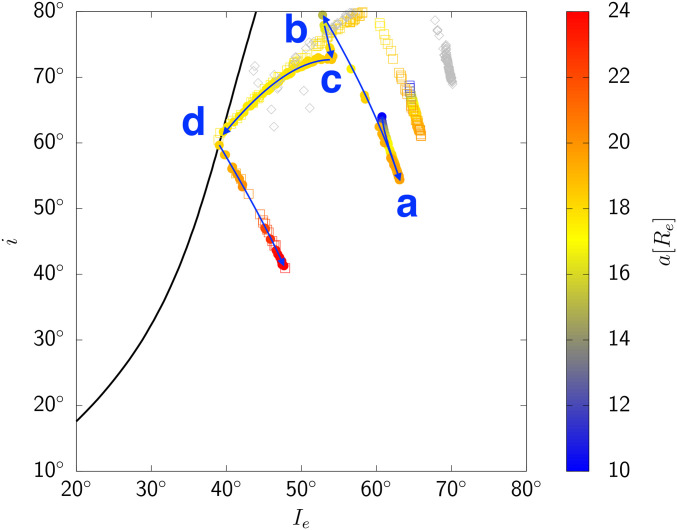
Examination of the simulations confirms this picture (Fig. 4). Whenever radians, with , we plot a point on the plane. The semimajor axis is not constant in the simulations, so we indicate the value of by a color. The evolution begins in the upper right. Once the system enters the LPT instability, the semimajor axis is roughly constant. During this phase, the colors are orange to yellow. The system evolves down diagonally to the left until the boundary between oscillation and circulation is reached. At this point, the trajectory on the plot changes direction. The semimajor axis then resumes its outward evolution, as indicated by the change of color to red. In this final phase, the stability diagram at fixed no longer applies. The eccentricity damps to zero, and no longer declines substantially.
Fig. 4.
versus whenever radians and for the simulations shown in Fig. 2, with initial conditions (in [, ]): (, 0.7 [circle]), (, 0.8 [square]), and (, 0.98 [diamond]). The color indicates the value of . Note that the three simulations, though started with different initial conditions, merge onto a common track. The black line marks the boundary between oscillating (to the right) and circulating for . For the simulation with initial , the arrows show the direction of time evolution, and the marks a–d correspond to the points in Fig. 2 with the same labels.
Constraint on Resonant Scenarios
The evection resonance and the evection-limit cycle involve a resonance between the precession of the lunar pericenter and the motion of the Earth around the Sun. Substantial AM can be lost in the form of a decrease in (1, 10–12). However, is conserved in the postresonance evolution. The late-accretional impacts can only modify by up to (either increase or decrease). Even the presence of solar tides and planetary perturbations can only decrease as much as . Therefore, for a scenario of evection resonance or evection limit cycle to be a possible representation of the Earth–Moon history, the postresonance state should have its close to (0.339): .
The evection resonance (1) and the near-resonance described in ref. 11 both involve high lunar eccentricities (). Such high eccentricities will lead to severe heating in the Moon and cause these mechanisms to quickly exit with little AM decreased (12). The evection limit cycle (near-resonance) described in refs. 10 and 12 leads to lower eccentricities and is thermally stable (12). However, the post-limit cycle minimum is 0.393 in ref. 10 and 0.404 in ref. 12, both with . It was then thought that the subsequent evolution would decrease , but the constraint rules out this possibility.
It was found in ref. 12 that a smaller can be produced with a larger (0.436, 0.404, and 0.389 for = 300, 400, and 500). With a large (103 to 104) in the early history of the Earth (31), the evection limit cycle remains a possible mechanism to drain the excess AM from a fast-spinning Earth.
Code Availability
The computer codes we used for the simulations in this paper are available at GitHub, https://github.com/zhenliangtian/em3d.
Conclusion
The constraint places limits on the possible orbital histories of the Earth–Moon system and thus limits the details of the Moon-forming giant impact. For a high-AM impact (1–3), which is able to produce a Moon with an Earth-like composition, the impact geometry is constrained to cases where the postimpact Earth has a small to medium obliquity.
Supplementary Material
Acknowledgments
This research was initiated in anticipation of the Moon Workshop, held October 14–16, 2019, at the American University of Beirut, Lebanon, organized by Jihad Touma. We thank Francis Nimmo for helpful discussions.
Footnotes
The authors declare no competing interest.
Data deposition: The computer codes we used for the simulations in this paper are available at GitHub, https://github.com/zhenliangtian/em3d.
*Even though Ćuk et al. (13) tried to match the present-day AM, , and, the values were not . They simulated the Earth–Moon history in two steps, first for and then for . After the first step, AM and get close to the present values, but is still much larger than . Then, in the second step, they concentrated on reducing to , but did not track . Actually, will increase in the second step, so the final state will not match the present values of AM, , and .
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2003496117/-/DCSupplemental.
References
- 1.Ćuk M., Stewart S. T., Making the Moon from a fast-spinning Earth: A giant impact followed by resonant despinning. Science 338, 1047–1052 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Canup R. M., Forming a Moon with an Earth-like composition via a giant impact. Science 338, 1052–1055 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lock S. J., et al. , The origin of the Moon within a terrestrial synestia. J. Geophys. Res. Planets 123, 910–951 (2018). [Google Scholar]
- 4.Lugmair G. W., Shukolyukov A., Early solar system timescales according to 53Mn-53Cr systematics. Geochim. Cosmochim. Acta 62, 2863–2886 (1998). [Google Scholar]
- 5.Wiechert M., et al. , Oxygen isotopes and the Moon-forming giant impact. Science 294, 345–348 (2001). [DOI] [PubMed] [Google Scholar]
- 6.Touboul M., Kleine T., Bourdon B., Palme H., Wieler R., Late formation and prolonged differentiation of the Moon inferred from W isotopes in lunar metals. Nature 450, 1206–1209 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Zhang J., Dauphas N., Davis A. M., Leya I., Fedkin A., The proto-Earth as a significant source of lunar material. Nat. Geosci. 5, 251–255 (2012). [Google Scholar]
- 8.Melosh H. J., An isotopic crisis for the giant impact origin of the Moon? Meteorit. Planet. Sci. Suppl. 72, 5104 (2009). [Google Scholar]
- 9.Touma J., Wisdom J., Resonances in the early evolution of the Earth-Moon system. Astron. J. 115, 1653–1663 (1998). [Google Scholar]
- 10.Wisdom J., Tian Z., Early evolution of the Earth-Moon system with a fast-spinning Earth. Icarus 256, 138–146 (2015). [Google Scholar]
- 11.Rufu R., Canup R. M., “Evection resonance in the Earth-Moon system” in 44th Lunar and Planetary Science Conference, Mackwell S. J., Stansbery E. K., Draper D. S., Eds. (Universities Space Research Association Houston, Houston, TX, 2019), p. 3029. [Google Scholar]
- 12.Tian Z., Wisdom J., Elkins-Tanton L., Coupled orbital-thermal evolution of the early Earth-Moon system with a fast-spinning Earth. Icarus 281, 90–102 (2017). [Google Scholar]
- 13.Ćuk M., Hamilton D. P., Lock S. J., Stewart S. T., Tidal evolution of the Moon from a high-obliquity, high-angular-momentum Earth. Nature 539, 402–406 (2016). [DOI] [PubMed] [Google Scholar]
- 14.Ward W. R., Canup R. M., Origin of the Moon’s orbital inclination from resonant disk interactions. Nature 403, 741–743 (2000). [DOI] [PubMed] [Google Scholar]
- 15.Pahlevan K., Morbidelli A., Collisionless encounters and the origin of the lunar inclination. Nature 527, 492–494 (2015). [DOI] [PubMed] [Google Scholar]
- 16.Atobe K., Ida S., Obliquity evolution of extrasolar terrestrial planets. Icarus 188, 1–17 (2007). [Google Scholar]
- 17.Tremaine S., Touma J., Namouni F., Satellite dynamics on the Laplace surface. Astron. J. 137, 3706–3717 (2009). [Google Scholar]
- 18.Lidov M. L., The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies. Planet. Space Sci. 9, 719–759 (1962). [Google Scholar]
- 19.Kozai Y., Secular perturbations of asteroids with high inclination and eccentricity. Astron. J. 67, 591–598 (1962). [Google Scholar]
- 20.Touma J., Wisdom J., Evolution of the Earth-Moon system. Astron. J. 108, 1943–1961 (1994). [Google Scholar]
- 21.Goldreich P., History of the lunar orbit. Rev. Geophys. 4, 411–439 (1966). [Google Scholar]
- 22.Bottke W. F., Walker R. J., Day J. M. D., Nesvorny D., Elkins-Tanton L., Stochastic late accretion to Earth, the Moon, and Mars. Science 330, 1527–1530 (2010). [DOI] [PubMed] [Google Scholar]
- 23.Marchi S., et al. , Widespread mixing and burial of Earth’s Hadean crust by asteroid impacts. Nature 511, 578–582 (2014). [DOI] [PubMed] [Google Scholar]
- 24.Brasser R., Mojzsis S. J., Werner S. C., Matsumura S., Ida S., Late veneer and late accretion to the terrestrial planets. Earth Planet Sci. Lett. 455, 85–93 (2016). [Google Scholar]
- 25.Genda H., Brasser R., Mojzsis S. J., The terrestrial late veneer from core disruption of a lunar-sized impactor. Earth Planet Sci. Lett. 480, 25–32 (2017). [Google Scholar]
- 26.Brasser R., Werner S. C., Mojzsis S. J., Impact bombardment chronology of the terrestrial planets from 4.5 Ga to 3.5 Ga. Icarus 338, 113514 (2020). [Google Scholar]
- 27.Wisdom J., Holman M., Symplectic maps for the N-body problem. Astron. J. 102, 1528–1538 (1991). [Google Scholar]
- 28.Kaula W. M., Tidal dissipation by solid friction and the resulting orbital evolution. Rev. Geophys. 2, 661–685 (1964). [Google Scholar]
- 29.Chen E. M. A., Nimmo F., Tidal dissipation in the lunar magma ocean and its effect on the early evolution of the Earth-Moon system. Icarus 275, 132–142 (2016). [Google Scholar]
- 30.Sussman G. J., Wisdom J., Structure and Interpretation of Classical Mechanics (MIT Press, Cambridge, MA, ed. 2, 2015). [Google Scholar]
- 31.Zahnle K. J., Lupu R., Dobrovolskis A., Sleep N. H., The tethered Moon. Earth Planet Sci. Lett. 427, 74–82 (2015). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.