Identifying tumor clones in sparse single-cell mutation data

Abstract

Motivation

Recent single-cell DNA sequencing technologies enable whole-genome sequencing of hundreds to thousands of individual cells. However, these technologies have ultra-low sequencing coverage (<0.5× per cell) which has limited their use to the analysis of large copy-number aberrations (CNAs) in individual cells. While CNAs are useful markers in cancer studies, single-nucleotide mutations are equally important, both in cancer studies and in other applications. However, ultra-low coverage sequencing yields single-nucleotide mutation data that are too sparse for current single-cell analysis methods.

Results

We introduce SBMClone, a method to infer clusters of cells, or clones, that share groups of somatic single-nucleotide mutations. SBMClone uses a stochastic block model to overcome sparsity in ultra-low coverage single-cell sequencing data, and we show that SBMClone accurately infers the true clonal composition on simulated datasets with coverage at low as $0.2\times$. We applied SBMClone to single-cell whole-genome sequencing data from two breast cancer patients obtained using two different sequencing technologies. On the first patient, sequenced using the 10X Genomics CNV solution with sequencing coverage $\approx 0.03\times$, SBMClone recovers the major clonal composition when incorporating a small amount of additional information. On the second patient, where pre- and post-treatment tumor samples were sequenced using DOP-PCR with sequencing coverage $\approx 0.5\times$, SBMClone shows that tumor cells are present in the post-treatment sample, contrary to published analysis of this dataset.

Availability and implementation

SBMClone is available on the GitHub repository https://github.com/raphael-group/SBMClone.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Single-cell DNA sequencing technologies that measure the genomes of individual cells are increasingly being used in cancer, metagenomics and other applications (Gawad et al., 2016). In cancer, single-cell DNA sequencing has been used to study the somatic evolution of tumors and identify distinct groups of cells, or clones, that are sensitive/resistant to treatment (10X Genomics, 2019; Laks et al., 2019; Navin, 2015; Navin et al., 2011; Wang et al., 2014). While single-cell DNA sequencing enables the measurement of genomic changes in individual cells, current single-cell sequencing technologies have limited accuracy and fidelity. Most single-cell DNA sequencing technologies rely on whole-genome amplification procedures like MDA or MALBAC that result in DNA amplification errors, undersampling and sequencing errors which complicate the identification of single-nucleotide mutations (Gawad et al., 2016; Navin, 2015).

To address the limitations in identifying mutations in single-cell sequencing data, a number of computational methods have been developed to improve mutation calling by grouping cells with similar mutational profiles (Borgsmueller et al., 2020; Roth et al., 2016) or shared cellular lineage (Ciccolella et al., 2018; El-Kebir, 2018; Jahn et al., 2016; Malikic et al., 2019; McPherson et al., 2016; Ross and Markowetz, 2016; Satas et al., 2019; Singer et al., 2018; Zafar et al., 2019). These methods have primarily been applied to analyze single-cell DNA sequencing data obtained from limited genomic regions: e.g. Single Cell Genotyper (SCG; Roth et al., 2016) and Bayesian non-parametric clustering (BnpC; Borgsmueller et al., 2020) have been applied to targeted single-cell sequencing datasets with up to 420 cells and up to 105 mutations (Gawad et al., 2014; McPherson et al., 2016), while BnpC and SCITE (Jahn et al., 2016) have been applied to whole-exome single-cell sequencing datasets with up to 65 cells and up to 79 mutations (Leung et al., 2017; Wu et al., 2017).

Recently, a number of new single-cell DNA sequencing technologies have been introduced that produce ultra-low coverage whole-genome sequencing data from hundreds to thousands of individual cells, with reads distributed approximately uniformly across the genome of each cell. These technologies include degenerate-oligonucleotide-primed polymerase chain reaction (DOP-PCR; Navin et al., 2011) with coverage of $0.1-0.5\times$ per cell, and the 10X Genomics Chromium CNV solution (10X Genomics, 2019) and Direct Library Preparation (Laks et al., 2019) with coverage of $0.02-0.05\times$ per cell. The initial application of these technologies has been to identify large (>1 Mb) copy-number aberrations (CNAs) in individual cells, a reasonable goal with such low coverage sequencing. Recent studies (Laks et al., 2019; Zaccaria and Raphael, 2019) showed that it was possible to identify single-nucleotide variants (SNVs) in ultra-low coverage DNA sequencing data by merging a large number of single cells with the same CNAs into a pseudo-bulk sample. However, CNAs will not always identify every distinct clone in a sample: some clones may have the same CNAs, or CNAs may not be present in any cells. In these cases, the previous merging approaches would fail to recover the complete clonal composition and may not reliably measure SNVs.

In this work, we aim to address a more difficult question: is it possible to detect SNVs directly from ultra-low coverage whole-genome single-cell sequencing data and to partition cells into clones according to their shared mutations? Obviously, one cannot expect to reliably identify single-nucleotide mutations in individual cells with sequencing coverage $\approx 0.5\times$. However, when reasonably sized clones are uniquely distinguished by a sufficiently large number of mutations, one may expect that cells from the same clone share a higher number of mutations than cells from different clones. We formulate this problem as the clone block inference (CBI) problem, where we combine sets of cells which share the same set of mutations into blocks. This problem is closely related to several well-studied problems in computer science, including co-clustering (Dhillon et al., 2003; Kumar et al., 2011), spectral clustering (Dhillon, 2001; Zha et al., 2001) and community detection (Alzahrani and Horadam, 2016; Fortunato and Hric, 2016). We show how to solve this problem by inferring a stochastic block model (SBM) (Karrer and Newman, 2011) that describes the data. This approach is substantially different from existing single-cell algorithms which focus either on clustering cells according to their mutation profiles or on clustering mutations according to the cells that contain them. With sparse mutation data, neither the cell nor mutation signal is sufficiently strong, but by simultaneously analyzing both cells and mutations, we are able to aggregate the two weaker signals into a stronger signal and recover a block structure.

We introduce SBMClone, a method that uses SBM inference algorithms (Peixoto, 2014a, b) to infer the clonal composition from single-cell whole-genome sequencing data. More specifically, SBMClone uses the measurements from n single-nucleotide mutations across m single cells to identify clones, which are subpopulation of cells with the same complements of mutations, and clusters of mutations that are present in the same clones. To assess the performance of SBMClone, we generated a diverse collection of simulated data using different parameters and experimental settings that mimic the features of existing whole-genome single-cell sequencing technologies with ultra-low coverage. We show that SBMClone can accurately recover the clonal composition in sequencing data with coverage as low as $0.2\times$, while three existing methods for single-cell mutation analysis—SCG (Roth et al., 2016), SCITE (Jahn et al., 2016) and BnpC (Borgsmueller et al., 2020)—cannot. We used SBMClone to analyze single-cell whole-genome sequencing data from two breast cancer patients (10X Genomics, 2019; Kim et al., 2018). On the first patient, where $4\hspace{0.17em}085$ cells were sequenced using the 10X Chromium platform with ultra-low coverage ($\approx 0.03\times$), SBMClone recovers the major clonal composition consistent with previous analysis when a small amount of additional information is incorporated. On the second patient, where 90 cells were sequenced using DOP-PCR with coverage $\approx 0.5\times$, we show that SBMClone identifies tumor cells present in the post-treatment sample, contrary to the published analysis of this dataset using CNAs only. By jointly clustering both cells and mutations, SBMClone enables the accurate inference of clonal composition using single-nucleotide mutations in ultra-low coverage single-cell whole-genome sequencing data.

2 Materials and methods

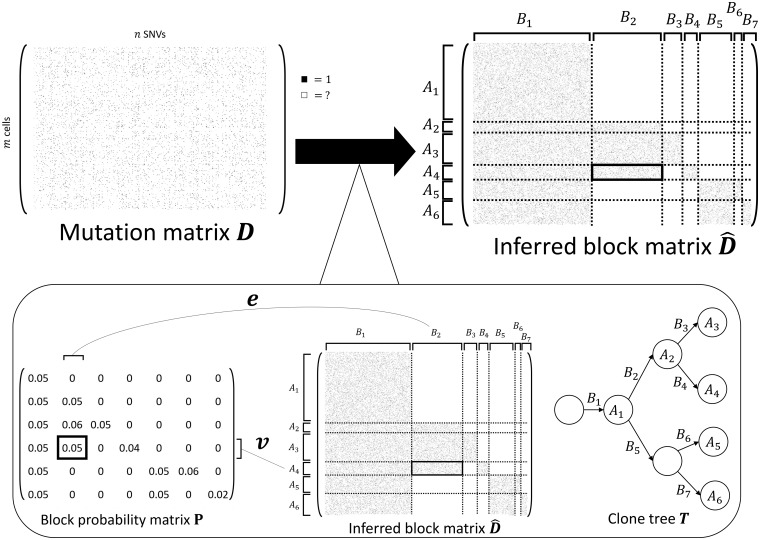
We measure mutations at n genomic loci in m evolutionarily related single cells using ultra-low-coverage ($\approx 0.5\times$) DNA sequencing. Because of this ultra-low coverage, there is substantial uncertainty in the detection of any particular mutation in any particular cell. In particular, most mutated locations will have no more than one sequencing read that aligns to the location. If this read contains the mutation, we may assume there is a reasonable chance that the cell has the mutation (with a small probability of being incorrect due to sequencing errors). However, if the sequencing read does not contain the mutation, we cannot be certain of the mutation status since generally there is more than one copy of a locus; e.g., there are two copies of all diploid regions of the human genome. We represent our measurements and the associated uncertainty using an m × n mutation matrix $D=[d_{i,j}]$ where $d_{i,j}=1$ if we observe a read in cell i containing the mutation j and $d_{i,j}=$? otherwise (Fig. 1). D is an extremely sparse matrix: on the 10X Genomics Chromium data studied below, only $\approx 0.11$% of entries are 1s.

Fig. 1.

SBMClone solves the CBI problem using an SBM. (Top) An example mutation matrix D with m cells (rows) and n mutations (columns) is composed of entries with either 1 or ‘?’ to indicate the measurement (black square) or lack of measurement (white square) of a mutation in each cell. The goal of the CBI problem is to infer the rearrangement of the rows and columns of D that form the inferred block matrix ${\widehat{D}}_{k,\ell }$ where rows are partitioned into k row blocks $A_1,\dots ,A_k$ (k = 6 here), columns are partitioned into $\ell$ column blocks $B_1,\dots ,B_{\ell }$ ($\ell =7$ here), and each block of $\widehat{D}$ has either high (many black squares) or low (no black squares) proportions of 1s. (Bottom left) SBMClone uses an SBM which is a generative model parameterized by the block probability matrix $P=[p_{r,s}]$. Each block probability $p_{r,s}$ indicates the expected proportion of 1s within the block composed of the cells in row block A_r and the mutations in column block B_s. (Bottom right) The mutation matrix D has a block structure because every row block A_r corresponds to a clone, which accumulate clusters of mutations that correspond to every column block B_s; this evolutionary process is described as the clone tree T where every node correspond to a clone and every edge is labeled by a mutation cluster

Although the mutation matrix D is sparse, the shared evolutionary history of the cells imposes structure on D. Specifically, there is a phylogenetic tree that describes the ancestral relationships between cells. At single-cell resolution, each node of this phylogenetic tree is a cell (either from the present time or ancestral) and each edge is labeled by the mutation(s) that distinguish the parental cell from the child cell. With ultra-low-coverage data, we have no hope of reconstructing this single-cell tree. (Even with higher-coverage single-cell sequencing data, it is often not possible to derive a fully resolved tree of single cells due to allelic dropout. For example, SCITE (Jahn et al., 2016), a method for inferring a phylogenetic tree from single-cell tumor DNA sequencing data, introduces the mutation tree to address uncertainty in the placement of cells on the tree.) While we cannot reconstruct a tree on single cells with a sparse mutation matrix D, the unknown tree imposes a structure on D. Specifically, we expect to find multiple groups of cells, with each group of cells distinguished by one or more groups of shared mutations.

In applications like cancer where there is selection on mutations, clonal expansions result in groups of cells, or clones, that share large groups of mutations, including the positively selected mutation and other passenger mutations that hitchhike with this mutation. Thus, the rows and columns of D can be rearranged to obtain a block matrix ${\widehat{D}}_{k,\ell }$ with row blocks $A_1,\dots ,A_k$ and column blocks $B_1,\dots ,B_{\ell }$ (Fig. 1). The row blocks correspond to cells that share the same mutations, or clones, and the column blocks correspond to clusters of mutations that are present in the same cells. The evolutionary relationships between clones are described by a clone tree T, where each row block A_r corresponds to a vertex in T and each column block B_s corresponds to an edge in T (Fig. 1). Note that we do not aim to reconstruct T, but rather T imposes a block structure on the mutation matrix D.

Our goal is to find such a block matrix ${\widehat{D}}_{k,\ell }$ where each block (r, s) has either many 1-entries (i.e. the cells in A_r contain the mutations in B_s) or few 1-entries (i.e. the cells in A_r do not contain the mutations in B_s). We formalize these ideas in the following problem.

CBI. Given a mutation matrix $D\in {\{1,?\}}^{m\times n}$, find a rearrangement of the rows and columns of D to form a block matrix ${\widehat{D}}_{k,\ell }\in {\{1,?\}}^{m\times n}$ with row blocks $A_1,\dots ,A_k$ and column blocks $B_1,\dots B_{\ell }$, and such that each block (A_r, B_s) has either a high or low proportion of 1s.

We note that this problem is very different from existing methods for analyzing mutations in single-cell sequencing data. Specifically, existing methods (Borgsmueller et al., 2020; Ciccolella et al., 2018; El-Kebir, 2018; Jahn et al., 2016; Malikic et al., 2019; McPherson et al., 2016; Ross and Markowetz, 2016; Roth et al., 2016; Satas et al., 2019; Singer et al., 2018; Zafar et al., 2019) attempt to directly model the error rates of observing individual mutations, or rely on distances between cells according to mutations or distances between mutations according to cells. In our case, because we have ultra-low-coverage data with very few mutations recorded as present in individual cells and no confidence in the absence of a mutation in an individual cell, such approaches are unlikely to work well. Instead, one needs to consolidate signals simultaneously between groups of mutations and groups of cells.

One might consider imposing additional constraints on blocks, such as a specific evolutionary model. Here, we impose no such constraints and instead solve the general problem. Note that the block structure does not depend on the infinite sites assumption (perfect phylogeny model) or any specific evolutionary model (Supplementary Material S1). Thus, we model the block structure of the mutation matrix D using the stochastic block model (SBM), which has been intensively studied as a model of community structure in networks (Abbe, 2017; Airoldi et al., 2008; Decelle et al., 2011; Fortunato and Hric, 2016; Goldenberg et al., 2010; Karrer and Newman, 2011; Larremore et al., 2014; Snijders and Nowicki, 1997; Zhou and Amini, 2019). The SBM is parameterized by a $k\times \ell$block probability matrix $P=[p_{r,s}]$ where $p_{r,s}$ indicates the probability of observing a 1-entry in row $i\in A_r$ and column $j\in B_s$, and by the block assignment variables v and e whose entries v_i and e_j indicate the block assignments of row i and column j, respectively. (While the SBM typically models a symmetric matrix encoding all pairwise relationships between objects, we use the bipartite SBM (Larremore et al., 2014) to avoid relationships between pairs of cells or pairs of mutations.) According to the SBM, each entry $d_{i,j}$ of the mutation matrix with block assignments v_i = r and e_j = s is sampled independently at random from Bernoulli (p_r,s). We emphasize that the inference of blocks with distinct probabilities $p_{r,s}$ is a positive feature for our applications, as the probability to observe mutations in different blocks may be influenced by CNAs.

We solve the CBI problem using the SBM inference algorithm in Peixoto (2014a). While this algorithm is based on a variant of the SBM that uses the Poisson distribution, the difference between this model and the Bernoulli-distributed SBM is negligible when entries in P are small (Perry and Wolfe, 2012), as is our case. This algorithm incorporates model selection to choose the number k of clones and the number $\ell$ of mutation clusters that best explains the observed data. We also apply a variant of the SBM inference algorithm, the hierarchical SBM (Peixoto, 2014b); the hierarchical SBM models block matrices with nested blocks, as might be expected in our case where the blocks of cells and mutations arise from the clone tree T.

3 Results

3.1 Simulated data

To assess the performance of SBMClone, we simulated mutation matrices obtained from ultra-low coverage DNA sequencing data for n mutations across m cells using a two-step procedure. First, we constructed a binary m × n complete block matrix $X=[x_{i,j}]$ where $x_{i,j}=1$ indicates that cell i contains mutation j, and $x_{i,j}=0$ otherwise. We defined k clones $A_1,\dots ,A_k$ and $\ell$ mutation clusters $B_1,\dots ,B_{\ell }$ such that, for each clone r and mutation cluster s, either all cells in r contain all mutations in s or no cells in r contain any mutations in s (i.e. either $\sum _{i\in A_r}\sum _{j\in B_s}{x}_{i,j}=\left|A_r\right|·\left|B_s\right|$ or $\sum _{i\in A_r}\sum _{j\in B_s}{x}_{i,j}=0$). We describe the specific block matrices X used to generate simulated data below. Second, given X and a block probability p, we generated the mutation matrix D such that if $x_{i,j}=1$ then $d_{i,j}=1$ with probability p, and $d_{i,j}=?$ otherwise. While the relationship between sequencing coverage and p is complex and highly dependent on read alignment and mutation calling, we estimated the block probability values from a previous 10X Chromium single-cell dataset (10X Genomics, 2019) and we found that an average per-cell sequencing coverage of $0.03\times$ corresponds to p = 0.0014, roughly a factor of 20 (see Supplementary Material S2 for a more detailed discussion).

Using this two-step procedure, we generated two types of mutation matrices D. First, we simulated data using block matrices X with m = 4000 cells divided into two clones and n = 5000 mutations divided into three mutation clusters (Section 3.1.1). Second, we simulated data using a tree-structured block matrix X based on the phylogenetic tree from Zaccaria and Raphael (2019). This phylogenetic tree was derived using CNAs and divides m = 4085 cells into 8 clones and n = 10 556 mutations into 15 clusters (Section 3.1.2). Since single-cell DNA sequencing technologies generally have different levels of technical variability and errors (e.g. false positives, amplification biases, doublets, etc.) (Gawad et al., 2016), we also simulated realistic tree-structured block matrices using an empirical block probability matrix $\widehat{P}$ that we derived from the previously identified clones (Section 3.1.2). For each complete block matrix X, we generated multiple mutation matrices D using different values of p.

We compared SBMClone to three existing methods for inferring clones from single-cell sequencing data, SCG (Roth et al., 2016), BnpC (Borgsmueller et al., 2020) and SCITE (Jahn et al., 2016), as well as a naive approach. This naive approach represented each cell i as the number of mutations it contains (i.e. its row sum) and applied k-means clustering (Arthur and Vassilvitskii, 2007) to this one-dimensional data. Both k-means and SCG were provided with the correct number k of clones, while BnpC infers the number of clones. We note that the single-cell methods were designed for much higher-coverage sequencing data and not for the ultra-low coverage whole-genome single-cell sequencing data that is the focus of this study. In particular, these methods have been applied only to mutation matrices with up to 3000 cells, up to 500 mutations and up to 60% missing entries.

We applied all methods to each simulated mutation matrix and measured the performance of each method by computing the adjusted Rand index (ARI) between the true and inferred partitions of cells (clones). Both SCITE (Jahn et al., 2016) and BnpC (Borgsmueller et al., 2020) did not scale to the large sizes of our simulated mutation matrices. SCITE required multiple days of computation on most instances, and exhibited poor performance on even the smallest instances. Therefore, we excluded SCITE from further analysis and we report additional details in Supplementary Material S7. For BnpC, some instances required >64 GB of memory or crashed with a floating point underflow error; these issues may be due to the very recent release of this method. Additional details on how BnpC and SCG were run are in Supplementary Materials S3 and S6.

3.1.1 Block mutation matrices

We simulated mutation matrices using a complete block matrix X composed of two clones, A₁ and A₂, and three mutation clusters, B₁, B₂ and B₃ (Fig. 2A). Mutations in B₁ were shared by both clones, while mutations in B₂ and B₃ were unique to A₁ and A₂, respectively. We simulated 1 228 880 mutation matrices, each with 100–4000 cells and 100–10 000 mutations. Moreover, we varied the number of cells in each of the two clones as well as the number of mutations in the three mutation clusters. We describe here results with m = 4000 cells, n = 5000 mutations, $\left|A_1\right|=1600,\hspace{0.17em}\left|A_2\right|=2400,\hspace{0.17em}\left|B_1\right|=1500,\hspace{0.17em}\left|B_2\right|=1400$ and $\left|B_3\right|=2100$. Additional results from SBMClone with varied block sizes are reported in Supplementary Material S4 and Figure S2.

Fig. 2.

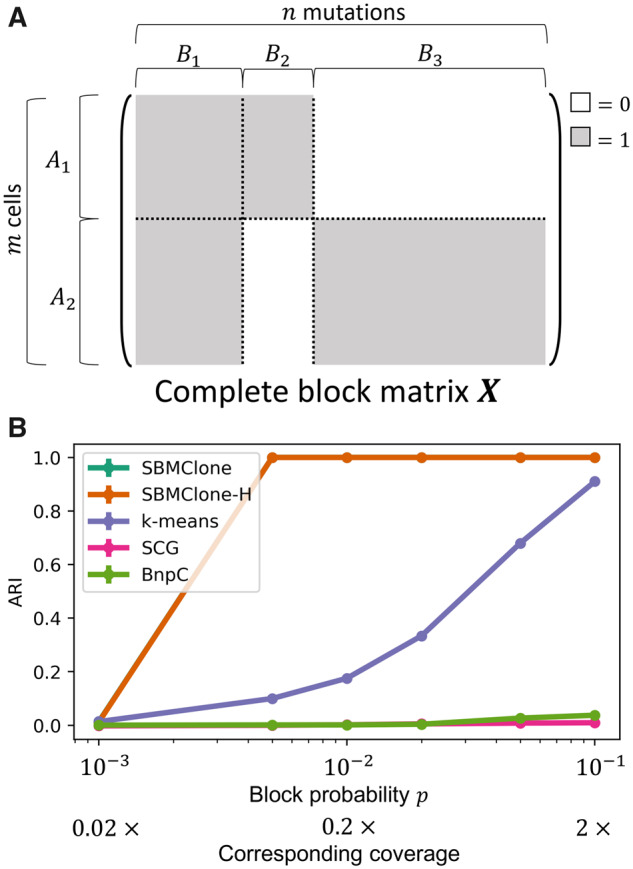
SBMClone outperforms existing methods on simulated mutation matrices with two clones and three clusters of mutations. (A) A complete block matrix X with m cells and n mutations is used to simulate two clones A₁ and A₂ that share mutations in the cluster B₁, while the two remaining clusters B₂ and B₃ of mutations are uniquely present in either A₁ or A₂, respectively. (B) ARI (y-axis) in recovering the simulated clones for SBMClone, SBMClone-H (hierarchical SBM), SCG (Roth et al., 2016), BnpC (Borgsmueller et al., 2020) and k-means clustering (k-means) applied to simulated mutation matrices with m=4000 cells divided into two clones, n=5000 mutations divided into three clusters, and with varying block probability p (x-axis in log-scale)

We found that SBMClone outperformed all other methods across a range of block probabilities p (Fig. 2B). While no method was able to accurately recover the true clonal composition with extremely low block probability ($p\le {10}^{-3}$, ARI$<0.01$), SBMClone perfectly recovered the clones with block probability $p\ge 5\times {10}^{-3}$ using either the hierarchical or non-hierarchical model. We also analyzed the number of clones inferred by SBMClone-H and found that when ARI $\ge 0.5$, SBMClone-H inferred the correct number of clones (Supplementary Material S10 and Fig. S5A). In contrast, the other methods performed poorly. BnpC and SCG were unable to recover clonal composition (ARI $<0.05$) for all block probabilities $p\le 0.1$ that were tested. The naive k-means clustering approach improved in performance as p increased, reaching an ARI of approximately 0.9 at the highest value p = 0.1, a value that corresponds approximately to a sequencing coverage of 2×. However, at lower values of p < 0.05 corresponding to sequencing coverage $<1\times$, in the range of current whole-genome single-cell sequencing technologies, k-means has ARI $<0.4$, considerably worse performance than SBMClone.

We also investigated the performance of SBMClone with varying tumor purity (i.e. the proportion of tumor cells in a sample) by including a population of normal cells without measured somatic mutations. We observed that SBMClone can accurately (ARI > 0.95) recover low proportions of tumor cells (as low as 5%) in simulated datasets with tumor purity as low as 25% and with block probability $p\ge 0.02$ (Supplementary Fig. S3 and Material S5).

3.1.2 Tree-structured block mutation matrices

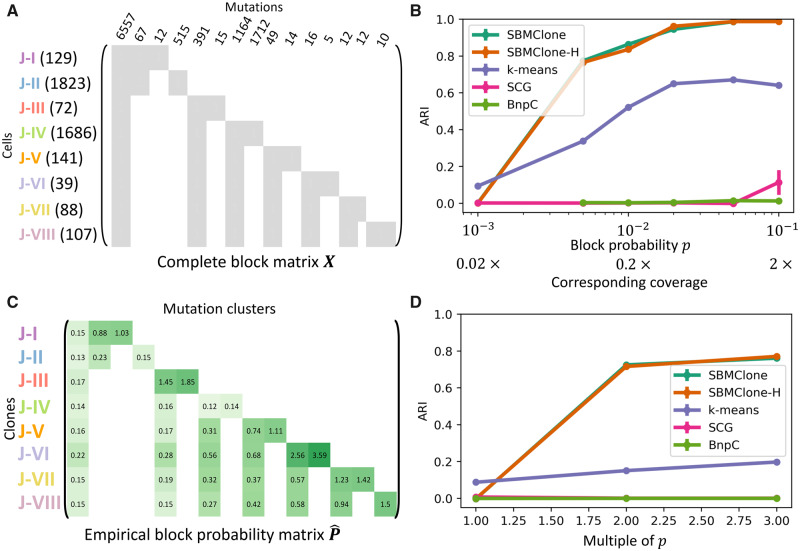
We also compared all methods on simulated tree-structured mutation matrices containing multiple blocks, whose organization was derived from a phylogenetic tree describing the evolution of the m cells that accumulated n mutations. Specifically, we used a phylogenetic tree on eight clones (labeled J–I through J–VIII) across 4085 breast tumor cells that was previously inferred using CNAs derived from single-cell whole-genome sequencing data using the CHISEL algorithm (Zaccaria and Raphael, 2019). This previous analysis also inferred 10 556 somatic mutations and placed them on the edges of this tree (Zaccaria and Raphael, 2019). Using the clonal structure encoded by the tree, we constructed a 4 085 × 10 556 complete block matrix X with k = 8 clones and $\ell =15$ mutation clusters, where blocks of 1s correspond to mutations that are present in each clone and blocks of 0s correspond to mutations that are not present (Fig. 3A).

Fig. 3.

SBMClone outperforms existing methods on tree-structured simulated mutation matrices with both uniform and empirical block probabilities. (A) The complete block matrix X is used to simulate tree-structured mutation matrices with eight tumor clones (J–I,…, J–VIII) of $4\hspace{0.17em}085$ cells and with 15 clusters of 10 556 mutations, according to a tumor phylogenetic tree previously inferred by the CHISEL algorithm from $4\hspace{0.17em}085$ breast tumor cells (Zaccaria and Raphael, 2019). The number of cells in each clone as well as the number of mutations in each cluster are reported for each row block and column block, respectively. (B) ARI measures the performance of SBMClone when applying either the SBM (SBMClone) or hierarchical SBM (SBMClone-H) inference algorithm, the other two existing methods [SCG (Roth et al., 2016) and BnpC (Borgsmueller et al., 2020)], and a k-means algorithm (k-means) to tree-structured simulated mutation matrices with a uniform block probability p across all blocks and with varying values of p (x-axis in log-scale). (C) The empirical block probability matrix P obtained from the 10X Chromium breast cancer data. Note that the values shown are percentages, i.e. the actual probability corresponding to each entry is 100 times smaller. Each entry is the observed proportion of 1-entries in the mutation matrix D when the cells and mutations are organized into the blocks given by the CHISEL phylogeny as in (A). (D) ARI measures the performance of SBMClone when applying either the SBM (SBMClone) or hierarchical SBM (SBMClone-H) inference algorithm, other two existing methods [SCG (Roth et al., 2016) and BnpC (Borgsmueller et al., 2020)], and a k-means algorithm (k-means) to tree-structured simulated mutation matrices with empirical block probabilities $\widehat{P}=[{\widehat{p}}_{r,s}]$ estimated from previous studies (Zaccaria and Raphael, 2019) and further scaled by a multiple (x-axis)

We simulated two sets of 4 085 × 10 556 mutation matrices. The first set of 60 mutation matrices was created using a constant block probability p across all blocks, varying this probability p from ${10}^{-3}$ to ${10}^{-1}$. These values of p correspond to sequencing coverages of $0.02\times$ and $2\times$, respectively. The second set of 30 mutation matrices was created using empirical block probabilities $\widehat{P}=[{\widehat{p}}_{r,s}]$ for each block (r, s) that we derived from the clones and mutation clusters identified in Zaccaria and Raphael (2019) (Fig. 3C). These empirical block probabilities partially account for errors and variability in single-cell DNA sequencing data; in fact, we note that empirical probabilities are lower than expected in some blocks due to the presence of errors (see Supplementary Material S8 for details). Moreover, to simulate higher sequencing coverage, we generated mutation matrices by proportionally increasing all values in $\widehat{P}$ by a constant multiple—e.g. a multiple of 2 signifies that each value ${\widehat{p}}_{r,s}$ is doubled to represent double the sequencing coverage (Fig. 3D).

We found that the performance of all methods was lower on this simulated data than on the simpler block matrices above. While no method was able to accurately recover the true clonal composition with extremely low uniformly sampled block probabilities ($p\le {10}^{-3}$, ARI $<0.1$) or unscaled empirical block probabilities (multiple $=1$, ARI $<0.1$), SBMClone using either the SBM or hierarchical SBM outperforms all other methods and perfectly recovers the clones from uniformly sampled matrices with $p\ge 0.05$. With lower block probabilities, SBMClone partially recovered the clonal structure: ARI $\approx \hspace{0.17em}0.85$ with a uniform block probability of $p={10}^{-2}$, and ARI $\approx \hspace{0.17em}0.72$ when considering simulated mutation matrices when the empirical block probabilities are doubled. In contrast, SCG and BnpC were unable to recover the clonal composition for all values of the block probability $p\le 0.1$ that were tested (ARI $<0.05$) or with triple the empirical block probabilities (ARI $<0.01$). While the naive k-means algorithm did not perform as poorly, it performed considerably worse than SBMClone on uniform simulations (Fig. 3B, ARI $<0.7$) as well as the non-uniform simulations (Fig. 3C, ARI $<0.2$). Across all tree-structured simulations, SBMClone correctly inferred the number of distinct clones when it obtained ARI $\ge 0.5$ (Supplementary Fig. S5B–D).

3.2 Cancer data

3.2.1 10X Genomics Chromium CNV solution

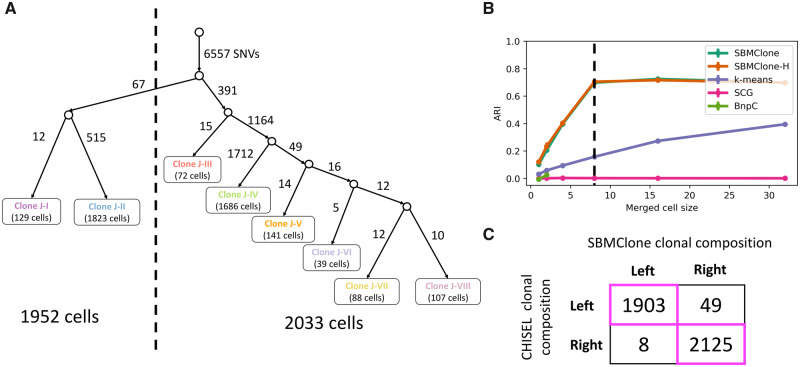
We used SBMClone to analyze the 10X Genomics Chromium single-cell DNA sequencing data from a breast cancer patient (10X Genomics, 2019). This dataset comprises 4085 tumor cells (over 10 202 cells in total), which have been sequenced with ultra-low coverage ($\approx 0.03$× per cell). The CHISEL algorithm (Zaccaria and Raphael, 2019) was used to identify allele- and haplotype-specific CNAs in these cells (Zaccaria and Raphael, 2019). This analysis identified eight distinct clones (labeled J–I through J–VIII) based on copy-number profiles, and constructed a phylogenetic tree relating these clones. The first branch in this tree separates the eight clones into two groups: a left branch containing 1952 cells from clones J–I to J–II, and a right branch containing 2033 cells from clones J–III to J–VIII (Fig. 4A). We investigated whether it was possible to recover this clonal composition by applying SBMClone to the 10 556 somatic single-nucleotide mutations that were previously identified and assigned to the corresponding branches of the phylogenetic tree (Zaccaria and Raphael, 2019).

Fig. 4.

SBMClone accurately recovers two distinct phylogenetic branches of $4\hspace{0.17em}085$ breast tumor cells from 10X Chromium single-cell DNA sequencing data by merging few cells. (A) A tumor phylogenetic tree that was previously reconstructed by Zaccaria and Raphael (2019) from the eight tumor clones (J–I, … , J–VIII) that were identified using the CHISEL algorithm and defined as the leaves of the tree (the corresponding number of cells is indicated for each leaf). The edges of the tree were also labeled by a total of 10 556 single-nucleotide mutations, with each edge labeled by the corresponding number of mutations. The phylogenetic tree separates the $4\hspace{0.17em}085$ cells from the eight clones into two distinct branches, a left branch comprising 1952 cells and a right branch comprising 2033 cells. (B) ARI (y-axis) for SBMClone, SBMClone-H (hierarchical SBM), SCG (Roth et al., 2016), BnpC (Borgsmueller et al., 2020) and k-means clustering (k-means) in recovering the eight tumor clones previously identified by the CHISEL algorithm from 10 556 single-nucleotide mutations, when merging a varying number of cells within the same clone (x-axis). (C) Clonal composition inferred by the previous copy-number analysis with CHISEL and by SBMClone, each separating cells into either the left or right evolutionary branch

All methods, including SBMClone, failed to recover the distinct clones from the single-nucleotide mutations. This result was not surprising and consistent with the simulations above, since the sequencing coverage of $\approx 0.03\times$ corresponds to a block probability of approximately $p<{10}^{-3}$ in simulated data (Fig. 3B). We saw in the tree-structured simulated data above that with slightly larger values of the block probability ($p\ge 0.02$), SBMClone could accurately recover the distinct clones (Fig. 3B, ARI $>0.95$). Since it was not possible to resequence the same cells with higher coverage, we created higher-coverage data in silico by merging mutation calls from multiple single cells that were reported to be in the same clone by CHISEL (see Supplementary Material S9 for details). While this approach may potentially propagate false-positive errors in the mutation calls of the mutation matrix D, we believe that these errors are much less common than the false negatives that we are addressing by merging mutation calls. We applied the same merging approach on our tree-structured simulated dataset with empirical block probabilities and found that merging cells (Supplementary Fig. S4) had a similar effect to increasing the value of block probability (Fig. 3C). On the real breast tumor dataset, we found that merging a small number of cells (≥8) was sufficient to enable SBMClone to accurately separate the cells into two distinct evolutionary branches that match the left and right branches in the CHISEL tree (Fig. 4B and C). We emphasize that merging such small numbers of cells still results in a dataset with ultra-low coverage (≈0.2×). Notably, we also found that a similar merging of cells did not appreciably improve the poor performance of other methods (Fig. 4B).

3.2.2 DOP-PCR

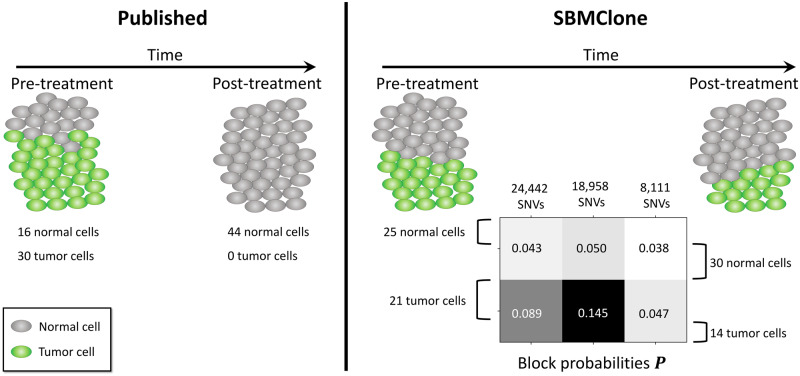
We used SBMClone to analyze the DOP-PCR single-cell DNA sequencing data from breast cancer patient P2 from Kim et al. (2018). This dataset includes ultra-low coverage ($\approx 0.5\times$) whole-genome sequencing of 90 cells from two different time points: 46 pre-treatment cells and 44 post-treatment cells. The published analysis of this dataset identified tumor cells only in the pre-treatment cells, and no tumor cells among the post-treatment cells (Kim et al., 2018) (Fig. 5). This observation led (Kim et al., 2018) to classify P2 as a patient with the ‘clonal extinction’ phenotype, where tumor cells were no longer detectable after treatment. Because of the low sequencing coverage, Kim et al. (2018) restricted their analysis to CNAs using the R package ‘copy-number’ (Nilsen et al., 2012). Thus, we aimed to investigate whether single-nucleotide mutations supported a different grouping of pre- and post-treatment cells.

Fig. 5.

SBMClone identifies tumor cells in both pre- and post-treatment samples from a breast cancer patient contrasting with published analysis. (Left) Published copy-number analysis of 90 cells from a breast cancer patient P2 (Kim et al., 2018) identified 16 tumor cells (green) in the pre-treatment sample, and no tumor cells in the post-treatment sample. (Right) SBMClone analysis of 51 511 SNVs from the 90 sequenced cells identified tumor cells (green) in both the pre-treatment sample (21 tumor cells) and the post-treatment sample (14 tumor cells). SBMClone’s results are supported by the identification of 18 958 SNVs that separate tumor from normal cells: these SNVs have a high block probability (0.145) in the tumor cells but a low block probability (0.050) in the normal cells

We jointly analyzed sequencing reads from all 90 cells using SBMClone. We used Bowtie2 (Langmead and Salzberg, 2012) to align DNA sequencing reads using the same procedure and reference genome hg19 as described in the published analysis (Kim et al., 2018). After removing putative germline variants using dbSNP (Sherry et al., 2001) and a pseudo-matched normal sample (see Supplementary Material S11 for details), we identified a total of 51 511 putative somatic SNVs. We applied SBMClone to the resulting 90 × 51 511 mutation matrix D and identified a block matrix with two distinct clones: one clone with 55 cells and the other clone with 35 cells. Unfortunately, we could not directly compare the clone assignments with the published results as the clone assignments from Kim et al. (2018) were not publicly available. However, SBMClone’s results are consistent with the published result of a normal diploid clone with more cells and a single tumor clone with fewer cells. Therefore, we hypothesized that the clone with 55 cells corresponds to the normal diploid clone, while the other clone with 35 cells corresponds to the tumor clone.

Interestingly, while the published analysis identified tumor cells only in the pre-treatment sample, SBMClone identified a tumor clone that consists of 21 pre-treatment tumor cells and 14 post-treatment tumor cells (Fig. 5). There are three main pieces of evidence corroborating this result. First, the 35 tumor cells identified by SBMClone are distinguished from the normal cells by blocks of mutations with substantially higher block probabilities, especially the middle block comprising 18 958 SNVs: these mutations have a much higher block probability in the tumor cells (0.145) than in the normal cells (0.050) (Fig. 5). Notably, we observed that 538 of the analyzed mutations are present exclusively in the 35 tumor cells identified by SBMClone (232, 87 and 219 in each mutation block, respectively). Second, we analyzed the read-depth profiles of all cells and found that both the pre- and post-treatment cells identified as tumor by SBMClone exhibit very similar read-depth profiles which are consistent with the large CNAs reported in the previous analysis by Kim et al. (2018), while the normal cells have constant read depth across the genome in both pre- and post-treatment samples (see Supplementary Material S11 and Fig. S6). Finally, we observed that SBMClone recovers nearly the same partition of cells when applied to a set of mutations that also includes germline variants (Supplementary Fig. S7). These analyses provide evidence against the ‘clonal extinction’ classification of this patient from the original publication (Kim et al., 2018), as SBMClone identified the presence of both pre- and post-treatment tumor cells. This result shows that analysis of single-nucleotide mutations can lead to important differences in the clonal composition from analysis of CNAs, and that both types of mutations must be carefully analyzed.

4 Discussion

Recent single-cell DNA sequencing technologies enable whole-genome sequencing of hundreds to thousands of individual cells. Unfortunately, the ultra-low coverage of such technologies has thus far limited their use to the analysis of large CNAs in individual cells (Casasent et al., 2018; Laks et al., 2019; Kim et al., 2018; Navin, 2015; Navin et al., 2011; Zaccaria and Raphael, 2019). While CNAs can often be used to effectively identify distinct clones, the clonal composition of a tumor is not determined solely by CNAs; single-nucleotide mutations are equally important, both in cancer studies and in other applications of single-cell whole-genome sequencing (Gawad et al., 2016). For example, distinct clones may be characterized by the same complement of CNAs but different single-nucleotide mutations, whose identification is thus crucial for recovering the correct clonal composition. Moreover, recent studies (Laks et al., 2019; Zaccaria and Raphael, 2019) showed that whole-genome single-cell DNA sequencing data can be used to identify single-nucleotide mutations by merging large sets of cells into a pseudo-bulk sample. However, such approaches lose the characteristic single-cell resolution provided by such technologies.

Here, we introduced SBMClone, a method that infers clonal composition from single-nucleotide mutations identified in ultra-low coverage whole-genome single-cell DNA sequencing data. Specifically, SBMClone uses SBM inference algorithms to partition cells into distinct clones containing different groups of mutations. While current methods infer the clonal composition by clustering either cells with similar mutation profiles or mutations present in the same sets of cells, SBMClone simultaneously groups both cells and mutations into distinct blocks.

We showed that SBMClone accurately infers clonal composition in simulated datasets of varying complexity with per-cell coverage as low as $0.2\times$. Even on much lower-coverage ($\approx 0.03\times$) data from a breast cancer patient sequenced on the 10X Chromium platform (10X Genomics, 2019), we showed that using a small amount of additional information we can recover clonal compositions that are corroborated by analysis of CNAs (Zaccaria and Raphael, 2019). On single-cell whole-genome DOP-PCR data from a breast cancer patient (Kim et al., 2018), we showed that SBMClone identifies post-treatment tumor cells that were not identified in the original copy-number analysis.

While SBMClone demonstrated the possibility of accurately inferring clonal composition from ultra-low coverage single-cell DNA sequencing data, there are several opportunities for future improvement. First, while our application of SBMClone focused on single-nucleotide mutations, the method could be extended to analyze other types of mutations—such as CNAs or structural variations—either individually or jointly. Indeed, a method that analyzes both single-nucleotide mutations and CNAs could be more powerful to detect low-frequency clones and more robust to the variability and errors in single-cell sequencing data. Second, while the sequencing coverage ($\approx 0.03\times$) of current 10X Genomics single-cell sequencing datasets appears to be insufficient to identify clonal structure using single-nucleotide mutations, our study demonstrates that an approximately eightfold increase in coverage per cell ($\approx 0.24\times$) or the higher coverage obtained by DOP-PCR ($\approx 0.5\times$) is sufficient for SBMClone to identify a subclone present in $\approx$20% of sequenced cells. Even higher coverage may enable accurate inference of clones with lower population frequency; indeed, the copy-number analysis of the same 10X data identified eight clones, including one clone representing <1% (39/4085) of the tumor cells (Zaccaria and Raphael, 2019). Third, while SBMClone infers clonal composition without enforcing any evolutionary constraints, one could incorporate a specific evolutionary model and jointly infer evolutionary structure and clonal composition. Finally, SBMClone could be extended to other applications, such as metagenomics or in vitro evolution studies, in the latter case helping to monitor changes in population dynamics over time.

Financial Support: none declared.

Conflict of Interest: B.J.R. is a cofounder of, and consultant to, Medley Genomics.