LinearPartition: linear-time approximation of RNA folding partition function and base-pairing probabilities

Abstract

Motivation

RNA secondary structure prediction is widely used to understand RNA function. Recently, there has been a shift away from the classical minimum free energy methods to partition function-based methods that account for folding ensembles and can therefore estimate structure and base pair probabilities. However, the classical partition function algorithm scales cubically with sequence length, and is therefore prohibitively slow for long sequences. This slowness is even more severe than cubic-time free energy minimization due to a substantially larger constant factor in runtime.

Results

Inspired by the success of our recent LinearFold algorithm that predicts the approximate minimum free energy structure in linear time, we design a similar linear-time heuristic algorithm, LinearPartition, to approximate the partition function and base-pairing probabilities, which is shown to be orders of magnitude faster than Vienna RNAfold and CONTRAfold (e.g. 2.5 days versus 1.3 min on a sequence with length 32 753 nt). More interestingly, the resulting base-pairing probabilities are even better correlated with the ground-truth structures. LinearPartition also leads to a small accuracy improvement when used for downstream structure prediction on families with the longest length sequences (16S and 23S rRNAs), as well as a substantial improvement on long-distance base pairs (500+ nt apart).

Availability and implementation

Code: http://github.com/LinearFold/LinearPartition; Server: http://linearfold.org/partition.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

RNAs are involved in multiple processes, such as catalyzing reactions or guiding RNA modifications (Bachellerie et al., 2002; Doudna and Cech, 2002; Eddy, 2001), and their functionalities are highly related to structures. However, structure determination techniques, such as X-ray crystallography (Zhang and Ferré-D’Amaré, 2014), nuclear magnetic resonance (Zhang and Keane, 2019) and cryo-electron microscopy (Lyumkis, 2019), though reliable and accurate, are extremely slow and costly. Therefore, fast and accurate computational prediction of RNA structure is useful and desired. Considering full RNA structure prediction is challenging (Miao et al., 2017), many studies focus on predicting secondary structure, the set of canonical base pairs in the structure (A-U, G-C and G-U base pairs) (Tinoco and Bustamante, 1999), as it is well-defined, and provides detailed information to help understand the structure–function relationship, and is a basis to predict full tertiary structure (Flores and Altman, 2010; Seetin and Mathews, 2011).

RNA secondary structure prediction is in general NP-complete (Lyngsø and Pedersen, 2000), but nested (i.e. pseudoknot-free) secondary structures can be predicted with cubic-time dynamic programming algorithms. Commonly, the minimum free energy (MFE) structure is predicted (Nussinov and Jacobson, 1980; Zuker and Stiegler, 1981). At equilibrium, the MFE structure is the most populated structure, but it is a simplification because multiple conformations exist as an equilibrium ensemble for one RNA sequence (Mathews, 2004). For example, many mRNAs in vivo form a dynamic equilibrium and fold into a population of structures (Lai et al., 2018; Long et al., 2007; Lu and Mathews, 2008; Tafer et al., 2008); Figure 1A and B shows the example of Tebowned RNA which folds into more than one structure at equilibrium. In this case, the prediction of one single structure, such as the MFE structure, is not expressive enough to capture multiple states of RNA sequences at equilibrium.

Fig. 1.

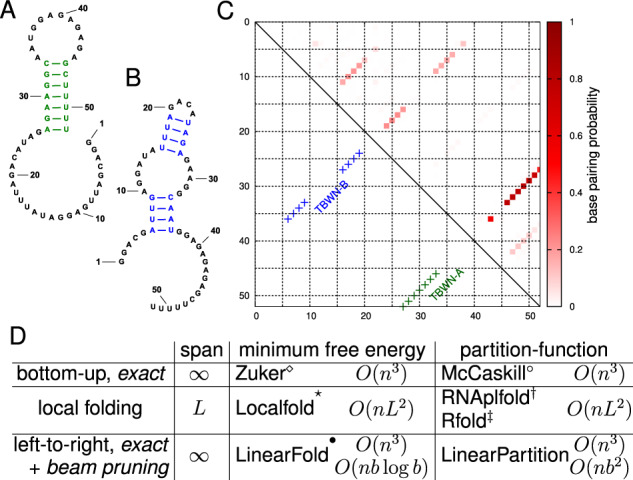
An RNA can fold into multiple structures at equilibrium. (A and B) Two secondary structures of Tebowned RNA: TBWN-A and TBWN-B (Cordero and Das, 2015). (C) Upper triangle shows the estimated base-pairing probability matrix for this RNA using Vienna RNAfold, where darker red squares represent higher probability base pairs; the lower triangle shows the two different structures; (D) Comparison between classical, local, and left-to-right algorithms for MFE and partition function calculation. ${}^{\diamond }$(Zuker and Stiegler, 1981), °(McCaskill, 1990), *(Lange et al., 2012), ${}^{†}$(Bernhart et al., 2006a), ${}^{‡}$(Kiryu et al., 2008) and ${}^{•}$(Huang et al., 2019). LinearFold and LinearPartition enjoy linear runtime because of a left-to-right order that enables heuristic beam pruning, and both become exact $O(n^3)$ algorithms without pruning. ‘Span’ denotes the window size (max. pair distance) ($\infty$ means no limit); it is a small constant in local methods (e.g. default L= 70 nt in RNAplfold)

Alternatively, we can compute the partition function, which is the sum of the equilibrium constants for all possible secondary structures, and is the normalization term for calculating the probability of a secondary structure in the Boltzmann ensemble. The partition function calculation can also be used to calculate base-pairing probabilities of each nucleotide i paired with each of possible nucleotides j (McCaskill, 1990; Mathews, 2004). In Figure 1C, the upper triangle presents the base-pairing probability matrix of Tebowned RNA using Vienna RNAfold, showing that base pairs in Tebowned RNA (TBWN)-A have higher probabilities (in darker red) than base pairs in TBWN-B (in lighter red). This is consistent with the experimental result, i.e. TBWN-A is the majority structure that accounts for 56% ± 16% of the ensemble, whereas TBWN-B takes up 27% ± 12% (Cordero and Das, 2015).

In addition to modeling multiple states at equilibrium, base-pairing probabilities are used for downstream prediction methods, such as maximum expected accuracy (MEA; Do et al., 2006; Knudsen and Hein, 2003), to assemble a structure with improved accuracy compared with the MFE structure (Lu et al., 2009). Other prediction methods, such as ProbKnot (Bellaousov and Mathews, 2010), ThreshKnot (Zhang et al., 2019), DotKnot (Sperschneider and Datta, 2010) and IPknot (Sato et al., 2011), use base-pairing probabilities to predict pseudoknotted structures with heuristics, which is beyond the scope of standard cubic-time algorithms. Additionally, the partition function is the basis of stochastic sampling, in which structures are sampled with their probability of occurring in the Boltzmann ensemble (Ding and Lawrence, 2003; Mathews, 2006).

Therefore, there has been a shift from the classical MFE-based methods to partition function-based ones. These latter methods, as well as the prediction engines based on them, such as partition function-mode of RNAstructure (Mathews and Turner, 2006), Vienna RNAfold (Lorenz et al., 2011) and CONTRAfold (Do et al., 2006), are all based on the seminal algorithm that McCaskill pioneered (McCaskill, 1990). It employs a dynamic program to capture all possible (exponentially many) nested structures, but its $O(n^3)$ runtime still scales poorly for longer sequences. This slowness is even more severe than the $O(n^3)$-time MFE-based ones due to a much larger constant factor. For instance, for Helicobacter pylori 23S rRNA (sequence length 2968 nt), Vienna RNAfold’s computation of the partition function and base-pairing probabilities is 9× slower than MFE (71 versus 8 s), and CONTRAfold is even 20× slower (120 versus 6 s). The slowness prevents their applications to longer sequences.

To address this $O(n^3)$-time bottleneck, we present LinearPartition, which is inspired by our recently proposed LinearFold algorithm (Huang et al., 2019) that approximates the MFE structure in linear time. Using the same idea, LinearPartition can approximate the partition function and base-pairing probability matrix in linear time. Like LinearFold, LinearPartition scans the RNA sequence from 5′-to-3′ using a left-to-right dynamic program that runs in $O(n^3)$ time, but unlike the classical bottom-up McCaskill algorithm (McCaskill, 1990) with the same speed, our left-to-right scanning makes it possible to apply the beam pruning heuristic (Huang and Sagae, 2010) to achieve linear runtime in practice (see Fig. 1D). Although the search is approximate, the well-designed heuristic ensures the surviving structures capture the bulk of the free energy of the ensemble. It is important to note that, unlike local folding methods in Figure 1D, our algorithm does not impose any limit on the base-pairing distance; in other words, it is a global partition function algorithm.

More interestingly, as Figure 2 shows, even with the $O(n^3)$-time McCaskill algorithm, the resulting number of base pairings with reasonable probabilities (e.g. >0.001) grows only linearly with the sequence length. This suggests that our algorithm, which only computes O(n) pairings by design, is a reasonable approximation.

Fig. 2.

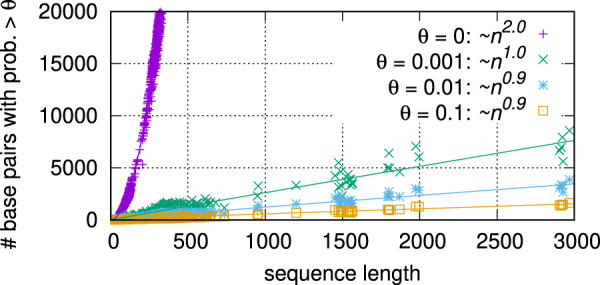
Although the total number of possible base pairings scales $O(n^2)$ with the sequence length n (using the probability matrix from Vienna RNAfold as an example), with any reasonable threshold θ, the number of surviving pairings (in colors for different θ) grows linearly, suggesting our approximation, only computing O(n) pairings, is reasonable

LinearPartition is 2771× faster than CONTRAfold for the longest sequence (32 753 nt) that CONTRAfold can run in the dataset (2.5 days versus 1.3 min.). Interestingly, LinearPartition is orders of magnitude faster without sacrificing accuracy. In fact, the resulting base-pairing probabilities are even better correlated with ground-truth structures, and when applied to downstream structure prediction tasks, they lead to a small accuracy improvement on longer families (small and large subunit rRNAs), as well as a substantial improvement on long-distance base pairs (500+ nt apart).

Although LinearPartition is inspired by LinearFold in many ways, the success of the former is not obvious at all given the latter. This is because, rather than finding one single optimal structure, LinearPartition needs to sum up exponentially many structures that capture the bulk part of the ensemble free energy. There are many algorithmic techniques that can speed up the search for the optimal or near-optimal solution (e.g. sparse folding; Backofen et al., 2011), but very few can speed up the summation of all solutions (see Section 4 for details). In addition, LinearPartition also results in more accurate downstream structure predictions than LinearFold.

Local partition function calculation algorithms (Bernhart et al., 2006a; Kiryu et al., 2008), on the other hand, also achieve linear runtime but can only consider pairs up to a fixed window size. More importantly, they cannot output the partition function or Boltzmann probabilities. Our work is the first to achieve linear runtime without constraints on pair distance, and can still output the partition function and Boltzmann probabilities, making it possible to do stochastic sampling (Ding and Lawrence, 2003).

2 The LinearPartition algorithm

We denote $\mathbf{x}=x_1\dots x_n$ as the input RNA sequence of length n, and $\mathcal{Y}(\mathbf{x})$ the set of all possible secondary structures of x. The partition function is:

$$Q(\mathbf{x})=\sum _{\mathbf{y}\in \mathcal{Y}(\mathbf{x})}{e}^{-\frac{\Delta G^{°}(\mathbf{y})}{RT}},$$

where $\Delta G^{°}(\mathbf{y})$ is the conformational Gibbs free energy change of structure y, R is the universal gas constant and T is the thermodynamic temperature. $\Delta G^{°}(\mathbf{y})$ is calculated using loop-based Turner free-energy model (Mathews et al., 1999, 2004), but for presentation reasons, we use a revised Nussinov–Jacobson energy model, i.e. a free energy change of $\delta (\mathbf{x},j)$ for unpaired base at position j and a free energy change of $\xi (\mathbf{x},i,j)$ for base pair of (i, j). For example, we can assign $\delta (\mathbf{x},j)=1$ kcal/mol and $\xi (\mathbf{x},i,j)=-3$ kcal/mol for CG pairs and −2 kcal/mol for AU and GU pairs. Thus, $\Delta G^{°}(\mathbf{y})$ can be decomposed as:

$$\Delta G^{°}(\mathbf{y})=\sum _{j\in \text{unpaired}(\mathbf{y})}\delta (\mathbf{x},j)+\sum _{(i,j)\in \text{pairs}(\mathbf{y})}\xi (\mathbf{x},i,j),$$

where $\text{unpaired}(\mathbf{y})$ is the set of unpaired bases in y, and $\text{paired}(\mathbf{y})$ is the set of base pairs in y. The partition function now decomposes as:

$$Q(\mathbf{x})=\sum _{\mathbf{y}\in \mathcal{Y}(\mathbf{x})}\left(\prod _{j\in \text{unpaired}(\mathbf{y})}{e}^{-\frac{\delta (\mathbf{x},j)}{RT}}\prod _{(i,j)\in \text{pairs}(\mathbf{y})}{e}^{-\frac{\xi (\mathbf{x},i,j)}{RT}}\right).$$

We first define span$[i,j]$ to be the subsequence $x_i\dots x_j$ (thus $[1,n]$ denotes the whole sequence x, and $[j,j-1]$ denotes the empty span between $x_{j-1}$ and x_j for any j in $\mathrm{1..}n$). We then define a state to be a span associated with its partition function:

$$[i,j]:Q_{i,j},$$

where $Q_{i,j}={\sum }_{\mathbf{y}\in \mathcal{Y}(x_i\dots x_j)}{e}^{-\frac{\Delta G^{°}(\mathbf{y})}{RT}}$ encompasses all possible substructures for span $[i,j]$, which can be visualized as

For simplicity of presentation, in the pseudocode in Figure 3, Q is notated as a hash table, mapping from $[i,j]$ to $Q_{i,j}$; see Supplementary Section A for details of its efficient implementation. As the base case, we set $Q_{j,j-1}$ to be 1 for all j, meaning all empty spans have partition function of 1 (Line 4). Our algorithm then scans the sequence from left-to-right (i.e. from 5′-to-3′), and at each nucleotide x_j ($j=\mathrm{1\dots }n$), we perform two actions:

Fig. 3.

Partition function calculation pseudocode of a simplified version of the LinearPartition algorithm [the inside phase; see Supplementary Fig. S1 for the pseudocode of beam pruning (Line 11)]. The base-pairing probabilities are computed with the combination of the outside phase (Supplementary Fig. S2) (see Supplementary Fig. S2 for the version with the Turner model)

• skip (Line 8): We extend each span $[i,j-1]$ in Q to $[i,j]$ by adding an unpaired base $y_j=$‘.’ (in the dot-bracket notation) to the right of each substructure in $Q_{i,j-1}$, updating $Q_{i,j}$:

  $$Q_{i,j} += Q_{i,j-1}·e^{-\frac{\delta (\mathbf{x},j)}{RT}}$$

which can be visualized as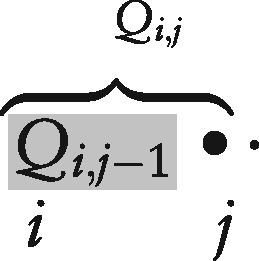

• pop (Lines 9–10): If $x_{i-1}$ and x_j are pairable, we combine span $[i,j-1]$ in Q with each combinable ‘left’ span $[k,i-2]$ in Q and update the resulting span $[k,j]$’s partition function

  $$Q_{k,j} += Q_{k,i-2}·Q_{i,j-1}·e^{-\frac{\xi (\mathbf{x},i-1,j)}{RT}}.$$

This means that every substructure in $Q_{i,j-1}$ can be combined with every substructure in $Q_{k,i-2}$ and a base pair $(i-1,j)$ to form one possible substructure in 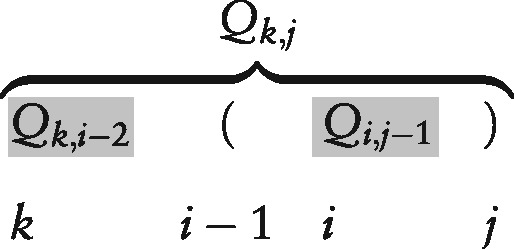$Q_{k,j}$:

Above we presented a simplified version of our left-to-right LinearPartition algorithm. We have three nested loops, one for j, one for i, and one for k, and each loop takes at most n iterations; therefore, the time complexity without beam pruning is $O(n^3)$, which is identical to the classical McCaskill Algorithm (see Fig. 1D). In fact, there is an alternative, bottom-up, interpretation of our left-to-right algorithm that resembles the Nussinov-style recursion of the classical McCaskill Algorithm:

$$Q_{k,j}=Q_{k,j-1}·e^{-\frac{\delta (\mathbf{x},j)}{RT}}+\sum _{k<i\le j}{Q}_{k,i-2}·Q_{i,j-1}·e^{-\frac{\xi (\mathbf{x},i-1,j)}{RT}}.$$

However, unlike the classical bottom-up McCaskill algorithm, our left-to-right dynamic programming, inspired by LinearFold, makes it possible to further apply the beam pruning heuristic to achieve linear runtime in practice. The main idea is, at each step j, among all possible spans $[i,j]$ that ends at j (with $i=\mathrm{1\dots }j$), we only keep the top b most promising candidates (b is the beam size), ranked by their partition functions $Q_{i,j}$ combined with the corresponding ‘prefix’ partition function for span $[1,i-1]$, i.e. states are ranked by $Q_{1,i-1}·Q_{i,j}$, in order to be fair for spans of different lengths (see Supplementary Fig. S1 for pseudocode). With such beam pruning, we reduce the number of states from $O(n^2)$ to O(nb), and the runtime from $O(n^3)$ to $O(n{b}^2)$. For details of the efficient implementation and runtime analysis, please refer to Supplementary Section A. Note b is a user-adjustable constant ($b=$100 by default).

After the partition-function calculation, also known as the ‘inside’ phase of the classical inside-outside algorithm (Baker, 1979), we design a similar linear-time ‘outside’ phase (see Supplementary Section SA.3) to compute the ‘outside’ partition function (only for those spans that survived the beam pruning in the ‘inside’ phase) and the base-pairing probabilities:

$$p_{i,j}=\sum _{\mathbf{y}\in \mathcal{Y}(\mathbf{x}),(i,j)\in \text{pairs}(\mathbf{y})}p(\mathbf{y}),$$

where $p_{i,j}$ is the probability of nucleotide i pairing with j, which sums up the probabilities of all structures that contain that pair, and $p(\mathbf{y})=e^{-\frac{\Delta G^{°}(\mathbf{y})}{RT}}/Q(\mathbf{x})$ is y’s Boltzmann probability in the ensemble.

3 Results

3.1 Efficiency and scalability

We present two versions of LinearPartition: LinearPartition-V using thermodynamic parameters (Mathews et al., 1999, 2004; Xia et al., 1998) following Vienna RNAfold (Lorenz et al., 2011), and LinearPartition-C using the learning-based parameters from CONTRAfold (Do et al., 2006). We benchmark on a Linux machine with 2.90 GHz Intel i9-7920X CPU and 64 G memory. We use RNAs from two datasets, ArchiveII (Mathews et al., 1999; Sloma and Mathews, 2016) [excluding 957 sequences from S-Processed dataset (Andronescu, 2007)] and RNAcentral (RNAcentral Consortium et al., 2017). See Supplementary Section B.1 for details of the datasets.

Figure 4 compares the efficiency and scalability between the two baselines, Vienna RNAfold and CONTRAfold, and our two versions, LinearPartition-V and LinearPartition-C. To make the comparison fair, we disable the downstream tasks (MEA prediction in CONTRAfold, and centroid prediction and visualization in RNAfold) which are by default enabled. Figure 4A shows that both LinearPartition-V and LinearPartition-C scale almost linearly with sequence length n. The runtime deviation from exact linearity is due to the relatively short sequence lengths in the ArchiveII dataset, which contains a set of sequences with well-determined structures (Sloma and Mathews, 2016). Figure 4A also confirms that the baselines scale cubically and the $O(n^3)$ runtimes are substantially slower than LinearPartition on long sequences. For the H.pylori 23S rRNA sequence (2968 nt, the longest in ArchiveII), both versions of LinearPartition take only 6 s, while RNAfold and CONTRAfold take 73 and 120 s, respectively.

Fig. 4.

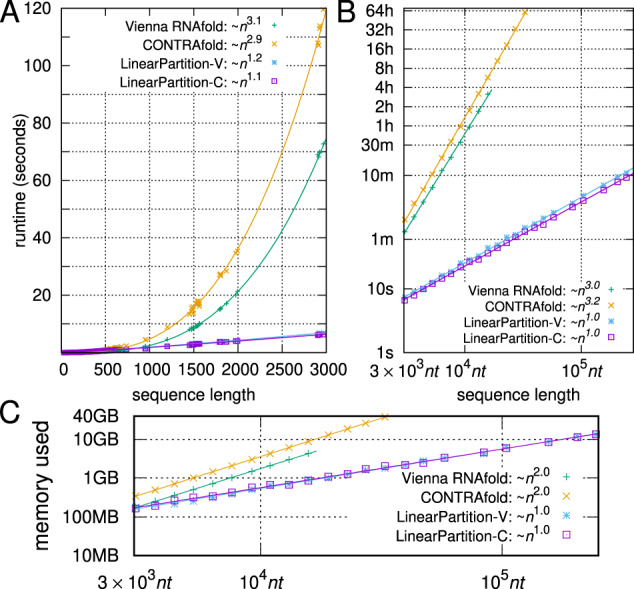
Total runtime and memory usage of computing both the partition function and base-pairing probabilities. (A) Runtime comparisons on the ArchiveII dataset; the curve-fittings were log-log in gnuplot with $n>{10}^3$. (B) Runtime comparisons on the RNAcentral dataset (log scale). The partition function computation takes about half of the total time shown here. (C) Memory usage comparisons on the RNAcentral dataset (log scale)

We also notice that both RNAfold and CONTRAfold have limitations on even longer sequences. RNAfold scales the magnitude of the partition function using a constant estimated from the MFE of the given sequence to avoid overflow, but overflows still occur on long sequences. For example, it overflows on the 19 071 nt sequence in the sampled RNAcentral dataset. CONTRAfold stores the logarithm of the partition function to solve the overflow issue, but cannot run on sequences longer than 32 767 nt due to using unsigned short to index sequence positions. LinearPartition, like CONTRAfold, performs computations in the log-space, but can run on all sequences in the RNAcentral dataset. Figure 4B compares the runtime of four systems on a sampled subset of RNAcentral dataset, and shows that on longer sequences the runtime of LinearPartition is exactly linear. For the 15 780 nt sequence, the longest example shown for RNAfold, LinearPartition-V is 256× faster (more than 3 h versus 44.1 s). Note that RNAfold may not overflow on some longer sequences, where LinearPartition-V should enjoy an even more salient speedup. For the longest sequence that CONTRAfold can run (32 753 nt) in the dataset, LinearPartition is 2771× faster (2.5 days versus 1.3 min.). Even for the longest sequence in RNAcentral [Homo sapiens Transcript NONHSAT168677.1 with length 244 296 nt (Zhao et al., 2016)], both LinearPartition versions finish in ∼10 min.

Figure 4C shows that RNAfold and CONTRAfold use $O(n^2)$ space while LinearPartition uses O(n).

Now that we have established the speed of LinearPartition, we move on to the quality of its output.

3.2 Correlation with ground-truth structures

We use ensemble defect (Zadeh et al., 2010; Fig. 5A and B) to represent the quality of the Boltzmann distribution. It is the expected number of incorrectly predicted nucleotides over the whole ensemble at equilibrium, and formally, for a sequence x and its ground-truth structure ${\mathbf{y}}^{*}$, the ensemble defect is

$$\Phi (\mathbf{x},{\mathbf{y}}^{*})=\sum _{\mathbf{y}\in \mathcal{Y}(\mathbf{x})}p(\mathbf{y})·d(\mathbf{y},{\mathbf{y}}^{*}),$$ (1)

where $p(\mathbf{y})$ is the probability of structure y in the ensemble $\mathcal{Y}(\mathbf{x})$, and $d(\mathbf{y},{\mathbf{y}}^{*})$ is the distance between y and ${\mathbf{y}}^{*}$, defined as the number of incorrectly predicted nucleotides in y:

$$\begin{array}{c}d(\mathbf{y},{\mathbf{y}}^{*})=\left|\mathbf{x}\right|-|\text{pairs}(\mathbf{y})\cap \text{pairs}({\mathbf{y}}^{*})|\hfill \\ -|\text{unpaired}(\mathbf{y})\cap \text{unpaired}({\mathbf{y}}^{*})|.\hfill \end{array}$$

Fig. 5.

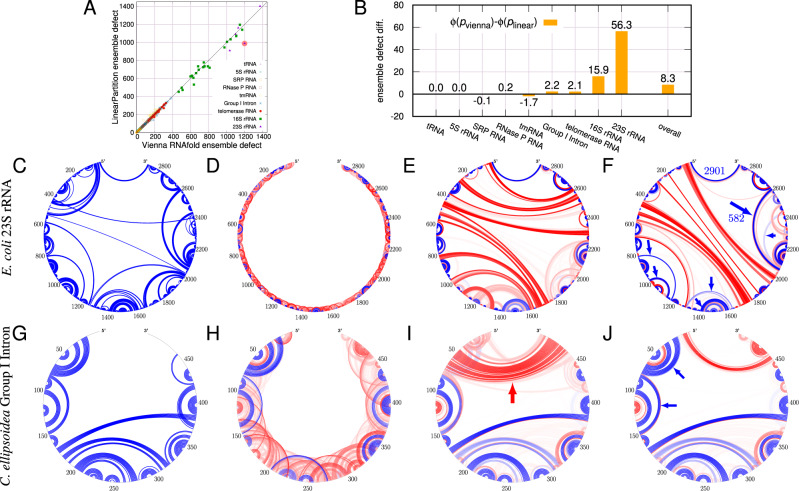
(A) Ensemble defect (expected number of incorrectly predicted nucleotides; lower is better) comparison between Vienna RNAfold and LinearPartition on the ArchiveII dataset. (B) Ensemble defect difference for each family. LinearPartition has lower ensemble defects for longer families: on average 56.3 less incorrectly predicted nucleotides on 23S rRNA and 8.3 less over all families. An example of E.coli 23S rRNA (shaded point in A). (C) Circular plot of the ground truth. (D–F) Base pair probabilities from RNAplfold (with default window size 70), RNAfold and LinearPartition, respectively; Blue denotes pairs in the known structure and Red denotes predicted pairs not in the known structure. The darkness of the line indicates pairing probability (G–J). Circular plots of C.ellipsoidea Group I Intron (see Fig. 6 for another view of this example)

The naïve calculation of Equation (1) requires enumerating all possible structures in the ensemble, but by plugging $d(\mathbf{y},{\mathbf{y}}^{*})$ into Equation (1) we have

$$\begin{array}{c}\Phi (\mathbf{x},{\mathbf{y}}^{*})=\left|\mathbf{x}\right|-2\sum _{(i,j)\in \text{pairs}({\mathbf{y}}^{*})}{p}_{i,j}-\sum _{j\in \text{unpaired}({\mathbf{y}}^{*})}{q}_j\hfill \end{array},$$

where $p_{i,j}$ is the probability of i pairing with j and q_j is the probability of j being unpaired, i.e. $q_j=1-\sum p_{i,j}$. This means we can now use base-pairing probabilities to compute the ensemble defect.

Figure 5A and B employs ensemble defect to measure the average number of incorrectly predicted nucleotides over the whole ensemble (lower is better). RNAfold and LinearPartition have similar ensemble defects for short sequences, but LinearPartition has lower ensemble defects for longer sequences, especially 16S and 23S rRNAs; in other words, LinearPartition’s ensemble has less expected number of incorrectly predicted nucleotides (or higher number of correctly predicted nucleotides). In particular, on 16S and 23S rRNAs, LinearPartition has on average 15.9 and 56.3 more correctly predicted nucleotides than RNAfold, and on average 8.3 more correctly predicted nucleotides over all families (Fig. 5B). Supplementary Figure S3 shows the relative ensemble defects (normalized by sequence lengths), where the same observations hold, and LinearPartition has on average 0.4% more correctly predicted nucleotides over all families. In both cases, the differences on tmRNA (worse) and Group I Intron (better) are statistically significant ().

This finding also implies that LinearPartition’s base-pairing probabilities are on average higher than RNAfold’s for ground-truth base pairs, and on average lower for incorrect base pairs. We use two concrete examples to illustrate this. First, we plot the ground-truth structure of Escherichia coli 23S rRNA (2904 nt) in Figure 5C, and then plot the predicted base-pairing probabilities from the local folding tool RNAplfold (with default window size 70), RNAfold, and LinearPartition in Figure 5D–F, respectively. We can see that local folding can only produce local pairing probabilities, while RNAfold misses most of the long-distance pairs from the ground-truth (except the 5′–3′ helix), and includes many incorrect long-distance pairings (shown in red). In contrast, LinearPartition successfully predicts many long-distance pairings that RNAfold misses, the longest being 582 nt apart (shown with arrows). Indeed, the ensemble defect of this example confirms that LinearPartition’s ensemble distribution has on average 211.4 more correctly predicted nucleotides (over 2904 nt, or 7.3%) than RNAfold’s.

As the second example, we use Corymnbia ellipsoidea Group I Intron (504 nt). First, in Figure 5G–J, we plot the circular plots in the same style as the previous example, where LinearPartition is substantially better in predicting four helices in the ground-truth structure: [17,24]–[72,79], [30,45]–[66,71], [44,48]–[54,58] and [80,83]–[148,151] (annotated with blue arrows). Next, in Figure 6A, we plot the base pairs (in triangle) and unpaired bases (in circle) with RNAfold probability on x-axis and LinearPartition probability on y-axis. We color the circles and triangles in blue where LinearPartition gives 0.2 higher probability than RNAfold (top left region), the opposite ones (bottom right region) in red, and the remainder (diagonal region, with probability changes < 0.2) in green. Then in Figure 6B, we visualize the ground-truth structure (Cannone et al., 2002) and color the bases as in Figure 6A. We observe that the majority of bases are in green, indicating that RNAfold and LinearPartition agree with for a majority of the structure features. But, the blue helices (near 5′-end and [80,83]–[148,151], see also Fig. 5J) indicate that LinearPartition favors these correct substructures by giving them higher probabilities than RNAfold. We also notice that all red features (where RNAfold does better than LinearPartition) are unpaired bases. This example shows that although LinearPartition and RNAfold give different probabilities, it is likely that LinearPartition prediction structure is closer to the ground-truth structure (which will be confirmed by downstream structure predictions in Section 3.3). The ensemble defect of this example also confirms that LinearPartition has on average 47.1 more correctly predicted nucleotides (out of 504 nt, or 9.3%) than RNAfold.

Fig. 6.

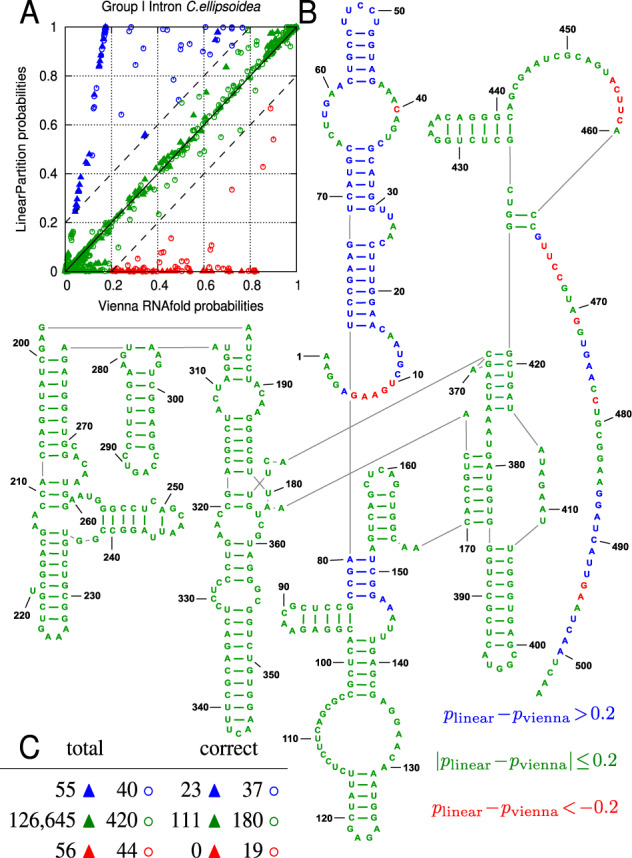
An example of C.ellipsoidea Group I Intron. (A) Solid triangles (▲ ▲ ▲) stand for base-pairing probabilities and unfilled circles (° ° °) stand for single-stranded probabilities. blue: $p_{\text{linear}}-p_{\text{vienna}}>0.2$; green: $|p_{\text{linear}}-p_{\text{vienna}}|\le 0.2$; red: $p_{\text{linear}}-p_{\text{vienna}}<-0.2$; (B) Ground-truth structure colored with the above scheme; (C) Statistics of this example. ‘Total’ columns are the total numbers of triangles and circles with different colors in (A), while ‘correct’ columns are the corresponding numbers in the ground-truth structure in (B), which is better correlated with LinearPartition’s probabilities than Vienna RNAfold’s (23 blue pairs and 0 red pairs)

Figure 6C gives the statistics of this example. We can see the green triangles in Figure 6A, which denote similar probabilities between RNAfold and LinearPartition are the vast majority. The total number of blue triangles, for which LinearPartition gives higher base-pairing probabilities, is 55, and among them 23 (41.8%) are in the ground-truth structure. On the contrary, 56 triangles are in red, but none of these RNAfold preferred base pairs are correct. For unpaired bases, LinearPartition also gives higher probabilities to more ground-truth unpaired bases: there are 40 blue circles, among which 37 (92.5%) are unpaired in the ground-truth structure, while only 19 out of the 44 red circles (43.2%) are in the ground-truth structure.

3.3 Accuracy of downstream predictions

An important application of the partition function is to improve structure prediction accuracy (over MFE) using base-pairing probabilities. Here we use two such ‘downstream prediction’ methods, MEA (Do et al., 2006) and ThreshKnot (Zhang et al., 2019) which is a thresholded version of ProbKnot (Bellaousov and Mathews, 2010), and compare their results using base-pairing probabilities from $O(n^3)$-time baselines and our O(n)-time LinearPartition. We use positive predictive value (PPV, the fraction of predicted pairs in the known structure, a.k.a. precision) and sensitivity (the fraction of known pairs predicted, a.k.a. recall) as accuracy measurements for each family, and get overall accuracy be averaging over families. When scoring accuracy, we allow base pairs to differ by one nucleotide in position (Mathews et al., 1999). We compare RNAfold and LinearPartition-V on the ArchiveII dataset in the main text, and provide the CONTRAfold versus LinearPartition-C comparisons in the Supplementary Figures S5 and S6.

Figure 7A shows MEA predictions (RNAfold + MEA and LinearPartition + MEA) are more accurate than MFE ones (RNAfold MFE and LinearFold-V), but more importantly, LinearPartition + MEA consistently outperforms RNAfold + MEA in both PPV and sensitivity with the same γ, a hyperparameter that balances PPV and sensitivity in MEA algorithm.

Fig. 7.

Accuracy of downstream prediction (MEA) using base-pairing probabilities from Vienna RNAfold and LinearPartition on the ArchiveII dataset. (A) Overall PPV-Sensitivity tradeoff of MFE (single point) and MEA with varying γ (which can be tuned for higher sensitivity or PPV by adjusting γ). (B and C) PPV and Sensitivity comparisons of MEA structures for each family. (D) Accuracy comparison of long-distance base pairs (>500 nt apart) in the MEA structures. We conclude that MEA predictions based on LinearPartition-V are consistently better in both PPV and Sensitivity than those based on Vienna RNAfold for all γ’s. LinearPartition-V is substantially better on long-range base pairs in MEA predictions

Figure 7B and C details the per-family PPV and sensitivity, respectively, for MFE and MEA ($\gamma =1.5$) results from Figure 7A. LinearPartition + MEA has similar PPV and sensitivity as RNAfold + MEA on short families (tRNA, 5S rRNA and SRP), but interestingly, is more accurate on longer families, especially the two longest ones, 16S rRNA (+0.86 on PPV and +1.29 on sensitivity) and 23S rRNA (+0.88 on PPV and +0.62 on sensitivity).

ProbKnot is another downstream prediction method that is simpler and faster than MEA; it assembles base pairs with reciprocal highest pairing probabilities. Recently, we demonstrated ThreshKnot (Zhang et al., 2019), a simple thresholded version of ProbKnot that only includes pairs that exceed the threshold, leads to more accurate predictions that outperform MEA by filtering out unlikely pairs, i.e. those whose probabilities fall under a given threshold θ.

As shown in Supplementary Figure S4A, LinearPartition + ThreshKnot is almost identical in overall accuracy to RNAfold + ThreshKnot at all θ’s, and is slightly better than the latter on long families (+0.24 on PPV and +0.38 on sensitivity for Group I Intron, +0.12 and +0.37 for telomerase RNA, and +0.74 and +0.62 for 23S rRNA; Supplementary Fig. S4B and C). We also perform a two-tailed permutation test (Aghaeepour and Hoos, 2013) to test the statistical significance, and observe that on tmRNA, both MEA and ThreshKnot structures of LinearPartition are significantly worse (p < 0.01) than their RNAfold-based counterparts in both PPV and Sensitivity.

Figure 7D and Supplementary Figure S4D show that LinearPartition-based predictions are subtantially better than RNAfold’s (in both PPV and sensitivity) for long-distance base pairs (those with 500+ nt apart), which are well known to be challenging for the current models. Supplementary Figure S7 details the accuracies on base pairs with different distance groups.

Supplementary Figures S5 and S6 show similar comparisons between CONTRAfold and LinearPartition-C using MEA and ThreshKnot prediction, with similar results to Figure 7 and Supplementary Figure S4, i.e. downstream structure prediction using LinearPartition-C is as accurate as using CONTRAfold, and (sometimes significantly) more accurate on longer families.

3.4 Approximation quality (default beam size)

LinearPartition uses beam pruning to ensure O(n) runtime, thus is approximate compared with standard $O(n^3)$-time algorithms. We now investigate its approximation quality at the default beam size 100.

First, in Figure 8, we measure the approximation quality of the partition function calculation, in particular, the ensemble folding free energy change (also known as ‘free energy of the ensemble’) which reflects the size of the partition function,

$$\Delta G_{\text{ensemble}}^{°}(\mathbf{x})=-RT\hspace{0.17em}\text{log}\hspace{0.17em}Q(\mathbf{x}).$$

Fig. 8.

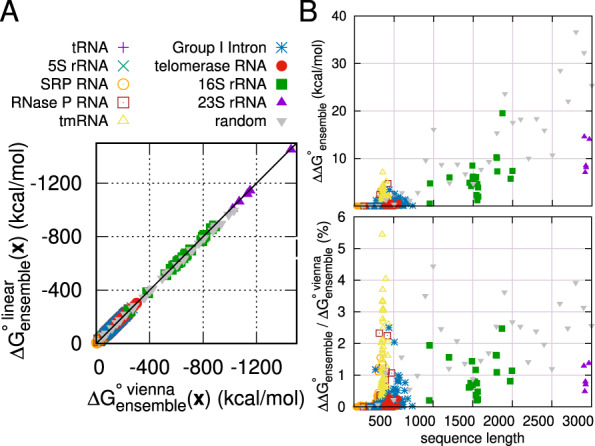
Approximation quality of partition function on ArchiveII dataset and random sequences. (A) The x and y axes are ensemble folding free energy changes $\Delta G_{\text{ensemble}}^{°}(\mathbf{x})$ of Vienna RNAfold and LinearPartition, respectively. (B) Difference of ensemble folding free energy change (top), $\Delta \Delta G_{\text{ensemble}}^{°}(\mathbf{x})$, between RNAfold and LinearPartition. and the relative differences (bottom), $\Delta \Delta G_{\text{ensemble}}^{°}(\mathbf{x})/\Delta G_{\text{ensemble}}^{°\hspace{0.17em}\text{vienna}}(\mathbf{x})$, in percentages

Figure 8A shows that the LinearPartition estimate for the ensemble folding free energy change is close to the RNAfold estimate on the ArchiveII dataset and randomly generated RNA sequences. The similarity shows that little magnitude of the partition function is lost by the beam pruning. For short families, free energy of ensembles between LinearPartition and RNAfold are almost the same. For 16S and 23S rRNA sequences and long random sequences (longer than 900 nt), LinearPartition gives a lower magnitude ensemble free energy change, but the difference,

$$\Delta \Delta G_{\text{ensemble}}^{°}(\mathbf{x})=\Delta G_{\text{ensemble}}^{°\hspace{0.17em}\text{vienna}}(\mathbf{x})-\Delta G_{\text{ensemble}}^{°\hspace{0.17em}\text{linear}}(\mathbf{x})\ge 0$$

is smaller than 20 kcal/mol for 16S rRNA, 15 kcal/mol for 23S rRNA and 37 kcal/mol for random sequences (Fig. 8B). The maximum difference for random sequence is larger than natural sequences (by 17.2 kcal/mol). This likely reflects the fact that random sequences tend to fold less selectively to probable structures (Fu et al., 2015), and the beam is therefore pruning structures in random that would contribute to the overall folding stability. Figure 8C shows the ‘relative’ differences in ensemble free energy changes, $\Delta \Delta G_{\text{ensemble}}^{°}(\mathbf{x})/\Delta G_{\text{ensemble}}^{°\hspace{0.17em}\text{vienna}}(\mathbf{x})$, are also very small: only up to 2.5% and 1.5% for 16S and 23S rRNAs, and up to 4.5% for random sequences.

Next, in Figure 9, we measure the approximation quality of base-pairing probabilities using root mean square deviation (RMSD) between two probability matrices p and $p\prime$ over the set of all possible Watson–Crick and wobble pairs on a sequence x. We define

$$\begin{array}{c}\text{pairings}\left(\mathbf{x}\right)=\{1\le i<j\le |\mathbf{x}\left|\right|\overline{)} j-i>3 \\ {\mathbf{x}}_i{\mathbf{x}}_j\in \{\text{CG}, \text{GC}, \text{AU}, \text{UA}, \text{GU}, \text{UG}\}\}\end{array}$$

and:

$$\text{RMSD}(p,p\prime )=\sqrt{\frac{1}{|\text{pairings}(\mathbf{x})|}\sum _{(i,j)\in \text{pairings}(\mathbf{x})}{(p_{i,j}-p{\prime }_{i,j})}^2}.$$

Fig. 9.

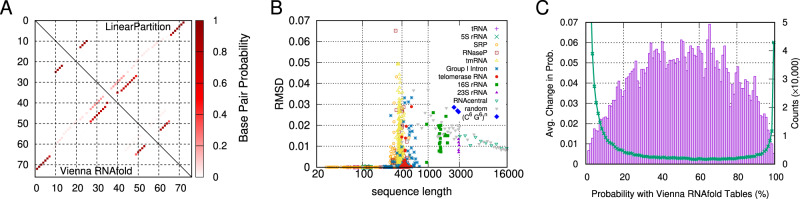
Comparison of base-pairing probabilities from Vienna RNAfold and LinearPartition. (A) LinearPartition (upper triangle) and RNAfold (lower triangle) result in identical base-pairing probability matrix for E.coli tRNA${}^{\mathit{Gly}}$. (B) The $\text{RMSD}(p_{\text{vienna}},p_{\text{linear}})$, is relatively small between RNAfold and LinearPartition; all tRNA and 5S rRNA sequences RMSD is close to 0 (e.g. RMSD$<{10}^{-5}$); the ${({\mathrm{C}}^6{\mathrm{G}}^6)}^n$ (blue diamonds) constructed sequences are repetitions of 6 C’s and 6 G’s. (C) Purple bars show mean absolute value of change in base-pairing probabilities between Vienna RNAfold and LinearPartition (left y-axis); these changes are averaged within every probability bin. The green line shows pair probability distribution of Vienna RNAfold (right y-axis); note that the right y-axis is limited to 50 000 counts, and the counts of first three bins (with probability <3%) are far beyond 50 000

Figure 9A and B confirms that our LinearPartition algorithm (with default beam size 100) can indeed approximate the base-pairing probability matrix reasonably well. Figure 9A shows the heatmap of probability matrices for E.coli tRNA${}^{\mathit{Gly}}$. RNAfold (lower triangle) and LinearPartition (upper triangle) yield identical matrices (i.e. $\text{RMSD}=0$). Figure 9B shows that the RMSD of each sequence in ArchiveII and RNAcentral datasets, and randomly generated artificial RNA sequences, is relatively small. The highest deviation is 0.065 for Ascaphus truei RNase P RNA, which means on average each base pair’s probability deviation in that worst-case sequence is about 0.065 between the cubic algorithm (RNAfold) and our linear-time one (LinearPartition). On the longest 23S rRNA family, the RMSD is about 0.015. We notice that tmRNA is the family with biggest average RMSD. The random RNA sequences behave similarly to natural sequences in terms of RMSD, i.e. RMSD is close to 0 (<10⁻⁵) for short ones, then becomes bigger around length 500 and decreases after that, but for most cases their RMSD’s are slightly larger than the natural sequences. This indicates that the approximation quality is relatively better for natural sequences. For RNAcentral-sampled sequences, RMSD’s are all small and around 0.01.

We hypothesize that LinearPartition reduces the uncertainty of the output distributions because it filters out states with lower partition function. We measure this using average positional structural entropy H(p), which is the average of positional structural entropy $H_2(i)$ for each nucleotide i (Garcia-Martin and Clote, 2015; Huynen et al., 1997):

$$\begin{array}{c}H(p)=\frac{1}{n}\sum _{i=1}^n{H}_2(i)=\frac{1}{n}\sum _{i=1}^n\left(-\sum _{j=0}^n{p}_{i,j}{\hspace{0.17em}\text{log}\hspace{0.17em}}_2{p}_{i,j}\right)\hfill \\ =-\frac{1}{n}\sum _{i=1}^n\sum _{j=0}^n{p}_{i,j}{\hspace{0.17em}\text{log}\hspace{0.17em}}_2{p}_{i,j},\hfill \end{array}$$

where p is the base-pairing probability matrix, and $p_{i,0}$ is the probability of nucleotide i being unpaired (q_i in Equation 1). The lower entropy indicates that the distribution is dominated by fewer base-pairing probabilities. Supplementary Figure S8A confirms LinearPartition distribution shifted to higher probabilities (lower average entropy) than RNAfold for most sequences.

Supplementary Figure S8B uses E.coli 23S rRNA to exemplify the difference in base-pairing probabilities. We sort all these probabilities from high to low and take the top 3000. The LinearPartition curve starts higher and finishes lower, confirming a lower entropy.

Supplementary Figure S8C follows a previous analysis method (Zuber et al., 2017) to estimate the approximation quality with a different perspective. We divide the base-pairing probabilities range [0,1] into 100 bins, i.e. the first bin is for base-pairing probabilities [0,0.01], and the second is for [0.01, 0.02], so on so forth. We visualize the averaged change of base-pairing probabilities between RNAfold and LinearPartition for each bin with purple bars. We can see that larger probability changes are in the middle (bins with probability around 0.5), and smaller changes on the two sides (with probability close to either 0 or 1). We illustrate the counts in each bin based on RNAfold base-pairing probabilities with green dots and line. We can see that most base pairs have low probabilities (near 0) or very high probabilities (near 1). From Figure 9C we can see that probabilities of most base pairs are near 0 or 1, where the differences between RNAfold and LinearPartition are relatively small. Supplementary Figure S9 provides the comparison of counts in each bin between RNAfold and LinearPartition-V. The count of LinearPartition-V in bin [99,100] is slightly higher than RNAfold, while the counts in bins near 0 (being capped at 50 000) are much less than RNAfold. This also confirms that LinearPartition prunes base pairs with tiny probabilities.

3.5 Adjustable beam size

Beam size in LinearPartition is a user-adjustable hyperparameter controlling beam prune, and it balances the approximation quality and runtime. A smaller beam size shortens runtime, but sacrifices approximation quality. With increasing beam size, LinearPartition gradually approaches the classical $O(n^3)$-time algorithm and the output is finally identical to the latter when the beam size is $\infty$ (no pruning). Figure 10A shows the changes in approximation quality of the ensemble free energy change, $\Delta G_{\text{ensemble}}^{°}(\mathbf{x})$, with $b=20\to 300$. Even with a small beam size (b = 20) the difference is only about 5%, which quickly shrinks to 0 as b increases. Figure 10B shows the changes in RMSD with changing b. With a small beam size b = 20 the average RMSD is < 0.035 over all ArchiveII sequences, which shrinks to < 0.005 at the default beam size (b = 100), and almost 0 with b = 500.

Fig. 10.

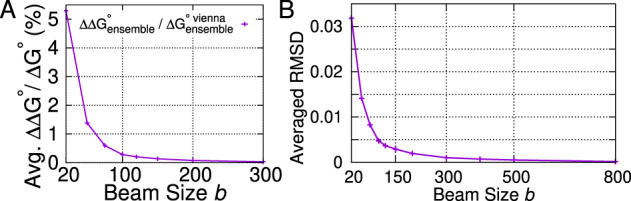
Impact of beam size. (A) Relative difference of ensemble folding free energy change, $\Delta \Delta G_{\text{ensemble}}^{°}/\Delta G_{\text{ensemble}}^{°}$, against beam size. (B) RMSD against beam size

Beam size also has impact on PPV and Sensitivity. Supplementary Figure S10A gives the overall PPV and Sensitivity changes with beam size. We can see both PPV and Sensitivity improve from b = 50 to  100, and then become stable beyond that. Supplementary Figure S10B and C present this impact for two selected families. Supplementary Figure S10B shows tmRNA’s PPV and Sensitivity both increase when enlarging beam size. Using beam size 200, LinearPartition achieves similar PPV and Sensitivity as RNAfold. However, increasing beam size is not beneficial for all families. Supplementary Figure S10C gives the counterexample of 16S rRNA. We can see both PPV and Sensitivity decrease with b from 50 to 100. After that, Sensitivity drops with no PPV improvement.

LinearFold uses k-best parsing (Huang and Chiang, 2005) to reduce runtime from $O(n{b}^2)$ to $O(nb\hspace{0.17em}\text{log}\hspace{0.17em}b)$ without losing accuracy. Basically, k-best parsing is to find the exact top-k (here $k=b$) states out of b² candidates in $O(b\hspace{0.17em}\text{log}\hspace{0.17em}b)$ runtime. If we applied k-best parsing here, LinearPartition would sum the partition function of only these top-b states instead of the partition function of b² states. This change would introduce a larger approximation error, especially when the differences of partition function between the top-b states and the following states near the pruning boundary are small. Therefore, in LinearPartition we do not use k-best parsing as in LinearFold, and the runtime is $O(n{b}^2)$ instead of $O(nb\hspace{0.17em}\text{log}\hspace{0.17em}b)$.

Finally, we note that the default beam size $b=100$ follows LinearFold and we do not tune it.

4 Discussion

4.1 Summary

The classical McCaskill (1990) algorithm for partition function and base-pairing probabilities calculations are widely used in many studies of RNAs, but its application has been impossible for long sequences (such as full length mRNAs and lncRNAs) due to its cubic runtime. To alleviate this, we design LinearPartition, a linear-time algorithm that dramatically reduces the runtime without sacrificing quality. We confirm that:

1. LinearPartition takes only linear runtime and memory usage, and is orders of magnitude faster on longer sequences (Fig. 4);

2. The base-pairing probabilities produced by LinearPartition are better correlated with the ground-truth structures on average (Figs 5 and 6);

3. When used with downstream structure prediction methods such as MEA and ThreshKnot, LinearPartitionhe base pair probabilities have similar overall accuracy (or even a small improvement on MEA structures) compared with RNAfold, as well as better accuracies on longer families and long-distance base pairs (Fig. 7);

4. LinearPartition has a reasonable approximation quality (Figs 8 and 9) in terms of RMSD.

There are two possible reasons why our approximation results in better base-pairing probabilities:

1. This is consistent with the findings in LinearFold, where approximate folding via beam search yields more accurate structures.

2. LinearPartitionin pruning of low-probability (sub)structures has a ‘regularization’ effect. It eliminates some noise in the current energy model which is highly inaccurate, especially for long-distance interactions.

The success of LinearPartition is arguably more striking than LinearFold, since the former needs to sum up exponentially many structures that capture the bulk part of the ensemble free energy, while the latter only needs to find one single optimal structure.

4.2 Extensions

Our work has potential extensions.

1. Existing methods and tools for bimolecular and multistrand base-pairing probabilities as well as accessibility computation (Bernhart et al., 2006b; Chitsaz et al., 2009; DiChiacchio et al., 2016; Dirks et al., 2007) are rather slow, which limits their applications on long sequences. LinearPartition will likely provide a much faster solution for these problems.

2. We will linearize the partition function-based heuristic methods for pseudoknot prediction such as IPknot and Dotknot. These heuristic methods use rather simple criteria to choose pairs from the base-pairing probability matrix, and their runtime bottleneck is still the $O(n^3)$-time calculation of the base-pairing probabilities. With LinearPartition we can overcome the costly bottleneck to get an overall much faster tool.

3. We can also speed up stochastic sampling of RNA secondary structures from Boltzmann distribution. The standard stochastic sampling algorithm runs in worst-case $O(n^2)$ time (Ding and Lawrence, 2003), but relies on the classical $O(n^3)$ partition function calculation. With LinearPartition, we can apply stochastic sampling to full length sequences such as mRNAs, and compute their accessibility based on sampled structures.

4.3 Related work

There are other algorithmic efforts to speed up RNA folding and partition function calculation, including sparsification (Backofen et al., 2011; Chitsaz et al., 2013). But our work differs from those efforts in the following ways: (i) our dynamic programming is left-to-right and theirs are bottom-up; (ii) our work guarantees linear runtime while theirs cannot; (iii) our search is inexact while theirs are exact.

A local partition function calculation (Bernhart et al., 2006a; Kiryu et al., 2008), on the other hand, also achieves linear runtime but can only consider pairs up to a fixed window size. Figure 5 shows the difference between the results of RNAplfold and LinearPartition. But more importantly, as pointed out by (Kiryu et al., 2008), RNAplfold only outputs approximate local base-pairing probabilities, because each $p_{i,j}$ is computed as an average over local pairing probabilities $p_{i,j}^{u,L}$ from all windows $[u,u+L]$ that contain the (i, j) pair. We further note that this approximation actually leads to a much more serious problem that the base-pairing probabilities do not normalize. Indeed, Supplementary Table S2 shows that, strikingly, almost all sequences in the ArchiveII dataset have at least one nucleotide whose unpaired probability from RNAplfold is negative, and about 40% of nucleotides in all sequences have that problem.

To compare RNAplfold and our work, we cannot use ensemble defect because RNAplfold’s unpaired probabilities can be negative. Furthermore, RNAplfold can only output (approximate) local base pair probabilities, and cannot output the partition function or the Boltzmann probabilities, making it impossible to do stochastic sampling (Ding and Lawrence, 2003).

So we compare the RMSDs. To do a fair comparison between two very different algorithms, we plot in Supplementary Figure S11 the RMSD against runtime, with varying L (window size) for RNAplfold and b (beam size) for LinearPartition. It is clear that LinearPartition can achieve substantially lower RMSDs with the same amount of computing time.

4.4 Limitations

Our work still has the following limitations:

1. We are unable to derive any guarantee of the approximation quality due to the ‘hard beam’ heuristic in pruning (only allowing a fixed number of states in each step). But, we also note that it is this very heuristic that guarantees linear runtime. An approximation guarantee would be possible if we had used a ‘soft beam’ heuristic that allows all states above a threshold to survive, but with the cost of linear runtime.

2. LinearPartition seems to be slightly worse on random sequences than natural sequences, and even worse on some special designed sequences such as ${({\mathrm{C}}^6{\mathrm{G}}^6)}^n$, i.e. repetitions of 6 C’s followed by 6 G’s, which would have rather flat distributions as there are so many competing pairing options. This is because the non-natural sequences tend to fold less selectively to probable structures (Fu et al., 2015), thus their distributions (both Boltzmann and base-pairing probabilities) are ‘flatter’ (i.e. higher entropy). This makes it harder for beam search to capture the bulk part of the ensemble free energy. Figure 9B confirms the RMSDs of ${({\mathrm{C}}^6{\mathrm{G}}^6)}^n$ is higher than random sequences, which are in turn higher than natural sequences.

Author Contributions

L.H. conceived the idea and directed the project. H.Z., L.H., and D.H.M. designed the algorithm, and H.Z. implemented it. D.H.M. guided the evaluation that H.Z. and L.Z. carried out. H.Z., L.H., and D.H.M. wrote the manuscript.

Funding

This work is supported in part by National Institutes of Health (R01 GM076485 to D.H.M.) and National Science Foundation (IIS-1817231 to L.H.).

Acknowledgements

We thank Kaibo Liu for designing the web server, Dezhong Deng for early discussions, and Rhiju Das for integrating LinearPartition into the EteRNA game.

Conflict of Interest: none declared.