Computer modeling tools to understand the causes of preterm birth

Abstract

The mechanical integrity of the soft tissue structures supporting the fetus may play a role in maintaining a healthy pregnancy and triggering the onset of labor. Currently, the level of mechanical loading on the uterus, cervix, and fetal membranes during pregnancy is unknown, and it is hypothesized that the over-stretch of these tissues contributes to the premature onset of contractility, tissue remodeling, and membrane rupture, leading to preterm birth. The purpose of this review article is to introduce and discuss engineering analysis tools to evaluate and predict the mechanical loads on the uterus, cervix, and fetal membranes. Here we will explore the potential of using computational biomechanics and finite element analysis to study the causes of preterm birth and to develop a diagnostic tool that can predict gestational outcome. We will define engineering terms and identify the potential engineering variables that could be used to signal an abnormal pregnancy. We will discuss the translational ability of computational models for the better management of clinical patients. We will also discuss the process of model validation and the limitations of these models. We will explore how we can borrow from parallel engineering fields to push the boundary of patient care so that we can work toward eliminating preterm birth.

Introduction

Preterm birth (PTB) is defined as a live birth that occurs before 37weeks’ gestation.¹ It is the leading cause of death in children under the age of five, reaching1.1million annually.² Each year there are an estimated 500,000 cases of preterm birthintheUS.¹ As many as 95% of cases are intractable to current therapies,³ suggesting the need for continued investigation sand medical discoveries. The average cost of a preterm newborn’s first year of life is over 10 times that of a normal term baby’s ($49,000 vs. $4,500).⁴ Furthermore, PTB often leads to lifelong health complications such as cerebral palsy, asthma, and numerous learning disabilities, and has an estimated societal cost of at least $26 billion in the United States each year.⁵

Throughout gestation, the fetus is supported and protected by biologically active soft tissue structures. These structures send mechanical signals that can trigger tissue remodeling and contractility through mechanosensitive cells(e.g., mechanotransduction). The mechanical integrity of the uterus, cervix, and fetal membranes are critical for a successful pregnancy, where the loss of structural integrity of these tissues is believed to contribute to spontaneous PTB. For example, in the case of cervical insufficiency (CI) the cervix dilates and shortens painlessly in the absence of uterine contractions.⁶ CI is hypothesized to be caused by premature cervical remodeling and softening of the tissue. Preterm labor is believed to be caused, in part, by uterine overdistention, as evidenced by the higher rate of preterm labor for multiple gestations or excessive amniotic fluid.^7,8 A recent study investigated uterine overdistention in nonhuman primates by inflating intra-amniotic balloons. Results showed uterine overdistention caused preterm labor triggering a cascade of cytokines and prostaglandins associated with inflammation.⁹ Premature preterm rupture of membranes (PPROM) occurs due to damage of the collagen in the chorioamnion, causing a mechanical tear in the membrane. Clinical studies show excessive collagen degradation in chorioamnion and amniotic fluid samples that have experienced PPROM.¹⁰ The hypothesized causes of PPROM include an insufficient cervix, hydramnios, trauma, and amniotic fluid infection.¹¹

Characterizing reproductive tissues in real time and accessing organs to measure anatomical and tissue properties throughout gestation is challenging. Hence, a driving engineering motivation is to use biomechanical models of pregnancy to understand the mechanical functions and dysfunctions of the tissues during pregnancy. The purpose of this review article is to introduce and discuss engineering analysis tools to evaluate and predict the mechanical loads on the uterus, cervix, and fetal membranes. Medical imaging such as magnetic resonance imaging (MRI) and ultrasound are minimally invasive, yet provide thorough anatomies of a patient’s anatomy. These anatomies can be implemented in biomechanical models to simulate gestational scenarios without providing any harm to pregnant patients. Here we will explore the potential of using computational biomechanics and finite element analysis to study the causes of preterm birth and to develop a diagnostic tool that can predict gestational outcome.

Engineering definitions

A biomechanical model quantitatively represents the geometry and mechanical properties for a single tissue, organ, or a system of load-bearing tissues and organs. The model aims to solve for the amount of tissue stress and stretch as the result of external mechanical loading. Mechanical models depend on strict definitions of force, deformation, stress, strain, and stretch. We briefly explain them here. The term stress represents the amount of force carried within the tissue normalized by its geometry. It is a three-dimensional term, where the amount of stress will vary depending on the direction. Simply put, stress (σ) is defined as a force (F) per unit area (A), σ F/A, with units of pressure N/m² or Pa in metric and lb/in² or psi in the English unit system. Due to its direction-dependence, there are multiple types of stress: normal stress occurs when the force vector is perpendicular to the surface, and shear stress occurs when the force vector is parallel to the surface. If the force vector is somewhere in between perpendicular and parallel to the surface, both stress components are present. Strain (ε) is a measure of deformation of the tissue due to stress, and it is also normalized by geometry. Because stress is direction-dependent, strain is also direction-dependent. Simply put, it can be expressed as the change in tissue length (Δl) over the original length (l₀), ε =Δl/l₀. Strain is often reported as a percentage. Stretch is similar to strain and is typically used for materials that undergo large deformations, such as soft biological tissues. Stretch (λ) is the ratio between the current length at a given applied force (l) and the original length (l₀) of the material, λ = l/l₀. It is reported as a unitless ratio and not a percentage.

In addition to accurately describe the shape and size, a biomechanical model also requires the mechanical properties of the tissues in the system. Tissue mechanical properties are the quantitative values that relate the amount of tissue stress σ with the amount of strain ε (or stretch λ). This mathematical relationship is called a material model, and the equation parameters are the material properties of the tissue. Material properties are found by isolating the tissue and conducting a series of mechanical tests. The most basic, and often most informative, mechanical test is a uniaxial tensile test. In this test, a uniform piece of tissue is gripped within a material tester by each of its end. The material tester displaces the grips by prescribed displacement values Δl, and the force F is measured as the tissue is pulled in tension. The material tester records force F as a function of grip displacement Δl, and stress σ and strain σ are then derived from these values and are normalized by the cross-sectional area A of the tissue.

The shape and magnitude of the experimental stress σ versus strain ε curve for a given material is the material behavior of the tissue. The mathematical equation describing the material behavior is the material model, where model parameters are tissue material properties (or tissue mechanical properties). Material properties must be strictly defined within each modeling context because the terms such as stiffness and strength have specific meanings in the field of mechanics. The simplest of material behavior is linear elastic, where there is a linear relationship between stress σ versus strain ε This type of material is described by two material parameters: the Young’s modulus E and the Poisson’s ratio ν. The Young’s modulus E of a material is often referred to as the stiffness of a material, and is the slope of the stress σ versus strain ε curve. Material compliance is the inverse of material stiffness 1/E, often thought of as the material’s flexibility. A material that deforms easily is said to be compliant, while a material that resists deformation is said to be stiff. Also identifiable on a stress–strain curve is the strength of a material. Yield strength is the point at which the stress–strain curve begins to deviate from a straight line, and represents the lowest stress that produces permanent deformation of a material. Poisson’s ratio of a material (ν) is the ratio of lateral strain to axial strain when a material is in tension: ν= −(ε_yy=ε_xx): In other words, it is the amount of transverse extension divided by the amount of axial compression. For example, when you stretch a rubber band, the band will become longer, but the width of the band will become narrower. Materials that are truly incompressible have a Poisson’s ratio ν of 0.5, since the sum of all their strains result in zero volume change.

Soft biological tissues have a complex material behavior because the material is made of an intricate network of long-chain proteins, cells, soft ground matrix, and interstitial water.¹² Therefore, it is often not sufficient to use a linear material model because the shape of the stress σ–strain ε curve of a soft tissue is governed by the non-linear, time-dependent, and direction-dependent material behavior of the individual biological components. For example, hydrated collagenous tissues have a soft compliant region when they are first stretched (referred to as the small-strain regime). Then as deformation continues, collagen fibers are recruited and begin to contribute to the tensile stiffness as they become straightened. The resulting stress σ–strain ε curve is non-linear and resembles a J-curve.¹³ Additionally, collagen fibers of organs often have a preferred-directionality and architecture depending on the direction of load they carry in the body. Therefore, the tissue will exhibit different stiffness properties in different directions. This type of a material is called anisotropic. Lastly, a time-dependent tissue will experience different levels of stress depending on the rate of mechanical loading or will continuously deform under a constant level of load in a behavior called creep. These examples provide an insight into the complexity of the mechanical behavior of soft biological tissues, and the material characterization of soft biological tissues represents an active field of study, with research groups aiming to develop microstructurally derived material models that accurately describe tissue material behavior. The most advanced material models aim to describe tissue material property evolution with age, disease, growth, and remodeling.

Finite Element Analysis

For simpler organs that carry a load in a single direction, the biomechanical model to determine tissue stress and stretch can be analytically solved with the standard force balance equations. For a complex system of organs, solving for physiologic tissue stress and stretch requires numerical simplification techniques to solve for the force balance equations. This type of biomechanical model is commonly referred to as a structural finite element analysis (FEA), a numerical technique that discretizes a complex domain to solve the equations of static equilibrium (Fig. 1). FEA has been used in numerous biomechanical fields such as cardiovascular, orthopedics, ocular, brain, and many more.^14–19 FEA was first brought into the field of biomechanics in 1972 to evaluate stresses in human bones.

Fig. 1 –

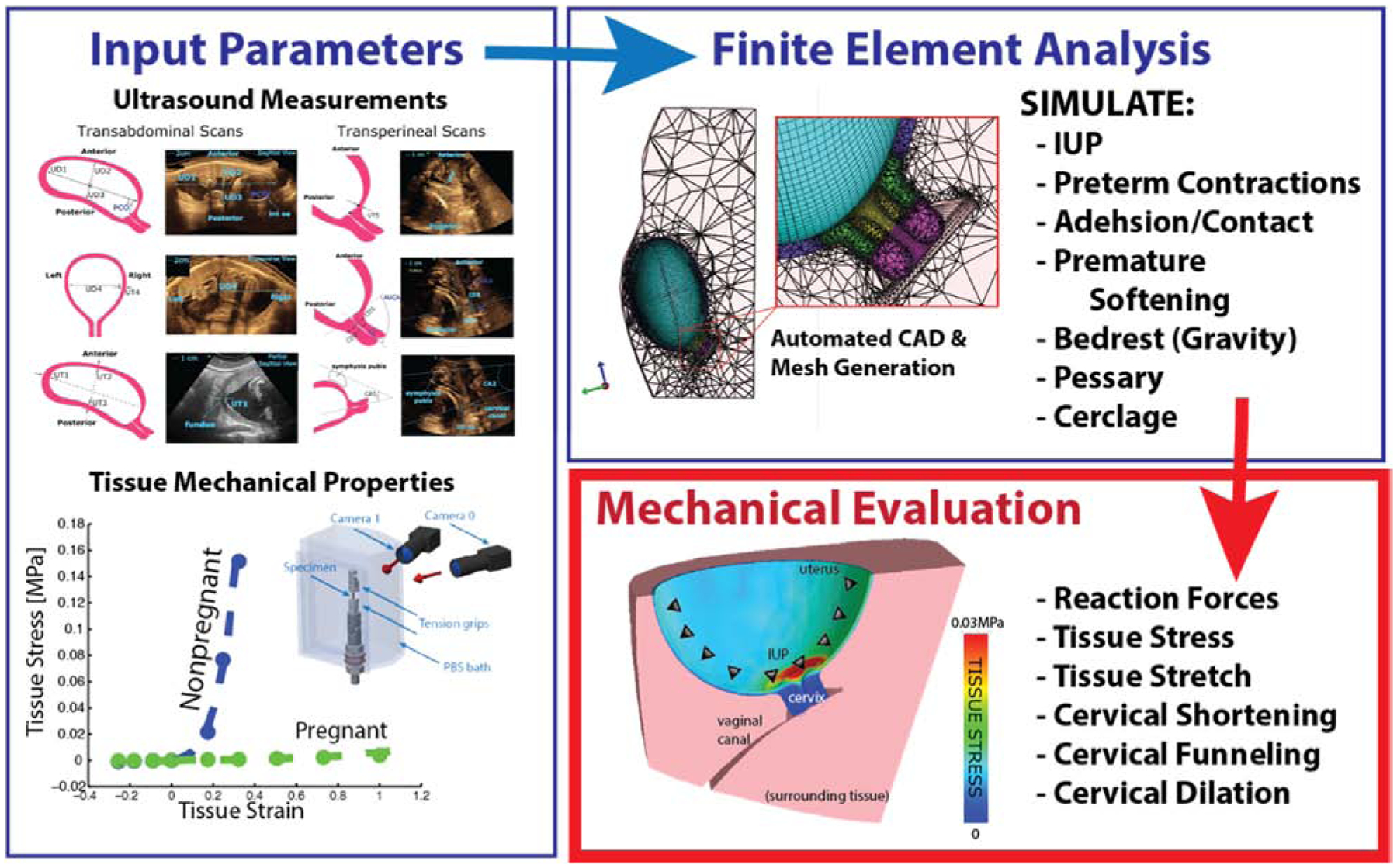
Formulation process for ultrasound-based finite element analysis of pregnancy. Models are informed with ultrasound dimensional data, experimental tissue mechanical properties, loading and boundary conditions. Mesh generation is automated in linear solver for mechanical evaluation of output parameters.

Finite element analysis requires the input of various parameters to obtain accurate results (Fig. 1). The finite element method consists of five steps. Pre-processing involves importing a solid model CAD geometry and creating a mesh to approximate the geometry. In the case of bio-mechanical models, these geometries are often obtained with medical imaging techniques. A mesh is created by separating the input geometry into multiple smaller geometries, called elements. Meshing is a crucial step of finite element analysis as the quality of the mesh reflects directly on the results generated. Next, element formation occurs when governing equations are developed for each element. These equations take into account user definitions of material properties, boundary and loading conditions, and model constraints. The equations either solve for tissue displacement given a prescribed stress, or they solve for tissue stress given a prescribed displacement. The material characteristics are determined from experimental mechanical testing of tissues under loading conditions similar to those experienced physiologically. Boundary conditions are sometimes made through assumptions, like organ surrounding ligamenture. After they are formed, these equations for the individual elements are solved. During final post-processing, output parameters are determined and result visualizations are created.

Since many input parameters in biomechanical models are still based on assumptions, developing new technologies for accurate data collection is still needed. In cardiovascular biomechanics, many technologies exist to characterize the heart’s electromechanics: electrophysiology measurements, stem-cell derived cell and tissue models, and rapidly improving imaging technologies for in vivo and clinical evaluations.^20–22 The field of cardiology has recently turned to patient-specific modeling approaches, obtaining individual geometries and structures of the heart from clinical images. Image modalities in cardiac mechanics include MRI, CT, positron emission tomography (PET) and ultrasound at the organ level, micro-CT, intravascular ultrasound (IVUS) and optical coherence tomography (OCT) at the tissue level, confocal, multi-photon microscopy, coherent anti-stokes Raman scattering (CARS) and electron tomography at the cellular level, and X-ray crystallography at the molecular level.¹⁴ Combining these with tissue-specific cellular models, electrophysiological, and mechanical information allows for dynamic patient-specific models.¹⁴ These models can be used in clinical scenarios to aid medical professionals in diagnosis and treatment decisions. If engineers and clinicians can come to a point where models accurately portray clinical scenarios, these models can act as non-invasive diagnostics which will allow for disease monitoring. But first, it is necessary to determine the most crucial model parameters, and to validate all material and mechanical assumptions.

Pregnancy is a protected environment and difficult to study in vivo. Biomechanical models of the growing and stretching uterus, cervix, and fetal membranes give the ability to assess and pinpoint biophysical factors causing tissue over-loading. These models can be used in discovery- and hypothesis-driven studies. For scientific exploration, models can assess sensitivity of tissue loading to anatomical and tissue material properties. In a clinical setting, forward-predicting models can evaluate risk of sPTB using mechanical threshold bio-markers assessed early in the pregnancy. Currently, biomechanical models of pregnancy are limited by the lack of time course data of the pregnant abdomen during gestation. Yet, it is possible to obtain pregnancy data from non-invasive medical imaging to create solid models of the pregnant abdomen.

Solid models of pregnant anatomy

Computer-aided design (CAD) is the use of software tools by engineers to design a countless number of products, such as buildings, bridges, robots, heavy machinery, etc. Solid CAD models are built from numerically defined primitives (cubes, cylinders, spheres, etc.), sweeps (extrusions, revolutions, etc.), and the Boolean operations of such objects.²³ 3D parametric modeling uses geometries that are easy to modify. For the case of the pregnant anatomy, both magnetic resonance imaging (MRI) and ultrasound have been used to build organ and tissue solid models (Fig. 2).^24–26 Solid models aid the visualization of the 3D anatomy, and can be converted into numerical models suitable for biomechanical modeling.²⁴ Converting medical images to numerical models can be time consuming and tedious.^27,28 To mediate this issue, it is sometimes beneficial to create simplified geometries which can capture the most sensitive aspects of the physiological anatomy.²⁶ Both more detailed and simplified models have their advantages. Complex geometries most accurately portray anatomical scenarios, consisting of layers of different tissues and boundary conditions like ligaments and fascia.^27,29 Simplified models have the potential to reduce preprocessing and computational time, while still capturing the most sensitive parameters of the desired physiology. Attempts are often made to determine exactly how much complexity a biomechanical simulation requires. Sensitivity studies determine the most crucial properties to accurately describe in a model. Model verification and validation are imperative to build credibility for models of intricate biological systems.³⁰

Fig. 2 –

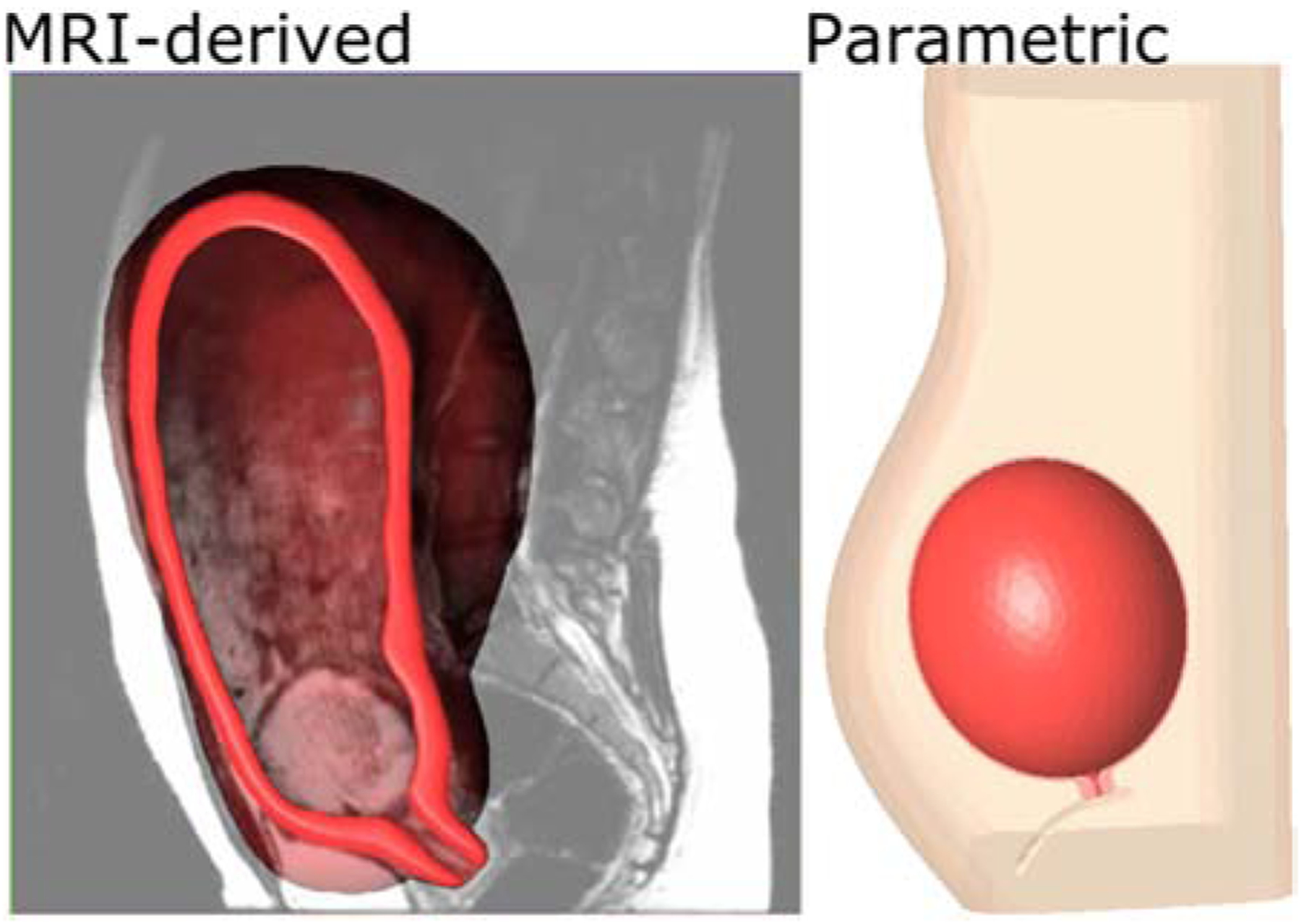
MRI-derived (left) and ultrasound-derived parametric (right) CAD models of pregnancy.

Meshing, boundary conditions, and loading

FEA works by partitioning the object into a finite number of elements, in a process called meshing, and then the analysis predicts full model behavior by summing the behavior of each individual element.²³ Finite elements come in various dimensional shapes. For purposes of biomechanical modeling, we will only discuss 3D shapes in this section. 3D solid elements can either be hexahedral (bricks) or tetrahedral (triangles), and they are connected at individual nodes. Hexahedral elements are more accurate than tetrahedral, but will often not work on complex geometries. In FEA of pregnancy, tetrahedral elements are often used to maximize meshing accuracy while preserving geometries (Fig. 1).

Finite element mesh quality is essential to model mathematical accuracy.²³ Ideal elements have uniform shapes like equilateral triangles, and have smooth transitions in mesh density. Density refers to the size and number of elements. Higher density is often required near areas of geometric curvature or high strains. Increased mesh density has more, smaller elements, and is typically more mathematically accurate. However, it is also more computationally demanding; increasing mesh density can increase model solving time by hours, days, or even weeks in highly complex models. Mesh convergence tests are often performed to optimize mesh density. This is the process of refining a mesh until results converge to asymptotic behavior.

Boundary conditions are constraints placed on the model which remove spatial degrees of freedom. These may be fixed, cylindrical, pinned, and frictionless. In a parametric finite element model of pregnancy, we fix only the outer abdomen of the model in all degrees of freedom. The fetal membranes are tied to the inner uterine wall to mimic membrane adhesion, and they are allowed to slide along the internal os of the cervix.²⁶

To predict model deformations, loads must be prescribed to the system. These can include forces, moments, pressures, temperatures, and accelerations. In pregnancy FEA, the intrauterine pressure (IUP) is usually the load applied to the inner amnion. It is necessary to define the load magnitude and orientation. The parametric FEA model of pregnancy applies contraction-magnitude IUP of 8.67 kPa uniformly around the entire membrane,³¹ and the next iteration of the model will include hydrostatic pressure of the amniotic fluid in future model iterations. One limitation to FEA in pregnancy is that in vivo geometries taken by medical images represent loaded model configurations. It is impossible to obtain unloaded reference configurations of the uterus and cervix throughout gestation. Experiments have been performed to try and estimate unloaded configurations of the fetal membranes,³² which is an important step in determining model input geometries.

Material models in pregnancy

Compared to musculoskeletal and cardiovascular tissues, the mechanical properties of the female reproductive system are understudied and are often limited to animal models. A recent review article details the available mechanical testing data and corresponding material properties for uterus, cervix, vaginal wall, and pelvic ligaments.³³ As discussed above, the material properties of soft collagenous tissues are non-linear, time-dependent, and direction-dependent. Additionally, the female reproductive system undergoes dramatic material property changes during pregnancy. The growth and remodeling of the reproductive tissue depend on the mechanical environment of the tissues in addition to their genetic makeup.³⁴ Histological and biochemical studies demonstrate evidence of both cervical growth and remodeling in pregnancy. Studies of human tissues show that compared to nonpregnant cervical tissue, pregnant tissue experiences a significant decrease in collagen alignment and organization.³⁵

A logical starting point for a large-scale FEA model is to model the tissues as linear elastic materials, using material stiffness properties measured within a reasonable physiologic range of stretches. For unknown gestation-timed material parameters, an estimation can be made by comparing the relative change between material properties measured in the nonpregnant state compared to tissue samples collected at term or rates of remodeling can be extrapolated from available mouse models of normal and abnormal pregnancy. Linear elastic models are convenient and useful to use in an FEA when attempting to isolate the contribution of anatomical shape changes in pregnancy.

A logical progression for improving the material models of the FEA is to explore the consequence of material non-linearity and tissue anisotropy. Tissue nonlinearity can be captured by using phenomenological mathematical expressions, such as a polynomial with more than one variable, fit to experimental data. These types of nonlinear models account for the fact that hydrated biologic tissues tend to be more compliant when they are first stretched. Researchers in biomechanics are moving towards more descriptive models that account for the tissue’s biological composition. For example, the cervix can be treated as a fiber composite material with a preferentially aligned collagen fiber network embedded in a soft compressible ground substance made of glycosaminoglycans.³⁶ Modeling the cervix in this manner accounts for the fact that the collagen fibers cannot give compressive resistance and can only hold a tensile force. Therefore, the resulting overall tissue behavior is very soft in compression and very strong in tension. An FEA model explored the different between modeling the cervix as a linear elastic material and a fiber composite material.²⁵ The linear elastic model fit to compression mechanical data drastically underestimates the effective stiffness of the tissue because it neglects the tensile contribution of the fibers. Therefore, the FEA results show an overestimation of tissue stretching at the internal os. Including the three-dimensional (3D) dispersion of the cervical collagen network will aid in supporting the loads in directions that are not aligned with the preferred fiber direction. The fibers of the 3D network are able to align and rotate in the directions of tissue stretch hence giving the cervix overall mechanical integrity. Active research is continuing to update material models to include time-dependent and growth and remodeling properties.

FEA results and validation

Biomechanical models of pregnancy reveal the positioning, symmetry, and shape of the organs play a large role in the mechanical stress state of the cervix. In an FEA model derived from magnetic resonance imaging (MRI) data, we found asymmetric anatomical features drive the pattern and magnitude of tissue stress and strain,²⁵ where the placement of the cervix within the abdomen and the shape of the uterus offset the stress concentration from the internal opening. The implications of this off-centering are not known, and leads to the question of how does the patient-specific pattern, location and magnitude influence tissue remodeling activities. Results also underscore the importance of capturing the interaction of the fetal membrane, uterus, and cervix. As fetal membrane stiffness and adhesion decrease, cervical stresses and corresponding strains increase (Fig. 3). With a stiff membrane that is tightly adhered to the uterine wall, the load is primarily being carried by the membrane and the uterine wall. Though, if the membrane experiences too much load, it will be at risk for premature preterm rupture. Therefore, this MRI-derived model allows us to distinguish the structural and material factors that influence the delicate balance between the soft tissues that support the fetus.

Fig. 3 –

Finite element tissue stretch over ranges of fetal membrane stiffness. Stiffness is prescribed to 1/5 of physiological stiffness (left), experimentally derived physiological stiffness (center), and 5 times physiological stiffness (right). Numerical values represent volume percentages of cervix internal os over a 1.25 stretch threshold. Increasing fetal membrane stiffness reduces tissue stretch at the internal os.

To increase the flexibility and computational efficiency of pregnant FEA models, reduce clinical costs, and ease patient research burden, ultrasound imaging has been adopted to determine patient anatomy. A clinical maternal ultrasound scan was developed, obtaining 15 dimensions of the uterine and cervical anatomies. A custom solid modeling parametric routine was then scripted to generate a meshed solid model of the pregnant abdomen based on ultrasonic dimensions.²⁶ To demonstrate the flexibility of this parametric model, sensitivity of tissue stress and stretch to cervical tissue properties and anatomical geometric parameters was evaluated. Geometric variations included anterior uterocervical angle, cervical length, and posterior cervical offset from the uterine axis. Cervical tissue stiffness was varied from non-pregnant measured values to pregnant term, where a softer cervix exhibited larger stretches at the internal os. Results indicate both the geometric and material properties of the cervix influence the distribution and magnitude of tissue stretch, where cervical tissue stiffness has the largest influence.

It is important to note that a parametric model may accomplish improved efficiency and flexibility at the expense of accuracy. Also, models rely on engineering assumptions considering not much is known about how pregnant anatomy progresses during gestation and it is nearly impossible to directly measure in vivo material parameters. Because of these factors, verification and validation procedures are needed. Verification and validation are processes which generate evidence and credibility to prove that a computer model yields sufficiently accurate results.³⁷ In particular, verification is the process of determining that a model accurately implements the physiological description and mathematical solution of the model.³⁸ Code verification is often done by the computational software. Calculation verification is conducted through mesh convergence studies mentioned previously. Validation is the process by which computational predictions are compared to experimental data that are not used to calibrate the model.³⁹ For example, pregnancy models can be built from ultrasound data of the patient lying on the table, and the model can then be validated by assessing the difference between model predictions of identifiable anatomic features of the uterus and cervix to the ultrasound data of the patient standing.

Previous finite element analysis of pregnancy

Finite element (FE) modeling of the pregnant anatomy has been used previously to investigate cervical tissue stretch. The cervix is the final passageway to allow for passage of the fetus during labor. Therefore, we hypothesize that the tissue stretch at the internal os is the most important output parameter. Since in vivo experiments are impossible to perform guaranteeing safety of the fetus, finite element modeling in pregnancy is imperative to simulate clinical scenarios without harming humans or animals.²⁹ Previous studies have investigated 2D FE models of the uterus and cervix,²⁹ 3D ultrasound-derived CAD-based FE models,²⁷ and 3D magnetic resonance imaging (MRI)-derived models.^25,40,41

Mahmoud et al. point out that little has been done to investigate the uterine–cervix interaction through finite element modeling of pregnancy. They state the importance of capturing the complex material behavior of the uterine and cervical tissue, as well as the detailed anatomy and accurate boundary conditions.²⁹ Though the authors present a valid approach to building a predictive model, their FE models are only two-dimensional, and exclude the necessary implementation of fetal membranes modeling.

House et al. used transabdominal 3D sonography images and segmented them to capture CAD geometries of the pregnant anatomy for six healthy patients and one patient with acute cervical insufficiency.²⁷ These FE analyses thoroughly modeled the uterus, cervix, fetal membranes, amniotic sac, endopelvic fascia, cardinal and uterosacral ligaments, abdominal cavity and fascia, and pelvic floor. House notes that the largest limitation of this study was the lengthy process of converting the ultrasound images to numerical models.

Paskaleva⁴⁰ used MRI image stacks obtained by House et al. to construct 3D FE models of the pregnant anatomy. The goal of this study was to feature cervical material growth and remodeling to simulate cervical insufficiency. Results demonstrated cervical loads were concentrated at the internal os, especially in the case where the fetal membranes were allowed to slide freely along the inner uterine wall. This result is consistent with the clinical procedure of fetal membranes stripping in order to induce labor. In addition, Paskaleva modeled various cerclage placement positions to investigate ideal scenarios. Models showed cerclage placement closer to the internal os as opposed to the external os resulted in decreased cervical funneling, predicting a minimized potential of cervical insufficiency. These results also coincide with clinical findings of cerclage placement to structurally support the cervix.

House and Socrate⁴¹ have also used MRI techniques to investigate cervical funneling in the TYVU deformation patterns. Models demonstrated the deformation by varying cervical material properties and applying representative pelvic loads. The authors were unable to determine if TYVU deformation is caused by weak cervical structure or if it is caused by another physiological process.

Fernandez et al.²⁵ used 3D MRI images of two pregnant patients to investigate the influence of anatomical geometry, cervical material properties, fetal membrane material properties and adhesion on the mechanical deformation and loading patterns of the cervix at the internal os. The study showed that the uterus, cervix, and fetal membranes all share load-bearing of the fetus and amniotic sac. Key mechanical and structural factors affecting cervical stretch were lower uterine segment and cervical geometries, material properties of the cervical tissue, and fetal membrane material properties and adhesion scenarios.

Previous studies sought to simplify pregnant anatomy geometries in order to expedite the finite element process.²⁶ Ultrasound images were used to create a parameterized model of the uterus, cervix, fetal membranes, vaginal canal, and abdomen. It lacked intricate anatomical details such as bumps and grooves as it modeled the uterus as an ellipsoid with uniform thickness, and the cervix as a hollow cylinder. Findings showed correlation to clinical practice, such as in the case of cervical length and angle. Intuitive results were also shown, where a softer cervix experienced more stretch than a stiffer cervix. New findings showed that the location of the cervix on lower uterine segment may also affect tissue stretch at the internal os. Though the geometries in this study were not as anatomically detailed as MRI-derived studies, the entire process from image collection to result visualization could be completed in a matter of hours, rather than days or weeks taken with previous methods.

Clincial significance

A crucial challenge to lowering the rate of sPTB and its subsequent costs is to identify women who are at the highest risk, to identify these women early in their pregnancy, and to develop etiology- and patient-specific interventions. Equally important to reducing costs related to sPTB, is the ability to identify women at the lowest risk to avoid unnecessary and costly interventions. Without knowing the underlying mechanisms that result in sPTB, empirically introducing treatments can be ineffective, potentially detrimental, and costly.^42,43 Additionally, conducting a clinical trial to determine what single factor or group of factors cause mechanical dysfunction in pregnancy is extremely timely and expensive.

Biomechanical models of pregnancy can specifically address these clinical needs by providing a simulation framework to identify the structural factors that cause mechanical dysfunction and aid in minimally invasive clinical diagnosis of preterm birth. Clinicians can use ultrasound to obtain anatomical dimensional data to inform patient-specific FEA. Computational results of tissue stress and stretch can then be reported within hours or even minutes. Furthermore, these models can guide mechanically based patient-specific therapeutic interventions to prevent PTB. When implemented in clinical practice, biomechanical models of pregnancy can implement “what if” scenarios that clinicians cannot test in vivo. For example, we can build a patient-specific model and insert a cerclage or cervical pessary to predict how certain interventions will change tissue mechanics and deformation. These simulations can predict treatment safety and efficacy with significantly lower costs and possible harm to patients.