Edges Impose Planar Alignment in Nematic Monolayers by Directing Cell Elongation and Enhancing Migration

Abstract

Boundaries play an important role in the emergence of nematic order in classical liquid crystal systems; we explore their importance for adhesive cells that form active nematics. In particular, we study how cells are affected by an edge, which in our experiments is a boundary between adhesive and non-adhesive domains on a planar surface. We find that such edges induce elongation and direct the migration of isolated fibroblasts. In confluent monolayers, these elongated cells co-align and migrate to form an active, two-dimensional nematic in which edges enforce planar alignment and provide local slip to streams of cells that move along them. On an adhesive square island of dimensions 1 mm × 1 mm, cells near edges in confluent nematic monolayers have enhanced alignment and velocity. The corners of the adhesive island seed defects with signs that depend on the direction of motion of the streams of cells that meet there. Distortions emerge with rotations of −π/2 to form a −1/4 defect for streams that move clockwise or counterclockwise, and +π/2 to form a +1/4 defect for converging streams. We explore how cells transmit alignment information to each other in the absence of an edge by studying cell pairs and find that while such pairs do co-align, this alignment is only transient and short lived. These results shed light on the importance of edges in imposing nematic order in confluent monolayers and how edges can be used as tools to pattern the long-range organization of cells for tissue engineering applications.

Graphical Abstract

The impact of microcontact printed edges on the emergence of nematic order in confluent monolayers of elongated fibroblasts is investigated.

Introduction

Cells respond to geometric cues of various length scales and dimensions, including linear fibers, curved surfaces, and fibrous meshes. Physical cues encountered by cells in vivo have motivated in vitro studies to elucidate how geometries influence cell behaviors. For example, the diameter of electrospun fibers in the range of hundreds of nanometers to microns influences cell proliferation, migration, and differentiation ^1–4. Additionally, fibroblasts and vascular smooth muscle cells reorganize their actin cytoskeletons and migrate in a directed manner in response to surface curvature of various two-dimensional surfaces ^5,6. Numerous studies address the emergence of structure in cells in more complex, three-dimensional microstructures, ranging from microchannels to structured gels, showing the importance of the geometry and dimension of cell niches on cell migration and organization ^7–10.

Even relatively simple planar surfaces provide rich platforms for the study of cell organization. Cells adhere to these surfaces in vitro when they are presented with adhesive ligand. The patterning of ligands on surfaces has long been studied as a means of directing the fate of individual cells ¹¹. More recently, adhesive islands have been used to study collective cell behavior. Densely packed monolayers of elongated cells, such as fibroblasts, neural progenitor, and epithelial cells, locally co-align with each other when cultured in confluent monolayers ^12–17. Before becoming overly packed, cells remain motile and migrate in ways reminiscent of molecular active nematics. For example, these systems generate topological defects that are typically ½-integer and these defects emerge and annihilate with each other over time ^18,19,. The monolayers are often cultured on micropatterned domains. The edges of these domains enforce parallel alignment of cells near the edge; that is, the edges enforce “planar” (as opposed to perpendicular) anchoring of the two-dimensional nematic.

While these studies exploit the collective parallel alignment enforced by edges to study the active nematic characteristics of confluent monolayers of cells, details about how edges influence cell behaviors are unclear. In this study, we aimed to understand how edges affect the morphology and migration of both isolated cells and cells within confluent monolayers.

To generate macroscale edges free of gradients in the concentration of the printed extracellular matrix protein fibronectin (FN), we used a stamp-off microcontact printing method. Using this method, we found that isolated mouse embryonic fibroblasts (MEFs) elongate and migrate along edges even when unconfined. When confined within confluent monolayers, the edge continues to pattern the morphology and to enhance the migration of cells near the edge compared to cells far from the edge. We find that topological defects emerge near corners at which edges with conflicting boundary conditions meet. The pattern of migration of cells at each edge dictates the type of defect that appears. Although edges provide a robust alignment cue for cells, we find that cells in pairs are unable to transmit alignment information to each other for extended periods of time owing to their limited body length. Together, these results emphasize the important role that edges and confinement play in patterning the active nematic order observed in monolayers of elongated cells.

Materials & Methods

Cell culture

Spontaneously immortalized mouse embryonic fibroblasts (MEFs) were cultured in growth medium containing 10 vol.% FBS, 2 mM L-glutamine, 2.5 μM HEPES, and 50 μg/mL gentamicin. Cells were maintained at 37 °C and 10% CO₂.

To track cell shape over time, immortalized MEFs were infected with adenoviral mCherry. The mCherry fluorophore was localized to the cytoplasm that had higher contrast than could be obtained with phase contrast for the analysis of cell shape. Cells in confluent monolayers were treated with 2 drops/mL of NucBlue (Invitrogen) for 30 minutes prior to imaging. Viability of cells treated with NucBlue decreased after ~6–8 hours, so they were only imaged for a maximum of 6 hours.

Microcontact Printing

The FN-coated regions were created using a stamp-off microcontact printing method adapted from a standard approach ^20,21 to form well defined edges between adhesive and non-adhesive domains (Fig. S1). Briefly, standard photolithography methods were used to generate an array of 1 mm × 1 mm squares on a silicon wafer. Poly(dimethylsiloxane) (PDMS) (Dow Corning) was prepared by mixing elastomer base and crosslinker at a ratio of 10:1. After degassing to remove bubbles, the liquid was poured onto the patterned wafer and cured by baking at 95 °C for at least two hours. Once cured, the PDMS was removed and cut into stamps. This process generated stamps with square holes instead of square pillars, which would typically be used for standard microcontact printing methods. A second set of flat PDMS stamps was created by curing PDMS in plastic 35 mm dishes and cutting the solid slabs into pieces slightly larger than the patterned stamps. To prepare the actual substrates on which cells were cultured, 300 μL of PDMS were leveled in each well of a 6-well plate before curing overnight at 65 °C.

All stamps were cleaned by sonication in 200 proof ethanol for 10 minutes. Then, both sets of stamps were dried under a stream of nitrogen gas. The flat stamps were inked by pipetting a sessile drop of fibronectin (FN) onto the clean, dry surface. The FN ink contained a mixture of unlabeled and Alexa Fluor 647- or Alexa Fluor 488-labeled bovine plasma FN (EMD). The labeled FN was prepared using Alexa Fluor 647 or Alexa Fluor 488 succinimidyl ester according to the manufacturer’s protocol (Molecular Probes). Once sessile drops were added to the flat stamps, the stamps were incubated at 37 °C for one hour. The PDMS-coated 6-well plate and square-hole stamps were treated with ultraviolet ozone (UVO) for 7 minutes to make the surfaces hydrophilic.

Once the flat stamps had been functionalized with FN for one hour, they were submerged and rinsed in phosphate buffered saline (PBS). Then, the flat stamps were dried under a constant stream of nitrogen gas. The dried flat stamps were placed FN side up in a separate dish and the UVO-treated square-hole stamps were placed hole side down onto the flat stamps. Light pressure was applied to ensure proper contact between the two stamps. The square-hole stamps were removed, leaving behind square islands of FN on the flat stamps. These flat stamps were then stamped onto the UVO-treated PDMS in the 6-well plate. Once the stamps were removed, a 0.2% solution of Pluronic F-127 was added to each well to render the regions surrounding the FN islands non-adherent to cells. The 6-well plate was incubated for 30 minutes at 37 °C. After incubation, the wells were rinsed with PBS and cell culture medium before cells were seeded at the desired surface density.

Some cells were cultured on unpatterned FN islands for cell pair studies. Instead of selectively removing FN from Stamp #1 as shown in Fig. S1C, the unperturbed FN on Stamp #1 as shown in Fig. S1B was stamped directly onto the substrate. This provided a larger area in which to observe cell pairs in the absence of edges.

Imaging

Cells were imaged on an EVOS FL Auto 2 inverted epifluorescence microscope with an incubated stage (Thermo Fisher Scientific; University of Pennsylvania Cell and Developmental Biology Microscopy Core). Isolated cells and cell pairs were imaged with a 20× objective and confluent monolayers were imaged with a 10× objective. Each square monolayer was captured in two fields of view that were stitched together in post-processing.

Image and Video Analysis

To analyze cell shape over time, images of cytoplasmic mCherry in MEFs infected with the fluorophore were processed in Fiji. Images were prepared for analysis by subtracting the background signal, despeckling to reduce noise, and adjusting brightness and contrast. Then, the Automated Detection and Analysis of Protrusions (ADAPT) plugin for Fiji was used to track cell shape and orientation²². Trajectories of MEFs expressing mCherry were measured from the centers of cell outlines in each frame. Data from ADAPT were further analyzed and plotted in custom MATLAB scripts. Trajectories of cells in pairs in longer experiments (~17 hr) were generated using the Fiji plugin MTrackJ ²³. These cells were not treated with NucBlue and the cytoplasmic mCherry signals of cells in pairs were often indistinguishable due to their close proximity. Instead of tracking either of these signals, nucleoli visible in phase contrast movies were tracked manually with MTrackJ. For the analysis of cell pairs, cell bodies were manually outlined in Fiji in every fifth frame. An ellipse was fit to each outline and the average angle of the fit ellipse over each analysed frame was calculated.

Analysis of confluent monolayers of MEFs on square islands began by stitching together two fields of view per square with a custom ImageJ script that utilized the Pairwise Stitching function ²⁴. Then, movies were rotated and cropped to the FN boundaries. Fiji was used to adjust the brightness and contrast of the NucBlue images before binarizing each frame. The Fiji plugin TrackMate was used to track the positions of binarized nuclei over time ²⁵. Nuclear shape was measured using Fiji’s Analyze Particles function.

Results

Isolated cells elongate and migrate along unconfined edges

To study how cells interact with unconfined edges, we created adhesive boundaries using a stamp-off microcontact printing method that was adapted from the standard microcontact printing technique ^20,21 (Fig. S1). Instead of preparing stamps with protrusions with the shape of interest (in this case, 1 mm × 1 mm squares), we made a negative with this shape in PDMS. This negative was used to remove FN from an initially uniform fibronectin layer on a planar PDMS stamp, leaving behind the desired shape on this planar layer. This method more reproducibly generated edges with no apparent gradients in FN concentration. All edges studied here were generated using the stamp-off method to ensure that the cell responses can be attributed to the edge geometry and not to concentration gradients, which are known to influence cell migration and elongation ²⁶. The edges in these experiments are the boundary between the adhesive FN islands and a non-adhesive sea of adsorbed surfactant (Pluronic F-127).

We studied the shape of MEFs interacting with edges by infecting them with adenoviral mCherry. Infected cells expressed the fluorescent protein in the cytoplasm and were imaged for ~17 hours (Fig. 1). We found that isolated cells that encountered edges were significantly more elongated than cells in the bulk of the FN islands (Fig. 1B). While others have shown that cells elongate along microcontact printed stripes that confine the cells on two sides ^27–29, here we find that the presence of a single edge is sufficient to induce cell elongation, although edges did not induce elongation of the nucleus (Fig. S2).

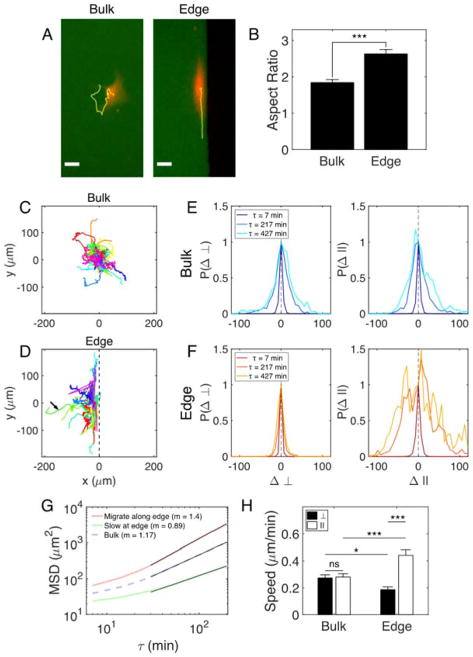
Figure 1. Edges induce elongation and enhance migration of isolated MEFs.

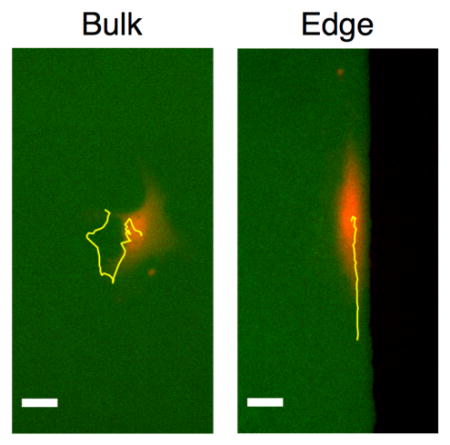
(A) MEFs expressing mCherry (red) cultured on microcontact-printed islands of FN (green). Yellow lines indicate trajectories of the cell centers over ~6 hr. Scale bars are 30 μm. (B) Aspect ratio of ellipses fit to cytoplasmic mCherry signals. Trajectories of mCherry-infected MEFs in the bulk (C) and at edges (D) of FN islands. Longest duration = 14 hr. Arrow indicates a cell that left the edge. 44 cells analysed in each environment. Normalized probability distributions for displacements of cells in the bulk (E) and cells that migrate along edges (F) for three lag times, τ. □, direction perpendicular to edge; ||, direction parallel to edge. (G) Mean square displacement (MSD) plots for cells that migrate along edges, cells that remain nearly stationary at edges, and cells in the bulk. Log-log slopes (m) for the fit lines (black) are reported. (H) Speed of mCherry-infected MEFs in the bulk and migrating along edges. Values are mean ± SEM.

In addition to altering cell shape, edges also direct migration and trap cells in their vicinity. By tracking the center of the mCherry signal in infected cells, we found that cells at edges migrate in the direction parallel to the edge (Fig. 1C,D). In Fig. 1D, cell centroids were tracked from the moment they contacted the wall until they left the field of view or the movie ended. The trajectories were shifted so that they start at y = 0 μm at t = 0 min. Most cells encountering edges remained near the edge for extended periods of time, but approximately 14% of cells left the edge (arrow, Fig. 1D). Cells that left edges were oriented at oblique angles to the edge, suggesting that the angle at which a cell interacts with an edge may influence whether it migrates along the edge (Fig. S3 and Movie S1).

Of the cells that remained near edges, two distinct populations were observed. Approximately 26% of these cells remained at the edge over the entire observation period, but migrated very little. These cells tended to elongate along the edge, but remained nearly stationary (Movie S2). The remaining 74% of cells migrated rapidly and persistently along the edge (Movie S3). To quantify this tendency to move along edges, we plotted normalized distributions of cell displacements in two orthogonal directions (Fig. 1E,F). Cells in the bulk of islands showed no difference in their displacement distributions in the horizontal (□) or vertical (||) directions, indicating that they have no preferential migration direction. Cells at edges, on the other hand, showed distinct displacement distributions in the directions perpendicular and parallel to the edge direction. Displacements from the original position in the direction perpendicular to the edge remained small even at long lag times. In the direction parallel to the edge, displacements grew quickly with lag time, indicating that cells moved greater distances along the parallel direction than the perpendicular direction. Thus, a single, simple adhesive boundary guides migration.

These findings are supported by differences in the mean square displacement (MSD) of cells in the bulk and cells at edges (Fig. 1G). Cells in the bulk were slightly superdiffusive with a log-log slope of 1.17. The cells that remained at edges but moved very little (“Slow at edge”) were slightly subdiffusive (m = 0.89), confirming that these cells became trapped at edges. The remaining majority of cells showed persistent superdiffusive behaviour with a slope of 1.4. Additionally, we find that edges enhance cell speed anisotropically (Fig. 1H); the cells that migrate along boundaries move significantly faster along those edges than cells in the bulk. The speed data also indicate that cells tend to be trapped near edges; they have a significantly lower speed in the direction perpendicular to the edge. Thus, edges have a profound impact on isolated cell shape, migration direction, and speed despite the fact that cells that encounter edges are unconfined and have the ability to migrate away from the edge and into the bulk.

Cell pairs far from edges only transiently and weakly transfer alignment signal

In confluent monolayers, elongated cells such as fibroblasts co-align with each other locally. We next aimed to understand how cells transmit alignment information to each other. When isolated, MEFs are elongated and could potentially act as a “soft edge” to neighboring cells. Can cells align along each other in the way that they align along edges? To approach this question, we studied pairs of MEFs that were isolated from other cells as well as boundaries.

By tracking the cytoplasmic mCherry signal of infected MEFs, we found that most cells in pairs stayed near each other over the roughly six hour experiments: Approximately 83% of cell pairs were separated by < 50 μm on average and 42% never separated from each other at all (Fig. 2A). These cells remain in close contact and can transmit alignment information to each other. To determine the extent of cell co-alignment, we used nuclear orientation as an indirect marker of cell orientation (Fig. S4). We measured the angle separating the two nuclei (Fig. 2B) and cell bodies (Fig. S5) averaged over the duration of the movie after the cells first made contact and found a broad distribution of separation angles. These data suggest that the cells do not strongly co-align with each other over a time scale of roughly six hours.

Figure 2. Cells in pairs only transiently co-align.

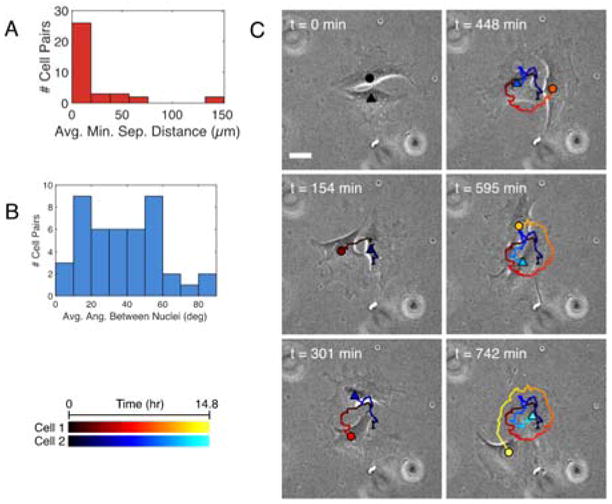
(A) Mean minimum separation distance of cytoplasmic mCherry signals of cells in pairs. 36 pairs analyzed in two independent experiments. (B) Mean angle between the orientations of the long axes of NucBlue-stained nuclei. 44 pairs analyzed in two independent experiments. (C) Three frames of a phase-contrast movie showing the morphology of two cells migrating around each other. Cell 1: circle in warm colors. Cell 2: triangle in cool colors. Gradient from dark to light shades indicates cell position over time (see scale in bottom left).

However, closer examination of individual migration patterns revealed that there were transient periods of co-alignment in some cell pairs. Over time, the nuclei of many cell pairs changed from a parallel arrangement to a perpendicular one, indicating that the relative orientations of the cells can change significantly within six hours (Fig. S6). Roughly 30% of cell pairs examined migrated around each other, some forming interwoven spiral trajectories (Fig. 2C and S6). These elongated cells co-aligned when their long edges were in contact, but co-alignment was lost once one cell passed around the short edge of the other. Once past the short edge, the cells then co-aligned again along their long edges. Although they might co-align temporarily, most cells in pairs (> 75%) are unable to co-align with each other over extended periods of time and confinement within larger, dense monolayers or by an edge appears to be a requirement for robust co-alignment.

Edges enhance elongation and migration of cells in nematic monolayers

To probe nematic alignment, we study cells in confined confluent monolayers. Microcontact printed edges are known to impose a planar boundary condition for elongated cells in confluent monolayers; that is, cells near edges align parallel to the edge direction ^14–16. We showed in Fig. 1 that edges can also influence cells to elongate and migrate along them for otherwise unconfined, isolated cells and aimed to better understand their effects on densely packed cells.

We studied confluent monolayers of MEFs on 1 mm × 1 mm square islands of FN. It was not possible to measure the shape of individual cells by infecting them with mCherry as described above because the cytoplasm signals from neighboring cells overlapped and made outlining each cell challenging. Instead, cells were treated with NucBlue, a blue DNA stain that labeled the nuclei of the living cells (Fig. 3). The nuclei of neighboring cells typically remained separated from each other, facilitating the analysis of each cell within the monolayer (Fig. 3B). We again used the orientation of the elongated nuclei as an indirect measure of the orientation of cells (Fig. S4).

Figure 3. Edges influence morphology and migration of nearby cells in confluent monolayers.

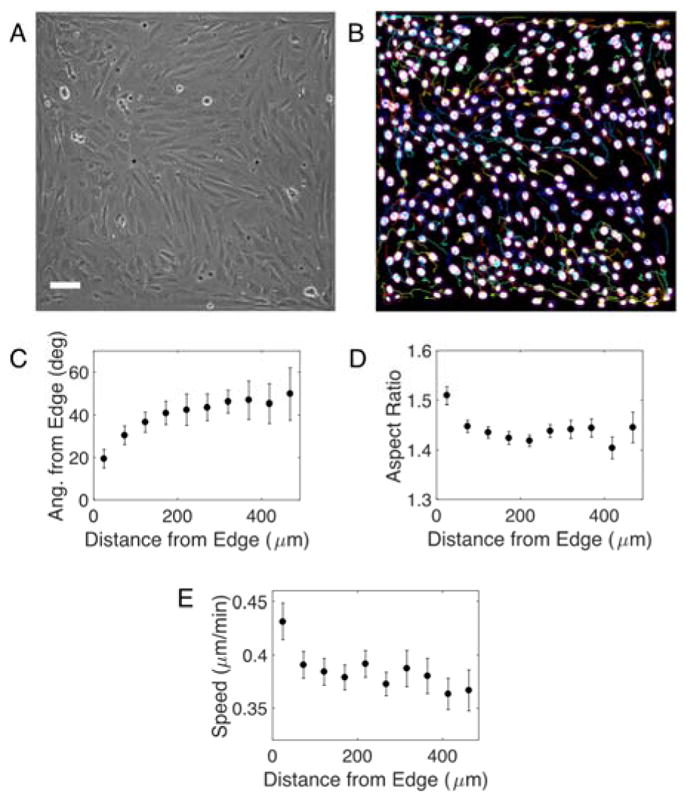
(A) Phase contrast image of a nematic monolayer on a 1 mm × 1 mm FN island. Edges of the image are edges of the island. Scale bar is 100 μm. (B) Binarized image of nuclei of cells in A stained with NucBlue. Colored lines indicate trajectories of each nuclei over 6 hr. (C) Angle of nuclei relative to the nearest edge vs. distance to that edge. Aspect ratio (D) and speed (E) of nuclei vs. distance from nearest edge. 20 squares analyzed in two independent experiments. Mean ± SEM.

Edge proximity strongly influenced nuclear orientation. Nuclei within 50 μm of an adhesive boundary aligned along it (Fig. 3C). This alignment decayed with distance; the orientation angles of nuclei far from edges were uncorrelated (i.e., the alignment angle approached 45°), indicating that the edge no longer influenced alignment. Here, we analyze the orientation of each nucleus (and, indirectly, each cell) and find that the edge has a strong influence on nuclear orientation over a distance of hundreds of microns, consistent with results based on phase contrast images of monolayers ¹⁴.

In addition to patterning orientation, edges also influence nuclear shape. The nuclei of cells within 50 μm of an adhesive boundary were more elongated than nuclei farther away (Fig. 3D). Thus, edges promote both co-alignment of nuclei with the edge and nuclear elongation.

To assess whether the faster migration along edges observed for isolated cells persisted in confluent monolayers, we studied the migration of cells within monolayers using the NucBlue signal and the Fiji plugin TrackMate. These data indeed reveal that edges generate a slip layer in which cell speed is significantly enhanced (Fig. 3E). This effect diminished over a short distance: Cells within ~50 μm of the edge migrated 10% faster than cells within 50–100 μm from the edge. Thus, microcontact printed edges strongly alter nuclear orientation, shape, and speed even for cells confined within nematic monolayers.

Migration pattern dictates topological defect formation at corners

Topological defects emerge within the nematic monolayers of MEFs (Movie S4). Within the bulk of the FN islands, these defects are half-integer, as predicted by theory ³⁰ and shown in other monolayer systems ^12,15–17. In these studies, cells were cultured on circular or long stripe micropatterns that do not induce the formation of defects near the edges naturally.

The four corners of the square geometry on which we culture cells are locations at which defects occur. Since both of the edges that meet at a right angle at a corner enforce alignment parallel to the edge, the director n cannot be specified at the corner. The nematogens (cells, in this case) attempt to satisfy both boundary conditions by bending or splaying the director field to form defects with winding numbers of −1/4 or +1/4, respectively (Fig. 4).

Figure 4. Migration near corners influences defect formation.

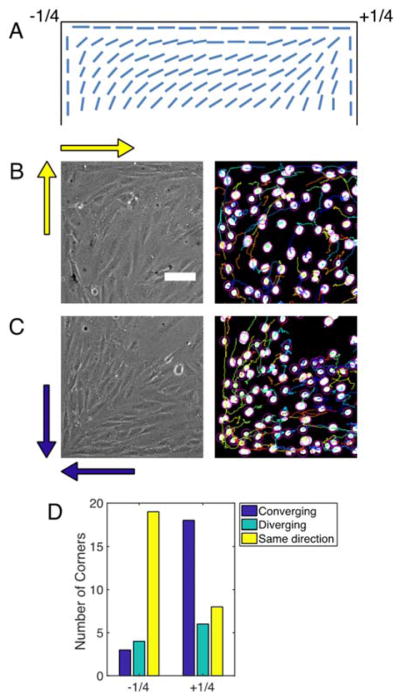
(A) Diagram showing bend and splay deformations with −1/4 and +1/4 winding numbers, respectively, that satisfy the conflicting boundary conditions at corners. (B) Phase contrast (left) and binarized image of NucBlue-stained nuclei (right) of −1/4 defect at the top left corner of the images. Yellow arrows indicate the migration directions of cells at each edge. (C) Phase contrast (left) and binarized image of NucBlue-stained nuclei (right) of +1/4 defect at the bottom left of the images. Blue arrows indicate the migration directions of cells at each edge. See Movie S5 to see the migrating cells. (D) Distribution of relative migration directions at edges that meet at corners and the types of defects that emerge at those corners.

We tracked the nuclei of confluent MEFs near corners and found that the relative flow directions at each edge control the type of defect that emerges when they meet at the corner. If the cells at both edges migrate in the same direction (i.e., both migrate in the clockwise or counterclockwise direction), then a −1/4 defect is most likely to emerge at that corner (Fig. 4D, Movie S5). If instead the cells converge at a corner, then a +1/4 defect is most likely to emerge. Thus, the local flow field of cells migrating near edges controls the formation of topological defects.

Discussion

The emergence active nematic order in cell monolayers on planar domains has been reported for various types of elongated cells, including fibroblasts, melanocytes, osteoblasts, and neural progenitor cells ^12,14–16. In many of these cases, cells confined within adhesive regions were observed to align along the edges of the domains. Here, we show that edges play a role in establishing active nematic behavior of cells beyond simply providing a static planar anchoring. We find that edges enhance the alignment and migration of cells that are isolated as well as those confined within confluent monolayers. Even when compressed against the edge by their neighbors, cells in confluent monolayers that are near edges migrate faster than their counterparts far from edges.

Epithelial cells near edges have also been observed to migrate more quickly than their counterparts in the bulk of small circular islands ³¹. On circular patterns that are roughly 8–12 cells wide (200 μm diameter), the few cells near the center migrated very little while the cells near the periphery migrated quickly in a single direction. We find that cells near edges migrate more quickly than cells in the bulk even in much larger monolayers that are too large to support coherent flows, suggesting that the edge effect decays quickly from the edge. Additionally, we have shown that fibroblasts also exhibit the migration enhancement at edges observed in epithelial monolayers.

The dynamics of living nematic systems have been addressed in terms of active turbulence, defined as “strong jets and vortices in the flow field and the continual creation and annihilation of pairs of topological defects” ³². Important aspects of active turbulence have been reported in monolayers of eukaryotic cells. While the flows in our monolayer of confluent MEFs, observed over a 6-hour time span, have no apparent defect formation or annihilation, jets and zones of high vorticity are observed. For example, the migration along edges to form +1/4 or −1/4 defects at corners could be considered a jet, with pronounced vorticity (i.e., strong path bending) at the +1/4 defects at which cells turn sharply to form the splay defect. There is weaker vorticity at the −1/4 defect, at which cells turn along edges to navigate the corner. These experiments were limited to roughly 6 hours due to the cytotoxicity of NucBlue. Duclos performed experiments using 3T3 cells, similar to ours, over far longer time scales (more than 80 hours). These researchers observed defect annihilation and large-scale displacement around the defect itself. They report that defect creation, however, did not occur. This remains, to our knowledge, an open issue. The long time scales and very slow motion in densely packed nematic monolayers of fibroblasts make these observations exceedingly challenging. Furthermore, if confinement to a monolayer is relaxed, new behaviors can emerge. For example, neural progenitor cell monolayers studied by Kawaguchi¹⁶ move along paths from fixed −1/2 defects to fixed +1/2 defects, building three dimensional structures of accumulated cells at the +1/2 defects over time¹⁶.

In bulk monolayers, +1/2 defects are motile while −1/2 are not¹⁵; this begs the comparison of dynamics of +1/4 vs. −1/4 corner defects. First, these defects can only exist in corners, and persist over the lifetime of our experiments. The local flow patterns for cells near corners correlate with the location of −1/4 or +1/4 defects. Simple continuity arguments explain the observed flow patterns. When cells moving along perpendicular edges converge at the corner, they must migrate toward the center of the island (+1/4 defect). When cells move along a continuous path, they can bend in a continuous stream around the corner (−1/4 defect). Thus, cells remain motile in both arrangements. The vorticity or path curvature is greater at the +1/4 defect than at the −1/4 defect. The continuity arguments assume that the cells, like those in our experiments, remain motile and adhered to the substrate. New degrees of freedom, like the ability to leave the monolayer, relax this relationship, as has been observed in the aforementioned study of Kawaguchi et al., in which neural progenitor cells rapidly accumulate at +1/2 defects¹⁶.

Recent work has revealed that confining edges can play an important role in controlling not only the orientation of defects within an active nematic, but also their spatial position ^33,34. In simulations of active nematics confined within small rectangular chambers, −1/2 defects become pinned near edges and +1/2 defects “dance” around each other in a manner reminiscent of a traditional Cèilidh dance ³³. The authors note that this dancing pattern emerges only in confined rectangular systems with an aspect ratio > 10. These predictions motivate future work; cells cultured on sufficiently long rectangular islands may reveal the extent to which the simulated systems model the defect and flow patterns present within confluent monolayers.

In addition to providing a valuable experimental tool for studying the active nematic behavior of mammalian cells, macroscale edges may serve as useful tools for tissue engineering. The traction forces generated by mouse fibroblasts have been used to fold thin pieces of thin elastomeric plates in “cell origami” ³⁵. The stress fibers within these cells contract along the long axis of the cell body and generate forces sufficiently large to fold plates into cubes and various other shapes. Using edges to guide alignment and the intrinsic co-alignment properties of cells within monolayers, large anisotropic forces could be generated in predictable patterns. Further studies of edges and nematic monolayers will thus not only shed light on how cells interact with physical cues within their environments, but may also provide guidelines for patterning cells over long distances (hundreds of microns) for engineering applications.

The question of how cells transmit alignment information to each other remains open. We found that cells in pairs can transiently transfer alignment information to one another, but their co-alignment is short-lived. The cells appear to act as soft, active edges: The cells remain in contact with each other and attempt to align with each other, but they are both migrating and rearranging so that co-alignment is not maintained for an extended period of time. Future work will reveal the role of confinement within monolayers on co-alignment of cells. How many cells in a nematic monolayer “droplet” are required to enforce strong co-alignment at the center? This knowledge will provide insight into the origin of nematic behavior in cellular monolayers as well as guiding principles for organizing cells over long distances in tissue-engineered constructs.

The molecular and microstructural mechanisms behind the emergence of co-alignment within nematic monolayers as well as edge alignment are unclear. We suspect that the actomyosin machinery, which has been implicated in cellular sensation of surface curvature, may play an important role in establishing nematic order and responding to edges. Fibroblasts and vascular smooth muscle cells respond to these curvature cues by aligning two distinct populations of stress fibers along the principal axes of the surface ^5,6. These bundles of F-actin are attributed to both the elongated cell shape and motility ³⁶. We suspect that stress fibers and other components of the actin cytoskeleton may play an important role in the observed alignment and migration responses to edges. A cell approaching and making contact with an edge must alter its polarization direction because it is unable to continue protruding its primary lamellipodium past the edge. The cell is likely to establish a new lamellipodium in one of the two directions parallel to the edge. Long-lived focal adhesions and their associated stress fibers may then form in response to this new direction, aligning themselves and the cell body in the parallel direction.

Conclusions

Edges of microcontact printed islands serve as important boundary conditions for cells. Our results suggest that the planar anchoring at edges observed in nematic monolayer systems is imparted even on isolated cells. Edges not only induce cell elongation, but also increase migration speed of both isolated cells and cells within confluent, nematic monolayers. The migration patterns near edges can be used to form bend and splay distortions within the two-dimensional nematic. Thus, cell alignment patterns can be predicted by theory of nematics and controlled over distances of hundreds of microns using simple adhesive boundaries.