Estimation of incubation period and generation time based on observed length‐biased epidemic cohort with censoring for COVID‐19 outbreak in China

Abstract

The incubation period and generation time are key characteristics in the analysis of infectious diseases. The commonly used contact‐tracing–based estimation of incubation distribution is highly influenced by the individuals' judgment on the possible date of exposure, and might lead to significant errors. On the other hand, interval censoring–based methods are able to utilize a much larger set of traveling data but may encounter biased sampling problems. The distribution of generation time is usually approximated by observed serial intervals. However, it may result in a biased estimation of generation time, especially when the disease is infectious during incubation. In this paper, the theory from renewal process is partially adopted by considering the incubation period as the interarrival time, and the duration between departure from Wuhan and onset of symptoms as the mixture of forward time and interarrival time with censored intervals. In addition, a consistent estimator for the distribution of generation time based on incubation period and serial interval is proposed for incubation‐infectious diseases. A real case application to the current outbreak of COVID‐19 is implemented. We find that the incubation period has a median of 8.50 days (95% confidence interval [CI] [7.22; 9.15]). The basic reproduction number in the early phase of COVID‐19 outbreak based on the proposed generation time estimation is estimated to be 2.96 (95% CI [2.15; 3.86]).

1. INTRODUCTION

In epidemiology, incubation period is the time between the infection of an individual by a pathogen and the manifestation of symptoms, while generation time is defined as the time between the infection of a primary case and its secondary cases (Fine, 2003; Svensson, 2007). Both are vital clinical characteristics that depict an epidemic and are essential for policy making. For example, a good understanding of incubation period offers an optimal length of quarantine, and a good understanding of generation time is essential in estimating the transmission potential of a disease measured by the basic reproduction number R ₀ (Farewell et al., 2005; Wallinga and Lipsitch, 2007; Nishiura, 2010).

In most of literature, such as Li et al. (2020) and Guan et al. (2020), the distribution of incubation period is either described through a parametric model, for example, log‐normal and Weibull, or, its empirical distribution based on the observed incubation period from contact‐tracing data. However, contact‐tracing data are usually difficult to obtain, and can be highly influenced by the individual's judgment on the possible date of exposure rather than the actual date of exposure, which, in turn, might not be accurately monitored and determined leading to significant errors (Cowling et al., 2007).

An alternative approach to study incubation period is to take advantage of the mechanism of truncation or censoring. Lui et al. (1988), De Gruttola and Lagakos (1989), Struthers and Farewell (1989), and Kuo et al. (1991) estimated incubation distribution of contagious diseases using external truncation or censoring information. Kuk and Ma (2005) studied the incubation period of SARS by deconvolution, but the proposed method was only feasible for the disease that is noninfectious during incubation period, which is not the case for COVID‐19. It also assumed that the ability of infectiousness is uniform during the infectious period, which is a strong assumption. In the studies of Lessler et al. (2009) and Reich et al. (2009), double censoring was used to characterize the problem caused by daily reports rather than continuous observed symptoms onset time. Nishiura and Inaba (2011) used 72 confirmed imported cases that traveled to Japan from Hawaii during the early phase of the 2009 H1N1 pandemic to estimate the incubation by addressing censoring and infection age.

For COVID‐19, Backer et al. (2020) and Linton et al. (2020) used confirmed cases detected outside Wuhan to estimate the distribution of the incubation by interval‐censoring likelihood. In their studies, for each selected case, a censored interval for incubation period was obtained by travel histories and dates of symptoms onset, and the distribution of incubation was then estimated by fitting censored intervals into Weibull, Gamma, and log‐normal. However, such estimations may lead to biased estimations of incubation period due to the biased sampling issues. Qin et al. (2020) adopted the theory from renewal process and carefully selected the studying cohort to overcome the biased sampling problems but fitted a continuous parametric model with discrete observations, while the discreteness of data is in fact a sort of interval censoring caused by daily reports.

To the best of our knowledge, generation time is usually directly estimated by the time difference between symptoms onset of successive cases in a chain of transmission rather than the actual time of infection, that is, the serial interval. This is because it is challenging to obtain both the corresponding infection dates of the primary case and its secondary cases in a chain of transmission, while the dates of symptoms onsets are relatively easier to obtain. However, the distribution of serial interval may be biased for estimating generation time, especially when the disease is infectious during incubation, in which the variance could be overestimated (Britton and Scalia Tomba, 2019). As a result, the subsequent quantities estimated based on the generation time is biased. For example, the basic reproduction number, indicating the spreading ability of an infectious disease, would be underestimated. Note that COVID‐19 is incubation‐infectious, hence the estimation of generation time simply based on observed serial intervals is not consistent.

To overcome the issues aforementioned, in this paper we estimate the distribution of incubation period using the well‐studied renewal process where there exists a censoring event within the incubation period. Vardi (1982a, 1982b, 1989) discussed nonparametric maximum likelihood estimation based on length‐biased sampling and renewal process with incomplete renewal data, and further the multiplicative censoring problem. A brief review can be found in Qin (2017). Issues related to the length‐biased sampling and interval‐censoring sampling are both taken into consideration in the estimation of incubation distribution in this study. We have shown that under mild assumptions, parameters in the incubation distribution are identifiable and enjoy desirable asymptotic properties. Furthermore, a consistent estimator for the distribution of generation time is also proposed based on incubation period and observed serial interval for incubation‐infectious and incubation‐noninfectious diseases, respectively. Our approaches increase available sample size and utilize censored information in the early phase of an epidemic outbreak.

The rest of this paper is organized as follows. Section 2 describes the motivation data. In Section 3, we propose algorithms to estimate the distribution of incubation period and show that under mild assumptions the model parameters are identifiable and enjoy desirable asymptotic properties. In Section 4, we propose algorithms to estimate the distribution of generation time. Simulation studies are performed in Section 5, and the analyzed results to the current outbreak of COVID‐19 in China are shown in Section 6. Further discussion is given in Section 7.

2. MOTIVATING DATA

The COVID‐19 outbreak in Wuhan, China, has attracted worldwide attention (Huang et al., 2020; Tu et al., 2020; Wang et al., 2020). Publicly available data were collected from provincial and municipal health commissions in China and ministry of health in other countries and areas. The following details were collected on each confirmed case: case ID, region, age, gender, date of symptoms onset, date of diagnosis, history of travel, or previous residency in Wuhan, and, if available, related information regarding contact history with other confirmed cases. As of March 31, 2020, a total of 14,829 lab‐confirmed COVID‐19 cases were reported outside Hubei Province by the National Health Commission of China.

In the collected data, 645 chains of transmission were found in the collected data, and $n=198$ of them have their dates of symptoms onset available, which can be used to calculate serial intervals (You et al., 2020). These 198 observed serial intervals, $\{s_j,j=1,\dots ,n\}$, range from −13 to 21 days, with a mean of 4.6 days and quartiles of 1, 4, and 7 days. The same subset of the data used in Qin et al. (2020) is considered in this study for the estimation of the incubation period. This subset includes the confirmed cases that left Wuhan between January 19 and January 23, 2020, and excludes cases that developed symptoms before leaving Wuhan. There is a total of $m=1211$ cases that meet such criteria in the collected data. These 1211 observed durations between departure from Wuhan and symptoms onset outside Hubei Province, $\{t_j,j=1,\dots ,m\}$, range from 0 to 22 days with a mean of 5.4 days and quartiles of 2, 5, and 8 days. It is worth noting that Bi et al. (2020) reported that 191 travelers developed symptoms 4.9 days on average after arriving in Shenzhen (Guangdong Province, China).

It is arguable that people who left Wuhan might have higher chance to be infected on the day of departure since it is easier to be exposed to the human‐to‐human transmitted virus in a crowded environment. Hence in our dataset, there might be two types of individuals: (a) those who got infected during their stay in Wuhan and developed symptoms outside Hubei Province, and (b) those who got infected at the time of leaving Wuhan, for example, at the airport, railway station, or on the way from Wuhan to their destinations. Thus, the observed durations between departure from Wuhan and symptoms onset are from a mixture of two distributions: the time between departure from Wuhan and symptoms onset (forward time), and the complete incubation period. Note that the selected cohort is length‐biased since the ones with shorter incubation periods who got infected were less likely to be captured as they had higher chance to develop symptoms before leaving Wuhan. The length‐biased issue cannot be tested easily in the data but has naturally arisen from the data collection process, since only those who developed symptoms after departure from Wuhan can be collected.

3. ESTIMATION OF INCUBATION PERIOD

In this section, the distribution of incubation is estimated through theory of renewal process and interval censoring with a mixture distribution. Here we have to assume that the distribution of incubation period is same between the Wuhan residents who had a schedule to leave Wuhan and the general population. Furthermore, given an individual who got infected in Wuhan and developed symptoms outside Wuhan, it is reasonable to assume that the event of departing from Wuhan is independent of the event of infection and manifestation of symptoms. Hence, we can consider the incubation period as a continuous random variable, I, as the sum of forward and backward times, and the duration between departure from Wuhan and onset of symptoms as the forward time V in renewal process (see Figure 1 as an illustration). Suppose that I and V are continuous and let $f_I(·)$ be the probability density function (pdf) of incubation period, and $h(·)$ be the pdf of forward time. According to Qin (2017) and Qin et al. (2020), we have

$$h(t)=\frac{S(t)}{E(I)}=\frac{{\int }_t^{+\infty }{f}_I(y)dy}{{\int }_0^{+\infty }y{f}_I(y)dy},t>0,$$ (1)

where $S(·)$ is the survival function and $E(I)$ is the expectation of I.

FIGURE 1.

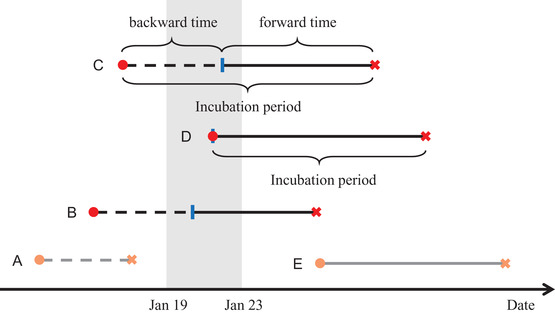
Illustration of complete incubation period and forward time Note. Red circle: getting infected; blue column: departure from Wuhan; red cross: symptoms onset. The shaded area is the period during which our cohort sample departed from Wuhan. This figure shows five types of individuals. Only those who departed from Wuhan in the shaded area were collected in our cohort. (A) Symptoms onset in Wuhan, not in our cohort; (B and C) captured in our cohort with infection before departure; (D) captured in our cohort with infection at departure; (E) infection outside Wuhan, not in our cohort. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

Note that I is not observable in our dataset but V is observable with observations of $\{t_j\},j=1,\dots ,m$. From Equation (1), we can see that the forward time V should have a monotonically decreasing density. However, the observed density of $\{t_j\}$ does not seem to be monotone (see Figure 3). A possible explanation toward it would be that $\{t_j\}$ are not observations of V only but mixture of V and I. As aforementioned, due to the nature of a human‐to‐human infectious disease, it is easier to get infected at the airport/train station or on the flight/train/bus, namely, the infection occurs at the departure. In such case, the duration between departure from Wuhan and onset of symptoms is no longer the forward time, but the complete incubation period. Taking such possibility into account, let π be the (unknown) probability of getting infected at the departure time from Wuhan, and $1-\pi$ be the probability of getting infected before departure. Therefore, the duration between departure from Wuhan and symptoms onset follows a mixture distribution with density

$$Q(t;\mathit{\theta },\pi )=\pi f_I(t;\mathit{\theta })+(1-\pi )h(t;\mathit{\theta }),t>0,$$ (2)

where θ is the model parameter in $f_I(·)$ and $h(·)$.

FIGURE 3.

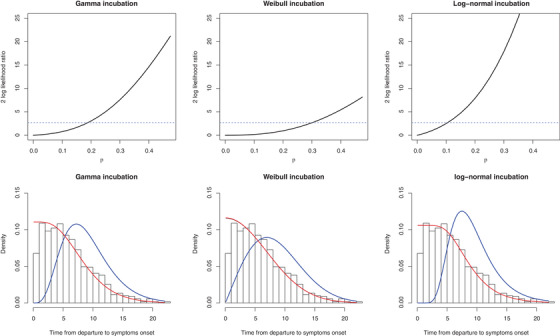
COVID‐19 data analysis result Note. Upper: twice of log‐likelihood ratio, $2[{\max }_{\mathit{\theta },\pi }\ell (\mathit{\theta },\pi )-{\max }_{\mathit{\theta }}\ell (\mathit{\theta },\pi )]$, versus π. The dashed line is at 2.71, the 90% quantile of chi‐squared distribution with 1 degree of freedom. In fact, the horizontal ordinate of the crossover point is the 95% upper bound of π by likelihood ratio, since $0.5+0.5{\chi }^2(2.71,1)=0.95$ (mixed chi‐squared distribution), where ${\chi }^2(·,1)$ is the cdf of chi‐squared distribution with 1 degree of freedom. Lower: incubation estimation; red line: forward time fit; blue line: incubation period fit; black line: mixed observed time fit (covered by the red line). This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

Accounting for the error caused by daily reports, we can simply let $t_j^{+}=t_j+0.5$ and $t_j^{-}=t_j-0.5$. The estimates of θ and π can be estimated by directly maximizing the likelihood function with interval censoring, that is,

$$\begin{array}{ccc}\hfill L(\mathit{\theta },\pi ;t_1,\dots ,t_m)& =& \prod _{j=1}^m\left[\pi \{F_I(t_j^{+};\mathit{\theta })-F_I(t_j^{-};\mathit{\theta })\}\right.\hfill \\ & & \left.+(1-\pi )\{H(t_j^{+};\mathit{\theta })-H(t_j^{-};\mathit{\theta })\}\right],\hfill \end{array}$$ (3)

where $F_I$ and H are the cumulative distribution functions (cdf) of I and V, respectively. We denote the maximum likelihood estimate of ${({\mathit{\theta }}^{\top },\pi )}^{\top }$ by ${({\widehat{\mathit{\theta }}}^{\top },\widehat{\pi })}^{\top }=arg{sup}_{\mathit{\theta },\pi }\ell (\mathit{\theta },\pi )$, where $\ell (\mathit{\theta },\pi )=\log L(\mathit{\theta },\pi ;t_1,\dots ,t_m)$. In Web Appendix B, we will provide an alternative interpretation for the likelihood function.

In general, it is difficult to derive asymptotic properties of the estimator for interval‐censoring cases (see Gentleman and Geyer, 1994; Lehmann and Romano, 2006). However, the asymptotic properties can be proved under our particular setting, in which we have identical interval lengths for all observations, namely $t_j^{+}-t_j^{-}=1$ for $j=1,\dots ,m$. Let $(t_j^{-},t_j^{+})$ for $j=1,\dots ,m$ be independently and identically distributed observations from the mixture model (2). Define a pseudo‐pdf for the mixed model (2) as

$$\begin{array}{ccc}\hfill Q^p(t_j;\mathit{\theta },\pi )& =& \pi \{F_I(t_j^{+};\mathit{\theta })-F_I(t_j^{-};\mathit{\theta })\}\hfill \\ & & +(1-\pi )\{H(t_j^{+};\mathit{\theta })-H(t_j^{-};\mathit{\theta })\}.\hfill \end{array}$$ (4)

It is straightforward to show that ${\int }_{-\infty }^{+\infty }{Q}^p(t;\mathit{\theta },\pi )dt=1$ by the Fubini theorem. For notational simplicity, let $F_I(t_j^{+};\mathit{\theta })-F_I(t_j^{-};\mathit{\theta })=f_I^p(t_j;\mathit{\theta })$ and $H(t_j^{+};\mathit{\theta })-H(t_j^{-};\mathit{\theta })=h^p(t_j;\mathit{\theta })$. The corresponding pseudo‐log‐likelihood (loglik) for the mixed model is

$$\ell (\mathit{\theta },\pi )=\sum _{j=1}^m\log \{\pi f_I^p(t_j;\mathit{\theta })+(1-\pi )h^p(t_j;\mathit{\theta })\}.$$ (5)

Define two likelihood ratio functions:

$$\begin{array}{ccc}\hfill R_1(\mathit{\theta },\pi )& =& 2\{\underset{\mathit{\theta },\pi }{sup}\ell (\mathit{\theta },\pi )-\ell (\mathit{\theta },\pi )\}=2\{\ell (\widehat{\mathit{\theta }},\widehat{\pi })-\ell (\mathit{\theta },\pi )\},\hfill \\ \hfill R_2(\pi )& =& 2\{\underset{\mathit{\theta },\pi }{sup}\ell (\mathit{\theta },\pi )-\underset{\mathit{\theta }}{sup}\ell (\mathit{\theta },\pi )\}=2\{\ell (\widehat{\mathit{\theta }},\widehat{\pi })\hfill \\ & & -\underset{\mathit{\theta }}{sup}\ell (\mathit{\theta },\pi )\}.\hfill \end{array}$$

Let ${({\mathit{\theta }}_0^{\top },{\pi }_0)}^{\top }$ be the true parameter value. For notational simplicity, let $g(t;\mathit{\phi })$ denote the density in (4) with $\mathit{\phi }={({\mathit{\theta }}^{\top },\pi )}^{\top }$, that is, $g(t;\mathit{\phi })=Q^p(t;\mathit{\theta },\pi )$. In addition, let $q_{\mathit{\theta }}$ denote the dimension of θ , ${\nabla }_{\mathit{\phi }}=\partial /\partial \mathit{\phi }$ and ${\nabla }_{\mathit{\phi }{\mathit{\phi }}^{\top }}={\partial }^2/(\partial \mathit{\phi }\partial {\mathit{\phi }}^{\top })$. The upcoming expectations are taken with respect to the true density $g(t;{\mathit{\phi }}_0)$, where ${\mathit{\phi }}_0={({\mathit{\theta }}_0^{\top },{\pi }_0)}^{\top }$. To establish the asymptotic result, we make the following regularity condition.

Condition 1

Let $T\sim g(t;{\mathit{\phi }}_0)$, and

• (a) $E\parallel {\nabla }_{\mathit{\phi }}\log \{g(T;{\mathit{\phi }}_0)\}\parallel <\infty$;
• (b) $U=-E[{\nabla }_{\mathit{\phi }{\mathit{\phi }}^{\top }}\log \{g(T;{\mathit{\phi }}_0)\}]$ is finite and nonsingular;
• (c) $E[{\nabla }_{\mathit{\phi }{\mathit{\phi }}^{\top }}\log \{g(T;\mathit{\phi })\}]$ is continuous for φ in a neighborhood of φ ₀.

The nonsingularity of U in Condition 1(b) excludes the cases where at least one of θ and π is not identifiable. Theorem 1 shows the asymptotic properties of the estimator ${({\widehat{\mathit{\theta }}}^{\top },\widehat{\pi })}^{\top }$ if the true parameter value is an interior point in the parameter space, while Theorem 2 shows the case if π₀ is at the boundary.

Theorem 1

Suppose that $g(t;\mathit{\phi })$ and φ ₀ satisfy Condition 1, and that ${({\mathit{\theta }}_0^{\top },{\pi }_0)}^{\top }$ is an interior point in the parameter space. As $m\to \infty$, (a) $\sqrt{m}{({\widehat{\mathit{\theta }}}^{\top }-{\mathit{\theta }}_0^{\top },\widehat{\pi }-{\pi }_0)}^{\top }\stackrel{d}{\to }N(0,U)$, where $\stackrel{d}{\to }$ means convergence in distribution; (b) $R_1({\mathit{\theta }}_0,{\pi }_0)\stackrel{d}{\to }{\chi }_{q_{\mathit{\theta }}+1}^2$; (c) $R_2({\pi }_0)\stackrel{d}{\to }{\chi }_1^2$.

We partition U as $U={(U_{ij})}_{1\le i,j\le 2}$, where U ₁₁ is a $q_{\mathit{\theta }}\times q_{\mathit{\theta }}$ matrix. Let $x_{+}=\max (x,0)$, $x_{-}=\min (x,0)$, $Y_1\sim N(0,I_{q_{\mathit{\theta }}})$, and $Y_2\sim N(0,1)$ such that Y ₁ and Y ₂ are independent of each other.

Theorem 2

Suppose that $g(t;\mathit{\phi })$ and φ ₀ satisfy Condition 1, and that θ ₀ is an interior point in the parameter space of θ and ${\pi }_0=1$. As $m\to \infty$,

$$\begin{array}{ccc}& & (a)\sqrt{m}\left(\begin{array}{c}\widehat{\mathit{\theta }}-{\mathit{\theta }}_0\\ \widehat{\pi }-{\pi }_0\end{array}\right)\stackrel{d}{\to }\hfill \\ & & \left(\begin{array}{c}{U}_{11}^{-1/2}{Y}_1-U_{11}^{-1}{U}_{12}{(U_{22}-U_{12}^{\top }{U}_{11}^{-1}{U}_{12})}^{-1/2}{(Y_2)}_{-}\\ {(U_{22}-U_{12}^{\top }{U}_{11}^{-1}{U}_{12})}^{-1/2}{(Y_2)}_{-}\end{array}\right);\hfill \end{array}$$

(b) $R_1({\mathit{\theta }}_0,{\pi }_0)\stackrel{d}{\to }\frac{1}{2}{\chi }_{q_{\mathit{\theta }}}^2+\frac{1}{2}{\chi }_{q_{\mathit{\theta }}+1}^2$; and (c) $R_2({\pi }_0)\stackrel{d}{\to }\frac{1}{2}{\chi }_0^2+\frac{1}{2}{\chi }_1^2$.

If ${\pi }_0=0$, then in the right‐hand side of the formula in (a) ${(Y_2)}_{-}$ should be replaced with ${(Y_2)}_{+}$.

The proof of Theorems 1 and 2 is given in Web Appendix C. We can easily verify that the interval‐censored mixture distribution (4) for Gamma, Weibull (except when shape parameter of Gamma or Weibull is 1, ie, the exponential distribution), or log‐normal distribution satisfies Condition 1 and thus the above two theorems hold for our estimates.

4. ESTIMATION OF GENERATION TIME

In this section, we study the estimation of generation time based on serial interval and incubation time under proper assumptions. The estimation of generation time only subjects to symptomatic population. Suppose an infector got infected at calendar time T ₀ and showed symptoms at T ₁. This infector infected an infetee at calendar time T ₂, and the infectee showed symptoms at T ₃. Let $G=T_2-T_0$ denote the generation time, $S=T_3-T_1$ denote the serial interval, $I_1=T_1-T_0$ and $I_2=T_3-T_2$ be the incubation period of infector and infectee, respectively. It is straightforward to see that $G=S+I_1-I_2$.

If a disease is noninfectious during the incubation period (eg, SARS; Lipsitch et al., 2003), then we can naturally assume 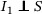and 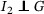. Then it follows that $f_G=f_S$, where $f_G$ and $f_S$ are the pdfs of G and S, respectively, and the generation time can be estimated by serial interval without inducing bias. However, such case does not apply for COVID‐19 as there were reported asymptomatic infections (Rothe et al., 2020). Instead, we assume 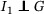, , 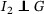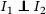. The first part states that the incubation period of the primary case is independent of its generation time. This is true if the disease is infectious during incubation period, and in addition, the ability to pass the pathogens to susceptible host is independent of whether the symptoms are being developed. The rest is straightforward due to the standard assumption of independence between individuals. In addition, we assume that the distribution of incubation period, generation time, and serial interval is homogeneous among all individuals. Furthermore, to ensure that the observed serial intervals could reflect the serial interval of general population, we assume that the missingness (failure of establishing contact‐tracing) was independent of the length of serial interval. Hence, we obtain that

$$f_G\ast f_{-I}\ast f_I=f_S,$$ (6)

where the symbol * represents convolution, $f_G$. $f_S$, $f_I$, and $f_{-I}$ are the pdfs of G, S, I, and $-I$, respectively. Thus, $f_G$ is identifiable through characteristic function (chf) (or Fourier transformation). The chf of G is ${\varphi }_G(t)={\varphi }_S(t)/{\varphi }_I(t){\varphi }_{-I}(t)$, where ${\varphi }_S(t)$, ${\varphi }_I(t)$ and ${\varphi }_{-I}(t)$ are the chf of S, I, and $-I$, respectively. By the continuous inversion formula (Durrett, 2019), the pdf of the generation time is

$$f_G(y)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{e}^{-ity}\frac{{\varphi }_S(t)}{|{\varphi }_I{(t)|}^2}dt,$$ (7)

where $i=\sqrt{-1}$, ${\varphi }_I(t)$ can be approximated through the estimated distribution of I introduced in previous section, and ${\varphi }_S(t)$ can be estimated by the observed serial intervals, $\{s_1,\dots ,s_n\}$, along with a proper kernel $K(·)$, that is,

$${\widehat{\varphi }}_S(t)={\int }_{-\infty }^{\infty }{e}^{ity}\frac{1}{n{h}_n}\sum _{j=1}^{n}K\left(\frac{y-s_j}{h_n}\right)dy=\frac{1}{n}\sum _{j=1}^n{e}^{it{s}_j}{\varphi }_K(t{h}_n),$$ (8)

where $h_n$ is the bandwidth. Note that G must be positive, so to account for the boundary bias, Karunamuni (2009) proposed to use boundary kernel $K_c(t;y)=a_0(y)K(t)+a_1(y)K^{\prime }(t)$ with

$$\left(\begin{array}{c}{a}_0(y)\\ a_1(y)\end{array}\right)={\left(\begin{array}{cc}{\int }_{-\infty }^{y/h_n}K(t)dt& {\int }_{-\infty }^{y/h_n}{K}^{\prime }(t)dt\\ {\int }_{-\infty }^{y/h_n}tK(t)dt& {\int }_{-\infty }^{y/h_n}t{K}^{\prime }(t)dt\end{array}\right)}^{-1}\left(\begin{array}{c}1\\ 0\end{array}\right).$$

at the point $y>0$. Denote the Fourier transformation ${\varphi }_{K_c}(t)={\int }_{-\infty }^{\infty }{e}^{itu}{K}_c(u)du$. Hence, a consistent estimator for $f_G$ is defined as

$$\begin{array}{cc}\hfill {\widehat{f}}_G(y)& =\frac{1}{2n\pi }\sum _{j=1}^n{\int }_{-M_n}^{M_n}Re{e}^{it(s_j-y)}\frac{{\varphi }_{K_c}(t{h}_n)}{|{\widehat{\varphi }}_I{(t)|}^2}dt,\hfill \end{array}$$ (9)

where $M_n\to \infty$, $h_n\to 0$ as $n\to \infty$, and $Re$ is the operator taking the real part of a complex value. This estimator is consistent at any interior point in the support of G, provided that the model for incubation period I is correctly specified (Liu and Taylor, 1989). It is equivalent to specifying a kernel density or a kernel chf, and possible choices are the Vallée Poussin (Fejér) kernels or Cesàro kernels (Devroye, 1989; Anastassiou, 2000). Note that the generation time must be positive. To correct the bias for devonvolution at the boundary $G=0$, a second‐order correction to remove the boundary effect was proposed by Karunamuni (2000, 2009). The density function ${\widehat{f}}_G$ can also be obtained by imposing a parametric model on generation time and fit the density for serial interval, which relies heavily on model specification. More details about the conditions and properties of deconvolution is shown in Web Appendix D.

5. SIMULATION STUDY

In this numerical study, we assess the performances of our proposed method and the following methods in estimation of incubation period:

• 1.The renewal process based mixture model in Qin et al. (2020), which is denoted as Qin's method hereafter, note that the original method in Qin et al. (2020) is not suitable to be applied in our simulation as the mixture proportion π was prefixed, hence we alter their method by estimating π simultaneously, as a result the Qin's method here is actually an improved version of the method in Qin et al. (2020) and the only difference between Qin's method and our method would be treating the observed $t_j$s with censored intervals.
• 2.The interval censoring–based method in Backer et al. (2020) and Linton et al. (2020), which is denoted as IC method hereafter.

In order to produce simulation settings similar to the collected dataset of COVID‐19, we consider three simulation settings for incubation period in the following numerical examples: the incubation period I follows (a) Gamma distribution Γ(5, 0.8), (b) Weibull distribution W(2, 8), and (c) log‐normal distribution $LN(1.8,0.4^2)$. The density functions of these distributions are given in Web Appendix A. For each setting, we mimic the length‐biased sampling process by letting the time from infection to departure C follow uniform distribution on (0,30) and recording the time from departure to symptoms onset (forward time) $V=I-C$ if $I>C$, until the designated sample size is achieved. The simulated values of V are then rounded up to the nearest integers. We vary the sample size m over 600, 1200, and 1800, and π over 0 and 0.2. Each setting is repeated for 1000 times.

Table 1 summarizes the estimates of parameters in incubation distribution using the Qin's method, interval‐censoring method, and our proposed method. We can see that when $\pi =0$, our proposed method and Qin's method provide similar results. For $\pi =0.2$, our approach has smaller bias in Weibull setting. Due to the fact that the loglik is too flat near the maximum, the estimates may be a little biased in finite sample. With larger sample size, the bias is getting smaller. The IC method does not perform well in our simulation as it does not take the length‐biased sampling issue and the cross infection probability π into consideration.

TABLE 1.

Estimation of incubation distribution in simulation

(a) Gamma incubation $f_I(t;\mathit{\theta })={\beta }^{\alpha }{t}^{\alpha -1}{e}^{-\beta t}/\mathrm{\Gamma }(\alpha )$; $\alpha =5$, $\beta =0.8$
		Proposed method			Qin's method			IC method
π	m	$\widehat{\alpha }$ (SE)	$\widehat{\beta }$ (SE)	$\widehat{\pi }$ (SE)	$\widehat{\alpha }$ (SE)	$\widehat{\beta }$ (SE)	$\widehat{\pi }$ (SE)	$\widehat{\alpha }$ (SE)	$\widehat{\beta }$ (SE)	$\widehat{\pi }$ (SE)
0	600	4.43	0.76	0.11	4.47	0.76	0.10	9.79	1.07	0
		(1.22)	(0.14)	(0.14)	(1.13)	(0.13)	(0.12)	(1.24)	(0.14)	(0)
	1200	4.47	0.76	0.09	4.49	0.76	0.08	9.72	1.06	0
		(0.94)	(0.10)	(0.11)	(0.89)	(0.10)	(0.09)	(0.88)	(0.10)	(0)
	1800	4.55	0.77	0.07	4.54	0.76	0.07	9.70	1.06	0
		(0.77)	(0.08)	(0.09)	(0.75)	(0.08)	(0.08)	(0.82)	(0.08)	(0)
0.2	600	5.36	0.83	0.20	5.37	0.83	0.19	9.61	1.00	0
		(1.64)	(0.17)	(0.15)	(1.62)	(0.17)	(0.14)	(1.21)	(0.13)	(0)
	1200	5.33	0.83	0.19	5.33	0.82	0.18	9.51	0.99	0
		(1.28)	(0.13)	(0.11)	(1.29)	(0.13)	(0.11)	(0.83)	(0.09)	(0)
	1800	5.25	0.82	0.19	5.25	0.82	0.19	9.49	0.99	0
		(1.08)	(0.10)	(0.10)	(1.10)	(0.11)	(0.10)	(0.67)	(0.07)	(0)

(b) Weibull incubation $f_I(t;\mathit{\theta })=k{(t/\lambda )}^{k-1}\exp \{-{(t/\lambda )}^k\}/\lambda$; $k=2$, $\lambda =8$
		Proposed method			Qin's method			IC method
π	m	$\widehat{k}$ (SE)	$\widehat{\lambda }$ (SE)	$\widehat{\pi }$ (SE)	$\widehat{k}$ (SE)	$\widehat{\lambda }$ (SE)	$\widehat{\pi }$ (SE)	$\widehat{k}$ (SE)	$\widehat{\lambda }$ (SE)	$\widehat{\pi }$ (SE)
0	600	1.92	7.49	0.11	2.00	7.89	0.02	3.49	11.99	0
		(0.24)	(0.86)	(0.17)	(0.19)	(0.47)	(0.05)	(0.24)	(0.30)	(0)
	1200	1.93	7.57	0.09	2.00	7.95	0.01	3.57	12.00	0
		(0.19)	(0.72)	(0.14)	(0.13)	(0.34)	(0.03)	(0.17)	(0.20)	(0)
	1800	1.93	7.62	0.07	2.00	7.97	0.01	3.56	12.00	0
		(0.16)	(0.64)	(0.12)	(0.11)	(0.27)	(0.02)	(0.14)	(0.17)	(0)
0.2	600	2.07	8.20	0.19	2.18	8.70	0.10	3.48	12.42	0
		(0.29)	(1.05)	(0.19)	(0.22)	(0.71)	(0.11)	(0.21)	(0.29)	(0)
	1200	2.04	8.17	0.19	2.17	8.73	0.09	3.46	12.44	0
		(0.23)	(0.88)	(0.15)	(0.16)	(0.59)	(0.09)	(0.15)	(0.20)	(0)
	1800	2.03	8.14	0.19	2.17	8.73	0.09	3.45	12.43	0
		(0.20)	(0.80)	(0.14)	(0.14)	(0.53)	(0.08)	(0.12)	(0.16)	(0)

(c) Log‐normal incubation $f_I(t;\mathit{\theta })=\exp \{-{(\log t-\mu )}^2/2{\sigma }^2\}/\sqrt{2\pi {\sigma }^2}t$; $\mu =1.8$, $\sigma =0.4$
		Proposed method			Qin's method			IC method
π	m	$\widehat{\mu }$ (SE)	$\widehat{\sigma }$ (SE)	$\widehat{\pi }$ (SE)	$\widehat{\mu }$ (SE)	$\widehat{\sigma }$ (SE)	$\widehat{\pi }$ (SE)	$\widehat{\mu }$ (SE)	$\widehat{\sigma }$ (SE)	$\widehat{\pi }$ (SE)
0	600	1.73	0.42	0.08	1.74	0.42	0.07	2.18	0.33	0
		(0.10)	(0.04)	(0.10)	(0.10)	(0.04)	(0.09)	(0.02)	(0.02)	(0)
	1200	1.74	0.42	0.06	1.75	0.42	0.05	2.18	0.33	0
		(0.08)	(0.03)	(0.07)	(0.07)	(0.03)	(0.07)	(0.02)	(0.02)	(0)
	1800	1.75	0.42	0.05	1.76	0.41	0.04	2.18	0.33	0
		(0.07)	(0.03)	(0.06)	(0.06)	(0.03)	(0.06)	(0.01)	(0.01)	(0)
0.2	600	1.82	0.39	0.18	1.83	0.39	0.18	2.22	0.33	0
		(0.11)	(0.04)	(0.11)	(0.10)	(0.04)	(0.11)	(0.02)	(0.02)	(0)
	1200	1.82	0.39	0.19	1.82	0.39	0.18	2.22	0.33	0
		(0.08)	(0.03)	(0.08)	(0.08)	(0.03)	(0.08)	(0.02)	(0.01)	(0)
	1800	1.81	0.40	0.19	1.81	0.40	0.19	2.22	0.33	0
		(0.06)	(0.03)	(0.07)	(0.06)	(0.03)	(0.07)	(0.01)	(0.01)	(0)

Note. Estimates and standard error. The first panel is our proposed method: mixture distribution with censoring. The second panel is Qin's method. The third panel is the IC method.

For generation time estimation, we assume that both generation time and incubation period follow Gamma distributions. The mean and variance of these two periods are listed in Figure 2. We generate 200 serial intervals. Note that it is possible that some serial intervals are negative. We choose the kernel chf ${\varphi }_K(t)={(1-t^2)}_{+}^3$, and according to Karunamuni (2009), ${\varphi }_{K_c}(t;y)=\{a_0(y)-i{a}_1(y)t\}{(1-t^2)}^{3}I(|t|\le 1)$, where

$$\begin{array}{ccc}\hfill \left(\begin{array}{c}{a}_0(y)\\ a_1(y)\end{array}\right)& =& {\left(\begin{array}{c}{\int }_{-\infty }^{y/h}\frac{48[t(t^2-15)\cos (t)+3(5-2t^2)\sin (t)]}{\pi t^7}dt\hfill \\ -{\int }_{-\infty }^{y/h}\frac{48[5t(2t^2-21)\cos (t)+(t^4-45t^2+105)\sin (t)]}{\pi t^8}dt\hfill \\ {\int }_{-\infty }^{y/h}\frac{48[t(t^2-15)\cos (t)+3(5-2t^2)\sin (t)]}{\pi t^6}dt\hfill \\ -{\int }_{-\infty }^{y/h}\frac{48[5t(2t^2-21)\cos (t)+(t^4-45t^2+105)\sin (t)]}{\pi t^7}dt\hfill \end{array}\right)}^{-1}\hfill \\ & & \times \left(\begin{array}{c}1\\ 0\end{array}\right).\hfill \end{array}$$

The results are displayed in Figure 2. The cyan line is the fitted Gamma density using observed positive serial interval data. The red line is the estimated generation time density by deconvolution. We can see that the estimated density of generation time by deconvolution is more close to the true density than fitting the serial intervals, although the deconvolution estimate may be negative in some area.

FIGURE 2.

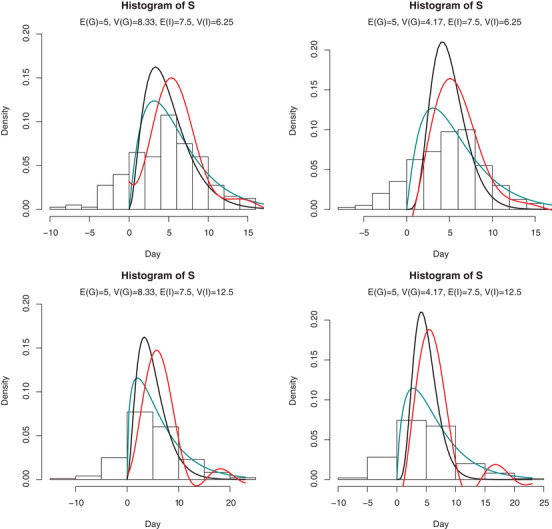
Histogram of serial interval data and density of generation time in simulation Note. The expectation and variance of generation time and incubation period are listed in each subfigure. Black line: true density; cyan line: Gamma fit of S by deleting negative observations; red line: estimated density. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

6. ANALYSIS RESULTS ON THE COVID‐19 OUTBREAK

In this section, we analyze the real data of COVID‐19 outbreak, originated from Wuhan, China. As described in Section 2, the times between departure from Wuhan and symptoms onset were collected for the 1211 cases that got infected in Wuhan and developed symptoms outside Hubei Province; see Figure 3 for the histogram of the collected observations.

Table 2 summarizes the estimates of model parameters as defined in Section 3 and quantiles in the incubation distribution with their 95% confidence intervals (CIs) by nonparametric bootstrap. The last two columns list the loglik and goodness‐of‐fit (GoF) χ² statistic of each parametric distribution of the incubation period, with higher loglik and lower GoF means a better fit of the model. The number in the bracket of GoF is the P‐value of GoF test, and all these three models have a good fit. More details about the GoF test is in Web Appendix E. Likelihood ratio test about π can be conducted based on the mixture distribution of half 0 and half chi‐squared distribution with 1 degree of freedom to infer the magnitude of π (Self and Liang, 1987; Susko, 2013). At significant level 0.05, the critical value is 2.71. Although the point estimate of π is zero, the loglik is flat in the region $\pi \in [0,0.2]$, which results in a situation where a null hypothesis such as $H_0:\pi >0.1$ or $H_0:\pi <0.1$ cannot be reject at significant level 0.05, since $2[{\max }_{\mathit{\theta }}\ell (\mathit{\theta },0)-{\max }_{\mathit{\theta }}\ell (\mathit{\theta },0.1)]<2.71$ (illustrated in Figure 3). Our model estimated that about 1% of patients have incubation periods longer than 21 days. This might influence the length of quarantine period in regions with a severe epidemic.

TABLE 2.

Estimation of incubation distribution for COVID‐19 data

(a) Gamma incubation
α	β	π	Mean	0.25 Q	Median	0.75 Q	0.90 Q	0.99 Q		GoF
95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	loglik	(P‐value)
4.97	0.55	0.00	9.10	6.13	8.50	11.43	14.57	21.17	−3260	13.46
[3.75;	[0.45;	[0.00;	[7.86;	[4.97;	[7.22;	[10.02;	[13.22;	[19.63;		(0.41)
6.25]	0.66]	0.15]	9.66]	6.80]	9.15]	11.98]	15.10]	22.07]

(b) Weibull incubation
k	λ	π	Mean	0.25 Q	Median	0.75 Q	0.90 Q	0.99 Q		GoF
95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI		(P‐value)
2.04	9.70	0.00	8.60	5.26	8.10	11.39	14.61	20.53	−3260	14.09
[1.72;	[7.88;	[0.00;	[7.03;	[3.84;	[6.40;	[9.52;	[12.69;	[18.58;		(0.37)
2.26]	10.25]	0.27]	9.08]	5.86]	8.67]	11.91]	15.11]	21.38]

(c) Log‐normal incubation
μ	σ	π	Mean	0.25 Q	Median	0.75 Q	0.90 Q	0.99 Q		GoF
95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	95% CI	loglik	(P‐value)
2.17	0.39	0.00	9.44	6.70	8.74	11.39	14.46	21.82	−3263	15.44
[2.08;	[0.35;	[0.00;	[8.81;	[6.03;	[8.02;	[10.76;	[13.78;	[20.59;		(0.28)
2.24]	0.43]	0.00]	9.99]	7.33]	9.36]	11.94]	15.02]	22.81]

Note. Model parameter estimates, incubation quantiles (with 95% CIs), log‐likelihood, goodness‐of‐fit statistic in the distribution estimation of incubation period.

Figure 3 plots the twice of loglik ratio, $2[{\max }_{\mathit{\theta },\pi }\ell (\mathit{\theta },\pi )-{\max }_{\mathit{\theta }}\ell (\mathit{\theta },\pi )]$, versus π. The dashed line is at 2.71, the 90% quantile of chi‐squared distribution with 1 degree of freedom. In fact, the horizontal ordinate of the crossover point is the 95% upper bound of π by likelihood ratio, since $0.5+0.5{\chi }^2(2.71,1)=0.95$ (mixed chi‐squared distribution), where ${\chi }^2(·,1)$ is the cdf of chi‐squared distribution with 1 degree of freedom.

From the last two columns in Table 2 we can see that Gamma distribution slightly outperforms among three distributions, having the smallest GoF statistic. The corresponding incubation period has an estimated mean of 9.10 days and median of 8.50 days, and possess a heavy tail. About 10% infected individuals would develop symptoms after 14.57 days and 1% after 21.17 days. Although the CI of π is relatively wide, variation of the results on the quantiles of incubation period is not significant as shown in Table 2. Figure 3 visualizes the estimate on the histogram of the time between leaving Wuhan and symptoms onset.

For the estimation of the distribution of generation time, we choose the kernel chf ${\varphi }_K(t)={(1-t^2)}_{+}^3$ in (9) with bandwidth $h=2$. The estimated probability density of generation time based on the estimated Gamma incubation period is displayed in Figure 4. We can see that the distributions of generation time has much smaller variance than the serial interval.

FIGURE 4.

Estimated generation time density (red line) using 71 observed serial intervals in COVID‐19 outbreak Note. The black line is the density of serial interval data. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

Based on the daily reported new cases from January 20 to January 30, 2020, the early phase of COVID‐19 outbreak, the exponential epidemic growth rate r (Malthusian coefficient) is estimated at 0.275 (SE 0.042) estimated by fitting a least square line to the daily number of reported new confirmed cases in a log‐scale outside Hubei Province (since only by regressing daily new confirmed cases rather than cumulative ones can the residuals be regarded independent). Note that the confirmed cases in Hubei Province were excluded here because there may be a significant underestimation of the number of infected individuals in Hubei Province and the first confirmed case outside Hubei Province was reported on January 20, 2020 (Imai et al., 2020; You et al., 2020). Hence the basic reproduction number can be calculated according to the Euler‐Lotka equation in a moment generating form

$${\widehat{R}}_0=\frac{1}{{\int }_0^{+\infty }{e}^{-rt}{f}_G(t)dt}.$$ (10)

The point estimate of the basic reproduction number is 2.96 with 95% CI [2.15; 3.86]. Note that the estimate of R ₀ is 2.18 using serial interval data instead of generation time, which severely underestimates the infectiousness ability of the disease.

7. DISCUSSION

In this paper, we proposed an estimation for incubation distribution, which only requires information on travel histories and dates of symptoms onset. Unlike the approach in Kuk and Ma (2005), our estimation of incubation period is feasible regardless that the disease is infectious or not during the incubation period. It enhances the estimation by increasing available sample size and utilizing censored information. We also took mixture distribution of forward time and complete incubation period and the interval censoring caused by daily reports into consideration, hence the result should be more robust than that in Qin et al. (2020).

According to the theory of renewal process, the density of forward time should be a decreasing function as it is proportional to the survival function of incubation period. If the density of the observed time between departure from Wuhan and symptoms onset is unimodal, it might be because of the fact that (a) the observations come from a mixture of forward time and full incubation period; (b) the discretized time. Hence, an estimation using mixture distribution together with the censored intervals is recommended if the observed density is not monotonically decreasing. Mixture distribution is robust in incubation analysis in that the potential problem due to the existence of short‐term tourists can be addressed by introducing π into the model. In addition, fewer observations of zeros than ones is still reasonable even if there is no full incubation period mixed in the cohort (when $\pi =0$), as the probability to be captured in our cohort is reduced by half if the “scheduled” departure from Wuhan and symptoms onset occur on the same day, which can be well reflected in the interval‐censoring situation since $F_I(0^{+};\mathit{\theta })-F_I(0^{-};\mathit{\theta })$ is just equal to $F_I(0^{+};\mathit{\theta })$.

Compared with the estimated incubation period in Li et al. (2020), Backer et al. (2020), and Linton et al. (2020), our estimation yields a longer estimate of incubation period. This is possibly because we avoided the selection bias by considering a longer follow‐up period after departure from Wuhan and successfully recruiting the cases with long incubation periods. However, a limitation here is raised by the possible violation of assumption that the individuals included in the study were either infected in Wuhan or on the way to their destination from Wuhan. Violation of such assumption (eg, a family departed from Wuhan together and infection occurred inside the family at destination) leads to an overestimation of incubation period.

Furthermore, a consistent estimation of generation time distribution was proposed under two different scenarios through deconvolution. The efficiency of deconvolution is influenced by the choices of kernel function and the corresponding bandwidth. For a relatively small sample size, the estimate of density function can be negative due to the integration of complex function. The choice of kernel and bandwidth is ad hoc for finite sample size. One possible approach to select kernel and bandwidth is by conducting simulation using prior distribution of generation time.

In the previous studies of the basic reproduction number of COVID‐19, Zhao et al. (2020a, 2020b) estimated R ₀ at 2.56 (95% CI [2.49; 2.63]) through the exponential growth using the distribution of serial interval, which might result in an underestimation due to the use of serial intervals rather than generation time (the serial intervals of SARS and MERS were used in their study rather than that of COVID‐19 due to the lack of information). Jung et al. (2020) estimated R ₀ at 2.1 (95% CI [2.0; 2.2]) and 3.2 (95% CI [2.7; 3.7]) also through the exponential growth under two scenarios using exported cases. Some other estimation were based on dynamic models, such as Wu et al. (2020) at 2.68 (95% CI [2.47; 2.86]) and Read et al. (2020) at 3.11 (95% CI [2.39; 4.13]). Our estimate of R ₀ is a little higher than those estimates obtained by exponential growth rate model that used serial intervals. Note that the recall bias embedded in epidemiology investigation is inevitable as long as contact‐tracing data were used for analysis, which might affect the estimation for generation time and basic reproduction number. It is worth mentioning that there is a large proportion of asymptomatic infected cases (Li et al., 2020). Whether the exponential growth rate can reflect the growth of all infected cases is untestable. If the asymptomatic cases have longer generation time, then the real distribution of generation time would be more variated and the R ₀ would be overestimated.

Supporting information

Web Appendix A, B, C, D and E referenced in Section 3–6, is available with this paper at the Biometrics website on Wiley Online Library.

Deng Y, You C, Liu Y, Qin J, Zhou X‐H. Estimation of incubation period and generation time based on observed length‐biased epidemic cohort with censoring for COVID‐19 outbreak in China. Biometrics. 2021;77:929–941. 10.1111/biom.13325

DATA AVAILABILITY STATEMENT

The data and R codes that support the findings in this paper are openly available on github https://github.com/naiiife/wuhan (Deng et al., 2020).