Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 17;36(27):7956–7964. doi: 10.1021/acs.langmuir.0c01211

Dynamic Surface Tension of Surfactants in the Presence of High Salt Concentrations

Mohsin J Qazi †,*, Simon J Schlegel ‡, Ellen HG Backus ‡,§, Mischa Bonn ‡, Daniel Bonn †, Noushine Shahidzadeh †
PMCID: PMC7366510  PMID: 32545966

Abstract

graphic file with name la0c01211_0013.jpg

We study the influence of high NaCl concentrations on the equilibrium and dynamic surface tensions of ionic (CTAB) and nonionic (Tween 80) surfactant solutions. Equilibrium surface tension measurements show that NaCl significantly reduces the critical micellar concentration (CMC) of CTAB but has no effect on the CMC of Tween 80. Dynamic surface tension measurements allow comparing the surface tension as a function of time for pure surfactant solutions and in the presence of NaCl. For the ionic surfactant, the dynamics agree with the usual diffusion-limited interfacial adsorption kinetics; however, the kinetics become orders of magnitude slower when NaCl is present. Sum-frequency generation spectroscopy experiments and the equilibrium adsorption measurements show that the presence of NaCl in CTAB solution leads to the formation of ion pairs at the surface, thereby neutralizing the charge of the head group of CTAB. This change, however, is not able to account for the slowing down of adsorption dynamics; we find that it is rather the decreases in the monomer concentration (CMC) in the presence of salt which has the major influence. For the nonionic surfactant, the kinetics of interfacial tension is seen to be already very slow, and the addition of salt does not influence it further. This also correlates very well to the very low CMC of Tween 80.

Introduction

Surface-active agents (surfactants) are one of the most commonly used compounds in both daily life as well as in diverse industrial processes. The ability of surfactants to partition at the interface makes them ideal candidates for influencing the surface properties even in very small concentrations.1,2 In addition to the equilibrium state of adsorbed surfactants at the interface, the kinetics at which the surfactants adsorb to the interface is also important in certain processes that involve fast wetting.3−6 For example, in ink-jet printing and pesticide spraying in agriculture, the wetting of surfaces takes place on time scales that can be of the order of milliseconds; consequently, the adsorption kinetics of surfactant molecules to the drop surface is of critical importance for the final result. In addition, adsorption at the liquid/air interface is of particular interest for studying the nucleation and growth of aerosol particles and other related atmospheric phenomena.7−9 In this regard, the understanding of time-dependent adsorption of different compounds at the interface and their interdependence is of crucial importance for atmospheric chemistry.

In principle, immediately after the (instantaneous) creation of a new surface in a surfactant solution, the surface tension has the same value as that of the pure liquid. Subsequently, the adsorption of surfactant in time at the interface leads to the decrease of the surface tension of the liquid until the equilibrium value in the presence of surfactants is reached. The dynamic surface tension (DST) is therefore controlled on the one hand by the nature of the surfactant, for example, chain length, size, and charge of the polar head, and on the other hand by the nature of the liquid and the presence of other additives. In many applications, salts are present or added as an extra additive to enhance the performance of surfactants. Salts can significantly affect the equilibrium surfactant behavior by changing the critical micellar concentrations (CMC), equilibrium surface tensions (γeq), aggregation number, or Krafft temperature.10−15 However, the effect of salts on the DST has received much less attention. Most of the results reported in the literature are limited to the small concentrations of salts (millimolar),16−19 although in several applications, like in crystallization control processes, the salt concentration reaches to very high levels (several molar for NaCl) before salt precipitation.

Beginning in 1907, Milner first suggested that the kinetics of adsorption of a specific surfactant (Sodium oleate) to the interface was limited by diffusion in the bulk of the solution.20 Later, Adam and Shute noted that for some surfactants, the adsorption process was slower than what could be expected from the diffusion of surfactant molecules to the interface.21 They proposed the presence of adsorption barriers to be responsible for slower adsorption of the surfactants to the interface. Reviewing DST data for different surfactants, most studies to date report the adsorption to be controlled by diffusion.22−25

In this study, we investigate both the equilibrium and dynamic behavior of the surfactants in the presence of sodium chloride at concentrations ranging from very low to very high, that is, the solubility limit of NaCl. We find that the kinetics of the ionic surfactant are rather fast compared to the nonionic one and both agree with the above mentioned notion of diffusion-limited adsorption. However, the dynamics of surface tension equilibration slows down dramatically for the ionic surfactant in the presence of a high concentration of salt.

Experimental Section

Materials

The cationic surfactant CTAB (>99% pure; Sigma-Aldrich) and the nonionic surfactant Tween 80 (polysorbate 80, Ameresco, proteomics grade) were chosen because of their exceptional stability in solution at high NaCl concentration; as we have shown previously,26 most surfactants are very sensitive to large amounts of salt and precipitate at high salt concentrations. Stock solutions of CTAB (4 mmolal) and Tween 80 (0.1 % wt, or 0.15 mmolal) were prepared with deionized Millipore water and were later diluted to make smaller concentrations. NaCl (Sigma-Aldrich, > 98% pure) at different concentrations was subsequently added to the surfactant solutions to make the ternary CTAB/NaCl/water and Tween 80/NaCl/water systems. The solutions were stirred and left to stabilize overnight. Densities of both binary and ternary solutions were measured by weighing a precise volume of the solution. We observed that the density of the surfactant solution remains the same as water (0.998 g/mL) for all the concentrations of the surfactants used. For the ternary solutions, that is, surfactant–salt solutions, the density of the solution was the same as the salt solution at this particular concentration [e.g., 1.18 g/L for 5.5 molal (m)]. Viscosities of both binary and ternary systems were measured using an Anton Paar MCR 302 rheometer equipped with a 50 mm 1-degree cone-plate geometry. The viscosities of surfactant solutions were the same as that of pure water (η = 0.001 Pa·s). For the ternary solutions, the viscosities were seen to be equivalent to the viscosity of the pure salt solutions (up to η = 0.0018 Pa·s for the highest salt concentration (5.5 m). Moreover, the viscosities remained constant over the range of shear rate measured (Figure 1), showing that the addition of salts to these surfactant solutions does not affect the shape of micelles in the solution, as has been reported in studies on other surfactants or under different conditions.27−31

Figure 1.

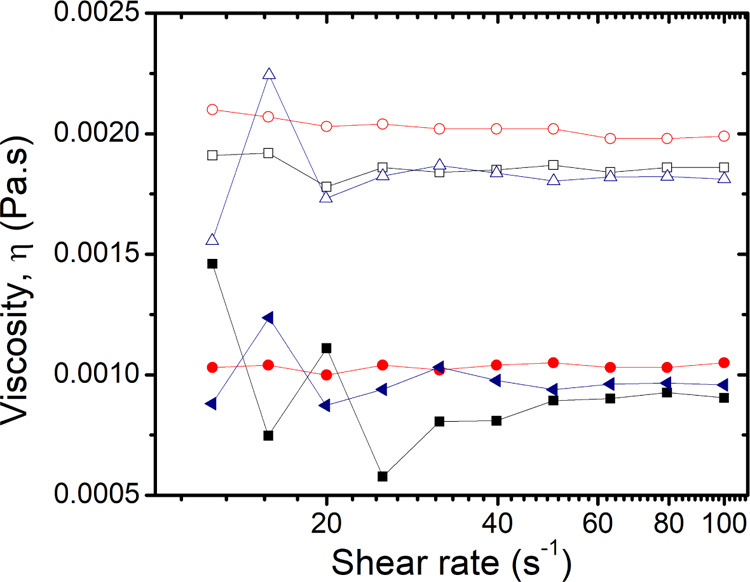
Figure 1

Open in a new tab

Viscosity (η) as a function of shear rate for binary and ternary surfactant solutions. Filled symbols correspond to binary aqueous solutions, and open symbols correspond to ternary solution with 5.5 m NaCl. (Black squares: water; red circles: 0.9 mM CTAB; and blue triangles: Tween 80).

Methods

Equilibrium Surface Tension Measurements

The equilibrium surface tension at different surfactant concentrations at a given salt concentration was measured by using a Kruss K100 tensiometer based on the du Noüy32 ring method equipped with two microdispensers for an automatic dilution system. When working with ternary surfactant–salt solutions, the dilution was achieved by using salt solutions, at the same salt concentration, as the ternary solution in order to keep the salt concentration constant throughout the measurement.

Dynamic Surface Tension

For DST measurements, depending upon the time scale of the surface tension decay, two different instruments were used. For pure surfactant solutions, with fast decay times of the surface tension (of the order of tens of milliseconds), the measurements were done by using a Kruss Maximum Bubble pressure (BP50) tensiometer. The maximum bubble pressure method has been widely used for measuring DST of surface tension.18,33−35 With the help of this instrument, the dynamics in the range of 14 milliseconds to 16 s has been measured. Unlike earlier versions, the latest model of BP50 controls the surface age instead of bubble frequency, thereby avoiding hydrodynamic errors and errors arising from dead time. For longer time-scale dynamics, a Kruss Easy Drop tensiometer based on the pendant drop method was used. The latter measures the surface tension by fitting the shape of the droplet to the Laplace equation, balancing interfacial tension and gravity. The adsorption of surfactants at the interface results in a change of the shape of the droplet in time from which surface tension can be deduced as a function of time. The time interval between each measurement was set to 1 s, and measurements were taken until the surface tension reaches its equilibrium value. In order to prevent the evaporation of droplet and hence concentration changes, the measurements were carried out in a controlled humidity chamber, in which the relative humidity was maintained at the equilibrium relative humidity above the solution throughout the measurement.

Results and Discussion

Cationic Surfactant CTAB

CMC and Surface Excess Concentration of CTAB in the Presence of NaCl

The impact of salt on the CMC and the surface excess concentration, Γ, was investigated by measuring the equilibrium surface tension of CTAB solutions as a function of the concentration of the surfactants at different NaCl concentrations. As can be observed in Figure 2a, the addition of NaCl to the CTAB solution shifts the CMC of CTAB rather drastically: from 9 × 10–4 molar without salt to 2 × 10–5 molar at high NaCl concentration (5.5 m). In addition to the decrease of the CMC, the addition of salt lowers the equilibrium surface tension at the CMC (Δγcmc ∼ 5 mN/m). These observations qualitatively agree with the earlier findings reported in the literature36,37 and at the same time extends these to (much) higher salt concentrations. The decrease of the CMC in the presence of electrolytes can be explained by the fact that the salt anions screen the electrostatic repulsion between the cationic head groups of the CTAB molecules, thereby facilitating their aggregation into micelles. With the addition of salt, fewer monomers will thus be present in the solution in equilibrium with micelles. It is interesting to note that the shift of the CMC to lower concentration happens until a certain concentration of NaCl (∼0.2 m), after which it remains constant (see black triangles in Figure 2b). This suggests that the maximum charge screening by the counterions is already reached, and the addition of more salt to the solution does not change the situation very much. The surface excess concentration (Γ) of the surfactant was determined from the slope of the curves, below the CMC (Figure 2b) using the Gibbs adsorption isotherm (eq 1)

graphic file with name la0c01211_m001.jpg 1

where n is the degree of dissociation of the surfactant (2 in case of CTAB if the Br– ion is split off), γ is the equilibrium surface tension, and C is the concentration of CTAB. The results are plotted in Figure 2b. The red line shows the surface excess in the absence of NaCl, using n = 2 in eq 1, being 2.45 × 10–6 mol/m2. As it is not a priori clear if upon adding salt, the surfactant forms ion pair with excess Cl–, and we calculate surface excess for both n = 1 (nondissociating ion pair) and n = 2 (dissociating). The results are depicted in Figure 2b in green and red squares. For n = 2, describing the case that the presence of NaCl has no influence on the dissociation of CTAB. The data indicate that in the presence of salt, the surface excess concentration decreases by a factor of 2. This seems unlikely, because as mentioned before, the main action of the salt should be to screen electrostatic interactions between the charged head groups, enabling the surfactants to pack more efficiently at the surface. However, if we assume ion-pair formation and thus n = 1, the surface excess concentration does not change upon adding salt. As such, we conclude a similar packing of molecules at the surface with and without salt is present because of the charge being screened by the counterions that are then bound to the surfactant.

Figure 2.

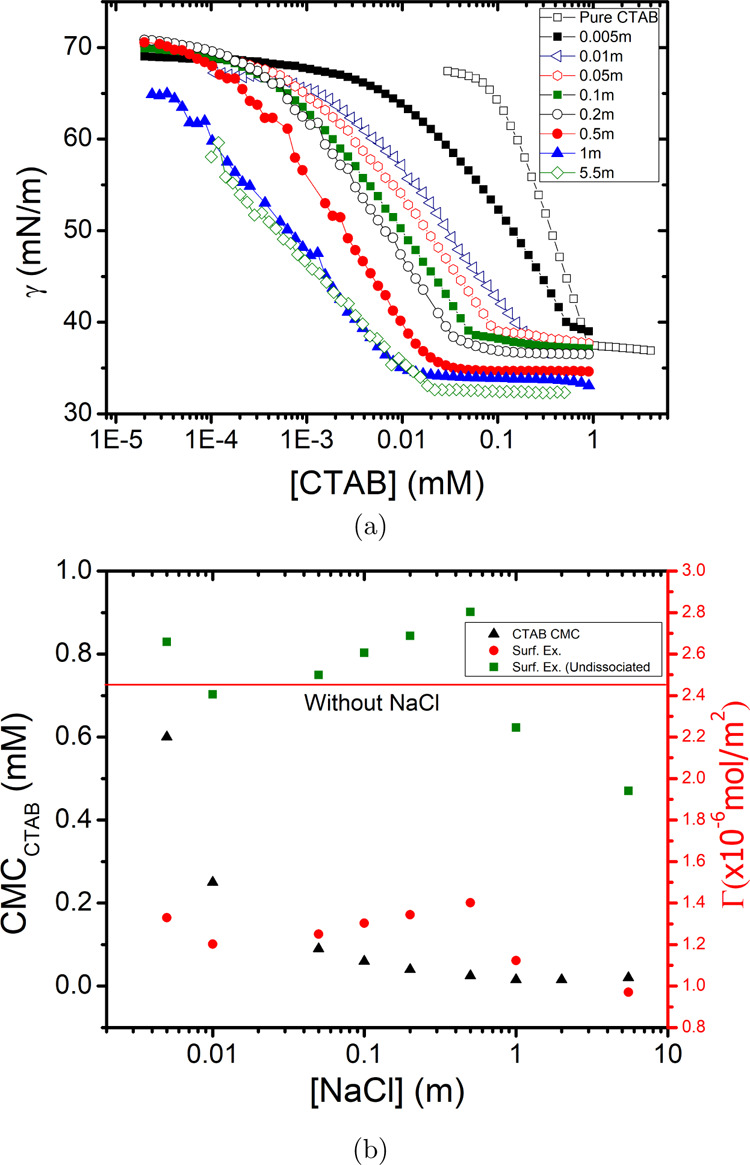
Figure 2

Open in a new tab

(a) Equilibrium surface tension as a function of CTAB concentration in the presence of different NaCl concentrations and (b) CMC and surface excess as a function of different NaCl concentrations used (Red line shows the surface excess concentration of pure CTAB solution).

To prove that the surfactant behavior at the interface is not changing significantly upon adding salt, we performed sum-frequency generation (SFG) spectroscopy. In SFG, a broadband infrared laser beam exciting molecular vibrations and a narrow band near-visible laser beam are overlapped in space and time at the interface. Because of the selection rule of the method, this process is forbidden in centrosymmetric media like bulk water. If the infrared light is in resonance with a molecular vibration, the sum-frequency signal is strongly enhanced. As such, the vibrational spectrum of only interfacial molecules is obtained. Here, we have probed the C–H stretch vibrations of the surfactants and the O–H stretch vibrations of the water molecules at the liquid/air interface. The result is depicted in Figure 3 for a 0.9 mM CTAB solution without and with 5.5 m NaCl. The peaks below 3000 cm–1 are C–H stretch vibrations and hence serve as signatures for the presence of CTAB at the interface. The signal above 3000 cm–1 originates from the water O–H stretch vibrations near the interface. The charge of the surfactant aligns the water molecules resulting in a large symmetry breaking and thus a relatively large O–H stretch signal.

Figure 3.

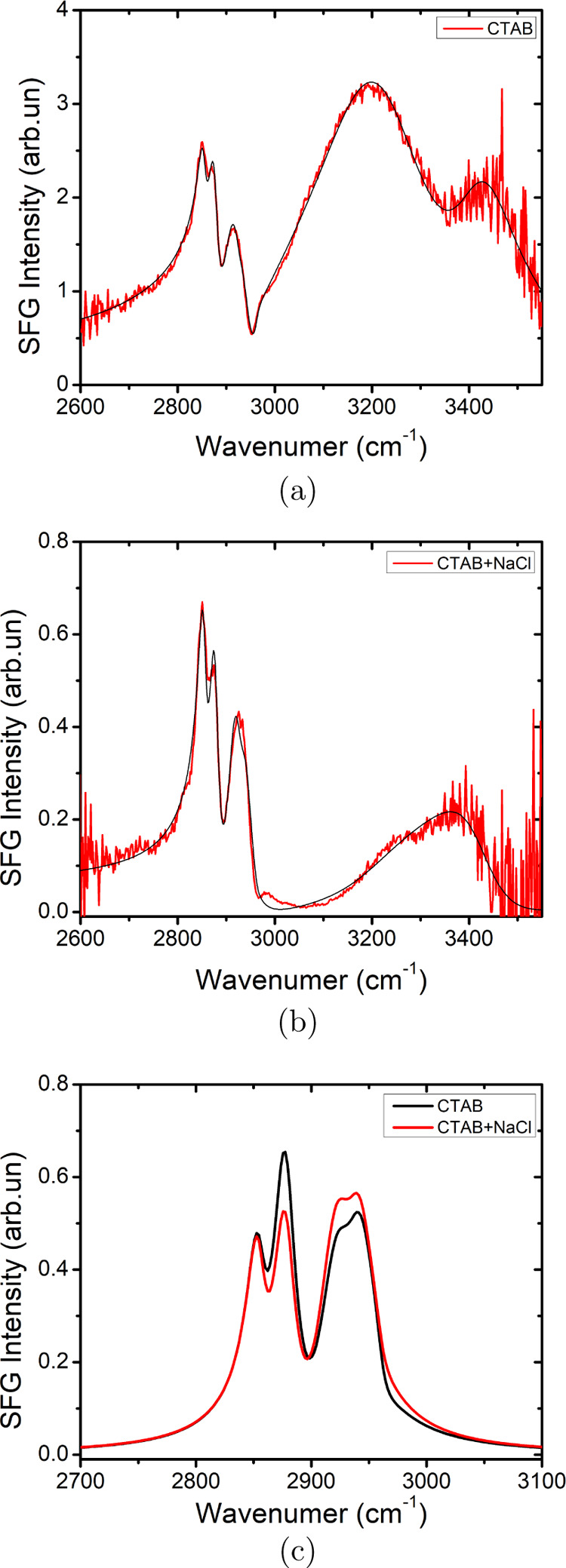
Figure 3

Open in a new tab

SFG spectra of CTAB (a) in the absence of salt (b) with 5.5 m NaCl. (c) Comparison of intensities of exclusively the peaks corresponding to C–H modes based on fits of (a,b). [Please note the different scale on the y-axis for panel (a,b)].

Upon adding salt, the water signal diminishes roughly by a factor of 10. Please note the different y-axis scale, as shown in Figure 3. This strong reduction clearly demonstrates that the effective surface charge has been reduced because of screening of the charge by Cl– ions. As a result, the water molecules are less aligned. The C–H signals seem also to reduce. However, because of interference with the water signal, it is impossible to draw conclusions about the C–H signals without analyzing the data quantitatively. The black lines in Figure 3a,b are fit with the Lorentzian lineshape model.38 Both datasets can be described with almost the same parameters for the C–H vibrations, see Figure 3c. The structure of the surfactant layer is apparently not changing significantly upon adding salt, consistent with the conclusion drawn above assuming ion-pair formation for CTAB.

DST of Pure CTAB Solutions

The DST of binary CTAB solutions (CTAB + water) was measured at a different concentration of CTAB, both below and above the CMC, by the maximum bubble pressure method, using Kruss BP50. The data obtained are presented in Figure 4. It can be seen that at higher surfactant concentrations, the equilibrium surface tension is reached faster.

Figure 4.

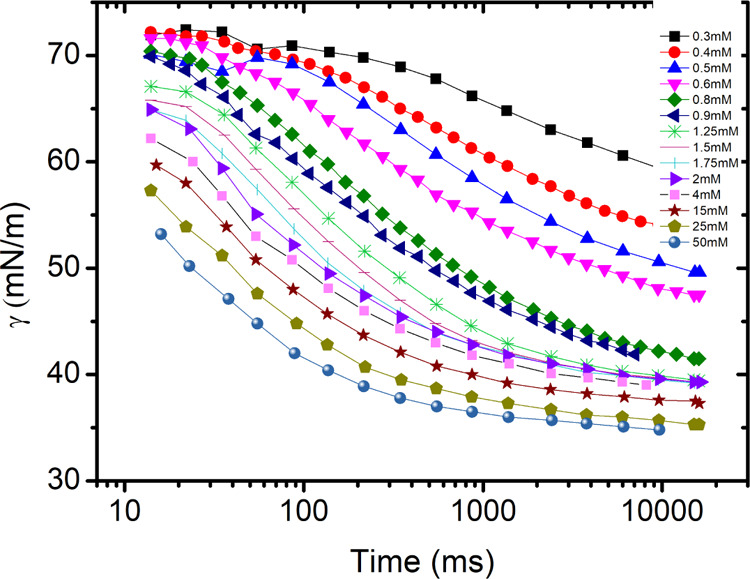
Figure 4

Open in a new tab

Surface tension as a function of time for different concentrations of CTAB measured by the maximum bubble pressure method.

In order to quantify the dynamics, for each concentration of surfactant, we determine the characteristic time (τ), which is the time needed to reach half of the total decrease of γ and is thus obtained by

graphic file with name la0c01211_m002.jpg 2

With γ0 and γ∞ being the initial and the equilibrium values, respectively.

For a diffusion-controlled surfactant adsorption, the mechanism reported by Ward and Tordai39,40 proposed that the characteristic time should vary with the surfactant concentration as 1/c2, as in eq 3

graphic file with name la0c01211_m003.jpg 3
graphic file with name la0c01211_m004.jpg 4

where D is the diffusion coefficient of surfactant molecules, Γ is the surface excess concentration, and c is the concentration of the surfactant in the solution. In Figure 5, the characteristic time is plotted against the concentration of CTAB for a range of concentrations, which fall well above and below the CMC.

Figure 5.

Figure 5

Open in a new tab

Characteristic time determined from DST plots (Figure 4) as a function of surfactant concentration.

Initially, τ decreases rapidly as a function of concentration. However, as the concentration reaches above CMC, there is very little change in the characteristic time (Figure 5). Moreover, the slope of the initial part of the log–log curve is −2, confirming that τ varies as 1/c2, and hence, the adsorption mechanism of the surfactant to the interface in this range of concentration is diffusion controlled, which is in agreement with the studies done on CTAB by Bain et al.41 In the second part of the curve, the variation of τ with concentration is minimal because as soon as the CMC is reached, there is no significant change in the monomer concentration of surfactant with increasing surfactant concentration anymore. This confirms that the adsorption is greatly affected by the concentration of surfactant monomers, and that the presence of micelles makes no difference in the adsorption dynamics. This is consistent with the theory of Ward and Tordai, which takes only monomer concentration into consideration while correlating it with the characteristic adsorption time.

Moreover, for concentration further above CMC, the slope does not remain quadratic anymore, implying that the higher concentration of ionic micelles leads to deviation of adsorption mechanism from purely monomer diffusion controlled to adsorption barrier or mixed diffusion–adsorption barrier controlled. Earlier studies by Ritacco et al.18 and Svitova et al.17 suggested the role of electrostatic adsorption barrier in the dynamics at pre-CMCs of CTAB, but our results at high salt concentrations suggest no such effect until a certain concentration above the CMC (∼3 × CMC) is reached, after which an adsorption barrier does seem to play a role.

DST of CTAB Solutions with a Fixed NaCl Concentration

We proceed to investigate the influence of high salt concentration on the adsorption mechanism of the ionic surfactant CTAB. Although keeping the concentration of NaCl constant and changing the surfactant concentration, we again observe that the equilibration time decreases with increasing the surfactant concentration (Figure 6). However, the dynamics become very slow compared to what was observed in pure surfactant solutions. The dynamics changes from the time scale of milliseconds to tens of seconds, as shown in Figure 6. An important point which needs to be noted here is that we could measure only the concentrations above the CMC. The reason being that the salts decreased the CMC to very low concentrations and also increased the equilibration time, which eventually makes DST measurements for pre-CMCs unfeasible.

Figure 6.

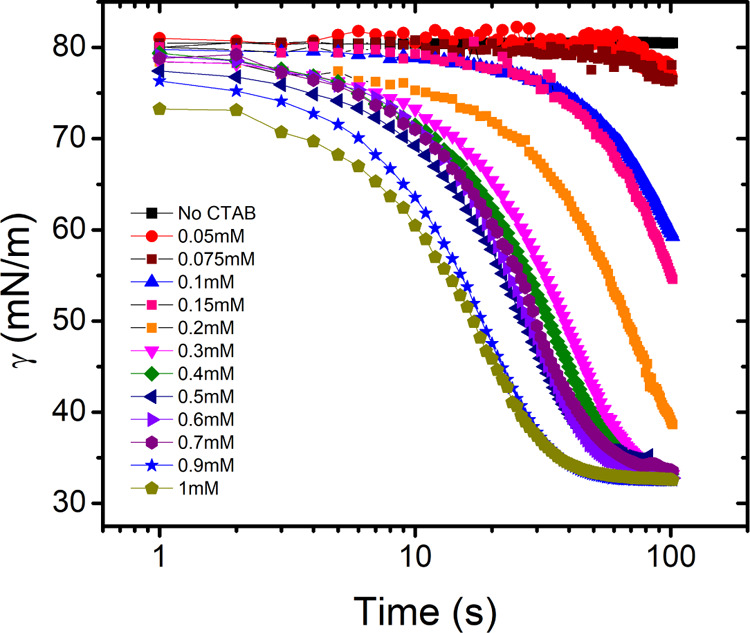
Figure 6

Open in a new tab

Surface tension as a function of time for different CTAB concentrations and fixed NaCl concentration (5.5 m), measured by the pendant drop method.

We employ the same approach as used for the pure CTAB solutions and deduce the characteristic time and correlate it with the CTAB concentration. The results, as shown in Figure 7, show a major difference from the pure surfactant case in the way that the characteristic time τ seems to be dependent on 1/c in contrast to 1/c2, as in the case of pure CTAB solution.

Figure 7.

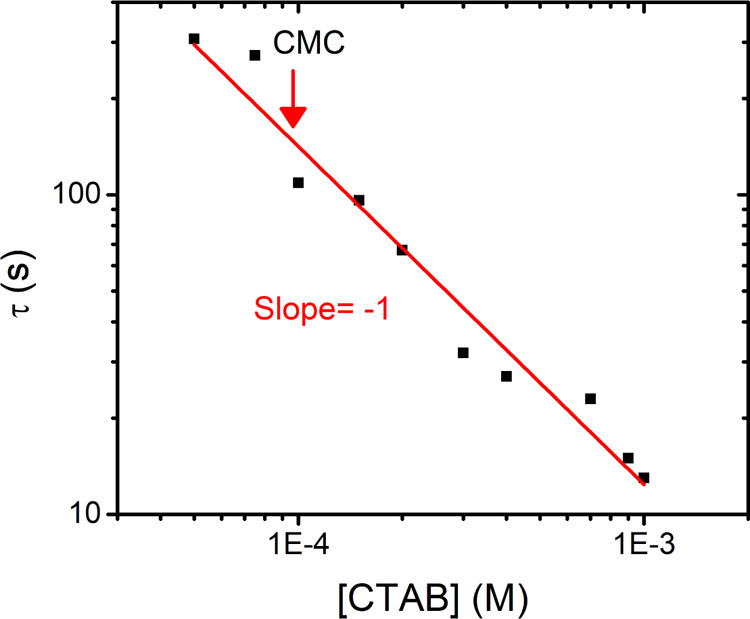
Figure 7

Open in a new tab

Characteristic time as a function of CTAB concentration with 5.5 m NaCl. (The red arrow shows the CMC of CTAB in the presence of 5.5 m NaCl).

As apparent from Figure 5, the characteristic time exhibits a 1/c2 dependence below the CMC while above the CMC, the dependence is much weaker. The 1/c dependence found here is then likely because of a combination of factors, of which the most important one is the shift of the CMC induced by the salt. Other factors could be that the high concentration of salt changes the diffusion constant or changes the properties of the surfactant itself. For the former, the high concentration of salt changes the viscosity by roughly a factor of 2 (Figure 1), which is too small to account for the observed change of more than an order of magnitude. For the latter, even if the surfactant forms ion pairs with the added salt, this should not affect the dynamics very significantly either. If anything, the charge neutralization by ion-pair formation rules out the possibility of any electrostatic barrier, which would slow down the adsorption. As far as the change in the surfactant monomers is concerned, the addition of salt leads to 2 orders of magnitude decrease in CMC, which in turn means that the concentration of monomers drops drastically in the presence of salt. The Ward and Tordai model accurately describes the characteristic time in terms of the monomer concentration, suggesting that the dramatic increase in the characteristic time is simply because of the lowering of the CMC. The linear instead of quadratic dependence of characteristic time, as shown in Figure 7, is likely due to the fact that all these concentrations are above CMC, and hence, the micelles rather than monomers are playing a central role in determining the adsorption dynamics, similar to the regime change that was seen above CMC in pure CTAB solutions (Figure 5). In a study by Song and Yuan42 using fluorescence microscopy, the transport of micelles from the bulk to interface and their demicellization in the subsurface was visualized. They suggested a combined influence of micellar diffusion and monomer adsorption on determining the overall adsorption kinetics. With the addition of salt, we have abundance of micelles, and hence, their diffusion is likely to play a major role. We will show below, after having discussed the results for Tween 80, that the Ward and Tordai model can quantitatively explain our data.

We confirm the transfer of CTAB molecules from the bulk to the interface as a function of time by taking kinetic SFG spectra with a time interval of 1 min. The signals below 3000 cm–1 represent the CTAB molecules at the interface. The results for pure 0.1 mM CTAB solution, as shown in Figure 8a, show no change in the SFG spectrum with time, suggesting that the interface is already saturated as soon as the first kinetic spectrum is recorded. However, the results for 0.1 mM CTAB in the presence of 5.5 m NaCl, as shown in Figure 8b, show an increase in the peak intensity with time. This confirms that the slower dynamic surface tension is directly correlated to the concentration of CTAB molecules at the interface.

Figure 8.

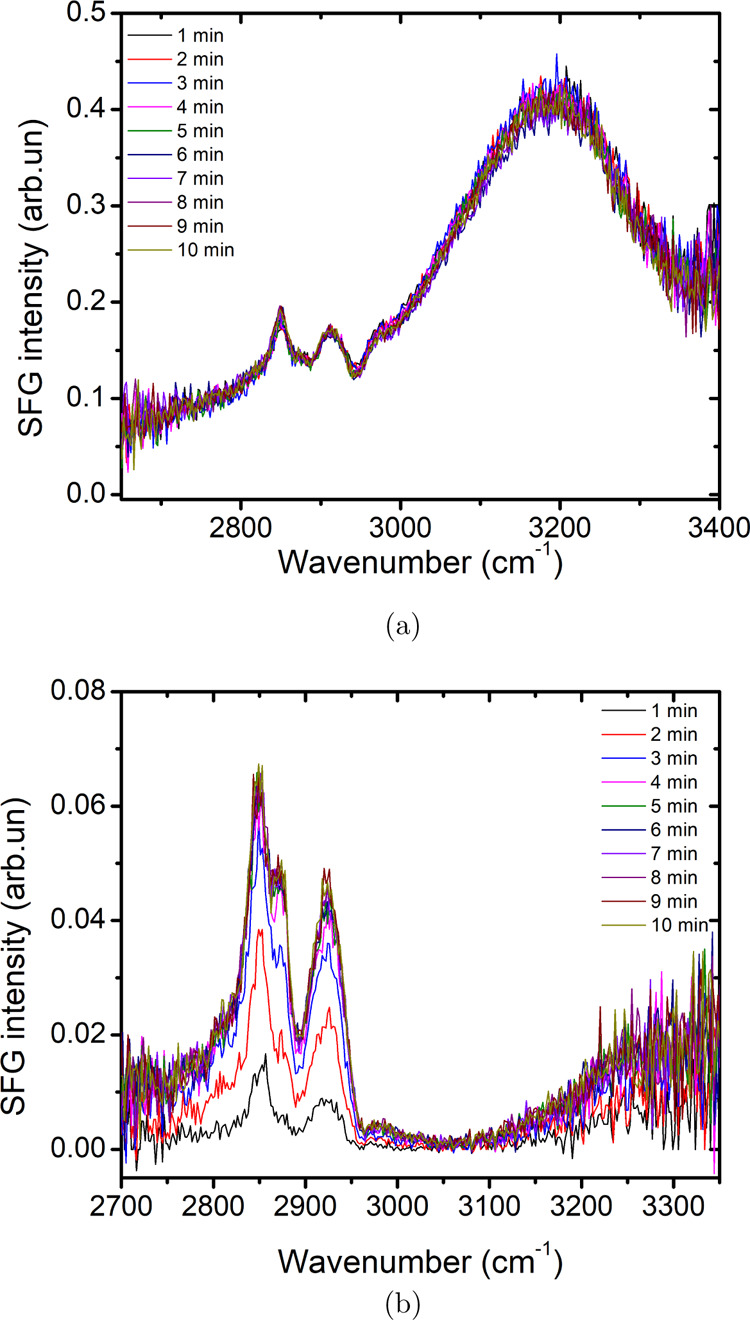
Figure 8

Open in a new tab

Kinetic SFG spectra of (a) 0.1 mM CTAB and (b) 0.1 mM CTAB + 5.5 m NaCl.

Anionic Surfactant—Tween 80

CMC and Surface Excess Concentration of Surfactants in the Presence of NaCl

Now in order to isolate the effect of polar heads of the cationic surfactant CTAB on the presence of salt, we investigate the influence of salts on the CMC of the nonionic surfactant Tween 80. In the same way as CTAB, the equilibrium surface tension as a function of Tween 80 concentration is measured in the pure Tween 80 solution as well as with the addition of different concentrations of NaCl. In literature, it has been reported that, like ionic surfactants, salts have depreciating influence on the CMC of nonionic surfactants also.10,43,44 However, in our experiments, the addition of NaCl has no effect on the CMC of Tween 80, which is around 1.5 × 10–5 molar. In addition, as the slope of the “γeq” versus concentration plot does not change with the addition of salt, the surface excess concentration is also not affected by the addition of salt. The surface excess concentration (Γ) of the surfactant is found to be (Γ = 8.5 × 10–7 mol m–2) using the slope of one of the curves, as shown in Figure 9.

Figure 9.

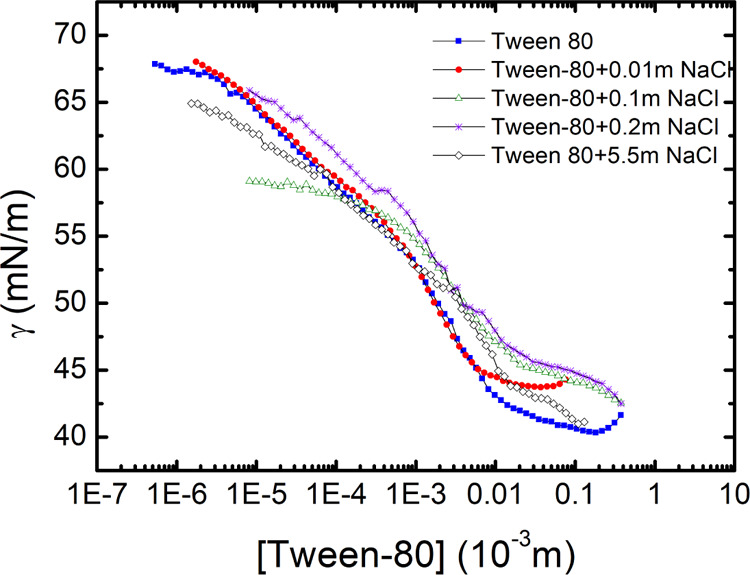
Figure 9

Open in a new tab

Equilibrium Surface tension (γeq) as a function of Tween 80 concentration for different salt concentrations. CMC ∼ 1.5 × 10–5 molar and the Γ ∼ 8.5 × 10–7 mol m–2.

DST of Tween 80 (with and Without NaCl)

In the same way as for CTAB, the DST of Tween 80 solutions was measured for (i) pure Tween 80 solutions and (ii) different Tween 80 concentrations at constant NaCl concentration.

In view of the slow surface tension decay with time, the pendant drop method was used to measure the time-dependent surface tension. The results, as shown in Figure 10a, show that the characteristic time decreases with the increase in the concentration of Tween 80, However, the time scale, in which the surface tension reaches to equilibrium, is of the order of tens of seconds in contrast the millisecond time scale as in the case of CTAB. Moreover, the addition of salt to the solution (Figure 10b) does not substantially affect the time scale of reaching the equilibrium value.

Figure 10.

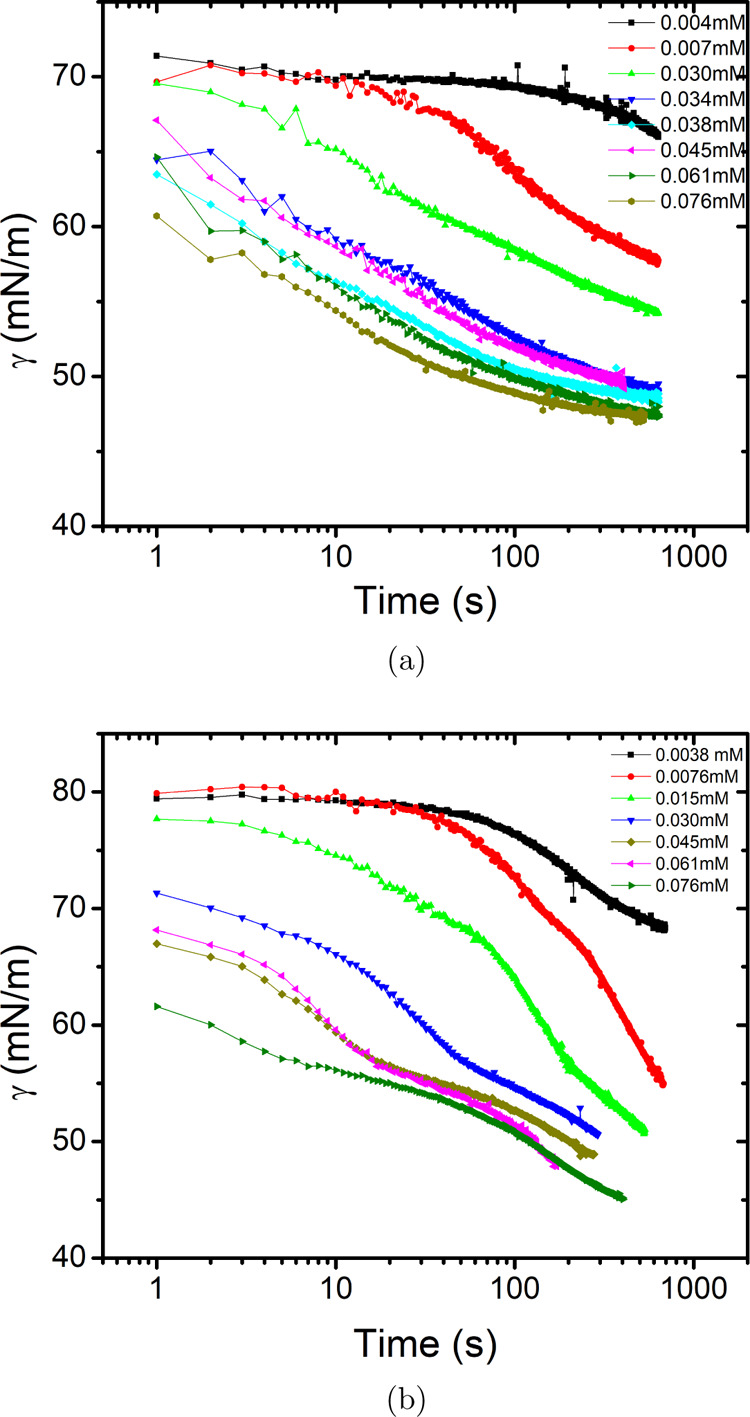
Figure 10

Open in a new tab

Surface tension as a function of time for (a) binary (Tween 80 + water) and (b) ternary solutions (Tween 80 + NaCl (5.5 m)+ water) measured using the pendant drop method.

In order to determine the mechanism of adsorption of the surfactant molecules to the interface, the characteristic time was determined for both binary and ternary solutions, as described previously, and plotted as a function of the concentration of Tween 80 (Figure 11). First, for pure Tween 80, the characteristic time varies as 1/c2, which suggests that the transport of surfactant molecules to the interface is diffusion controlled. The addition of salt does not affect this behavior.

Figure 11.

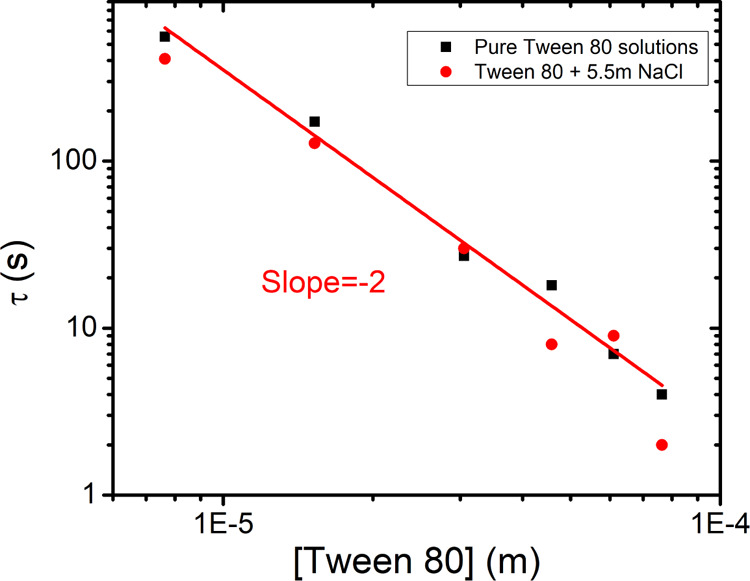
Figure 11

Open in a new tab

Characteristic time (determined from the DST data of Figure 10) as a function of Tween 80 concentration.

Although the DST data agree with the Ward and Tordai model and confirm that the adsorption is diffusion controlled, the question remains why the process is so slow. For this, we once again refer to the earlier explanation considering the surfactant monomer concentrations. As is clear from Figure 9, the CMC of Tween 80 is very low compared to most common surfactants, which means that the monomer concentration stops to increase at a very low concentration. Hence, as in case of CTAB with NaCl, the small number of monomers present at a certain time is responsible for the slow adsorption of Tween 80. The applicability of Ward and Tordai equation, even in the micellar concentrations, suggests that Tween 80 micelles have negligible influence on the adsorption kinetics. Because of neutral nature, the micelles do not cause any electrostatic effects, and micelle diffusion and dissociation equilibria do not seem to be playing a significant enough role either. Moreover, in cases of Tween 80, the addition of salt does not change the CMC and thus also not the concentration of monomers. As a result, no change in the adsorption dynamics upon addition of salt (Figure 10b) is observed. Noskov et al.45,46 studied the adsorption of neutral polymer chains and the influence of salt on it. They reported that addition of salt made the adsorption kinetics faster, and the adsorption rate was proportional to the salt concentration. We do not see any enhancement of adsorption rate by adding salt, and the reason could be that in case of polymer chains, the salts are affecting the chain configuration, which is not the case in Tween 80. In order to get a perspective of the very low monomer concentration and its influence on DST, we plot the characteristic time for the concentrations closest to the CMC along with the characteristic times for CTAB (plotted in Figure 5). The data points corresponding to CTAB + NaCl fall on the same trend line as in case of pure CTAB (Figure 12). This confirms that it is actually the reduction in the number of monomer molecules causing the slow dynamics. Hence, the mechanism, in which the salt slows down the adsorption, is by favoring the micellization, which leads to decrease in the monomer concentration.

Figure 12.

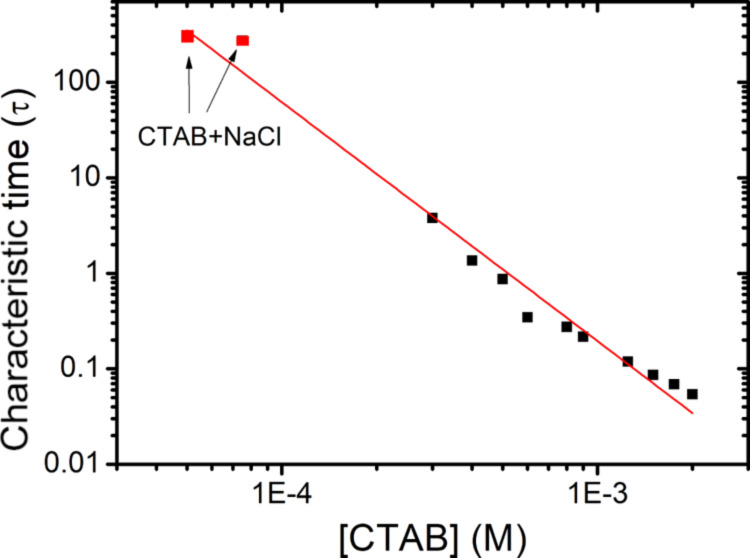
Figure 12

Open in a new tab

Extrapolation of τ vs c graph for CTAB (Figure 5) to lower concentrations while adding the data points from CTAB + NaCl to illustrate the correlation of characteristic time with monomer concentration. This lends one more confirmation to the argument that the concentration of monomers determines the DST trends despite the presence of large quantities of electrolyte impurities.

Conclusions

The effect of salt (sodium chloride) with concentrations up to 5.5 molal on both equilibrium and DST properties is studied for an ionic (CTAB) and nonionic (Tween 80) surfactants. In case of equilibrium surface tension, we show that the salt affects the CMC and the equilibrium surface tension only in case of an ionic surfactant. The CMC of ternary CTAB solutions is shifted to lower concentration, and the equilibrium surface tension is also reduced (ΔγCMC ∼ 5 mN/m). The shift of the CMC occurs up to a certain concentration of NaCl, after which it remains constant. Consequently, with the addition of salt, much fewer monomers will be present in the solution in equilibrium with micelles. Although from the data, it appears that NaCl decreases the surface excess concentration of CTAB, the precise factor of 2 decrease suggests that it can be the result of ion-pair formation, which makes the ionic surfactant in the presence of salt behave more like a nonionic surfactant. Our SFG results confirm this hypothesis by showing that the surface concentration of CTAB does not change significantly upon the addition of salt.

From the DST data of pure ionic surfactant solutions, we show, by using the Ward and Tordai model, that the adsorption kinetics is controlled by a diffusion mechanism, and that the rate depends specifically on the concentration of monomers in bulk. We show that the addition of salt slows down the adsorption dynamics very strongly. As soon as the concentration exceeds the CMC, its effect on the DST becomes much smaller, indicating that the dynamics of the micelles do not contribute very much to the DST. The existence of an adsorption barrier has previously been proposed as a possible rate-limiting step for the adsorption of surfactants; however, its origin remains debated. There have been various propositions, including the electrostatic repulsion between surfactants, or between interfacial water molecules and the surfactant molecules, the orientation of molecules before adsorbing to the interface, and steric repulsion by molecules already adsorbed at the interface.3,47,48 However, our surface excess measurements supported by SFG data suggest that high salt concentration leads to the formation of ion pairs between the excess anions and the CTAB molecules, which leads to neutralization of charges. This rules out the possibility that an electrostatic barrier is playing a role in slowing down the monomer adsorption to the interface. The equilibrium surface tension data rather show that the CMC decreases significantly, which effectively decreases the number of monomer molecules. This depletion in the number of molecules eventually makes the dynamics slow.

For nonionic surfactant Tween 80, the rate of adsorption is already very slow, and the addition of salt does not change the time scale. Here, the equilibrium surface tension data showed that NaCl does not affect the CMC of Tween 80 either. Consequently, the slow dynamics in case of Tween 80 can also be explained by the very low CMC, which leads to existence of very small number of monomers compared to pure CTAB solutions but similar to the CTAB + NaCl case (i.e., ion pairs formation). To confirm this, we plot the data points corresponding to CTAB + NaCl along with the pure CTAB, and we observe that they fall right on the trend line.

The authors declare no competing financial interest.

References

  1. Rosen M. J.; Kunjappu J. T.. Surfactants and interfacial phenomena; Wiley, 2012; pp 1–4. [Google Scholar]
  2. Schramm L. L.; Marangoni G. Surfactants: Fundamentals and applications in the petroleum industry. Chem. Eng. J. 2001, 83, 63. [Google Scholar]
  3. Eastoe J.; Dalton J. S. Dynamic surface tension and adsorption mechanisms of surfactants at the air - water interface. Adv. Colloid Interface Sci. 2000, 85, 103–144. 10.1016/s0001-8686(99)00017-2. [DOI] [PubMed] [Google Scholar]
  4. Nozière B.; Baduel C.; Jaffrezo J.-L. The dynamic surface tension of atmospheric aerosol surfactants reveals new aspects of cloud activation. Nat. Commun. 2014, 5, 3335. 10.1038/ncomms4335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Yunfei H.; Yazhuo S.; Honglai L.; Dominique L.; Anniina S. Surfactant adsorption onto interfaces: Measuring the surface excess in time. Langmuir 2012, 28, 3146–3151. 10.1021/la2047454. [DOI] [PubMed] [Google Scholar]
  6. Yuan X.H.; Rosen M. J. Dynamic surface tension of aqueous surfactant solutions. J. Colloid Interface Sci. 1988, 124, 652–659. [Google Scholar]
  7. Knipping E. M.; Lakin M. J.; Foster K. L.; Jungwirth P.; Tobias D. J.; Gerber R. B.; Dabdub D.; Finlayson-Pitts B. J. Experiments and simulations of ion-enhanced interfacial chemistry on aqueous NaCl aerosols. Science 2000, 288, 301–306. 10.1126/science.288.5464.301. [DOI] [PubMed] [Google Scholar]
  8. Ghosal S.; Hemminger J. C.; Bluhm H.; Mun B. S.; Hebenstreit E. L. D.; Ketteler G.; Ogletree D. F.; Requejo F. G.; Salmeron M. Electron Spectroscopy of Aqueous Solution Interfaces Reveals Surface Enhancement of Halides. Science 2005, 307, 563. 10.1126/science.1106525. [DOI] [PubMed] [Google Scholar]
  9. Li Z.; Williams A. L.; Rood M. J.; Li Z.; Williams A. L.; Rood M. J. Influence of Soluble Surfactant Properties on the Activation of Aerosol Particles Containing Inorganic Solute. J. Atmos. Sci. 1998, 55, 1859–1866. . [DOI] [Google Scholar]
  10. Carale T. R.; Pham Q. T.; Blankschtein D. Salt effects on intramicellar interactions and micellization of nonionic surfactants in aqueous solutions. Langmuir 1994, 10, 109–121. 10.1021/la00013a016. [DOI] [Google Scholar]
  11. Roy J. C.; Islam M. N.; Aktaruzzaman G. The effect of NaCl on the Krafft temperature and related behavior of cetyltrimethylammonium bromide in aqueous solution. J. Surfactants Deterg. 2014, 17, 231–242. 10.1007/s11743-013-1510-0. [DOI] [Google Scholar]
  12. Wan L. S. C.; Poon P. K. C. Effect of salts on the surface/interfacial tension and critical micelle concentration of surfactants. J. Pharm. Sci. 1969, 58, 1562–1567. 10.1002/jps.2600581238. [DOI] [PubMed] [Google Scholar]
  13. Woolfrey S. G.; Banzon G. M.; Groves M. J. The effect of sodium chloride on the dynamic surface tension of sodium dodecyl sulfate solutions. J. Colloid Interface Sci. 1986, 112, 583–587. 10.1016/0021-9797(86)90129-3. [DOI] [Google Scholar]
  14. Alexandridis P.; Holzwarth J. F. Differential Scanning Calorimetry Investigation of the Effect of Salts on Aqueous Solution Properties of an Amphiphilic Block Copolymer (Poloxamer). Langmuir 1997, 13, 6074–6082. 10.1021/la9703712. [DOI] [Google Scholar]
  15. Benrraou M.; Bales B. L.; Zana R. Effect of the Nature of the Counterion on the Properties of Anionic Surfactants. 1. Cmc, Ionization Degree at the Cmc and Aggregation Number of Micelles of Sodium, Cesium, Tetramethylammonium, Tetraethylammonium, Tetrapropylammonium, and Tetrabutylammoniu. J. Phys. Chem. B 2003, 107, 13432–13440. 10.1021/jp021714u. [DOI] [Google Scholar]
  16. Adamczyk Z.; Para G.; Warszyński P. Influence of Ionic Strength on Surface Tension of Cetyltrimethylammonium Bromide. Langmuir 1999, 15, 8383–8387. 10.1021/la990241o. [DOI] [Google Scholar]
  17. Svitova T. F.; Wetherbee M. J.; Radke C. J. Dynamics of surfactant sorption at the air/water interface: continuous-flow tensiometry. J. Colloid Interface Sci. 2003, 261, 170–179. 10.1016/s0021-9797(02)00241-2. [DOI] [PubMed] [Google Scholar]
  18. Ritacco H.; Langevin D.; Diamant H.; Andelman D. Dynamic Surface Tension of Aqueous Solutions of Ionic Surfactants: Role of Electrostatics. Langmuir 2011, 27, 1009–1014. 10.1021/la103039v. [DOI] [PubMed] [Google Scholar]
  19. Colegate D. M.; Bain C. D. Adsorption Kinetics in Micellar Solutions of Nonionic Surfactants. Phys. Rev. Lett. 2005, 95, 198302. 10.1103/physrevlett.95.198302. [DOI] [PubMed] [Google Scholar]
  20. Milner S. R. On surface concentration, and the formation of liquid films. Phil. Mag. 1907, 13, 96–110. 10.1080/14786440709463586. [DOI] [Google Scholar]
  21. Adam N. K.; Brown R. C.; Murray R. C.; Ramsden W.; Lottermoser A. General discussion. Trans. Faraday Soc. 1935, 31, 204. 10.1039/tf9353100204. [DOI] [Google Scholar]
  22. Ferri J. K.; Stebe K. J.; Stebe K. J. Which Surfactants Reduce Surface Tension Faster? A Scaling Argument for Diffusion-Controlled Adsorption. Adv. Colloid Interface Sci. 2000, 85, 61–97. 10.1016/s0001-8686(99)00027-5. [DOI] [PubMed] [Google Scholar]
  23. Chang C.-H.; Franses E. I. Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms. Colloid. Surface. Physicochem. Eng. Aspect. 1995, 100, 1–45. 10.1016/0927-7757(94)03061-4. [DOI] [Google Scholar]
  24. Dong C.; Hsu C.-T.; Chiu C.-Y.; Lin S.-Y. A Study on Surfactant Adsorption Kinetics: Effect of Bulk Concentration on the Limiting Adsorption Rate Constant. Langmuir 2000, 16, 4573–4580. 10.1021/la991001b. [DOI] [Google Scholar]
  25. Miller R.; Joos P.; Fainerman V. B. Dynamic surface and interfacial tensions of surfactant and polymer solutions. Adv. Colloid Interface Sci. 1994, 49, 249–302. 10.1016/0001-8686(94)80017-0. [DOI] [Google Scholar]
  26. Qazi M. J.; Liefferink R. W.; Schlegel S. J.; Backus E. H. G.; Bonn D.; Shahidzadeh N. Influence of Surfactants on Sodium Chloride Crystallization in Confinement. Langmuir 2017, 33, 4260–4268. 10.1021/acs.langmuir.7b00244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ikeda S.; Hayashi S.; Imae T. Rodlike micelles of sodium dodecyl sulfate in concentrated sodium halide solutions. J. Phys. Chem. 1981, 85, 106–112. 10.1021/j150601a024. [DOI] [Google Scholar]
  28. Goyal P. S.; Dasannacharya B. A.; Kelkar V. K.; Manohar C.; Srinivasa Rao K.; Valaulikar B. S. Shapes and sizes of micelles in CTAB solutions. Phys. B 1991, 174, 196–199. 10.1016/0921-4526(91)90606-f. [DOI] [Google Scholar]
  29. Das N. C.; Cao H.; Kaiser H.; Warren G. T.; Gladden J. R.; Sokol P. E. Shape and size of highly concentrated micelles in CTAB/NaSal solutions by small angle neutron scattering (SANS). Langmuir 2012, 28, 11962–11968. 10.1021/la2022598. [DOI] [PubMed] [Google Scholar]
  30. Sammalkorpi M.; Karttunen M.; Haataja M. Ionic Surfactant Aggregates in Saline Solutions: Sodium Dodecyl Sulfate (SDS) in the Presence of Excess Sodium Chloride (NaCl) or Calcium Chloride (CaCl2). J. Phys. Chem. B 2009, 113, 5863–5870. 10.1021/jp901228v. [DOI] [PubMed] [Google Scholar]
  31. Shahidzadeh N.; Bonn D.; Aguerre-Chariol O.; Meunier J. Large Deformations of Giant Floppy Vesicles in Shear Flow. Phys. Rev. Lett. 1998, 81, 4268–4271. 10.1103/physrevlett.81.4268. [DOI] [Google Scholar]
  32. du Noüy P. An Interfacial Tensiometer For Universal Use. J. Gen. Physiol. 1925, 7, 625–631. 10.1085/jgp.7.5.625. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Christov N. C.; Danov K. D.; Kralchevsky P. A.; Ananthapadmanabhan K. P.; Lips A. Maximum Bubble Pressure Method: Universal Surface Age and Transport Mechanisms in Surfactant Solutions. Langmuir 2006, 22, 7528–7542. 10.1021/la061239h. [DOI] [PubMed] [Google Scholar]
  34. Yoshimura T.; Ishihara k.; Esumi K. Sugar-Based Gemini Surfactants with Peptide Bonds Synthesis, Adsorption, Micellization, and Biodegradability. Langmuir 2005, 21, 10409–10415. 10.1021/la051614q. [DOI] [PubMed] [Google Scholar]
  35. Stanimirova R.; Marinova K.; Tcholakova S.; Denkov N. D.; Stoyanov S.; Pelan E. Surface Rheology of Saponin Adsorption Layers. Langmuir 2011, 27, 12486–12498. 10.1021/la202860u. [DOI] [PubMed] [Google Scholar]
  36. Li F.; Li G.-Z.; Wang H.-Q.; Xue Q.-J. Studies on cetyltrimethylammonium bromide (CTAB) micellar solution and CTAB reversed microemulsion by ESR and 2H NMR. Colloid. Surface. Physicochem. Eng. Aspect. 1997, 127, 89–96. 10.1016/s0927-7757(96)03889-7. [DOI] [Google Scholar]
  37. Beyer K.; Leine D.; Blume A. The demicellization of alkyltrimethylammonium bromides in 0.1M sodium chloride solution studied by isothermal titration calorimetry. Colloids Surf., B 2006, 49, 31–39. 10.1016/j.colsurfb.2006.02.003. [DOI] [PubMed] [Google Scholar]
  38. Ohno P. E.; Wang H.-f.; Geiger F. M. Second-order spectral lineshapes from charged interfaces. Nat. Commun. 2017, 8, 1032. 10.1038/s41467-017-01088-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ward A. F. H.; Tordai L. Time-Dependence of Boundary Tensions of Solutions I. The Role of Diffusion in Time-Effects. J. Chem. Phys. 1946, 14, 453–461. 10.1063/1.1724167. [DOI] [Google Scholar]
  40. Aytouna M.; Bartolo D.; Wegdam G.; Bonn D.; Rafaï S. Impact dynamics of surfactant laden drops: dynamic surface tension effects. Exp. Fluid 2010, 48, 49–57. 10.1007/s00348-009-0703-9. [DOI] [Google Scholar]
  41. Bain C. D.; Manning-Benson S.; Darton R. C. Rates of Mass Transfer and Adsorption of Hexadecyltrimethylammonium Bromide at an Expanding Air–Water Interface. J. Colloid Interface Sci. 2000, 229, 247–256. 10.1006/jcis.2000.7026. [DOI] [PubMed] [Google Scholar]
  42. Song Q.; Yuan M. Visualization of an adsorption model for surfactant transport from micelle solutions to a clean air/water interface using fluorescence microscopy. J. Colloid Interface Sci. 2011, 357, 179–188. 10.1016/j.jcis.2011.01.096. [DOI] [PubMed] [Google Scholar]
  43. Aydogan N.; Abbott N. L. Effect of electrolyte concentration on interfacial and bulk solution properties of ferrocenyl surfactants with anionic headgroups. Langmuir 2002, 18, 7826–7830. 10.1021/la025737b. [DOI] [Google Scholar]
  44. Miyagishi S.; Okada K.; Asakawa T. Salt Effect on Critical Micelle Concentrations of Nonionic Surfactants, N-Acyl-N-methylglucamides (MEGA-n). J. Colloid Interface Sci. 2001, 238, 91–95. 10.1006/jcis.2001.7503. [DOI] [PubMed] [Google Scholar]
  45. Noskov B. A.; Nuzhnov S. N.; Loglio G.; Miller R. Dynamic Surface Properties of Sodium Poly(styrenesulfonate) Solutions. Macromolecules 2004, 37, 2519–2526. 10.1021/ma030319e. [DOI] [Google Scholar]
  46. Noskov B. A.; Akentiev A. V.; Miller R. Dynamic Surface Properties of Poly(vinylpyrrolidone) Solutions. J. Colloid Interface Sci. 2002, 255, 417–424. 10.1006/jcis.2002.8614. [DOI] [PubMed] [Google Scholar]
  47. Lunkenheimer K.; Miller R. A criterion for judging the purity of adsorbed surfactant layers. J. Colloid Interface Sci. 1987, 120, 176–183. 10.1016/0021-9797(87)90337-7. [DOI] [Google Scholar]
  48. Mysels K. J.; Florence A. T. The Effect of Impurities on Dynamic Surface Tension– Basis for a Valid Surface Purity Criterion. J. Colloid Interface Sci. 1973, 43, 577–582. 10.1016/0021-9797(73)90405-0. [DOI] [Google Scholar]

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES