Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2020 Aug 1.
Published in final edited form as: J Appl Ecol. 2019 Jul 1;56(8):2057–2068. doi: 10.1111/1365-2664.13455

Predicting the fundamental thermal niche of crop pests and diseases in a changing world: A case study on citrus greening

Rachel A Taylor 1,2, Sadie J Ryan 3,4,5, Catherine A Lippi 3,4, David G Hall 6, Hossein A Narouei-Khandan 4,7, Jason R Rohr 1,8, Leah R Johnson 9
PMCID: PMC7367095  NIHMSID: NIHMS1604352  PMID: 32684639

Abstract

  1. Predicting where crop pests and diseases can occur, both now and in the future under different climate change scenarios, is a major challenge for crop management. One solution is to estimate the fundamental thermal niche of the pest/disease to indicate where establishment is possible. Here, we develop methods for estimating and displaying the fundamental thermal niche of pests and pathogens and apply these methods to Huanglongbing (HLB), a vector-borne disease that is currently threatening the citrus industry worldwide.

  2. We derive a suitability metric based on a mathematical model of HLB transmission between tree hosts and its vector Diaphorina citri, and incorporate the effect of temperature on vectortraits using data from laboratory experiments performed at different temperatures. We validate the model using data on the historical range of HLB.

  3. Our model predicts that transmission of HLB is possible between 16 and 33°C with peak transmission at ~25°C. The greatest uncertainty in our suitability metric is associated with the mortality of the vectors at peak transmission, and fecundity at the edges of the thermal range, indicating that these parameters need further experimental work.

  4. We produce global thermal niche maps by plotting how many months each location is suitable for establishment of the pest/disease. This analysis reveals that the highest suitability for HLB occurs near the equator in large citrus-producing regions, such as Brazil and South-East Asia. Within the Northern Hemisphere, the Iberian peninsula and California are HLB suitable for up to 7 months of the year and are free of HLB currently.

  5. Policy implications. We create a thermal niche map which indicates the places at greatest risk of establishment should a crop disease or pest enter these regions. This indicates where surveillance should be focused to prevent establishment. Our mechanistic method can be used to predict new areas for Huanglongbing transmission under different climate change scenarios and is easily adapted to other vector-borne diseases and crop pests.

Keywords: Asian Citrus Psyllid, Bayesian inference, crop management, Huanglongbing, risk of establishment, species distribution models, transmission suitability, vector-borne disease

1 |. INTRODUCTION

The quality and quantity of yields for many crop systems can be significantly reduced by pests and disease. For example, the wheat aphid reduces yields of grain crops (Merrill, Holtzer, Peairs, & Lester, 2009), Pierce’s disease vectored by the glassy-winged sharpshooter diminishes grape yields (Bruening, Kirkpatrick, Esser, & Webster, 2014), codling moth damages apple orchards (Rafoss & Sæthre, 2003), and Huanglongbing (HLB) vectored by the Asian citrus psyllid (ACP) decimates citrus crops (da Graça et al., 2016). The pests and/or vectors of disease are often small arthropods that are sensitive to environmental conditions, including temperature and humidity (Mordecai et al., 2013; Tsai, Wang, & Liu, 2002). Therefore, predicting when and where these pests or disease vectors will occur, and hence potential loss of crops, is often highly dependent on environmental conditions, and thus a changing climate. Some crops are already experiencing reduced yields associated with climate change (Challinor et al., 2014), an undesired outcome that could be exacerbated if it coincides with increases in pest populations or disease transmission (Cammell & Knight, 1992). However, predicting realistic impacts of climate change on living systems, such as pests and disease vectors, is a major challenge in ecology (Rohr et al., 2011).

With the pressing need to understand the effects of climate change on food production, we provide a method to estimate and display the fundamental thermal niche of a crop pest or disease. The fundamental thermal niche is the set of temperatures under which populations of a species would be expected to persist, all else being equal (Angilletta & Sears, 2011). It can be used to predict where pests or disease can currently establish outside of their existing range, as well as predict future locations of pest and disease outbreaks associated with a changing climate. This, in turn, can facilitate targeting risk-based surveillance and prophylactic interventions. Consequently, our method for estimating the fundamental thermal niche of a crop pest or disease should be an important tool for current and future agricultural planning.

In this study, we borrow approaches established for human vector-borne diseases (Mordecai et al., 2017, 2013) to simultaneously estimate the fundamental thermal niche of a crop pathogen and its insect vector. More specifically, we first develop a mechanistic model of disease transmission where the parameters of the model are fitted to data from temperature-dependent laboratory studies. A metric derived from this model is then used to indicate how suitable locations are based on average monthly temperatures. Finally, we validate the model by assessing how well it corresponds with observational data on known disease occurrence (Mordecai et al., 2013). Additionally, we use Bayesian inference to incorporate uncertainty arising from the use of multiple data sources and uncertainty in temperature dependence of each of the vector’s life history traits to estimate the overall uncertainty in the suitability metric (Johnson et al., 2015). Our method allows for the inclusion of the intrinsic reasons behind why an organism is found where it is and the potential interplay when different traits of organisms respond disparately to changes in extrinsic factors (Angilletta & Sears, 2011).

To develop our methods, we leverage data on the effect of temperature on bacteria of citrus that cause the disease HLB (or citrus greening) and their primary vector, the ACP (Diaphorina citri Kuwayama). Citrus is a commercially important crop grown throughout the world including South-East Asia, Australia, the Mediterranean, South Africa, South and Central America and southern states of USA (FAO, 2017). HLB is a devastating disease of citrus trees that has spread globally from its origin in Asia (Bové, 2006). It affects the quality and quantity of citrus fruit on a tree, for all citrus species, leading to misshapen fruit, bitter taste, and fruit dropping early (Bové, 2006). The symptoms can be difficult to detect, and may take months to appear on a tree, but include chlorosis of leaves with eventual dieback and death of the tree (Gottwald, 2010; Lee et al., 2015). HLB is caused by three bacteria: Candidatus Liberibacter asiaticus (CLas), Candidatus Liberibacter africanus (CLaf), and Candidatus Liberibacter americanus (CLam) (Bové, 2006). The predominant bacterium, and the focus in this study, is CLas, which occurs in all HLB-infected areas (Gottwald, 2010) apart from South Africa (where CLaf is present). CLam occurs primarily in South America alongside CLas, and is responsible for only a minority of cases there (Gottwald, 2010). Transmission of both the CLas and CLam bacteria occurs due to feeding of the ACP (Grafton-Cardwell, Stelinski, & Stansly, 2013; Hall, Richardson, Ammar, & Halbert, 2013). ACP and HLB have spread throughout the world mostly via worldwide trade (Byrne et al., 2018) and now exist in nearly all citrus producing regions (Hall et al., 2013). The cost of this disease to the citrus industry is huge, and interventions to prevent its spread and reduce the deleterious effects of the disease are, for the most part, ineffective (Hodges & Spreen, 2012). Here, we map the suitability metric of HLB around the world to provide a planning tool for citrus growers, whilst the method itself is applicable to all crop diseases spread by vectors or to crop pests.

2 |. MATERIALS AND METHODS

2.1 |. Formulation of S(T)

To determine the thermal niche of citrus greening, we characterize the possibility of an introduction of citrus greening persisting at a local level, for different locations around the world. We use an estimate of the basic reproductive number R0. When R0 > 1, the disease is likely to spread and lead to an epidemic, whereas if R0 < 1, the disease will die out. We determine an equation for R0 for the spread of citrus greening on a single grove by using a previously developed model for citrus greening (Taylor, Mordecai, Gilligan, Rohr, & Johnson, 2016). In this mechanistic model, trees and psyllids are split into different compartments based on their disease status. Trees are susceptible, asymptomatic (infected, but no symptoms) or infected (with symptoms). Psyllids are susceptible, exposed or infected (Figure 1). Death of trees and roguing (removing trees from a grove due to high levels of infection) are included, as well as replacement of all removed trees with susceptible trees. For full details of this model, see Appendix S1. The basic reproductive number R0 is then calculated as (Taylor et al., 2016):

R0=(FEpEADPa2bcFNμ3(3ϕ3ϕ+μ)3e−rτ(1γ+r+γ(γ+r)r1))1/2. (1)

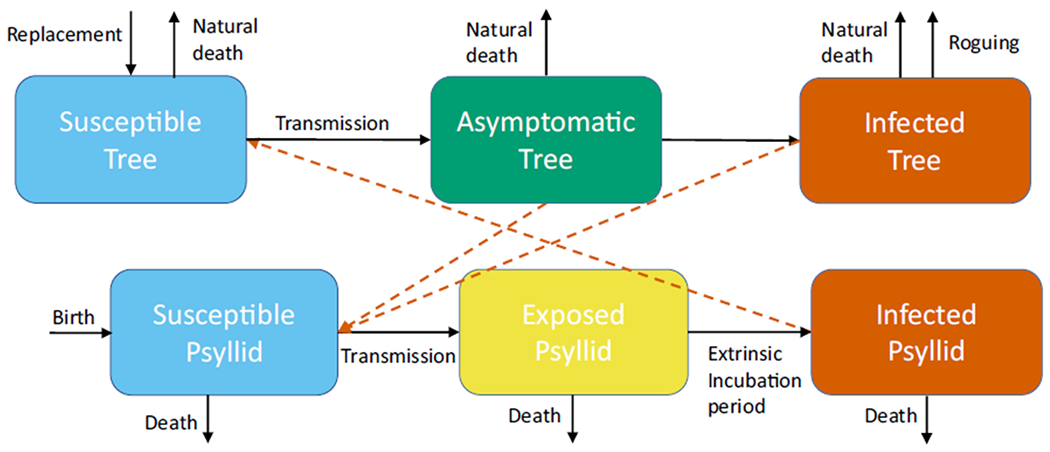
FIGURE 1.

FIGURE 1

Open in a new tab

A schematic of the model for HLB transmitted between trees and psyllids. Trees are susceptible, asymptomatic, or infected. Psyllids are susceptible, exposed or infected. Dead and rogued trees are replaced by susceptible trees. Black arrows show the transitions between the compartments. Orange dashed arrows show the necessary interactions between trees and psyllids to obtain transmission

This equation for R0 can be understood by considering how disease propagates through the citrus system. The number of psyllids in the population is determined by:

V=FEpEADPFμ2 (2)

which includes the fecundity of adult psyllids (FE), the probability of egg to adult survival (pEA), the development rate from egg to adult (DP), the mortality rate of adult psyllids (μ) and the amount of trees flushing (F) within the grove which varies throughout the year. These adult psyllids are in contact with the single infected tree based on the bite rate (a) with a probability of transmission from tree to psyllid (c). The psyllids undergo an extrinsic incubation period before becoming infectious given by rate (ϕ). But they can die during this time which leads to the term (3ϕ3ϕ+μ)3 for the number of psyllids that survive the extrinsic incubation period. These infectious psyllids are in contact with susceptible trees (total N), once again with bite rate a and a probability of transmission from psyllid to tree (b). The term e−rτ represents the proportion of trees that survive the incubation period (τ) to become infectious. The final combined term in the equation determines how long a tree is infectious, during both the asymptomatic stage and the infected stage, and includes the rate at which trees develop symptoms (γ), the death rate of asymptomatic trees (r) and the death rate of infected trees (r1).

We define our measure of thermal suitability for HLB as the vector/infection components of R0 that depend on temperature, T, only. That is, the suitability, S(T), is given by:

S(T)=C(FE(T)pEA(T)DP(T)μ(T)3)1/2(3ϕ3ϕ+μ(T))3/2, (3)

where C is a constant that scales the mean suitability to lie between 0 and 1. Thus, the suitability is zero when temperature is predicted to fully exclude transmission and 1 at maximal transmission. In the results, we will primarily focus on predictions based on two suitability regimes: a “permissive” thermal niche corresponding to temperatures where S(T) > 0; and a “highly suitable” thermal niche corresponding to temperatures such that S(T) > 0.75 (i.e. the highest quartile of suitability).

2.2 |. Bayesian fitting of thermal traits in S(T)

It has been widely recognized that performance traits of ectotherms, such as survival, reproduction, and movement, exhibit unimodal responses to temperature (Amarasekare & Savage, 2012, p. 134; Dell, Pawar, & Savage, 2011). Following the approach introduced in Mordecai et al. (2013), we fit unimodal temperature responses to laboratory data for traits of the vector that appear in the equation for S(T). These curves can then be inserted into the equation for S(T) to determine how transmission depends upon temperature. As in Johnson et al. (2015), we take a Bayesian approach to fitting. Thus, we can quantify the uncertainty in the temperature relationship of individual components and explore the emergent uncertainty in S(T) overall that is due to the uncertainty in the components. Complete details of the approach are presented in Appendix S2.

Here, we focus on four psyllid traits for which there exists data across sufficient temperatures to quantify the responses: fecundity (FE); probability of egg to adult survival (pEA); average longevity (the inverse of the mortality rate, 1/μ); and the development rate of psyllidsfrom eggs into adults (DP).The majority of the data comes from Liu and Tsai (2000), which has a range of 15°C up to 30°C for all four parameters, with additional data at 10 and 33°C for some of the parameters. Hall, Wenninger, and Hentz (2011) and Hall and Hentz (2014) provide data on high and low extreme temperatures that prevent development of the psyllids and/or lead to mortality. However, Hall et al. (2011) also provide information on fecundity of female psyllids across a temperature range of 11–41°C. We include both datasets for fecundity, and consider whether they generate different predictions. Hereafter, Liu and Tsai (2000) and Hall et al. (2011) will be referred to as LT00 and H11, respectively, and, when referring to the S(T) output created by either dataset, LT00 S(T) and H11 S(T) will be used.

For all sets of data, we fit two functions to describe the mean relationship between the trait and temperature: quadratic, giving a symmetric relationship (f(T)=qn(T–T0)(T–TM)); Brière, giving an asymmetric relationship (f(T)=cT(T–T0)(T–TM))1/2, Brière, Pracros, Roux, & Pierre, 1999). All responses were fitted using a Bayesian approach. After specifying the mean relationship, probability distributions appropriate to describe the variability around this mean were chosen, and priors specified (Appendix S2). We chose priors to limit parameters for the minimum and maximum temperature thresholds to approximate known limits to psyllid survival. For instance, the prior on the thermal limits was set uniformly over the interval from 30 to 50°C to acknowledge that exposing psyllids to the very high temperatures kills them almost immediately, while being wide enough to allow the laboratory data primacy in the analysis. Priors for other parameters of the mean were chosen to be relatively uninformative but scaled appropriately for the response. Priors on variance parameters were typically also chosen to be relatively uninformative, although the precise specification varied due to differences in the scale of the responses and to improve mixing and convergence of the Markov Chain Monte Carlo sampling scheme. All responses were fitted in r (R Development Core Team, 2008) using the jags/rjags packages (Plummer, 2003, 2013). After fitting both quadratic and Briére responses to each dataset, the preferred response was chosen via deviance information criterion as implemented in rjags.

Once samples of the posterior distributions of parameters for the preferred model were obtained, these were used to calculate the posterior samples of the response across temperature. Then, at each temperature the mean/median of the response and the 95% highest posterior density (HPD) interval were calculated. The posterior samples of each trait response were then combined to create samples from the overall response of S(T) to temperature. As with the individual thermal responses, these posterior samples of S(T) across temperature were used to calculate the mean and 95% HPD interval around the mean of S(T).

2.3 |. Uncertainty in response of S(T) to temperature

The uncertainty for each parameter in S(T) is calculated using the variation in S(T) at each temperature when all parameters, apart from the one of interest, are held constant at their mean posterior values for that temperature. We calculate the 2.5 and 97.5 quantiles of the S(Tm) posterior distribution and plot the difference between the quantiles against Tm, where we use Tm to represent the temperature with all bar one parameter held at their mean values. We do this for values of Tm in our temperature range, and then for all parameters in S(T). This method indicates which parameters have the greatest variation at each temperature and hence which parameters have the greatest uncertainty at that temperature. This allows us to know when our estimate of S(T) is uncertain and which parameter is causing this.

2.4 |. Mapping suitability across space

To communicate the potential suitability of the world’s land surface for transmission of HLB, we mapped the months of suitability as a function of mean monthly temperatures. We used the WorldClim dataset (version 1.4, www.worldclim.org) (Hijmans, Cameron, Parra, Jones, & Jarvis, 2005), which corresponds to a climate period of 1960–1990, used to represent a long term period in the 20th century; this appropriately represents the date range of the validation occurrence data, from 1956 to 2014. Using this “baseline” long term climate data reduces any biases that may arise from recent warming signals mis-representing the earlier part of the validation data. We took the posterior mean S(T) curves for the H11 and LT00 models across temperatures and extracted the temperatures corresponding to the top 25th percentile of the S(T) curve (i.e. S(T) > 0.75, Appendix S5) for the highly suitable thermal niche, and temperatures corresponding to the transmission limits (S(T) > 0) for the permissive thermal niche (Ryan et al., 2015). These values were used with the climate models (see Section 2.4.1) to determine, on average, the number of months each year that each pixel is either permissive or highly suitable.

2.4.1 |. Climate models

We mapped the suitability measures onto rasters of current mean monthly temperature data at 0.1°C intervals. Data were derived from WorldClim version 1.4 dataset at 5 min resolution (roughly 10 km2 at the equator). The scaled suitability model was projected onto the climate data using the raster package (Hijmans, 2016) in R (R Development Core Team, 2008). Visualizations were generated in ArcMap. For each of the scenarios, we created global maps and insets for areas of citrus growing concern in the Northern Hemisphere: California, Florida and the Iberian peninsula.

2.5 |. Validation of suitability measure

Narouei-Khandan, Halbert, Worner, and Bruggen (2016) present spatially explicit data on locations with confirmed presence of the ACP or HLB (CLas form specifically). These are presence-only data, so we cannot examine how well our model partitions predictions between suitable and unsuitable areas. Instead, we focus on a more qualitative assessment of model adequacy. For each location in the dataset, we calculate the number of months that the average temperature falls within the bounds of the permissive or the highly suitable thermal ranges of ACP from our model. If our model can adequately capture temperature conditions related to transmission and vector establishment, then most locations of HLB presence will have many months in the suitable range. We restrict ourselves to locations from the dataset that are not from mountainous regions (i.e. exclusion of ACP [n = 26] and HLB [n = 12] points) by removing those coinciding with named mountain ranges. This is because, at the spatial scale we use for climate layers, these areas tend to have much more true variation in temperature, leading to higher uncertainty in the temperature predictor than in other locations. This removal alleviates the risk of introducing bias in either warmer or colder directions.

3 |. RESULTS

3.1 |. Posterior distributions of thermal traits

The probability of egg to adult survival (pEA) and longevity (1/μ) are both fitted best by quadratic curves, while development rate from egg to adult (DP) is best fitted by a Briére curve (Figure 2). However, fecundity (FE) switches from a Briére to a quadratic depending on whether we use the data from Liu and Tsai (2000) or Hall et al. (2011) respectively (Figure 2d,e). The data sources also predict different upper thermal limits for fecundity: LT00 predicts no fecundity above 31°C, whereas fecundity is possible up to 41°C according to H11. Full posterior plots of the parameters are in Appendix S3.

FIGURE 2.

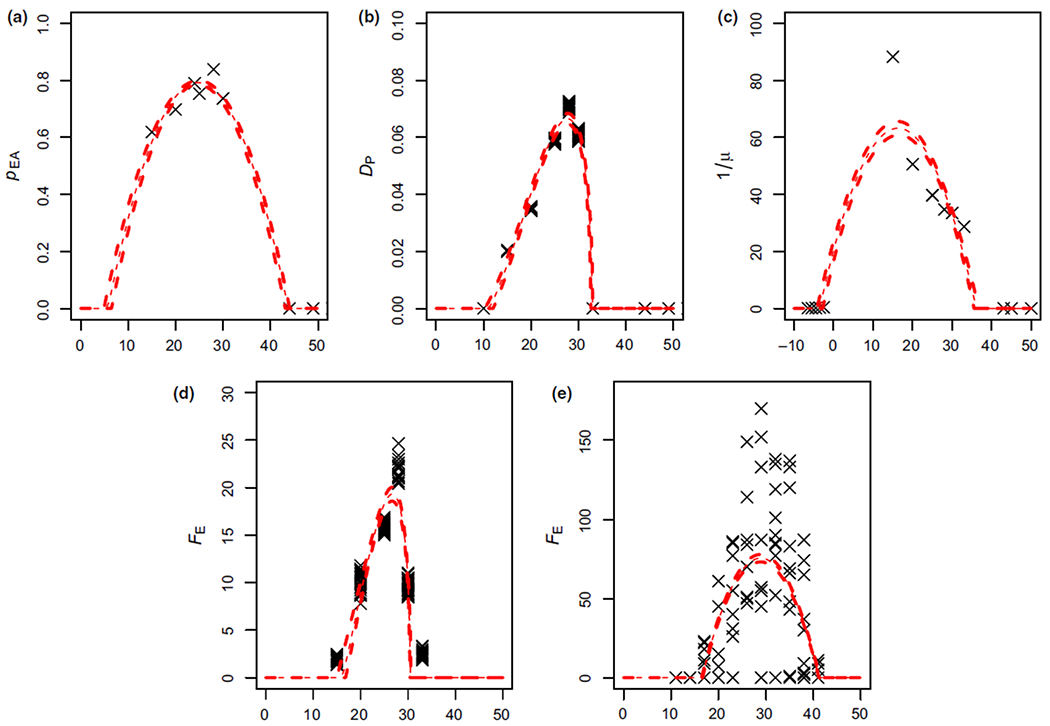
FIGURE 2

Open in a new tab

Psyllid trait data against temperature (°C) with the best fit plotted as a solid line and 95% quantiles as dashed lines. In (a), the probability of egg to adult survival (pEA); in (b), the development rate from egg to adult psyllid (DP); in (c), the longevity of adult psyllids (1/μ); in (d), the fecundity of adult psyllids (FE) with only Liu and Tsai (2000) data used; and in (e) the fecundity of adult psyllids (FE) with only the Hall et al. (2011) data is used

3.2 |. Posterior distribution of S(T)

The lower thermal bound of the posterior distributions of LT00 and H11 S(T) are in agreement, predicted using the two different datasets for fecundity, although LT00 S(T) has more uncertainty (Figure 3, Appendix S4). The temperature at which the peak of S(T) occurs is also very closely aligned. However, the value of S(T) at that peak temperature and the upper thermal limit are very different. When scaled so that the LT00 S(T) has a maximum of 1, the peak of H11 S(T) is 1.35 times larger. LT00 S(T) is driven to 0 at approximately 31°C because fecundity is not possible for higher temperatures. However, H11 S(T) still has a transmission predicted up to 33°C.

FIGURE 3.

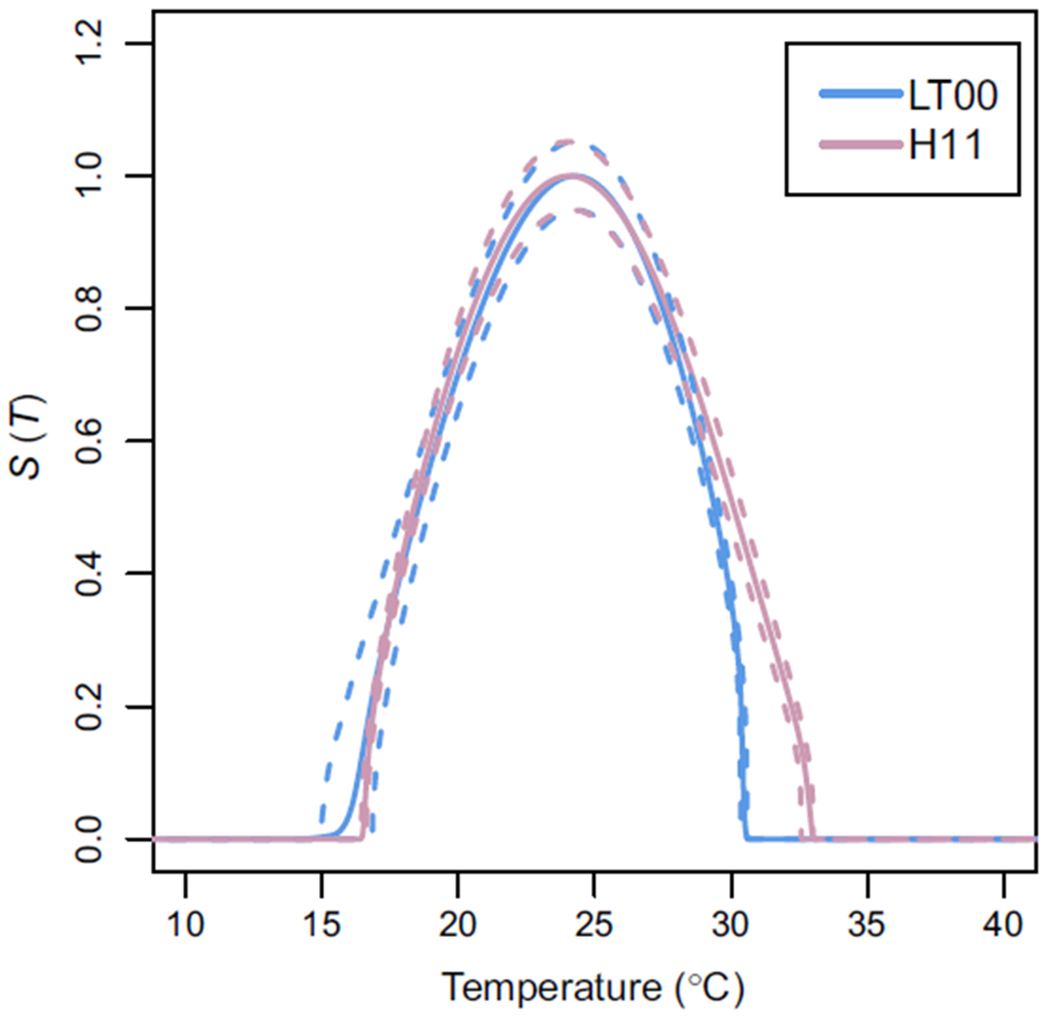
FIGURE 3

Open in a new tab

Posterior distribution of S(T) against temperature (°C) using data from Liu and Tsai (2000) (LT00, in blue) and Hall et al. (2011) (H11, in pink). Mean S(T) for both models is plotted using solid lines, 95% credible intervals are plotted with dashed lines. Both are independently scaled so that their maximum is 1

3.3 |. Sources of uncertainty in S(T)

The uncertainty of each parameter on S(T) is plotted against temperature as all other parameters are held constant at their means (Figure 4). We can use Figure 4 to understand what drives S(T) at different temperatures, and therefore it indicates how best to affect S(T) at those temperatures, if the aim is intervention. In Figure 4a, fecundity (FE) is the main parameter driving variability in S(T) during the range 15–20°C as well as when S(T) is decreasing to 0 at 31°C. However, adult mortality (μ) is the main proponent of uncertainty during the mid to high temperatures of 20–30°C. In comparison, in Figure 4b, adult mortality (μ) leads to the most uncertainty over the whole temperature range. While adult fecundity is once again important at low temperatures, it is the development rate (DP) that emerges as producing the most variability in S(T) at high temperatures.

FIGURE 4.

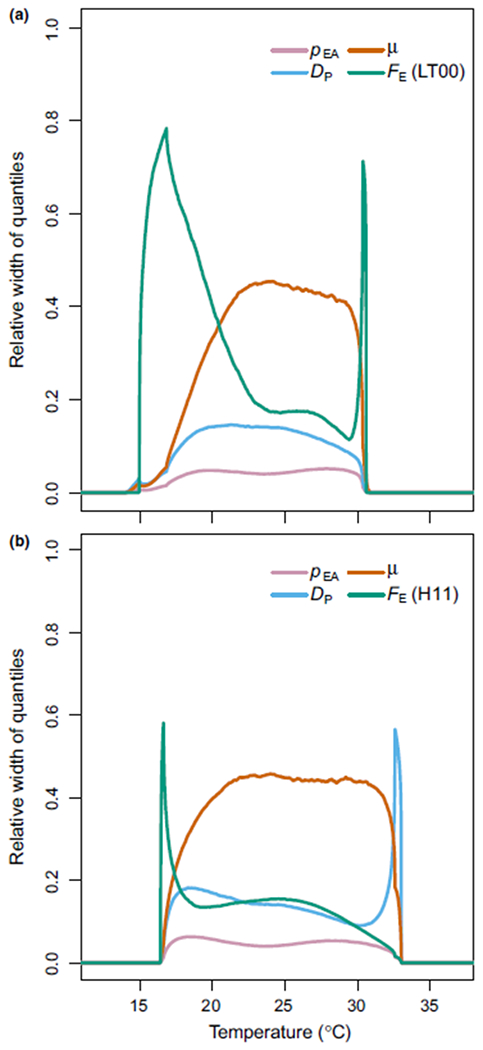
FIGURE 4

Open in a new tab

The uncertainty of S(T) propagated through each parameters’ relation to temperature. In (a) uncertainty in LT00 S(T) and in (b) uncertainty in H11 S(T). This is produced based upon the posterior of S(T), holding all parameters constant at their predictive mean apart from the parameter of interest. The 2.5% and 97.5% quantiles of the resultant estimation of S(T) are then calculated at each temperature and the difference between these quantiles is plotted

3.4 |. Validation

We present histograms of the number of months that the average temperature falls within the bounds of both the permissive or the highly suitable thermal ranges (Figure 5, based on the H11 model) at each location in the dataset from Narouei-Khandan et al. (2016).

FIGURE 5.

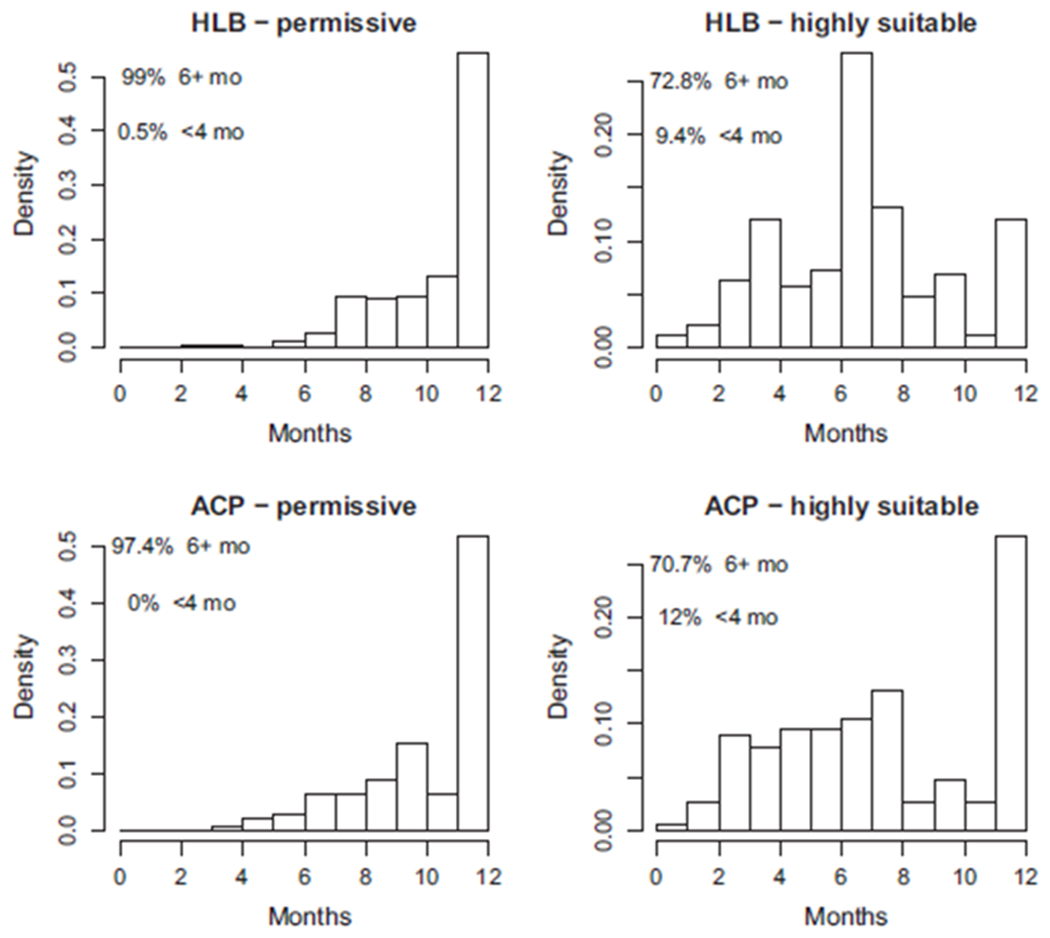
FIGURE 5

Open in a new tab

The number of months that every location with current HLB or ACP presence is either permissive or highly suitable according to our H11 S(T) model. Top row: locations in the validation dataset where HLB is present. Bottom row: locations in the validation dataset where ACP is present. We define permissive suitability as S(T) > 0 and high suitability as S(T) > 0.75

Most locations with HLB or ACP have permissive temperature ranges for at least 6 months of the year. Over 82% of locations are in the permissive range for nine or more months of the year, and more than 50% have permissive temperatures year round. Locations with year round highly suitable conditions account for 12% and 28% of records for HLB and ACP, respectively, and over 70% of locations have highly suitable conditions for 6 months or more. There are almost no locations with HLB or ACP present that the conditions are permissive for less than 3 months. Results based on the data by Liu and Tsai (2000) are similar, as are the results that include mountainous areas (see Appendix S6).

3.5 |. Thermal niche of HLB

In Figures 6 and 7, we present the mapped outputs of the permissive and highly suitable regions, respectively, for H11 S(T). Similar maps for the LT00 S(T) model are presented in Appendix S7 and maps with the HLB and ACP validation points included are provided in Appendix S8. Many locations in the Southern Hemisphere are permissive for HLB all months of the year (Figure 6), including in South America and Southwest Asia where the disease is currently present. Australia and many countries in Africa, which are large citrus producing regions, are permissive for HLB all or many months of the year, but CLas HLB is not currently present. The insets highlight that southern Florida is permissive for HLB all months of the year, and for at least 7 months in the north. This is confirmed on the ground as HLB is present throughout the whole state of Florida. California and the Iberian peninsula have similar suitability profiles to each other, with up to 7 months permissive in the south of the Iberian peninsula, and up to 8 months at the very south of California. As expected, more northerly regions of the world, which are not suitable for growing citrus, are also not able to maintain ACP populations.

FIGURE 6.

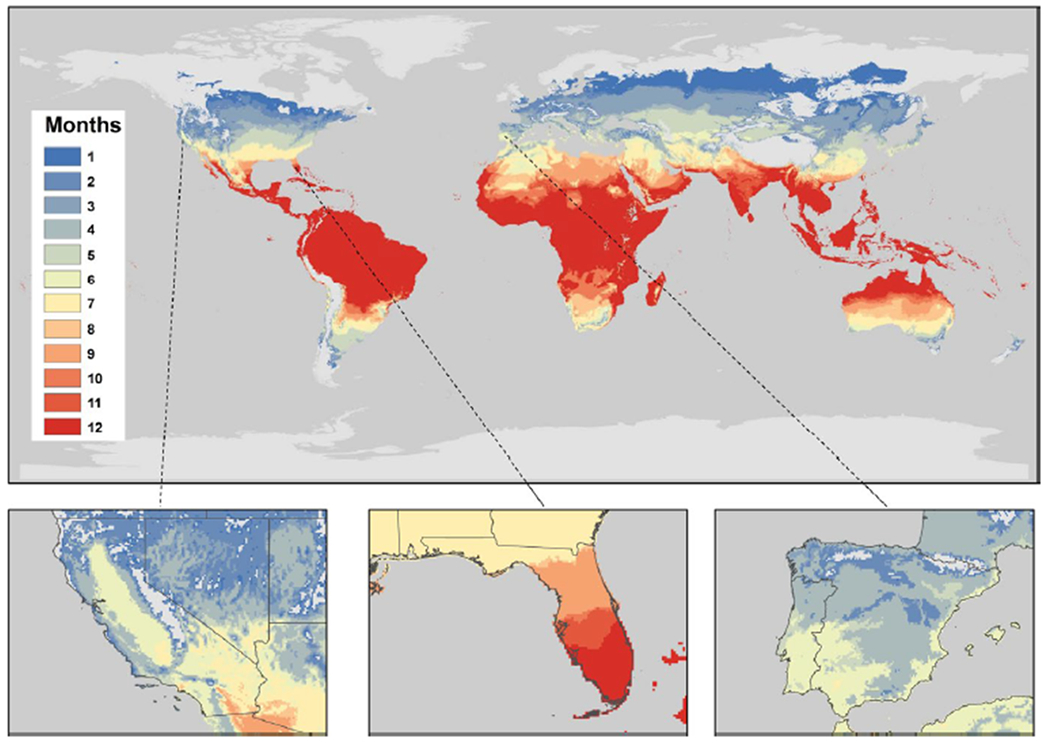
FIGURE 6

Open in a new tab

The number of months a year that locations have permissive temperatures according to our H11 S(T) model. Inset plots of California, Florida and the Iberian peninsula, respectively, are included. We define permissive temperatures for suitability as S(T) > 0. Locations in grey have zero months suitable for HLB transmission

FIGURE 7.

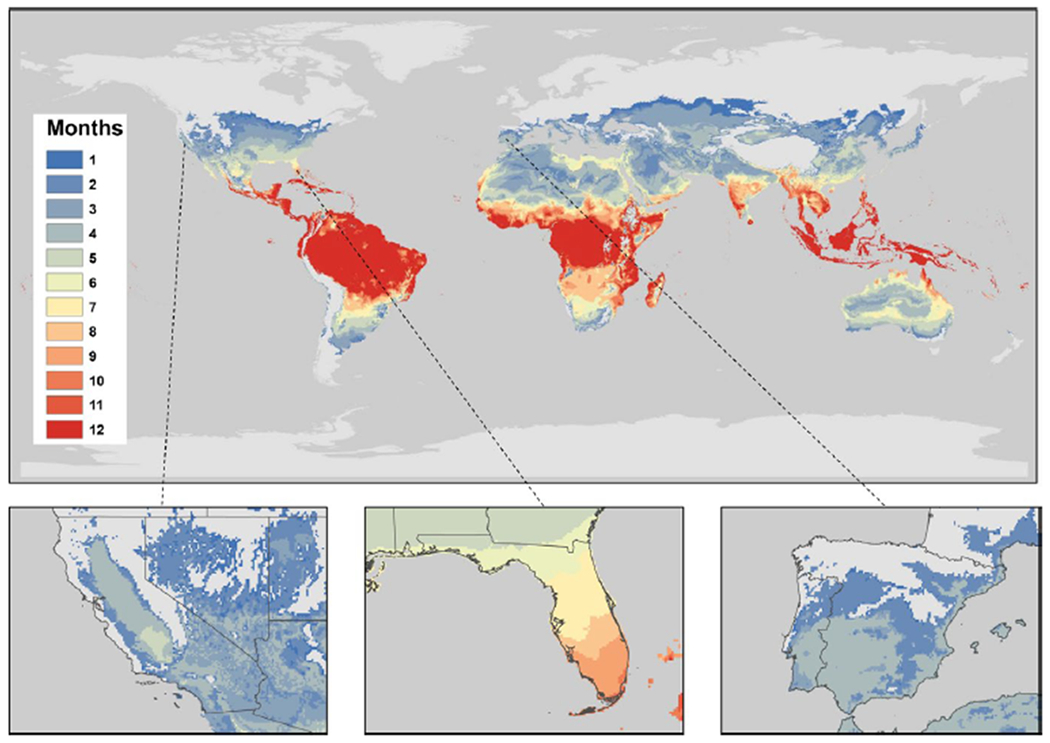
FIGURE 7

Open in a new tab

The number of months a year that locations have highly suitable temperatures according to our H11 S(T) model. Inset plots of California, Florida and the Iberian peninsula, respectively, are included. We define highly suitable temperatures as S(T)>0.75. Locations grey have zero months suitable for HLB transmission

The pattern for suitability is similar for the highly suitable map (Figure 7) but with lower numbers of months satisfying this stricter criteria. South America maintains year round high suitability for the disease across much of the continent. Similarly, Southwest Asia maintains suitability year-round, whereas Australia is reduced to 7 months or less across the country. California and the Iberian peninsula are highly suitable for 4–5 months of the year, whereas Florida is still highly suitable for up to 9 months each year.

4 |. DISCUSSION

In this paper, we presented a model of suitability for a specific crop disease, HLB. This method of demonstrating duration of risk of potential disease emergence and transmission, as a function of thermal suitability, has been successfully used for human vector-borne diseases such as dengue, Zika and malaria (Mordecai et al., 2017, 2013). This climate-predictive mapping framework provides a tool for planning and intervention, and is adaptable to multiple systems, including vector-borne diseases of crops and thermally sensitive crop pests. While we have demonstrated this approach for a coupled vector–pathogen system, and thus used R0 as a starting point to create a transmission-based suitability metric, the method to create a fundamental thermal niche for invasive crop pests is readily possible using population models (in which R0 represents the likelihood of population persistence rather than disease persistence). Given the availability of rigorous laboratory experiments on the thermal responses of other crop pest or disease systems (Deutsch et al., 2008), this approach is broadly applicable to many systems.

Our model outputs a suitability metric S(T) for transmission of HLB dependent on temperature. Conditional on the data we use to parameterize S(T), we predict that transmission can occur between 16°C and 30–33°C with peak transmission at approximately 25°C. While the lower bound and peak temperature predictions are similar regardless of which of the two fecundity datasets we use for parameterization, i.e. those from Hall et al. (2011) (H11) or Liu and Tsai (2000) (LT00), the predicted upper limit of suitability of the peaks differ depending on the data used (Figure 3). More specifically, the range is wider for the H11 data. Thus, based on the suitability index, there might be more areas strictly suitable for transmission if we assume the H11 data are more representative of psyllid populations in the field. Furthermore, when we consider our uncertainty analysis, there are additional differences between the two data sources (Figure 4). The main uncertainty in the LT00 model arises from fecundity at lower temperatures and mortality for higher temperatures, whereas for the H11 model, mortality is the main driver of uncertainty overall. In both cases, mortality of ACP is the most important parameter when S(T) is near its peak at 25°C. Together, these indicate that focus should be on further experimental understanding of mortality rates and fecundity near the edges of the thermal tolerances of psyllids to refine our estimates of the thermal niche.

We use our suitability metric to predict regions which are permissive or highly suitable for HLB around the world. Our maps indicate that regions close to the equator have the greatest number of months permissive for HLB transmission, especially in South America, Africa and South East Asia. South America and South East Asia are, in particular, large citrus producing regions, and HLB is already present in both (Coletta-Filho et al., 2004; Garnier & Bové, 1996, 2000; Torres-Pacheco et al., 2013). The fact that HLB is not only permissive all 12 months of the year, but is actually highly suitable year-round, indicates the scale of the potential problem in those areas. However, the HLB epidemic in São Paulo State in Brazil, the major citrus-producing region in the country, is successfully managed in those areas that have adhered to strict recommendations for control (Belasque et al., 2010). The disease entered the state in 2004 (Coletta-Filho et al., 2004). By 2012, incidence of disease was estimated as low as 1% for symptomatic trees across a third of the citrus acreage in the state (Bové, 2012). In comparison, in Florida, where the disease was first discovered in 2005, growers in a survey in 2015 were asked to estimate both the percentage of their citrus acres with at least one tree infected and the percentage of all their citrus trees infected, with results indicating 90% and 80%, respectively (Singerman & Useche, 2016). This is despite the fact that our suitability metric estimates the northern regions of Florida to be highly suitable for HLB only 6 months of the year. While Brazil might have managed to control HLB successfully in some regions, the disease is still spreading throughout the country in those regions which have not been as proactive in their control (Belasque et al., 2010); a reminder that, without strict control measures, the disease can spread quickly and devastatingly, with 100% HLB incidence possible in infected groves (Bové, 2012).

Within the Northern Hemisphere, we highlight the suitability of California and the Iberian peninsula for HLB transmission. Although California has had incursions of the disease, with the first occurring in 2012 (Kumagai et al., 2013), all have been in trees at residential properties and hence the citrus industry in California is currently free from disease (Byrne et al., 2018). Similarly, the Iberian peninsula has had no cases of HLB (Cocuzza et al., 2017). However, both regions have high citrus production and thus the potential consequences of incursion of HLB are high. They have similar suitability profiles with permissive suitability of HLB on average about 6 months of the year in both regions. While disease transmission might not be permissible all year round, trees can remain infected with HLB indefinitely unless they are rogued, thus allowing over-wintering of the disease during the seasons that ACP will not be active (Gottwald, 2010). Therefore, for these two regions to maintain HLB-free status, they need to deal with incursions promptly to ensure infected trees are removed. However, California has the added disadvantage that its neighbouring country and many neighbouring states have the disease or have ACP present (Torres-Pacheco et al., 2013). Indeed, the initial incursion of ACP into California is most likely to have occurred from Mexico (Bayles, Thomas, Simmons, Grafton-Cardwell, & Daugherty, 2017). This makes it harder to reduce the likelihood of HLB incursion as it is difficult to control the movement of vectors across borders. For the Iberian peninsula, it has been suggested that incursion of HLB is most likely through contaminated trade, such as infected plant materials (Cocuzza et al., 2017).

Our analysis has been performed for the transmission of the CLas form of HLB by the vector ACP and thus does not quantify the spread of CLaf HLB around the world from the African citrus psyllid (AfCP). Therefore, the suitability for HLB transmission might be underestimated in some areas of the world since AfCP has a different temperature profile than ACP, as it prefers higher elevations and lower temperatures and the two psyllids have not been found in the same locations (da Graça et al., 2016). In 2014, AfCP was first discovered in mainland Spain, alarming the citrus industry in Spain and Portugal (Cocuzza et al., 2017). Thus, it is possible that the Iberian peninsula is permissive for HLB for more months of the year than we have predicted if AfCP is the primary vector there.

We have validated this model using spatially explicit records of HLB and ACP presence. Most areas with confirmed HLB or ACP are in regions our model predicts as permissive or highly suitable for most of the year, indicating that our temperature-only model can capture an important component of the environment that constrains the spatial distribution of HLB. Narouei-Khandan et al. (2016) used species distribution modelling with climatic variables to also create a HLB niche model, finding that annual precipitation levels, resulting in higher humidity, are the greatest predictor of HLB presence around the world. Unfortunately, there are not enough laboratory experiments assessing the effect of humidity on psyllid life history traits for us to include this in our model. Whilst our validation results indicate that we have successfully characterized a significant component of HLB transmission using temperature, our predictions could undoubtedly improve if we also included the effects of humidity. Our model produces similar results to the model of Narouei-Khandan et al. (2016), although it is difficult to make comparisons between number of permissive months (our model) versus the probability of occurrence (Narouei-Khandan et al., 2016 model). The Narouei-Khandan et al. (2016) model predicts greater areas in Australia suitable for HLB and ACP establishment than our model but only coastal areas of California are predicted to have a high probability of HLP and ACP occurrence with a low probability elsewhere in California. In contrast, our model predicts up to 7 months of permissive suitability across much of California.

Our method for creating the thermal niche is adaptable to other crop diseases and pests due to its strength of being built using mechanistic models. Spatially explicit data of disease presence are typically used to build ecological niche models in other contexts (Gething et al., 2011; Peterson, Martínez-Campos, Nakazawa, & Martínez-Meyer, 2005). A mechanistic model with additional on-the-ground validation is likely to predict more robustly how temperature constrains transmission than a correlative approach based on presence-only data. It also enables clean projections for future climate scenarios, as it is not limited by unquantifiable changes in land cover.

Our use of two datasets for one parameter highlights how our understanding of a disease/pest population can change significantly depending on the data we use to parameterize our models. The best way to avoid this and reduce our uncertainty is to use multiple data sources combined, but this requires multiple experiments from different laboratories estimating the same parameter across a range of temperatures using the same empirical approaches. Often multiple experiments like this do not take place because of a perceived lack of novelty, but as we show here, they are potentially important to fully understand the impact of temperature on the persistence and establishment of vector-borne diseases and pest populations.

As our mapping of suitability is performed at the pixel level, approximately 10 km2 at the equator, this allows us to predict suitability to a very fine scale. Therefore, our map for HLB suitability can be used as a tool to determine surveillance and management strategies at a fine spatial scale. Furthermore, the general method is applicable for other vector-borne crop diseases or pests. Suitability does not indicate where incursions of the disease are likely to occur, but it does highlight the regions where it is most likely to establish and therefore where it is most necessary to avoid incursion. For example, for HLB in California, surveillance should be targeted mostly towards the southern part of the state (Figure 6). Furthermore, for those countries with disease present already, the suitability maps can indicate which regions should have different management aims: a strict management policy to keep incidence levels low or complete eradication in regions with lower suitability. A more focused surveillance and management strategy can save time, money and resources, which is necessary considering the economic costs currently involved in managing crop diseases (Challinor et al., 2014). São Paulo State, Brazil, demonstrates that it is possible to keep incidence of HLB low, even in a region which is highly suitable for HLB all 12 months of the year. Vera-Villagrán et al. (2016) estimated the economic benefits of implementing a Brazilian strategy in Mexico and found that it was cost-effective, assuming all growers abide by the regulations. The costs of implementing such a strict control strategy may be prohibitive, but it gives hope for the industry that control is possible, especially if implemented as soon as HLB is discovered (Belasque et al., 2010). Similarly, for other vector-borne diseases of crops and crop pests, successful management and control are possible if implemented quickly and extensively after disease or pest emergence (Bruening et al., 2014; Enkerlin et al., 2015). Overall, our suitability maps provide an additional tool, alongside modelling of intervention strategies, cost–benefit analysis, experimental studies, development of disease-resistant trees and other inventions, in the fight against vector-borne crop diseases and pests.

Supplementary Material

Supplementary Appendices S1-S8

ACKNOWLEDGEMENTS

L.R.J., S.J.R., C.A.L. and J.R.R. were supported by the National Science Foundation (DEB-1518681; https://nsf.gov/). S.J.R. was also supported by the National Institutes of Health (R01AI136035-01; https://www.nih.gov/). L.R.J. was supported by NSF (DMS/DEB-1750113). J.R.R. was supported by the NSF (EF-1241889 and IOS-1754868), National Institutes of Health (R01GM109499 and R01TW010286-01), and US Department of Agriculture (2009-35102-0543; https://www.usda.gov/wps/portal/usda/usdahome).

Funding information

Division of Mathematical Sciences, Grant/Award Number: 1750113; Division of Integrative Organismal Systems, Grant/Award Number: IOS-1754868; U.S. Department of Agriculture, Grant/Award Number: 2009-35102-0543; Division of Environmental Biology, Grant/Award Number: DEB-1518681; Division of Emerging Frontiers, Grant/Award Number: EF-1241889; National Institutes of Health, Grant/Award Number: R01AI136035-01, R01GM109499 and R01TW010286-01

Footnotes

DATA AVAILABILITY STATEMENT

Code available via Zenodo https://doi.org/10.5281/zenodo.3235271 (Taylor et al., 2019).

SUPPORTING INFORMATION

Additional supporting information may be found online in the Supporting Information section at the end of the article.

REFERENCES

  1. Amarasekare P, & Savage V (2012). A framework for elucidating the temperature dependence of fitness. The American Naturalist, 179, 178–191. 10.1086/663677 [DOI] [PubMed] [Google Scholar]
  2. Angilletta MJ Jr, & Sears MW (2011). Coordinating theoretical and empirical efforts to understand the linkages between organisms and environments. Integrative and Comparative Biology, 51, 653–661. 10.1093/icb/icr091 [DOI] [PubMed] [Google Scholar]
  3. Bayles BR, Thomas SM, Simmons GS, Grafton-Cardwell EE, & Daugherty MP (2017). Spatiotemporal dynamics of the southern California Asian citrus psyllid (Diaphorina citri) invasion. PLoS ONE, 12, e0173226 10.1371/journal.pone.0173226 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Belasque J, Bassanezi RB, Yamamoto PT, Ayres AJ, Tachibana A, Violante AR, … Bové JM (2010). Lessons from Huanglongbing management in São Paulo state, Brazil. Journal of Plant Pathology, 92, 285–302. [Google Scholar]
  5. Bové JM (2006). Huanglongbing: A destructive, newly-emerging, century-old disease of citrus. Journal of Plant Pathology, 88, 7–37. [Google Scholar]
  6. Bové JM (2012). Huanglongbing and the future of citrus in São Paulo state, Brazil. Journal of Plant Pathology, 94, 465–467. [Google Scholar]
  7. Brière JF, Pracros P, Le Roux AY, & Pierre JS (1999). A novel rate model of temperature-dependent development for arthropods. Environmental Entomology, 28, 22–29. 10.1093/ee/28.1.22 [DOI] [Google Scholar]
  8. Bruening G, Kirkpatrick B, Esser T, & Webster R (2014). Managing newly established pests: Cooperative efforts contained spread of Pierce’s disease and found genetic resistance. California Agriculture, 68, 134–141. 10.3733/ca.v068n04p134 [DOI] [Google Scholar]
  9. Byrne FJ, Grafton-Cardwell EE, Morse JG, Olguin AE, Zeilinger AR, Wilen C, … Daugherty MP (2018). Assessing the risk of containerized citrus contributing to Asian citrus psyllid (Diaphorina citri) spread in California: Residence times and insecticide residues at retail nursery outlets. Crop Protection, 109, 33–41. 10.1016/j.cropro.2018.02.024 [DOI] [Google Scholar]
  10. Cammell ME, & Knight JD (1992). Effects of climatic change on the population dynamics of crop pests. Advances in Ecological Research, 22, 117–162. [Google Scholar]
  11. Challinor AJ, Watson J, Lobell D, Howden S, Smith D, & Chhetri N (2014). A meta-analysis of crop yield under climate change and adaptation. Nature Climate Change, 4, 287 10.1038/nclimate2153 [DOI] [Google Scholar]
  12. Cocuzza GEM, Alberto U, Hernández-Suárez E, Siverio F, Di Silvestro S, Tena A, & Carmelo R (2017). A review on Trioza erytreae (African citrus psyllid), now in mainland Europe, and its potential risk as vector of Huanglongbing (HLB) in citrus. Journal of Pest Science, 90, 1–17. 10.1007/s10340-016-0804-1 [DOI] [Google Scholar]
  13. Coletta-Filho HD, Targon MLPN, Takita MA, De Negri JD, Pompeu J Jr, Machado MA, … Muller GW (2004). First report of the causal agent of Huanglongbing (“Candidatus Liberibacter asiaticus”) in Brazil. Plant Disease, 88, 1382–1382. [DOI] [PubMed] [Google Scholar]
  14. da Graça JV, Douhan GW, Halbert SE, Keremane ML, Lee RE, Vidalakis G, & Zhao H. (2016). Huanglongbing: An overview of a complex pathosystem ravaging the world’s citrus. Journal of Integrative Plant Biology, 58, 373–387. 10.1111/jipb.12437 [DOI] [PubMed] [Google Scholar]
  15. Dell AI, Pawar S, & Savage VM (2011). Systematic variation in the temperature dependence of physiological and ecological traits. Proceedings of the National Academy of Sciences of the United States of America, 108, 10591–10596. 10.1073/pnas.1015178108 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Deutsch CA, Tewksbury JJ, Huey RB, Sheldon KS, Ghalambor CK, Haak DC, & Martin PR (2008). Impacts of climate warming on terrestrial ectotherms across latitude. Proceedings of the National Academy of Sciences of the United States of America, 105, 6668–6672. 10.1073/pnas.0709472105 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Enkerlin W, Gutiérrez-Ruelas JM, Cortes AV, Roldan EC, Midgarden D, Lira E, … Arriaga FJT (2015). Area freedom in Mexico from Mediterranean fruit fly (Diptera: Tephritidae): A review of over 30 years of a successful containment program using an integrated area-wide SIT approach. Florida Entomologist, 98, 665–681. 10.1653/024.098.0242 [DOI] [Google Scholar]
  18. FAO (2017). Food and agriculture organization of the United Nations. FAOSTAT; Retrieved from http://www.fao.org/faostat [Google Scholar]
  19. Garnier M, & Bové JM (1996). Distribution of the Huanglongbing (greening) Liberobacter species in fifteen African and Asian countries. International Organization of Citrus Virologists Conference Proceedings (1957–2010) (Vol. 13). [Google Scholar]
  20. Garnier M, & Bové JM (2000). Huanglongbing in Cambodia, Laos and Myanmar. International Organization of Citrus Virologists Conference Proceedings (1957–2010) (Vol. 14). [Google Scholar]
  21. Gething PW, Patil AP, Smith DL, Guerra CA, Elyazar IR, Johnston GL, … Hay SI (2011). A new world malaria map: Plasmodium falciparum endemicity in 2010. Malaria Journal, 10, 378 10.1186/1475-2875-10-378 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gottwald TR (2010). Current epidemiological understanding of citrus Huanglongbing. Annual Review of Phytopathology, 48, 119–139. 10.1146/annurev-phyto-073009-114418 [DOI] [PubMed] [Google Scholar]
  23. Grafton-Cardwell EE, Stelinski LL, & Stansly PA (2013). Biology and management of Asian citrus psyllid, vector of the Huanglongbing pathogens. Annual Review of Entomology, 58, 413–432. 10.1146/annurev-ento-120811-153542 [DOI] [PubMed] [Google Scholar]
  24. Hall DG, & Hentz MG (2014). Asian Citrus Psyllid (Hemiptera: Liviidae) tolerance to heat. Annals of the Entomological Society of America, 107, 641–649. 10.1603/AN13169 [DOI] [Google Scholar]
  25. Hall DG, Richardson ML, Ammar ED, & Halbert SE (2013). Asian citrus psyllid, Diaphorina citri, vector of citrus Huanglongbing disease. Entomologia Experimentalis et Applicata, 146, 207–223. [Google Scholar]
  26. Hall DG, Wenninger EJ, & Hentz MG (2011). Temperature studies with the Asian citrus psyllid, Diaphorina citri: Cold hardiness and temperature thresholds for oviposition. Journal of Insect Science, 11, 83. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hijmans RJ (2016). raster: Geographic Data Analysis and Modeling. R package version 2.5-8. [Google Scholar]
  28. Hijmans RJ, Cameron SE, Parra JL, Jones PG, & Jarvis A (2005). Very high resolution interpolated climate surfaces for global land areas. International Journal of Climatology, 25, 1965–1978. 10.1002/joc.1276 [DOI] [Google Scholar]
  29. Hodges AW, & Spreen TH (2012). Economic impacts of citrus greening (HLB) in Florida: 2006/07 – 2010/11. Tech, rep, Food and Resource Economics Department, Florida Cooperative Extension Service, Institute of Food and Agricultural Sciences, University of Florida. [Google Scholar]
  30. Johnson LR, Ben-Horin T, Lafferty KD, McNally A, Mordecai E, Paaijmans KP, … Ryan SJ (2015). Understanding uncertainty in temperature effects on vector-borne disease: A Bayesian approach. Ecology, 96, 203–213. 10.1890/13-1964.1 [DOI] [PubMed] [Google Scholar]
  31. Kumagai LB, LeVesque CS, Blomquist CL, Madishetty K, Guo Y, Woods PW, … Polek M(2013). First report of Candidatus Liberibacter asiaticus associated with citrus Huanglongbing in California. Plant Disease, 97, 283. [DOI] [PubMed] [Google Scholar]
  32. Lee JA, Halbert SE, Dawson WO, Robertson CJ, Keesling JE, & Singer BH (2015). Asymptomatic spread of Huanglongbing and implications for disease control. Proceedings of the National Academy of Sciences of the United States of America, 112, 7605–7610. 10.1073/pnas.1508253112 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Liu YH, & Tsai JH (2000). Effects of temperature on biology and life table parameters of the Asian citrus psyllid, Diaphorina citri Kuwayama (Homoptera: Psyllidae). Annals of Applied Biology, 137, 201–206. 10.1111/j.1744-7348.2000.tb00060.x [DOI] [Google Scholar]
  34. Merrill SC, Holtzer TO, Peairs FB, & Lester PJ (2009). Modeling spatial variation of Russian wheat aphid overwintering population densities in Colorado winter wheat. Journal of Economic Entomology, 102, 533–541. 10.1603/029.102.0210 [DOI] [PubMed] [Google Scholar]
  35. Mordecai EA, Cohen JM, Evans MV, Gudapati P, Johnson LR, Lippi CA, … Weikel DP (2017). Detecting the impact of temperature on transmission of Zika, dengue, and chikungunya using mechanistic models. PLoS Neglected Tropical Diseases, 11, e0005568 10.1371/journal.pntd.0005568 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mordecai EA, Paaijmans KP, Johnson LR, Balzer C, Ben-Horin T, Moor E, … Lafferty KD (2013). Optimal temperature for malaria transmission is dramatically lower than previously predicted. Ecology Letters, 16, 22–30. 10.1111/ele.12015 [DOI] [PubMed] [Google Scholar]
  37. Narouei-Khandan HA, Halbert SE, Worner SP, & van Bruggen AHC (2016). Global climate suitability of citrus Huanglongbing and its vector, the Asian citrus psyllid, using two correlative species distribution modeling approaches, with emphasis on the USA. European Journal of Plant Pathology, 144, 655–670. 10.1007/S10658-015-0804-7 [DOI] [Google Scholar]
  38. Peterson AT, Martínez-Campos C, Nakazawa Y, & Martínez-Meyer E (2005). Time-specific ecological niche modeling predicts spatial dynamics of vector insects and human dengue cases. Transactions of the Royal Society of Tropical Medicine and Hygiene, 99, 647–655. 10.1016/j.trstmh.2005.02.004 [DOI] [PubMed] [Google Scholar]
  39. Plummer M (2003). Jags: A program for analysis of {B}ayesian graphical models using Gibbs sampling. In: Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003) March pp. 20–22. [Google Scholar]
  40. Plummer M (2013). rjags: Bayesian graphical models using MCMC. R package version 3.10. [Google Scholar]
  41. R Development Core Team (2008). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
  42. Rafoss T, & Sæthre MG (2003). Spatial and temporal distribution of bioclimatic potential for the codling moth and the Colorado potato beetle in norway: Model predictions versus climate and field data from the 1990s. Agricultural and Forest Entomology, 5, 75–86. 10.1046/j.1461-9563.2003.00166.x [DOI] [Google Scholar]
  43. Rohr JR, Dobson AP, Johnson PT, Kilpatrick AM, Pauli SH, Raffel TR, … Thomas MB (2011). Frontiers in climate change–disease research. Trends in Ecology & Evolution, 26, 270–277. 10.1016/j.tree.2011.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Ryan SJ, McNally A, Johnson LR, Mordecai EA, Ben-Horin T, Paaijmans K, & Lafferty KD (2015). Mapping physiological suitability limits for malaria in Africa under climate change. Vector-Borne and Zoonotic Diseases, 15, 718–725. 10.1089/vbz.2015.1822 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Singerman A, & Useche P (2016). Impact of citrus greening on citrus operations in Florida. University of Florida/lnstitute of Food and Agricultural Sciences Extension; FE983. [Google Scholar]
  46. Taylor RA, Mordecai EA, Gilligan CA, Rohr JR, & Johnson LR (2016). Mathematical models are a powerful method to understand and control the spread of Huanglongbing. PeerJ, 4, e2642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Taylor RA, Ryan SJ, Lippi CA, Hall DG, Narouei-Khandan HA, Rohr JR, & Johnson LR (2019). Predicting the fundamental thermal niche of crop pests and diseases in a changing world: A case study on citrus greening: R code. Zenodo, 10.5281/zenodo.3235271 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Torres-Pacheco I, López-Arroyo JI, Aguirre-Gómez JA, Guevara-González RG, Yänez-López R, Hernández-Zul MI, & Quijano-Carranza JA (2013). Potential distribution in Mexico of Diaphorina citri (Hemiptera: Psyllidae) vector of Huanglongbing pathogen. Florida Entomologist, 96, 36–47. [Google Scholar]
  49. Tsai JH, Wang JJ, & Liu YH (2002). Seasonal abundance of the {A}sian citrus psyllid, Diaphorina citri (Homoptera: Psyllidae) in southern Florida. Florida Entomologist, 85, 446–451. 10.1653/0015-4040(2002)085[0446:SAOTAC]2.0.CO;2 [DOI] [Google Scholar]
  50. Vera-Villagrán E, Sagarnaga-Villegas LM, Salas-González JM, Leos-Rodríguez JA, De De Miranda SHG, & Adami ACDO (2016). Economic impact analysis for combating HLB in key lime citrus groves in Colima, Mexico, assuming the Brazilian approach. Custos E Agronegocio Online, 12, 344–363. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Appendices S1-S8
NIHMS1604352-supplement-Supplementary_Appendices_S1-S8.pdf (19.2MB, pdf)

RESOURCES