Resistive amplitude fingerprints during translocation of linear molecules through charged solid-state nanopores

Abstract

We report the first analytical theory on the amplitude of resistive signals during molecular translocation through charged solid-state nanopores with variable cross-sectional area and piecewise-constant surface charge densities. By providing closed-form explicit algebraic expressions for the concentration profiles inside charged nanopores, this theory allows the prediction of baseline and translocation resistive signals without the need for numerical simulation of the electrokinetic phenomena. A transversely homogenized theory and an asymptotic expansion for weakly charged pores capture DC or quasi-static rectification due to field-induced intrapore concentration polarization (as a result of pore charge inhomogeneity or a translocating molecule). This theory, validated by simulations and experiments, is then used to explain why the amplitude of a single stranded DNA molecule can be twice as high as the amplitude of its double stranded counterpart. It also suggests designs for intrapore concentration polarization and volume exclusion effects that can produce biphasic and other amplitude fingerprints for high-throughput and yet discriminating molecular identification.

I. INTRODUCTION

Nanopore sensing devices can count individual biomolecules through the detection of changes in electrical current (resistive signal) produced by charged molecules transiting through them.^1–6 Their simplicity and sensitivity have rendered them as viable portable biomedical sensors, particularly for point-of-care applications.⁷ They can be classified into three general categories:^8,9 biological protein nanopores,^10–12 solid-state nanopores,^4,7,13 and hybrid nanopores.¹⁴ Single-molecule resolution is achieved either with very small sub-10 nm protein pores^10–12 or much larger conic solid-state pores that only register translocation events at the nanoscale tip.^1,7,15,16 The larger (10 nm–100 nm) solid-state nanopores offer the necessary high throughput to assay a large number of molecules. However, the short translocation time (1 µs–10 µs per single stranded nucleotide^17–19) responsible for their high throughput also prevents them from differentiating between different RNAs from their translocation duration, particularly for short regulatory microRNAs (miRNAs) of comparable length that are important disease biomarkers, and even between probe hybridized duplexes from their unhybridized single stranded counterparts.^7,16 Recently, small protein nanopores were shown to be capable of differentiating non-target miRNAs from target miRNA duplexes with ion-current tags.¹⁰ While the miRNA translocation time is short for these protein nanopores (ms), the capture time is nearly 1 min per molecule even at concentrations much higher than physiological values, since the miRNAs need to linearize before they can enter the protein nanopore.²⁰ There is, then, a considerable conformation entropy barrier for entry into such small nanopores.^21,22 With this low throughput (<10³ molecules/h) due to the entry barrier, only a small fraction of the molecules can be interrogated.¹⁶ Protein nanopores are, hence, highly selective in identifying (even sequencing) target molecules, but too slow for diagnostic applications. Solid-state nanopores, on the other hand, offer rapid counting but are not selective in their molecular identification.

Different methods of increasing the translocation times through solid-state nanopores have been pursued. They range from modifying the properties (mostly viscosity) of the electrolytes^23–25 to using protein tags to slow down the motion of the nucleic acids.^14,26,27 Electrical gating by induced or passive nanopore surface charge has also been explored, succeeding to increase translocation times by at least one order of magnitude.^{16,18,19,28–31} Due to their mechanical strength, robustness, good insulating properties, and high chemical stability, Si₃N₄, SiO₂, SiC, and Al₂O₃ films are currently used to modify solid-state nanopores.^9,32–34 It has been found that Al₂O₃ has better resolution and lower noise than other materials, while also being able to slow down the translocation events due to strong electrostatic interactions.^8,19 In the last few years, the use of single layer materials, such as graphene, boron nitride, and molybdenum disulfide, has been suggested.²⁰ As these membranes have a thickness comparable with the size of a DNA nucleotide (0.34 nm), they promise an increase of spatial resolution in sequencing measurements. However, the strong interaction between nucleobases and graphene surfaces leads to severe clogging after a few translocation events, such that the throughput is again severely reduced for these sensors.⁹ In addition, for charged coatings, interaction between the modified surface and the translocating molecule will also change the amplitude of the resistive signal. Amplitude signatures of molecules translocating through a solid-state nanopore have not been analyzed, although they are obviously the basis for protein nanopore sequencing. Unlike the smaller protein nanopores, a continuum approach is necessary for the disruption of ion distribution within the solid-state nanopores by the translocating molecule. In particular, thermal diffusion and concentration polarization play an important role in solid-state nanopores but not in protein nanopores.

Such amplitude signatures may enhance the selectivity of solid-state nanopore sensors even with short and indistinguishable translocation times, perhaps to the extent that one does not need to increase the translocation time. There is ample earlier work that suggests this may be possible. Discontinuities on the surface charge^35–39 and spatial asymmetry of the pore^16,40–51 have been shown for many decades to lead to very high DC current rectification because of intrapore ion enrichment and depletion phenomena. Hence, asymmetric geometries and coating designs have been introduced such that the translocating molecules can produce unique resistive signatures because of quasi-static rectification effects.^16,52,53 One such design is to use a high electric field to distort the ion cloud of a translocating molecule to produce biphasic signals.^54,55

Another design is to allow adsorption of translocating molecules during the translocation.^56,57 Biphasic patterns have been observed during the translocation of bovine serum albumin into track-etched polymeric nanochannels coated with thin high-permittivity dielectric films.⁵³ Bullet-shaped polymer nanopores coated with thin high-permittivity dielectric films have shown comparable current drops during the translocation of single and double stranded molecules, defying the intuition of usual current blockage theories.¹⁶ Adsorption prolongs the translocation signal in a solid-state pore and introduces a larger charge in homogeneity than a freely translocating molecule. It also suggests the possibility of grafting probes onto the pore to produce distinct amplitude signals for specific molecules.^57–59 The amplitude signals they produce are preferred over translocation duration signals, as the latter often exhibit broad Poisson distributions due to the large ensemble of adsorbed or entry states for a linear molecule.^60,61 For cylindric Si₃N₄ nanopores, the coefficient of variance (CV) for the translocation time can be above 20%, while the amplitude CV is only 5%. For track-etched conical nanopores modified by atomic layer deposition, these coefficients take the values of 40% for the Gaussian amplitude distribution and up to 600% for the Poisson translocation time distribution^16,53 (see Fig. 1). The amplitude signatures of different molecules are hence more distinct than their translocation duration (dwell time) signals. There would also be a larger bandwidth to differentiate different molecules. Despite such potential advantages, we are not aware of any analytical theory on the amplitude signal when a molecule adsorbs onto the pore surface—or even for freely translocating molecules translocating through a charged nanopore.

FIG. 1.

Experimental translocation times and amplitudes of 22-base-pairs-long dsDNA molecules translocating through an atomic-layer-deposition modified track-etched conical nanopore. The dashed line represents our theoretical estimate for the amplitude as calculated in Sec. III by approximating the nanopore through a cylindrical pore of length 100 nm, radius 4 nm, and with a junction placed 3 nm into the entrance of the nanopore such that the surface charge density is 0.075 C/m² on the upper region and 0 on the lower one. An ionic concentration of 1 M is used.

Extensive numerical and experimental studies have described the translocation of spherical and cylindrical particles through charged nanopores.^62–66 Ai and Qian⁶⁵ have simulated the effect due to field blockage, which is the dominant mechanism when the pore radius is large compared to the Debye length at relatively high ionic strengths. However, at the other extreme of length ratio, the ionic strength and conductivity can increase drastically at the gap between the molecule and wall. Ion enrichment and depletion can also occur at the two ends of the molecule to change the ionic strength and conductivity there. Such concentration polarization during translocation, which can sometimes over-compensate the field blockage effect to produce a current increase, is captured here for the first time with an asymptotic theory and a closed-form explicit expression. As expected, such concentration polarization effects are most pronounced for large-aspect ratio pores, like ion-track nanopores, as in conjunction with a long molecule, the concentration polarization can be sustained over a long domain. Moreover, our recent work on RNA sensing¹⁶ indicates that adsorption can only occur for long pores because of the longer transit time. Such adsorption in long pores can then produce unique concentration polarization effects and ion current amplitude fingerprints, which is a major focus of the current report. Fortuitously, such long pores also simplify our analysis, as they permit transverse homogenization and omission of end and electro-osmotic flow effects.^67,68 Such long pores are difficult to resolve numerically, and, in fact, most prior numerical efforts are for short pores whose lengths are comparable to their radius.

We begin with a DC rectification theory due to true surface charge inhomogeneities and then extend the theory to pores with variable cross-sectional area, which leads to a quasi-static theory for a freely translocating molecule or an adsorbed linear molecule to capture the transient amplitude fingerprints. We use this theory to quantitatively capture several reported amplitude signatures for both experimental and simulated solid-state nanopores, as well as to predict new amplitude signatures that have not yet been observed.

II. THEORETICAL MODEL

A. Single junction with constant cross-sectional area

Consider a nanopore with length L and radius a connected to two reservoirs with identical bulk ionic concentrations C = C₀. This pore has two segments with surface charge densities σ_T and σ_B such that there is a drastic change in surface charge at their junction z = z_m. We will assign σ_T to the surface charge density of the segment spanning from z = 0 to z = z_m, and σ_B to the surface charge density of the segment spanning from z = z_m to z = L. The electric potentials on the farthest borders of the top and bottom reservoirs are set to 0 and V₀, respectively, as shown in Fig. 2. For large aspect-ratio nanopores (length over aperture radius), entrance contributions may be neglected, and the current is the result of intrapore ion dynamics. Under this hypothesis and for high ionic strengths, 1D analytical approximations have been shown to be in good agreement with 3D numerical results. Ion dynamics inside this nanopore are ruled by the Poisson–Nernst–Planck (PNP) equations coupled with the Poisson–Boltzmann (PB) and Navier–Stokes (NS) equations. Neglecting the contribution of pressure driven and electro-osmotic flows, NS equations can be safely omitted.^37,67

FIG. 2.

Schematic of a nanopore with a single junction.

In the absence of electro-osmotic convection^67,68 in our long pores, the ionic flux of univalent anions and cations can be written as

$$J_{\pm }=-D_{\pm }\nabla C_{\pm }\mp \left(\frac{F{D}_{\pm }}{RT}\right)C_{\pm }\nabla \varphi ,$$ (1)

where F is the Faraday constant, R is the gas constant, T is the temperature of the system, ϕ is the electric potential, C₊ and C₋ are the concentrations of cations and anions, respectively, and D₊ and D₋ are their diffusion coefficients, presumed to be identical and assigned a typical value of D = 2 × 10⁻⁹ m²/s for a KCl solution.

As shown by Yan et al.,⁵¹ the transverse variation across a slender pore is weak, and the longitudinal gradients in (1) are dominant. Radial variations become insignificant for slender pores, particularly when the radial length scale is either much smaller or much larger than the Debye length. One can hence obtain a one-dimensional transversely homogeneous model. (For convenience, we retain the gradient notation even in one dimension.) This homogeneity in the transverse direction also allows us to neglect all azimuthally asymmetric effects and model the translocating molecule to be locally along the central axis. Similar homogenization in the transverse direction for the Poisson equation that stipulates the effective space charge density at each longitudinal position ρ_T must include both the true space charge with density ρ and the effective volume density of the surface charge with density σ(z). The resulting transversely homogenized Poisson equation is

$${\nabla }^2\varphi =-\frac{{\rho }_T}{ϵ}=-\frac{1}{ϵ}\left[F\left(C_{+}-C_{-}\right)+\frac{2\sigma \left(z\right)}{a}\right],$$ (2)

where ϵ is the permittivity of the solution (ϵ ≈ 80ϵ₀, with ϵ₀ the permittivity of vacuum), a is the local pore radius, and the true space charge ρ = F(C₊ − C₋). The averaged transport equations for the ion and current flux densities and the averaged Poisson equation can then be written as

$$J=J_{+}+J_{-}=-D\nabla \left(C_{+}+C_{-}\right)-\left(\frac{D}{RT}\right)\rho \nabla \varphi ,$$ (3)

$$I=J_{+}-J_{-}=-\left(\frac{D}{F}\right)\nabla \rho -\left(\frac{FD}{RT}\right)\left(C_{+}+C_{-}\right)\nabla \varphi ,$$ (4)

$${\nabla }^2\varphi =-\frac{1}{ϵ}\left(\rho +F{C}_0\chi \left(z\right)X\right),$$ (5)

where a dimensionless parameter for the tip surface charge strength X = 2|σ_T|/FC₀a has been defined and χ(z) = σ(z)/|σ_T| is the scaled discontinuous charge density, normalized by the tip charge density σ_T ≠ 0, assumed to be finite. The key dimensionless parameter X represents the ratio of the effective space charge density due to surface charge to the bulk electrolyte concentration and is a good measure of the ion-selectivity of a pore or membrane. With a surface charge |σ_T| = 5 mC/m² and for a nanopore of diameter 10 nm, the parameter X is 0.01 at 1 M KCl and 10 at 1 mM KCl. Our asymptotic theory will be for small X, corresponding to high bulk ionic strength relative to the surface charge. It is a quasi-steady theory and hence both fluxes in (3) and (4) are constant. One can take one more derivative to convert them into second order equations that must be solved with boundary conditions at both ends.

Consistent with the high ionic strength conditions that lead to a weakly selective pore without external concentration polarization,^51,69,70 we will impose Donnan equilibrium conditions at the boundaries at z = 0 and z = L,

$$\begin{array}{cc}\hfill \varphi \left(z\right)& =-\frac{RT}{F}{\text{sinh}}^{-1}\left(\frac{\chi \left(z\right)X}{2}\right),\hfill \\ \hfill C_{\pm }& =C_0{e}^{\mp \frac{F\varphi \left(z\right)}{RT}},\rho \left(z\right)=-\chi \left(z\right)XF{C}_0,\hfill \end{array}$$ (6)

and an additional voltage bias V₀ at z = L.

The characteristic parameters for scaling these equations are the bulk concentration C₀, the pore length L, the characteristic flux density DC₀/L, the thermal potential RT/F, and the space charge density FC₀. Therefore, defining

$${Ĉ}_{\pm }=\frac{C_{\pm }}{C_0},Ĵ=\frac{J}{\frac{D{C}_0}{L}},\widehat{z}=\frac{z}{L},\widehat{\varphi }=\frac{\varphi }{\frac{RT}{F}},Î=\frac{I}{\frac{D{C}_0}{L}},$$ (7)

and Ĉ = Ĉ₊ + Ĉ₋, $\widehat{\rho }={Ĉ}_{+}-{Ĉ}_{-}$, our transport equations can be expressed in their dimensionless form as

$$Ĵ=-\widehat{\nabla }Ĉ-\widehat{\rho }\widehat{\nabla }\widehat{\varphi },$$ (8)

$$Î=-\widehat{\nabla }\widehat{\rho }-Ĉ\widehat{\nabla }\widehat{\varphi },$$ (9)

$${\widehat{\nabla }}^2\widehat{\varphi }=-\alpha \left[\widehat{\rho }+\chi \left(\widehat{z}\right)X\right].$$ (10)

The geometric parameter $\alpha =F^2{L}^2{C}_0/RTϵ={\left(L/{\lambda }_D\right)}^2/2$ is a dimensionless measure of the pore length L, with λ_D the Debye length of the solution. At high ionic concentration (1 M KCl), α is expected to be of the order of X⁻² for a nanopore of length 100 nm, while at lower concentrations (1 mM KCl), it is expected to be of order X, with X ≪ 1. We will analyze the former case and define α = α₀X⁻². At this order, we do not need to solve the Poisson equation to leading order, and the leading order potential distribution is just a linear one, corresponding to a chargeless nanopore with ionic strength equal to the bulk and without mobile space charge or a net charge. The recursive derivation of our expansion will then solve the next-order correction from the Poisson equation with a surface charge. However, this surface charge is balanced by the space charge, and the nanopore remains neutral at $\mathcal{O}\left(X\right)$. It is not until the second order correction that a local net charge appears and is shown to produce an induced dipole due to charge polarization along the pore, without a net charge appearing over the entire pore.

Boundary conditions (6) can likewise be rendered dimensionless and expanded for small X,

$$\begin{array}{cc}\hfill Ĉ\left(0\right)& =2+{\left(\frac{{\chi }_T}{2}\right)}^2{X}^2,Ĉ\left(1\right)=2+{\left(\frac{{\chi }_B}{2}\right)}^2{X}^2,\hfill \\ \hfill \widehat{\rho }\left(0\right)& =-{\chi }_{T}X,\widehat{\rho }\left(1\right)=-{\chi }_{B}X,\hfill \\ \hfill \widehat{\varphi }\left(0\right)& =\frac{{\chi }_T}{2}X,\widehat{\varphi }\left(1\right)={\widehat{V}}_0+\frac{{\chi }_B}{2}X.\hfill \end{array}$$ (11)

We carry out an expansion in X and solve each order of (8)–(10) successively with boundary conditions (11), Ĉ = Ĉ⁰ + XĈ¹, $\widehat{\rho }={\widehat{\rho }}^0+X{\widehat{\rho }}^1$, $\widehat{\varphi }={\widehat{\varphi }}^0+X{\widehat{\varphi }}^1$, Î = Î⁰ + Xι, and Ĵ = Ĵ⁰ + XĴ¹. The leading order solution of $\mathcal{O}\left(1\right)$ corresponds to a pore without charge, Ĉ⁰ = 2, ${\widehat{\rho }}^0=0$, ${\widehat{\varphi }}^0={\widehat{V}}_0\widehat{z}$, Ĵ⁰ = 0, and $Î=-2{\widehat{V}}_0$.

To $\mathcal{O}\left(X\right)$, the Poisson equation (10) is just the electroneutrality condition ${\widehat{\rho }}^1=-\chi \left(\widehat{z}\right)$. Inserting this leading order space charge into the ion flux Eq. (8), one concludes that induced concentration polarization C¹ is piecewise linear, with slope equal to $-{Ĵ}^1-\chi \left(\widehat{z}\right){\widehat{V}}_0$. As the Donnan boundary condition for concentration Ĉ¹ is zero at this order, we conclude that Ĉ¹ must have slopes of different sign in each region so it can be continuous at the junction. The continuity at the junction selects the constant flux density Ĵ¹. One can then obtain an estimate of the intrapore concentration polarization profile Ĉ¹ and the ion flux density, where longitudinally inhomogeneous electromigration (caused by inhomogeneous surface charge) is balanced by diffusion to maintain the constant ion flux density,

$${Ĉ}^1=\frac{{\widehat{V}}_0}{2}\left({\chi }_T-{\chi }_B\right)\left({\widehat{z}}_m+\widehat{z}-2\widehat{z}{\widehat{z}}_m-|\widehat{z}-{\widehat{z}}_m|\right),$$ (12)

$${Ĵ}^1={\widehat{V}}_0\left[{\chi }_T{\widehat{z}}_m+{\chi }_B\left(1-{\widehat{z}}_m\right)\right].$$ (13)

Integrating the current flux (9) along the length of the nanopore and imposing the Donnan charge boundary conditions at this order, we obtain the correction to the current due to intrapore ion polarization,

$${Î}^1=-\left({\chi }_T-{\chi }_B\right)\frac{{\widehat{V}}_0^2}{2}{\widehat{z}}_m\left(1-{\widehat{z}}_m\right),$$ (14)

leading to the net current

$$Î=-2{\widehat{V}}_0\left[1+\frac{\mathrm{\Gamma }}{2}\right],$$ (15)

where the factor Γ, representing a dimensionless excess (induced) conductance, is related to the location of the surface charge discontinuity ẑ_m, where the change in ionic strength ${Ĉ}^1\left({\widehat{z}}_m\right)={\widehat{V}}_0\left({\chi }_T-{\chi }_B\right){\widehat{z}}_m\left(1-{\widehat{z}}_m\right)$ is highest,

$$\begin{array}{cc}\hfill \mathrm{\Gamma }& =\frac{Ĉ\left({\widehat{z}}_m\right)-{Ĉ}^0}{{Ĉ}^0}=\frac{X}{2}{Ĉ}^1\left({\widehat{z}}_m\right)\hfill \\ \hfill & ={\widehat{V}}_{0}X\left({\chi }_T-{\chi }_B\right){\widehat{z}}_m\left(1-{\widehat{z}}_m\right)/2.\hfill \end{array}$$ (16)

Although the excess conductance Γ should theoretically be small because of our small X expansion, we will show that its validity extends to |X| < 0.5. However, the ionic strength Ĉ(ẑ_m) cannot be lower than 0. Therefore, the current Î is set to zero if Γ < −1. Ours is the first theory for arbitrary piecewise constant surface charge density. In the limiting case of ẑ_m = 1/2 and χ_T = −χ_B, our expression is in agreement with that derived by Cheng and Guo⁷¹ under the hypothesis of Ĵ = 0. As seen in (13), however, the ion flux density is not zero in general.

It is interesting to note that, as in the steady state ∇ · Î = 0, to third order in $\widehat{\rho }$, we have a local charge buildup as

$$\frac{{\partial }^2}{\partial {\widehat{z}}^2}{\widehat{\varphi }}^1\left(\widehat{z}\right)=\left\{\begin{array}{cc}-\frac{1}{2}{\widehat{V}}_0^2\left({\chi }_T-{\chi }_B\right)\left(1-{\widehat{z}}_m\right)\hfill & \widehat{z}<{\widehat{z}}_m,\hfill \\ \frac{1}{2}{\widehat{V}}_0^2\left({\chi }_T-{\chi }_B\right){\widehat{z}}_m\hfill & \widehat{z}>{\widehat{z}}_m.\hfill \end{array}\right.$$ (17)

Multiplying the first term by ẑ_m and the second by (1 − ẑ_m), we observe that there is no net charge buildup over the entire pore. Instead, an induced dipole is formed due to field-induced charge polarization. A similar expansion can be carried out for α of orders less than or equal to 0. When $\alpha \sim \mathcal{O}\left(1\right)$, net electroneutrality is only valid for ${\widehat{V}}_0\ll L/{\lambda }_D$ (see supplementary material S.1), as higher electric fields have been shown to significantly remove the ions surrounding charged surfaces.⁵⁴ An induced monopole develops at the nanopore in that limit. Hence, the length of the nanopore with respect to the Debye length, as represented by α, has a profound effect on the induced charge and induced dipole in the nanopore.

Our theory was extensively tested against FEM simulations of the PNP–PB equations for unipolar (χ_B = 0) and bipolar (χ_T = −χ_B) nanopores (see supplementary material S.2 for comparisons of our theory to simulations, and Subsection 1 of the Appendix for details on simulation protocols) for |X| < 0.5 and $\left|{\widehat{V}}_0\right|<40$, to excellent agreement. Figure 3(a) compares our theory to experimental I–V curves for a unipolar nanopore reported in the literature.³⁷ Figure 3(b) presents the change in concentration at the junction, Γ, as a function of the position of the junction for unipolar and bipolar nanopores, showing that placing the junction in the middle of the nanopore maximizes enrichment when ${\widehat{V}}_0\left({\chi }_T-{\chi }_B\right)>0$ and depletion when ${\widehat{V}}_0\left({\chi }_T-{\chi }_B\right)<0$. Defining the rectification factor as $\mathcal{R}=|Î\left(\widehat{V}\right)/Î\left(-\widehat{V}\right)|$ where ${\widehat{V}}_0>0$,

$$\mathcal{R}=\left|\frac{2+\mathrm{\Gamma }\left(\widehat{V}\right)}{2-\mathrm{\Gamma }\left(\widehat{V}\right)}\right|.$$ (18)

Figure 3(c) compares theoretical rectifications with simulation results of the PNP–PB equations solved with FEM. We can also define the charge selectivity of the nanopore through $\mathcal{S}=|I/J|$, term that may be theoretically estimated through

$$\mathcal{S}=\frac{1}{X}\left|\frac{2+\mathrm{\Gamma }\left({\widehat{V}}_0\right)}{{\chi }_T{\widehat{z}}_m+{\chi }_B\left(1-{\widehat{z}}_m\right)}\right|.$$ (19)

Note that $\mathcal{S}$ goes to infinity for a bipolar nanopore with a junction in the middle, while $\mathcal{S}$ goes to infinity for a unipolar nanopore only if the junction is placed infinitely close to the entrance of the pore [see Fig. 3(d)].

FIG. 3.

(a) Data from Nasir et al.³⁷ and calculated I–V curves for a unipolar nanopore with χ_T = 0, χ_B = 1, C₀ = 100 mM, a = 18 nm, ẑ_m = 1/2, L = 12 μm, and σ_T = 0.16 C/m². (b) Simulated (symbols) and theoretical (lines) changes in concentration Γ as a function of the position of the junction ẑ_m for unipolar and bipolar nanopores. L = 150 nm, C₀ = 1 M, a = 10 nm, σ_T = ±0.01 C/m², and ${\widehat{V}}_0=\pm 4$. (c) Simulated (symbols) and theoretical (lines) rectification factors as a function of Γ for L = 150 nm, C₀ = 1 M, a = 10 nm, ẑ_m ∈ {0.1, 0.25, 0.5, 0.75, 0.9}, and multiple voltages and surface charge densities such that $\left|{\widehat{V}}_0\right|\le 20$ and |X| ≤ 0.5. (d) Simulated (symbols) and theoretical (lines) charge selectivity factors as a function of the position of the junction for unipolar and bipolar nanopores. L = 150 nm, C₀ = 1 M, a = 10 nm, σ_T = ±0.01 C/m², and ${\widehat{V}}_0=\pm 4$. All simulations were performed using the finite element method (FEM) with the PNP–PB equations (see Subsection 1 of the Appendix).

B. Multiple junctions with cross-sectional area change

If the cross-sectional area S along the nanopore is variable, Ĵ and Î are no longer continuous, and the continuity of total ion and charge fluxes SĴ and SÎ must be imposed. To keep our approach nondimensional, we will consider Ŝ = S/S_n, where S_n is the cross-sectional area of the bottom region of the nanopore. We will also consider a nanopore with n charged regions with surface charge densities ${\left\{{\chi }_i\right\}}_{i=1}^n$ and cross-sectional areas ${\left\{{Ŝ}_i\right\}}_{i=1}^n$ separated by n − 1 different junctions ${\left\{{\widehat{z}}_{i,i+1}\right\}}_{i=1}^{n-1}$. A first-order expansion of our transport terms as a function of X, under the same hypotheses previously stated, leads to the following transport equations:

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{J}}}^0+X{\widehat{\mathcal{J}}}^1& =\hfill & -\frac{\partial }{\partial \widehat{z}}\left[Ŝ\left(\widehat{z}\right){Ĉ}^0+XŜ\left(\widehat{z}\right){Ĉ}^1\right]\hfill \\ \hfill & \hfill & -\left({\widehat{\rho }}^0+X{\widehat{\rho }}^1\right)\frac{\partial }{\partial \widehat{z}}\left[{\widehat{\mathcal{E}}}^0+X{\widehat{\mathcal{E}}}^1\right],\hfill \end{array}$$ (20)

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{Y}}}^0+X{\widehat{\mathcal{Y}}}^1& =\hfill & -\frac{\partial }{\partial \widehat{z}}\left[Ŝ\left(\widehat{z}\right){\widehat{\rho }}^0+XŜ\left(\widehat{z}\right)\widehat{{\rho }^1}\right]\hfill \\ \hfill & \hfill & -\left({Ĉ}^0+X{Ĉ}^1\right)\frac{\partial }{\partial \widehat{z}}\left[{\widehat{\mathcal{E}}}^0+X{\widehat{\mathcal{E}}}^1\right],\hfill \end{array}$$ (21)

$$X^2\frac{{\partial }^2}{\partial {\widehat{z}}^2}\left[{\widehat{\mathcal{E}}}^0+X{\widehat{\mathcal{E}}}^1\right]=-{\alpha }_0Ŝ\left(\widehat{z}\right)\left[{\widehat{\rho }}^0+X{\widehat{\rho }}^1+\chi \left(\widehat{z}\right)X\right],$$ (22)

where we wrote α = α₀X⁻², $\widehat{\mathcal{J}}=ĴŜ$, $\widehat{\mathcal{Y}}=ÎŜ$, and $\widehat{\mathcal{E}}=\widehat{\varphi }Ŝ$. The final dimensionless variable represents the net potential over the local pore area.

Poisson equation (22) and boundary conditions again suggest the usual electroneutral space charge limit for the leading order solution ${\widehat{\rho }}^0=0$ for the pore without and net electroneutrality for the next order ${\widehat{\rho }}^1=-\chi \left(\widehat{z}\right)$. Hence, ${\widehat{\mathcal{J}}}^0=-\partial Ŝ{Ĉ}^0/\partial \widehat{z}$ and ${\widehat{\mathcal{Y}}}^0=-{Ĉ}^0\partial {\widehat{\mathcal{E}}}^0/\partial \widehat{z}$. As in the steady state $\nabla \cdot \widehat{\mathcal{J}}=0$ and imposing the zeroth order boundary conditions, we conclude Ĉ⁰ = 2 and ${\widehat{\mathcal{J}}}^0=0$, and the net field over the cross-sectional area of a pore without charge $\partial {\widehat{\mathcal{E}}}^0/\partial \widehat{z}$ takes the same values for all ẑ, in consistency with the Gauss law. Imposing continuity of ${\widehat{\varphi }}^0=0$, we obtain

$${\widehat{\mathcal{E}}}^0\left(\widehat{z}\right)={\widehat{\mathcal{E}}}_0\widehat{z}=\frac{{\prod }_{i=1}^n{Ŝ}_i}{\left[{\sum }_{i=1}^{n-1}{\widehat{z}}_{i,i+1}\left({Ŝ}_{i+1}-{Ŝ}_i\right){\prod }_{j\notin \left\{i,i+1\right\}}{Ŝ}_j\right]+{\prod }_{i\ne n}{Ŝ}_i}{\widehat{V}}_0\widehat{z},$$ (23)

and, therefore, $\widehat{\mathcal{Y}}=-2{\widehat{\mathcal{E}}}^0$. To the next order,

$$\frac{\partial }{\partial \widehat{z}}Ŝ\left(\widehat{z}\right){Ĉ}^1\left(\widehat{z}\right)=-{\widehat{\mathcal{J}}}^1+\chi \left(\widehat{z}\right){\widehat{\mathcal{E}}}_0,$$ (24)

$$\frac{\partial }{\partial \widehat{z}}{\widehat{\mathcal{E}}}^1\left(\widehat{z}\right)=\frac{1}{2}\left[-{\widehat{\mathcal{Y}}}^1+\frac{\partial }{\partial \widehat{z}}Ŝ\left(\widehat{z}\right)\chi \left(\widehat{z}\right)-{Ĉ}^1\left(\widehat{z}\right){\widehat{\mathcal{E}}}_0\right].$$ (25)

From our equation for ${\widehat{\mathcal{J}}}^1$, Ĉ¹ is piecewise linear, and therefore we may calculate Ĉ¹(ẑ) by imposing Ĉ¹(0) = Ĉ¹(1) = 0 as well as continuity at the junctions. Integrating (21) along the length of the nanopore and imposing ${\widehat{\varphi }}^1\left(0\right)={\chi }_1/2$, ${\widehat{\varphi }}^1\left(1\right)={\chi }_n/2$ as well as continuity in the junction, we can estimate the current from the concentrations at the junctions as

$$\widehat{\mathcal{Y}}=-2{\widehat{\mathcal{E}}}_0-X{\widehat{\mathcal{E}}}_0\frac{{\sum }_{i=1}^n\frac{\left({\widehat{z}}_{i,i+1}-{\widehat{z}}_{i-1,i}\right)\left({Ĉ}^1\left({\widehat{z}}_{i,i+1}\right)+{Ĉ}^1\left({\widehat{z}}_{i-1,i}\right)\right)}{2{Ŝ}_i}}{{\sum }_{i=1}^n\frac{{\widehat{z}}_{i,i+1}-{\widehat{z}}_{i-1,i}}{{Ŝ}_i}},$$ (26)

where we defined ẑ_0,1 = 0 and ẑ_n,n+1 = 1. To determine the concentrations, we must impose our boundary conditions, which can be performed systematically by solving an (n + 1) × (n + 1) system of equations,

$$\begin{array}{ccc}\hfill & \hfill & \left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill \left(\frac{1}{{Ŝ}_2}-\frac{1}{{Ŝ}_1}\right){\widehat{z}}_{\mathrm{1,2}}\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill \left(\frac{1}{{Ŝ}_3}-\frac{1}{{Ŝ}_2}\right){\widehat{z}}_{\mathrm{2,3}}\hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill -1\hfill & \hfill \left(\frac{1}{{Ŝ}_n}-\frac{1}{{Ŝ}_{n-1}}\right){\widehat{z}}_{n-1,n}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 1\hfill & \hfill -\frac{1}{{Ŝ}_n}\hfill \end{array}\right]\left[\begin{array}{c}\hfill K_1\hfill \\ \hfill K_2\hfill \\ \hfill K_3\hfill \\ \hfill \dots \hfill \\ \hfill K_n\hfill \\ \hfill \widehat{\mathcal{J}}\hfill \end{array}\right]\hfill \\ \hfill & \hfill & ={\widehat{\mathcal{E}}}_0\left[\begin{array}{c}\hfill 0\hfill \\ \hfill \left(\frac{{\chi }_2}{{Ŝ}_2}-\frac{{\chi }_1}{{Ŝ}_1}\right){\widehat{z}}_{\mathrm{1,2}}\hfill \\ \hfill \left(\frac{{\chi }_3}{{Ŝ}_3}-\frac{{\chi }_2}{{Ŝ}_2}\right){\widehat{z}}_{\mathrm{2,3}}\hfill \\ \hfill \dots \hfill \\ \hfill \left(\frac{{\chi }_n}{{Ŝ}_n}-\frac{{\chi }_{n-1}}{{Ŝ}_{n-1}}\right){\widehat{z}}_{n-1,n}\hfill \\ \hfill -\frac{{\chi }_n}{{Ŝ}_n}\hfill \end{array}\right],\hfill \end{array}$$ (27)

as in each region, we can express the piecewise linear induced concentration profile as ${Ĉ}_i^1\left(\widehat{z}\right)={Ŝ}_i^{-1}\left[-{\widehat{\mathcal{J}}}^1+\chi \left(\widehat{z}\right){\widehat{\mathcal{E}}}_0\right]\widehat{z}+K_i$. Analytical expressions can be found for this system for any number of regions. For n = 2, as ${\widehat{\mathcal{E}}}_0={Ŝ}_1{Ŝ}_2{\widehat{V}}_0/\left[{Ŝ}_1\left(1-{\widehat{z}}_{\mathrm{1,2}}\right)+{Ŝ}_2{\widehat{z}}_{\mathrm{1,2}}\right]$, the concentration at the junction follows ${Ĉ}^1\left({\widehat{z}}_{\mathrm{1,2}}\right)={\widehat{z}}_{\mathrm{1,2}}\left(1-{\widehat{z}}_{\mathrm{1,2}}\right)\left({\chi }_1-{\chi }_2\right){\widehat{\mathcal{E}}}_0^2/{Ŝ}_1{Ŝ}_2{\widehat{V}}_0$ and thus $\widehat{\mathcal{Y}}=-{\widehat{\mathcal{E}}}_0\left[2+X{Ĉ}^1\left({\widehat{z}}_{\mathrm{1,2}}\right)/2\right]$. Explicit solutions for n = 3 as well as examples are provided in supplementary material S.3.

C. DNA translocation through a pore with a highly charged tip or focused geometry

It is important to note that, from the leading order estimates for both bipolar pores and pores with multiple charged regions of different cross section, the sign of current change (whether net intrapore enrichment or depletion occurs) is determined by the jump in conductance per unit length (product of conductivity and cross-sectional area) at the junctions. Classical theories suggest that, during a translocation event, the change in ionic current results from both geometric exclusion of ions and field as well as introduction of new ions brought into the nanopore by the ionic cloud of the charged molecule.³ The volume exclusion effect is captured by Ŝ_i, and the surface charge of the translocating molecule can be included in the surface charge density distribution χ_i. Accordingly, we model the translocating molecule as a cylindric particle of length L_m, radius r_m, and effective charge q and modify the pore geometry locally to a narrower nanopore due to volume exclusion, with a modified surface charge density (see Fig. 4). For any molecule that translocates without adsorption, its effect on the local ion distribution will be the same as the one that translocates along the axis of the nanopore in our transversely homogeneous theory, independent of its actual radial location. We will hence assign a factor to the surface charge density to account for the presence of the molecule,

$$\mathrm{\Sigma }=\frac{{\sigma }_b^{\prime }}{\sigma }=\left(\frac{1+\frac{q}{2\pi \sigma L_{m}a}}{\sqrt{1-{\left(\frac{r_m}{a}\right)}^2}}\right)=\left(\frac{1+\eta }{\sqrt{1-{\left(\frac{r_m}{a}\right)}^2}}\right),$$ (28)

where η = q/2πσL_ma represents the ratio of the molecular charge to the net surface charge. We note that η can take on positive or negative values, depending on whether the molecule has the same or opposite charge from the pore surface. We must also correct for the change in cross-sectional area, the change which is imposed by defining $\mathrm{\Lambda }={Ŝ}^{\prime }/Ŝ=1-{\left(r_m/a\right)}^2$.

FIG. 4.

Schematic of our multi-polar nanopore model for a translocation event. (a) Translocation of a cylindrical molecule through the middle of a unipolar nanopore. (b) Equivalent multi-polar nanopore with variable cross-sectional area.

We use the above correction to look at one useful limiting case, that of a nanopore with only one charged section near ẑ = 0. This also corresponds to a focused geometry where the only detection section is the tip and the rest of the channel becomes irrelevant even if it is charged. The charged region at the tip has a junction at ẑ_1,2 and has dimensionless surface charge χ₁. We compare its current to the case when the entire charged region is occupied by a molecule. With the change in both local conductivity and area due to the molecule by the above model, our theory can capture both cases and we obtain that the current change due to molecule entry is

$$\frac{{\widehat{\mathcal{Y}}}_1-{\widehat{\mathcal{Y}}}_0}{{\widehat{\mathcal{Y}}}_0}\sim {\widehat{z}}_{\mathrm{1,2}}\left(1-\frac{1}{\mathrm{\Lambda }}+\text{sgn}\left({\chi }_1\right)\frac{X}{4}{\widehat{V}}_0\left(\frac{\mathrm{\Sigma }}{\mathrm{\Lambda }}-1\right)\right),$$ (29)

where ${\widehat{\mathcal{Y}}}_0$ and ${\widehat{\mathcal{Y}}}_1$ are the baseline current and the current obtained when the molecule occupies the upper region of the pore, respectively, and χ₁ is the normalized surface charge of the charged region in the absence of a translocating molecule (see supplementary material S.4). This estimate suggests a competition between volume exclusion and the ionic enriching or depleting effect of the charge of the molecule on the conductivity near the junction, which can lead to either positive or negative resistive signals.

If the molecule adsorbs into the surface (that is, if the molecule is found in close proximity to the pore walls), we propound to correct the surface charge density by a factor

$$\mathrm{\Sigma }=\frac{{\sigma }_s^{\prime }}{\sigma }=\left(\frac{\left(1-\frac{r_m}{a}\right)+\frac{q}{4\pi \sigma L_{m}a}}{\sqrt{1-{\left(\frac{r_m}{a}\right)}^2}}\right)=\left(\frac{\left(1-\frac{r_m}{a}\right)+\frac{\eta }{2}}{\sqrt{1-{\left(\frac{r_m}{a}\right)}^2}}\right),$$ (30)

which can be even smaller than (28), as ions do not see the region of the nanopore that is covered by the molecule, and about half of the surface of the molecule is not exposed to the environment. Note that, for a free-floating molecule, $\mathrm{\Sigma }=\left(1+\eta \right)/\sqrt{\mathrm{\Lambda }}$, while for an adsorbed one ${\mathrm{\Sigma }}_s=\left(1-\sqrt{1-\mathrm{\Lambda }}+\eta /2\right)/\sqrt{\mathrm{\Lambda }}$. For example, for double stranded (dsDNA) and single stranded (ssDNA) DNA molecules with 22 base-pairs (nucleotides for ssDNA), we use linear charge densities of q/L_m = −0.2 C/nm and q/L_m = −0.02 C/nm with radii rm of 1.185 nm and 0.838 nm, respectively. On a unipolar pore of a = 4 nm and σ = 0.075 C/m² (such as the one modeled in Fig. 1), we obtain η = −0.12 and −0.012 for dsDNA and ssDNA molecules. This produces values of (Σ/Λ) − 1 and (Σ_s/Λ) − 1 of 0 and −0.26 for dsDNA and 0.05 and −0.17 for ssDNA, as well as values of 1 − (1/Λ) of −0.09 for dsDNA and −0.04 for ssDNA. It is obvious then that, with positive bias, a free-floating dsDNA molecule can reduce more current than its free-floating ssDNA counterpart, whereas higher current drops can be obtained when an adsorbed ssDNA molecule translocates through the pore. One can easily tune the surface charge, so the adsorbed molecule has a much larger current drop than the free one. It is hence highly desirable to have the target molecule adsorbed to the surface due to a specific probe or due to its conformation. We will demonstrate in Sec. III B that ssDNA molecules have a higher affinity for hydrophobic surface than their double stranded counterparts. This adsorption produces a resistive signal amplitude that exceeds free-floating ones by as much as a factor of 2, a magnitude much larger than the CV.

We also observe that, for free-floating ssDNA molecules, the amplitude of the resistive signal can become negative (the current increases), as the effect of its charge dominates the dynamics at larger voltages, overcoming volume exclusion. Based on the above analysis, a dimensionless parameter can be defined to determine the relative effects of the molecule on ionic strength and field blocking for freely translocating and adsorbed molecules,

$$\mathrm{\Omega }=\text{sgn}\left({\chi }_1\right)\frac{X}{4}{\widehat{V}}_0\left(\frac{\mathrm{\Lambda }-\mathrm{\Sigma }}{1-\mathrm{\Lambda }}\right).$$ (31)

The denominator of this parameter is always positive. However, the numerator can be either negative or positive depending on the properties of the system and of the translocating agent. As

$$\frac{{\widehat{\mathcal{Y}}}_1-{\widehat{\mathcal{Y}}}_0}{{\widehat{\mathcal{Y}}}_0}\sim -{\widehat{z}}_{\mathrm{1,2}}\left(\frac{1-\mathrm{\Lambda }}{\mathrm{\Lambda }}\right)\left[1+\mathrm{\Omega }\right]$$ (32)

for molecules such that Ω < −1, we observe current enhancements, while all other values lead to current drops. Figure 5 compares Ω with current changes from FEM simulations of the PNP–PB equations for the translocation of DNA molecules, which occupy only the upper region of a unipolar nanopore with a single junction, showing good agreement of our simulation results with our Eq. (32) and verifying the capacity of estimating the sign of the change in resistive signals upon entrance of the translocating agent from the parameter Ω.

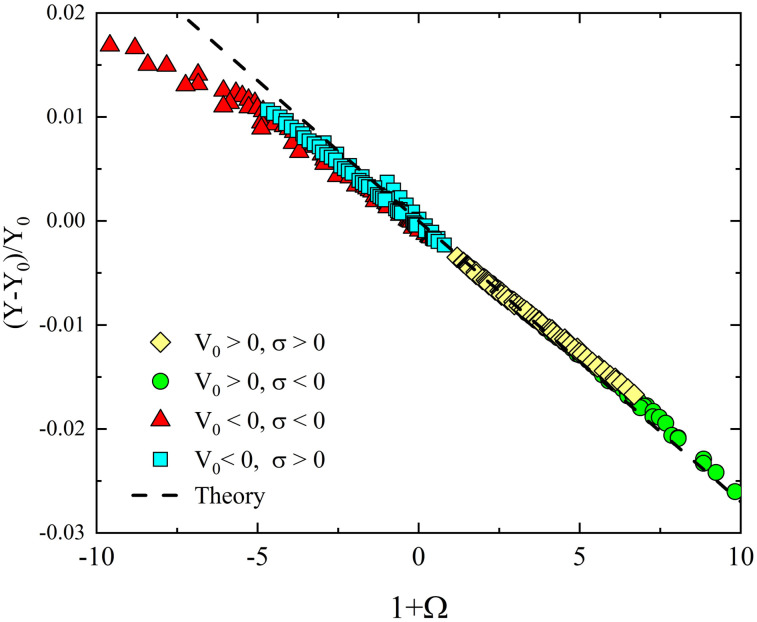
FIG. 5.

Simulated changes in current as a function of our theoretical Ω for the translocation of a 3-nm-long double stranded DNA molecule through a cylindric nanopore with a diameter of 4 nm, a length of 100 nm, and a junction placed 3 nm after the pore entrance. The upper surface charge density of the pore is varied from −0.075 C/m² to 0.075 C/m², while the lower charge is taken as zero. Voltages ${\widehat{V}}_0$ span from −40 to 40 and an ionic concentration of 1 M is considered. Simulations were performed using the FEM with the PNP–PB equations as explained in Subsection 1 of the Appendix. All data collapse according to Eq. (32), represented by the dotted line.

When the molecule is exiting the pore, the change in current may be estimated through

$$\frac{{\widehat{\mathcal{Y}}}_1-{\widehat{\mathcal{Y}}}_0}{{\widehat{\mathcal{Y}}}_0}\sim -\left(\frac{1-\mathrm{\Lambda }}{\mathrm{\Lambda }}\right)l,$$ (33)

where 0 < l < 1 is a dimensionless parameter associated with the amount of molecule still inside the pore (see supplementary material S.4). This estimate suggests that, if the molecule is exiting the nanopore, far from the junction, its charge has no significant effect in the signal, leading to a drop in current due to volume exclusion. Biphasic signals can hence occur in nanopores if Ω < −1, and the surface charge is dominant at the entrance.

We tested Eq. (32) with our nanopores with the following parameters: 0.075 C/m² surface charge, 4 nm radius, and 100 nm length, assuming a charged region of 3 nm due to surface modification. For a 22-bp dsDNA and a bias voltage of ${\widehat{V}}_0=20$, we estimate Ω = 0, X = 0.39, Λ = 0.91, and Σ = 0.91, and hence we obtain an amplitude reduction of 0.3% or an actual reduction current signal of 50 pA. This result is derived for the case when only 3 nm of the dsDNA molecule are inside the pore (about 40%). Better results are obtained by considering the entirety of the molecule inside the pore, leading to a reduction of 1.6% (275 pA), in agreement with experimental results (see Fig. 1). A more detailed comparison will then be carried out in Sec. III when the entire current evolution will be simulated, not just when the molecule is either far from the junction or occupies exactly the charged region of the nanopore. There is also no reason why the dominant charge region should be at the entrance, although this is probably the easiest to fabricate. Biphasic signals can also be produced by a charged region in the middle of the pore. However, their analytical expressions become tedious, and we thus suggest the numerical application of our theory for those systems.

III. RESULTS

A. Biphasic signals in unipolar nanopores

In the last few years, biphasic signals have been reported on conical glass nanopores (σ ∼ −0.01 C/m²), where translocation of DNA molecules into confinement (positive bias) showed current blockages, while translocations out of confinement (negative bias) showed biphasic patterns.⁵² For large nanopores at negative bias, where a negative molecule enters through ẑ = 1 and exits through ẑ = 0 (see Fig. 6), entrance effects do not modify the local conductivity inside the pore, which is dominated by the concentration at the junction. However, they do modify the local conductance, leading to current drop due to volume exclusion [see Eq. (33)]. On the other hand, when the molecule is leaving the pore through ẑ = 0, the current can either increase or decrease depending on the value of Ω, one of which may give rise to biphasic current signatures. Figure 6 presents simulation results of the translocation of a dsDNA molecule through a cylindrical nanopore with a negatively charged junction near its tip (placed at z = 3 nm). All simulations were performed using the FEM with the PNP–PB equations. At negative bias, both (16) and simulation results suggest conductance enhancement for the baseline. When the dsDNA molecule is entering the pore (far from the junction), a drop in current due to volume exclusion is observed, in accordance with (33). When the dsDNA molecule is leaving the pore (near the junction), the conductance enhancement near the junction is magnified by the negative charge of the DNA molecule, which overrules the effect of volume exclusion (Λ − Σ < −1), leading to Ω < −1 and thus an increase in current. We then observe a biphasic signal compatible with our theory as well as experimental results.

FIG. 6.

(a) Simulation for a translocation event of a 66-base-pairs-long DNA molecule moved along the axis of a unipolar nanopore from right to left at negative bias. At this bias, the DNA molecule moves from larger to smaller values of ẑ. Colored regions represent the values of Γ, showing how DNA translocation enriches the nanopore during entrance (near ẑ = 1) and depletes it as the molecule leaves the pore (near ẑ = 0). A voltage of ${\widehat{V}}_0=-20$ is imposed at the right reservoir as well as a surface charge density of −0.01 C/m² in the first 3 nm of the nanopore on the left (z ∈ [0 nm, 3 nm]) and a zero surface charge density in the rest of the nanopore. (b) Simulated change in current as a function of the distance of the tip of the molecule to the left end of the nanopore (where it exits).

On cylindrical pores much longer than the molecule, the enrichment section does not contribute significantly to the overall resistance. Therefore, most pores only exhibit a reduction in current due to depletion during the exit. Nevertheless, entrance effects may be amplified by either considering a discontinuous pore charge density or a smaller pore at the tip—a conical or bullet shaped pore. Due to their capacity to focus the electric field in nanometric regions, bullet-shaped and conically shaped nanopores are of great interest for sensing applications.^16,53 This focusing effect strongly converges the electric field at the pore tip, making the current be highly sensitive to the tip conditions. The tip region of these nanopores is then called the detection zone of the nanopore, and we will focus in these regions for our blockage analysis. Importantly, atomic layer deposition on bullet-shaped pores often creates a tip layer with a high surface charge density.

Current blockages on a cylindrical nanopore with a surface charge density discontinuity near the tip of the nanopore (ẑ = 0), such as those resulting from atomic layer deposition techniques,⁵³ were analyzed. Unipolar nanopores with length L = 100 nm, radius a = 4 nm, and a charged region placed at the tip of the nanopore of length z_m = 3 nm are considered at an ionic strength of 1 M. Surface charge densities with values 0 C/m², ±0.0025 C/m², ±0.005 C/m², ±0.0075 C/m², ±0.01 C/m², ±0.025 C/m², ±0.05 C/m², and ±0.075 C/m² are considered, leading to values of |X| < 0.5, and cylindrical particles with surface charge densities 0 C/m², ±0.013 64 C/m², and ±0.027 28 C/m², radii r_m = 0.888 nm, 1.185 nm, 1.481 nm, and 1.77 nm, and lengths 3.74 nm, 7.48 nm, 14.96 nm, 22.44 nm, and 29.92 nm are placed inside these pores. Note that these lengths correspond to double stranded molecules with 11, 22, 44, 66, and 88 base-pairs, respectively, molecules that present radii of 1.185 nm and surface charge densities of −0.027 28 C/m². As the most peculiar current changes happen when the molecule is close to the junction, we focus on the case when the molecule just entered the nanopore and is completely inside it, as shown in Fig. 4. Imposing a voltage drop ${\widehat{V}}_0$ and defining ${\widehat{\mathcal{Y}}}_1$ as the current measured with the molecule inside the pore and ${\widehat{\mathcal{Y}}}_0$ as the baseline current, we obtain excellent agreement of our theory with normalized change in current $\left({\widehat{\mathcal{Y}}}_1-{\widehat{\mathcal{Y}}}_0\right)/{\widehat{\mathcal{Y}}}_0$ obtained from FEM simulations of the PNP–PB equations (see supplementary material S.5). Both positive and negative resistive signals are obtained, suggesting that our theory can accurately predict both the amplitude and sign of translocation events.

B. Binding of DNA molecules to the pore walls

As seen in Sec. III A, the amplitude signal is most pronounced when the molecule begins to exit. The enrichment and depletion at two ends of the molecule produce opposite concentration polarization that cancel each others’ effect. When it begins to exit, only concentration polarization at the trailing end occurs and hence the signal is amplified. Although the example in Sec. III A involves a charged section at the exit end of the pore, the same principle can be applied to the case where the charged section is at the entrance end of the pore. The positive (larger resistance) amplitude signal would be further amplified if the molecule entering is already adsorbed. This would ensure an entire length near the entrance where the surface charge is compensated by the adsorbed molecule, as described by (30), and the conductance is significantly lower because of both size exclusion and surface charge reduction effects of the molecule. There are many ways to induce adsorption prior to entry.

Short-range interactions allow charged molecules, such as DNAs, to bind to hydrophobic surfaces, even in the case of electrostatic repulsion.^72,73 On nanopores, binding and unbinding events can lead to atypical resistive signals, such as multiple-level blockage events⁶¹ and biphasic signals.⁵³ Adding a thin alumina coating to insulating conic polymer nanopores has been shown to increase the translocation time and current blockage of single stranded molecules above the values of their double stranded counterparts,¹⁶ which is counter-intuitive as double stranded molecules have larger charges and cross-sectional areas than single stranded molecules. Molecular dynamics (MD) simulations suggest that single stranded DNA molecules are more strongly attracted to hydrophobic surfaces than their double stranded counterparts, both due to their flexibility and due to hydrophobic interactions between the exposed aromatic rings of the single stranded molecule and the hydrophobic surface.⁷⁴ These interactions between double stranded DNA molecules and hydrophobic surfaces are much weaker, as they require the breakage of the hydrogen bonds that stabilize a complementary base-pair.^73,75,76

As the persistence length of single stranded molecules is of the order of 1 nm,^77,78 an important question to address is whether this higher blockage is because these molecules translocate in a coiled state through these nanopores. To address this issue, multiple walker metadynamics simulations⁷⁹ were performed for a short (8-nucleotides-long) single stranded molecule on top of an uncharged amorphous SiO₂ surface. As reaction coordinates, we select the distance of the center of mass of the molecule to the surface, and the end-to-end distance of the DNA molecule. Small end-to-end distances suggest that either the molecule is coiled or it takes a circular conformation; however, large end-to-end distances suggest that the molecule is stretched and uncoiled, being the maximum end-to-end distance possible about 0.64 nm per nucleotide (where the molecule is perfectly linear).⁸⁰ Before performing our metadynamics simulations, our molecule was equilibrated in bulk for 300 ns. We observe that, in bulk, this molecule equilibrates to a coiled conformation, as shown in Fig. 7(a). Figure 7(b) shows the results of our free energy calculations, suggesting the preference of single stranded molecules to stay in an uncoiled conformation to maximize the number of hydrophobic attachments. They hence will absorb onto the pore surface, particularly at the tip because field leakage there can reduce the electrostatic repulsion.¹⁶

FIG. 7.

(a) Examples of conformations taken by ssDNA molecules in bulk (top) and in proximity to a surface (bottom). (b) Free energy profile for the attachment of a ssDNA oligomer into an uncharged amorphous silica surface. The horizontal axis is a reaction coordinate for deposition of the molecule into the surface, while the vertical axis assesses the end-to-end distance of the molecule, showing a preference toward an uncoiled, stretched conformation.

As suggested by our theoretical model, adsorption and desorption of biomolecules to nanopore walls can modulate the ionic conductivity inside them, leading to characteristic signals. In Fig. 8, we report both FEM simulated and theoretical current drops for a single stranded molecule bound to the walls of a cylindrical nanopore with a junction placed near its tip (at z = 3 nm). These results are compared with translocation signals of double and single stranded molecules translocating through the middle of the nanopore, showing that adsorption can modulate the ionic conductivity enough as to lead to comparable current drops for double and single stranded molecules. Figure 9 compares FEM simulations of the current drops for these same molecules with experimental results,¹⁶ in excellent agreement with our estimated surface charge density of 0.075 C/m², which is plotted as a vertical dashed line in Fig. 9. We note that both the amplitude signal of the absorbed ssDNA and the freely translocating dsDNA are captured within the CV of the data. At the elevated charge density of our tip, adsorbed ssDNA molecules produce twice as large a resistive amplitude as free-floating dsDNA molecules of the same length and more than 3 times as large an amplitude as free-floating ssDNAs. All these amplitude ratios are significantly larger than the CV of the data, as is evident in Fig. 9. This underscores the advantage of using the amplitude of the resistive signal.

FIG. 8.

Comparison between theoretical (lines) and FEM simulated (symbols) current blockages for single (rectangle) and double (triangle) stranded DNA molecules with different surface charge densities in the top region of the nanopore, where either the molecule translocates through the middle of the nanopore (red and green) or sticks to its inner walls (blue). As adsorption of single stranded molecules breaks the symmetry of the nanopore, 3D simulations were performed for those cases when the molecule sticks to the walls. Our analytical theory, without fitting parameters, is in good agreement with simulation results for dsDNA and ssDNA molecules that translocate through the middle [Eq. (28)] or are adsorbed [Eq. (30)]. Some parameter fitting can further improve the latter case for ssDNA but the FEM simulation itself becomes error prone when the molecules are in contact with the wall. Error bars are obtained by comparison of baselines of 3D and 2D nanopore models. The parameters are length 100 nm, radius 4 nm, and with a junction placed 3 nm into the entrance of the nanopore such that there is surface charge only on the upper region. An ionic concentration of 1 M is used. Simulation details are presented in Subsection 1 of the Appendix.

FIG. 9.

Experimental translocation resistive pulse signals of double stranded (a) and single stranded (b) molecules on a single polymeric bullet-shaped nanopore with a 3 nm thick Al₂O₃ coating. (c) Comparison between experimental (dashed regions) and FEM simulated (symbols-solid lines) current blockages. The surface charge density 0.075 C/m² that is closest to the experimental amplitude data is marked as a vertical dashed line. The pink dashed region corresponds to double stranded molecules, while the cyan region corresponds to single stranded molecules. Red circles correspond to double stranded molecules translocating through the middle of the pore, while blue triangles correspond to single stranded molecules translocating through the middle. Cyan triangles correspond to single stranded molecules translocating through the inner walls of the nanopore. The horizontal axis corresponds to the surface charge density of the tip of the bullet-shaped. As adsorption of single stranded molecules breaks the symmetry of the nanopore, 3D simulations were performed for those cases when the molecule sticks to the walls. Simulation error bars are obtained by comparison of baselines of 3D and 2D nanopore models.

IV. CONCLUSIONS AND AMPLITUDE TAGS WITH SPECIFIC FINGERPRINTS

We have shown analytically and through numerical simulations that intra-pore enrichment can produce negative resistive signals if it is more dominant than the volume exclusion effect. Such enrichment results from a conductance discontinuity of bipolar pores and also when a linear molecule translocates through a uniform pore. We are hence able to analytically capture the rectification factor of a bipolar pore and to define a key parameter that determines whether a translocating molecule will lead to an increase or a decrease of the current. The key interval in time is when the molecule is near the junction, where its effect in the conductivity of the pore is the most important. We showed from our theory that ssDNA and dsDNA molecules far from the junction of a nanopore always produce positive resistive signals (reductions of baseline current), independent of the pore size and density. However, a negative resistive signal (increase from the base line current) is possible upon exiting, particularly if the exit is highly charged. We also showed that the amplitude of an adsorbed ssDNA is significantly different from its free-floating counterpart or even a free-floating dsDNA of the same length, and differences of as much as a factor of 2 can be easily obtained.

With the critical parameter Ω, we can now design probes or oligos to produce distinct amplitude fingerprints for each molecule. We have already seen that, with proper tuning of the surface charge, we can create large amplitude differences in ssDNA and dsDNA of the same length, even if both exhibit positive resistive signals for all conditions. Unlike DNAs, linear proteins have very different charge densities and are known to exhibit biphasic and more complex signals.^53,81,82 One can then design the surface charge at the tip so that Ω < −1 for a certain molecule in question. These molecules (alpha helices, beta sheets, etc.) would then produce distinct negative resistive spikes at those locations. Adsorption or association with surface antibodies can also produce similar negative resistive signals if Ω is designed to be the correct value. Likewise, hybridization of short oligos with nanoparticles or highly charged tags can also produce very distinct resistive signals that ssDNA or dsDNA molecules cannot otherwise produce. With sufficient resolution, a bar code can even be developed with tags with different amplitude signatures. Another possible direction is to have multiple nanopores in sequence, each with different end charged regions so that different molecules can produce different pulse sequences of positive and negative spikes in the current signal. If such amplitude fingerprints can be developed, the millisecond translocation time of solid-state nanopores need not be prolonged. We were able to analyze the data of Figs. 1 and 9 even though the translocation time is as low as milliseconds and the capture time as short as 10 ms. We would hence have both the advantage of high throughput and clear identification of different molecules.

SUPPLEMENTARY MATERIAL

Supplementary material S.1 presents the derivation of the current on a nanopore with a single junction and constant cross-sectional area when the length of the nanopore is of the same order of the Debye length ($\alpha \sim \mathcal{O}\left(1\right)$. Supplementary material S.2 compares our analytical theory with FEM simulations of multiple bipolar and unipolar nanopores. Supplementary material S.3 presents the analytical solution of the current on a nanopore with two junctions and variable cross-sectional area. Supplementary material S.4 presents the analytical expression for the blockage of a single junction nanopore by a molecule when it is either at its entrance or exit. Supplementary material S.5 compares our analytical theory with FEM simulations of blockage events when a molecule of length L_m is placed along the axis of the nanopore near its entrance, occupying z ∈ [0, L_m].

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.

APPENDIX: METHODS

1. Finite element method (FEM) protocols

Figure 10(a) depicts a cylindrical nanopore embedded within an isolating membrane, which connects two identical reservoirs on either side. The computational domain is restricted to the fluid domain Ω_f, enclosed by segments ACBHGFEED. The nanopore consists on a cylindrical section GFE of length L and radius a. The length and radius of the reservoirs are sufficiently large to ensure that the numerical results are independent of the reservoir size. The two reservoirs are filled with a 1–1 symmetric electrolyte solution containing ions with equal mobility, at the bulk ionic concentration C₀, density $\tilde{\rho }$, dynamic viscosity μ, and relative permittivity ϵ. An electric potential difference ${\widehat{V}}_0$ is applied between the bottom (AD) and the top (BC) of the reservoirs to generate the ionic current through the nanopore.

FIG. 10.

(a) Schematic of the axisymmetric geometry used for a cylindric nanopore in the 2D simulations. (b) Schematic of the geometry used for a bullet-shaped nanopore. Parameters of the system are ϵ = 80, $\tilde{\rho }=1000$ kg/m³, μ = 0.0024 Pa s, D₊ = D₋ = 2 × 10⁻⁹ m²/s, and z₊ = z₋ = 1, where z₊ and z₋ are the valency of the positive and negative ions, respectively.

Poisson–Nernst–Planck equations are solved for this axisymmetric geometry with the commercial finite element method (FEM) software COMSOL 5.3a⁸⁴ using the coupled Multiphysics modules of electrostatics and transport of diluted species. An exhaustive study of the proper meshing is performed to ensure that the numerical results are independent of meshing. Finer meshing is generated in the region close to the charged portions of the nanopore. Axial symmetry is imposed on AB. Zero normal electric field is imposed on BHID as well as on GH and EI. As segments CH, HG, GF, FE, EI, and ID are the walls of the reservoirs and the nanopore, no ion flux is imposed on these boundaries. Segments AD and BC are far from the nanopore, and thus the ionic concentrations at both boundaries are the bulk concentrations C₀. A junction is placed at F such that different surface charge densities are imposed on GF and FE. To characterize the current drop during a translocation event, FEM simulations of the translocation of double and single stranded molecules through the middle of the nanopore were performed. dsDNA molecules were modeled as cylinders with radius 1.185 nm, height 0.34 nm per base-pair, and surface charge density −0.027 28 C/m² whose axis aligns with the axis of the simulation box, while ssDNA molecules were modeled as cylinders with a radius 0.838 nm, height 0.64 nm per nucleotide, and surface charge density −0.0047 C/m². These particles were moved along the axis of the nanopore, and the net current through the nanopore was measured through

$$I={\int }_{S}F\sum _{i=\mathrm{1,2}}\left(z_i{N}_i\right)\cdot ndS,$$ (A1)

where S is the cross-sectional area of the nanopore, z_i and N_i are the valency and ionic fluxes of the positive and negative ions, respectively, and n is the unit normal vector pointed from S into the fluid.

Bullet-shaped nanopores were modeled as in Fig. 10(b), with a junction at G such that HG is 3 nm long and GF is 7 nm long. Segment FE is placed at an angle of 9° with respect to the vertical axis. Adsorption of ssDNA molecules into the walls of the nanopore breaks the symmetry, and thus 3D simulations of our nanopore were considered. An exhaustive study of the proper meshing was performed to ensure that the numerical results were independent of the meshing. An adsorbed ssDNA molecule was modeled as a half-cylinder with radius 1.185 nm, height 0.64 nm per nucleotide, and surface charge density −0.003 902 C/m², leading to an equal volume and net surface compared to the model for the single stranded molecule translocating through the middle of the nanopore. A representation of this system is presented in Fig. 10(c).

2. Molecular dynamics (MD) protocols

Molecular dynamics simulations were performed in National Alliance of Market Developers (NAMD)⁸⁵ with the Chemistry at Harvard Molecular Mechanics (CHARMM36) force field.⁸⁶ To obtain a more proper characterization of the interaction between the charged and hydrophobic groups of DNA, the CUFIX modification of the CHARMM force field was implemented.⁸⁷ A single stranded molecule, 5′-CACGGCTC-3′, a short molecule typically considered for fundamental studies of kinetics of nucleic acid reactions, was immersed in a TIP-3P explicit water box⁸⁸ of dimensions 60 × 15 × 15 nm³. Lithium ions were placed by calculating the Coulombic potential due to the DNA molecule in the nearby volume, and the ions were placed at points of minimal energy using the cionize plugin of visual molecular dynamics (VMD).⁸⁹ After this placement, enough lithium and chlorine ions were added to the solution in order to obtain a molar strength of 1 M. After equilibration, this molecule was placed at a distance of 40 A from an uncharged amorphous silica oxide surface⁹⁰ (see Fig. 11), and its backbone was held fixed for 100 ns to allow ions to accumulate on the surface. Metadynamics calculations were performed in 24-cores CPUs with 20 walkers for a total simulation time of 10 µs. Each simulation is performed on a 9 × 9 × 8 nm³ box, being the long dimension normal to the silica surface. There are 17 500 water molecules in the box, the number of which was adjusted to achieve a mass density of 1 g/cm³. The thickness of the silica surface is 0.5 nm, and this surface is held together in its initial location with harmonic constraints (10 kcal/mol/A²). Two reaction coordinates were employed: the vertical distance between the center of mass of the DNA molecule and the surface, and the end-to-end distance of the DNA molecule. The temperature of the system was held constant at 295 K using a Langevin thermostat with a damping frequency of 1 THz. A Nose–Hoover Langevin piston was applied to maintain the pressure at 1.013 25 bar. A time step of 2 fs was considered, and outputs of the trajectory were saved every 100 000 steps. A distance cutoff of 12.0 A was applied to short-range, non-bonded interactions, and 10.0 A for the smothering functions.

FIG. 11.

Simulation box used as a starting configuration for our metadynamics simulations.