Modeling the Role of LHCII-LHCII, PSII-LHCII, and PSI-LHCII Interactions in State Transitions

Abstract

The light-dependent reactions of photosynthesis take place in the plant chloroplast thylakoid membrane, a complex three-dimensional structure divided into the stacked grana and unstacked stromal lamellae domains. Plants regulate the macro-organization of photosynthetic complexes within the thylakoid membrane to adapt to changing environmental conditions and avoid oxidative stress. One such mechanism is the state transition that regulates photosynthetic light harvesting and electron transfer. State transitions are driven by changes in the phosphorylation of light harvesting complex II (LHCII), which cause a decrease in grana diameter and stacking, a decrease in energetic connectivity between photosystem II (PSII) reaction centers, and an increase in the relative LHCII antenna size of photosystem I (PSI) compared to PSII. Phosphorylation is believed to drive these changes by weakening the intramembrane lateral PSII-LHCII and LHCII-LHCII interactions and the intermembrane stacking interactions between these complexes, while simultaneously increasing the affinity of LHCII for PSI. We investigated the relative roles and contributions of these three types of interaction to state transitions using a lattice-based model of the thylakoid membrane based on existing structural data, developing a novel algorithm to simulate protein complex dynamics. Monte Carlo simulations revealed that state transitions are unlikely to lead to a large-scale migration of LHCII from the grana to the stromal lamellae. Instead, the increased light harvesting capacity of PSI is largely due to the more efficient recruitment of LHCII already residing in the stromal lamellae into PSI-LHCII supercomplexes upon its phosphorylation. Likewise, the increased light harvesting capacity of PSII upon dephosphorylation was found to be driven by a more efficient recruitment of LHCII already residing in the grana into functional PSII-LHCII clusters, primarily driven by lateral interactions.

Significance

For photosynthesis to operate at maximum efficiency, the activity of the light-driven chlorophyll-protein complexes, photosystems I and II, must be fine-tuned to environmental conditions. Plants achieve this balance through a regulatory mechanism known as the state transition, which modulates the relative light harvesting antenna size and therefore excitation rate of each photosystem. State transitions are driven by changes in the extent of the phosphorylation of light harvesting complex II, which modulate the interactions between photosystem I, photosystem II, and light harvesting complex II. Here, we developed a novel algorithm to simulate protein complex dynamics and then ran Monte Carlo simulations to understand how these interactions cooperate to affect the organization of the photosynthetic membrane and bring about state transitions.

Introduction

The plant chloroplast thylakoid membrane is the site of the light reactions of photosynthesis. Here, the integral membrane protein complexes, light harvesting complex II (LHCII), photosystem II (PSII), cytochrome b₆f (cytb₆f), photosystem I (PSI), and ATP synthase, carry out light harvesting and electron and proton transport, culminating in the synthesis of NADPH and ATP, which are utilized in the stroma for CO₂ fixation. The thylakoid membrane is partitioned into the grana and stromal lamellae regions (1, 2, 3). The grana are cylindrical stacks of 2–30 appressed membranes 400–500 nm in diameter, enriched in LHCII and PSII. The stromal lamellae are flat sheet-like structures that wrap helically around the grana, interconnecting one stack to another and are enriched in PSI and ATP synthase (4, 5, 6). The cytb₆f complex is evenly distributed between the two domains (1,7,8). The division of the thylakoid into the grana and stromal lamellae depends on the presence of positively charged counterions to overcome the net negative charge on the membranes (9,10). In the presence of cations, attractive lateral interactions between PSII and LHCII drive the lateral segregation of these complexes from PSI and ATP synthase (10, 11, 12). In the presence of screening levels of cations, attractive van der Waals and hydrophobic interactions between the flat stromal surfaces of these PSII-LHCII macrodomains then allow these complexes to self-associate with PSII-LHCII regions in neighboring membranes to form three-dimensional grana stacks (11,13,14). An entropic driving force through the influence of macromolecular crowding may also contribute to grana stacking (15). At the molecular level, the interaction of two LHCII trimers across the stromal gap has been calculated to be of the order of 4 K_BT, where K_B is Boltzmann’s constant and T is the temperature in K (16).

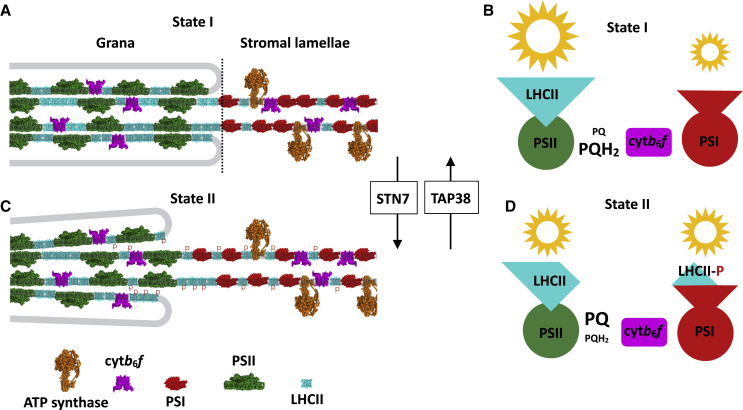
The light environment of land plants fluctuates by orders of magnitude over timescales as little as a second. Such dramatic variations can cause mismatches between the amount of light absorbed and its utilization in photosynthesis, leading to metabolic and oxidative stress that lowers plant growth and productivity (17,18). Fortunately, plants have evolved a complex repertoire of mechanisms that can alter the efficiency of light harvesting and electron transfer in the thylakoid membrane (19). One such mechanism is the state transition that balances the relative excitation level of PSI and PSII to optimize photosynthesis (Fig. 1; (20,21)). The relative excitation balance between PSI and PSII varies with light spectral quality because of their differing absorption spectra and may also be adjusted to account for differences in the required ratio of linear (PSII and PSI) to cyclic (PSI only) photosynthetic electron transfer (22,23). State transitions are regulated by the redox state of the photosynthetic electron transfer chain (24). When PSII is overexcited relative to PSI, the Q_p site on the cytb₆f complex is occupied by plastoquinol, leading to activation of the kinase STN7 (25). STN7 phosphorylates the stromal-facing N-terminus of the LHCII subunits LHCB1 and 2, weakening its tendency to associate with PSII and increasing its affinity for PSI (state II) (Fig. 1; (26)). In this way, the relative light harvesting antenna sizes of PSI and PSII are altered to rebalance their relative excitation rates, ensuring the redox homeostasis of the electron transfer chain. When PSI is overexcited relative to PSII, the plastoquinone (PQ) pool is oxidized, STN7 is inactivated, and LHCII is dephosphorylated by the constitutively active phosphatase TAP38 (state I) (Fig. 1; (27,28)). Alternatively, state I can also be induced in high light in which the PQ pool remains reduced through the inhibitory effect of reduced thioredoxin and/or ΔpH on STN7 (29,30).

Figure 1.

Mechanism of state transitions in plants. (A) The plant photosynthetic thylakoid membrane is divided into stacked grana and unstacked stromal lamellae domains. PSII and LHCII are concentrated mostly in the grana, whereas PSI and ATP synthase are exclusively found in the stromal lamellae. cytb₆f is found in both domains. (B) When light conditions favor PSII excitation (see text), the plastoquinone electron carrier pool becomes reduced (PQH₂). This activates the kinase STN7, which phosphorylates LHCII. (C) Phosphorylation of LHCII (forming LHCII-P) weakens the lateral and stacking interactions that sustain the grana structure and leads to increased association between PSI and LHCII. (D) Association of LHCII-P with PSI rebalances the relative excitation rates of PSI and PSII, allowing reoxidation of the plastoquinone pool (to PQ). The state transition is reversed by the phosphatase TAP38, which dephosphorylates LHCII when PSI excitation is favored. To see this figure in color, go online.

Although the LHCII phosphorylation is clearly established as the mechanistic basis of state transitions, it remains unclear precisely how the thylakoid macro-organization changes to bring about the relative change in the PSI/PSII antenna size. STN7-dependent phosphorylation of LHCII causes a reduction in grana diameter and the number of membrane layers per stack while simultaneously increasing the number of grana per chloroplast (23,31). Puthiyaveetil et al. (14) calculated, by solving the Poisson-Boltzmann equation for average surface charge across the grana, the changes in the stacking forces due to LHCII phosphorylation. They found that at physiologically relevant cation concentrations, the balance between attractive van der Waals and hydrophobic interactions and repulsive electrostatic interactions is carefully poised. The net result is that increasing the negative surface charge density on LHCII by phosphorylation is sufficient to weaken the lateral and stacking interactions that sustain grana organization (13,14). These changes bring about a reduction in grana diameter and effectively increase the contact area between the grana and stromal lamellae, which may facilitate the exchange of LHCII between the domains (23,31,32). The changes in thylakoid stacking were also found to weaken the connectivity between PSII reaction centers, again contributing to the relative shift in antenna size (33).

In addition to LHCII phosphorylation, molecular recognition through the presence of specific binding sites on PSI is also crucial to state transitions (20,34). Binding of phospho-LHCII (LHCII-P) to PSI via the PsaL/O and H subunits gives rise to the PSI-LHCII-P supercomplex (35,36). A second probably weaker binding site for LHCII-P involving the LHCI (LHCA1-4) subunits of PSI also exists (37,38). The psal and lhca mutants of Arabidopsis thus largely lack state transitions despite unchanged or even increased levels of LHCII phosphorylation (34,37).

Early structural analysis using freeze-fracture electron microscopy revealed that LHCII migrates from the grana to stromal lamellae upon transition to state II in isolated thylakoids, consistent with a decrease in the chlorophyll a/b ratio of this domain (39). However, later biochemical studies in which state transitions were first induced in leaves before thylakoid isolation and those using in situ fluorescence microscopy suggested PSI and LHCII encountered one another in the margins where the two domains meet, and exchange of LHCII between domains was very limited (40,41). Unfortunately, recent cryo-electron tomography data have cast doubt on the existence of a defined margins region with intermediate composition relative to the grana and stromal lamellae (5,8). Moreover, it is now clear that a population of LHCII energetically connected to PSI resides in the stromal lamellae even in state I and that the transition to state II rather increases the proportion (42). The relative importance of the changes in thylakoid membrane stacking and changes in the lateral interactions brought about by LHCII phosphorylation thus remain unclear, and indeed, they may fulfill distinct as well as complimentary roles in regulating electron transfer and light harvesting.

Given the unanswered questions that remain on the precise mechanism of state transitions, new approaches are needed to clarify how the altered balance of forces upon LHCII phosphorylation affect the thylakoid macro-organization. The structural model of the thylakoid membrane at the individual protein complex level presented here was made possible by recent breakthroughs in elucidating thylakoid organization and dynamics used in atomic force microscopy (AFM) (7,23,43) and structured illumination microscopy (SIM) (31,44) and publication of high-resolution structures of the key protein complexes involved in the light reactions (45, 46, 47, 48, 49, 50). Recently developed algorithms, which made the calculation of whether two or more particles spatially overlap tractable, were also essential (see Materials and Methods). Thanks to these advances, we were able to model the behavior of protein complexes using structures obtained directly from the Protein Data Bank, whereas previous studies relied on simplified protein geometries (16,51). Previous models revealed that relatively weak (2 K_BT) interaction between LHCII trimers, including strong and moderately bound trimers of the PSII-LHCII supercomplex, give rise to complex emergent behavior, including the formation of the crystalline domains of PSII and LHCII (51,52). The model presented in the current study extends those of Schneider and Geissler (16) and Lee et al. (51) to include cytb₆f, PSI, and ATP synthase as well as introducing separate thylakoid regions: the grana and the stromal lamellae. We used this molecular model as a basis for Monte Carlo simulations to investigate the role of specific lateral intermolecular interactions and changes in grana stacking forces in modifying the distribution of photosynthetic complexes between the two domains and on the connectivity of LHCII with PSI and PSII. In particular, we address the question of whether the lateral and stacking interactions have functionally distinct or cooperative roles in state transitions. To achieve this, we developed a lattice-based algorithm for overlap detection of particles of arbitrary geometry. This algorithm was shown to be computationally effective for a large number of protein complexes, rendering feasible the mesoscale Monte Carlo simulation of protein structures directly from the Protein Data Bank.

Materials and Methods

Construction of the thylakoid model

A model of the thylakoid membrane was constructed using high-resolution structures of plant photosynthetic complexes, obtained from the Protein Data Bank (PSII-LHCII (C₂S₂M₂), PDB: 5XNL (48); PSII-LHCII (C₂M₂), PDB: 3JCU (49); cytb₆f, PDB: 6RQF (45); LHCII, PDB: 1RWT (50); PSI-LHCI, PDB: 4Y28 (53); ATP synthase, PDB: 6FKF (46)), on a square lattice with a spacing of 1 nm (Fig. 2 A). The densities of particles in the grana (dimeric PSII-LHCII and dimeric cytb₆f, 1.14 × 10⁻³ nm⁻²) and monomeric PSI-LHCI in the stromal lamellae (2.45 × 10⁻³ nm⁻²) were determined in a previous AFM study (23). We assumed a 1:1 ratio of PSII and PSI reaction centers (1) and a 1:1 ratio of C₂S₂ to C₂S₂M₂ PSII-LHCII dimers (23). A number of free LHCII particles were added to the grana area to a total of five LHCII (including strong and moderately PSII bound) per PSII reaction center (54). cytb₆f particles were distributed between the grana and stromal lamellae at a ratio of an equal area density to a total of 0.5 times the number of PSII reaction centers (1,7). The ATP synthase was added to the stromal lamellae at a density of 0.7 of the number of PSII reaction centers (1,55). Monomeric PSII was added to the stromal lamellae and represented 10% of the total number of PSII reaction centers (1). The geometry of the thylakoid model was based on previous work (23,56) wherein the grana is considered a circular plane, and stromal lamellae is a concentric ring surrounding the grana. The outer edge of the stromal lamellae is considered impermeable to all proteins (zero-flux, aperiodic boundary conditions), and the barrier between the grana and the stromal lamellae is semipermeable (in this study, only LHCII was permitted to move between the grana and the stromal lamellae). The radius of the stromal lamellae (r_sl) was calculated using the following equation:

$$r_{sl}=\sqrt{\frac{N_{PSI}}{\pi D_{PSI}}+r_{gran{a}^2}},$$

where r_grana is the grana radius, N_PSI is the number of PSI particles, and D_PSI is the density of PSI in the stromal lamellae.

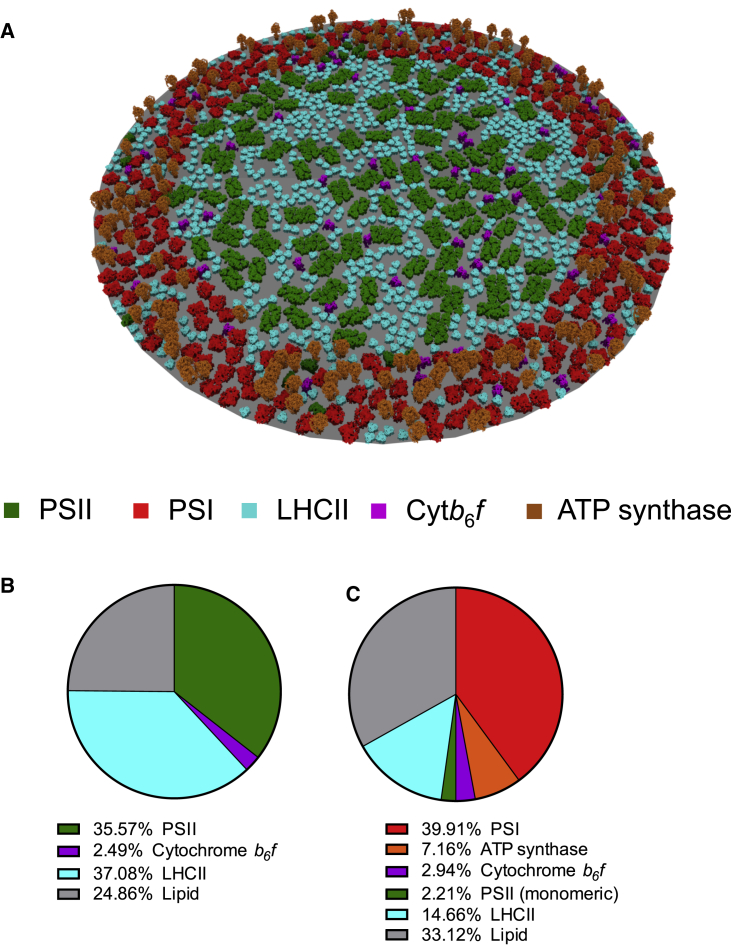
Figure 2.

A structural model of the thylakoid membrane. (A) A visual representation of the model is shown. (B) The percentage of grana area occupied by constituents of the grana is shown. (C) The percentage of stromal lamellae area occupied by constituents of the stromal lamellae is shown. To see this figure in color, go online.

Monte Carlo simulations

LHCII lateral and stacking interactions were modeled using the potentials described in Schneider and Geissler (16) except that intralayer interactions were nonspecific; we did not specify an angular difference threshold for binding. This is because specific interactions were considered from the outset by including C₂S₂M₂ and C₂S₂ PSII-LHCII supercomplexes in the model in equal numbers. We note that the S and M LHCII trimers of C₂S₂M₂ and C₂S₂ PSII-LHCII are not directly involved in state transitions in vivo (57). We introduced a PSI-LHCII interaction, based on Pan et al. (36), when LHCII was phosphorylated. This was modeled as a square-well interaction and varied between 2 and 16 K_BT with a distance threshold of 1 nm. Simulations included two grana layers of equal composition. Equilibrium properties of the thylakoid membrane system were sampled using the standard Metropolis-Hastings algorithm. For each perturbation in the Monte Carlo simulations, a particle was selected at random from one of the two layers and moved by plus or minus 1 nm (lattice spacing) in x or y and rotated by plus or minus π/33. 10⁷ perturbations were made for each simulation, and sampling was only carried out when the system was in equilibrium (Fig. S1). Overlap of particles was forbidden during simulations. Spatial overlap was implied when the total number of lattice sites occupied by all particles was less than the sum of the number of lattice sites occupied by individual particles (Fig. S2). A thorough discussion is given in Appendix 1. Before all simulations, the models were initialized with 10⁷ Monte Carlo perturbations in the absence of any potentials. This was to ensure randomization of the arrangements of proteins and allow equilibration of LHCII between the grana and stromal lamellae (with the exception of diffusion simulations in Fig. 5, which initialized from state II). Test simulations were performed with only LHCII complexes (Fig. S3) or with only LHCII and PSI complexes to test PSI-LHCII interactions.

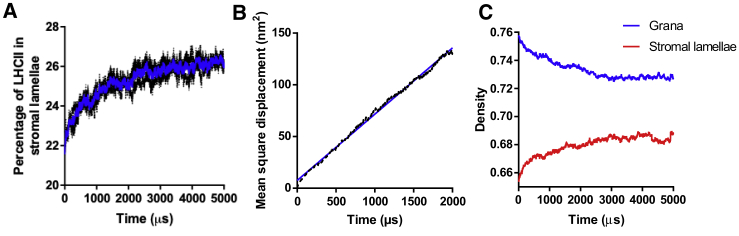
Figure 5.

The diffusion-based timescale for the migration LHCII into the stromal lamellae is sub-millisecond. (A) Shown are the kinetics of the percentage of LHCII in the stromal lamellae during the transition from state I to the random state (blue solid line: average of three traces; black dashed lines: individual traces). (B) The mean-square displacement of LHCII over time is shown (blue solid line: linear fit; black dashed line: raw values). (C) The kinetics of the density of the grana (blue) and stromal lamellae (red) during the transition from state I to the random state is shown. To see this figure in color, go online.

Diffusion in protein complex dynamics

Translational (D_T) and rotational (D_R) diffusion coefficients of protein complexes in the thylakoid membrane were calculated according to Saffman and Delbrück (58):

$$D_T=\frac{R^2}{4t}=\frac{k_{B}T}{4\pi {\mu }_m{r}_{e}h}\left(\log \left(\frac{{\mu }_{m}h}{{\mu }_w{r}_e}-\gamma \right)\right),$$

$$D_R=\frac{{\theta }^2}{2t}=\frac{k_{B}T}{4\pi {\mu }_m{r}_{r}2h},$$

where μ_m = 200 mPa s (based on the range of viscosities of lipid membranes of 160–260 mPa s (59)) and μ_u = 1 mPa s are the viscosities of the lipid membrane and water, respectively, h = 4 nm is the thickness of the lipid bilayer, γ ≈ 0.577 is the Euler-Mascheroni constant, and is the effective radius of the particle

$$r_e=\sqrt{\frac{Particlearea\left(\mathrm{n}{\mathrm{m}}^2\right)}{\pi }}.$$

The effective radius therefore makes the simplifying assumption that the particle is circular. In diffusion simulations, translations were ±1 nm (in x and y directions), and rotations were ±π/33 radians (π/33 radians was chosen because this results in movements to the only neighboring lattice site for larger particles). A single time step of 1 μs was used. To compensate for the variety of diffusion coefficients, we used a probabilistic approach whereby translations and rotations, where accepted, are given the following criteria:

$$Accepttranslationwithprobability\frac{1}{1\mu \mathrm{s}}\frac{\Delta X^2}{4D_T},$$

$$Acceptrotationwithprobability\frac{1}{1\mu \mathrm{s}}\frac{\Delta {\theta }^2}{4D_R}.$$

That is, movements were accepted with a probability defined by the predicted time (from the Einstein equation (Δx² = 4DΔt)) divided by 1 μs. The 1-μs time step was chosen such that the probability of acceptance was always less than one. Translations and rotations were considered independent.

Graphical analysis of antennae size and PSII connectivity

The PSII-LHCII chlorophyll antenna network was modeled as a graph network using the NetworkX package in Python (Fig. S4). Each PSII or LHCII complex was represented by a node in the graph. Edges were introduced between any two nodes in the graph if any chlorophyll in the particle represented by the first node was within a given distance (referred to as the distance threshold) of any chlorophyll in the complex represented by the other node (Fig. S4). We measured two properties of the graph, termed the antennae size and the PSII connectivity. The antenna size was defined as the average number of LHCII, over all PSII complexes, and at a given distance threshold, for which there exists a connecting path (a sequence of edges connecting the two nodes). The PSII connectivity was defined in terms of PSII clusters. If there existed a path between any two PSII complexes, they were defined as belonging to the same cluster of PSII complexes. The PSII connectivity was therefore defined as the average number of reaction centers per PSII cluster.

Code availability

Source code is freely available under a creative commons license at https://github.com/WhjWood/Thylakoid_Model.

Results

The thylakoid model

A model of the plant thylakoid membrane was constructed, based on realistic protein complex geometries and densities (Fig. 2 A). The densities of PSII and PSI were obtained from AFM images on isolated grana and stromal lamellae membranes from spinach (23). The relative number of other complexes in the membrane (LHCII, cytb₆f, and ATP synthase) were taken from the current literature (see Materials and Methods). The model produced a number of predictions that agreed with the experimental literature. We first calculated chlorophyll a/b ratio of the thylakoid model. As the model was constructed using published data on the density and stoichiometry of protein complexes but had no constraints on relative amounts of chlorophyll a and chlorophyll b, there was no guarantee a priori that the predicted chlorophyll a/b ratio from the model would match experimental values determined using the chlorophyll assay (60). The predicted chlorophyll a/b ratio of 3.2 was found to agree with those taken from spinach leaves grown at 150 μmol photons m⁻² s⁻¹ (Fig. S5), which demonstrates that the model composition is realistic with respect to this parameter. In this model, the grana area, PSII density, PSI density, and PSI:PSII stoichiometry were fixed parameters based on experimental data. The number of PSII complexes was calculated by multiplying the PSII density by the grana area. Because of the fixed PSI:PSII ratio, this resulted in a fixed number of PSI complexes. The radius and therefore the area of the stromal lamellae was calculated such that it resulted in the correct PSI density. In this model, we choose a 1:1 stoichiometry of PSI and PSII. This resulted in the radius of the thylakoid, including stromal lamellae, to be 252 nm when the grana radius was set at 190 nm (23) and predicted the area of grana as a percentage of total thylakoid area to be 54%. We found this prediction to be within the range of 50–80% proposed in the literature (61,62). In general, we found that for any choice of PSI to PSII stoichiometry in the range of 0.5–1.2, the resulting area of grana as a percentage of total thylakoid was within the observed range (Fig. S6). This largely agrees with the range of PSI:PSII ratios of 0.54–1.4 observed in the literature (63). We calculated the area occupation of each type of complex in the membrane as the number of lattice sites occupied by the complexes divided by the total number of lattice sites in the grana or stromal lamellae. The area fraction (the fraction of lattice sites occupied) of protein complexes were 0.75 in the grana (Fig. 2 B) and 0.67 in the stromal lamellae (Fig. 2 C). The lower density of proteins in the stromal lamellae compared to the grana was confirmed with AFM analysis of grana and stromal lamellae membranes (Fig. S7) and previous work (64). The overall protein area occupation as a percentage within the thylakoid was 72%, in agreement with the previous estimates of around 70% (65). In particular, LHCII dominates the grana with free LHCII trimers, accounting for almost 40% of the grana area (Fig. 2 C). Including four LHCII timers bound to each C₂S₂M₂ PSII complex and two LHCII trimers bound to each C₂S₂ PSII complex increases the area occupation of LHCII to around 55% of the grana area. The area of the stromal lamellae was found to be predominantly occupied by PSI (Fig. 2 C). At 40%, the area occupancy of PSI in the stromal lamellae was greater than every other protein complex in the stromal lamellae combined, which was ∼30%.

State transitions change the molecular organization of the thylakoid membrane

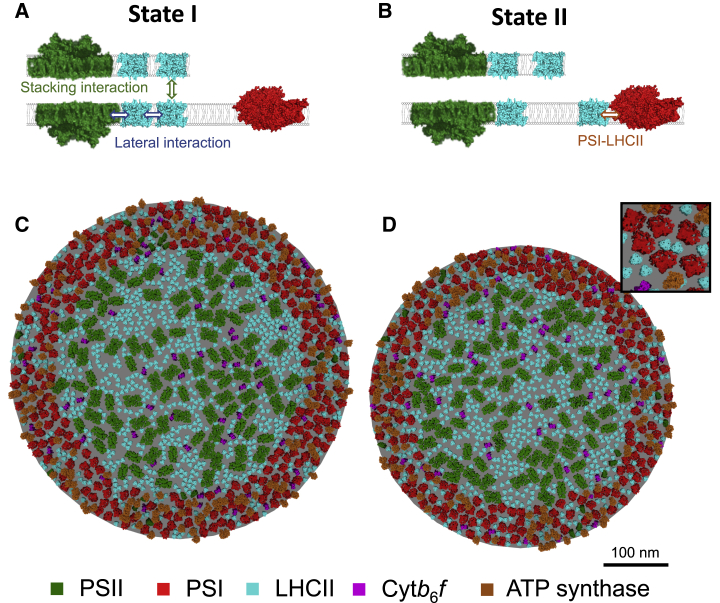
We investigated the phenomenon of state transitions at an individual complex level. In the dephosphorylated state I, LHCII trimers interact with one another both within the same membrane via specific protein-protein interactions (hereafter, lateral interactions) and across the stromal gap of the grana via electrostatic interactions mediated by cation screening (hereafter, stacking interactions) (Fig. 3 A). It is important to note that the distribution of LHCII complexes in state I between grana and stromal lamellae is determined by the balance between the stacking/lateral forces (defined as in (13)), pulling LHCII into the grana, and the lower protein density in the stromal lamellae exerting the opposite effect (Fig. 3, A and C). Thus, even in state I, a significant amount of LHCII resides in the stromal lamellae even in the absence of phosphorylation, a fact consistent with a range of biochemical data (23,37,40,42). Both the stacking and lateral interactions are greatly diminished when LHCII is phosphorylated in state II (13,14). There is, however, the appearance of the PSI-LHCII complex when LHCII is phosphorylated (Fig. 3 B; (35)). We modeled state II by removing the stacking and lateral interactions and introducing a square-well interaction between LHCII and PSI (Fig. 3, B and D). In both cases, only LHCII was allowed to move between the grana and stromal lamellae, consistent with the majority of the biochemical data (31,40,42). The grana radius was set to 190 and 170 nm for state I and state II, respectively, as observed in structured illumination microscopy images of spinach chloroplasts (23). The densities of PSII and PSI were unchanged from state I to state II as was the area of grana as a percentage of total thylakoid area (31,57). The latter fact is explained by the increased number of grana per chloroplast that offsets the decrease in grana diameter in state II (31). Monte Carlo simulations were used to sample the partitioning of LHCII into the grana and stromal lamellae at equilibrium. Sampling was carried out after 10⁷ Monte Carlo perturbations for state I and state II (Fig. S1).

Figure 3.

Modeling state transitions. (A) State I is mediated by grana stacking attractive interactions and LHCII-LHCII association, including PSII-bound LHCII trimers. (B) State II is mediated by PSI-LHCII attractive interactions only. Visual representations of the model in state I (C) and state II (D) show differences in the organization of thylakoid membrane. To see this figure in color, go online.

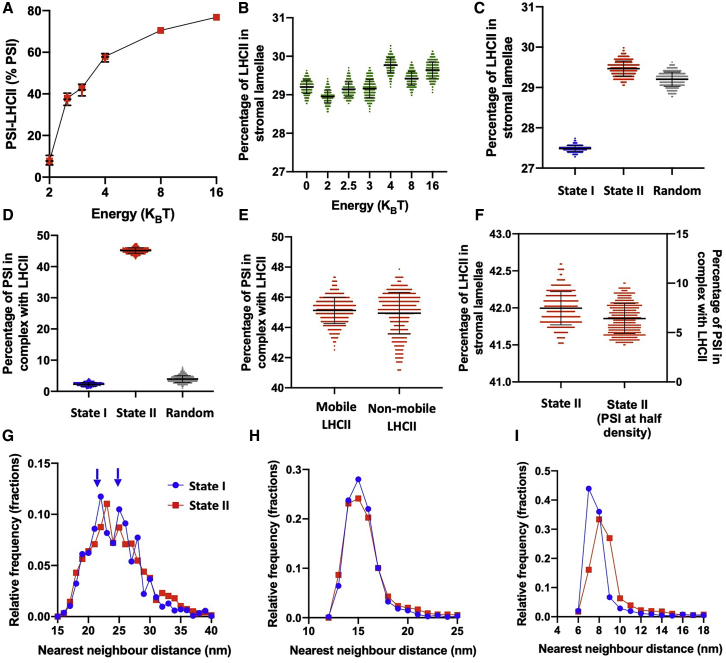
We defined the presence of the PSI-LHCII complex by the criterion of LHCII in close proximity (≤1 nm) to the PSI binding site described in Pan et al. (36). We observed an increase in the fraction of PSI in complex with LHCII from 7.5 to 80% as we varied the PSI-LHCII interaction strength from 2.5 to 16 K_BT in our state II condition (Fig. 4 A). An interaction of 3 K_BT reproduced a figure of 42% of PSI in complex with LHCII in state II in line with experimental data (Fig. 4 A; (37,66)). We therefore chose 3 K_BT as representative of the PSI-LHCII interaction in state II. Interestingly, we found that the strength of the PSI-LHCII interaction did not dramatically affect the percentage of LHCII partitioned into the stromal lamellae (Fig. 4 B). Consistent with this, the random state (in which all interactions are removed from the model) resulted in a very similar percentage of LHCII in the stromal lamellae as state II (Fig. 4 C). In contrast, the presence of the lateral and stacking interactions in state I caused a decrease in the proportion of LHCII partitioned into the stromal lamellae from 29.5 to 27.5% (Fig. 4 C). However, although the random state and state II shared a similar amount of LHCII in the stromal lamellae, they were dramatically different in terms of PSI in complex with LHCII (Fig. 4 D). This result suggests that the amount of LHCII present in the stromal lamellae is predominantly controlled by the strength of the lateral and stacking interactions rather than the PSI-LHCII interaction, a finding which is consistent with experimental data that shows the reduction in grana diameter, and stacking in state II is not dependent on the presence of the PsaL subunit of PSI (31). Our modeling suggests that the formation of PSI-LHCII complexes in state II is not limited by LHCII migration from the grana. To test this further, we ran a separate state II simulation in which LHCII was not permitted to migrate between the grana and the stromal lamellae and found that the percentage of PSI present PSI-LHCII complexes was not significantly reduced (Fig. 4 E). Thus, the partitioning of LHCII between the grana and stromal lamellae did not account for the magnitude of the increase in the number of PSI-LHCII supercomplexes as a fraction of the total number of PSI complexes in state II. It is possible that the migration of LHCII in the stromal lamellae is restricted because of the high density of the stromal lamellae. To test whether the number of PSI-LHCII complexes would increase in state II if the density of proteins in the stromal lamellae was lower, we increased the area of the stromal lamellae, effectively reducing the density by half, while keeping the grana area the same (Fig. 4 F). This led to a large increase in the percentage of LHCII in the stromal lamellae, reaching 42% in state II. Counterintuitively, the decreased density also led to a decrease in the number of PSI-LHCII complexes from 42 to 6.4% (Fig. 4 F). We speculate that this decrease may be due to an increased entropic cost of forming the PSI-LHCII complex when the density of the stromal lamellae is low.

Figure 4.

LHCII interactions control the partitioning of LHCII between the grana and the stromal lamellae and affect the organization of PSII but not PSI. (A) The percentage of PSI in complex with LHCII with varying strength of the PSI-LHCII interaction is shown (dashed lines show experimentally observed range of the percentage of PSI-LHCII). (B) The percentage of LHCII in the stromal lamellae with varying strength of the PSI-LHCII interaction is shown. (C) The percentage of LHCII complexes partitioned into the stromal lamellae in state I (blue), state II (red), and with no interactions present (random, gray) is shown. (D) Shown is the percentage of PSI in complex with LHCII (defined as LHCII ≤1 nm from binding site) in state I, state II, and random simulations. (E) Shown is the percentage of PSI in complex with LHCII in state II when LHCII is or is not allowed to migrate between the grana and the stromal lamellae. (F) The percentage of LHCII complexes partitioned into the stromal lamellae and the percentage of PSI in complex with LHCII after the density of the PSI in the stromal lamellae was decreased by half (this was achieved by increasing the area of the stromal lamellae). Error bars in (A)–(F) indicate mean ± standard deviation. (G) Shown is the nearest-neighbor distribution (center-to-center distances) of PSII-LHCII supercomplexes in state I (blue circles) and state II (red squares). The two modes arising in state I are indicated by blue arrows. (H) The nearest-neighbor distribution (center-to-center distances) of PSI in state I and state II is shown. (I) The nearest-neighbor distribution (center-to-center distances) of LHCII in state I and state II is shown. To see this figure in color, go online.

We next investigated whether the movement of LHCII led to reorganization of the thylakoid membrane by analyzing the nearest-neighbor distributions of PSII (including C₂S₂M₂ and C₂S₂ supercomplexes). In our model, PSII-LHCII did not form grana-spanning semicrystalline domains as has been seen previously (52); however, we did observe a more ordered arrangement of PSII supercomplexes in state I (Fig. 4 G). The peaks at 22 and 25 nm in the nearest-neighbor distribution of PSII were found to be in agreement with the center-to-center separation of PSII in AFM images of grana membranes (Fig. 4 G, blue arrows; Fig. S8). The observation that the peaks are more prominent in state I in our model is in agreement with the observation that PSII is more ordered or more likely to be found in a crystalline arrangement under this condition compared to state II (7,23,43,57,67). Despite the increase in the number of LHCII and PSI-LHCII complexes in the stromal lamellae in state II compared to state I, PSI nearest-neighbor distributions were indistinguishable (Fig. 4 H). This is in contrast with the observed increased amount PSI dimerization is state I observed in AFM images of stromal lamellae membranes (23). Here, as with PSII, it is difficult to ascertain at present as to whether the discrepancy between the results of the model with previous experiments is due to artifacts resulting from the detergent-based isolation of membranes in Wood et al. (23) or that the dimerization of PSI is due to an interaction not included in the model. We note that Wietrzynski et al. (8), using cryo-electron tomography, found no evidence of such PSI dimers in Chlamydomonas thylakoids, although its PSI structure is different to plants (68). A large difference between state I and state II was observed in the nearest-neighbor distribution of LHCII (Fig. 4 I). The mean nearest-neighbor distances of LHCII in state I and state II were found to be 8.27 and 9.02 nm, respectively. This can be seen in the clustering of LHCII in state I (Fig. 3 C) compared to the seemingly more random LHCII organization in state II (Fig. 3 D).

A diffusion-based lower bound for the time taken for the transition from state I to state II

The transition from state I to state II relies on the phosphorylation of LHCII (26). This is followed by the diffusion of a portion of LHCII into the stromal lamellae. However, which of the two processes, phosphorylation or diffusion, is the slowest and therefore rate limiting is unclear. We performed time-resolved simulations with the intention of estimating the time taken for a state transition to occur if LHCII phosphorylation was immediate (the diffusion-limited case). We could not simulate directly the state I to state II transition in a time-resolved manner as this would require a kinetic Monte Carlo simulation, which is computationally unfeasible for this model. Instead, we substituted a model that lacked any interactions (hereafter referred to as a random distribution) in place of state II, which, in relation to the amount of LHCII in the stromal lamellae, is highly similar to state II (Fig. 4 C). The diffusion coefficients of the thylakoid protein complexes were calculated using the Saffman-Delbrück model (58) (see Materials and Methods). Table 1 shows the calculated D_T and D_R diffusion coefficients used in the simulations. We found the half-time for the transition from state I to random as measured by the proportion of LHCII in the stromal lamellae was 0.95 ms (Fig. 5 A). This is much faster than state transition occurrences in vivo, which have a half-time of around 3–8 min (34), suggesting the limiting factor in the time taken for state transitions to occur is not the diffusion of LHCII but is perhaps the action of the STN7 kinase, consistent with the conclusions made by Consoli et al. (69). By analysis of the mean-square displacement of LHCII in the random state, we calculated the effective diffusion coefficient of LHCII to be 1.6 × 10⁻¹⁰ cm² s⁻¹ (Fig. 5 B). This is within the range observed for LHCII and phosphorylated LHCII in vivo, which were found to be 8.4 × 10⁻¹¹ and 2.7 × 10⁻¹⁰ cm² s⁻¹, respectively (69). It is evident in this model that LHCII migration into the stromal lamellae is driven by the higher density of protein complexes in the grana in state I. During the course of the transition, LHCII continues to flow from the grana into the stromal lamellae until they are almost at equal area densities (Fig. 5 C).

Table 1.

Effective Radii, Translation Diffusion Coefficients D_T, and Rotational Diffusion Coefficients D_R

Particle	Effective Radius (nm)	DT (× 10−9 cm2s−1)	DR (× 103 rad2s−1)
PSII (C2S2M2)	12.7	1.46	0.25
PSII (C2S2)	10.1	1.55	0.40
B6F	5.3	1.82	1.50
LHCII	4.5	1.88	2.00
PSI	7.2	1.69	0.78
ATP Synthase	3.7	1.97	3.06
PSII (monomeric)	5.8	1.78	1.20

Calculated using the Saffman and Delbrück model (58).

Lateral and stacking interactions of LHCII cooperate to increase the light harvesting antenna size and the connectivity of PSII-LHCII in state I

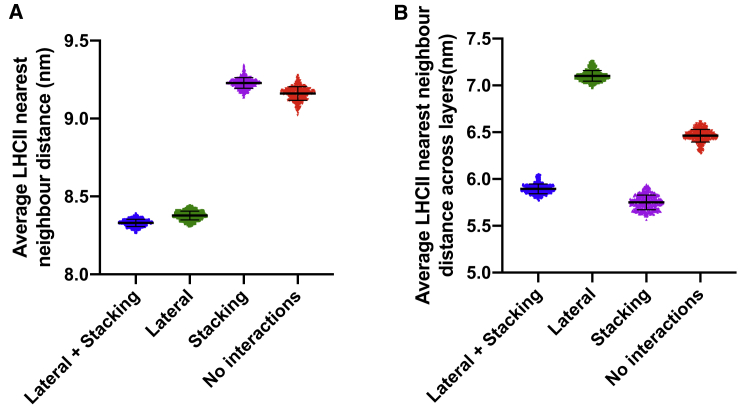
We investigated the effects of the lateral and stacking interactions of LHCII individually to ascertain their impacts on the properties of the thylakoid membrane. Simulations were carried out containing either both lateral and stacking interactions, lateral interactions only, stacking interactions only, or no interactions. We found that the lateral interactions caused the LHCII complexes to cluster as shown by a decrease in the nearest-neighbor distances (Fig. 6 A). Stacking interactions did not cause clustering of LHCII complexes in the same layer (Fig. 6 A), but the attraction between LHCII complexes on opposing layers did lead to increased correlation between LHCII complexes as shown by a decreased nearest-neighbor distance when considering only neighbors on the opposing thylakoid layer (Fig. 6 B). These results were also replicated in simulations containing LHCII only (Fig. S3).

Figure 6.

Lateral and stacking interactions affect the organization of LHCII. (A) Shown are the average nearest-neighbor distances of LHCII with the same layer in simulations containing lateral and stacking interactions (blue), lateral interactions only (green), stacking interactions only (magenta), or no interactions (red). (B) Shown are the average nearest-neighbor distances between LHCII complexes in layer 1 and layer 2 (across layers) in simulations as described in (A). Error bars indicate mean ± standard deviation. To see this figure in color, go online.

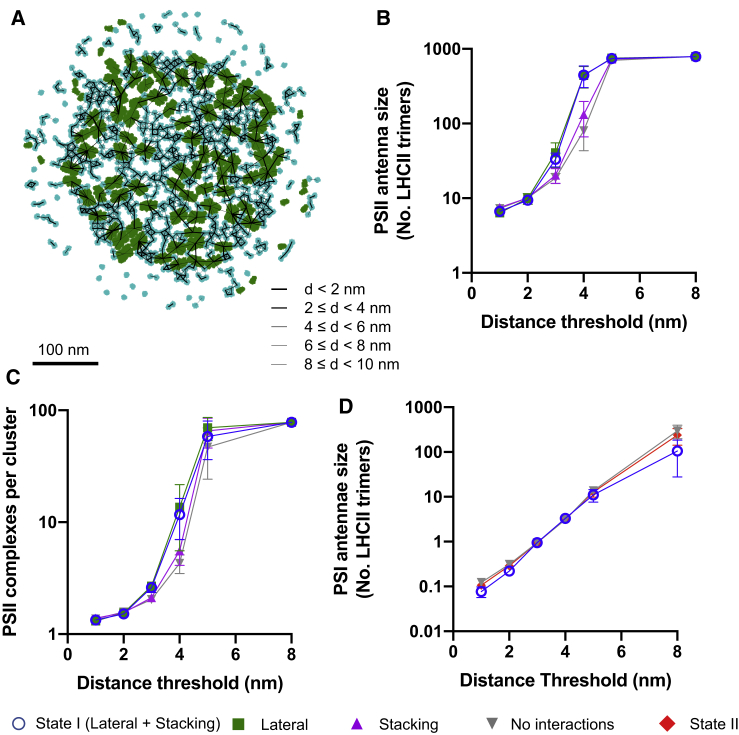
Questions naturally arise from the simulations outlined above as to how the increased density and clustering of LHCII in the grana in state I are implicated in the observed increase of antenna size and connectivity of PSII observed in vivo (33,70). We investigated the structure of the PSII-LHCII chlorophyll light harvesting antenna using a network-based topological analysis. The antenna network consisted of LHCII trimers connected to PSII reaction centers (Fig. 7 A), which collectively made up the vertices of the graph. Edges between neighboring LHCII trimers and/or PSII supercomplexes were introduced if there were chlorophylls in each complex close enough together. That is, the Euclidean distance was less than a given value called the distance threshold (Fig. 7 A; Fig. S4). Reaction centers were assumed to be connected to bound LHCII trimers within the same C₂S₂M₂ or C₂S₂ PSII-LHCII supercomplex. The quantitative properties of the antenna network are highly sensitive to the chosen distance threshold for this type of analysis. For this reason, we describe the phenomena observed for a range of distance thresholds and show that the qualitative conclusions drawn are independent of the distance threshold. We note that in reality, Förster resonance energy transfer is unlikely to happen over distances greater than 5 nm. First, for any given distance threshold, we found that the PSII and LHCII network was arranged in functional clusters, with a defined number of reaction centers and associated LHCII trimers akin to the heterogeneous photosynthetic unit model of Lavergne and Trissl (71). At low distance thresholds (<1 nm), one retrieves the average antenna properties of the C₂M₂S₂ and C₂S₂ supercomplexes (at equal stoichiometry), namely around three LHCII trimers and two reaction centers per cluster. With lateral and stacking interactions together or only lateral interactions, the size of the clusters was increased, leading to a larger antenna size (Fig. 7 B) and more PSIIs per cluster (Fig. 7 C). The increase in number of reaction centers per cluster is in agreement with the increase in PSII connectivity observed in state I by Kyle et al. (33). We found only a slight increase in the antennae size and the number of PSIIs per cluster when only stacking interactions were present (Fig. 7, B and C) compared to when no interactions were present. Using the same approach, we investigated the structure of the PSI-LHCII chlorophyll network (Fig. 7 D). We observed a slight increase in the network-based PSI antenna size (Fig. 7 D) in state II, and no interactions compared to state I. This can be seen to occur at low (<3 nm) and high (>5 nm) distance thresholds but not in the intermediate range.

Figure 7.

Analysis of changes in the structure of the chlorophyll light harvesting antennae network, resulting from lateral and stacking interactions. (A) Chlorophyll network are produced by simulations containing lateral and stacking interactions. PSII and LHCII complexes are shown in green and cyan, respectively. Black lines between the centers of any two complexes indicate that there exists a chlorophyll on one complex less than 10 nm from a chlorophyll on the other and are weighted by the distance (shorter distances (<2 nm) are shown by the thickest lines). (B) Shown is the number of LHCII complexes per PSII in the presence of lateral and stacking interactions (blue circles), lateral interactions only (green squares), stacking interactions only (magenta triangles), or no interactions (inverted gray triangles). (C) Shown is the number of PSII complexes per cluster resulting from simulations labeled in accordance with (B). (D) Shown is the number of LHCII complexes per PSI is state I (blue circles), state II (red diamonds), and no interactions (inverted gray triangles). Error bars indicate mean ± standard deviation. To see this figure in color, go online.

Discussion

STN7-dependent LHCII phosphorylation leads to structural changes in the thylakoid membrane in which grana diameter and the number of membrane layers per stack decreases, whereas the number of grana per chloroplast increases (23,31,44). This process is driven by an increase in the repulsive electrostatic force between LHCII trimers across the stromal gap of appressed grana membranes (14). In addition to STN7-dependent LHCII phosphorylation, state transitions require specific interactions between LHCII-P and the PsaL/H/O subunits of PSI, which lead to the formation of the PSI-LHCII supercomplex (34, 35, 36). In this study, we developed a molecular model of the thylakoid membrane as a basis for Monte Carlo simulations to investigate the role of lateral intermolecular interactions, changes in grana stacking forces, and specific PSI-LHCII interactions in modifying the distribution of photosynthetic complexes between the two domains and the relative antenna sizes of PSI and PSII during state transitions. The value of a theoretical model is the ability to clearly separate the effects of these three forces and understand the extent to which they likely cooperate to bring about the changes observed in vivo. Our results show three forces act largely separately to bring about specific facets of the structural changes observed in state transitions.

The first question we addressed was how the three forces affected the distribution of LHCII between the grana and stromal lamellae. Removal of the lateral and stacking interactions from our model increased the percentage of LHCII found in the stromal lamellae because of the lower density of complexes in this region. In contrast, altering the strength of the PSI-LHCII interaction did not cause dramatic changes in the amount of LHCII in the stromal lamellae (Fig. 4 B). This suggests that the two effects of LHCII phosphorylation, a disruption of the lateral and stacking interactions that sustain the grana and promotion of the interaction of LHCII-P with PSI, are independent phenomena. This finding is in line with experimental results that show that although mutants lacking the PsaL/O/H LHCII-P binding site on PSI lack state transitions, they still show a transition to smaller grana in state II indicative of a movement of LHCII from grana to stromal lamellae (31). The next question was how the number of PSI-LHCII supercomplexes formed was affected. As the specific PSI-LHCII interaction was increased from 0 to 16 K_BT, the number of PSI-LHCII supercomplexes increased to from 0 to 80%. In vivo 30–50% of PSI are found in PSI-LHCII supercomplexes (37,42,57). We therefore chose 3 K_BT, which resulted in 42% of PSI in complex with LHCII, as representative of state II in our simulations. Interestingly, the number of PSI-LHCII supercomplexes was not significantly higher, even if the protein density of the stromal lamellae was reduced by 50%, which increased the LHCII percentage in the stromal lamellae to 42%. The availability of LHCII in the stromal lamellae therefore does not limit the amount of PSI-LHCII supercomplexes that are formed in our model, and thus, a large-scale redistribution of LHCII between grana and stromal lamellae would appear unnecessary for achieving an increase in PSI antenna size, a finding consistent with previous studies (40,41). Indeed, even in state I, significant amounts of LHCII are found in the stromal lamellae, according to a range of biochemical data (23,37,40,42). Our model does not take into account PSI-LHCII complexes involving the weaker digitonin-sensitive LHCI binding sites (37,38), which may further augment PSI antenna size. The simplified geometry of our thylakoid model may lead to boundary effects. Most apparent is the exclusion of LHCII from PSI binding sites in the vicinity of the boundary at the outer edge of the stromal lamellae. Indeed, we find that the percentage of PSI-LHCII complexes decreases toward the outer edge with a difference of 12% from the inner to the outer edge of the stromal lamellae (Fig. S9). However, this difference is small compared to the difference between states I and II (Fig. 4 D) and therefore does not affect the conclusions drawn in this study.

In state I, we found that the cooperative effects of the lateral and stacking interactions led to a larger average PSII-LHCII cluster size and, moreover, more LHCII trimers per reaction center in each cluster. This was not due to a mere increase in the number of LHCII complexes in the grana, which only increased by 5%. Instead, it was due to the more efficient recruitment of free LHCII trimers in the grana into the functional PSII-LHCII clusters. A decrease in light harvesting capacity of PSII (antenna size and connectivity) when lateral and stacking interactions are removed (Fig. 7, B and C) has been observed in vivo (33). This effect has primarily been attributed to the mixing of PSII and PSI in destacked thylakoids and the consequent spillover of energy from PSII to PSI (32,72). Previous hypotheses have dismissed the idea that the role of grana is to prevent excitation energy spillover (73) on the basis that cyanobacteria lack grana yet are seemingly not largely afflicted by spillover. However, we have shown that lateral and stacking interactions may increase photosynthetic efficiency, even when strict separation of PSII and PSI is maintained. The findings presented here reopen this debate as they have shown that an evolutionary advantage of grana stacking could be an increased light harvesting efficiency of the PSII photosynthetic unit by more efficient recruitment of LHCII.

In conclusion, our model reveals that LHCII phosphorylation, that is the exchange of LHCII-LHCII and LHCII-PSII lateral and stacking interactions for specific PSI-LHCII interactions, affects the antenna structure of the two photosystems differently. Although the change in PSII is an emergent property of large-scale network structure, the change in PSI is modulated largely by individual LHCII binding events. This idea is consistent with the fact that PSII forms an interconnected photosynthetic unit (antenna lake), whereas PSI connectivity is much more limited (74).

Author Contributions

W.H.J.W. carried out the simulations. M.P.J. and W.H.J.W. co-wrote the manuscript.

Editor: Markus Deserno.