Abstract
Phase separation is thought to underlie spatial and temporal organization that is required for controlling biochemical reactions in cells. Multivalence of interaction motifs, also known as stickers, is a defining feature of proteins that drive phase separation. Intrinsically disordered proteins with stickers uniformly distributed along the linear sequence can serve as scaffold molecules that drive phase separation. The sequence-intrinsic contributions of disordered proteins to phase separation can be discerned by computing or measuring sequence-specific phase diagrams. These help to delineate the combinations of protein concentration and a suitable control parameter, such as temperature, that support phase separation. Here, we present an approach that combines detailed simulations with a numerical adaptation of an analytical Gaussian cluster theory to enable the calculation of sequence-specific phase diagrams. Our approach leverages the known equivalence between the driving forces for single-chain collapse in dilute solutions and the driving forces for phase separation in concentrated solutions. We demonstrate the application of the theory-aided computations through calculation of phase diagrams for a set of archetypal intrinsically disordered low-complexity domains. We also leverage theories to compute sequence-specific percolation lines and thereby provide a thermodynamic framework for hardening transitions that have been observed for many biomolecular condensates.
Significance
Intrinsically disordered proteins that have the requisite valence of adhesive linear motifs can drive phase separation and give rise to membraneless biomolecular condensates. Knowledge of how phase diagrams vary with amino acid sequence and changes to solution conditions is essential for understanding how proteins contribute to condensate assembly and dissolution. In this work, we introduce a new, to our knowledge, two-pronged computational approach to predict sequence-specific phase diagrams. This approach starts by extracting key parameters from simulations of single-chain coil-to-globule transitions. We use these parameters in our numerical implementation of the Gaussian cluster theory for polymer solutions to construct sequence-specific phase diagrams. The method is efficient and demonstrably accurate and should pave the way for high-throughput assessments of phase behavior.
Introduction
Intrinsically disordered proteins (IDPs) that have the requisite valence of adhesive linear motifs—stickers—can drive phase separation and give rise to membraneless biomolecular condensates (1, 2, 3, 4, 5). Knowledge of how phase diagrams vary with amino acid sequence and changes to solution conditions is an essential component of understanding how proteins contribute to condensate assembly and their regulated dissolution (1, 2, 3, 4,6). Comparative assessments of sequence-specific phase diagrams are also invaluable for enabling the design of novel disordered low-complexity domains (LCDs) that give rise to synthetic condensates for engineering applications (7, 8, 9, 10, 11, 12, 13). In this work, we introduce a two-pronged computational approach to predict sequence-specific phase diagrams that describe phase separation. We start by extracting key parameters from simulations of single-chain coil-to-globule transitions. We use these in our numerical implementation of the Gaussian cluster theory (GCT) for polymer solutions (14,15) to construct sequence-specific phase diagrams.
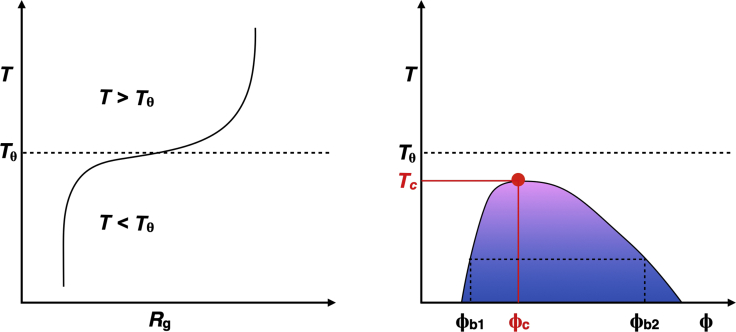
Our approach leverages the known equivalence between the driving forces for coil-to-globule transitions of individual polymer molecules in dilute solutions and phase separation that arises from collective interactions among polymer molecules in concentrated solutions (10,14, 15, 16, 17, 18, 19). For systems with an upper critical solution temperature (UCST) (Fig. 1), the coil-to-globule transition is characterized by indifferent solvent conditions at the θ temperature (Tθ), poor solvent conditions below Tθ, and good solvent conditions above Tθ (11). At finite concentrations, for T < Tθ, chains overlap with one another, and because of cohesive interactions among chain molecules, there exist temperature-dependent threshold volume fractions above which the system separates into two phases, namely a dilute solution that coexists with a dense phase. For a temperature T < Tθ, we denote the volume fractions of the coexisting dilute and dense phases as ϕb1 and ϕb2, respectively (Fig. 1). Although the dilute arm of the binodal, namely ϕb1 as a function of T, can be obtained via a range of experimentally tractable approaches, accurate estimates of the dense phase concentration—i.e., ϕb2 as a function of T—are plagued with several challenges. These include the need for high concentrations of protein, artifacts from fluorescent reporters, the impact of finite size effects, and slow equilibration within dense phases (7). As a result, despite their overarching importance for characterizing condensates, measurements of system-specific coexistence curves (binodals) are available for only a handful of LCDs (3,8, 9, 10,20).
Figure 1.
Equivalence between single-chain coil-to-globule transitions and phase separation. The schematic depicts expectations for a system that shows UCST behavior. Coil-to-globule transitions whereby coils form at temperatures above Tθ (dashed line) and globules form below Tθ. At Tθ, the radius of gyration scales as N0.5 with chain length N. There is a system-specific collapse temperature Tcollapse below which Rg ∼N0.33. The crossover regime, whose width is defined by the ratio of the two-/three-body interaction coefficient, corresponds to the interval Tcollapse < T < Tθ, where the scaling exponent for Rg lies between 0.33 and 0.5. Expected phase diagram for a flexible polymer that shows UCST behavior. The critical point defined by the critical temperature (Tc) and critical volume fraction (ϕc) is the point at which the binodal and spinodal coincide. The binodal is shown as the contour that delineates the two-phase regime (shown in colored shading, where the colors become cooler away from the critical point). For a given temperature T < Tθ and T < Tc, there exists a volume fraction above which the system separates into two coexisting phases, a dilute and dense phase characterized by volume fractions ϕb1(T) and ϕb2(T). The difference between ϕb1(T) and ϕb2(T) decreases as T approaches Tc. To see this figure in color, go online.
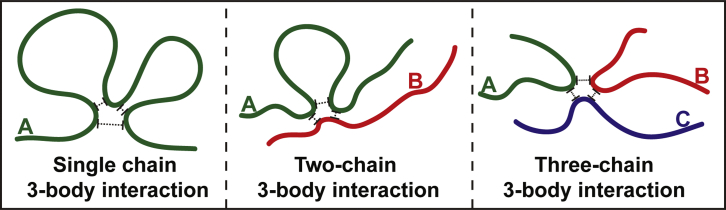
The driving forces for temperature-dependent coil-to-globule transitions and phase separation are governed by the three-way interplay among chain-chain, chain-solvent, and solvent-solvent interactions (16). The consequences of this three-way interplay are captured via an effective two-body interaction coefficient B, which has units of inverse volume. The value of B is positive below Tθ for a system with UCST behavior and negative for a system above Tθ for a system with a lower critical solution temperature (LCST). These features of B signify net attractions among monomer units below Tθ for a UCST system and above Tθ for a LCST system. The three-body interaction coefficient w (Fig. 2) is always positive, and to first approximation, it is taken to be independent of temperature (16); the magnitude of w is determined, in part, by the local persistence length or thickness of the chain. The steepness of coil-to-globule transitions and the temperature-dependent values of ϕdense are governed by the ratio of the two-/three-body coefficient (14,15).
Figure 2.
Depicting how three-body interactions are realized. Three-body interactions are realizable in at least three different ways: within a single polymer (left), between pairs of polymers (middle), or among three polymers (right). The interactions are always repulsive, and this derives from the finite thickness and steric impenetrability of polymers. To see this figure in color, go online.
Disordered LCDs (as well as folded domains) can be mapped onto “stickers-and-spacers” architectures (10,21, 22, 23, 24, 25). Stickers are attractive groups (26,27) that include short linear motifs or individual residues that form reversible physical (noncovalent) cross-links with one another; conversely, the excluded volumes of spacers control the extent of compaction of individual chains and the cooperativity of phase transitions that give rise to two coexisting phases (25). Recent studies have shown that the correspondence between coil-to-globule transitions and phase separation, which is well established for flexible homopolymers, is also applicable for describing the phase behavior of disordered LCDs (18,28). For this correspondence to apply, the stickers have to be uniformly distributed along the linear sequence (10). Intriguingly, a significant fraction of naturally occurring disordered LCDs, specifically prion-like domains, and designed sequences have the requisite sequence features that should enable correspondence between the driving forces that control coil-to-globule transitions and phase separation (9, 10, 11,29, 30, 31, 32).
We reasoned that it should be possible to compute complete phase diagrams using quantitative analysis of sequence-specific coil-to-globule transitions in conjunction with a requisite theoretical framework that directly connects coil-to-globule transitions to phase separation. Accordingly, we deployed a two-pronged strategy for calculating sequence-specific phase diagrams of disordered LCDs. First, all-atom or coarse-grained simulations are used to obtain temperature-dependent profiles for coil-to-globule transitions, and the results are analyzed to extract Tθ, B, and w. Next, these parameters are used in our numerical adaptation of the GCT for polymer solutions (14,15) to construct full phase diagrams in the two-parameter (ϕ,T) space.
The GCT was developed for generic homopolymers, each comprising N monomers connected by N − 1 bonds of length l0. The distributions of intramolecular and intermolecular distances are described in terms of distances between statistical Kuhn segments instead of monomers. At their specific theta temperatures, any homopolymer can be reduced to a freely jointed chain of Kuhn segments, where the latter refers to the length scale beyond which the chemical details of the repeating units can be ignored (33). If ns is the number of bonds per Kuhn segment, then the number of Kuhn segments is defined as nK = (N − 1)/ns and the mean-square length of each Kuhn segment is written as , where C∞ is the characteristic ratio of the chain (33). The GCT assumes Gaussian forms for the distributions of intrachain and interchain distances between Kuhn segments (14,15). The main parameters of the Gaussian distributions are Tθ, B(T), and w. Mean-field free energies, written in terms of moments of the Gaussian distributions, describe the temperature dependence of intrachain and interchain interactions. Minimization of the sum of single- and multichain free energies allows us to extract temperature-dependent values of and , respectively. The locus of these temperature-dependent values defines the coexistence curve, or “binodal”; likewise, the locus of points at which the second derivative of the sum of single- and multichain free energies is zero helps define the instability curve, or “spinodal.” In this way, we can compute system-specific full phase diagrams by minimization of the overall free energy for a polymer solution based on parameters obtained from single-chain coil-to-globule transitions.
The remainder of the manuscript is organized as follows: first, we summarize the main tenets of the GCT. Next, we detail how simulations of coil-to-globule transitions of individual LCDs are used to extract parameters for use in the GCT and demonstrate how we use our numerical implementation of the GCT to compute sequence-specific, temperature-dependent binodals and spinodals. We then illustrate the accuracy of our two-pronged approach by computing phase diagrams for LCDs in which temperature-dependent binodals have been measured. We further illustrate the methodology by computing full phase diagrams for distinct synthetic systems that have UCSTs and LCSTs, respectively. In doing so, we compare the calculated binodals with recent experimental measurements of binodals for the A1-LCD system and designed variants of this sequence (10). We conclude with a discussion of how the GCT-aided two-pronged method might be useful for high-throughput characterizations of phase diagrams of disordered LCDs.
Materials and Methods
Systems of interest
We demonstrate the application of GCT-aided calculation of phase diagrams using simulations of coil-to-globule transitions for a series of systems. We start with the 137-residue LCD from the hnRNP-A1 protein (34). Recently, Martin et al. (10) characterized the phase behavior of this system and three designed variants that differ from the wild-type (WT) sequence in terms of the number (valence) of aromatic stickers. The sequences of interest are referred to as WT-A1; Aro+, which was designed to have higher valence of aromatic residues than WT-A1; and Aro− and Aro− −, which have lower numbers of aromatic stickers than the WT (10). For these systems, we use coarse-grained simulations of coil-to-globule transitions that are based on PIMMS (10,35), which is a lattice-based simulation engine.
Polyglutamine (polyQ) expansions are associated with Huntington’s disease and at least eight other neurodegenerative disorders (36). Considerable effort has focused on characterizing the conformational equilibria of individual polyQ chains and the phase equilibria of these systems (19,37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52). Homopolymers of polyQ forms globules in aqueous solvents; additionally, experiments and simulations point to UCST phase behavior for polyQ (37,45,52,53). Evidence has also been presented for the prospect of disordered, oligomeric or liquid-like phases serving as precursors of fibril formation (37,38,52,54,55). Here, we use the ABSINTH implicit solvation model (56) to perform all-atom simulations of coil-to-globule transitions. We use these simulations to demonstrate how the GCT can be used to construct phase diagrams for a biologically relevant system of homopolypeptides.
Finally, systems that undergo thermoresponsive phase behavior are of considerable interest for the design of biomaterials (9,29, 30, 31). As the third set of systems, we demonstrate the applicability of the two-pronged approach for constructing temperature-dependent phase diagrams of two systems, viz. (QGQSPYG)9 and (TPKAMAP)9. These synthetic systems are designed to have UCST and LCST behaviors, respectively.
Coarse-grained and all-atom simulations of coil-to-globule transitions
PIMMS is a lattice-based simulation engine that uses a single bead per amino acid residue (10,35). Simulations of coil-to-globule transitions of WT-A1, Aro+, Aro−, and Aro− − were performed using a stickers-and-spacers representation of these sequences. Here, aromatic residues are stickers, and all other residues are spacers. In our model, we set kB = 1 and T is in the interval 30 ≤ T ≤ 60. Martin et al. (10) showed that sticker-sticker energies of −14, sticker-spacer energies of −5, and spacer-spacer energies of −2 provide a minimalist model that reproduces the variation of Rg with sticker valence in dilute solutions and experimentally measured binodals in the space of ϕ and T, with suitable conversions between the reduced temperature units and Kelvin (10). In this work, we use results from PIMMS simulations as the touchstone for comparative assessments of GCT-derived phase diagrams, and we use unitless, reduced temperatures, setting kBT = 1 for comparative calculations on the four systems, WT-A1, Aro+, Aro−, and Aro2−.
The all-atom simulations for polyQ sequences denoted as Qn (n = 20, 30, 40, 50, 60, 70) and the two sequences (QGQSPYG)9 and (TPKAMAP)9 were performed using version 2.0 of the CAMPARI modeling suite (http://campari.sourceforge.net/). The N- and C-termini are capped using N-acetyl and N′-methylamide groups, respectively. All simulations use the ABSINTH implicit solvent model and force field paradigm. The parameters were derived based on the OPLS-AA/L force field, and all the parameters are implemented in the abs_3.2_opls.prm parameter set. Parameters for proline residues were based on the work of Radhakrishnan et al. (57). The cutoff for the short-range Lennard-Jones potential is set to be 10 Å. The cutoff for electrostatic interactions between different sites on neutral groups is 14 Å. There are no cutoffs among charge groups that carry a net charge, and these pertain to solution ions as well as charge groups on the side chains. In systems with charged residues, specifically (TPKAMAP)9, nine Cl− ions, modeled using the parameters developed by Mao and Pappu (58), were included to ensure electroneutrality. In addition, ion pairs were included to mimic an excess NaCl concentration of 1 mM. For the temperature dependence of macroscopic dielectric constant of water, we use the form adapted by Wuttke et al. (59).
ABSINTH uses experimentally derived reference free energies of solvation for model compounds (56,60). The reference free energies of solvation have weak temperature dependencies for polar compounds. Accordingly, we use the reference values at 298 K for the model compounds that mimic side chains of Gln, Ser, Gly, Pro, and Tyr. However, to model LCST behavior for (TPKAMAP)9, we adapt the generalization introduced by Wuttke et al. (59). Specifically, we set the reference free energies of solvation for the backbone amide and the model compounds that mimic the side chains to be temperature dependent. The parameters for the enthalpy and heat capacity that are used in the Gibbs-Helmholtz equation to estimate temperature-dependent free energies of solvation are summarized in Table S1.
Standard Metropolis Monte Carlo (MMC) simulations aided by thermal replica exchange (61) were used to sample conformations of polyQ systems and the two synthetic sequences. Move sets for MMC simulations include side-chain torsions, concerted rotations, pivot moves, translations of ions, and translations and rotations of individual molecules (10,57,60,62). Details regarding the number of replicas and the temperature schedule for each system are listed in Table S2. Swaps between neighboring replicas were proposed once every 5 × 104 MMC simulation steps. Simulations were initiated using a randomly generated self-avoiding conformation for each polypeptide. All simulations use a spherical droplet, and the droplet is large enough to ensure against confinement artifacts. Multiple independent replica exchange simulations were performed—three for (TPKAMAP)9 and four for the other systems—and each independent replica exchange simulation comprises a total of 6 × 107 MMC simulation steps.
Theory
GCT for a single chain
The workflow for constructing full phase diagrams using simulations of single-chain coil-to-globule transitions and the use of GCT based on parameters extracted from the single-chain simulations is summarized in Fig. 3. We first connect the GCT formalism to results from single-chain simulations and show how this connection allows us to estimate Tθ, the two-body interaction coefficient B, and the three-body interaction coefficient w. The GCT prescribes specific forms for the distribution of intrachain and interchain distances between chain segments (14,15). The segments of interest are Kuhn segments. Formally, a real chain of N residues can be reduced to an effective freely jointed chain of nK Kuhn segments. For polypeptides, the length of a Kuhn segment can be calculated using l0 = 3.8 Å as the length of a virtual bond between adjacent α-carbon atoms for all-atom simulations and l0 = 1 lattice unit for PIMMS simulations. We set nK to be five for polyQ and the WT-A1 system as well as variants of this system. This choice is a robust estimate for systems that have the local flexibility of generic polypeptides, which refers to systems in which proline residues make up less than 10% of the sequence (63). For the synthetic systems, we set nK to be 7, which is identical to the number of residues within each repeat. Systematic calibrations showed that the calculated phase diagrams are insensitive to the choice made for nK.
Figure 3.
Workflow summarizing the overall two-pronged approach that leverages the GCT formalism. We use the prescribed approach to connect results from single-chain simulations of coil-to-globule transitions to calculations of phase diagrams using the GCT.
The GCT assumes a Gaussian form for ρ(r), the distribution of intersegment distances within a single chain (14,15), which is written as
| (1) |
Here, is the ensemble-averaged value of the mean-square radius of gyration for a single chain. To simplify the algebra, the theory introduces three parameters, viz. the reduced temperature τ, the parameter σ that quantifies the standard deviation of the Gaussian distribution for ρ(r), and the contraction ratio αs:
| (2) |
| (3) |
and
| (4) |
Notice that τ < 0 for T < Tθ. Allegra and Ganazzoli (64) showed that the strain ratio for low wavenumbers (k) in Fourier space, which translates to large separations r in real space, can be defined as αk = . Accordingly, the strain ratio in Fourier space and the contraction ratio in real space depend on a single auxiliary parameter q, known as the compression parameter (14,15). Here, q tends to zero as T approaches Tθ, whereas q approaches ∞ in the nonphysical limit at which the chain is compressed down to a single point. Based on the relationship between ρ(r) and its Fourier transform, which is also a Gaussian distribution in k-space, we rewrite ρ(r) and r in terms of q; moments such as can be evaluated in terms of q. Allegra and co-workers have shown that (64,65)
| (5) |
here, L(q) is the Langevin function L(q) = (33). From Eqs. 3, 4, and 5, it follows that σ, Rg = , and the contraction ratio αs are functions of q.
The mean-field free energy A1(q; τ) of a single chain at a relative temperature τ is written in terms of the compression parameter q. Given that q is a continuous parameter that quantifies the dependence of chain dimensions on T, we have an analytical route to relate the temperature-dependent chain dimensions to the free energy of the chain. At equilibrium, the free energy of a single chain is minimized by setting .The desired free energy A1(q; τ) is a sum of the effects of intrachain interactions Aintra(q; τ) and the elastic term Ael(q) that quantifies contributions of conformational entropy. Accordingly,
| (6) |
At equilibrium, the free energy (see Appendix) of a single chain at fixed τ is minimized by setting = 0. This yields a relationship between τ and the compression parameter q, which allows us to estimate q by solving the transcendental equation below:
| (7) |
Extraction of Tθ, B, and w by comparing GCT to results from single-chain simulations
Equation 7 provides the central connection between simulations of coil-to-globule transitions and parameters of the GCT. The protocol for its usage is as follows:
-
1)
Coarse-grained or all-atom simulations are used to extract the system-specific profile for as a function of simulation temperature T. This information is converted into a profile for the contraction ratio αs vs. T using Eqs. 3 and 4. Additionally, for a given temperature, we extract internal scaling profiles, which plot vs. |j − i|. Here, refers to ensemble-averaged mean distance between all pairs of residues i and j that are |j − i| apart along the linear sequence.
-
2)
If the system of interest is a perfect homopolymer or can be reduced to a perfect homopolymer, then simulations of coil-to-globule transitions are performed for a series of chain lengths or numbers of repeats. In this scenario, Tθ is estimated as the intercept along the temperature axis at which plots of vs. T intersect with one another. This is reflective of the tricritical nature of the θ-point (14,15,66,67). Alternatively, given temperature-dependent profiles for plot vs. |j − i|, we identify Tθ as the temperature for which = R0|j − i|0.5 (68).
-
3)
Next, we fit a smooth curve to the profile of αs vs. T. From this profile, we estimate T∗, defined as the temperature at which . Here, is the minimal value of the contraction ratio from the simulations. For the UCST system, is the contraction ratio at the lowest sampled temperature. For the LCST system, it is the value of the contraction ratio at the highest sampled temperature.
-
4)
From the GCT, it follows that the transition temperature has to satisfy . Accordingly, given prior knowledge of Tθ and T∗, we can estimate the value of B. Raos and Allegra have shown that a ≈ −0.35 for generic homopolymers (14). We use this to set bounds on the value of a and develop a numerical procedure (Fig. S1) to estimate T∗.
-
5)
The relationship in Eq. 7 is used to rewrite the compression parameter q as a function of τ. This, in conjunction with the definitions introduced in Eqs. 3 and 4, leads to numerical profiles for the contraction ratio as a function of .
-
6)
We then estimate w using a parameter scan in which the constraint is the requirement that the theoretical profile for the contraction ratio versus be coincident with the profile derived from the single-chain simulations.
In practice, we identify a putative transition region for the location of T∗, choose different values of T∗ in this region, and simultaneously choose values for B and w using the bounds based on the constraint prescribed in step 4. We then identify the combination that minimizes the difference between the simulated contraction ratio and the one calculated using Eq. 7 from the GCT. We have developed two distinct approaches for estimating B and w, and these approaches are described in the pseudocode shown in Fig. S1. It helps to have roughly 10 distinct temperatures that span the transition region and the region where the contraction ratio plateaus as the chain forms a globule. A detailed sensitivity analysis for choosing parameters from simulations of coil-to-globule transition profiles is presented in the Supporting Materials and Methods.
GCT for phase separation used to calculate full phase diagrams
The GCT assumes that in a cluster comprising ν distinct polymers, the distribution of distances for polymer i vis-à-vis all other polymers is a Gaussian of the form (14,15)
| (8) |
In Eq. 8, Ri and Rj denote the centers-of-mass of polymers i and j; the parameter is related to the ensemble-averaged mean-square distance between chains, , in a cluster of ν distinct molecules. As with the single-chain case, the GCT introduces a few key variables. These are defined in terms of , the ensemble-averaged mean-square radius of gyration of a single chain within a cluster of ν molecules; , the ensemble-averaged mean-square radius of gyration of a cluster of ν molecules; and αs,ν, the contraction ratio of a single chain within the cluster. Accordingly,
| (9) |
For a given value of τ, the free energy Aν of a cluster of ν molecules, with as the ensemble-averaged mean-square distance between chains in the cluster and q as the value of the compression parameter for a single chain, is the sum of three terms:
| (10) |
The contact free energy Ainter,ν combines contributions from two- and three-body contacts among chain segments. Following the derivation shown in the Appendix, for specific values of ϕ and τ, there should be a single value of q that minimizes the system free energy. This is estimated from a generalization of the expression in Eq. 7, now rewritten for a single chain in a polymer solution as
| (11) |
To compute the phase diagram, we need an expression for the chemical potential μP of the polymer as a function of values of ϕ. The chemical potential is the partial derivative of avol with respect to the number of polymer molecules; here, avol denotes the free energy per unit volume in the polymer solution (see Appendix). The chemical potential takes the form
| (12) |
For fixed values of τ, B, and w, the chemical potential is a function of the compression parameter q and the volume fraction ϕ. Because there is a one-to-one numerical mapping between q and ϕ, it follows that we can calculate μP for different values of ϕ given prior knowledge of the two- and three-body interaction coefficients B and w, respectively.
Calculation of full phase diagrams
The mapping between q and ϕ is extracted numerically from Eq. 11. For this mapping we use values of B and w derived from the analysis of single-chain coil-to-globule transitions. Next, for fixed τ, we calculate the locations of spinodals by computing the values of ϕ that are solutions of the equation = 0. This yields two solutions, viz. ϕs1(τ) and ϕs2(τ). Next, to generate the coexistence curve, we compute the locations of coexisting dilute and dense phases, viz. ϕb1(τ) and ϕb2(τ). For fixed τ, the two coexisting phases represent points for which the chemical potential (μP) and osmotic (Π) pressure are equalized along the horizontal tie line that connects the points ϕb1 and ϕb2. Accordingly, it follows that
| (13) |
The osmotic pressure is calculated using the expression
| (14) |
Here, and . For fixed τ, B, and w, we use the expressions in Eqs. 12, 13, and 14 and numerically identify the points ϕb1 and ϕb2 that lie on the same tie line. The locus of points ϕb1(τ) and ϕb2(τ) obtained for different values of τ yield the desired binodal in the (ϕ,τ) or (ϕ,T) plane.
Results
We demonstrate the application of the two-pronged approach wherein we obtain system-specific parameters from coarse-grained or all-atom simulations of coil-to-globule transitions of individual chains and incorporate them into the GCT to obtain full phase diagrams. Here, full phase diagrams refer to system-specific binodals and spinodals that are calculated and shown in the two-parameter space with volume fraction ϕ along the abscissa and simulation temperature T along the ordinate. Note that T is unitless for phase diagrams computed using PIMMS because it is written in terms of reduced temperatures used by Martin et al.(10). For phase diagrams computed using all-atom simulations, the temperature is in units of degree-Kelvin.
Phase diagrams for Aro+, WT-A1, Aro−, and Aro2− variants
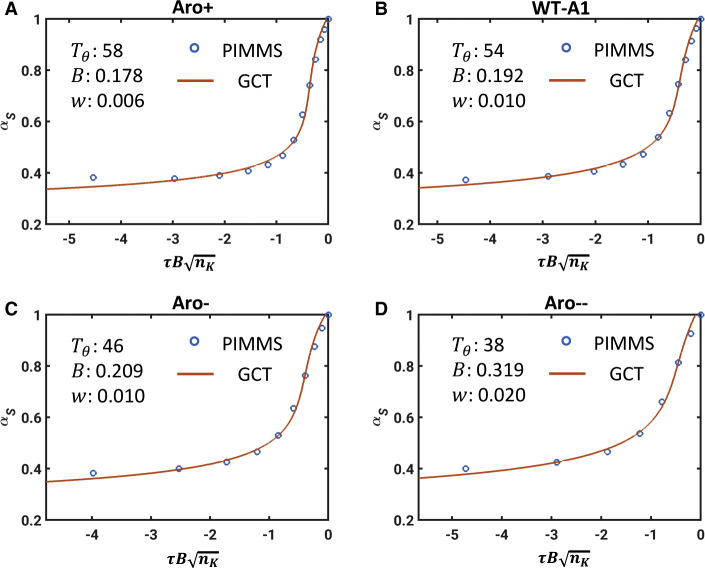
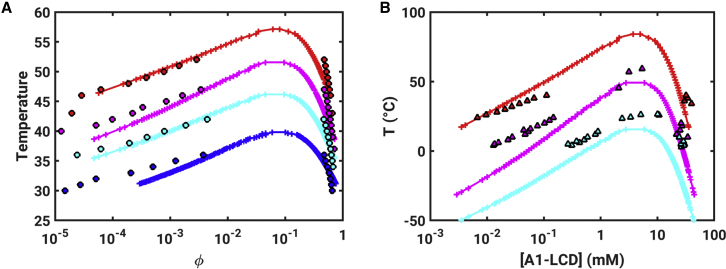
First, we extract the theta temperature by analyzing the internal scaling profiles obtained from PIMMS simulations of coil-to-globule transitions for each of the four systems. This analysis is summarized in Fig. S2. Additionally, Fig. S3 shows plots of as a function of τ for each of the four constructs. The system-specific estimates for Tθ are summarized in each of the panels of Fig. 4. Each panel in Fig. 4 also shows a system-specific profile for the contraction ratio plotted as a function of . Fig. 5 A shows a comparison between binodals obtained using GCT and those obtained directly from PIMMS simulations. Fig. 5 B shows a direct comparison between the experimentally measured binodals and those calculated using our two-pronged approach. To facilitate this comparison, we used the approach of Martin et al. (10) and converted the reduced temperature to Kelvin using T = 6.25TPIMMS; concentrations in molar units were computed using c = ρϕ, where ϕ is the mole fraction to be converted into molar units and ρ = 61.869 mM. The results are shown in Fig. 5 B. They indicate that the binodals obtained using GCT, based on the parameters extracted from single-chain simulations, are in good agreement with binodals obtained from direct simulation of phase separation using PIMMS and with experimentally measured binodals. The critical temperature, as well as the width of the two-phase regimes, decreases with decreasing sticker valence, and these trends are accurately captured by the GCT-derived binodals.
Figure 4.
Profiles of contraction ratios for Aro+, WT-A1, Aro−, and Aro2−. In each panel, the blue circles are results from PIMMS simulations of single chains, and the red curves are contraction ratios obtained using Eq. 9 that best fit the simulation results. The best-fit, system-specific parameters for Tθ, B, and w are shown as legends in each of the four panels. B has units of inverse volume, and w has units of the square of the inverse volume. To see this figure in color, go online.
Figure 5.
Comparison of binodals obtained using direct simulations based on PIMMS and numerical implementation of the GCT formalism that uses parameters extracted from single-chain simulations. (A) The PIMMS results are shown as circles, and the results using GCT are shown as + marks. Here, the binodals for the different systems are shown using symbols of different colors: red (Aro+), magenta (WT-A1), cyan (Aro−), and blue (Aro− −). The binodals obtained using GCT were shifted upward along the ordinate by 10.5 units and along the abscissa by −0.3 units to bring them onto the same scale as the PIMMS-derived binodals. (B) A comparison of binodals calculated using GCT to the three binodals measured experimentally by Martin et al. (10). The coexisting concentrations obtained from experiments (in molar units) are shown as triangles (red for Aro+, magenta for WT-A1, and cyan for Aro−). The GCT-derived values are shown using the + symbol, and lines join these symbols as guides to the eye. To see this figure in color, go online.
Direct simulations of phase separation enable the extraction of sequence- or architecture-specific phase diagrams (10,18,22,28). However, identifying the critical point is challenging because the amplitudes of conformational fluctuations become commensurate with chain dimensions as T approaches Tc. Similarly, as ϕ approaches ϕc, the amplitudes of concentration fluctuations become equivalent or even larger than the simulation volume. It is also challenging to estimate the low- and high-concentration arms of spinodals because this requires direct observation of the onset of instabilities. These challenges are readily overcome in the GCT-aided calculation of phase diagrams.
Details regarding the width of the metastable region and its dependence on T are direct determinants of the mechanisms of phase separation (16). For a given T < Tc, if ϕ0(T) is the initial value of ϕ and ϕb1(T) < ϕ0(T) < ϕs1(T), then the system is in the metastable regime. The rate of nucleation of phase separation from an initial homogeneous one-phase state will be governed by two parameters, viz. , which is a measure of the width of the two-phase regime, and , which is a measure of the supersaturation (69). An analogous relationship exists for the initial conditions ϕs2(T) < ϕ0(T) < ϕb2(T), in which the starting conditions are in the high-concentration metastable regime. For simplicity, we will focus here on the low-concentration metastable regime because this is the most relevant scenario for biological systems. If ϕs1(T) < ϕ0(T) < ϕs2(T), then the dynamics of phase separation follow spinodal decomposition (16,70). The dynamics of phase separation, given a prior functional for the free energy of a solution, can be modeled using the Cahn-Hilliard formalism (71). The quench depth relative to the binodal and spinodal directly determines the dynamics of phase separation. Knowledge of the quench depth helps one discern whether the dynamics can be modeled using a Cahn-Hilliard formalism (72,73) or whether advances in chemical-kinetics-approaches-based modernizations of nucleation theories (74,75) can be brought to bear on modeling the dynamics of phase separation.
Calculations of full phase diagrams should aid in the assessment of comparative dynamics for similar quench depths across different systems and for different quench depths of the same system. Fig. 6, A–D show the GCT-derived binodals and spinodals for WT-A1. For this analysis, we define τc = (T − Tc)/Tc, where Tc is the system-specific critical temperature. The predicted spinodal is manifest only for larger volume fractions (ϕ > 10−2), which would correspond to initial concentrations that are in the millimolar range for WT-A1. Accordingly, concentrations corresponding to initial conditions in typical in vitro experiments are likely to lie between the binodal and spinodal thereby implicating nucleation as the dominant mechanism for phase separation. Further, the low endogenous concentrations that one expects in vivo are also likely to correspond to the metastable regime. The sizable gap between the binodal and the spinodal that we report for each of the four constructs (Fig. 6) implicates primary, secondary, and possibly heterogeneous nucleation as the dominant mechanisms for phase separation in vivo (55,74, 75, 76). The width of the metastable region determines the interplay between nucleation-dependent phase separation and spinodal decomposition (14,15,65). Accordingly, clusters that form in the metastable regime are likely to be key contributors to nucleating the growth of dense phases (15). Indeed, super-resolution methods have made headway in identifying such clusters as signatures of first-order phase transitions in vivo (77).
Figure 6.
Assessments of binodals, spinodals, and percolation lines for the WT-A1 and three designed variants. To see this figure in color, go online.
Fig. S4 shows that the gap between the low arms of the spinodal and binodal, which we can compute as Δϕm = [ϕs1(T) − ϕb1(T)], varies with (Tc − T) for Aro+, WT-A1, Aro−, and Aro− −, respectively. This width approaches zero as T approaches Tc. In general, for (Tc − T) > 2, Δϕm is on the order of 10−2, and for a given value of T, Δϕm is smallest for Aro+ and largest for Aro2−. Additionally, Δϕm varies most steeply with (Tc − T) for Aro− −, followed by Aro−, WT-A1, and Aro+, respectively. These results indicate that the width of the metastability region decreases and shows a weaker dependence on temperature as the system becomes a stronger driver of phase separation.
Connecting phase diagrams to hardening transitions of LCDs
Condensates formed by LCDs undergo “hardening transitions” as a function of time (6,21,78,79). This refers to the development of irregular morphologies, drastic slowing of the exchange of molecules between condensates and their surroundings, and increased inability of condensates to fuse and grow. Heteropolymers with stickers-and-spacers architectures also undergo a networking transition known as “percolation” that is enabled by noncovalent (physical) cross-links among stickers. Percolation is essentially gelation, and it occurs above a system-specific concentration known as the percolation threshold that is designated as ϕperc (22). Above ϕperc, the collection of multivalent macromolecules in solution form a system-spanning network; if ϕsat < ϕperc < ϕdense, then multivalent macromolecules will undergo “phase-separation-aided percolation” (25). Systems that conform to stickers-and-spacers architectures undergo phase-separation-aided percolation. Accordingly, dense phases are condensate-spanning networks characterized by intracondensate cross-links among stickers that are aided by features of spacers.
In the physical literature, hardening represents the formation of dynamically arrested phases that arise because of the coupling between phase separation and percolation (80). At a given temperature, the likelihood that a condensate will undergo a hardening transition will be governed by the magnitude of the gap between the percolation line and the high-concentration arm of the binodal, which we quantify in terms of the difference between ϕdense and ϕperc and designate as ϕgap. Large values of ϕgap lead to increased chances of forming randomly networked assemblies because of physical cross-links among stickers of polymers that overlap with one another in dense phases. Large values of ϕgap also imply that the cross-links are significantly stronger than kBT, and this leads to long-lived cross-links that cause dynamical arrest and irregular morphologies. These features were illustrated in recent results obtained by Boeynaems et al. (35), who demonstrated dynamically arrested phase separation in a model protein-RNA system (35). Irregular, void-rich condensates that do not rearrange rapidly or fuse with one another are signatures of dynamical arrest. The timescales associated with the making and breaking of physical cross-links are governed by the free energy barrier for bond dissociation. This and the extent of cross-linking, both of which contribute to ϕgap, are the causes of dynamical arrest.
Building on the calculations of sequence-specific binodals and spinodals we also estimated the percolation line, i.e., ϕperc as a function of temperature. For this, we used a recent generalization (23,24) of the mean-field theory developed by Semenov and Rubinstein (27). Specifically, we set ϕperc(T; τ) = −1, where na is the number of aromatic stickers and λ(T; τ) = −Bτ is a simple estimate for the temperature dependence of the intersticker interaction strengths. The A1-LCD has 19 aromatic stickers. In the designed variants, the valence of aromatic stickers is either increased (to 24 in Aro+) or decreased (to 13 in Aro− and 6 in Aro− −) (10). The calculated, system-specific percolation lines are overlaid on the binodals for the WT A1-LCD and three designed variants as shown in each of the panels in Fig. 6.
We plotted ϕgap vs. τc to compare the likelihoods of hardening transitions across different systems (Fig. 7). This enables comparisons across different sequences with different critical points. Note that only large positive ϕgap-values are relevant for the dynamical arrest of condensates. We find that ϕgap decreases as τc approaches zero, which happens as the temperature approaches the critical point (Fig. 7); for fixed τc, the value of ϕgap is larger for Aro+, followed by WT, Aro−, and Aro− −, respectively. This implies that stronger driving forces for phase separation, which in this case are governed by the increased valence of stickers, also lead to larger gaps between the percolation lines and the high-concentration arms of binodals. Therefore, at identical values of τc, it follows that sequences encoding stronger driving forces for phase separation will also have larger values of ϕgap, and such sequences are likely to be more susceptible to hardening transitions.
Figure 7.
ϕgap vs. τc for each of WT-A1 LCD and the three designed variants. To see this figure in color, go online.
Phase diagrams for polyQ and synthetic IDPs
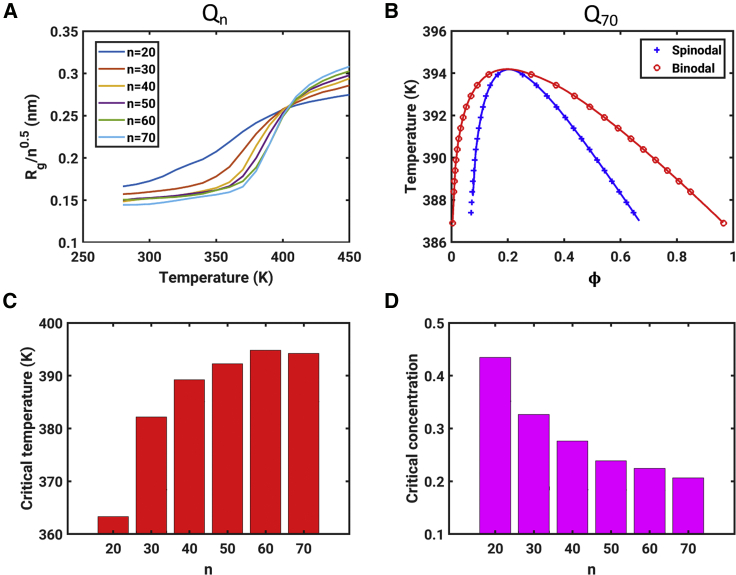
The results shown in Fig. 5 illustrate the accuracy of the GCT-derived binodals as compared to binodals obtained using PIMMS for four closely related systems. Next, we computed full phase diagrams using parameters extracted from all-atom simulations that were based on the ABSINTH implicit solvation model. We present results for three separate systems, viz. polyQ and two synthetic IDPs, one with UCST behavior and another showing LCST behavior. The results for the polyQ system are shown in Fig. 8.
Figure 8.
Results for the polyQ system. (A) Normalized Rg for different chain lengths as a function of simulation temperature T. The θ temperature (Tθ ≈ 405 K) corresponds to the point at which the curves coincide with one another. Note that previous simulations based on the ABSINTH model estimated a value of 390 K for the Tθ of polyQ (44,60). The discrepancy between published and current estimates comes from our current usage of a temperature-dependent functional form for the macroscopic dielectric constant of water (59). (B) Full phase diagrams for the Q70 system. The binodal and spinodal coincide at the critical point. The smooth red and blue curves join the dots along the binodal and spinodal, respectively, and they are used to guide the eye. (C) A bar plot showing the increase of the critical temperature (Tc) with polyQ length. (D) A bar plot showing the decrease of the critical volume fraction (ϕc) with increasing polyQ length. To see this figure in color, go online.
Crick et al. previously measured the temperature dependence of the solubility limit for different constructs with polyQ tracts (37). The measured saturation concentrations, which are in the low micromolar range, decrease to be in the submicromolar range for longer polyQ molecules. These measured concentrations translate to volume fractions that are ∼10−5 and are what we obtain for the low arms of binodals (Fig. 8). Further, Crick et al. showed that polyQ has UCST behavior with a critical temperature that is above the boiling point of water—a feature that is recapitulated by the simulations and the GCT-aided calculations. Simulation results, summarized in Fig. 8 A, were used to identify the theta temperature for this system. Here, Tθ ≈ 405 K. Fig. 8 B shows the full phase diagrams, including binodals and spinodals for phase separation. These data are shown for the Q70 system. Fig. 8, C and D show that the critical temperature (Tc) increases with increasing polyQ length, whereas the critical volume fraction (ϕc) decreases with increasing polyQ length. This is in accord with general trends expected from mean-field theories for the phase separation of homopolymers (16).
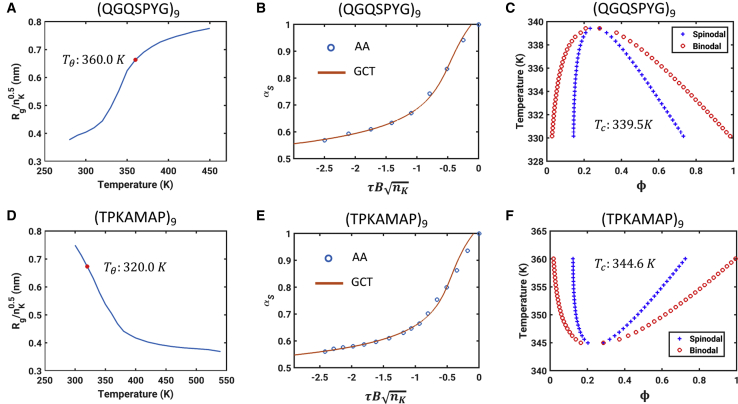
Finally, Fig. 9 summarizes results obtained for the two synthetic IDPs with UCST and LCST behavior. Recent attention has focused on IDPs derived from resilin- and elastin-like polypeptides that are designed to have UCST versus LCST behavior, respectively (31,81). We show results for two archetypal systems. The θ temperatures for these systems were estimated by analyzing the temperature-dependent internal scaling profiles. Fig. 9, A–C, respectively, show the profile of the normalized Rg plotted as a function of simulation temperature, the contraction ratio as a function of , and the resultant phase diagram for the (QGQSPYG)9 system that shows UCST behavior. Fig. 9, D–F show the corresponding results for the (TPKAMAP)9 system that has LCST phase behavior. Systems that are perfect repeats of specific peptide sequences may be thought of as homopolymers on length scales that are longer than one repeat. Accordingly, these systems are amenable to a joint computational approach that combines simulations of single chains with GCT to extract computed phase diagrams. The results demonstrate that the GCT is applicable for calculating phase diagrams of systems with LCST behavior. All that is required is that simulations at the single-chain level demonstrate a collapse transition at higher temperatures, which we observe for the (TPKAMAP)9 system if we use temperature-dependent reference free energies of solvation as prescribed by Wuttke et al. (59); see Fig. 8 D.
Figure 9.
Results for synthetic systems that show UCST behavior (top row) and LCST behavior (bottom row). (A) Normalized Rg plotted as a function of simulation temperature for (QGQSPYG)9. The intercept along the abscissa from the red circle corresponds to the location of the theta temperature. (B) Contraction ratio plotted against for (QGQSPYG)9. (C) Binodal and spinodal for (QGQSPYG)9. The critical point is at which the binodal and spinodal coincide and the estimated UCST is Tc ≈ 340 K. The symbols represent the temperatures for which the points on the binodal and spinodal were obtained from the GCT theory. (D) Plot that is equivalent to (A) for the system (TPKAMAP)9 that has LCST behavior. This system undergoes a robust collapse transition above the θ temperature, which is the intercept along the abscissa that passes through the red circle. (E) Plot of the contraction ratio for (TPKAMAP)9 as a function of . Note that B is positive for UCST systems and negative for LCST systems. Accordingly, is always negative. (F) Full phase diagram, including the binodal and spinodal for (TPKAMAP)9. The LCST (∼345 K) corresponds to the temperature at which the binodal and spinodal coincide. To see this figure in color, go online.
Discussion
In this work, we have adapted and deployed the GCT of Raos and Allegra (14,15) to compute full phase diagrams for archetypal LCDs using parameters extracted from single-chain simulations of coil-to-globule transitions. Our motivation for adapting and deploying the GCT-aided approach comes from recent observations showing that mean-field theories based on the Flory-Huggins theory (82,83) can be reliably used to describe experimentally measured binodals for LCDs (3,8, 9, 10). Bioinformatics analyses have identified a uniform linear distribution of stickers as a defining feature of LCDs that are implicated in liquid-liquid phase separation (10,84,85). This suggests that, to zeroth order, LCDs that are drivers of liquid-liquid phase separation can be treated as effective homopolymers. Additionally, recent theoretical, computational, and experimental work has shown that there is a one-to-one correspondence between the driving forces for chain collapse in dilute solutions and phase separation in concentrated solutions of LCDs (10,18,28,68,86,87). The theoretical work of Lin and Chan, based on a random phase-approximation-based mean-field approach to incorporate the effects of sequence patterning and cation-π as well as π-π interactions, showed an inverse correlation between the extent of collapse in polyampholytes and the critical temperature (86). Overall, the observations to date are suggestive of the swapping of intrachain interactions for interchain interactions as being a key determinant of phase separation (17). Therefore, we reasoned that a theory designed to connect single-chain coil-to-globule transitions to phase separation should be suitable for numerical adaptation. We selected the GCT for our two-pronged approach because, to the best of our knowledge, this is one of the few theories that describes both single-chain conformational equilibria and multichain phase equilibria using a single set of parameters. A detailed analysis of the robustness of the parameterization procedure is presented in the Supporting Materials and Methods (see Figs. S5 and S6).
Use of the GCT approach requires a priori numerical characterization of single-chain coil-to-globule transition profiles. These can be extracted from all-atom or coarse-grained simulations, which are accessible via different approaches. For example, a recent study (88), which draws on our presentation at the 64th annual meeting of the Biophysical Society (89), demonstrated the use of the Raos-Allegra theory for computing phase diagrams for the protein FUS using data for coil-to-globule transitions obtained using the transferrable coarse-grained model of Dignon et al. (18,28,90). Computational methods based on the ABSINTH implicit solvation model and novel refinements to explicit solvent models have enabled increasingly accurate and efficient simulations of conformational equilibria of a range of IDPs (39,40,59,63,91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107). Many of these approaches can use experimental data as inputs to generate accurate coarse-grained descriptions for conformational ensembles of IDPs (108,109). These methods can be brought to bear for accurate characterization of coil-to-globule transitions. Here, we focused on temperature as the control parameter; however, one can conceive of other intensive parameters such as pH (110) or the chemical potentials of solution ions or small molecules as control parameters (8,11,20,111).
Our method of extracting parameters from single-chain coil-to-globule transitions and computing phase diagrams using a numerical approach based on the GCT is similar in spirit to the field-theoretic approaches that have been adapted from the polymer literature for the study of LCD phase separation (112,113). The essential differences are that the GCT, unlike field-theoretic approaches, remains primarily a mean-field theory. This implies that effects of fluctuations are ignored in the GCT formalism. This is likely to create issues in describing how the width of the two-phase regime varies as the critical temperature is approached (114). However, as a rapid and potentially easy to deploy strategy, the GCT should afford a useful approach for high-throughput comparative assessments of phase diagrams, providing we have results from simulations of coil-to-globule transitions. This GCT-driven approach is likely to be useful for the design of repetitive sequences with bespoke phase behavior—a problem of considerable interest in the design of novel biomaterials as well as synthetic condensates. It can be combined with field-theoretic approaches to obtain improved descriptions of near critical regions and of the effects of density fluctuations engendered by conformational fluctuations.
Efficiency considerations
There are three major categories of methods that enable the numerical calculation of sequence- and/or architecture-specific phase diagrams of intrinsically disordered regions (IDRs) and chimeras of IDRs and folded domains. Lattice-based methods were introduced by Harmon et al. (25,115), to demonstrate the relevance of the stickers-and-spacers model for chimeric systems. The underlying physics of bond fluctuation models used by Harmon et al. was formalized in the LASSI engine for modeling phase separation and percolation of IDRs and chimeric systems comprising IDRs tethered to folded domains (22). An analogous lattice-based approach, known as PIMMS, that mainly uses a single bead per amino acid resolution (although this is not an absolute constraint) has been deployed for simulations of phase behaviors of IDRs in different contexts (10,35,116). LASSI and PIMMS are analogous engines, although the latter is intended to enable “on the fly” discovery of stickers and spacers because it can be deployed with a transferrable or a learned model. In contrast, LASSI requires an a priori delineation of stickers versus spacers. LASSI, however, affords the incorporation of anisotropic interactions, and it can, in theory, be generalized to incorporate stickers with higher coordination numbers.
Off-lattice models include those developed by Dignon et al. (18,28,90). Their approach and code base are gaining traction and usage (88,117) because they are built on a transferrable model for the interactions between coarse-grained beads that mimic individual amino acids or groups of residues. An alternative to the transferrable model of Dignon et al. is the machine-learning-aided off-lattice approach developed by Ruff et al. (41) that derives system-specific parameters by bootstrapping against all-atom simulations for individual molecules and pairs of molecules. Finally, the field-theoretic strategy pioneered by Fredrickson and co-workers (118) has gained usage for modeling phase behavior of polyelectrolytic and polyampholytic IDPs (112,113). The field-theoretic approach requires numerical solution of dynamical equations that incorporate free energy functionals derived from simulations of single chains.
In our two-pronged approach that leverages the GCT, the main bottleneck remains the simulation of single-chain coil-to-globule transitions. Once we have this information, all that remains is calculation of the chemical potential and osmotic pressure system for each combination of ϕ and T. The total time for the calculation of the phase diagram is therefore linearly related to the number of ϕ and T pairs of that are of interest. A typical calculation, such as the one that yields the phase diagrams shown in Fig. 6 for the WT-A1 system, takes an average of 58 s on a single 4 Intel i5-7600 processor. The code used in this study is provided as Data S1.
Summary and prognosis
Our use of the GCT rests on the validity of the assumption that the driving forces for single-chain collapse in dilute solutions are the same as the ones that drive interchain associations in concentrated solutions. We refer to this as the “strong coupling regime” and note that the correspondence required for the use of GCT need not always prevail (20,114). For example, a direct prediction of the GCT, which we have not called out here explicitly, is the fact that the chain conformations in the dense phase are likely to be distinct from those in the coexisting dilute phase. Well below the θ temperature, chains in dilute solutions should form globules, whereas chains in the dense phase are likely to behave like random walks because intermolecular interactions weaken the driving force for collapse (15). Therefore, systems characterized by limited conformational change across the phase boundary are poor candidates for the use of GCT. This will be true as we approach the critical temperature at which the two-phase regime narrows, giving rise to ultradilute droplet phases, which has been observed in recent studies (20).
Predictions from the GCT can be tested by explicit measurements of binodals and by characterizing the dimensions of individual chains in both the dilute and dense phases as a function of temperature or any other control parameter of interest. This should be feasible using advances in small angle x-ray scattering as well as multiparameter single-molecule fluorescence spectroscopies (102,119,120). A problem of considerable interest would be the use of GCT to analyze published results for low-concentration arms of binodals and derive coil-to-globule transition profiles in the dilute solutions and reconstruct full phase diagrams using parameters from the inferred coil-to-globule transitions. This follow-up work is currently underway.
Author Contributions
Conceptualization, X.Z. and R.V.P.; all-atom simulations and GCT implementation, X.Z.; PIMMS simulations, A.S.H.; Analysis, X.Z. and R.V.P.; writing, R.V.P.; editing, X.Z., A.S.H., A.C., T.M., and R.V.P.; funding, A.C., T.M., and R.V.P.
Acknowledgments
We thank Mina Farag for helpful discussions and critical inputs.
This work was supported by grants DMR 1729783 from the US National Science Foundation (to A.C. and R.V.P.), RGP0034/2017 from the Human Frontier Science Program (to R.V.P.), 5R01NS056114 from the US National Institutes of Health (to R.V.P.), and the St. Jude Children’s Research Collaborative on Membraneless Organelles (to T.M. and R.V.P.).
Editor: Scott Showalter.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.06.014.
Appendix: Mathematical Details That Lead to Eqs. 7 and 11
From the assumption of a Gaussian distribution for intrasegment distances within a chain, it follows that Aintra(q; τ) is written in terms of q, τ, the two-body interaction coefficient B (where B > 0), and the three-body interaction coefficient w as
| (15) |
The parameter τB is the second virial coefficient that reflects the interplay of pairwise segment-segment, segment-solvent, and solvent-solvent interactions. Note that for UCST systems, τB is negative for T < Tθ because B here is positive; conversely, for LCST systems, B is negative and the second virial coefficient τB is negative for T > Tθ. The parameter w is a direct measure of the third virial coefficient defined by three-way interactions of polymer segments (Fig. 2).
The elastic free energy is written in terms of the compression parameter q as
| (16) |
These expressions lead to Eq. 7, which is the lynchpin of the theory for extracting parameters from simulated coil-to-globule transition profiles for single chains.
Free Energy For A System With Multiple Chain Molecules
Using the assumption of a Gaussian distribution for W(Ri), it follows that
| (17) |
where
| (18) |
and
| (19) |
νAel is the elastic free energy of individual chains in the cluster, whereas Aconf is the free energy cost associated with confining ν molecules into a cluster. The confinement term accounts for the loss of translational entropy. It also includes a combinatorial Gibbs-like correction term that accounts for the indistinguishability of chains within a cluster. The expression for Aconf derived by Raos and Allegra is as follows:
| (20) |
Phase separation is an infinitely cooperative process (121), and accordingly, the cluster free energy is minimized in the limit ν → ∞. In this limit, it is useful to work in terms of the volume fraction ϕ. Raos and Allegra show that the free energy per chain in a polymer solution ach is written in the limit ν → ∞ as
| (21) |
Here, and . The expression in Eq. 17 is then used to estimate the free energy per unit volume in the polymer solution denoted as avol. Here, avol = ach.
Supporting Material
A Zip Archive of the Commented MATLAB Code and the Data Files Used to Extract System-Specific Phase Diagrams Using Our Adaptation of the Gaussian Cluster Theory All relevant details are found within the README file in the archive.
References
- 1.Banani S.F., Lee H.O., Rosen M.K. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017;18:285–298. doi: 10.1038/nrm.2017.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brangwynne C.P., Tompa P., Pappu R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015;11:899–904. [Google Scholar]
- 3.Shin Y., Berry J., Brangwynne C.P. Spatiotemporal control of intracellular phase transitions using light-activated optoDroplets. Cell. 2017;168:159–171.e14. doi: 10.1016/j.cell.2016.11.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Martin E.W., Mittag T. Relationship of sequence and phase separation in protein low-complexity regions. Biochemistry. 2018;57:2478–2487. doi: 10.1021/acs.biochem.8b00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shin Y., Brangwynne C.P. Liquid phase condensation in cell physiology and disease. Science. 2017;357:eaaf4382. doi: 10.1126/science.aaf4382. [DOI] [PubMed] [Google Scholar]
- 6.Alberti S., Saha S., Hyman A.A. A user’s guide for phase separation assays with purified proteins. J. Mol. Biol. 2018;430:4806–4820. doi: 10.1016/j.jmb.2018.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Posey A.E., Holehouse A.S., Pappu R.V. Phase separation of intrinsically disordered proteins. Methods Enzymol. 2018;611:1–30. doi: 10.1016/bs.mie.2018.09.035. [DOI] [PubMed] [Google Scholar]
- 8.Brady J.P., Farber P.J., Kay L.E. Structural and hydrodynamic properties of an intrinsically disordered region of a germ cell-specific protein on phase separation. Proc. Natl. Acad. Sci. USA. 2017;114:E8194–E8203. doi: 10.1073/pnas.1706197114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Simon J.R., Carroll N.J., López G.P. Programming molecular self-assembly of intrinsically disordered proteins containing sequences of low complexity. Nat. Chem. 2017;9:509–515. doi: 10.1038/nchem.2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Martin E.W., Holehouse A.S., Mittag T. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science. 2020;367:694–699. doi: 10.1126/science.aaw8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ruff K.M., Roberts S., Pappu R.V. Advances in understanding stimulus-responsive phase behavior of intrinsically disordered protein polymers. J. Mol. Biol. 2018;430:4619–4635. doi: 10.1016/j.jmb.2018.06.031. [DOI] [PubMed] [Google Scholar]
- 12.Faltova L., Küffner A.M., Arosio P. Multifunctional protein materials and microreactors using low complexity domains as molecular adhesives. ACS Nano. 2018;12:9991–9999. doi: 10.1021/acsnano.8b04304. [DOI] [PubMed] [Google Scholar]
- 13.Linsenmeier M., Kopp M.R.G., Arosio P. Dynamics of synthetic membraneless organelles in microfluidic droplets. Angew. Chem. Int. Ed. Engl. 2019;58:14489–14494. doi: 10.1002/anie.201907278. [DOI] [PubMed] [Google Scholar]
- 14.Raos G., Allegra G. Chain collapse and phase separation in poor-solvent polymer solutions: a unified molecular description. J. Chem. Phys. 1996;104:1626–1645. [Google Scholar]
- 15.Raos G., Allegra G. Macromolecular clusters in poor-solvent polymer solutions. J. Chem. Phys. 1997;107:6479–6490. [Google Scholar]
- 16.Rubinstein M., Colby R.H. Oxford University Press; New York: 2003. Polymer Physics. [Google Scholar]
- 17.Panagiotopoulos A.Z., Wong V., Floriano M.A. Phase equilibria of lattice polymers from histogram reweighting Monte Carlo simulations. Macromolecules. 1998;31:912–918. [Google Scholar]
- 18.Dignon G.L., Zheng W., Mittal J. Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA. 2018;115:9929–9934. doi: 10.1073/pnas.1804177115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pappu R.V., Wang X., Crick S.L. A polymer physics perspective on driving forces and mechanisms for protein aggregation. Arch. Biochem. Biophys. 2008;469:132–141. doi: 10.1016/j.abb.2007.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wei M.T., Elbaum-Garfinkle S., Brangwynne C.P. Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat. Chem. 2017;9:1118–1125. doi: 10.1038/nchem.2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang J., Choi J.-M., Hyman A.A. A molecular grammar governing the driving forces for phase separation of prion-like RNA binding proteins. Cell. 2018;174:688–699.e16. doi: 10.1016/j.cell.2018.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Choi J.-M., Dar F., Pappu R.V. LASSI: a lattice model for simulating phase transitions of multivalent proteins. PLoS Comput. Biol. 2019;15:e1007028. doi: 10.1371/journal.pcbi.1007028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Choi J.-M., Holehouse A.S., Pappu R.V. Physical principles underlying the complex biology of intracellular phase transitions. Annu. Rev. Biophys. 2020;49:107–133. doi: 10.1146/annurev-biophys-121219-081629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Choi J.-M., Hyman A.A., Pappu R.V. Generalized models for bond percolation transitions of associative polymers. arXiv. 2020 doi: 10.1103/PhysRevE.102.042403. arXiv:2004.03278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Harmon T.S., Holehouse A.S., Pappu R.V. Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. eLife. 2017;6:e30294. doi: 10.7554/eLife.30294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rubinstein M., Dobrynin A.V. Solutions of associative polymers. Trends Polym. Sci. (Regul. Ed.) 1997;5:181–186. [Google Scholar]
- 27.Semenov A.N., Rubinstein M. Thermoreversible gelation in solutions of associative polymers. 1. Statics. Macromolecules. 1998;31:1373–1385. [Google Scholar]
- 28.Dignon G.L., Zheng W., Mittal J. Sequence determinants of protein phase behavior from a coarse-grained model. PLoS Comput. Biol. 2018;14:e1005941. doi: 10.1371/journal.pcbi.1005941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dzuricky M., Roberts S., Chilkoti A. Convergence of artificial protein polymers and intrinsically disordered proteins. Biochemistry. 2018;57:2405–2414. doi: 10.1021/acs.biochem.8b00056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Roberts S., Harmon T.S., Chilkoti A. Injectable tissue integrating networks from recombinant polypeptides with tunable order. Nat. Mater. 2018;17:1154–1163. doi: 10.1038/s41563-018-0182-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Quiroz F.G., Chilkoti A. Sequence heuristics to encode phase behaviour in intrinsically disordered protein polymers. Nat. Mater. 2015;14:1164–1171. doi: 10.1038/nmat4418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pierce W.K., Grace C.R., Mittag T. Multiple weak linear motifs enhance recruitment and processivity in SPOP-mediated substrate ubiquitination. J. Mol. Biol. 2016;428:1256–1271. doi: 10.1016/j.jmb.2015.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Flory P.J., Volkenstein M. Statistical mechanics of chain molecules. Biopolymers. 1969;8:699–700. [Google Scholar]
- 34.Molliex A., Temirov J., Taylor J.P. Phase separation by low complexity domains promotes stress granule assembly and drives pathological fibrillization. Cell. 2015;163:123–133. doi: 10.1016/j.cell.2015.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Boeynaems S., Holehouse A.S., Gitler A.D. Spontaneous driving forces give rise to protein-RNA condensates with coexisting phases and complex material properties. Proc. Natl. Acad. Sci. USA. 2019;116:7889–7898. doi: 10.1073/pnas.1821038116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Walker F.O. Huntington’s disease. Semin. Neurol. 2007;27:143–150. doi: 10.1055/s-2007-971176. [DOI] [PubMed] [Google Scholar]
- 37.Crick S.L., Ruff K.M., Pappu R.V. Unmasking the roles of N- and C-terminal flanking sequences from exon 1 of huntingtin as modulators of polyglutamine aggregation. Proc. Natl. Acad. Sci. USA. 2013;110:20075–20080. doi: 10.1073/pnas.1320626110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Posey A.E., Ruff K.M., Pappu R.V. Profilin reduces aggregation and phase separation of huntingtin N-terminal fragments by preferentially binding to soluble monomers and oligomers. J. Biol. Chem. 2018;293:3734–3746. doi: 10.1074/jbc.RA117.000357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Newcombe E.A., Ruff K.M., Hatters D.M. Tadpole-like conformations of huntingtin exon 1 are characterized by conformational heterogeneity that persists regardless of polyglutamine length. J. Mol. Biol. 2018;430:1442–1458. doi: 10.1016/j.jmb.2018.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Warner J.B., IV, Ruff K.M., Lashuel H.A. Monomeric huntingtin exon 1 has similar overall structural features for wild-type and pathological polyglutamine lengths. J. Am. Chem. Soc. 2017;139:14456–14469. doi: 10.1021/jacs.7b06659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ruff K.M., Harmon T.S., Pappu R.V. CAMELOT: a machine learning approach for coarse-grained simulations of aggregation of block-copolymeric protein sequences. J. Chem. Phys. 2015;143:243123. doi: 10.1063/1.4935066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ruff K.M., Khan S.J., Pappu R.V. A coarse-grained model for polyglutamine aggregation modulated by amphipathic flanking sequences. Biophys. J. 2014;107:1226–1235. doi: 10.1016/j.bpj.2014.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Williamson T.E., Vitalis A., Pappu R.V. Modulation of polyglutamine conformations and dimer formation by the N-terminus of huntingtin. J. Mol. Biol. 2010;396:1295–1309. doi: 10.1016/j.jmb.2009.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vitalis A., Lyle N., Pappu R.V. Thermodynamics of beta-sheet formation in polyglutamine. Biophys. J. 2009;97:303–311. doi: 10.1016/j.bpj.2009.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Vitalis A., Wang X., Pappu R.V. Atomistic simulations of the effects of polyglutamine chain length and solvent quality on conformational equilibria and spontaneous homodimerization. J. Mol. Biol. 2008;384:279–297. doi: 10.1016/j.jmb.2008.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wetzel R. Physical chemistry of polyglutamine: intriguing tales of a monotonous sequence. J. Mol. Biol. 2012;421:466–490. doi: 10.1016/j.jmb.2012.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kar K., Jayaraman M., Wetzel R. Critical nucleus size for disease-related polyglutamine aggregation is repeat-length dependent. Nat. Struct. Mol. Biol. 2011;18:328–336. doi: 10.1038/nsmb.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Thakur A.K., Jayaraman M., Wetzel R. Polyglutamine disruption of the huntingtin exon 1 N terminus triggers a complex aggregation mechanism. Nat. Struct. Mol. Biol. 2009;16:380–389. doi: 10.1038/nsmb.1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Slepko N., Bhattacharyya A.M., Wetzel R. Normal-repeat-length polyglutamine peptides accelerate aggregation nucleation and cytotoxicity of expanded polyglutamine proteins. Proc. Natl. Acad. Sci. USA. 2006;103:14367–14372. doi: 10.1073/pnas.0602348103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bhattacharyya A.M., Thakur A.K., Wetzel R. Polyglutamine aggregation nucleation: thermodynamics of a highly unfavorable protein folding reaction. Proc. Natl. Acad. Sci. USA. 2005;102:15400–15405. doi: 10.1073/pnas.0501651102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chen S., Ferrone F.A., Wetzel R. Huntington’s disease age-of-onset linked to polyglutamine aggregation nucleation. Proc. Natl. Acad. Sci. USA. 2002;99:11884–11889. doi: 10.1073/pnas.182276099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Walters R.H., Murphy R.M. Examining polyglutamine peptide length: a connection between collapsed conformations and increased aggregation. J. Mol. Biol. 2009;393:978–992. doi: 10.1016/j.jmb.2009.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Crick S.L., Jayaraman M., Pappu R.V. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc. Natl. Acad. Sci. USA. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lee C.C., Walters R.H., Murphy R.M. Reconsidering the mechanism of polyglutamine peptide aggregation. Biochemistry. 2007;46:12810–12820. doi: 10.1021/bi700806c. [DOI] [PubMed] [Google Scholar]
- 55.Vitalis A., Pappu R.V. Assessing the contribution of heterogeneous distributions of oligomers to aggregation mechanisms of polyglutamine peptides. Biophys. Chem. 2011;159:14–23. doi: 10.1016/j.bpc.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Vitalis A., Pappu R.V. ABSINTH: a new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009;30:673–699. doi: 10.1002/jcc.21005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Radhakrishnan A., Vitalis A., Pappu R.V. Improved atomistic Monte Carlo simulations demonstrate that poly-L-proline adopts heterogeneous ensembles of conformations of semi-rigid segments interrupted by kinks. J. Phys. Chem. B. 2012;116:6862–6871. doi: 10.1021/jp212637r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mao A.H., Pappu R.V. Crystal lattice properties fully determine short-range interaction parameters for alkali and halide ions. J. Chem. Phys. 2012;137:064104. doi: 10.1063/1.4742068. [DOI] [PubMed] [Google Scholar]
- 59.Wuttke R., Hofmann H., Schuler B. Temperature-dependent solvation modulates the dimensions of disordered proteins. Proc. Natl. Acad. Sci. USA. 2014;111:5213–5218. doi: 10.1073/pnas.1313006111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Choi J.-M., Pappu R.V. Improvements to the ABSINTH force field for proteins based on experimentally derived amino acid specific backbone conformational statistics. J. Chem. Theory Comput. 2019;15:1367–1382. doi: 10.1021/acs.jctc.8b00573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sugita Y., Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 62.Vitalis A., Pappu R.V. Methods for Monte Carlo simulations of biomacromolecules. Annu. Rep. Comput. Chem. 2009;5:49–76. doi: 10.1016/S1574-1400(09)00503-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Das R.K., Pappu R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA. 2013;110:13392–13397. doi: 10.1073/pnas.1304749110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Allegra G., Ganazzoli F. Polymer collapse in dilute solution: equilibrium and dynamical aspects. J. Chem. Phys. 1985;83:397–412. [Google Scholar]
- 65.Raos G., Allegra G., Ganazzoli F. The collapse of chains with different architectures. J. Chem. Phys. 1994;100:7804–7813. [Google Scholar]
- 66.Stephen M.J. Collapse of a polymer chain. Phys. Lett. A. 1975;53:363–364. [Google Scholar]
- 67.De Gennes P.G. Collapse of a polymer chain in poor solvents. Journale de Physique Letters. 1975;36:55–57. [Google Scholar]
- 68.Holehouse A.S., Garai K., Pappu R.V. Quantitative assessments of the distinct contributions of polypeptide backbone amides versus side chain groups to chain expansion via chemical denaturation. J. Am. Chem. Soc. 2015;137:2984–2995. doi: 10.1021/ja512062h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Oxtoby D.W., Kashchiev D. A general relation between the nucleation work and the size of the nucleus in multicomponent nucleation. J. Chem. Phys. 1994;100:7665–7671. [Google Scholar]
- 70.Cahn J.W. On spinodal decomposition. Acta Metall. 1961;9:795–801. [Google Scholar]
- 71.Cahn J.W., Hilliard J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958;28:258–267. [Google Scholar]
- 72.Berry J., Brangwynne C.P., Haataja M. Physical principles of intracellular organization via active and passive phase transitions. Rep. Prog. Phys. 2018;81:046601. doi: 10.1088/1361-6633/aaa61e. [DOI] [PubMed] [Google Scholar]
- 73.Berry J., Weber S.C., Brangwynne C.P. RNA transcription modulates phase transition-driven nuclear body assembly. Proc. Natl. Acad. Sci. USA. 2015;112:E5237–E5245. doi: 10.1073/pnas.1509317112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Michaels T.C.T., Šarić A., Knowles T.P.J. Chemical kinetics for bridging molecular mechanisms and macroscopic measurements of amyloid fibril formation. Annu. Rev. Phys. Chem. 2018;69:273–298. doi: 10.1146/annurev-physchem-050317-021322. [DOI] [PubMed] [Google Scholar]
- 75.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. From macroscopic measurements to microscopic mechanisms of protein aggregation. J. Mol. Biol. 2012;421:160–171. doi: 10.1016/j.jmb.2012.02.031. [DOI] [PubMed] [Google Scholar]
- 76.Šarić A., Buell A.K., Frenkel D. Physical determinants of the self-replication of protein fibrils. Nat. Phys. 2016;12:874–880. doi: 10.1038/nphys3828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Narayanan A., Meriin A., Cisse I.I. A first order phase transition mechanism underlies protein aggregation in mammalian cells. eLife. 2019;8:e39695. doi: 10.7554/eLife.39695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Patel A., Lee H.O., Alberti S. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell. 2015;162:1066–1077. doi: 10.1016/j.cell.2015.07.047. [DOI] [PubMed] [Google Scholar]
- 79.Alberti S., Gladfelter A., Mittag T. Considerations and challenges in studying liquid-liquid phase separation and biomolecular condensates. Cell. 2019;176:419–434. doi: 10.1016/j.cell.2018.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Sciortino F., Bansil R., Alstrøm P. Interference of phase separation and gelation: a zeroth-order kinetic model. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1993;47:4615–4618. doi: 10.1103/physreve.47.4615. [DOI] [PubMed] [Google Scholar]
- 81.Varanko A.K., Su J.C., Chilkoti A. Elastin-like polypeptides for biomedical applications. Annu. Rev. Biomed. Eng. 2020;22:343–369. doi: 10.1146/annurev-bioeng-092419-061127. [DOI] [PubMed] [Google Scholar]
- 82.Flory P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942;10:51–61. [Google Scholar]
- 83.Huggins M.L. Solutions of long chain compounds. J. Chem. Phys. 1941;9:440. [Google Scholar]
- 84.Nott T.J., Petsalaki E., Baldwin A.J. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell. 2015;57:936–947. doi: 10.1016/j.molcel.2015.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Schmidt H.B., Barreau A., Rohatgi R. Phase separation-deficient TDP43 remains functional in splicing. Nat. Commun. 2019;10:4890. doi: 10.1038/s41467-019-12740-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Lin Y.-H., Chan H.S. Phase separation and single-chain compactness of charged disordered proteins are strongly correlated. Biophys. J. 2017;112:2043–2046. doi: 10.1016/j.bpj.2017.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Lin Y.-H., Brady J.P., Ghosh K. A unified analytical theory of heteropolymers for sequence-specific phase behaviors of polyelectrolytes and polyampholytes. J. Chem. Phys. 2020;152:045102. doi: 10.1063/1.5139661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Chou H.-Y., Aksimentiev A. Single-protein collapse determines phase equilibria of a biological condensate. J. Phys. Chem. Lett. 2020;11:4923–4929. doi: 10.1021/acs.jpclett.0c01222. [DOI] [PubMed] [Google Scholar]
- 89.Zeng X., Pappu R.V. Combined theoretical and computational approach for calculating sequence-specific phase diagrams of thermoresponsive intrinsically disordered homopolypeptides. Biophys. J. 2020;118(Suppl 1):304a. [Google Scholar]
- 90.Dignon G.L., Zheng W., Mittal J. Temperature-controlled liquid-liquid phase separation of disordered proteins. ACS Cent. Sci. 2019;5:821–830. doi: 10.1021/acscentsci.9b00102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Sherry K.P., Das R.K., Barrick D. Control of transcriptional activity by design of charge patterning in the intrinsically disordered RAM region of the Notch receptor. Proc. Natl. Acad. Sci. USA. 2017;114:E9243–E9252. doi: 10.1073/pnas.1706083114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Das R.K., Huang Y., Pappu R.V. Cryptic sequence features within the disordered protein p27Kip1 regulate cell cycle signaling. Proc. Natl. Acad. Sci. USA. 2016;113:5616–5621. doi: 10.1073/pnas.1516277113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Das R.K., Ruff K.M., Pappu R.V. Relating sequence encoded information to form and function of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2015;32:102–112. doi: 10.1016/j.sbi.2015.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Das R.K., Crick S.L., Pappu R.V. N-terminal segments modulate the α-helical propensities of the intrinsically disordered basic regions of bZIP proteins. J. Mol. Biol. 2012;416:287–299. doi: 10.1016/j.jmb.2011.12.043. [DOI] [PubMed] [Google Scholar]
- 95.Staller M.V., Holehouse A.S., Cohen B.A. A high-throughput mutational scan of an intrinsically disordered acidic transcriptional activation domain. Cell Syst. 2018;6:444–455.e6. doi: 10.1016/j.cels.2018.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Fuertes G., Banterle N., Lemke E.A. Decoupling of size and shape fluctuations in heteropolymeric sequences reconciles discrepancies in SAXS vs. FRET measurements. Proc. Natl. Acad. Sci. USA. 2017;114:E6342–E6351. doi: 10.1073/pnas.1704692114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Ripaud L., Chumakova V., Hipp M.S. Overexpression of Q-rich prion-like proteins suppresses polyQ cytotoxicity and alters the polyQ interactome. Proc. Natl. Acad. Sci. USA. 2014;111:18219–18224. doi: 10.1073/pnas.1421313111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Gibbs E.B., Showalter S.A. Quantification of compactness and local order in the ensemble of the intrinsically disordered protein FCP1. J. Phys. Chem. B. 2016;120:8960–8969. doi: 10.1021/acs.jpcb.6b06934. [DOI] [PubMed] [Google Scholar]
- 99.Metskas L.A., Rhoades E. Conformation and dynamics of the troponin I C-terminal domain: combining single-molecule and computational approaches for a disordered protein region. J. Am. Chem. Soc. 2015;137:11962–11969. doi: 10.1021/jacs.5b04471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Robustelli P., Piana S., Shaw D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA. 2018;115:E4758–E4766. doi: 10.1073/pnas.1800690115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Best R.B., Zheng W., Mittal J. Balanced protein-water interactions improve properties of disordered proteins and non-specific protein association. J. Chem. Theory Comput. 2014;10:5113–5124. doi: 10.1021/ct500569b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Zheng W., Zerze G.H., Best R.B. Inferring properties of disordered chains from FRET transfer efficiencies. J. Chem. Phys. 2018;148:123329. doi: 10.1063/1.5006954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Best R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017;42:147–154. doi: 10.1016/j.sbi.2017.01.006. [DOI] [PubMed] [Google Scholar]
- 104.Zerze G.H., Best R.B., Mittal J. Sequence- and temperature-dependent properties of unfolded and disordered proteins from atomistic simulations. J. Phys. Chem. B. 2015;119:14622–14630. doi: 10.1021/acs.jpcb.5b08619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Best R.B., Zheng W., Mittal J. Correction to balanced protein-water interactions improve properties of disordered proteins and non-specific protein association. J. Chem. Theory Comput. 2015;11:1978. doi: 10.1021/acs.jctc.5b00219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Ganguly D., Chen J. Modulation of the disordered conformational ensembles of the p53 transactivation domain by cancer-associated mutations. PLoS Comput. Biol. 2015;11:e1004247. doi: 10.1371/journal.pcbi.1004247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Lee K.H., Chen J. Optimization of the GBMV2 implicit solvent force field for accurate simulation of protein conformational equilibria. J. Comput. Chem. 2017;38:1332–1341. doi: 10.1002/jcc.24734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Milles S., Salvi N., Jensen M.R. Characterization of intrinsically disordered proteins and their dynamic complexes: from in vitro to cell-like environments. Prog. Nucl. Magn. Reson. Spectrosc. 2018;109:79–100. doi: 10.1016/j.pnmrs.2018.07.001. [DOI] [PubMed] [Google Scholar]
- 109.Salvi N., Abyzov A., Blackledge M. Atomic resolution conformational dynamics of intrinsically disordered proteins from NMR spin relaxation. Prog. Nucl. Magn. Reson. Spectrosc. 2017;102–103:43–60. doi: 10.1016/j.pnmrs.2017.06.001. [DOI] [PubMed] [Google Scholar]
- 110.Fossat M.J., Pappu R.V. q-canonical Monte Carlo sampling for modeling the linkage between charge regulation and conformational equilibria of peptides. J. Phys. Chem. B. 2019;123:6952–6967. doi: 10.1021/acs.jpcb.9b05206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Holehouse A.S., Sukenik S. Controlling structural bias in intrinsically disordered proteins using solution space scanning. J. Chem. Theory Comput. 2020;16:1794–1805. doi: 10.1021/acs.jctc.9b00604. [DOI] [PubMed] [Google Scholar]
- 112.McCarty J., Delaney K.T., Shea J.-E. Complete phase diagram for liquid-liquid phase separation of intrinsically disordered proteins. J. Phys. Chem. Lett. 2019;10:1644–1652. doi: 10.1021/acs.jpclett.9b00099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Lin Y., McCarty J., Han S. Narrow equilibrium window for complex coacervation of tau and RNA under cellular conditions. eLife. 2019;8:e42571. doi: 10.7554/eLife.42571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Muthukumar M. Thermodynamics of polymer solutions. J. Chem. Phys. 1986;85:4722–4728. [Google Scholar]
- 115.Harmon T.S., Holehouse A.S., Pappu R.V. Differential solvation of intrinsically disordered linkers drives the formation of spatially organized droplets in ternary systems of linear multivalent proteins. New J. Phys. 2018;20:045002. [Google Scholar]
- 116.Guillen-Boixet J., Kopach A., Franzmann T.M. RNA-induced conformational switching and clustering of G3BP drive stress granule assembly by condensation. Cell. 2020;181:346–361.e17. doi: 10.1016/j.cell.2020.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Espinosa J.R., Joseph J.A., Collepardo-Guevara R. Liquid network connectivity regulates the stability and composition of biomolecular condensates with many components. Proc. Natl. Acad. Sci. USA. 2020;117:13238–13247. doi: 10.1073/pnas.1917569117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Fredrickson G.H., Ganesan V., Drolet F. Field-theoretic computer simulation methods for polymers and complex fluids. Macromolecules. 2002;35:16–39. [Google Scholar]
- 119.Aznauryan M., Delgado L., Schuler B. Comprehensive structural and dynamical view of an unfolded protein from the combination of single-molecule FRET, NMR, and SAXS. Proc. Natl. Acad. Sci. USA. 2016;113:E5389–E5398. doi: 10.1073/pnas.1607193113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Schuler B., Soranno A., Nettels D. Single-molecule FRET spectroscopy and the polymer physics of unfolded and intrinsically disordered proteins. Annu. Rev. Biophys. 2016;45:207–231. doi: 10.1146/annurev-biophys-062215-010915. [DOI] [PubMed] [Google Scholar]
- 121.Sugar I.P. Cooperativity and classification of phase transitions. Application to one- and two-component phospholipid membranes. J. Phys. Chem. 1987;91:95–101. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
A Zip Archive of the Commented MATLAB Code and the Data Files Used to Extract System-Specific Phase Diagrams Using Our Adaptation of the Gaussian Cluster Theory All relevant details are found within the README file in the archive.