The emergent interactions that govern biodiversity change

Significance

Predicting how ecological communities respond to change requires an understanding of the direct effects of environment and the indirect effects that emerge when environment is propagated through food webs of interacting species. A probabilistic, dynamic framework for inference identifies these environment–species interactions. Results show how environmental effects translate into nonlinear responses, how they can be estimated from data, and the insight they provide on the relative importance of direct and indirect (through other species) responses to change. Because these effects include uncertainty from the model and data, they can guide management that has to weigh the utility of efforts to protect critical habitat (or not) against the risk for species that respond through the responses of others.

Abstract

Observational studies have not yet shown that environmental variables can explain pervasive nonlinear patterns of species abundance, because those patterns could result from (indirect) interactions with other species (e.g., competition), and models only estimate direct responses. The experiments that could extract these indirect effects at regional to continental scales are not feasible. Here, a biophysical approach quantifies environment– species interactions (ESI) that govern community change from field data. Just as species interactions depend on population abundances, so too do the effects of environment, as when drought is amplified by competition. By embedding dynamic ESI within framework that admits data gathered on different scales, we quantify responses that are induced indirectly through other species, including probabilistic uncertainty in parameters, model specification, and data. Simulation demonstrates that ESI are needed for accurate interpretation. Analysis demonstrates how nonlinear responses arise even when their direct responses to environment are linear. Applications to experimental lakes and the Breeding Bird Survey (BBS) yield contrasting estimates of ESI. In closed lakes, interactions involving phytoplankton and their zooplankton grazers play a large role. By contrast, ESI are weak in BBS, as expected where year-to-year movement degrades the link between local population growth and species interactions. In both cases, nonlinear responses to environmental gradients are induced by interactions between species. Stability analysis indicates stability in the closed-system lakes and instability in BBS. The probabilistic framework has direct application to conservation planning that must weigh risk assessments for entire habitats and communities against competing interests.

The nonlinear distributions of species along environmental gradients that result from species interactions have frustrated efforts to understand biodiversity at least since G. E. Hutchinson defined the “realized” and “fundamental niche” (1). They are a persistent challenge for today’s efforts to anticipate global change. If the dynamics of communities are dominated by interactions between species, then both fast disturbance and slow climate change could have impacts that are nonlinear, unpredictable, and hard to attribute to any specific cause. Models used to quantify risk could fail to detect food webs that are destabilized by climate change or by extreme events when environmental responses are mediated by species interactions that are only partially observed (2–4). Neither species distribution models (SDMs) (5, 6) nor joint SDMs (JSDMs) (7–9) can fit or predict nonlinear gradient responses that are induced by environment–species interactions, such as temperature responses that come from strong competition in warm climates (e.g., ref. 10). A framework for evaluating environment–species interactions that allows for variables that are measured, observations, and parameters could improve our understanding of carrying capacities (11–14), food web stability (15–18), and resilience to change (19–24). Full uncertainty is important for its application to policy, where utility of a conservation plan has to be weighed against the risks of action or inaction (25, 26). Here we apply a dynamic, biophysical framework that identifies the combined impacts of environment and species interactions from the data that ecologists collect. We demonstrate the insights it provides on the different ways that environment–species interactions can operate in contrasting ecosystems.

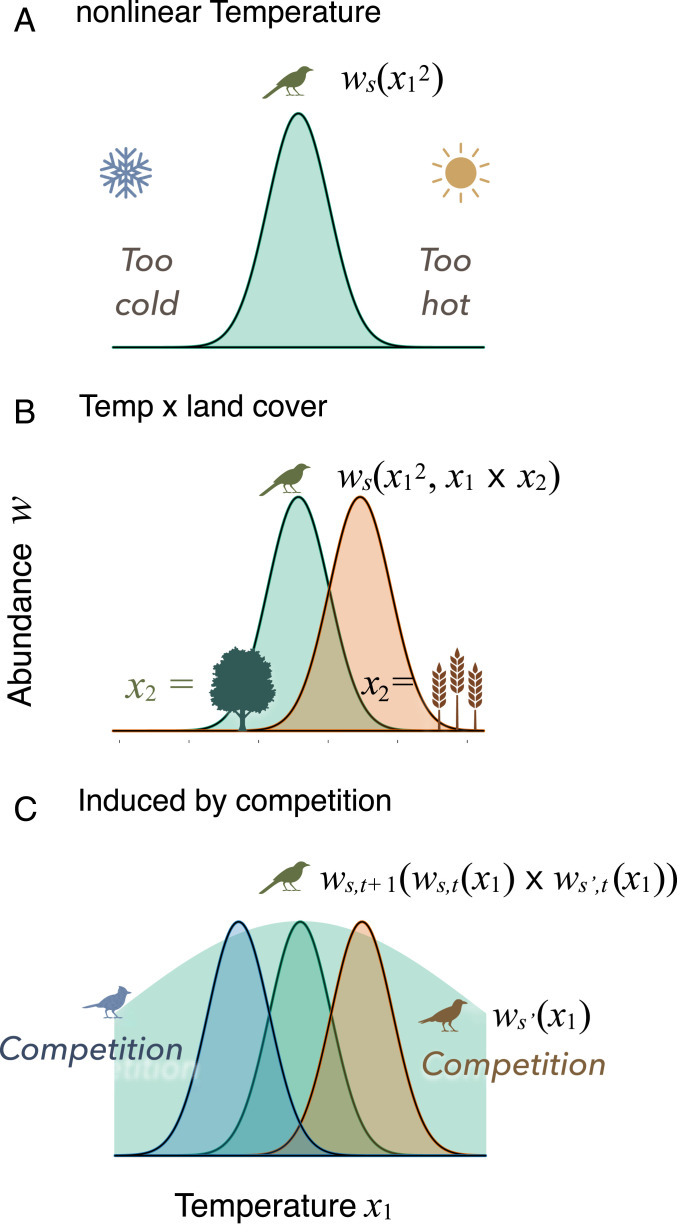
Our approach addresses two foundational challenges facing community ecology. First, can the simple models that could be parameterized from data predict the nonlinear effects of the environment that are induced instead by trophic interactions (Fig. 1C)? The term “environment–species interaction” (ESI) is used here to integrate biotic and abiotic effects of environment that depend on population size—just as species interactions depend on population density (species compete most when they are abundant), environmental fluctuations such as drought are amplified by competition for moisture at high density. Environmental variation penetrates the web of competitors, natural enemies, and prey through its effects on each species. The impacts ramify through species interactions with others (14, 27). However, traditional models that are used to estimate climate effects fit nonlinear responses directly to environmental variables (e.g., refs. 28 and 29). Application of this traditional approach to a temperature gradient estimates parameter values that assign low population density to conditions that are either too hot or too cold (Fig. 1A). Our approach offers an alternative: Competition between species with different temperature responses could explain nonlinear distributions, even without direct nonlinear responses (Fig. 1C). Likewise, explanations for the dependence of temperature responses on land cover type (Fig. 1B) could come, instead, from interactions between species that differ in their responses to both variables.

Fig. 1.

Nonlinear and interaction responses to environment. (A) Nonlinear response of species $s$ to a temperature gradient ($x_1$) is fitted with a model containing a quadratic term, $x_1^2$. (B) Combined effects of temperature and land cover ($x_2$) are fitted with an additional interaction term, $x_1\times x_2$, where response to temperature might differ in forests and fields. (C) Alternatively, nonlinear and interaction responses enter indirectly though products with other species $s\prime$ (blue and brown) that depend on temperature $x_1$, but require the time dimension. The background shading in C describes Hutchinson’s concept of the fundamental niche that might be realized by species $s$ in the absence of other species.

Understanding how ESI affects these responses indirectly (1) would have to come from dynamic data at relevant spatial and temporal scales (30). Static data snapshot food webs that are tracking climate trends and recovering from short-term disturbances. Static observations misrepresent how species influence one another (14, 31); finding that two species tend to occur together can support the interpretation that competition is weak (otherwise, they would repel each other) or that it is strong (similar requirements put them in direct conflict). For this reason, theory defines species interactions as the effects of density on the growth rates of others. The assumption that species abundances are in equilibrium with the environment is an additional source of uncertainty (32, 33). Incorrectly attributing the effects of other species to the direct effects of environment can propagate to prediction errors that will change, depending on which species are present now and in the future. It is important to ask whether these errors are large enough to mislead. If dynamic models that allow for interactions and model errors can predict nonlinear and interaction gradient responses, then there may be potential for understanding their contributions to data and vulnerability to change.

If simple models that could be fitted to data can predict the nonlinear effects that are induced by species interactions, then can estimates of ESI be used to predict equilibrium communities, their stability properties, and their regulation by trophic interactions as opposed to environmental constraints (15–17, 34)? If estimates of equilibrium abundances can be extended to include ESI, then stability analysis might aid understanding of how ESI contributes to model behavior (35). The capacity to identify those communities that are strongly regulated by environmental constraints versus trophic interactions would have direct application to the risks of climate change, species invasions, and harvesting.

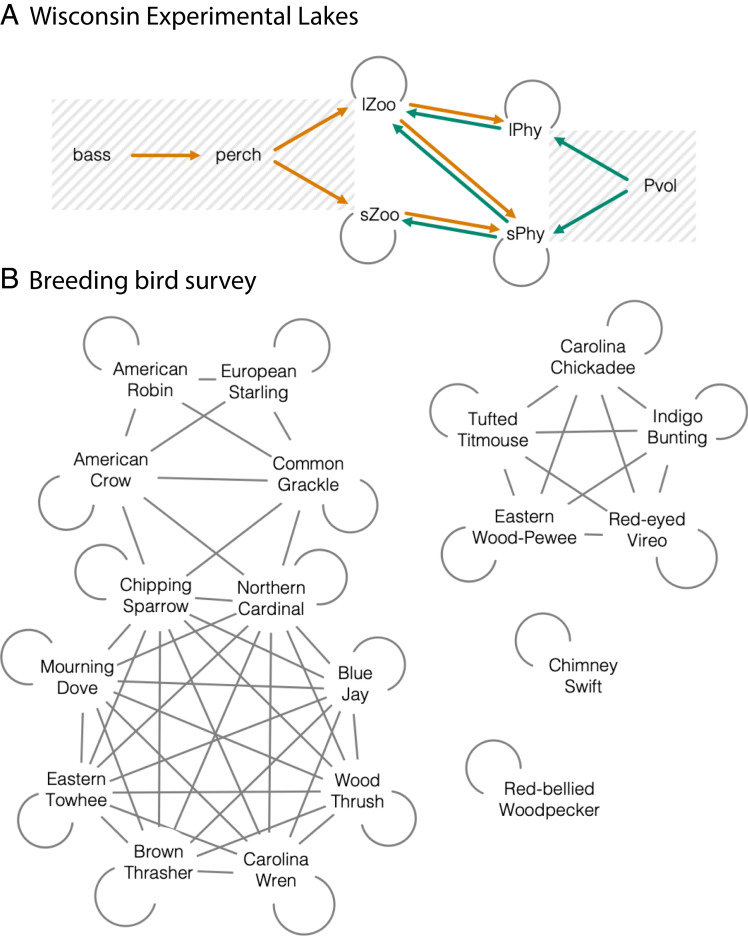
Two examples illustrate the challenges. The Wisconsin Experimental Lakes (WEL) example (Fig. 2A) follows a manipulation of nutrients and largemouth bass to determine the combined effects of bottom-up and top-down forces relevant for biomanipulation (35). Species with similar trophic roles are aggregated into four groups. Others are omitted due to limited information and a focus on key trophic interactions. The Breeding Bird Survey (BBS) example (Fig. 2B) (36) comes from data that have been used to assess declines linked to habitat degradation, pesticides, and climate change (37, 38). As is typical of biodiversity data, most counts for most species are zero (39). The BBS network was not designed to study food webs, but dynamics do depend on ESI. Unlike the WEL example, where aggregated species groups emphasize trophic relationships, the BBS monitors each species from a taxonomic group that includes insectivores, granivores, frugivores, and omnivores. Competition results from resource limitation that reduces territory size, body condition, fecundity, and/or survival. Species interact within communities that include mammals, invertebrates, reptiles, amphibians, and mast- and seed-producing plants, none of which are monitored at BBS sites.

Fig. 2.

Species assemblages that include ESIs. (A) WEL data were analyzed as a closed system over multiple years with competition for nutrients and light between sPhy and lPhy. Treatments include manipulation of largemouth bass predation on the perch that consume lZoo and nutrient enrichment (Pvol). Both zooplankton groups are subject to predation from small planktivorous fish (perch). The sZoo and lZoo feed on phytoplankton, with sZoo restricted by size to feed on sPhy. Gray lines are competition (negative), and orange and green arrows indicate the negative and positive effects of predation, respectively. (B) BBS data include guilds of species that might compete based on diet and habit.

A second contrast between examples is the open nature of a BBS location. Whereas seasonal dynamics within a lake result largely from in-lake processes, the breeding season BBS records both year-round residents and seasonal migrants. Migrants suffer from competition for food and territories in both the breeding season and the winter range (40, 41). The combined effects are expected to smear out over a map as territories shift from one year to the next (42). In other words, the “population growth” inferred for a specific location includes not just births and deaths of the in situ population but also movement between locations. This ubiquitous feature of real communities, where each participant is reacting to others on different scales, remains challenging for food web theory and its application (2, 43).

We applied a dynamic, biophysical framework to the contrasting examples in Fig. 2 to determine 1) whether probabilistic modeling can capture the nonlinear patterns of abundance that come from trophic relationships and 2) whether stability analysis and equilibrium responses from a model that includes ESI, with full uncertainty, can lend insight into community regulation. The framework includes six features: 1) dynamics; 2) ESIs that affect movement, population growth, and carrying capacities; 3) probabilistic parameters, process, and observations; 4) operates on the observation scale; 5) accommodates zero-dominant data; and 6) admits food web theory through prior distributions. Products of the analysis include estimates of 1) ESI strength, 2) equilibrium abundances, and 3) stability. Interaction strength is needed to determine how a community is structured by relationships between species, reaction to the environment, and combinations of the two. Equilibrium abundance is needed to translate observations of a dynamic process to a reference state for the system. Stability analysis of the equilibrium provides insight on whether or not it might be encountered in nature.

The framework adopted here resolves challenges that have made valid inference on communities difficult. We started from the well-studied generalized Lotka–Volterra (LV) model, expanding it to accommodate environmentally influenced movement and interactions, serial dependence, and missing information. The standard LV model expresses rate of change in the density of a species $s$ in terms of density-independent rate ${\rho }_s$ and density-dependent rate ${\alpha }_{s,s\prime }{w}_{s\prime }$ that depends on the abundance of species $s\prime$ and its interaction effect ${\alpha }_{s,s\prime }$. The basic LV model for $S$ species, $d{w}_s/dt=w_s\left({\rho }_s+{\sum }_{s\prime =1}^S{\alpha }_{s,s\prime }{w}_{s\prime }\right)$, is extended here to include ESI in three terms,

$$\begin{array}{c}\hfill \frac{d{w}_s}{dt}\hspace{0.17em}=\hspace{0.17em}\stackrel{\mathrm{m}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}{\overbrace{{\mathbf{\text{x}}}^{\prime }{\mathit{\beta }}_s}}+\stackrel{\mathrm{D}\mathrm{I}\hspace{0.17em}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\overbrace{\left(w_s\times {\mathbf{\text{x}}}^{\prime }\right){\mathit{\rho }}_s}}+\stackrel{\text{DD growth}}{\overbrace{\left(w_s\times {\mathbf{\text{w}}}^{\prime }\right){\mathit{\alpha }}_s}}+\stackrel{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}{\overbrace{{ϵ}_s}}\end{array}.$$ [1]

The first term includes a vector of coefficients ${\mathit{\beta }}_s$ describing the response to environmental variables in a vector $\mathbf{\text{x}}$. This term can include any effects of environment that do not depend on population density $w_s$. It is most often used in the literature to represent immigration and/or emigration. To simplify discussion, we refer to this term as “movement.” The second term includes coefficients ${\mathit{\rho }}_s$ describing the response to the interaction between density and environment, $w_s\times \mathbf{\text{x}}$. This is the standard density-independent (DI) growth of LV, expanded here to interactions with environment. The third term includes coefficients in a vector ${\mathit{\alpha }}_s$ to describe density-dependent (DD) effects of abundances of all $S$ species held in the vector $\mathbf{\text{w}}$. There is one equation for each of $S$ species, so coefficient vectors become matrices, $\mathit{\beta }$, $\mathit{\rho }$, and $\mathit{\alpha }$, each with $S$ rows. In our model, the $S$ equations are additionally linked by an $S\times S$ covariance matrix $\mathit{\Sigma }$ (SI Appendix, section S2) for the error $ϵ$.

Fitting Eq. 1 to data confronts long-standing challenges of community data that are amplified in the dynamic, nonlinear setting. First, most species abundance data are dominated by zeros (often $>90\%$). This can motivate model fitting on a logarithmic scale (e.g., Poisson regression) where coefficients and covariances do not have a direct interpretation (39). Second, the uncertainties in parameters, model, and observations are omitted or not specified in ways that account for serial dependence in time series data. Third, interacting species are often measured in different ways and on different scales (Fig. 2A).

Our approach merges the dynamic ESI in Eq. 1 with full uncertainty for the different ways in which species are observed. Species abundance $w_{s,i,t}$ at a location $i$ at time $t$ is a continuous, nonnegative, latent variable that is linked to an observed species abundance $y_{s,i,t}$ that can be a discrete count. Inputs to the model are the predictors in a design vector ${\mathbf{\text{x}}}_{i,t}$ and the observed abundances of $S$ species in a vector ${\mathbf{\text{y}}}_{i,t}$. Generalized joint attribute modeling (GJAM) (39) is implemented to model change in abundance by linking the observed ${\mathbf{\text{y}}}_{i,t}$ to the dynamic model of Eq. 1 on the observation scale, important because it allows interactions to be readily interpreted, and potentially different for each species.

The dynamic process admits missing knowledge in two ways, through prior distributions that blend current and previous information (not all of Fig. 2 will be informed by a given data set) and through model misspecification. Food web understanding is used to limit dimensionality a priori that would otherwise be overfitted. There are many parameters, due to the potentially large number of interactions. For a total of $S$ species, there are $S^2$ coefficients in the matrix $\mathit{\alpha }$ alone. However, many of these terms must be zero (e.g., species that have nonoverlapping diets and do not compete for territories). For others, the sign of the interaction is known (e.g., one is a predator of another).

Redefining the challenge to allow for ESI suggests a strategy for food web analysis, focusing on how posterior distributions diverge from the prior as an alternative to variable selection. Traditional variable-selection criteria (e.g., lowest Deviance Information Criterion) are used to limit variables in a model to those that are “significantly different from zero.” However, model fitting has not two but three possible outcomes: The estimate is different from zero or not, but, importantly, is it different from the prior? Posterior–prior comparisons can be especially relevant for food webs, due to the fact that interactions are many, constantly shifting, and mostly unobserved (2). The connections shown in Fig. 2 are hypotheses that, although essentially correct, might not be identified in a given data set; they are interactions that could occur, but data miss too much of the process, or they are too weak to influence dynamics. Where the data do not offer Bayesian learning on a specific interaction, the preferable (and Bayesian) action is intermediate between traditional methods: Retain the interaction in the model with its prior-dominated estimate. If the prior is informed by life history knowledge or observations of shared resources, then it is the best estimate available. The posterior distribution over potential interactions includes the true uncertainty, which is certainly not the same as assuming zeros. We expect that a given model fit will identify only some of the ESIs, but we capture the uncertainty that includes the prior knowledge that an interaction could be important.

Materials and Methods summarizes gjamTime, which embeds GJAM within a dynamic state space framework. Details are provided in the SI Appendix and the model is demonstrated with a reproduced analysis in ref. 44. In the next section, we provide analytical and simulation results for the capacity to estimate parameters and predict abundances, followed by application.

Results

We addressed our two foundational questions through 1) simulation studies, 2) analytical model analysis, and 3) applications to food webs in Fig. 2.

Simulation Validates Fitting and Prediction.

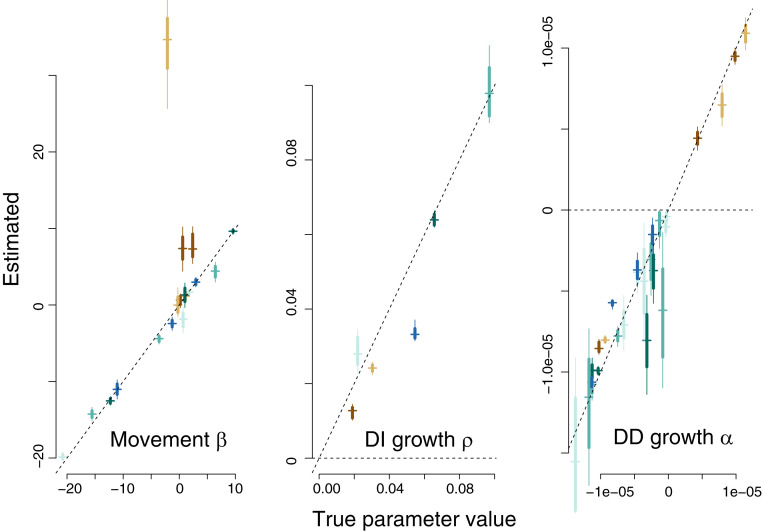
We first determined that gjamTime predicts the data used to fit the model, indicating that the algorithm is correct. However, data prediction is not enough, because a model with many parameters can be overfitted. An important test is to demonstrate that parameters used to simulate data are recovered from the fitted model. All of the reasons why a parameter estimate might be “insignificant” in a simple model are amplified where species abundances and environmental predictors could have limited variation or their products in the ESI terms could exhibit collinearity. This is a consideration that pertains to any effort to model species interactions. Confidence in the fit comes from the ability to both predict the data and recover parameters.

Simulation studies (SI Appendix, section S3) demonstrate that the model can recover the contributions of movement, DI growth, and DD growth, but only if we allow for each in SI Appendix, Eq. S2.5. When all sources of uncertainty are included, the interpretation of parameters is essentially correct. Of the contributions from movement, DI growth, and DD, only one of the movement coefficients in $\mathit{\beta }$ is clearly missed (Fig. 3). Our gjamTime recovers parameters as well as could be expected from a static model applied to static data, but, in this case, it resolves the challenges of ESI in a dynamic setting. A simple LV model that lacks the six features of gjamTime would produce misleading results; even within the dynamic framework of gjamTime, estimates are affected by omission of movement. Inaccurate interpretation can also come from limited sampling, which is important given the small counts that are often available for ecological data (44).

Fig. 3.

Parameter recovery when the correct model (that includes the three terms of gjamTime in Eq. 1) is fitted to data, including movement ($\mathit{\beta }$), DI growth ($\mathit{\rho }$), and DD growth ($\mathit{\alpha }$).

As with any model-fitting exercise, there can be no general claims about parameter recovery, because the balance of signal in three of the four terms of Eq. 1 (movement, DI growth, DD growth, and residual variance) will differ for each dataset. The important result here is that, given signal, simulation studies confirm that parameters can be recovered, and they provide a tool for exploring the impacts of individual contributions in the model. The SI Appendix summarizes these effects using a simple food web, consisting of four competitors, two of which are prey to both of two predators (SI Appendix, Fig. S2.2, left). All species experience intraspecific density dependence, and some compete with one another. Given that parameters are recovered in simulation, it is important next to understand whether nonlinearities can be induced by ESIs and, if so, why.

Analytical Nonlinear Gradients from Linear Direct Effects.

Analytical methods confirm that, in the absence of interactions with other species or direct nonlinear effects, there are no nonlinear gradient responses (SI Appendix, Eq. S2.11). Of course, a nonlinear response to a gradient can be fitted by including a quadratic term in either movement or DI growth (the first two terms of Eq. 1), as depicted in Fig. 1A. Likewise, an interaction between two predictors (Fig. 1B) can be included in either of these terms. In either case, predictions build in the assumption that species are responding directly to the environment. The question is, can these nonlinear responses be predicted without assuming direct environmental effects?

Model analysis demonstrates that both nonlinear and interaction responses can be induced by other species, and the model can predict them. From SI Appendix, section S2, the gradient response of a species is affected by other species in two ways, 1) conditionally, through indirect effects contained in the residual covariance, and 2) through species interactions. The residual covariance absorbs variation coming from all variables that are not included in the model—many are unobserved; those that are observed may not be measured on the scales that organisms experience them. These unobserved effects can influence all species and contribute to residual covariance. If the abundance of one species is known, it can be used to help interpret responses of others. In this conditional case, the residual covariance becomes a matrix of regression coefficients that alters the slopes of other species (second term of SI Appendix, Eq. S5.18). This indirect effect depends on how strongly species respond to the same gradient (SI Appendix, Eq. S5.16). In other words, species can indirectly increase or decrease the conditional responses of one another if they have residual covariance, and if they each respond to the same gradient. This effect can appear when the abundance of a species is viewed conditional on others, but it is linear.

All induced nonlinearities and interactions come through other species, but they do not engage the residual covariance. The response is nonlinear for a species that is influenced by other species responding (even linearly) to the same gradient. A nonlinear response to a temperature gradient $x$ requires product terms, for example, $x^2$ (Fig. 1A). If such terms are not included in the matrix of covariates $\mathbf{\text{x}}$ of Eq. 1, then the nonlinear response can still emerge through dynamics and the interactions with other species. If two species respond to $x$ at time $t$, then those responses are transferred as a product to time $t+1$, in the third term of Eq. 1. The nonlinearity comes from the strength of the species interactions in matrix $\mathit{\alpha }$. Thus, two species that respond to the same predictor and affect the growth rate of a third species contribute these nonlinearities.

Interactive responses along environmental gradients (Fig. 1B) emerge from the same mechanism. Two species that respond to different predictors and affect the growth rate of a third species contribute these product terms, here again through $\mathit{\alpha }$.

Because ESIs do not come through residual covariance, they are not estimated or predicted by static JSDMs; they require the dynamic view that captures the effect of a variable on more than one species that is transferred to others through density dependence. Interestingly, the stronger the response of each species to a predictor (the ${\rho }_{q,s}$ coefficients) and the more strongly species interact with one another (the ${\alpha }_{s,s\prime }$ coefficients), the greater the induced ESI. Because abundance is not only spatial but also dynamic, the nonlinearities and interactions induced by other species in space are changing over time. For reference purposes, SI Appendix, Eq. S5.18 can be evaluated at the equilibrium abundance $\mathbf{\text{w}}*$, which, importantly, is not an estimate of observed abundance. Examples of nonlinearities and interactions induced by other species appear in the applications to real food webs in the next section.

Applications to Data.

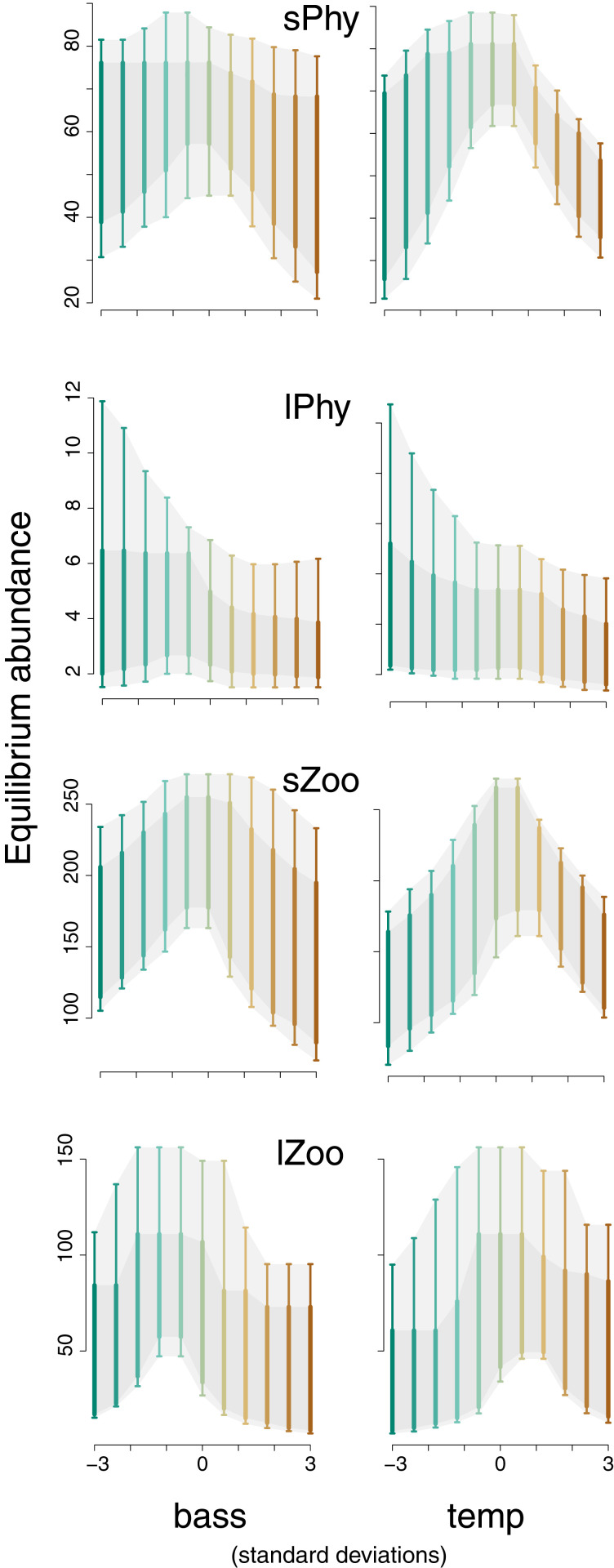
Applications to field data confirm analytical predictions of emergent nonlinear and interactive responses to environment. The highly aggregated species groups in the WEL example (Fig. 2A) were tracked at weekly intervals for multiple years in three lakes (SI Appendix, Table S7.2). Again, small zooplankton (sZoo) mostly consume small phytoplankton (sPhy), which compete with large phytoplankton (lPhy) for nutrients and light (Fig. 2). Due to their large body size, large zooplankton (lZoo) are especially vulnerable to predation by fish. Many species are unobserved; the four species groups were abstracted from a food web that includes wading and diving birds, amphibians, reptiles, mammals, and littoral macrophytes. Covariates for this analysis included bass, nutrient enrichment, and temperature for DI growth, but we omitted movement (first term of Eq. 1), under the assumption that a lake is effectively closed. Bass and nutrient enrichment were included in an earlier analysis of these data (35). We also included temperature, due to its strong seasonal trend (SI Appendix, Fig. S7.4) that could impact metabolic rates of phytoplankton, zooplankton, and fish. To explore nonlinear responses induced by species interactions, we included only linear terms for main effects. As discussed in SI Appendix, section S6, the prior distribution is flat over parameters in $\mathit{\rho }$ and $\alpha$, where bounds provide liberal coverage for realistic effects. In the case of DI growth rate (the “intercept” row 1 in $\mathit{\rho }$), bounds of $\left(-0.05,0.1\right)$ allow for a doubling time of 7 wk to a $50\%$ decline in 14 wk. These bounds are wide, because they describe growth that would occur in the absence of density dependence.

As anticipated by analytical analysis, we observed nonlinear predictions for equilibrium abundances along gradients in bass abundance and temperature (Fig. 4). Zooplankton have maximum equilibrium abundances at intermediate bass predation, while lPhy are high at low bass predation, as might be expected for high planktivory on lZoo where perch are unregulated by bass predation. Maximum abundances on the temperature gradient range from lPhy at low temperatures to other groups at intermediate temperatures. These predictions include the effects of environment that comes through its effects on other species, that is, the ESI.

Fig. 4.

Predictive equilibrium abundances $\mathbf{\text{w}}*$ along the bass abundance (Left) and temperature (temp) (Right) gradients for four species groups in the WEL example. Envelopes bound $68\%$ and $95\%$ predictive intervals.

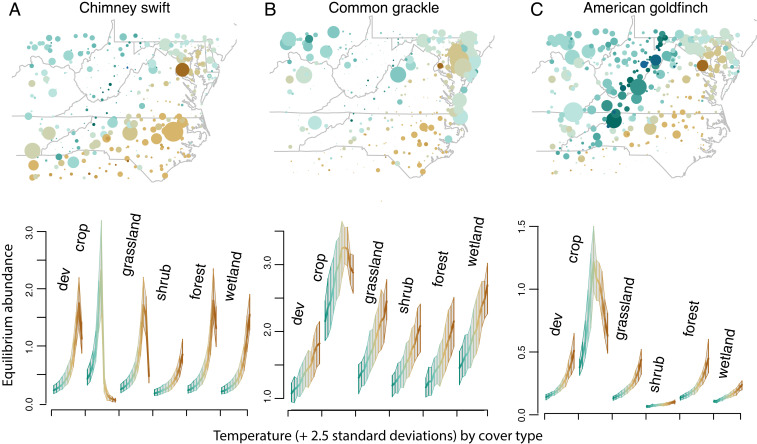
From the BBS example (Fig. 2B), we obtained not only nonlinear effects of temperature, but also strong ESI between temperature and land cover. As with the WEL example, the prior bounds used for DI growth in BBS spanned beyond the biologically reasonable range of $\left(-0.05,0.1\right)\hspace{0.17em}{\mathrm{y}}^{-1}$, that is, up to 10$\%$ increase per year at mean environmental conditions. This model included effects of wind conditions on movement (activity levels can decline with high winds), and June temperature, summer moisture deficit, and land cover on DI growth. June temperature is low (green in Fig. 5) along the Appalachian Mountains and, with the exception of urban areas, in the north. The moisture deficit is high when low precipitation coincides with high temperatures during the breeding season. Land cover affects nesting sites, cover, and food. The areas of highest mean counts per effort (maps in Fig. 5) need not coincide with equilibrium predicted abundances, because many species are changing over time.

Fig. 5.

Predictive equilibrium abundances $\mathbf{\text{w}}*$ along a temperature gradient (cold green to warm brown), with a response curve for each of six land covers, including (A) chimney swift, (B) common grackle, and (C) American goldfinch. Maps show mean counts per observation effort by BBS route since 1996. Temperature responses across cover types demonstrate nonlinearities and interactions, neither of which are specified in the model. The land-cover type “dev” refers to developed lands.

Nonlinear equilibrium abundances ${\mathbf{\text{w}}}^{*}$ plotted along the temperature gradient below maps in Fig. 5 are predicted by a model that includes them only as linear effects. Predictive distributions for chimney swift are narrow and strongly unimodal across all cover types except shrub and wetland (Fig. 5A). This nonlinear response comes from interactions with species that have different temperature responses. Common grackle (Fig. 5B) and American goldfinch (Fig. 5C) responses likewise emphasize the nonlinear and interaction responses along environmental gradients that emerge from species interactions. Induced interactions are clear from the responses to temperature that depend on land cover, despite the fact that the model does not include an interaction between land cover and temperature. In fact, there is a rich diversity of responses to these variables, as unimodal responses to temperature in one cover type (e.g., crop) shift to simple trends in others (e.g., forest). Just as nonlinear responses emerge from interacting species that vary with temperature, ESIs emerge when interacting species differ in their responses to two different gradients, in this case, temperature and land cover.

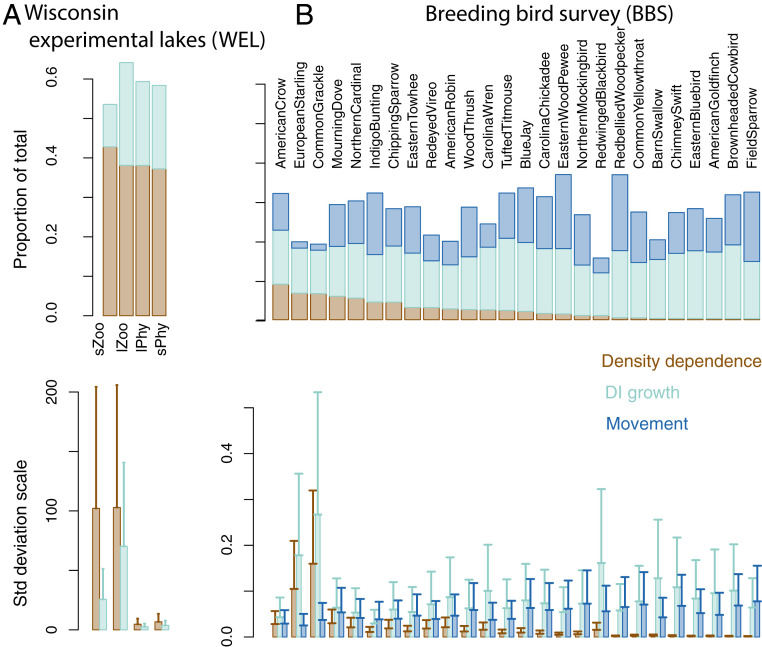
The two applications show contrasting contributions to overall dynamics from movement, DI growth, and species interactions. The strong density dependence in WEL compared with BBS (Fig. 6, Upper) would be expected from a closed lake system that is controlled by trophic interactions compared with an open, loosely connected BBS assemblage. The proportion of variation explained by DD is similar across the four species groups in WEL, suggesting that these groups collectively account for much of the food web variation. For an assemblage like BBS, where population growth is weakly connected to abundances, we can expect a limited effect of DD from the population 1 y ago (Fig. 6B, Upper). This does not mean that DD does not occur within summer and winter ranges, only that it can be a weak predictor of abundances at the same location the subsequent year. In BBS, the abundant species like common grackle, American crow, and European starling show the strongest contribution of DD.

Fig. 6.

Contributions to dynamics in contrasting food webs. Movement (light blue) in B comes from redistribution of birds from year to year; it is not included in the WEL example in A. DI growth (light blue) is high where environmental variables play a large role. DD (brown) comes through species interactions. On a proportionate basis (Upper), DD is more important in the closed lake food web, where interactions are comparatively strong. Species groups in A are sZoo, lZoo, and small and large algae (sPhy, lPhy). Lower plots show SDs for the three contributions on the observation scale.

Do the contrasting contributions of DD in Fig. 6 mean that DD is actually stronger in WEL or that data are simply more informative? Prior–posterior comparisons show clear Bayesian learning in WEL (SI Appendix, Fig. S8.7). In the case of WEL, all information points to dynamics steered by species interactions. For BBS, the data update priors for movement and DI growth (SI Appendix, Fig. S8.10), but many DD parameters are weakly informed by data (SI Appendix, Fig. S8.11). In the case of BBS, the fit is guided not only by data but also by prior information, allowing for the fact that interactions could be poorly informed by observations. BBS dynamics could be importantly affected by DD, but will require more data than analyzed here to clearly estimate them.

Stability analysis differs for the two examples. The structure of interactions in the matrix $\mathit{\alpha }$ provides insights on whether or not a given community might be expected to persist. A stable community is interpreted where the eigenvalues of $\mathit{\alpha }$ have all negative real parts. An unstable community can often be “stabilized” by extinction of one or more species. The estimated $\mathit{\alpha }$ for BBS has several eigenvalues with positive real parts indicating instability for the equilibrium abundances. This result is not at odds with numerous studies reporting bird declines over the period covered by this analysis (38) and with predictive distributions from our analysis that include zero for a number of species (SI Appendix, section S8). WEL has all eigenvalues with negative real parts indicating stability. This result agrees with predicted positive equilibrium abundances for all species groups.

Discussion

The biggest questions in community ecology persist, at least in part, due to the limited means for incorporating interactions into models at the relevant scales. Observational studies have not yet convincingly shown that climate gradients directly control the species and community responses that are observed across continents. The experiments that would be needed to dissect biotic versus climatic contributions to community composition at relevant scales may never justify the cost. Without a means for estimating how ESIs control trophic structure and species distributions, predictions for the future will be treated with skepticism. The large variability in population data requires a full accounting of uncertainty (45–48). The framework that can generate those estimates is needed to anticipate environmental change (19, 49). It will be needed to fully exploit observational networks like BBS and, more recently, the National Ecological Observation Network (NEON). Solutions might improve ties between a 50-y legacy of theoretical insights (15–17, 34, 50, 51) and advances in data analysis (14, 52, 53). Inference and prediction for basic community theory developed here build from previous efforts (35, 54, 55) by incorporating movement and ESI in growth and DD, while accommodating the uncertainty in data, model misspecification, and parameters.

Our gjamTime can identify ESI effects on multiple species, because movement, DI growth, and DD interactions each affect dynamic data in distinct ways. This fully probabilistic approach could help to identify sources of variation when traditional methods give different answers, even when applied to simple microcosms (e.g., figure 2 in ref. 56). Application to the 26 most prevalent species in BBS from our region exceeds the community sizes that are usually fitted to dynamic data in the food web literature (e.g., refs. 35 and 56). The capacity to estimate large food webs depends not only on dynamic data but also on dimension reduction for the residual covariance (57), prior accommodation of food web theory (Fig. 2), and a structure that allows for direct sampling in posterior simulation (SI Appendix, section S7). Valid interpretation requires both synthesis of ESI contributions (Fig. 6) and transparency on where the information is coming from (SI Appendix, Figs. S8.7, S8.10, and S8.11).

Although gjamTime can be applied to networks of single-species groups (e.g., BBS), understanding dynamic food webs will benefit most from monitoring multiple species groups at the same locations. Currently, NEON may be the only initiative that offers this potential. Analysis of large communities will be most productive where there are extensive data, because large communities have more parameters to estimate. For this reason, networks spanning a range of habitat types have the greatest potential, and that potential will expand as observations accumulate over time.

Applications of the approach show that the rich nonlinear and interactive responses of communities in nature can be fitted and predicted even when we do not build them into models as direct responses to the environment. For example, the model fitted to the WEL data includes a linear term for effects of temperature on growth rates, but it predicts nonlinear temperature response (Fig. 4) that agrees with data (SI Appendix, Fig. S8.5). BBS responses to gradients are both nonlinear and interactive, again without assuming that they are direct (SI Appendix, Fig. S8.8) and, again, that agrees with observation (SI Appendix, Fig. S8.8). The only other way that models could estimate these relationships would be to assume that they result from direct responses to temperature, moisture, or other environmental gradients (29, 58, 59). Because ESIs emerge unconditionally from a model that includes only direct, linear, and noninteractive responses to environmental gradients, they address the increasing interest to expand SDMs in ways that could accommodate species interactions (60, 61).

It is important to recognize that nothing in the model specifies the unimodal predictive distributions that emerge for species in both of our applications (Figs. 4 and 5). The model is unconstrained by biological assumptions that abundance should peak somewhere within a gradient or even that inverted gradient abundances could be unrealistic (maximum abundances at both ends). Yet, the model clearly finds the biologically plausible gradient responses that might be expected from ecological arguments (62–65).

The demonstration that nonlinear effects of species interactions can be estimated from data does not mean that direct nonlinear effects should be omitted from models. Our gjamTime allows for both (the design matrix $\mathbf{\text{x}}$ can include quadratic and interaction terms). Because we already know that nonlinear responses can be predicted as direct effects, it was important to demonstrate here that they can also be generated indirectly.

Paradoxically, the stronger the responses of species individually to environment and the stronger their interactions with one another, the greater the potential for emergent ESIs. We might expect that strongly nonlinear patterns in abundance signal environment effects that overwhelm species interactions. The opposite can be true—strong species interactions insure that responses of any one are transferred to others. Due to the product terms in predictors that are induced by interacting species (SI Appendix, section S5), nonlinear, interactive patterns are an inevitable outcome of species interactions.

If it comes as no surprise that a model with multiple species can predict nonlinear gradient responses, it is important to appreciate that static JSDMs cannot predict such responses. The expanding interest in estimating species interactions from data (66, 67) has understandably focused on residual covariance—it is the only place in JSDMs where other species appear. Recalling that residual covariance is simply that—unexplained variance—highlights the role of unmeasured environmental variables and species that contribute to residual covariance. The residual covariance involves species interactions only as one of many sources of unexplained variation (8). However, if those arguments are unconvincing, then the inability of JSDMs to predict nonlinear gradient responses (SI Appendix, section S5) is additional evidence that JSDMs cannot be capturing the effects of species interactions. Our dynamic, biophysical approach accommodates these interactions as the effect of abundances on growth rates of others, with uncertainty at each stage.

The nonlinear and interactive responses that engage both direct and indirect effects of environment should temper expectations for precise forecasting of future communities. Complex, nonlinear systems are notoriously hard to predict. The rapid degradation of numerical weather predictions with lead time (essentially, days) provides extensive experience with such systems. Results here add to the known sources of nonlinearities in food webs. These results can motivate future efforts to identify the spatial scales where prediction could be most effective, weighing the gain in signal-to-noise as observations are aggregated at coarse spatial scales against the degradation of links between predictors (e.g., habitat) and population responses. Ecological forecasting of community change requires new efforts to refine how ESI vary with the scale of monitoring efforts.

The equilibrium analysis of Figs. 4 and 5 yields a reference for each system, not a prediction for the future. By the end of the experiment, Carpenter et al. (68) described how the WEL system continued to respond, including through age structure of bass populations that shift from planktivory to piscivory as they increase in size. Likewise, BBS data track populations that are responding to continuing climate change, compounded by habitat shifts (38). The equilibrium state will generally be an extrapolation outside of the data for any food web that is in flux—the equilibrium state is not part of the data used to fit the model. Still, this equilibrium benchmark can be valuable for referencing differences between food webs and over time, one that incorporates the ES evidence from dynamic data. It moves beyond the snapshot perspective offered by analysis with SDMs.

Synthesis of results from monitoring networks like NEON and BBS with field experiments at other scales will require analyses that can generate results like SI Appendix, Figs. S8.7, S8.10, and S8.11. Long-term monitoring data must be translated into estimates of responses and interactions. The utility of gjamTime is not limited to observational data from large networks on large numbers of species. Longitudinal data on multiple response variables are now common in ecology. Both experimental and observational data confront many of the same challenges for traditional models that motivated gjamTime, including response variables measured on multiple scales, large numbers of zeros, and the potential benefits of parameter estimates on the observation scale. Our gjamTime accommodates experimental treatments, including factors and interactions, on “communities” as simple as two species studied at a single site. These estimates provide the basis for the next generation of questions and experiments needed to answer them. Important next steps will explore the data that are needed to separate direct and indirect nonlinear responses.

Managers recognize that habitat quality for many threatened species is shaped, in large part, by the other species that define food webs, and those species assemblages are changing (63). Management has to combine the utility assigned to alternative decisions with predictive uncertainty (25, 69) that includes ESI. Examples include species loss, habitat protection, and management for climate change. The probabilistic treatment of uncertainty in parameters, model, and data in gjamTime adds an important tool to current methods for estimating species interactions (e.g., ref. 56).

These results demonstrate that guidance on the vulnerability of whole communities to fast disturbance and slow climate change may come from the perspective of a dynamic biophysical approach. Building from confident estimates, gjamTime extends inference to the important ESIs that emerge from dynamics (Fig. 6). The large differences in controls by species interactions in a closed lake versus DI growth and movement in loosely organized breeding bird assemblages have direct implications for reactions to disturbance and climate change.

Materials and Methods

The process described by Eq. 1 is embedded within the data model for species collected on multiple scales that is GJAM (39). We combine GJAM with a structure that resolves technical challenges of nonlinear, multivariate, state space modeling (SI Appendix, section S1). This integration allowed us to move from the traditional LV-based theory to fully probabilistic species–environment interactions, equilibrium abundance, and stability. In SI Appendix, we discuss the discrete time, stochastic version of the continuous LV model, referred to here as gjamTime, with connections to current models in the literature (e.g., refs. 35, 54, and 55).

The model is (state-space) hierarchical Bayes, with model fitting by Markov chain Monte Carlo (52, 53). The observation model is a flat, censored interval defined by observation effort (39). Rather than the more typical Gaussian observation model, which places positive probability on negative values, censoring allows for discrete values, including zeros (SI Appendix, Table S2.1). Dimension reduction of the residual covariance matrix allows for large communities (57).

Parameter estimates in the movement matrix $\mathit{\beta }$, DI growth matrix $\mathit{\rho }$, and species interaction matrix $\mathit{\alpha }$ determine growth rates, the strength of ESIs, equilibrium abundances, and stability. Prior information is used to sparsify (zero out) and/or bound coefficients a priori, for example, positive (mutualist, prey on predator) or negative (competition, predator on prey) ranges. Interaction coefficients in the matrix $\mathit{\alpha }$ have further constraints defined by extremes for the potential effects of interactions on growth rates (SI Appendix, section S6). Environmental variation contributes to dynamics through movement matrix $\mathit{\beta }$ (SI Appendix, Eq. S4.12) and growth matrix $\mathit{\rho }$. The relative contributions of species–environment interactions through movement, DI growth, and DD can be evaluated from these coefficients (SI Appendix, section S4).

This nonlinear model with movement offers a numerical solution for equilibrium abundances $\mathbf{\text{w}}*$ obtained by setting $\mathrm{\Delta }{\mathbf{\text{w}}}_t=0$ in SI Appendix, Eq. S2.5. That equilibrium incorporates effects of species (${\mathbf{\text{w}}}_t$ occurs in second and third terms with $\mathit{\rho }$ and $\mathit{\alpha }$) and environment (${\mathbf{\text{x}}}_t$ occurs in first and second terms with $\mathit{\beta }$ and $\mathit{\rho }$). These equilibrium values are shown across gradients in Figs. 4 and 5. Equilibrium abundance is a (probabilistic) predictive distribution obtained by numerical integration (39). Local stability of the equilibrium $\mathbf{\text{w}}*$ is indicated by eigenvalues of $\mathit{\alpha }$ having all negative real parts.

Data Archival.

Data used in this study are available from refs. 35 and 36. Code to analyze the data is available at https://rpubs.com/jimclark/631209.