Estimating rates and patterns of diversification with incomplete sampling: a case study in the rosids

Abstract

Premise

Recent advances in generating large‐scale phylogenies enable broad‐scale estimation of species diversification. These now common approaches typically are characterized by (1) incomplete species coverage without explicit sampling methodologies and/or (2) sparse backbone representation, and usually rely on presumed phylogenetic placements to account for species without molecular data. We used empirical examples to examine the effects of incomplete sampling on diversification estimation and provide constructive suggestions to ecologists and evolutionary biologists based on those results.

Methods

We used a supermatrix for rosids and one well‐sampled subclade (Cucurbitaceae) as empirical case studies. We compared results using these large phylogenies with those based on a previously inferred, smaller supermatrix and on a synthetic tree resource with complete taxonomic coverage. Finally, we simulated random and representative taxon sampling and explored the impact of sampling on three commonly used methods, both parametric (RPANDA and BAMM) and semiparametric (DR).

Results

We found that the impact of sampling on diversification estimates was idiosyncratic and often strong. Compared to full empirical sampling, representative and random sampling schemes either depressed or inflated speciation rates, depending on methods and sampling schemes. No method was entirely robust to poor sampling, but BAMM was least sensitive to moderate levels of missing taxa.

Conclusions

We suggest caution against uncritical modeling of missing taxa using taxonomic data for poorly sampled trees and in the use of summary backbone trees and other data sets with high representative bias, and we stress the importance of explicit sampling methodologies in macroevolutionary studies.

With recent advances in generating very large phylogenetic trees (e.g., Smith and O’Meara, 2012; Stamatakis, 2014; Hinchliff et al., 2015; Nguyen et al., 2015; Eiserhardt et al., 2018; Smith and Brown, 2018), and in analytical methods (e.g., Nee et al., 1994a, b; Pybus and Harvey, 2000; Paradis et al., 2004; Alfaro et al., 2009; Stadler, 2011; Pennell et al., 2014; Rabosky, 2014; Höhna et al., 2016; Morlon et al., 2016), assessing macroevolutionary patterns for globally distributed clades with available biodiversity information has become common (e.g., Jetz et al., 2012; Morlon, 2014; Scholl and Wiens, 2016; Magallón et al., 2018; Rabosky et al., 2018; Upham et al., 2019 [Preprint]). Analyses of diversification rates have shed light on potential drivers of diversity gradients across wide phylogenetic and geographic scales (Jetz et al., 2012; Landis et al., 2018; Rabosky et al., 2018). However, inferring diversification processes solely on the basis of extant species phylogenies is very challenging (Etienne et al., 2011; Didier et al., 2017; Sauquet and Magallón, 2018; Mitchell et al., 2019; Louca and Pennell, 2020), and the accuracy of these methods is an area of intensive research and sometimes heated controversy (Moore et al., 2016; O’Meara and Beaulieu, 2016; Rabosky et al., 2017; Meyer et al., 2018; Rabosky, 2018). Many contemporary analytical workflows for studying diversification have seen little vetting to date with empirical data sets (but see Title and Rabosky, 2017), and much remains to be explored about the response of diversification methods to missing and biased species sampling (Sauquet and Magallón, 2018).

On the empirical side, incomplete sampling of molecular phylogenetic data for many clades represents a long‐standing constraint on assembling data sets to adequately explore large‐scale macroevolutionary questions (e.g., Linder et al., 2005; Cusimano et al., 2012; Thomas et al., 2013; Folk et al., 2018; Sun et al., 2019 [Preprint]). Diversification models generally have no information from which to draw inferences other than branching order and branch length among extant species, both of which can be dramatically affected by (1) absolute taxon coverage (FitzJohn et al., 2009; Title and Rabosky, 2017; Burin et al., 2018; Rabosky, 2018; Revell, 2018) and (2) sampling method at a given level of taxon coverage (Höhna et al., 2011; Cusimano et al., 2012; Höhna, 2014). Hence, not only absolute taxon coverage, but also potential bias in this coverage, is important in interpreting diversification results, yet the identification and use of explicit sampling strategies remains uncommon in the field (O’Meara et al., 2016). Inclusion of data representing all extant lineages with molecular data from resources such as GenBank, without an explicit sampling methodology, is perhaps the most common analytical strategy (e.g., Jetz et al., 2012; Zanne et al., 2014; Upham et al., 2019 [Preprint]; but see, e.g., O’Meara et al., 2016; Magallón et al., 2018).

A second commonly used approach is taxonomically representative sampling, including family‐level or genus‐level backbone trees (e.g., Magallón et al., 2018), which preferentially sample species to represent deep phylogenetic divergences to the exclusion of recent divergences. Representative sampling is the community standard for molecular phylogenetic studies, meaning that databases such as GenBank implicitly contain representative bias (reviewed in Cusimano et al., 2012; Höhna, 2014; O’Meara et al., 2016; Sauquet and Magallón, 2018). Finally, random sampling procedures that sample extant species with equal probability are perhaps the least frequently used (although this approach corresponds best to common model assumptions; see O’Meara et al., 2016).

Most current diversification approaches are able to model incomplete sampling, and several such methods have been widely used in recent diversification studies (as a small sample across taxa, see Jetz et al., 2012; Magallón et al., 2018; Rabosky et al., 2018). Methods of accounting for missing taxa make strong assumptions about the structure of missing species, typically assuming they are randomly missing, an assumption not matched in many empirical data sets (Höhna et al., 2011; Cusimano et al., 2012; Thomas et al., 2013; Revell, 2018), and the impact of alternative sampling approaches is not clear. An additional poorly understood area is the impact of methods for incorporating described taxonomic diversity for which molecular phylogenetic data are unavailable. The increased availability of very large synthetic phylogenetic products with backbone taxonomy such as the Open Tree of Life (hereafter “OpenTree”; Hinchliff et al., 2015), as well as probabilistic methods for inserting backbone taxonomic information (e.g., polytomy resolver [Kuhn et al., 2011]; PASTIS [Thomas et al., 2013]; and TACT [Rabosky et al., 2018; Chang et al., 2019]), creates opportunities for very large analyses with complete sampling of known diversity. However, while these methods are often used (e.g., Jetz et al., 2012; Rabosky et al., 2018; see review by Rabosky, 2015), the properties of diversification inference with contemporary methods using such backbone taxonomies remain poorly characterized.

Here, we use the rosid clade in the flowering plants as a test case to explore how different sampling schemes influence the estimation of diversification with empirical data. Rosids (Rosidae; Cantino et al., 2007; Wang et al., 2009; APG IV, 2016) have great potential to contribute to our understanding of the evolution and diversification of angiosperms, considering their enormous species richness (~90,000 species, representing ~25% of all angiosperms; Govaert, 2001; Hinchliff et al., 2015; Folk et al., 2018). The clade, containing such globally important families as grapes, legumes, oaks and beeches, squash and melons, and mustards (respectively, Vitaceae, Fabaceae, Fagaceae, Cucurbitaceae, and Brassicaceae), originated in the early to late Cretaceous (115 to 93 million years ago [Myr]), followed by rapid diversification in perhaps as little as 4 to 5 million years to yield the crown groups of fabids (112 to 91 Myr) and malvids (109 to 83 Myr; Wang et al., 2009; Bell et al., 2010; Magallón et al., 2015). The rise of the rosids yielded today’s forests, which largely remain dominated by rosid species. The advent of these forests spurred diversification in many other lineages of life (e.g., ants: Moreau et al., 2006; Moreau and Bell, 2013; amphibians: Roelants et al., 2007; mammals: Bininda‐Emonds et al., 2007; fungi: Hibbett and Matheny, 2009; liverworts: Feldberg et al., 2014; ferns: Schneider et al., 2004; Watkins and Cardelús, 2012; Testo and Sundue, 2016). However, biodiversity knowledge in the rosids remains limited, with perhaps only 23% of species having usable molecular data for phylogenetics (i.e., not repetitive DNA and other non‐conserved markers; Folk et al., 2018). Species sampling is likewise biased (Sun et al., 2019 [Preprint]); species coverage is highly uneven, with economically important groups including the legume and beech orders (Fabales, Fagales) overrepresented compared to important but less familiar tropical groups such as Malpighiales (Folk et al., 2018).

Despite previous efforts to assess the impact of incomplete sampling (e.g., Cusimano et al., 2012; Höhna, 2014; Title and Rabosky, 2017), much remains unknown about how incomplete and biased taxon‐sampling approaches impact diversification estimates, particularly with empirical supermatrices. Additionally, much of the methodological literature cited above does not include use of the most recent methods now widely used in the community. Hence, incomplete taxon coverage in the rosids is an opportunity to characterize the robustness of contemporary methods with a large, typical empirical data set covering a wide range of sampling levels, as a complement to numerous recent simulation studies.

We used a recently constructed, five‐locus, 19,700‐taxon tree for rosids (molecular data only; hereafter “20k‐tip tree”; Sun et al., 2019 [Preprint]) to compare with a previously published four‐gene, 8855‐taxon rosid phylogeny (molecular data only; hereafter “9k‐tip tree”; Sun et al., 2016) as well as a rosid tree with complete species sampling extracted from the inclusive seed plant phylogeny (molecular data and taxonomic data; Smith and Brown, 2018; hereafter “100k‐tip tree”), which used the taxonomy of the OpenTree (Hinchliff et al., 2015). We explored results generated using these phylogenies from a suite of commonly used diversification approaches, comprising two parametric methods, RPANDA (Morlon et al., 2016) and BAMM (Rabosky, 2014) and one semiparametric method (the DR statistic; Jetz et al., 2012).

We focused on the following questions: (1) Do commonly used contemporary methods differ in their robustness to poor overall sampling? (2) Do data sets generated by random and representative sampling strategies result in different diversification inferences? (3) Does adding backbone taxonomic information improve diversification inference? To answer these questions, we examined both variation in empirical sampling patterns in major rosid clades and a series of sampling perturbations to simulate random and representative sampling methods. Using the workflow summarized in Fig. 1, we document a remarkably complex impact of taxon sampling on inference of macroevolutionary patterns.

Figure 1.

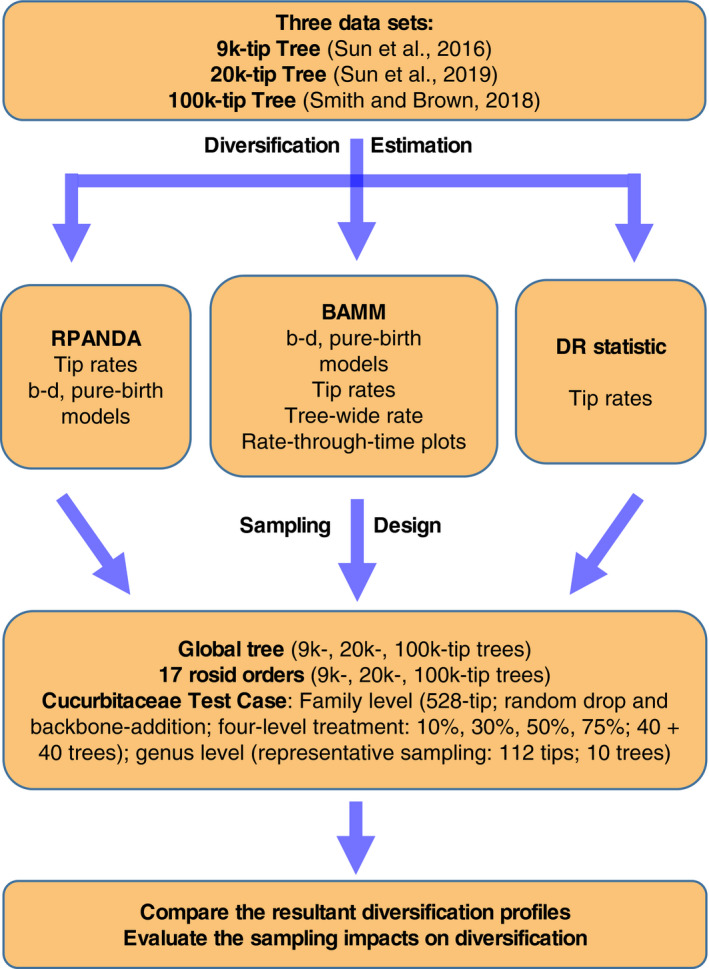
Workflow employed for empirical data and simulations in this study. Abbreviation notes: 9k‐tip tree = four‐gene, 8855‐species rosid tree from Sun et al. (2016); 20k‐tip tree = five‐locus, 19,740‐species rosid tree from Sun et al. (2019 [Preprint]); 100k‐tip tree = 106,910‐species tree extracted from Smith and Brown (2018); b–d = nine birth‐death models from RPANDA and BAMM (see Appendix S1a); pure‐birth model analyses conducted by RPANDA and BAMM (see Appendix S3b, c). “Tree‐wide rate” means speciation rate averaged throughout the tree.

MATERIALS AND METHODS

Study context

Studies of the performance of diversification estimation and other macroevolutionary methods on empirical data sets have been rare. In contrast to simulation studies, we do not have a completely sampled “true” tree for comparison, and to some extent all comparisons are on relative terms. However, characterizing representative empirical data sets offers three key advantages over simulation. First, we can obviate the need to choose realistic data‐set‐generating parameters like speciation rates, which do not need to be assumed with empirical data or derived with some degree of circularity from diversification models. Second, the choice of a large and globally distributed clade such as the rosids, covering a broad range of sampling efforts and underlying diversification regimes, also obviates concerns about selecting a sufficiently representative group from which to derive insight (see Beaulieu and O’Meara, 2018) or exploring a meaningful set of predefined generative parameters. Finally, the use of empirical data means we have implicitly included numerous sources of heterogeneity that are always present in macroevolutionary approaches but often incompletely addressed in simulation studies. While it is common to model gene tree estimation error, parameters on the broader sources of phylogenetic heterogeneity (e.g., the degree of incomplete lineage sorting, gene tree estimation error, model violations) are usually unknown. It is therefore challenging to model large, heterogeneous supermatrix data sets, but investigations of empirical data sets have the advantage of implicitly containing all of these unknown generating processes at once. Hence, our approach complements a large body of simulation literature while identifying novel patterns relevant to a broad range of empirical inquiries based on diversification models.

The 9k‐tip tree

This is the four‐gene tree of Sun et al. (2016) based on three chloroplast loci (atpB, rbcL, and matK) and one mitochondrial locus (matR). The data set consists of 8855 ingroup species with 59.26% missing data, and the tree is largely congruent with other phylogenetic results for rosids (e.g., Wang et al., 2009; Soltis et al., 2011; Ruhfel et al., 2014; Gitzendanner et al., 2018).

The 20k‐tip tree

The 20k‐tip tree was built by adding the nuclear ITS locus to the four genes in the matrix of Sun et al. (2016), resulting in a five‐locus matrix with 19,740 ingroup species (135 families and 17 orders) and 70.55% missing data (see Sun et al., 2019 [Preprint]). All families are monophyletic, and this phylogeny is also largely congruent with other inferences of rosid phylogeny (e.g., Wang et al., 2009; Soltis et al., 2011; Sun et al., 2016; Gitzendanner et al., 2018).

The 100k‐tip tree

We also assembled a complete species‐level tree with branch lengths for all named rosid species from Smith and Brown (2018). We pruned the rosid clade from a recent phylogeny dating all seed plants using the OpenTree taxonomy (see details in Smith and Brown, 2018; https://github.com/FePhyFoFum/big_seed_plant_trees/releases; file “ALLOTB.tre”), removed non‐species designations, and smoothed the branch lengths after pruning. These steps were completed via functions from Phyx (Brown et al., 2017) and scripts from OpenTree PY Toys (https://github.com/blackrim/opentree_pytoys). The final cleaned tree contained 106,910 tips.

Divergence time analyses for these three trees (9k‐, 20k‐, and 100k‐tip) were conducted previously (see details provided by Sun et al. [2019 (Preprint)] and Smith and Brown [2018], respectively; Fig. 2). Briefly, Sun et al. (2019 [Preprint]) used treePL with 59 fossil constraints for the 9k‐tip (Sun et al., 2016) and the 20k‐tip phylogenies; likewise, Smith and Brown (2018) used treePL with 590 constraints extracted from Magallón et al. (2015) for dating all seed plants.

Figure 2.

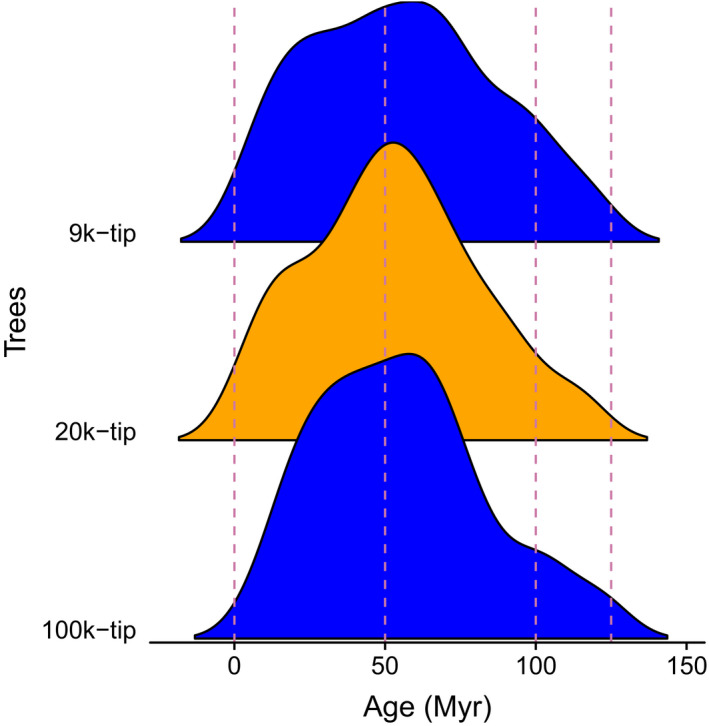
Age distribution of crown ages for rosid clades extracted from the 9k‐, 20k‐, and 100k‐tip trees. The dating method used is treePL. The 9k‐tip and 100k‐tip trees are shown in blue, and 20k‐tip tree is in orange. For the dated treePL trees used in this study, the probability density distributions of clade dates were very similar across very different sampling levels.

Diversification analyses and comparisons

To understand the impact of sampling strategies, we first used trends in empirical sampling across the three trees to investigate the correlation between sampling and inferred diversification. We compared patterns for three overall trees and for the 17 orders (each monophyletic and recognized by APG IV [2016]) of the rosid clade, the species‐level sampling of which differs by up to eightfold among the trees. For the 17 order‐level clades from all three rosid trees (9k‐tip, 20k‐tip, and 100k‐tip trees), we consistently applied three widely used contemporary methods: RPANDA (Morlon et al., 2016), BAMM (Rabosky, 2014), and the DR statistic (Jetz et al., 2012; for implementation details, see below).

Despite our use of birth‐death models, we focus on reporting speciation rates hereafter. We were motivated to focus on speciation alone because, as recently shown by Title and Rabosky (2019), semiparametric methods for estimating “diversification” rates measure speciation rate alone. Despite uncertainty about best practices in the use of parametric and semiparametric approaches, both are popular in the community, and our wish to include the most commonly used methods motivated the use of speciation rates. We focused on the speciation rate of present‐day lineages in particular (i.e., speciation rate at time zero or “tip rate”). This approach has the advantage of generating a metric that is directly comparable across all of the methods employed and commonly used across a wide variety of investigations (see Title and Rabosky, 2019; but see also Diaz et al., 2019). Extinction rates are challenging to estimate from extant‐only phylogenies, and estimates are often unrealistically low (Rabosky, 2010, 2016). Reported estimates likely exhibit systematic bias, and as a result there is reason for caution in drawing empirical insight from these statistics. Nevertheless, this focus means we are unable to disentangle the possibility of differential effects of methodological choices on speciation and extinction estimation; such impacts merit further investigation beyond the present study. We used both global tip speciation rates (i.e., speciation rates estimated at present, averaging across species; RPANDA and BAMM) and distributions of rates for individual contemporary species (= “tip rates”; BAMM and DR). For BAMM, we additionally examined speciation rates throughout the timeline of the phylogeny, using both averages across the entire tree (hereafter “tree‐wide speciation rates”) and rate‐through‐time plots.

Sampling treatments: Cucurbitaceae test case

To examine diversification patterns further by generating known sampling patterns, we used the best‐sampled rosid family (Cucurbitaceae; ~64% sampling), following Flora of North America (Nesom, 2015) and Flora of China (Lu et al., 2011).

We extracted the Cucurbitaceae clade (a subset of 528 tips) from the 20k‐tip tree to maximize species representation with molecular data alone. We simulated both random and representative sampling schemes, the former with and without backbone taxonomies. First, we simulated randomly missing species by randomly dropping extant species from the original Cucurbitaceae tree at four sampling levels (10%, 30%, 50%, and 75% of sampled species), with 10 replicates for each sampling treatment. Second, we simulated randomly missing species that are added in via backbone taxonomies (hereafter “backbone‐addition”) via randomly dropping extant species at four sampling levels (10%, 30%, 50%, and 75% of sampled species) and then adding them back to the phylogeny by attaching them to the most recent common ancestor (MRCA) of the genus, with the tip branch length extended to the present, similar to the method used in Smith and Brown (2018). If there were not at least two species of a genus sampled to generate a genus node, the missing taxon was attached to the root of the tree (i.e., it was assignable to the family Cucurbitaceae, but not to any sampled genus node). These steps were done in 10 replicates with OpenTree PY Toys (https://github.com/blackrim/opentree_pytoys). Finally, to simulate representative sampling, we pruned this tree to a genus‐level phylogeny by randomly selecting one species in each genus in 10 replicates. Across these scenarios, we repeated the diversification methods for empirical trees (above) on these replicate trees.

Diversification methods

We used RPANDA version 1.4 (Morlon et al., 2016), a likelihood method, to fit nine diversification models representing constant, linear, and exponential time‐dependent birth‐death and pure‐birth models (Morlon et al., 2014; Appendices S1a and S3b). The best model was chosen individually across all empirical data sets, and simulated replicates and parameters presented are always from the individual best model (but see also Appendix S3a for Akaike‐weighted parameter averages across models). We accounted for incomplete sampling in each analysis to test whether this is adequately modeled by RPANDA, basing the sampling ratio on the total species number in the Open Tree Taxonomy (OTT) database (Table 1). We extracted the speciation rate parameter at the present for downstream analyses as a metric comparable to commonly used per‐species “tip rates” derived below from BAMM and DR. This quantity represents global speciation rates estimated for extant taxa (hereafter “global tip speciation rate”).

Table 1.

Ordinal‐level summary sampling table for the 9k‐tip and 20k‐tip rosid sampling compared to the rosid clade of the Open Tree Taxonomy (OTT) database version 3.0 (https://devtree.opentreeoflife.org/about/taxonomy‐version/ott3.0; Hinchliff et al., 2015) and matching taxon names between these data sets. Orders follow APG IV (2016). A summary table at the family level for the 20k‐tip tree is available in Sun et al. (2019).

Order	9k‐tip Tree		20k‐tip Tree
	Matched genus (%)	Matched species (%)	Matched genus (%)	Matched species (%)
Brassicales	36.85	7.49	71.12	28.50
Celastrales	59.45	13.34	61.26	18.15
Crossosomatales	92.85	29.26	92.86	29.27
Cucurbitales	85.71	13.93	87.97	26.60
Fabales	66.66	8.25	76.04	21.95
Fagales	44.59	10.91	48.65	21.92
Geraniales	60.00	12.16	75.00	30.67
Huerteales	100.00	23.33	100.00	23.33
Malpighiales	64.98	8.33	65.77	17.37
Malvales	54.81	9.72	62.96	16.54
Myrtales	48.21	4.05	54.11	8.28
Oxalidales	59.42	4.21	62.32	8.25
Picramniales	66.66	8.77	66.67	8.77
Rosales	54.03	3.38	60.45	8.22
Sapindales	56.98	11.21	62.07	18.34
Vitales	60.00	3.63	60.00	9.52
Zygophyllales	62.96	10.58	66.67	17.65
Total	57.80	7.28	66.34	16.25

We used BAMM version 2.5.0 (Rabosky, 2014), a Bayesian approach, to estimate tip speciation rates as with RPANDA (above). We also used BAMM to explore non‐contemporary speciation rates, examining both tree‐wide speciation rates (i.e., speciation rates averaged across all tree time frames including the present) and rate‐through‐time plots (i.e., speciation rates averaged in temporal windows; Appendix S1b). We also accounted for incomplete sampling in BAMM (see details in Appendix S1b), parameterizing this identically to RPANDA (above).

As an additional examination of common practices, we used BAMM to explore the impact of a global sampling probability (one missing species proportion imposed as the parameter for the entire tree) and species‐specific sampling probabilities (missing species parameters for arbitrarily defined clades, often named taxa) on diversification rates implemented in BAMM. We confirmed convergence of the Markov chain Monte Carlo (MCMC) chains and effective sample sizes >200 for the number of both shifts and log likelihoods (Appendix S2a), after discarding at least 10% burn‐in when necessary. The exception was in order‐level BAMM analyses for the 100k‐tip tree, for which six orders (Brassicales, Fabales, Malpighiales, Myrtales, Rosales, and Sapindales) could not reach suitable effective sample sizes despite runs in some cases exceeding 400 million generations; in these cases we imposed a 90% burn‐in to ensure adequate convergence and reduce downstream computational time. We present results from these orders for comparison; results were qualitatively similar to other orders in the 100k‐tip tree (see below).

Lastly, we employed the DR statistic (Jetz et al., 2012), one of the most widely used semiparametric approaches to diversification estimation. The DR statistic quantifies the “splitting rate” from each extant species to the tree root as a likelihood‐free estimate of diversification rate. Methods followed those described in Jetz et al. (2012) and Harvey et al., 2017). There is no straightforward way to model incomplete sampling with the DR statistic (but see Rabosky et al., 2018); aside from calculating DR for our 100k‐tip synthetic tree, we did not account for missing taxa in order to represent the most typical way in which this statistic has been used. For BAMM, it was impossible to achieve convergence in the global 20k‐tip and 100k‐tip trees, so we ran this method only on the 17 rosid orders (APG IV, 2016); global tree results were successfully generated only in DR and RPANDA.

Finally, given that we use a mix of pure‐birth approaches (DR and some RPANDA best models) and birth‐death models (BAMM) as discussed above, we verified that pure‐birth models in BAMM give similar results (Appendix S3). Parameters for suboptimal RPANDA models are also presented in Appendix S3.

RESULTS

Diversification analyses

Empirical diversification patterns

RPANDA

Both the 9k‐tip and 20k‐tip trees favored a birth‐death model with speciation and extinction rates varying exponentially with time; the optimal model for the 100k‐tip tree was a pure birth model with linear speciation rate with respect to time (Appendices S1a and S2b). The tip speciation rate was highest for the 9k‐tip tree (1.3905 Myr⁻¹), with similarly high results from the 20k‐tip tree (1.3058 Myr⁻¹); estimated rates for the 100k‐tip tree were much lower (0.0446 Myr⁻¹; Fig. 3A). Likewise, the best models based on model selection and estimated speciation rates among the 17 orders are generally similar among the 9k‐tip, 20k‐tip, and 100k‐tip trees described above (Appendix S2b). We calculated the Akaike‐weighted averages of speciation rates from a pool of models, and they are extremely similar to the best‐model values (see Appendices S2b and S3a).

Figure 3.

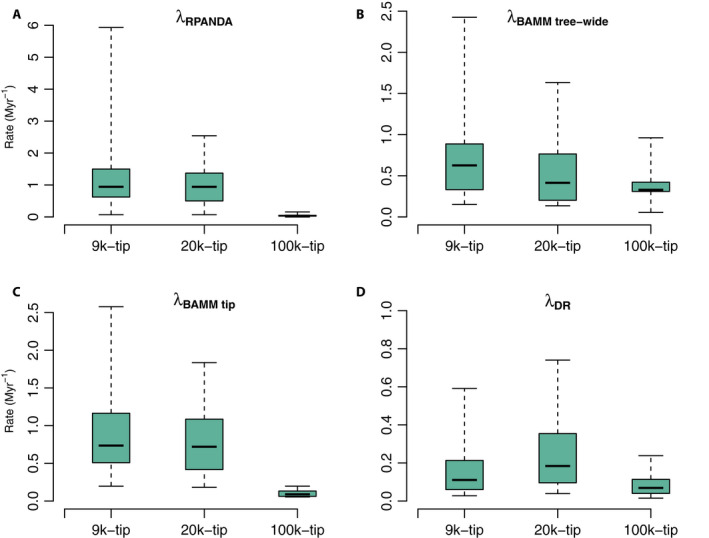
Tip speciation rate box plots across the three empirical data sets (i.e., 9k‐tip, 20k‐tip, and 100k‐tip trees). Panels A–D correspond to contemporary speciation rates (λ) estimated by RPANDA (λ_RPANDA), BAMM (speciation rate: λ_{BAMM tree‐wide}; and tip rate: λ_{BAMM tip}), and DR (λ_DR), respectively. The boxes and whiskers represent the 0.25–0.75 and the 0.05–0.95 quantile ranges.

BAMM

The values of both mean tip speciation rates and mean tree‐wide speciation rates from the 9k‐tip tree (1.1527 Myr⁻¹ and 0.7829 Myr⁻¹, respectively) are higher than those from the 20k‐tip tree (1.0731 Myr⁻¹ and 0.5601 Myr⁻¹; Appendix S2a and Fig. 3) and much higher than those from the 100k‐tip tree (0.1136 Myr⁻¹ and 0.3914 Myr⁻¹; Appendix S2a and Fig. 3B, C). Among the 17 orders, both the tip and tree‐wide speciation rates from the 9k‐tip tree are likewise generally slightly higher than those from the 20k‐tip tree and much higher than those from the 100k‐tip tree (Appendix S2a and Fig. 3B, C).

DR

On average, DR tip rates estimated from the 20k‐tip tree yielded the highest value (0.4644 Myr⁻¹), the 9k‐tip tree was intermediate at 0.1889 Myr⁻¹, while the 100k‐tip tree yielded the lowest (0.0902 Myr⁻¹; Appendix S2c and Fig. 3D). As with the previous methods, this overall tree‐dependent scaling was also generally true across the 17 orders (Appendix S2c).

Sampling and diversification among rosid orders

RPANDA and BAMM showed a negative relationship between sampling ratio and estimated rates across the empirical data for the 17 rosid orders (i.e., orders with less sampling effort had greater estimated speciation rates, suggesting an inflation of estimates). However, this correlation was not significant (cf. Fig. 4). The DR method, which does not model sampling effort, showed a strong positive correlation (P = 1.658e‐07) between sampling ratios and estimated rates, meaning that decreasing sampling effort predicts lower estimated speciation rates using this method (Fig. 4).

Figure 4.

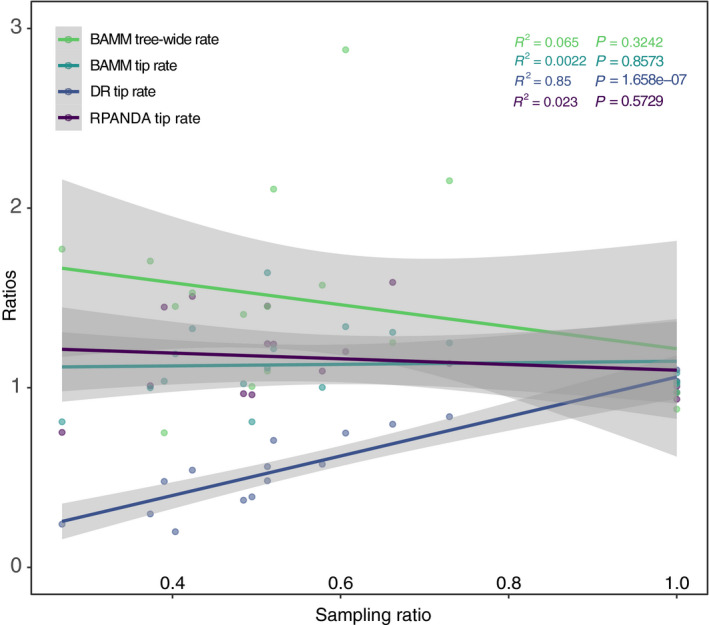
Correlation between sampling effort and speciation rates among the 17 rosid orders from 9k‐tip and 20k‐tip trees. The x‐axis is the ratio of sampling percentages; the y‐axis is the ratio of speciation rates (9k‐tip/20k‐tip in both cases; values closer to one indicate values closer to the more fully sampled 20k‐tip tree); each dot represents a single rosid order. The R ² and P values are color‐coded following the legend colors. Gray plot zones indicate curve 95% confidence intervals. Only the DR statistic showed a significant positive relationship between sampling percentage and diversification rate; for other methods, the rosid orders do not show a significant relationship between sampling effort and estimated speciation rate.

Rate‐through‐time curves across all orders showed strong differences among the three trees (Appendix S4). The 9k‐tip and 20k‐tip trees were most similar across analyses; however, the improved sampling of the 20k‐tip tree allowed for the detection of recent bursts within the past 15 million years in several orders that were not inferred in the 9k‐tip tree (e.g., Brassicales, Cucurbitales, Fabales, Malpighiales, and Vitales; Appendix S4). The difference between the 100k‐tip tree and the 9k‐tip and 20k‐tip trees was more substantial. In the 100k‐tip tree, with the exception of Huerteales, all order‐level analyses detected early bursts of speciation not found in other trees, with lower estimated tip rates (i.e., rates at time zero) than the 9k‐tip and 20k‐tip trees (also see Fig. 3C).

Cucurbitaceae test case: Random sampling simulation

RPANDA

With randomly incomplete sampling, the estimated global tip speciation rate increased with decreasing sampling effort, ranging about 1.5‐fold from 0.4687 Myr⁻¹ (10% random drop) to 0.7263 Myr⁻¹ (75% random drop; Fig. 5A and Appendix S2d). The 75% random‐drop treatment was significantly higher in tip speciation rate than all other treatments; no other treatment comparisons were significantly different (Tukey’s HSD; see Appendix S2e).

Figure 5.

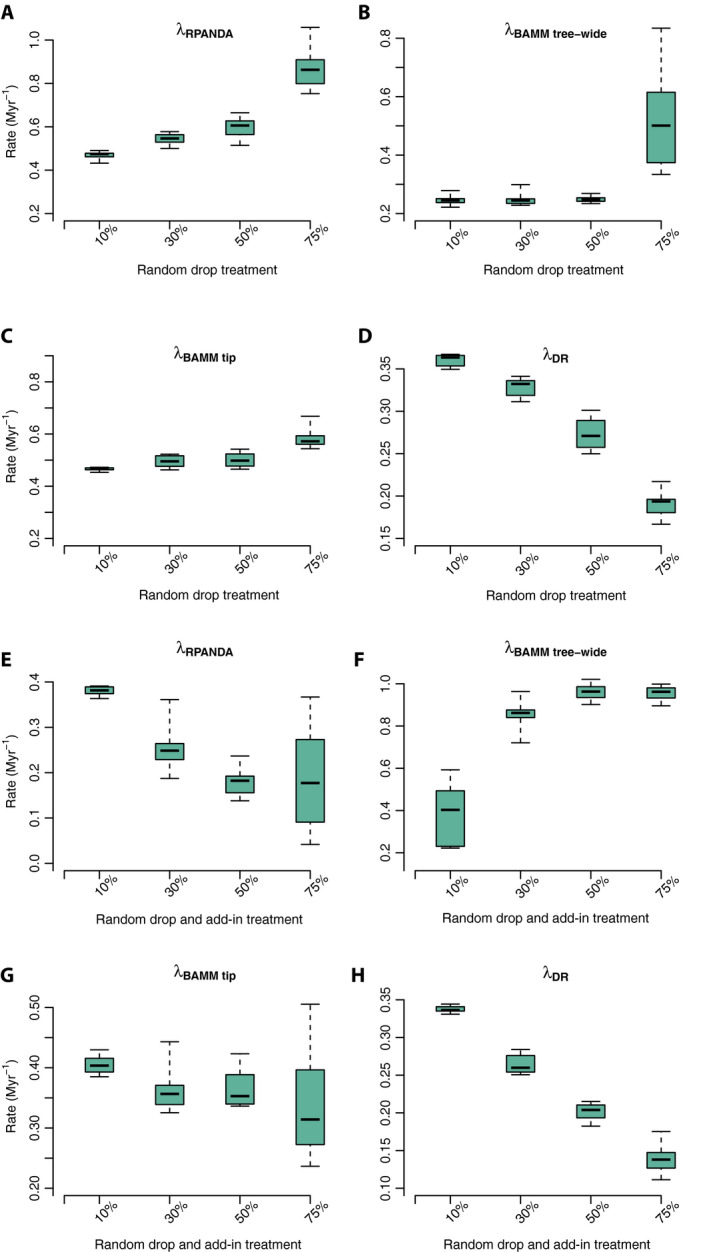
Sampling simulation box plots with four treatments and three different rate metrics using the Cucurbitaceae tree. Contemporary speciation rates (λ) estimated by RPANDA (λ_RPANDA), BAMM (speciation rate: λ_{BAMM tree‐wide}; and tip rate: λ_{BAMM tip}), and DR (λ_DR). Panels A–D correspond to the random sampling simulations; panels E–H correspond to the random sampling simulations with backbone‐addition following similar labeling conventions to A–D.

BAMM

As with RPANDA, higher estimated mean tip speciation rates and tree‐wide speciation rates were both associated with decreasing sampling effort under random sampling, ranging from 0.4658 Myr⁻¹ to 0.6508 Myr⁻¹ for mean tip speciation rates and from 0.2466 Myr⁻¹ (10% randomly dropped) to 0.5261 Myr⁻¹ (75% randomly dropped) for mean tree‐wide speciation rates (Fig. 5B, C; see Appendix S2d). These rates were statistically identical for all treatments except the 75% random‐drop treatment (Tukey’s HSD; see Appendix S2e).

Rate‐through‐time plots from the trees show a similar pattern (Fig. 6) to those observed for tip speciation rates. All of the sampling treatments tend to be similar in rate magnitude and curve shape to the complete tree except for the 75% random drop treatment; in this treatment the overall speciation rates are higher in all time frames, and the curves tend to be flattened and linearized, with few of the complex details apparent with greater sampling (Fig. 6).

Figure 6.

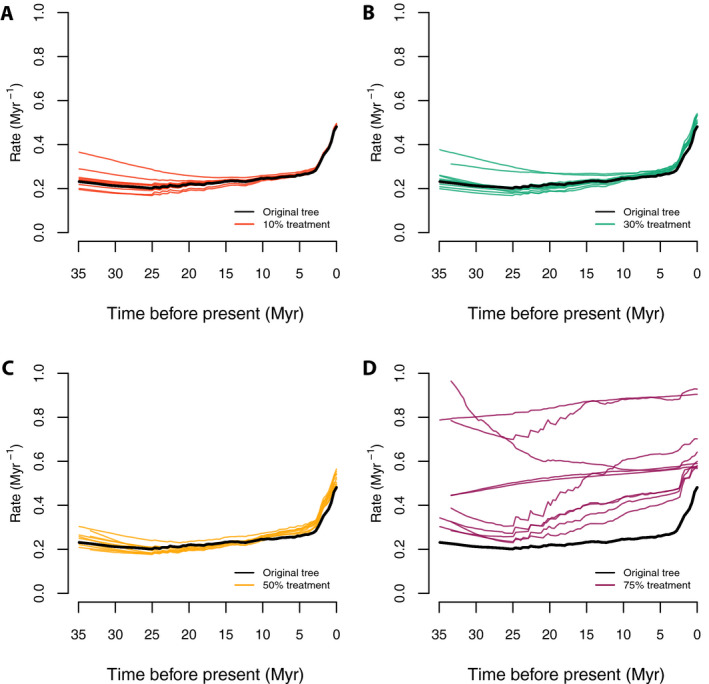
Speciation rate‐through‐time plots with the random sampling simulations. Panels A–D correspond to the color‐coded rate‐through‐time curves generated by 10 random trees each, under 10%, 30%, 50%, and 75% of taxa randomly dropped, respectively; the thick black lines stand for the original Cucurbitaceae 528‐tip tree. The results for all sampling treatments were similar to the full empirical sampling result except for the most extreme experiment (75% of tips dropped).

DR

In contrast to RPANDA and BAMM, DR rates decreased with decreasing sampling effort from 0.3599 Myr⁻¹ (10% random drop) to 0.1910 Myr⁻¹ (75% random drop; Fig. 5D and Appendix S2d). The DR rates were significantly different across all treatment comparisons (Tukey’s HSD; see Appendix S2e).

Summary

As observed with empirical sampling among the 17 rosid orders (above), the estimated contemporary speciation rates increased in RPANDA and BAMM with decreasing sampling effort (10% to 75% random drop; Fig. 5A, C), while rates estimated in DR decreased with decreased sampling (Fig. 5D).

Cucurbitaceae test case: Random sampling simulation with backbone taxonomic addition

RPANDA

Under randomly incomplete sampling with addition of taxa via backbone taxonomies, the estimated tip speciation rate decreased with decreasing sampling effort (in contrast to random sampling alone; see above), ranging about fourfold from 0.3740 Myr⁻¹ (10% backbone‐addition; comparable to the 10% random drop treatment, above) to 0.0966 Myr⁻¹ (75% backbone‐addition; Appendix S2d). The 10% backbone‐addition treatment was significantly higher in contemporary speciation rate than all other treatments (Fig. 5E); no other treatment comparisons were significant (Tukey’s HSD; see Appendix S2f).

BAMM

As with RPANDA, estimated mean tip speciation rates decreased with decreasing sampling effort and backbone‐addition, although the effect was smaller, ranging from 0.4054 (10% random drop and add‐in) Myr⁻¹ to 0.3412 (75% random drop and add‐in; Fig. 5G and Appendix S2d). The 10% backbone‐addition treatment was significantly higher in contemporary speciation rates than all other treatments; the remaining treatment comparisons were not significant (Tukey’s HSD; see Appendix S2f).

Unlike tip speciation rates, decreasing sampling effort with backbone‐addition resulted in increased estimated tree‐wide speciation rates, ranging from 0.3871 Myr⁻¹ (10% random drop and add‐in) to 0.9545 Myr⁻¹ (75% random drop and add‐in; Fig. 5F and Appendix S2d). In this case, the tree‐wide rates were higher than the tip rates, indicating that the sampling scenario induced early‐burst inferences (below). The 10% backbone‐addition treatment was significantly lower in contemporary speciation rates than all other treatments; no other treatment comparisons were significant (Tukey’s HSD; see Appendix S2f).

Rate‐through‐time plots from these backbone‐addition trees all show a similar pattern of inferring spurious early bursts of diversification (Fig. 7) that were not reconstructed in the original Cucurbitaceae tree (Fig. 7; black curve). Unsurprisingly, these bursts correspond to nodes where backbone taxonomic data were added in these trees.

Figure 7.

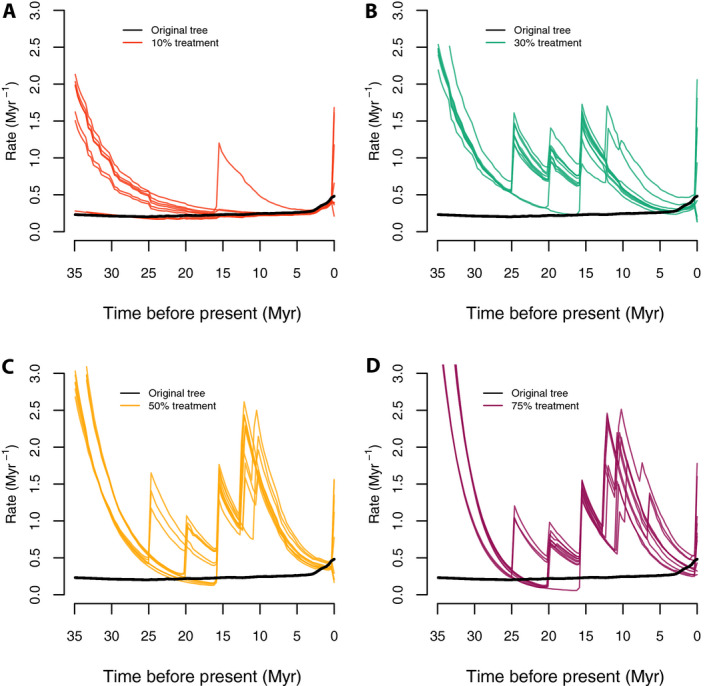
Speciation rate‐through‐time plots with the random sampling and backbone‐addition simulations. Panels A–D correspond to the color‐coded rate‐through‐time curves generated by 10 random trees each under 10%, 30%, 50%, and 75% of taxa randomly dropped and added in as backbone taxonomic data, respectively; the thick black lines stand for the original Cucurbitaceae 528‐tip tree. With moderate missing taxa (10% of tips dropped), few spurious early bursts were inferred, but these were frequent with more missing taxa.

DR

DR rates decreased with decreasing sampling effort from 0.3372 Myr⁻¹ (10% random drop and add‐in) to 0.1397 Myr⁻¹ (75% random drop and add‐in; Fig. 5H and Appendix S2d). The DR rates estimated from all four‐level backbone‐addition treatments were significantly different for all group comparisons (Tukey’s HSD; see Appendix S2f).

Summary

Using backbone taxonomic addition to account for missing taxa did not prevent under‐ or overestimated tip speciation rates. Adding backbone taxa tended to result in the inference of spurious early bursts of diversification (Fig. 7), consistent with the empirical results for the 100k‐tip tree (above).

Cucurbitaceae test case—Representative sampling simulation

RPANDA

Under a representative sampling scenario, the mean tip speciation rate for representative sampling simulations was 0.3022 Myr⁻¹ (Fig. 8; see Appendix S2g), about 1.5× lower than that for the complete Cucurbitaceae tree (0.4635 Myr⁻¹); hence, estimated speciation rates decreased with decreased sampling, opposite the pattern recovered above with random sampling, but similar to that recovered with random sampling with backbone‐addition.

Figure 8.

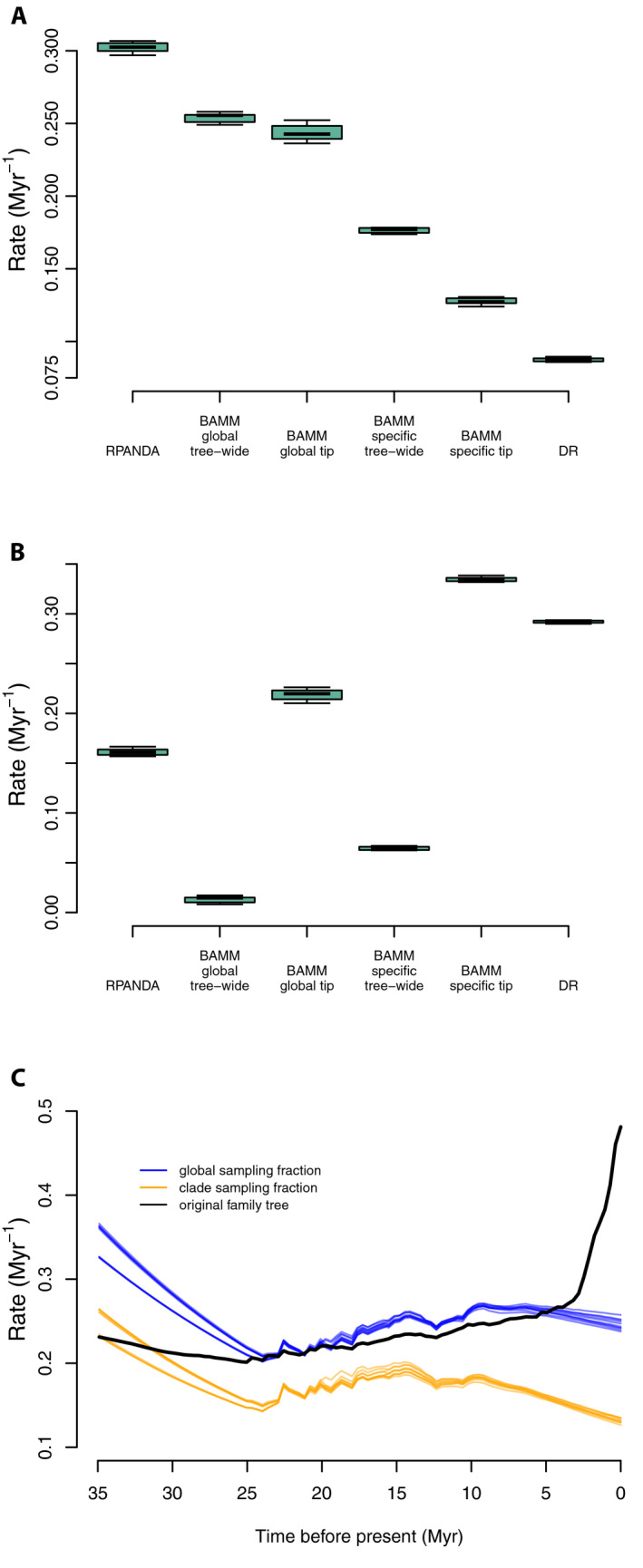
Comparisons of tip speciation rate for full empirical and representative sampling levels for RPANDA, BAMM, and DR using Cucurbitaceae data. (A) Box plot of contemporary speciation rate and tree‐wide rate (BAMM) of the 10 random genus‐level tree results estimated by RPANDA, BAMM, and DR. (B) Box plot showing rate differences by subtracting rates in panel A from those inferred from the family‐level 528‐tip tree; zero would indicate identical results. Note that in some cases the magnitude of the difference is nearly as large as the overall speciation rate. (C) Color‐coded rate through time plots in BAMM showing rate differences among global sampling fraction (blue), clade‐specific sampling fraction (orange), and original family tree (black). Abbreviations: BAMMglobal tip = tip speciation rates estimated with global sampling fractions; BAMMglobal tree‐wide = tree‐wide speciation rates estimated with global sampling fractions; BAMMspecific tip = tip speciation rates estimated with clade‐specific sampling fractions; BAMMspecific tree‐wide = tree‐wide speciation rates estimated with clade‐specific sampling fractions.

BAMM

Unlike RPANDA, BAMM has two approaches for handling incomplete sampling, both implemented here: specifying either clade‐specific or global missing taxon parameters. While global sampling fractions were used elsewhere, we included clade‐specific sampling fractions here to match common methods used for family‐level trees and other backbone phylogenetic data. In the global sampling fraction scenario, mean tip speciation rates (0.1275 Myr⁻¹) were lower than those estimated from the global tree (0.4625 Myr⁻¹), while mean tree‐wide speciation rates (0.2539 Myr⁻¹) were higher than those estimated from the global tree (0.2408 Myr⁻¹). Clade‐specific sampling fractions resulted in unilaterally lower estimated speciation rates; both mean tip rates (0.1275 Myr⁻¹) and mean tree‐wide speciation rates (0.1764 Myr⁻¹) were lower than those estimated from the global tree (0.4625 Myr⁻¹ and 0.2408 Myr⁻¹, respectively; Fig. 8 and Appendix S2g).

Rate‐through‐time plots (Fig. 8C) were similar to the mean rate results. Global sampling factions tended to increase the scaling of the entire rate curve, with up to about 2× higher speciation rates (at the present), compared to assigning cladewise sampling fractions; the global sampling fraction result was closer to that for the total Cucurbitaceae tree. While the scaling was different, the rate‐through‐time curves were similar in completely failing to detect the burst of speciation rates toward the present seen in the total Cucurbitaceae tree (Fig. 8C); instead, BAMM inferred a spurious early burst of speciation rates at the root (see also backbone‐addition, above).

DR

The mean DR tip rate for the representative sampling trees was 0.0875 Myr⁻¹, far lower than for the total Cucurbitaceae tree (0.3794 Myr⁻¹), as well as lower than the other rates estimated by RPANDA and BAMM (Fig. 8A, B).

Summary

Across methods, representative sampling results in lower tip speciation rate estimates, an effect similar to that obtained with backbone‐addition (above). Both patterns appear to be solely driven by biases in sampling ancestral nodes, whether failing to sample nodes representing recent divergences (representative sampling) or sampling recent divergences but pushing them back in relative time (backbone‐addition). Tree‐wide speciation rates were typically higher with these sampling strategies; rate‐through‐time curves (Fig. 8C) showed that this behavior is due to failure to detect recent bursts of speciation and instead inferring higher rates of evolution at earlier time intervals (see also Cusimano et al., 2010).

DISCUSSION

We found surprisingly diverse effects of sampling effort on inferences of diversification using the methods we employed. Overall, BAMM, the only method we used that can model taxon‐specific patterns of incomplete sampling, showed the greatest robustness to incomplete sampling under the widest variety of scenarios. In BAMM, all random taxon‐dropping treatments resulted in statistically identical tip speciation rates, with the exception of the most extreme treatment (dropping 75% of taxa; Fig. 5B, C), where the estimated tip speciation rate increased dramatically (Appendix S2d). BAMM also tended to be more robust to the other sampling scenarios that are more divergent from the modeling assumptions, with the exception of representative sampling, where no method was robust. Tree‐wide speciation rates and rate‐through‐time curves in BAMM showed patterns similar to the speciation rates on which we have primarily focused (Figs. 6 and 7), although in most cases these metrics were more sensitive to incomplete sampling than tip speciation rates. Interestingly, tip rates were also less perturbed by the choice of pure‐birth models (Appendices S3b–d) or birth‐death models than other summary statistics. For most orders in rosids, the rate curve estimated under a pure‐birth model loses much of the fine‐scale temporal dynamics in speciation rate compared with birth‐death models (see the solid lines vs. dashed lines in Appendix S3d), which indicates that pure‐birth models are not realistic and practical.

In contrast to BAMM, both RPANDA and DR were highly sensitive to missing taxa. For most analyses, the effect of all incomplete sampling scenarios using RPANDA and DR was disturbingly near linear (e.g., Fig. 5A, D), in contrast to the threshold behavior of BAMM, despite the substantial differences between these two approaches. Methods also differed in the direction of parameter bias in response to incomplete sampling; DR in all cases resulted in underestimates of tip speciation rates, consistent with a failure to account for incomplete sampling. BAMM and RPANDA, by contrast, alternatively under‐ or overestimated speciation rates compared to the complete tree depending on sampling scenario, suggesting a relatively unpredictable ability to account for incomplete sampling.

Opposing bias patterns in representative and random sampling

Under the random sampling scenarios simulated here, speciation estimates increased in both RPANDA and BAMM with decreasing sampling efforts (i.e., they were overestimated; Fig. 5). By contrast, representative sampling resulted in decreased estimates of tip speciation rate across methods. In contrast to random sampling, BAMM tip rates were not robust to representative sampling strategies, and these simulations exhibited some of the greatest differences in estimated rates from the complete Cucurbitaceae tree (Fig. 8B and Appendix S2g).

Only BAMM and RPANDA showed differential bias patterns in taxon‐removal experiments, whereas with DR (which does not model taxon absence), decreased sampling always resulted in underestimates of speciation rates. Similarly, results across the 17 rosid orders showed that poorly sampled lineages had higher speciation rates in BAMM and RPANDA. These results suggest that modeling taxon absence can result in a potentially problematic “correction” that inflates rate parameters. These results make intuitive sense and are consistent, to some extent, with previous literature (e.g., Cusimano and Renner, 2010). While we attempted to account for incomplete sampling, typically, missing species must be modeled as randomly missing in most implementations of diversification methods. Representative sampling can be seen as a form of sampling bias in that it selectively preserves long phylogenetic branches while dropping short branches. This will have the effect of masking recent, shallow radiation events (which will have disproportionately poor sampling) and pushing apparent diversification patterns backwards in time and depressing estimates of extinction (see Cusimano and Renner, 2010; Höhna et al., 2011). Rate‐through‐time plots in BAMM exemplify this effect (Fig. 8C and Appendix S4); representative sampling flattened inferred curves and essentially erased any signal of recent diversification, an effect seen only in random sampling with the most extreme scenario (75%; Fig. 6). Instead of a recent burst, representative sampling tends to result in spurious inferences of early bursts not evident with improved sampling (see also Cusimano and Renner, 2010). Understanding this bias is important, as typical molecular phylogenetic sampling schemes seek to represent deep phylogenetic branches disproportionately (Höhna et al., 2011); hence, genetic resources such as GenBank are likely to be populated primarily by data from studies that used representative sampling schemes.

Comparison with an angiosperm‐wide study

As an additional exploration of sampling protocols, our BAMM mean speciation rates for the molecular‐only trees (9k‐tip and 20‐k tip; Appendix S2a) can be directly compared to a recent angiosperm‐wide analysis in BAMM exemplifying very coarse representative sampling (Magallón et al., 2018; cf. Supplemental Data) covering 792 species or ~0.2% of angiosperm species richness. While Magallón et al. (2018) accounted for incomplete sampling with similar methods to the present study, the difference in results is remarkable. Our estimates of speciation rate with stronger sampling in the same rosid orders (including tree‐wide averages and rate‐through‐time plots) were uniformly higher, the difference sometimes exceeding an order of magnitude (e.g., compare Sapindales, Myrtales, and Vitales; Magallón et al., 2018: fig. 3). The mean clade speciation rates we obtained from BAMM ranged up to ~2.5 Myr⁻¹ for the 9k‐tip tree and ~1.7 Myr⁻¹ for the 20‐tip tree, all values consistent with other rapidly diversifying plant taxa (scaling of plant diversification rates is reviewed in Lagomarsino et al., 2016). All mean clade speciation rates reported in Magallón et al. (2018) were at least 5× smaller in magnitude, and even the highest speciation rates for individual lineages were at least 2× smaller, an overall low scaling that has been recovered before in studies relying heavily on taxonomic data and backbone trees, regardless of approach (e.g., semiparametric methods in Magallón and Sanderson, 2001). The magnitude of this downscaling of speciation rate likewise is similar to that between our molecular‐only trees (9k‐tip and 20k‐tip) and our tree with added lineages based on backbone taxonomies (100k‐tip; Appendix S4), suggesting that taxonomic backbone data may be directly responsible for this discrepancy. Unsurprisingly, an angiosperm backbone tree fails to recover signatures of recent diversification; rate curves (Magallón et al., 2018: fig. 3) were strongly flattened compared to our results, particularly for rate variation within the past ~15 million yr, consistent with our representative sampling experiments (Fig. 8C and Appendix S4). These observations, along with our sampling manipulation experiments, suggest a degree of caution in interpreting the results from diversification studies sampling a very small proportion of species‐level diversity with backbone trees (= representative sampling bias) and relying heavily on taxonomic data to cover sampling gaps.

Impact of backbone taxonomic addition

Diversification patterns observed with the 100k‐tip tree using backbone taxonomies were remarkably divergent from the other trees across methods. The differences mainly comprised (1) spurious inference of early bursts of speciation and (2) depression or inflation of tip speciation rates. This difference was consistent across analyses despite a similar phylogenetic backbone across all trees and a similar overall distribution of clade dates between the 100k‐tip tree and the 9k‐tip and 20k‐tip trees (Fig. 2), without obvious overall bias in node age. Despite considerable interest in using synthetic trees for evolutionary studies, we are aware of no similar studies of the behavior of taxon addition by MRCA, as commonly used in large synthetic phylogenies (e.g., Smith and Brown, 2018; for alternative probabilistic methods, see Thomas et al., 2013; Rabosky, 2015; Rabosky et al., 2018). While a conservative approach from the taxonomic point of view, MRCA insertion substantially changes tree shape by adding numerous early‐diverging lineages. Correspondingly, among the three diversification methods we used (RPANDA, BAMM, and DR), the 100k‐tip tree always resulted in estimated tip speciation rates far lower than those observed with the 9k‐tip and 20k‐tip trees, usually around 10× smaller in magnitude (Fig. 3 and Appendices S2a–c and S4). Although the magnitude of the discrepancy is surprising, this pattern makes intuitive sense given that synthetic phylogenies (100k‐tip) were built by insertion of missing taxa at the MRCA of the least inclusive clade of which membership is known (e.g., genus or family). Assuming correct taxonomic assignments, this approach will result in consistently older node ages than would be inferred with molecular data alone (e.g., the 9k‐tip and 20k‐tip trees), pushing back the apparent timing of diversification and therefore depressing estimates of tip speciation rate (Fig. 3C and Appendix S4). Simulating this behavior in our backbone‐addition experiments confirmed that this practice results in lower estimates of tip speciation rates (Fig. 5E–H and Appendix S2d), and rate curves showed that this is largely driven by inferring spurious early bursts of evolution (Fig. 7 and Appendix S4). The divergence of the results for the 100k‐tip tree from those in the molecular‐only trees suggests that the underlying methods used to generate phylogenies can drive results more than incomplete sampling. As with the random sampling scenario, tip rates in BAMM were most robust to backbone‐addition among the methods employed (Fig. 5G), although, overall, BAMM rates were very sensitive (Fig. 5F).

CONCLUSIONS

We found strong impacts of sampling on diversification inference, impacts that were surprisingly diverse and potentially large enough in magnitude to change evolutionary conclusions. For example, our representative and backbone‐addition sampling simulations were sufficient to generate spurious inferences of early bursts of speciation and erase the signals of recent bursts of speciation. Our results parallel those of Stadler (2009), who found that speciation, extinction, and sampling fraction cannot be co‐estimated (see also Louca and Pennell, 2020). We correspondingly find that diversification rates can be highly contingent on assumed sampling pattern and effort, although the exact reasons behind such high sensitivity remain to be investigated. Although improvement of molecular taxon sampling to overcome this heterogeneity would be ideal, for large clades this is not always feasible, necessitating methods that adequately account for missing biodiversity knowledge. Our results indicate greater robustness to moderate incomplete sampling in BAMM, likely due primarily to its taxon‐specific modeling of sampling, and an especially high robustness for estimating tip speciation rate (but see Diaz et al., 2019). That rate metrics focusing on the recent past may be more robust (see also Louca and Pennell, 2020) is an important outcome for poorly sampled data sets that makes intuitive sense. In an extant‐only phylogeny, the present time frame has the most complete lineage sampling in the presence of extinction, and hence the most data from which to derive inferences.

A frequently used alternative to adding molecular data to a given phylogenetic tree is to incorporate taxonomic knowledge with presumed phylogenetic placements, often using lineage addition via backbone taxonomies. To date, the benefits of backbone taxonomic addition (e.g., Jetz et al., 2012; Rabosky et al., 2018; Stein et al., 2018) have largely been assumed rather than demonstrated with test cases. We found that adding taxa without molecular data had unpredictable effects, was not necessarily better than other approaches, and perhaps was sometimes harmful. Based on the dramatic inferential differences we observed among analyses, we advise strong caution in the inference of diversification using very poorly sampled trees, regardless of method, and in using summary backbone phylogenies and other data sets where incomplete sampling assumptions are unlikely to be met. We also recommend the use of sensitivity analyses similar to those we implemented in Cucurbitaceae to assess whether empirical results are conditional on methods that account for missing taxa. Nevertheless, strong differences in robustness exist both among commonly used methods and among the summary statistics that can be extracted from them. Armed with this information and the right strategy, empiricists can derive meaningful macroevolutionary insights from incomplete but sufficiently characterized data sets.

AUTHOR CONTRIBUTIONS

R.A.F. and M.S. designed the study. M.A.G. advised with data mining. M.S. conducted the analyses. M.S and R.A.F. conducted data interpretation. M.S., R.A.F., and D.E.S. drafted the manuscript. M.A.G., P.S.S., Z.C., and R.P.G. revised the manuscript. P.S.S., Z.C., D.E.S., and R.P.G. supervised the work. All authors contributed to and approved the final manuscript.

Supporting information

APPENDIX S1 Supplemental Methods:

Appendix S1a. Diversification analyses implemented by RPANDA.

Appendix S1b. Diversification analyses implemented by BAMM.

APPENDIX S2 Supplemental Tables:

Appendix S2a. Summary table for BAMM analyses (also see Appendix S1b).

Appendix S2b. Best models and speciation rates estimated for 9k‐, 20k‐, and 100k‐tip trees and each of 17 rosid orders from these trees using RPANDA with nine birth‐death models (cf. Appendix S1a).

Appendix S2c. Summary table for the DR statistic.

Appendix S2d. Summary table for diversification simulations in the Cucurbitaceae test case.

Appendix S2e. Tukey’s HSD test across the RPANDA, BAMM, and DR methods for the Cucurbitaceae test case under the random taxon‐dropping scenario.

Appendix S2f. Tukey’s HSD test across the RPANDA, BAMM, and DR methods for the Cucurbitaceae test case under the backbone‐addition scenario.

Appendix S2g. Summary table for diversification analyses for the Cucurbitaceae test case under the representative sampling scenario.

APPENDIX S3 Supplemental Note: Justification for comparing speciation rates under different models across different methods.

Appendix S3a. Model‐weighted mean speciation rates estimated for 9k‐, 20k‐, and 100k‐tip trees and each of 17 rosid orders using RPANDA with nine mixed models (cf. Appendix S1a).

Appendix S3b. Summary table of speciation rates estimated from RPANDA under three pure‐birth models (cf. Methods in Appendix S1a).

Appendix S3c. Rate comparison for 20k‐tip tree under birth‐death and pure‐birth models in BAMM analysis.

Appendix S3d. Comparison of rate‐through‐time plots for each of the 17 rosid orders from 20k‐tip tree under birth‐death model (solid line) and pure‐birth model (dashed line), respectively.

APPENDIX S4 Supplemental Figure: Comparison of rate‐through‐time plots for each of the 17 rosid orders (a–q).

Sun, M. , Folk R. A., Gitzendanner M. A., Soltis P. S., Chen Z., Soltis D. E., and Guralnick R. P.. 2020. Estimating rates and patterns of diversification with incomplete sampling: a case study in the rosids. American Journal of Botany 107(6): 895–909.

Data Availability

All results of downstream analyses and R scripts are available at https://github.com/Cactusolo/Rosids_AJB‐D‐19‐00298 (https://doi.org/10.5281/zenodo.3725025) (Sun et al., 2020).