Abstract
Increasingly prevalent extreme weather events have caused resilience to become an essential sustainable development component for resource and infrastructure networks. Existing resilience metrics require detailed knowledge of the system and potential disruptions, which is not available in the early design stage. The lack of quantitative tools to guide the early stages of design for resilience, forces engineers to rely on heuristics (use physical redundancy, localized capacity, etc.). This research asserts that the required quantitative guidelines can be developed using the architecting principles of biological ecosystems, which maintain a unique balance between pathway redundancy and efficiency, enabling them to be both productive under normal circumstances and survive disruptions. Ecologists quantify this network characteristic using the ecological fitness function. This paper presents the required reformulation required to enable the use of this metric in the design and analysis of resource and infrastructure networks with multiple distinct, but interdependent, interactions. The proposed framework is validated by comparing the resilience characteristics of two notional supply chain designs: one designed for minimum shipping cost and the other designed using the proposed bio-inspired framework. The results support using the proposed bio-inspired framework to guide designers in creating resilient and sustainable resource and infrastructure networks.
Keywords: Resilience, Critical infrastructure, Supply chains, Ecological network analysis, Bio-inspired design, Sustainability
Nomenclature
- ENA
Ecological Network Analysis
- [T]
Flow matrix
- TSTp
Total System Throughput
- AMI
Average Mutual Information
- H
Shannon Index
- Hc
Conditional Entropy
- DoSO
Degree of System Order
- RECO
Ecological Fitness Function
- FOM
Figure of Merit
1. Introduction
Resource and infrastructure networks are critical to the functioning of society. These networks include electric power distribution networks, municipal water supply and wastewater treatment networks, public transportation systems, and supply chain networks. Traditionally the design of these networks aims to minimize their capital and operational costs [1], [2] and increase their efficiency. Efficiency as a system design goal can be tricky as it is defined and quantified differently depending on the field. Thermodynamic engines define efficiency (first law efficiency) as the ratio of useful work extracted to the energy used [3]. Network efficiency [4] can be described as using the shortest path or the minimum number of paths to meet an end [5], [6]. Economic efficiency is the smart allocation of sunken costs and imports to maximize profit from useful exports [7], [8]. Sustainability-related efficiency seeks to minimize emissions [9], [10], minimize resource consumption, and minimize waste generation [11], [12].
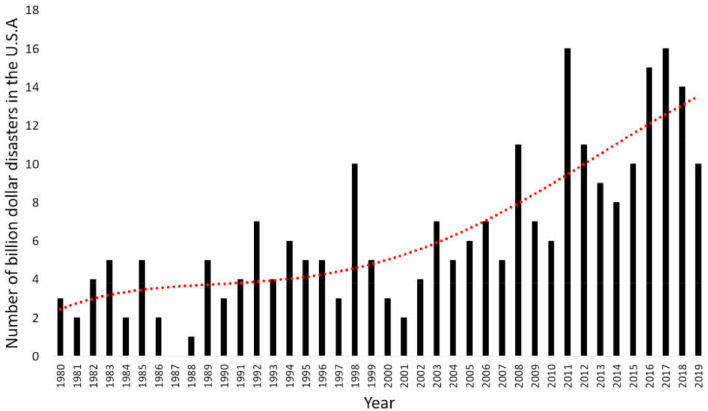
Efficiency objectives are essential, especially at a time when economic growth and technology enable almost everything to be connected, but their exclusive use fails to account for a system's ability to respond to external disruptions. Natural disasters and extreme weather events are becoming more prevalent, presenting a counter-argument against single-minded efficiency goals. The United States has sustained more than 254 weather and climate disasters with damages of $1 billion or more (CPI adjustment to 2019) since 1980, with a total cost exceeding 1.7 trillion USD [13] (Fig. 1 ). Resource and infrastructure networks need to be capable of withstanding and recovering from disruptive events like these, a characteristic known as system resilience.
Fig. 1.
The number of billion-dollar disasters in the United States from 1980 to 2019 (raw data from [13], data valid as of October 8, 2019). The red dotted line represents a trend line of their increasing prevalence.
1.1. Resilience in engineered systems
Resilience is the ability of a system to withstand and recover, as defined by normal performance levels, from a disruptive event [14]. Readers looking for a comprehensive review of the emergence of the concept of engineering resilience and progress made towards quantitatively assessing its various aspects are encouraged to refer to [15], [16], [17].
System resilience is a multifaceted quantity. Currently, there is no single, universally accepted measure of resilience (efforts are being made in this direction, notably Ayyub [18], Henry and Ramirez-Marquez [19], and Yodo and Wang [20]). Based on a survey of available literature [17], [21], [22], [23], [24], [25], the following measures of resilience were selected: survivability, time to recovery, and recoverability. Survivability measures the ratio of the avoided drop in system functionality following a disruption against the maximum possible drop in system functionality. This definition is recast as Eq. (1) using the nomenclature of this paper, where F(t) is a time-dependent measure of a system's performance (Figure of Merit, FOM [19]). F(t0) is the system performance before the disruption, F(tm)worst is the lowest performance that the system can drop to after a disruption (this may be assumed to be zero), F(tm) is the actual minimum system functionality after a disruption, and F(ts) is the system functionality at the post-recovery steady state. The duration of recovery efforts can be calculated as the time passed from the disruptive event to the new steady-state (Eq. (2)). System recoverability is defined here as the fraction of the system performance at the post-recovery steady-state to its performance pre-disruption (Eq. (3)).
| (1) |
| (2) |
| (3) |
Another vital aspect is resilience loss, which measures the loss of useful system outputs/functionality over the disruption-recovery period. This was first quantified by Bruneau et al. [26]. Eq. (4) presents this metric in the nomenclature of the current paper. This metric is especially helpful in highlights the economic impact of resilience. A system that is not resilient will result in lost profits when disrupted.
| (4) |
1.2. Resilience and sustainability
Sustainable development, as defined by the United Nations Brundtland Commission in 1987, is the development that meets the needs of the present without harming the natural systems that society depends on or the ability of future generations to meet their needs [27]. Resilience and sustainability can be seen as interconnected qualities of complex systems with common goals [28], [29]. An environmentally benign system that is not resilient will not survive disruptions to be able to meet needs and is therefore not sustainable, also termed as fragile sustainability [30]. Resilience is inherently tied to the three pillars of sustainability: social, environmental and economic. A system that can effectively recover from a disaster is sustainable in that it can restore the original quality of life and function for the environment, society, and the economy [31], [32].
The need for an integrated outlook on sustainability and resilience has been recognized in the field of ecosystems management, and urban infrastructure [24], [33], [34], [35], [36], [37], [38], [39], [40]. Blackmore & Plant [37] presented the argument that if a system is to be designed for sustainability, it must take into account vulnerabilities to possible disruptions. Fiksel [38], [39] advocated the need to move on from the ‘steady-state’ model of sustainability, acknowledging the importance of resilience for communities and economic enterprises in achieving sustainable development. The concept of a stable state that, once-achieved, will continue to exist in perpetuity (is fail-safe) conflicts with the emerging dynamic concept of sustainability and the “rapidly changing threats and opportunities [41]” that resilience strives to mitigate. It is more apt, therefore, to try and design systems that can maintain at least partial functionality during failures and recover from them without losing its essential characteristics (‘fail-soft’, or ‘safe-to-fail’) [40].
Holling [42] defined resilience (of ecological systems) as the capacity of a system to absorb and adapt to change without altering fundamental properties. Sustainability in this context can be understood as a set of critical system qualities needed for the survival and recovery from disruptions: to promote sustainable development, the desirable system functionalities must be resilient to disruptions. This conclusion has been echoed in recent scientific literature. Elmqvist et al. [28] suggested that the ability to adhere to or strengthen a certain desirable quality in the face of disruptions is the key factor in achieving sustainable growth. Marchese et al. [29] emphasized the importance of analyzing and improving the resilience of the sustainable (or desirable) components of systems.
1.3. Novelty and contributions of present research
Currently, only general design principles exist to guide engineers toward resilient system solutions, like physical redundancy, functional redundancy, localized capacity (amongst others) [15]. Quantifiable objectives are needed to act as guidelines for resilient systems design. The metrics presented in Section 1.1 only provide design engineers with tools to assess a system's resilience to disruptions after its design. These entail an analysis or simulation conducted using a detailed description of the system in question and specific knowledge of potential disruptions to the system, which are not available in the early stages of design.
Recent literature has identified that incorporating inter-disciplinary approaches (such as from ecology) may provide novel design approaches for resilience [43]. Ecosystems have been repeatedly found to exhibit the ability to return to their previous state or find a new sustainable, stable state after disturbances [44], [45], [46]. This ability suggests that ecological systems are inherently resilient to perturbations. Ecologists developed a metric called the ecological fitness function (detailed in Section 2) to quantitatively assess the trade-offs between pathway efficiency and redundancy in ecological networks and relate it to ecosystem resilience [47]. They found that ecological networks maintain a unique balance between pathway redundancy and efficiency that allows them to be productive under normal circumstances as well as survive disruptions [48], [49], [50], [51].
Resource and infrastructure networks and ecological networks can be viewed as analogous in many ways: the exchange of resources and services between components of an infrastructure network (e.g. industries, and consumers) are analogous to species in ecosystems exchanging energy and nutrients. In both cases, survival and maintenance of functionality in the face of disruptions is highly desirable. Ecological architecting principles, if they are found to lead to the design of more resilient resource and infrastructure networks, would be invaluable tools for the early stages of network design when detailed information is often not yet available. The ecological fitness function requires only information regarding the network architectures and their interactions, unlike the simulations and analyses commonly used that require detailed threat models.
The ecological fitness function, when applied to power grid and industrial water networks, presents promising improvements in the ability of the network to absorb disruptions [52], [53]. The existing mathematical formulation of the ecological fitness function however is limited to application on networks with only one type of flow (interaction). Modifications are required to enable its application in resource and infrastructure networks where multiple interdependent interactions are the norm. The required modifications are presented and tested on an electric motor supply chain case study (an interdependent infrastructure network with multiple flow types), validating the new formulation through resilience analysis. While previous studies focused primarily on the possible improvements in a network's ability to absorb disruptions through the use of the ecological fitness function [52], [53], here we also investigate the recovery following disruptions, providing a more holistic view of the relationship between the ecological fitness function and the resilience of engineering networks.
The rest of the paper is organized as follows: Section 2 provides details of the ecological fitness function evaluation framework and the proposed modifications, Section 3 outlines the case-study and the validation procedure, Sections 4 and 5 present the results and relevant discussion, and Section 6 discusses the potential, limitations and requirements for future work.
2. Ecological network analysis and the ecological fitness function
Ecological Network Analysis (ENA) is a tool used by ecologists to study the complex interactions among species at the systems level. ENA provides a set of metrics that link structure and behavior in ecological networks [54]. ENA requires the identification of a quantity of interest (energy, nutrients, etc.) between the actors (or species) inside the selected system boundaries. Individual species or actors in the system are grouped based on common functions, becoming nodes in a directional graph (or digraph). The interactions between the nodes then become the directed edges (or links).
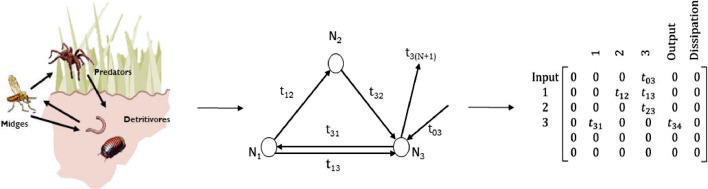
Flow magnitude information between the nodes within the system boundaries, as well as those with the surrounding environment (system inputs, outputs, and dissipations), are stored in the (N + 3) x (N + 3) flow matrix T (where N is the number of actors within the network). The nodes 1 to N in the flow matrix represent the actors within the specified system boundary. The nodes 0, N + 1, and N + 2 are the system imports (row “zero” in the T matrix), system exports, and dissipations (columns N + 1 and N + 2, respectively). The matrix element Tij represent the magnitude of flow from node i (producers/prey) to node j (consumers/predators). The hypothetical food web of Fig. 2 for example shows that midges (node 1) are consumed by predators (node 2) and predators are consumed by detritivores (node 3). An ENA models these food web interactions as caloric (energy) transfers between the nodes and the flow information is saved in the elements T12 and T23 (flow is from rows to columns) of the flow matrix, respectively. Readers interested in a more detailed description may refer to Fath et al. [56].
Fig. 2.
A schematic of the modeling procedure used in ENA, illustrated using a hypothetical food web, based on [55].
ENA metrics that quantify information about system structure and qualities such as flow cycling, synergism, mutualism, etc. are calculated from [T] [54], [57], [58], [59]. The ENA metric of interest here is ecological robustness, also known as the ecological fitness function – as will be used in this paper to avoid confusion with engineering robustness.
Eqs. (5)-11 are needed to calculate the ecological function. Eq. (5) quantifies the Total System Throughput (TSTp, also abbreviated as T in some texts), which represents the total magnitude of flow that passes through the network. Network Ascendancy (ASC) is an indicator of the organizational development of a network, which translates to the network becoming more organized (and therefore efficient) at transporting material from one point to another [60]. Network Ascendancy, when normalized by the Total System Throughput, becomes Average Mutual Information (AMI, Eq. (6)) of the flow network. According to nature's laws, nothing can grow without bounds. The upper limit on ASC is given by the metric Development Capacity (DC) [60]. The Development Capacity, normalized by the Total System Throughput, becomes the Shannon Index (H, Eq. (7)). The difference between Network Ascendancy and Development Capacity is the part of the system that has yet to be constrained and therefore provides flexibility to the system in the form of redundancy. This is called the Total System Overhead (TSO), and normalized by the Total System Throughput it becomes the metric Conditional Entropy (Hc, Eq. (8)). Readers interested in the rigorous mathematical derivation of these metrics from the concepts of Information theory are encouraged to refer to Ulanowicz et al. [47], [60] and Fath et al. [48].
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Where,
| (10) |
| (11) |
The ratio AMI/H (or ASC/DC) is used to calculate the ecological fitness function (RECO, Eq. (9)). This ratio is called the Degree of System Order (DoSO) and varies from zero to one. A value of DoSO close to zero signifies a large number of redundant pathways in the flow network. A value of DoSO close to one indicates that the network has highly constrained (or efficient) flow pathways. These extreme cases correspond to either a network where all actors are connected to each other (value of zero), or a linear chain network with each actor receives flow from only one node and provides flow to only one other node (value of one). Neither of these extreme cases results in a ‘fit’ network. An excessively redundant network is not effective at utilizing the available resources, and an excessively efficient network will be vulnerable to disruptions [47]. Consequently, RECO is zero when DoSO is one and tends towards zero again when DoSO approaches zero.
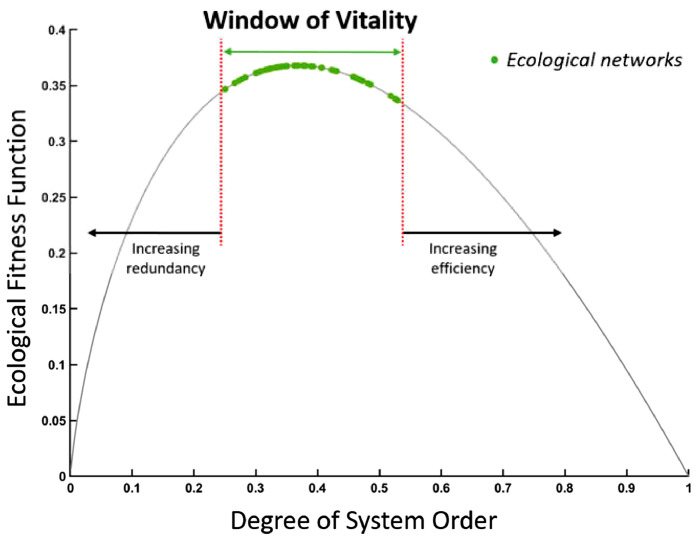
An analysis of experimentally derived networks (with 12 or more participating species) from ecosystem models revealed that the ecosystems existed in a narrow range of DoSO values centered around a DoSO slightly higher than 1/e [49]. This region was named the ‘window of vitality’ [50] and was assumed to represent designs that would reap maximal fitness for survival and evolution (see Fig. 3 ). Therefore, the ecological fitness function was formulated to peak at DoSO ~1/e. That ecosystems favor this peak suggests that this maximum is a point of natural sustainability [49] that considers both the efficiency goals of the system during normal circumstances and requirements for alternate pathways in case of external perturbations.
Fig. 3.
The ecological fitness function (RECO, Eq. (9)) curve with food webs taken from the datasets of Borrett et al. [61] plotted on the curve fit to illustrate the “window of vitality” [50], where mature ecosystems reside. Figure based on [48].
Ecologists primarily focus on energy (caloric) transfers between species (producers, consumers, decomposers, etc.), and so the ability to analyze a network with only one kind of flow is sufficient. Resource distribution and infrastructure networks, on the other hand, are made up of various types/modes of independent interactions between actors, and disruptions in any layer of interactions can result in cascading failures in other layers as well [62], [63], [64]. Therefore, modifications are needed to accommodate the multiple distinct and interdependent flows between the system actors in engineering networks. An initial modified formulation to calculate the ecological fitness function was presented by the authors in [65] and is further developed here following Eqs. (12) and (13). These modified equations AMI and H can be utilized for networks with multiple currencies of flow and be input directly back into Eq. (9). The symbols retain their original meaning, with the additional subscript l signifies the m different types (mediums) of flows in the network.
| (12) |
| (13) |
3. Methodology
A hypothetical electric motor supply chain (based on [20]) is utilized as a case-study to test if resilience characteristics of resource and infrastructure networks can be improved using the formulation proposed in Section 2. Before proceeding further, the authors would like to clarify that supply chain modeling and/or a resilience analysis is not the focus of this paper. The supply chain is chosen as a case-study due to its ability to be modeled as a flow network and its complexity of multiple distinct but interdependent flows (see Fig. 4 ). Readers specifically interested in supply chain resilience are referred to scholarly works such as [66], [67], [68], [69], [70], [71], [72].
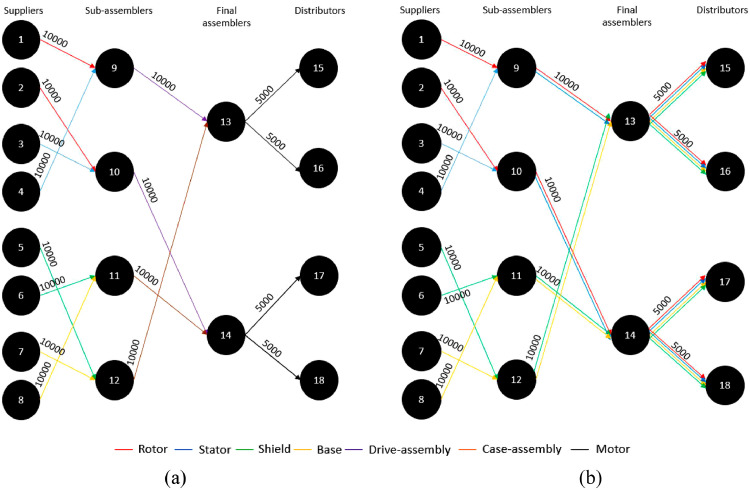
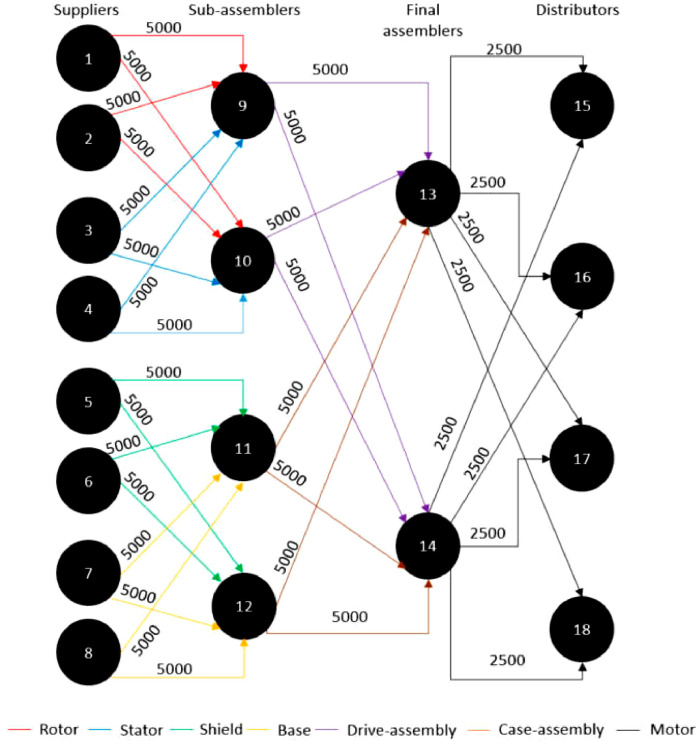
Fig. 4.
Schematic of an (a) electric motor supply chain network based on [20] and (b) how it can be modeled as a multi-currency flow network of the four primary components.
The validation was performed by comparing the resilience characteristics of two notional supply chain designs: one designed for minimum shipping cost (baseline) and the other designed using the proposed bio-inspired framework. The general features and network modeling assumptions of the supply chain are described in Section 3.1. The steps involved in generating the two network design instances are detailed in Section 3.2. Section 3.3 details the disruption and recovery scenarios used to assess the resilience characteristics of the two designs.
3.1. Case-study description: electric motor supply chain
The electric motor supply chain network consists of four different layers of actors: (1) eight suppliers, (2) four sub-assemblers, (3) two final assemblers, and (4) four distributors. The eight suppliers are equally divided into four different classes, supplying one of the four primary components of the electric motor: rotors (actors 1 and 2), stators (actors 3 and 4), shields (actors 5 and 6), and bases (actors 7 and 8). The four sub-assemblers are divided into two groups: actors 9 and 10 assemble the rotors and stators into drive assemblies, and actors 12 and 13 assemble the shields and bases into case assemblies. The final assemblers (actors 13 and 14) assemble the electric motor from the drive and case assemblies and ship them to the distributors (actors 15, 16, 17, and 18). Fig. 4a illustrates the supply chain network and Fig. 4b illustrates the multiple distinct but interdependent flow interactions in the network. The first layer of connections, between the suppliers and sub-assemblers, exchange the four primary components. The second layer of connections, between the sub assemblers and the final assemblers, exchange the drive assemblies and case assemblies. The transfer of drive-assemblies is the transfer of the two primary components, rotors and stators. Similarly, the transfer of case assemblies is a dual flow of the primary components - shields and bases. Finally, the transfers of the fully assembled motors are flows made up of a combination of flows of each of the primary components.
The total shipping cost was calculated based on the parameter s (shipping cost per unit primary per mile, $/unit-mile). The location of each actor in the network (city and state) and the shipping distance between them (provided in Appendix A) were found using Google MapsⓇ services. Two actors in the same city were assigned a shipping distance of 20 miles. The frequency of shipping between each layer of the supply chain was assumed to be weekly. The profit on each unit exported by the distributors was assumed to be ‘p’ [$/unit]. These parameters enabled the costs of shipping to be weighed against the potential profit losses in the case of disruption of regular activity.
The fiscal comparison was made using the following assumptions for the parameters s and p:
-
1
Shipping cost: The weight of a fully assembled 100 HP electric motor is ~ 1200 lbs [73]. A DOE report estimated a median rate of 0.65 cents per pound for shipping between 350 and 3000 miles in this weight range [74]. Taking a 1500-mile distance and the weight mentioned above, the shipping cost parameter for each primary component (assumed a fourth of the complete unit) per mile was estimated as ~ $0.13.
-
2
Profit: The sales-weighted average markup on electric motors is 139% [74]. The cost of a heavy-duty 100 HP motor is ~ $11,500 [73], making the profit per unit sold ~ $3225.
3.2. Generating two designs for comparison
Two designs of the electric motor supply chain were generated. The baseline design minimizes shipping costs. The bio-inspired design mimics (in as far as was possible) the ecological balance of efficient and redundant pathways. The two designs utilize the same 18 factories (actors) with the same production capabilities, import the same amount of raw materials, and export the same number of completed electric motors (20,000) during normal operations. Only the distribution and supply of components between the actors are different, creating a significant difference in the sunk costs due to shipping costs, justifying the choice of minimum shipping cost as the objective for the baseline design. The methodology used for developing both the designs follows:
Step 1: Thirty-two total possible flow paths were identified. Each route corresponds to the transfer of a specific component, sub-assembly, or the complete motor. The design variables are the number of units of the specific component shipped along that route. A lower limit of zero and an upper limit of ten thousand units were set for each route. A value of zero indicates that the route is not utilized. The significance of each of the 32 design variables is presented in Appendix A.
Step 2: The following design constraints were identified (mathematical formulations of the constraints provided in Appendix B):
-
a
The sub-assemblers cannot produce assembled structures more than the minimum of the number of two primary components they receive.
-
b
Similarly, each of the final assemblers cannot assemble electric motors more than the minimum of the number of drive or case assemblies they receive.
-
c
All actors of the same functional groups were set to operate at equal capacities in the fully functional state (no preference towards any actor). This was done by setting constraints of equal output from actors supplying the same components, sub-assemblies, and assembled motors:
-
d
The supply chain was required to export 20,000 units per week. Since each of the distributors was required to operate at equal capacity, exporting 5000 electric motors weekly, each must receive a shipment of 5000 assembled motor units every week.
Step 3: Finally, the two designs were developed by optimizing for the desired characteristics.
-
1The objective of the first design was to minimize the shipping cost. The cost of shipping along each route (for one transfer) was calculated using Eqs. (14a)-c:
(14a) (14b) (14c)
The shipping cost per unit per mile of the drive and case assemblies and the cost of shipping one unit of a completely assembled motor were assumed to be twice and four times that of a single primary component, respectively, due to the joint weight. The network design was then optimized for the objective function presented in Eq. (15) subject to the constraints explained above using MATLAB's gradient-based optimization tool fmincon:
| (15) |
-
1The optimization objective for the second, bio-inspired, design was to achieve the value of the ecological fitness function metric (Eq. (9)), for the supply chain network, closest to the maximum possible value of RECO ~ 1/e. The flows of each primary component (design variables) in the network were arranged in corresponding flow matrices, in the manner discussed in Section 2. AMI and H were calculated using Eqs. (12) and (13). Mathematically, the objective function for this optimization is given by Eq. (16):
(16)
A system design, where the flows of components between suppliers and consumers were equally distributed, was found to result in a system design that most closely mimics ecosystems, given the design constraints.
Fig. 4a is a schematic of the design for minimum shipping cost. This design presents no redundant pathways. The weekly shipping cost and ecological fitness value of the baseline design were calculated as $18,785,000/week, and 0.1326, respectively. Fig. 5 presents a schematic of the bio-inspired electric motor supply chain, illustrating the utilization of multiple redundant pathways. The weekly shipping cost and ecological fitness value of the bio-inspired design were calculated as $22,737,000/week, and 0.3037, respectively.
Fig. 5.
Schematic of the bio-inspired supply chain design, utilizing multiple redundant pathways.
3.3. Disruption and recovery scenario
In order to compare the resilience of the two electric motor supply chain designs developed, a disruption and recovery scenario was simulated. Yodo and Wang [20] stated that based on historical data and surveys, natural disasters like floods hurricanes and tornados are most likely to disrupt the operations of the rotor supplier in Kansas City (KS), the shields supplier in Minneapolis (MN) and the final assembler in Wichita (KS). The resilience of the baseline supply chain network was assessed against that of the bio-inspired supply chain network using this disruption scenario. Assumptions regarding the recovery timeline were made based on approximately 12 months of recovery time reported for infrastructure rebuilding time after three major storms in the recent past (Katrina, Sandy, and Ike) [75]. A total repair time of approximately two months was assumed based on the following rationale: (1) not all such disruptions will be as devastating as these three, and (2) the time it takes to repair damages and restart a plant can be significantly less than the recovery time for city-wide infrastructure. The recovery timeline assumed for the simulation is listed below:
-
a)For the disrupted suppliers:
-
1Four weeks to reach 25% functionality.
-
2Five weeks to reach 50% functionality.
-
3Six to reach 75% functionality.
-
4Seven weeks to reach 100% functionality.
-
1
-
b)For the disrupted final assembler
-
1Six weeks to reach 25% functionality.
-
2Seven weeks to reach 50% functionality.
-
3Eight weeks to reach 75% functionality.
-
4Nine weeks to reach 100% functionality.
-
1
The disruption and recovery simulation was performed with discrete time steps of one week, corresponding to the frequency of shipments between different layers of actors in the supply chain under normal circumstances. Two system performance metrics are used to assess the system functionality of the two designs during the disruption and recovery period:
-
1
Export performance: The number of fully assembled electric motors exported by the distributors at a given time.
-
2
System health: When an actor's functioning is disrupted, both its suppliers and consumers are affected [76]. This metric indicates the health of the system through the number of active actors at a given time. An active actor is defined as an actor that is either fully or partially fulfilling its role in the supply chain.
Other viable measures could be used as system performance metrics, for example, stock utilization. Previous work has noted that the resilience of systems is often assessed only from a single perspective of interest [77]. These two metrics were selected due to their representation of two distinct and equally important perspectives regarding the supply chain's operation.
The export performance metric assesses the supply chain from the corporation's standpoint. A drop in export by distributors is loss of business and profits. The fiscal perspective of this analysis is further explored by calculating the loss of profits during the disruption and recovery period. Eq. (17) (based on Eq. (4) discussed in Section 1.1) gives the loss of profits due to reduced exports (assuming a normal export level of 20,000 units) after the disruption and until full recovery. The time when the disruption occurs is td, the time to full recovery is tr, and p is the profit per assembled motor exported.
| (17) |
The system health metric provides an assessment of the supply chain from a societal perspective. More actors shut down due to cascading failures in the system, corresponding to more lost wages and an impact on the financial well-being of the employees.
4. Results
Fig. 6 illustrates the system performance metrics through the disruption and recovery process for both the baseline (dashed red line) and the bio-inspired supply chain network design (solid green line). The disruption is simulated at time td (td = 1 week in Fig. 7 ). The system does not instantly lose full functionality due to assumed properties such as latent storage, instead losing functionality over a period of time slightly after td to tm (for example, tm = 4 weeks for the baseline design), when the system bottoms out at its minimal functionality. Recovery efforts start right after the disruptive event and continue until time tm when a new steady state is reached (in the case study this new state is the same as before the disturbance). An animated representation of the disruption and recovery timeline is provided as supplementary material (S1). A week by week description of the state of the supply chain designs, during the disruption and recovery period, is also provided in Appendix C.
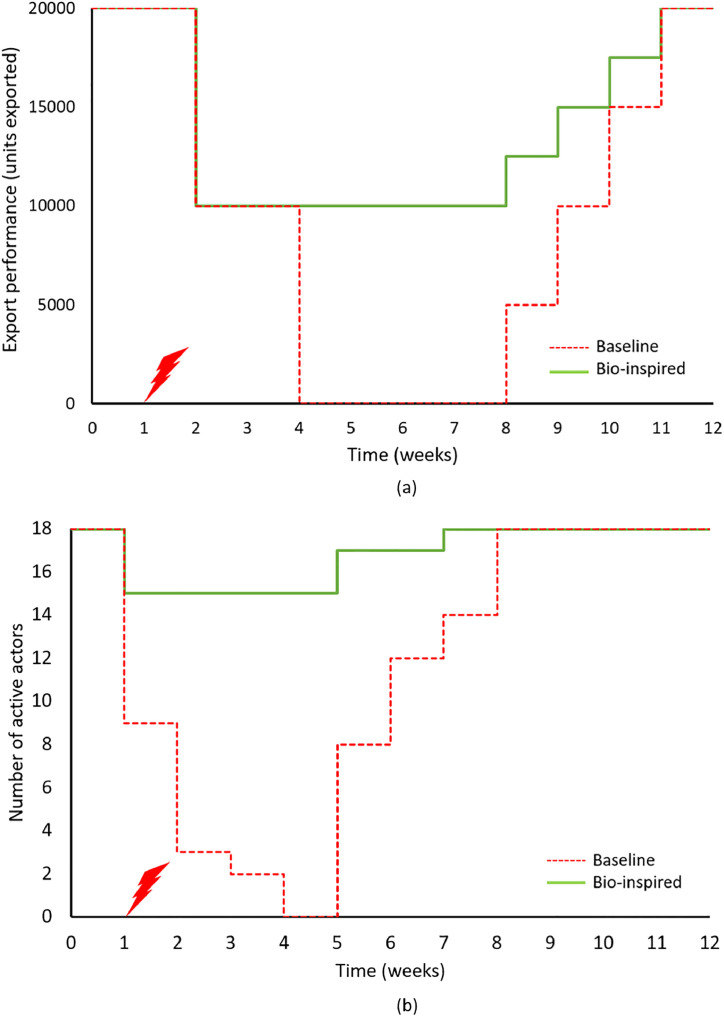
Fig. 6.
Simulated (a) export performance and (b) the number of active actors (system health, right) of both supply chain designs through the disruption and recovery period.
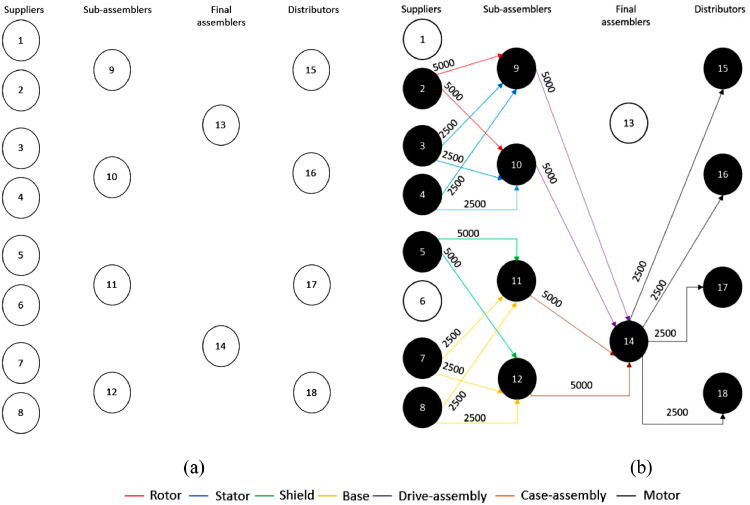
Fig. 7.
Predicted state of the (a) baseline and (b) bio-inspired supply chain designs three weeks after the disruption that originally shuts down actors 1, 6, and 13. The solid circles represent actors that are still active. The empty circles represent actors that are directly or indirectly shut down.
Both performance measures (export performance, and system health) indicate that the bio-inspired supply chain network loses less functionality than the baseline design. The survivability, time to recovery, and recoverability metrics Eqs. (1)-(3) are calculated for both export performance and system health for both designs and are tabulated in table 1 . The loss of profits sustained by the baseline, and bio-inspired supply chain designs during the ten-week disruption and recovery period simulated were $419,250,000 and $241,875,000.
Table 1.
Survivability, time to recovery, and recoverability of the two supply chain designs for export performance and system health (number of active actors).
| Design | Survivability | Time to recovery | Recoverability | |
|---|---|---|---|---|
| Export Performance | Baseline | 0% | 10 weeks | 100% |
| Bio-inspired | 50% | 10 weeks | 100% | |
| System Health | Baseline | 0% | 7 weeks | 100% |
| Bio-inspired | 83.33% | 6 weeks | 100% | |
5. Discussion
The survivability of the baseline supply chain design is 0% against the disruption simulated in this analysis for both the export performance and system health metrics. The system degrades to its worst state three weeks after the disruption. At this point, all the system actors are forced to shut down their operations, and export performance is 0% of its pre-disruption value. On the other hand, most of the system actors in the bio-inspired supply chain design only experience a reduced operational capacity after the disruption. The export performance does not fall below 50%, and only the three actors directly affected by the natural disaster are forced to shut-down, namely suppliers 1 and 6 and final assembler 13. A comparison of both the systems at their worst possible states (at t = 4 weeks) is shown in Fig. 7.
The highly pathway efficient nature of the baseline design allows many actors only a single consumer or supplier. Due to this, shut down of any actor forces its suppliers and producers to shut down as well, even though they were not directly affected by the natural disaster. When the supply of one component (or sub is cut off to a sub-assembler or final assembler, the demand for its counterpart is canceled too because the component with the minimum supply limits production. This makes the baseline supply chain design highly susceptible to cascading failures. The bio-inspired supply chain design allows actors to have multiple suppliers and consumers. This reduces the importance/criticality of any one actor and ensures that no actor faces complete loss of supply or demand in case one (or a few) of them are disrupted.
The disrupted actors, in both designs, are assumed to be able to regain their original performance levels after the repair work is completed. The time to full recovery for export performance was found to be equal for both the designs. The time to recovery for the system health metric was one week shorter for the bio-inspired supply chain design. This is also a result of the bio-inspired design protecting the system against cascading failures. Only the actors directly affected by the disruptive events are forced to shut down in the bio-inspired design, and therefore the time to restore operations is equal to the duration of recovery efforts to restart operations of actors 1, 6, and 13. All the actors in the baseline design are forced to shut down due to cascading effects. These cascading effects require an extra week for the distributors to restart operations after the critical final assembler 13 is repaired sufficiently to restart operation (by week 7).
The bio-inspired design constantly out-performs the baseline design during the time to recovery, both in terms of export performance and the number of active actors. Under normal operations, the bio-inspired design has approximately 21% higher weekly shipping cost, but following a disruptive event the baseline design will suffer approximately 73% greater loss of profits. A break-even analysis showed that the difference between the profit losses during the recovery period is worth the difference in shipping costs for approximately 45 weeks between the baseline and bio-inspired supply chain designs. A similar disruption that is expected nearly once a year would negate the savings on shipping cost by the baseline design. In the case that more than one such disruption is expected, the bio-inspired design would be significantly more profitable than the baseline design. The annual average of extreme weather events (over 2014 to 2018) is recorded to be 12.6 events [13], providing strong support for the bio-inspired network design approach from a fiscal perspective. The results indicate that the ecologically inspired concept of the “window of vitality” can provide quantitative guidelines to design supply chain networks in a zone of “balanced resilience” (optimal trade-off between operational costs and exposure to threats) [78].
The financial analysis assumes that the supply chain could recover to its original performance level after the disrupted actors are repaired. In reality, a significant drop in export performance could lead to the enterprise losing demand. The system then would not be able to return to its original performance level without sufficient demand for the completed motor units. This assumption results in a lower bound on the benefits of the bio-inspired design: higher functionality post recovery would be expected by the bio-inspired design because it maintains a higher level of export performance during the disruption and recovery period. The analysis also assumes that fixed costs associated with maintaining multiple producer-consumer relationships in the bio-inspired design are negligible. This assumption may not hold true, depending upon the scale of the supply chain operation and the setup of incentives, and may affect the results of the break-even analysis. Even if these fixed costs are not negligible, the break-even analysis could be expected to prefer the design for higher resilience given the US annual rate of 12.6 extreme weather events [13]. Future work focusing on a parametric analysis with different conditions of required fixed costs, scale of operations, and expected annual disruptions is required to answer these questions conclusively.
All actors except suppliers 1 and 6 and final assembler 13 in the bio-inspired design remain operational throughout the restoration period. On the other hand, every actor in the baseline supply chain design is shut down for at least 3 weeks, with most being shut down for four or more weeks. From a societal perspective, this indicates a significantly higher financial distress for employees of the enterprise in the baseline supply chain design compared to a bio-inspired design.
The disruption scenario was selected based on those actors that were most likely to be affected by extreme weather events (Section 3), but other sets of actors may be affected as well. Three other disruption scenarios were explored to cover a broader group of actors. The survivability metric, which was most improved by the bio-inspired design, is compared for the bio-inspired and baseline designs in these new scenarios (table 2 ).
Table 2.
The survivability of the bio-inspired vs. baseline supply chain designs using export performance and system health as system performance metrics.
| Actors Disrupted | Baseline Design |
Bio-inspired Design |
||
|---|---|---|---|---|
| Export Performance | System Health | Export Performance | System Health | |
| Suppliers 1 and 2, and Sub-assembler 9 | 0% | 0% | 0% | 0% |
| Suppliers 1, sub-assembler 11 and final assembler 13 | 0% | 0% | 25% | 83.33% |
| Suppliers 1 and 6, and sub-assembler 9 | 0% | 0% | 50% | 83.33% |
The bio-inspired design maintains a minimum level of performance in two out of these three cases, while the baseline design is unable to do so in any scenario. The bio-inspired design loses full functionality only when the two disrupted suppliers are both supplying the same component. The same will be seen if two sub-assemblers of the same type or both final assemblers are affected. Similar components are sourced from multiple suppliers for this exact reason: if one fails, the other is still available. Truly random events are unlikely to disrupt two geographically dispersed actors providing the same functionality to the system. These results show that the bio-inspired design has a greater capacity to absorb disruptions and maintain functionality, promoting a higher survivability.
6. Concluding remarks
The validation in this study was performed using a notional supply chain case-study, but the proposed framework can be applied to any resource and infrastructure network that can be modeled as a network of flows (for example see [52], [53], [79]). A novel feature of the bio-inspired design framework presented here is that it does not merely advocate adding actors of the same functionality, but rather intelligent set up of interactions between existing actors. The proposed framework thus improves resilience without necessarily requiring large capital investments to increase redundancy. While the results of this investigation are encouraging, some questions must be answered before any standardized framework for resilient resource and infrastructure networks can be developed using the ecological fitness function.
Comparing and understanding the advantages and limitations of the proposed bio-inspired framework against other novel resilience analysis and optimization techniques is essential (proposed in recent literature for supply chains [80], [81], [82], [83], [84], [85], [86] as well as infrastructure networks in general [87], [88], [89], [90]). The bio-inspired design must be tested and validated with a variety of disruption scenarios (e.g. disruption of links/pathways) to understand under what circumstances this framework may be more suited. Another interesting avenue of future work is to explore the scope of this novel design methodology for the newly proposed concept of supply chain (or other infrastructure networks’) viability: the ability of the network to re-configure or replan for long-term survival under changing conditions (refer for viability with respect to the COVID-19 pandemic [91], [92]).
The ecological literature has hypothesized that given the unique constraints and threat levels of different types of systems, maximal fitness may occur at different DoSO values [47]. Additional investigations of this framework is needed before standardized design guidelines can be developed. Using the ecological fitness function as a design guideline is not a magical solution that can remedy every disruption scenario. The prevalence and strength of disturbances are not constant across all systems. Mimicking an ecosystem's balance between efficiency and redundancy may not make sense for some engineering systems. Thermodynamic power cycles, for example, do not need redundancy because they are closed systems that do not experience extreme weather events or disturbances [93], [94].
In summary, the results obtained in this study provide strong support for further exploration of mimicking the natural balance of efficient and redundant pathways in designing for resilient engineered systems. Improved resilience, in turn, promotes both fiscal and societal sustainability for systems that are prone to disruptive events. Not only is the ecological fitness function a potential source for design guidelines for resilient engineered systems, but it can also be used to analyze the changes in system characteristics based on design decisions early in the design process. This could help understand the development of integrated systems and the interactions between them and can serve as a single high-level indicator of sustainability and resilience of infrastructure systems.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors would like to thank Texas A&M University for supporting this research and fellow BiSSL members Colton Brehm and Tirth Dave for insightful comments and discussions.
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.ress.2020.107142.
Appendix A. Description of supply chain flows
Table A.1.
Significance of design variables used in the notional designs and the approximate shipping distances.
| # | Component | From | To | Distance (miles) |
|---|---|---|---|---|
| 1 | Rotors | 1 (Kansas City, KS) | 9 (Kansas City, KS) | 20 |
| 2 | Rotors | 1 (Kansas City, KS) | 10 (Tupelo, MS) | 600 |
| 3 | Rotors | 2 (Tupelo, MS) | 9 (Kansas City, KS) | 600 |
| 4 | Rotors | 2 (Tupelo, MS) | 10 (Tupelo, MS) | 20 |
| 5 | Stators | 3 (Tupelo, MS) | 9 (Kansas City, KS) | 600 |
| 6 | Stators | 3 (Tupelo, MS) | 10 (Tupelo, MS) | 20 |
| 7 | Stators | 4 (Aberdeen, SD) | 9 (Kansas City, KS) | 600 |
| 8 | Stators | 4 (Aberdeen, SD) | 10 (Tupelo, MS) | 1200 |
| 9 | Shields | 5 (Casper, WY) | 11 (St. Louis, MO) | 1000 |
| 10 | Shields | 5 (Casper, WY) | 12 (Medford, OK) | 850 |
| 11 | Shields | 6 (Minneapolis, MN) | 11 (St. Louis, MO) | 560 |
| 12 | Shields | 6 (Minneapolis, MN) | 12 (Medford, OK) | 700 |
| 13 | Bases | 7 (Ashland, MO) | 11 (St. Louis, MO) | 150 |
| 14 | Bases | 7 (Ashland, MO) | 12 (Medford, OK) | 400 |
| 15 | Bases | 8 (St. Louis, MO) | 11 (St. Louis, MO) | 20 |
| 16 | Bases | 8 (St. Louis, MO) | 12 (Medford, OK) | 500 |
| 17 | Drive-assemblies | 9 (Kansas City, KS) | 13 (Wichita, KS) | 200 |
| 18 | Drive-assemblies | 9 (Kansas City, KS) | 14 (Knoxville, IA) | 200 |
| 19 | Drive-assemblies | 10 (Tupelo, MS) | 13 (Wichita, KS) | 700 |
| 20 | Drive-assemblies | 10 (Tupelo, MS) | 14 (Knoxville, IA) | 660 |
| 21 | Case-assemblies | 11 (St. Louis, MO) | 13 (Wichita, KS) | 450 |
| 22 | Case-assemblies | 11 (St. Louis, MO) | 14 (Knoxville, IA) | 300 |
| 23 | Case-assemblies | 12 (Medford, OK) | 13 (Wichita, KS) | 80 |
| 24 | Case-assemblies | 12 (Medford, OK) | 14 (Knoxville, IA) | 470 |
| 25 | Motors | 13 (Wichita, KS) | 15 (San Diego, CA) | 1370 |
| 26 | Motors | 13 (Wichita, KS) | 16 (Dallas, TX) | 470 |
| 27 | Motors | 13 (Wichita, KS) | 17 (New York, NY) | 1400 |
| 28 | Motors | 13 (Wichita, KS) | 18 (Seattle, WA) | 1850 |
| 29 | Motors | 14 (Knoxville, IA) | 15 (San Diego, CA) | 1770 |
| 30 | Motors | 14 (Knoxville, IA) | 16 (Dallas, TX) | 750 |
| 31 | Motors | 14 (Knoxville, IA) | 17 (New York, NY) | 1100 |
| 32 | Motors | 14 (Knoxville, IA) | 18 (Seattle, WA) | 1800 |
Appendix B. : Mathematical formulation of the electric motor supply chain design constraints
Mathematical formulations of the constraints listed in Section 3.2 . Generating two designs for comparison are provided here (physical significance of specific design variables can be found in Appendix A):
-
aThe number of sub-assemblies produced by the sub-assemblers is limited by the minimum of the number of two primary components they receive.
-
I
-
II
-
III
-
IV
-
I
-
bSimilarly, the number of final assemblies produced by the final assemblers is limited by the minimum of the number of drive or case assemblies they receive.
-
I
-
II
-
I
-
cAll actors of the same functional groups were set to operate at equal capacities in the fully functional state (no actor considered more important than the others). This was done by setting constraints of equal exports from actors supplying the same components:
-
I
-
II
-
III
-
IV
-
V
-
VI
-
VII
-
I
-
dSince each of the distributors are required to operate at equal capacity, exporting 5000 electric motors – each must receive a shipment of 5000 assembled motor units during normal operations.
-
I
-
II
-
III
-
IV
-
I
-
eFinally it was assumed that each of the suppliers import enough materials for supplying 10,000 units of raw materials for their respective primary components. Thus they must supply 10,000 units primary components each to the sub-assemblers during normal operations:
-
I
-
II
-
III
-
IV
-
V
-
VI
-
VII
-
VIII
-
I
Appendix C. : Week by week description of the state of the supply chain designs
Table C.1.
Disruption and recovery timeline comparison of the two supply chain designs.
| Week | Baseline (shipping cost-optimized) design | Bio-inspired design |
| 1 | • Suppliers 1 and 6 and Final assembler 13 are directly affected and forced to shut down. Supplier 4 is indirectly forced to shut down because, without the supply of rotors from 1 to sub-assembler 9, there is no demand for stators at 9 either. A similar situation is seen with supplier 8 because of the shutdown of supplier 6. The shutdown of final assembler 13 cuts off the demand for supply from sub-assembler 9 and 13 and subsequently forces suppliers 5 and 7 to shut down. • Suppliers 2 and 3 remain active, supplying to sub-assembler 10. Sub-assemblers 10 and 11 are still able to supply to final assembler 14, however, 11 is only able to do so using supplies from the previous week. The final assembler 14 remains operational too. • All distributors remain active, thus export performance does not drop down immediately. Distributors 15 and 16 are only operational using supply from the previous week. |
• Suppliers 1 and 6 and Final assembler 13 are directly affected and forced to shut down. No other actor is faced with a complete loss of supply or demand due to all actors having multiple suppliers and consumers. • When final assembler 13 is fully shut down, the sub-assemblers can only supply to final assemble 14, causing the sub-assemblers to operate at 50%. • The suppliers 3, 4, 7, and 8 also operate at 50% capacity. Suppliers 2 and 5 continue to operate at 100% capacity to meet the demand for rotors and shields by the sub-assemblers (because suppliers 1 and 6 are not operational). • Distributors maintain 100% export with the supplies received in the previous week. |
| 2. | • The lack of supply causes distributors 15 and 16 to shut down, cutting the export performance in half. Sub-assembler 11 also runs out of required input and cannot supply case-assemblies to final assembler 14. This indirectly cuts off the demand of drive assemblies as well and sub-assembler 10 is forced to shut down. Subsequently suppliers 2 and 3 no longer have a demand upstream and are forced to shut down. • Final assembler 14 remains operational with supplies from the previous week. Distributors 17 and 18 remain operational maintaining a 50% export performance. |
• Distributors only receive 50% of the normal supply of assembled units in the previous week and export performance drops to 50%. • All other actors remain in the same state. |
| 3. | • Final assembler 14 runs out of required input and shuts down. Distributors 17 and 18 remain operational with supplies received in the previous week, keeping the export performance at 50% | • All actors remain in the same state as the previous week. |
| 4. | • Distributors 17 and 18, no longer have any stock left and export performance drops to 0%. All actors are shut down between weeks 4 and 5. | • All actors remain in the same state as the previous week. |
| 5. | • Repair efforts allow suppliers 1 and 6 to restart production at 25%. All other suppliers can restart only at 25% as well, because all components are required in equal numbers, any extra component of a type will be wasted if there is not an equal supply of its counterpart. Eg. since supplier 1 supplies only 2500 rotors to sub-assembler 9, there is only demand for 2500 stators from supplier 4 as well. | • Repair efforts allow suppliers 1 and 6 to restart production at 25%. Suppliers 2 and 5 maintain operations at 100% and the rest of the suppliers’ increments their operations to 62.5% capacity. • This increment is possible as the final assembler 13 is expected to resume operations at 25% capacity in two weeks. After one week, sub assemblers will need to increase their production to meet the supply needs that allow final assembler 13 to start operations. Subsequently, there is a demand for a higher number of primary components from the suppliers to the sub-assemblers too. |
| 6. | • Since the final assembler 13 will be able to resume operations at 25% capacity from week 7, the sub-assemblers have demand for their output again. With the supplies (25% of normal) received between week 5 and week 6 from the suppliers, the sub-assemblers can all resume function and supply to the final assemblers. • Suppliers increment their output to 50% of normal operations as suppliers 1 and 2 recover further. |
• Suppliers 1 and 6 increment their output to 50% of normal operations. • Sub-assemblers increase their production to 62.5% expecting final assembler 13 to resume operation next week. |
| 7. | • Repair efforts allow final assembler 13 restarts at 25% capacity. Final Assembler 14 also starts at 25% capacity because of the limited supply of sub-assemblies. • Suppliers increment to 75% capacity due to further repair of suppliers 1 and 6. Sub-assemblers are able to increase their output to 50% as well, due to the supplies received during the previous week and the fact that the final assembler will be able to operate at 50% the next week, thus producing the demand. |
• Repair efforts allow final assembler 13 restarts at 25% capacity. • Sub-assemblers increase their production to 75%, anticipating further improvement of final assembler 13 and supplied sufficiently by the corresponding increase in production and shipment of primary components by the suppliers. • Suppliers 1 and 6 now operate at 75%. • All actors are, at least, partially operational. |
| 8. | • Distributors finally receive assembled motor units (25% of usual supply) from the partially operational final assemblers. Export performance improves to 25%. • All suppliers now operate at 100%, as repair efforts at 1 and 6 are completed. • With the continued expected improvement of sub-assembler 13, the demand on the sub-assemblers also increases steadily. Sub-assemblers now operate at 75% capacity. • The final assemblers operate at 50% capacity based on repair efforts at 13 and the amount of supplies received from sub-assemblers in the last week. • All actors are, at least, partially operational. |
• Supply of assembled motors to distributors increases as final assembler 13 resumed operations last week. Export performance increases to 62.5%. • All suppliers now operate at 100%, as repair efforts at 1 and 6 are completed. • With the continued expected improvement of sub-assembler 13, the demand on the sub-assemblers also increases steadily. Sub-assemblers now operate at 87.5% capacity. |
| 9. | • Following the pattern of the past weeks, sub-assemblers increase operations to 100%, final assemblers to 75% and the distributors to 50%. | • Following the pattern of the past weeks, sub-assemblers increase operations to 100%, final assemblers to 75% and the distributors to 75%. |
| 10. | • All actors except the distributors are now operational at 100% as the repairs are completed at final assembler 13. • The distributors operate at 75% exports because they only received 75% of the normal number of assembled motors in the previous week. |
• All actors except the distributors are now operational at 100% as the repairs are completed at final assembler 13. • The distributors operate at 87.5% of the normal export level. |
| 11. | • The distributors also receive a full supply of assembled motor units and 100% export performance is recovered. | • The distributors also receive a full supply of assembled motor units and 100% export performance is recovered. |
Appendix D. Supplementary materials
References
- 1.Geem Z.W. Optimal cost design of water distribution networks using harmony search. Eng Optim. 2006;38(3):259–277. doi: 10.1080/03052150500467430. [DOI] [Google Scholar]
- 2.Arias-Albornoz M., Sanhueza-Hardy H. Distribution network configuration for minimum energy supply cost. IEEE Trans Power Syst. 2004;19(1):538–542. doi: 10.1109/TPWRS.2003.820697. [DOI] [Google Scholar]
- 3.Borgnakke C., Sonntag R.E. 9e. ed. John Wiley & Sons, Inc; Hoboken, NJ: 2017. Fundamentals of thermodynamics. [Google Scholar]
- 4.Bertsekas D.P. Athena Scientific; Belmont: 1998. Network optimization: continuous and discrete models. [Google Scholar]
- 5.Dijkstra E.W. A note on two problems in connexion with graphs. Numerische Mathematik. 1959;1(1):269–271. doi: 10.1007/bf01386390. [DOI] [Google Scholar]
- 6.Latora V., Marchiori M. Efficient Behavior of Small-World Networks. Phys Rev Lett. 2001;87(19) doi: 10.1103/PhysRevLett.87.198701. [DOI] [PubMed] [Google Scholar]
- 7.Azad A.V., Amidpour M. Economic optimization of shell and tube heat exchanger based on constructal theory. Energy. 2011;36(2):1087–1096. doi: 10.1016/j.energy.2010.11.041. [DOI] [Google Scholar]
- 8.Ren H., Gao W., Ruan Y. Economic optimization and sensitivity analysis of photovoltaic system in residential buildings. Renew Energy. 2009;34(3):883–889. doi: 10.1016/j.renene.2008.06.011. [DOI] [Google Scholar]
- 9.Ramudhin A. 2008 IEEE international conference on industrial engineering and engineering management. 2008. Carbon market sensitive green supply chain network design. [DOI] [Google Scholar]
- 10.Elhedhli S., Merrick R. Green supply chain network design to reduce carbon emissions. Transp Res Part D. 2012;17(5):370–379. doi: 10.1016/j.trd.2012.02.002. [DOI] [Google Scholar]
- 11.de Faria D.C., Ulson de Souza A.A., Guelli Ulson de Souza S.M.d.A. Optimization of water networks in industrial processes. J Clean Prod. 2009;17(9):857–862. doi: 10.1016/j.jclepro.2008.12.012. [DOI] [Google Scholar]
- 12.Gomes J.F.S., Queiroz E.M., Pessoa F.L.P. Design procedure for water/wastewater minimization: single contaminant. J Clean Prod. 2007;15(5):474–485. doi: 10.1016/j.jclepro.2005.11.018. [DOI] [Google Scholar]
- 13.NOAA. U.S. Billion-Dollar Weather and Climate Disasters. 2019 [11/13/2019] Available from: https://www.ncdc.noaa.gov/billions/.
- 14.Hollnagel E., Woods D.D., Leveson N. Ashgate Publishing, Ltd; 2006. Resilience engineering: concepts and precepts. [Google Scholar]
- 15.Jackson S., Ferris T.L.J. Resilience principles for engineered systems. Syst Eng. 2013;16(2):152–164. doi: 10.1002/sys.21228. [DOI] [Google Scholar]
- 16.Uday P., Marais K. Designing resilient systems-of-systems: a survey of metrics, methods, and challenges. Syst Eng. 2015;18(5):491–510. doi: 10.1002/sys.21325. [DOI] [Google Scholar]
- 17.Hosseini S., Barker K., Ramirez-Marquez J.E. A review of definitions and measures of system resilience. Reliab Eng Syst Saf. 2016;145:47–61. doi: 10.1016/j.ress.2015.08.006. [DOI] [Google Scholar]
- 18.Ayyub B.M. Systems resilience for multihazard environments: definition, metrics, and valuation for decision making. Risk Anal. 2014;34(2):340–355. doi: 10.1111/risa.12093. [DOI] [PubMed] [Google Scholar]
- 19.Henry D., Emmanuel Ramirez-Marquez J. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab Eng Syst Saf. 2012;99:114–122. doi: 10.1016/j.ress.2011.09.002. [DOI] [Google Scholar]
- 20.Yodo N., Wang P. Resilience modeling and quantification for engineered systems using bayesian networks. J Mech Desn. 2016;138(3) doi: 10.1115/1.4032399. 031404-031404-12. [DOI] [Google Scholar]
- 21.Uday P., Marais K.B. Resilience-based System Importance Measures for System-of-Systems. Procedia Comput Sci. 2014;28:257–264. doi: 10.1016/j.procs.2014.03.033. [DOI] [Google Scholar]
- 22.Barker K., Ramirez-Marquez J.E., Rocco C.M. Resilience-based network component importance measures. Reliab Eng Syst Saf. 2013;117:89–97. doi: 10.1016/j.ress.2013.03.012. [DOI] [Google Scholar]
- 23.Pumpuni-Lenss G., Blackburn T., Garstenauer A. Resilience in complex systems: an agent-based approach. Syst Eng. 2017;20(2):158–172. doi: 10.1002/sys.21387. [DOI] [Google Scholar]
- 24.Bocchini P. Resilience and sustainability of civil infrastructure: toward a unified approach. J Infrastruct Syst. 2014;20(2) doi: 10.1061/(ASCE)IS.1943-555X.0000177. [DOI] [Google Scholar]
- 25.Castet J.-.F., Saleh J.H. On the concept of survivability, with application to spacecraft and space-based networks. Reliab Eng Syst Saf. 2012;99:123–138. doi: 10.1016/j.ress.2011.11.011. [DOI] [Google Scholar]
- 26.Bruneau M. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthquake Spectra. 2003;19(4):733–752. doi: 10.1193/1.1623497. [DOI] [Google Scholar]
- 27.Brundtland G.H., Khalid M., Agnelli S., Al-Athel S., Chidzero B. New York; 1987. Our common future; p. 8. [Google Scholar]
- 28.Elmqvist T. Sustainability and resilience for transformation in the urban century. Nature Sustain. 2019;2(4):267–273. doi: 10.1038/s41893-019-0250-1. [DOI] [Google Scholar]
- 29.Marchese D. Resilience and sustainability: similarities and differences in environmental management applications. Sci Total Environ. 2018;613-614:1275–1283. doi: 10.1016/j.scitotenv.2017.09.086. [DOI] [PubMed] [Google Scholar]
- 30.Ahern J. Urban landscape sustainability and resilience: the promise and challenges of integrating ecology with urban planning and design. J Landscape Ecol. 2013;28(6):1203–1212. doi: 10.1007/s10980-012-9799-z. [DOI] [Google Scholar]
- 31.Bozza A., Asprone D., Manfredi G. Developing an integrated framework to quantify resilience of urban systems against disasters. Natural Hazards. 2015;78(3):1729–1748. doi: 10.1007/s11069-015-1798-3. [DOI] [Google Scholar]
- 32.Korhonen J., Seager T.P. Beyond eco-efficiency: a resilience perspective. Business Strategy Environ. 2008;17(7):411–419. doi: 10.1002/bse.635. [DOI] [Google Scholar]
- 33.Achour N. Integration of resilience and sustainability: from theory to application. Int J Disaster Resilience Built Environ. 2015;6(3):347–362. doi: 10.1108/IJDRBE-05-2013-0016. [DOI] [Google Scholar]
- 34.Roostaie S., Nawari N., Kibert C.J. Sustainability and resilience: a review of definitions, relationships, and their integration into a combined building assessment framework. Build Environ. 2019;154:132–144. doi: 10.1016/j.buildenv.2019.02.042. [DOI] [Google Scholar]
- 35.Levin S.A. Ecosystems and the biosphere as complex adaptive systems. Ecosystems. 1998;1(5):431–436. doi: 10.1007/s100219900037. [DOI] [Google Scholar]
- 36.Common M., Perrings C. Towards an ecological economics of sustainability. Ecol Econ. 1992;6(1):7–34. doi: 10.1016/0921-8009(92)90036-R. [DOI] [Google Scholar]
- 37.Blackmore J.M., Plant R.A.J. Risk and resilience to enhance sustainability with application to urban water systems. J Water Resour Plann Manag. 2008;134(3):224–233. doi: 10.1061/(ASCE)0733-9496(2008)134:3(224). [DOI] [Google Scholar]
- 38.Fiksel J. Designing resilient, sustainable systems. Environ Sci Technol. 2003;37(23):5330–5339. doi: 10.1021/es0344819. [DOI] [PubMed] [Google Scholar]
- 39.Fiksel J. Sustainability and resilience: toward a systems approach. Sustainability: Science, Practice and Policy. 2006;2(2):14–21. doi: 10.1080/15487733.2006.11907980. [DOI] [Google Scholar]
- 40.Ahern J. From fail-safe to safe-to-fail: sustainability and resilience in the new urban world. Landsc Urban Plan. 2011;100(4):341–343. doi: 10.1016/j.landurbplan.2011.02.021. [DOI] [Google Scholar]
- 41.Fiksel J., Goodman I., Hecht A. Resilience: navigating toward a sustainable future. Solut J. 2014;5(5):38–47. https://www.thesolutionsjournal.com/article/resilience-navigating-toward-a-sustainable-future/ [Google Scholar]
- 42.Holling C.S. Resilience and stability of ecological systems. Annu Rev Ecol Syst. 1973;4:1–23. http://www.jstor.org/stable/2096802 [Google Scholar]
- 43.Raz A.K., Kenley C.R. 2019 IEEE international conference on Systems, Man and Cybernetics (SMC) 2019. Multi-disciplinary perspectives for engineering resilience in systems. [DOI] [Google Scholar]
- 44.Evans, D.M., M.J.O. Pocock, and J. Memmott, The robustness of a network of ecological networks to habitat loss. 2013.16(7): p. 844–852. DOI: 10.1111/ele.12117. [DOI] [PubMed]
- 45.Gross T. Generalized models reveal stabilizing factors in food webs. Science. 2009;325(5941):747–750. doi: 10.1126/science.1173536. https://science.sciencemag.org/content/sci/325/5941/747.full.pdf [DOI] [PubMed] [Google Scholar]
- 46.Staniczenko, P.P.A., et al., Structural dynamics and robustness of food webs. 2010.13(7): p. 891–899. DOI: 10.1111/j.1461-0248.2010.01485.x. [DOI] [PubMed]
- 47.Ulanowicz R, et al. Quantifying sustainability: resilience, efficiency and the return of information theory, 2009;6:27–36. doi: 10.1016/j.ecocom.2008.10.005. [DOI]
- 48.Fath B.D. Quantifying economic and ecological sustainability. Ocean Coast Manag. 2015;108:13–19. doi: 10.1016/j.ocecoaman.2014.06.020. [DOI] [Google Scholar]
- 49.Ulanowicz R.E. The dual nature of ecosystem dynamics. Ecol Modell. 2009;220(16):1886–1892. doi: 10.1016/j.ecolmodel.2009.04.015. [DOI] [Google Scholar]
- 50.Zorach A.C., Ulanowicz R.E. Quantifying the complexity of flow networks: how many roles are there? Complexity. 2003;8(3):68–76. doi: 10.1002/cplx.10075. [DOI] [Google Scholar]
- 51.Ulanowicz R.E., Holt R.D., Barfield M. Limits on ecosystem trophic complexity: insights from ecological network analysis. Ecol Lett. 2014;17(2):127–136. doi: 10.1111/ele.12216. [DOI] [PubMed] [Google Scholar]
- 52.Panyam V. Bio-inspired design for robust power grid networks. Appl Energy. 2019;251 doi: 10.1016/j.apenergy.2019.113349. [DOI] [Google Scholar]
- 53.Dave T., Layton A. Designing ecologically-inspired robustness into a water distribution network. J Clean Prod. 2020;254 doi: 10.1016/j.jclepro.2020.120057. [DOI] [Google Scholar]
- 54.Ulanowicz R.E. Quantitative methods for ecological network analysis. Comput Biol Chem. 2004;28(5):321–339. doi: 10.1016/j.compbiolchem.2004.09.001. [DOI] [PubMed] [Google Scholar]
- 55.Layton A., Bras B., Weissburg M. Ecological principles and metrics for improving material cycling structures in manufacturing networks. J Manuf Sci Eng. 2016;138(10) doi: 10.1115/1.4033689. 101002-101002-12. [DOI] [Google Scholar]
- 56.Fath B.D. Ecological network analysis: network construction. Ecol Modell. 2007;208(1):49–55. doi: 10.1016/j.ecolmodel.2007.04.029. [DOI] [Google Scholar]
- 57.Layton A., Bras B., Weissburg M. Designing industrial networks using ecological food web metrics. Environ Sci Technol. 2016;50(20):11243–11252. doi: 10.1021/acs.est.6b03066. [DOI] [PubMed] [Google Scholar]
- 58.Fath B.D., Patten B.C. Network synergism: emergence of positive relations in ecological systems. Ecol Modell. 1998;107(2):127–143. doi: 10.1016/S0304-3800(97)00213-5. [DOI] [Google Scholar]
- 59.Fath B.D. Network mutualism: positive community-level relations in ecosystems. Ecol Modell. 2007;208(1):56–67. doi: 10.1016/j.ecolmodel.2007.04.021. [DOI] [Google Scholar]
- 60.Ulanowicz R.E. iUniverse; 1986. Growth and development: ecosystems phenomenology.https://books.google.com/books?id=vSkFAAAACAAJ [Google Scholar]
- 61.Borrett S.R., Lau M.K. enaR: an r package for ecosystem network analysis. Method Ecol Evolut. 2014;5(11):1206–1213. doi: 10.1111/2041-210x.12282. [DOI] [Google Scholar]
- 62.Singh A.N., Gupta M.P., Ojha A. Identifying critical infrastructure sectors and their dependencies: an Indian scenario. Int J Crit Infrast Protect. 2014;7(2):71–85. doi: 10.1016/j.ijcip.2014.04.003. [DOI] [Google Scholar]
- 63.Klein P., Klein F. Dynamics of interdependent critical infrastructures – A mathematical model with unexpected results. Int J Crit Infrastruct Protect. 2019;24:69–77. doi: 10.1016/j.ijcip.2018.11.002. [DOI] [Google Scholar]
- 64.Thompson J.R. Interdependent Critical Infrastructure Model (ICIM): an agent-based model of power and water infrastructure. Int J Crit Infrastruct Protect. 2019;24:144–165. doi: 10.1016/j.ijcip.2018.12.002. [DOI] [Google Scholar]
- 65.Chatterjee A., Layton A. ASME 2019 international design engineering technical conferences and computers and information in engineering conference. 2019. Bio-inspired human network design: a multi-currency robustness metric inspired by ecological network analysis. [DOI] [Google Scholar]
- 66.Pires Ribeiro J., Barbosa-Povoa A. Supply chain resilience: definitions and quantitative modelling approaches – A literature review. Comput Ind Eng. 2018;115:109–122. doi: 10.1016/j.cie.2017.11.006. [DOI] [Google Scholar]
- 67.Ivanov D., Sokolov B. Control and system-theoretic identification of the supply chain dynamics domain for planning, analysis and adaptation of performance under uncertainty. Eur J Oper Res. 2013;224(2):313–323. doi: 10.1016/j.ejor.2012.08.021. [DOI] [Google Scholar]
- 68.Ivanov D., Dolgui A. Low-Certainty-Need (LCN) supply chains: a new perspective in managing disruption risks and resilience. Int J Product Res. 2019;57(15–16):5119–5136. doi: 10.1080/00207543.2018.1521025. [DOI] [Google Scholar]
- 69.Hosseini S., Ivanov D., Dolgui A. Ripple effect modelling of supplier disruption: integrated Markov chain and dynamic Bayesian network approach. Int J Product Res. 2019:1–20. doi: 10.1080/00207543.2019.1661538. [DOI] [Google Scholar]
- 70.Hosseini S., Ivanov D., Dolgui A. Review of quantitative methods for supply chain resilience analysis. Transp Res Part E. 2019;125:285–307. doi: 10.1016/j.tre.2019.03.001. [DOI] [Google Scholar]
- 71.Dolgui A., Ivanov D., Sokolov B. Ripple effect in the supply chain: an analysis and recent literature. Int J Prod Res. 2018;56(1–2):414–430. doi: 10.1080/00207543.2017.1387680. [DOI] [Google Scholar]
- 72.Demirel G. Identifying dynamical instabilities in supply networks using generalized modeling. J Oper Manag. 2019;65(2):136–159. doi: 10.1002/joom.1005. [DOI] [Google Scholar]
- 73.Wholesale, E.M., 2019, 100HP BALDOR 1785RPM 405T TEFC 3PH MOTOR ECP4400T-4, http://www.electricmotorwholesale.com/BALDOR-ECP4400T-4/. Accessed: 6/24/2019.
- 74.U.S. Dept of Energy, Chapter 6. Markups Analysis, in Preliminary Technical Support Document: Energy Efficiency Program for Commercial Equipment. 2012.
- 75.Recovering after a hurricane: how long does it take?2017September 15, 2019]; Available from: https://webassets.inman.com/wp-content/uploads/2017/10/BuildFax-Hurricane-Recovery-Study.pdf.
- 76.Valenzuela-Venegas G. A resilience indicator for Eco-Industrial Parks. J Clean Prod. 2018;174:807–820. doi: 10.1016/j.jclepro.2017.11.025. [DOI] [Google Scholar]
- 77.Mulligan M. Keywords in planning: what do we mean by ‘community resilience’? Int Plan Stud. 2016;21(4):348–361. doi: 10.1080/13563475.2016.1155974. [DOI] [Google Scholar]
- 78.Pettit T., Fiksel J., Croxton K. Ensuring supply chain resilience: development of a conceptual framework. J Bus Logist. 2010;31:1–21. doi: 10.1002/j.2158-1592.2010.tb00125.x. [DOI] [Google Scholar]
- 79.Layton, A., B. Bras, and M. Weissburg, Ecological robustness as a design principle for sustainable industrial systems. 2015(57113): p. V004T05A047. DOI: 10.1115/DETC2015-47560.
- 80.Ivanov D., Pavlov A., Sokolov B. Optimal distribution (re)planning in a centralized multi-stage supply network under conditions of the ripple effect and structure dynamics. Eur J Oper Res. 2014;237(2):758–770. doi: 10.1016/j.ejor.2014.02.023. [DOI] [Google Scholar]
- 81.Ivanov D. Disruption-driven supply chain (re)-planning and performance impact assessment with consideration of pro-active and recovery policies. Transp Res Part E. 2016;90:7–24. doi: 10.1016/j.tre.2015.12.007. [DOI] [Google Scholar]
- 82.Ivanov D. Minimization of disruption-related return flows in the supply chain. Int J Product Econ. 2017;183:503–513. doi: 10.1016/j.ijpe.2016.03.012. [DOI] [Google Scholar]
- 83.Ivanov D. Disruption tails and revival policies: a simulation analysis of supply chain design and production-ordering systems in the recovery and post-disruption periods. Comput Ind Eng. 2019;127:558–570. doi: 10.1016/j.cie.2018.10.043. [DOI] [Google Scholar]
- 84.Paul S.K. A mathematical modelling approach for managing sudden disturbances in a three-tier manufacturing supply chain. Ann Oper Res. 2019;280(1):299–335. doi: 10.1007/s10479-019-03251-w. [DOI] [Google Scholar]
- 85.Dixit V., Seshadrinath N., Tiwari M.K. Performance measures based optimization of supply chain network resilience: a NSGA-II+Co-Kriging approach. Comput Ind Eng. 2016;93:205–214. doi: 10.1016/j.cie.2015.12.029. [DOI] [Google Scholar]
- 86.Pavlov A. Optimization of network redundancy and contingency planning in sustainable and resilient supply chain resource management under conditions of structural dynamics. Ann Oper Res. 2019 doi: 10.1007/s10479-019-03182-6. [DOI] [Google Scholar]
- 87.Ouyang M., Dueñas-Osorio L., Min X. A three-stage resilience analysis framework for urban infrastructure systems. Struct Saf. 2012;36-37:23–31. doi: 10.1016/j.strusafe.2011.12.004. [DOI] [Google Scholar]
- 88.Ouyang M., Wang Z. Resilience assessment of interdependent infrastructure systems: with a focus on joint restoration modeling and analysis. Reliab Eng Syst Saf. 2015;141:74–82. doi: 10.1016/j.ress.2015.03.011. [DOI] [Google Scholar]
- 89.Hossain N.U.I. A framework for modeling and assessing system resilience using a Bayesian network: a case study of an interdependent electrical infrastructure system. Int J Critic Infrastruct Protect. 2019;25:62–83. doi: 10.1016/j.ijcip.2019.02.002. [DOI] [Google Scholar]
- 90.Attoh-Okine N.O., Cooper A.T., Mensah S.A. Formulation of resilience index of urban infrastructure using belief functions. IEEE Syst J. 2009;3(2):147–153. doi: 10.1109/JSYST.2009.2019148. [DOI] [Google Scholar]
- 91.Ivanov D. Viable supply chain model: integrating agility, resilience and sustainability perspectives—Lessons from and thinking beyond the COVID-19 pandemic. Ann Oper Res. 2020 doi: 10.1007/s10479-020-03640-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Ivanov D., Dolgui A. Viability of intertwined supply networks: extending the supply chain resilience angles towards survivability. A position paper motivated by COVID-19 outbreak. International Journal of Production Research. 2020;58(10):2904–2915. doi: 10.1080/00207543.2020.1750727. [DOI] [Google Scholar]
- 93.Panyam, V., T. Dave, and A. Layton, Understanding ecological efficiency and robustness for network design using thermodynamic power cycles. 2018(51845): p. V007T06A053. DOI: 10.1115/DETC2018-85404.
- 94.Layton A. Correlation between thermodynamic efficiency and ecological cyclicity for thermodynamic power cycles. PLoS ONE. 2012;7(12):e51841. doi: 10.1371/journal.pone.0051841. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.