Abstract
As a substrate for function, large-scale brain structural networks are crucial for fundamental and systems-level understanding of primate brains. However, it is challenging to acquire a complete primate whole-brain structural connectome using track tracing techniques. Here, we acquired a weighted brain structural network across 91 cortical regions of a whole macaque brain hemisphere with a connectivity density of 59% by predicting missing links from the CoCoMac-based binary network with a low density of 26.3%. The prediction model combines three factors, including spatial proximity, topological similarity, and cytoarchitectural similarity—to predict missing links and assign connection weights. The model was tested on a recently obtained high connectivity density yet partial-coverage experimental weighted network connecting 91 sources to 29 target regions; the model showed a prediction sensitivity of 74.1% in the predicted network. This predicted macaque hemisphere-wide weighted network has module segregation closely matching functional domains. Interestingly, the areas that act as integrators linking the segregated modules are mainly distributed in the frontoparietal network and correspond to the regions with large wiring costs in the predicted weighted network. This predicted weighted network provides a high-density structural dataset for further exploration of relationships between structure, function, and metabolism in the primate brain.
Keywords: hemisphere-wide weighted network, link prediction, macaque brain connectome, segregation and integration, structural network
Introduction
A complex brain network consisting of a large number of anatomical interareal pathways forms the structural substrate of brain functional performance (Purves et al. 2004; Bressler and Menon 2010; Park and Friston 2013). Research into the fundamental and systems-level mechanisms of brain functional performance and cognitive behavior depends heavily on the accurate and complete data of the structural brain connectome (Fuster 2000; Miller and Cohen 2001; Jacobs and Scheibel 2002; Elston 2003; Kaiser 2007; Spruston 2008; Fornito et al. 2013; Harris and Shepherd 2015; Misic et al. 2015; Bratislav et al. 2016; Luebke 2017). A large amount of analysis and modeling work have been carried out on the brain connectome in the last decade to investigate the structure-function relationship of the brain across various species (Sporns et al. 2004; Markram 2006; Elston 2007; Honey et al. 2007; Sporns 2014; Chaudhuri et al. 2015); nonetheless, there remains a need for a more complete and reliable mesoscopic anatomical connectome of the primate brain across cortical regions, and the search for this information is a major challenge in the field. Thus, one of the key issues in several large brain projects is to obtain a complete mesoscopic mapping of large-scale brain connectivity (Koch and Reid 2012; Kandel et al. 2013; Van Essen et al. 2013; Sejnowski et al. 2014; Alivisatos et al. 2015; Jorgenson et al. 2015; Mainen et al. 2016; Poo et al. 2016).
The macaque monkey, given its phylogenetic proximity to humans (Kaas 1992; Goldman-Rakic 1995; Preuss 1995; Rakic 1995; Goldman-Rakic 1996; Kaas 1997; Goldman-Rakic 1999; Preuss 2000; Rakic 2009; Goldman-Rakic 2011; Bianchi et al. 2013), is the ideal animal species to explore the structural and functional mechanisms of the primate brain (Poo et al. 2016). Invasive track-tracing techniques applicable to animal brains can detect the axon projections among brain regions more reliably than the noninvasive techniques (Oh et al. 2014; Rubinov et al. 2015). Previously, data on the macaque connectome were collated into the CoCoMac dataset (Kotter 2004) by reviewing the projections identified in numerous anterograde and retrograde tracing experiments from independent studies (Lanciego and Wouterlood 2011). However, the different datasets have inconsistency for axon projections, even for the network statistical properties (Bezgin et al. 2012), and thus it is highly challenging to combine different datasets to construct the whole brain connectome. Yet, some datasets are relatively more consistent than other (Bezgin et al. 2012), such as datasets of FV91 (Felleman and Van Essen 1991), LV00 (Lewis and Van Essen 2000a, 2000b), and PHT00 (Paxinos et al. 2000). Notably, FV91 is a systematic analysis of macaque anatomical connections proposing the hierarchical structure based on the laminar pattern, and most broadly applied afterwards (Buzsaki 2006; Bullmore and Sporns 2009; Friston 2010). Previous work combined the FV91 dataset with LV00, two consistent maps to build the macaque cortical network (Kaiser and Hilgetag 2006), which was further improved by combining PHT00 to overcome the relative rough area division for motor cortex (Chen et al. 2013, 2017). This previously applied dataset (dataset 1, 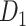 ) combining three datasets and covering the whole brain has a connectivity density of approximately 26.3%. However, the CoCoMac dataset only provides a qualitative assessment of connection weight, using categories such as weak, moderate, and strong (Bakker et al. 2012).
) combining three datasets and covering the whole brain has a connectivity density of approximately 26.3%. However, the CoCoMac dataset only provides a qualitative assessment of connection weight, using categories such as weak, moderate, and strong (Bakker et al. 2012). 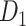 provides structural network with a rather complete coverage of cortical regions and thus has been widely used in the analysis and modeling of brain networks, but the crude weight information is seldom used in the analysis (Honey et al. 2007; Sporns et al. 2007; Chen et al. 2013, 2017). Meanwhile, the CoCoMac dataset was not acquired systematically under uniform experimental conditions but collated from various studies with different parcellation schemes (Markov, Ercsey-Ravasz, et al. 2014).
provides structural network with a rather complete coverage of cortical regions and thus has been widely used in the analysis and modeling of brain networks, but the crude weight information is seldom used in the analysis (Honey et al. 2007; Sporns et al. 2007; Chen et al. 2013, 2017). Meanwhile, the CoCoMac dataset was not acquired systematically under uniform experimental conditions but collated from various studies with different parcellation schemes (Markov, Ercsey-Ravasz, et al. 2014).
Recently, an improved retrograde tracing method has been applied to macaque monkeys to systematically obtain projections and corresponding quantitative projection strength (connection weight) from 91 areas to 29 injection areas of one hemisphere to form a new dataset (dataset 2, 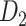 ) (Markov, Ercsey-Ravasz, et al. 2014). Importantly, this improved tract-tracing method has revealed many weak projections. The binary connectivity density of 61.2% (whether two areas are connected or not, irrespective of the projection strength) in this new weighted directed
) (Markov, Ercsey-Ravasz, et al. 2014). Importantly, this improved tract-tracing method has revealed many weak projections. The binary connectivity density of 61.2% (whether two areas are connected or not, irrespective of the projection strength) in this new weighted directed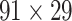 network is much higher than the value in the CoCoMac dataset (
network is much higher than the value in the CoCoMac dataset ( ), overturning the view of brain as a sparse network (Markov, Ercsey-Ravasz, et al. 2014). The aforementioned quantitative projection weights span five orders of magnitude (Markov, Ercsey-Ravasz, et al. 2014), statistically decaying with projection distance. However, these high-resolution anatomical data are still far from being complete because they cover only approximately one-third (29/91 regions) of the cortical areas. The connectivity data of 29 target areas of the hemisphere were obtained through labor-intensive histology and imaging procedures in 28 macaque monkeys (Markov, Ercsey-Ravasz, et al. 2014). It would be highly labor intensive, time consuming, and costly to obtain complete cortical coverage, which would require sacrificing a large number of macaque monkeys. Therefore, there are currently two distinct datasets on the connectivity of the macaque brain: 1) the CoCoMac-based network (
), overturning the view of brain as a sparse network (Markov, Ercsey-Ravasz, et al. 2014). The aforementioned quantitative projection weights span five orders of magnitude (Markov, Ercsey-Ravasz, et al. 2014), statistically decaying with projection distance. However, these high-resolution anatomical data are still far from being complete because they cover only approximately one-third (29/91 regions) of the cortical areas. The connectivity data of 29 target areas of the hemisphere were obtained through labor-intensive histology and imaging procedures in 28 macaque monkeys (Markov, Ercsey-Ravasz, et al. 2014). It would be highly labor intensive, time consuming, and costly to obtain complete cortical coverage, which would require sacrificing a large number of macaque monkeys. Therefore, there are currently two distinct datasets on the connectivity of the macaque brain: 1) the CoCoMac-based network ( ), which has high brain coverage but low connectivity density and crude weight information, and 2) a directed and weighted
), which has high brain coverage but low connectivity density and crude weight information, and 2) a directed and weighted 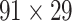 network (
network ( ), which is more accurate but has only partial cortical coverage. Despite being incomplete, the directed and weighted partial network
), which is more accurate but has only partial cortical coverage. Despite being incomplete, the directed and weighted partial network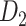 has provided new insights into the organization of the brain (Markov, Vezoli, et al. 2014; Song et al. 2014; Chaudhuri et al. 2015; Donahue et al. 2016; Mejias et al. 2016). In the present era, it will be of great value to use the two existing datasets to obtain a more complete, high-density, directed, and weighted connectome across a whole macaque brain hemisphere before proceeding with expensive experiments to complete it.
has provided new insights into the organization of the brain (Markov, Vezoli, et al. 2014; Song et al. 2014; Chaudhuri et al. 2015; Donahue et al. 2016; Mejias et al. 2016). In the present era, it will be of great value to use the two existing datasets to obtain a more complete, high-density, directed, and weighted connectome across a whole macaque brain hemisphere before proceeding with expensive experiments to complete it.
In this work, we propose a three-factor multiple-iteration predictive model to map the hemisphere-wide weighted structural network based on the previous CoCoMac dataset 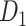 (Kotter 2004; Chen et al. 2013, 2017). The high-density, weighted, yet partial macaque brain structural network
(Kotter 2004; Chen et al. 2013, 2017). The high-density, weighted, yet partial macaque brain structural network 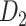 , showing projections from 91 regions to 29 regions (Markov, Ercsey-Ravasz, et al. 2014), is used to calibrate and optimize the parameters of the predictive model and to examine the sensitivity and specificity of the predicted links and connection weights. The predictive model here combines three factors that have been found to relate to brain connectivity, including 1) “spatial proximity,” measuring the spatial distance between two regions (Ercsey-Ravasz et al. 2013); 2) “topological similarity,” measuring the similarity of the connection profiles of two regions in the network (Song et al. 2014); and 3) “cytoarchitectural similarity,” describing the relationship between the density and anatomical complexity (or computational capacity) of neurons in the two regions (Elston et al. 1999; Elston 2000; Elston et al. 2001; Elston and Rockland 2002; Elston et al. 2005; Herculano-Houzel et al. 2007; Collins et al. 2010; Beul et al. 2017). First, we use the model to acquire the predicted binary network
, showing projections from 91 regions to 29 regions (Markov, Ercsey-Ravasz, et al. 2014), is used to calibrate and optimize the parameters of the predictive model and to examine the sensitivity and specificity of the predicted links and connection weights. The predictive model here combines three factors that have been found to relate to brain connectivity, including 1) “spatial proximity,” measuring the spatial distance between two regions (Ercsey-Ravasz et al. 2013); 2) “topological similarity,” measuring the similarity of the connection profiles of two regions in the network (Song et al. 2014); and 3) “cytoarchitectural similarity,” describing the relationship between the density and anatomical complexity (or computational capacity) of neurons in the two regions (Elston et al. 1999; Elston 2000; Elston et al. 2001; Elston and Rockland 2002; Elston et al. 2005; Herculano-Houzel et al. 2007; Collins et al. 2010; Beul et al. 2017). First, we use the model to acquire the predicted binary network 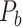 reaching the same connectivity density (61.2%) in the
reaching the same connectivity density (61.2%) in the 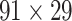 subsystem as that in
subsystem as that in 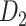 (Markov, Ercsey-Ravasz, et al. 2014). Second, we assign all connection weights in
(Markov, Ercsey-Ravasz, et al. 2014). Second, we assign all connection weights in 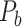 based on the prediction scores to obtain weighed network
based on the prediction scores to obtain weighed network 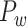 . This new predicted weighed network
. This new predicted weighed network 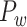 reveals some important features, such as the following: 1) structural modules closely match anatomical functional domains; 2) the connector regions with high participation coefficients (PCs) among anatomical functional domains are mainly distributed in the frontoparietal network (FPN); and 3) the connector regions are those with large total axon projection length (wiring cost).
reveals some important features, such as the following: 1) structural modules closely match anatomical functional domains; 2) the connector regions with high participation coefficients (PCs) among anatomical functional domains are mainly distributed in the frontoparietal network (FPN); and 3) the connector regions are those with large total axon projection length (wiring cost).
Materials and Methods
Macaque Brain Connectome
Two datasets are applied in this work to acquire a large-scale, high-density macaque structural connectome. 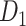 is the previous brain connectivity dataset from CoCoMac (“http://cocomac.org”) (Kotter 2004), which has the complete cortical coverage across the macaque hemisphere but a low connectivity density of 26.3%. In our previous work (Chen et al. 2013, 2017), we collected and constructed a binary brain network with 2512 connections among 103 regions (i.e., a 103
is the previous brain connectivity dataset from CoCoMac (“http://cocomac.org”) (Kotter 2004), which has the complete cortical coverage across the macaque hemisphere but a low connectivity density of 26.3%. In our previous work (Chen et al. 2013, 2017), we collected and constructed a binary brain network with 2512 connections among 103 regions (i.e., a 103 103 binary matrix) from CoCoMac.
103 binary matrix) from CoCoMac. 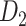 , with partial cortical coverage, contains the projections from 91 regions to 29 regions as identified by systematic experiments with improved retrograde tracing methods (Markov, Ercsey-Ravasz, et al. 2014). With the help of the new method,
, with partial cortical coverage, contains the projections from 91 regions to 29 regions as identified by systematic experiments with improved retrograde tracing methods (Markov, Ercsey-Ravasz, et al. 2014). With the help of the new method, 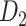 achieves a connectivity density of 61.2%, much higher than that of
achieves a connectivity density of 61.2%, much higher than that of 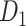 , and contains the projection weights (extrinsic fraction of weighted neurons, FLNe), which is not presented in
, and contains the projection weights (extrinsic fraction of weighted neurons, FLNe), which is not presented in 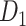 . FLNe is defined as the number of labeled neurons in a source region i divided by the total number of labeled neurons from all source regions extrinsic to a targeted region j injected with the tracers.
. FLNe is defined as the number of labeled neurons in a source region i divided by the total number of labeled neurons from all source regions extrinsic to a targeted region j injected with the tracers.
In this work, we developed a three-factor multiple-iteration predictive model to predict the missing links from 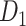 and assigned all projection weights to form a new weighted connectome network
and assigned all projection weights to form a new weighted connectome network  (see below for the predictive model). The model was calibrated according to
(see below for the predictive model). The model was calibrated according to 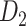 . The three connectomes
. The three connectomes 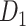 ,
, 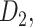 and
and 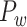 were all registered on the same template of 91 regions as the M132 atlas, covering the whole hemisphere shared by the CARET database (http://sumsdb.wustl.edu/sums/index.jsp). We used the M132 atlas (Paxinos et al. 2000; Saleem and Logothetis 2012) as a reference for the 3D coordinates of all voxels. The average surface 3D coordinate of the voxels of a cortical region in the atlas was taken as the spatial position of the brain region. All maps in this work were displayed on the M132 atlas using the BrainNet viewer (Xia et al. 2013).
were all registered on the same template of 91 regions as the M132 atlas, covering the whole hemisphere shared by the CARET database (http://sumsdb.wustl.edu/sums/index.jsp). We used the M132 atlas (Paxinos et al. 2000; Saleem and Logothetis 2012) as a reference for the 3D coordinates of all voxels. The average surface 3D coordinate of the voxels of a cortical region in the atlas was taken as the spatial position of the brain region. All maps in this work were displayed on the M132 atlas using the BrainNet viewer (Xia et al. 2013).
We also used the neuron densities of two regions as one of the factors to predict the missing links between them, as neuron density can be used to characterize cytoarchitectural similarity between the two regions (Elston et al. 2005). Neuron density was reported in a series of previous publications (Dombrowski et al. 2001; Elston and Rockland 2002; Barbas et al. 2005; Karaoglu et al. 2005; Collins et al. 2010; Elston et al. 2010; Elston, Benavides-Piccione, et al. 2011; Elston, Oga, et al. 2011; Amunts and Zilles 2012; Young et al. 2013; Herculano-Houzel et al. 2014; Herculano-Houzel et al. 2015; van den Heuvel et al. 2015; Collins et al. 2016). We relied mainly on a published dataset from a previous study (Dombrowski et al. 2001); this dataset was also applied in (Beul et al. 2017).
Further details of data and data processing are presented in Supplementary Material I.
Link Prediction Model
Three Factors Involved in Link Prediction
The missing links were predicted for unconnected pairs of regions in 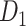 with high prediction scores in the model. The prediction score
with high prediction scores in the model. The prediction score 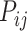 indicates the probability of connectivity between regions i and j in terms of three factors: spatial proximity
indicates the probability of connectivity between regions i and j in terms of three factors: spatial proximity 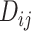 , topological similarity
, topological similarity 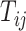 , and cytoarchitectural similarity
, and cytoarchitectural similarity 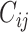 . Previous studies found that the connectivity probability between a pair of regions follows a statistical pattern of exponential decay with the spatial distance between the corresponding regions (Song et al. 2014). Therefore, we took the spatial proximity
. Previous studies found that the connectivity probability between a pair of regions follows a statistical pattern of exponential decay with the spatial distance between the corresponding regions (Song et al. 2014). Therefore, we took the spatial proximity 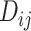 as
as 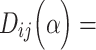
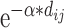 , where
, where 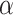 is the decay parameter and
is the decay parameter and 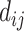 , the distance between regions i to j, is measured by the Euclidean distance of their respective centers of mass. Furthermore, the connectivity probability was assumed to be proportional to the topological similarity, which is quantified by the portion of input or output connections held in common by a pair of regions (Song et al. 2014). Here, we applied 13 different methods to measure the topological similarity
, the distance between regions i to j, is measured by the Euclidean distance of their respective centers of mass. Furthermore, the connectivity probability was assumed to be proportional to the topological similarity, which is quantified by the portion of input or output connections held in common by a pair of regions (Song et al. 2014). Here, we applied 13 different methods to measure the topological similarity 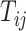 (see Supplementary material II.1) and selected the best among them by calibration with dataset
(see Supplementary material II.1) and selected the best among them by calibration with dataset 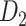 . Recent studies have also revealed that cytoarchitectural features, particularly the neuron density, were strongly associated with connections between different regions (Beul et al. 2017). Pairs of regions with similar neuron densities have a high probability of being connected, independent of the influence of spatial proximity (Hilgetag and Grant 2010; Beul et al. 2017). We applied the measure of cytoarchitecture similarity used in a previous study (Beul et al. 2017),
. Recent studies have also revealed that cytoarchitectural features, particularly the neuron density, were strongly associated with connections between different regions (Beul et al. 2017). Pairs of regions with similar neuron densities have a high probability of being connected, independent of the influence of spatial proximity (Hilgetag and Grant 2010; Beul et al. 2017). We applied the measure of cytoarchitecture similarity used in a previous study (Beul et al. 2017), 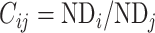 , where
, where 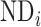 and
and 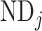 represent the neuron density of source region i and target region j, respectively (see map of neuron density in Supplementary Fig. 1). Taking these three factors together into account, the connectivity probability
represent the neuron density of source region i and target region j, respectively (see map of neuron density in Supplementary Fig. 1). Taking these three factors together into account, the connectivity probability 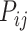 (prediction score) in the predictive model is subsequently defined as
(prediction score) in the predictive model is subsequently defined as
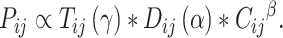 |
(1) |
Here 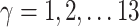 different measures of topological similarity (Supplementary Table 1). The parameters
different measures of topological similarity (Supplementary Table 1). The parameters 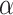 ,
, 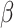 , and
, and 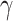 were optimized by calibration with dataset
were optimized by calibration with dataset 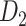 . The predictive model is described in further detail in Supplementary Material II.1.
. The predictive model is described in further detail in Supplementary Material II.1.
Prediction Process
The predictive model contained a multiple iteration process. The missing links were predicted and added into the initial network 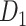 in batches after each of the multiple iteration steps. The multiple iteration process terminated when the connectivity density in the corresponding subset (91
in batches after each of the multiple iteration steps. The multiple iteration process terminated when the connectivity density in the corresponding subset (91 29) achieved 61.2%, the same as that of
29) achieved 61.2%, the same as that of 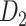 . For the 91
. For the 91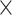 29 subset, there are 888 missing links in
29 subset, there are 888 missing links in 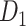 compared with
compared with 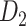 . Setting the total iteration steps as
. Setting the total iteration steps as 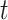 , at each iteration step, we predicted a number of new links
, at each iteration step, we predicted a number of new links 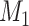 across the whole hemisphere (i.e., in the 91
across the whole hemisphere (i.e., in the 91 91 matrix) to guarantee
91 matrix) to guarantee 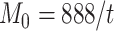 links generated in the 91
links generated in the 91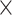 29 subset at each iteration. Thus,
29 subset at each iteration. Thus, 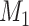 may vary slightly from step to step. For the
may vary slightly from step to step. For the 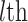 iteration step, the prediction scores for the remaining unconnected pairs of regions were calculated based on the new connectome network (
iteration step, the prediction scores for the remaining unconnected pairs of regions were calculated based on the new connectome network (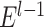 ) up to the
) up to the 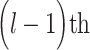 step, which included all the newly added links from the previous
step, which included all the newly added links from the previous 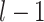 steps. At each step l, the
steps. At each step l, the 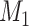 connections with the top prediction scores were chosen. By varying the values of parameters (α, β, and
connections with the top prediction scores were chosen. By varying the values of parameters (α, β, and 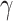 ) to adjust different combinations of the three factors in equation (1), we acquired different groups of
) to adjust different combinations of the three factors in equation (1), we acquired different groups of 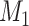 tentative links. The
tentative links. The 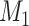 links with the highest prediction precision were added into the network
links with the highest prediction precision were added into the network 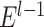 to produce the new network
to produce the new network 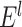 . After a total of
. After a total of 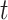 iteration steps, the process yielded the final binary structural connectome (
iteration steps, the process yielded the final binary structural connectome (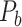 ) with high connectivity density; this connectome included the existing links in the initial network
) with high connectivity density; this connectome included the existing links in the initial network 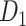 and all the links predicted during the iterations. Different total numbers of iteration steps
and all the links predicted during the iterations. Different total numbers of iteration steps 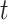 were considered, and the one with the highest sensitivity in the final predicted network (
were considered, and the one with the highest sensitivity in the final predicted network (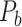 ) was used.
) was used.
Assigning Connection Weights
The experimentally identified connection weights in 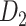 were highly heterogeneous, with values spanning five orders of magnitude (Ercsey-Ravasz et al. 2013) (Fig. 5A). Thus, the predicted binary network was not accurate and could be misleading in practical application because it treats weak connections and strong connections as equally important. As shown in previous studies (Ercsey-Ravasz et al. 2013; Song et al. 2014; Beul et al. 2017), the three factors of spatial proximity, topological similarity, and cytoarchitectural similarity are related not only to connectivity probability but also to the connection weights (FLNe). Thus, we also applied equation (1) to assign weights for all links in the predicted binary network (
were highly heterogeneous, with values spanning five orders of magnitude (Ercsey-Ravasz et al. 2013) (Fig. 5A). Thus, the predicted binary network was not accurate and could be misleading in practical application because it treats weak connections and strong connections as equally important. As shown in previous studies (Ercsey-Ravasz et al. 2013; Song et al. 2014; Beul et al. 2017), the three factors of spatial proximity, topological similarity, and cytoarchitectural similarity are related not only to connectivity probability but also to the connection weights (FLNe). Thus, we also applied equation (1) to assign weights for all links in the predicted binary network (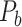 ). Since FLNe follows different forms of exponential decay at various distance bins from the experimental dataset (Fig. 5A), we optimized the parameters in equation (1) for links in different distance bins to refine weight assignment. Initially, we assigned weights to all connections in
). Since FLNe follows different forms of exponential decay at various distance bins from the experimental dataset (Fig. 5A), we optimized the parameters in equation (1) for links in different distance bins to refine weight assignment. Initially, we assigned weights to all connections in 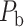 according to the prediction scores based on equation (1), where parameters were chosen when the correlation between the assigned and experimental weights achieves the maximal value for the overlapping connections in
according to the prediction scores based on equation (1), where parameters were chosen when the correlation between the assigned and experimental weights achieves the maximal value for the overlapping connections in  and
and  . Then, we refined the prediction of weights by allowing different model parameters for connections in the n different distance bins to further increase the correlation values. Different distance bin numbers
. Then, we refined the prediction of weights by allowing different model parameters for connections in the n different distance bins to further increase the correlation values. Different distance bin numbers  were considered, and the one generating the highest correlation value was used.
were considered, and the one generating the highest correlation value was used.
Figure 5.
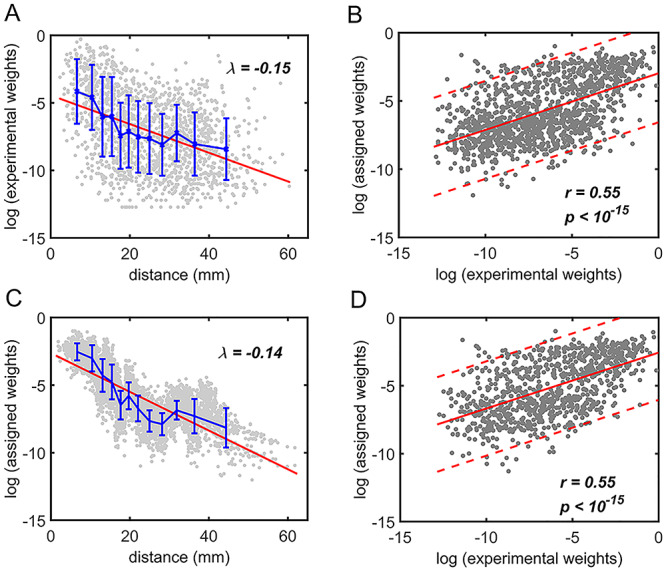
Comparison between assigned and experimental weights in the 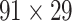 subset. (A) Decay of experimental weights with distance in the 91
subset. (A) Decay of experimental weights with distance in the 91 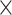 29 dataset in
29 dataset in 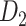 . (B) Assigned weight versus experimental weight (in log-scale) in the 91
. (B) Assigned weight versus experimental weight (in log-scale) in the 91 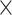 29 subset for each of the TP links (dots) of the final predicted network with an overall connectivity density of 59%. (C) Assigned weights for all links in the final 91
29 subset for each of the TP links (dots) of the final predicted network with an overall connectivity density of 59%. (C) Assigned weights for all links in the final 91 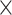 91 predicted network
91 predicted network 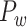 as a function of spatial distance. The exponential decay parameter is −0.14, very close to that from the experimental value of −0.15 (Ercsey-Ravasz et al. 2013). The red lines in (A) and (C) are the exponential fitting. The blue lines in (A) and (C) show the mean values and the standard deviation of the logarithm of experimental connection weights and assigned weights in each of the 12 distance bins, respectively, which interestingly captures the small peak of relatively high weights for long-distance links. (D) The same as (B), but for the assigned weight versus experimental weight in the 91
as a function of spatial distance. The exponential decay parameter is −0.14, very close to that from the experimental value of −0.15 (Ercsey-Ravasz et al. 2013). The red lines in (A) and (C) are the exponential fitting. The blue lines in (A) and (C) show the mean values and the standard deviation of the logarithm of experimental connection weights and assigned weights in each of the 12 distance bins, respectively, which interestingly captures the small peak of relatively high weights for long-distance links. (D) The same as (B), but for the assigned weight versus experimental weight in the 91 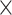 29 subset for each of the TP links (dots) of the predicted network with an overall connectivity density of 40%.
29 subset for each of the TP links (dots) of the predicted network with an overall connectivity density of 40%.
Validation Analysis
To evaluate the reliability of the model prediction, we examined the influences of different strategies for measuring topological similarity (see Supplementary Material II.1) and different parameters for predicting binary connection and connection weights. The validation analysis is described in further detail below.
For the multiple iteration prediction of binary connections, we compared the prediction performance in the training and testing groups to avoid overfitting and evaluated the sensitivity by studying the influence of total iteration steps t. 1) For training and testing of the predictive model, we randomly separated 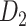 into two subsets and repeated the random division to obtain 500 realizations. For each training subset at different realizations, we applied the multiple-iteration predictive model and conducted the receiver operating characteristic (ROC) analysis (Fawcett 2006) (Supplementary Fig. 2). 2) To further confirm the reliability of the predictive model, we evaluated the similarity of sensitivity in the 91
into two subsets and repeated the random division to obtain 500 realizations. For each training subset at different realizations, we applied the multiple-iteration predictive model and conducted the receiver operating characteristic (ROC) analysis (Fawcett 2006) (Supplementary Fig. 2). 2) To further confirm the reliability of the predictive model, we evaluated the similarity of sensitivity in the 91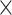 14 training subset and 91
14 training subset and 91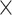 15 testing subset. Moreover, we applied the Kolmogorov–Smirnov test to quantify the discrepancy in the sensitivity distributions (across the 500 realizations) between the training and testing subsets (Supplementary Fig. 3). 3) We further compared the precision and AUC of the prediction model by three factors and the models from different combinations of two factors or the single factor (Supplementary Figs 4 and 5). 4) We conducted separate analyses under different total iteration steps t to search for the optimal t value that maximizes the sensitivity of the final predicted network (Supplementary Fig. 6). After determining the number of iteration steps t, we applied the validated model to make predictions from
15 testing subset. Moreover, we applied the Kolmogorov–Smirnov test to quantify the discrepancy in the sensitivity distributions (across the 500 realizations) between the training and testing subsets (Supplementary Fig. 3). 3) We further compared the precision and AUC of the prediction model by three factors and the models from different combinations of two factors or the single factor (Supplementary Figs 4 and 5). 4) We conducted separate analyses under different total iteration steps t to search for the optimal t value that maximizes the sensitivity of the final predicted network (Supplementary Fig. 6). After determining the number of iteration steps t, we applied the validated model to make predictions from 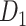 using all of
using all of 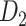 (91
(91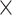 29) as the training set. Further details on validating and testing the model are presented in Supplementary Material III.
29) as the training set. Further details on validating and testing the model are presented in Supplementary Material III.
For the weight assignments, we evaluated the influence of the number of distance bins n. We examined the weight assignment by training (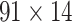 ) and testing (
) and testing (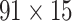 ) samples from
) samples from 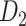 at different numbers of distance bins n. After comparing the correlation between the experimental and assigned weights for correctly predicted links in the testing sample at different numbers n of distance bins, we acquired the optimal value of n (Supplementary Fig. 7). After n was determined, weight assignment was applied to all the links in the predicted binary network
at different numbers of distance bins n. After comparing the correlation between the experimental and assigned weights for correctly predicted links in the testing sample at different numbers n of distance bins, we acquired the optimal value of n (Supplementary Fig. 7). After n was determined, weight assignment was applied to all the links in the predicted binary network 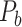 , using the weight of the overlapping links in all of
, using the weight of the overlapping links in all of 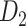 (91
(91 29) as the training set.
29) as the training set.
Network Measures
After obtaining the predicted hemisphere-wide, high-density weighted network 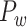 , we explored the prominent features of segregation and integration organization in the network and contrast to the initial CoCoMac-based network
, we explored the prominent features of segregation and integration organization in the network and contrast to the initial CoCoMac-based network . We applied and compared the following broadly used network properties to reveal the features.
. We applied and compared the following broadly used network properties to reveal the features.
Modularity.
We adopted the well-established community detection algorithm (Newman 2006) to find module partition by maximizing the modularity, defined as
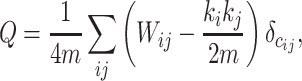 |
(2) |
where 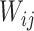 represents the weighted connections between regions i and j, of which the weighted degrees (total output weight) of the two regions are denoted by
represents the weighted connections between regions i and j, of which the weighted degrees (total output weight) of the two regions are denoted by 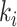 and
and 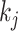 , m represents the total weights for all edges in the network, and
, m represents the total weights for all edges in the network, and 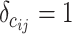 if the two regions belong to the same module
if the two regions belong to the same module 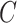 ; otherwise,
; otherwise, 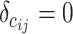 .
.
Participation coefficient.
This variable measures how uniformly the connections for a given region i are distributed among different modules, defined as (Newman 2006)
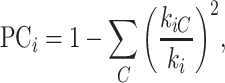 |
(3) |
where 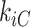 indicates the total weights of connections from region i to regions in module C, among the total weighted connections
indicates the total weights of connections from region i to regions in module C, among the total weighted connections 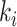 of the region (e.g., its degree) in the whole network (Guimera and Amaral 2005). A region with a PC close to 0 is unimodal (with connections just to one module), and one with a PC close to 1.0 is a connector in the network involving functional integration among the modules.
of the region (e.g., its degree) in the whole network (Guimera and Amaral 2005). A region with a PC close to 0 is unimodal (with connections just to one module), and one with a PC close to 1.0 is a connector in the network involving functional integration among the modules.
Wiring cost
This variable estimates the total length of the axon projections from region i to others, defined as
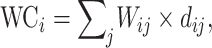 |
(4) |
where 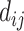 is the Euclidean distance between region i and j. The Euclidean distance is supposed to be an approximation of the length of the fiber projection broadly applied in previous studies (Bullmore and Sporns 2012; Harriger et al. 2012). Geodesic distance measures the length of a shortest trajectory going through white matter between barycenters from 91 regions to 29 regions (Markov et al. 2013), which could provide a good estimation of the fiber length. For this subnetwork, the Euclidean distance is highly correlated to the geodesic distance (r = 0.91, P <
is the Euclidean distance between region i and j. The Euclidean distance is supposed to be an approximation of the length of the fiber projection broadly applied in previous studies (Bullmore and Sporns 2012; Harriger et al. 2012). Geodesic distance measures the length of a shortest trajectory going through white matter between barycenters from 91 regions to 29 regions (Markov et al. 2013), which could provide a good estimation of the fiber length. For this subnetwork, the Euclidean distance is highly correlated to the geodesic distance (r = 0.91, P < 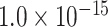 ). Currently, it is still lacking for the geodesic distance for the whole brain. Moreover, our analysis of human brain showed that the streamline length between the pairs of brain regions is strongly correlated with Euclidean distance within each hemisphere (left hemisphere: r = 0.89, P <
). Currently, it is still lacking for the geodesic distance for the whole brain. Moreover, our analysis of human brain showed that the streamline length between the pairs of brain regions is strongly correlated with Euclidean distance within each hemisphere (left hemisphere: r = 0.89, P < 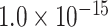 ; right hemisphere: r = 0.83, P <
; right hemisphere: r = 0.83, P < 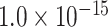 ). Thus, Euclidean distance is also reliable as a good approximation compared with geodesic distance. This is plausible, since the wiring cost constraint plays an important role in shaping the connectivity of fiber among different regions in mammal brains; thus the fiber tracts tend to follow relatively straight lines in the white matter to minimize the total projection length under wiring cost constraint. Therefore, in this study, we represent the streamline length with Euclidean distance as in many previous studies (Bullmore and Sporns 2012), since the information about the streamline is missing for both the existing connections in D1 and the newly predicted connections. With the weights (extrinsic fraction of weighted neurons, FLNe) reflecting the axon projection number (Markov, Ercsey-Ravasz, et al. 2014), the wiring cost defined in equation (4) indicates the total length of the axon projections from region i to other regions in the whole network.
). Thus, Euclidean distance is also reliable as a good approximation compared with geodesic distance. This is plausible, since the wiring cost constraint plays an important role in shaping the connectivity of fiber among different regions in mammal brains; thus the fiber tracts tend to follow relatively straight lines in the white matter to minimize the total projection length under wiring cost constraint. Therefore, in this study, we represent the streamline length with Euclidean distance as in many previous studies (Bullmore and Sporns 2012), since the information about the streamline is missing for both the existing connections in D1 and the newly predicted connections. With the weights (extrinsic fraction of weighted neurons, FLNe) reflecting the axon projection number (Markov, Ercsey-Ravasz, et al. 2014), the wiring cost defined in equation (4) indicates the total length of the axon projections from region i to other regions in the whole network.
In addition to the Materials and Methods summarized above, further details are presented in Supplementary Material.
Results
The Final Binary Network (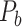 ) Predicted by the Predictive Model
) Predicted by the Predictive Model
First, we validated the three-factor, multiple-iteration predictive model on the training and testing groups from the 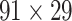 experimental network
experimental network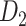 (see Supplementary Material I) and determined the best number of iteration steps t (iteration steps t = 12, see Supplementary Fig. 6 for the validation of the iteration steps). Then, we applied the predictive model trained by the whole
(see Supplementary Material I) and determined the best number of iteration steps t (iteration steps t = 12, see Supplementary Fig. 6 for the validation of the iteration steps). Then, we applied the predictive model trained by the whole 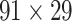 experimental network
experimental network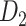 to acquire the large-scale network with high connectivity density. Starting from the original binary network from CoCoMac dataset
to acquire the large-scale network with high connectivity density. Starting from the original binary network from CoCoMac dataset 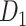 ,
, 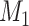 of the most likely links (corresponding to the highest prediction scores) are predicted and added to the 91
of the most likely links (corresponding to the highest prediction scores) are predicted and added to the 91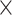 91 network so that exactly
91 network so that exactly 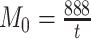 links are added to the
links are added to the 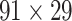 subset at each iteration step; thus,
subset at each iteration step; thus, 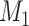 may have some variation from step to step during the iteration. The process repeats to predict another
may have some variation from step to step during the iteration. The process repeats to predict another 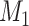 links from the updated network until the density of the final network for the
links from the updated network until the density of the final network for the 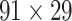 subsystem reaches 61.2%, the same density of
subsystem reaches 61.2%, the same density of 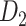 (see Materials and Methods). The precision (whether a predicted link is correct among all the predicted links; see Supplementary Material) of the
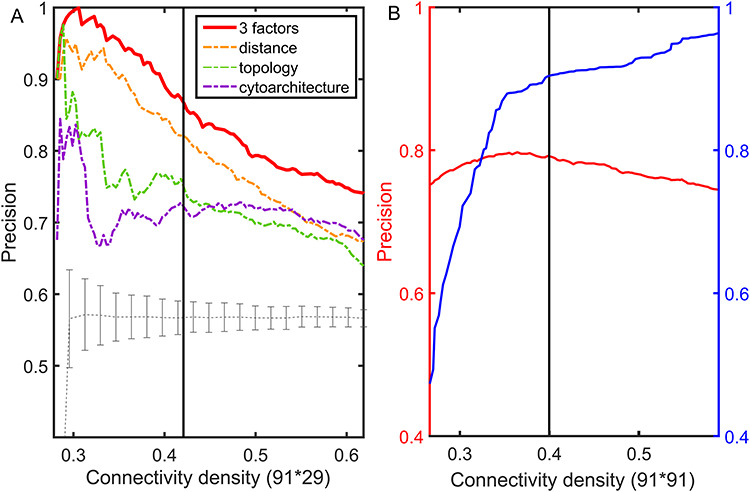
(see Materials and Methods). The precision (whether a predicted link is correct among all the predicted links; see Supplementary Material) of the 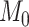 newly predicted links in the subset will decrease as the connectivity density of the predicted network increases (Fig. 1A). Nevertheless, when the connectivity density of the 91
newly predicted links in the subset will decrease as the connectivity density of the predicted network increases (Fig. 1A). Nevertheless, when the connectivity density of the 91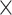 29 subset in the predicted network reaches 61.2%, the precision for the newly predicted links remains at a high level of 74.1%. This result from the combination of three factors is clearly higher than that from the models using only a single factor (spatial proximity 67.3%, topological similarity 65.0%, and cytoarchitectural similarity 67.4%; see Fig. 1A), and is also higher than the models using different combinations of two factors (topological similarity and spatial proximity: 71.8%; cytoarchitecture similarity and spatial proximity: 72.1%; cytoarchitecture similarity and topological similarity: 72.1%; see Supplementary Fig. 4 for the plots of all the models). We have compered the goodness of the models by AUC. The three-factor model has AUC = 0.75, P <
29 subset in the predicted network reaches 61.2%, the precision for the newly predicted links remains at a high level of 74.1%. This result from the combination of three factors is clearly higher than that from the models using only a single factor (spatial proximity 67.3%, topological similarity 65.0%, and cytoarchitectural similarity 67.4%; see Fig. 1A), and is also higher than the models using different combinations of two factors (topological similarity and spatial proximity: 71.8%; cytoarchitecture similarity and spatial proximity: 72.1%; cytoarchitecture similarity and topological similarity: 72.1%; see Supplementary Fig. 4 for the plots of all the models). We have compered the goodness of the models by AUC. The three-factor model has AUC = 0.75, P < 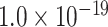 when compared with the random benchmark (Supplementary Fig. 2). Compared with the three-factor model, the two-factor models have smaller values (AUC = 0.69, P <
when compared with the random benchmark (Supplementary Fig. 2). Compared with the three-factor model, the two-factor models have smaller values (AUC = 0.69, P < 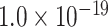 for topological similarity and spatial proximity; AUC = 0.72, P <
for topological similarity and spatial proximity; AUC = 0.72, P < 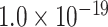 for cytoarchitecture similarity and spatial proximity; and AUC = 0.72, P <
for cytoarchitecture similarity and spatial proximity; and AUC = 0.72, P < 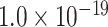 for cytoarchitecture similarity and topological similarity). AUC for single factor is even smaller (AUC = 0.67, P <
for cytoarchitecture similarity and topological similarity). AUC for single factor is even smaller (AUC = 0.67, P < 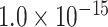 for spatial proximity; AUC = 0.67, P <
for spatial proximity; AUC = 0.67, P < 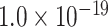 cytoarchitecture similarity; and AUC = 0.61, P < 0.001 for topological similarity). The ROC curves for two factors and single factors are shown in Supplementary Figure 5. The whole predicted network
cytoarchitecture similarity; and AUC = 0.61, P < 0.001 for topological similarity). The ROC curves for two factors and single factors are shown in Supplementary Figure 5. The whole predicted network 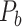 combining those newly predicted links with the originally existing ones of the initial CoCoMac-based network
combining those newly predicted links with the originally existing ones of the initial CoCoMac-based network 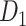 is shown in Figure 2B (and Supplementary Fig. 8 for more details of correctly and wrongly predicted links). The precision of
is shown in Figure 2B (and Supplementary Fig. 8 for more details of correctly and wrongly predicted links). The precision of 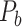 in the 91
in the 91 29 subnetwork is rather stable with respect to increasing connectivity density, varying between 74% and 80% (Fig. 1B, red curve), reaching 74.5% in the final predicted network
29 subnetwork is rather stable with respect to increasing connectivity density, varying between 74% and 80% (Fig. 1B, red curve), reaching 74.5% in the final predicted network .In addition, we investigated the weight recovery rate (
.In addition, we investigated the weight recovery rate (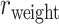 ) by summing the weights for the correctly predicted links over the total weights for all links in the
) by summing the weights for the correctly predicted links over the total weights for all links in the 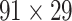 subset
subset 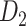 (see Supplementary Material II.2). In the early stage of iterations (up to an overall density of approximately 35%), the predicted links have relatively high prediction scores, and they also have high precision compared with the experimental data in
(see Supplementary Material II.2). In the early stage of iterations (up to an overall density of approximately 35%), the predicted links have relatively high prediction scores, and they also have high precision compared with the experimental data in 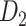 (Fig. 1A);
(Fig. 1A); 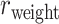 accordingly increases rapidly, suggesting that those early-predicted links have large weights in
accordingly increases rapidly, suggesting that those early-predicted links have large weights in 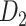 (Fig. 1B). The increase slows down considerably with further prediction of those links with relatively weak weights. Interestingly, the weight recovery rate (
(Fig. 1B). The increase slows down considerably with further prediction of those links with relatively weak weights. Interestingly, the weight recovery rate (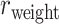 ) of the final predicted binary network
) of the final predicted binary network 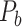 comes to 96.4%, much higher than the aforementioned binary precision (74.5%), suggesting that the high-weight links have been largely recovered in
comes to 96.4%, much higher than the aforementioned binary precision (74.5%), suggesting that the high-weight links have been largely recovered in 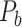 and that the unrecovered links are rather weak (representing approximately 100%–74.5% ~ 25.5% of the total links but occupying only 4.6% of the total weight).
and that the unrecovered links are rather weak (representing approximately 100%–74.5% ~ 25.5% of the total links but occupying only 4.6% of the total weight).
Figure 1.
The precision and weight recovery rate by the predictive model. The predicted network in the 91  29 subsystem is compared with the corresponding high-resolution
29 subsystem is compared with the corresponding high-resolution  experimental network
experimental network  . (A) The precision (correctness of predicted links) in the predicted network based on different predictive models (three factors vs. single factor) with respect to connectivity density for the 91
. (A) The precision (correctness of predicted links) in the predicted network based on different predictive models (three factors vs. single factor) with respect to connectivity density for the 91 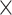 29 subsystem. The gray dashed line is a random benchmark (including error bars from 5000 independent realizations of randomly adding links). (B) The precision (red line) and the weight recovery rate (
29 subsystem. The gray dashed line is a random benchmark (including error bars from 5000 independent realizations of randomly adding links). (B) The precision (red line) and the weight recovery rate (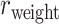 , blue line) of the predicted network after combining with the initial CoCoMac-based network
, blue line) of the predicted network after combining with the initial CoCoMac-based network 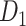 , versus the overall connectivity density in the whole 91
, versus the overall connectivity density in the whole 91 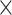 91 network. In both subplots, the black vertical line indicates the overall connectivity density of the
91 network. In both subplots, the black vertical line indicates the overall connectivity density of the 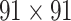 network at 40%.
network at 40%.
Figure 2.
Comparison of the CoCoMac-based network  across the whole hemisphere before prediction (density 26.3%) (A) and the final predicted network
across the whole hemisphere before prediction (density 26.3%) (A) and the final predicted network  (density 59%) from the three-factor predictive model (B). Each dot shows a binary link from region i (row) to region j (column). The areas are grouped according to functional systems: V (visual), S (somatosensory), M (motor), T (temporal), and F (frontal).
(density 59%) from the three-factor predictive model (B). Each dot shows a binary link from region i (row) to region j (column). The areas are grouped according to functional systems: V (visual), S (somatosensory), M (motor), T (temporal), and F (frontal).
This work predicted the missing links from the CoCoMac-based network (Fig. 2A), thus generating predicted network across the whole hemisphere (Fig. 2B) with the same connectivity density (61.2% in the 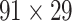 subsystem) as the high-resolution
subsystem) as the high-resolution 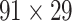 experimental network
experimental network 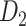 (Markov, Ercsey-Ravasz, et al. 2014), along with high precision and a high weight recovery rate. The predicted hemisphere-wide
(Markov, Ercsey-Ravasz, et al. 2014), along with high precision and a high weight recovery rate. The predicted hemisphere-wide 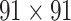 network
network 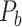 reaches a density of 59%, more than twice the density of 26.3% in the initial CoCoMac-based network
reaches a density of 59%, more than twice the density of 26.3% in the initial CoCoMac-based network 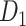 .If we consider a predicted network only up to an overall density of 40% (vertical black lines in Fig. 1), the precision for the newly predicted links is 88% (Fig. 1A), and the link precision and weight recovery rate are 79% and 90%, respectively, when the existing links in the CoCoMac data
.If we consider a predicted network only up to an overall density of 40% (vertical black lines in Fig. 1), the precision for the newly predicted links is 88% (Fig. 1A), and the link precision and weight recovery rate are 79% and 90%, respectively, when the existing links in the CoCoMac data 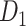 are included (Fig. 1B). Thus, we have added 1135 new and important links [
are included (Fig. 1B). Thus, we have added 1135 new and important links [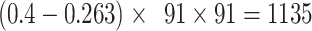 ] with very high confidence (see Supplementary Fig. 8B for this network). Experimentally identifying so many new links across the hemisphere would be highly labor intensive and costly.
] with very high confidence (see Supplementary Fig. 8B for this network). Experimentally identifying so many new links across the hemisphere would be highly labor intensive and costly.
Next, we further evaluated the performance of prediction from two aspects, namely weight and spatial distance of the connections in four quadrants (Fig. 3A), by evaluating the sensitivity (ratio of correctly predicted links [true positive, TP] over all the links in 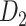 , see Supplementary Material II.2) of the predicted networks with three factors compared with only a single factor. In the three-factor predictive model, the sensitivity for the predicted high-weight links (FLNe > 0.0015, half of the weight range on a log scale) (right quadrants of Fig. 3A) is 0.86, while the sensitivity for low-weight links (FLNe < 0.0015) is clearly lower at 0.67 (Fig. 3B). For both groups, the sensitivity from the three-factor model is higher than that from single-factor models (spatial proximity 0.84 and 0.62; topological similarity 0.80 and 0.63; and cytoarchitectural similarity 0.79 and 0.65, respectively, for high- and low-weight links). These results further validate that the prediction is more accurate for the high-weight links in the 91
, see Supplementary Material II.2) of the predicted networks with three factors compared with only a single factor. In the three-factor predictive model, the sensitivity for the predicted high-weight links (FLNe > 0.0015, half of the weight range on a log scale) (right quadrants of Fig. 3A) is 0.86, while the sensitivity for low-weight links (FLNe < 0.0015) is clearly lower at 0.67 (Fig. 3B). For both groups, the sensitivity from the three-factor model is higher than that from single-factor models (spatial proximity 0.84 and 0.62; topological similarity 0.80 and 0.63; and cytoarchitectural similarity 0.79 and 0.65, respectively, for high- and low-weight links). These results further validate that the prediction is more accurate for the high-weight links in the 91 29 subnetwork than for the low-weight links. More specifically, upon further dividing the high- or low-weight links into two groups based on the distance of the connections, we found that most links in both groups had short distances (d < 31.3 mm, half of the distance range, Fig. 3A). Clearly, the sensitivity for the short-distance links predicted by the three-factor model is quite high for both high-weight (0.93) and low-weight (0.85) links (Fig. 3C). These values for short-distance links are slightly smaller than those in the model with only spatial proximity but higher than those in single-factor models with only cytoarchitectural similarity or topological similarity. The sensitivity for the short-distant links achieves the highest for both high-weight (1.0) and low-weight (1.0) links by the two-factor model with cytoarchitecture similarity and spatial proximity (Supplementary Fig. 9B). The long-distance links (>31.3 mm), irrespective of weights, are especially challenging to predict by the model with spatial proximity alone; surprisingly, however, the links can be predicted much more effectively by topological similarity and even better by cytoarchitectural similarity. When the three factors are combined, a trade-off is achieved to maximize the overall prediction power for the whole dataset (Fig. 1A).
29 subnetwork than for the low-weight links. More specifically, upon further dividing the high- or low-weight links into two groups based on the distance of the connections, we found that most links in both groups had short distances (d < 31.3 mm, half of the distance range, Fig. 3A). Clearly, the sensitivity for the short-distance links predicted by the three-factor model is quite high for both high-weight (0.93) and low-weight (0.85) links (Fig. 3C). These values for short-distance links are slightly smaller than those in the model with only spatial proximity but higher than those in single-factor models with only cytoarchitectural similarity or topological similarity. The sensitivity for the short-distant links achieves the highest for both high-weight (1.0) and low-weight (1.0) links by the two-factor model with cytoarchitecture similarity and spatial proximity (Supplementary Fig. 9B). The long-distance links (>31.3 mm), irrespective of weights, are especially challenging to predict by the model with spatial proximity alone; surprisingly, however, the links can be predicted much more effectively by topological similarity and even better by cytoarchitectural similarity. When the three factors are combined, a trade-off is achieved to maximize the overall prediction power for the whole dataset (Fig. 1A).
Figure 3.
Prediction performance for links with different weights and distance. (A) Four classes of links from the  experimental network
experimental network 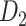 grouped according to link weight (w) and distance (d). Dots represent all links in
grouped according to link weight (w) and distance (d). Dots represent all links in 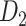 , including the existing links from CoCoMac dataset
, including the existing links from CoCoMac dataset 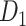 . Red and blue dots represent links that can be correctly predicted (TP) or cannot be predicted by a three-factor predictive model, respectively. (B) and (C) compare the sensitivity for different classes of links after applying predictive models with three factors or a single factor. (B) The sensitivity for the links with high (FLNe > 0.0015, black bars) or low (FLNe < 0.0015, white bars) experimental weights that are predicted by different models. (C) The sensitivity separately for the four classes shown in (A) by different models. Long (short)-distance links correspond to the pairs of connected regions with distances greater than 31.3 mm (less than half of the distance range).
. Red and blue dots represent links that can be correctly predicted (TP) or cannot be predicted by a three-factor predictive model, respectively. (B) and (C) compare the sensitivity for different classes of links after applying predictive models with three factors or a single factor. (B) The sensitivity for the links with high (FLNe > 0.0015, black bars) or low (FLNe < 0.0015, white bars) experimental weights that are predicted by different models. (C) The sensitivity separately for the four classes shown in (A) by different models. Long (short)-distance links correspond to the pairs of connected regions with distances greater than 31.3 mm (less than half of the distance range).
Furthermore, we compared the sensitivity of the predicted links within or between different brain function domains in the final predicted network 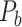 by the three-factor predictive model. Overall, the sensitivity for the intrafunctional links was very high, reaching 0.97 (random benchmark 0.73 ± 0.01), clearly higher than that for interfunctional links, which is 0.62 (random benchmark 0.42 ± 0.01). If only the high-weight links (FLNe > 0.0015) were considered, the sensitivity for intrafunctional links increased slightly to 0.98, and the sensitivity for interfunctional links increases to 0.75 (Fig. 4). For low-weight links, the sensitivity decreased slightly for intrafunctional links but clearly for interfunctional links when compared with high-weight links. Overall, the sensitivity for interfunctional links is quite high (>0.8), except for links between visual and frontal regions or from motor to visual regions and some links of temporal regions (with very limited number), which have lower sensitivity (see Supplementary Fig. 10 for sensitivity of links among different functional systems). The sensitivity for intrafunctional links under the predictive model combining three factors is much higher than that under a single factor (Supplementary Fig. 11).
by the three-factor predictive model. Overall, the sensitivity for the intrafunctional links was very high, reaching 0.97 (random benchmark 0.73 ± 0.01), clearly higher than that for interfunctional links, which is 0.62 (random benchmark 0.42 ± 0.01). If only the high-weight links (FLNe > 0.0015) were considered, the sensitivity for intrafunctional links increased slightly to 0.98, and the sensitivity for interfunctional links increases to 0.75 (Fig. 4). For low-weight links, the sensitivity decreased slightly for intrafunctional links but clearly for interfunctional links when compared with high-weight links. Overall, the sensitivity for interfunctional links is quite high (>0.8), except for links between visual and frontal regions or from motor to visual regions and some links of temporal regions (with very limited number), which have lower sensitivity (see Supplementary Fig. 10 for sensitivity of links among different functional systems). The sensitivity for intrafunctional links under the predictive model combining three factors is much higher than that under a single factor (Supplementary Fig. 11).
Figure 4.
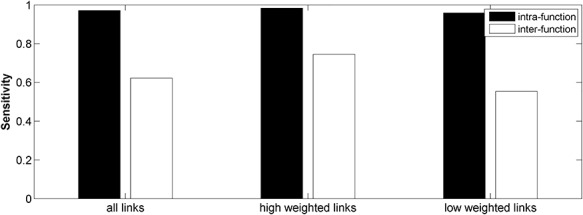
Comparison of sensitivity for the intra- and interfunctional links involving all the predicted links (left group) or including only the high-weight (FLNe > 0.0015, middle group) or low-weight links (FLNe < 0.0015, right group) in the 91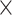 29 subsystem of the predicted network
29 subsystem of the predicted network 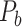 . Here, the intra- and interfunctional links are within or between five functional domains (visual, somatosensory, motor, temporal, and frontal regions).
. Here, the intra- and interfunctional links are within or between five functional domains (visual, somatosensory, motor, temporal, and frontal regions).
Assigning Connection Weights in the Final Predicted Network Binary 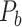 to Obtain the Weighted Network
to Obtain the Weighted Network 
An important feature provided by the high-resolution 91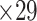 experimental network
experimental network  is the connection weights (FLNe) (Markov et al. 2011; Markov, Ercsey-Ravasz, et al. 2014), which follow a statistical pattern of exponential decay with distance (Fig. 5A). To assign the connection weights in the predicted binary network
is the connection weights (FLNe) (Markov et al. 2011; Markov, Ercsey-Ravasz, et al. 2014), which follow a statistical pattern of exponential decay with distance (Fig. 5A). To assign the connection weights in the predicted binary network  , we estimated the connection weight of binary links in
, we estimated the connection weight of binary links in 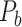 by the score
by the score 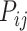 in equation (1). Assignment of connection weights was optimized according to different distance bins (using different parameters
in equation (1). Assignment of connection weights was optimized according to different distance bins (using different parameters 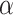 ,
, 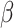 , and
, and 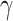 for different distance bins; see further details in Materials and Methods and Supplementary Material II.1, and Supplementary Figure 7 for validating the proper number of distance bins n = 12). For the correctly predicted links of the final predicted network with a connectivity density of 59%, the maximal correlation between the assigned and experimental weights is relatively high (r = 0.55, P <
for different distance bins; see further details in Materials and Methods and Supplementary Material II.1, and Supplementary Figure 7 for validating the proper number of distance bins n = 12). For the correctly predicted links of the final predicted network with a connectivity density of 59%, the maximal correlation between the assigned and experimental weights is relatively high (r = 0.55, P < 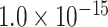 ) (Fig. 5B). Here, the predicted connection weight for the whole network follows an exponential form,
) (Fig. 5B). Here, the predicted connection weight for the whole network follows an exponential form, 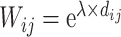 , (Fig. 5C), where
, (Fig. 5C), where 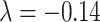 is very close to the experimental result in the 91
is very close to the experimental result in the 91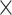 29 subset (
29 subset (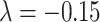 , Fig. 5A). Moreover, the assigned weights (Fig. 5C) capture the fluctuation of experimental connection weights (Fig. 5A) with respect to connection distance, although the range of weight spreading is not as strong as in the experimental data. For the correctly predicted links in the predicted network with an overall connectivity density of 40%, the correlation between assigned and experimental weights is also high (r = 0.55, P <
, Fig. 5A). Moreover, the assigned weights (Fig. 5C) capture the fluctuation of experimental connection weights (Fig. 5A) with respect to connection distance, although the range of weight spreading is not as strong as in the experimental data. For the correctly predicted links in the predicted network with an overall connectivity density of 40%, the correlation between assigned and experimental weights is also high (r = 0.55, P < 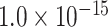 ) (Fig. 5D). Thus, the predicted networks with low connection density (e.g., ~ 40%) have both high accuracy in the recovery of binary links (Fig. 1B) and connection strength (Fig. 5D). For comparison, a previous study proposed to assign weight using only the single factor of spatial distance,
) (Fig. 5D). Thus, the predicted networks with low connection density (e.g., ~ 40%) have both high accuracy in the recovery of binary links (Fig. 1B) and connection strength (Fig. 5D). For comparison, a previous study proposed to assign weight using only the single factor of spatial distance, 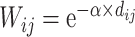 (Ercsey-Ravasz et al. 2013). We found that under this single factor, the correlation between the real and estimated weights in
(Ercsey-Ravasz et al. 2013). We found that under this single factor, the correlation between the real and estimated weights in 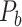 is clearly reduced (
is clearly reduced ( ).
).
In total, there are 418 predicted projections as the false-positive links, which are shown as empty in  yet wrongly taken as existing projections by our prediction model. However, it is important to note that the predicted weights of false-positive links are significantly smaller than the TP predicted links (
yet wrongly taken as existing projections by our prediction model. However, it is important to note that the predicted weights of false-positive links are significantly smaller than the TP predicted links (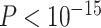 ). It suggests that there are unavoidable false-positive links in the predicted network, but these wrong connections are weak in weight and may not significantly affect the analysis of the relationships between network connectivity, wiring cost, modules, and participation.
). It suggests that there are unavoidable false-positive links in the predicted network, but these wrong connections are weak in weight and may not significantly affect the analysis of the relationships between network connectivity, wiring cost, modules, and participation.
Feature Analysis of the Predicted Hemisphere-Wide Weighted Network  of the Macaque Brain
of the Macaque Brain
We have obtained a hemisphere-wide, high-density weighted network of the macaque brain. Compared with the CoCoMac-based network 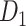 with a binary connectivity density of 26.3%, the final predicted network binary
with a binary connectivity density of 26.3%, the final predicted network binary  has a greatly increased connectivity density of 59% across the hemisphere, close to that of the partial-coverage
has a greatly increased connectivity density of 59% across the hemisphere, close to that of the partial-coverage  experimental network
experimental network (61.2%). In the following section, we explore important features revealed by the large-scale weighted macaque network
(61.2%). In the following section, we explore important features revealed by the large-scale weighted macaque network  rather than the CoCoMac-based binary network
rather than the CoCoMac-based binary network 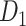 . Here, we mainly considered three features from the weighted network: 1) modular segregation, 2) integration measured by the functional PC, and 3) regional wiring cost.
. Here, we mainly considered three features from the weighted network: 1) modular segregation, 2) integration measured by the functional PC, and 3) regional wiring cost.
Functional Segregation and Module Partition
Information processing is segregated in different functional domains in the macaque brain, including visual (primary and advanced visual subsystems), somatosensory, motor, temporal (auditory, olfactory, etc.), and frontal regions (Lewis and Van Essen 2000). Previously, functional segregation was reflected by module analysis on the functional network based on the BOLD signal from fMRI (Sporns et al. 2004; Sporns 2013). It is not yet clear whether functional segregation is well reflected in the structural network in the primate brain. Here, we explored whether the predicted brain network would be a better match than the CoCoMac-based binary network for the functional segregation of the macaque brain. Applying the module detection algorithm (see Materials and Methods) to the CoCoMac-based binary network 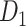 yielded only two modules (modularity Q = 0.32). One module covers most of the occipital regions and temporal lobes, and the other covers frontal and parietal lobes (Fig. 6A). While the first module largely aligns with visual regions, the other functional systems (somatosensory, motor, temporal, and frontal) fail to be properly segregated into different modules (Fig. 6B). In sharp contrast, in the predicted weighted network
yielded only two modules (modularity Q = 0.32). One module covers most of the occipital regions and temporal lobes, and the other covers frontal and parietal lobes (Fig. 6A). While the first module largely aligns with visual regions, the other functional systems (somatosensory, motor, temporal, and frontal) fail to be properly segregated into different modules (Fig. 6B). In sharp contrast, in the predicted weighted network 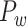 , the same module detection algorithm revealed five modules with modularity (Q = 0.58). To overcome the difficulty of comparing the modularity of the predicted weighted network and the CoCoMac-based network with different connection densities (Sporns and Betzel 2016), we calculated Z-score of modularity for the two networks compared with the corresponding random benchmarks. We first generated 1000 random networks based on the two networks. Particularly, we randomly shuffled the weighted connections by rewiring them while keeping the weights to generate the group of random networks from the predicted weighted network. Then, for two groups of the random networks, we measured modularity, respectively. The Z-score of modularity for the CoCoMac-based network is 44.5, while that for the final prediction network is 50.6. It indicates that the final prediction network has stronger modularity than the CoCoMac-based network. The frontal, parietal, temporal, and occipital lobes are clearly divided into different modules (Fig. 6D). Notably, there are two modules in the frontal lobe. One contains regions 12, 44, 45A/B, 8 l, F4, F5, and ProM, involving most of the dorsal frontal cortex. The other module contains the rest frontal regions (Fig. 6C), involving most of the ventral frontal cortex. We compared the number of matched regions between different functional domains and structural connectivity modules in the CoCoMac-based network
, the same module detection algorithm revealed five modules with modularity (Q = 0.58). To overcome the difficulty of comparing the modularity of the predicted weighted network and the CoCoMac-based network with different connection densities (Sporns and Betzel 2016), we calculated Z-score of modularity for the two networks compared with the corresponding random benchmarks. We first generated 1000 random networks based on the two networks. Particularly, we randomly shuffled the weighted connections by rewiring them while keeping the weights to generate the group of random networks from the predicted weighted network. Then, for two groups of the random networks, we measured modularity, respectively. The Z-score of modularity for the CoCoMac-based network is 44.5, while that for the final prediction network is 50.6. It indicates that the final prediction network has stronger modularity than the CoCoMac-based network. The frontal, parietal, temporal, and occipital lobes are clearly divided into different modules (Fig. 6D). Notably, there are two modules in the frontal lobe. One contains regions 12, 44, 45A/B, 8 l, F4, F5, and ProM, involving most of the dorsal frontal cortex. The other module contains the rest frontal regions (Fig. 6C), involving most of the ventral frontal cortex. We compared the number of matched regions between different functional domains and structural connectivity modules in the CoCoMac-based network 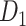 (Fig. 6B) as well as the predicted weighted network
(Fig. 6B) as well as the predicted weighted network  (Fig. 6D). The matched regions refer to the regions in the same functional domain, for example, the motor system, which occupy over 50% of regions in one of the given modules (pie charts in Fig. 6D). For the CoCoMac-based network
(Fig. 6D). The matched regions refer to the regions in the same functional domain, for example, the motor system, which occupy over 50% of regions in one of the given modules (pie charts in Fig. 6D). For the CoCoMac-based network  , there are 34 matched regions, covering 37.4% of all regions. For the predicted weighted network
, there are 34 matched regions, covering 37.4% of all regions. For the predicted weighted network  , up to 63 regions were matched, covering 69.2% of all regions. Thus, the large-scale predicted weighted network can much better reveal the segregation of the macaque brain into different functional modules.
, up to 63 regions were matched, covering 69.2% of all regions. Thus, the large-scale predicted weighted network can much better reveal the segregation of the macaque brain into different functional modules.
Figure 6.
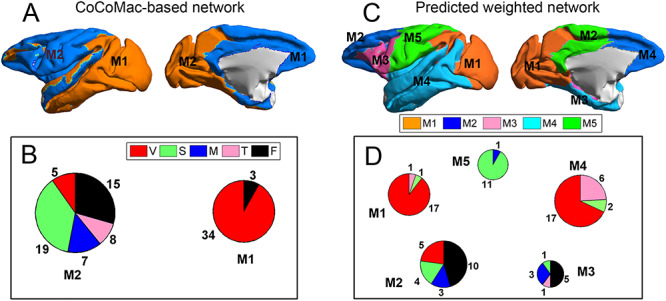
Comparison between the segregation of functional modules in the CoCoMac-based binary network 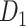 (A and B) and the predicted weighted network
(A and B) and the predicted weighted network 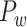 (C and D). The module detection algorithm (Newman 2006) has identified two modules (M1, M2) in the CoCoMac-based network with modularity Q = 0.32, Z-score = 44.5 (A) but five modules (M1–M5) in the predicted weighted network with Q = 0.58, Z-score = 50.6 (C). For both networks, (B) and (D) correspondingly exhibit the functional domains (red: visual; green: somatosensory; blue: motor; pink: temporal; and black: frontal) for the regions in each module represented by a pie chart. The areas shown in different colors in each pie denote the numbers of regions belonging to the corresponding functional domains for each module.
(C and D). The module detection algorithm (Newman 2006) has identified two modules (M1, M2) in the CoCoMac-based network with modularity Q = 0.32, Z-score = 44.5 (A) but five modules (M1–M5) in the predicted weighted network with Q = 0.58, Z-score = 50.6 (C). For both networks, (B) and (D) correspondingly exhibit the functional domains (red: visual; green: somatosensory; blue: motor; pink: temporal; and black: frontal) for the regions in each module represented by a pie chart. The areas shown in different colors in each pie denote the numbers of regions belonging to the corresponding functional domains for each module.
Integration among Structural Modules
Since the predicted high-density weighted network much better reflected the functional segregation than the previous dataset, we next explored how the structural connectors that link the segregated functional modules in the predicted network are distributed and whether they overlap with some functional integrators based on previous fMRI studies.
The importance of the cortical region in functional integration can be quantified by its functional PC based on the predicted weighted network (see Materials and Methods). Regions with high PC distribute connection weights rather uniformly among different structural modules and are thus normally considered connectors in the structural network (Sporns 2013; Rubinov et al. 2015). In the predicted weighted network, there are five modules corresponding to one somatosensory, two visual subsystems, and two frontal subsystems (Fig. 6D). The regions as connectors with high PC distribute connections rather uniformly among the five modules. We found that the connector regions (PC at top 15%) cover the FPN, including SII, Prostriate, 7B, F4, STPc, AIP, 7A, 46v, 8r, 31, 46d, TEO, 9/46v, and 5 (Fig. 7A).
Figure 7.
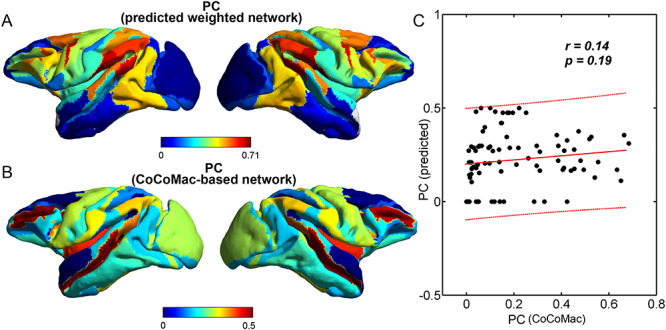
Comparison between PC in the predicted weighted network and the CoCoMac-based network. (A) Map of the PCs in the predicted weighted network  . (B) Map of the PCs in the CoCoMac-based network
. (B) Map of the PCs in the CoCoMac-based network 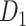 . (C) Scatter plot of the PCs (dots) in the CoCoMac-based network versus the predicted weighted network. The two measures are uncorrelated (r = 0.14, P = 0.19).
. (C) Scatter plot of the PCs (dots) in the CoCoMac-based network versus the predicted weighted network. The two measures are uncorrelated (r = 0.14, P = 0.19).
The previous CoCoMac-based network (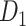 ) has only two modules without proper functional segregation. The high PC regions in
) has only two modules without proper functional segregation. The high PC regions in 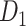 are regions DP, OPAl, F7, 8B, V4, V3, 25, V6A, and V2 (Fig. 7B). Clearly, most of the high PC regions in
are regions DP, OPAl, F7, 8B, V4, V3, 25, V6A, and V2 (Fig. 7B). Clearly, most of the high PC regions in 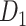 concentrate on the primary visual and motor regions, not on the advanced functional domain. The PC in the predicted weighed network is uncorrelated with PC in
concentrate on the primary visual and motor regions, not on the advanced functional domain. The PC in the predicted weighed network is uncorrelated with PC in 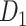 (r = 0.14, P = 0.19) (Fig. 7C).
(r = 0.14, P = 0.19) (Fig. 7C).
Generally, the predicted weighted network revealed segregation and integration in the structural network closely matching the functional domains and advanced frontoparietal regions.
Connector Regions Align with Regions Having Long Axon Fiber Lengths
As shown above, the new large-scale predicted weighted network 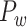 revealed that some frontoparietal regions may be connectors through by distributing connections among functionally segregated structural modules. Next, we further explored other features revealed by the new predicted weighted network for the important connector regions. As shown in Fig. 6C, the functionally segregated modules are also spatially segregated. Thus, the connector regions with high PC should have projection to distant regions and may have long axon projection lengths.
revealed that some frontoparietal regions may be connectors through by distributing connections among functionally segregated structural modules. Next, we further explored other features revealed by the new predicted weighted network for the important connector regions. As shown in Fig. 6C, the functionally segregated modules are also spatially segregated. Thus, the connector regions with high PC should have projection to distant regions and may have long axon projection lengths.
Indeed, the predicted weighted network across the whole hemisphere also revealed regions with large total axon projection lengths (called wiring cost, eq. (4)). The regional wiring cost reflects the total axon projection length in individual regions. The regions with the top 15% wiring cost were mainly distributed in the frontal and somatosensory regions, including Prostriate, 5, SII, 7B, 7A, thalamus, 46v, AIP, TEpd, 8r, 31, 46d, TEO, and 9/46v (Fig. 8A). Interestingly, many regions with high wiring costs overlap with high PC, for example, Prostriate, 5, SII, 7B, 7A, 46v, AIP, 8r, 31, TEO, and 9/46v. There is a strong correlation between PC and wiring cost across the whole brain regions (r = 0.52, P < 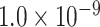 , Fig. 8B). For comparison, the regions with high wiring cost in the CoCoMac-based network (
, Fig. 8B). For comparison, the regions with high wiring cost in the CoCoMac-based network ( ) mainly concentrate on visual and motor primary regions (Fig. 8C). The regional wiring cost in
) mainly concentrate on visual and motor primary regions (Fig. 8C). The regional wiring cost in 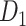 is uncorrelated with PC in the predicted weighted network (r = 0.19, P = 0.07) (Fig. 8D).
is uncorrelated with PC in the predicted weighted network (r = 0.19, P = 0.07) (Fig. 8D).
Figure 8.
Comparison between PC and regional wiring cost in the predicted weighted network. (A) Map of wiring cost based on the predicted weighted network  . (B) Scatter plot of PCs versus regional wiring cost in the predicted network (dots). The two measures are strongly correlated (r = 0.52, P <
. (B) Scatter plot of PCs versus regional wiring cost in the predicted network (dots). The two measures are strongly correlated (r = 0.52, P <  ). The region prostriate has the maximal wiring cost, which is clearly larger than the others. Without considering this region, the wiring cost and PCs are still significantly correlated (r = 0.48, P <
). The region prostriate has the maximal wiring cost, which is clearly larger than the others. Without considering this region, the wiring cost and PCs are still significantly correlated (r = 0.48, P < 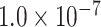 ). (C) Map of the regional wiring cost calculated from CoCoMac-based binary network
). (C) Map of the regional wiring cost calculated from CoCoMac-based binary network 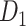 . (D) Scatter plot of the PCs in the predicted weighted network versus regional wiring cost in the CoCoMac-based network, which are uncorrelated (r = 0.19, P = 0.07).
. (D) Scatter plot of the PCs in the predicted weighted network versus regional wiring cost in the CoCoMac-based network, which are uncorrelated (r = 0.19, P = 0.07).
Notably, the regions with large wiring cost means that their total fiber length is long, which do not necessarily refer to regions with long-range connections but could also include regions with short-/median-range connections with high weights. Thus, to better consider the spatial-range of the connections across different regions, we further calculate the ratio of total fiber length of individual region in the predicted network to that of the corresponding region with the same weights in the benchmark random network. When the ratio is high, the corresponding region tends to project long-range connections, compared with random benchmark. The participation of regions is highly correlated with this ratio of long-range projections (r = 0.67, P < 1.0 × 10−15). Comparing the regions with large total fiber length due to high weight but short-/median-range connections, the connector regions are more contributed by the regions tending to have long-range connections.
Discussion
It would be both highly expensive and challenging to experimentally acquire the structural connectome among brain regions using track-tracing methods across the whole macaque brain. Also, it is challenging to obtain an integrated dataset from several existing CoCoMac maps which are not consistent. In this work, we proposed an iterative predictive model to computationally predict missing links and assign weights to all existing and predicted links to obtain the hemisphere-wide large-scale weighted connectivity network 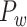 with high density by integrating two existing connectivity datasets, the widely applied CoCoMac-based whole hemisphere brain map (
with high density by integrating two existing connectivity datasets, the widely applied CoCoMac-based whole hemisphere brain map ( ) which integrates three relatively more consistent maps in CoCoMac and the newly acquired high resolution, but partial coverage dataset (
) which integrates three relatively more consistent maps in CoCoMac and the newly acquired high resolution, but partial coverage dataset (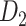 ) and cytoarchitecture information describing the relationship between the density and anatomical complexity (or computational capacity) of neurons in the two regions (Elston et al. 2005). The predictive model integrated three important factors, namely topological similarity, spatial proximity, and cytoarchitectural similarity, to assess the prediction score from previous hemisphere-wide binary structural network with relatively low density (CoCoMac-based dataset
) and cytoarchitecture information describing the relationship between the density and anatomical complexity (or computational capacity) of neurons in the two regions (Elston et al. 2005). The predictive model integrated three important factors, namely topological similarity, spatial proximity, and cytoarchitectural similarity, to assess the prediction score from previous hemisphere-wide binary structural network with relatively low density (CoCoMac-based dataset 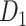 ). Thus, an additional cytoarchitecture dataset showing neuron density for different regions is also applied in this study. Model parameters are trained and optimized using the recently obtained partial-coverage yet high-resolution weighted
). Thus, an additional cytoarchitecture dataset showing neuron density for different regions is also applied in this study. Model parameters are trained and optimized using the recently obtained partial-coverage yet high-resolution weighted 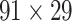 experimental network (
experimental network ( ). Since the 29 target regions were chosen rather uniformly from different functional domains, it was argued that the 29 target regions are representative of five major functional domains of the cortex (Markov, Ercsey-Ravasz, et al. 2014); thus, it is plausible to use
). Since the 29 target regions were chosen rather uniformly from different functional domains, it was argued that the 29 target regions are representative of five major functional domains of the cortex (Markov, Ercsey-Ravasz, et al. 2014); thus, it is plausible to use 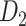 to calibrate the predictive model. The final predicted binary network (
to calibrate the predictive model. The final predicted binary network (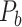 , including existing links in
, including existing links in  with an overall connectivity density of 59% has a prediction sensitivity of 74.1% in
with an overall connectivity density of 59% has a prediction sensitivity of 74.1% in 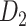 . In particular, the predictive model showed a very high sensitivity of 86% for the high-weight links and 97% for intrafunctional links. We further assigned weights for all links in
. In particular, the predictive model showed a very high sensitivity of 86% for the high-weight links and 97% for intrafunctional links. We further assigned weights for all links in 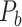 to obtain the high-density weighted network
to obtain the high-density weighted network 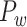 , and the assigned weights were significantly correlated with the experimental ones in
, and the assigned weights were significantly correlated with the experimental ones in 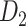 . The unavoidable false-positive link has significantly weaker link weights compared with true-positive links. Further analysis of the structural modules of the high-density weighted network
. The unavoidable false-positive link has significantly weaker link weights compared with true-positive links. Further analysis of the structural modules of the high-density weighted network 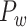 revealed that the identified modules of brain regions closely match physiological function domains. Moreover, structural connectors with high PCs for the connections among the modules are mainly distributed in the FPN. Furthermore, the PCs and regional wiring cost were shown to be significantly correlated, revealing an important organization feature of the brain connectome: integration among the well-segregated structural modules demands high wiring cost and long-range connections. Therefore, the predicted large-scale weighted structural network
revealed that the identified modules of brain regions closely match physiological function domains. Moreover, structural connectors with high PCs for the connections among the modules are mainly distributed in the FPN. Furthermore, the PCs and regional wiring cost were shown to be significantly correlated, revealing an important organization feature of the brain connectome: integration among the well-segregated structural modules demands high wiring cost and long-range connections. Therefore, the predicted large-scale weighted structural network 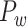 could serve as a high-resolution and high-density structural connectome to facilitate future studies of the primate brain. The methods developed here may also be further extended to acquire a more complete/reliable connectome in the human brain from the backbone detected by diffusion MRI (dMRI). Below, we discuss these aspects of the work in more detail.
could serve as a high-resolution and high-density structural connectome to facilitate future studies of the primate brain. The methods developed here may also be further extended to acquire a more complete/reliable connectome in the human brain from the backbone detected by diffusion MRI (dMRI). Below, we discuss these aspects of the work in more detail.
Improved Prediction by the Combination of Multiple Factors
Previous studies have noted that several factors are associated with the interregional connection probability from the observed projections. A broadly discussed factor is the spatial distance between the regions (Bullmore and Sporns 2012; Ercsey-Ravasz et al. 2013). For efficient signal transmission under limited energy cost, the wiring diagram of the brain structural network is presumed to minimize the wiring cost (Bullmore and Sporns 2012; Chen et al. 2013, 2017). A number of studies found that most structural connections in the brains of different species satisfy wiring cost minimization (Kaiser and Hilgetag 2006; Bullmore and Sporns 2012; Rubinov et al. 2015; Chen et al. 2017). Recent analysis on the 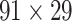 experimental macaque brain network (
experimental macaque brain network (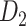 ) revealed that the connectivity probability decays sharply with spatial distance (Ercsey-Ravasz et al. 2013) (Fig. 5A), consistent with cost minimization to make short-range projections. Another important factor, topological similarity, was also discovered to influence the connectivity probability. That is, pairs of regions with more similar connection profiles in the network tend to have a higher probability of being connected directly (Song et al. 2014). More recently, it was also found that regions with similar cytoarchitecture (especially neuron density) have a higher chance to be connected (Beul et al. 2017). The neuron density, as an important cytoarchitectural feature, has been systematically studied and found to range from low density in regions with few layers that lack an inner granular layer (agranular) to high density in regions with six distinct layers, such as the striate cortex (Beul et al. 2017). Notably, variation in the neuron density implies the potential inverse relationship with average neuron size (Herculano-Houzel et al. 2014). Regions with high neuron density, such V1, may have large chance to have small size of neurons, which accordingly have small dendritic arbors with few inputs (Elston 2002; Collins et al. 2016). Thus, along with large variation of neuron density, the pyramidal cell structure and the number of input for individual neuron vary across different brain regions (Elston 2002). Thus, cortical regions with similar neural density may have similar neural circuits to support similar functional processing and may have high probability to be directly connected by fiber projection to facilitated similar functional processing. Interestingly, these three factors capture different aspects that affect existing connections in the primate brain connectome, and they may compensate for each other. Considering the cytoarchitectural similarity and spatial proximity as examples, previous studies showed that although the likelihood of a connection decreases with long distance (or large difference in cytoarchitecture), it would be mitigated if the regions have similar neuron density (or close to each other), which is attributed to the independency of neuron density from the influence of spatial proximity (Hilgetag and Grant 2010; Beul et al. 2017).
) revealed that the connectivity probability decays sharply with spatial distance (Ercsey-Ravasz et al. 2013) (Fig. 5A), consistent with cost minimization to make short-range projections. Another important factor, topological similarity, was also discovered to influence the connectivity probability. That is, pairs of regions with more similar connection profiles in the network tend to have a higher probability of being connected directly (Song et al. 2014). More recently, it was also found that regions with similar cytoarchitecture (especially neuron density) have a higher chance to be connected (Beul et al. 2017). The neuron density, as an important cytoarchitectural feature, has been systematically studied and found to range from low density in regions with few layers that lack an inner granular layer (agranular) to high density in regions with six distinct layers, such as the striate cortex (Beul et al. 2017). Notably, variation in the neuron density implies the potential inverse relationship with average neuron size (Herculano-Houzel et al. 2014). Regions with high neuron density, such V1, may have large chance to have small size of neurons, which accordingly have small dendritic arbors with few inputs (Elston 2002; Collins et al. 2016). Thus, along with large variation of neuron density, the pyramidal cell structure and the number of input for individual neuron vary across different brain regions (Elston 2002). Thus, cortical regions with similar neural density may have similar neural circuits to support similar functional processing and may have high probability to be directly connected by fiber projection to facilitated similar functional processing. Interestingly, these three factors capture different aspects that affect existing connections in the primate brain connectome, and they may compensate for each other. Considering the cytoarchitectural similarity and spatial proximity as examples, previous studies showed that although the likelihood of a connection decreases with long distance (or large difference in cytoarchitecture), it would be mitigated if the regions have similar neuron density (or close to each other), which is attributed to the independency of neuron density from the influence of spatial proximity (Hilgetag and Grant 2010; Beul et al. 2017).
It has been shown that generative models combining spatial proximity and topological similarity can reproduce some statistical properties of actual cortical connectivity, such as the formation of network modules and probability distributions of clustering, degree, betweenness, and edge length (Betzel et al. 2016). These results imply the important joint roles of these factors in shaping the features of the structural network. Here, our objective for the predictive model is not to recover statistical features but to predict the missing links and build a high-density weighted structural network across the hemisphere of the macaque brain.
With the combination of the three representative factors and integrating three datasets (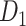 ,
, 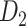 , and the neuron density dataset), the predictive model can much more effectively predict the binary links. Since a large number of high-weight projections have a short spatial distance (Fig. 3A) (Ercsey-Ravasz et al. 2013; Markov, Ercsey-Ravasz, et al. 2014), prediction by the single factor of spatial proximity could recover most (82%) of the high-weight links (Fig. 3B) in the
, and the neuron density dataset), the predictive model can much more effectively predict the binary links. Since a large number of high-weight projections have a short spatial distance (Fig. 3A) (Ercsey-Ravasz et al. 2013; Markov, Ercsey-Ravasz, et al. 2014), prediction by the single factor of spatial proximity could recover most (82%) of the high-weight links (Fig. 3B) in the 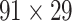 experimental network (
experimental network ( ), which is further improved by combining the additional factor of cytoarchitecture similarity (84%). However, for links with high weights and long distances, which may play an important role in processing signals across remote functional domains, the sensitivity of the predictive model with the single factor of spatial proximity dropped to only 23% (Fig. 3C). In contrast, the other two factors, topological similarity and cytoarchitectural similarity, strongly improved the prediction of connections with high weights and long distance (Fig. 3C, 53–69%). The combination of these two factors could predict 52% of links with high weights and long distance, while it also has high sensitivity (86%) to predict the links with high weights and short distance, which is better than that by the model with any single one from these two factors. The situation is similar for weak but long-distance connections. With the combination of all three factors, the precision of the predicted network would largely increase compared with only a single factor, or even two factors (Fig. 1A and Supplementary Fig. 9), up to 90.4% in the predicted network with a connectivity density of 40% and 74.1% in the final predicted network with a density of 59%. Here, we did not use black-box machine learning methods because our predictive model combining the three factors can provide insights into the organization mechanism underlying the heterogeneously weighted connectome in the primate brain.
), which is further improved by combining the additional factor of cytoarchitecture similarity (84%). However, for links with high weights and long distances, which may play an important role in processing signals across remote functional domains, the sensitivity of the predictive model with the single factor of spatial proximity dropped to only 23% (Fig. 3C). In contrast, the other two factors, topological similarity and cytoarchitectural similarity, strongly improved the prediction of connections with high weights and long distance (Fig. 3C, 53–69%). The combination of these two factors could predict 52% of links with high weights and long distance, while it also has high sensitivity (86%) to predict the links with high weights and short distance, which is better than that by the model with any single one from these two factors. The situation is similar for weak but long-distance connections. With the combination of all three factors, the precision of the predicted network would largely increase compared with only a single factor, or even two factors (Fig. 1A and Supplementary Fig. 9), up to 90.4% in the predicted network with a connectivity density of 40% and 74.1% in the final predicted network with a density of 59%. Here, we did not use black-box machine learning methods because our predictive model combining the three factors can provide insights into the organization mechanism underlying the heterogeneously weighted connectome in the primate brain.
Notably, even by our predictive model with three factors and iterative process, the long-distance links are still relatively hard to predict when compared with the short-distance ones. Our previous study (Chen et al. 2013) showed that the majority (approximately 65%) of the long-range links are interfunctional connections, especially between the visual and frontal systems. Such interfunctional connections between spatially segregated regions have relatively low topological and cytoarchitectural similarities; hence, they are difficult to predict by the proposed model (Supplementary Fig. 10). For the 91 29 subset covered by the experimental weighted network, all intrafunctional links for the five functions and some interfunctional links of somatosensory or frontal regions have a sensitivity near or above 90%. However, over 80% of incorrectly predicted (false negative) links are the interfunctional links of visual regions with motor or frontal regions. Fortunately, the predicted weights of false-positive links are significantly smaller than the TP predicted links. Thus, these links may not significantly affect the analysis of the relationships between structure (network connectivity), metabolism (e.g., wiring cost), and function (e.g., modules and participation). The formation of long-range connections in the brain may be attributed to the requirement of advanced functional integration in the connectome, which is not yet sufficiently quantified to be considered as an influential factor in the predictive model. This line of research would be interesting to pursue in the future.
29 subset covered by the experimental weighted network, all intrafunctional links for the five functions and some interfunctional links of somatosensory or frontal regions have a sensitivity near or above 90%. However, over 80% of incorrectly predicted (false negative) links are the interfunctional links of visual regions with motor or frontal regions. Fortunately, the predicted weights of false-positive links are significantly smaller than the TP predicted links. Thus, these links may not significantly affect the analysis of the relationships between structure (network connectivity), metabolism (e.g., wiring cost), and function (e.g., modules and participation). The formation of long-range connections in the brain may be attributed to the requirement of advanced functional integration in the connectome, which is not yet sufficiently quantified to be considered as an influential factor in the predictive model. This line of research would be interesting to pursue in the future.
Notably, the probabilistic tractography based on dMRI revealed relatively dense macaque structural connectome using a consistency-based thresholding method (Donahue et al. 2016; van den Heuvel et al. 2015; Azadbakht et al. 2015; Shen et al. 2019). The probabilistic tractography data provide binary connections and connection weights from streamline. However, previous works also pointed out that the AUC of the dMRI structural network for both the binary and weighted networks is not higher than the estimation of new links based on the single factor of distance. AUC of binary connections from dMRI is 0.68, which is worse than AUC = 0.75 (Shen et al. 2019) from geodesic distance-based estimates of connectivity by a regression model from the 29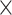 29 subset of the Markov dataset
29 subset of the Markov dataset 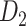 . Here, in our method, AUC from the same geodesic distance-based estimates of connectivity by the prediction model achieves 0.77 in the 29
. Here, in our method, AUC from the same geodesic distance-based estimates of connectivity by the prediction model achieves 0.77 in the 29 29 subset. However, the geodesic distance for the whole brain is still lacking till now. Next, we compared AUC from the Euclidean distance in the same testing sample of the 29
29 subset. However, the geodesic distance for the whole brain is still lacking till now. Next, we compared AUC from the Euclidean distance in the same testing sample of the 29 29 subset in
29 subset in 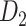 . AUC for the single factor of distance equals to 0.71. This difference is probably mainly because in our method, the prediction score depends on deterministic distance ranking from low to high, which may not be as good as the statistic regression model that could better account for distance-related fluctuation as the statistic regression in (Shen et al. 2019). When considering the two-factor model with distance and cytoarchitecture similarity, the multiple-iteration process would obtain a better prediction with AUC = 0.76. AUC is even higher, equaling to 0.78 for the three-factor predicting model in the 29
. AUC for the single factor of distance equals to 0.71. This difference is probably mainly because in our method, the prediction score depends on deterministic distance ranking from low to high, which may not be as good as the statistic regression model that could better account for distance-related fluctuation as the statistic regression in (Shen et al. 2019). When considering the two-factor model with distance and cytoarchitecture similarity, the multiple-iteration process would obtain a better prediction with AUC = 0.76. AUC is even higher, equaling to 0.78 for the three-factor predicting model in the 29 29 testing sample. The latter two AUC values are higher than the AUC of dMRI and even the best single factor model in the previous work (Shen et al. 2019). Thus, we still suggest to apply the three-factor model to predict the macaque brain network across the whole brain by using the Markov 91
29 testing sample. The latter two AUC values are higher than the AUC of dMRI and even the best single factor model in the previous work (Shen et al. 2019). Thus, we still suggest to apply the three-factor model to predict the macaque brain network across the whole brain by using the Markov 91 29 subnetwork
29 subnetwork 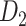 as the best available testing sample.
as the best available testing sample.
Reciprocity of the Connectivity in the Predicted Connectome
We stress that the predictive model also took the directionality of the connections into consideration, since several measures of topological similarity explicitly considered both the input and output connections (Supplementary Table 1). Previous studies have shown that cortical connectivity has a relatively low portion of unidirectional connections (Zamora-Lopez et al. 2008; Markov, Ercsey-Ravasz, et al. 2014). The 29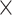 29 submatrix covered by the experimental network
29 submatrix covered by the experimental network 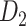 (Markov, Ercsey-Ravasz, et al. 2014) contains 20% of unidirectional connections, and the others are reciprocal (weights may be different). This is consistent with the CoCoMac-based dataset
(Markov, Ercsey-Ravasz, et al. 2014) contains 20% of unidirectional connections, and the others are reciprocal (weights may be different). This is consistent with the CoCoMac-based dataset 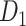 (Kotter 2004; Chen et al. 2013) with 23% unidirectional connections. However, it was also noted that at least 10% of all cortical pathways are genuinely unidirectional due to the possible confounding factor of areal heterogeneity (Markov, Ercsey-Ravasz, et al. 2014). In our work, the predicted hemisphere-wide 91
(Kotter 2004; Chen et al. 2013) with 23% unidirectional connections. However, it was also noted that at least 10% of all cortical pathways are genuinely unidirectional due to the possible confounding factor of areal heterogeneity (Markov, Ercsey-Ravasz, et al. 2014). In our work, the predicted hemisphere-wide 91 91 network (
91 network (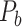 ) with an overall connection density of 59% contains 8% unidirectional connections. Therefore, the predicted network (
) with an overall connection density of 59% contains 8% unidirectional connections. Therefore, the predicted network (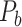 ) has relatively higher reciprocity than the two previous datasets (
) has relatively higher reciprocity than the two previous datasets (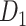 and
and 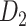 ). Interestingly, the interfunctional connections have low reciprocity and contribute 84% of unidirectional connections in the predicted network. In particular, 73% of unidirectional connections belong to the interfunctional connections of visual (more output, mainly due to sending bottom-up signals) or frontal (more input, mainly due to receiving bottom-up signals). The relatively low portion of unidirectional connections is mainly due to the difficulty of predicting such weak, long-distance, interfunctional unidirectional connections (Fig. 3, Supplementary Fig. 10).
). Interestingly, the interfunctional connections have low reciprocity and contribute 84% of unidirectional connections in the predicted network. In particular, 73% of unidirectional connections belong to the interfunctional connections of visual (more output, mainly due to sending bottom-up signals) or frontal (more input, mainly due to receiving bottom-up signals). The relatively low portion of unidirectional connections is mainly due to the difficulty of predicting such weak, long-distance, interfunctional unidirectional connections (Fig. 3, Supplementary Fig. 10).
Recovery of Connection Weights
The weights of projections (FLNe) in the 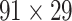 experimental network (
experimental network (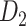 ) span five orders of magnitude (from
) span five orders of magnitude (from 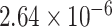 to 0.88) (Markov, Ercsey-Ravasz, et al. 2014). Compared with the CoCoMac-based network (
to 0.88) (Markov, Ercsey-Ravasz, et al. 2014). Compared with the CoCoMac-based network (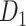 ), the dataset
), the dataset 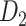 revealed many more projections, mostly weak, but also including many high-weight links. This detailed weight index observed in
revealed many more projections, mostly weak, but also including many high-weight links. This detailed weight index observed in 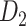 deepened the understanding of the macaque connectome (Markov, Ercsey-Ravasz, et al. 2014). Notably, the experimental weights may follow different distance-dependent rules at various distance bins. The weights decay rapidly for short-distance connections and more slowly for the long-distance connections (Markov, Ercsey-Ravasz, et al. 2014) (also see Fig. 5). Here, we assigned the weights of all the links in the final 91
deepened the understanding of the macaque connectome (Markov, Ercsey-Ravasz, et al. 2014). Notably, the experimental weights may follow different distance-dependent rules at various distance bins. The weights decay rapidly for short-distance connections and more slowly for the long-distance connections (Markov, Ercsey-Ravasz, et al. 2014) (also see Fig. 5). Here, we assigned the weights of all the links in the final 91 91 predicted binary network
91 predicted binary network 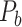 by the prediction scores under the combination of the three factors in different distance bins, which was shown to enhance the correlation between the assigned and experimental weights in
by the prediction scores under the combination of the three factors in different distance bins, which was shown to enhance the correlation between the assigned and experimental weights in 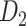 . Interestingly, for the early predicted links (iteration until reaching overall binary density 40%), the precision of the newly predicted links is very high (88%), and the overall precision (including the initial existing links in the CoCoMac-based network) was 79%; those correct links in the
. Interestingly, for the early predicted links (iteration until reaching overall binary density 40%), the precision of the newly predicted links is very high (88%), and the overall precision (including the initial existing links in the CoCoMac-based network) was 79%; those correct links in the 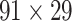 subset are accounted for 90.4% of all link weights in
subset are accounted for 90.4% of all link weights in 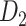 (Fig. 1). These results suggest that we may also apply a version of the predicted weighted network with relatively low binary density (e.g., 40%) in potential applications of the macaque brain connectome, as such a network is more accurate (in terms of precision in binary link and link weights). Compared with the CoCoMac-based network, this network has [(0.4–0.263)
(Fig. 1). These results suggest that we may also apply a version of the predicted weighted network with relatively low binary density (e.g., 40%) in potential applications of the macaque brain connectome, as such a network is more accurate (in terms of precision in binary link and link weights). Compared with the CoCoMac-based network, this network has [(0.4–0.263)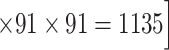 new and important links with very high confidence and good estimation of all connection weights. Identifying these links experimentally will be highly labor intensive and costly. This result demonstrated the value of computational prediction in this work.
new and important links with very high confidence and good estimation of all connection weights. Identifying these links experimentally will be highly labor intensive and costly. This result demonstrated the value of computational prediction in this work.
Segregation in the Predicted Weighted Macaque Connectome
The brain network is segregated into different functional groups to correspondingly perform various specialized functions (Krubitzer and Kaas 1989; Kaas 1992; Preuss 1995; Kaas 1997; Preuss 2000; Karlen and Krubitzer 2007; Bullmore and Sporns 2012; Sporns 2013; Yeo et al. 2014). Previous studies have focused on the relationship between different cognitive functional domains and the network modules detected from functional connectivity based on fMRI data (Yeo et al. 2014; Bertolero et al. 2015). Modular structure with dense intramodule and sparse intermodule connections supports the segregation of each function and avoids excessive interference by other functional systems. However, the modular division in the CoCoMac-based macaque binary structural network 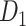 cannot properly capture the functional segregation. There are only two modules that roughly separate the visual and frontal systems (Fig. 6A,B), both mixed with other functional regions (Chen et al. 2017). In sharp contrast, the predicted weighted network
cannot properly capture the functional segregation. There are only two modules that roughly separate the visual and frontal systems (Fig. 6A,B), both mixed with other functional regions (Chen et al. 2017). In sharp contrast, the predicted weighted network  has successfully revealed a more diverse organization of five modules, much better matching the functional domains (Fig. 6C,D). Therefore, the predicted high-density weighted structural network may provide deeper insight into how the structural substrate of connectivity modules supports functional segregation.
has successfully revealed a more diverse organization of five modules, much better matching the functional domains (Fig. 6C,D). Therefore, the predicted high-density weighted structural network may provide deeper insight into how the structural substrate of connectivity modules supports functional segregation.
Structural Connectors as Functional Integrators
Together with proper functional segregation, the brain system also requires the organization of connectors to integrate segregated information processing in different functional domains (Elston 2007; Zamora-Lopez et al. 2010; Sporns 2013; van den Heuvel and Sporns 2013; Bertolero et al. 2015). Previous studies on the functional connectors with uniform link distributions on the functional modules from BOLD signals (He et al. 2009; Power et al. 2013; van den Heuvel and Sporns 2013) found that the FPN, as a flexible functional connector, plays a central role in cognitive control and adaptive implementation in the human brain (Barbas and Pandya 1989; Goldman-Rakic 1995, 1996; Pandya and Yeterian 1996; Barbas and Rempel-Clower 1997; Cavada et al. 1997; Goldman-Rakic 1999; Cavada et al. 2000; Goldman-Rakic 2011; Cole et al. 2013). In the macaque brain, although many previous works have discussed the relationship between various cortical regions and cognitive behavior (Preuss and Goldman-Rakic 1991; Funahashi et al. 1993; Lund et al. 1993; Miller 1999; Elston et al. 2001; Elston et al. 2006; Elston, Benavides-Piccione, et al. 2011), the relationship between functional connectors in the functional network from fMRI data and cognitive behavior has not been well explored. However, other studies in the macaque brain suggest parts of the default mode network (Miranda-Dominguez et al. 2014), which has elevated fMRI activity in the resting state, as an important functional integrator (Vincent et al. 2007; Hutchison et al. 2011; Mantini et al. 2011; Matsui et al. 2011; Miranda-Dominguez et al. 2014; Barttfeld et al. 2015). The default mode network in the macaque brain includes the regions TPOc, SII, 8, 9-46d, and 23. Our analysis of structural connectors integrating the structural modules from the predicted weighted network  includes almost all regions of the default mode network, except for region 23. Interestingly, the structural connectors in the macaque brain and functional connectors in the human brain are both in the FPN (Braver and Barch 2006; Dosenbach et al. 2008). This consistency implies that functional integrators may have the structural basis of uniformly distributed structural connections among functional domains.
includes almost all regions of the default mode network, except for region 23. Interestingly, the structural connectors in the macaque brain and functional connectors in the human brain are both in the FPN (Braver and Barch 2006; Dosenbach et al. 2008). This consistency implies that functional integrators may have the structural basis of uniformly distributed structural connections among functional domains.
Although previous studies showed that the overall wiring cost of rich club regions tend to have relatively higher wiring cost (Harriger et al. 2012; van den Heuvel et al. 2012), it is still lack of quantitative comparison, especially at regional level, between the wiring cost and the PC as a direct measure of integration among different modules. Interestingly, this work showed that on the regional level, the functional PCs, measuring how uniform a region distributes its connections across different modules, is correlated with the regional wiring cost (Fig. 8). Compared with the regions with large total fiber length (wiring cost) due to high weight but short-/median-range connections, the connector regions are more contributed by the regions tending to have long-range connections. This result clearly shows the property that the connector regions distribute long-range connections to integrate the spatial segregated modules. A similar relationship was also found in the human brain, and both functional participation and regional wiring cost were found to be related to an important metabolic parameter, the rate of aerobic glycolysis (Chen et al. In preparation). Previous studies on the microstructure showed that myelinated axons are related to metabolic consumption (Vaishnavi et al. 2010; Funfschilling et al. 2012; Lee et al. 2012; Saab and Nave 2017). Notably, two factors, integrative capacity for individual neurons and neuron density, both contributing to metabolism demand, may have an inverse relationship in their variation across brain regions; namely, regions with high neuron density typically have lower integrative capacity (Elston 2007; Herculano-Houzel et al. 2008; Elston and Garey 2009; Elston and Garey 2013; Elston and Manger 2014; Herculano-Houzel et al. 2014). However, compared with the regions with high neuron density and low integrative capacity of pyramidal neurons, such as V1 (Elston and Garey 2009; Elston and Garey 2013), regions with high integrative capacity of pyramidal neurons and low neuron density, such as PFC (Elston and Garey 2009; Elston and Garey 2013), have high metabolic consumption, suggesting that integrative capacity might be dominant in metabolism demand. Together with these observations, our results suggest that brain regions playing important roles in integrating information from functionally segregated subsystems may require high metabolic energy due to the large wiring cost in the underlying structural connectome to link spatially segregated functional domains. These findings suggest that the predicted weighted network can be applied to study the structure-function-metabolism relationship in the primate brain.
Conclusion and Further Considerations
This work used computational methods to acquire a weighted network across a hemisphere of the macaque brain with more than twice the density of the previous CoCoMac-based binary network. Including the predicted weights, this new macaque connectome dataset was shown to provide a complete and more accurate network substrate underlying several aspects in the structure-function-metabolic relationship for the primate brain. Therefore, this dataset can be of great value until the necessary expenses and experimental efforts are invested to systematically complete the remaining two-third of the connectivity of the macaque brain compared with the recently established partial dataset 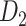 . The future studies on tract tracing experiments will provide empirical data that will ultimately determine the power of the prediction model in this work.
. The future studies on tract tracing experiments will provide empirical data that will ultimately determine the power of the prediction model in this work.
Our work also provides a basis to investigate the missing links in the future from the dMRI-based backbone of the human connectome. Currently, many works consider that the backbone of the human brain structural connectome that can be reliably detected by noninvasive dMRI has a much lower connectivity density of 7%–15% (Hagmann et al. 2008; Gong et al. 2009), and such backbone has been widely used in graph theoretical analysis of the brain connectome (Bullmore and Sporns 2009, 2012; Rubinov and Sporns 2010; van den Heuvel and Sporns 2011; Harriger et al. 2012). Using a consistency-based thresholding method rather than a weight-based one can produce reliable connectomes of 30% density (Roberts et al. 2017). However, binary connections and connection weights from streamline number provided by the dMRI structural network do not outperform the estimation based on the single factor of distance (Shen et al. 2019), which gives worse prediction than the prediction model with two or three factors here. Therefore, due to the need for noninvasiveness and the limitations of dMRI, such as fiber crossing and missed tracing for short fibers, it has been quite challenging to access human brain high-resolution structural connectome thus far (Mori et al. 2002; Dauguet et al. 2007; Jones 2010; Jones et al. 2013). The prediction model based on the connection rules with the combination of cytoarchitecture (He et al. 2007; Wagstyl et al. 2018), spatial distance, and topology of the backbone (Hagmann et al. 2008) may help to construct a more complete, accurate structural connectome for the human brain in the future.
Funding
Hong Kong Baptist University (HKBU) Strategic Development Fund; Hong Kong Research Grant Council (GRF12302914); HKBU FRG2/17-18/011; HKBU Research Committee, Interdisciplinary Research Clusters Matching Scheme 2018/19 (RC-IRCMs-18-19-SCI-01); Natural Science Foundation of China (Grant Nos. 81601560, 81620108016, 11275027, 11328501, and 61673151); Major Project of the National Social Science Fund of China (Grant No. 19ZDA324); Zhejiang Provincial Natural Science Foundation of China (Grant No. LR18A050001).
Notes
Conflict of Interest: None declared.
Supplementary Material
References
- Alivisatos AP, Chun M, Church GM, Greenspan RJ, Roukes ML, Yuste R. 2015. A national network of neurotechnology centers for the BRAIN initiative. Neuron. 88:445–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amunts K, Zilles K. 2012. Architecture and organizational principles of Broca's region. Trends Cogn Sci. 16:418–426. [DOI] [PubMed] [Google Scholar]
- Azadbakht H, Parkes LM, Haroon HA, Augath M, Logothetis NK, de Crespigny A, D’Arceuil HE, Parker GJ. 2015. Validation of high-resolution tractography against in vivo tracing in the macaque visual cortex. Cereb Cortex. 25:4299–4309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakker R, Wachtler T, Diesmann M. 2012. CoCoMac 2.0 and the future of tract-tracing databases. Front Neuroinform. 6:30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbas H, Hilgetag CC, Saha S, Dermon CR, Suski JL. 2005. Parallel organization of contralateral and ipsilateral prefrontal cortical projections in the rhesus monkey. BMC Neurosci. 6:32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbas H, Pandya DN. 1989. Architecture and intrinsic connections of the prefrontal cortex in the rhesus monkey. J Comp Neurol. 286:353–375. [DOI] [PubMed] [Google Scholar]
- Barbas H, Rempel-Clower N. 1997. Cortical structure predicts the pattern of corticocortical connections. Cereb Cortex. 7:635–646. [DOI] [PubMed] [Google Scholar]
- Barttfeld P, Uhrig L, Sitt JD, Sigman M, Jarraya B, Dehaene S. 2015. Signature of consciousness in the dynamics of resting-state brain activity. Proc Natl Acad Sci U S A. 112:887–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertolero MA, Yeo BT, D'Esposito M. 2015. The modular and integrative functional architecture of the human brain. Proc Natl Acad Sci U S A. 112:E6798–E6807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betzel RF, Avena-Koenigsberger A, Goni J, He Y, de Reus MA, Griffa A, Vertes PE, Misic B, Thiran JP, Hagmann P et al. 2016. Generative models of the human connectome. NeuroImage. 124:1054–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beul SF, Barbas H, Hilgetag CC. 2017. A predictive structural model of the primate connectome. Sci Rep. 7:43176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezgin G, Vakorin VA, van Opstal AJ, McIntosh AR, Bakker R. 2012. Hundreds of brain maps in one atlas: registering coordinate-independent primate neuro-anatomical data to a standard brain. NeuroImage. 62:67–76. [DOI] [PubMed] [Google Scholar]
- Bianchi S, Stimpson CD, Duka T, Larsen MD, Janssen WG, Collins Z, Bauernfeind AL, Schapiro SJ, Baze WB, McArthur MJ et al. 2013. Synaptogenesis and development of pyramidal neuron dendritic morphology in the chimpanzee neocortex resembles humans. Proc Natl Acad Sci U S A. 110(Suppl 2):10395–10401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bratislav M, Betzel RF, de Reus MA, van den Heuvel MP, Berman MG, Mcintosh AR, Olaf S. 2016. Network-level structure-function relationships in human neocortex. Cereb Cortex. 26:3285–3296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braver TS, Barch DM. 2006. Extracting core components of cognitive control. Trends Cogn Sci. 10:529–532. [DOI] [PubMed] [Google Scholar]
- Bressler SL, Menon V. 2010. Large-scale brain networks in cognition: emerging methods and principles. Trends Cogn Sci. 14:277–290. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 10:186–198. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. 2012. The economy of brain network organization. Nat Rev Neurosci. 13:336–349. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. 2006. Rhythms of the Brain. New York: Oxford University Press. [Google Scholar]
- Cavada C, Company T, Tejedor J, Cruz-Rizzolo RJ, Reinoso-Suarez F. 2000. The anatomical connections of the macaque monkey orbitofrontal cortex. A review. Cereb Cortex. 10:220–242. [DOI] [PubMed] [Google Scholar]
- Cavada C, Hernández-González A, Tejedor J, Reinoso-Suárez F. 1997. Multiple processing streams versus global visual perception. A binding hypothesis based on the anatomical organization of the neural networks of primate visual association cortices In: Sakata H, Mikami A, Fuster J, editors. The association cortex, structure and function. Amsterdam: Harwood; pp. 129–136. [Google Scholar]
- Chaudhuri R, Knoblauch K, Gariel MA, Kennedy H, Wang XJ. 2015. A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron. 88:419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Lin Q, Hornbeck R, Liao X, Courture L, Raichle M, Zhou C, He Y forthcoming 2020. Association of aerobic glycolysis with wiring cost of the structural connectome reveals benefit-risk balancing mechanism in the human brain. [DOI] [PMC free article] [PubMed]
- Chen Y, Wang S, Hilgetag CC, Zhou C. 2013. Trade-off between multiple constraints enables simultaneous formation of modules and hubs in neural systems. PLoS Comput Biol. 9:e1002937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Wang S, Hilgetag CC, Zhou C. 2017. Features of spatial and functional segregation and integration of the primate connectome revealed by trade-off between wiring cost and efficiency. PLoS Comput Biol. 13:e1005776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Reynolds JR, Power JD, Repovs G, Anticevic A, Braver TS. 2013. Multi-task connectivity reveals flexible hubs for adaptive task control. Nat Neurosci. 16:1348–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins CE, Airey DC, Young NA, Leitch DB, Kaas JH. 2010. Neuron densities vary across and within cortical areas in primates. Proc Natl Acad Sci U S A. 107:15927–15932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins CE, Turner EC, Sawyer EK, Reed JL, Young NA, Flaherty DK, Kaas JH. 2016. Cortical cell and neuron density estimates in one chimpanzee hemisphere. Proc Natl Acad Sci U S A. 113:740–745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dauguet J, Peled S, Berezovskii V, Delzescaux T, Warfield SK, Born R, Westin C-F. 2007. Comparison of fiber tracts derived from in-vivo DTI tractography with 3D histological neural tract tracer reconstruction on a macaque brain. NeuroImage. 37:530–538. [DOI] [PubMed] [Google Scholar]
- Dombrowski SM, Hilgetag CC, Barbas H. 2001. Quantitative architecture distinguishes prefrontal cortical systems in the rhesus monkey. Cereb Cortex. 11:975–988. [DOI] [PubMed] [Google Scholar]
- Donahue CJ, Sotiropoulos SN, Jbabdi S, Hernandezfernandez M, Behrens TE, Dyrby TB, Coalson T, Kennedy H, Knoblauch K, Van Essen DC. 2016. Using diffusion tractography to predict cortical connection strength and distance: a quantitative comparison with tracers in the monkey. J Neurosci. 36:6758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Cohen AL, Schlaggar BL, Petersen SE. 2008. A dual-networks architecture of top-down control. Trends Cogn Sci. 12:99–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elston G. 2007. Evolution of the pyramidal cell in primates: evolution of nervous systems. New York: Academic Press. [Google Scholar]
- Elston G, Garey L. 2009. Prefrontal cortex: Brodmann and Cajal revisited: prefrontal cortex: roles, interventions and traumas. New York: Nova Science Publishers. [Google Scholar]
- Elston G, Manger P. 2014. Pyramidal cells in V1 of African rodents are bigger, more branched and more spiny than those in primates. Front Neuroanat. 8:4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elston GN. 2000. Pyramidal cells of the frontal lobe: all the more spinous to think with. J Neurosci. 20:RC95–RC95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elston GN. 2002. Cortical heterogeneity: implications for visual processing and polysensory integration. J Neurocytol. 31:317–335. [DOI] [PubMed] [Google Scholar]
- Elston GN. 2003. Cortex, cognition and the cell: new insights into the pyramidal neuron and prefrontal function. Cereb Cortex. 13:1124–1138. [DOI] [PubMed] [Google Scholar]
- Elston GN, Benavides-Piccione R, DeFelipe J. 2001. The pyramidal cell in cognition: a comparative study in human and monkey. J Neurosci. 21:RC163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elston GN, Benavides-Piccione R, Defelipe J. 2005. A study of pyramidal cell structure in the cingulate cortex of the macaque monkey with comparative notes on inferotemporal and primary visual cortex. Cereb Cortex. 15:64–73. [DOI] [PubMed] [Google Scholar]
- Elston GN, Benavides-Piccione R, Elston A, Manger PR, Defelipe J. 2011. Pyramidal cells in prefrontal cortex of primates: marked differences in neuronal structure among species. Front Neuroanat. 5:2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elston GN, Benavides-Piccione R, Elston A, Zietsch B, Defelipe J, Manger P, Casagrande V, Kaas JH. 2006. Specializations of the granular prefrontal cortex of primates: implications for cognitive processing. Anat Rec A Discov Mol Cell Evol Biol. 288:26–35. [DOI] [PubMed] [Google Scholar]
- Elston GN, Garey LJ. 2013. The cytoarchitectonic map of Korbinian Brodmann: arealisation and circuit specialisation In: Microstructural Parcellation of the Human Cerebral Cortex. Berlin, Heidelberg: Springer, pp. 3–32. [Google Scholar]
- Elston GN, Oga T, Okamoto T, Fujita I. 2011. Spinogenesis and pruning in the anterior ventral inferotemporal cortex of the macaque monkey: an intracellular injection study of layer III pyramidal cells. Front Neuroanat. 5:42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elston GN, Okamoto T, Oga T, Dornan D, Fujita I. 2010. Spinogenesis and pruning in the primary auditory cortex of the macaque monkey (Macaca fascicularis): an intracellular injection study of layer III pyramidal cells. Brain Res. 1316:35–42. [DOI] [PubMed] [Google Scholar]
- Elston GN, Rockland KS. 2002. The pyramidal cell of the sensorimotor cortex of the macaque monkey: phenotypic variation. Cereb Cortex. 12:1071–1078. [DOI] [PubMed] [Google Scholar]
- Elston GN, Tweedale R, Rosa MG. 1999. Cortical integration in the visual system of the macaque monkey: large-scale morphological differences in the pyramidal neurons in the occipital, parietal and temporal lobes. Proc Biol Sci. 266:1367–1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ercsey-Ravasz M, Markov NT, Lamy C, Van Essen DC, Knoblauch K, Toroczkai Z, Kennedy H. 2013. A predictive network model of cerebral cortical connectivity based on a distance rule. Neuron. 80:184–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fawcett T. 2006. An introduction to ROC analysis. Pattern Recognit Lett. 27:861–874. [Google Scholar]
- Felleman DJ, Van Essen DC. 1991. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1:1–47. [DOI] [PubMed] [Google Scholar]
- Fornito A, Zalesky A, Breakspear M. 2013. Graph analysis of the human connectome: promise, progress, and pitfalls. NeuroImage. 80:426–444. [DOI] [PubMed] [Google Scholar]
- Friston K. 2010. The free-energy principle: a unified brain theory? Nat Rev Neurosci. 11:127. [DOI] [PubMed] [Google Scholar]
- Funahashi S, Chafee MV, Goldman-Rakic PS. 1993. Prefrontal neuronal activity in rhesus monkeys performing a delayed anti-saccade task. Nature. 365:753–756. [DOI] [PubMed] [Google Scholar]
- Funfschilling U, Supplie LM, Mahad D, Boretius S, Saab AS, Edgar J, Brinkmann BG, Kassmann CM, Tzvetanova ID, Mobius W et al. 2012. Glycolytic oligodendrocytes maintain myelin and long-term axonal integrity. Nature. 485:517–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuster JM. 2000. Cortical dynamics of memory. Int J Psychophysiol. 35:155–164. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. 1995. Cellular basis of working memory. Neuron. 14:477–485. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. 1996. The prefrontal landscape: implications of functional architecture for understanding human mentation and the central executive. Philos Trans R Soc Lond Ser B Biol Sci. 351:1445–1453. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. 1999. The "psychic" neuron of the cerebral cortex. Ann N Y Acad Sci. 868:13–26. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. 2011. Circuitry of primate prefrontal cortex and regulation of behavior by representational memory. Compr Physiol. Wiley Online Library, 373–417. [Google Scholar]
- Gong G, He Y, Concha L, Lebel C, Gross DW, Evans AC, Beaulieu C. 2009. Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb Cortex. 19:524–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guimera R, Amaral LAN. 2005. Functional cartography of complex metabolic networks. Nature. 433:895–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O. 2008. Mapping the structural core of human cerebral cortex. PLoS Biol. 6:e159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harriger L, van den Heuvel MP, Sporns O. 2012. Rich club organization of macaque cerebral cortex and its role in network communication. PLoS One. 7:e46497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, Shepherd GM. 2015. The neocortical circuit: themes and variations. Nat Neurosci. 18:170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Evans AC. 2007. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex. 17:2407–2419. [DOI] [PubMed] [Google Scholar]
- He Y, Wang J, Wang L, Chen ZJ, Yan C, Yang H, Tang H, Zhu C, Gong Q, Zang Y et al. 2009. Uncovering intrinsic modular organization of spontaneous brain activity in humans. PLoS One. 4:e5226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herculano-Houzel S, Catania K, Manger PR, Kaas JH. 2015. Mammalian brains are made of these: a dataset of the numbers and densities of neuronal and nonneuronal cells in the brain of glires, primates, scandentia, eulipotyphlans, afrotherians and artiodactyls, and their relationship with body mass. Brain Behav Evol. 86:145–163. [DOI] [PubMed] [Google Scholar]
- Herculano-Houzel S, Collins CE, Wong P, Kaas JH. 2007. Cellular scaling rules for primate brains. Proc Natl Acad Sci U S A. 104:3562–3567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herculano-Houzel S, Collins CE, Wong P, Kaas JH, Lent R. 2008. The basic nonuniformity of the cerebral cortex. Proc Natl Acad Sci U S A. 105:12593–12598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herculano-Houzel S, Manger PR, Kaas JH. 2014. Brain scaling in mammalian evolution as a consequence of concerted and mosaic changes in numbers of neurons and average neuronal cell size. Front Neuroanat. 8:77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilgetag CC, Grant S. 2010. Cytoarchitectural differences are a key determinant of laminar projection origins in the visual cortex. NeuroImage. 51:1006–1017. [DOI] [PubMed] [Google Scholar]
- Honey CJ, Kotter R, Breakspear M, Sporns O. 2007. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc Natl Acad Sci U S A. 104:10240–10245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Leung LS, Mirsattari SM, Gati JS, Menon RS, Everling S. 2011. Resting-state networks in the macaque at 7 T. NeuroImage. 56:1546–1555. [DOI] [PubMed] [Google Scholar]
- Jacobs B, Scheibel AB. 2002. Regional dendritic variation in primate cortical pyramidal cells. USA: Cortical Areas CRC Press, pp. 123–144. [Google Scholar]
- Jones DK. 2010. Challenges and limitations of quantifying brain connectivity in vivo with diffusion MRI. Imaging Med. 2:341–355. [Google Scholar]
- Jones DK, Knosche TR, Turner R. 2013. White matter integrity, fiber count, and other fallacies: the do's and don'ts of diffusion MRI. NeuroImage. 73:239–254. [DOI] [PubMed] [Google Scholar]
- Jorgenson LA, Newsome WT, Anderson DJ, Bargmann CI, Brown EN, Deisseroth K, Donoghue JP, Hudson KL, Ling GS, MacLeish PR et al. 2015. The BRAIN initiative: developing technology to catalyse neuroscience discovery. Philos Trans R Soc Lond Ser B Biol Sci. 370:20140164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaas JH. 1992. Do humans see what monkeys see? Trends Neurosci. 15:1–3 [DOI] [PubMed] [Google Scholar]
- Kaas JH. 1997. Theories of visual cortex organization in primates In: Extrastriate cortex in primates. Boston, MA: Springer, pp. 91–125. [Google Scholar]
- Kaiser M. 2007. Brain architecture: a design for natural computation. Philos Trans A Math Phys Eng Sci. 365:3033–3045. [DOI] [PubMed] [Google Scholar]
- Kaiser M, Hilgetag CC. 2006. Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Comp Biol. 2:e95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandel ER, Markram H, Matthews PM, Yuste R, Koch C. 2013. Neuroscience thinks big (and collaboratively). Nat Rev Neurosci. 14:659–664. [DOI] [PubMed] [Google Scholar]
- Karaoglu H, Lee CM, Meyer W. 2005. Survey of simple sequence repeats in completed fungal genomes. Mol Biol Evol. 22:639–649. [DOI] [PubMed] [Google Scholar]
- Karlen SJ, Krubitzer L. 2007. The functional and anatomical organization of marsupial neocortex: evidence for parallel evolution across mammals. Prog Neurobiol. 82:122–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch C, Reid RC. 2012. Neuroscience: observatories of the mind. Nature. 483:397–398. [DOI] [PubMed] [Google Scholar]
- Kotter R. 2004. Online retrieval, processing, and visualization of primate connectivity data from the CoCoMac database. Neuroinformatics. 2:127–144. [DOI] [PubMed] [Google Scholar]
- Krubitzer LA, Kaas JH. 1989. Cortical integration of parallel pathways in the visual system of primates. Brain Res. 478:161–165. [DOI] [PubMed] [Google Scholar]
- Lanciego JL, Wouterlood FG. 2011. A half century of experimental neuroanatomical tracing. J Chem Neuroanat. 42:157–183. [DOI] [PubMed] [Google Scholar]
- Lee Y, Morrison BM, Li Y, Lengacher S, Farah MH, Hoffman PN, Liu Y, Tsingalia A, Jin L, Zhang PW et al. 2012. Oligodendroglia metabolically support axons and contribute to neurodegeneration. Nature. 487:443–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis JW, Van Essen DC. 2000a. Corticocortical connections of visual, sensorimotor, and multimodal processing areas in the parietal lobe of the macaque monkey. J Comp Neurol. 428:112–137. [DOI] [PubMed] [Google Scholar]
- Lewis JW, Van Essen DC. 2000b. Mapping of architectonic subdivisions in the macaque monkey, with emphasis on parieto-occipital cortex. J Comp Neurol. 428:79–111. [DOI] [PubMed] [Google Scholar]
- Luebke JI. 2017. Pyramidal neurons are not generalizable building blocks of cortical networks. Front Neuroanat. 11:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lund JS, Yoshioka T, Levitt JB. 1993. Comparison of intrinsic connectivity in different areas of macaque monkey cerebral cortex. Cereb Cortex. 3:148–162. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Hausser M, Pouget A. 2016. A better way to crack the brain. Nature. 539:159–161. [DOI] [PubMed] [Google Scholar]
- Mantini D, Gerits A, Nelissen K, Durand JB, Joly O, Simone L, Sawamura H, Wardak C, Orban GA, Buckner RL et al. 2011. Default mode of brain function in monkeys. J Neurosci. 31:12954–12962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markov NT, Ercsey-Ravasz M, Lamy C, Gomes ARR, Magrou L, Misery P, Giroud P, Barone P, Dehay C, Toroczkai Z. 2013. The role of long-range connections on the specificity of the macaque interareal cortical network. Proc Natl Acad Sci U S A. 110:5187–5192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markov NT, Ercsey-Ravasz MM, Ribeiro Gomes AR, Lamy C, Magrou L, Vezoli J, Misery P, Falchier A, Quilodran R, Gariel MA et al. 2014. A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cereb Cortex. 24:17–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markov NT, Misery P, Falchier A, Lamy C, Vezoli J, Quilodran R, Gariel MA, Giroud P, Ercsey-Ravasz M, Pilaz LJ et al. 2011. Weight consistency specifies regularities of macaque cortical networks. Cereb Cortex. 21:1254–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markov NT, Vezoli J, Chameau P, Falchier A, Quilodran R, Huissoud C, Lamy C, Misery P, Giroud P, Ullman S et al. 2014. Anatomy of hierarchy: feedforward and feedback pathways in macaque visual cortex. J Comp Neurol. 522:225–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H. 2006. The blue brain project. Nat Rev Neurosci. 7:153–160. [DOI] [PubMed] [Google Scholar]
- Matsui T, Tamura K, Koyano KW, Takeuchi D, Adachi Y, Osada T, Miyashita Y. 2011. Direct comparison of spontaneous functional connectivity and effective connectivity measured by intracortical microstimulation: an fMRI study in macaque monkeys. Cereb Cortex. 21:2348–2356. [DOI] [PubMed] [Google Scholar]
- Mejias JF, Murray JD, Kennedy H, Wang XJ. 2016. Feedforward and feedback frequency-dependent interactions in a large-scale laminar network of the primate cortex. Sci Adv. 2:e1601335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK. 1999. The prefrontal cortex: complex neural properties for complex behavior. Neuron. 22:15–17. [DOI] [PubMed] [Google Scholar]
- Miller EK, Cohen JD. 2001. An integrative theory of prefrontal cortex function. Annu Rev Neurosci. 24:167–202. [DOI] [PubMed] [Google Scholar]
- Miranda-Dominguez O, Mills BD, Grayson D, Woodall A, Grant KA, Kroenke CD, Fair DA. 2014. Bridging the gap between the human and macaque connectome: a quantitative comparison of global interspecies structure-function relationships and network topology. J Neurosci. 34:5552–5563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misic B, Betzel RF, Nematzadeh A, Goni J, Griffa A, Hagmann P, Flammini A, Ahn YY, Sporns O. 2015. Cooperative and competitive spreading dynamics on the human connectome. Neuron. 86:1518–1529. [DOI] [PubMed] [Google Scholar]
- Mori S, Kaufmann WE, Davatzikos C, Stieltjes B, Amodei L, Fredericksen K, Pearlson GD, Melhem ER, Solaiyappan M, Raymond GV. 2002. Imaging cortical association tracts in the human brain using diffusion-tensor-based axonal tracking. Magn Reson Med. 47:215–223. [DOI] [PubMed] [Google Scholar]
- Newman ME. 2006. Modularity and community structure in networks. Proc Natl Acad Sci U S A. 103:8577–8582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM. 2014. A mesoscale connectome of the mouse brain. Nature. 508:207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandya DN, Yeterian EH. 1996. Comparison of prefrontal architecture and connections. Philos Trans R Soc Lond Ser B Biol Sci. 351:1423–1432. [DOI] [PubMed] [Google Scholar]
- Park HJ, Friston K. 2013. Structural and functional brain networks: from connections to cognition. Science. 342:1238411. [DOI] [PubMed] [Google Scholar]
- Paxinos G, Huang X-F, Toga AW. 2000. The rhesus monkey brain in stereotaxic coordinates. San Diego, USA: Academic Press. [Google Scholar]
- Poo MM, Du JL, Ip NY, Xiong ZQ, Xu B, Tan T. 2016. China brain project: basic neuroscience, brain diseases, and brain-inspired computing. Neuron. 92:591–596. [DOI] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL, Lessov-Schlaggar CN, Petersen SE. 2013. Evidence for hubs in human functional brain networks. Neuron. 79:798–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preuss T. 1995. The argument from animals to humans in cognitive neuroscience In: Gazzaniga M, editor. The cognitive neurosciences. Cambridge (MA): MIT Press. [Google Scholar]
- Preuss TM. 2000. What’s human about the human brain. New Cogn Neurosci. 2:1219–1234. [Google Scholar]
- Preuss TM, Goldman-Rakic PS. 1991. Ipsilateral cortical connections of granular frontal cortex in the strepsirhine primate Galago, with comparative comments on anthropoid primates. J Comp Neurol. 310:507–549. [DOI] [PubMed] [Google Scholar]
- Purves D, Augustine GJ, Fitzpatrick D, Katz LC, LaMantia A-S, JO MN, Williams SM. 2004. Neuroscience. USA: Sinauer Associates. [Google Scholar]
- Rakic P. 1995. A small step for the cell, a giant leap for mankind: a hypothesis of neocortical expansion during evolution. Trends Neurosci. 18:383–388. [DOI] [PubMed] [Google Scholar]
- Rakic P. 2009. Evolution of the neocortex: a perspective from developmental biology. Nat Rev Neurosci. 10:724–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts JA, Perry A, Roberts G, Mitchell PB, Breakspear M. 2017. Consistency-based thresholding of the human connectome. NeuroImage. 145:118–129. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. 2010. Complex network measures of brain connectivity: uses and interpretations. NeuroImage. 52:1059–1069. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Ypma RJ, Watson C, Bullmore ET. 2015. Wiring cost and topological participation of the mouse brain connectome. Proc Natl Acad Sci U S A. 112:10032–10037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saab AS, Nave KA. 2017. Myelin dynamics: protecting and shaping neuronal functions. Curr Opin Neurobiol. 47:104–112. [DOI] [PubMed] [Google Scholar]
- Saleem KS, Logothetis NK. 2012. A combined MRI and histology atlas of the rhesus monkey brain in stereotaxic coordinates. London, UK: Academic Press. [Google Scholar]
- Sejnowski TJ, Churchland PS, Movshon JA. 2014. Putting big data to good use in neuroscience. Nat Neurosci. 17:1440–1441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen K, Goulas A, Grayson DS, Eusebio J, Gati JS, Menon RS, McIntosh AR, Everling S. 2019. Exploring the limits of network topology estimation using diffusion-based tractography and tracer studies in the macaque cortex. NeuroImage. 191:81–92. [DOI] [PubMed] [Google Scholar]
- Song HF, Kennedy H, Wang XJ. 2014. Spatial embedding of structural similarity in the cerebral cortex. Proc Natl Acad Sci U S A. 111:16580–16585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O. 2013. Network attributes for segregation and integration in the human brain. Curr Opin Neurobiol. 23:162–171. [DOI] [PubMed] [Google Scholar]
- Sporns O. 2014. Contributions and challenges for network models in cognitive neuroscience. Nat Neurosci. 17:652–660. [DOI] [PubMed] [Google Scholar]
- Sporns O, Betzel RF. 2016. Modular brain networks. Annu Rev Psychol. 67:613–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, Hilgetag CC. 2004. Organization, development and function of complex brain networks. Trends Cogn Sci. 8:418–425. [DOI] [PubMed] [Google Scholar]
- Sporns O, Honey CJ, Kotter R. 2007. Identification and classification of hubs in brain networks. PLoS One. 2:e1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N. 2008. Pyramidal neurons: dendritic structure and synaptic integration. Nat Rev Neurosci. 9:206–221. [DOI] [PubMed] [Google Scholar]
- Vaishnavi SN, Vlassenko AG, Rundle MM, Snyder AZ, Mintun MA, Raichle ME. 2010. Regional aerobic glycolysis in the human brain. Proc Natl Acad Sci U S A. 107:17757–17762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Kahn RS, Goni J, Sporns O. 2012. High-cost, high-capacity backbone for global brain communication. Proc Natl Acad Sci U S A. 109:11372–11377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Scholtens LH, Feldman Barrett L, Hilgetag CC, de Reus MA. 2015. Bridging cytoarchitectonics and connectomics in human cerebral cortex. J Neurosci. 35:13943–13948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Sporns O. 2011. Rich-club organization of the human connectome. J Neurosci. 31:15775–15786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Sporns O. 2013. An anatomical substrate for integration among functional networks in human cortex. J Neurosci. 33:14489–14500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium WU-MH . 2013. The WU-Minn human connectome project: an overview. NeuroImage. 80:62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent JL, Patel GH, Fox MD, Snyder AZ, Baker JT, Van Essen DC, Zempel JM, Snyder LH, Corbetta M, Raichle ME. 2007. Intrinsic functional architecture in the anaesthetized monkey brain. Nature. 447:83–86. [DOI] [PubMed] [Google Scholar]
- Wagstyl K, Lepage C, Bludau S, Zilles K, Fletcher PC, Amunts K, Evans AC. 2018. Mapping cortical laminar structure in the 3d bigbrai. Cereb Cortex. 28:2551–2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia M, Wang J, He Y. 2013. BrainNet Viewer: a network visualization tool for human brain connectomics. PLoS One. 8:e68910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Krienen FM, Chee MW, Buckner RL. 2014. Estimates of segregation and overlap of functional connectivity networks in the human cerebral cortex. NeuroImage. 88:212–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young NA, Collins CE, Kaas JH. 2013. Cell and neuron densities in the primary motor cortex of primates. Front Neural Circuits. 7:30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamora-Lopez G, Zhou C, Kurths J. 2010. Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks. Front Neuroinform. 4:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamora-Lopez G, Zlatic V, Zhou C, Stefancic H, Kurths J. 2008. Reciprocity of networks with degree correlations and arbitrary degree sequences. Phys Rev E Stat Nonlinear Soft Matter Phys. 77:016106. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


