Abstract
With the rapid development of high-throughput technologies, a growing amount of multi-omics data are collected, giving rise to a great demand for combining such data for biomedical discovery. Due to the cost and time to label the data manually, the number of labelled samples is limited. This motivated the need for semi-supervised learning algorithms. In this work, we applied a graph-based semi-supervised learning (GSSL) to classify a severe chronic mental disorder, schizophrenia (SZ). An advantage of GSSL is that it can simultaneously analyse more than two types of data, while many existing models focus on pairwise data analysis. In particular, we applied GSSL to the analysis of single nucleotide polymorphism (SNP), functional magnetic resonance imaging (fMRI) and DNA methylation data, which accounts for genetics, brain imaging (endophenotypes), and environmental factors (epigenomics) respectively. While parameter selection has been an open challenge for most models, another key contribution of this work is that we explored the parameter space to interpret their meaning and established practical guidelines. Based on the practical significance of each hyper-parameter, a relatively small range of candidate values can be determined in a data-driven way to both optimize and speed up the parameter tuning process. We validated the model through both synthetic data and a real SZ dataset of 184 subjects from the Mental Illness and Neuroscience Discovery (MIND) Clinical Imaging Consortium. In comparison to several existing approaches, our algorithm achieved better performance in terms of classification accuracy. We also confirmed the significance of several brain regions associated with SZ.
Keywords: multi-view learning, graph-based analysis, parameter selection, schizophrenia
I. Introduction
With the rapid progress of advanced high-throughput technologies along with various bioinformatics tools, an era of precision medicine is coming. Both clinical and molecular profiles of individuals are available, which can lead to a better understanding of various diseases and developing tailored disease prevention and treatment strategies. For this reason, in recent years various omics studies have been boosted, including genomics, epigenomics, transcriptomics, proteomics, and metabolomics.
However, studies on a single type of omics can only provide limited insight on the etiology. Most complex diseases are caused by an elaborate interplay of genetic and environmental factors[1], indicating that human genome is complex and regulated at multiple levels[2]. Thus, there is a great desire for jointly analysing multi-omics data to represent the complex biological systems. In fact, there have been considerable research efforts dedicated to multi-omics data integration to study various diseases[2–8]. In these studies, multi-omics data integration has been applied to achieve various tasks, including biomarker identification[3–5], disease prediction[6, 7] and optimal treatment[2, 8].
In this work, we focus on the prediction of schizophrenia (SZ) through the integration of multi-omics data. As a severe chronic mental disorder, SZ affects more than 23 million people worldwide and devastates patients with various disabling symptoms including paranoid delusions, auditory hallucinations, and thought disorders. While it has been studied for more than 100 years, the underlying neuropathology remains unclear. Because of this, current treatments can only focus on eliminating the outward symptoms. Treatments include antipsychotic medications, psychosocial treatment, and coordinated specialty care. Thus, it is of great significance to predict SZ when no syndromes are present or to diagnose SZ at an early stage when symptoms are relatively minor. Early detection can raise vigilance and allow these individuals to work with doctors to develop a prevention strategy or to seek early treatment.
In this study, we improved the model proposed in [9], a graph-based semi-supervised learning algorithm (GSSL). We applied it to combine single nucleotide polymorphism (SNP), DNA methylation and functional magnetic resonance imaging (fMRI) for SZ prediction as illustrated by Fig. 1. As a transformation-based integration method, GSSL can preserve view-specific information and is also robust to different data measurement scales[10]. The algorithm shares a similar idea with network-based SVM by embedding the data into a network[11, 12]. However, in GSSL, the generated kernel matrices are allowed to be sparse without introducing local minima into the optimization process[9]. This gives GSSL an advantage in computational efficiency.
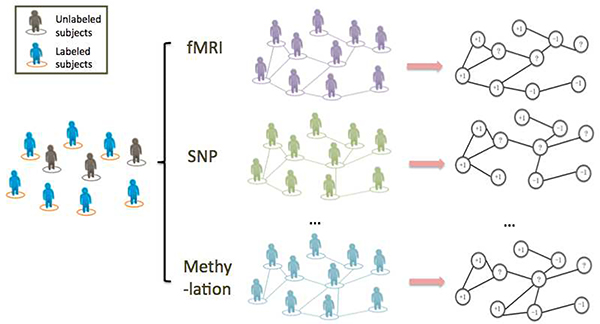
Fig. 1:
Graph construction from views of data: when performing a binary classification task on a group of people, no matter labelled or not, similarity matrices can be extracted from various types of data (e.g., fMRI, SNP or DNA methylation data). All entries of the similarity matrices are non-negative and the (i,j)th entry of one particular similarity matrix measures the strength of the connection between subject i and subject j in the corresponding view. Then each matrix can be depicted as an undirected graph that consists of two parts: nodes that represent individuals, and edges connecting the nodes. Nodes corresponding to labelled subjects are labelled as either ‘+1’ or ‘−1’ based on their phenotype. Unlabelled nodes are marked with’?’ and the goal is to predict their class using the graph. Edges connecting the nodes measure the pairwise similarity. If there is no edge connecting two nodes, the similarity between these two is neglectable. To combine the information from different data is equivalent to integrating the extracted graphs.
In GSSL, a sparse similarity matrix is extracted from one type of omics data, which can be depicted as an undirected graph (Fig. 1). The graph consists of two components: the nodes representing individuals, and the edges connecting the nodes. If the similarity between two subjects can be neglected, there is no edge connecting the corresponding nodes. After the construction of the graphs, a novel integration method is used to make predictions for the unlabelled subjects (nodes).
We applied GSSL in this study to integrate multi-omics data and reached a successful SZ classification. While parameter selection was challenging, we proposed a data-driven way to determine ranges of hyper-parameters for this model, which can both optimize and speed up the tuning procedure. We also showed how to extend this model to multi-class classification settings.
The rest of the paper is organized as follows. We describe the original algorithm and compare it with its formulation to similar models in Section II A. We interpret the meaning of hyper-parameters in this model and propose a data-driven guideline in Section II B. The extension of this model to multi-classes version is presented in Section II C. We present in Section III A the simulation results on testing the robustness of GSSL against noise and demonstrate its advantage of extracting information with limited label information. The real data analysis is presented in Section III B, where we conducted the classification of SZ. In Section IV, we conclude our findings and discuss possible future directions for this work.
II. Method
A. Binary classification with graphs
First, we work on binary classification tasks with a single dataset. Given n subjects, suppose the first l subjects are labelled and the last u subjects are not. We use {x1, y1;x2, y2;…xl, yl} to represent labelled ones, where yi ∈ [−1,+1] represents the phenotype, and {xl+1; xl+2; …xl+u} to represent unlabelled ones. Denoting the data of labelled subjects as Xl and their label information as yl, the least absolute shrinkage and selection operator (LASSO) regression aims at estimating prediction coefficients ω = [ω1, ω2, …ωp]T through the minimization of the following objective function:
| (1) |
Then the estimated ω values are applied to unlabelled data Xu to predict their labels. While this is a classic approach for classification tasks, it is a supervised learning that fails to make use of the information contained in unlabelled data. To this end, it would be more practical to adopt semi-supervised learning algorithms, among which graph-based learning is particularly useful. In LASSO, the phenotype of an individual is evaluated based on the value of xω. Since our main goal is to predict the phenotype, ranking the importance of each feature is not necessary. Motivated by this, we use a real-value score f to replace xω to accelerate the estimation and establish the relationship between the labelled data and the unlabelled ones.
Given the measurement X, an n × n symmetric similarity matrix S can be extracted from the measurement to represent the connections between subjects. The non-negative (i, j)th entry sij measures the similarity between subject i and j. It can be treated as an undirected graph: each subject is represented by a vertex and sij represents the strength of linkage between node i and j. Then we define an n-dimensional realvalued score vector f = (f1, f2, …, fn)T for all nodes. Among these n nodes, the first l ones are labelled as either yi = +1 or −1 based on their phenotypes, and the remaining nodes are unlabelled. To derive the function for f, we require that the scores of adjacent nodes are similar and the scores of labelled nodes should be consistent with the given labels. This leads to the following optimization problem on f:
| (2) |
The right side of Equation (2) is a quadratic energy function investigated in [13]. However, because the scores of labelled subjects are strictly fixed, we find the data fitting with Equation (2) is too restrictive which can easily lead to over-fitting problems. In addition, Equation (2) fails to consider scenarios where mislabelled data in the training group exist. This will jeopardize the estimation of the scores of unlabelled nodes. To address this issue, the following optimization problem is proposed:
| (3) |
where the first term is the loss function characterizing the data fitting on labelled subjects; the second term is a regularization term to keep the scores of unlabelled subjects within a reasonable range; the third term is a smoothness term c to constrain the difference in scores of adjacent nodes. Both μ and c are trade-off parameters.
In this study, we focus on the special case μ = 1, which allows for a quick closed solution[9][14]. By defining an ndimensional label vector , and calculating the graph Laplacian matrix L = D−S, where , Equation (3) can be transformed to solve the following optimization problem:
| (4) |
Note that, this can also be regarded as a manifold regularized learning problem:
| (5) |
where ω is defined in the same way as in LASSO: ω = [ω1, ω2, …ωp]T. Parameters λ and c are trade-off hyper-parameters that control the importance of each penalty term.
With the similarity matrix S being diagonally symmetric, the graph Laplacian matrix L is diagonally symmetric. Hence, the solution to the minimization problem Equation (4) can be obtained explicitly as:
| (6) |
where I is an n × n identity matrix.
Note that, Equation (4) can also be rewritten in the following constrained form:
| (7) |
For multiple types of data, namely N views of data in total, the k-th view of data is denoted as X(k). Then N graphs can be constructed and reflected by the corresponding Laplacian matrices L1, L2, …,LN. The information contained in each graph can be integrated by extending the optimization problem (7) to the following minimization problem with multiple constraints:
| (8) |
This optimization problem has been discussed and solved in [7, 9]. Its solution is given as follows:
| (9) |
where βk ≥ 0. Denoting β = [β1, …βk, …βN], it can be obtained by solving the following minimization problem:
| (10) |
Comparing the solution to the optimization problem of a single graph (Equation (6)) and that to multiple graphs (Equation (9)), they have similar formulations, where in the latter replaces cL. Furthermore, due to the constraints that weight of the graph represented byP Lk and thus can serve as βk ≥ 0 and , βk can be seen as the combination weight of the graph represented by Lk and thus can serve as the evaluation of the importance of a particular graph in terms of data fitting. Therefore, the proposed method can be called as multi-view integration with optimized weights.
Upon calculating the score vector f, by comparing its every element fi to the threshold zero, if fi is greater than zero, the label of node i is predicted as +1; otherwise, it is predicted as 1. The training error is defined as the ratio between the number of misclassified subjects and that of all training groups. The testing error is defined accordingly on the testing group.
B. Parameter selection and interpretation
1). Gaussian kernel bandwidth selection
The Gaussian kernel has been widely used to construct similarity matrices, and in this research we also focus on graphs constructed through Gaussian kernel. Given a view , an n × n symmetric similarity matrix W can be computed. The (i,j)th entry of W, denoted by wij, represents the strength of the edge connecting node i and node j in the graph, which is given by the following equation:
| (11) |
If xi is not in xj’s k-nearest neighbourhood or vice versa, the connection between these two nodes can be neglected and wij is set as zero.
An important parameter to determine when using the Gaussian kernel is the value of σ. In practice, we need to ensure that the graph is fully connected so that the geometrical structure of the data is captured. The connectivity of the graph is merely controlled by the value of σ. Silimar to σ, the bandwidth of Gaussian kernel is defined as ϵ = σ2. It is obvious that: if ||xi − xj||2 < ϵ, a high similarity is suggested between the node i and node j; Otherwise, if ||xi − xj||2 ≫ ϵ, the similarity between this pair is negligible and no connection is assumed in the graph. To ensure that every node in the graph is connected to at least one other node[15] so that the graph is connected, the bandwidth ϵconnected should satisfy the following criterion:
| (12) |
While the kernel bandwidth ϵ has to satisfy this requirement, it should also be sufficiently small so that only the most important connection is captured and kept. In [16], a more specific selection criterion on the bandwidth was proposed:
| (13) |
where K is empirically set within the range of 2∼3 to guarantee that the graph is connected while sparse and each node is connected to several other nodes[16].
However, since our task is to predict the labels for the unlabelled nodes, there is no need to enforce the above-mentioned restraint. In other words, we do not require a connected graph. However, in order to classify the unlabelled subjects, there has to be a connection between every unlabelled node and at least one labelled node, and the connection does not necessarily need to be direct. As a result, instead of generating a fully connected graph, we allow the graph to be disconnected, while each connected sub-graph containing unlabelled nodes has to have at least one labelled node. To find the optimal bandwidth that fits this condition, we calculate the following values as the candidates:
| (14) |
Then there are at most u different candidate values to choose from and we denote the set of candidate values as Λ. The lower boundary of Λ is ; this ensures that every unlabelled node is directly connected to at least one labelled node. The upper bound of Λ is ; it generates a graph that only one unlabelled node is directly connected to a labelled node. To select the optimal ϵ∗ that satisfies our requirement, we propose Algorithm 1.
Algorithm 1.
Bandwidth selection
| Require: |
| Node set consisting of labelled nodes set and unlabelled nodes set ; |
| Bandwidth candidate values set Λ |
| Ensure: |
| 1: Find the median value ϵmedian, lower bound ϵlb and upper bound ϵub of set Λ |
| 2: Calculate similarity matrix W using the median bandwidth value ϵmedian; |
| 3: Initialize a node set ; |
| 4: Update the node set by adding nodes i to it if wij > 0 for every node j that belongs to node set till node set stops growing |
| 5: If then update Λ = [ϵlb,…ϵmedian], otherwise update Λ = [ϵmedian,…ϵub] go to Step 1 till there is only one element in updated Λ, which is denoted as ϵ∗ |
| 6: return ϵ∗ |
2). Hyperparameter c selection
To determine the parameter c in the optimization objective function (3), we need to understand its impact and to interpret its significance. Let us revisit our original optimization function (3) with μ = 1. For simplicity, we define δ = 1/c, and then by setting the derivative of f with respect to fi to zero,for a single node i in the graph, we have:
| (15) |
The first part of the solution corresponds to the smooth term in energy function (3), and the second part corresponds to the loss function in function (3).
To interpret this, we imagine a particle walking along the constructed graph starting from a random node i. In the graph, there are paths from node i to node j if wij is positive, and the probability of visiting node j from node i in one step is . However, there is also a ‘mirror’ node to node i that it might visit. The connection of node i to its mirror node has the strength of and the score of the mirror node is yi. This mirror node represents the prior knowledge (its label) we have for individual i and if yi = 0, it means we do not have any prior knowledge. This is also used as the baseline for adjusting the score of the node. The probability of visiting this mirror node in one step is . Then function (15) calculates the expectation of the score of the node that it will reach in one step:
| (16) |
As , it is clear that the larger di is, the node i is closer to other nodes in general. Thus, the labels/scores of its neighbour nodes can better reflect what this node’s label/score should be. In this case, we have more confidence on the smoothness term to modify the scores after data fitting. On the other hand, the smaller di is, the more isolated node i is in the graph. For such a lonely node, the labels/scores of its ‘neighbour’ nodes do not provide a lot reference to its score, so the loss function should have a larger weight. In other words, if the particle starts walking from an isolated node, it is more likely to visit the mirror node within one step because the starting point is too far away from any other nodes.
If di ≫ δ, the score of node i can be written as . In this case, is very close to zero, which means the mirror node does not have much effect on the value of fi. The value of fi is largely adjusted from the value yi based on the scores of its adjacent nodes. In this case, if individual i is labelled, then its score is adjusted based on its (strong) similarity to other nodes to infer the degree of its type. Meanwhile, if individual i is unlabelled, based on its strong connection to other nodes, we have enough information to infer its type and its score is calculated from the scores of its adjacent individuals.
On the other hand, if δ ≫ di, the node i can be considered as an isolated node, then Pii is very close to one, and the score of node i is almost yi. In this case, the nodes in node i’s ‘nearest neighborhood’ are not actually near. Thus the value of fi is merely decided based on our prior knowledge: if individual i is labelled, the score of fi stays at the value yi; if individual i is not labelled, then we don’t have enough information to classify it and the score of node i stays close to zero.
Given a type of data, matrix D can be calculated and then c (or δ) can be chosen based on the distribution of di. With multiple datasets, we combine all the candidate values of parameter c calculated for each single dataset as the selecting pool.
C. The extension to multi-class classification problem
Furthermore, this algorithm can be easily extended to multi-class classification setting. For this model, the most direct solution is to use different values to represent different groups. However, it is challenging to decide and justify the value for each class and the thresholds to distinguish the groups. In addition, from Equation (3), the second term encourages scores of unlabelled nodes to stay relatively close to zero. As a result, it is not applicable to extend GSSL in this way, since we intend to stay focused on the special case where μ is 1 to allow for an explicit and quick solution.
A task of classifying N different groups can be divided into several binary classification tasks through conducting one-vs-all or all-vs-all classification. Inspired by this, we propose to use a matrix to represent the classes of labelled subjects, where:
| (17) |
That is, each labelled subject belongs to only one particular group, and the corresponding entry in label matrix Y is one. Similarly, we also re-define a score matrix , where the entry Fij represents the relative possibility of subject i belonging to the j-th group.
Then the optimization problem can be re-formulated as follows:
| (18) |
where Fi and Yi are the ith row vector of F and of Yl respectively. By setting μ = 1 and extending class matrix Y∗ to Y = [Yl;Yu] where , the solution of F can be found by solving:
| (19) |
where Tr is the trace of the matrix. By calculating the derivation of this equation in terms of F and setting it to zero, the solution is obtained as follows:
| (20) |
After calculating F, and by locating the largest value of Fi, the ith subject is then classified into the corresponding group. For multiview setting (N views), the integration problem can be formulated in a similar way:
| (21) |
The solution can be obtained as:
| (22) |
To validate the effectiveness of the proposed multi-class classification model, we did a simple test on Iris dataset1. We used 60% of the data as training. Overall, the testing error is 10.00% and the training error is 5.56%. The total accuracy is 92.67%.
III. Results
In this section, we present experimental results of the proposed method on both synthetic and real data. Since omics data are commonly high-dimensional, containing many redundant features and noise, we used the Student’s test to perform a preliminary feature reduction if not stated otherwise. The Gaussian kernel is applied to construct the similarity matrix/graph throughout the study. By performing classification experiments and comparing the performance with other commonly used methods, we evaluate the proposed method from different aspects. The details are described below.
A. Results on synthetic data
Before testing on real datasets, we validated the algorithm on simulated toy datasets. We first generated single-view toy datasets following the two-spiral pattern (also known as two-moon pattern). Each dataset contained a number of 200 subjects with binary phenotypes and two-dimensional measurements (as shown in Fig. S1 in supplementary document). The algorithm to generate the measurement and phenotype is described in Algorithm 2.
For each simulation, the degree of each spiral was set as 540°, and the noise level was increased gradually so that the intertwining spirals became closer. We imported the datasets into our algorithm and also into SVM with radius basis kernel function(RBF) for a comparison.
During this simulation test, for the purpose of simplicity, we adopted the kernel bandwidth based on Equation (13) and set K = 1. This setting makes the similarity matrix irrelevant to the partition of the data: no matter which subjects are used as training data, the similarity matrix can remain the same and is only relevant to the local structure of the whole data. The calculated similarity matrices are also presented in Fig. S1.
Algorithm 2.
Two-spiral pattern toy dataset simulation
| Require: |
| The number of subjects of each phenotype N |
| The radian of each spiral R |
| The noise level L; |
| Ensure: |
| Simulate a two-dimensional measurement that follows two-spiral pattern |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: return X and Y |
We first tested the classification performance using 80% ~ 90% of the whole data as training data. Both GSSL and SVM achieved classification accuracy of over 95% when the noise level L ≤ 1, and over 90% when L ≤ 3. There was no significant difference in terms of classification accuracy between the two algorithms (p value < 0.05) in these circumstances.
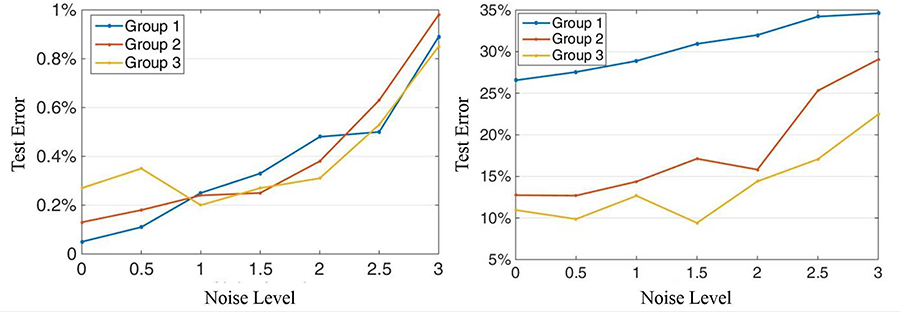
However, in real applications, labelling the data is labour-intensive so massive amount of data is unlabelled. Considering this situation, we continued to test the algorithm performance with lower ratio between training data and testing data. The result is presented in Fig. 2. Note that, compared with using 90% of the data as training group, the test error of GSSL actually dropped at all noise levels.
Fig. 2:
Classification performance using (a) GSSL algorithm and (b) SVM with RBF kernel. Group 1 to 3 correspond to using 10%, 20% and 25% of the whole data as training group. The y-axis represents test error, and the x-axis represents the noise level L.
Based on the classification accuracy with limited labelled training data, GSSL outperformed SVM at all noise levels. As the noise level rose, the classification accuracy dropped for both GSSL and SVM. Another important conclusion that can be drawn from Fig. 2 is that the classification accuracy of GSSL was not as sensitive to the ratio between training and testing data as SVM was.
To further validate the algorithm, we also tested on high dimensional synthetic data with multiple views. We simulated three high-dimensional data. We began with generating explanatory variables , where the first 400 components of each variable were drawn from Gaussian distribution, while the rest components were set to zeros. Continuous labels were generated from these explanatory variables and then transformed to z-scores. We kept the subjects whose scores were at the two ends (5% on each side) and ended up with n = 120 subjects. Binary labels were assigned to them based on the scores. In addition, we generated extra components to serve as cross-correlated variables so as to mimic the assumed links among real data. First, we generated three components from Gaussian distribution as ‘pair-correlated’ variables and another component as ‘all-correlated’ variables. The synthetic data were then made of three views for 120 subjects, and each view was represented by a 120×1200 matrix. Second, we added Gaussian noise to the data to test the robustness against disturbances.
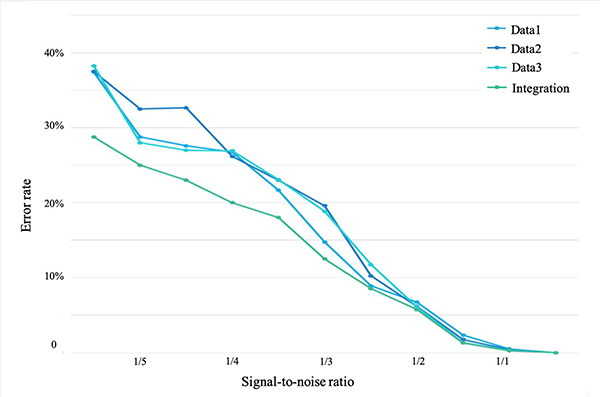
The results are shown in Fig. 3. It is clear that the integration of three views of data can better predict unlabelled points than using a single one at different noise levels. Also, it is more robust against noise compared to single dataset, due to the fact that noise in different views is unlikely to share the same patterns; in other words, by extracting common information carried in various views, the noise is to some extent reduced.
Fig. 3:
The classification performance using high dimensional synthetic data with multiviews. With growing signal-to-noise ratio, the testing error is reduced. In general, the method is robust to noise within a reasonable range.
B. Schizophrenia classification
1). Data acquisition and pre-processing
For real data analysis, we tested the algorithm using SNP, fMRI and DNA methylation data collected by the Mental Illness and Neuroscience Discovery Clinical Imaging Consortium (MCIC)[17] with the task of classifying SZ patients.
The fMRI data used in this study were collected when participants were performing the auditory oddball (AOD) task. As one of the most popular fMRI paradigms, AOD task has been proven to be successful in capturing the abnormalities in brain activations presented in SZ patients [18, 19]. It required participants to detect and respond to the random infrequent target sound stimuli by pressing a button. The detailed experiment setting for the fMRI AOD paradigm can be found in [17, 20]. The preprocessing of fMRI data was achieved by the SPM software2. After a successive processing including realignment, spatial normalization and smoothing, data were analysed by multiple regression considering factors including the audio stimulus. As a result, a 53 × 63 × 46 stimulus- on versus stimulus-off contrast image was then extracted for each participant. After excluding voxels with missing measurements, each image consists of 41236 voxels in total, which can be divided into 116 ROIs based on the Automated Anatomical Labeling (AAL) template.
The DNA was extracted from blood samples obtained from participants at the Harvard Partners Center for Genetics and Genomics. Genotyping was then performed at the Mind Research Network using the Illumina Infinium HumanOmni1Quad BeadChip. Details can be found in [17]. After quality control using PLINK software package3, the final dataset contained information of 722,177 SNP loci for each subject. Each SNP was categorized into three clusters based on their genotype and was represented by discrete numbers: 0 for BB(no minor allele), 1 for AB (one minor allele) and 2 for AA (two minor alleles).
The DNA methylation data were also extracted from the blood samples. After excluding intensity outliers, data were normalized using the R package wateRmelon [21]. After further quality control and normalization [22], the data contained information on 27,508 CpG sites. Each entry was between 0 ~ 1, representing the degree of methylation of each CpG island.
The total number of subjects included in this study was 184, including 104 healthy controls (HCs) (32.37±11.06 years old, 66 males and 38 females) and 80 SZ patients (33.75 ± 10.55 years old, 60 males and 20 females), and all three types of data were available for each subject. The SZ patients were assessed based on the 4th edition of Diagnostic and Statistical Manual of Mental Disorders (DSM-IV) diagnostic criteria and most patients were in early stages of illness and anti-psychotic drug naive. The requirement for HCs was that they were free of psychiatric illness including substance abuse or dependence.
To further verify if gender or age can be excluded from our analysis, we conducted a one-way analysis of variance (ANOVA). The null hypothesis for gender was that the probability of a male participants being diagnosed as a SZ patient was equal to that of a female participant. The p value calculated was 0.0959, which was higher than 0.05. Thus, the null hypothesis was not rejected and gender was not considered as a contributive factor in terms of SZ. Similarly, we tested on the age influence, and the p value was calculated as 0.2972, which was also higher than 0.05. As a result, we didn’t consider age to be an influence factor either. The same conclusion can be drawn if we conducted a Student’s t-test.
More details about data collection and preprocessing can be found in [23, 24].
2). Result data analysis
We first applied Gaussian kernels to the entire data set (SNP: 184×722177, fMRI: 184×41236 and DNA methylation: 184×27508 ) to construct the similarity matrix. Two types of kernel bandwidth ϵconnected and ϵ∗ were calculated using Equation (13) and Algorithm 1 respectively, and were applied to construct similarity matrices. After obtaining the similarity matrices of each view of data, we calculated matrix D to find a proper range for parameter c. By plotting the histogram of the matrix D calculated from the weight matrix (Fig. S2), it is clear that most subjects/nodes are very close to others while few subjects/nodes are rather isolated from others. Based on this, if the dataset satisfies our cluster assumption, we know that for these isolated subjects, we have less confidence on their label prediction. Through the test on a single view, denoting the minimum value in D as Dlb and maximum value as Dub, we performed cross-validation to select the parameter 1/c (which is δ) from the range of 0.1Dlb to 5Dub. We found that the best value of 1/c always lies within 0.5Dlb ~ 0.5(Dlb + Dub). Thus, in further experiments carried out, we selected from this small range during cross-validation.
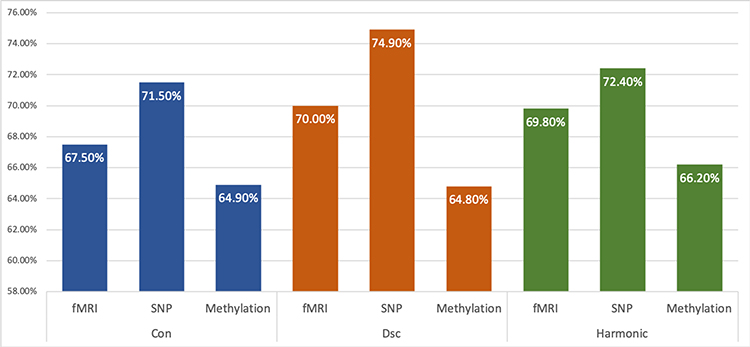
We first applied GSSL to single omics data and the classification accuracy is presented in Fig. 4. For GSSL, we used two types of graphs: the fully connected graphs using kernel bandwidth ϵconnected (Equation (13) and denoted as ‘Con’) and the disconnected graphs where each subgraph has at least one labelled node using ϵ∗ (Algorithm 1 and denoted as ‘Dsc’). We also compared with the results of another semi-supervised learning algorithm: the harmonic algorithm proposed in [13] (denoted as ‘Harmonic’) using disconnected graphs (with kernel bandwidth ϵ∗). There was no significant difference in the performance of three methods applied to DNA methylation data. When predicting SZ using SNP data, GSSL with disconnected graphs gave a significantly better accuracy than the other two methods (p < 0.05). Both GSSL and Harmonic algorithm with disconnected graphs outperformed GSSL with fully connected graphs when applied to fMRI data. Another observation was made during these experiments: while ϵ∗ takes longer time to compute than ϵconnected, disconnected graphs can accelerate classification process due to its higher sparsity than that of fully connected graphs.
Fig. 4:
A comparison of SZ classification accuracy (100% minus testing error) using single type of omics data with different graph-based method. From left to right: 1. ‘Con’: GSSL with fully connected graphs; 2. ‘Dsc’: GSSL with disconnected graphs where each subgraph has at least one labelled node;3. ‘Harmonic’: harmonic function proposed in [13] with disconnected graphs where each subgraph has at least one labelled node.
Overall, in graph-based analysis on single omics data, SNP delivered the best accuracy of diagnosing SZ, followed next by fMRI, and DNA methylation gave the lowest accuracy.
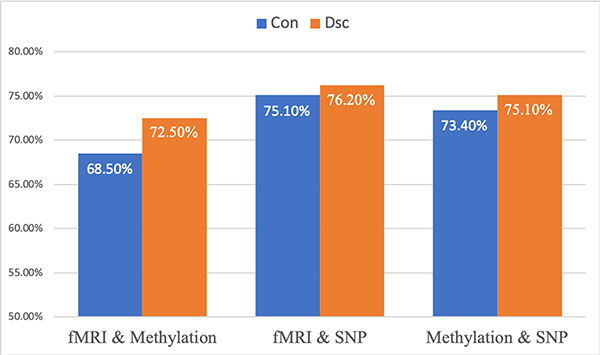
Next we tested the performance of pairwise combination of omics data using GSSL with optimized weights and the results are presented in Fig. 5. We tested the performance of graphs constructed using ϵconnected (‘Con’) and using ϵ∗ (‘Dsc’). With the same type of graphs, the combination of fMRI and SNP data gave the best classification accuracy, followed by the combination of SNP and DNA methylation data, and then the combination of fMRI and DNA methylation data. These pairwise combinations all outperformed the corresponding single omics data analysis (with the same type of graphs). This validates the ability of GSSL to extract complementary information from multiple views of data. While for the combination of fMRI and SNP data, there was no significant difference between fully-connected graphs and disconnected graphs, integration with disconnected graphs significantly outperformed fully-connected graphs for the two other combinations (p < 0.05). The results also confirm that the better each graph at prediction, the higher accuracy is generated by the integration using optimized GSSL.
Fig. 5:
SZ classification accuracy (100% minus testing error) with pair-wise combination of omics data. From left to right: optimized combination : 1. fMRI and DNA methylation data; 2. fMRI and SNP data; 3. DNA methylation and SNP data. Blue and orange bars correspond to fully-connected graphs and disconnected graphs, respectively.
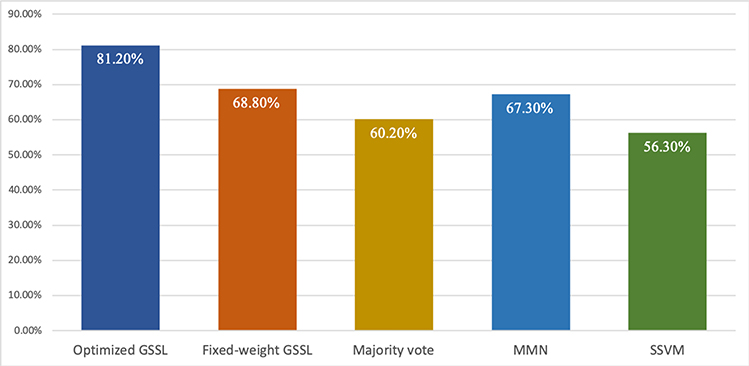
Then we integrated all three types of omics data using GSSL and compared with other integration methods, and the results are presented in Fig. 6. Other integration methods we tested include: 1. majority vote which is based on GSSL on single omics data with fully connected graphs (calculate the average of the scores from single GSSL and then apply thresholds); 2. majority-neighbourh mean fusion (MMN) [23]; 3. Similarity-network-fusion-based SVM (SSVM) [25].
Fig. 6:
SZ classification accuracy (100% minus testing error) with integration of SNP, DNA methylation and fMRI data with different methods. From left to right: 1. GSSL with optimized weights; 2. GSSL with fixed weight; 3. GSSL with majority vote; 4. majority-neighborhood-based classification by mean fusion (MMN); 5. similarity-network-fusion-based SVM (SSVM).
Based on the classification accuracy, GSSL gave higher accuracy in classifying SZ than other integration methods. Besides, integration of three types of data with optimized-weight GSSL gave a higher accuracy than GSSL with any single omics data or pairwise combination. On the other hand, the classification accuracy of majority vote with three types of data was even lower than that of any single omics data. This further validates the superiority of GSSL method in data integration than other methods.
To validate the necessity of calculating optimized weights for graphs integration (Equation (10)), we tested integration performance using GSSL with fixed weights which is defined as following:
| (23) |
where c is a hyper parameter that constrains the sum of all weights, and N is the number of views of data (in this experiment, it is 3).
The results are present in Fig. 6. It is evident that optimized-weight GSSL gave a significantly higher accuracy than fixed-weight GSSL (p < 0.05). This confirms the advantage of integration with optimized weights and proves that the proposed model can optimally combine multiple types of omics data.
While the classification accuracy with GSSL is satisfactory, many researches on SZ using fMRI alone have shown good results, which motivated us to do more investigation on fMRI data. For GSSL, the choice of features used for similarity matrices construction is crucial. Based on findings in [18] and [20], we selected 40 regions (regions defined by automated anatomical labeling (AAL) template) to further investigate their significance. The selected regions of interests (ROIs) are listed in Table S1 in supplementary document. During this part of experiment, no t-test is involved to select features. As disconnected graphs yield better classification accuracy than fully connected graphs when using fMRI alone, we only investigate this type of graphs.
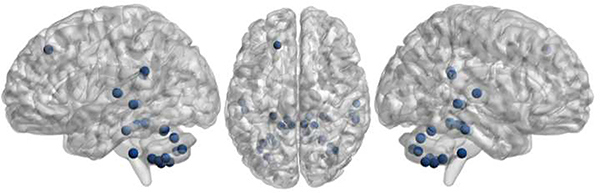
One hundred subjects (50 SZ patients and 50 HCs) were selected as training group. We conducted 10 fold cross validation on the training group and the accuracy of these nodes is shown in Fig. S3. The classification accuracy indicates that the following regions have better performance: left superior frontal gyrus, left inferior parietal lobule, bilateral posterior cingulate gyrus, right thalamus, cerebellum, bilateral superior temporal gyrus, left middle and inferior temporal gyrus, and right putamen. These ROIs are visualized in Fig. 7.
Fig. 7:
Visualization of 14 important brain regions confirmed by our analysis.
The association between these regions and schizophrenia has been validated by other independent research. For example, numerous studies have found abnormality in the thalamus in SZ patients including neuronal loss and volume reduction [26–28]. It is associated with cognitive functions of SZ patients including declarative memory [29] and attentional sub-process [30, 31]. Meanwhile, the cerebellum is among the most affected brain regions in SZ patients [32]. Besides motor coordination, cerrebellum is also involved in cognitive function such as attention, working memory, verbal learning, and sensory discrimination [33]. The superior frontal gyrus is associated with self-awareness [34]; the posterior cingulate gyrus forms a central node in the default mode network(DMN) and is a central hub for information exchange in the brain [35]. Thus they can be linked with the distortions of self-experience of SZ patients. Inferior parietal lobule is involved with the perception of emotions and interpretation of sensory information [36], related to the the reduced social engagement and emotional expression of SZ patients. Volumetric abnormalities have been found in the superior, middle and inferior temporal gyrus of SZ patients [37, 38]. The superior temporal gyrus is related to the production of hallucinations [39], developmental mechanisms of brain lateralization and the pathogenesis of language-related SZ symptoms [40]. The main functions of middle and inferior temporal gyrus include language and semantic memory processing, and visual perception[41]. Research works have pointed out their association with the auditory verbal hallucinations of SZ patients [42, 43]. Volumetric abnormality has been observed in the putamen in SZ patients, and the putamen infarct is suggested to cause psychotic symptoms in SZ patients [44, 45].
After identifying these regions, we integrated them with optimized weights using GSSL. We tested on the testing group (the remaining 84 subjects) with 10 fold cross validation. The average classification accuracy reached 72.5%. This is higher than using the whole fMRI data, confirming the association of these ROIs with SZ. Testing the performance of single nodes can also be regarded as a feature selection process and these 14 nodes are considered as important regions for SZ classification.
We then integrated the fMRI data of these 14 ROIs with SNP and DNA methylation data using the optimized GSSL model. With a 10-fold cross validation, the averaged classification accuracy reached 86.11%. This is higher than integrating the whole fMRI data with (epi)genetics data, indicating that proper feature selection process can enhance the classification performance of a single graph and that of its integration with other graphs.
IV. Discussion and Conclusions
This study focuses on the GSSL algorithm. This method can be applied to both single omics analysis and integration of multiple omics data. Each view of data is transformed into a graph to measure the similarity between subjects. The phenotypes of unlabelled subjects are predicted based on the graphs. Unlike network-based SVM, these graphs are allowed to be sparse. Given a large amount of samples, this can reduce computational burden. Through testing the classification performance with graphs of different connectivity degrees, it is proved that the sparsity of the graphs can also improve the accuracy. This indicates that the sparse graphs contain the most important information, which also makes GSSL robust to noise. This is validated through simulation experiments, too.
In many real-world problems, labelling the data is manually expensive. There is an unbalanced ratio between labelled data and labelled data. In one of our simulation experiments, we tested the classification performance of GSSL and SVM when different proportion of the data were labelled. While there was no significant difference when over 80% of the data were labelled, the advantage of GSSL over SVM was evident when labelled subjects were not more than 25%. This confirms that GSSL can cope with the unbalanced ratio between labelled and unlabelled data as a semi-supervised algorithm.
For real data analysis, we applied GSSL to SZ classification using MCIC data. We adopted SNP, DNA methylation and fMRI data, which accounts for genetics, epigenetics and brain imaging respectively. In single omics analysis, SNP and fMRI data gave better results than DNA methylation data, validating the genetic heritability of SZ and the important role played by potential endophenotype fMRI. As for combining three types of data, GSSL gave a higher accuracy than using single omics data. This validates the ability of GSSL to extract complementary information from multiple views of data. Also, optimized-weight GSSL gave a significantly higher accuracy for diagnosing SZ compared with other popular integration methods and also fixed-weight GSSL. This further confirms the classification ability of optimized-weight GSSL.
While GSSL aimed at classification, during single omics analysis, we confirmed 14 important brain regions associated with SZ by testing each ROI’s performance. The combination of these 14 regions yielded higher accuracy than using the whole fMRI data. This indicates that GSSL can also be applied to confirm important biomarkers and such prior feature selection can improve classification accuracy.
A major contribution of this work is on the choice of hyper-parameters, which has been an open and challenging problem in many models. By interpreting the significance of each parameter, we proposed a practical strategy to determine the weight c for smoothness term and the kernel bandwidth ϵ for graph construction. We validated the advantage of the strategy in both simulation test and real data analysis. With this guideline, an optimal value of kernel bandwidth and a suitable range for hyper-parameter c can be determined based on the data. We also offered a way to extend the model to multi-class setting, which can be applied to various practical problems. This is one of our future directions.
While we selected Gaussian kernel to construct the graph, we are aware that classification performance can vary if the similarity matrix is constructed in other ways. For example, subspace clustering can also be used to construct similarity matrices for high-dimensional data[46–48]. The choice of similarity metrics construction method is dependent on the dataset. Gaussian kernel is generally a good fit to most datasets especially with prior feature selection[24, 49]. Besides, aided by the proposed guideline for kernel bandwidth selection, Gaussian kernel was proved efficient for SZ classification with MCIC data.
However, this study has only focused on exploring the case when the weight for the regularization term in Equation (3) μ = 1. While this renders the solution easier to find, we can investigate more general cases in the future.
Supplementary Material
Acknowledgments
The authors would like to thank the partial support by NIH (P20GM103472, R01EB005846, R01GM109068, R01MH104680, R01MH107354, R01MH094524) and NSF (#1539067).
Footnotes
Contributor Information
Yuntong Bai, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118, USA.
Zille Pascal, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118, USA.
Vince Calhoun, Tri-institutional Center for Translational Research in Neuroimaging and Data Science (TReNDS), Georgia State University, Georgia Institute of Technology, Emory University, Atlanta, GA 30030.
Yu-Ping Wang, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118, USA.
Reference
- [1].Higdon R, Earl RK, Stanberry L, Hudac CM, Montague E, Stewart E, et al. The promise of multi-omics and clinical data integration to identify and target personalized healthcare approaches in autism spectrum disorders. Omics: a journal of integrative biology, 19(4):197–208, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Huang S, Chaudhary K, and Garmire LX More is better: Recent progress in multi-omics data integration methods. Frontiers in Genetics, 8:84, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Miao R, Luo H, Zhou H, Li G, Bu D, Yang X, et al. Identification of prognostic biomarkers in hepatitis b virus-related hepatocellular carcinoma and stratification by integrative multi-omics analysis. Journal of hepatology, 61(4):840–849, 2014. [DOI] [PubMed] [Google Scholar]
- [4].Cisek K, Krochmal M, Klein J, and Mischak H The application of multi-omics and systems biology to identify therapeutic targets in chronic kidney disease. Nephrology Dialysis Transplantation, 31(12):2003–2011, 2015. [DOI] [PubMed] [Google Scholar]
- [5].Wheelock CE, Goss VM, Balgoma D, Nicholas B, Brandsma J, Skipp PJ, et al. Application of omics technologies to biomarker discovery in inflammatory lung diseases. European Respiratory Journal, 42(3):802–825, 2013. [DOI] [PubMed] [Google Scholar]
- [6].Huang H, Vangay P, McKinlay CE, and Knights D Multi-omics analysis of inflammatory bowel disease. Immunology letters, 162(2):62–68, 2014. [DOI] [PubMed] [Google Scholar]
- [7].Kim D, Joung J, Sohn K, Shin H, Park YR, Ritchie MD, et al. Knowledge boosting: a graph-based integration approach with multi-omics data and genomic knowledge for cancer clinical outcome prediction. Journal of the American Medical Informatics Association, 22(1):109–120, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Tebani A, Afonso C, Marret S, and Bekri S Omicsbased strategies in precision medicine: toward a paradigm shift in inborn errors of metabolism investigations. International journal of molecular sciences, 17(9):1555, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Tsuda K, Shin H, and Scholkopf B ¨ Fast protein classification with multiple networks. Bioinformatics, 21(suppl 2):ii59–ii65, 2005. [DOI] [PubMed] [Google Scholar]
- [10].Ritchie MD, Holzinger ER, Li R, Pendergrass SA, and Kim D Methods of integrating data to uncover genotype–phenotype interactions. Nature Reviews Genetics, 16(2):85, 2015. [DOI] [PubMed] [Google Scholar]
- [11].Schwarz E, Izmailov R, Spain M, Barnes A, Mapes JP, Guest PC, et al. Validation of a blood-based laboratory test to aid in the confirmation of a diagnosis of schizophrenia. Biomarker insights, 5:39, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Fan Y, Shen D, and Davatzikos C Classification of structural images via high-dimensional image warping, robust feature extraction, and svm. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2005, pages 1–8, 2005. [DOI] [PubMed] [Google Scholar]
- [13].Zhu X, Ghahramani Z, and Lafferty J Semi-supervised learning using gaussian fields and harmonic functions. ICML-03, 20th International Conference on Machine Leraning, 2003. [Google Scholar]
- [14].Zhou D, Bousquet O, Lal TN, Weston J, and Scholkopf B Learning with local and global consistency. In Advances in neural information processing systems, pages 321–328, 2004. [Google Scholar]
- [15].Dov D, Talmon R, and Cohen I Kernel-based sensor fusion with application to audio-visual voice activity detection. IEEE Transactions on Signal Processing, 64(24):6406–6416, 2016. [Google Scholar]
- [16].Keller Y, Coifman RR, Lafon S, and Zucker SW Audio-visual group recognition using diffusion maps. IEEE Transactions on Signal Processing, 58(1):403–413, 2010. [Google Scholar]
- [17].Gollub RL, Shoemaker JM, King MD, White T, Ehrlich S, Sponheim SR, Clark VP, et al. The mcic collection: a shared repository of multi-modal, multisite brain image data from a clinical investigation of schizophrenia. Neuroinformatics, 11(3):367–388, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Kiehl KA, Stevens MC, Celone K, Kurtz M, and Krystal JH Abnormal hemodynamics in schizophrenia during an auditory oddball task. Biological psychiatry, 57(9):1029–1040, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Dae Il Kim, Mathalon DH, Ford JM, Mannell M, Turner JA, Brown GG, Belger A, Gollub R, Lauriello J, Wible C, et al. Auditory oddball deficits in schizophrenia: an independent component analysis of the fmri multisite function birn study. Schizophrenia bulletin, 35(1):67–81, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Kiehl KA and Liddle PF An event-related functional magnetic resonance imaging study of an auditory oddball task in schizophrenia. Schizophrenia research, 48(2):159–171, 2001. [DOI] [PubMed] [Google Scholar]
- [21].Pidsley Ruth, Chloe CY Wong Manuela Volta, Lunnon Katie, Mill Jonathan, and Leonard C Schalkwyk. A data-driven approach to preprocessing illumina 450k methylation array data. BMC genomics, 14(1):293, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Hass Johanna, Walton Esther, Wright Carrie, Beyer Andreas, Scholz Markus, Turner Jessica, Liu Jingyu, Smolka Michael N, Roessner Veit, Sponheim Scott R, et al. Associations between dna methylation and schizophrenia-related intermediate phenotypesa gene set enrichment analysis. Progress in NeuroPsychopharmacology and Biological Psychiatry, 59:31–39, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Deng S, Hu W, Calhoun VD, and Wang Y Schizophrenia prediction using integrated imaging genomic networks. Advances In Science, Technology and Engineering Systems Journal Vol.2, No. 3, 702–710, 2017. [Google Scholar]
- [24].Bai Y, Zille P, Calhoun VD, and Wang Y Biomarker identification through integrating fmri and epigenetics. IEEE transactions on Biomedical Engineering, 2019. DOI: 10.1109/TBME.2019.2932895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wang B, Mezlini AM, Demir F, Fiume M, Tu Z, Brudno M, et al. Similarity network fusion for aggregating data types on a genomic scale. Nature methods, 11(3):333–337, 2014. [DOI] [PubMed] [Google Scholar]
- [26].Byne William,Buchsbaum Monte S, Mattiace Linda A, Hazlett Erin A, Kemether Eileen, Elhakem Sharif L, Purohit Dushyant P, Haroutunian Vahram, and Jones Liesl. Postmortem assessment of thalamic nuclear volumes in subjects with schizophrenia. American Journal of Psychiatry, 159(1):59–65, 2002. [DOI] [PubMed] [Google Scholar]
- [27].Byne William, Hazlett Erin A, Buchsbaum Monte S, and Kemether Eileen. The thalamus and schizophrenia: current status of research. Acta neuropathologica, 117(4):347, 2009. [DOI] [PubMed] [Google Scholar]
- [28].Pergola Giulio, Selvaggi Pierluigi, Trizio Silvestro, Bertolino Alessandro, and Blasi Giuseppe. The role of the thalamus in schizophrenia from a neuroimaging perspective. Neuroscience & Biobehavioral Reviews, 54:57–75, 2015. [DOI] [PubMed] [Google Scholar]
- [29].Andrews Jessica, Wang Lei, Csernansky John G, Gado Mokhtar H, and Barch Deanna M. Abnormalities of thalamic activation and cognition in schizophrenia. American Journal of Psychiatry, 163(3):463–469, 2006. [DOI] [PubMed] [Google Scholar]
- [30].Salgado-Pineda Pilar, Junqué Carme, Vendrell Pere, Baeza Immaculada, Bargalló Nuria, Falcón Carles, and Bernardo Miquel. Decreased cerebral activation during cpt performance: structural and functional deficits in schizophrenic patients. Neuroimage, 21(3):840–847, 2004. [DOI] [PubMed] [Google Scholar]
- [31].Tregellas Jason R, Davalos Deana B, Rojas Donald C, Waldo Merilyne C, Gibson Linzi, Wylie Korey, Yiping P, and Freedman Robert. Increased hemodynamic response in the hippocampus, thalamus and prefrontal cortex during abnormal sensory gating in schizophrenia. Schizophrenia research, 92(1–3):262–272, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Andreasen Nancy C and Pierson Ronald. The role of the cerebellum in schizophrenia. Biological psychiatry, 64(2):81–88, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Yeganeh-Doost Peyman, Gruber Oliver, Falkai Peter, and Schmitt Andrea. The role of the cerebellum in schizophrenia: from cognition to molecular pathways. Clinics, 66:71–77, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Goldberg Ilan I, Harel Michal, and Malach Rafael. When the brain loses its self: prefrontal inactivation during sensorimotor processing. Neuron, 50(2):329–339, 2006. [DOI] [PubMed] [Google Scholar]
- [35].Leech Robert, Braga Rodrigo, and Sharp David J. Echoes of the brain within the posterior cingulate cortex. Journal of Neuroscience, 32(1):215–222, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Radua Joaquim, Phillips Mary L, Russell Tamara, Lawrence Natalia, Marshall Nicolette, Kalidindi Sridevi, El-Hage Wissam, McDonald Colm, Giampietro Vincent, Michael J Brammer, et al. Neural response to specific components of fearful faces in healthy and schizophrenic adults. Neuroimage, 49(1):939–946, 2010. [DOI] [PubMed] [Google Scholar]
- [37].Ohi Kazutaka, Matsuda Y, Shimada T, Yasuyama T, Oshima K, Sawai K, Kihara H Nitta Y, Okubo H, Uehara Takashi, et al. Structural alterations of the superior temporal gyrus in schizophrenia: Detailed subregional differences. European Psychiatry, 35:25–31, 2016. [DOI] [PubMed] [Google Scholar]
- [38].Onitsuka Toshiaki, Shenton Martha E, Salisbury Dean F, Dickey Chandlee C, Kasai Kiyoto, Toner Sarah K, Frumin Melissa, Kikinis Ron, Jolesz Ferenc A, and McCarley Robert W. Middle and inferior temporal gyrus gray matter volume abnormalities in chronic schizophrenia: an mri study. American Journal of Psychiatry, 161(9):1603–1611, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Rajarethinam RP, DeQuardo JR, Nalepa R, and Tandon R. Superior temporal gyrus in schizophrenia: a volumetric magnetic resonance imaging study. Schizophrenia research, 41(2):303–312, 2000. [DOI] [PubMed] [Google Scholar]
- [40].Matsumoto Hideo, Simmons Andrew, Williams Steven, Hadjulis Michael, Pipe Roderic, Murray Robin, and Frangou Sophia. Superior temporal gyrus abnormalities in early-onset schizophrenia: similarities and differences with adult-onset schizophrenia. American Journal of Psychiatry, 158(8):1299–1304, 2001. [DOI] [PubMed] [Google Scholar]
- [41].Zhang Linchuan, Li Baojuan, Wang Huaning, Li Liang, Liao Qimei, Liu Yang, Bao Xianghong, Liu Wenlei, Yin Hong, Lu Hongbing, et al. Decreased middle temporal gyrus connectivity in the language network in schizophrenia patients with auditory verbal hallucinations. Neuroscience letters, 653:177–182, 2017. [DOI] [PubMed] [Google Scholar]
- [42].McGuire PK, David AS, Murray RM, Frackowiak RSJ, Frith CD, Wright I, and Silbersweig DA. Abnormal monitoring of inner speech: a physiological basis for auditory hallucinations. The Lancet, 346(8975):596–600, 1995. [DOI] [PubMed] [Google Scholar]
- [43].Lennox Belinda R, Bert S, Park G, Medley Ian, Morris Peter G, and Jones Peter B. The functional anatomy of auditory hallucinations in schizophrenia. Psychiatry Research: Neuroimaging, 100(1):13–20, 2000. [DOI] [PubMed] [Google Scholar]
- [44].Mamah Daniel, Wang Lei, Barch Deanna, de Erausquin Gabriel A, Gado Mokhtar, and Csernansky John G. Structural analysis of the basal ganglia in schizophrenia. Schizophrenia research, 89(1–3):59–71, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Farid Faisal and Mahadun Prem. Schizophrenia-like psychosis following left putamen infarct: a case report. Journal of medical case reports, 3(1):7337, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Zhang C, Fu H, Liu S, Liu G, and Cao X Low-rank tensor constrained multiview subspace clustering. In Proceedings of the IEEE international conference on computer vision, pages 1582–1590, 2015. [Google Scholar]
- [47].Cao X, Zhang C, Fu H, Liu S, and Zhang H Diversity-induced multi-view subspace clustering. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 586–594, 2015. [Google Scholar]
- [48].Zhang C, Fu H, Hu Q, Cao X, Xie Y, Tao D, et al. Generalized latent multi-view subspace clustering. IEEE transactions on pattern analysis and machine intelligence, 2018. [DOI] [PubMed] [Google Scholar]
- [49].Bai Y, Zille P, Calhoun VD, and Wang Y Extraction of co-expressed discriminative features of schizophrenia in imaging epigenetics framework In Medical Imaging 2019: Biomedical Applications in Molecular, Structural, and Functional Imaging, volume 10953, page 109530X International Society for Optics and Photonics, 2019. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.