Abstract
Recent single-cell RNA-sequencing studies have suggested that cells follow continuous transcriptomic trajectories in an asynchronous fashion during development. However, observations of cell flux along trajectories are confounded with population size effects in snapshot experiments and are therefore hard to interpret. In particular, changes in proliferation and death rates can be mistaken for cell flux. Here, we present pseudodynamics, a mathematical framework that reconciles population dynamics with the concepts underlying developmental trajectories inferred from timeseries single-cell data. Pseudodynamics models population distribution shifts across trajectories to quantify selection pressure, population expansion, and developmental potentials. Applying this model to time-resolved single-cell RNA-sequencing of T-cell and pancreatic β-cell maturation, we characterize proliferation and apoptosis rates and identify key developmental checkpoints, inaccessible to existing approaches.
Single-cell experiments, such as single-cell RNA-sequencing (scRNA-seq)1, single-cell qPCR2, mass cytometry3 and flow cytometry enable the study of heterogeneity of cell populations. In development, this often corresponds to the distribution of asynchronously4,5 developing cells across intermediate cellular states. Pseudotemporal ordering methods, which describe development as a transition in transcriptomic state (i.e. a ‘trajectory’) rather than a transition in real time4,5, have been devised to capture such trajectories. These trajectory-learning approaches are complemented by methods which learn the overall topology of the data set and thereby infer the connectivity between trajectories: monocle26, graph abstraction7, and others4,8. One can merge overlapping snapshots from multiple time points across a developmental process to learn a trajectory that covers the full range of cell states accessible in this process; this is however still a static description. Accordingly, a trajectory does not uncover the dynamic behavior of individual cells in state space and time - this dynamic information is lost in population snap-shot experiments. Hence pseudotime does not directly correspond to real time but is rather a cell state space metric4. In contrast, one can recover population dynamics, such as developmental potentials and source and sink positions, from a time-series of snapshot experiments. Population dynamics govern distributional shifts in cellular systems and are key to understand how cell type frequencies change in response to developmental and environmental cues which underlie physiological mechanisms of health and disease. An example scenario with such a frequency change is as follows: The relative proportion of a given cell type A may decrease during a process because its proliferation rate decreases, its death rate increases or because A differentiates to other cell types. It is crucial to understand the nature of this shift if a frequency shift in A is associated with a disease, such as a decrease in pancreatic β-cell frequency is associated with diabetes.
Population dynamics have been previously modeled in the context of cell cycle transitions9,10, and in the context of scRNA-seq under steady state assumptions11. The problem of developmental trajectory estimation from time series data is typically non-stationary (Fig. 1a) as recently addressed via an optimal transport framework for discrete transitions12, and secondly from a dynamic point of view for low dimensional systems13. However, it remains difficult to disentangle the effects of population sources and sinks and effects of directed development which both contribute to the observed distribution in a snapshot experiment11.
Figure 1.
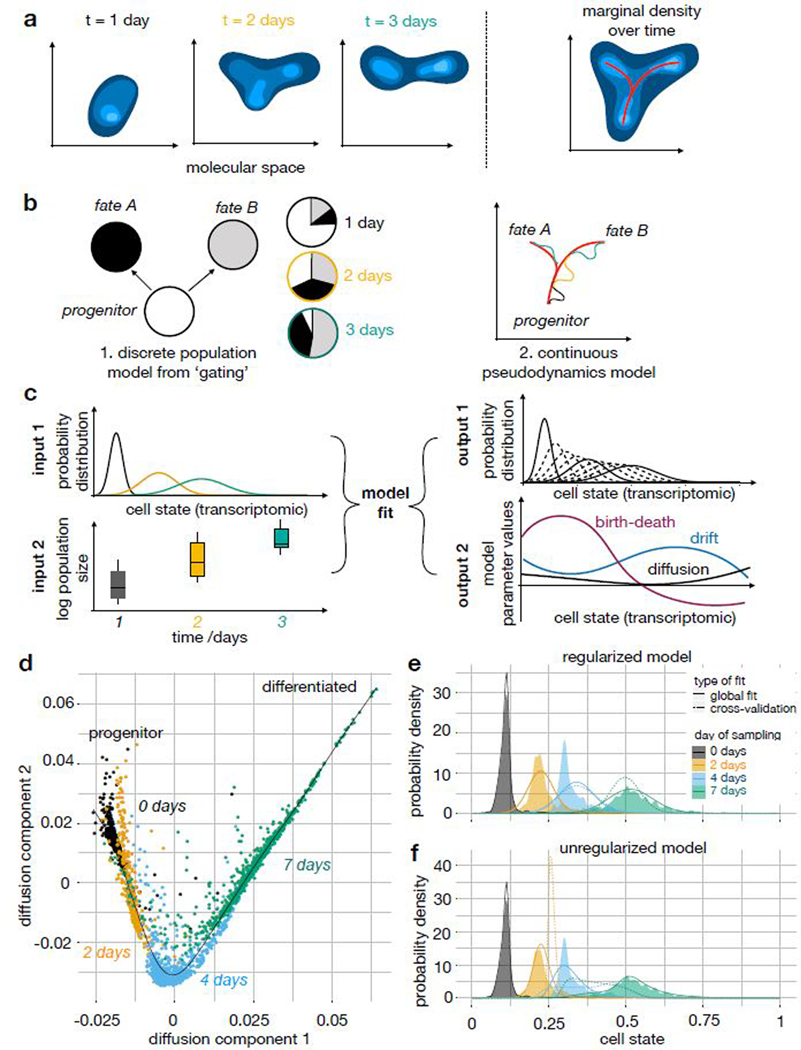
A population-based view of single-cell RNA-seq time-series experiments: Concept of pseudodynamics and example fits on a mouse embryonic stem cell differentiation data set. (a) Development can be modeled as the temporal progression of a population density in transcriptome (cell state) space. Here, the developmental process is a branched lineage from a progenitor to two terminal fates. (b) Dimension reductions of the full cell state space are useful for dynamic modelling. Discrete cell types, such as from FACS gates, were previously used for ordinary differential equation models. Branched trajectories with pseudotime coordinates can be used in the context of pseudodynamics. (c) Conceptual overview of the pseudodynamics algorithm: The input consists of developmental progress data (normalized distributions across cell state) and population size data (number of cells) for each time point. The output contains interpretable parameter estimates and imputed samples at unseen time points (dotted densities). (d) Diffusion map of mouse embryonic stem cell development in vitro after leukemia inhibitory factor (LIF) removal1. Color: days after LIF removal in cell culture. (e,f) Kernel density estimate and simulated density of cells across cell state coordinate (diffusion pseudotime) at four sampled time points (n0=933, n2=303, n4=683, n7=798 cells) for regularized (rho = 1) and unregularized (rho = 0) model fits. Colored density: kernel density estimate, solid line: simulated density based on model fitted to all data, dotted line: simulated density in leave-one-time-point-out cross-validation.
Here, we present pseudodynamics, a mathematical framework that uses population size and single-cell snapshot data in an integrated model of development which can distinguish population size and differentiation effects (Fig. 1a-c). Pseudodynamics adds layers of information to developmental graphs, in particular state-resolved proliferation and death and developmental potentials, an approximation of Waddington’s landscape. Firstly, we apply our model to T-cell maturation and uncover the population dynamics of beta-selection. Secondly, we apply our model to maturation of pancreatic β-cells in neonatal mice and we find that there is no evidence for extracellular regulation of proliferation.
Results
Pseudodynamics models single-cell time series measurements along developmental trajectories
A population of cells observed in a single-cell experiment is a sample from a probability distribution on the molecular space (such as transcriptome or proteome). During development, this distribution changes as a function of time (Fig. 1a). The molecular space is high-dimensional and typically transformed for interpretation, such as through space discretization or dimension reduction (Fig 1b). Pseudodynamics describes the population dynamics in such a low-dimensional space which we denote the cellular state s.
The time-dependence of a distribution of cells of a population, u(s,t), across discrete bins s with known connectivity has been traditionally described by a system of ordinary differential equations14 (Fig. 1b). We propose to describe the time-dependence of the number density u(s,t) across a set of continuous states s by a partial differential equation model. We model the dynamic process as a reaction-diffusion-advection partial differential equation, a population balance model11,15 (online methods eq. 1): The diffusion term represents undirected or stochastic movement of cells on the trajectory. The advection (‘drift’) parameter models directed movement across the trajectory. Weinreb et al. refer to the drift as the gradient of the development potential function11. The reaction term describes proliferation and death.
We allow all parameters to depend on the cell state (online methods eq. 1) and therefore define diffusion, drift and birth-death rates as continuous functions (splines) of state s. The cell state-dependent parameters encode local characteristics of the system in the cell state space such as proliferative compartments (high birth-death rates) or regions of increased cell death (negative birth-death rate). One can also introduce a time-dependence of the parameters to model changes in regulation over time (Supp. Note 1 eq. SN1.3).
We estimate the cell state-dependent parameters by maximizing a likelihood function that contains terms for developmental progress and total population size (online methods eq. 11). As inputs, the model takes a) time-resolved, normalized samples of the population obtained through a single-cell method and b) separate time-resolved measurements of the total number of cells in the entire system (Fig. 1c). Such total population size estimates can be approximated based on flow cytometry counts or cell counting in tissue sections. By integrating total population size measurements, pseudodynamics can infer state-specific birth-death parameters. It is necessary to forward simulate a dynamical system at each iteration of the parameter estimation to evaluate the likelihood function given a set of parameters. We achieved numerical stability and accuracy of the forward simulations of the partial differential equation system with the finite volumes method (online methods) and validated the robustness of the parameter estimation in multiple simulation studies (Supp. Note 2). Moreover, we showed that cell type sampling bias correction is possible within pseudodynamics16,17 (Supp. Note 2 sec. SN2.2.3).
We fit the continuous pseudodynamics model to a pseudotemporal ordering of scRNA-seq observations from four time points along mouse embryonic stem cell differentiation1,4 (Fig. 1d, online methods) without population size observations. Pseudodynamics was able to fit the samples along this transcriptomic trajectory and allowed imputation of unobserved time points (Fig. 1e,f, Supp. video 1). With lower regularization parameters, the model fit is better but has worse predictive power as shown by leave-one-time-point-out cross-validation (Fig. 1e,f).
Pseudodynamics extends previous models of T-cell maturation
T-cell maturation has been previously described as a sequence of transitions between cell states defined based on surface marker protein expression18. Here, we propose a trajectory model for T-cell maturation (Fig. 2), and show that pseudodynamics yields a comprehensive description of the T-cell maturation process. This includes quantitative analyses of the size of the proliferative burst after beta-selection, magnitude of selection on double-positive T-cells and position of beta-selection on the trajectory (Fig. 3,4).
Figure 2.
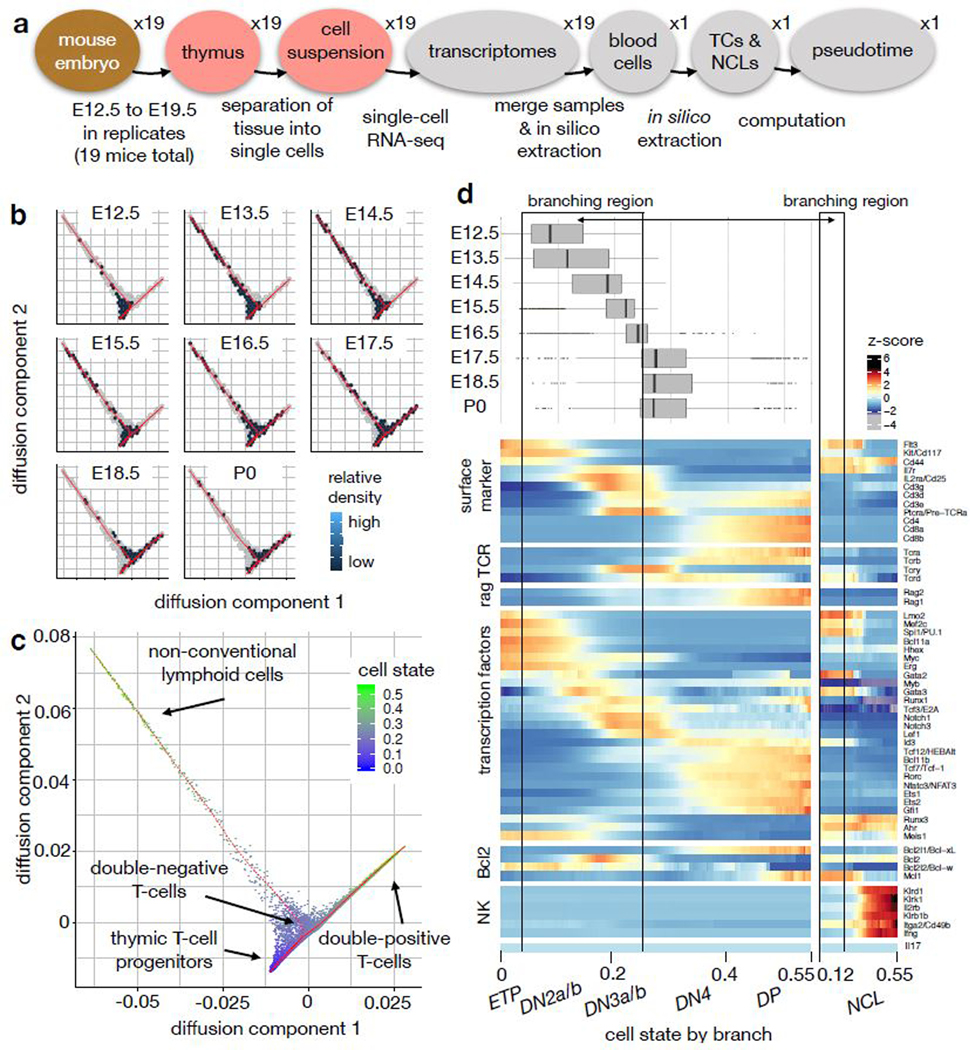
A trajectory model for T-cell maturation yields a description with higher resolution than a discretized description of the cell state space. (a) Design of the single-cell RNA-seq experiment. TCs: T-cells, NCLs: non-conventional lymphoid cells. (b) 2D density estimate in hexagonal bins of population by time point in the diffusion map. The density is encoded by the hexagon color (dark: low density, bright: high density, white: no cells observed, grey: non-zero density in the union of all samples). The diffusion map was computed based on TCs and NCLs from all time points. (c) Diffusion map based on TCs and NCLs only with cell state (diffusion pseudotime) superimposed. (d) Summary of the trajectory model for T-cell maturation. The boxplots show the sampled density of cells across cell state by time point. The boxplots are based on nE12.5=366 cells, nE13.5=1611 cells, nE14.5= 981, nE15.5= 974, nE16.5= 2492, nE17.5= 1908, nE18.5= 857, nP0= 890. The center of each boxplots is the sample median, the whiskers extend from the upper (lower) hinge to the largest (smallest) data point no further than 1.5 times the interquantile range from the upper (lower) hinge. The heatmap shows z-scores of sliding window expression estimates across cell state in the T-cell lineage (n=10079 cells) and the NCL lineage (n=793 cells). ETP: early thymic progenitors, DN2a/b, DN3a/b, DN4: double-negative stages, DP: double-positive stage.
Figure 3.
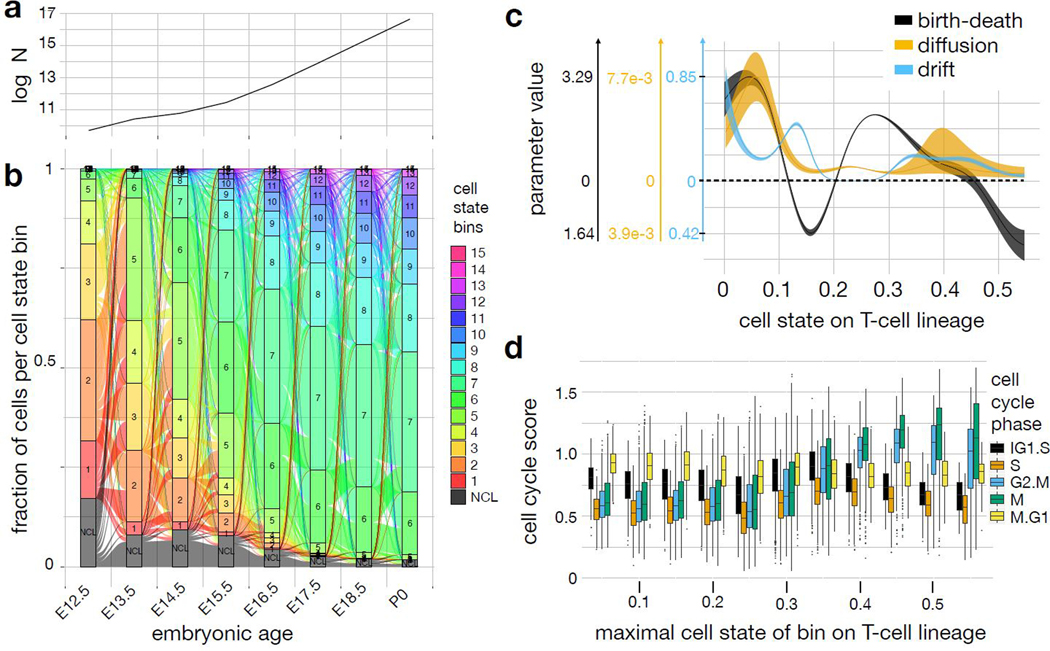
Pseudodynamics density and parameter fits extend the stationary description of T-cell maturation. (a) Simulated population size by time point. log N: log number of total cells. (b) Alluvial plot showing the flows between intervals of cell state bins across time. Each bar plot corresponds to one time point. The height of the boxes of each bin within a bar is proportional to the fraction of cells of all cells in that bin. The T-cell trajectory was divided into 15 equidistant bins in cell state (labelled 1–15), the non-conventional lymphoid cell branch was summarized to one bin (labelled NCL). The resulting 16 bins and their outflows are color coded. Outflow width represents the fraction of surviving cells transitioning into each bin at the old time point. Inflow width represents the contribution of each flow to the population size in a bin at the new time point. The alluvial plot is explained in Supp. Note 3 sec. SN3.2.2.7 and also provided as Supp. video 3. (c) Parameter estimates of pseudodynamics as function of cell state on the αβ-T-cell lineage with confidence intervals for regularization parameter rho=10. Shaded area: spline fit to 99% confidence interval boundary on spline nodes. (d) Transcriptome-based cell cycle state scores (online methods) per cell by cell state bin. The cell state was binned into intervals of length 0.05. The boxplots are based on nx cells observed per bin x (sorted ascending in cell state): n1=500, n2=930, n3=623, n4=1078, n5=3624, n6=2580, n7=646, n8=368, n9=276, n10=186, n11=61. The center of each boxplots is the sample median, the whiskers extend from the upper (lower) hinge to the largest (smallest) data point no further than 1.5 times the interquantile range from the upper (lower) hinge.
Figure 4.
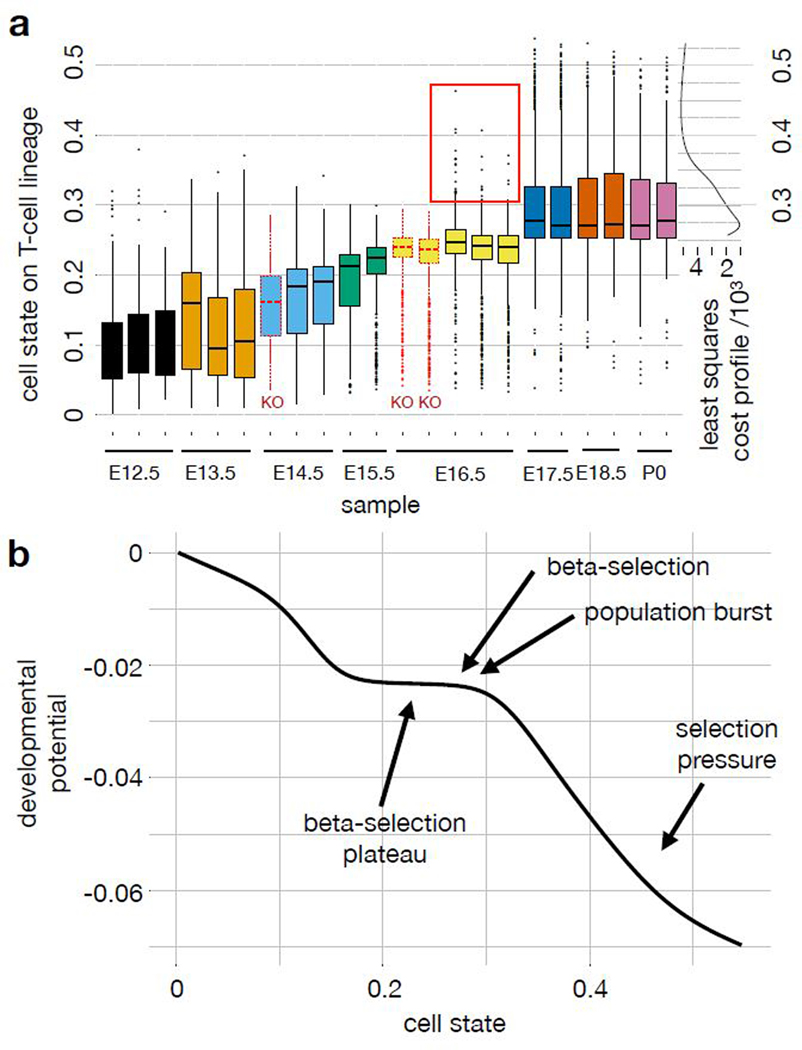
Pseudodynamics annotates a trajectory model with the position of a developmental checkpoint based on knock-out data, with the developmental potential and with developmental phases. (a) Boxplots of population density in cell state on T-cell lineage by sample with least squares cost profile of proposed beta-selection point as function of cell state based on the following number of cells per sample: n={215, 145, 55} at t=12.5; n={664, 603, 462} at t=13.5; n={436} at t=14.5 in the Rag2KO sample; n={487, 531} at t=14.5 in the wild-type samples; n={420, 560} at t=15.5; n={694, 896} at t=16.5 in the Rag1KO samples; n={784, 828, 865} at t=16.5 in the wild-type samples; n={929, 936} at t=17.5; n={429, 405} at t=18.5; n={378, 427} at t=19.5. Here, cell state coordinates are computed based on all replicates. Replicates are independent Drop-seq samples which are based on separate thymus samples, the two replicates at P0 are based on the two lobes of a single thymus. The red box denotes high cell state outliers at E16.5 only observed in wild-type. The cost profile shows the fit of the mutant data to the pseudodynamics parameterization which reflects the position of beta-selection in cell state space as a free parameter (online methods eq. 20). Color: time point, black solid outline: wild-type mice, red dotted outline: Rag1/2KO mice. The center of each boxplots is the sample median, the whiskers extend from the upper (lower) hinge to the largest (smallest) data point no further than 1.5 times the interquantile range from the upper (lower) hinge. (b) Approximation of developmental potential of the proposed model of T-cell maturation with other pseudodynamics output annotated. The developmental potential is the integral of the drift parameter on the T-cell lineage across cell state (online methods eq. 22).
Pseudotime inference identifies continuous states in T-cell maturation.
We constructed a cell state trajectory for T-cell maturation based on 19 scRNA-seq thymus samples (Drop-seq protocol1) from mouse embryos at eight different time points spanning 12.5 to 19.5 days after fertilization (E12.5-P0)19 (Fig. 2a,b). The data set contains clusters of putative myleloid and dendritic cells19 (Supp. Fig. 1-3), T-cells (Supp. Fig. 3,4) and innate lymphoid cells and γδ-T-cells (Supp. Fig. 5). The set of innate lymphoid cells and γδ-T-cells was previously grouped as non-conventional lymphocytes (NCLs)19. We filtered a branch of putative myeloid or dendritic cells from the set of all lymphocytes (Supp. Fig. 6a, online methods) to generate a data set consisting of T-cells and NCLs only (online methods). The diffusion map20 of this gated data set uncovers one branching region between the T-cell lineage and the NCL lineage (Fig. 2b,c, Supp. Fig. 6b). This branching is also found by partition-based graph abstraction7 (Supp. Fig. 1i) and has been discussed in detail recently19. The branching is consistent with the previous result that T-cells and NCLs are derived from the same progenitor in the thymus21,22,23. We used diffusion pseudotime as a one dimensional cell state coordinate with the tip cell of the progenitor branch as a root cell. The cell state therefore captures transcriptomic progression along the T-cell and the NCL lineages. We performed a linear partition in the branching region to distinguish the T-cell and the NCL trajectories (Supp. Fig. 6c). The expression profiles along the T-cell lineage recapitulate the previously established sequence of developmental stages from double negative to double positive cells which are defined based on surface marker proteins18 (Fig. 2d, Supp. Fig. 7a-c) and transcription factors18 (Supp. Fig. 7d,e). TCRα (Tcra) and TCRβ (Tcrb) expression together with surface marker expression suggest that the T-cell lineage trajectory in the diffusion map corresponds to the αβ-T-cell lineage (Fig. 2d, Supp. Fig. 7a, Supp. Fig. 8a,b). We found TCRγ (Tcrg)- and TCRδ (Tcrd)-expressing cells on this T-cell lineage before the upregulation of double-positive stage markers (Fig. 2d) which could correspond to γδ-T-cells or to temporary expression of TCRγ and TCRδ on the αβ-T-cell lineage. Expression profiles across the trajectory have a higher resolution than across previously used discrete cell stages and highlight the order of activity of gene regulatory modules of interest (Supp. Fig. 7d). Moreover, expression profiles along the trajectory can be used to suggest putative surface marker proteins for particular developmental stages (Supp. Fig. 7b,c).
Pseudodynamics identifies a proliferative burst and selection pressure during T-cell maturation.
We fit the continuous pseudodynamics model to the developmental tree with a single branching region between the T-cell and putative NCL lineages (Supp. Note 3 sec. SN3.2.2). Population size observations of the total number of lymphocytes per thymus were collected separately24. The model provides a continuous interpolation of the density across cell state in time and predicts the time-resolved flux of cells through the cell state space (Fig. 3a,b): The normalized distribution across bins reaches a steady state during the last three observed time points (Fig. 2d), while the overall population size is still increasing (Fig. 3a,b). We found the predictive power of pseudodynamics to impute missing time points (Supp. video 2) to depend on the sampling density (Supp. Fig. 9).
We extended the continuous cell state description of T-cell development by annotating the cell states with the parameter fits from the pseudodynamics model. The T-cell lineage drift parameter fit (Fig. 3c) uncovers two intervals of rapid transcriptomic development (high drift parameter) which peak at cell states 0.13 and 0.35. They correspond to transcriptomic states in which transcription factors are sequentially regulated, for example Notch1 and Notch3 in interval one, and Id3 and Rorc in interval two. This sequential regulation leads to directed transcriptomic development and to deterministic behavior of individual cells. Indeed, we observed global changes in transcription factor activity at these stages (Fig. 2d, Supp. Fig. 7e). Downregulation of Bcl2 and Mcl1, up-regulation of Bcl-xL (Bcl2l1)18 and double-positive stage markers (Fig. 2d, Supp. Fig. 8c) suggest that the developmental checkpoint is beta-selection and lies around cell state 0.23. Pseudodynamic parameter fits capture this checkpoint as an area of non-deterministic development with low drift and non-zero diffusion. This is a saddle point of the developmental potential function (Fig. 4b).
T-cells that pass beta-selection divide rapidly and then undergo positive and negative selection18. The cell state-specific division and death rates are captured as a high birth-death rate after the putative point of beta-selection, which then monotonically decreases with cell state and eventually becomes negative (Fig. 3c). The parameter trends are qualitatively similar across a range of regularization hyperparameters (Supp. Fig. 10). We fit a single-trajectory pseudodynamics model without branching to a pseudotemporal ordering inferred with monocle26 (Supp. Fig. 11, Supp. Fig. 12a-c, Supp. Note 3 sec. SN3.2.2.5). The inferred peak of the birth-death parameter at beta-selection and the negative interval during selection are robust with respect to the underlying state space (Supp. Fig. 12d-f, Supp. Note 3 sec. SN3.2.2.6). Transcriptome-derived M- and G2.M-phase scores (online methods) were increased in the cell states with negative birth-death rates (Fig. 3d). The transcriptome-derived scores reflect expansion of the cells that survive selection as only these surviving cells are observed in scRNA-seq. These scores do not capture the global population size effect of selection, which the pseudodynamics framework can recover.
Pseudodynamics can map developmental check-points based on knock-out data.
Rag1 and Rag2 knockout (KO) mice produce T-cells that cannot overcome beta-selection as they are unable to rearrange the T-cell receptor genes25. We took scRNA-seq samples from these knockout mice to validate the prediction of the position of beta-selection in cell state space. We fit a diffusion map to the union of all wild-type samples, an E14.5 Rag2KO at and two E16.5 Rag1KO samples (Supp. Fig. 13, online methods). The T-cell populations in the knock-out mice are significantly delayed in transcriptomic development along the αβ-T-cell trajectory compared to age-matched wild-type samples, and lack high cell state outliers at these time points (Fig. 4a, Supp. Fig. 14a,b). Beyond trends in cell state space, we also observed a reduced mean expression of double-positive stage markers in the knock-out animals compared to age-matched wild-type mice (Supp. Fig. 14c,d). We trained the pseudodynamics model on wild-type samples and adapted the inferred parameters to account for the arrest expected at beta-selection with the position of beta-selection as a free parameter (online methods). Then, we computed a least squares cost profile (Supp. Note 1 sec. SN1.6) of the mutant data across the beta-selection position (Fig. 4a). The resulting estimator of the beta-selection point at cell state 0.27 is in agreement with the Bcl-xL expression profile and lies at the end of the low drift parameter interval in cell state (Fig. 4b). We obtained similar beta-selection estimates for multiple regularization parameters (Supp. Fig. 14e,f). This probabilistic model for the position of beta-selection is better defined than a model based on marker gene changes and is not as sensitive to resampling as the maximal pseudotime coordinate in the knock-out cells would be.
Pseudodynamics attributes variation in proliferation rates of pancreatic β-cells across time to a state-dependent effect
Pancreatic β-cell proliferation in young mice was previously observed as the fraction of cycling cells in tissue sections and was shown to decrease with age26,27. Above, we showed that average cell state often changes during development (Fig. 1e, 2d). Hence, both state- and time-dependent birth parameters induce variation in proliferation rates across time. State-dependent birth parameters may occur if there are proliferative stages along a developmental trajectory, such as in the T-cell system. In contrast, cell state-invariant time-dependence of parameters requires extracellular regulators (Fig. 5a) if the cell state variable captures the full molecular state of the cell. To inform hypotheses about extracellular cues, it is important to distinguish the state-dependent from time-dependent regulation.
Figure 5.
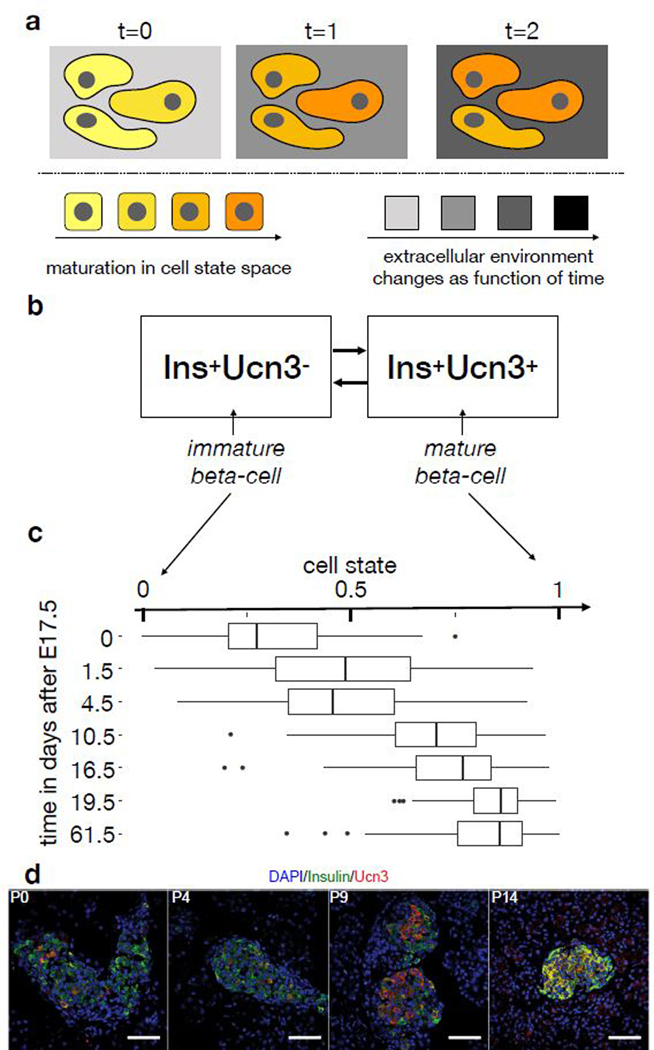
Cell state space discretization and time-dependence of models of pancreatic β-cell maturation and proliferation. (a) Concept of state- and time-dependent effects in vivo. Cell state-dependent effects (cell color) directly depend only on the molecular state of the cell. Time-dependent effects (background color) are invariant with respect to the cell state. Time-dependent effects depend directly only on extracellular regulators if the cell state variable captures the full molecular state of a cell. (b) Surface marker-based compartment model for β-cell maturation. Here, the presence of Ucn3 is used as a marker for maturation within the set of Ins+ cells. (c) Continuous trajectory model of β-celll maturation in cell state space. Here, pseudotime quantifies maturation as cell state in a continuous interpolation of the two states shown in (b). The boxplots show the distribution of single-cell RNA-seq samples across cell state space by sampled time point with nx cells per time point x: n0=61, n1.5=84, n4.5=88, n10.5=81, n16.5=59, n19.5=71, n61.5=131. The center of each boxplots is the sample median, the whiskers extend from the upper (lower) hinge to the largest (smallest) data point no further than 1.5 times the interquantile range from the upper (lower) hinge. (d) Maturation quantification of β-cells in pancreas sections via co-staining of DAPI, insulin (β-cells) and Ucn3 (β-cell maturation) at multiple time points (P0, P4, P9, P14). The fractions of cells in the two compartments shown in (b) can be directly counted in these sections. We quantified the proliferation of 1000–3300 β-cells in 3 animals per animal per time point. White scale bar: 50 μm.
State- and time-dependence of proliferation have been previously analyzed based on a two-stage compartment model of β-cell maturation with the marker Flattop (Fltp, Cfap126): The proliferation rate was measured as the fraction of cycling cells in the Fltp- (immature) and Fltp+ (mature) compartment at multiple time points and was found to vary with age in both compartments27. We modeled such a discrete state space using the pseudodynamics likelihood with a two-state ordinary differential equation model. For input data, we collected pancreatic β-cell population size measurements28 (Supp. Note 3 sec. SN3.2.3) and measured the distribution of the population across two maturation compartments based on the marker Ucn3 by counting cells in stained sections (Fig. 5d). Likelihood-based model selection between models with different parameterizations suggests a state- and time-dependence of the birth-death rate in this two-stage description (Supp Note 2 sec. SN2.2.4).
Time-dependence may arise not because of extrinsic signals but because discretizing the state space lowers resolution so that cell state alone can no longer explain proliferation. Accordingly, we also fit the continuous pseudodynamics model to a trajectory model based on scRNA-seq data26 (Fig. 5c). To distinguish state- and time-dependent proliferation, we fit the model with two different parameterizations of the birth-death rate, namely a function of the cell state only (state model) and a function of cell state and time (state-time model). We accounted for the time-dependence in the state-time model with a factor based on an additional spline of the time coordinate (Supp. Note 1 eq. SN1.3). Both models were able to fit the cell state density and the total population size well (Supp. Fig. 15). To validate predictions of the birth-death rates, we estimated the fraction of cycling β-cells using Ki67-stainings across multiple time points, and computed birth rates based on an estimate of the cell cycle length in pancreatic β-cells29 (Fig. 6a). We only detected subtly cleaved caspase-3 positive β-cells at P9 (Fig. 6b). Thus, the death rates are close to zero. This conclusion is supported by low apoptosis rates in pancreatic β-cells of neonatal rats observed in propidium iodide staining assays30. As the death rates are close to zero, the birth rate measurements approximate the birth-death rate. These measurements are independent of the estimates from the pseudodynamics model and confirm both magnitude and decreasing trend of the predicted birth-death rates (Fig. 6c). We performed model selection with a likelihood-ratio test between the state (null) model and state-time (alternative) model (Fig. 6d): The test did not reject the null hypothesis for any regularization. Therefore, the state-dependent proliferation model is sufficient to explain the observations.
Figure 6.
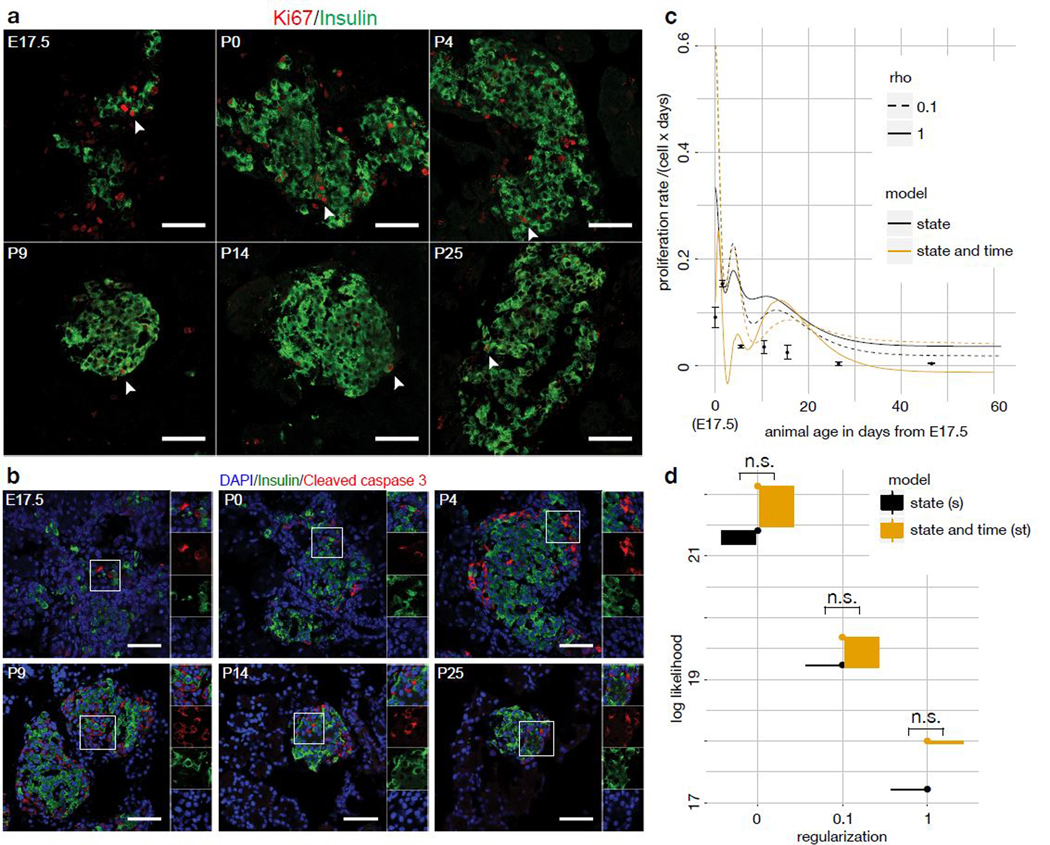
Likelihood-based model selection favors a state-dependent birth-death model over a state- and time-dependent model for β-cell maturation. (a,b) Proliferation (Ki67, a) and apoptosis (cleaved caspase-3, b) quantification of β-cells in pancreas sections via co-staining with DAPI and insulin (β-cells) at multiple time points (E17.5, P0, P4, P9, P14, P25). The fraction of proliferating and apoptotic β-cells can be directly counted, similarly to Fig. 5d. We observed the apoptosis and maturation status of 1900–3600 β-cells in 3 animals per time point. White scale bar: 50 μm. (c) Average birth-death rate per time point by model and observed proliferation rates by time point with one standard deviation around the mean as error bars. The birth-death rates at a given time point are computed as the convolution of the simulated population density at that time point with the parameter fit, both functions of cell state (Supp. Note 3 sec. SN3.2.3.3). The parameter fit is multiplied by the value of the time dependent birth-death function at that time point in the case of the time-dependent model. Two regularization hyper-parameters (rho) are shown for each model. (d) Likelihood of ten best fits by birth-death rate model for different regularization hyper-parameters. The interval shown is the interval between the best and the worst fit. Model selection was performed via a likelihood ratio test between of the best fit of each model (n.s.: not significant at threshold of 0.05).
The previously observed temporal variation of proliferation rates by cell state26,27 may be caused by the discretization of the β-cell maturation trajectory into two compartments. Pseudodynamics is able to overcome these discretization problems given a continuous cell state space. This yields a mechanistic hypothesis: The observed proliferation rates of pancreatic β-cells can be explained with a maturation-dependent proliferation model and there is no evidence for extracellular regulation.
Discussion
The order of cells along developmental trajectories can be inferred from large and high-dimensional single-cell data sets. However, temporal sample coordinates encode dynamic information which is not exploited in transcriptome-based embeddings. Secondly, population size measurements, that encode information on proliferation and death events, have been neglected in this context. We showed that a description solely based on transcriptomic data uncovers many known aspects of T-cell maturation in an unbiased fashion. We used pseudodynamics to integrate scRNA-seq and population size observations to infer the dynamics underlying T-cell maturation and found that this process is biphasic. One may think of this class of dynamic models as a step towards approximating the developmental potential previously termed “Waddington’s landscape”31. The inclusion of population size into the diffusion-advection framework allowed us to map selection pressure and population expansion on the cell state coordinate, which was not possible in previous dynamic models of cellular development in transcriptome space11,13. Moreover, we showed via model selection that the variation of proliferation across time in pancreatic β-cells is consistent with a state-dependent effect in a continuous cell state space.
Here, we chose a pseudotemporal ordering as the developmental progression space. Possible extensions include different cell state spaces, such as from coarsened graphs32, protein measurements, coordinates determined by lineage tracing33,34 or coordinates informed by RNA velocities35. Pseudodynamics bridges the concepts of pseudotemporal ordering and cell state dynamics in a probabilistic framework that adds layers of information with uncertainty quantification to a developmental lineage.
Online Methods
Ethical approval
The thymus study protocol was approved by The University of Massachusetts Medical School Institutional Animal Care and Use Committee (IACUC). The animal experiments for the pancreas study were carried out in compliance with the German Animal Protection Act, the guidelines of the Society of Laboratory Animals (GV-SOLAS) and Federation of Laboratory Animal Science Associations (FELASA).
Statistics
We used a log-likelihood ratio test to perform model selection between pseudodynamics model fits on the pancreatic β-cell data as explained in the main text. We used false-discovery rate-corrected p-values for differential expression based on a multivariate Wald test in Supp. Fig. 7. We used a one-sided Kolmogorov-Smirnov test to test the developmental delay of the T-cell population in the knockout versus the wild-type animals (Supp. Fig. 14a,b).
The continuous pseudodynamics model:
See also (Supp. Note 1 sec. SN1.3). Pseudodynamics describes the development of a population of single cells in time and cell state. We consider the number density of cells over a cell state coordinate at a time point . The integral of over an interval =[0,i], provides the number of cells with cell state in . Due to differentiation and growth dynamics this density changes during development. In pseudodynamics, the change in this density over time is modeled by a reaction-diffusion-advection partial differential equation (PDE) across the 1D transcriptomic progression (“cell state”) coordinate (eq. 1). The model includes directed movement of cells along the cell state coordinate (drift) with drift parameter , random fluctuations in cell state modeled by a diffusion term with a diffusion parameter , and population growth with growth rate . A detailed discussion of the influence of the parameters on the model behavior can be found in the Supp. Note 1 sec. SN1.3.3. All rates can depend on cell state and time . The parameters are parameterized as natural cubic splines in cell state or time.
| (1) |
Boundary conditions for pseudodynamics should be chosen to correspond to the biological setting. For the applications in this work, we assumed no-flux boundary conditions at both boundaries of the 1D domain. To improve numerical stability, the drift is decreased to zero on the right hand side:
| (2) |
| (3) |
Accordingly, one can formulate a pseudodynamics model for a process with one branching region as a system of two coupled partial differential equations. The first PDE describes the evolution of the population along the main trajectory from a progenitor state to a chosen terminal cell fate (eq. 4) and the second equation describes the evolution along the side branch starting at the branching region (eq. 5) to the alternative terminal cell fate. Both equations are coupled at the branching region in which cells can switch between main and side branch with propensities for change from branch to branch :
| (4) |
| (5) |
Here, the function defines a branching region in state space: is one inside the branching region and zero outside of it. On each branch we assume no-flux boundary conditions. Analogous to (3), the drift parameter is decreased to zero at each right boundary:
| (6) |
| (7) |
| (8) |
| (9) |
The population size at a time point is computed as the sum of the integrals of the corresponding density with respect to cell state summed over branches ,
| (10) |
The initial conditions for the system can be derived from the experimental data at the initial time point, i.e., the population size and the initial distribution of cells are initialized as the (mean) observed population size and cell distribution at the first measurement time point. In principle, it is also possible to include these as additional parameters.
Likelihood, regularization and parameter estimation
See also (Supp. Note 1 sec. SN1.5). The parameters of the pseudodynamics model are estimated from a given dataset using a maximum likelihood estimation. The likelihood (eq. 11) accounts for the cell state distribution of the population, the population size, and the proportion of cells on each branch. The data consist of samples b,t, of cell state observations of single cells in a population at time points cdf and in branches , a set of mean population sizes observed at time points N, and of the standard error in the population size observations per time point σtN. From the cell state sample b,t the empirical cumulative density function (ECDF) at cell state , time point and branch , as well as the fraction of cells observed on a branch at time , b,t , and the corresponding standard deviation can be computed. Using these data the log-likelihood can be formulated as:
| (11) |
where is the set of parameters of the pseudodynamics model. Note that the likelihood term on the fraction of cells per branch does not need to be evaluated on one branch as the proportions across all branches sum to one. For numerical reasons, we minimize the negative log-likelihood and add regularization terms on the parameter splines with regularization parameter ρ to counteract overfitting. This yields the objective function:
| (12) |
where bD, b and bg are the number of nodes of the natural cubic splines and D, v, and g the associated parameter vectors on each branch out of branches. Similarly, time-dependent parameterizations can be regularized (Supp. Note 1 sec. SN1.5.3). The regularization parameter ρ can be chosen via cross-validation (Supp. Note 1 sec. SN1.5.3.1).
The likelihood of observing the cell state distribution for given parameters is evaluated based on the area between the ECDF of the observed data and simulated cumulative density function. In the case of branching, this is done per branch. The simulated cumulative density function is:
| (13) |
where b is the simulated density on branch . We assumed that area between the curves (A) is normally distributed with standard deviation σA() and mean μA() estimated per time point on the area between the curves of the ECDF of each experimental replicate to the ECDF of the union of all cells (t) of a given time point , yielding the likelihood function
| (14) |
For the population size, we assumed normally distributed errors. We estimated the standard deviation of the measurement noise per time point as the standard error of the population size observation at that time point tN. Accordingly, the likelihood for the population size observations is a normal distribution:
| (15) |
which has the square of the standard error of the population size observations as variance and which has the integral of the simulated density over cell state as a mean parameter (eq. 10).
Implementation of the parameter estimation of the continuous model
See also (Supp. Note 1 sec. SN1.5, Supp. Note 3). The estimation of the parameters of the pseudodynamics models is non-trivial as the PDE has to be forward simulated for each likelihood evaluation. The numerical implementation of the forward simulation of the pseudodynamics model was based on the method of lines. The model was discretized in cell state using finite volumes. For the solution of the resulting system of ordinary differential equations we employed the Sundials CVODE suite36 and AMICI37 (https://github.com/ICB-DCM/AMICI/) as Matlab interface. For the optimization, we used a multi-start approach (with gradient information) that is implemented in the Matlab toolbox PESTO38 (https://github.com/ICB-DCM/PESTO). We supplied the optimizer with the analytical gradient as this increases efficiency in comparison to gradients computed using finite differences39. Uncertainty analysis and computation of confidence intervals was performed using profile likelihoods (also implemented in PESTO) or asymptotic confidence intervals. To determine the regularization parameter, we performed leave-one-out cross validation successively leaving out the data corresponding to a time point and estimating the parameters for the reduced data set. For these parameters we were able to evaluate the likelihood on the whole data set and compare prediction accuracy (Supp. Note 1 sec. SN1.5.3.1).
Estimation of the cell state coordinate of beta-selection with pseudodynamics
(See also Supp. Note 1 sec. SN1.6). To compute a least squares cost profile of the point of beta-selection across the cell state coordinate , we calibrated the pseudodynamics model on the wild-type data subset of the combined wild-type and knock-out sample diffusion pseudotime model. To estimate the point of beta-selection, *, we considered the discrepancy between the calibrated pseudodynamics model that was modified to include developmental arrest at some time point ’ and the mutant data. The estimator for the point of beta-selection was then chosen as the arrest point that minimizes this discrepancy (eq. 17). The model was adjusted for developmental arrest at a proposed cell state ’ by setting the drift parameter at the cell state coordinates beyond the proposed point of arrest to zero (eq. 18,19) and the growth parameter to -3, a lower bound of estimated birth-death parameters. We computed a least squares cost profile of ’ between the smallest cell state grid point not observed at the initial time point and the highest cell state observed on the T-cell lineage by computing the fit of the model with arrest at ’ to the knock-out data for every ’ in that range. As no replicates were available, we used a least squares objective function to evaluate the fit (eq. 20).
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
where 𝜃mut contains the adjusted parameters as described in eq. 18,19 and the wild-type drift parameter. We trained the pseudodynamics model and computed the least squares cost profile based on cell state coordinates derived from diffusion pseudotime ordering computed on the union of all wild-type and mutant cells. This diffusion pseudotime coordinate (WT+KO) is different from the diffusion pseudotime computed only on the set of wild-type cells (WT). We mapped the cell state WT+KO back to WT to interpret the beta-selection point in the context of the T-cell maturation description established based on the wild-type data (Fig. 2). We note that WT+KO is a monotonously increasing function of WT. Accordingly, we performed the mapping with a smooth function class (degree 5 natural cubic splines) (Supp. Fig. 14f).
Computation of the developmental potential function
We assume that the gradient of the developmental potential function with respect to cell state can be approximated by the drift parameter estimate of the pseudodynamics model (eq. 21). Accordingly, one can approximate as the integral of the negative drift parameter trajectory with respect to cell state (eq. 22).
| (21) |
| (22) |
We approximated the integral (eq. 22) with Euler’s method by setting (0) = 0 and by using the negative drift parameter fit to do stepwise finite difference approximation of in (eq. 23), where Δ is the grid spacing of the drift parameter fit in cell state.
| (23) |
We note that this approach to approximate the developmental potential function only yields approximations of along the observed developmental trajectories.
Generation of Drop-seq dataset of T cell development
Detailed description of isolation of thymus resident cells and generation of Drop-seq datasets are provided in19. Briefly, C57BL6/J and Rag1 knockout mice were obtained from The Jackson Laboratory, and thymus tissue was isolated from timed pregnant mice. Live cells were enriched using FACS and immediately processed for Drop-seq analysis. Drop-seq was performed following the online protocol provided from the McCarroll lab at Harvard Medical School (Drop-seq Laboratory Protocol version 3.1; http://mccarrolllab.com/dropseq/).
Drop-seq data processing and analysis
Drop-seq libraries were sequenced at paired-end (20–50) on a Nextseq500. Alignment was done as described in Supp. Note 3 sec. SN3.2.2.5. We rescaled raw molecule counts of each cell to sum to 10,000, and we transformed the resulting values via X→log2(1+X) . The number 10,000 was chosen by rounding the median unique molecular identifier (UMI) count up to the nearest power of 10.
T-cell receptor alignment was improved by augmenting the reference genome. The augmented reference contained an artificial TCR contig in which known constant, joining, and variable regions of the TCR were concatenated. TCR regions were extracted from TRACER40 annotation files. The boundaries were annotated as splice junctions, allowing the extensive spliced alignment capabilities of STAR to position reads, despite TCR rearrangement. Reads aligning to the TCR contig were subsetted, and transcript quantification was performed as above. We made two alterations: in place of MIN_NUM_GENES_PER_CELL=1000; we used cell barcodes established using the conventional alignment pipeline, and we specified READ_MQ=1. TCR realignment was performed after the initial analysis, and this did not affect the set of cells classified as thymic hematopoietic cells.
In silico isolation of wild-type thymic hematopoietic cells E12.5-E16.5
Quality control and thymic hematopoietic isolation were conducted using the R language (https://www.R-project.org/) and the package Seurat41 (http://www.satijalab.org/seurat). The main goals for quality control were to verify exclusion of female embryos; to exclude empty droplets; and to deplete cell doublets. Only male embryos were analyzed to avoid biological confounding by sex. To remove empty droplets, we excluded any cell expressing less than 1000 genes. We also excluded any gene expressed in less than 10 cells. Doublet depletion was carried out, followed by isolation of the thymic hematopoietic cells. Both steps used unsupervised machine learning.
For doublet depletion and thymic hematopoietic cell isolation, we used two pipelines that differ only in their final steps. Each began by compensating for variation due to the cell cycle. For each of five cell cycle phases (IG1.S, S, G2.M, M, M.G1), scores were computed by averaging expression within each cell over a set of genes found in the second workbook of table S2 from a reference42. Seuraťs RegressOut function was used to replace expression levels with standardized residuals from linear regressions (one per gene). In each regression, observations are cells; the response variable is log-normalized expression; and the covariates are the five cell cycle scores. After cell-cycle correction, we enriched for informative genes by applying Seuraťs MeanVarPlot function (with x.low.cutoff = 0.1 and y.cutoff = 0.5). Principal components analysis (PCA) was run on the selected genes using as features the normalized residuals from RegressOut.
The first difference in the two pipelines occurs after PCA. For doublet removal, the top 20 principal components (PCs) were used as input to Barnes-Hut t-Stochastic Neighbor Embedding (tSNE). DBSCAN was used to isolate and remove outlying cells and clusters showing markers from multiple cell types. In DBSCAN, the t-SNE embedding was used as input, and the parameters were 1.1 (neighborhood size) and 5 (minPts). In total, 52 putative doublets and 80 outlying cells were excluded from downstream analyzes.
For isolation of thymic hematopoietic cells, the entire process up to PCA was repeated after doublet depletion. Clustering was then carried out using Seuraťs FindClusters function, which applies a variant of the Louvain algorithm43 to a shared-nearest-neighbor graph constructed in the principal subspace (20 PCs, resolution 0.5). Results were visualized as before via tSNE. Six contiguous clusters were manually labeled as thymic hematopoietic cells based on expression of known markers. Different parameter choices for variable gene selection and for the number of PCs were explored and results remained qualitatively consistent.
In silico isolation of E17.5-P0 wild-type thymic hematopoietic cells and E14.5 Rag2 knockout thymic hematopoietic cells
The thymic hematopoietic cells from these later time points were aligned following the same procedure. Data were filtered for at least 1000 genes per cell, but the requirement was relaxed to at least 3 cells per gene due to the smaller total number of cells. No doublet removal was attempted. Thymic hematopoietic cell isolation was performed via the pipeline described above using x.low.cutoff = 0.1 and y.cutoff = 1.2 for gene selection, 25 PCs, and the Louvain algorithm with resolution 0.5. Two clusters lacked Ptprc and expressed thymic stromal markers, and these were manually removed. Different parameter choices were explored for variable gene selection and for the number of PCs; relabeled results remained relatively robust. Wild-type cells were processed together and Rag2 knockout cells were processed separately.
In silico isolation of E16.5 Rag1 knockout thymic hematopoietic cells
For whole-thymus samples from Rag1 knockout embryos, the same alignment, quantification, and quality control steps were performed (>1000 genes per cell, >3 cells per gene). Cells were classified by k-nearest-neighbors (k = 25) after projection into a 20-dimensional principal subspace, with both PCA and classifier trained on the E12.5-E16.5 wild-type data. Cells classified into any of the six thymic hematopoietic cell clusters were retained for analysis.
Preparation of pseudodynamics input from thymic hematopoietic cell transcriptomes
See also (Supp. Note 3 sec. SN3.2.2) and (Supp. data 1.2, 1.3). We fit diffusion pseudotime with one branching point to the union of all lymphocytes from all samples with scanpy44 (k = 100, knn = False) (diffusion map A). We classified the resulting four groups of cells based on markers genes as progenitors/intermediate cells, T-cells, non-conventional lymphoid cells (NCL) and putative myeloid and dendritic cells (Supp. Fig. 3–5). We discarded the putative myeloid and dendritic cell group to obtain a data set that contains a single branching between the αβ-T-cell lineage and the NCL lineage and fit a new pseudotemporal ordering on this data set with scanpy (k = 100, knn = False) (diffusion map B). We defined the allocations of cells to branches and the branching region in diffusion map B based on pseudotime coordinates and diffusion component 1 and 2 coordinates. We repeated the workflow from diffusion map A to diffusion map B separately for the wild-type only and the wild-type with knock-out samples data sets. We discarded the putative myeloid and dendritic cell group and the NCL group from diffusion map A to obtain a data set that contains no branching and only the T-cell lineage (used for monocle2-based cell state coordinates6).
Preparation of pseudodynamics input from pancreatic β-cell transcriptomes
See also (Supp. Note 3 sec. SN3.2.3) and (Supp. data 1.4). We fit diffusion pseudotime with no branching points to all pancreatic β-cells from all time points with scanpy44 (k = 30, knn = False). We obtained total β-cell population size measurements for mice at ages P10 and P45 (via extrapolation from counts in cross-sections) from Herbach et al.28. We generated rough estimates in the same fashion for E17.5, P4, P9 and P14. We extrapolated our P9 and P14 observations with a linear model to P10 and used the relative difference to the P10 observation from Herbach et al. as a scaling factor which we applied to all of our observations. We note that such cell counting is very laborious and we therefore restricted our data collection to relative counts which we scaled to the accurate data of Herbach et al.. The state-dependent model parameter s as a function of time s, shown in Fig. 6c, is the integral over the product of the density at a given time point, and the birth-death parameter spline with respect to cell state s.
| (24) |
Mice for pancreas study
For pancreas dissection C57BL6/J mice were sacrificed at each of the tested developmental stages.
Cryosections of pancreas
The dissected pancreas was fixed in 4% paraformaldehyde (PFA) for 2–24 hours at 4 °C. After fixation, the tissues were cryoprotected in a sequential gradient of 10% and 30% sucrose in PBS (1–2 hours each at room temperature). Next, the pancreas was incubated in 30% sucrose and tissue embedding medium (Leica) (1:1) at 4 ºC overnight (O/N). The pancreas was orientated in an embedding mold, frozen using dry ice and stored at -80 °C. Cryosections were cut into 20 μm sections using a cryostat (Leica), mounted on a glass slide (Thermo Fisher Scientific) and dried for 10 min at RT before use or storage at -20 °C.
Immunostaining of pancreatic cryosections
Cryosections were rehydrated by 3 times washing with 1X PBS, permeabilized with 0.2% Triton X-100 in H2O for 15 min and blocked in blocking solution (PBS, 0.1% Tween-20, 1% donkey serum, 5% FCS) for 1–2 hrs. Afterwards, the sections were incubated with primary antibody in blocking solution at 4 °C overnight. Prior to the incubation with secondary antibodies in blocking solution the sections were rinsed 3 times and washed 3 times with 1X PBS. Finally after incubated for 3–5 hrs with the secondary antibodies, the sections were stained for DAPI (1:500 in 1X PBS) for 30 min, rinsed and washed 3 times with 1X PBS and mounted by Elvanol. Confocal pictures were taken using a Leica DMI 6000 microscope and LAS AF software. For all quantifications, the sections were ≥ 100 μm apart. The primary and secondary antibodies used are listed Reporting Summary.
Microscopy & analysis of pancreatic cryosections
The acquired images were analyzed using Leica LAS AF software and/or Image J software.
Supplementary Material
ACKNOWLEDGEMENTS
We would like to express our gratitude towards Ping Xu and Kashfia Neherin for mouse husbandry and tissue preparation. F.J.T. acknowledges financial support by the Graduate School QBM, the German Research Foundation (DFG) within the Collaborative Research Centre 1243, Subproject A17, by the Helmholtz Association (Incubator grant sparse2big, ZT-I-0007) and by the Chan Zuckerberg Initiative DAF (advised fund of Silicon Valley Community Foundation, 182835). R.M. acknowledges financial support by the Leona M. and Harry B. Helmsley Charitable Trust (2015PG-T1D035), a Charles H. Hood Foundation Child Health Research Award, the Glass Charitable Foundation and the National Institutes of Health (1DP3DK111898, R01 AI132963, UC4 DK104218). J.H. acknowledges financial support by the German Research Foundation (DFG) (HA 7376/1–1) and the German Federal Ministry of Education and Research (BMBF) within the SYS-Stomach project (01ZX1310B). H.L. acknowledges financial support by the Helmholtz Society and German Center for Diabetes Research (DZD e.V.). D.S.F. acknowledges financial support by a German research foundation (DFG) fellowship through the Graduate School of Quantitative Biosciences Munich (QBM) (GSC 1006) and by the Joachim Herz Stiftung.
Footnotes
CONFLICT OF INTEREST
The authors declare no competing interests.
Data availability
The Rag2 knockout Drop-seq data have been deposited in GEO under the accession number GSE126579. The remaining thymic hematopoietic cell data are available from GEO under the accession number GSE107910.
Code availability
The pseudodynamics model code and the presented examples are available through GitHub (https://github.com/theislab/pseudodynamics) and in the Supp. Code.
Main references
- 1.Klein AM et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 161, 1187–1201 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Taniguchi K, Kajiyama T & Kambara H. Quantitative analysis of gene expression in a single cell by qPCR. Nat. Methods 6, 503–506 (2009). [DOI] [PubMed] [Google Scholar]
- 3.Bandura DR et al. Mass cytometry: technique for real time single cell multitarget immunoassay based on inductively coupled plasma time-of-flight mass spectrometry. Anal. Chem. 81, 6813–6822 (2009). [DOI] [PubMed] [Google Scholar]
- 4.Haghverdi L, Büttner M, Wolf FA, Buettner F & Theis FJ Diffusion pseudotime robustly reconstructs lineage branching. Nat. Methods 13, 845–848 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Trapnell C et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 32, 381–386 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Qiu X et al. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods 14, 979–982 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wolf FA et al. Graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. bioRxiv (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Saelens W, Cannoodt R, Todorov H & Saeys Y A comparison of single-cell trajectory inference methods: towards more accurate and robust tools. (2018). doi: 10.1101/276907 [DOI] [PubMed] [Google Scholar]
- 9.Kafri R et al. Dynamics extracted from fixed cells reveal feedback linking cell growth to cell cycle. Nature 494, 480–483 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kuritz K, Stöhr D, Pollak N & Allgöwer F. On the relationship between cell cycle analysis with ergodic principles and age-structured cell population models. J. Theor. Biol. 414, 91–102 (2017). [DOI] [PubMed] [Google Scholar]
- 11.Weinreb C, Wolock S, Tusi BK, Socolovsky M & Klein AM Fundamental limits on dynamic inference from single-cell snapshots. Proc. Natl. Acad. Sci. U. S. A. 115, E2467–E2476 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schiebinger G et al. Optimal-Transport Analysis of Single-Cell Gene Expression Identifies Developmental Trajectories in Reprogramming. Cell 176, 928–943.e22 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hashimoto T, Gifford D & Jaakkola T Learning Population-Level Diffusions with Generative RNNs. in International Conference on Machine Learning 2417–2426 (2016). [Google Scholar]
- 14.Buchholz VR et al. Disparate individual fates compose robust CD8+ T cell immunity. Science 340, 630–635 (2013). [DOI] [PubMed] [Google Scholar]
- 15.Cho H et al. Modelling acute myeloid leukaemia in a continuum of differentiation states. Letters in Biomathematics 5, S69–S98 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Segerstolpe Å et al. Single-Cell Transcriptome Profiling of Human Pancreatic Islets in Health and Type 2 Diabetes. Cell Metab. 24, 593–607 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Haber AL et al. A single-cell survey of the small intestinal epithelium. Nature 551, 333–339 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yui MA & Rothenberg EV Developmental gene networks: a triathlon on the course to T cell identity. Nat. Rev. Immunol. 14, 529–545 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kernfeld EM et al. A Single-Cell Transcriptomic Atlas of Thymus Organogenesis Resolves Cell Types and Developmental Maturation. Immunity (2018). doi: 10.1016/j.immuni.2018.04.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Haghverdi L, Buettner F & Theis FJ Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics 31, 2989–2998 (2015). [DOI] [PubMed] [Google Scholar]
- 21.Vosshenrich CAJ et al. A thymic pathway of mouse natural killer cell development characterized by expression of GATA-3 and CD127. Nat. Immunol. 7, 1217–1224 (2006). [DOI] [PubMed] [Google Scholar]
- 22.Ribeiro VSG et al. Cutting edge: Thymic NK cells develop independently from T cell precursors. J. Immunol. 185, 4993–4997 (2010). [DOI] [PubMed] [Google Scholar]
- 23.Tang Y et al. Emergence of NK-cell progenitors and functionally competent NK-cell lineage subsets in the early mouse embryo. Blood 120, 63–75 (2012). [DOI] [PubMed] [Google Scholar]
- 24.Cook AM Proliferation and lineage potential in fetal thymic epithelial progenitor cells. (2010). [Google Scholar]
- 25.Germain RN T-cell development and the CD4-CD8 lineage decision. Nat. Rev. Immunol. 2, 309–322 (2002). [DOI] [PubMed] [Google Scholar]
- 26.Qiu W-L et al. Deciphering Pancreatic Islet β Cell and α Cell Maturation Pathways and Characteristic Features at the Single-Cell Level. Cell Metab. 25, 1194–1205.e4 (2017). [DOI] [PubMed] [Google Scholar]
- 27.Bader E et al. Identification of proliferative and mature β-cells in the islets of Langerhans. Nature 535, 430–434 (2016). [DOI] [PubMed] [Google Scholar]
- 28.Herbach N, Bergmayr M, Göke B, Wolf E & Wanke R. Postnatal Development of Numbers and Mean Sizes of Pancreatic Islets and Beta-Cells in Healthy Mice and GIPRdn Transgenic Diabetic Mice. PLoS One 6, e22814 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hija A et al. G0-G1 Transition and the Restriction Point in Pancreatic β-Cells In Vivo. Diabetes 63, 578 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Scaglia L, Cahill CJ, Finegood DT & Bonner-Weir S. Apoptosis participates in the remodeling of the endocrine pancreas in the neonatal rat. Endocrinology 138, 1736–1741 (1997). [DOI] [PubMed] [Google Scholar]
- 31.Waddington CH Organisers and Genes by C. H. Waddington. (1940). [Google Scholar]
- 32.Wolf FA et al. Graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. (2017). doi: 10.1101/208819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.McKenna A et al. Whole-organism lineage tracing by combinatorial and cumulative genome editing. Science 353, aaf7907 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Spanjaard B et al. Simultaneous lineage tracing and cell-type identification using CRISPR–Cas9-induced genetic scars. Nat. Biotechnol. 36, 469 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.La Manno G et al. RNA velocity of single cells. Nature 560, 494–498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Methods references
- 36.Cohen SD, Hindmarsh AC & Dubois PF CVODE, a stiff/nonstiff ODE solver in C. Computers in physics (1996). [Google Scholar]
- 37.Fröhlich F, Theis FJ, Rädler JO & Hasenauer J. Parameter estimation for dynamical systems with discrete events and logical operations. Bioinformatics 33, 1049–1056 (2017). [DOI] [PubMed] [Google Scholar]
- 38.Stapor P et al. PESTO: Parameter EStimation TOolbox. Bioinformatics 34, 705–707 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Raue A et al. Lessons learned from quantitative dynamical modeling in systems biology. PLoS One 8, e74335 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Stubbington MJT et al. T cell fate and clonality inference from single-cell transcriptomes. Nat. Methods 13, 329–332 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Satija R, Farrell JA, Gennert D, Schier AF & Regev A. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 33, 495–502 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Macosko EZ et al. Highly Parallel Genome-wide Expression Profiling of Individual Cells Using Nanoliter Droplets. Cell 161, 1202–1214 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Waltman L & van Eck NJ A smart local moving algorithm for large-scale modularity-based community detection. Eur. Phys. J. B 86, 471 (2013). [Google Scholar]
- 44.Wolf FA, Angerer P & Theis FJ SCANPY: large-scale single-cell gene expression data analysis. Genome Biol. 19, 15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


