Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV₃Sb₅

The anomalous Hall effect soars when Dirac quasiparticles meet frustrated magnetism.

Abstract

The anomalous Hall effect (AHE) is one of the most fundamental phenomena in physics. In the highly conductive regime, ferromagnetic metals have been the focus of past research. Here, we report a giant extrinsic AHE in KV₃Sb₅, an exfoliable, highly conductive semimetal with Dirac quasiparticles and a vanadium Kagome net. Even without report of long range magnetic order, the anomalous Hall conductivity reaches 15,507 Ω⁻¹ cm⁻¹ with an anomalous Hall ratio of ≈ 1.8%; an order of magnitude larger than Fe. Defying theoretical expectations, KV₃Sb₅ shows enhanced skew scattering that scales quadratically, not linearly, with the longitudinal conductivity, possibly arising from the combination of highly conductive Dirac quasiparticles with a frustrated magnetic sublattice. This allows the possibility of reaching an anomalous Hall angle of 90° in metals. This observation raises fundamental questions about AHEs and opens new frontiers for AHE and spin Hall effect exploration, particularly in metallic frustrated magnets.

INTRODUCTION

The electronic anomalous Hall effect (AHE), where charge carriers acquire a velocity component orthogonal to an applied electric field without an external magnetic field, is one of the most fundamental and widely studied phenomena in physics. Since its discovery more than a century ago, the AHE has been extensively studied both theoretically and experimentally (1). Historically, spontaneous AHEs have been explored in materials with internally broken time-reversal symmetry (TRS), due to ferro- or ferrimagnetic ordering (2–5). Recently, there has been a surge of interest in the exploration of nonspontaneous AHEs, which require the application of an external magnetic field to break the TRS. The resulting Hall response is not commensurate with the magnitude of the applied field, thus making it distinct from the ordinary Hall effect (OHE). Such a nonspontaneous AHE has been seen in nonmagnetic ZrTe₅ (6) and in dilute magnetically doped Kondo systems (7). Large AHEs can arise from a variety of effects, and a particularly interesting limit to explore is when the anomalous Hall angle (AHA) approaches 90°; one characteristic of the intrinsic quantum AHE observed in TRS breaking topological insulators (8–10). In these insulators, the anomalous Hall conductivity (σ_AHE) becomes modulated by the conductance quantum, while the longitudinal conductivity (σ_xx) approaches zero, resulting in the AHA (tan⁻¹($\frac{{\sigma }_{\text{AHE}}}{{\sigma }_{\text{xx}}}$))approaching 90° (11, 12).

The AHE can be broadly divided into two categories: intrinsic and extrinsic (1). The intrinsic AHE is governed by the electronic structure of a material that causes an electron to acquire a transverse momentum as it travels in-between scattering events (2, 13–15). This is the dominant mechanism in topological materials like Co₃Sn₂S₂ and Co₂MnGa, which have AHEs on the order of 1000 Ω⁻¹cm⁻¹ (16–18). The extrinsic AHEs, on the other hand, are dependent on electrons scattering off of sudden changes in the periodic potential of a crystal, caused by structural defects or chemical and magnetic impurities (3, 4, 19). They can be further categorized into the “dirty regime” (low conductivity, small scattering time, τ) (19, 20) and the “clean regime” (high conductivity, large scattering time) (3, 4), which is dominated by skew scattering and is the focus of this work.

Much effort has been dedicated to understanding the different mechanisms that can give rise to skew scattering AHEs, as illustrated in Fig. 1A. In clean ferromagnets with spontaneously ordered magnetic moments, such as Fe, an AHE can be induced by electrons deflecting transversely by nonmagnetic impurities (21–23). In paramagnetic systems, such as ZnO/MnZnO, spin-dependent electron scattering on localized magnetic moments can give rise to an AHE (24). Recently, scattering off of spin clusters, local groups of coupled spins, has been proposed: tilted magnetic clusters, like magnetic atoms in a Kagome net, can generate an enhanced skew scattering potential (25) and thus a large AHE. Triangular materials, like those often explored as geometrically frustrated magnets and spin liquid candidates, as well as other types of cluster magnets, are particularly likely to exhibit this type of AHE (25–28). However, the necessity of a combination of high conductivity in a spin-cluster lattice has contributed to its lack of experimental observation.

Fig. 1. Skew scattering mechanisms, basic ARPES, and transport characteristics of KV₃Sb₅.

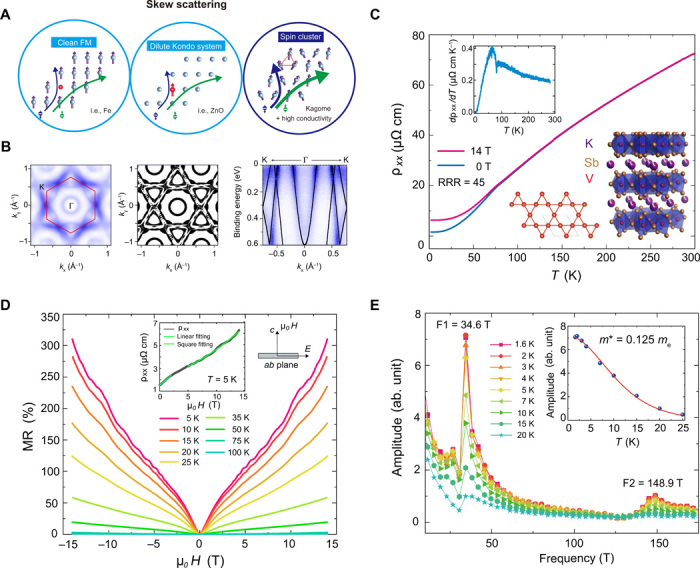
(A) Schematic representation of three different skew scattering mechanisms, including clean ferromagnetic (FM) model, Kondo model, and spin cluster model. (B) Left: Experimentally measured Fermi surface of KV₃Sb₅. The hexagonal Brillouin zone is marked by the red line. Middle: DFT-calculated Fermi surface. Right: Band dispersion along K-Γ-K direction overlayed with the ARPES measurement. (C) Temperature dependence of longitudinal resistivity in zero field and in a field of 14 T. The inset on the top left shows the temperature dependence of differential longitudinal resistivity in zero field, in which a kink at 80 K corresponds to the magnetic transition. The inset on the bottom right shows the crystal structure of KV₃Sb₅ and its Kagome lattice. The Residual Resistivity Ratio (RRR) of the sample is 45. (D) MR measured at various temperatures, exhibiting linear field dependence below 3 T and quadratic field dependence at higher field (inset). (E) Extracted FFT frequency showing two identifiable periods of 34.6 and 148.9 T. The inset shows the Lifshitz-Kosevich fit of the 34.6 T orbit with an extracted effective mass of 0.125 m_e.

One avenue for realizing this is by introducing electronic topology into magnetically frustrated systems. The electronic topology can generate a spin-orbit field that couples to magnetic fluctuations (for example, in a tiled spin cluster lattice), which can act analogously to impurity centers, a mechanism that is fundamentally distinct from the Berry phase mechanisms (25). This is advantageous for allowing cleaner crystals, without chemical disorder or atomic impurities, which have very high conductivities. The coupling of magnetic fluctuations and Dirac quasiparticles generates a novel field of study, previously unconsidered, for skew scattering. Topological frustrated magnets, which can host both magnetic fluctuations and Dirac quasiparticles, are highly sought after class of compounds. Metallic materials with frustrated magnetic sublattices, particularly when combined with relativistic carriers, are uncommon, and investigation of their Hall effects has been sparsely performed. For example, the metallic spin liquids, Pr₂Ir₂O₇ and LiV₂O₄ are a Luttinger semimetal and heavy-fermion metal, respectively; neither of these has Dirac band crossings or low-mass carriers (29–32).

In this work, we present the observation of a giant extrinsic AHE in KV₃Sb₅, which is a high-conductivity semimetal with Dirac quasiparticles and geometric frustration due to its vanadium Kagome net. The highly dispersive Dirac bands of KV₃Sb₅ are observed using angle-resolved photoelectron spectroscopy (ARPES) as shown in Fig. 1B, along with the density functional theory (DFT)–calculated band structure. The DFT and ARPES match well, both in terms of band dispersion and the Fermi surface geometry with the experimentally determined Fermi level appearing to be slightly below the predicted level (≈−10 meV). Although there has been no report of magnetic ordering of KV₃Sb₅ down to 0.25 K (33), the anomalous Hall conductivity (AHC), at 2 K, reaches as high as ≈15,507 ohm⁻¹cm⁻¹ with an anomalous Hall ratio (AHR) of ≈1.8%; an order of magnitude larger than Fe (34) and one of the largest AHEs ever observed. Unexpectedly, this AHE scales quadratically with σ_xx, deviating from the linear scaling predicted from current skew scattering theories. This is the first example of a giant AHE without ferromagnetic ordering in a magnetic system and prompts investigations into previously unconsidered material families, particularly metallic geometrically frustrated magnets, spin liquid candidates, and cluster magnets. It also raises new questions on the fundamental theory regarding AHE mechanisms in the high-conductivity regime and poses the possibility of realizing an AHA of 90° in metallic systems. This observation opens a new frontier for the AHE [and spin Hall effect (SHE)] born from the intersection of geometrically frustrated/cluster magnets and topological semimetals/metals, inviting exploration not only from theoretical and experimental physicists but also materials scientists and solid-state chemists.

RESULTS

KV₃Sb₅ crystallizes in the P6/mmm space group (SG: 191) and as shown in the inset of Fig. 1C, and its stacking is composed of a Kagome lattice of vanadium coordinated by antimony in distorted octahedra with potassium intercalated between layers. Previous work by Ortiz et al. (33) found that the compound displays paramagnetic behavior at high temperatures, before undergoing a transition at 80 K to either a dilute trimerized state from orbital ordering effects or a highly frustrated state with localized moments. Considering the vanadium Kagome net, geometrical frustration of the magnetic sublattice is expected. DFT + U calculations carried out by Ortiz et al. (33) comparing disordered AFM and ferrimagnetic ordering also support this expectation. Transport experiments on those same crystals were carried out here on a series of KV₃Sb₅ nanoflakes of different thicknesses. Figure 1C shows the typical temperature dependence of ρ_xx for a 105-nm-thick device (see the Supplementary Materials for fabrication information); with decreasing temperature, a kink is visible in ρ_xx around 80 K, corresponding to the known magnetization and heat capacity anomaly (33). At low temperature, the ρ_xx reaches ≈1.5 µΩ cm, which is comparable to that of high purity bulk Bismuth (35). The magnetoresistance (MR) at various temperatures is shown in Fig. 1D, with Shubnikov de Hass (SdH) oscillations clearly visible above 4 T. Below 3 T, the MR is linear, while at higher field, it adopts a standard quadratic dependence with μ₀H (μ₀H is the applied magnetic field; Fig. 1D, inset). Fitting the quadratic field dependence, the average carrier mobility at 5 K is extracted to be ≈1000 cm² V⁻¹ s⁻¹. The fast Fourier transforms (FFTs) below 35 K reveal two identifiable periods at 34.6 and 148.9 T, as shown in Fig. 1E. Tracking the temperature dependence of the FFT amplitude, the Lifshitz-Kosevich fit yields an effective mass of 0.125 m_e for carriers related to the 34.6 T orbit. Such a low effective mass corresponds well with the highly dispersive Dirac bands near the Fermi level. Angle-dependent MR and SdH oscillation analysis (see fig. S2) shows the 34.6 T peak deviates from the 1/cos(θ) line below ≈ 20°, implying that the 34.6 T pocket is not strictly two dimensional.

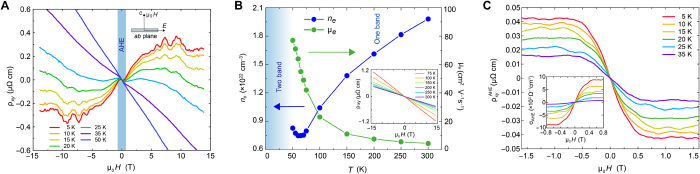
The SdH oscillations are also clearly visible in the Hall response as shown in Fig. 2A, when the current is applied in the ab plane and μ₀H is applied along the c axis. In the high-field region (above 10 T) and below 15 K, there is a sudden change of habit resulting in a field-independent Hall response; this may correspond to a spin flop or other magnetic transition, which changes symmetry and modifies the Fermi surface. Future investigations into the rich high-field magnetic and electronic properties of KV₃Sb₅ are necessary to elucidate the cause of this behavior.

Fig. 2. Hall effects in KV₃Sb₅.

(A) The Hall resistivity of KV₃Sb₅ with the current applied in the ab plane and the magnetic field applied along the c axis. The AHE shows up as antisymmetric S shape in the low-field region for all temperature below 50 K. At low temperatures and high-field regime, the Hall resistivity exhibits a typical two-band behavior. (B) Extracted electron carrier concentration and mobility in the one-band regime. Inset: The Hall response of KV₃Sb₅ above 75 K. (C) Extracted ${\mathrm{\rho }}_{\mathit{xy}}^{\mathit{\text{AHE}}}$ taken by subtracting the local linear ordinary Hall background at various temperatures. The inset shows the converted ${\mathrm{\sigma }}_{\mathit{xy}}^{\mathit{\text{AHE}}}$ at various temperatures by inverting the resistivity tensor.

In the low-field region, highlighted by the blue shading in Fig. 2A, an antisymmetric sideways “S” shape is observed, which is a characteristic of either an AHE or a two-band OHE. Below 35 K, ρ_xy exhibits a second broad hump centered around 7 T, but as the temperature is increased, this hump is gradually lost and a one band linear field dependence is recovered (Fig. 2B, inset). The S-shaped Hall resistivity feature, however, persists throughout this changeover and remains visible at higher temperature where the Hall resistivity appears to be linear. This indicates that the high-field behavior of the Hall effect is related to the two-band OHE and that the low-field S shape is related to an AHE. Within the one-band temperature range, the electron concentrations (n_e) and mobilities (μ_e) are extracted from linear fitting of the OHE and shown in Fig. 2B (the simultaneous fitting of the two-band model with MR and Hall is not possible due to the linear MR behavior in this regime). As the temperature is lowered, μ_e monotonically increases, while n_e shows a minimum at around 65 K, which may be related to the magnetic transition mentioned above. Figure 2C shows the extracted ${\mathrm{\rho }}_{\mathit{xy}}^{\text{AHE}}$ taken by subtracting the local linear OHE background. The magnitude of the AHE monotonically decreases with increasing temperature until it is lost at around 50 K. To precisely extract the AHC (${\mathrm{\sigma }}_{\mathit{xy}}^{\text{AHE}}$) when ρ_xy < ρ_xx with no approximation, we first obtained the Hall conductivity by inverting the resistivity matrix, σ_xy = −ρ_xy/(ρ_xx² + ρ_xy²). Afterward, the local linear ordinary Hall conductivity background is subtracted, leaving the ${\mathrm{\sigma }}_{\mathit{xy}}^{\text{AHE}}$, as shown in Fig. 2C (inset).

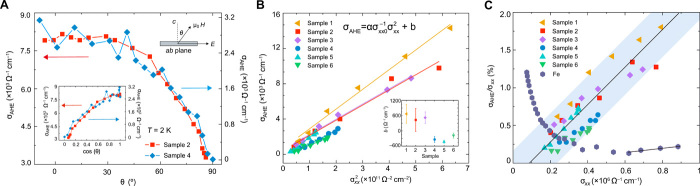
To further confirm the AHE nature of the low-field anomaly, we carried out a detailed angle-dependent measurements. Figure 3A shows the σ_AHE dependence on the angle of μ₀H relative to the applied electric field, and the inset shows σ_AHE against the cos(θ). The AHC is angle independent until μ₀H is tilted away from the z axis by about 30°, after which it rapidly decreases until it reaches 0 at μ₀H∥E. The fact that σ_AHE does not linearly scale with the out-of-plane component of μ₀H solidifies its AHE origin and that the AHE extraction is robust: If the OHE was not properly subtracted, then the angle-dependent behavior would be skewed toward the expected linear response. Furthermore, as expected from a real Hall response, the sign of the AHE flips when rotated past 90° (see fig. S3). The extracted σ_AHE for several devices with thicknesses ranging from 30 to 128 nm is plotted against each device’s ${\mathrm{\sigma }}_{\mathit{xx}}^2$ (which was varied by changing the temperature) in Fig. 3B. The skew scattering and intrinsic components of the AHE can be fitted to ${\mathrm{\sigma }}_{\mathit{\text{AHE}}}=\mathrm{\alpha }{\mathrm{\sigma }}_{\mathit{xx}0}^{-1}{\mathrm{\sigma }}_{\mathit{xx}}^2+b$, where α is the skew constant, σ_xx0 is the residual resistivity, and b is the intrinsic AHC (22). Samples 1, 2, and 3 were fabricated from freshly exfoliated crystals, while samples 4, 5, and 6 were fabricated a few weeks after exfoliation. All devices follow a square dependence with α varying from 0.0075(2) to 0.0172(5); more than an order of magnitude larger than Fe and Ni [0.00149 (22, 34) and 0.0007 (36), respectively]. The inset shows the extracted intrinsic σ_AHE, which average to positive 500 Ω⁻¹cm⁻¹ for samples 1 to 3 in the high-conductivity regime and negative 325 Ω⁻¹cm⁻¹ for samples 4 to 6 in the low-conductivity regime. We use an assumed ferromagnetic splitting of the bands to reveal that the intrinsic mechanism cannot account for the markedly larger observed signal in high-conductivity regime. The DFT-calculated intrinsic values (see the Supplementary Materials) represent an upper limit for the intrinsic contribution to the Hall conductivity and, together with the Hall sign change around the Fermi level, are in agreement with the experimentally extracted intrinsic values. This further confirms the robustness of the AHC extraction. The AHR percentages ($\frac{{\mathrm{\sigma }}_{\text{AHE}}}{{\mathrm{\sigma }}_{\mathit{xx}}}\times 100$) for various KV₃Sb₅ devices and for Fe (23) are shown in Fig. 3C. Throughout the measured σ_xx range, the AHR of KV₃Sb₅ rises monotonically with σ_xx, unlike Fe, which has a decreasing AHR throughout its intrinsic region until σ_xx ≈0.6 × 10⁶ Ω⁻¹cm⁻¹, at which point its skew scattering mechanism begins to dominate. Because of its smaller skew constant, the rate of increase of its AHR is smaller compared to KV₃Sb₅ (37, 38).

Fig. 3. AHE in KV₃Sb₅.

(A) Angular dependence of σ_AHE at 2 K as the μ₀H is tilted from out-of-plane to in-plane. The inset shows the σ_AHE against cos(θ). (B) Extracted σ_AHE versus ${\mathrm{\sigma }}_{\mathit{xx}}^2$ for various devices with thickness ranging from 30 to 128 nm. Solid lines are fittings to the equation shown in the inset to extract the skew scattering constant (α) and intrinsic AHC (b) for each device. The inset shows the extracted intrinsic σ_AHE for all six devices. Larger error is seen for samples 1 to 3 due to the size of the dominating extrinsic component. (C) The ratio between σ_AHE and σ_xx for six KV₃Sb₅ devices and for Fe. The black lines guide the eye to illustrate the increasing tendency of σ_AHE/σ_xx for KV₃Sb₅ and for Fe.

DISCUSSION

To compare the observed AHE of KV₃Sb₅ with that of other materials, σ_AHE versus σ_xx for a variety of materials spanning the various AHE regimes from the dirty regime (localized hopping regime) through to the skew scattering regime are plotted in Fig. 4 (23, 39–43). The different scaling relationships for the localized hopping regime (${\mathrm{\sigma }}_{\mathit{xx}}^{1.6}$) and skew scattering regimes (σ_xx) as well as the quadratic scaling behavior of Fe (${\mathrm{\sigma }}_{\mathit{xx}}^2$) are shown by black dotted lines. Purple lines show three AHRs and their corresponding AHA values. The AHE in KV₃Sb₅, for devices of varying thickness with its scaling shown as the red dotted line, begins its quadratic scaling at σ_xx ≈ 10⁵ Ω⁻¹cm⁻¹, an order of magnitude before Fe, and dwarfs most materials by σ_xx ≈ 2 × 10⁵ Ω⁻¹cm⁻¹.

Fig. 4. Map of AHEs for various materials.

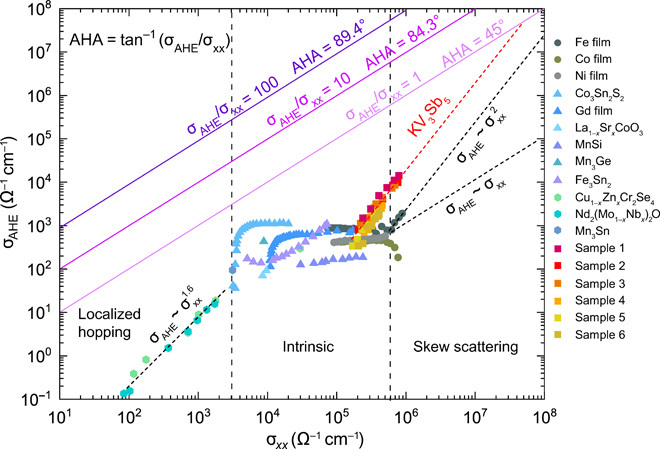
σ_AHE versus σ_xx for a variety of materials spanning the various AHE regimes from the side-jump mechanism through the intrinsic and skew scattering regimes (23, 39–43).

With an AHE this large, there are few known systems that are comparable to KV₃Sb₅. It is fundamentally distinct from Fe in that has both Dirac quasiparticles and a triangular magnetic sublattice. It is also fundamentally distinct from the AHEs recently observed in topological materials (e.g., Co₃Sn₂S₂ and Co₂MnGa), which are intrinsically driven by Berry curvature (σ_AHE ∼ 10³ Ω⁻¹cm⁻¹) (16–18). To the best of our knowledge, KV₃Sb₅ is the first material to showcase an enhanced extrinsic AHE in a frustrated system; other frustrated systems, like Mn₃Sn and Nd₂Mo₂O₇, have been shown to be dominated by the intrinsic mechanism (40, 44, 45). KV₃Sb₅ appears to follow the recently proposed “spin cluster” mechanism by Ishizuka and Nagaosa (25). Here, a triangular spin cluster or tiled clusters as in a Kagome net can act like a “compound magnetic scattering center” when, due to an external field, a distortion of the local order results in a net magnetization and magnetic fluctuations act as scattering centers generating an enhanced skew scattering potential (25). Upon further examination of the AHE shown in the massive Dirac Kagome ferromagnet, Fe₃Sn₂, we find that its AHC also follows a quadratic scaling with a similar skew constant (0.013) as KV₃Sb₅, but due to its low longitudinal conductivity, the magnitude is 10 times smaller. However, the spin cluster theory predicts that a σ_AHE is proportional to σ_xx relationship, which assumes weak magneto-electron coupling that excludes spin-orbit coupling (SOC) in the derivation. A theoretical treatment of Dirac quasiparticles in spin cluster systems where SOC is included will have additional terms in the scattering potential that may recover the quadratic dependence.

A combination of enhanced skew scattering parameters and the quadratic scaling grant the KV₃Sb₅-like materials the potential to realize another fascinating effect: to achieve an AHA approaching 90° extrinsically, which has not been previously proposed or observed. Quadratic dependence of σ_AHE means that the AHA increases quickly with increasing σ_xx, allowing a very large σ_AHE at reasonable σ_xx. For example, extrapolating the evident quadratic scaling of KV₃Sb₅ shown in Fig. 4, an AHA = 45° is reached by σ_xx of 5 × 10⁷ Ω⁻¹cm⁻¹. These are very large conductivities but not implausible; the Dirac semimetal Cd₃As₂ (46), Weyl semimetal NbAs (47), and encapsulated graphene (48) all are known to reach this conductivity regime. A similar extrapolation for Fe would require an unrealistic σ_xx of >10⁸ Ω⁻¹cm⁻¹.

Intuitively, however, one would expect a saturation of the AHA as one approaches large σ_xx values, as the magnetic scattering events are expected to become increasingly rare when the system is exceptionally clean and defect free. However, in the case of materials with some form of backscattering protection, σ_xx can increase without requiring vanishing defects. This has been seen in the Weyl semimetal WTe₂, where the Fermi surface has spin-polarized pockets resulting in spin-flip protection that suppresses backscattering (49); and in the Dirac semimetal Cd₃As₂ where the quantum scattering lifetime is several orders of magnitude less than the backscattering lifetime, meaning that, although the electrons are scattering often, they are not backscattering often (46). In the limit of 90° AHA due to skew scattering, the time between skew scattering events would need to be much less than the time between backscattering events, such that an electron traveling through a soup of magnetic scattering centers in an applied magnetic field would have a very high probability to undergo an orthogonal scattering event before undergoing a backscattering event. In the case of a high conductivity, enhanced skew scattering material like KV₃Sb₅, the addition of some form of backscattering suppression should allow extremely large AHAs to be realizable as one could envision the scenario of a high concentration of scattering centers that do not prohibit σ_xx from increasing but do provide a high probability of orthogonal scattering. Rigorous theoretical handling of this limit is needed.

In summary, a giant extrinsic AHE as large as 15,507 Ω⁻¹ cm⁻¹ is observed in the highly conductive frustrated magnet candidate, KV₃Sb₅. It hosts a Kagome net of vanadium atoms, without magnetic ordering down to 0.25 K, as well as Dirac quasiparticles at the Fermi level. The observed σ_AHE is proportional to ${\mathrm{\sigma }}_{\mathit{xx}}^2$ and, combined with an enhanced skew constant, the AHA rapidly rises with increasing σ_xx; a phenomena not clearly demonstrated before. This points to the possibility of extremely large AHAs at reasonable conductivity values including an AHA of 45° by ≈5 ×10⁷ Ω⁻¹ cm⁻¹ and an AHA of ≈90° if the skew scattering constant can be further enhanced by an order of magnitude. Materials with S > ¹/₂ may lead to stronger itinerant spin coupling, which can result in even larger skew constants, further lowering the σ_xx threshold for an AHA = 90°. This raises fundamental questions about the extrinsic limits of the AHE as one of the effects of quantum anomalous Hall insulators may be replicated in a highly conductive metal. We conclude that the Kagome sublattice in KV₃Sb₅ is acting as tilted spin clusters, giving rise to an enhanced skew scattering effect in accordance with a recent proposal by Ishizuka and Nagaosa (25) but with highly mobile Dirac quasiparticles enhancing the conductivity. This suggests that future theoretical studies on understanding the coupling of relativistic electrons to the magnetic texture with SOC are necessary to reveal the detailed scaling relations. Studies on sister compounds RbV₃Sb₅ and CsV₃Sb₅ could elucidate the effect of increased SOC strength. Since these materials also have weakly bound alkali earth interstitials, the Fermi level can be tuned through intercalation control; ionic liquid gating on few layer samples is an ideal way to vary σ_xx and explore the AHE response. In addition, the high exfoliatability of these compounds makes them ideal platforms for thickness-dependent and monolayer exploration of the AHE and observing the cross-over from the extrinsic-dominated AHE to the intrinsic-dominated regime. This combination of exotic band structures with metallic geometrically frustrated systems provides a novel route for the study of extrinsic Hall effects. Also, since the magnetic fluctuations can be tuned with external perturbations, a new type of experiment where the AHE is further enhanced by modifying the skew scattering potential in situ is possible. In addition, the skew scattering SHE arises from a similar mechanism as the skew scattering AHE; therefore, very large spin Hall angles may also be discovered in KV₃Sb₅ and other similar materials. This is another particularly important avenue of research as large spin Hall angles in highly conductive systems (and therefore low power) are extremely sought after for spintronic applications.

METHODS

High-quality single crystals of KV₃Sb₅ were synthesized from K (ingot, Alfa 99.8%), V (powder, Sigma 99.9%), and Sb (shot, Alfa 99.999%) via the flux method as described by Ortiz et al. (33). Flux mixtures containing 5 mole percent of KV₃Sb₅ were heated to 1000°C, soaked for 24 hours, and then subsequently cooled at 2°C per hour. KV₃Sb₅ crystals were structurally and chemically characterized by powder x-ray diffraction to confirm bulk purity and scanning electron microscopy energy-dispersive x-ray for chemical analysis.

A Quantum Design physical property measurement system (PPMS) was used for transport measurements with Keithley 6221 and Keithley 2182 electronics. Hall measurements were taken in a five-wire configuration, while the MR of KV₃Sb₅ samples was measured using the four-point method. The rotator insert (Quantum Design) was used to tilt the angle between the magnetic field and the current direction.

ARPES measurements were performed at Beamline I05 of the Diamond Light Source using the Scienta R4000 analyzer. The angle and energy resolutions were <0.2° and <15 meV, respectively.

The electronic structure calculations were performed in the framework of DFT using the wien2k (50) code with a full-potential linearized augmented plane wave and local orbitals [FP-LAPW + lo] basis (51) together with the Perdew Burke Ernzerhof parametrization of the generalized gradient approximation as the exchange-correlation functional. The Fermi surface was plotted with the program XCrySDen.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/31/eabb6003/DC1