Toward reliable measurements of perceptual scales in multiple contexts

Abstract

A central question in psychophysical research is how perceptual differences between stimuli translate into physical differences and vice versa. Characterizing such a psychophysical scale would reveal how a stimulus is converted into a perceptual event, particularly under changes in viewing conditions (e.g., illumination). Various methods exist to derive perceptual scales, but in practice, scale estimation is often bypassed by assessing appearance matches. Matches, however, only reflect the underlying perceptual scales but do not reveal them directly. Two recently developed methods, MLDS (Maximum Likelihood Difference Scaling) and MLCM (Maximum Likelihood Conjoint Measurement), promise to reliably estimate perceptual scales. Here we compared both methods in their ability to estimate perceptual scales across context changes in the domain of lightness perception. In simulations, we adopted a lightness constant, a contrast, and a luminance-based observer model to generate differential patterns of perceptual scales. MLCM correctly recovered all models. MLDS correctly recovered only the lightness constant observer model. We also empirically probed both methods with two types of stimuli: (a) variegated checkerboards that support lightness constancy and (b) center-surround stimuli that do not support lightness constancy. Consistent with the simulations, MLDS and MLCM provided similar scale estimates in the first case and divergent estimates in the second. In addition, scales from MLCM–and not from MLDS–accurately predicted asymmetric matches for both types of stimuli. Taking experimental and simulation results together, MLCM seems more apt to provide a valid estimate of the perceptual scales underlying judgments of lightness across viewing conditions.

Introduction

One goal of visual perception research is to characterize the relationship between visual experiences and the physical world. Mathematics and physics provide us with sophisticated tools to measure variables in the physical world, but we struggle to provide equally sophisticated tools to characterize the variables of visual experience.

The most widely used tool to assess people's subjective experiences is still Fechner's method of adjustment (Koenderink, 2013), or simply matching. In matching, an observer adjusts the intensity of a test stimulus so that it looks identical to a given target stimulus. When the test stimulus varies only along a single dimension, the method can be likened to measuring the unknown length of a rod with a ruler.

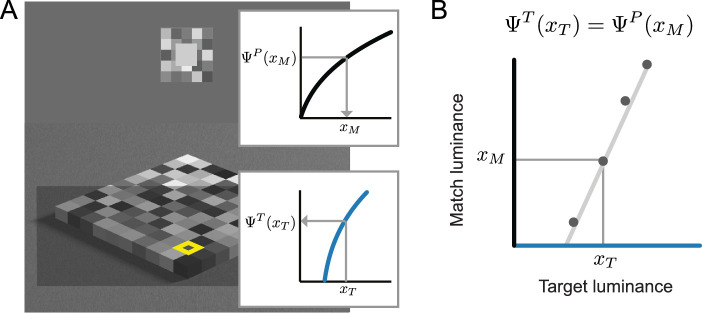
The analogy is not exactly right, because matching procedures rely on a linking assumption whereby observers’ matches reflect the function that relates physical and visual magnitudes but do not reveal the shape of the function directly (see, e.g., Maertens and Shapley, 2013; Wiebel et al., 2017). Figure 1 illustrates the relationship between matches and internal scales. A target of a certain physical intensity x_T (i.e., luminance), evokes a response on the perceptual dimension of interest Ψ(x_T) (i.e., lightness). To perform a matching, the observer chooses a physical match intensity, x_M, which evokes a perceptual response, Ψ(x_M), that is as close as possible to the perceptual response to the target. The functions that relate Ψ(x) and x are known as perceptual scales, transducer functions (e.g., Kingdom and Prins, 2010), or transfer functions in lightness perception (Adelson, 2000). It is evident from Figure 1 that one and the same pattern of matching data (Figure 1B) may be consistent with different combinations of internal response functions (Figure 1A). Thus, matching data alone are insufficient to infer perceptual scales.

Figure 1.

Matching procedures and underlying perceptual processes. (A) The target is the check with a yellow frame in the checkerboard and observers adjust the intensity of the test check embedded in a small coplanar checkerboard so as to match the perceived lightness of the target. It is assumed that at match and target positions, physical luminances (x_M, x_T) are mapped to perceived lightness (Ψ^P(x_M), Ψ^T(x_T)) by unique transducer functions, Ψ^T in transparency and Ψ^P in plain view (see insets). (B) The matching procedure assesses the luminances x_M and x_T, which evoke equal perceived lightnesses, so that Ψ^P(x_M) = Ψ^T(x_T). After Wiebel et al. (2017).

A more straightforward approach to measure perceptual scales are scaling procedures. A variety of scaling procedures has been developed in the history of psychophysical research, from Fechner's integration of just noticeable differences (jnds) to Stevens's direct scaling techniques (for a review, see, e.g., Gescheider, 1997; Marks and Gescheider, 2002), but their validity has been a topic of debate. For example, integrating jnds is problematic, practically, because the error in each JND estimation propagates to the subsequent estimation, and theoretically, because the shapes of the estimated functions will differ as a function of the noise underlying the perceptual judgments (Kingdom and Prins, 2010; Kingdom, 2016). Stevens's direct methods (e.g., magnitude estimation, ratio estimation) might be affected by the choice of the numerical categorization and hence are not guaranteed to provide a meaningful perceptual scale either (see, e.g., Treisman, 1964; Krueger, 1989).

More recently, Maloney and Yang (2003) presented a new type of psychophysical scaling method based on judgments of perceived differences, Maximum Likelihood Difference Scaling (MLDS). MLDS promises to reliably estimate perceptual scales and to be more robust when compared with other scaling methods (Knoblauch and Maloney, 2008). The method uses a stochastic model of difference judgments, which allow maximum likelihood estimation of the underlying perceptual scale. Practically, an MLDS experiment can be executed with the “method of triads” or the “method of quadruples” (Knoblauch and Maloney, 2012). In the method of triads, the observer is presented with three ordered stimuli and has to judge which of the two extremes is more different from the one in between, a procedure rather intuitive for the observer.¹ Using simulations, we showed that MLDS is able to recover different ground truth perceptual scales regardless of whether we assumed the underlying noise to be additive or multiplicative, that is, constant or proportionally increasing across the scale (Aguilar et al., 2017).

MLDS is straightforward when the goal is to characterize a single perceptual scale. However, more often the goal is to characterize how the mapping between a physical and a perceptual variable changes when certain aspects of the viewing conditions are varied, that is, across viewing contexts. In matching, this has been identified as a problem in situations in which the context renders target and match so different that the best the observer can do is a minimum difference “match” (see, e.g., Logvinenko and Maloney, 2006; Ekroll et al., 2004). MLDS avoids the problem of comparisons across contexts because all elements of a triad are always shown in one context. Perceptual scales are estimated from analogous triad comparisons in all contexts the experimenter is interested in. This raises the question of whether the scales measured in different contexts can be meaningfully compared. In this article, we evaluate whether MLDS allows for cross-context comparisons between perceptual scales. We also evaluate a second difference scaling procedure called Maximum Likelihood Conjoint Measurement (MLCM; Knoblauch and Maloney, 2012). We will describe the details of the method below.

Experimental testbed for scaling procedures

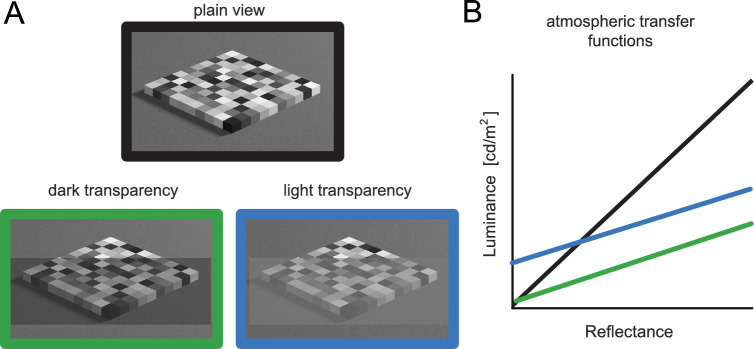
As a testbed for the method comparison, we use scales of perceived lightness for stimuli that do and do not support lightness constancy (Wiebel et al., 2017; Zeiner and Maertens, 2014; Maertens and Shapley, 2013). Lightness constancy describes the phenomenon that observers perceive surfaces of equal reflectance as equally light despite strong variations in illumination (e.g., indoors vs. outdoors) and hence strong variations in the luminance that is reflected to the eye. Figure 2A shows the stimulus that supports lightness constancy, a variegated checkerboard in different viewing conditions. Figure 2B shows how the mapping between check reflectances and luminances differs between different viewing conditions. A lightness constant observer does not respond to the luminances but perceives the lowest luminance as black and the highest as white regardless of the absolute luminance values (see Figure 4A).

Figure 2.

Variegated checkerboards (A) and atmospheric transfer functions (B). The functions show the mapping between check's reflectance and luminance for the two transparency conditions (green and blue lines) and plain view (black line).

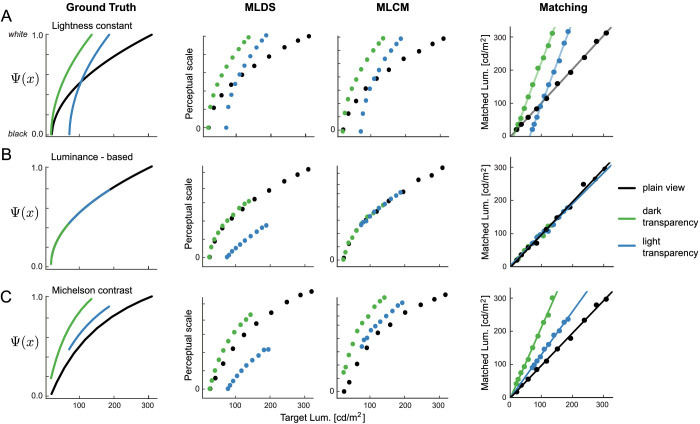
Figure 4.

(A, left panel) Lightness constant observer model represented as ground-truth functions that map luminance (x-axis) to the internal lightness dimension Ψ(x) (y-axis) for the three different viewing contexts (color legend). These functions were used to simulate three different experiments: MLDS, MLCM, and asymmetric matching. The middle left and middle right panels show the outcome of estimating perceptual scales by MLDS or MLCM from the simulated responses. The right panel depicts the outcome of a simulated asymmetric matching experiment. (B) and (C) show the same simulation logic for the luminance-based and the contrast-based observer model.

Figure 3C and D shows the stimuli that do not support lightness constancy. We chose a simple center-surround display that is known to induce lightness judgments that are either based on absolute luminance or on contrast (e.g., Ekroll et al., 2004).² The putatively underlying perceptual scales are described in more detail below (see section Simulation of perceptual scales).

Figure 3.

Stimuli and task for MLDS and MLCM experiments.

We measured perceptual scales with MLDS and with MLCM. In MLDS, the observer judges which of two checks, x₁ or x₃, is more different in lightness from x₂ (Figure 3A and C). The observer only compares triads within the same context as indicated by the two example stimuli in Figure 3A and C. In MLCM, the observer judges which of two checks, x₁ or x₂, is lighter (Figure 3B and D). As indicated in the figure, in MLCM, the paired comparison can be done within the same viewing condition (upper panel) or between different viewing conditions (lower panel). MLDS estimates independent scales for each viewing condition. By default, each scale is anchored to zero at the minimum stimulus value. The maximum is inversely proportional to the noise estimated for each condition. The noise is assumed to be additive. The estimated scales are interval scales.

MLCM has been introduced as an extension of MLDS to model the effect of more than one stimulus dimension onto a single perceived dimension, for example, perceived gloss (Ho et al., 2008; Hansmann-Roth and Mamassian, 2017), color (Rogers et al., 2016), or the watercolor effect (Gerardin et al., 2014, 2018). For the scale estimation, one context is defined as “reference.” Here we use the checkerboard in plain view or the center-surround analogue to plain view as reference (see Methods). The reference scale's minimum is anchored to zero and the maximum is inversely proportional to the estimated noise. Since perceptual comparisons are made within and across viewing conditions, the minimum and maximum anchors for all non-reference scales can be estimated from the data and expressed relative to the reference scale. The estimated scales are also interval scales and the noise is assumed to be additive and equal for all comparisons.

Simulation of perceptual scales

To better understand the differences between methods, we adopt a simulation approach. We define three observer models of lightness perception as ground truth. We then use each of the models to generate response data for an MLDS and MLCM experiment (Figure 4). We use a lightness constant observer, a luminance-based observer, and a contrast-based observer. The lightness constant observer maps the reduced luminance range of surfaces seen through a transparency (x-axis) to a full range of perceived lightness values (Ψ(x), Figure 4A, left). This is an inversion of the mapping from reflectance to luminance shown in Figure 2. Both methods, MLDS and MLCM, recover the ground-truth model.

A luminance-based observer (Figure 4B, left) responds directly to the luminances. The mapping between stimulus input and perceived lightness, Ψ(x), is thus a one-to-one mapping with luminance values in different transparent media covering different parts of the luminance range. MLCM is able to recover the luminance-based observer model when plain view is specified as the reference scale. MLDS anchoring policy erroneously shifts the luminance range of the light transparent medium from its actual value to zero and hence does not recover the ground-truth model.

A contrast-based observer (Figure 4C, left) responds to the relative luminance within a local region. The mean luminance of the surround is subtracted from the luminance of the target, and the difference between target and surround luminance is divided by their sum (Michelson contrast). To make the computation only dependent on the target luminance, the same mean luminance was used in all contrast computations. Again, MLCM recovered the ground-truth model and correctly anchored the minimum of the scale for the light transparency. MLDS imposed the “minimum at zero” constraint and relative to ground truth, it erroneously anchored the scale at zero. This led to a qualitative differentiation in the predicted result pattern for the light transparent medium. In MLDS, the scale would be below the plain-view scale, and in MLCM it would be above it.

Outline

We measured MLDS and MLCM scales in variegated checkerboards and center-surround stimuli, presumably supporting and not supporting lightness constancy, respectively. We repeated the measurements in the same observers to maximally differentiate between the methods. We also simulated and collected data for a matching experiment (see Figure 4, right column). The simulated matching data do not allow recovering the ground-truth observer models, but the method is so prevalent that we included it for the sake of comparison. Given the results from the simulation, we expect both MLDS and MLCM to estimate perceptual scales for the variegated checkerboard that are consistent with each other and consistent with a lightness constant observer model (Figure 4, top row). For the center-surround stimulus, we expect MLCM to estimate perceptual scales consistent with a contrast-based or a luminance-based observer model (Figure 4, middle and bottom rows). We do not expect MLDS to estimate the scales in this condition consistently with MLCM.

Methods

Observers

Eight observers participated in the study; two were the authors (O1/GA, O2/MM), one was an experienced observer (O4/MK), and the rest were volunteers naïve to the purpose of the experiment. All observers had normal or corrected to normal visual ability, and naïve observers were reimbursed for participation. Informed written consent was given by all observers except the authors prior to the experiment. All experiments adhered to the Declaration of Helsinki.

Stimuli

Variegated checkerboards

The stimuli were images of variegated checkerboards composed of 10 × 10 checks (Figure 2A; see also Wiebel et al., 2017). The images were rendered using povray (Persistence of Vision Raytracer Pty. Ltd., Williamstown, Victoria, Australia, 2004). The position of the checkerboard, the light source, and the camera were kept constant across all images. Checks were assigned 1 of 13 surface reflectance values according to the experimental design (see below). In plain view, the luminances ranged from 15 to 415 cd/m². To keep the local contrast of each target check in the checkerboard comparable, we used the same eight reflectances for the surround checks but shuffled their positions. The mean luminance of the surround was equal to the mean luminance of all 13 reflectance values (Suppl. Table S3). The remaining checks in the checkerboard (73 in MLDS and 82 in MLCM) were randomly assigned 1 of the 13 reflectance values. The only constraint was that no two adjacent checks had the same reflectance. A different checkerboard was rendered for each trial in each of the procedures and for each observer.

In the transparency conditions, a transparent layer was placed between the checkerboard and the camera (Figure 2). The transparency is simulated using alpha blending (i.e., an episcotister model), where the resulting luminance of a region in transparency l′ is obtained by linearly combining the luminance of the check in plain view l and the luminance of the foreground transparency when rendered opaque l_τ, weighted by the transparency's transmittance α:

$$l^{\text{'}}=\alpha ·l+(1-\alpha )·l_{\tau }$$

We used two different transparencies: a dark transparency that had a reflectance value of 0.35 in povray (arbitrary) reflectance units (l_τ = 19 cd/m²) and a light transparency that had a reflectance value of 2 (l_τ = 110 cd/m²). The transmittance for both transparencies was α = 0.4. Supplementary Table S3 provides the luminance values for each reflectance in each viewing condition.

Center-surround stimuli

The stimulus was a center-surround display consisting of the target squares, two or three, depending on the task and the background (Figure 3). For within-context comparisons, targets were presented on a homogeneous surround region. For the between-contexts comparisons in MLCM, the background was divided into two luminance plateaus that were connected by a linear luminance gradient (Shapley and Reid, 1985; Maertens et al., 2015). Target luminances were identical to those used in the variegated checkerboards. Background luminances were matched to the mean luminance of the checks in the variegated checkerboard that were viewed through a transparent medium or to the mean of the checks seen in plain view, respectively.

External matching field

In the matching experiment, a test field was presented above the stimulus to assess observers’ lightness matches. The test field was embedded in a coplanar surround checkerboard that was composed of 5 × 5 checks of different luminance. The mean luminance of this surround was 178 cd/m², which was identical to the mean luminance of the checkerboard seen in plain view. To keep the luminance and geometric structure of the surround with respect to the match comparable between trials, we used the same surround checkerboard but presented it in different orientations, rotated from the original in steps of 90 deg.

Apparatus

Stimuli were presented on a linearized 21-inch Siemens SMM2106LS monitor (400 × 300 mm, 1,024 × 768 px, 130 Hz). Observers were seated 130 cm away from the screen in a dark experimental cabin. Presentation was controlled by a DataPixx toolbox (Vpixx Technologies, Inc., Saint-Bruno, QC, Canada) and custom presentation software (http://github.com/computational-psychology/hrl). Observers’ responses were registered with a ResponsePixx button-box (VPixxTechnologies, Inc.).

Design and procedure

We measured perceptual scales using MLDS, MLCM, and asymmetric matching.

MLDS experiment

We used MLDS with the method of triads (Knoblauch and Maloney, 2012). In each trial, three target reflectances (x₁, x₂, x₃) are drawn from the set of possible reflectance values and presented in descending or ascending order at the target positions (see Figure 3). Observers judged which of the extremes (x₁ or x₃) was more different in perceived lightness from the central one (x₂; see Figure 3). To indicate their judgment, they pressed the left or right button on the response box, respectively.

We used 13 different reflectances for the checks in the checkerboard and 10 of these reflectances were used to measure the scales (p = 10). For 10 stimulus intensities, the set of possible triads is 120 (n = p!/((p − 3)! · 3!)) in each viewing condition. Each unique set of triads was repeated 10 times, resulting in a total of 3,600 trials for each observer (120 unique triads × 3 viewing conditions × 10 repeats). Trial sequence was randomized across conditons and repeats, and it was also randomized whether a triad was presented in ascending or descending order. We divided the total number of trials into 10 blocks of 360 trials, which took observers between 40 and 50 minutes to complete.

MLCM experiment

We used MLCM with the method of paired comparisons. Two targets were presented at the positions of targets x₁ and x₃ in the MLDS experiment (see Figure 3). Observers were asked to judge which of the targets was lighter (Figure 3) and they indicated their choice by pressing the left or right key in the response box. No time limit was imposed.

Again we measured scales for 10 reflectances in three viewing conditions, resulting in 30 different stimulus values. With 30 stimuli, there are 435 (30 · (30 − 1)/2) possible pairs of stimuli to be compared. We only included pairs seen in the same viewing conditions and pairs in which one of the viewing conditions was plain view (i.e., comparisons between checks seen through light and dark transparency were excluded). This was legitimate because we only wanted to anchor the scales relative to plain view, and it reduced the number of comparisons to 335. This unique set of comparisons was repeated 10 times, resulting in a total of 3,350 trials per observer. Trials were presented in random order and divided into 10 blocks of 335 trials, which lasted about 25 min each.

Matching experiment

Target reflectances were identical to those used in MLDS and MLCM. The target position was the position of target x₂ in MLDS. Observers adjusted the external test field so as to match the target in perceived lightness. There were two buttons for coarse and two buttons for fine adjustments. A fifth button was used to indicate a match. This triggered the presentation of the next trial. No time limit was imposed. Each judgment was repeated 10 times, resulting in a total of 300 matching trials (10 reflectance values × 3 viewing conditions × 10 repeats).

Experiment order

Observers completed the whole experiment in multiple sessions of about 1 to 2 hours (including breaks) over several days. They were free to chose how many blocks they wanted to do in each session (maximum was 5). The order of experiments was fixed: MLDS, MLCM, and matching for the variegated checkerboard and MLDS, MLCM, and matching for the center-surround stimulus.

Scale estimation

Perceptual scales were estimated using the software packages MLDS (Knoblauch and Maloney, 2008) and MLCM (Knoblauch and Maloney, 2014) in the R programming language (R Core Team, 2017). For both methods, scales are estimated via maximizing the likelihood of a generalized linear model (GLM), derived in detail in Knoblauch and Maloney (2012). Confidence intervals for the scale values were obtained using bootstrap techniques. The goodness of fit for the scales was also evaluated using bootstrap techniques (see Knoblauch and Maloney, 2012; Wood, 2006). In the supplementary material, we describe the details of the goodness-of-fit evaluation for our data set.

Results

Variegated checkerboards

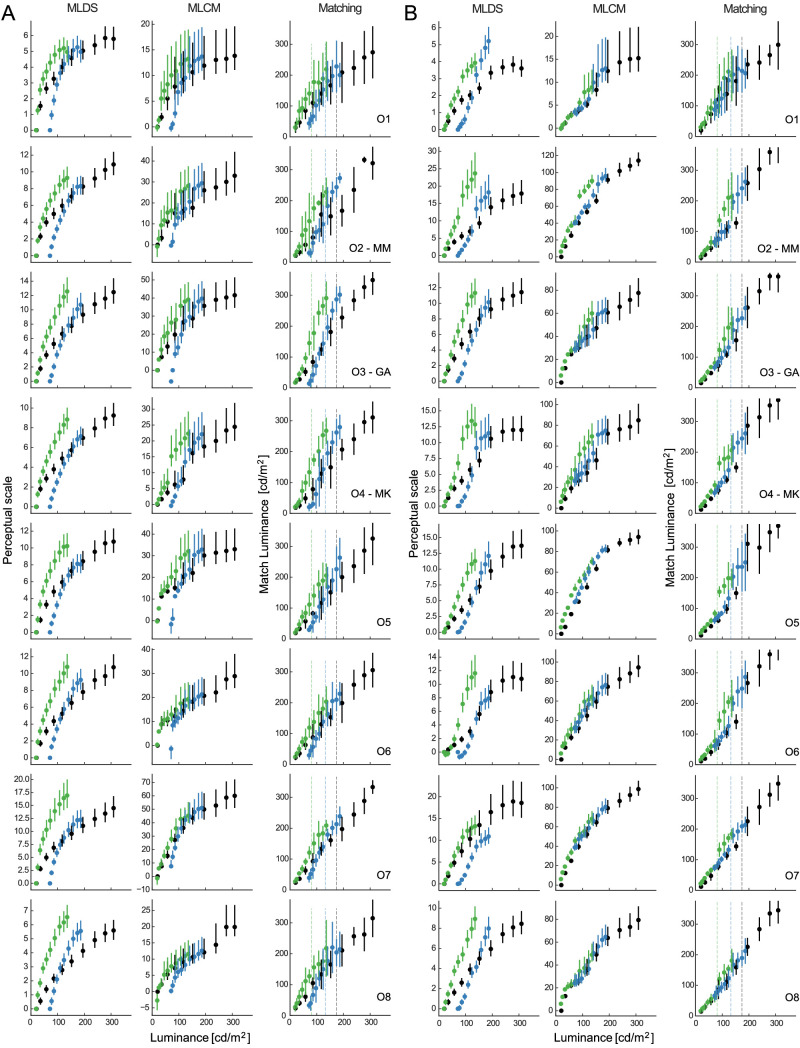
Figure 5A shows MLDS scales, MLCM scales, and matching data for each of the eight observers. Visual inspection of the figure shows that the data of five observers (O1–O5) are consistent among each other and qualitatively more consistent with a lightness constant than with the other two observer models (compare Figure 4). The critical features we are looking for are (a) a parallel shift of the scales in transparencies and (b) a crossing of the plain view and the light transparent scale at an x value of 110 cd/m² (this corresponds to the luminance of the light transparent medium when rendered as an opaque surface; see Methods). The MLDS scales for the remaining observers are also indicative of a lightness constant observer model, whereas the MLCM scales indicate a mixture between a lightness constant and a contrast or luminance-based observer.

Figure 5.

Results from MLDS, MLCM, and matching experiments for observers judging (A) variegated checkerboards and (B) center-surround stimuli. Observers were sorted according to the similarity between MLDS and MLCM scales for the variegated checkerboards. Errorbars are 95% CI for MLDS and MLCM scales, and ± 2 SD for matching. Color legend as in Figure 4. Scales’ maxima relate inversely to the noise in the judgments estimated by MLDS or MLCM (see Noise estimation section).

To quantitatively compare the similarity between MLDS and MLCM results, we normalize the individual scales derived with each method with respect to their maximum in plain view. We then plot the normalized scales against each other (Figure 6A). If both methods produced identical scales, all scales values would line up on the main diagonal. The amount of disagreement can be read from the magnitude of the deviation from the main diagonal. We quantify the agreement by calculating the sum of the squared differences (SSD) between each scale value and the unity line along the x and the y dimension. The SSD measure ranged from 0.24 (O1) to 4.28 (O8, average 1.21) as seen in the inset annotations in Figure 6. To put this into perspective, we computed the SSD measure for scale values that were randomly sampled between 0 and 1. The resulting SSD measure had an average value of 10 and a standard deviation of 2.2.

Figure 6.

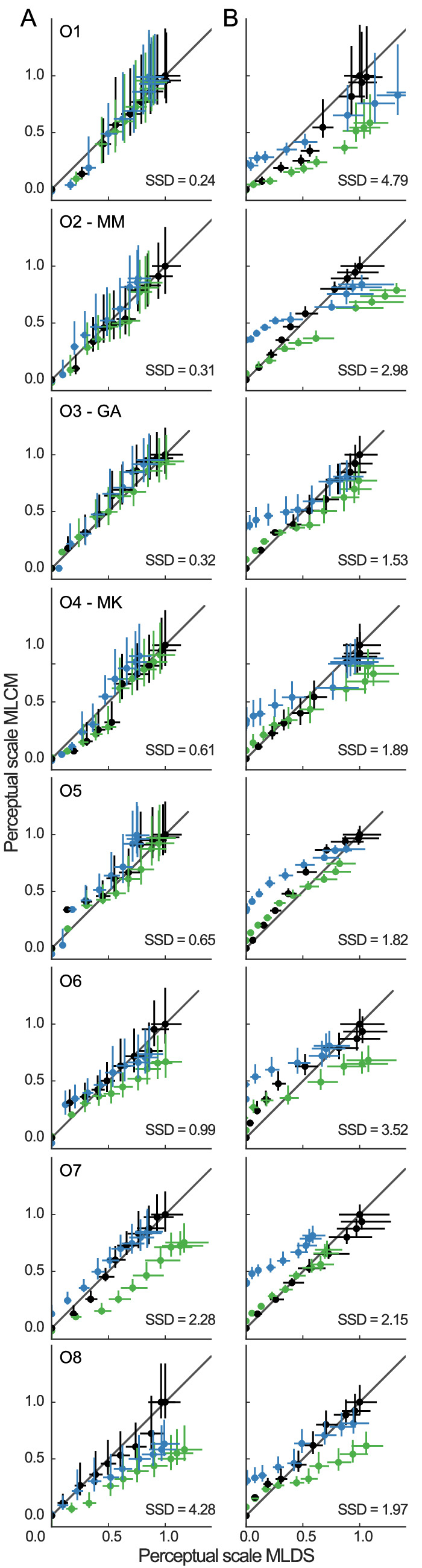
Comparison between perceptual scales estimated by MLDS and MLCM for the (A) variegated and (B) center-surround stimuli. Errorbars are 95% CI Color legend as in Figure 4.

Center-surround stimuli

Panel B in Figures 5 and 6 shows the analogous data and analyses as in panel A but for the center-surround stimulus. For all observers, the MLDS procedure yields a different pattern of perceptual scales than the MLCM procedure. The MLDS scales are mostly consistent with a lightness constant observer, whereas the MLCM scales are more consistent with a luminance-based observer (see Figure 4 for comparison). This observation is quantitatively confirmed by a higher SSD measure for all of our observers (average 2.58 vs. 1.21 in the variegated checkerboards). The disagreement is mostly due to the perceptual scale in the light transparent medium (blue in Figure 5B), because in MLDS, that scale is anchored to zero (by default), whereas in MLCM, it is anchored to an intermediate value relative to plain view (estimated from the comparisons).

Asymmetric matching

Figure 5 also shows the results of the asymmetric matching task. For the variegated checkerboards (Figure 5A), we obtained matches that are consistent with lightness constancy in agreement with the perceptual scales and with previous work (Wiebel et al., 2017). The matching functions are roughly linear, which, according to our matching logic (see Figure 1; Maertens and Shapley, 2013), is a consequence of underlying scales that have a similar non linearity. For the center-surround stimuli (Figure 5B), we obtained matching functions consistent with a luminance-based observer, that is, the matching functions mostly overlap on the main diagonal (Figure 4B).

For the center-surround stimulus, we observed what has been referred to as “crispening effect,” an abrupt change in lightness for targets that are closely above or below the luminance of the surround (e.g., Whittle, 1994; Ekroll et al., 2004). In Figure 5B, the effect is seen as a “push away” of the data points from a linear function near the background luminance (vertical dashed lines). The effect is more visible in the matching data (e.g., see observer O2/MM in plain view) than in the perceptual scales. The effect was absent in the variegated checkerboards.

Consistency between scales and matching

We explained in the Introduction (see Figure 1) how asymmetric matches are a reflection of the internal perceptual scales that relate physical stimulus intensity and perceived intensity at the target and the match positions. Following this logic, we can use the estimated scales to predict the data of an observer in an asymmetric matching task (Wiebel et al., 2017). For each luminance value in transparency, x_T, we find its corresponding value on the perceptual axis, Ψ^T(x_T), using the perceptual scale measured in this condition (Ψ^T). We then find the numerically identical value Ψ^P(x_M) on the perceptual axis of the plain-view scale, Ψ^P, and use that scale to find the corresponding luminance value, x_M. In this way, x_M and x_T are the luminance values that produce equal values on the perceptual dimension, that is, Ψ^T(x_T) = Ψ^P(x_M).

We used this readout procedure to predict asymmetric matching data from MLCM and from MLDS scales for variegated checkerboards and for center-surround stimuli. We compared the predicted with the actual match luminances that observers set in the asymmetric matching task. The average of that comparison across observers is shown in Figure 7 (individual observer data can be found in the Suppl. Figures S3–S6). If the prediction and the data would be in agreement, then the data points would fall on the main diagonal. To quantify the agreement between the prediction and data, we calculate Pearson's correlation coefficient (inset values r in Figure 7). In MLCM, predicted and actual matches were correlated with coefficients of r = 0.997 and r = 0.996 for the variegated checkerboard and the center-surround stimulus, respectively. In MLDS, the correlation coefficients were r = 0.95 for the variegated checkerboards and r = 0.889 for the center-surround stimuli.

Figure 7.

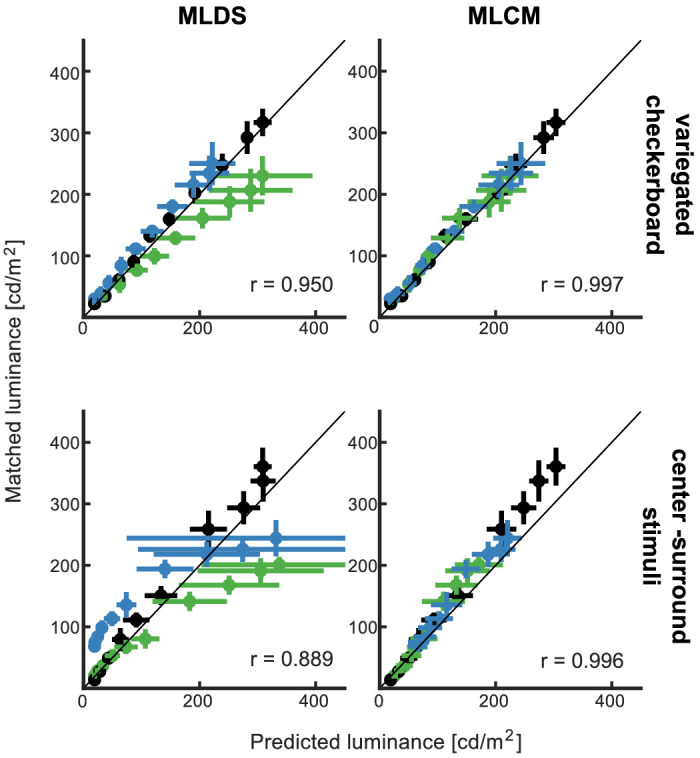
Consistency between matching data and prediction from perceptual scales aggregated for all observers. Data points represent mean ± SD Color legend as in Figure 4.

Goodness of fit

We evaluated goodness of fit for MLDS and MLCM scales using the routines provided in the respective software packages and as suggested in Knoblauch and Maloney (2012). In variegated checkerboards, goodness of fit was appropriate in 29 out of 32 cases (91%, 23 out of 24 for MLDS and 6 out of 8 for MLCM). In center-surround stimuli, goodness of fit was appropriate in 13 out of 32 cases (41%, 12 out of 24 for MLDS and 2 out of 8 for MLCM). For the scales that did not have a satisfactory goodness of fit on a first pass, we employed a suggested outlier removal and checked goodness of fit again (see supplementary material). The procedure removed the trials that had a high deviance residual. After outlier removal, all the scales measured with variegated checkerboards passed the goodness-of-fit test. For center-surround stimuli, 30 out of 32 cases (94%, 22 out of 24 for MLDS and 8 out of 8 for MLCM) passed the goodness of fit.

Discussion

We compared two scaling methods, MLDS and MLCM, with respect to their ability to estimate perceptual scales in the domain of lightness perception. In simulations, we adopted three different observer models that are consistent with a different pattern of perceptual scales under different viewing conditions. MLDS and MLCM were differently able to recover the underlying observer models from simulated data. MLCM was able to correctly recover the lightness constant, the luminance-based observer, and the contrast-based observer. MLDS correctly recovered the lightness constant observer but incorrectly anchored the scales for the other two observer models.

In order to empirically probe different observer models, we used two types of stimuli. Variegated checkerboards have been shown to support lightness constancy (e.g., Wiebel et al., 2017; Zeiner and Maertens, 2014), whereas center-surround stimuli do not support lightness constancy, and their lightness is judged rather on the basis of luminance or contrast (Ekroll et al., 2004). For the variegated checkerboards, we thus expected both MLCM and MLDS to produce similar scales that would be indicative of lightness constancy. The experimental data confirmed this expectation. Contrarily, with center-surround stimuli, we expected luminance- or contrast-based judgments that would produce different scales from MLDS and MLCM. In the experiments, MLDS still produced perceptual scales indicative of lightness constancy. MLCM produced perceptual scales that were consistent with a luminance-based judgment.

Our empirical data corroborated the simulation results. Thus, taking both of them together, we conclude that MLCM is more apt to provide a valid estimate of the perceptual scales putatively underlying judgments of perceived lightness. At least for the current scenario, in which the underlying perceptual scales vary in particular ways between different viewing conditions, the simulations indicated that MLDS's default anchoring to zero is erroneous relative to ground truth, because the numerical equality at zero cannot be interpreted as perceptual equality (Figure 4).

We also measured asymmetric matches with both stimuli. We used the perceptual scales derived with MLDS and MLCM to predict asymmetric matches and compared the predictions with the actual matching data. Scales from MLCM accurately predicted asymmetric matches for both types of stimuli, whereas MLDS accurately predicted the matches in the variegated checkerboard but not in the center-surround stimulus. The failure to predict matches from MLDS scales for the center-surround stimulus is consistent with our above reasoning that the MLDS scales in this condition are not valid estimates of the true underlying scales.

Comparing MLCM and MLDS

Scaling methods carry the prospect of revealing the mapping between variations on a perceptual dimension and variations in some physical variable, that is, the perceptual scale. It would be particularly insightful to characterize how a perceptual scale might change with changes in viewing conditions, because these viewing conditions change the input to the visual system. However, measuring perceptual scales in different contexts has turned out to be a challenge in psychophysical research (Gescheider, 1997). Commonly the appearance of stimuli in different contexts is assessed with asymmetric matching, but, as we outlined in the Introduction, the context might render target and match so different that observers resort to a minimum difference match, which invalidates the method (Logvinenko and Maloney, 2006).

Here, we compared MLDS and MLCM with respect to their ability to measure scales in different contexts and in the following, we summarize the differences in experimental procedures and in the assumptions underlying scale estimation (see Table 1).

Table 1.

Comparison of the methods with respect to their required procedures and the assumptions underlying scale estimation in MLDS and MLCM.

	Asymmetric matching	MLDS	MLCM
Procedure
Comparison	Across-context	Within-context	Within- and across-context
Judgment	Equality	Difference between intervals	Simple difference
Task	Adjust until equal	Triad comparison	Paired comparison
Outcome	Matches in unit of interest	Perceptual scales	Perceptual scales
Assumptions
Noise	–	Additive noise, separate for each scale	Single additive noise for all scales
Scale minimum	–	Each scale at zero	Reference scale at zero, others estimated from data relative to reference
Scale maximum	–	Inverse of estimated noise for each scale	Inverse of estimated noise for reference scale, others estimated from data relative to reference

Cross-context comparisons and perceived differences

MLDS and MLCM both avoid the problem of matching by asking observers to report differences about the test stimuli in a forced-choice setting. MLDS avoids the problem of cross-context comparisons, because the stimuli belonging to one triad are all shown in the same context. In MLCM, observers do not have to produce equality but judge which of the stimuli is higher on some perceptual dimension. Thus, even though in MLCM, sometimes stimuli are compared across contexts, this comparison is not as problematic as producing perceptual equality as in asymmetric matching (see below).

Task

MLCM and MLDS both ask observers to judge perceived differences between stimuli. MLCM uses the method of paired comparisons where observers judge which of the two stimuli is higher along some perceptual attribute of interest, that is, higher in lightness. In MLDS, the observer compares two perceptual intervals and judges which one is bigger, that is, which two stimuli are more different in lightness. Observers unanimously reported that the paired comparison in MLCM was easier than the triad comparison in MLDS. However, both comparisons were easier than asymmetric matching, which was reported to be sometimes difficult and even frustrating. Also theoretically, paired comparisons are the easier task as they involve the comparison of two values compared to three in the triad comparison. Taken together, from a procedural point of view of the observer, MLCM is the preferred task, followed by MLDS and then asymmetric matching.

Model assumptions

In MLDS, by default, the scale minimum is anchored to zero. The scale maximum is inversely related to the magnitude of the estimated noise on the perceptual dimension (the “unconstrained” parametrization; see Knoblauch and Maloney, 2012). When MLDS is used to estimate scales in different contexts, the maxima might differ, because the noise in different context might differ. The minima will all be set to zero, but that does not mean that the lowest value will actually appear identical across contexts. For a lightness constant observer (see Figure 4A), the true perceptual minima and maxima are in fact identical across contexts, and hence MLDS's anchoring policy leads to successful scale estimations. For a luminance- or a contrast-based observer, the true minima and maxima are different in different contexts (see Figure 4B and C). MLDS will still anchor the minimum of all scales at zero, but this results in scale estimates that cannot be meaningfully compared across contexts. Thus, whether or not MLDS can be reasonably used for cross-context comparisons of perceptual scales depends on the perceptual dimension under study. We did this in a previous study on lightness perception (Wiebel et al., 2017) and our scales were in good agreement with data from asymmetric matching. But, as our current simulations show, this was the case because our variegated checkerboard stimuli happened to support lightness constancy. The adequacy of MLDS's anchoring rules needs to be scrutinized for each and every case, and it is up to the experimenter to check their validity. This is an aspect of the method that has not yet been discussed explicitly in the MLDS literature, and we think it is of extreme relevance for experimenters to be aware of this anchoring policy when they use MLDS.

The second scaling method that we tested was conjoint measurement. Conjoint measurement was designed to measure the combined effect of multiple physical dimensions on one perceptual dimension of interest (Luce and Tukey, 1964; Krantz et al., 1971). The maximum likelihood version of conjoint measurement—MLCM—arose as a natural extension of MLDS to more than one physical dimension (Knoblauch and Maloney, 2012).

So far, MLCM has been used, for example, to evaluate the relative effects of physical gloss and roughness on the respective perceptual attributes (Ho et al., 2008), the effect of physical gloss and albedo on perceived gloss and lightness (Hansmann-Roth and Mamassian, 2017), or stimulus’ frequency and amplitude on perceived saturation in the watercolor effect (Gerardin et al., 2014, 2018). In these cases, the stimulus dimensions were continuous variables, and the conjoint measurement is evaluated with an additive model, in which the perceptual judgments are explained by the sum of the effects of each individual stimulus dimension (Knoblauch and Maloney, 2012).

However, the method can also be applied differently in order to measure scales in multiple viewing contexts, and this is what we used it for. Instead of testing several continuous stimulus dimensions, we tested one continuous stimulus dimension (luminance) and a second categorical stimulus dimension (three contexts). For our scenario, the usual additive model is insufficient to recover the scaling functions, because it cannot capture full affine transformations among scales. Specifically, it only captures models with an (additive) offset but not with an offset and a multiplicative factor as it was the case for the scales in the transparency condition (Figure 4; see supplementary material and Suppl. Fig. S2 that illustrate this point). Consequently, we used the alternative and more general saturated model provided by MLCM. This model includes almost as many parameters (29) as combinations of stimuli (30, 10 test reflectances × 3 contexts). We collected sufficient data to fit the saturated model and used the nested likelihood ratio test to check whether the saturated model provided a better fit to the data than the additive model (Knoblauch and Maloney, 2012).³ This was the case for all experimental data.

In MLCM, only the minimum of the reference scale (plain view) is anchored to zero, whereas the minima and maxima of all other scales are estimated from the data. This means that MLCM provides a way to empirically recover the “ground-truth” functions for the observer models that we evaluated here (Figure 4).

Noise estimation

Both MLDS and MLCM take into account that human observers’ judgments are inherently stochastic, or noisy. Both methods model the source of noise at the decision stage and they provide an estimate of that noise $\widehat{\sigma }$, which is equal to the inverse of the scale's maximum (in MLCM the maximum of the reference scale). The decision variable in MLDS is

$$\begin{array}{c}\hfill {\Delta }_{\mathrm{MLDS}}=\left[{\Psi }^i\left(x_3\right)-{\Psi }^i\left(x_2\right)\right]-\left[{\Psi }^i\left(x_2\right)-{\Psi }^i\left(x_1\right)\right]+\epsilon \end{array}$$ (1)

where Ψⁱ(x) is the perceptual scale in the ith context. The observer perceives the pair (x₂, x₃) as being more different from (x₂, x₁) when Δ_MLDS > 0.

The decision variable in MLCM is

$${\Delta }_{\mathrm{MLCM}}=\left[{\Psi }^j\left(x_2\right)-{\Psi }^i\left(x_1\right)\right]+\epsilon$$ (2)

where the perceptual scales can be from the same or different contexts (i could be different from j), and the observer perceives x₂ as lighter than x₁ when Δ_MLCM > 0. In both cases, the decision variable is corrupted by additive Gaussian noise with variance σ² (ϵ ∼ N(0, σ²)). The scale maximum of either method equals the inverse of the estimated variability, that is, $1/{\widehat{\sigma }}_{\mathrm{MLDS}}$ and $1/{\widehat{\sigma }}_{\mathrm{MLCM}}$. If the noise is additive and Gaussian and if both methods are probing the same underlying dimension, Ψ(x), then the noise estimates from both methods should be related in the following way:

$${\widehat{\sigma }}_{\mathrm{MLCM}}=\frac{\sqrt{2}}{2}{\widehat{\sigma }}_{\mathrm{MLDS}}$$ (3)

where ${\widehat{\sigma }}_{\mathrm{MLCM}}$ and ${\widehat{\sigma }}_{\mathrm{MLDS}}$ are the noise estimates by MLCM and MLDS, respectively (see supplementary material for the derivation).

Injecting the above assumptions into the lightness constant observer model, we obtained the above relationship between the noise estimates in MLDS and MLCM. It is meaningful to compare the noise estimates in this way when the maxima of the ground truth functions are equal across conditions, as it is the case for the lightness constant observer (Figure 4). For the other two observer models, this was not the case, but we can still use the scales estimated in “plain view” for a cross-method comparison of the noise estimates.

Figure 8 shows the respective noise estimates for the “plain-view” scale for MLDS (x-axis) and MLCM (y-axis) for our experimental data. The diagonal line indicates the theoretical relationship as described in Equation 3. All data points fall below the diagonal, but for the variegated checkerboards, the noise estimates that five out of eight observers are close to the expected theoretical relationship. For the center-surround stimuli, the relationship is less clear. In general, the noise estimates in MLCM were smaller than those in MLDS. One possible explanation for this is that there might be other sources of noise, in addition to decision noise, which may have a smaller effect on responses in MLCM than in MLDS. This would be in agreement with our own impression and informal reports of observers that the paired comparison task in MLCM is easier than the triad comparison in MLDS.

Figure 8.

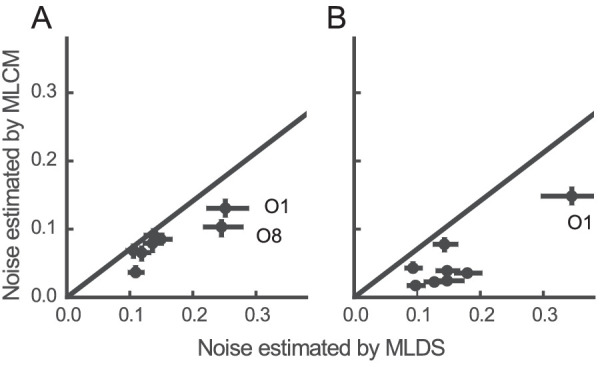
Noise estimated by both scaling methods for variegated checkerboards (A) and for the center-surround stimuli (B). The black line indicates the expected relationship between the two estimates ($\sqrt{2}/2$; see text).

A general issue associated with scaling methods is to what extent the method can recover the shape of the function irrespective of the type of noise. For convenience, it is often assumed that the noise is additive. Discrimination scales constructed from summation of JNDs are sensitive to differences in noise type (Kingdom and Prins, 2010; Kingdom, 2016). Scales constructed from judgments of interval differences (“difference scaling”), on the other hand, have been shown to be insensitive to whether the noise is additive or multiplicative. This applies to all partition scaling methods and hence to MLDS (Kingdom and Prins, 2010; Aguilar et al., 2017). Furthermore, MLDS has been shown to provide robust estimates also for non-Gaussian noise distributions (e.g., Chauchy, Uniform, or Laplace; Maloney and Yang, 2003). These are clear advantages of MLDS compared to other scaling methods when perceptual scales are measured in a single viewing context. It needs to be tested in the future to what extent MLCM scales might be affected by different types or distributions of noise.

Conclusions

We compared MLDS and MLCM as methods to estimate lightness scales using variegated checkerboards and center-surround stimuli. In simulations, we showed that MLCM and not MLDS could recover the underlying functions of three different observer models. In experiments, we found that MLCM scales were consistent with the expected lightness functions and quantitatively predicted asymmetric matches. We conclude that MLCM is better suited to measure perceptual scales across different viewing conditions, because its experimental and estimation procedures involve comparisons across conditions and hence allow for meaningful anchoring of the scales. However, MLCM makes a strong assumption about a single additive noise source that needs to be scrutinized by experimental tests in the future.