Abstract
Hazardous waste management is of paramount importance due to the potential threats posed to the environment and local residents. The design of a hazardous waste management system involves several important decisions, i.e., the determination of the locations and sizes of treatment, recycling and disposal facilities, and organizing the transportation of hazardous waste among different facilities. In this paper, we proposed a novel stochastic bi-objective mixed integer linear program (MILP) to support these decisions in order to reduce the population exposure to risk while simultaneously maintaining a high cost efficiency of the transportation and treatment of hazardous waste. Moreover, considering the inherent uncertainty within the planning horizon, the cost, demand and affected population are defined as stochastic parameters. A sample average approximation based goal programming (SAA-GP) approach is used to solve the mathematical model. The proposed model and solution method are validated through numerical experiments whose results show that uncertainty may not only affect the objective value but also lead to different strategic decisions in the network design of a hazardous waste management system. In this regard, the strategic decisions obtained by the stochastic model is more robust to the change of external environment. Finally, the model is applied in a real-world case study of healthcare waste management in Wuhan, China, in order to show its applicability.
Keywords: Hazardous waste, Location problem, Network design, Hazardous materials, Multi-objective optimization, Stochastic optimization
1. Introduction
With the rapid increase on production and consumption, a large amount of hazardous waste is now generated from a wide range of industries and service sectors (Rabbani et al., 2019), e.g., production and manufacturing, chemical processes, construction, healthcare, and household activities. Hazardous waste is, however, an inevitable by-product of industrial processes and can be found in several forms, e.g., solid, sludge, liquid, packaged or containerized gases, etc., from both large-scale industrial sectors and small businesses (Alumur and Kara, 2007). Any type of waste can be classified as hazardous if it possesses any of the following properties: ignitability, reactivity, corrosiveness or toxicity (Alumur and Kara, 2007). Because of these characteristics, if hazardous waste is treated or disposed of in an inappropriate manner, the nearby residents and the environment will be exposed to substantial risk and threats. Therefore, the management of hazardous waste is of prime importance.
Hazardous waste management consists of several activities including collection, transportation, treatment, recycling and disposal (Samanlioglu, 2013). The network design of a hazardous waste management system consists of the determination of the locations and sizes of treatment, recycling and disposal facilities and organizing the transportation of hazardous waste among these facilities. It is a complex decision making problem due to the conflicting perspectives from different stakeholders (Alumur and Kara, 2007). For instance, the primary objective of a waste management company is to minimize its cost. However, on the other hand, the government’s perspective is to minimize exposure of the population to risk. An optimal decision is usually made through a trade-off between cost efficiency and population exposure risk. Furthermore, based on the characteristics of hazardous waste, different treatment technologies, i.e., chemical or biological process, incineration, and immobilization are required (Boyer et al., 2013). Thus, the network decisions are also affected by the compatibility between hazardous waste and the adopted technology.
Another important issue is uncertainty. The network design of a hazardous waste management system is a long-term strategic decision and is therefore influenced by a high level of uncertainty within the planning horizon, i.e., the generation and composition of hazardous waste, the cost of facility operation and transportation, and so forth, which further complicates the decision making problem. However, most mathematical models for hazardous waste management are developed with deterministic inputs and the proper control of the uncertainty related to the parameters is insufficient. In reality, decision making with all the input parameters fully known in advance is impossible (King and Wallace, 2012) and the incapability of coping with uncertainty may reduce the robustness of a model’s outputs. When a strategic facility location decision is made for hazardous waste management, it will be extremely expensive to alter, and the lack of robustness may thus limit the use of a deterministic decision-support model. For these reasons, we formulate a novel two-stage stochastic multi-objective model for the network planning of a hazardous waste management system under an uncertain environment.
In this paper, by using a mathematical programming approach, we aim at answering the following research questions:
-
•
How is the decision making on the network configuration of a hazardous waste management system affected by the uncertainty?
-
•
What benefits can be achieved by using a stochastic model?
The rest of the paper is organized as follows. Section 2 presents an extensive literature review. Section 3 describes the problem and formulates the mathematical model. Section 4 develops a solution method for the proposed model. The numerical experiments, result and sensitivity analyses are given in Section 5. Section 6 presents a real-world case study of healthcare waste management in Wuhan, China. Section 7 concludes the paper with a summary of contributions and research opportunities.
2. Literature review
The hazardous waste management problem has been the subject of many research works, and this section provides a literature review considering four basic elements of the decision-support models, namely, the types of decisions modeled, the objective functions of the models, the solution approaches, and the treatment of uncertainty. Finally, the literature gaps are identified and the contributions of this research are summarized.
2.1. Types of decisions
The modeling efforts focus on three different types of decisions, namely, facility location, routing or allocation, and integrated network design problem. The strategic facility location problem of hazardous waste management was extensively investigated in late 1980s and was described an “obnoxious” or “undesirable” facility location problem (Erkut and Neuman, 1989). The target of these models is to minimize nuisance sometimes at the expense of service cost (Alumur and Kara, 2007). Recently, Li et al. (2015) developed an integer linear program (ILP) to select the locations of collection and treatment facilities for industrial hazardous waste. Based on a covering problem, Chauhan and Singh (2016) proposed a hybrid method combining interpretive structural modeling, fuzzy AHP, and a fuzzy TOPSIS to select the locations of healthcare waste disposal facilities in a sustainable manner. The second group of models focuses on short-term decisions, i.e., routing and allocation. For instance, Paredes-Belmar et al. (2017) formulated an ILP for minimizing the cost of hazardous waste collection problem, where only the routing decisions were considered. Considering the route selection of a hazardous waste management system, Zografos and Androutsopoulos (2008) formulated a bi-objective ILP to simultaneously minimize the cost and risk associated with the transportation of hazardous waste. Sheu (2007) formulated a bi-objective linear program (LP) to determine the allocation of hazardous waste over several periods considering the minimization of both cost and risk. The third strand of literature models the integrated network design problem that aims at determining both strategic and operational decisions, for example, location-routing and location-allocation problems. Due to the effectiveness in simultaneously solving both complex decision making problems (Rabbani et al., 2018), most recent publications belong to this group, as shown in Table 1 .
Table 1.
A comparison of relevant literature in the network design of hazardous waste management system.
| Papers | Decisions |
Material flow |
Objective function |
Environment |
Solution |
Validation methodology | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Location | Allocation/Routing | Others | Single | Multiple | Single | Multiple | Certain | Uncertain | Exact | Approximation | ||
| Nema and Gupta (2003) | × | × | × | × | × | × | Numerical experiment | |||||
| Alumur and Kara (2007) | × | × | × | × | × | × | Case study | |||||
| Emek and Kara (2007) | × | × | × | × | × | × | Case study | |||||
| Sheu (2007) | × | × | × | × | × | Numerical experiment | ||||||
| Zografos and Androutsopoulos (2008) | × | × | × | × | Case study | |||||||
| Das et al. (2012) | × | × | × | × | × | Case study | ||||||
| Xie et al. (2012) | × | × | × | × | × | × | Case study | |||||
| Boyer et al. (2013) | × | × | × | × | × | × | Case study | |||||
| Samanlioglu (2013) | × | × | × | × | × | × | Case study | |||||
| Berglund and Kwon (2014) | × | × | × | × | × | × | × | Numerical experiment | ||||
| Jiang et al. (2014) | × | × | × | × | × | × | Case study | |||||
| Ardjmand et al. (2015) | × | × | × | × | × | × | Numerical experiment | |||||
| Li et al. (2015) | × | × | × | × | × | Case study | ||||||
| Zhao and Verter (2015) | × | × | × | × | × | × | Case study | |||||
| Ardjmand et al. (2016) | × | × | × | × | × | × | Numerical experiment | |||||
| Lee et al. (2016) | × | × | × | × | × | Case study | ||||||
| Yu and Solvang (2016) | × | × | × | × | × | × | Numerical experiment | |||||
| Zhao et al. (2016) | × | × | × | × | × | × | × | Case study | ||||
| Yu and Solvang (2017a) | × | × | × | × | × | × | Numerical experiment | |||||
| Asgari et al. (2017) | × | × | × | × | × | × | Case study | |||||
| Farrokhi-Asl et al. (2017) | × | × | × | × | × | × | Numerical experiment | |||||
| Paredes-Belmar et al. (2017) | × | × | × | × | × | Case study | ||||||
| Yilmaz et al. (2017) | × | × | × | × | × | × | Case study | |||||
| Rabbani et al. (2018) | × | × | × | × | × | × | Numerical experiment | |||||
| Rabbani et al. (2019) | × | × | × | × | × | × | × | Numerical experiment | ||||
| Zhao and Huang (2019) | × | × | × | × | × | × | Case study | |||||
| This study | × | × | × | × | × | × | Numerical experiment and case study | |||||
2.2. Objective functions
The network design of a hazardous waste management system considers three objectives related to economic performance, risk, and equity (Rabbani et al., 2018). The maximization of equity in hazardous waste management was mainly modeled in the early 1990s. However, it may result in a higher number of facilities to be opened and in a lower utilization rate in order to evenly allocate the risk to different communities (Alumur and Kara, 2007). Thus, the recent modeling efforts mainly focus on the cost and risk objectives. From the waste management companies’ perspective, efficiency is the primary target. In this regard, several models were developed to minimize the cost related to collection, transportation, and treatment of hazardous waste. Emek and Kara (2007) developed a mixed integer linear program (MILP) for selecting of the optimal locations for incarnation plants. This model aims at minimizing the cost, while at the same time fulfilling the emission requirement for air pollution, which is measured using a Gaussian plume equation (Sykes et al., 1986). Lee et al. (2016) developed a MILP to design the reverse logistics network of a municipal solid waste (MSW) management system. The objective is to minimize the total cost through the determination of optimal facility locations, number of trips and allocation of MSW among different facilities.
The transportation and treatment of hazardous waste may impose a significant risk to the population exposure and the environment, so the primary objective of most mathematical models is to balance the trade-off between economic efficiency and risk through formulating a multi-objective optimization model. In this regard, several researches formulated multi-objective MILPs to balance the trade-off between the cost and risk related to the facility operation and the transportation of hazardous waste (Yu and Solvang, 2016). Das et al. (2012) developed a bi-objective routing optimization model which simultaneously minimizes both cost and risk related to the transportation of hazardous waste. Considering multiple transportation modes, Jiang et al. (2014) improved a bi-objective location-routing model of a multi-commodity hazardous waste management system. Xie et al. (2012) proposed an integer non-linear program to determine the optimal locations of transfer yards and routing plan for hazardous waste management. Zhao and Verter (2015) investigated an improved weighted goal programming (GP) method for the location-routing problem of used oil treatment. This model simultaneously minimizes the system’s operating cost and environment risk from the treatment and transportation of used oil. In addition, the recent multi-objective optimization models have attempted to better reflect real-world situations by incorporating the waste-to-technology compatibility and the multi-product material flow (see, e.g., Rabbani et al. (2018)).
2.3. Solution approaches
Due to the involvement of multiple objectives, the network design of a hazardous waste management system is a complicated optimization problem that can be solved by both exact and approximation methods. To obtain exact solutions, commercial optimization packages like CPLEX and LINGO have been widely used for the implementation of several scalarization methods, i.e., the weighting method (Nema and Gupta, 2003), the GP (Zhao and Verter, 2015), the lexicographic weighted Tchebycheff method (Samanlioglu, 2013) and the augmented -constraint method (Yu and Solvang, 2016), in order to generate the Pareto-optimal solutions. With a focus on improving the computational performance, several highly effective and efficient approximation methods have been implemented for hazardous waste network design problems. Farrokhi-Asl et al. (2017) and Rabbani et al. (2018) evaluated the performance of two meta-heuristic algorithms called non-dominated sorting genetic algorithm (NSGA-II) and multi-objective particle swarm optimization (MOPSO) on solving a large-scale bi-objective location-routing problem for waste collection. Ardjmand et al. (2015) developed an improved genetic algorithm to calculate efficient Pareto-optimal solutions of a single-product single-period location-routing problem of hazardous materials. Asgari et al. (2017) developed an effective memetic algorithm to solve a multi-objective hazardous waste location-routing problem.
2.4. Treatment of uncertainty
Strategic decision making usually involves many uncertainties related to the input information, so taking control of uncertainty is of importance. However, most network design models for hazardous waste management were formulated under a deterministic environment and, to our knowledge, the only exceptions were provided by Berglund and Kwon (2014), Ardjmand et al. (2016) and Rabbani et al. (2019). Considering the budgeted uncertainty related to the number of trucks required in a shipment and the exposure risk, Berglund and Kwon (2014) developed a robust optimization model for hazardous waste location-routing problem. The most widely used approach in modeling the uncertainty of a robust logistics network is stochastic programming (Hatefi and Jolai, 2014). In this regard, Ardjmand et al. (2016) investigated a single-product single-objective hazardous waste location-routing problem to balance the trade-off between cost and risk under a stochastic environment. Even though the risk of hazardous waste management was considered in Berglund and Kwon (2014) and Ardjmand et al. (2016), it was directly monetized and combined in the cost objective. Thus, their models are the extension of a single-objective MILP and the different measures of the cost and the risk are, however, not fully considered. The most recent research work is that of Rabbani et al. (2019) who formulated a multi-product multi-objective location-routing problem for hazardous waste management. The model was first developed in a deterministic form and an integrated sim-heuristic with both NSGA-II and Monte Carlo simulation was then proposed to generate a set of Pareto-optimal solutions in a stochastic environment.
2.5. Summary and contributions
Table 1 summarizes the relevant literature. With the help of multi-objective optimization, the previous modeling efforts have led to a well-established methodological framework for the formulation of and the balance between the economic performance and the risk of hazardous waste management. Furthermore, the research focus has also been given to the development of improved solution approach and algorithm in order to effectively and efficiently solve the complex optimization problems. However, one major limitation is the input parameters of most previous models are deterministic and are therefore incapable of dealing with the uncertainty. In the real world, uncertainty may have a significant impact on the robustness of a solution, and the incapability to cope with uncertainty can significantly limit the use of a decision-support model. Besides, the three exceptions of Berglund and Kwon (2014), Ardjmand et al. (2016) and Rabbani et al. (2019) only evaluate the impact of uncertainty on the objective values but not on the strategic facility locations in the hazardous waste management system. Compared with a deterministic model, the most significant benefit of using a stochastic model is to generate more realistic estimations and robust decisions (King and Wallace, 2012). When a facility location is selected, it is extremely expensive to change. Moreover, different from commercial logistics systems, the treatment of hazardous waste requires strict qualifications, which limits the flexibility of the network. Therefore, a robust strategic decision under an uncertain environment is particularly worth investigating. In addition, these three models mainly consider the uncertainty related to demand and cost but not to other important parameters, i.e., the waste composition and the possible change of affected population over the planning horizon. Besides, none of them has been applied in real-world case studies. For these reasons, in order to fill the literature gap, we formulate a novel mathematical model for the network design of a hazardous waste management system. The contributions are summarized as follows:
-
•
We model the uncertainty of the generation and composition of hazardous waste, the fluctuations on the cost of facility operation and transportation, and the demographic change.
-
•
We evaluate the impact of uncertainty on both the objective values and the strategic facility location decisions in hazardous waste management.
-
•
We introduce a sample average approximation based goal programming (SAA-GP) algorithm to effectively solve the proposed model.
-
•
We validate the model and algorithm with a set of numerical experiments and a real-world case study in order to show the trade-off between economic performance and the risk of hazardous waste management under a stochastic environment.
3. Problem description and mathematical model
We now describe the problem under study and provide a mathematical model for it.
3.1. Problem description
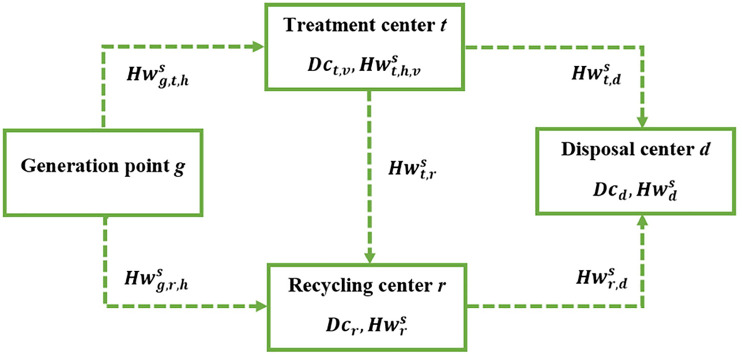
Fig. 1 illustrates the network structure of a hazardous waste management system. Different types of hazardous waste are first collected at the generation points and thence distributed to respective recycling centers and treatment centers in accordance with their composition and characteristics. It is noteworthy that hazardous waste can be sent for treatment only when a compatible technology is installed at the respective treatment center. For instance, explosive hazardous waste cannot be treated at an incineration plant. After the treatment operations, some non-hazardous recyclable parts and components can be sent for recycling, and the non-recyclables and hazardous components are dispatched for proper disposal. In addition, the waste residue from the recycling centers will also go to the disposal centers.
Fig. 1.
A General network structure of a hazardous waste management system.
The aim of the model is to simultaneously balance the system operating cost and the risk to the population of exposure from hazardous waste management through an optimal network configuration. In essence, the planning of a hazardous waste management is a two-stage decision making process. In the first stage, strategic decisions are made to design the network structure through the determination of facility locations and technologies installed. Then, through allocation and route planning, the second stage tactical or operational decisions determine how the network for hazardous waste management is used in an optimal fashion.
Nevertheless, decision making in the real world is rarely made with all the necessary information perfectly known in advance (King and Wallace, 2012). Usually, several uncertainties are encountered within the lifespan of a system, but some important decisions have to be made with imperfect information about the future. Hence, it is of prime importance to properly control the uncertainty related to the input parameters of the network design. To this end, a two-stage stochastic model can be used to formulate such a decision making problem. In a scenario-based stochastic optimization model, discrete scenarios as well as their probabilities of occurrence are used to formulate different conditions, and the decisions will be made taking into account future uncertain conditions. In accordance with King and Wallace (2012), considering the nature of decisions, a modeling choice for a decision is to be either robust or flexible.
-
•
Robust: A robust decision means that it should be able to withstand the change of environment and has a proper performance. For example, the decision on a bus schedule should be robust even if the future demand may be uncertain when the bus schedule is planned.
-
•
Flexible: A flexible decision should be able to adapt the change of environment in order to maximize the performance of a system. For instance, the daily route planning of an express delivery company may be adjusted based on changes in customer demands in order to improve the resource utilization and efficiency.
In the hazardous waste network design problem, the first stage strategic facility location decisions will not change with respect to the realization of different scenarios and are therefore robust. On the other hand, the second stage allocation and routing decisions are flexible and can be adjusted according to the realizations of different scenarios in order to optimize the overall effectiveness and efficiency of the hazardous waste management system. Therefore, considering the nature of the decision making, the determination of the network structure through the first-stage decision variables are more important due to their robust nature. These decisions will have a long-term impact on the system performance and cannot be easily altered without a significant cost.
3.2. Mathematical model
The modeling structure of a hazardous waste network design problem comprises four basic elements, namely, decision variables, parameters, objective functions and constraints. First, two types of variables are needed for the decision making at different stages. The binary variables are modeled to determine the facility locations and the continuous variables are formulated to make allocation decisions. Then, the input information is modeled as the parameters of the model, and the parameters with high uncertainty are modeled as scenario-dependent stochastic parameters. The model includes two objective functions in order to minimize both the cost and the risk related to collection, transportation, treatment and disposal of hazardous waste. Meanwhile, the model needs to be solved under several logistical constraints, i.e., demand fulfillment, flow balance, capacity limitation, compatibility requirement, etc.
Taking into account the requirements on the modeling structure, we develop a novel two-stage stochastic bi-objective MILP on the basis of the hazardous waste location-routing problem formulated by Alumur and Kara (2007) and Samanlioglu (2013). The main differences are summarized as follows:
-
1.
We extend the model in a stochastic environment in order to control uncertainty arising from different input parameters.
-
2.
We consider not only the facility selection problem, but also the operation of facility as well as its risk impact on the population exposure.
-
3.
We enhance the risk assessment formula by considering the combined risk impact from the different types of hazardous waste and different treatment technologies implemented.
The mathematical notation used in the model is first given in Table 2 .
Table 2.
Mathematical notation.
| Sets | |
| N = (P, Q) | Network of hazardous waste management system with nodes P and arcs Q |
| G, g | Set and index of generation points of hazardous waste, |
| T, t | Set and index of potential locations for treatment centers, |
| R, r | Set and index of potential locations for recycling centers, |
| D, d | Set and index of potential locations for disposal centers, |
| H, h | Set and index of different types of hazardous waste |
| V, v | Set and index of different treatment technologies |
| S, s | Set and index of scenarios |
| Parameters | |
| Fixed cost of opening a treatment center at location with technology | |
| , | Fixed cost of opening a recycling center at location and a disposal center at location |
| Variable cost of operating a treatment center at location with technology in scenario | |
| , | Variable cost in scenario of operating a recycling center at location and a disposal center at location |
| , | Cost of transporting one unit of hazardous waste in scenario on arc and on arc |
| , , | Cost of transporting one unit of residue in scenario on arc , on arc and on arc |
| Population risk along the arc for transporting hazardous waste in scenario | |
| Population risk along the arc in scenario | |
| Risk compensation multiplier for hazardous waste | |
| Population along the arc for transporting the waste residue in scenario | |
| Population risk around the potential location for treatment center with technology in scenario | |
| , | Population around the potential location for treatment center and around the potential location for disposal center in scenario |
| Risk compensation multiplier for technology | |
| Probability of the realization of scenario | |
| Generation of hazardous waste at point in scenario | |
| Recyclable fraction of hazardous waste in scenario | |
| , | Percentage of weight reduction of hazardous waste with technology and at recycling center |
| , | Recyclable fraction and disposal fraction of hazardous waste treated by technology , where |
| , | Capacity and minimum utilization rate of treatment center with technology |
| , | Capacity and minimum utilization rate of recycling center |
| , | Capacity and minimum utilization rate of disposal center |
| Compatibility between hazardous waste and technology . , If hazardous waste can be treated with the specific technology, , otherwise |
|
| An arbitrarily large number | |
| First-stage decision variables | |
| , , | Binary decision variable determines if a new facility is opened at respective candidate location |
| Second-stage decision variables | |
| Quantity of hazardous waste treated at with technology in scenario | |
| , | Quantity of waste treated at recycling center and at disposal center in scenario |
| , | Quantity of hazardous waste transported in scenario on arc and on arc |
| , , | Quantity of residue transported in scenario on arc , on arc and on arc |
The objective functions are formulated in Eqs. (1), (2) where the uncertainty is described by discrete scenarios from a probability distribution. Depending on the characteristics of the problems, the scenarios can be generated by different methods, e.g., sampling, statistical approaches, and simulation. The comparison of different scenario generation methods has been given by Di Domenica et al. (2007) and Löhndorf (2016). Eq. (1) minimizes the overall cost of opening and operating a hazardous waste management system. The first three terms are the fixed cost of establishing the network through opening different facilities, and they only involve the first-stage decision variables which should be robust throughout all the possible scenarios. The rest of Eq. (1) calculates the variable facility operating cost and transportation cost of hazardous waste management. The decision variables specify the second-stage and scenario-dependent decisions, through which the optimal operational plan of the hazardous waste management system is determined:
| (1) |
| (2) |
The second objective Eq. (2) minimizes the population exposure risk. In this equation, the first term calculates the transportation risk of hazardous waste and residue on arcs (g, t) and (t, d), and the second term represents the facility operating risk of the treatment facilities and disposal facilities. In risk management, the combined risk impact can be measured by the probability of occurrence of an event, multiplied by the value of the consequence of that event (Erkut and Verter, 1995). This idea has been widely adopted in hazardous waste management problems for risk assessment since the mid-1990s (Erkut and Verter, 1995), in which the probability of occurrence is proportional to the usage of arcs and facilities, and the value of the consequence is proportional to the population exposure (Current and Ratick, 1995). Besides, the methods developed in the 1990s (see, e.g. ReVelle et al. (1991) and Nema,and Gupta (1999)) have become the theoretical foundation for quantifying the parameters in the risk minimization objective function and have been applied in today’s modeling efforts. Traditionally, the facility operating risk has been formulated through the first-stage binary variables (Alumur and Kara, 2007), which means that if a facility is opened, there is an equal risk to the surrounding population regardless of the facility usage. However, for the same probability of occurrence of risk events, more facility usage leads to a higher probability of adverse events. Therefore, the formula for the measurement of facility operating risk can be improved with the second-stage continuous variables related to the facility usage (refer to Table 2 for the notation):
| (2a) |
| (2b) |
In this model, the risk minimization objective function is improved through the compensation of the consequence of the events in Eq. (2). As argued in Yu and Solvang (2016), the consequence of an event on the population exposure may vary significantly when transporting different types of hazardous waste or operating a facility with different technologies. Compared with other types of hazardous waste, a higher consequence is encountered when accidents happen on the transportation of explosive or radiative waste. For instance, the explosion of a tanker truck of hazardous materials on June 13th, 2020, caused 19 casualties and 170 injuries in Zhejiang, China (BBC, 2020). Therefore, the consequence of an event is not only determined by the population exposed, but also by the type and quantity of hazardous waste transported and the treatment technology implemented. Eqs. (2a), (2b) are used to compensate the technology-related risk on facility and waste-related risk on arc (g, t) to the population exposure, which imply the transportation and treatment of different types of hazardous waste may impose different levels of risk.
Seven sets of constraints are formulated as follows. The first set is the demand fulfillment constraint. Eq. (3) requires the hazardous waste generated at each generation point to be totally collected and sent for recycling or treatment in all scenarios. Eq. (4) specifies that different types of the hazardous waste can be recycled with a fraction which is a quality-dependent stochastic parameter:
| (3) |
| (4) |
Eqs. (5), (6), (7) are the mass balance constraints at the treatment facilities of hazardous waste. There will be a mass loss of the input of hazardous waste treated with different technologies. For different types of hazardous waste, they can be converted to recyclable fraction and disposal fraction at a fixed rate:
| (5) |
| (6) |
| (7) |
Eqs. (8), (9) are the mass balance constraints at the recycling centers. Eq. (8) calculates the input amount from both generation points and treatment centers. Eq. (9) calculates the output amount of the residue sent to disposal centers:
| (8) |
| (9) |
Eq. (10) is the mass balance constraint at the disposal centers, which adds the input amount from both the recycling centers and the treatment centers:
| (10) |
Constraints (11–16) are the capacity and utilization requirements for treatment centers, recycling centers and disposal centers, respectively, through which the upper and lower limits of a facility are specified:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Constraints (17) are the compatibility constraint for treatment facilities, which require the hazardous waste to be processed at a treatment center only when the type of hazardous waste is compatible with the treatment technology installed:
| (17) |
The last constraints define the domains of the decision variables:
| (18) |
| (19) |
4. Algorithm
Stochastic multi-objective problems are highly complicated optimization problems, especially in view of the fact that the conflict among several objective functions and the influence from different uncertainties have to be simultaneously considered. Hence, we use a sample average approximation based goal programming (SAA-GP) approach to solve the model heuristically.
4.1. Sample average approximation (SAA)
An optimal solution of a stochastic programming model is one with the best and most reliable performance throughout all the possible scenarios (Yu and Solvang, 2018). The number of scenarios in a stochastic optimization problem can be very large, which may lead to a significant computational challenge. In this regard, sample average approximation (SAA) has been extensively applied to solve a wide variety of problems, e.g. network design (Ayvaz et al., 2015), vehicle routing (Verweij et al., 2003), and supply chain operations (Schütz et al., 2009). SAA is a Monte Carlo simulation based approach used to solve stochastic optimization problems with a large number of scenarios. Instead of solving the original problem, SAA approximates its optimal solution value with a high level of confidence through repeatedly solving a number of smaller sized problems:
| (20) |
Eq. (20) defines a two-stage stochastic minimization problem, where and are first-stage decisions and second-stage decisions within a finite feasible solution space (e.g. a finite set of ). is a random vector with probability , is the expected resource value of a given first-stage decision and probability . The purpose of Eq. (20) is to minimize the sum of the first-stage value and expected resource value with respect to the first-stage decisions, and the real value of can be calculated as: (Kleywegt et al., 2002). In SAA as well as other sampling methods, a sample with a set of discrete scenarios is generated based in using the probability distribution . Instead of calculating the real value of , the expected resource value can be approximated by the sample average function (Verweij et al., 2003). Eq. (21) shows the converted SAA problem of the original stochastic optimization problem given in Eq. (20):
| (21) |
The optimal solution of Eq. (21) with respect to scenarios is and the optimal solution value is . With the increase on the sample size , converges to the optimal solution value of the original stochastic optimization problem (Kleywegt et al., 2002). Even though several attempts have been made to give a theoretical basis for determining the sample size required for a SAA problem (Shapiro, 2003; Kleywegt et al., 2002), the number calculated with these formulas is usually much more than what is required to obtain a solution with acceptable performance (King and Wallace, 2012). Hence, in practice, different sample sizes may be tested taking into account of the balance between the quality of solution and computational efforts required.
The implementation of the SAA method can be described through the following procedure:
Step 1: independent samples with scenarios are randomly generated based upon a given probability distribution. Then, Eq. (21) is repeatedly solved times, and the optimal values and the candidates for the first-stage decisions are , …, and , …, respectively:
| (22) |
| (23) |
Step 2: The average value and variance of all the optimal value are calculated by Eqs. (22), (23), and a statistical lower bound of the original stochastic optimization problem is estimated by (Mak et al., 1999):
| (24) |
Step 3: This step is to estimate the upper bound of the original stochastic optimization problem with a feasible candidate of the first-stage decisions (e.g. the one with the best ) and a reference sample with scenarios, as shown in Eq. (24). The reference sample is generated independently with a large number of scenarios and hence is used to represent the original problem. Since the first-stage decisions have already been made by , the problem becomes a linear program which consists of determining only the second-stage decisions, which is computationally manageable even if is much larger than . Then, the variance of is estimated by Eq. (25):
| (25) |
Step 4: In order to evaluate the quality of the solutions obtained by solving the SAA problem, the estimators of the optimality gap and the corresponding variance are calculated by Eqs. (26), (27):
| (26) |
| (27) |
Step 5: This step evaluates the performance and if the convergence criterion is fulfilled (e.g. the gap estimator and variance estimator are reasonable), the procedure can be stopped, and the optimal value as well as the optimal first-stage decisions of the original stochastic optimization problem can be approximated by selecting the candidate solutions with the best performance in the reference sample . Otherwise, the above procedures must be repeated with increased or until the convergence criterion is met.
4.2. Goal programming (GP)
The network design of a hazardous waste management system is a multi-objective optimization problem which aims at simultaneously balancing the trade-off between system operating cost and the risk related to facility operation and transportation. An optimal solution to a multi-objective optimization problem is called “Pareto-optimal solution”. In such a solution, the value of one objective function cannot be improved without deteriorating the value on the other objectives (Sakawa et al., 2013). Goal Programming (GP) is an a priori method for determining the Pareto-optimal solution of a multi-objective optimization problem, in which the priority or relative importance of each objective has to be determined in advance (e.g. with lexicographic method or weight). The GP method was put forward by Charnes et al. (1955), and its objective is to minimize the overall unwanted deviations from the target value of all the objective functions. Eq. (28) presents a general form of GP given by Charnes and Cooper (1977):
| (28) |
The objective function minimizes the sum of the overachievement () and underachievement () from the goal value of all the objective functions. The second and third equations are called goal constraint and system constraint, respectively. The last constraint requires the deviations from the goal value is non-negative. It is noteworthy that both the overachievement and the underachievement to one goal cannot happen at the same time, so that . The advantage of GP in the context of a multi-objective optimization problem is the simplicity of its implementation and the clarity of the result interpretation. When using GP, the goal value of each objective is first determined usually by solving each individual single objective optimization problem. Then the relative importance of each objective is specified. In this paper, weighted GP is used to represent the importance of each objective in decision making, as shown in Eq. (29):
| (29) |
Finally, a Pareto-optimal solution with respect to the goal value and corresponding importance of the objective functions can be calculated. In addition, because the units of different objective functions may not be comparable (e.g. the units for cost and risk in hazardous waste management), the deviations from the goal are first normalized before they are weighted and summed in Eq. (29).
4.3. Stepwise procedures for the SAA-GP method
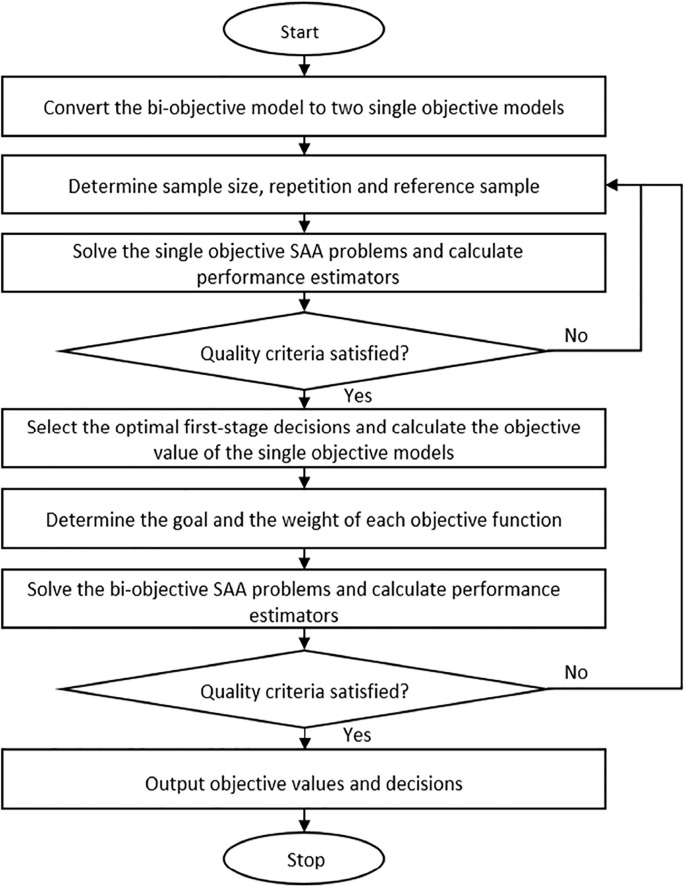
Fig. 2 shows the flowchart of the SAA-GP algorithm for solving the proposed mathematical model, which can be implemented by the following procedure:
Step 1: Convert the original bi-objective stochastic model into two individual single objective stochastic optimization problems:
Fig. 2.
Flowchart of the SAA-GP algorithm.
Cost minimization: Eq. (1) and constraints (3–19).
Risk minimization: Eq. (2) and constraints (3–19).
Step 2: Set up the number of scenarios , the number of repetitions and the size of the reference sample (considered as the original stochastics problem) in the experiment. Then, using a given probability distribution of the stochastic parameters, independent samples with scenarios as well as the reference sample are generated.
Step 3: Solve both cost minimization and risk minimization repeatedly for times, and then the lower and upper bound estimators for performance evaluation can be calculated by Eqs. (22), (23), (24), (25), (26), (27).
Step 4: Evaluate the performance of the estimators with respect to and for both cost minimization and risk minimization. The lower bound estimators evaluate the in-sample stability of the SAA problems and the upper bound estimators evaluate the quality of the SAA to the original problem. If the quality requirements are fulfilled, proceed to Step 5. Otherwise, the Steps 2–4 should be iterated with increased sample size or repetitions until all the quality requirements are met.
Step 5: Calculate the optimal objective value and selecting the optimal first-stage decision for both single objective optimization problems by testing each candidate in the reference sample.
Step 6: Set the goals of each objective to its optimal value obtained in the previous step and demeaning the weight combination. The original bi-objective stochastic problem is then converted to a weighted GP by Eq. (29).
Step 7: Repeatedly optimize the weighted GP with scenarios for times. Then, calculate the estimators for performance evaluation to the corresponding cost and risk in each optimal solution by Eqs. (22), (23), (24), (25), (26), (27).
Step 8: Evaluate the performance, and if the quality requirements are fulfilled, proceed to the next step. Otherwise, repeat Steps 2–8 with increased sample size or repetitions until all the quality requirements are met.
Step 9: Choose the optimal first-stage decision on location selection and, by solving the reference sample with the given weight combination, calculate the objective values and the deviation of cost and risk from their goals.
5. Numerical experiments, discussion and sensitivity analyses
In this section, we present numerical experiments in order to validate the proposed mathematical model and the SAA-GP method.
5.1. Test instances
The numerical experiments include eight generation points, five candidates for treatment facility, five candidates for recycling facility and three candidates for disposal facility. All the parameter values are randomly generated within a given interval. Table 3 presents the facility-related parameters used in the numerical experiments.
Table 3.
Parameters of the candidate locations for treatment facility, recycling center and disposal center.
| Facility | Parameter | Candidate locations |
||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Treatment | Fixed cost | 6,113,721 | 6,038,976 | 6,029,742 | 7,936,913 | 6,798,470 |
| Compensation factor | 1.64 | 1.66 | 1.66 | 1.26 | 1.47 | |
| Capacity | 2594 | 2943 | 2388 | 2579 | 2353 | |
| Recycling | Fixed cost | 4,236,571 | 5,261,293 | 4,376,145 | 5,281,432 | 4,934,609 |
| Capacity | 1610 | 1737 | 1829 | 1781 | 1639 | |
| Disposal | Fixed cost | 4,899,205 | 4,449,917 | 3,209,821 | ||
| Compensation factor | 2.04 | 2.25 | 3.12 | |||
| Capacity | 4490 | 3514 | 4332 | |||
Within the planning horizon, the model considers the uncertainty existed in several input parameters related to the generation, composition, treatment and transportation of hazardous waste. These stochastic parameters follow a discrete uniform distribution. Table 4 provides the generation intervals of the stochastic parameters, based on which all test problems are randomly generated. Furthermore, to implement the SAA-GP method, we tested different sample sizes with 20, 40 and 60 scenarios, and the number of repetition was set to 10. The size of the reference sample was set to 500 scenarios, and is considered to be the original stochastic optimization problem. For comparison purposes, a deterministic counterpart with the mean value of all stochastic parameters was also tested. All the optimization problems were coded and solved by a commercial optimization solver: LINGO 17.0 on a computer with Inter Core i5 2.2 GHz CPU and 8 GB RAM operated under Windows 10 operating system.
Table 4.
Generation intervals of the stochastic parameters.
| Stochastic parameter | Generation interval |
|---|---|
| Unif (400, 600) | |
| Unif (600, 800) | |
| Unif (200, 300) | |
| Unif (4000, 6000) | |
| Unif (3000, 4000) | |
| Unif (600, 1000) | |
| Unif (500, 800) | |
| Unif (500, 800) | |
| Unif (800, 1200) | |
| Unif (600, 800) | |
| Unif (6000, 10000) | |
| Unif (3000, 5000) | |
| Unif (600, 900) | |
| Unif (20%, 40%) |
6. Results and discussion
In the initial step, two single objective optimization problems for cost minimization and risk minimization were solved. Table 5 presents the statistical lower bounds, upper bounds and the estimators for quality evaluation of samples with increased sizes: 20, 40 and 60. The statistical lower bound is the mean of the optimal value of 10 repetitions (Mak et al., 1999), and the upper bound is calculated through optimizing the reference sample with one of the feasible first-stage decisions obtained from the SAA problems. For the lower bounds, the variances decrease significantly with the increase on the sample size for both cost and risk objectives. However, the variances are stable for the upper bounds. It is noteworthy that the estimated optimality gap of cost minimization remains relatively stable when increases from 20 to 40, but it reduces dramatically when = 60. Comparing it with the cost minimization objective, the estimated optimality gap of risk minimization objective is much higher when = 20, and it decreases consistently and considerably with the increase in the sample size.
Table 5.
Statistical lower bounds, upper bounds and the estimators for quality evaluation.
| Sample size | Repetition | Objective | Lower bound |
Upper bound |
Gap estimators |
||||
|---|---|---|---|---|---|---|---|---|---|
| % | |||||||||
| = 20 | = 10 | Cost | 43,186,456 | 175,394 | 43,250,895 | 809,434 | 64,439 | 0.15 | 828,219 |
| Risk | 96,467,552 | 1,512,030 | 97,711,236 | 8,528,440 | 1,243,684 | 1.29 | 8,661,439 | ||
| = 40 | = 10 | Cost | 43,181,245 | 130,564 | 43,250,895 | 809,434 | 69,650 | 0.16 | 819,896 |
| Risk | 97,021,695 | 1,016,312 | 97,402,577 | 8,596,540 | 380,882 | 0.39 | 8,656,408 | ||
| = 60 | = 10 | Cost | 43,252,268 | 86,316 | 43,250,895 | 809,434 | −1373 | 0 | 814,023 |
| Risk | 97,723,873 | 651,248 | 97,513,812 | 8,681,283 | −210,061 | −0.22 | 8,705,676 | ||
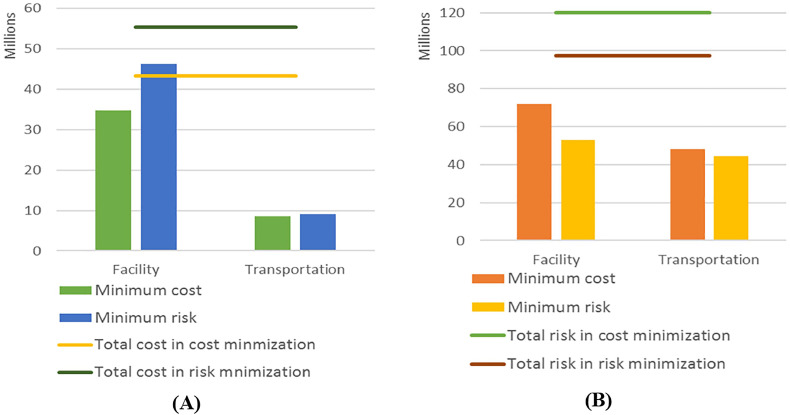
As can be seen, the quality of solutions improves greatly with the increase of sample size, so = 60 was selected to test the GP problem. One of the most important benefits of repeatedly solving SAA problems is to obtain a robust first-stage decision of the original stochastic optimization problem (Schütz et al., 2009), which yields the best performance in the reference sample. For the cost minimization objective, the first-stage decisions are stable and identical through all the SAA problems, where t = (2, 3), r = (1, 3, 5) and d = (3) are selected and the minimum cost is 43,250,900. For the risk minimization objective, 10 candidates found by the SAA problems are tested in the reference sample. In the optimal solution, t = (1, 4, 5), r = (3, 4, 5) and d = (1) are opened and the minimum risk is 97,402,580. Fig. 3 compares the optimal results of the cost minimization and risk minimization objectives. Compared with transportation, facility operation has more impact on both cost and risk performance of the tested numerical example. With the risk minimization objective, more facilities are selected, which leads to a significant increase in the facility operating cost.
Fig. 3.
Comparison of the optimal solutions of the cost minimization and risk minimization objectives: (A): Total cost, facility operation cost and transportation cost; (B) Total risk, facility operation risk and transportation risk.
The minimum cost and minimum risk obtained from the single objective optimization are considered as the goals of the GP. In order to minimize the weighted deviations from the goals, a weight combination with w 1 = 0.5 and w 2 = 0.5 was tested. The corresponding SAA-GP problems with = 60 were repeatedly solved 10 times and the result is given in Table 6 . This table presents the cost, the risk as well as the deviations from their goals in the optimal solution of each repetition, and the first-stage decisions are also provided. In the SAA-GP problem, the optimal solution is obtained through optimizing the trade-off between the weighted cost deviation and the risk deviation. The performance between the different objectives and between the first-stage decisions may vary significantly throughout the repetitions.
Table 6.
Cost, risk, deviation and first-stage decisions in the 10 repetition with = 60 and w1 = 0.5.
| Repetition | Cost | Deviation % | Risk | Deviation % | First-stage decisions |
||
|---|---|---|---|---|---|---|---|
| t | R | d | |||||
| 1 | 47,892,370 | 10.73 | 97,739,620 | 0.35 | 4, 5 | 1, 3, 5 | 1 |
| 2 | 45,822,090 | 5.94 | 101,572,500 | 4.28 | 2, 5 | 1, 3, 5 | 1 |
| 3 | 47,248,020 | 9.24 | 100,896,900 | 3.59 | 2, 4 | 1, 3, 5 | 1 |
| 4 | 47,021,950 | 8.72 | 98,681,730 | 1.31 | 2, 4 | 1, 3, 5 | 1 |
| 5 | 45,273,500 | 4.68 | 103,533,700 | 6.30 | 1, 2 | 1, 3, 5 | 1 |
| 6 | 45,308,100 | 4.76 | 103,358,100 | 6.11 | 1, 2 | 1, 3, 5 | 1 |
| 7 | 47,127,450 | 8.96 | 98,989,440 | 1.63 | 1, 4 | 1, 3, 5 | 1 |
| 8 | 47,029,250 | 8.74 | 98,493,990 | 1.12 | 1, 4 | 1, 3, 5 | 1 |
| 9 | 47,095,480 | 8.89 | 99,711,530 | 2.37 | 2, 4 | 1, 3, 5 | 1 |
| 10 | 45,154,750 | 4.4 | 103,590,000 | 6.35 | 2, 3 | 1, 3, 5 | 1 |
Table 7 shows the statistical lower bound, the upper bound and the estimators for quality evaluation for both the cost and the risk objectives. Compared with the single objective optimization, the estimated optimality gaps are much higher for both objectives in the SAA-GP problems, but they are still at an acceptable level to guarantee a confident solution. Through the repetitions, six candidates are generated and tested in the reference sample, and the best one is to open t = (1, 2), r = (1, 3, 5) and d = (1). In the best solution, the cost deviation is 4.64% and the risk deviation is 6.34%.
Table 7.
Statistical lower bound, upper bound and the estimators for quality evaluation for 10 repetition with = 60 and w1 = 0.5.
| Goal | Lower bound |
Upper bound |
Gap estimators |
||||
|---|---|---|---|---|---|---|---|
| % | |||||||
| Cost | 46,497,296 | 999,620 | 47,088,714 | 803,281 | 591,418 | 1.27 | 1,282,381 |
| Risk | 100,656,751 | 2,256,733 | 99,560,882 | 9,314,344 | −1,095,869 | −1.09 | 9,583,833 |
For comparison purposes, the problem was also solved in its deterministic form by replacing the stochastic parameters by their mean value. The optimal solution of the deterministic model is to open t = (1, 4), r = (1, 3, 5) and d = (1), and the cost deviation is 8.37% and the risk deviation is 1.44%. The first-stage decision from the optimization of the deterministic model was tested in the reference sample. It is infeasible due to the capacity limitation of the treatment facilities and more facilities should be opened to deal with the demand fluctuation in the stochastic problem. This eventually results in an increase in both cost and risk.
Fig. 4 shows a comparison of both cost and risk between the optimal solutions obtained by the stochastic model and deterministic model. The difference in performance can be measured by the expected value of modeling uncertainty (EVMU) or by the value of the stochastic solution (VSS) (Birge and Louveaux, 2011). The EVMU is an indicator used to illustrate the benefit achieved by using a stochastic model. The procedure applied to calculate EVMU is first to replace the stochastic parameters with their mean value and then solve the mean - value problem in order to obtain the first-stage decision. Then, using that first-stage decision to optimize the corresponding stochastic problem, and the EVMU can be calculated with Eq. (30):
| (30) |
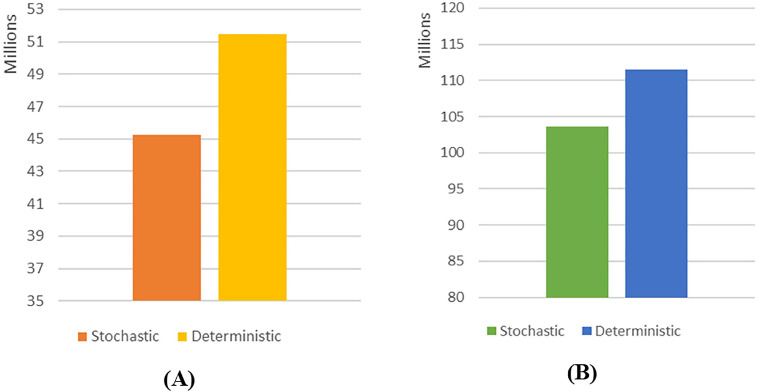
Fig. 4.
Comparison of the performance of the first-level decisions obtained by both deterministic and stochastic models in the original stochastic problem: (A) Cost; (B) Risk.
With a stochastic model, by installing only 7.04% more capacity for the treatment centers, the overall performance of the hazardous waste management system can be dramatically improved, with a 12.07% reduction in total cost and a 7.17% reduction in total risk, respectively, compared with the optimal decision computed through a deterministic model. Even if some authors argue that the network flexibility may be used to overcome the demand fluctuation, e.g., by outsourcing (King and Wallace, 2012) or by reducing the service level (Yu and Solvang, 2017b), it may not be a solution for hazardous waste management in which stringent regulations are implemented in order to yield a timely and proper treatment for all the hazardous waste generated within a certain period. In addition, due to the complex nature of hazardous waste treatment and transportation, only a few highly qualified companies and service providers can be involved, which limits the outsourcing options and network flexibility. Hence, in this regard, a robust decision on network configuration obtained by a stochastic programming model may significantly outperform its deterministic counterpart.
6.1. Sensitivity analyses
Sensitivity analyses with different weight combinations were also performed. To this end, 11 scenarios were tested with the weight of the cost deviation gradually decreasing from 1 to 0 by steps of 0.1 in each scenario, while the weight of risk deviation increases in the opposite way. Table 8 shows the lower bounds, the upper bounds and the estimators of the optimality gap in the sensitivity analysis, and the gap between lower bound and upper bound in all the test scenarios is acceptable for generating solutions having a sufficient confidence level.
Table 8.
Statistical lower bounds, upper bounds and the estimators for quality evaluation in the sensitivity analysis with changing weight combination.
| Weight | Goal | Lower bound |
Upper bound |
Gap estimators |
||||
|---|---|---|---|---|---|---|---|---|
| % | ||||||||
| w1 = 1 | Cost | 43,252,268 | 86,316 | 43,250,895 | 809434 | −1373 | 0 | 814,023 |
| Risk | 119,952,310 | 967,360 | 119,895,022 | 10,839,277 | −57,288 | −0.05 | 10,882,358 | |
| w1 = 0.9 | Cost | 43,475,060 | 148,551 | 43,281,984 | 813,666 | −193,076 | −0.44 | 827,115 |
| Risk | 117,960,070 | 1,269,067 | 118,560,005 | 10,703,293 | 599,935 | 0.51 | 10,778,266 | |
| w1 = 0.8 | Cost | 43,425,067 | 120,239 | 43,349,774 | 815,638 | −75,293 | −0.17 | 824,452 |
| Risk | 117,384,540 | 964,128 | 104,244,613 | 9,809,252 | 51,613 | 0.05 | 9824,419 | |
| w1 = 0.7 | Cost | 45,115,179 | 100,370 | 45,090,960 | 809,304 | −24,219 | −0.05 | 815,504 |
| Risk | 104,193,000 | 545,693 | 104,244,613 | 9,809,252 | 51,613 | 0.05 | 9,824,419 | |
| w1 = 0.6 | Cost | 45,151,484 | 105,368 | 45,132,280 | 814,186 | −19,204 | −0.04 | 820,976 |
| Risk | 103,933,240 | 594,219 | 104,066,758 | 9,783,581 | 133,518 | 0.13 | 9,801,610 | |
| w1 = 0.5 | Cost | 46,497,296 | 999,620 | 47,088,714 | 803,281 | 591,418 | 1.27 | 1,282,381 |
| Risk | 100,656,751 | 2,256,733 | 99,560,882 | 9,314,344 | −1,095,869 | −1.09 | 9,583,833 | |
| w1 = 0.4 | Cost | 47,281,433 | 309,679 | 47,106,247 | 806,902 | −175,186 | −0.37 | 864,287 |
| Risk | 99,134,692 | 1,046,516 | 99,528,192 | 9,309,252 | 393,500 | 0.40 | 9,367,890 | |
| w1 = 0.3 | Cost | 47,304,111 | 299,695 | 47,118,668 | 810,118 | −185,443 | −0.39 | 863,776 |
| Risk | 99,106,560 | 1,042,259 | 99,512,380 | 9,304,577 | 405,820 | 0.41 | 9,362,770 | |
| w1 = 0.2 | Cost | 47,313,976 | 296,886 | 47,133,044 | 811,360 | −180,932 | −0.38 | 863,971 |
| Risk | 99,099,020 | 1,041,099 | 99,501,415 | 9,303,115 | 402,395 | 0.41 | 9,361,188 | |
| w1 = 0.1 | Cost | 50,023,629 | 3,383,297 | 53,930,043 | 813,174 | 3,906,414 | 7.81 | 3,479,648 |
| Risk | 98,370,287 | 818,338 | 97,516,075 | 8,681,971 | −854,212 | −0.87 | 8,720,453 | |
| w1 = 0 | Cost | 59,850,556 | 3,259,162 | 60,620,437 | 825,052 | 769,880 | 1.29 | 3,361,970 |
| Risk | 97,723,873 | 651,248 | 97,513,812 | 8,681,283 | −210,061 | −0.22 | 8,705,676 | |
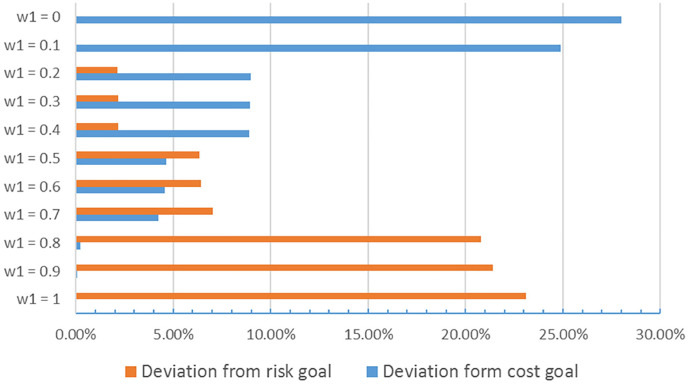
Fig. 5 presents the cost deviation and risk deviation of the Pareto-optimal solutions with varying weight combinations. When w 1 = 0 and 0.1, the risk level is minimized, but there is a large deviation in the cost goal. On the other hand, when w 1 = 0.8, 0.9 and 1, the cost approaches the optimal value, but the risk significantly deviates from its goal. In the other scenarios, the deviations from the cost and risk goals must be balanced with one another, so it is of particular interest to investigate the system behavior under these scenarios.
Fig. 5.
Sensitivity analysis with varying weight combination.
One of the most important purposes of using a two-stage stochastic programming model is to obtain a robust first-stage decision. Table 9 compares the first-stage decisions generated by both the deterministic model and the stochastic model. We first observe that the network configuration varies greatly with the change of focus on the system design. Second, in some scenarios (w 1 = 0, 0.1, 0.7, 0.8, 0.9 and 1), a deterministic model can also yield a good first-stage decision. However, in the other scenarios, especially when the balance between cost deviation and risk deviation is emphasized, the decisions made by a stochastic model are much better with respect to system performance. Third, in a multi-objective optimization problem under uncertainty, even though the overall system performance is better with the decision made by a stochastic model, the performance of individual objectives may increase monotonically, as can be seen when w 1 = 0.2 and 0.3.
Table 9.
Fist-stage decisions obtained by both deterministic and stochastic model as well as the EVMU in percentage in the sensitivity analysis with change weight combinations.
| Weight | First-stage decisions |
EVMU % |
||||||
|---|---|---|---|---|---|---|---|---|
| Deterministic |
Stochastic |
Cost | Risk | |||||
| t | r | d | t | r | d | |||
| w1 = 1 | 2, 3 | 1, 3, 5 | 3 | 2, 3 | 1, 3, 5 | 3 | 0 | 0 |
| w1 = 0.9 | 1, 2 | 1, 3, 5 | 3 | 1, 2 | 1, 3, 5 | 3 | 0 | 0 |
| w1 = 0.8 | 2, 3 | 1, 3, 5 | 3 | 2, 3 | 1, 3, 5 | 3 | 0 | 0 |
| w1 = 0.7 | 2, 3 | 1, 3, 5 | 1 | 2, 3 | 1, 3, 5 | 1 | 0 | 0 |
| w1 = 0.6 | 1, 3 | 1, 3, 5 | 1 | 1, 2 | 1, 3, 5 | 1 | 8.64 | 9.93 |
| w1 = 0.5 | 1, 4 | 1, 3, 5 | 1 | 1, 2 | 1, 3, 5 | 1 | 12.07 | 7.17 |
| w1 = 0.4 | 4, 5 | 1, 3, 5 | 1 | 2, 4 | 1, 3, 5 | 1 | 9.74 | 9.96 |
| w1 = 0.3 | 4, 5 | 1, 3, 5 | 1 | 2, 4 | 1, 3, 5 | 1 | 12.72 | −2.15 |
| w1 = 0.2 | 4, 5 | 1, 3, 5 | 1 | 2, 4 | 1, 3, 5 | 1 | 12.72 | −2.15 |
| w1 = 0.1 | 4, 5 | 1, 3, 5 | 1 | 1, 4, 5 | 1, 3, 5 | 1 | 0 | 0 |
| w1 = 0 | 4, 5 | 3, 4, 5 | 1 | 1, 4, 5 | 3, 4, 5 | 1 | 0 | 0 |
7. Case study
The model was applied in a case study of healthcare waste management from the third-level grade-A hospitals in Wuhan, which are the top tier hospitals in China. Wuhan is the capital of Hubei province and is a megacity with more than 10 million residents. The total generation of healthcare waste in Wuhan is 17,300 tons (Ministry of Ecology and Environment of People’s Republic of China, 2019), which are mainly from four types of healthcare institutions including hospitals, healthcare centers, community health service centers, and maternity and child care hospitals. Table 10 illustrates the number of beds and the utilization rate of beds at these healthcare institutions, based on which the annual generation of healthcare waste per bed can be estimated by and is 0.216 tons/bed/year. There are 30 third-level grade-A hospitals, which have 35,769 clinical beds in total and contribute to 41.2% healthcare waste generation in Wuhan (Statistical yearbook of Wuhan, 2018). It is assumed the total healthcare waste generation in the planning horizon will be increased by 30%, and the healthcare waste generation is proportional to the number of beds and the utilization rate at each healthcare institution. Based on these assumptions, the number, name, total number of beds, and projected annual healthcare waste generation of the third-level grade-A hospitals in Wuhan are given in Table A1 (Appendix A).
Table 10.
Number of beds and utilization rate of beds at different healthcare institutions in Wuhan.
| Healthcare institutions | Number of beds (Units) | Utilization rate of beds (%) |
|---|---|---|
| Hospitals | 78,447 | 92.51 |
| Healthcare centers | 4530 | 66.24 |
| Community health service centers | 6215 | 45.47 |
| Maternity and child care centers | 1877 | 99.61 |
Data source: Statistical yearbook of Wuhan (2018).
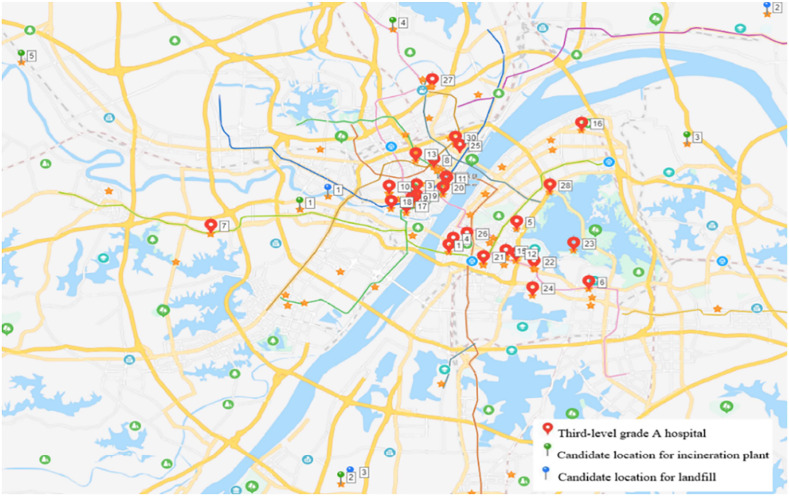
Due to the highly infectious nature, the recycling of healthcare waste is not performed at the current stage in Wuhan. Instead, the healthcare waste is first treated at a specialized incineration plant at Guodingshan before they are sent to the landfill. In this study, we considered all the five incineration plants in Wuhan as candidate locations for opening specialized facility for the treatment of healthcare waste. The residue from incineration plants can be sent to the landfills at Zixiaguan, Changshankou and Chenjiachong. The Baidu map (https://map.baidu.com) was used to identify the locations of hospitals, incineration plants and landfills and also to calculate the distance among these locations. Fig. 6 shows the locations of respective nodes. The distance matrixes between hospitals and incineration plants and between incineration plants and landfills are given in Tables A2 and A3, respectively. The parameters of the candidate locations for treatment centers and disposal centers are given in Table 11 . The transportation cost of healthcare waste is proportional to the travel distance between two nodes and the unit transportation cost is set to 40 yuan/km (Zhao et al., 2016).
Fig. 6.
Locations of the third-level grade-A hospitals, incineration plants and landfills in Wuhan.
Table 11.
Parameters of the candidate locations.
| Facility | Candidate number | Location (District) | Population density (people/sq. km) | Fixed cost (yuan/year) | Unit processing cost (yuan/ton) | Capacity (ton/year) |
|---|---|---|---|---|---|---|
| Incineration plant | 1 | Hanyang | 5898 | 10,000,000 | 1200 | 11,000 |
| 2 | Jiangxia | 453 | 8,000,000 | 1200 | 11,000 | |
| 3 | Qingshan | 9349 | 12,000,000 | 1200 | 11,000 | |
| 4 | Huangpi | 437 | 8,000,000 | 1200 | 11,000 | |
| 5 | Dongxihu | 1133 | 9,000,000 | 1200 | 11,000 | |
| Landfill | 1 | Hanyang | 5898 | 8,000,000 | 900 | 8000 |
| 2 | Xinzhou | 616 | 6,000,000 | 900 | 8000 | |
| 3 | Jianxia | 453 | 5,000,000 | 900 | 8000 |
Data source of population density: Statistical yearbook of Wuhan (2018).
In order to evaluate the risk impact of the healthcare waste management system, the population exposure within a bandwidth of 800 m along each transportation route was first estimated (ReVelle et al., 1991; Alumur and Kara, 2017). Then, the population exposure was calculated by (Zhao and Huang, 2019). Furthermore, the risk impact to population exposure of the transportation of untreated healthcare waste is higher than that of the residue. Hence, the was set to 1.3 in this study. The waste-to-residue conversion rate at the incineration plant was assumed to 0.2 (Zhao et al., 2016). The risk of facility operation is related to both population exposure and the implemented technologies. The population exposure within a radius of 3 km from the facility was used and was thus calculated by . Considering the diffusion of hazardous smoke from the combustion of healthcare waste, the risk impact to the population exposed to incineration plants was compensated by .
The model parameters were first generated in deterministic forms. Taking into account the randomness of the input information, the stochastic parameters were then generated from an uniform distribution on . Herein, and are the lower bound and the upper bound of the parameter interval, which can be calculated by and , respectively (Pishvaee and Razmi, 2012). The samples size was set to 60. In the case study, the value of was set to 10%, 20% and 30%. We compared three scenarios with different weight combinations , and . The computational results are presented in Table 12 . With the change of from 10% to 30%, the computational results, in general, show high stability in both objective values and facility location decisions. Besides, when increases from 0.5 to 0.7, the network configuration and objective values are not changed. However, when decreases from 0.5 to 0.3, one more incineration plant is opened at Hankounan, which result in changes in both cost and risk. Finally, under the realistic situation, another set of experiments was tested in order to evaluate the model’s computational performance, where the weight combination was set to and the sample size was set to 20. The result is presented in Table 13 .
Table 12.
Computational result.
| Scenario | Objective value |
Facility selection |
CPU time (s) | |||
|---|---|---|---|---|---|---|
| Cost (yuan) | Risk | Incineration | Landfill | |||
| S1 | 10% | 39,289,706 | 1,880,790,279 | Changshankou | Changshankou | 51 |
| 20% | 39,297,148 | 1,891,555,270 | Changshankou | Changshankou | 45 | |
| 30% | 39,233,298 | 1,864,974,160 | Changshankou | Changshankou | 19 | |
| S2 | 10% | 39,289,706 | 1,880,790,279 | Changshankou | Changshankou | 186 |
| 20% | 39,297,148 | 1,891,555,270 | Changshankou | Changshankou | 78 | |
| 30% | 39,233,298 | 1,864,974,160 | Changshankou | Changshankou | 55 | |
| S3 | 10% | 44,468,037 | 1,711,485,811 | Changshankou and Hankoubei | Changshankou | 13 |
| 20% | 44,534,915 | 1,698,147,950 | Changshankou and Hankoubei | Changshankou | 16 | |
| 30% | 44,723,216 | 1,655,355,272 | Changshankou and Hankoubei | Changshankou | 15 | |
Table 13.
Computational performance.
| Instance | Problem size |
Computational performance |
||||
|---|---|---|---|---|---|---|
| Hospital | Incineration | Disposal | CPU time (s) | Solver type | Solver interactions | |
| 1 | 30 | 10 | 10 | 6 | B-and-B | 16,661 |
| 2 | 30 | 20 | 20 | 49 | B-and-B | 117,310 |
| 3 | 30 | 30 | 30 | 71 | B-and-B | 157,765 |
| 4 | 50 | 30 | 30 | 331 | B-and-B | 953,295 |
| 5 | 50 | 40 | 40 | 537 | B-and-B | 1,524,667 |
| 6 | 50 | 50 | 50 | 539 | B-and-B | 983,286 |
| 7 | 80 | 50 | 50 | 694 | B-and-B | 1,167,708 |
| 8 | 80 | 80 | 80 | 4644 | B-and-B | 2,329,267 |
| 9 | 100 | 80 | 80 | 4422 | B-and-B | 2,115,509 |
| 10 | 150 | 100 | 100 | 12,572 | B-and-B | 7,046,249 |
Compared with the current incineration plant at Guodingshan, the computational results suggest opening a new incineration plant for healthcare waste at Changshankou is a better choice. Even though the total transportation cost could be minimized by operating a healthcare waste incineration plant at Guodingshan due to its close proximity to the city center, it imposes significant risks to a large population exposed and has thus been complained by nearby residents for many years (Hu et al., 2015). Furthermore, when the decision making on network design favors more on risk control and minimization, another healthcare waste incineration plant would be selected at Hankoubei and would thus be significantly increase the facility operating cost. However, on the other hand, the healthcare waste generated at different hospitals can be allocated to these two incineration plants based on the proximity, which optimizes the transportation network and reduces both risk and cost related to the transportation. Moreover, the focus on risk control equips the system with a larger capacity that may be used to better deal with the future uncertainty. For instance, the outbreak of the novel coronavirus disease (COVID-19) from December 2019 (Wu et al., 2020) in Wuhan causes several challenges in the prevention of epidemic spread, among which the transportation and treatment of highly infectious and rapidly increased healthcare waste is one of the most significant logistical problems (Yu et al., 2020). In this regard, a system planning with more focus on risk minimization may be of vital importance in order to deliver timely and responsive logistical service for removing the infectious healthcare waste at hospitals, which may drastically reduce the exposure risk for both medical staffs and patients. In addition, taking into account the uncertainty related to the input information, the cost estimation given by the stochastic model may be more realistic (King and Wallace, 2012), so it may result in a more robust and reliable decision making.
8. Conclusions
The network design of a hazardous waste management system is a complex decision making problem that needs to achieve a trade-off between system operating cost and population exposure risk. It is also influenced by a high level of uncertainty within the planning horizon. Unlike the network design of the other logistical systems and supply chains, only a few companies are qualified to perform operations in hazardous waste management, which greatly limits the system flexibility. In this paper, a novel two-stage stochastic bi-objective mathematical model was formulated in order to optimize the trade-off between cost and risk through the network decisions. In contrast to most of the other models which predominantly focus on simultaneously making both strategic decisions (location), and tactical and operational decisions (allocation, routing and inventory), our model takes into account the robust and flexible nature of the decision making and thus emphasizes the robustness of the strategic location decisions in the first-stage under an uncertain environment.
We have applied a Monte Carlo simulation based SAA-GP heuristic to solve the multi-objective stochastic optimization problem. The application of the model and the algorithm were accessed through extensive numerical experiments and a real-world case study. Based on the experimental results, three implications for hazardous waste network design emerge in order to answer the proposed research questions:
-
•
Considering future uncertainty may lead to a significant change not only in the objective values of the model but also in the strategic location decisions that are extremely difficult to alter. In this regard, the stochastic model for hazardous waste network design takes a large number of possible scenarios, e.g., fluctuations of cost and waste generation, into decision making and may thus obtain a more realistic estimation and generate more robust location decisions.
-
•
The optimal facility locations obtained under a stochastic environment can better reflect the infrastructural preparedness for the worst situations. Different from other logistics systems that enjoy the benefits of fulfilling fluctuate demands with several flexible options, e.g., outsourcing, hiring of seasonal workers, etc., a hazardous waste management system usually has a much lower flexibility due to the limited number of qualified companies and personnel in this sector. In this regard, the better infrastructural preparedness suggested by the stochastic model is important to effectively deal with the fluctuation of waste generation and react to emergency situations.
-
•
Even though a stochastic program may improve the objective value and the location decisions under an uncertain environment, this is more effective with a single objective function. However, in a multi-objective optimization, the improvement may not be monotonic in all objectives. The performance of some objective values obtained by the stochastic model may be weakened when they become less important in the decision making of hazardous waste network design.
Preparedness for the worst is of vital importance for a hazardous waste management system which lacks flexibility. The better decisions on facility selection and locations obtained by using a stochastic model may improve the long-term performance of a hazardous waste management system. For example, due to the COVID-19 outbreak, the daily generation of medical waste i.e., used respirators, waste medical masks and protective clothes, increases drastically all over the world and a robust network configuration for hazardous waste management may help to better react to these kinds of public health emergency.
Extensions of the current research could consist of improving the effectiveness and efficiency of the model computation for large-size instances using, for example, decomposition methods (e.g. Bender’s decomposition) and metaheuristics. The incorporation of emergency response of risk event in the network planning of a hazardous waste management system is also of interest for future investigation.
CRediT authorship contribution statement
Hao Yu: Conceptualization, Formal analysis, Writing - original draft, Methodology. Xu Sun: Conceptualization, Data curation. Wei Deng Solvang: Conceptualization, Supervision. Gilbert Laporte: Conceptualization, Writing - original draft, Methodology. Carman Ka Man Lee: Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to in fluence the work reported in this paper.
Acknowledgement
Thanks are due to the referees for their valuable comments. This work was partly supported by the Research Council of Norway under Transport 2025 Programme under grand 283084 and by the Canadian Natural Sciences and Engineering Research Council under grant 2015–06189. Both grants are gratefully acknowledged.
Handling editor. Prof. Jiri Jaromir Klemeš
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jclepro.2020.123566.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Alumur S., Kara B.Y. A new model for the hazardous waste location-routing problem. Comput. Oper. Res. 2007;34:1406–1423. [Google Scholar]
- Ardjmand E., Weckman G., Park N., Taherkhani P., Singh M. Applying genetic algorithm to a new location and routing model of hazardous materials. Int. J. Prod. Res. 2015;53:916–928. [Google Scholar]
- Ardjmand E., Young W.A., Ii, Weckman G.R., Bajgiran O.S., Aminipour B., Park N. Applying genetic algorithm to a new bi-objective stochastic model for transportation, location, and allocation of hazardous materials. Expert Syst. Appl. 2016;51:49–58. [Google Scholar]
- Asgari N., Rajabi M., Jamshidi M., Khatami M., Farahani R.Z. A memetic algorithm for a multi-objective obnoxious waste location-routing problem: a case study. Ann. Oper. Res. 2017;250:279–308. [Google Scholar]
- Ayvaz B., Bolat B., Aydın N. Stochastic reverse logistics network design for waste of electrical and electronic equipment. Resour. Conserv. Recycl. 2015;104:391–404. [Google Scholar]
- BBC . 2020. China explosion: tanker truck blows up, killing 19 people.https://www.bbc.com/news/world-asia-china-53039831 Available from: [Google Scholar]
- Berglund P.G., Kwon C. Robust facility location problem for hazardous waste transportation. Network. Spatial Econ. 2014;14:91–116. [Google Scholar]
- Boyer O., Sai Hong T., Pedram A., Mohd Yusuff R.B., Zulkifli N. A mathematical model for the industrial hazardous waste location-routing problem. J. Appl. Math. 2013;2013 [Google Scholar]
- Birge J.R., Louveaux F.V. Springer Science & Business Media; New York: 2011. Introduction to Stochastic Programming. [Google Scholar]
- Charnes A., Cooper W.W., Ferguson R.O. Optimal estimation of executive compensation by linear programming. Manag. Sci. 1955;1:138–151. [Google Scholar]
- Charnes A., Cooper W.W. Goal programming and multiple objective optimizations: Part 1. Eur. J. Oper. Res. 1977;1:39–54. [Google Scholar]
- Chauhan A., Singh A. A hybrid multi-criteria decision making method approach for selecting a sustainable location of healthcare waste disposal facility. J. Clean. Prod. 2016;139:1001–1010. [Google Scholar]
- Current J.R., Ratick S.J. A model to assess risk, equity and efficiency in facility location and transportation of hazardous materials. Locat. Sci. 1995;3(3):187–201. [Google Scholar]
- Das A., Mazumder T., Gupta A. Pareto frontier analyses based decision making tool for transportation of hazardous waste. J. Hazard Mater. 2012;227:341–352. doi: 10.1016/j.jhazmat.2012.05.068. [DOI] [PubMed] [Google Scholar]
- Di Domenica N., Mitra G., Valente P., Birbilis G. Stochastic programming and scenario generation within a simulation framework: an information systems perspective. Decis. Support Syst. 2007;42(4):2197–2218. [Google Scholar]
- Emek E., Kara B.Y. Hazardous waste management problem: the case for incineration. Comput. Oper. Res. 2007;34:1424–1441. [Google Scholar]
- Erkut E., Neuman S. Analytical models for locating undesirable facilities. Eur. J. Oper. Res. 1989;40(3):275–291. [Google Scholar]
- Erkut E., Verter V. A framework for hazardous materials transport risk assessment. Risk Anal. 1995;15:589–601. doi: 10.1111/0272-4332.216179. [DOI] [PubMed] [Google Scholar]
- Farrokhi-Asl H., Tavakkoli-Moghaddam R., Asgarian B., Sangari E. Metaheuristics for a bi-objective location-routing-problem in waste collection management. Journal of Industrial and Production Engineering. 2017;34:239–252. [Google Scholar]
- Hatefi S.M., Jolai F. Robust and reliable forward–reverse logistics network design under demand uncertainty and facility disruptions. Appl. Math. Model. 2014;38(9–10):2630–2647. [Google Scholar]
- Hu H., Li X., Nguyen A.D., Kavan P. A critical evaluation of waste incineration plants in Wuhan (China) based on site selection, environmental influence, public health and public participation. Int. J. Environ. Res. Publ. Health. 2015;12(7):7593–7614. doi: 10.3390/ijerph120707593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y., Zhang X., Rong Y., Zhang Z. A multimodal location and routing model for hazardous materials transportation based on multi-commodity flow model. Procedia–Social and Behavioral Sciences. 2014;138:791–799. [Google Scholar]
- King A.J., Wallace S.W. Springer Science & Business Media; New York: 2012. Modeling with Stochastic Programming. [Google Scholar]
- Kleywegt A.J., Shapiro A., Homem-De-Mello T. The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 2002;12:479–502. [Google Scholar]
- Lee C., Yeung C., Xiong Z., Chung S. A mathematical model for municipal solid waste management–A case study in Hong Kong. Waste Manag. 2016;58:430–441. doi: 10.1016/j.wasman.2016.06.017. [DOI] [PubMed] [Google Scholar]
- Li L., Wang S., Lin Y., Liu W., Chi T. A covering model application on Chinese industrial hazardous waste management based on integer program method. Ecol. Indicat. 2015;51:237–243. [Google Scholar]
- Löhndorf N. An empirical analysis of scenario generation methods for stochastic optimization. Eur. J. Oper. Res. 2016;255(1):121–132. [Google Scholar]
- Mak W.-K., Morton D.P., Wood R.K. Monte Carlo bounding techniques for determining solution quality in stochastic programs. Oper. Res. Lett. 1999;24:47–56. [Google Scholar]
- Ministry of Ecology and Environment of People’s Republic of China . 2019. Annual Report of Solid Waste Management in Major Cities of China in 2019 (Chinese Version)http://www.mee.gov.cn/ywgz/gtfwyhxpgl/gtfw/201912/P020191231360445518365.pdf Available at: [Google Scholar]
- Nema A.K., Gupta S.K. Multiobjective risk analysis and optimization of regional hazardous waste management system. Pract. Period. Hazard. Toxic, Radioact. Waste Manag. 2003;7:69–77. [Google Scholar]
- Nema A.K., Gupta S.K. Optimization of regional hazardous waste management systems: an improved formulation. Waste Manag. 1999;19:441–451. [Google Scholar]
- Paredes-Belmar G., Bronfman A., Marianov V., Latorre-Núñez G. Hazardous materials collection with multiple-product loading. J. Clean. Prod. 2017;141:909–919. [Google Scholar]
- Pishvaee M.S., Razmi J. Environmental supply chain network design using multi-objective fuzzy mathematical programming. Appl. Math. Model. 2012;36(8):3433–3446. [Google Scholar]
- Rabbani M., Heidari R., Yazdanparast R. A stochastic multi-period industrial hazardous waste location-routing problem: integrating NSGA-II and Monte Carlo simulation. Eur. J. Oper. Res. 2019;272:945–961. [Google Scholar]
- Rabbani M., Heidari R., Farrokhi-Asl H., Rahimi N. Using metaheuristic algorithms to solve a multi-objective industrial hazardous waste location-routing problem considering incompatible waste types. J. Clean. Prod. 2018;170:227–241. [Google Scholar]
- ReVelle C., Cohon J., Shobrys D. Simultaneous siting and routing in the disposal of hazardous wastes. Transport. Sci. 1991;25(2):138–145. [Google Scholar]
- Sakawa M., Yano H., Nishizaki I., Nishizaki I. Science & Business Media; New York: 2013. Linear and Multiobjective Programming with Fuzzy Stochastic Extensions. [Google Scholar]
- Samanlioglu F. A multi-objective mathematical model for the industrial hazardous waste location-routing problem. Eur. J. Oper. Res. 2013;226:332–340. [Google Scholar]
- Schütz P., Tomasgard A., Ahmed S. Supply chain design under uncertainty using sample average approximation and dual decomposition. Eur. J. Oper. Res. 2009;199:409–419. [Google Scholar]
- Shapiro A. Monte Carlo sampling approach to stochastic programming. ESAIM Proc. 2003:65–73. EDP Sciences. [Google Scholar]
- Sheu J.-B. A coordinated reverse logistics system for regional management of multi-source hazardous wastes. Comput. Oper. Res. 2007;34:1442–1462. [Google Scholar]
- Sykes R.I., Lewellen W.S., Parker S.F. A Gaussian plume model of atmospheric dispersion based on second-order closure. J. Clim. Appl. Meteorol. 1986;25:322–331. [Google Scholar]
- Verweij B., Ahmed S., Kleywegt A.J., Nemhauser G.L., Shapiro A. The sample average approximation method applied to stochastic routing problems: a computational study. Comput. Optim. Appl. 2003;24:289–333. [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020 doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Y., Lu W., Wang W., Quadrifoglio L. A multimodal location and routing model for hazardous materials transportation. J. Hazard Mater. 2012;227:135–141. doi: 10.1016/j.jhazmat.2012.05.028. [DOI] [PubMed] [Google Scholar]
- Yilmaz O., Kara B.Y., Yetis U. Hazardous waste management system design under population and environmental impact considerations. J. Environ. Manag. 2017;203:720–731. doi: 10.1016/j.jenvman.2016.06.015. [DOI] [PubMed] [Google Scholar]
- Yu H., Solvang W.D. An improved multi-objective programming with augmented ε-constraint method for hazardous waste location-routing problems. Int. J. Environ. Res. Publ. Health. 2016;13:548. doi: 10.3390/ijerph13060548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H., Solvang W.D. A multi-objective location-allocation optimization for sustainable management of municipal solid waste. Environment Systems and Decisions. 2017;37:289–308. [Google Scholar]
- Yu H., Solvang W.D. A carbon-constrained stochastic optimization model with augmented multi-criteria scenario-based risk-averse solution for reverse logistics network design under uncertainty. J. Clean. Prod. 2017;164:1248–1267. [Google Scholar]
- Yu H., Solvang W.D. Incorporating flexible capacity in the planning of a multi-product multi-echelon sustainable reverse logistics network under uncertainty. J. Clean. Prod. 2018;198:285–303. [Google Scholar]
- Yu H., Sun X., Solvang W.D., Zhao X. Reverse logistics network design for effective management of medical waste in epidemic outbreaks: insights from the coronavirus disease 2019 (COVID-19) outbreak in Wuhan (China) Int. J. Environ. Res. Publ. Health. 2020;17(5):1770. doi: 10.3390/ijerph17051770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J., Huang L. Multi-period network design problem in regional hazardous waste management systems. Int. J. Environ. Res. Publ. Health. 2019;16(11):2042. doi: 10.3390/ijerph16112042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J., Huang L., Lee D.-H., Peng Q. Improved approaches to the network design problem in regional hazardous waste management systems. Transport. Res. E Logist. Transport. Rev. 2016;88:52–75. [Google Scholar]
- Zhao J., Verter V. A bi-objective model for the used oil location-routing problem. Comput. Oper. Res. 2015;62:157–168. [Google Scholar]
- Zografos K.G., Androutsopoulos K.N. A decision support system for integrated hazardous materials routing and emergency response decisions. Transport. Res. C Emerg. Technol. 2008;16:684–703. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.