SUMMARY
The goals in clinical and cohort studies often include evaluation of the association of a time-dependent binary treatment or exposure with a survival outcome. Recently, several impactful studies targeted the association between initiation of aspirin and survival following colorectal cancer (CRC) diagnosis. The value of this exposure is zero at baseline and may change its value to one at some time point. Estimating this association is complicated by having only intermittent measurements on aspirin-taking. Commonly used methods can lead to substantial bias. We present a class of calibration models for the distribution of the time of status change of the binary covariate. Estimates obtained from these models are then incorporated into the proportional hazard partial likelihood in a natural way. We develop non-parametric, semiparametric, and parametric calibration models, and derive asymptotic theory for the methods that we implement in the aspirin and CRC study. We further develop a risk-set calibration approach that is more useful in settings in which the association between the binary covariate and survival is strong.
Keywords: Interval censoring, Last-value-carried-forward, Missing data, Proportional hazard
1. Introduction
One benefit of the Cox proportional hazards (PH) model for the analysis of time-to-event data (Cox, 1972) is the simplicity of including time-dependent covariates, while preserving desirable theoretical properties. Classical methods assume that time-dependent covariates are measured continuously. However, in practice, they are often measured intermittently, leading to bias in effect estimates if treated naïvely (Andersen and Liestøl, 2003; Cao and others, 2015). We consider a time-dependent binary covariate having zero value at baseline that may change its value to one at some point, and if a change has occurred, the covariate retains this value for the rest of the follow-up time. Real-life scenarios of this nature are widespread, including the onset of a irreversible medical condition (e.g., HIV infection, Langohr and others, 2004) or a treatment with a constant effect that is administrated in a different time for each patient (Austin, 2012). Goggins and others (1999) described data arising from a clinical trial where the goal was to study the effect of Cytomegalovirus (CMV) shedding on the risk of developing active CMV disease.
In the problems motivating this article (Chan and others, 2009; Liao and others, 2012; Hamada and others, 2017), the researchers were interested in the association between initiating aspirin use and survival after colorectal cancer (CRC) diagnosis. The data were obtained from two cohort studies: the Nurses’ Health Study (NHS) and the Health Professionals Follow-Up Study (HPFS). Following their enrollment to the studies, participants have been receiving questionnaires biennially and answering questions about life-style and other characteristics. Patients diagnosed with CRC who had been taking aspirin typically stop taking aspirin at the time of diagnosis as part of their preparations for surgery. Post-diagnosis aspirin-initiation is a time-dependent binary covariate. The time a participant started to take aspirin is known to lie within the interval between the time of the last questionnaire answered as no aspirin-taking and the time of the first questionnaire answered as aspirin-taking.
Researchers target the association between aspirin-initiation and survival and not aspirin-use and survival (Chan and others, 2009; Liao and others, 2012; Bastiaannet and others, 2012; Barron and others, 2015; Hamada and others, 2017) because aspirin-use might be stopped after initiation due to a deteriorating health status of the participants, resulting in reverse causality. A recently published study (Murphy and others, 2017) has found that among cancer patients that initiated aspirin use, the probability of continuing to take aspirin was much lower for those who were nearing death, compared to matched survivors.
The relevant existing literature is limited. Andersen and Liestøl (2003) studied the attenuation in effect estimates caused by having infrequently measured covariates. Cao and others (2015) developed kernel-based weighted score methods. Goggins and others (1999) proposed an EM algorithm to estimate the association between a binary covariate and survival time when the change-time of the binary covariate is interval-censored, and Kim (2016) proposed a modified estimating equation for the same problem, when there are no additional covariates affecting the outcome.
In this article, we propose a novel analysis framework for the problem of interval-censored change-time and suggest a two-stage approach. In the first stage, we fit a model for the change-time of the binary covariate. This model may be non-parametric, semiparametric or fully parametric, and may include baseline covariates that affect the change-time. For this first stage, we exploit existing methods, theory and efficient algorithms for interval-censored data (Sun, 2007; Huang, 1996; Anderson-Bergman, 2017; Wang and others, 2016). In the second stage, we incorporate the first-stage model into the main PH model. We construct a partial likelihood using the conditional hazard with respect to the available history, which, in the CRC and aspirin dataset, includes the timing of the last questionnaire, corresponding aspirin status and baseline covariates.
Our goal in this article is 3-fold. First, we develop a conceptual framework for the analysis of time-to-event data under the common practice of infrequent updates of a binary covariate of interest. Second, we present a rigorous analysis of data arisen from several impactful studies in the area of CRC. Third, we provide the R package ICcalib that implements our flexible methodology under a wide range of models. Unlike existing methods, our flexible approach allows to include variables related to aspirin-initiation, utilizing the available data and subject-matter knowledge in a novel way.
The rest of the article is structured as follows. In Section 2, we describe the motivating data. In Section 3, we define the main model, and in Section 4, we develop our proposed methods. Section 5 contains asymptotic properties. In Section 6, we describe our simulation study. In Section 7, we present the analysis of the CRC data and in Section 8, we reanalyze the CMV data of Goggins and others (1999). We offer concluding remarks in Section 9.
2. Data description
The data were formed from two large cohorts: the NHS, to which 121 701 female nurses enrolled in 1976, and the HPFS that began in 1986 with the enlistment of 51 529 males in various health professions. Description of the studies, and eligibility conditions for inclusion in the CRC survival studies can be found in Hamada and others (2017).
Participants have been receiving questionnaires biennially. During each questionnaire cycle, participants returned their answers in varying times. CRC researchers are interested in the first 5 or 10 years following the diagnosis. In our analyses, we considered 10 years follow-up. We limited our analyses to participants with Stages 1–3 CRC or missing stage data. In the span of 10 years, 249 CRC-related deaths were observed. Table A.1 of the supplementary material available at Biostatistics online presents descriptive statistics of the main variables.
In the three CRC studies that motivated this article (Chan and others, 2009; Liao and others, 2012; Hamada and others, 2017), evidence was presented for differential association of aspirin-initiation with CRC mortality across the following molecular subtypes, by considering the interaction terms of the aspirin-taking status and these molecular subtypes. The three molecular subtypes were PTGS2 (cyclooxygenase-2) overexpression (Chan and others, 2009), PIK3CA mutation (Liao and others, 2012), and low CD274 (PD-L1) expression (Hamada and others, 2017). These subtype definitions are not exclusive; a tumor may be included in zero, one, two, or three of these subtypes. The goal of our analyses was to evaluate the association between post-diagnosis aspirin initiations and CRC-related mortality within the subpopulation of each tumor subtype.
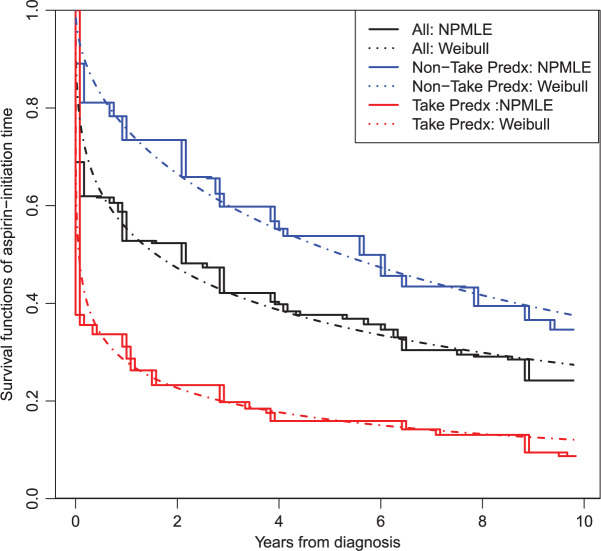
The post-diagnosis aspirin-initiation time varied. Figure 1 presents estimated time-to-aspirin-initiation curves, for the entire sample and by pre-diagnosis aspirin-taking status. Patients diagnosed with CRC were asked to stop taking aspirin to prepare for surgery. It is likely that patients who had been taking aspirin prior to CRC diagnosis were more inclined to initiate aspirin, once it was possible. This is consistent with the rapid drop right after the baseline in the curve for pre-diagnosis aspirin-takers.
Fig. 1.
Survival curve estimation of aspirin-initiation time for the entire sample (middle curve) and by pre-diagnosis (Predx) aspirin-taking status (takers vs non-takers; bottom vs top curves). Solid lines are the NPMLE, dashed lines are survival curves obtained from Weibull model fitting.
3. The main model
Let 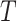 be the time to event of interest, e.g., time-to-death following CRC diagnosis.
be the time to event of interest, e.g., time-to-death following CRC diagnosis. 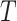 is possibly right censored by a censoring time
is possibly right censored by a censoring time 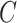 . Let
. Let 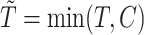 and
and 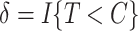 be the observed time and censoring indicator, respectively. Of main interest is the association of the monotone non-decreasing binary covariate
be the observed time and censoring indicator, respectively. Of main interest is the association of the monotone non-decreasing binary covariate 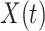 with
with 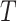 . For presentational simplicity, we henceforth refer to
. For presentational simplicity, we henceforth refer to 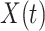 as the exposure, although it can be a treatment or any other binary covariate. As explained in Section 1, when studying aspirin and survival following cancer diagnosis, researchers prefer to study the exposure aspirin-initiation and not aspirin-taking (e.g., Bastiaannet and others, 2012; Barron and others, 2015; Hamada and others, 2017 to avoid misinterpretation of the results due to reverse causality. Let
as the exposure, although it can be a treatment or any other binary covariate. As explained in Section 1, when studying aspirin and survival following cancer diagnosis, researchers prefer to study the exposure aspirin-initiation and not aspirin-taking (e.g., Bastiaannet and others, 2012; Barron and others, 2015; Hamada and others, 2017 to avoid misinterpretation of the results due to reverse causality. Let 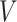 be the change-time in the value of
be the change-time in the value of 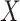 . That is,
. That is, 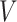 is the first time when
is the first time when 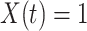 . Let
. Let 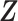 be a vector of covariates presumably associated with
be a vector of covariates presumably associated with 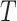 . For simplicity of presentation, we assume that
. For simplicity of presentation, we assume that 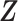 is time-independent. The proposed methods can be straightforwardly applied to time-dependent covariates
is time-independent. The proposed methods can be straightforwardly applied to time-dependent covariates 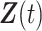 . The Cox PH model (Cox, 1972) for the hazard function of
. The Cox PH model (Cox, 1972) for the hazard function of 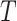 given
given 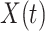 and
and 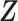 is
is
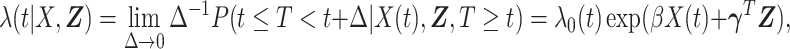 |
(3.1) |
where 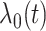 is an unspecified baseline function and
is an unspecified baseline function and 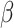 and
and 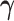 are parameters to be estimated. We are mainly interested in
are parameters to be estimated. We are mainly interested in 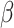 . We refer to this PH model for
. We refer to this PH model for 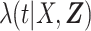 as the main model. The partial likelihood for
as the main model. The partial likelihood for 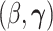 is
is
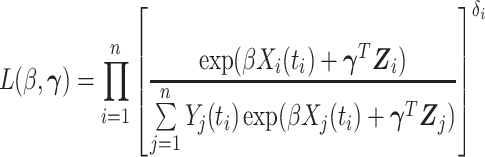 |
(3.2) |
where 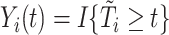 is an at-risk indicator. If
is an at-risk indicator. If 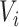 was known, we could simply set the time-dependent exposure to be equal to zero for all
was known, we could simply set the time-dependent exposure to be equal to zero for all 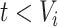 and to one after that time, i.e.,
and to one after that time, i.e., 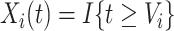 . However, the data collected from questionnaires are often limited. The aspirin-initiation status
. However, the data collected from questionnaires are often limited. The aspirin-initiation status 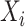 was measured only at a series of
was measured only at a series of  discrete time points:
discrete time points: 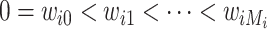 , with
, with 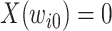 . If
. If 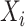 was not measured at any time point before
was not measured at any time point before 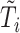 , then
, then 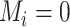 . When the main event is terminal (e.g., death), exposure data are available only until the event or censoring time; that is,
. When the main event is terminal (e.g., death), exposure data are available only until the event or censoring time; that is, 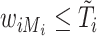 . In other studies, data on the exposure can be obtained even after the main event has occurred.
. In other studies, data on the exposure can be obtained even after the main event has occurred.
Let 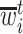 denote the last time
denote the last time 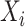 was measured before time
was measured before time 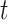 ;
; 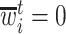 if
if 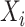 was not previously measured. If
was not previously measured. If 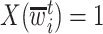 , then
, then 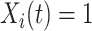 . However, if
. However, if 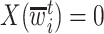 , then
, then 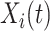 can be either one or zero. Therefore, the likelihood (3.2) cannot be calculated from the observed data.
can be either one or zero. Therefore, the likelihood (3.2) cannot be calculated from the observed data.
Two common methods for addressing this type of missing data are the last-value-carried-forward (LVCF) and midpoint imputation (MidI) methods. The LVCF method imputes missing values as the last observed values, 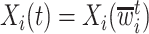 . That is, a participant is assumed to not initiate aspirin, until the first time she reports aspirin-taking. The MidI method imputes the change-time (
. That is, a participant is assumed to not initiate aspirin, until the first time she reports aspirin-taking. The MidI method imputes the change-time (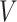 ) in the middle of the interval in which the change is known to have occurred. For example, if a participant reported she was not taking aspirin 1 year after diagnosis, and then reported she is taking aspirin 2.5 years after diagnosis, then MidI would assume
) in the middle of the interval in which the change is known to have occurred. For example, if a participant reported she was not taking aspirin 1 year after diagnosis, and then reported she is taking aspirin 2.5 years after diagnosis, then MidI would assume 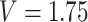 for that participant; LVCF would assume
for that participant; LVCF would assume 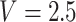 . These are ad hoc methods that may lead to substantially biased results. This calls for a new conceptual framework.
. These are ad hoc methods that may lead to substantially biased results. This calls for a new conceptual framework.
First, we can describe the missing data problem in terms of the random variable 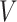 . For each participant, the data available on
. For each participant, the data available on 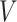 include the measurement times and the corresponding exposure status. The data can be summarized in a form of an interval
include the measurement times and the corresponding exposure status. The data can be summarized in a form of an interval 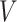 is censored into, denoted by
is censored into, denoted by 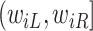 , where
, where
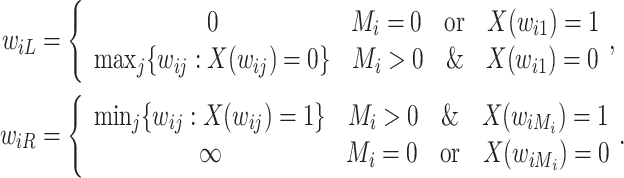 |
If 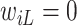 ,
, 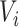 is left-censored, and if
is left-censored, and if 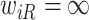 ,
, 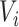 is right-censored. Note that data about measurements of
is right-censored. Note that data about measurements of  before
before 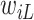 or after
or after 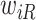 do not add information about
do not add information about 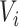 .
.
Let 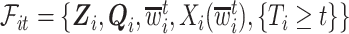 be the history until time
be the history until time 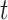 of an at-risk participant
of an at-risk participant 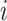 , where
, where 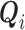 are covariates informative about
are covariates informative about 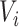 (and hence on
(and hence on 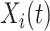 ), and
), and 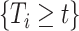 means that participant
means that participant 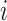 has been event-free so far. In our application,
has been event-free so far. In our application, 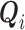 includes, among other covariates, the pre-diagnosis aspirin-use status, which is clearly informative about
includes, among other covariates, the pre-diagnosis aspirin-use status, which is clearly informative about 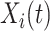 , as previously demonstrated in Figure 1. If a covariate affects both
, as previously demonstrated in Figure 1. If a covariate affects both 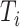 and
and 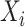 , it is included in both
, it is included in both 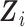 and
and 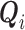 .
.
Before turning to our proposed methods, we present our assumptions. For all 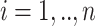 ,
,
Assumption 1
Conditionally on
,
and
are independent,
Assumption 2
Conditionally on
and
, the probability of event at time
is independent of
,
, and
.
Assumption 3
.
Assumption 1 is the standard independent censoring assumption for the main event time 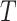 . Assumption 2 is plausible, as it states that for a participant surviving at least until time
. Assumption 2 is plausible, as it states that for a participant surviving at least until time 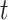 , given all covariates
, given all covariates 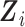 , if
, if 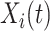 is known, then the history of
is known, then the history of 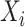 and timing of past questionnaires are not informative about the event occurrence at time
and timing of past questionnaires are not informative about the event occurrence at time 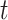 . This assumption could be relaxed and replaced with a model for the relationship between the history of
. This assumption could be relaxed and replaced with a model for the relationship between the history of 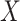 and
and 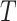 . Assumption 3 is the standard independent censoring assumption for interval-censored data (Sun, 2007, Section 1.3.5). It states that
. Assumption 3 is the standard independent censoring assumption for interval-censored data (Sun, 2007, Section 1.3.5). It states that 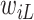 and
and 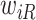 do not contain additional information about
do not contain additional information about 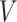 , other than that
, other than that 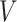 is within interval
is within interval 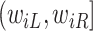 . This assumption would not exactly hold when the main event is terminal and
. This assumption would not exactly hold when the main event is terminal and 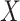 and
and 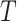 are associated (
are associated (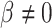 ). If, for example, aspirin is strongly protective against death (
). If, for example, aspirin is strongly protective against death (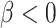 and
and  is large), a finite value of
is large), a finite value of 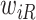 implies that the participant survived until
implies that the participant survived until 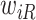 , and hence it is more likely that this participants started to take aspirin early (i.e.,
, and hence it is more likely that this participants started to take aspirin early (i.e., 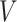 close to
close to 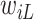 ). This assumption, its validity, and potential solutions to deviations from this assumptions are discussed in Sections 4.2 and 9.
). This assumption, its validity, and potential solutions to deviations from this assumptions are discussed in Sections 4.2 and 9.
4. A calibration approach
To present our methods, we first note that under model (3.1) and Assumption 2, the hazard function of 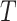 conditional on
conditional on 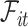 is
is
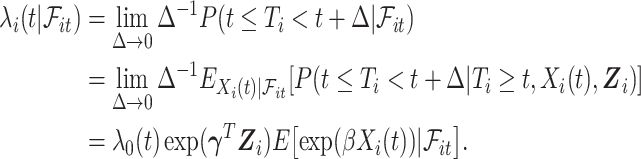 |
A similar mathematical derivation was presented for the case of measurement error in a time-dependent continuous covariate (Prentice, 1982). It is readily seen that 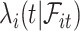 is also a PH model (Prentice, 1982) and therefore we can consider the partial likelihood
is also a PH model (Prentice, 1982) and therefore we can consider the partial likelihood
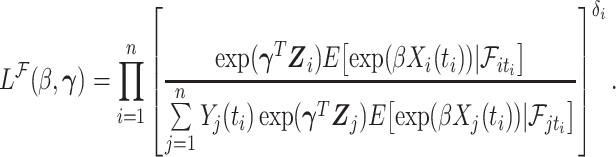 |
(4.1) |
The fact that 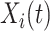 is binary allows us to explicitly write the expectation in (4.1) as
is binary allows us to explicitly write the expectation in (4.1) as
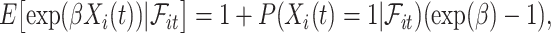 |
(4.2) |
where 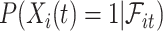 can be expressed using the distribution of
can be expressed using the distribution of 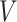 as
as
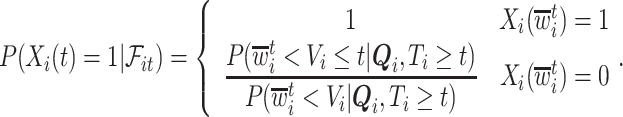 |
(4.3) |
In words, the probability of a positive aspirin-initiation status at time 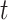 , conditionally on the personal history, equals to one, if the participant previously reported she is taking aspirin, and if she did not report aspirin-taking previously, it equals to the probability of a change in the aspirin-initiation status between the last questionnaire time
, conditionally on the personal history, equals to one, if the participant previously reported she is taking aspirin, and if she did not report aspirin-taking previously, it equals to the probability of a change in the aspirin-initiation status between the last questionnaire time 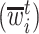 and time
and time 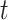 , conditionally on no aspirin-initiation at time
, conditionally on no aspirin-initiation at time 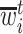 . Combining (4.2) and (4.3), it is evident that
. Combining (4.2) and (4.3), it is evident that 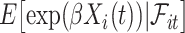 is a functional of the distribution of
is a functional of the distribution of 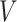 conditionally on
conditionally on 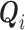 and
and 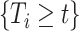 . If the distribution of
. If the distribution of 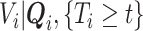 was known, we could have obtained valid estimates for
was known, we could have obtained valid estimates for 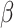 and
and 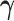 by substituting (4.2) and (4.3) into
by substituting (4.2) and (4.3) into 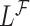 . However, the distribution of
. However, the distribution of 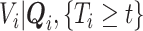 is unknown for all
is unknown for all 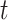 .
.
Because the distribution of 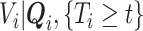 can be very complicated due to the conditioning on
can be very complicated due to the conditioning on 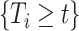 , we start with a simple solution. Let
, we start with a simple solution. Let 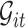 be
be 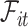 without the survival information, i.e.,
without the survival information, i.e., 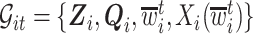 . Our first proposal is to estimate
. Our first proposal is to estimate 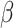 and
and 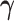 by applying two modifications to
by applying two modifications to 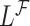 . First, we replace
. First, we replace 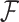 by
by 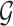 in the expectations in (4.1) to get
in the expectations in (4.1) to get 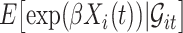 . The second modification involves replacing expectations of the form
. The second modification involves replacing expectations of the form 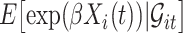 by estimators
by estimators 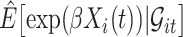 . Our ordinary calibration (OC) estimator
. Our ordinary calibration (OC) estimator 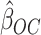 is the maximizer of
is the maximizer of
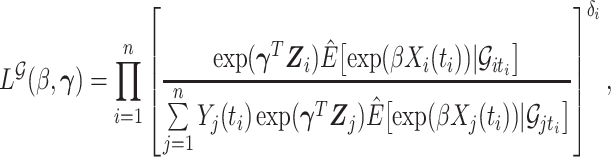 |
with respect to 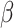 and
and 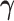 . Noting the simplicity of this likelihood function, maximization can be done in a straightforward way, e.g., using the Newton–Raphson algorithm.
. Noting the simplicity of this likelihood function, maximization can be done in a straightforward way, e.g., using the Newton–Raphson algorithm.
The expectation 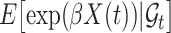 can be expressed as a functional of the distribution of
can be expressed as a functional of the distribution of 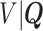 , as in (4.2) and (4.3), with
, as in (4.2) and (4.3), with  replaced by
replaced by  , and omitting
, and omitting 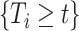 in (4.3). Therefore, we first estimate the distribution of
in (4.3). Therefore, we first estimate the distribution of 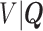 and then calculate
and then calculate 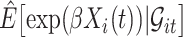 using the estimated distribution.
using the estimated distribution.
4.1. Calibration models fitted from interval-censored data
Let 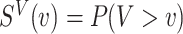 be the survival function of
be the survival function of 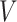 . We refer to the model for the distribution of
. We refer to the model for the distribution of 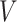 as the calibration model. Under Assumption 3, the likelihood of interval-censored time-to-event data is (Sun, 2007)
as the calibration model. Under Assumption 3, the likelihood of interval-censored time-to-event data is (Sun, 2007)
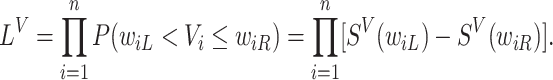 |
(4.4) |
The nonparametric maximum likelihood estimator (NPMLE) estimator has been studied as an extension of the Kaplan–Meier estimator to interval-censored data. Algorithms suggested to find the NPMLE were previously developed (Turnbull, 1976; Groeneboom and Wellner, 1992; Wellner and Zhan, 1997). Consistency and asymptotic distribution (at a 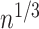 rate) were proved by Groeneboom and Wellner (1992).
rate) were proved by Groeneboom and Wellner (1992).
Parametric or semiparametric models for the distribution of 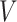 can also be used, and are especially appealing when the distribution of
can also be used, and are especially appealing when the distribution of 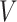 is likely to depend on additional covariates, previously denoted by
is likely to depend on additional covariates, previously denoted by 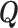 . In the CRC studies, pre-diagnosis aspirin-taking status is strongly associated with post-diagnosis aspirin-initiation time (Figure 1). Additional covariates include risk factors for cardiovascular and cerebrovascular events, because aspirin is often taken to reduce the risk of these events among high-risk patients; see Section 7.
. In the CRC studies, pre-diagnosis aspirin-taking status is strongly associated with post-diagnosis aspirin-initiation time (Figure 1). Additional covariates include risk factors for cardiovascular and cerebrovascular events, because aspirin is often taken to reduce the risk of these events among high-risk patients; see Section 7.
Let 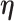 denote a vector of parameters characterizing the distribution of
denote a vector of parameters characterizing the distribution of 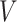 . An estimator of
. An estimator of 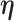 is obtained by maximizing the equivalent of (4.4) under a model for
is obtained by maximizing the equivalent of (4.4) under a model for 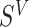 that possibly accommodates the covariates. See Chapter 2 of Sun (2007) for discussion of parametric models for interval-censored time-to-event data. A more flexible model is a PH regression model with an unspecified baseline hazard function. Finkelstein (1986) discussed PH models for interval-censored data and suggested discretization of the baseline hazard function. Algorithms for computation of the MLE were previously proposed and asymptotic theory was studied (Huang, 1996; Pan, 1999).
that possibly accommodates the covariates. See Chapter 2 of Sun (2007) for discussion of parametric models for interval-censored time-to-event data. A more flexible model is a PH regression model with an unspecified baseline hazard function. Finkelstein (1986) discussed PH models for interval-censored data and suggested discretization of the baseline hazard function. Algorithms for computation of the MLE were previously proposed and asymptotic theory was studied (Huang, 1996; Pan, 1999).
We adopt the recently developed framework of Wang and others (2016), which uses flexible I-splines (Ramsay, 1988) for the cumulative baseline hazard function. Wang and others (2016) further developed a fast EM algorithm, which we apply in our simulations and data analysis. Let 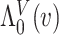 and
and 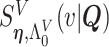 be the cumulative baseline hazard function and the survival function of
be the cumulative baseline hazard function and the survival function of 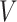 , respectively, which under the PH model are
, respectively, which under the PH model are
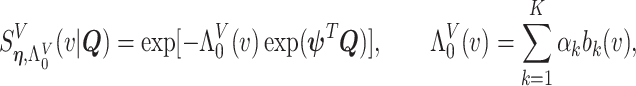 |
(4.5) |
where 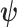 is a coefficient vector relating the covariates
is a coefficient vector relating the covariates 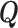 to the survival function of
to the survival function of 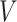 , and where for all
, and where for all 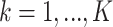 ,
, 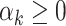 are unknown parameters and
are unknown parameters and 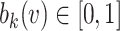 are integrated spline basis functions, that are non-decreasing. The spline basis functions are calculated according to the user specification of
are integrated spline basis functions, that are non-decreasing. The spline basis functions are calculated according to the user specification of 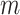 interior knots and a polynomial degree for the basic functions. The resulting
interior knots and a polynomial degree for the basic functions. The resulting 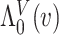 is guaranteed to be monotone increasing. See Ramsay (1988) and Wang and others (2016) for further details and discussion about I-splines in general and for the PH model, respectively.
is guaranteed to be monotone increasing. See Ramsay (1988) and Wang and others (2016) for further details and discussion about I-splines in general and for the PH model, respectively.
4.2. Risk-set calibration
The OC estimator 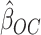 may suffer from asymptotic bias. It is calculated as the maximizer of
may suffer from asymptotic bias. It is calculated as the maximizer of 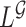 while the partial likelihood is
while the partial likelihood is 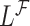 . The degree of divergence between
. The degree of divergence between 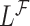 and
and 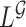 depends on how different
depends on how different 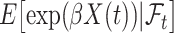 and
and 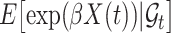 are. Recall that
are. Recall that 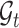 was defined by omitting
was defined by omitting 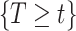 from
from 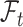 . If the probability that
. If the probability that 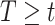 is close to one, as in the case of rare events, the bias should be attenuated. If
is close to one, as in the case of rare events, the bias should be attenuated. If  has no effect on
has no effect on 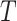 ,
, 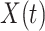 is independent of
is independent of 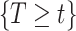 and
and  . If
. If 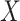 has a s strong effect on
has a s strong effect on 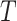 then the
then the 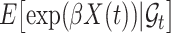 will not approximate
will not approximate 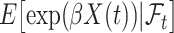 very well. In that scenario, the fact that
very well. In that scenario, the fact that 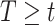 carries information on the distribution of
carries information on the distribution of 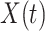 . This implies that as the absolute value of
. This implies that as the absolute value of 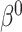 , the true value of
, the true value of 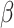 , increases, a larger bias may be expected.
, increases, a larger bias may be expected.
Another source of bias stems from fitting the calibration model under the independent interval-censoring assumption (Assumption 3). However, in our studies, the time to event, 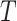 , is informative about the censoring in the calibration model. If, for example, aspirin reduces the risk of death, then the aspirin-initiation time is more likely to be right censored (
, is informative about the censoring in the calibration model. If, for example, aspirin reduces the risk of death, then the aspirin-initiation time is more likely to be right censored (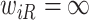 ) in non-aspirin-taking patients. This may cause bias in the estimation of
) in non-aspirin-taking patients. This may cause bias in the estimation of 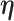 when fitting the calibration model. As before, if the event is rare, the censoring of
when fitting the calibration model. As before, if the event is rare, the censoring of 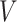 is most likely due to administrative reasons, and hence Assumption 3 approximately holds. Furthermore, under the null (i.e., when
is most likely due to administrative reasons, and hence Assumption 3 approximately holds. Furthermore, under the null (i.e., when 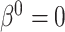 ), the censoring interval is independent of
), the censoring interval is independent of 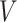 . As before, larger
. As before, larger 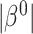 typically implies more substantial bias. We investigate this point in the simulation studies in Section 6 and Appendix C of the supplementary material available at Biostatistics online. In studies with non-terminal event, Assumption 3 may be more plausible, because data on
typically implies more substantial bias. We investigate this point in the simulation studies in Section 6 and Appendix C of the supplementary material available at Biostatistics online. In studies with non-terminal event, Assumption 3 may be more plausible, because data on 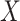 can be collected after the main event has occurred.
can be collected after the main event has occurred.
In order to reduce potential bias, we propose a risk-set calibration (RSC) procedure, an adaption of risk-set regression calibration previously developed in the context of error-prone covariates in survival analysis (Xie and others, 2001; Ye and others, 2008; Liao and others, 2011). This method uses 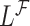 , and estimate the distribution of
, and estimate the distribution of 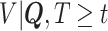 by refitting the calibration model for
by refitting the calibration model for 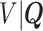 at each observed event time, using only the members of the risk set at that time, so only participants with
at each observed event time, using only the members of the risk set at that time, so only participants with 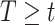 are used. Then, at each risk set, we plug-in the estimated distribution of
are used. Then, at each risk set, we plug-in the estimated distribution of 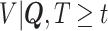 in (4.3), leading to
in (4.3), leading to 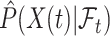 which is then substituted in (4.2) to obtain
which is then substituted in (4.2) to obtain 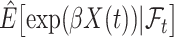 for
for 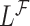 .
.
The RSC is expected to lead to less bias than OC, especially when 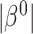 is large (Xie and others, 2001). However, some asymptotic bias in the RSC estimator may be expected, due to model misspecification. Even if the PH model for the distribution of
is large (Xie and others, 2001). However, some asymptotic bias in the RSC estimator may be expected, due to model misspecification. Even if the PH model for the distribution of 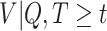 holds at
holds at 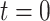 , it is not likely to hold for all
, it is not likely to hold for all 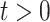 . The RSC estimator is also expected to have larger variance, due to increased number of parameters, and the decreasing (in
. The RSC estimator is also expected to have larger variance, due to increased number of parameters, and the decreasing (in 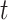 ) sample size for the RSC models. Therefore, it is advised to use this estimator when the
) sample size for the RSC models. Therefore, it is advised to use this estimator when the 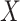 -
-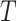 association is strong, and the sample size is large.
association is strong, and the sample size is large.
5. Asymptotic properties
We focus on the PH model under the I-splines representation for 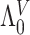 of Wang and others (2016). The results can be straightforwardly extended to parametric models for
of Wang and others (2016). The results can be straightforwardly extended to parametric models for 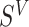 . Let
. Let 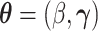 ,
, 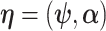 and let
and let
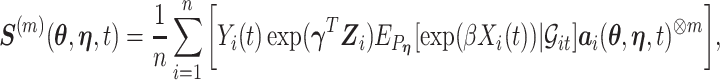 |
where 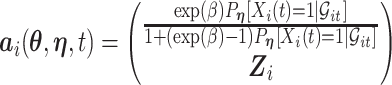 and where for any vector
and where for any vector 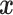 ,
, 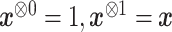 , and
, and  . Recall that
. Recall that 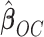 is obtained by maximizing
is obtained by maximizing 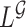 , or alternatively, by solving
, or alternatively, by solving 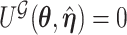 where
where
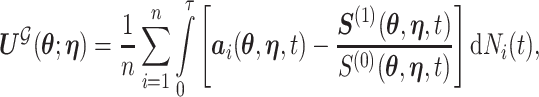 |
with 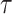 being the study end-time and
being the study end-time and 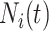 the counting process associated with
the counting process associated with 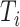 . Under certain regularity assumptions ,
. Under certain regularity assumptions , 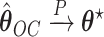 . These regularity assumption and the proof are given in Appendix A of the supplementary material available at Biostatistics online. Furthermore,
. These regularity assumption and the proof are given in Appendix A of the supplementary material available at Biostatistics online. Furthermore, 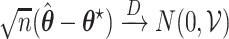 and
and 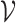 can be estimated by a sandwich estimator
can be estimated by a sandwich estimator
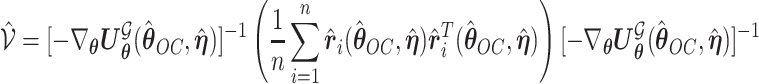 |
(5.1) |
with 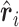 being a sample version of
being a sample version of 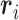 given in Appendix A of the supplementary material available at Biostatistics online.
given in Appendix A of the supplementary material available at Biostatistics online.
For the RSC estimator, results of similar nature are given and proved in Appendix A of the supplementary material available at Biostatistics online. Main modifications in the results are that 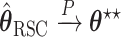 , where
, where 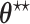 is possibly different from
is possibly different from 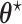 , and that
, and that 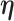 is replaced by
is replaced by 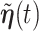 , a time-dependent parameter vector.
, a time-dependent parameter vector.
As explained in Section 4.2, The limiting values 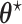 and
and 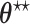 are not necessarily the true values of
are not necessarily the true values of 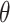 . Under the null (
. Under the null (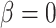 ), they are. We investigate the direction and magnitude of the asymptotic bias when
), they are. We investigate the direction and magnitude of the asymptotic bias when 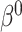 is non-zero in Section 6 and in Appendix C of the supplementary material available at Biostatistics online.
is non-zero in Section 6 and in Appendix C of the supplementary material available at Biostatistics online.
6. Simulation study
We carried out simulation studies to assess the finite-sample performance of our methods and to compare them to the näive methods. We simulated 1000 datasets per scenario.
For the main model, the hazard function of 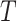 was
was  , with
, with 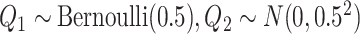 and
and 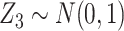 , all independent of each other. We took the Gompertz baseline hazard function
, all independent of each other. We took the Gompertz baseline hazard function 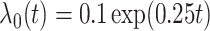 , and
, and 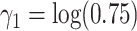 ,
, 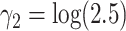 and
and 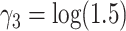 . For
. For 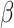 , we considered the values
, we considered the values 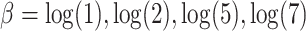 . We simulated time-to-event data with time-dependent covariate as described in Austin (2012). We took exponential censoring (mean = 5) and additional censoring at time 5. The resulting censoring rates varied between 42% and 63%, depending on the value of
. We simulated time-to-event data with time-dependent covariate as described in Austin (2012). We took exponential censoring (mean = 5) and additional censoring at time 5. The resulting censoring rates varied between 42% and 63%, depending on the value of 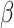 .
.
For the calibration model, we considered a PH calibration model in our main simulation study and used the setup of Wang and others (2016), with 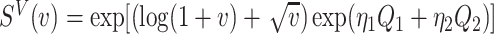 , where
, where 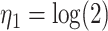 ,
, 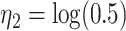 , and
, and 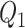 and
and 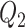 are the same covariates as in the main model. For each observation,
are the same covariates as in the main model. For each observation, 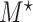 questionnaire time points were simulated from the intervals on the equally spaced grid of
questionnaire time points were simulated from the intervals on the equally spaced grid of 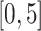 . For example, under
. For example, under 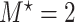 , the first questionnaire time point was simulated from
, the first questionnaire time point was simulated from 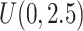 , and the second from
, and the second from 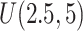 . However, to mimic the motivating studies, we considered a terminal main event, and kept only questionnaire time points before
. However, to mimic the motivating studies, we considered a terminal main event, and kept only questionnaire time points before 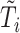 .
.
The PH calibration model fitting was done for each simulated dataset with 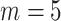 equally-spaced interior knots and a quadratic order for the basic functions of the I-splines. Standard errors were estimated by (5.1) and confidence intervals were calculated using the asymptotic normal distribution.
equally-spaced interior knots and a quadratic order for the basic functions of the I-splines. Standard errors were estimated by (5.1) and confidence intervals were calculated using the asymptotic normal distribution.
Table 1 summarizes the results for the LVCF, the PH calibration model (PH-OC) and PH risk-set calibration models (PH-RSC), for 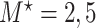 . Under the null, all three methods were valid. As the association between
. Under the null, all three methods were valid. As the association between 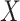 and
and 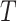 got stronger, a more substantial bias was observed. The OC estimator preformed generally well, with increased bias and lower coverage rates of the 95% confidence interval for the combination of
got stronger, a more substantial bias was observed. The OC estimator preformed generally well, with increased bias and lower coverage rates of the 95% confidence interval for the combination of 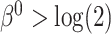 and
and 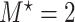 . The RSC estimator had lower bias in these scenarios. These observed biases were much smaller (in absolute value) than the bias of the LVCF estimator.
. The RSC estimator had lower bias in these scenarios. These observed biases were much smaller (in absolute value) than the bias of the LVCF estimator.
Table 1.
Simulation study results under a calibration PH model. Methods compared are LVCF, PH calibration model (PH-OC), and PH risk-set calibration models (PH-RSC). The table presents mean estimates (Mean), empirical standard deviations (EMP.SE), mean estimated standard errors (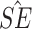 ), and empirical coverage rate of 95% confidence intervals (CP95%) for
), and empirical coverage rate of 95% confidence intervals (CP95%) for 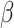
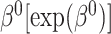
|
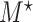
|
Method | Mean | EMP.SE |
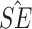
|
CP95% |
|---|---|---|---|---|---|---|
| 0.000 | 2 | LVCF | -0.002 | 0.141 | 0.135 | 0.944 |
|
PH-OC | 0.003 | 0.183 | 0.178 | 0.950 | |
| PH-RSC | 0.004 | 0.183 | 0.177 | 0.952 | ||
| 5 | LVCF | 0.003 | 0.122 | 0.124 | 0.955 | |
| PH-OC | 0.007 | 0.138 | 0.146 | 0.956 | ||
| PH-RSC | 0.007 | 0.138 | 0.142 | 0.956 | ||
| 0.693 | 2 | LVCF | 0.462 | 0.119 | 0.118 | 0.498 |
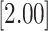
|
PH-OC | 0.680 | 0.175 | 0.179 | 0.936 | |
| PH-RSC | 0.684 | 0.177 | 0.175 | 0.938 | ||
| 5 | LVCF | 0.572 | 0.107 | 0.110 | 0.810 | |
| PH-OC | 0.690 | 0.132 | 0.145 | 0.958 | ||
| PH-RSC | 0.689 | 0.132 | 0.137 | 0.957 | ||
| 1.609 | 2 | LVCF | 0.968 | 0.110 | 0.109 | 0.000 |
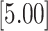
|
PH-OC | 1.472 | 0.179 | 0.210 | 0.869 | |
| PH-RSC | 1.516 | 0.190 | 0.195 | 0.897 | ||
| 5 | LVCF | 1.212 | 0.096 | 0.099 | 0.013 | |
| PH-OC | 1.577 | 0.139 | 0.166 | 0.951 | ||
| PH-RSC | 1.575 | 0.137 | 0.151 | 0.948 | ||
| 1.946 | 2 | LVCF | 1.130 | 0.112 | 0.110 | 0.000 |
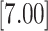
|
PH-OC | 1.695 | 0.182 | 0.230 | 0.723 | |
| PH-RSC | 1.773 | 0.198 | 0.205 | 0.816 | ||
| 5 | LVCF | 1.410 | 0.097 | 0.098 | 0.000 | |
| PH-OC | 1.890 | 0.148 | 0.187 | 0.933 | ||
| PH-RSC | 1.890 | 0.147 | 0.158 | 0.929 |
Table A.2 of supplementary material available at Biostatistics online presents more results from this simulation scenario. It includes the results for 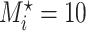 ,
, 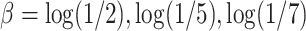 , and the MidI estimator. In terminal main event scenarios, MidI had a very large bias, even under the null. This is because a finite interval is only observed for observations with left- or interval-censored exposure times. Right-censored exposure times are dealt with differently (e.g., using LVCF, as we did) from left- or interval-censored observations, and a right-censored exposure time is the result of the main event occurring before a change in
, and the MidI estimator. In terminal main event scenarios, MidI had a very large bias, even under the null. This is because a finite interval is only observed for observations with left- or interval-censored exposure times. Right-censored exposure times are dealt with differently (e.g., using LVCF, as we did) from left- or interval-censored observations, and a right-censored exposure time is the result of the main event occurring before a change in 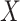 was observed. This creates a negative dependency between the imputed
was observed. This creates a negative dependency between the imputed 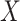 and
and 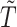 , even under the null. In studies with non-terminal events, the MidI method is valid under the null, but not when
, even under the null. In studies with non-terminal events, the MidI method is valid under the null, but not when 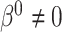 . A small simulation study (not presented here) confirmed these claims.
. A small simulation study (not presented here) confirmed these claims.
To investigate the performance of our methods in other settings, we have considered additional simulation studies without any covariates affecting the time-to-exposure (i.e., no 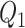 and
and 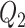 in the calibration model) and compared Weibull and non-parametric calibration models when the true calibration model was Weibull, and when it was piecewise exponential. The results, presented in the supplementary materials available at Biostatistics online, generally agreed with the results we have descried in this section.
in the calibration model) and compared Weibull and non-parametric calibration models when the true calibration model was Weibull, and when it was piecewise exponential. The results, presented in the supplementary materials available at Biostatistics online, generally agreed with the results we have descried in this section.
7. Results of aspirin and CRC survival analyses
Our first step was to construct a calibration model for the aspirin-initiation time. The 113 participants without available questionnaire data were not used for fitting the calibration model, and the calibration model was fitted using the remaining 1258 participants. The baseline potential covariates included gender, age-at-diagnosis, pre-diagnosis body mass index (BMI), pre-diagnosis aspirin-taking status, and the following tumor characteristics: disease stage (1–3 and missing), differentiation (poor vs well-moderate) and location (proximal colon, distal colon, or rectum). We considered three PH calibration models: (I) a model with all the aforementioned covariates, (II) a model with all non-tumor-related baseline covariates and disease stage, (III) a model with all non-tumor-related baseline covariates. Model (III) minimized the BIC (Schwarz, 1978). In addition, including strong determinants of the terminal event, such as the disease stage, is undesired. An association between disease stage and aspirin-initiation could be the result of violation of Assumption 3. That is, the association of the disease stage with aspirin-initiation could be only due to an association between disease stage and death.
Model (III) is logically sound from a subject-matter perspective. Aspirin is a preventive care for patients in high-risk for vascular diseases. Therefore, determinants of vascular diseases would also increase the probability of aspirin-initiation. The covariates in Model (III), age, gender, and BMI, are all well-established risk factors for vascular diseases. Therefore, we adopted Model (III) as our calibration model. Table 2 presents the results of fitting this PH model to the data. We used the same PH calibration model for all the analyses since there is no reason to believe that the tumor subtype, that was not even known at the time of diagnosis, informs the aspirin-initiation time.
Table 2.
The PH calibration model for aspirin-initiation time, using cubic order and 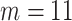 interior knots. Covariates include pre-diagnosis aspirin status (Predx-asp, taker vs non-taker), pre-diagnosis BMI (Predx-BMI), age-at-diagnosis (Age-at-dx), and gender (Female)
interior knots. Covariates include pre-diagnosis aspirin status (Predx-asp, taker vs non-taker), pre-diagnosis BMI (Predx-BMI), age-at-diagnosis (Age-at-dx), and gender (Female)
Est (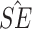 ) ) |
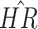
|
CI |
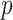 -value -value |
|
|---|---|---|---|---|
| Predx-asp | 1.135 (0.074) | 3.113 |
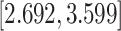
|
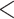 0.001 0.001 |
| Predx-BMI | 0.027 (0.006) | 1.028 |
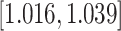
|
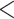 0.001 0.001 |
| Age-at-dx | 0.010 (0.001) | 1.010 |
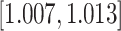
|
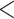 0.001 0.001 |
| Female |
 0.181 (0.073) 0.181 (0.073) |
0.834 |
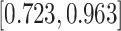
|
0.013 |
As suggested by Wang and others (2016), we used BIC to choose the number of equally spaced interior knots, which led to 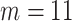 . We used the flexible cubic order for the spline basis functions. The number of interior knots according to the AIC criterion (Akaike, 1974) was
. We used the flexible cubic order for the spline basis functions. The number of interior knots according to the AIC criterion (Akaike, 1974) was 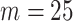 . The final results did not substantially change when we took
. The final results did not substantially change when we took 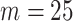 .
.
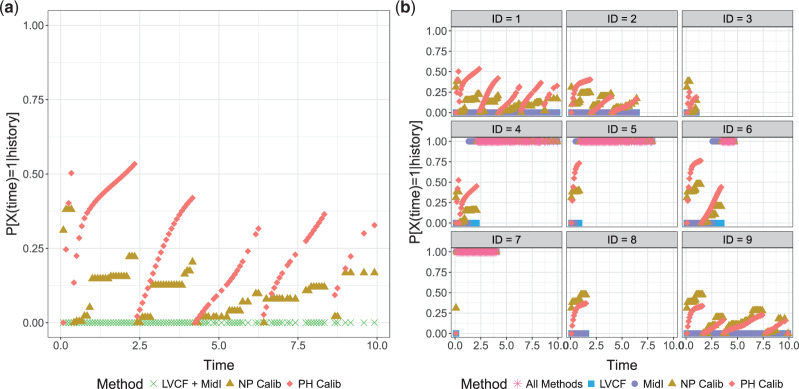
The simulation results presented in Section 6 and the Supplementary materials available at Biostatistics online have shown that when there are covariates affecting the time-to-exposure, the PH-OC estimator is preferable over the näive methods, namely LVCF and MidI. Figure 2 illustrates the difference between the methods. On its right panel, we drew the probabilities 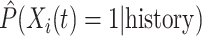 vs
vs 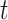 , for the first nine participants in our data. Once
, for the first nine participants in our data. Once 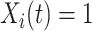 was observed, all methods assign
was observed, all methods assign 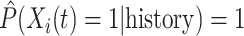 for the rest of the relevant risk sets. The left panel of Figure 2 presents the same probabilities as the right panel of the figure, but for the first participant only. This person did not report aspirin taking during the 10 years follow-up (
for the rest of the relevant risk sets. The left panel of Figure 2 presents the same probabilities as the right panel of the figure, but for the first participant only. This person did not report aspirin taking during the 10 years follow-up (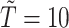 ). From the data, this person was a 75 years old (at diagnosis time) male, who was taking aspirin at baseline. From Table 2, we would expect the probability of this person to take aspirin to be higher than in the general population. This aligns with this person having larger estimated probabilities under the PH model comparing to the NP calibration model.
). From the data, this person was a 75 years old (at diagnosis time) male, who was taking aspirin at baseline. From Table 2, we would expect the probability of this person to take aspirin to be higher than in the general population. This aligns with this person having larger estimated probabilities under the PH model comparing to the NP calibration model.
Fig. 2.
(a) First participant; (b) First 9 participants. 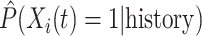 using LVCF, MidI, non-parametric (NP) calibration, and the PH calibration model, for the first 9 participants. Panel (a) corresponds to the top left corner of Panel (b).
using LVCF, MidI, non-parametric (NP) calibration, and the PH calibration model, for the first 9 participants. Panel (a) corresponds to the top left corner of Panel (b).
We included in the RSC models the covariates of Model (III). To avoid destabilization of the calibration model fittings, we grouped the risk sets in intervals of size 0.5. That is, we refitted the calibration model every 6 months.
Turning to the main model, we included baseline covariates that are known to be associated with CRC-related death. These included age-at-diagnosis, pre-diagnosis BMI, family history of CRC, and the following tumor characteristics: stage, differentiation, and location. Table 3 shows estimates and corresponding standard errors, confidence intervals, and 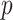 -values for the association between aspirin-initiation and survival in the three motivating studies and in the entire data. Compared to LVCF, stronger protective associations were estimated by our methods in all three subtype-specific analyses. Compared to the OC estimates, the RSC estimates were only slightly further from null. This could be partially explained by the high censoring rate (
-values for the association between aspirin-initiation and survival in the three motivating studies and in the entire data. Compared to LVCF, stronger protective associations were estimated by our methods in all three subtype-specific analyses. Compared to the OC estimates, the RSC estimates were only slightly further from null. This could be partially explained by the high censoring rate (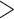 80%). Even though the sample sizes and case numbers were low to moderate, there was evidence for strong protective effect of aspirin for PIK3CA subtype CRC. The point estimates for aspirin in low CD274 subtype imply negative association between aspirin and death, but, possibly due to limited power, the null hypothesis was not rejected.
80%). Even though the sample sizes and case numbers were low to moderate, there was evidence for strong protective effect of aspirin for PIK3CA subtype CRC. The point estimates for aspirin in low CD274 subtype imply negative association between aspirin and death, but, possibly due to limited power, the null hypothesis was not rejected.
Table 3.
Results for the main model in the three CRC studies and in all data. Results presented for the aspirin effect. The main model also included family history of CRC, pre-diagnosis BMI, age-at-diagnosis, gender, disease stage, differentiation, and location
| Study | Method | Est (SE) |
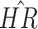
|
CI 95%(for HR) |
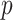 -value -value |
|---|---|---|---|---|---|
| All data | LVCF |
 0.34 (0.15) 0.34 (0.15) |
0.71 |
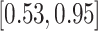
|
0.020 |
(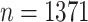 ) ) |
PH-OC |
 0.32 (0.18) 0.32 (0.18) |
0.73 |
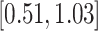
|
0.072 |
(No. of events 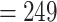 ) ) |
PH-RSC |
 0.32 (0.18) 0.32 (0.18) |
0.73 |
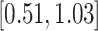
|
0.073 |
Low CD274
|
LVCF |
 0.64 (0.35) 0.64 (0.35) |
0.53 |
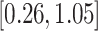
|
0.067 |
(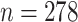 ) ) |
PH-OC |
 0.77 (0.40) 0.77 (0.40) |
0.46 |
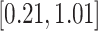
|
0.054 |
(No. of events 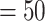 ) ) |
PH-RSC |
 0.79 (0.40) 0.79 (0.40) |
0.45 |
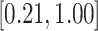
|
0.049 |
PIK3CA
|
LVCF |
 2.13 (0.64) 2.13 (0.64) |
0.12 |
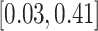
|
0.001 |
(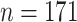 ) ) |
PH-OC |
 2.22 (0.65) 2.22 (0.65) |
0.11 |
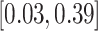
|
0.001 |
(No. of events 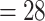 ) ) |
PH-RSC |
 2.23 (0.66) 2.23 (0.66) |
0.11 |
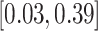
|
0.001 |
PTGS2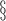
|
LVCF |
 0.30 (0.20) 0.30 (0.20) |
0.74 |
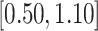
|
0.138 |
(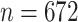 ) ) |
PH-OC |
 0.32 (0.24) 0.32 (0.24) |
0.73 |
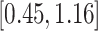
|
0.185 |
(No. of events 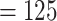 ) ) |
PH-RSC |
 0.32 (0.24) 0.32 (0.24) |
0.72 |
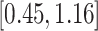
|
0.181 |
8. Reanalyzing the data in Goggins and others (1999)
The motivating application of Goggins and others (1999) was an analysis of AIDS Clinical Trial Group (ACTG) 181 (Finkelstein and others, 2002). The event of interest, active CMV disease, was non-terminal. Their binary covariate was CMV shedding. Based on the joint likelihood for 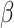 and the distribution of
and the distribution of 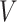 (
(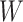 in their notation), they proposed an EM algorithm where the E-step is carried out with respect to the ordering of CMV shedding among the study participants. They further developed a Gibbs sampler to improve computational efficiency.
in their notation), they proposed an EM algorithm where the E-step is carried out with respect to the ordering of CMV shedding among the study participants. They further developed a Gibbs sampler to improve computational efficiency.
Our methodology has several improvements over the method of Goggins and others (1999). First, we exploit modern and fast procedures for estimating the distribution of 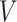 , by the NPMLE. Second, we can (but do not have to) include parametric modeling assumptions on the distribution of
, by the NPMLE. Second, we can (but do not have to) include parametric modeling assumptions on the distribution of 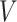 , if appropriate. Third, since we fit the calibration and main models separately, we can include in our analysis participants without data about the covariate of interest. Finally, and most importantly, we can include measured covariates affecting the time-to-exposure
, if appropriate. Third, since we fit the calibration and main models separately, we can include in our analysis participants without data about the covariate of interest. Finally, and most importantly, we can include measured covariates affecting the time-to-exposure 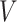 .
.
We analyzed the ACTG 181 data (Finkelstein and others, 2002) using our non-parametric calibration method. The results are presented in Appendix D of the supplementary material available at Biostatistics online. We observed a divergence between the OC and RSC estimates. The RSC estimates were further away from the null, and similar to those obtained by Goggins and others (1999). The confidence intervals were quite wide, as one may obtain for hazard ratios of strong effects when the sample size is moderate.
9. Conclusion
We have presented a novel calibration approach for studying the association between a time-dependent binary exposure and survival time, when the data about the monotone time-dependent exposure is only available intermittently. Our proposed approach allows for a wide range of calibration models. In practice, an adequate model should be chosen by combination of subject-matter knowledge and the available data. The R package ICcalib implementing our methods is available from CRAN. The package is described in Appendix B of the supplementary material available at Biostatistics online. The simulations and CMV data analysis can be reproduced using the Github repository ICcalibReproduce.
When the association between exposure and survival is strong, and a terminal event is non-rare, our calibration framework may suffer from bias, that can be reduced, though not eliminated, by RSC. Unlike regression calibration methods for error-prone covariates, additional data (e.g., reliability or validation data) is not needed to fit the calibration model, as the covariate measurements are inherently part of the available data. To address deviations from Assumption 3, future research may incorporate methods for analyzing data subject to dependent interval-censoring (Sun, 2007, Section 10.5) into our approach.
The problem described in this article and the proposed conceptual framework open the way for further research. A main question of interest is whether 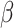 can be estimated consistently from the data, and what is the nature of further assumptions and methods to ensure consistency. Our model is a type of a joint model for time-to-event and longitudinal data (Rizopoulos, 2012). Potential alternative methods may model the binary covariate directly (Faucett and others, 1998; Larsen, 2004; Rizopoulos and others, 2008). Additionally, in scenarios the binary variable may change its value again, from 1 to 0, a potential approach would model the transition times between the two stages, although the assumptions and data needed for such an approach might be different from what we described in this article. Finally, future research may consider the case of a non-terminal main event that is assessed at the same time as the covariate. Then, both the main event time and the covariate change-time are interval-censored.
can be estimated consistently from the data, and what is the nature of further assumptions and methods to ensure consistency. Our model is a type of a joint model for time-to-event and longitudinal data (Rizopoulos, 2012). Potential alternative methods may model the binary covariate directly (Faucett and others, 1998; Larsen, 2004; Rizopoulos and others, 2008). Additionally, in scenarios the binary variable may change its value again, from 1 to 0, a potential approach would model the transition times between the two stages, although the assumptions and data needed for such an approach might be different from what we described in this article. Finally, future research may consider the case of a non-terminal main event that is assessed at the same time as the covariate. Then, both the main event time and the covariate change-time are interval-censored.
In conclusion, we presented a new conceptual framework accompanied by flexible and simple methodology to preform time-to-event analysis under the problem of infrequently updated binary covariate, a common problem in medical and epidemiological research.
Supplementary Material
Acknowledgments
We thank two anonymous reviewers and the associate editor for useful comments and suggestions that improved the article. Conflict of Interest: None declared.
Funding
National Institutes of Health (NIH) (P01 CA55075, P01 CA87969, R01 CA118553, R01 CA151993, R01 CA169141, R35 CA197735, U01 CA167552, UM1 CA167552, and UM1 CA186107).
References
- Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control 19, 716–723. [Google Scholar]
- Andersen, P. K. and Liestøl, K. (2003). Attenuation caused by infrequently updated covariates in survival analysis. Biostatistics 4, 633–649. [DOI] [PubMed] [Google Scholar]
- Anderson-Bergman, C. (2017). An efficient implementation of the EMICM algorithm for the interval censored NPMLE. Journal of Computational and Graphical Statistics 26, 463–467. [Google Scholar]
- Austin, P. C. (2012). Generating survival times to simulate Cox proportional hazards models with time-varying covariates. Statistics in Medicine 31, 3946–3958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barron, T. I., Murphy, L. M., Brown, C., Bennett, K., Visvanathan, K. and Sharp, L. (2015). De-novo post-diagnosis aspirin use and mortality in women with stage I–III breast cancer. Cancer Epidemiology and Prevention Biomarkers. 24, 898–904. [DOI] [PubMed] [Google Scholar]
- Bastiaannet, E., Sampieri, K., Dekkers, O. M., De Craen, A. J. M., van Herk-Sukel, M. P. P., Lemmens, V., Van Den Broek, C. B. M., Coebergh, J. W., Herings, R. M. C., Van De Velde, C. J. H. and others (2012). Use of aspirin postdiagnosis improves survival for colon cancer patients. British Journal of Cancer 106, 1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao, H., Churpek, M. M., Zeng, D. and Fine, J. P. (2015). Analysis of the proportional hazards model with sparse longitudinal covariates. Journal of the American Statistical Association 110, 1187–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan, A. T., Ogino, S. and Fuchs, C. S. (2009). Aspirin use and survival after diagnosis of colorectal cancer. Journal of the American Medical Association 302, 649–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, D. R. (1972). Regression models and life-tables. Journal of the Royal Statistical Society. Series B (Methodological) 34, 187–220. [Google Scholar]
- Faucett, C. L., Schenker, N. and Elashoff, R. M. (1998). Analysis of censored survival data with intermittently observed time-dependent binary covariates. Journal of the American Statistical Association 93, 427–437. [Google Scholar]
- Finkelstein, D. M. (1986). A proportional hazards model for interval-censored failure time data. Biometrics 42, 845–854. [PubMed] [Google Scholar]
- Finkelstein, D. M., Goggins, W. B. and Schoenfeld, D. A. (2002). Analysis of failure time data with dependent interval censoring. Biometrics 58, 298–304. [DOI] [PubMed] [Google Scholar]
- Goggins, W. B., Finkelstein, D. M. and Zaslavsky, A. M. (1999). Applying the Cox proportional hazards model when the change time of a binary time-varying covariate is interval censored. Biometrics 55, 445–451. [DOI] [PubMed] [Google Scholar]
- Groeneboom, P. and Wellner, J. A. (1992). Information Bounds and Nonparametric Maximum Likelihood Estimation. Basel: Birkhauser. [Google Scholar]
- Hamada, T., Cao, Y., Qian, Z. R., Masugi, Y., Nowak, J. A., Yang, J., Song, M., Mima, K., Kosumi, K., Liu, L.. and others (2017). Aspirin use and colorectal cancer survival according to tumor CD274 (programmed cell death 1 ligand 1) expression status. Journal of Clinical Oncology 35, 1836–1844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, J. (1996). Efficient estimation for the proportional hazards model with interval censoring. The Annals of Statistics 24, 540–568. [Google Scholar]
- Kim, Y.-J. (2016). A modified estimating equation for a binary time varying covariate with an interval censored changing time. Communications for Statistical Applications and Methods 23, 335–341. [Google Scholar]
- Langohr, K., Gómez, G. and Muga, R.. (2004). A parametric survival model with an interval-censored covariate. Statistics in Medicine 23, 3159–3175. [DOI] [PubMed] [Google Scholar]
- Larsen, K. (2004). Joint analysis of time-to-event and multiple binary indicators of latent classes. Biometrics 60, 85–92. [DOI] [PubMed] [Google Scholar]
- Liao, X., Lochhead, P., Nishihara, R., Morikawa, T., Kuchiba, A., Yamauchi, M., Imamura, Y., Qian, Z. R., Baba, Y., Shima, K.. and others (2012). Aspirin use, tumor pik3ca mutation, and colorectal-cancer survival. New England Journal of Medicine 367, 1596–1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao, X., Zucker, D. M., Li, Y. and Spiegelman, D. (2011). Survival analysis with error-prone time-varying covariates: a risk set calibration approach. Biometrics 67, 50–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy, L., Brown, C., Smith, A., Cranfield, F., Sharp, L., Visvanathan, K., Bennett, K. and Barron, T. I. (2017). End-of-life prescribing of aspirin in patients with breast or colorectal cancer. BMJ Supportive & Palliative Care. DOI: 10.1136/bmjspcare-2017-001370. [DOI] [PubMed] [Google Scholar]
- Pan, W. (1999). Extending the iterative convex minorant algorithm to the Cox model for interval-censored data. Journal of Computational and Graphical Statistics 8, 109–120. [Google Scholar]
- Prentice, R. L. (1982). Covariate measurement errors and parameter estimation in a failure time regression model. Biometrika 69, 331–342. [Google Scholar]
- Ramsay, J. O. (1988). Monotone regression splines in action. Statistical Science 3, 425–441. [Google Scholar]
- Rizopoulos, D. (2012). Joint Models for Longitudinal and Time-to-event Data: With Applications in R. Boca Raton, FL: CRC Press. [Google Scholar]
- Rizopoulos, D., Verbeke, G., Lesaffre, E. and Vanrenterghem, Y. (2008). A two-part joint model for the analysis of survival and longitudinal binary data with excess zeros. Biometrics 64, 611–619. [DOI] [PubMed] [Google Scholar]
- Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics 6, 461–464. [Google Scholar]
- Sun, J. (2007). The Statistical Analysis of Interval-Censored Failure Time Data. New York: Springer Science & Business Media. [Google Scholar]
- Turnbull, B. W. (1976). The empirical distribution function with arbitrarily grouped, censored and truncated data. Journal of the Royal Statistical Society. Series B (Methodological) 38, 290–295. [Google Scholar]
- Wang, L., McMahan, C. S., Hudgens, M. G. and Qureshi, Z. P. (2016). A flexible, computationally efficient method for fitting the proportional hazards model to interval-censored data. Biometrics 72, 222–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wellner, J. A. and Zhan, Y. (1997). A hybrid algorithm for computation of the nonparametric maximum likelihood estimator from censored data. Journal of the American Statistical Association 92, 945–959. [Google Scholar]
- Xie, S. X., Wang, C. Y. and Prentice, R. L. (2001). A risk set calibration method for failure time regression by using a covariate reliability sample. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 63, 855–870. [Google Scholar]
- Ye, W., Lin, X. and Taylor, J. M. G. (2008). Semiparametric modeling of longitudinal measurements and time-to-event data—a two-stage regression calibration approach. Biometrics 64, 1238–1246. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.