Summary
In stepped wedge designs (SWD), clusters are randomized to the time period during which new patients will receive the intervention under study in a sequential rollout over time. By the study’s end, patients at all clusters receive the intervention, eliminating ethical concerns related to withholding potentially efficacious treatments. This is a practical option in many large-scale public health implementation settings. Little statistical theory for these designs exists for binary outcomes. To address this, we utilized a maximum likelihood approach and developed numerical methods to determine the asymptotic power of the SWD for binary outcomes. We studied how the power of a SWD for detecting risk differences varies as a function of the number of clusters, cluster size, the baseline risk, the intervention effect, the intra-cluster correlation coefficient, and the time effect. We studied the robustness of power to the assumed form of the distribution of the cluster random effects, as well as how power is affected by variable cluster size. % SWD power is sensitive to neither, in contrast to the parallel cluster randomized design which is highly sensitive to variable cluster size. We also found that the approximate weighted least square approach of Hussey and Hughes (2007, Design and analysis of stepped wedge cluster randomized trials. Contemporary Clinical Trials 28, 182–191) for binary outcomes under-estimates the power in some regions of the parameter spaces, and over-estimates it in others. The new method was applied to the design of a large-scale intervention program on post-partum intra-uterine device insertion services for preventing unintended pregnancy in the first 1.5 years following childbirth in Tanzania, where it was found that the previously available method under-estimated the power.
Keywords: Cluster randomization, Implementation science, Power calculation, Stepped wedge design, Study design, Time effect
1. Introduction
Traditional clinical trials are designed to assess the efficacy of an intervention. After establishing efficacy, effectiveness of the intervention can next be assessed in a large-scale real-life setting. Often at this stage, a gold standard individually randomized clinical trial may not be feasible or ethical. Cluster randomized trials (CRTs) that randomize clusters or groups of people, rather than individuals, to interventions may be more appropriate for administrative, political, or ethical reasons. CRTs have often been conducted to measure the effects of public health interventions in developing countries, as well as to examine the effects of interventions in institutions such as schools, factories, and medical practices (Hayes and Moulton, 2009).
There are three main types of CRT designs: (i) the parallel cluster randomized design (pCRD), (ii) the crossover design, and (iii) the stepped wedge design (SWD) (Brown and Lilford, 2006). To date, the pCRD has been the most frequently used. In a pCRD, at the start of the trial, typically half the clusters are randomly assigned to one of two interventions. In a crossover design, each cluster receives both the treatment and control interventions, often separated by a “washout” period. In this article, we develop methods for the SWD. The SWD is a special case of a cluster-level crossover design that begins with no clusters randomized to the intervention and ends with all clusters assigned to the intervention, eliminating ethical concerns related to withholding interventions which have previously been shown to be efficacious. Pre-specified time points, called steps, are chosen at which clusters are crossed over from the control arm to the treatment arm in one direction only. The step at which clusters are phased into the intervention is randomized. SWDs are useful when it is difficult to implement an intervention simultaneously at many facilities, perhaps due to budgetary or logistical reasons, as is often the case in large-scale evaluations of public health interventions. For example, the FIGO study described later in Section 4 measures the impact of post-partum intrauterine device (PPIUD) use in Tanzania (Canning and others, 2016). PPIUD meets, at least in part, women’s need for long-term but reversible contraceptive protection following childbirth. During the year following the birth of a child, two in three women are estimated to have an unmet need for contraception. In response to growing interest among a number of developing countries, FIGO launched an initiative for the institutionalization of immediate PPIUD services as a routine part of antenatal counseling and delivery room services. This paper will develop methodology for the design of studies such as this, for example, to ensure that there is adequate power to detect the effectiveness of PPIUD in preventing unintended pregnancy for 1.5 years following the index birth.
Although most outcomes in health care trials are binary, methods that account for the binary nature of the outcome data have not yet been developed for the SWD. Hussey and Hughes (2007) proposed a weighted least square (WLS) approach for SWDs of continuous outcomes, and suggested an approximation to their method for studies with binary outcomes. A recent literature review by Martin and others (2016) identified 60 SWDs between 1987 and 2014. Approximately 30% of the studies used the Hussey and Hughes methodology for power calculations. There have been more recent developments for the SWD, but all have used the Hussey and Hughes approximation for binary outcome data (Hemming and others, 2015; Hemming and Taljaard, 2016). In this article, following Hussey and Hughes and related papers, we consider a two-arm setting with the risk difference as the parameter of interest. We derive the asymptotic variance of the maximum likelihood estimator (MLE) for the risk difference to obtain power and sample size formulas for SWDs of binary outcomes, avoiding Hussey and Hughes’ approximation.
This article is organized as follows. In Section 2, we develop a maximum likelihood method for power calculations in the SWD based on a generalized linear mixed model (GLMM). We present the general results for power calculations in Section 3, and compare it with the WLS approach in Hussey and Hughes (2007) and to the power of the pCRD. In Section 3, we also investigate the robustness of SWD power based on this maximum likelihood approach to different between-cluster random effects distributions, and evaluate the impact of unequal cluster sizes on power. In Section 4, we apply the new method to the design of the Tanzanian PPIUD study. We conclude the article with a discussion in Section 5.
2. Methods
We consider a SWD with 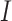 clusters, and there are
clusters, and there are
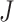 steps per cluster.
steps per cluster. 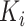 individuals
join the study at each step in each cluster
individuals
join the study at each step in each cluster 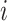 and the sample size of each
cluster is
and the sample size of each
cluster is 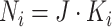 . At each step in each cluster,
new individuals join the trial, so there are no repeated measurements. For designs with
equal cluster sizes,
. At each step in each cluster,
new individuals join the trial, so there are no repeated measurements. For designs with
equal cluster sizes, 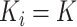 , and there are
, and there are
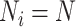 individuals per cluster. Thus, the total
sample size is
individuals per cluster. Thus, the total
sample size is 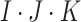 . In a standard SWD,
. In a standard SWD,
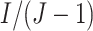 is an integer, so that there are
is an integer, so that there are
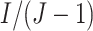 clusters randomized to each of
clusters randomized to each of
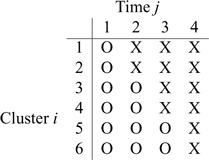
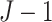 intervention patterns. The following table
illustrates a standard SWD with 6 clusters and 4 steps, where “X” represents the
intervention periods and “O” represents standard of care. In this example,
intervention patterns. The following table
illustrates a standard SWD with 6 clusters and 4 steps, where “X” represents the
intervention periods and “O” represents standard of care. In this example,
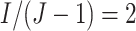 clusters are rolled over to the
intervention at each step.
clusters are rolled over to the
intervention at each step.
Unlike the pCRD, the SWD can incorporate time effects in design and analysis. We first derive a maximum likelihood method for power calculations for SWDs assuming no time effects in Section 2.1, and then extend the method to include time effects in Section 2.2.
2.1. Power calculations for the MLE of binary models: the case of no time effects
Suppose time effects do not need to be included in the model. This scenario is likely for
trials of short duration, and when the effect of calendar time on the outcome is believed
to be small. We consider a binary intervention, 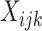 , and a binary
outcome,
, and a binary
outcome, 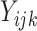 , for participant
, for participant
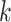 in cluster
in cluster 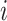 at step
at step
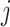 . A GLMM (Breslow and Clayton, 1993) with the identity link is assumed,
. A GLMM (Breslow and Clayton, 1993) with the identity link is assumed,
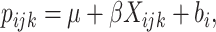 |
(2.1) |
where 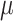 is the probability of the outcome in the
comparison group,
is the probability of the outcome in the
comparison group, 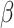 is the intervention effect,
is the intervention effect,
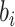 is the random cluster effect, and
is the random cluster effect, and
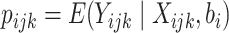 . By
design,
. By
design, 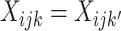 for all
for all
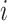 and
and 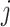 . Following Hussey and Hughes (2007), the normal distribution for
random effects,
. Following Hussey and Hughes (2007), the normal distribution for
random effects, 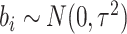 , is assumed, although
in Section 3.3, we will explore the sensitivity
of the methods to departures from this assumption.
, is assumed, although
in Section 3.3, we will explore the sensitivity
of the methods to departures from this assumption.
When time effects are not included in the model, the outcomes 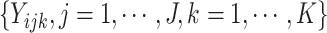 for individuals in cluster
for individuals in cluster 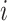 can be re-organized as
can be re-organized as
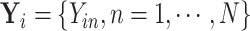 , with
, with
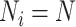 for all
for all 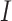 clusters.
Correspondingly, the intervention indicators
clusters.
Correspondingly, the intervention indicators 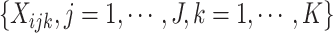 can
be re-ordered as
can
be re-ordered as 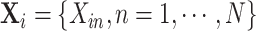 .
Model (2.1) can then be rewritten as
.
Model (2.1) can then be rewritten as
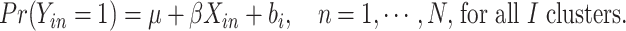 |
(2.2) |
The object of inference is the parameter 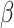 , the risk difference,
and the goal of the study is to test
, the risk difference,
and the goal of the study is to test 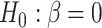 versus
versus
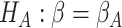 , where
, where
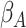 is the value of
is the value of
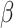 under the alternative hypothesis
under the alternative hypothesis
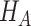 . We base power calculations on the Wald
test for the MLE under its assumed asymptotic normal distribution. As usual, the
asymptotic power is
. We base power calculations on the Wald
test for the MLE under its assumed asymptotic normal distribution. As usual, the
asymptotic power is
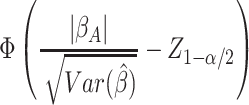 |
(2.3) |
where 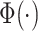 denotes the standard cumulative
normal distribution, and
denotes the standard cumulative
normal distribution, and 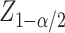 is the
is the
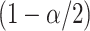 th quantile of the standard
normal distribution function with
th quantile of the standard
normal distribution function with 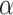 being the Type I error rate. The
challenge here is to derive and compute the asymptotic variance of
being the Type I error rate. The
challenge here is to derive and compute the asymptotic variance of
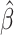 .
.
The full data likelihood for the model parameters 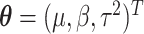 from (2.2) is
from (2.2) is
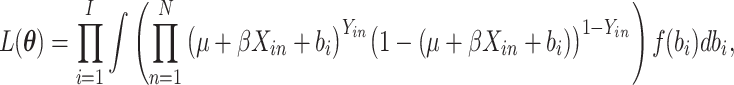 |
and the log-likelihood is
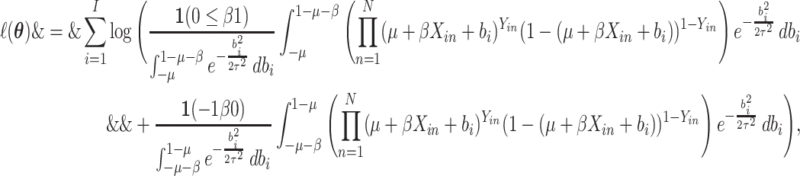 |
(2.4) |
where the limits of the integral over 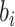 are imposed to ensure
that the probabilities
are imposed to ensure
that the probabilities 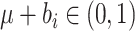 and
and
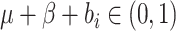 , and
, and
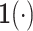 is the indicator function.
The factors
is the indicator function.
The factors 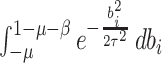 and
and 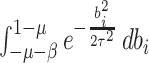 in the denominator normalize the integral to 1.
in the denominator normalize the integral to 1.
Because there are four possible configurations of 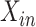 and
and
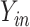 in this framework, (0,0), (0,1), (1,0)
and (1,1), the study data for a single cluster can be written in terms of cell counts
in this framework, (0,0), (0,1), (1,0)
and (1,1), the study data for a single cluster can be written in terms of cell counts
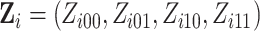 as shown below
as shown below
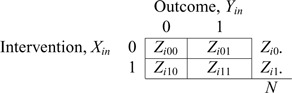
where 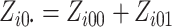 is
the number of individuals in cluster
is
the number of individuals in cluster 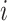 who receive the standard of care,
who receive the standard of care,
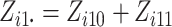 is
the number of individuals in cluster
is
the number of individuals in cluster 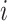 who receive the intervention, and the
cluster size is
who receive the intervention, and the
cluster size is 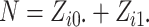 .
Both
.
Both 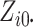 and
and
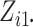 are fixed by
design, i.e.,
are fixed by
design, i.e., 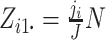 and
and
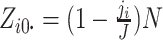 ,
where
,
where 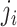 is the number of steps in cluster
is the number of steps in cluster
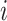 randomly assigned to the intervention. We
can rewrite log-likelihood (2.4) by
utilizing
randomly assigned to the intervention. We
can rewrite log-likelihood (2.4) by
utilizing 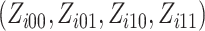 as
follows
as
follows
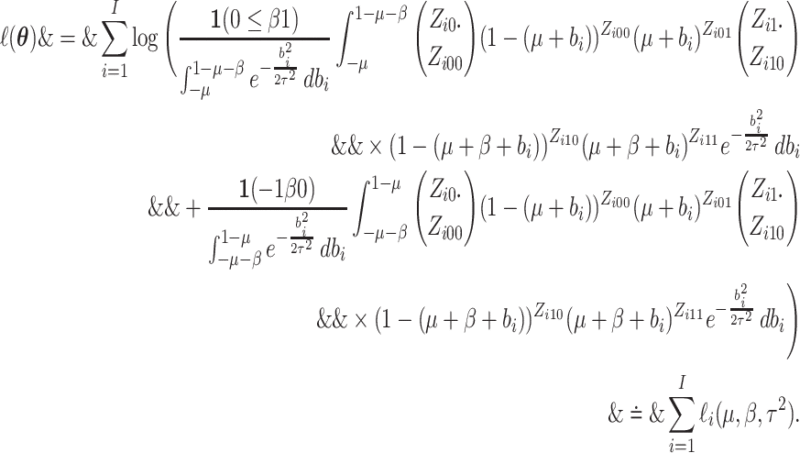 |
(2.5) |
Gauss-Legendre quadrature can be used to calculate this integral numerically.
Asymptotically, the variance of 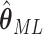 is given by
is given by
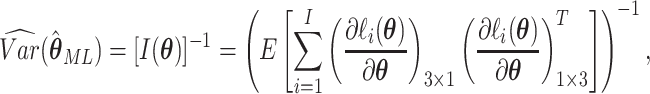 |
(2.6) |
where 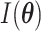 is the expected
Fisher information matrix. Let
is the expected
Fisher information matrix. Let
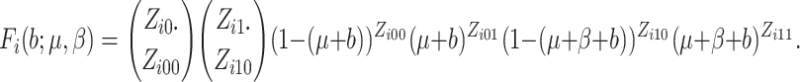 |
(2.7) |
By Leibniz’s rule for differentiation with integration, we obtain the derivatives of the
log-likelihood function, as given in (S1.1) (S1.6) of the supplementary material available at
Biostatistics online. Noting that
(S1.6) of the supplementary material available at
Biostatistics online. Noting that
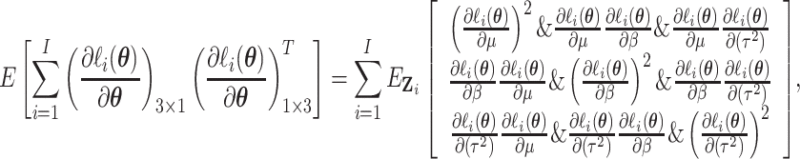 |
(2.8) |
we calculate the expectations of the matrix elements in (2.8) with respect to 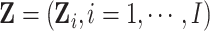 . For
example,
. For
example,
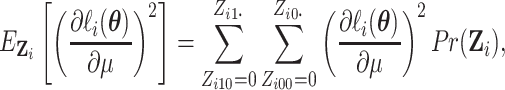 |
(2.9) |
where 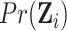 is given by
is given by
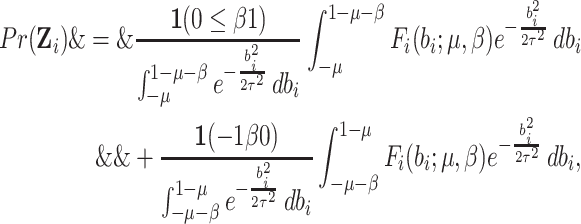 |
(2.10) |
and similarly for the expectation of other matrix elements in (2.8). Then, summation over all the
clusters gives the expectation matrix (2.8) and 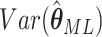 is
obtained from the appropriate element of its inverse. Hence,
is
obtained from the appropriate element of its inverse. Hence, 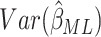 , the
, the
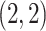 element of
element of 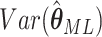 , is
, is
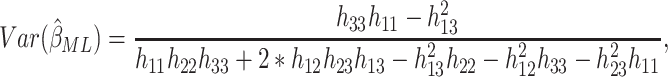 |
(2.11) |
where 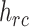 is the
is the 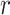 th row and
th row and
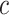 th column of (2.8).
th column of (2.8).
The formula (2.11) works well when
the cluster size, 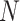 , is not too big, say, less than several
hundreds, as in many clinical trials. However, in public health interventions,
, is not too big, say, less than several
hundreds, as in many clinical trials. However, in public health interventions,
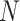 may be greater than 1000 or even 10 000, as
in the FIGO study in Section 4. The large
may be greater than 1000 or even 10 000, as
in the FIGO study in Section 4. The large
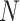 leads to several numerical issues. First,
when
leads to several numerical issues. First,
when 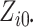 and
and
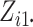 are greater than
1000, the combinatorial numbers
are greater than
1000, the combinatorial numbers 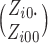 or
or 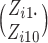 will likely exceed the limit of machine precision, precluding exact binomial probability
calculations. Second, when
will likely exceed the limit of machine precision, precluding exact binomial probability
calculations. Second, when 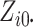 and
and
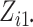 are large,
are large,
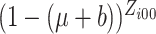 ,
,
 ,
,
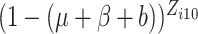 , or
, or
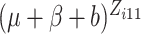 in (2.7) is small, sometimes below the limit
of machine precision and will then be treated as zero, leading to inaccurate calculation.
In these cases, we propose to use the normal approximation to the binomial,
in (2.7) is small, sometimes below the limit
of machine precision and will then be treated as zero, leading to inaccurate calculation.
In these cases, we propose to use the normal approximation to the binomial,
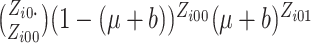 and
and 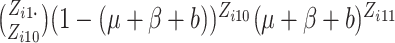 in (2.7) as follows,
in (2.7) as follows,
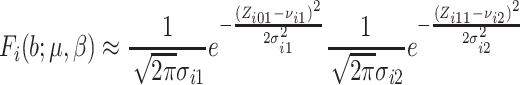 |
(2.12) |
where 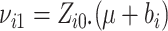 ,
,
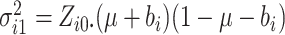 ,
,
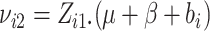 ,
and
,
and 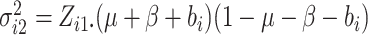 .
.
Related work found that there was little effect on inference due to mis-specification of
the random effects distribution under a logistic model for the binary outcome (Heagerty and Kurland, 2001; Neuhaus and others, 2011). Herein, we consider a gamma
distribution for between-cluster random effects in model (2.1), similar to the one considered by Heagerty and Kurland (2001), i.e. 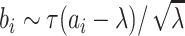 ,
where
,
where 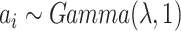 with the density
function
with the density
function 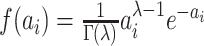 ,
,
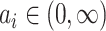 . The density function of
. The density function of
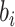 is then given by
is then given by
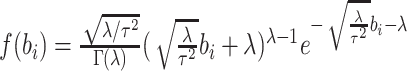 with
with 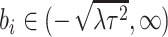 , with
, with
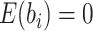 and
and 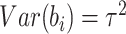 ,
matching the first two moments of the assumed normal random effects distribution. Under
this between-cluster random effect distribution, the log-likelihood (2.5) becomes
,
matching the first two moments of the assumed normal random effects distribution. Under
this between-cluster random effect distribution, the log-likelihood (2.5) becomes
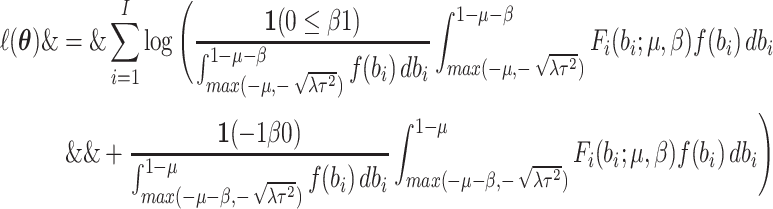 |
where 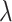 is varied to obtain differently
shaped distributions. Power based on different random effect distributions will be
compared in Section 3.
is varied to obtain differently
shaped distributions. Power based on different random effect distributions will be
compared in Section 3.
When time effects are not included in the model, we note that the SWD is mathematically equivalent to a design where subjects in a cluster are randomly assigned to the intervention or standard of care with a cluster-specific allocation ratio (taking the trial in Section 4 as an example, 3:1 in the first three hospitals and 1:3 in the last three hospitals). However, this design may be difficult to implement in practice because subjects in the same cluster are assigned to different arms, as in an individually randomized clinical trial. Typically, in large scale efficacy trials, cluster-level randomization is required, logistically and because the intervention has cluster level components.
2.2. Power calculations for the MLE of binary models: the case for time effects
In this section, we extend the method of the previous section to the situation with time effects. Accordingly, a generalized linear mixed model (GLMM) with the identity link is defined as follows,
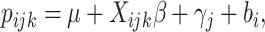 |
(2.13) |
where 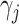 is the time effect corresponding
to step
is the time effect corresponding
to step 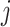 (
(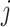 in
in
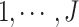 , and
, and 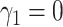 for
identifiability), and it is assumed that
for
identifiability), and it is assumed that 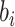 follows a normal
distribution,
follows a normal
distribution, 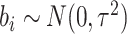 . Since the
probabilities
. Since the
probabilities 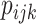 in (2.13) are between 0 and 1,
in (2.13) are between 0 and 1, 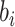 is not allowed to take
any value as for a normal distribution. Thus, for an identity link,
is not allowed to take
any value as for a normal distribution. Thus, for an identity link,
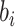 now follows a truncated normal
distribution.
now follows a truncated normal
distribution.
The full data likelihood for the model parameters 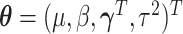 ,
where
,
where 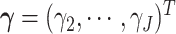 ,
based on (2.13) is
,
based on (2.13) is
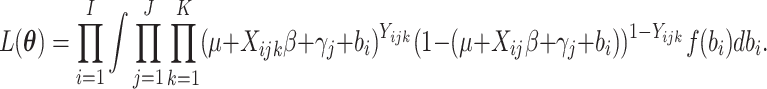 |
(2.14) |
The data for cluster 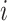 at step
at step 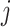 can be
summarized as
can be
summarized as 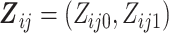 ,
where
,
where 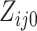 and
and 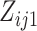 are the
numbers of individuals having outcome 0 and 1, respectively, at step
are the
numbers of individuals having outcome 0 and 1, respectively, at step
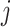 from cluster
from cluster 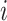 , and
, and
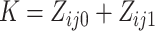 . With a slight abuse of
notation, the full data log-likelihood function is
. With a slight abuse of
notation, the full data log-likelihood function is
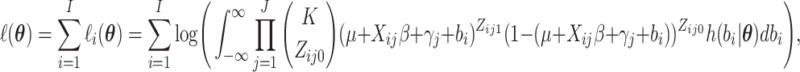 |
(2.15) |
where 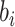 follows a truncated normal distribution
follows a truncated normal distribution
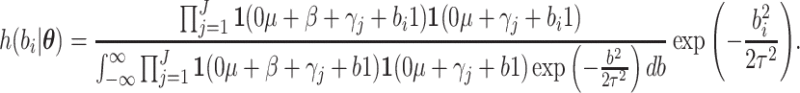 |
Gauss Legendre quadrature can be used for
numerical integration. To simplify this formula, denote
Legendre quadrature can be used for
numerical integration. To simplify this formula, denote 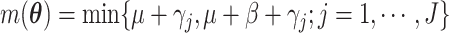 and
and 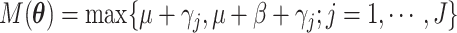 .
Then, the distribution of
.
Then, the distribution of 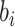 can be rewritten as
can be rewritten as
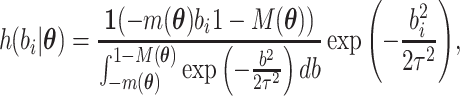 |
and 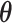 must satisfy
must satisfy
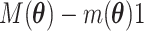 to make the distribution valid.
to make the distribution valid.
The asymptotic variance of the maximum likelihood estimator 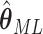 is,
is,
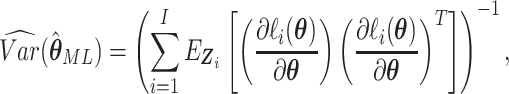 |
where 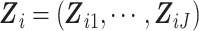 .
With a slight abuse of notation, we define
.
With a slight abuse of notation, we define
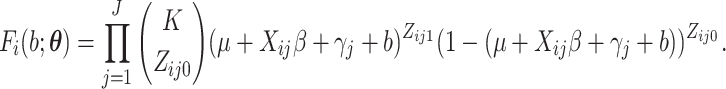 |
By Leibniz’s rule, we obtain the derivatives as given in (S1.7) (S1.10) supplementary material available at
Biostatistics online. The expectation with respect to
(S1.10) supplementary material available at
Biostatistics online. The expectation with respect to 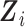 can be
calculated as
can be
calculated as
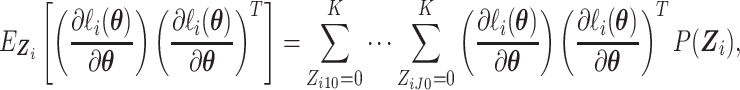 |
(2.16) |
where 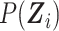 is given by
is given by
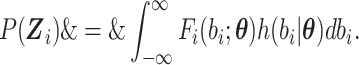 |
(2.17) |
Then the variance of 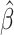 in (2.3) is given by the corresponding
component of estimated variance-covariance matrix
in (2.3) is given by the corresponding
component of estimated variance-covariance matrix 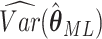 .
.
When 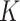 is large, numerical issues discussed in
Section 2.1 are even more challenging. The
normal approximation can be applied accordingly. Specifically,
is large, numerical issues discussed in
Section 2.1 are even more challenging. The
normal approximation can be applied accordingly. Specifically, 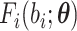 in (2.17) and in supplementary material available at
Biostatistics online (S1.7)
in (2.17) and in supplementary material available at
Biostatistics online (S1.7) (S1.10) can be replaced
with
(S1.10) can be replaced
with 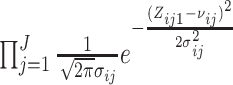 ,
where
,
where 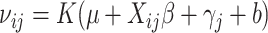 and
and 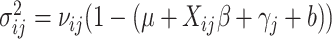 .
In addition, with time effects, the computations are even more intensive than that without
time effects in the model. For example, consider the FIGO study (
.
In addition, with time effects, the computations are even more intensive than that without
time effects in the model. For example, consider the FIGO study (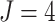 ,
,
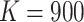 ) in Section 4. When there are no time effects, we need to compute the derivatives in
supplementary material
available at Biostatistics online (S1.1)
) in Section 4. When there are no time effects, we need to compute the derivatives in
supplementary material
available at Biostatistics online (S1.1) (S1.6) and the
probability distribution in (2.10)
for each possible combination of
(S1.6) and the
probability distribution in (2.10)
for each possible combination of 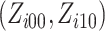 of cluster
of cluster
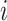 in (2.9). The number of possible combinations is
in (2.9). The number of possible combinations is
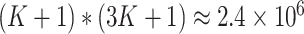 for a
single cluster. Without time effects in the model, the running time for the power
calculation was about 85 s at our computational facility. However, when time effects are
included in the model, we consider all possible combinations of
for a
single cluster. Without time effects in the model, the running time for the power
calculation was about 85 s at our computational facility. However, when time effects are
included in the model, we consider all possible combinations of 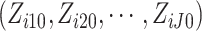 of cluster
of cluster
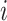 in (2.16). In each cluster, there are
in (2.16). In each cluster, there are 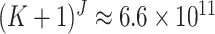 combinations
for which (S1.7)
combinations
for which (S1.7) (S1.10) of the supplementary material available at
Biostatistics online and (2.17) must be evaluated, leading to an estimated running time
of over 1000 days at our high performance facility. We thus developed a partition method
to approximate the power. At step
(S1.10) of the supplementary material available at
Biostatistics online and (2.17) must be evaluated, leading to an estimated running time
of over 1000 days at our high performance facility. We thus developed a partition method
to approximate the power. At step 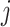 in cluster
in cluster 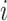 ,
,
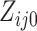 may take on values
may take on values
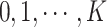 . We divide these
. We divide these
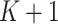 numbers into
numbers into 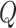 equal
partitions, and use their center values to represent these partitions. For example,
suppose
equal
partitions, and use their center values to represent these partitions. For example,
suppose 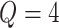 . The partitions are
. The partitions are
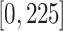 ,
, 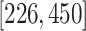 ,
,
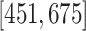 , and
, and 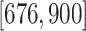 ,
centered at 112, 338, 563, and 788. We use these center values to approximate the
expectation in (2.16) as
,
centered at 112, 338, 563, and 788. We use these center values to approximate the
expectation in (2.16) as
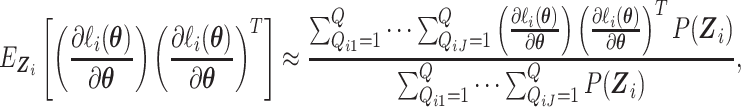 |
where the center values are about at 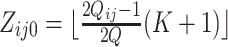 and
and 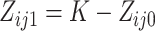 , for
, for
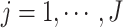 , with
, with
 being the greatest
integer function. To choose
being the greatest
integer function. To choose 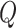 , we start from a small value, and then
gradually increase until the difference between two consecutive calculated powers is less
than 1%. In the FIGO study, starting from
, we start from a small value, and then
gradually increase until the difference between two consecutive calculated powers is less
than 1%. In the FIGO study, starting from 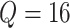 , and then
, and then
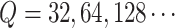 , the power calculation
stopped at
, the power calculation
stopped at 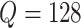 . When
. When 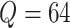 , the
calculation took about 0.6 hours, and when
, the
calculation took about 0.6 hours, and when 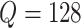 the running time was
about 10.3 h. This partition method was very efficient, reducing the computational cost in
this example from over 1000 days to 10.3 h.
the running time was
about 10.3 h. This partition method was very efficient, reducing the computational cost in
this example from over 1000 days to 10.3 h.
3. Results
3.1. General observations
To explore the properties of the methods proposed in Section 2, we first studied the asymptotic power as a function of the risk difference and the number of steps.
To design a study, the assumed parameter values must be specified. The values of
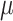 and
and 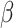 can be determined by
can be determined by
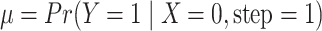 and
and
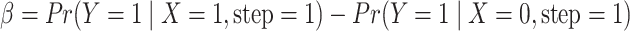 .
When time effects are included in the model, we assumed that the effects are linear across
the time steps. If the change over the study duration is
.
When time effects are included in the model, we assumed that the effects are linear across
the time steps. If the change over the study duration is 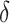 ,
,
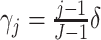 . To
illustrate the methods, we will consider
. To
illustrate the methods, we will consider 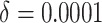 and
and
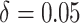 . The time effect for
. The time effect for
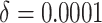 is almost negligible, and it
is moderate for the other. The value of
is almost negligible, and it
is moderate for the other. The value of 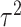 is determined by the
intra-cluster correlation coefficient (ICC),
is determined by the
intra-cluster correlation coefficient (ICC), 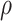 , which measures the
correlation between individuals in the same cluster. Following Hussey and Hughes (2007), in models (2.1) and (2.13),
, which measures the
correlation between individuals in the same cluster. Following Hussey and Hughes (2007), in models (2.1) and (2.13), 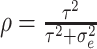 ,
where
,
where 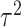 is the variance of cluster-specific
random effects and the residual variance
is the variance of cluster-specific
random effects and the residual variance 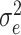 can be
reasonably assumed to be
can be
reasonably assumed to be 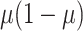 , giving
, giving
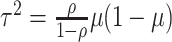 .
.
For an assumed baseline risk of outcome 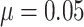 , we considered
risk ratios in the range of 1.8 to 4.2, corresponding to risk differences
, we considered
risk ratios in the range of 1.8 to 4.2, corresponding to risk differences
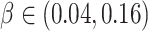 . Figure 1 shows the power as a function of the risk difference,
. Figure 1 shows the power as a function of the risk difference,
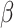 , for different numbers of steps and
different ICCs. Here, the number of clusters is
, for different numbers of steps and
different ICCs. Here, the number of clusters is 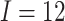 , the number of steps
was varied as
, the number of steps
was varied as 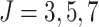 , and the ICC was set to 0.1 and
0.001 to represent large and small correlations, respectively. The cluster size was fixed
at
, and the ICC was set to 0.1 and
0.001 to represent large and small correlations, respectively. The cluster size was fixed
at 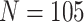 . In Figures 1(a) and (b), model (2.1) was used with no time effects. In
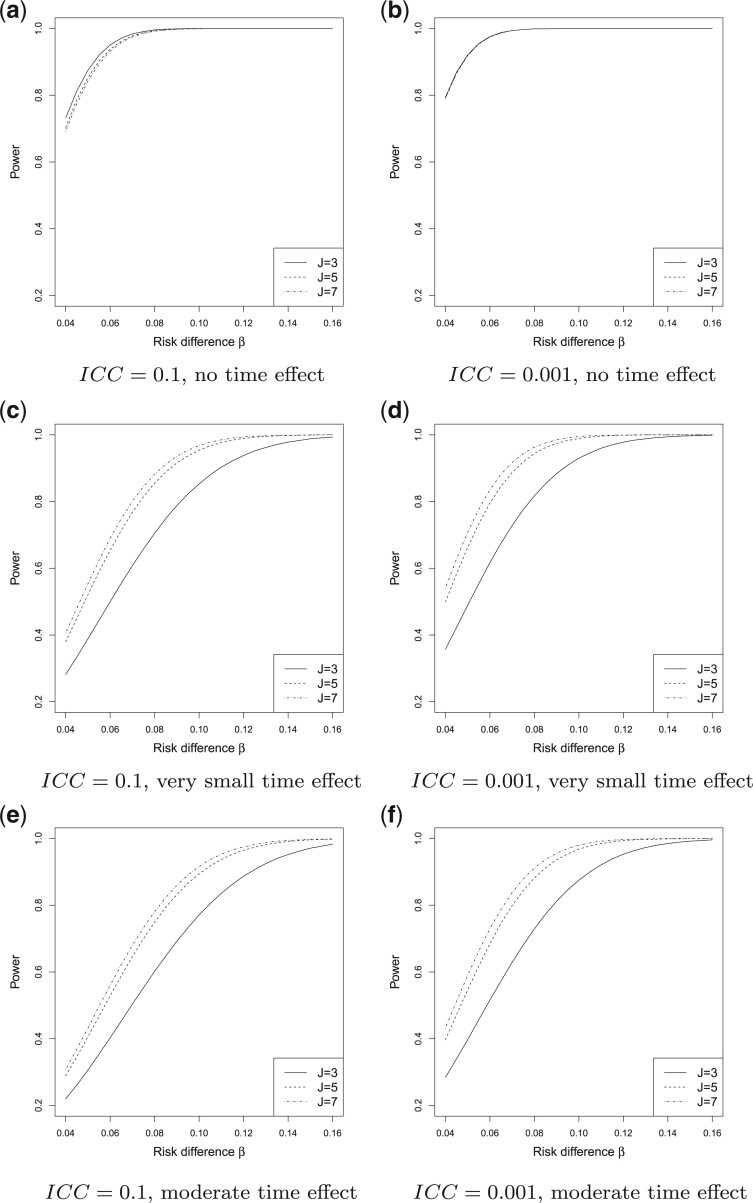
Figure 1(a), when the ICC was large
(
. In Figures 1(a) and (b), model (2.1) was used with no time effects. In
Figure 1(a), when the ICC was large
(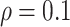 ), power became slightly lower as
the number of steps increased. Because no time effect was included, the data become more
unbalanced within a cluster between the intervention and control groups as the number of
steps increases, and hence power decreases accordingly. When
), power became slightly lower as
the number of steps increased. Because no time effect was included, the data become more
unbalanced within a cluster between the intervention and control groups as the number of
steps increases, and hence power decreases accordingly. When 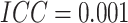 was
small, it can be seen in Figure 1(b) that the effect
of the number of steps on power decreases as the time effect diminishes, and the effect
almost vanished as the ICC approached zero when there were no time effects. For example,
for
was
small, it can be seen in Figure 1(b) that the effect
of the number of steps on power decreases as the time effect diminishes, and the effect
almost vanished as the ICC approached zero when there were no time effects. For example,
for 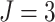 , when
, when 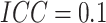 , there
was 80% power to detect a risk difference of 0.0445, which corresponds to a risk ratio of
1.89; when
, there
was 80% power to detect a risk difference of 0.0445, which corresponds to a risk ratio of
1.89; when 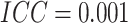 , the minimum detectable risk
difference was 0.0405, corresponding to a risk ratio of 1.81, for 80% power.
, the minimum detectable risk
difference was 0.0405, corresponding to a risk ratio of 1.81, for 80% power.
Fig. 1.
Power vs. risk difference 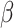 , for
, for 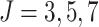 and
and
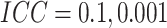 , with cluster size
, with cluster size
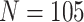 and baseline risk
and baseline risk
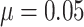 . For figures in the left
column,
. For figures in the left
column, 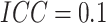 ; while for figures in the right
column,
; while for figures in the right
column, 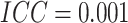 . There are no time effects
(
. There are no time effects
(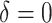 ) in the first row, very small
time effects (
) in the first row, very small
time effects (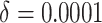 ) in the second row, and
moderate time effects (
) in the second row, and
moderate time effects (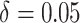 ) in the third row.
) in the third row.
In Figure 1(c) and (d), although the time effects were very small (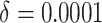 ),
model (2.13) was used for power
calculations. Unlike what was seen in Figure 1(a) and
(b), when time effects are included in the model,
power increases with the number of steps. This may be because, in addition to the
comparisons available between intervention and standard of care at the same step, the
number of comparisons within cluster also increases as the number of steps increases. For
),
model (2.13) was used for power
calculations. Unlike what was seen in Figure 1(a) and
(b), when time effects are included in the model,
power increases with the number of steps. This may be because, in addition to the
comparisons available between intervention and standard of care at the same step, the
number of comparisons within cluster also increases as the number of steps increases. For
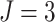 , when
, when 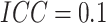 there
was 80% power to detect a risk difference of 0.092, corresponding to a risk ratio of 2.84;
when
there
was 80% power to detect a risk difference of 0.092, corresponding to a risk ratio of 2.84;
when 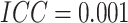 , the risk difference with 80%
power was 0.078, corresponding to a risk ratio of 2.56. The power in Figure 1(c) was much lower than the power in Figure 1(a), similar to the comparison between Figure 1(d) and (b). When time
effects are anticipated to be negligible, the model without time effects is much more
powerful.
, the risk difference with 80%
power was 0.078, corresponding to a risk ratio of 2.56. The power in Figure 1(c) was much lower than the power in Figure 1(a), similar to the comparison between Figure 1(d) and (b). When time
effects are anticipated to be negligible, the model without time effects is much more
powerful.
In Figure 1(e) and (f), the time effects were moderate (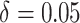 ). Specifically,
for
). Specifically,
for 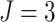 , when
, when 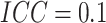 there
was 80% power to detect a risk difference of 0.105 (risk ratio 3.1); when
there
was 80% power to detect a risk difference of 0.105 (risk ratio 3.1); when
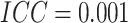 the minimum detectable risk
difference with 80% power was 0.0885 (risk ratio 2.77). Again, the power increased with
the number of steps.
the minimum detectable risk
difference with 80% power was 0.0885 (risk ratio 2.77). Again, the power increased with
the number of steps.
In summary, when time effects are not included in the model, the power decreases with increasing number of steps given fixed cluster size and sample size; in contrast, when time effects are included in the model, the power increases with more time steps. When time effects are negligible, the model without time effects is much more powerful than the model with time effects.
3.2. Comparison of the power of SWDs with equal and unequal cluster sizes
So far we have assumed equal cluster sizes, 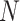 . In practice, however,
studies often have variable cluster sizes. Therefore, it is of interest to compare the
efficiency of a SWD with equal cluster sizes to one with unequal cluster sizes. Previous
work has considered the relative efficiency of unequal versus equal cluster sizes in the
pCRD (van Breukelen and others,
2007; Candel and Van Breukelen, 2016),
where it was found that power tends to decrease drastically as the variation in cluster
sizes increases. We conducted numerical experiments to investigate the impact of variable
cluster size on the power of the SWD. Two parameters need to be taken into account. One is
the cluster size coefficient of variation (CV), defined as the square root of the variance
of the cluster sizes divided by the mean cluster size; and the other is the
intervention-control allocation ratio (TCR), defined as the ratio of study participants
randomized to the intervention vs. those not. When the cluster sizes are equal, the
cluster size CV is 0 and the TCR is 1. When the cluster sizes are unequal, the design then
has a positive CV and a TCR that departs from 1, both of which could affect the study
power.
. In practice, however,
studies often have variable cluster sizes. Therefore, it is of interest to compare the
efficiency of a SWD with equal cluster sizes to one with unequal cluster sizes. Previous
work has considered the relative efficiency of unequal versus equal cluster sizes in the
pCRD (van Breukelen and others,
2007; Candel and Van Breukelen, 2016),
where it was found that power tends to decrease drastically as the variation in cluster
sizes increases. We conducted numerical experiments to investigate the impact of variable
cluster size on the power of the SWD. Two parameters need to be taken into account. One is
the cluster size coefficient of variation (CV), defined as the square root of the variance
of the cluster sizes divided by the mean cluster size; and the other is the
intervention-control allocation ratio (TCR), defined as the ratio of study participants
randomized to the intervention vs. those not. When the cluster sizes are equal, the
cluster size CV is 0 and the TCR is 1. When the cluster sizes are unequal, the design then
has a positive CV and a TCR that departs from 1, both of which could affect the study
power.
The sample size of the numerical examples in this section was fixed at 480. Consider a
SWD with 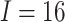 clusters, a mean cluster size
clusters, a mean cluster size
 , and
, and 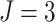 steps. We
first fixed the TCR to be 1 and varied the cluster size CV. The cluster size was 30 for
each cluster in the equal cluster size design, while for the unequal cluster size design,
we randomly assigned 240 individuals to the first eight clusters using a multinomial
distribution with
steps. We
first fixed the TCR to be 1 and varied the cluster size CV. The cluster size was 30 for
each cluster in the equal cluster size design, while for the unequal cluster size design,
we randomly assigned 240 individuals to the first eight clusters using a multinomial
distribution with 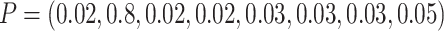 ,
and then another 240 individuals to the second eight clusters using a multinomial
distribution with
,
and then another 240 individuals to the second eight clusters using a multinomial
distribution with 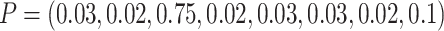 .
Thus, the TCR was still 1 although the cluster size CV = 2.0. For baseline risk
.
Thus, the TCR was still 1 although the cluster size CV = 2.0. For baseline risk
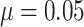 and
and 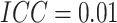 , the
power curves versus risk differences are displayed in Figure S1(a) of the supplementary material available at
Biostatistics online without time effects, in Figure S1(c) of the supplementary material available at
Biostatistics online with very small time effects, and in Figure S1(e)
of the supplementary material
available at Biostatistics online with moderate time effects. We can see
that there is virtually no difference between these curves. Overall, with TCR = 1, power
was very similar between the two designs.
, the
power curves versus risk differences are displayed in Figure S1(a) of the supplementary material available at
Biostatistics online without time effects, in Figure S1(c) of the supplementary material available at
Biostatistics online with very small time effects, and in Figure S1(e)
of the supplementary material
available at Biostatistics online with moderate time effects. We can see
that there is virtually no difference between these curves. Overall, with TCR = 1, power
was very similar between the two designs.
We next varied the TCR from 1 to 0.7 by setting the total sample size of the first eight
clusters to 96 and the total sample size of the second eight clusters to 384, or,
equivalently, by setting the cluster size of the first eight clusters to 12, and to 48 for
the second eight clusters, which produced a cluster size CV = 0.6. In addition, we created
another design by randomly assigning 96 individuals to the first eight clusters using a
multinomial distribution with 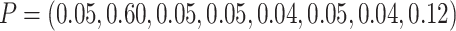 .
We then assigned another 384 individuals to the second eight clusters using a multinomial
distribution with
.
We then assigned another 384 individuals to the second eight clusters using a multinomial
distribution with 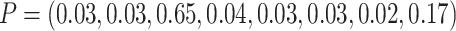 ,
to obtain a TCR of 0.7 and a cluster size CV of 2.0. We then changed TCR to 1.5 by setting
the total sample size of the first eight clusters to be 384 and the total sample size of
the second eight clusters to be 96. We assigned subjects to the clusters as previously, so
the cluster size CVs were still 0.6 and 2.0, respectively. We plotted the power curves for
these two TCRs in red and in blue, respectively, along with the plots explored previously
in Figure S1(a) of the supplementary
material available at Biostatistics online without time effects,
in Figure S1(c) of the supplementary
material available at Biostatistics online with very small time
effects, and in Figure S1(e) of the supplementary material available at Biostatistics online with
moderate time effects, in the supplementary material. We can see that the two power curves with the same TCR
were very close, although they had quite different cluster size CVs, again verifying the
previous observation that SWD power is insensitive to different cluster size CVs for a
fixed TCR.
,
to obtain a TCR of 0.7 and a cluster size CV of 2.0. We then changed TCR to 1.5 by setting
the total sample size of the first eight clusters to be 384 and the total sample size of
the second eight clusters to be 96. We assigned subjects to the clusters as previously, so
the cluster size CVs were still 0.6 and 2.0, respectively. We plotted the power curves for
these two TCRs in red and in blue, respectively, along with the plots explored previously
in Figure S1(a) of the supplementary
material available at Biostatistics online without time effects,
in Figure S1(c) of the supplementary
material available at Biostatistics online with very small time
effects, and in Figure S1(e) of the supplementary material available at Biostatistics online with
moderate time effects, in the supplementary material. We can see that the two power curves with the same TCR
were very close, although they had quite different cluster size CVs, again verifying the
previous observation that SWD power is insensitive to different cluster size CVs for a
fixed TCR.
When there were no time effects as in Figure S1(a) of the supplementary material available at
Biostatistics online, the effect of TCR on power is small. However, for
the model with time effects, TCR had a marked impact on power (Figures S1(c) and (e) of
the supplementary material
available at Biostatistics online). When TCR=1, i.e. half the
participants are randomized to the intervention, the SWD was the most efficient. To
further investigate the role of TCR on SWD power, we repeated the above numerical study
with a baseline risk 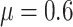 (Figures S1(b), (d) and (f) of the
supplementary material
available at Biostatistics online). Similar patterns were observed.
(Figures S1(b), (d) and (f) of the
supplementary material
available at Biostatistics online). Similar patterns were observed.
Overall, the findings from these numerical studies suggest that the effect of cluster size CV on power in the SWD is, in general, small, for a fixed TCR. Without time effects, there is little effect of TCR on power, while with time effects, TCR has a much greater effect. However, when a SWD is well randomized, the TCR will not depart too much from 1. It is reasonable to conclude that the power of the SWD is robust to variable cluster size.
3.3. Comparison of power with different assumed random effect distributions
Now, we consider the gamma random effect distribution discussed in Section 2.1, with 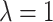 and
and
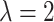 , to incorporate a wide range of
shapes. The density plots of the gamma distributions considered are given in Figure S2 of
the supplementary material
available at Biostatistics online. The gamma distribution with
, to incorporate a wide range of
shapes. The density plots of the gamma distributions considered are given in Figure S2 of
the supplementary material
available at Biostatistics online. The gamma distribution with
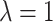 looks very different from the
standard normal distribution, while the shape of the density function is closer to normal
with
looks very different from the
standard normal distribution, while the shape of the density function is closer to normal
with 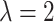 .
.
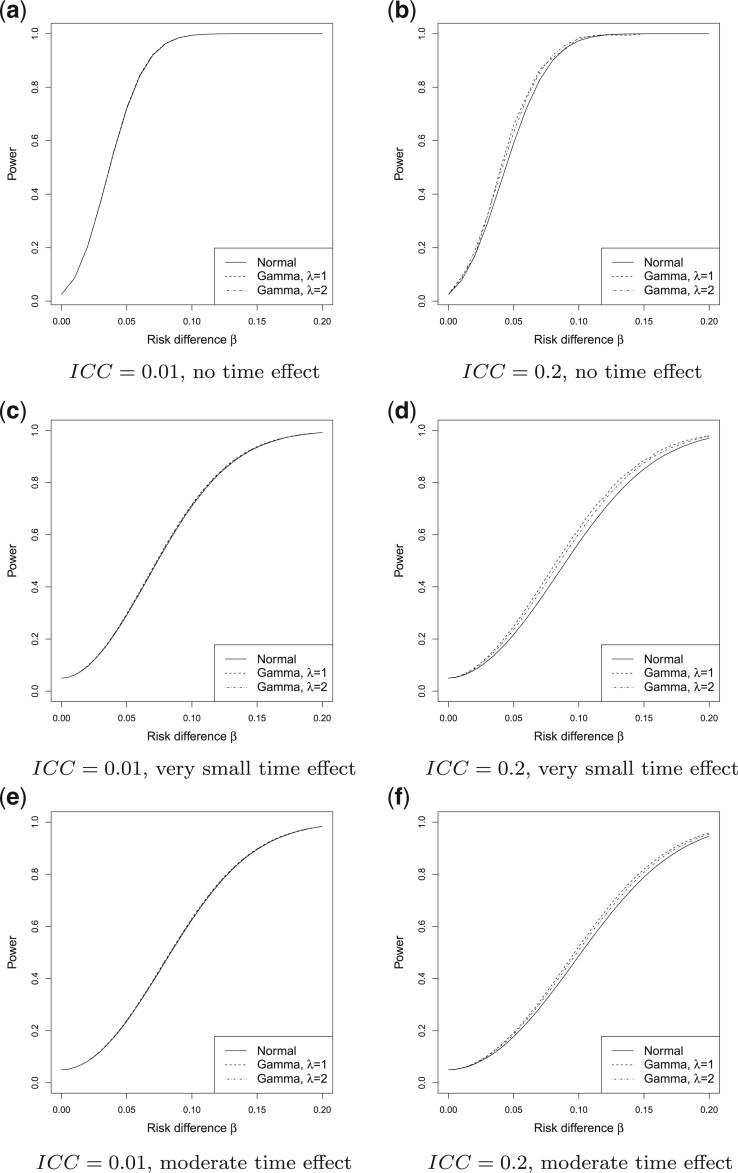
In Figure 2, assuming a SWD with
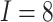 ,
, 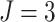 , and a cluster size
, and a cluster size
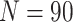 , we show power curves with different
distributions of the cluster random effects. There were no time effects in Figure 2(a) and (b).
When the
, we show power curves with different
distributions of the cluster random effects. There were no time effects in Figure 2(a) and (b).
When the 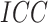 was small (
was small (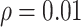 ), in
Figure 2(a), the power curves for the three
distributions were nearly identical. In Figure 2(b),
when
), in
Figure 2(a), the power curves for the three
distributions were nearly identical. In Figure 2(b),
when 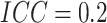 was substantially larger, a bigger
difference between these three power curves was observed, although they were still quite
close. When the time effects were very small (Figure
2(c) and (d) ) or moderate (Figure 2(e) and (f))
the power curves from different random effects distributions were also very similar. These
observations suggest that, for random effects distributions with the same mean and
variance but different higher order moments, the distribution of the cluster random
effects has little effect on the power of a SWD, as has previously reported (Heagerty and Kurland, 2001; Neuhaus and others, 2011).
was substantially larger, a bigger
difference between these three power curves was observed, although they were still quite
close. When the time effects were very small (Figure
2(c) and (d) ) or moderate (Figure 2(e) and (f))
the power curves from different random effects distributions were also very similar. These
observations suggest that, for random effects distributions with the same mean and
variance but different higher order moments, the distribution of the cluster random
effects has little effect on the power of a SWD, as has previously reported (Heagerty and Kurland, 2001; Neuhaus and others, 2011).
Fig. 2.
Power vs. the risk difference 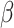 for different cluster random
effect distributions, with baseline risk
for different cluster random
effect distributions, with baseline risk 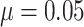 , number of
steps
, number of
steps 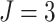 , number of clusters
, number of clusters
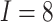 , and cluster size
, and cluster size
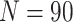 . For figures in the left column,
. For figures in the left column,
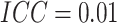 ; while for figures in the
right column,
; while for figures in the
right column, 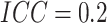 . There are no time effects
(
. There are no time effects
(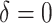 ) in the first row, very small
time effects (
) in the first row, very small
time effects (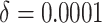 ) in the second row, and
moderate time effects (
) in the second row, and
moderate time effects (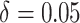 ) in the third row.
) in the third row.
3.4. Comparison to the Hussey and Hughes (2007) method
Next, we compared the efficiency of the MLE estimator for a SWD to that of the WLS estimator of Hussey and Hughes (2007). First, we assumed no time effects. In Hussey and Hughes (2007), the variance of the WLS estimator based on model (2.1) is
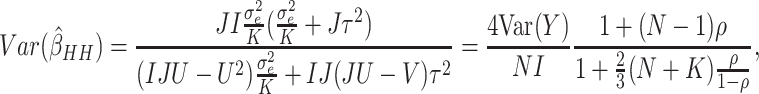 |
(3.1) |
where 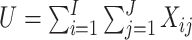 ,
,
 with
with
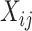 an indicator of the intervention
status randomly assigned to cluster
an indicator of the intervention
status randomly assigned to cluster 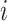 at time
at time 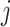 ,
,
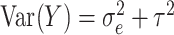 , and
, and
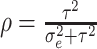 is
the ICC. This simplified expression was given by Zhou
and others (2017). An extra factor of
is
the ICC. This simplified expression was given by Zhou
and others (2017). An extra factor of
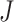 was omitted from equation (9) in Hussey and Hughes (2007) but is included in the
numerator of (3.1) (Liao and others, 2015).
was omitted from equation (9) in Hussey and Hughes (2007) but is included in the
numerator of (3.1) (Liao and others, 2015).
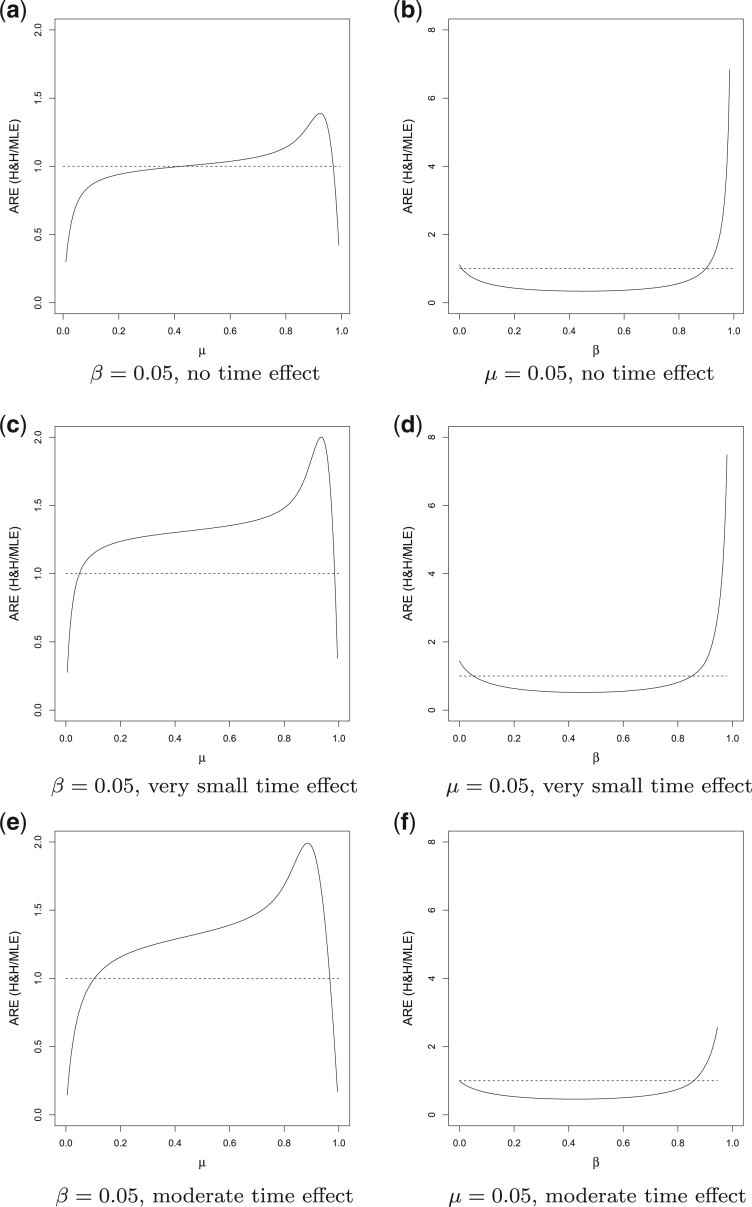
In Figure 3(a) and (b), we compared the relative variances (ARE) of 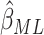 and
and 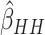 using (3.1) for models without time effects,
over different values of the baseline risk
using (3.1) for models without time effects,
over different values of the baseline risk 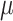 , and the risk
difference
, and the risk
difference 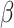 , in a SWD of eight clusters with 90
subjects in each cluster, five steps, and
, in a SWD of eight clusters with 90
subjects in each cluster, five steps, and 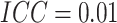 . The variance of
. The variance of
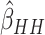 was over-estimated (i.e.
the ARE was greater than 1) for some values of
was over-estimated (i.e.
the ARE was greater than 1) for some values of 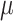 and
and
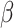 , and under-estimated for others.
, and under-estimated for others.
Fig. 3.
ARE of 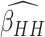 relative to
relative to
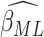 . Figures in the
left column show ARE vs. baseline risk
. Figures in the
left column show ARE vs. baseline risk 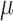 with the risk
difference
with the risk
difference 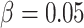 ; Figures in the right column
show ARE vs. risk difference
; Figures in the right column
show ARE vs. risk difference 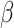 with the baseline risk
with the baseline risk
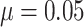 . There are no time effects
(
. There are no time effects
(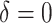 ) in the first row, very small
time effects in the second row (
) in the first row, very small
time effects in the second row (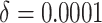 ), and moderate time
effects in the third row (
), and moderate time
effects in the third row (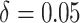 ). The number of clusters
). The number of clusters
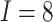 , the number of steps
, the number of steps
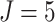 , the cluster size
, the cluster size
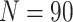 , and
, and 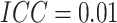 .
.
When there are time effects, the variance of the WLS estimator is given by
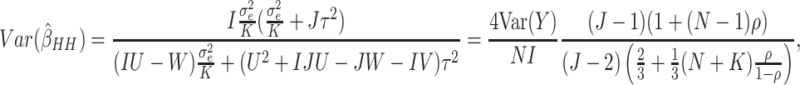 |
(3.2) |
where 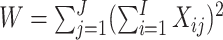 .
Again, this simplified expression was given by Zhou
and others (2017). Figure
3(c)–(f) compared the relative variances (ARE) of
.
Again, this simplified expression was given by Zhou
and others (2017). Figure
3(c)–(f) compared the relative variances (ARE) of 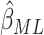 and
and 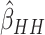 for model (2.13) with very small or moderate time
effects. As with no time effects, the variance of
for model (2.13) with very small or moderate time
effects. As with no time effects, the variance of 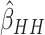 was
over-estimated for some values of
was
over-estimated for some values of 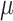 and
and 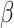 , and
under-estimated for others.
, and
under-estimated for others.
Since Hussey and Hughes (2007) assumed that the
within-cluster variance was 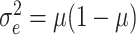 , the variance in
(3.1) and (3.2) does not depend on the underlying
risk difference
, the variance in
(3.1) and (3.2) does not depend on the underlying
risk difference 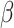 , while the variance of the MLE does,
as is the case with binomial data in general. This approximation likely leads to
inaccuracies in the calculation of
, while the variance of the MLE does,
as is the case with binomial data in general. This approximation likely leads to
inaccuracies in the calculation of 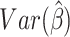 . In addition, the WLS
approach assumes that
. In addition, the WLS
approach assumes that 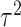 is known, which will not be true in
practice, or at least, that its estimate is uncorrelated with the estimate of the mean
function parameters as would be the case in a linear model under normality assumptions. In
contrast, the MLE takes into account the estimation of
is known, which will not be true in
practice, or at least, that its estimate is uncorrelated with the estimate of the mean
function parameters as would be the case in a linear model under normality assumptions. In
contrast, the MLE takes into account the estimation of 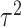 in
deriving the variance, as well as its correlation with
in
deriving the variance, as well as its correlation with 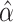 ,
,
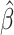 , and
, and 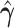 , and thus it will be
a more honest assessment of the power although it may be less efficient because it
estimates an additional parameter. Thus, our findings suggest that power calculations for
the SWD should be based on the variance of the MLE or the variance of another consistent
estimator which accounts for these key features of binomially distributed outcome
data.
, and thus it will be
a more honest assessment of the power although it may be less efficient because it
estimates an additional parameter. Thus, our findings suggest that power calculations for
the SWD should be based on the variance of the MLE or the variance of another consistent
estimator which accounts for these key features of binomially distributed outcome
data.
3.5. Comparison of the SWD to the parallel cluster randomized design
It is also of interest to compare the SWD to the pCRD, in which, at the start of the study, typically half of the clusters are randomized to the intervention group and half to the control group. As given by Donner and Klar (2000),
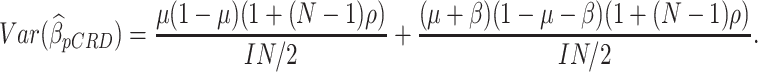 |
(3.3) |
Firstly, consider the SWD without time effects, as shown in the left column of Figure 4. Figure
4(a) displays the power of the SWD and pCRD as a function of the number of
clusters, varying from 8 to 80, with 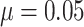 ,
, 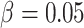 , and
, and
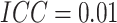 . The power curves for the SWD and
pCRD as a function of the risk difference, which varies from 0 to 0.2, are shown in Figure 4(c), with fixed baseline risk
. The power curves for the SWD and
pCRD as a function of the risk difference, which varies from 0 to 0.2, are shown in Figure 4(c), with fixed baseline risk
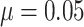 and for several values of
and for several values of
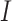 , the number of clusters. We can see that
the SWD has greater power than the pCRD in all scenarios explored. Figure 4(e) and Figure S3(a) of the supplementary material available at
Biostatistics online show the power curves for the SWD and pCRD as a
function of the ICC for different numbers of clusters and different baseline risks. We can
see that the power of the pCRD decreases quickly as the ICC increases, while the power of
SWD barely changed either in Figure 4(e) for a small
baseline risk
, the number of clusters. We can see that
the SWD has greater power than the pCRD in all scenarios explored. Figure 4(e) and Figure S3(a) of the supplementary material available at
Biostatistics online show the power curves for the SWD and pCRD as a
function of the ICC for different numbers of clusters and different baseline risks. We can
see that the power of the pCRD decreases quickly as the ICC increases, while the power of
SWD barely changed either in Figure 4(e) for a small
baseline risk 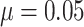 (rare outcome), or in Figure S3(a)
of the supplementary material
available at Biostatistics online for a big baseline risk
(rare outcome), or in Figure S3(a)
of the supplementary material
available at Biostatistics online for a big baseline risk
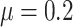 (common outcome). Also, the rate of
the change of the power function with increasing ICC was very similar in the SWD for
different numbers of clusters as can be seen in Figure
4(a). But for the pCRD, the power declined even faster with increasing ICC as the
number of clusters increased. In Section S3 of the supplementary material available at Biostatistics
online, we prove that the power of the SWD based on the MLE variance (2.11) is always bigger than that of the
pCRD based on the variance (3.3),
emphasizing the efficiency advantage of the SWD over the pCRD, when there are no time
effects included in the model. Intuitively, this point seems obvious. There are only
between-cluster comparisons in the pCRD, while there are, in addition, within-cluster
comparisons in the SWD (Zhou and others,
2017).
(common outcome). Also, the rate of
the change of the power function with increasing ICC was very similar in the SWD for
different numbers of clusters as can be seen in Figure
4(a). But for the pCRD, the power declined even faster with increasing ICC as the
number of clusters increased. In Section S3 of the supplementary material available at Biostatistics
online, we prove that the power of the SWD based on the MLE variance (2.11) is always bigger than that of the
pCRD based on the variance (3.3),
emphasizing the efficiency advantage of the SWD over the pCRD, when there are no time
effects included in the model. Intuitively, this point seems obvious. There are only
between-cluster comparisons in the pCRD, while there are, in addition, within-cluster
comparisons in the SWD (Zhou and others,
2017).
Fig. 4.
Comparison between SWD and pCRD. There are no time effects in the model for figures
in the left column, and moderate time effects in the model for figures in the right
column. (a) and (b) power vs. the number of clusters, with baseline risk
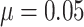 , the risk difference
, the risk difference
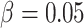 , the cluster size
, the cluster size
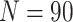 , and
, and 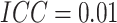 ;
(c) and (d) power vs. the risk difference
;
(c) and (d) power vs. the risk difference 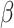 , with baseline
risk
, with baseline
risk 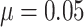 , the cluster size
, the cluster size
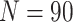 , the
, the 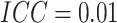 ,
and the number of steps
,
and the number of steps 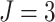 ; (e) and (f) power vs. ICC, for
different baseline risks
; (e) and (f) power vs. ICC, for
different baseline risks 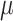 , where the risk difference
, where the risk difference
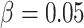 , the cluster size
, the cluster size
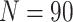 , and the number of steps
, and the number of steps
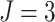 .
.
Next, we considered the comparison with the pCRD when time effects were included in the
model for the SWD. Suppose that for the pCRD, individuals at different time steps are well
balanced in each cluster. That is, the formula (3.3) is still appropriate, since the time step is not a
confounder in the pCRD. The comparison between SWD and pCRD is shown in the right column
of Figure 4, when the time effects are moderate
(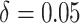 ). Figure 4(b) and (d) display the power of
the SWD and pCRD as a function of the number of clusters, and as a function of the risk
difference, respectively, with
). Figure 4(b) and (d) display the power of
the SWD and pCRD as a function of the number of clusters, and as a function of the risk
difference, respectively, with 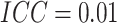 . The SWD has lower power than the
pCRD, since the SWD has to estimate
. The SWD has lower power than the
pCRD, since the SWD has to estimate 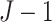 more parameters,
more parameters,
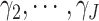 , in the model.
However, as the ICC increases, as shown in Figure
4(f) and Figure S3(b) of the supplementary material available at Biostatistics online, the
SWD still provides better power. As seen previously, the power of SWD barely changed as
the ICC increases.
, in the model.
However, as the ICC increases, as shown in Figure
4(f) and Figure S3(b) of the supplementary material available at Biostatistics online, the
SWD still provides better power. As seen previously, the power of SWD barely changed as
the ICC increases.
4. Illustrative example
In collaboration with the International Federation of Gynaecology and Obstetrics (FIGO) and the Association of Gynaecologists and Obstetricians of Tanzania (AGOTA), the Harvard T.H. Chan School of Public Health (HSPH) designed a study of the impact and performance of a postpartum IUD (PPIUD) intervention in Tanzania (Canning and others, 2016). The FIGO/AGOTA intervention will take place over 1-year (9 months in the first group of three hospitals and 3 months in the second group of three hospitals). The study design is illustrated below, with X = PPIUD intervention and O = standard of care.
| Time (months) | 1–3 | 4–6 | 7–9 | 10–12 | |
|---|---|---|---|---|---|
| Group 1 | Hospital 1 | O | X | X | X |
| 2 | O | X | X | X | |
| 3 | O | X | X | X | |
| Group 2 | 4 | O | O | O | X |
| 5 | O | O | O | X | |
| 6 | O | O | O | X |
In this SWD, there are 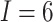 clusters (hospitals) and
clusters (hospitals) and
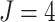 steps, each 3 months long. Although this
is not a standard SWD, our method still applies, using the treatment assignments in the
above table. The primary outcome is the pregnancy rate within 18 months of the index
birth. Based on data from the 2010 Tanzania Demographic and Health Survey, the 18-month
new pregnancy rate was 18.1% and the ICC was 0.022. Approximately 300 women per month will
join the study in each of the six participating Tanzanian hospitals, yielding
steps, each 3 months long. Although this
is not a standard SWD, our method still applies, using the treatment assignments in the
above table. The primary outcome is the pregnancy rate within 18 months of the index
birth. Based on data from the 2010 Tanzania Demographic and Health Survey, the 18-month
new pregnancy rate was 18.1% and the ICC was 0.022. Approximately 300 women per month will
join the study in each of the six participating Tanzanian hospitals, yielding
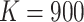 per cluster per step. Hence, each
cluster size is
per cluster per step. Hence, each
cluster size is 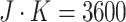 and the total sample size is
and the total sample size is
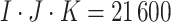 . As we discussed in
Sections 2.1 and 2.2, this cluster size is very large, requiring the use of the
normal approximation for the model without time effects, and in addition the partition
method for the model with time effects.
. As we discussed in
Sections 2.1 and 2.2, this cluster size is very large, requiring the use of the
normal approximation for the model without time effects, and in addition the partition
method for the model with time effects.
For illustrative purposes, we first considered a smaller cluster size scenario, namely
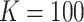 and cluster size
and cluster size
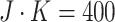 . With this scenario, we were
able to compare the power obtained with the exact calculations to that with the numerical
approximations, to assess their accuracy. When there were no time effects, the exact
calculations of (2.7) produced a
power of 62.3% for detecting a risk ratio of 0.8, corresponding to a
. With this scenario, we were
able to compare the power obtained with the exact calculations to that with the numerical
approximations, to assess their accuracy. When there were no time effects, the exact
calculations of (2.7) produced a
power of 62.3% for detecting a risk ratio of 0.8, corresponding to a
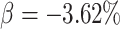 decrease in the 18 month
pregnancy rate, compared with 62.0% for the normal approximation; the power was 19.7% for
detecting a risk ratio of 0.9, corresponding to a
decrease in the 18 month
pregnancy rate, compared with 62.0% for the normal approximation; the power was 19.7% for
detecting a risk ratio of 0.9, corresponding to a 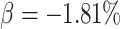 decrease, for
both the exact calculation and normal approximation methods. When the time effect over one
year study period is assumed to correspond to a 10% decrease in the baseline risk
(
decrease, for
both the exact calculation and normal approximation methods. When the time effect over one
year study period is assumed to correspond to a 10% decrease in the baseline risk
(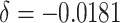 ), the exact calculation
method yielded a power of 28.4% for a risk ratio of 0.8, and 10.3% for a risk ratio of
0.9. For the normal approximation and partition method with a maximum
), the exact calculation
method yielded a power of 28.4% for a risk ratio of 0.8, and 10.3% for a risk ratio of
0.9. For the normal approximation and partition method with a maximum
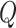 of 32, the calculated powers were 28.3% and
10.4% for risk ratios of 0.8 and 0.9, respectively. These results suggest excellent
performance for the numerical techniques we have proposed.
of 32, the calculated powers were 28.3% and
10.4% for risk ratios of 0.8 and 0.9, respectively. These results suggest excellent
performance for the numerical techniques we have proposed.
When the cluster size was set to 3600 as in the actual study, computational limitations
required the use of the normal approximation and the partition method for power
calculations. We considered possible time effects over the one-year study period: (i) no
time effects (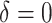 ); (ii) negligible time effects
(
); (ii) negligible time effects
(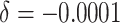 ); (iii) 5% decrease of the
baseline risk (
); (iii) 5% decrease of the
baseline risk (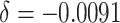 ); (iv) 10% decrease of the
baseline risk (
); (iv) 10% decrease of the
baseline risk (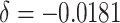 ). We also compared the power
based on the MLE variance to that based on the WLS variance. The results are given in
Table 1. When there were no time effects, the ARE
of MLE to Hussey and Hughes’ WLS method is 1.275 for detecting a risk ratio of 0.8 and
1.207 for detecting a risk ratio of 0.9, indicating that if Hussey and Hughes’ method were
used for power calculations, the study budget/sample size would be nearly 25% greater than
necessary. When there were time effects, we used the partition method. The procedure for
choosing
). We also compared the power
based on the MLE variance to that based on the WLS variance. The results are given in
Table 1. When there were no time effects, the ARE
of MLE to Hussey and Hughes’ WLS method is 1.275 for detecting a risk ratio of 0.8 and
1.207 for detecting a risk ratio of 0.9, indicating that if Hussey and Hughes’ method were
used for power calculations, the study budget/sample size would be nearly 25% greater than
necessary. When there were time effects, we used the partition method. The procedure for
choosing 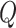 is given in Table S1 of the supplementary material available at
Biostatistics online. As shown in Table
1, the power was roughly insensitive to the time effects, and was higher in our
approach than the WLS method. Notice that when the time effects are negligible, the power
was much lower than that without time effects when the intervention effect was
is given in Table S1 of the supplementary material available at
Biostatistics online. As shown in Table
1, the power was roughly insensitive to the time effects, and was higher in our
approach than the WLS method. Notice that when the time effects are negligible, the power
was much lower than that without time effects when the intervention effect was
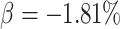 , corresponding to a risk ratio
of 0.9.
, corresponding to a risk ratio
of 0.9.
Table 1.
Power of the PPIUD study in Tanzania, for several plausible time effects and hypothesized risk ratios
| Time effects | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
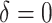
|
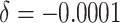
|
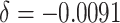
|
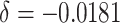
|
|||||||||
| Risk ratio | Risk ratio | Risk ratio | Risk ratio | |||||||||
| 0.8 | 0.9 | 0.8 | 0.9 | 0.8 | 0.9 | 0.8 | 0.9 | |||||
| Power | MLE | 1.000 | 0.908 | 0.976 | 0.480 | 0.981 | 0.494 | 0.984 | 0.506 | |||
| H&H | 1.000 | 0.850 | 0.935 | 0.412 | 0.935 | 0.412 | 0.935 | 0.412 | ||||
| ARE | 1.275 | 1.207 | 1.288 | 1.208 | 1.348 | 1.254 | 1.387 | 1.291 | ||||
5. Discussion
Little statistical theory for SWDs for binary outcome data has been developed to date—this
article fills that gap. In this article, we developed a numerical method calculating the
asymptotic power for a SWD with a binary outcome. Numerical integration over the
distribution of the unobserved random cluster effects is required. By doing so, we were able
to appropriately account for the binary nature of the outcome data using maximum likelihood
theory. We showed through several design scenarios that the resulting power did not agree
with that given by Hussey and Hughes (2007) using
their closed form approximation. There are two sources of discrepancies. One is that the
Hussey and Hughes estimator incorrectly assumes that the variance of the outcome is
constant, since the variance of a binomial distribution is related to its mean. Thus, the
Hussey and Hughes estimator could be either over- or under-powered. The other is that the
variance, 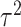 , of between-cluster random effects is
assumed known in Hussey and Hughes (2007). This
assumption is invalid in practice, and likely results, all other things being equal, in an
over-estimation of the power. The maximum likelihood method developed in this article does
not make either of these assumptions and, in addition, was found to be robust against
different random effect distributions.
, of between-cluster random effects is
assumed known in Hussey and Hughes (2007). This
assumption is invalid in practice, and likely results, all other things being equal, in an
over-estimation of the power. The maximum likelihood method developed in this article does
not make either of these assumptions and, in addition, was found to be robust against
different random effect distributions.
In this article, we have developed power calculations for binary outcomes modeled either as a function of time or not. A natural question is which model should be used in practice for study design. When we are quite sure about the existence of time effects, the model with time effects should be used. However, it is often the case that the time effects are believed to be small or negligible during the study period, if they exist at all, particularly with studies of short duration. A recent review by Martin and others (2016) found that, among 45 studies which reported a sample size calculation, 36% allowed for time effects, while 31% did not. If time effects are considered at the design stage, a much larger sample size will be required, as seen in Sections 3 and 4. However, if we assume that there are no time effects at the design stage, and a time trend is found, the estimated intervention effect will be biased unless it is adjusted for time in the analysis. Adjusting for this unanticipated time trend at the analysis phase will likely lead to an underpowered study. Subject matter considerations, prior knowledge, and common sense will have to guide these decisions.
In this work, we considered a random intercept in models (2.1) and (2.13). Recently, others have proposed models that include random time effects (Hughes and others, 2015) and random treatment effects (Hooper and others, 2016) for continuous outcomes. Theoretically, it is straightforward to extend our method to include such variation with binary outcomes. To do so, would require developing accurate and efficient numerical methods for multiple integration, a challenging task. It will be of great interest to investigate these extensions in future work.
Following the seminal work of Hussey and Hughes (2007), in this article, we considered the identity link so that the intervention effect is given on the risk difference scale. In future work, we will consider extensions to the log link and logistic link, where the parameter of interest is the risk ratio and odds ratio. User-friendly software based on our method is available online at https://github.com/xinzhoubiostat/swdpower.
Supplementary Material
Supplementary Data
Acknowledgments
Conflict of Interest: None declared.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
National Institute of Environmental Health Sciences [DP1ES025459]; National Institute of Allergy and Infectious Diseases [R01AI112339]; Food and Drug Administration [U01FD00493].
References
- Breslow N. E. and Clayton D. G. (1993). Approximate inference in generalized linear mixed models. Journal of the American Statistical Association 88, 9–25. [Google Scholar]
- Brown C. A. and Lilford R. J. (2006). The stepped wedge trial design: a systematic review. BMC Medical Research Methodology 6,54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candel M. J. J. M. and Van Breukelen G. J. P. (2016). Repairing the efficiency loss due to varying cluster sizes in two-level two-armed randomized trials with heterogeneous clustering. Statistics in Medicine 35, 2000–2015. [DOI] [PubMed] [Google Scholar]
- Canning D., Shah I., Pearson E., Pradhan E., Karra M., Senderowicz L., Barnighausen T., Spiegelman D. and Langer A. (2016). Institutionalizing postpartum intrauterine device (PPIUD) services in sri lanka, tanzania, and nepal: study protocol for a longitudinal cluster-randomized stepped wedge trial. BMC Pregnancy and Childbirth 16, 362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donner A. and Klar N. (2000). Design and Analysis of Cluster Randomization Trials in Health Research. London: Arnold. [Google Scholar]
- Hayes R. J. and Moulton L. H. (2009). Cluster Randomised Trials. Boca Raton, FL: Chapman and Hall/CRC. [Google Scholar]
- Heagerty P. J. and Kurland B. F. (2001). Misspecified maximum likelihood estimates and generalised linear mixed models. Biometrika 88, 973–985. [Google Scholar]
- Hemming K., Haines T. P., Chilton P. J., Girling A. J. and Lilford R. J. (2015). The stepped wedge cluster randomised trial: rationale, design, analysis, and reporting. BMJ 350, h391. [DOI] [PubMed] [Google Scholar]
- Hemming K. and Taljaard M. (2016). Sample size calculations for stepped wedge and cluster randomised trials: a unified approach. Journal of Clinical Epidemiology. 69, 137–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooper R., Teerenstra S., De Hoop E. and Eldridge S. (2016). Sample size calculation for stepped wedge and other longitudinal cluster randomised trials. Statistics in Medicine 35, 4718–4728. [DOI] [PubMed] [Google Scholar]
- Hughes J. P., Granston T. S. and Heagerty P. J. (2015). Current issues in the design and analysis of stepped wedge trials. Contemporary Clinical Trials 45, 55–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussey M. A. and Hughes J. P. (2007). Design and analysis of stepped wedge cluster randomized trials. Contemporary Clinical Trials 28, 182–191. [DOI] [PubMed] [Google Scholar]
- Liao X., Zhou X. and Spiegelman D. (2015). A note on “Design and analysis of stepped wedge cluster randomized trials”. Contemporary Clinical Trials 45, 338–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin J., Taljaard M., Girling A. and Hemming K. (2016). Systematic review finds major deficiencies in sample size methodology and reporting for stepped-wedge cluster randomised trials. BMJ Open 6, e010166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuhaus J. M., McCulloch C. E. and Boylan R. (2011). A note on Type II error under random effects misspecification in generalized linear mixed models. Biometrics 67, 654–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Breukelen G. J. P., Candel M. J. J. M. and Berger M. P. F. (2007). Relative efficiency of unequal versus equal cluster sizes in cluster randomized and multicentre trials. Statistics in Medicine 26, 2589–2603. [DOI] [PubMed] [Google Scholar]
- Zhou X., Liao X. and Spiegelman D. (2017). “Cross-sectional” stepped wedge designs always reduce the required sample size when there is no effect of time. Journal of Clinical Epidemiology 83, 108–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Data