Quantifying Epigenetic Stability with Minimum Action Paths

Abstract

Chromatin can adopt multiple stable, heritable states with distinct histone modifications and varying levels of gene expression. Insight on the stability and maintenance of such epigenetic states can be gained by mathematical modeling of stochastic reaction networks for histone modifications. Analytical results for the kinetic networks are particularly valuable. Compared to computationally demanding numerical simulations, they often are more convenient at evaluating the robustness of conclusions with respect to model parameters. In this communication, we developed a second-quantization based approach that can be used to analyze discrete stochastic models with a fixed, finite number of particles using a representation of the SU(2) algebra. We applied the approach to a kinetic model of chromatin states that captures the feedback between nucleosomes and the enzymes conferring histone modifications. Using a path integral expression for the transition probability, we computed the epigenetic landscape that helps to identify the emergence of bistability and the most probable path connecting the two steady states. We anticipate the generalizability of the approach will make it useful for studying more complicated models that couple epigenetic modifications with transcription factors and chromatin structure.

I. Introduction

A remarkable achievement of multicellular organisms is the formation of distinct cell types with identical genomes. Covalent modifications of histone proteins, of which DNA wraps around to form chromatin, are expected to be crucial for the emergence of cellular diversity [1]. These epigenetic marks can regulate the output of the genome by promoting or restricting the accessibility of the DNA sequence. They are known to impact the openness of chromatin and global genome organization, though the molecular mechanisms are only beginning to emerge [2–5]. Therefore, multistability in chromatin states formed by various histone modifications or combinations thereof can potentially give rise to distinct patterns of gene expression and inheritable phenotypes [6–9]. Evidence for bistable and inheritable epigenetic marks has indeed been found that can be attributed to the presence of positive feedback loops wherein nucleosomes that carry a particular modification recruit, either directly or indirectly, enzymes that catalyze the same modification on neighboring nucleosomes [10–14].

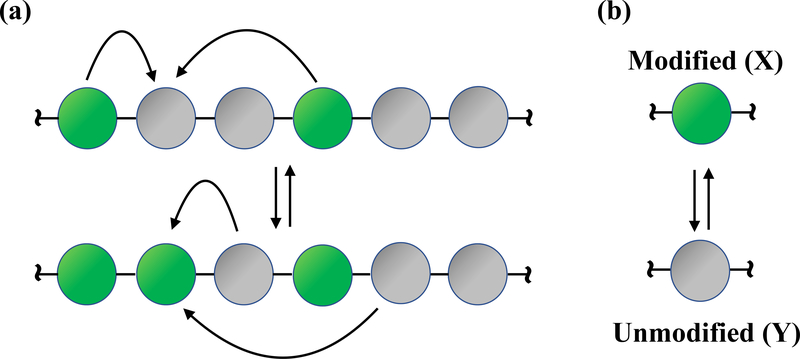
Mathematical modeling of the reaction networks of histone modifications can help determine factors that are crucial for epigenetic stability. Distilling the essence of feedback mechanisms, Dodd and coworkers introduced a simplified kinetic model with bistable chromatin states [15]. One envisions a system of N nucleosomes, where a nucleosome can exist in either a modified or an unmodified state (see Fig. 1). As a first approximation, spatial organization of chromatin is neglected, and the kinetics of the system can be described with the non-linear dynamics given below

$$X+X+Y\stackrel{c_1}{\to }3X,Y+Y+X\stackrel{c_1}{\to }3Y,$$ (1)

$$X\stackrel{c_2}{\to }Y,Y\stackrel{c_2}{\to }X.$$ (2)

The reactions governing the dynamics in Eq. (1) and (2) represent recruited and thermalized, noisy conversions respectively. From analysis of regulatory circuits, we know that in deterministic systems, bistability requires not only positive feedback but also nonlinearity in the feedback loop [10, 16–18]. However, sufficient noise can produce bistability with fewer constraints on the deterministic system [19, 20]. The model presented is nonlinear, since the recruited conversion of Y to X (or X to Y) is bimolecular in X (or Y) and unimolecular in Y (or X). Thus the rate of production for a given nucleosome type responds to increases in its own concentration in a nonlinear fashion. This produces bistability in the determinstic system, wherein noise can allow for transitions between the two stable attractors.

FIG. 1.

Illustration of the kinetic model for the interconversion between modified (green, X) and unmodified nucleosomes (grey, Y). (a) Recruited conversion defined in Eq. 1 that requires a pair of (un-)modified nucleosomes to alter the state of a nucleosome. (b) Noisy conversion (Eq. 2) with first order kinetics.

Far from being a trifle toy-model, the kinetic scheme above is not unlike the mating type silencing in S. Cerevisiae [15, 21–24]. Generalizing the above model to more than 2 epigenetic states has been attempted as well [24–28]. Their elegance and biological relevance have inspired numerous theoretical studies of these models [6]. A popular approach used in these studies to investigate epigenetic stability is to posit deterministic rate equations followed by bifurcation analysis. Insight into the switching among chromatin states is missed in such deterministic analyses, however. To study the rare transition events between steady states, Dodd and coworkers introduced an approximate Fokker-Planck equation, from which an epigenetic landscape can be constructed.

II. Results

In this work, we present an alternative way to analyze such zero-dimensional models. We turn to the original master equation, which is an exact stochastic description of the underlying process describing the temporal evolution of the system’s configurational probability, and reformulate it using second-quantization (or Fock-Space) methods (Doi-Peliti approach) [29–33]. While canonical approaches rely on bosonic creation and annihilation operators, we employ operators that are a representation of the SU(2) algebra, in order to treat the constraint that fixes the total number of nucleosome types (X + Y ≡ N) in a more mathematically natural fashion. The Doi-Peliti method has been successfully employed in the study of reaction-diffusion processes [34], gene switches [35, 36], and other systems [37]. We outline the main results here and the detailed derivations are consigned to Appendix A. The Doi-Peliti approach allows us to reformulate the time evolution of the original master equation as an imaginary time Schrödinger equation

$${\partial }_t|\psi (t)\rangle =-H|\psi (t)\rangle ,$$ (3)

where we have introduced formally a state vector |ψ(t)〉 as a superposition of all possible occupation number configurations weighted with their corresponding probabilities (a generating function),

$$|\psi (t)\rangle =\sum _{\left\{n_x,n_y\right\}}P\left(\left\{n_x,n_y\right\};t\right)|n_x,n_y\rangle .$$ (4)

Following standard procedures [35–37], H is usually expressed in a second-quantized form

$$\begin{gathered} H=\frac{c_1}{{(2j)}^3}[a_x^{†3}{a}_x^2{a}_y-a_x^{†2}{a}_x^2{a}_y^{†}{a}_y]+\frac{c_1}{{(2j)}^3}[a_y^{†3}{a}_y^2{a}_x-a_y^{†2}{a}_y^2{a}_x^{†}{a}_x] \\ +\frac{c_2}{2j}[a_y^{†}{a}_x-a_x^{†}{a}_x]+\frac{c_2}{2j}[a_x^{†}{a}_y-a_y^{†}{a}_y]. \end{gathered}$$ (5)

a_i and $a_i^{†}$ for i ∈ {x,y} are bosonic creation and annihilation operators that obey the canonical commutation relations

$$[a_i,a_j^{†}]={\mathit{\delta }}_{ij}\text{and}[a_i,a_j]=0=[a_i^{†},a_j^{†}].$$ (6)

The action of a_x, $a_x^{†}$ on ket vectors |n_x, n_y〉 is given by ax|n_x, n_y〉 = n_x|n_x −1,n_y〉, $a_x^{†}|n_x,n_y\rangle =|n_x+1,n_y\rangle$, and $a_x^{†}{a}_x|n_x,n_y\rangle =n_x|n_x,n_y\rangle$. Similar operations can be defined for a_y, $a_y^{†}$. Since for a vacuum state |0,0〉, a_i |0,0〉 = 0, one can obtain any arbitrary ket state as $|n_x,n_y\rangle ={(a_x^{†})}^{n_x}{(a_y^{†})}^{n_y}|0,0\rangle$.

While it is straightforward to apply the standard formalism up until this point, one notices that the total number of nucleosomes in our system $N={\widehat{n}}_x+{\widehat{n}}_y=a_x^{†}{a}_x+a_y^{†}{a}_y$ is constant. This is evident from the fact that our Hamiltonian commutes with the total number operator, $a_x^{†}{a}_x+a_y^{†}{a}_y$. One might also find it slightly philosophically troubling, to use bosonic ladder operators to describe a system with a large, but still finite number of particles. Moreover, not all combinations of states X and Y are allowed, but only those satisfying n_x + n_y = N. In conventional quantum mechanics, bosonic ladder operators allow for neither an exclusion principle, nor a cap on the total particle number. However, since the Hamiltonian conserves particle number, we aren’t remiss in our formalism. We can take any equilibrium solution of the master equation and project down to the subspace where the conserved quantity takes a fixed value and we will get another equilibrium solution. In probability theory we would say we are conditioning on the conserved quantity taking a definite value. Thus if our initial state |ψ(0)〉 is a configuration such that ${\widehat{n}}_x+{\widehat{n}}_y=N$ holds true, and then given our prescription of stochastic Hamiltonian all subsequent states will meet this condition as well. However, given that there is essentially only one independent variable, namely n_x, we can perhaps phrase this problem in a more natural framework. We develop this framework in the sections that follow.

The starting point of this reformulation is the Jordan-Schwinger map [38, 39], where we introduce (see Appendix A, Eqs. A3, A4)

$$J_{+}=a_x^{†}{a}_y{J}_{-}=a_y^{†}{a}_x.$$ (7)

For notational convenience we set N = 2j. Here the operators satisfy the commutation relations of SU(2) algebra

$$\left[J_z,J_{\pm }\right]=\pm J_{\pm }\left[J_i,J_j\right]=i{\overleftrightarrow{\epsilon }}_{ijk}\forall i,j,k\in \{x,y,z\},$$ (8)

where the structure constant ${\overleftrightarrow{\epsilon }}_{ijk}$ is the Levi-Civita symbol. Re-defining the ket |n_x, n_y〉 = |n_x, 2j – n_x〉 ≡ |n〉, their action is given by

$$\begin{gathered} J_{+}|n\rangle =(2j-n)|n+1\rangle , \\ {J}_{-}|n\rangle =n|n-1\rangle , \\ {J}_z|n\rangle =(n-j)|n\rangle , \end{gathered}$$ (9)

$$\begin{gathered} {\widehat{n}}_x|n\rangle =\left(J_z+j\right)|n\rangle =n|n\rangle , \\ {\widehat{n}}_y|n_y\rangle =\left(j-J_z\right)|n\rangle =(2j-n)|n\rangle . \end{gathered}$$ (10)

The Hamiltonian can be reformulated as

$$\begin{gathered} H=\frac{c_1}{{(2j)}^3}[J_{+}{\widehat{n}}_x^{\underset{\_}{2}}-{\widehat{n}}_x^{\underset{\_}{2}}{\widehat{n}}_y]+\frac{c_1}{{(2j)}^3}[J_{-}{\widehat{n}}_y^{\underset{\_}{2}}-{\widehat{n}}_y^{\underset{\_}{2}}{\widehat{n}}_x] \\ +\frac{c_2}{2j}[J_{-}-{\widehat{n}}_x]+\frac{c_2}{2j}[J_{+}-{\widehat{n}}_y], \end{gathered}$$ (11)

where we have used ${\widehat{n}}_i^{\underset{\_}{2}}={\widehat{n}}_i({\widehat{n}}_i-1))$ to denote the falling factorial to write down the Hamiltonian in a more compact form.

A great advantage of the second quantization approach is its relative convenience for deriving analytical solutions. For example, a formal solution to Eq. 3 is given by

$$|\psi (t)\rangle =\exp (-Ht)|\psi (0)\rangle .$$ (12)

In addition, the transition probability of starting in a state with particle number n_i at time t = 0 and ending up in a state with particle number n_f at t_f can be defined as

$$\langle \psi \left(t_f\right)\left|e^{-tH}\right|\psi (0)\rangle \equiv \langle n_f\left|e^{-tH}\right|n_i\rangle .$$ (13)

We next seek for a path integral expression of the transition probability that is useful for finding steady states and transition pathways between them. We discretize the time interval [0, t_f] into N_t time slices, and then insert a resolution of identity between each time slice. Finally, taking the limit N_t → ∞ we get,

$$\begin{gathered} \mathbb{P}\left({\rho }_f;t_f\mid {\rho }_i;0\right)=\langle n_f\left|e^{-tH}\right|n_i\rangle \\ =\int \mathcal{D}\left[z_i,z_f\right]\langle n_f\mid z_f\rangle \langle z_f\left|e^{-tH}\right|z_i\rangle \langle z_i\mid n_i\rangle \\ =\int \mathcal{D}\left[{\overline{z}}_i,z_f\right]\int \mathcal{D}[\overline{z},z]e^{-S}, \end{gathered}$$ (14)

where we have introduced, ρ = n/2j. By definition, ρ represents an order parameter that quantifies the fraction of modified nucleosomes. After performing the integration over z_i, ${\overline{z}}_i$, z_f, ${\overline{z}}_f$. we introduce one final re-parametrization in terms of the density ρ. Using

$$\rho =\frac{\langle z\left|j+J_z\right|z\rangle }{2j}=\frac{z\overline{z}}{1+z\overline{z}},$$ (15)

we can rewrite

$$z=\frac{\rho }{1-\rho }\exp (-\tilde{\rho }),\overline{z}=\exp (\tilde{\rho })$$ (16)

with ρ(0) = ρ_i and ρ(t) = ρ_f and $\tilde{\rho }(t)$, $\tilde{\rho }(0)$ unconstrained. Making these substitutions, the action finally reads,

$$S[\tilde{\rho },\rho ]=2j{\int }_0^{t_f}\text{d}t\left[\tilde{\rho }{\partial }_t\rho -H(\tilde{\rho },\rho )\right],$$ (17)

where

$$\begin{gathered} H(\tilde{\rho },\rho )=-\frac{1}{2j^2}{e}^{-\tilde{\rho }}\left(e^{\tilde{\rho }}-1\right)\left[c_1(j-1)(2j-1) \\ (\rho -1)\rho \left(\rho +\rho e^{\tilde{\rho }}-1\right)+2c_2{j}^2\left(\rho +(\rho -1)e^{\tilde{\rho }}\right)\right]. \end{gathered}$$ (18)

Correspondingly, the time-dependent transition probability (propagator) can be expressed as

$$\mathbb{P}\left({\rho }_f;t_f\mid {\rho }_i;0\right)=\int \mathcal{D}[\tilde{\rho },\rho ]\exp (-S[\tilde{\rho },\rho ]).$$ (19)

Eq. 17 is the main result of this paper. It allows the computation of both steady state and kinetic results for the model in terms of the order parameter ρ. In particular, for 2j ≫ 1, i.e., the small noise regime with many nucleosomes, the path integral in Eq. 19 will be dominated by contributions from the minimum action path [40–44]. The variational derivatives that minimize the action yield the classical Hamiltonian equations

$$\begin{gathered} \dot{\rho }=\frac{\partial H}{\partial \tilde{\rho }}, \\ \dot{\tilde{\rho }}=-\frac{\partial H}{\partial \rho }. \end{gathered}$$ (20)

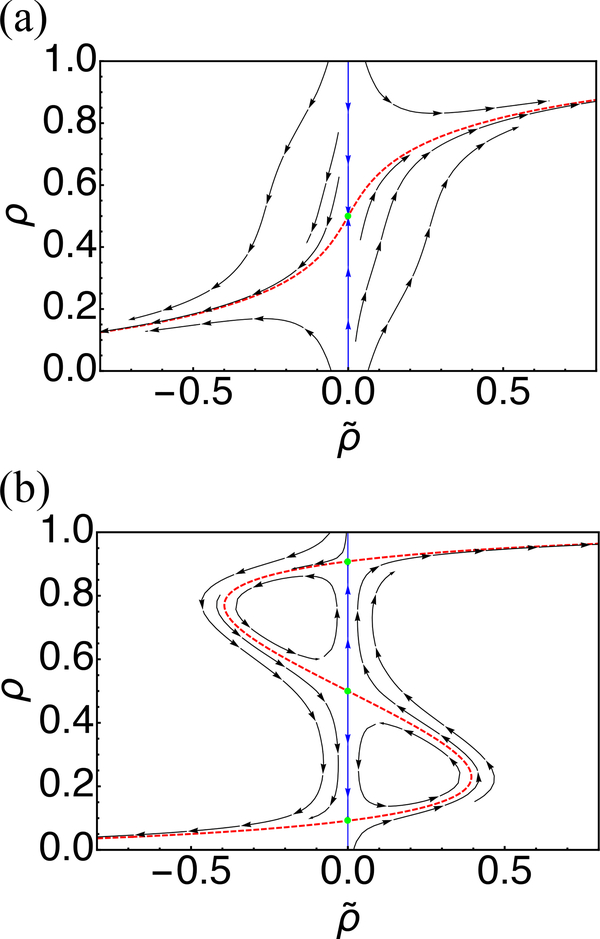
We note that $\tilde{\rho }\equiv 0$ is always a solution to the above Hamiltonian equation. As shown in Figure 2 in blue color, these paths correspond to deterministic dynamics flowing towards steady-state solutions (green dots). The resulting deterministic equation (see Eq. A17) is identical to that presented in Ref. 15, which was obtained using phenomenological arguments. For the Hamiltonian paths with non-zeros $\tilde{\rho }$, the zero-energy path with H ≡ 0 is of particular interest as it represents fluctuations away from the steady states. In bistable regimes, the zero-energy path connects the two steady states via the saddle point (see Fig. 2b red), and corresponds to the maximum likelihood transition path [45, 46].

FIG. 2.

Phase portrait determined using Eq. (20) with kinetic parameters c₁/c₂ = 3 (a) and 12 (b). The red dashed lines are zero-energy paths and green dots are steady state solutions. The blue paths represent deterministic trajectories. The number of nucleosomes was held fixed at N = 60.

Quantitative results of the kinetic model can be obtained with the definition of a quasi-potential, Φ, in the Friedlin-Wentzell sense [47] in terms of the least-action path (denoting $\phi =\{\rho ,\tilde{\rho }\}$)

$$\mathrm{\Phi }\left(x_1,x_2\right)=\underset{t>0}{\inf }\underset{\phi \in {\gamma }_{x_1}^{x_2}(0,T)}{\inf }S(\phi ),$$ (21)

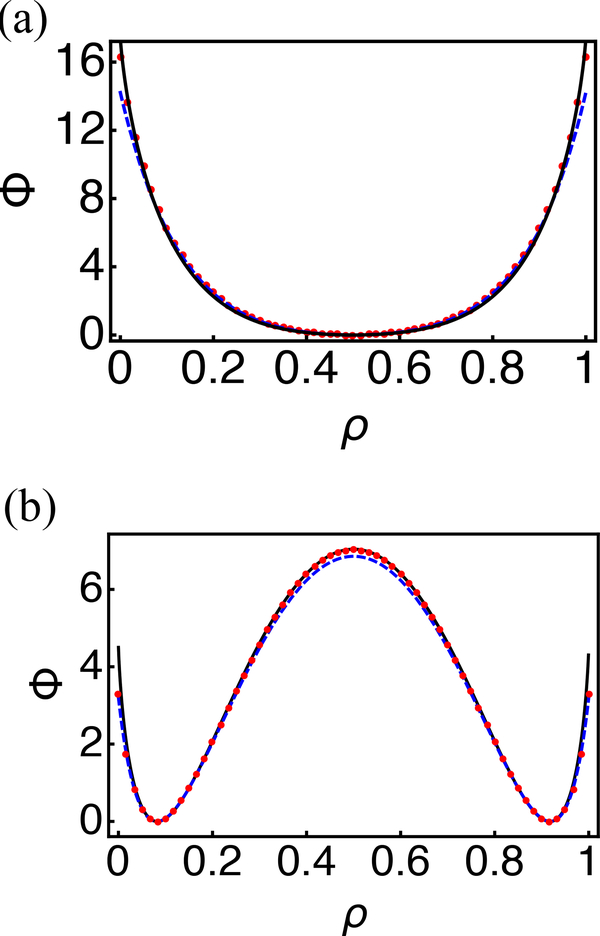
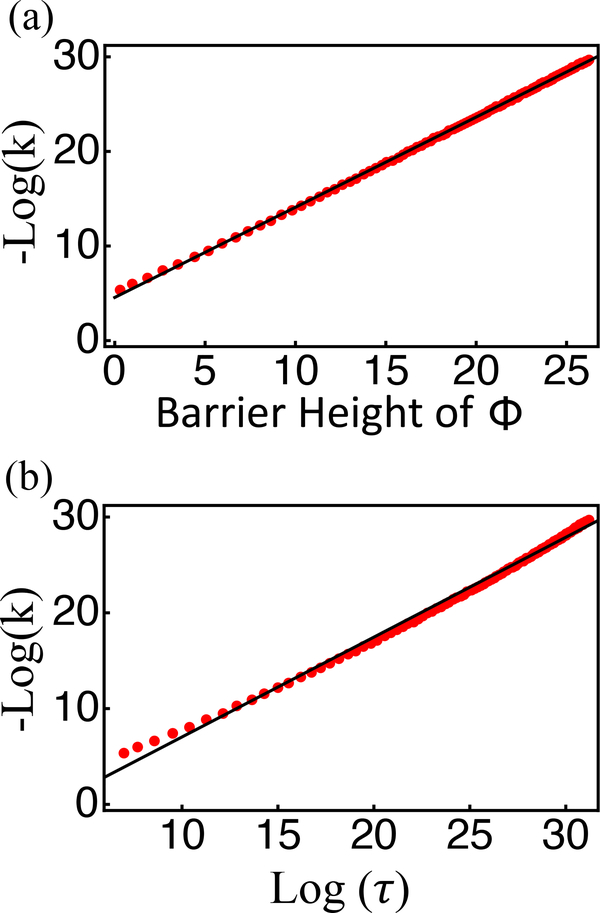
where ${\gamma }_{x_1}^{x_2}(0,t)$ is the set of continuous curves f connecting two points x₁,x₂ in configuration space, such that f(0) = x₁, f(t) = x₂. The minima of the Friedlin-Wentzell quasi-potential correspond to attractors of the dynamical system, and the height of the barrier corresponds to the ease of transition between two stable fixed points. As shown in Fig. 3, the quasi-potential correctly captures the emergence of bistability as the parameter c₁/c₂ varies from 3 to 12. c₁ and c₂ are the rate coefficients for recruited and random nucleosome conversions defined in Eqs. 1 and 2. In addition, we found that in both cases, the quasi-potential agrees well with the negative-log of the steady state probability distribution determined using the zero eigenvalue eigenvector of the transition rate matrix (see Appendix B for details). When compared to the transitions rates between the two steady states, the barriers of the saddle point determined from the quasi-potential strongly correlate with the numerical values over a wide range of parameters (see Fig. 4).

FIG. 3.

Comparison between the steady state distribution (−logP_eq, red dots) and the quasi potential (Φ) computed using Eq. 21 (black solid line) and the Fokker-Planck equation (blue dashed line) for c₁/c₂ = 3 (a) and 12 (b). The number of nucleosomes was held fixed at N = 60.

FIG. 4.

Correlation between the exact transition rates (k) computed from diagonalizing the transition matrix and the barrier height of the quasi-potential (a) or the mean first passage time (τ) estimated using the Fokker-Planck equation (b). Each data point corresponds to an independent calculation for integer values of the parameter c₁/c₂ between 5 and 120. The total nucleosome number was fixed as N = 60.

III. Discussion

In this communication, we applied the Doi-Peliti approach to a reaction network that captures the emergence of epigenetic stability from histone modifications [15]. Together with a transformation enabled by the SU(2) algebra, it allowed for the derivation of analytical results that rigorously account for the constraints imposed by a fixed number of particles. The semi-classical treatment of the path integral expression for transition probability further provided a fresh view of the stochastic reaction network in the guise of a “pseudo-mechanical system”. Hamilton’s equation of motion and the quasi-potential, much like their counterparts in classical mechanics, provide intuition regarding the dynamics and landscape of the reaction network.

We note that the steady state distribution and transition rate for the chromatin state model can be obtained from the Fokker–Planck equation introduced in Ref. 15 as well. The Fokker–Planck equation may, in fact, seem more appealing compared to the Doi-Peliti approach used here due to its mathematical simplicity. As shown in Figs. 3 and 4, the accuracy of the two methods is comparable. The Doi-Peliti approach slightly outperforms in reproducing solutions obtained from diaogonalizing the master equation, due to its improved treatment of larger deviations.

The advantage of the Doi-Peliti approach will become more evident for more complex problems with coupled reaction networks, such as a chromatin switch coupled to a self-activating gene. There, due to the high dimensionality, analytical/numerical solutions of the Fokker-Planck equation cannot be readily obtained. On the other hand, robust algorithms have been introduced to compute the minim action paths of complex networks [48]. These most probable paths could be used to quantify epigenetic stability and investigate the mechanism for switching between steady states [36]. We note that both the Fokker-Planck equation and the minimum action approximation are only valid at the small-noise limit. When the number of nucleosomes is small (<30), significant deviations from the analytical results presented here may occur. The small number regime, though physically interesting, is of less biological interest as epigenetic domains are large and can cover a long stretch of DNA (10 ~ 100 Kb). In addition, estimations based on the minimum action can, in principle, be improved by including higher-order terms from a functional Taylor expansion of Eq. 19 [49].

V. Appendix

A. Constructing the coherent states path integral

For completeness let us start with the master equation for our system (with N = 2j),

$$\begin{gathered} {\partial }_{t}P\left(n_x,n_y\right)=\frac{c_1}{{(2j)}^3}\left[\left(n_x-1\right)\left(n_x-2\right)\left(n_y+1\right)P\left(n_x-1,n_y+1\right) \\ -n_x{n}_y\left(n_x-1\right)P\left(n_x,n_y\right)\right] \\ +\frac{c_1}{{(2j)}^3}[\left(n_y-1\right)\left(n_y-2\right)\left(n_x+1\right)P\left(n_x+1,n_y-1\right) \\ -n_x{n}_y\left(n_y-1\right)P\left(n_x,n_y\right)] \\ +\frac{c_2}{2j}\left[\left(n_x+1\right)P\left(n_x+1,n_y-1\right)-n_{x}P\left(n_x,n_y\right)\right] \\ +\frac{c_2}{2j}\left[\left(n_y+1\right)P\left(n_x-1,n_y+1\right)-n_{y}P\left(n_x,n_y\right)\right]. \end{gathered}$$ (A1)

As mentioned in the main text, following the second quantization approach [29, 30, 35–37] and by introducing the state vector |ψ(t)〉, the time evolution of the original master equation can be recast into an imaginary time Schrödinger equation (Eq. 3), and the Hamiltonian is defined in terms of the bosonic creation and annihilation operators as Eq. 5. Now we can begin reformulating this system using the Jordan-Schwinger map [38]. For convenience, let us define the following vectors (Eq. A2), to which we then apply the Jordan transformation to obtain (Eq. A3), where σ_μ denotes the usual Pauli Matrices.

$$\mathit{a}\equiv \left(\begin{array}{l}{a}_x\\ a_y\end{array}\right),{\mathit{a}}^{†}\equiv \left(\begin{array}{l}{a}_x^{†}\\ a_y^{†}\end{array}\right).$$ (A2)

$$\begin{gathered} Q_{\mu }={\mathit{a}}^{†}{\mathit{\sigma }}_{\mu }\mathit{a} \\ {J}_{\pm }=Q_1\pm i{Q}_2 \\ {J}_{+}=a_x^{†}{a}_y{J}_{-}=a_y^{†}{a}_x, \end{gathered}$$ (A3)

Also for convenience, we define the auxiliary operators (Eq. A4). The operators J_± satsify the same commutation relations as SU(2) algebra, given in Eq. 8

$$\begin{gathered} J_x=\frac{\left(J_{+}+J_{-}\right)}{2} \\ {J}_y=\frac{\left(J_{+}-J_{-}\right)}{2i} \\ \left[J_{+},J_{-}\right]=2J_z. \end{gathered}$$ (A4)

Using these rules, the stochastic pseudo-hamiltonian was reformulated as in Eq. 11. In order to now construct a path integral for the transition probability, one introduces the following left and right spin-coherent states [50, 51], and a resolution of identity,

$$|z\rangle =\frac{1}{{(1+z\overline{z})}^j}{e}^{z{J}_{+}}|0\rangle ={(1+z\overline{z})}^{-j}\sum _{0\le n}^{2j}\left(\begin{array}{c}2j\\ n\end{array}\right)z^n|n\rangle ,$$ (A5)

$$\begin{gathered} \langle z|=\frac{1}{{(1+z\overline{z})}^j}\langle 0|e^{\overline{z}{J}_{-}}={\left(1+z\overline{z}\right)}^{-j}\sum _{0\le n}^{2j}\langle n|{\overline{z}}^n, \\ \int \frac{2j+1}{\pi }\frac{d^{2}z}{{(1+z\overline{z})}^2}|z\rangle \langle z|=\mathbb{1}. \end{gathered}$$ (A6)

The details and subtleties regarding the construction of spin coherent state path integrals have been discussed in the literature [39, 52–55]. However, for completeness we give a brief overview. Starting with the propagator between two normalized coherent states, 〈z_f|e^−tH|z_i〉, we discretize the time interval [0,t] into N_t time slices, and then insert a resolution of identity of the form (A6) between each time slice. Finally, taking the limit N_t → ∞ we get,

$$\langle z_f|e^{-tH}|z_i\rangle =\int \mathcal{D}[\overline{z},z]\exp (-S),$$ (A7)

where,

$$\begin{gathered} S=-j\log \frac{\left(1+{\overline{z}}_{f}z(t)\right)\left(1+\overline{z}(0)z_i\right)}{\left(1+{\overline{z}}_f{z}_f\right)\left(1+{\overline{z}}_i{z}_i\right)} \\ +2j{\int }_0^t\text{d}t\left[\frac{1}{2}\frac{\overline{z}\dot{z}-\dot{\overline{z}}z}{1+\overline{z}z}-H(\overline{z},z)\right], \end{gathered}$$ (A8)

and $H(\overline{z},z)=\langle z|H|z\rangle$. Next, we derive an expression for the physical propagator between and 〈n_f| and |n_i〉 representing states of fixed initial and final number of particles respectively. This represents the probability of starting in state with particle number n_i at time t = 0 and ending up in a state with particle number n_f at t_f. To do so one takes,

$$\begin{gathered} \mathbb{P}\left(n_f;t_f\mid n_i;0\right)=\langle n_f|e^{-tH}|n_i\rangle \\ =\int \mathcal{D}\left[z_i,z_f\right]\langle n_f\mid z_f\rangle \langle z_f|e^{-tH}|z_i\rangle \langle z_i\mid n_i\rangle . \end{gathered}$$ (A9)

To get the physical propagator from (A7) one needs to subtract log〈z_i|n_i〉 + log〈n_f|z_f〉 from the action, and then integrate over z_i, ${\overline{z}}_i$, z_f, ${\overline{z}}_f$. Then,

$$\mathbb{P}\left({\rho }_f;t_f\mid {\rho }_i;0\right)=\int \mathcal{D}\left[{\overline{z}}_i,z_f\right]\int \mathcal{D}[\overline{z},z]e^{-S},$$ (A10)

where we have introduced, ρ = n/2j. Here S is now given by,

$$\begin{gathered} S=-j\log [\left(1+{\overline{z}}_{f}z(t)\left(1+\overline{z}(0)z_i\right)\right] \\ +2j{\int }_0^t\text{d}t\left[\frac{1}{2}\frac{\overline{z}\dot{z}-\dot{\overline{z}}z}{1+\overline{z}z}-H(\overline{z},z)\right] \\ +2j[-{\rho }_i\log {\overline{z}}_i-{\rho }_F\log {\overline{z}}_f+{\rho }_f\log {\rho }_f+\left(1-{\rho }_f\right)\log \left(1-{\rho }_f\right) \\ +\log \left(\left(+{\overline{z}}_f{z}_f\right)\left(1+z_i{\overline{z}}_i\right)\right)]. \end{gathered}$$ (A11)

Now we can integrate over z_i, z_f, ${\overline{z}}_i$, ${\overline{z}}_f$ using the saddle-point method. The derivatives of (A11) fix the initial and final conditions,

$$\frac{1}{2j}\frac{\partial S}{\partial z_i}=\frac{{\overline{z}}_i}{1+{\overline{z}}_i{z}_i}-\frac{\overline{z}(0)}{1+\overline{z}(0)z_i},$$ (A12a)

$$\frac{1}{2j}\frac{\partial S}{\partial {\overline{z}}_f}=\frac{z_f}{1+{\overline{z}}_f{z}_f}-\frac{z(t)}{1+z(t)z_f},$$ (A12b)

$$\frac{1}{2j}\frac{\partial S}{\partial {\overline{z}}_i}=\frac{z_i}{1+{\overline{z}}_i{z}_i}-\frac{{\rho }_i}{{\overline{z}}_i},$$ (A12c)

$$\frac{1}{2j}\frac{\partial S}{\partial z_f}=\frac{{\overline{z}}_f}{1+{\overline{z}}_f{z}_f}-\frac{{\rho }_f}{{\overline{z}}_f}.$$ (A12d)

Thus, we get the following four conditions $\overline{z}(0)={\overline{z}}_i$, z(t) = z_f, ${\rho }_i=\frac{{\overline{z}}_i{z}_i}{1+{\overline{z}}_i{z}_i}$ and ${\rho }_f=\frac{{\overline{z}}_f{z}_f}{1+{\overline{z}}_f{z}_f}$. After performing the integration the action now reads,

$$\begin{gathered} S={2j\left[\frac{z\overline{z}}{1+z\overline{z}}\log \overline{z}-\log (1+z\overline{z})\right]|}_f^i \\ +2j{\int }_0^t\text{d}{t}^{t^{\prime }}\left[\frac{1}{2}\frac{\overline{z}\dot{z}-\dot{\overline{z}}z}{1+\overline{z}z}-H(\overline{z},z)\right]. \end{gathered}$$ (A13)

We introduce one final re-parametrisation in terms of the density ρ. Using

$$\rho =\frac{\langle z|j+J_z|z\rangle }{2j}=\frac{z\overline{z}}{1+z\overline{z}},$$ (A14)

one rewrites

$$z=\frac{\rho }{1-\rho }\exp (-\tilde{\rho }),\overline{z}=\exp (\tilde{\rho })$$ (A15)

with ρ(0) = ρ_i and ρ(t) = ρ_f and $\tilde{\rho }(t)$, $\tilde{\rho }(0)$ unconstrained. The Jacobian for the change of variables is (1 − ρ)², and $\int \frac{2j+1}{\pi }\frac{d^{2}z}{{(1+z\overline{z})}^2}$ is replaced by $\int \frac{2j+1}{\pi }{d}^2\rho$. Doing so we finally recover 17 and 19 of the main text. To get the deterministic rate equations, we evaluate,

$$\dot{\rho }={\frac{\partial H}{\partial \tilde{\rho }}|}_{\tilde{\rho }=0}=\frac{(1-2\rho )\left(c_1(j-1)(2j-1)(\rho -1)\rho +2c_2{j}^2\right)}{2j^2}$$ (A16)

which for j ≫ 1, gives

$$\dot{\rho }=(1-2\rho )\left(c_1(\rho -1)\rho +c_2\right).$$ (A17)

This equation is in agreement with Micheelsen et.al. [15], and it yields a single stable real fixed point, ρ* = 0.5 when c₁/c₂ < 4 and an unstable fixed point at ρ* = 0.5 and 2 stable fixed points at ${\rho }^{*}=0.5\pm 0.5\sqrt{\left(c_1-4c_2\right)/c_1}$ when c₁/c₂ > 4.

B. Details of Transition Matrix Calculations

The transition rate matrix corresponding to the reaction network of the chromatin state model is a N × N tridiagonal matrix with off-diagonal elements defined as

$$\begin{gathered} H_{i,j}={\delta }_{i,i+1}\left(\frac{c_1}{N^3}i(i-1)(N-i)+\frac{c_2}{N}(N-i)\right) \\ +{\delta }_{i,i-1}\left(\frac{c_1}{N^3}i(N-i)(N-i-1)+\frac{c_2}{N}i\right). \end{gathered}$$ (B1)

The diagonal elements were defined to ensure that each column of the matrix sums to zero, namely,

$$H_{i,i}=-\sum _i{H}_{i,j}.$$ (B2)

The smallest (in absolute value) non-zero eigenvalue of the matrix corresponds to the transition rate between two steady states. The eigenvector for the zero eigenvalue quantifies the steady state probability distribution.