A mechanism-aware and multiomic machine-learning pipeline characterizes yeast cell growth

Significance

Linking genotype and phenotype is a fundamental problem in biology, key to several biomedical and biotechnological applications. Cell growth is a central phenotypic trait, resulting from interactions between environment, gene regulation, and metabolism, yet its functional bases are still not completely understood. We propose and test a machine-learning approach that integrates large-scale gene expression profiles and mechanistic metabolic models, for characterizing cell growth and understanding its driving mechanisms in Saccharomyces cerevisiae. At its core, a custom-built multimodal learning method merges experimentally generated and model-generated data. We show that our approach can leverage the advantages of both machine learning and metabolic modeling, revealing unknown interactions between biological domains, incorporating mechanistic knowledge, and therefore overcoming black-box limitations of conventional data-driven approaches.

Abstract

Metabolic modeling and machine learning are key components in the emerging next generation of systems and synthetic biology tools, targeting the genotype–phenotype–environment relationship. Rather than being used in isolation, it is becoming clear that their value is maximized when they are combined. However, the potential of integrating these two frameworks for omic data augmentation and integration is largely unexplored. We propose, rigorously assess, and compare machine-learning–based data integration techniques, combining gene expression profiles with computationally generated metabolic flux data to predict yeast cell growth. To this end, we create strain-specific metabolic models for 1,143 Saccharomyces cerevisiae mutants and we test 27 machine-learning methods, incorporating state-of-the-art feature selection and multiview learning approaches. We propose a multiview neural network using fluxomic and transcriptomic data, showing that the former increases the predictive accuracy of the latter and reveals functional patterns that are not directly deducible from gene expression alone. We test the proposed neural network on a further 86 strains generated in a different experiment, therefore verifying its robustness to an additional independent dataset. Finally, we show that introducing mechanistic flux features improves the predictions also for knockout strains whose genes were not modeled in the metabolic reconstruction. Our results thus demonstrate that fusing experimental cues with in silico models, based on known biochemistry, can contribute with disjoint information toward biologically informed and interpretable machine learning. Overall, this study provides tools for understanding and manipulating complex phenotypes, increasing both the prediction accuracy and the extent of discernible mechanistic biological insights.

The analysis of complex, high-dimensional biological data from heterogeneous sources is currently one of the main bottlenecks in molecular biology. Such data are generated by a range of high-throughput devices that target specific biomolecules or biological processes and are collectively known as omic data. Representative examples are the global genetic composition of an organism—the genome—and the overall activation level of its genes at a certain time—the transcriptome.

Popular technologies permit the monitoring of various phenomena on a genetic and epigenetic level. However, in several applications, information on genes may have limited relevance to the task at hand, describing only a part of the processes taking place in biological organisms. Metabolic data are closer to the cellular phenotype but, despite recent innovations in omic technologies, sampling metabolic activity on a large scale is still challenging (1). Machine learning provides tools to identify and exploit patterns within this metabolic information, which can aid in our understanding of the underlying biological mechanisms (2). In this context, the heterogeneity of omic data has fostered the development and application of multimodal learning methods (3).

Machine-learning techniques generally ignore previous biological knowledge in driving the pattern analysis, limiting the trustworthiness and interpretability of any obtained model. To fill these gaps, constraint-based modeling (CBM) can be used to simulate steady-state metabolism on a cellular scale. Metabolic flux profiles generated in silico have been previously used to inform specific machine-learning models (4–9), in some cases providing predictive advantages, as recently reviewed (10). However, an integrative approach that fully exploits the multimodal learning potential to integrate such models with experimental omics and is therefore able to incorporate mechanistic biological knowledge in the learning process is still lacking.

In this work, we propose a multimodal learning framework that leverages both transcriptomic data and strain-specific metabolic models to predict phenotypic traits of interest. We use this framework to predict the cellular growth for 1,143 strains of Saccharomyces cerevisiae, one of the main eukaryotic platforms in basic research as well as in biotechnology and, more recently, used for characterizing the processes associated with human diseases (11).

Cellular growth and gene expression are closely related in unicellular organisms, as they coparticipate in mutual regulation. On the one hand, growth is sustained by genes implicated in ribosomal and translational functions. In parallel, the expression of genes is affected by global and unspecific regulation originating from the physiological state of the cell (12). This relationship has yet to be fully understood, and therefore predicting cellular growth following genetic manipulations is still challenging. Understanding and controlling cellular growth have important applications in disease modeling, in biotechnology, and for the development of efficient cell factories (13). CRISPR-Cas9–enabled genetic engineering now allows modifying yeast DNA with single-nucleotide precision in vivo (14), achieving engineered strains that maximize a desired output. However, the identification of such strains is a complex issue (15). For instance, streamlining yeast metabolism for the production of valuable compounds often requires the deletion of multiple genes and efficient diversion of resources toward production pathways (16).

In an attempt to fully elucidate relationships between cellular growth and other processes, mathematical models have been developed, particularly in bacteria and yeast (17–19). For instance, coarse-grained models were designed to describe the global relationship between the allocation of resources toward protein synthesis and growth (20). Further, extensive models of metabolic networks are commonly used to simulate cellular metabolism under different growth conditions (21, 22). These models offer quantitative mechanistic representations of molecular processes, but often require detailed knowledge about uptake rates from the environment to achieve precise estimates.

On the other hand, accurate and flexible models connecting gene expression and cell growth can be obtained by data-driven statistical and machine-learning methods. As gene expression maintains a steady state during the log phase (23), it is possible to predict the growth rate even in cases where experimental measurements are not feasible. This is particularly relevant in the development of synthetic systems, where phenotypic traits have to be tightly controlled. Previous research has focused on building linear predictive models for yeast growth (24) and more recently machine learning for both Escherichia coli and S. cerevisiae (25). While both studies used gene expression profiles alone, metabolic activity is also tightly bound to cell growth (26).

Our idea is that reconnecting metabolic activity to cell growth with a data-driven and multiview approach should support more accurate machine-learning predictions, while incorporating biological mechanisms within the learning process. To investigate this idea, we used a compendium of 1,143 single-gene knockout S. cerevisiae strains, with their genome-wide expression profiles as training data to build models that predict cell doubling times. We augmented the array of biological predictors by incorporating a metabolic modeling phase, wherein we use transcriptomic profile integration in CBM to simulate strain-specific metabolism using parsimonious flux balance analysis (pFBA). From these simulations, we extracted reaction fluxes as additional features (fluxomic data). We then applied machine-learning methods using the transcriptomic and fluxomic datasets combined across 27 data–method combinations, testing different approaches for their multiview integration. When the integration of the two omics was performed within a neural network architecture, we found a significant improvement compared to using transcriptomic data alone. Upon finding that the proposed model, a multimodal artificial neural network, achieves the best performance, we tested it on a further 86 “unseen” strains generated in a different experiment and not used in the training phase, verifying its robustness to this independent dataset.

Our contributions thus focus on two aspects: 1) an investigation into the viability of building predictive models using transcriptomic and fluxomic information through a comparison of machine-learning, feature selection, and multiview data integration approaches and 2) an examination of the benefits of using metabolic modeling in building multimodal machine-learning predictive models, evaluating to what extent these mechanistic data are used to drive the learning process.

Results

Our goal was to develop and evaluate a multiomic mechanism-aware pipeline for predicting S. cerevisiae growth rate. To this end, we developed the workflow summarized in Fig. 1. In brief, we used CBM of metabolism to estimate the metabolic activity of each yeast mutant in the exponential growth phase, starting from their transcriptional activity. Then, we built and cross-compared 27 machine-learning models of yeast growth from a combination of transcript abundance and metabolic flux information. These steps and their output are described in detail in the following.

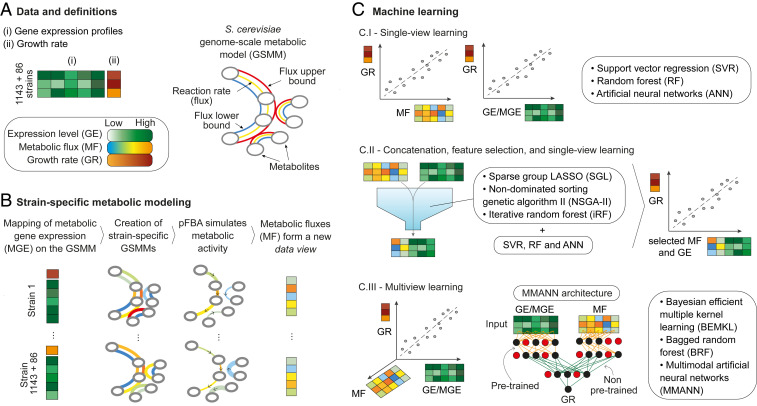
Fig. 1.

Our multiomic integration and prediction framework, including all of the datasets and machine-learning methods used in this study. The input is a gene expression screen of 1,143 single-knockout yeast strains (plus 86 single- and double-knockout strains used for independent validation), coupled with their relative growth rate and a GSMM of S. cerevisiae (A). Our methodology is divided into two main stages. In the metabolic modeling stage (B), we extracted the gene expression (GE) data for the genes involved in metabolism (MGE) and used the data to tailor the flux constraints of the GSMM in a strain-specific manner. Next, we applied pFBA to such strain-specific GSMMs to obtain the associated metabolic fluxes (MFs). In the machine-learning stage (C), we used the GE, MGE, and MF data to construct machine-learning models of yeast growth. This was achieved through (C.I) single-view learning—using only GE, MGE, or MF; (C.II) concatenation, feature selection, and single-view learning—reducing the number of GE and MF predictors; and (C.III) multiview learning—integrating the multiomic data with algorithms designed for multiple data sources (also referred to as data modes or data views). In total, 27 dataset–model combinations were tested in this stage, including a custom multimodal neural network (MMANN).

Strain-Specific Metabolic Modeling of Yeast Mutants.

Genome-scale metabolic models (GSMMs) aim to capture and simulate the entire metabolic activity within a cell. Since different transcription rates lead to alterations of cell behavior, we used gene expression data to create 1,229 strain-specific models that emulate the corresponding metabolism. Through these simulations, we extracted a measure of this metabolic activity in the form of reaction fluxes for each strain (fluxomic data).

In particular, we focused on a transcriptomic dataset with 1,143 single deletion strains of S. cerevisiae (27) and a second dataset comprising 86 single and double mutants (28), for a total of 1,229 strains. The former was used as the main resource for model training, optimization, and testing, while the latter served as an experimentally independent test set in the predictive modeling stage. We used a recently refined GSMM of yeast metabolism (29) in conjunction with Eq. 2 in Materials and Methods to build the corresponding 1,229 strain-specific models. This was achieved through a set of 908 genes involved in metabolism, represented within the yeast GSMM and put in relation to the biochemical reactions they control. In the following, we refer to the full transcriptomic profiles as “gene expression” (GE) data and to the reduced transcript information from these 908 genes as “metabolic gene expression” (MGE), as depicted in Fig. 1B.

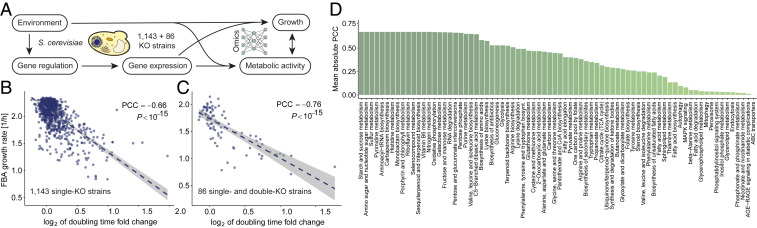
To create the strain-specific metabolic models, we altered the reaction bounds within the yeast GSMM based on expression fold-change levels in the MGE dataset. To reproduce nutritional conditions, we set the uptake rates according to the feed composition used in the original study (Materials and Methods). We then used pFBA to determine the reaction fluxes for the entire network by maximizing the biomass accumulation rate subject to model constraints. In this setting, we ensure that metabolic activity is coupled with gene expression and independent of environmental conditions, which are homogeneous across all strains (Fig. 2A). Fig. 2 B and C shows the relationship between the pFBA-predicted biomass accumulation rate and the experimentally measured relative cell doubling time in the two sets of mutants. As expected, we obtained a clear negative correlation between the two quantities, with a Pearson’s correlation coefficient (PCC) $=-0.66$, $P<10^{-15}$ in the first set and PCC $=-0.76$, $P<10^{-15}$ in the second set.

Fig. 2.

Results of strain-specific metabolic modeling of yeast knockouts. (A) Relationship between cell growth and the main biological processes. While most models consider either gene expression or metabolism, here we seek to integrate both views within a unified computational framework. In our study, environmental conditions are fixed, and hence cellular growth and metabolism are mainly driven by the influence of varying gene regulation and expression conditions. (B and C) Yeast mutant experimental relative doubling time plotted against their biomass accumulation rate, computationally estimated by strain-specific pFBA, both for the initial set (B) and for the experimentally independent test set (C). The negative correlation suggests that our strain-specific constraint-based modeling approach recapitulates the measured yeast growth. (D) Mean absolute correlation between experimental relative doubling time and strain-specific GSMM reaction fluxes within each metabolic pathway. High correlations were identified for meiosis, amino acids, and carbohydrates metabolism.

Metabolic modeling of the yeast mutant populations also allowed us to identify pathways of biological interest that are highly correlated with growth, therefore providing means to assess the mechanistic knowledge supporting the machine-learning models we developed in the next stage. Fig. 2D shows the mean absolute correlation of fluxes inside each pathway with the relative doubling time. Among those pathways that correlate most strongly with growth ($\left|\text{PCC}\right|\ge 0.6$) we found amino acid and aminoacyl-tRNA metabolism, as well as pathways involved in producing the fuel for growth such as starch, sucrose, riboflavin, and fructose metabolism, in keeping with previous experimental results (30). Other highly correlated pathways act as intermediaries between processes that are important for cell growth, such as C5-branched dibasic acid and galactose metabolism. Furthermore, we identified purine metabolism, which has been found to regulate cell growth (31); RNA degradation, which has been shown to be strongly correlated with yeast growth rates (32); and sulfur metabolism, which can actively promote initial cell division (33). Finally, the fact that growth rate is also correlated with pyrimidine supports recent research suggesting that its limitation causes the depletion of UTP and CTP, which in turn limits RNA biosynthesis, a limiting factor for cell growth (34).

Prediction of Cellular Growth Based on Transcriptomic and Fluxomic Profiles.

Starting from GE and metabolic flux (MF) profiles of yeast mutants as two data views, we used the associated relative growth rate as a target to train our predictive machine-learning models. As the nutritional conditions are fixed for all of the strains, we assumed that variation on the level of gene regulation and expression is the main contributor to metabolism and growth. In this stage, we adopted the workflow depicted in Fig. 1C.

First, we explored three traditional machine-learning techniques, each one with previous encouraging results in biological predictive tasks: 1) support vector regression (SVR)—often the learning tool of choice in computational biology due to its nonlinear decision boundary and ability to handle high-dimensional datasets (35, 36); 2) random forest (RF)—able to handle heterogeneous data types in high dimensions and to account for both correlation and interaction among features, which has led to success in predictive modeling in multiple biological domains (37); and 3) artificial neural networks (ANNs)—extremely effective in learning and modeling complex systems, with recent research reconstructing cell functionality (38) and predicting phenotypes from multiomic data (39). We applied these methods to GE, MGE, and MF data separately, in a single-view fashion, to obtain a baseline performance for the following steps.

In a second stage, we studied the integration of base omic datasets. Because our combined data represent two distinct views on the same biological systems, to thoroughly investigate the use of complementary information we explored three data strategies: 1) early integration, where GE and MF are concatenated and treated as a single dataset denoted as GE-MF; 2) intermediate integration, where model building is carried out on a combined transformation of the input views; and 3) late integration, where a model is separately built within each view and then the models are fused (3).

For intermediate and late integration, we used three multiview methods based on those employed in the single-view scenario. First, we considered Bayesian efficient multiple-kernel learning (BEMKL) (40), applying separate radial basis kernels to the MF and GE datasets. Second, we used bagged random forest (BRF) with distinct forests learned on transcriptomic and fluxomic profiles. Finally, we designed and built a multimodal artificial neural network (MMANN) to independently extract latent information from the two omic views and then fuse it together via additional neural layers (see SI Appendix for details).

The multiomic datasets considered in our predictive framework have a large number of features, which in general can contribute to various extents toward the predicted growth value. Noncontributing features add noise to the data, therefore giving potentially weaker predictive models while increasing the training effort. To overcome this “curse of dimensionality,” feature selection and regularization techniques were incorporated with the aim of isolating the most predictive features. Also in this task, we explored three state-of-the-art approaches: 1) sparse group lasso (SGL) (41), due to its ability to take into account the correlated and modular nature of biological functions; 2) nondominated sorting genetic algorithm II (NSGA-II) (42), for its ability to optimize multiple objectives; and 3) iterative random forests (iRF) (43), for its ability to capture nonlinear interactions among features (SI Appendix). Each of these techniques offers a different perspective on feature selection and is applied to GE-MF as an additional step of early integration. We thereby created three further datasets (SGL data, NSGA-II data, and iRF data, respectively) comprising the features identified by each of these approaches.

Comparison of 27 Multiomic Machine-Learning Models of Yeast Growth.

The methods outlined in the previous section globally constitute a wide and diversified collection of state-of-the-art data-driven prediction tools, applicable to different sets of omic data. To identify the most effective approach, we performed a systematic comparison of their predictive accuracy, covering 27 dataset–method combinations. We evaluated each combination by training and optimizing a model with 80% of the 1,143 samples in our primary dataset and testing it with the remaining 20%. The hyperparameters were selected by grid search as described in Materials and Methods. The entire procedure was repeated 100 times to capture the random variation in training and validation, while maintaining the same final test set.

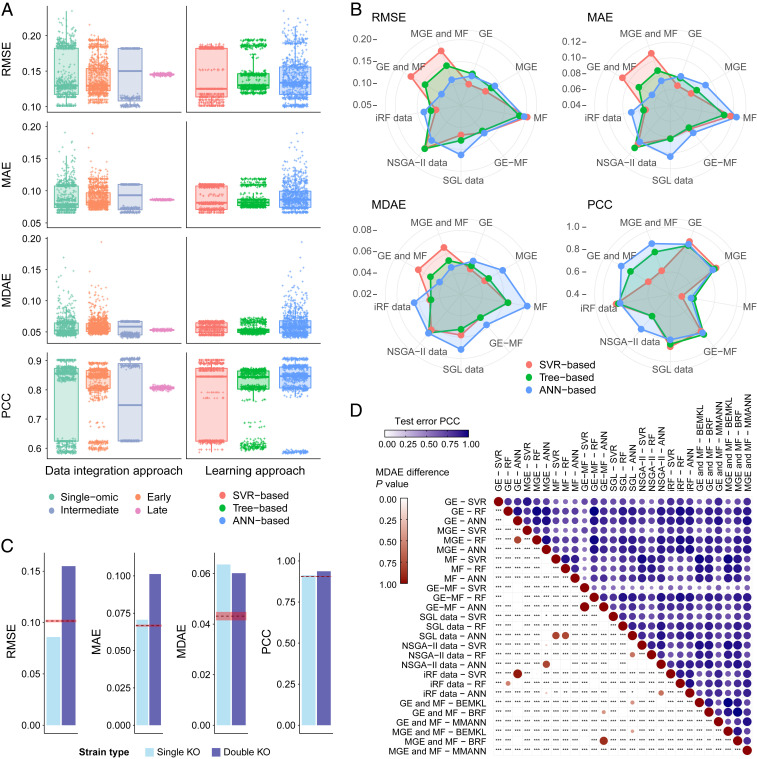
Table 1 and Fig. 3 give a breakdown of the predictive modeling results. First, we found highly variable scores for single-omic predictions, depending on whether they referred to transcriptomic or fluxomic data. In fact, both GE and MGE consistently achieved higher accuracy than MF profiles. Analogously, the complete GE performs better than the MGE subset, therefore highlighting the importance of metabolic or nonmetabolic genes that are not currently used by the yeast GSMM. Second, our results suggest that early- and late-integration approaches on average do not improve single-omic accuracy, although also this trend is associated with large variation depending on the specific data–method combination. Conversely, a small but tangible improvement was observed for intermediate integration approaches. Third, SVR- and ANN-based approaches generally tend to be more accurate than tree-based approaches. It is interesting to observe that, overall, the most accurate dataset–method combination is the MMANN model using both GE and MF, immediately followed by SVR trained on GE alone, with statistically significant median absolute error (MDAE) differences between the two (Fig. 3D).

Table 1.

Full set of accuracy scores across all 27 dataset–algorithm combinations, shown in Fig. 3: root-mean-squared error (RMSE), mean absolute error (MAE), median absolute error (MDAE), Pearson’s correlation coefficient (PCC), and fluxomic features representation (FFR, the percentage of metabolic flux features over the total number of features)

Dataset(s)	Method	RMSE	MAE	MDAE	PCC	FFR, %
Single omics
GE	SVR	0.102 $\pm$ 3e-04*	0.067 $\pm$ 0.001*	0.045 $\pm$ 0.004	0.902 $\pm$ 0.001	0
GE	RF	0.127 $\pm$ 0.001	0.077 $\pm$ 4e-04	0.049 $\pm$ 0.001	0.864 $\pm$ 0.002	0
GE	ANN	0.122 $\pm$ 0.007	0.079 $\pm$ 0.008	0.053 $\pm$ 0.010	0.876 $\pm$ 0.004	0
MGE	SVR	0.115 $\pm$ 0.003	0.070 $\pm$ 4e-04	0.046 $\pm$ 2e-04	0.872 $\pm$ 0.006	0
MGE	RF	0.130 $\pm$ 0.001	0.079 $\pm$ 4e-04	0.050 $\pm$ 0.001	0.855 $\pm$ 0.002	0
MGE	ANN	0.139 $\pm$ 0.008	0.091 $\pm$ 0.008	0.065 $\pm$ 0.011	0.838 $\pm$ 0.005	0
MF	SVR	0.203 $\pm$ 0.006	0.117 $\pm$ 0.003	0.065 $\pm$ 3e-04	0.504 $\pm$ .033	100
MF	RF	0.185 $\pm$ 0.002	0.109 $\pm$ 0.001	0.065 $\pm$ 0.002	0.611 $\pm$ 0.009	100
MF	ANN	0.196 $\pm$ 0.009	0.125 $\pm$ 0.016	0.083 $\pm$ 0.021	0.588 $\pm$ 0.003	100
Early integration
GE-MF	SVR	0.132 $\pm$ 0.009	0.079 $\pm$ 0.004	0.048 $\pm$ 0.004	0.828 $\pm$ 0.029	36
GE-MF	RF	0.126 $\pm$ 0.001	0.077 $\pm$ 0.001	0.048 $\pm$ 0.001	0.866 $\pm$ 0.003	36
GE-MF	ANN	0.132 $\pm$ 0.007	0.085 $\pm$ 0.009	0.057 $\pm$ 0.011	0.847 $\pm$ 0.006	36
SGL data	SVR	0.117 $\pm$ 0.001	0.082 $\pm$ 3e-04	0.058 $\pm$ 0.001	0.867 $\pm$ 0.002	34
SGL data	RF	0.130 $\pm$ 0.001	0.082 $\pm$ 5e-04	0.053 $\pm$ 0.001	0.844 $\pm$ 0.003	34
SGL data	ANN	0.163 $\pm$ 0.011	0.105 $\pm$ 0.013	0.072 $\pm$ 0.019	0.805 $\pm$ 0.005	34
NSGA-II data	SVR	0.178 $\pm$ 0.014	0.103 $\pm$ 0.005	0.063 $\pm$ 0.002	0.653 $\pm$ 0.069	24
NSGA-II data	RF	0.179 $\pm$ 0.020	0.110 $\pm$ 0.010	0.067 $\pm$ 0.004	0.653 $\pm$ 0.077	24
NSGA-II data	ANN	0.154 $\pm$ 0.011	0.100 $\pm$ 0.014	0.067 $\pm$ 0.017	0.804 $\pm$ 0.013	24
iRF data	SVR	0.108 $\pm$ 0.002	0.072 $\pm$ 0.001	0.050 $\pm$ 0.001	0.891 $\pm$ 0.002	0
iRF data	RF	0.120 $\pm$ 0.001	0.074 $\pm$ 3e-04	0.049 $\pm$ 0.001	0.870 $\pm$ 0.002	0
iRF data	ANN	0.136 $\pm$ 0.008	0.090 $\pm$ 0.010	0.065 $\pm$ 0.014	0.854 $\pm$ 0.003	0
Intermediate and
late integration
GE and MF	BEMKL	0.182 $\pm$ 1e-04	0.110 $\pm$ 2e-04	0.066 $\pm$ 1e-04	0.626 $\pm$ 0.001	36
GE and MF	BRF	0.145 $\pm$ 0.001	0.086 $\pm$ 3e-04	0.053 $\pm$ 0.001	0.810 $\pm$ 0.003	36
GE and MF	MMANN	0.102 $\pm$ 0.001*	0.067 $\pm$ 0.001*	0.043 $\pm$ 0.002*	0.906 $\pm$ 0.002*	36
MGE and MF	BEMKL	0.182 $\pm$ 7e-05	0.110 $\pm$ 1e-04	0.067 $\pm$ 2e-04	0.625 $\pm$ 3e-04	79
MGE and MF	BRF	0.147 $\pm$ 0.001	0.087 $\pm$ 4e-04	0.054 $\pm$ 0.001	0.803 $\pm$ 0.003	79
MGE and MF	MMANN	0.112 $\pm$ 0.001	0.073 $\pm$ 0.001	0.047 $\pm$ 0.002	0.882 $\pm$ 0.003	79

Values in boldface type represent the best scores for each data integration scenario, while the best global performance for each measure is highlighted by an asterisk. The MMANN model consistently outperforms all other models and, with 36% of the features being fluxomic, demonstrates the utility of the additional metabolic modeling stage in our pipeline.

Fig. 3.

Machine-learning yeast growth prediction results. (A) Comparison of model predictive performance across data integration strategy and machine-learning model type. Intermediate integration is overall the most effective approach and notably better than single-omic models. Concomitantly, ANN- and SVR-based techniques appear generally more effective than tree-based techniques. (B) Comparison of model accuracy for all dataset–learning algorithm combinations, corresponding to numeric results shown in Table 1. The MMANN using both GE and MF profiles is overall the most accurate model, followed by GE-based SVR. (C) Error scores on the experimentally independent test set. Dashed red lines represent the corresponding error score on the main test set, while shaded areas represent their associated SD. (D) In blue, Pearson’s correlation between error score vectors on the test set, for each pair of data–method combination. In red, P values are shown of Wilcoxon rank-sum tests assessing the significance of MDAE differences, for each pair of data–method combination. *, **, and *** represent significance at thresholds of 0.05, 0.01, and 0.001, respectively, rescaled by Bonferroni correction.

By examining the predictive scores achieved by single-view and multiview ANNs, we notice a clear improvement of multiomic models against the stand-alone GE- and MGE-based models, in contrast to other multiview methods. It thus emerges that ANNs constitute the most suitable framework for the integration of transcriptomic and fluxomic data in terms of predictive benefits, among those considered here. Our results also suggest that, despite the relatively weak performance of the fluxes alone, their useful information cannot be discerned from GE and is therefore complementary to it. This is supported by examining the prediction output correlations shown in Fig. 3D, where the models produced using the fluxomic data have a prediction set that largely differs from the other models. MMANNs seem thus to use the metabolic modeling to gain information that cannot be acquired from the gene expression alone. Additionally, using fluxes as additional features improves the ability to mechanistically explain the predictions from ANNs, making them biologically interpretable.

Furthermore, data condensation through feature selection (SGL, NSGA-II, and iRF data) increases the predictive capability of SVR and occasionally RF, but our results indicate that this is not the case with ANNs. Since our ANNs include at least two hidden layers, this suggests that ANNs can identify predictive nonlinear relationships among genes and metabolic reactions that involve a larger set of features.

Generalization to an Experimentally Independent Dataset.

For a machine-learning model to be considered generalizable and of high utility, performance stability is paramount. Especially in those settings where new data are collected in environments that differ from those of the training data, it is imperative that the prediction accuracy does not degrade under this new and unseen setting. However, this can be challenging to achieve when all of the training, validation, and test data originate from a single experiment (44). To verify the ability of our MMANN model to generalize to experimentally independent data, we applied it to a different set of yeast mutants cultivated in the same nutritional conditions. Importantly, the new mutants not only comprise single-knockout strains, but also double knockouts, exposing our model to epistatic effects on which it was not trained (28). This analysis therefore allowed us to investigate the additional question of whether our multiomic MMANN model, trained only on single mutants, could also generate reasonable predictions for double mutants (further details can be found in Materials and Methods).

Fig. 3C shows the results on the experimentally independent test set. In the single-knockout case, mean absolute error (MAE) and MDAE increase, but root-mean-squared error (RMSE) and Pearson’s correlation coefficient (PCC) improve compared to the first test case. This might be caused by potential batch effects across experiments that represent a source of systematic error, often particularly visible on the level of MDAE (45). However, the key patterns are captured as RMSE and PCC are consistent with previous tests. Double knockouts were not present in the training dataset and therefore, expectedly, the model performs less well in this scenario. We note also that, even in this out-of-distribution double-gene knockout setting, the correlation with target growth rates is particularly strong. This suggests that, if a relative rather than absolute strain identification is required, then training on single knockouts and testing on double knockouts using the MMANN approach would give a setting from which strains could be compared with confidence. Taken together, assuming an appropriate training environment and batch effect corrections, these results support the use of MMANN as a strong predictive method for this task and demonstrate robust generalization across experiments.

Functional Classification of Relevant Multiomic Predictors.

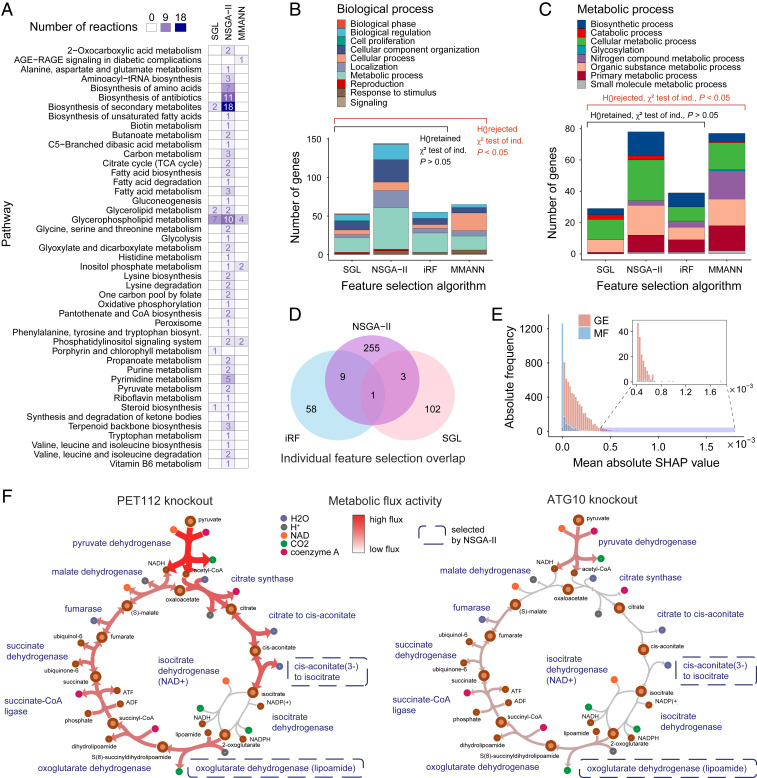
As described above, the application of feature selection methods allowed us to reduce the number of biological variables to facilitate model learning. At the same time, it provided us with concise sets of predictors that hold a strong association with the cellular growth from a data-driven point of view. We found that SGL yields 71 GE and 36 MF features as most relevant, while iRF identifies 68 unique GE features. Third, with the NSGA-II feature selection, nine variable sets are selected as members of the Pareto front of possible optimal solutions (SI Appendix), which include 218 GE and 51 MF unique features. Fig. 4A shows the metabolic pathways associated with the GSMM reactions selected by each of these algorithms, while Fig. 4B illustrates the main functional categories for the selected genes, obtained by querying the PANTHER classification system (46).

Fig. 4.

Contribution of the omic features to the learning process. (A) Pathway classification of the metabolic features selected by SGL, NSGA-II, and MMANN. (B and C) Functional classification of the genes selected by SGL, NSGA-II, iRF, or MMANN, based on Gene Ontology biological processes and metabolic molecular functions, respectively. The number of features per functional class is independent of the selection method for SGL, NSGA-II, and iRF (${\chi }^2$ test of independence, null hypothesis $H_0$ retained, $P=0.72>0.05$ for biological processes and $P=0.18>0.05$ for metabolic processes), but dependent for MMANN (null hypothesis $H_0$ rejected, $P=6.3\cdot 10^{-4}<0.05$ for biological processes and $P=2.2\cdot 10^{-3}<0.05$ for metabolic processes). (D) Overlap in the individual features selected by SGL, NSGA-II, and iRF. A single feature is shared among iRF, NSGA-II, and SGL, represented by the expression of gene YDR472W. This suggests that individual features are used interchangeably by the feature selection methods (e.g., highly correlated gene expression values or reactions with similar flux in a linear pathway) while, at a higher functional level, the pathway-level selected signal is consistent across all methods (as shown in B). (E) Distribution of feature importance in the MMANNs. These distributions are extracted from the MF and GE components of the MMANN models. Although the GE SHAP values have an overall higher contribution, the MF has a small number of features determined as highly contributing, demonstrating their predictive utility. (F) Metabolic flux through the citric acid cycle in two mutants: PET112 (Left) and ATG10 (Right), illustrating how condition-specific CBM can capture metabolic perturbations generated by the knockout of two genes not present in the GSMM, whose fluxes are exploited downstream by the machine-learning approaches. The color scale from gray (low) to red (high) indicates the amount of flux carried by each reaction in the pathway.

Among all biological processes, metabolic processes are the most prominent class for all three feature selection algorithms. By examining the organic metabolic processes, we found that a large proportion of reactions and pathways correspond to the biosynthesis and metabolism of macromolecules and organic compounds, such as factors for transcription, translational initiation, and elongation (Fig. 4C). This is consistent with the role in protein synthesis played by the translational machinery, which is critical for cell growth (47). No functional class was found statistically enriched, indicating that the joint contribution of multiple processes determines the actual growth rate. Regarding MF features, SGL selected reactions largely involved in the metabolism of glycerolipids, glycerophospholipids, and secondary metabolites, whereas reactions selected by NSGA-II encapsulate a more diverse variety of functions (Fig. 4A), ranging from the biosynthesis of amino acids and secondary metabolites to the metabolism of fatty acids, glycerophospholipids, and nucleotides.

The gene YDR472W (also known as TRS31) was selected by all three feature selection methods and encodes a core component of a subunit present in TRAPP complexes, which are responsible for Rab-mediated vesicle trafficking (48). All other selected genes and metabolic reactions are exclusive to one or two methods. Among the nine features selected by both iRF and NSGA-II, there are genes encoding binding proteins and transporters (Dataset S1). Similarly, the genes selected by SGL and NSGA-II also coded for mitochondrial transport and mRNA binding. The selection of genes linked to tRNA and cellular amino acid-related metabolic processes is consistent with the process of translational elongation during the assembly of amino acids into proteins, which consequently affects cellular growth and maximization of biomass. Despite the limited overlap among the features selected by the three methods (Fig. 4D), their high-level functional classification is statistically coherent (${\chi }^2$ tests of independence, null hypothesis retained, $P=0.72$ for biological processes and $P=0.18$ for metabolic processes). This is consistent with the nature of cell systems, based on functional modularity and redundancy, and characterized by widespread cross-correlated omic cues.

For metabolic genes or reactions, their contribution to cell growth could be inferred also through CBM-only approaches, e.g., by simulating the effect of their artificial alterations. To compare a CBM-only approach with our multimodal machine-learning approach, we performed a sensitivity analysis through in silico single-gene knockdown directly within the metabolic model, examining the impact on the biomass accumulation rate (SI Appendix). The genes and pathways that have the greatest effect on the biomass are listed in Dataset S1, among which we found some overlap with the feature selection algorithms. The down-regulation of genes related to tRNA metabolic processes and the biosynthesis of amino acids such as arginine and phenylalanine resulted in zero biomass flux, consistent with the features identified by SGL and NSGA-II. From the perspective of individual algorithms, overlapping iRF-selected genes are related to pyrimidine and phospholipid biosynthesis and to the pentose phosphate pathway. The NSGA-II genes whose deletion resulted in zero biomass are related to the metabolism of vitamin D and sphingolipid biosynthesis.

Analogously, we carried out a flux-coupling analysis to identify reaction fluxes on which growth rate is mutually dependent (fully coupled) or unilaterally dependent (directionally coupled) (49) (see SI Appendix for details). A total of 234 reactions were classified in either one of the two categories (Dataset S1). Also in this case, we observed an overlap between some features that were selected by SGL or NSGA-II. Of the 36 reactions selected by SGL, only 3 reactions are coupled with the biomass pseudoreaction (with 1 fully coupled and 2 directionally coupled reactions), whereas 19 of the 51 reactions selected by NSGA-II were found to be coupled (with 1 fully coupled and 18 directionally coupled reactions). However, it should be noted that CBM approaches are limited to the enzymes included in the genome-scale metabolic model and overlook the role of external biological factors. Thus, we argue that our integrative framework can be complementary to more traditional CBM approaches and capture cross-omic relationships missed by them.

Interestingly, when examining rules within the GSMM that dictate the gene–protein-reaction associations, some of the reactions selected uncover formerly overlooked connections. For instance, the reactions involved in glycerophospholipid metabolism are selected by SGL but the corresponding genes are not. In fact, a closer inspection of these results revealed that the functionalities of the selected gene and reaction features hardly overlap. Five reactions that constitute part of the glycerophospholipid metabolic pathway are controlled either exclusively or partially by the gene YPR140W, which is essential for maintaining the phospholipid content of the mitochondrial membrane. Indeed, S. cerevisiae is a popular choice of organism for studying glycerophospholipid homeostasis in eukaryotes, owing to tolerance with respect to its membrane lipid composition (50). These results support the case for the inclusion of both flux and gene features to augment the machine-learning model with more data, while improving our mechanistic understanding of the role that each omic plays in the wider biological context.

Finally, given the high prediction accuracy of MMANN models, we sought to determine their most contributing features. To this end, we exploited recent advances in ANN interpretation via the SHapley Additive exPlanations (SHAP) method (51), a general approach for determining the contribution (called SHAP value) of individual features to model outputs. We applied SHAP to a randomly selected model from the set of MMANN models, selecting features with absolute mean SHAP values in the top percentile as highly relevant and obtaining 71 belonging to the transcriptomic domain and 10 to GSMM reaction fluxes (Dataset S1). MMANN-associated GE features yield statistically significant differences from those selected by the feature selection methods in terms of functional classification (Fig. 4 B and C, ${\chi }^2$ tests of independence, null hypothesis rejected, $P=6.3\cdot 10^{-4}$ for biological processes and $P=2.2\cdot 10^{-3}$ for metabolic processes). The information extracted by these models thus seems notably distinct, which may explain the higher performance of MMANNs. Among the top-contributing genes in MMANNs, many produce proteins binding to RNA, with several genes acting as mRNA splicing factors involved in preprocessing via the spliceosome. Some genes encode proteins that bind to DNA to repair mismatched nucleotides, as well as proteins responsible for dephosphorylation and protein/tRNA modification. This, along with the presence of an amino acid transporter gene, reaffirms the role of protein synthesis in relation to growth. Among the top-contributing reactions, the main pathways (glycerophospholipid and inositol metabolism) are very closely linked, since inositol signaling is responsible for homeostasis and regulation of lipid metabolism (52).

Contribution of Fluxomic Information in Multiomic Machine-Learning Models.

Although from the single-omic results it is clear that a large contribution in the most accurate multimodal learning model (MMANN) comes from the transcriptomic data, we showed that a significant and complementary amount of relevant signal is present in the metabolic view. Thus, we further investigated the extent to which this method exploits the information in MF rather than in GE. The variable importance distribution for each data source, estimated through SHAP, is plotted in Fig. 4E. Although transcriptomic features have a higher mean absolute SHAP value and constitute the majority of the information used, fluxomic features also contribute a subset with high SHAP values. This shows that the predictive improvement obtained by the addition of MF profiles is directly attributable to active information sourcing from this data view.

Finally, to ascertain how the addition of MF affected the predictive accuracy on individual knockout strains, we compared the absolute error differences between ANNs (using only GE) and MMANNs (using both GE and MF). The knockout strains that recorded the highest differences between the mean errors were regarded as providing a more accurate prediction of growth rate due to the addition of MF to the model. The full list of strains for this analysis can be found in Dataset S2. Among the 20 highest differences were many gene knockouts that played a role in DNA transcription or RNA processing, as well as enzymes involved in the sorting and modification of proteins. Interestingly, only 2 of these 20 genes are present within the GSMM. This shows that MF and machine learning can jointly contribute toward extracting more accurate and biologically interpretable predictions by indirectly propagating perturbations on biological components into a GSMM, even when such components are not explicitly included in the GSMM. As an example, Fig. 4F displays the difference in metabolic flux in the citric acid cycle between two different mutants, illustrating how our condition-specific CBM approach can capture metabolic perturbations generated by the knockout of genes not present in the GSMM (PET112 and ATG10), which in turn can be exploited by a data-driven model used downstream. This advocates the use of metabolic reactions as features for machine-learning methods, using ad hoc feature selection techniques for any given application.

Discussion

This work investigates the application of multiview and multistage learning to integrating experimental and in silico-generated omic data for the prediction of yeast cellular growth. This framework is proposed and systematically evaluated across several machine-learning approaches. The wide spectrum of models and data integration techniques considered here provides a useful starting point for future benchmarking. We verified that combining experimental transcriptomic and artificial fluxomic data can increase the prediction strength over individual omics, although the improvement is subject to the predictive model choice. In our study, the largest improvement was obtained through artificial neural networks, with multimodal neural networks being the strongest predictive model overall. Additionally, we demonstrated that the advantages in terms of prediction accuracy and biological insights can reach beyond what is directly captured mechanistically by the metabolic reconstruction used to generate the fluxomic profiles.

Although transcriptomic-constrained flux balance analysis is widely used in genome-scale metabolic modeling, there are additional methods that can inject further constraints in flux simulations (53–55). Similarly, additional information may lie in the solution space of strain-specific models. For instance, additional features could be extracted from a metabolic model, e.g., from the results of flux variability analysis or sampling. While in this work we focused on cross-comparing machine-learning methods, an analogous survey could be performed on the level of constraint-based modeling techniques to generate reaction-level fluxes, as well as on the level of different base metabolic reconstructions. Furthermore, in this work, we adopted transcriptomic data as a benchmark, given their widespread use across biology and biotechnology studies. In the cases where further omic data are available, they could be implemented to perform predictions across different biological layers (5). Similarly, our framework could be extended to investigating varying environmental conditions.

It is interesting to note that multimodal artificial neural networks achieve higher accuracy compared to single-view neural networks and to other methods overall, but also transcriptomics-based support vector regression achieves good performance scores. Indeed, multiomic data integration does not always guarantee improved predictions, especially when benchmarking over gene expression (56). While any difference in accuracy generally depends on the task, our findings demonstrate that the knowledge embedded in genome-scale metabolic models is complementary to gene expression and may support its exploitation by data-driven models in a variety of scenarios. Therefore, support vector regression also appears to be a promising framework for further improving the predictions guided by transcriptomic and fluxomic data, once such complementarity is fully exploited.

Finally, it is important to note that metabolic flux information has a straightforward mechanistic interpretation, as it is directly linked to the underlying biochemistry. Data augmentation based on metabolic networks, combined with multiview learning, can therefore increase predictivity while providing direct mechanistic insights into the condition-specific interaction of metabolites that give rise to the phenotypic outcome. This can translate into advantages in terms of human ability to trust and employ more biologically interpretable machine-learning models, especially in scenarios where it is important to understand the effect of cell or metabolic engineering operations (10). Our results thus support the extension of such data- and knowledge-based multiomic machine learning to biological engineering and to other relevant phenotypic targets, such as the secretion of metabolites for drug development.

Materials and Methods

Transcriptomic and Growth Data.

The main transcriptomic dataset used in this work was collected in a previous study (27), which provides two-channel microarray profiles for 1,484 single-gene deletion strains of S. cerevisiae during the midlog phase. We downloaded these data from the supplementary material of a second study (57), which provides also relative growth rates compared to the wild type for 1,312 strains, expressed as the ${\log }_2$ of the doubling-time ratio between each strain and the wild type. After merging transcriptomic profiles and growth rates, we obtained 1,143 samples with their associated growth rates, which we used in the following stages.

An independent dataset for testing the proposed MMANN was obtained from a third study (28), providing gene expression profiles for single and double gene deletion strains of S. cerevisiae on the same microarray platform. Among these strains, we selected the single mutants that do not overlap with those in our primary dataset (14 strains) and all of the double mutants (72 strains). In this second dataset, 58 of the genes present in the main training dataset were missing. To ensure consistency of features, i.e., the same gene sets, and feed these new data into our pretrained models, we imputed the gene expression values for the missing genes by linear regression based on the other variables. Upon imputation of missing values, the obtained 86 mutants represented an experimentally independent set of conditions and served as a real-case scenario for using our proposed MMANN method.

Genome-Scale Metabolic Modeling.

A GSMM is a collection of all known biochemical reactions and transmembrane transporters that occur within an organism. The reaction network is mathematically represented as a stoichiometric matrix $\mathbf{S}$, capturing the exact proportions of reactants and products involved in each biochemical transformation (58). Reaction rates (fluxes) are mass and energy balanced assuming a metabolic steady state and can be described by a vector $\mathbf{v}$ of reaction fluxes through the network, limited by their lower and upper bounds ${\mathbf{v}}_{lb}$ and ${\mathbf{v}}_{ub}$. The constraints given by ${\mathbf{v}}_{lb}$ and ${\mathbf{v}}_{ub}$ can be modified to model varying genetic or environmental factors, yielding a context-specific metabolic model consistent with experimental data.

We estimated the metabolic fluxes associated to each transcriptional condition by solving the following parsimonious FBA problem:

$$\begin{array}{c}\underset{\mathbf{v}}{min}\hspace{0.5em}\Vert {\mathbf{v}\Vert }_1\\ subjectto\hspace{0.17em}\hspace{0.5em}{\mathbf{w}}^{\top }\mathbf{v}=f,\\ \mathbf{S}\hspace{0.17em}\mathbf{v}=0,\\ {\mathbf{v}}_{lb}\hspace{0.17em}\mathrm{\Theta }\le \mathbf{v}\le {\mathbf{v}}_{ub}\hspace{0.17em}\mathrm{\Theta }.\end{array}$$ [1]

Here $\mathbf{w}$ is a binary vector expressing the biomass pseudoreaction as a unique objective, while $f$ is the maximal growth rate achievable by the network under the given constraints. The impact of each transcriptional condition is represented by $\mathrm{\Theta }$, which is the gene set expression vector obtained by mapping the expression of the individual genes onto the associated reactions. This involves converting logical gene–protein-reaction association rules into max/min operations, as

$$\begin{array}{cc}\hfill & \mathrm{\Theta }\left(g_1\wedge g_2\right)=min\left\{\theta \left(g_1\right),\theta \left(g_2\right)\right\}\hfill \\ \hfill & \mathrm{\Theta }\left(g_1\vee g_2\right)=max\left\{\theta \left(g_1\right),\theta \left(g_2\right)\right\},\hfill \end{array}$$ [2]

where $\theta \left(g\right)$ represents the expression level of a gene $g$, and $\mathrm{\Theta }$ represents the effective expression level of the gene set $\left\{g_1,g_2\right\}$ (59). We refer the reader to SI Appendix for more details regarding the nutritional conditions.

In this work, we used the iSce926 yeast GSMM, which includes 926 genes, 3,494 reactions, and 2,223 metabolites (29). Among these 926 genes, a total of 908 (98%) are present in our main transcriptomic dataset. To solve Eq. 1, we used the COBRA toolbox 3.0 (60) with the PDCO solver. The solutions provide steady-state fluxes for every reaction in the iSce926 GSMM across the 1,143 yeast strains from the main dataset and the 86 strains from the experimentally independent dataset.

Machine-Learning Models.

To predict the relative doubling time, expressed as the ${\log }_2$ of the doubling-time ratio with respect to the wild type, we started from the transcriptomic and fluxomic profiles as features, and we used the following supervised learning methods: SVR (35), RF (37), and ANNs (61). To integrate omic profiles and obtain multiomic machine-learning models, we employed the following multiview methods: BEMKL (40), BRF, and MMANNs. Further, to reduce the number of omic predictors, we employed SGL (41), NSGA-II (42), and iRF (43) (see SI Appendix for details on each of these methods).

Machine-Learning Model Selection, Training, and Testing.

To assess model generalization, we randomly split our samples into train and test subsets composing 80% and 20% of the main dataset, respectively. Training data were used for fitting the models and learning latent patterns present in the data, which can predict the relative doubling time of yeast mutants. Since many of the adopted methods have hyperparameters that can impact the learning process, we performed a grid search to identify the optimal hyperparameter settings with the use of validation data subsets. Using the 80% data portion, we applied fivefold cross-validation repeated three times for all methods, except the ANN-based models, for which we used a fixed 10% of the training set for validation. After selecting the hyperparameters, we trained each model again, this time using the full training data—validation samples included. To measure model performance, we used the obtained models to make predictions on all of the samples in the test set, which are disjoint from those in the training and hyperparameter selection phases.

To account for stochastic variability—whether in cross-validation or during the optimization process in the case of ANN—we repeated the training–test procedure 100 times for each combination of dataset and ANN-based model and repeated the selection–training–test procedure 100 times for each other dataset–method combination. Feature selection methods were optimized and applied one time only. Finally, we applied a randomly selected MMANN model to the experimentally independent test set to simulate a real-use scenario. To ensure full reproducibility, we provide the train–test split indexes and the random seed used, along with details on methods, software packages, and hyperparameter search spaces in SI Appendix.

Data Normalization and Performance Metrics.

When feeding the different data views to the machine-learning techniques, we used $z$-score normalization, where the mean and SD of the training data were also used to normalize the test data to prevent information leakage. We used the normalized data in all of the learning approaches due to the different data distributions of the two views (fluxes and gene expression), also noting in general that normalization is a requirement for SVR and enables faster convergence in ANNs.

The hyperparameter selection focused on minimizing the RMSE,

$$\text{RMSE}=\sqrt{\frac{{\sum }_{i=1}^n{\left({ŷ}_i-y_i\right)}^2}{n}},$$ [3]

where model predictions $y_i$ are compared with observed growth rates $\widehat{y_i}$ across all $n$ strains. The RMSE emphasizes incorrect predictions. When evaluating and comparing models, we used three additional metrics, namely the MAE,

$$\text{MAE}=\frac{{\sum }_{i=1}^n|{ŷ}_i-y_i|}{n};$$ [4]

the MDAE,

$$\text{MDAE}=median\left(|{ŷ}_1-y_1|,\dots ,|{ŷ}_n-y_n|\right);$$ [5]

and the PCC. MDAE statistical differences across data–method pairs were estimated by Wilcoxon rank-sum tests through the wilcox.test R function, whose $P-$ values were adjusted via Bonferroni correction.

Artificial Neural Network Interpretation.

To quantify the variable contributions in the MMANN models, we used the SHAP method (51). SHAP uses a game-theoretic approach to determine the importance of a particular feature to individual data inputs. SHAP values are thus feature importance scores defined to satisfy local accuracy, missingness, and consistency properties. We used a variant of the SHAP method specifically designed for ANN models, called Deep SHAP (51), whose working principle is the back propagation of unit activation differences to input features. The top-contributing features inspected in terms of biological classification were chosen as those in the largest mean SHAP value percentile, where the mean was computed over the training samples.

Biological Feature Classification.

The biological classification for the genes identified by the feature selection methods and SHAP was obtained with the PANTHER classification system (46). The KEGG pathway annotation (62) for GSMM reactions was obtained from a curated S. cerevisiae GSMM (63). The statistical enrichment tests on PANTHER were run with default parameters. To assess associations between the feature selection methods and the selected gene features, ${\chi }^2$ independence tests were run on biological and metabolic process classification classes via the chisq.test R function. These tests were performed first across SGL, NSGA-II, and iRF and finally with the inclusion of the MMANN features obtained through SHAP.

Data Availability.

The microarray and growth data obtained for this study are available on Gene Expression Omnibus (GEO) (accession nos. GSE42526, GSE42527, and GSE42536), on Array Express (E-MTAB-1383, E-MTAB-1384, and E-MTAB-1385), and as flat files from the authors of the original studies (27, 28, 57). The yeast metabolic model can be found in the supplementary material of the corresponding paper (29). All data, models, and code used in this work are also available on GitHub at https://github.com/multiOmicMechanismAwareML/CodeBase, along with the information for replicating the results presented.