A cancer biologist’s primer on machine learning applications in high-dimensional cytometry

Abstract

The application of machine learning and artificial intelligence to high-dimensional cytometry datasets has increasingly become a staple of bioinformatic data analysis over the past decade. This is especially true in the field of cancer biology, where protocols for collecting multiparameter single-cell data in a high-throughput fashion are rapidly developed. As the use of machine learning methodology in cytometry becomes increasingly common, there is a need for cancer biologists to understand the basic theory and applications of a variety of algorithmic tools for analyzing and interpreting cytometry data. We introduce the reader to several keystone machine learning-based analytic approaches with an emphasis on defining key terms and introducing a conceptual framework for making translational or clinically relevant discoveries. The target audience consists of cancer cell biologists and physician-scientists interested in applying these tools to their own data, but who may have limited training in bioinformatics.

Introduction

Single-cell cytometry has proven to be a robust and flexible tool in both research and clinical laboratories since the early 1970s.¹ In recent years, the advent of high-dimensional fluorescence cytometry,² mass cytometry,³ and sequence-based cytometry⁴ in particular have allowed for the generation of richer, more complex single-cell data than ever before. For basic scientists, these innovations have provided low-cost, high-throughput methods of profiling the phenotypic and functional characteristics of millions of individual cells across a wide array of human tissues. For clinicians, cytometry has become a mainstay of diagnosing (and guiding the treatment of) numerous medical conditions including infection, malignancy, and immunodeficiency.⁵ While much of the cytometry field has focused on characterizing the identity of and relationships between subpopulations of immune cells, an emerging field of particular significance is the application of high-dimensional cytometry to the study of cancer cell diversity and heterogeneity, which are difficult to characterize without many multiparameter, single-cell observations.⁶

Historically, cytometry data have been analyzed “manually” via direct inspection of 2-dimensional biaxial plots and the sequential application of Boolean gates that are hand-drawn based on the marker intensity distributions of individual cells.⁷ While this approach is familiar to many biologists and clinicians, it suffers from significant limitations—including high between-individual user bias, lack of scalability in the face of many markers or many individual samples, and a dependence on a priori knowledge regarding which cell populations are important for the biological question at hand.⁸ Importantly, these limitations are especially cumbersome in the study of cancer cells, whose segmentation into cellular subpopulations is generally less defined (and far more contentious) than that of healthy cells, which can often be divided into discrete lineages relatively easily based on cell-surface marker expression.

In large part due to the limitations of manual gating-based analytic approaches, it is becoming increasingly common to analyze single-cell cytometry data using high-dimensional computational tools. In particular, the application of machine learning algorithms to cytometry datasets has increased significantly in the past 20 years, as has the application of artificial intelligence to biomedical datasets in general (Figure 1). Many machine learning approaches have been recently adapted specifically for the analysis of cytometry data and have been shown to perform at least as well (and often better) than human experts on a variety of tasks.8-⁹ Yet, despite the fact that these tools now exist, they are often nontrivial to understand and utilize to their full potential for most cancer biologists—and certainly clinicians—due to their stark departure from traditional manual gating workflows.^10–11 Similarly, machine learning analyses are often too complex for direct use in a clinical environment or require significantly larger datasets than are available to practicing physicians. Together, these issues demonstrate the difficulty of bridging the gap between data science and cancer systems biology in order to use cytometry data to answer important clinical or translational questions.¹²

Figure 1 – An increasing number of studies are using machine learning to analyze biomedical data.

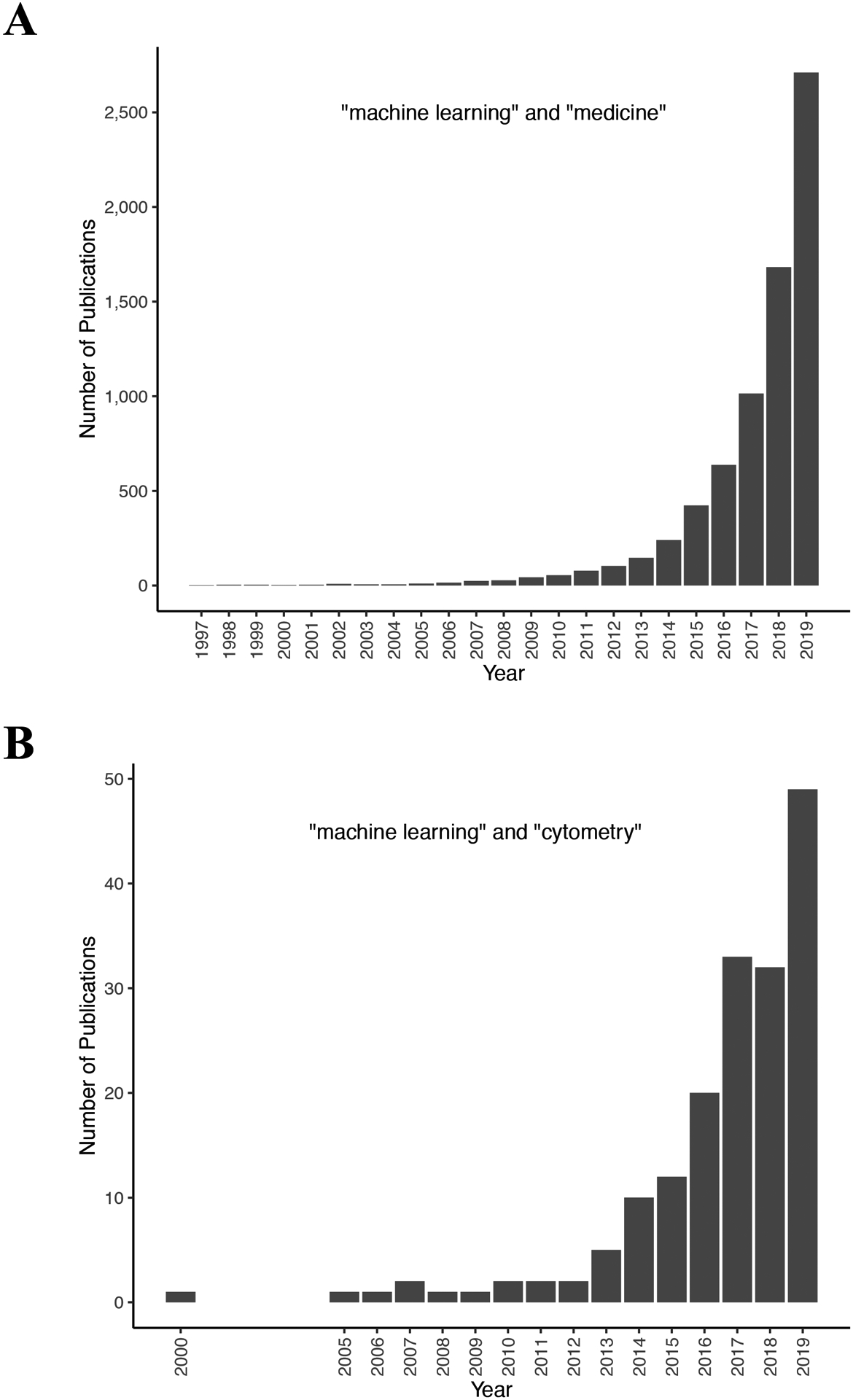
Bar graphs indicating the number of PubMed Central search results for (A) the query “machine learning” and “medicine” since 1997 and (B) the query “machine learning” and “cytometry” since 2000.

Here, we describe the main machine learning algorithms that have been used to analyze high-dimensional cytometry data in cancer biology, with an emphasis on what kinds of translational insights each of them can yield for the user. In doing so, we present the reader with a practical workflow for analyzing cytometry data by first starting with more exploratory, unsupervised machine learning approaches before working towards more targeted analytical methods. The primary audience for this review is cancer cell biologists and physician-scientists interested in applying machine learning algorithms to cytometry data in a clinically focused way, but who may have little to no bioinformatics background. Thus, what we present here is not meant to be an exhaustive guide, but rather a primer that will orient the reader and lead them towards relevant, in-depth, and up-to-date resources for further learning.

An overview of machine learning and high-dimensional cytometry

We use the term “machine learning” here to refer to a broad range of computational techniques that involve training an arbitrary model to find, classify, or predict patterns in data according to a carefully selected set of rules.¹³ While some data scientists explicitly distinguish between traditional statistical models (such as linear or logistic regression) and more complex procedures such as building artificial neural networks (NNs) or conducting clustering analyses, we deliberately avoid this distinction here in order to provide a broad discussion of as many of the currently available tools as possible. Specifically, we give close consideration to three kinds of data analysis: dimensionality reduction, clustering, and predictive modeling (with feature selection), each of which have been successfully applied to cytometry datasets in cancer research. Importantly, each of these analytic strategies yield distinct insights and, in turn, are associated with specific input and output data formats that are critical for them to be used effectively by an investigator.

Dimensionality reduction and clustering are two forms of “unsupervised” machine learning. Unsupervised machine learning algorithms seek to describe how data are organized—either along a continuum or within distinct groups or clusters—based solely on the measurements associated with each observation. In the case of cytometry data, these measurements can correspond to a cell’s transcript or protein expression levels, readouts of its genomic or epigenomic status, and/or information about its morphological or higher-level spatial features.^14–15 Using these measurements, dimensionality reduction algorithms project the data into a lower-dimensional (generally two- or three-dimensional) space in a way that preserves as much of the original information as possible and that can be easily visualized.⁷ Somewhat similarly, clustering algorithms increase the ease of visualizing and interpreting high-dimensional data by explicitly partitioning each observation—or, in the case of cytometry data, each cell—into discrete groups based on their similarity to one another. This allows cluster size and characteristics to be compared across multiple samples, experimental conditions, or treatment groups such that novel cell types of interest can be identified and characterized.¹⁰

In contrast to dimensionality reduction and clustering, predictive modeling (of which there are many kinds) represents a form of “supervised” machine learning. Supervised machine learning relates the measurements associated with each observation in a dataset to the corresponding value of an outcome variable of some kind. In cancer biology, outcome variables of interest are generally diagnostic or prognostic in nature, such as a patient’s cancer type or subtype, their response to a specific therapy or therapies, or their likelihood of disease recurrence following remission.¹⁶ In addition to their direct application as predictive tools, supervised models are often informative because many of them can perform “feature selection,” a process in which only the most important features for predicting a particular outcome are identified and included in the final model.¹⁷ Often, these selected features are biologically informative and can represent candidate therapeutic targets, molecular mechanisms of disease, or biomarkers in the diagnosis or surveillance of a particular cancer.¹⁸

Together, dimensionality reduction, clustering, and predictive modeling can be used to guide a first-pass analysis of high-dimensional cytometry data by respectively allowing for easy data visualization, characterization of distinct cellular subpopulations, and selection of candidate features that most strongly predict the clinical or experimental outcomes of interest for the study at hand (Figure 2). This framework, while by no means exhaustive, is explicit in its emphasis on focusing the analysis towards clinically useful insights. In general, clinical cytometry analyzes fewer simultaneous parameters than research cytometry, with clinical cytometers utilizing only 2–8 colors on average for a given diagnostic test.¹⁹ For cancer specifically, flow cytometry is generally used in several well-defined ways: (i) quantifying the presence of rare, aberrant cell populations such as in the detection of minimal residual disease (MRD) in the surveillance of leukemia,²⁰ (ii) measuring the expression level of a particular protein or combination of proteins within a patient’s tumor cells,²¹ or (iii) identifying the clonality or lineage status of a patient’s bulk tumor population relative to a reference control.²²

Figure 2 – Schematic diagram representing the analysis strategy described in this review.

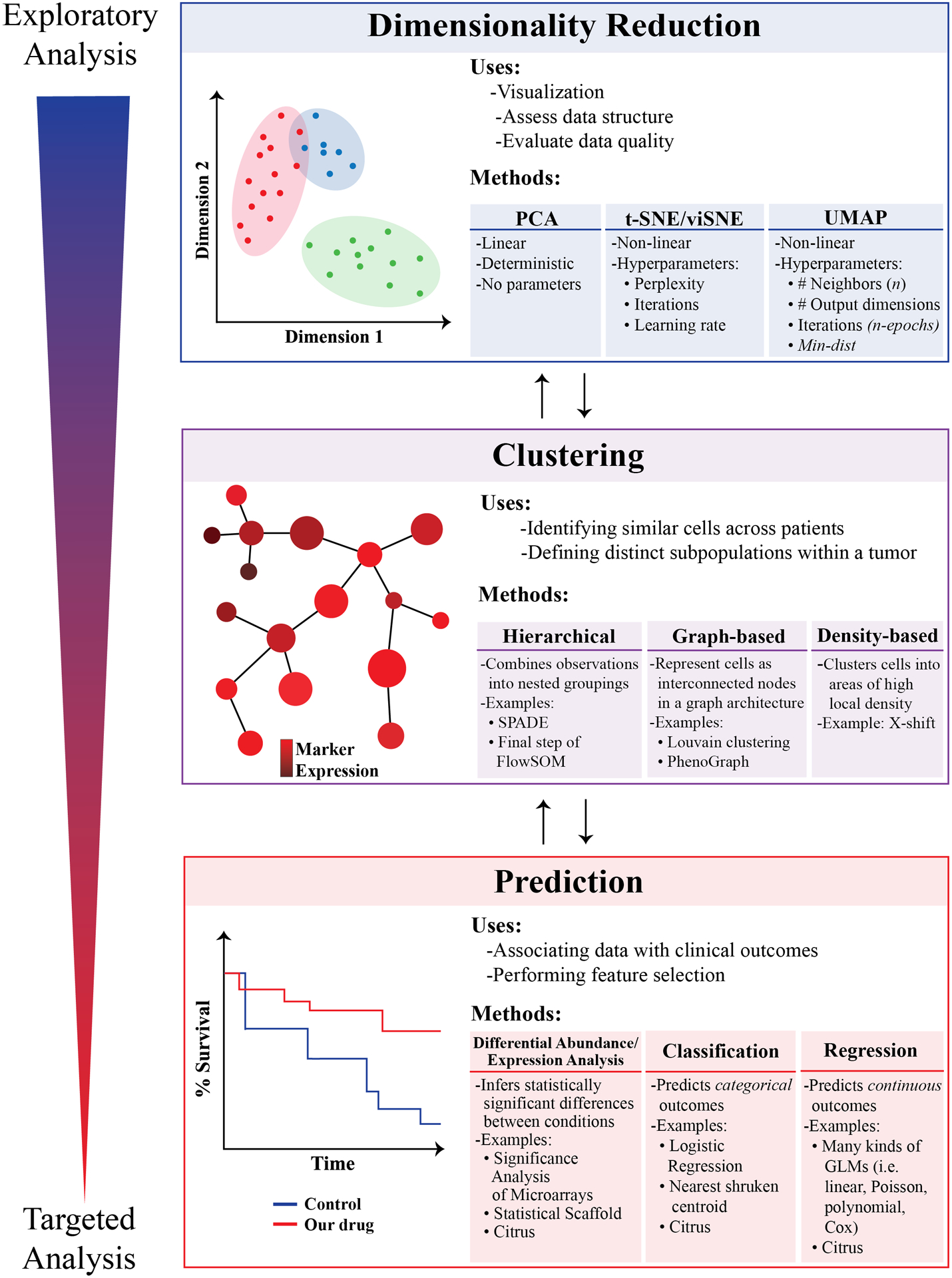
We encourage the reader to begin their analyses using exploratory approaches such as dimensionality reduction and basic visualization, later progressing to unsupervised clustering and predictive modeling/correlative biology. Bidirectional arrows are included in the diagram to emphasize that each stage of an analysis will influence multiple other stages, with results from earlier stages often informing the analytic approach in the subsequent stage (and vice versa). Throughout the figure, exploratory analyses are coded as blue, whereas more targeted analyses are coded as red.

Given these restrictions on clinical cytometry in practice, it makes sense to organize translational cytometry studies around identifying a small number of specific surface markers, intracellular signals, or cell populations that could be potentially measured in a clinical lab. Organizing one’s analysis first on dimensionality reduction, then on clustering, and then on predictive modeling is one way of doing so.²³ The following sections outline each part of this three-step workflow in closer detail while providing examples from the literature of how each of these strategies have been successfully applied to cancer cytometry data. In addition, the Glossary defines several key terms that appear in each of the sections below.

Before you start: Quality control and data pre-processing

Some readers will be familiar with the phrase “garbage in, garbage out” that is often used to describe a frustrating reality in the field of artificial intelligence: that is, if low-quality data are provided to even the best machine learning algorithm, it is unlikely that the results will be robust, reproducible, or even interpretable in a meaningful way.²⁴ In the specific context of high-dimensional cytometry data, this means that datasets collected using flawed experimental design practices or in which technical artifacts have not been corrected are likely to produce spurious findings when analyzed with any machine learning tool. Furthermore, it is often more difficult to detect such errors after complex analyses have been performed. For these reasons, the importance of quality control and data pre-processing cannot be overstated. A full, in-depth discussion of high-dimensional cytometry experimental design and data cleaning is beyond the scope of this review, but it has been thoroughly discussed elsewhere (see 22, 25, 26, and 27 for several comprehensive descriptions).

In general, the best way to guard against spurious results and data misinterpretation is a fastidious approach to experimental design before starting an experiment as well as attention to data cleaning and quality checks after data have been collected. During the experimental design phase of a project, careful consideration should be given to the inclusion of batch controls, using consistent experimental protocols and reagents, and balancing case and control groups during sample acquisition. After data is obtained, it may need to undergo compensation to correct for spillover from overlapping fluorochromes or metal isotopes, transformation to the logarithmic or hyperbolic arcsine scale to improve data scaling, and normalization to correct for batch effects, technical variation between cytometers, and longitudinal differences in samples collected across broad timescales (i.e. weeks or months).^28,29,30,31 Finally, data should also undergo a “sanity check” for quality assessment. This may include detecting outliers, technical errors in individual samples, or larger-than-expected between-sample variability and can frequently be accomplished by visualizing data distributions and computing summary statistics to discern how much each sample deviates from the norm.^32,33 Often, machine learning tools are applied to data that have not yet been manually explored to identify routine sources of error; instead, these sources of error are left to quietly wreak havoc on the analysis until the late stages of a project in which they are more difficult to identify (and after a great deal of one’s time may have already been spent). Ensuring appropriate experimental design and quality control before undertaking any complex analyses can help to avoid these frustrating pitfalls.

Step 1: Dimensionality Reduction

Dimensionality reduction is a common method of succinctly visualizing single-cell data either to reveal broad trends in how cells are distributed in high-dimensional space or to roughly assess data quality across multiple experiments or datasets. Here, we discuss several methods of dimensionality reduction including Principal component analysis (PCA), t-distributed stochastic neighborhood embedding (tSNE or viSNE), and uniform manifold approximation and projection (UMAP). Example applications of each of these dimensionality reduction approaches to a recently-published cancer cytometry dataset are provided in Figure 3.

Figure 3 – Dimensionality reduction using 3 commonly-used approaches: PCA, t-SNE, and UMAP.

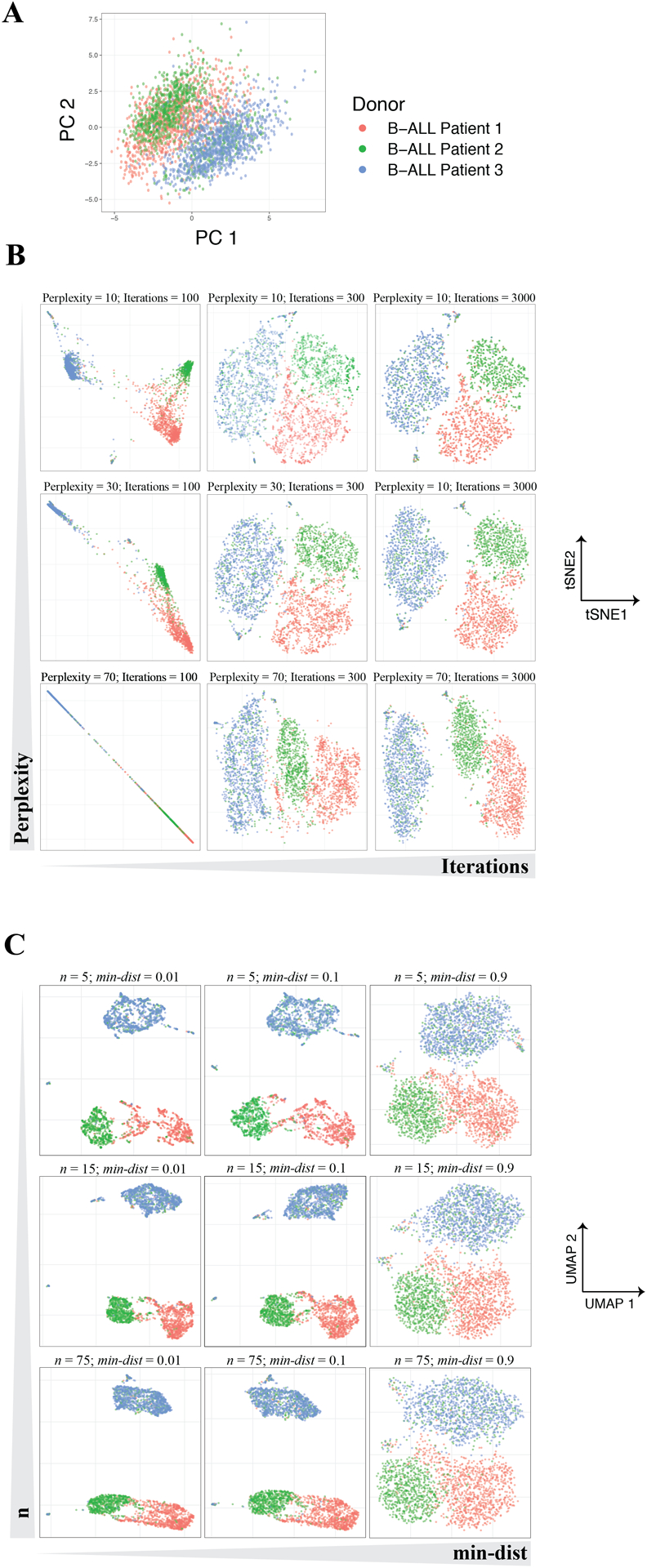
10,000 cells were subsampled from 3 B-cell Progenitor Acute Lymphoblastic Leukemia (BCP-ALL) patient samples analyzed using mass cytometry. Data were obtained from the GitHub repository from Good et al. (2018).⁹⁶ (A) Two-dimensional plot of 3 patient samples along their first (PC1) and second (PC2) principal component axes. Note that PCA does not require the user to set any hyperparameters and will return the same result each time it is used. (B) Two-dimensional plot after performing t-SNE on the same cells as in A across several t-SNE hyperparameter values. Note that samples fail to separate from one another when the number of iterations is too low and that neither inter-sample distances or dispersion are conserved across perplexity settings. (C) Two-dimensional plot computed using the same cells as in A-B across varying levels of min-dist and n. Slightly different embeddings result from different hyperparameter settings, although global relationships are more robust to these changes than those observed in t-SNE embeddings.

Principal Component Analysis (PCA).

Principal Component Analysis (PCA) is one of the most commonly-used dimensionality reduction techniques and is often the first algorithm applied to new high-dimensional datasets. PCA reduces the dimensionality of an input dataset by recombining its variables into so-called principal components (PCs), a set of new, uncorrelated variables that are rank-ordered by the amount of variance from the original data that they explain. Thus, principal component 1 (PC1) explains the largest amount of variance from the input dataset, principal component 2 (PC2) explains the second largest amount, and so on. Importantly, each principal component represents a linear combination of the original variables and, for cytometry data, can be conceptualized as a composite dimension of markers (or other cellular features) that contain similar information across all of the cells being analyzed.³⁴

In general, PCA is often used to visualize the structure of high-dimensional cytometry data by plotting cells along the first two (or sometimes three) PCs, and this can be useful for observing broad separations in cellular phenotype.³⁵ In addition, most statistical software capable of performing PCA will also report the contribution of each individual marker to all of the PCs (called “loadings”). Factor loadings can be helpful in determining which markers contribute most of the variance to a dataset and can be used in preliminary experiments to narrow down an antibody panel for high-dimensional flow cytometry or mass cytometry (for an example of this approach, see 36).

Both because of its rapid compute time (due to its relationship with a linear algebra concept called the singular value decomposition, see Glossary) and lack of tuning parameters, PCA is an exceedingly convenient tool for analyzing broad patterns within a dataset.³⁴ For instance, the EuroFlow Consortium recently used PCA to develop a highly-sensitive method for detecting minimal residual disease in B-cell precursor acute lymphoblastic leukemia (BCP-ALL).^37–38 In their study, bone marrow aspirates from 178 BCP-ALL patients were collected before treatment, after induction therapy, and 1 year after ending treatment and were analyzed using PCA in order to develop an antibody panel that best separated leukemic blasts from healthy B-cell precursors. Yet despite PCA’s usefulness for tasks like this, it also suffers from an inability to meaningfully represent highly complex, nonlinear relationships between variables. Biological data is inherently non-linear because of the complex regulatory structures that abound in molecular biology—including processes like thresholding, saturation, signal amplification, and both positive- and negative-feedback. Thus, biological variables commonly have polynomial, exponential, or otherwise highly complex relationships with one another. This results in irregular distributions and relationships that may not be easily captured by PCA.³⁹ Because of these common properties of biological data, dimensionality-reduction algorithms that can accommodate non-linear relationships are often used to detect more subtle relationships than those represented by PCA.

T-distributed Stochastic Neighbor Embedding (tSNE).

Although PCA is limited to the detection of linear patterns, not all dimensionality reduction algorithms are. The first of the non-linear algorithms we will discuss is t-distributed stochastic neighbor embedding (t-SNE; often also called “viSNE” when used for visualization).⁴⁰ The t-SNE algorithm has been implemented in most programming languages commonly used for scientific computing including R, Python, and MATLAB. In addition, it is available for use as a graphical user interface (GUI) on both the FlowJo and Cytobank analysis platforms.

Like PCA, t-SNE analyses start with high-dimensional input data in which single cells are associated with corresponding measurements of protein marker expression in flow cytometry, sequence reads in single-cell nucleic acid sequencing, or cellular neighborhood information in multiplexed imaging. However, whereas PCA reduces dimensionality through a series of linear transformations based on the input data’s global variance structure, t-SNE more accurately captures non-linear relationships by emphasizing differences in the data’s local structure.⁴¹ In brief, it does so in three steps. First, the pairwise distances between individual cells and each of their close neighbors are calculated in high-dimensional space and represented as a set of normal (Gaussian) probability distributions. Second, each cell is placed randomly on a pair of arbitrary axes to give an “initial” 2-dimensional representation of the data in which distances between close neighbors are calculated using the t-distribution.⁴² And third, the probability distribution of the high-dimensional and initial 2-dimensional representations are compared, and the 2-dimensional representation is iteratively adjusted until it matches the high-dimensional representation as closely as possible. Ultimately, this means that t-SNE analysis places similar cells close to one another in the resulting plot such that distinct cellular subpopulations emerge visually.⁴⁰

Importantly, t-SNE requires the user to set several hyperparameters before an analysis is run—including the algorithm’s number of iterations, learning rate, and perplexity—and these parameters can have significant effects on the final result. Perhaps the most important of these values is “perplexity,” which represents the rough balance between the input data’s local and global structure that is emphasized in the construction of t-SNE’s low-dimensional representation. When perplexity is low, each data point is assumed to have a small number of close neighbors and local structure predominates; when perplexity is high, the opposite is true.⁴² Thus, a recommended best practice for conducting a t-SNE analysis is to test a variety of perplexity values (keep in mind that the recommended range is 5–50) on a given dataset and observe which underlying patterns in the data are consistently observed.⁴⁰ In addition, it is important to test multiple values for the number of iterations that the algorithm will use when constructing the low-dimensional representation, as values that are too low will fail to represent the data accurately. Importantly, several variations on the t-SNE algorithm—including hierarchical tSNE (HSNE)⁴³ and opt-SNE⁴⁴—have been developed since its initial description to improve its accuracy and compute time on large datasets.

t-SNE has been successfully applied to variety of high-dimensional cytometry datasets in the study of human cancer. For example, in t-SNE’s initial application to cytometry data, Amir et al. used it to show that bone marrow aspirates taken from acute myeloid leukemia (AML) patients contain cells distinct from both healthy bone marrow populations and one another.⁴⁰ More recently, t-SNE analysis has been used in multiple studies characterizing the differences between circulating and infiltrating immune cell populations in patients with solid tumors. For example, one recent study applied t-SNE analysis to mass cytometry data acquired from hepatocellular carcinoma (HCC) patient biopsies to show that immune cells within the HCC tumor microenvironment express higher levels of immunosuppressive surface markers than those outside the tumor. Specifically, the authors were first able to identify subsets of tissue resident memory CD8+ T-cells and T-regulatory cells (T-regs) expressing high levels of T-cell exhaustion markers—including PD-1, Tim-3, and Lag-3—after these cells segregated from other cell types on a series of t-SNE plots.⁴⁵ Furthermore, a similar approach demonstrated a nearly identical result in a recent study of glioblastoma multiforme (GBM), in which t-SNE analysis helped to identify GBM tumor-resident T-regs cells that, when compared to T-regs in circulation, demonstrated both higher PD-1 expression and an elevated molecular signature of T-cell exhaustion.⁴⁶ Together, these examples indicate that t-SNE can be especially useful during the exploratory phase of data analysis by parsing out broad population dynamics and standout cellular subsets on easily-visualized, low-dimensional plots.

Yet, while t-SNE is a powerful tool for representing high-dimensional, non-linear patterns in two or three dimensions, it can be easy to misinterpret. Even when t-SNE’s tunable parameters are appropriately set, the algorithm does not preserve density or global distances between observations. This means two important things. First, it means that the relative size of a subpopulation on a t-SNE plot does not necessarily correspond to its actual size in high-dimensional space. Second, it means that the distance between distant “clusters” in a t-SNE plot does not always accurately reflect their similarity to one another.^11,42 Thus, interpreting distances on a t-SNE plot quantitatively can be misleading, although some studies have precariously done so to make claims regarding leukemic cell identity along the hematopoietic developmental trajectory.^47–48 Importantly, it should also be noted that t-SNE is stochastic, which means that it can yield slightly different low-dimensional representations when applied to the same data multiple times, although differences tend to be minor when the algorithm’s parameters are chosen well.⁴²

Uniform Manifold Estimation and Projection (UMAP).

While t-SNE is the most commonly used non-linear dimensionality reduction technique in high-dimensional cytometry data analysis, it is limited to analyzing a relatively small number of cells due to its slow computation time (which scales quadratically with the number of cells being analyzed).⁴¹ Due to this and other constraints on t-SNE’s performance, an algorithm called Uniform Manifold Approximation and Projection (UMAP) was recently developed as an alternative dimensionality reduction approach.^49,50 Because UMAP was so recently developed, there are limited examples of its application to the study of cancer biology specifically; however, UMAP is becoming increasingly widespread in the field of bioinformatics in general, which is why it warrants discussion here.^51,52,53 UMAP has been implemented as software packages in both Python and R.

Like t-SNE, UMAP seeks to represent the high-dimensional structure of an input data matrix in low-dimensional space such that local relationships between nearby cells are conserved. Unlike t-SNE, however, UMAP leverages manifold theory and Riemannian geometry to accomplish this by first approximating the high-dimensional surface on which the data sits, then utilizing a weighted k-nearest neighbor graph architecture to project that surface onto a low-dimensional layout.⁴⁹ While UMAP is derived using mathematical theory that most biologists will be unfamiliar with, in practice UMAP and tSNE can be used for similar purposes. UMAP’s particular strengths derive from its significantly faster compute time and greater emphasis on global data structure relative to t-SNE, as well as its ability to add new observations to an existing plot, of which t-SNE is not directly capable.⁵⁰ This ability to embed additional data points on an existing plot is particularly useful for biological data analysis, as it has direct applications in longitudinal disease monitoring (i.e. tracking individual patients over time throughout disease progression or treatment) as well as in the detection of batch effects when new samples are analyzed. Importantly, UMAP’s greater preservation of a dataset’s global structure means that comparing distances between clusters on a UMAP embedding might be a bit more meaningful than doing so on a t-SNE plot.⁵⁴ However, because local distances are used to compute both t-SNE and UMAP embeddings, global distances (particularly between very distant data points) are difficult to interpret. In most cases, it is less precarious to simply compute distances in the original, high-dimensional data space, making use of the distance metric that best suits your particular dataset (see “Distance metrics” in the Glossary).

UMAP requires the user to tune several hyperparameters, including n, the number of neighbors that UMAP will use to learn local data structure; d, the target number of output embedding dimensions; min-dist, the minimum distance allowed between close points in the low-dimensional representation; and n-epochs, the number of iterations the algorithm should use to find a stable low-dimensional representation.⁴⁹ Arguably the most important of these parameters is n, for which larger values will emphasize global data structure over local structure (similar to t-SNE’s perplexity parameter; see Figure 3c). By contrast, min-dist is a purely aesthetic parameter for which low values will result in more closely-packed plots. In general, users should expect to test a variety of values for n and min-dist while using values of d and n-epochs that provide stable output in the desired number of dimensions (generally 2 or 3).

When choosing between PCA, t-SNE, and UMAP in practice, there are several considerations to keep in mind. For instance, PCA is an optimal choice when computational speed, interpretability and simplicity (due to PCA’s lack of hyperparameters) are important. By contrast, t-SNE and UMAP are stronger choices when an analysis requires the visual separation of cell types whose measurements have highly non-linear relationships with one another or whose differences are poorly resolved using PCA in 2 or 3 dimensions. Finally, longitudinal data analyses are best performed using PCA and UMAP due to their ability to embed new samples into a coordinate system that has already been computed on previous samples, thereby allowing the direct comparison of old and new data. That being said, outside of these specific criteria, many data scientists also choose between these dimensionality reduction methods using trial-and-error—generally by starting with PCA due to its speed and working up to slower, more complex methods like UMAP and t-SNE if necessary.

Step 2: Clustering

While dimensionality reduction algorithms are useful for exploratory data analysis and visualization, they do not explicitly compare cell subpopulation structure between samples. To accomplish this, investigators can utilize clustering algorithms that stratify cells into quantifiable subsets that are (for the purposes of the clustering) assumed to be similar. This allows the bulk characteristics of different clusters to be compared both to one another and across sample types. While there are many kinds of clustering algorithms that work in different ways, they all seek the explicit goal of assigning observations into distinct groups such that similar observations are assigned to the same group and dissimilar observations are assigned to different groups. While clustering ultimately leads to the loss of single-cell resolution when applied to cytometry data, it also allows investigators to make inferences about which phenotypes—shared among many cells—are present in their data. Such inferences are frequently important in cancer biology, where deconvolving heterogeneous mixtures of cells within bulk tumor populations is a common experimental goal.^55–56

In this section, we give an overview of the most common clustering approaches used in the analysis of cancer cytometry data including hierarchical clustering, k-means clustering, density-based clustering, and graph-based clustering (Figure 4). We also provide examples of how these algorithms have been applied to specific questions in cancer biology and adapted specifically for the analysis of cytometry data. Importantly, many existing clustering tools are associated with built-in visualization strategies, but clusters can also be visualized using any of the dimensionality reduction strategies described in the previous section.

Figure 4 – Comparison of clustering results using SPADE, K-means clustering, PhenoGraph, and FlowSOM.

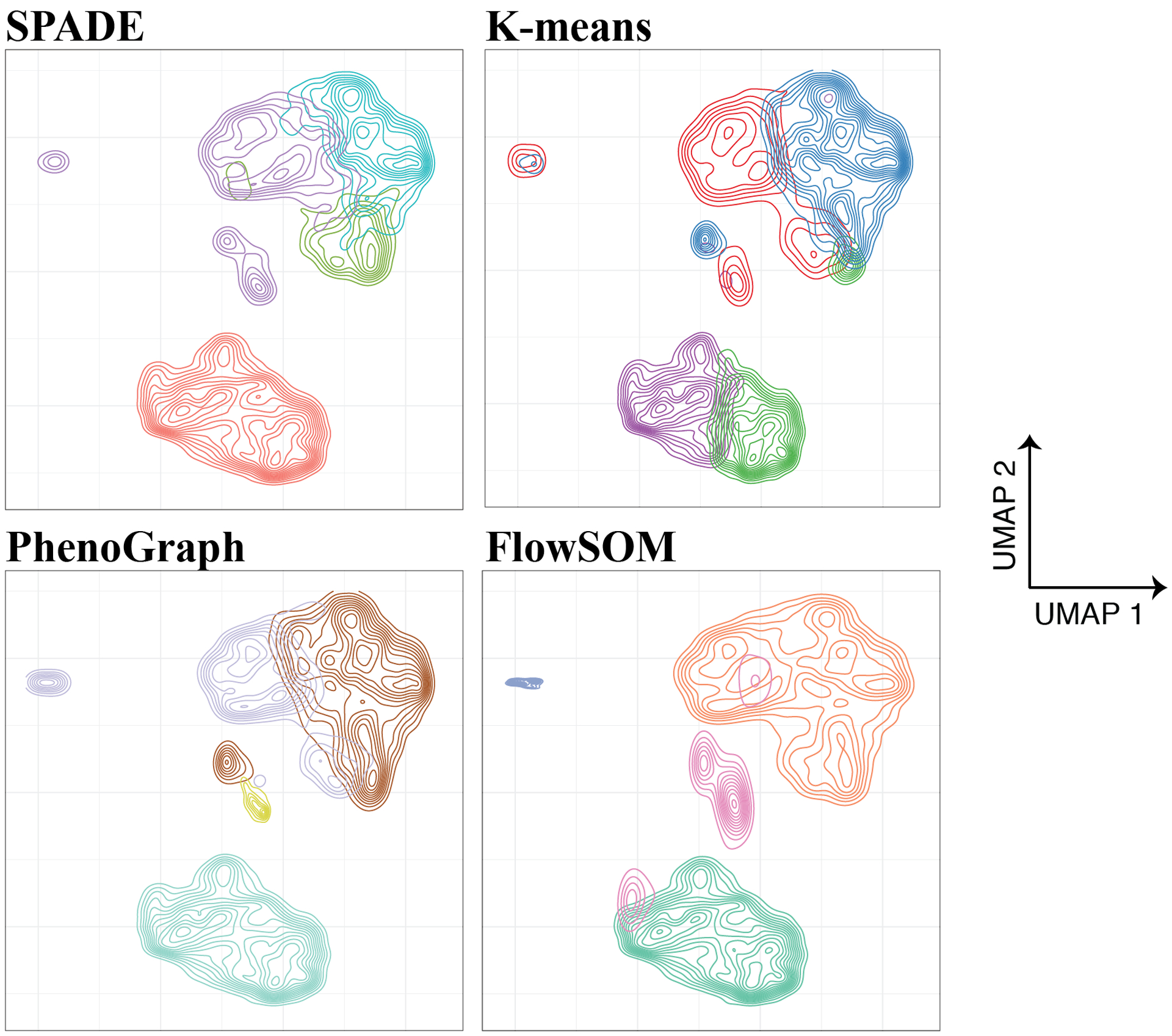
10,000 cells were subsampled from each of 3 B-cell Progenitor Acute Lymphoblastic Leukemia (BCP-ALL) patient samples analyzed using mass cytometry. Data were obtained from the GitHub repository from Good et al. (2018)⁹⁶ and analyzed using R implementations of SPADE, k-means clustering, PhenoGraph, and FlowSOM. PhenoGraph automatically detected the presence of 4 clusters, so this number of clusters was specified for the 3 remaining algorithms in order to compare results; otherwise, default parameters were used. Contour plots were embedded within UMAP axes computed using all 30,000 subsampled cells, with distinct clusters identified by each algorithm represented with a unique color in each panel. Across all clustering methods, markers used for clustering were the following: CD19, CD20, CD24, CD34, CD38, CD127, CD179a, CD179b, IgM (intracellular and extracellular), and terminal deoxynucleotidyl transferase. Notably, different clustering approaches identify subtly different cellular subsets even within this relatively simple dataset. Often, iteratively testing different clustering approaches, visualizing the results, and adjusting hyperparameters can help to determine which method fits best for one’s particular dataset.

Hierarchical clustering.

By far the most commonly-used clustering technique in bioinformatics is hierarchical clustering. Hierarchical clustering operates either by iteratively combining observations into progressively larger groups (the bottom-up or “agglomerative” approach) or by iteratively dividing observations into progressively smaller groups (the top-down or “divisive” approach).⁵⁷ In the agglomerative approach, each cell is initially assigned to its own cluster and, as the algorithm iterates through multiple steps, clusters are combined with similar clusters one-by-one until the desired number of clusters is reached. In the divisive approach, all cells are initially assigned to a single cluster that is repeatedly divided into smaller clusters such that the dissimilarity between the resulting clusters is maximized. As in the agglomerative approach, this splitting process continues until the desired number of clusters is reached.⁵⁸ In both approaches, the investigator must choose the desired number of clusters in the final result a priori—and while this is the only hyperparameter that hierarchical clustering requires, users should be cautious to avoid choosing a number of clusters that is too small, which can limit the analysis’s resolution by forcing dissimilar cell types to be grouped together spuriously.

Importantly, hierarchical clustering approaches vary in how they define the dissimilarity or distance between clusters. In single-linkage hierarchical clustering, the distance between two clusters is defined as the smallest distance between any point in the first cluster and any point in the second cluster. By contrast, complete-linkage hierarchical clustering does so by instead using the largest distance between any data point in the first cluster and any data point in the second cluster. As something of an intermediary between single-linkage and complete-linkage, average-linkage hierarchical clustering uses the average distance between all data points in one cluster and all data points in a second cluster to define inter-cluster distance.⁵⁹ Each of these linkage types produce slightly different results, and they are each capable of using a variety of distance metrics. While Euclidian distance is a common choice, other similarity metrics (such as Manhattan distance, Pearson’s correlation, and others) are frequent alternatives.

In the analysis of high-dimensional cytometry data in particular, a commonly-used application of hierarchical clustering is spanning-tree analysis of density-normalized events (SPADE), an algorithm best known for its application to the analysis and visualization of mass cytometry data, originally applied by Bendall et al.³ After an initial density-dependent subsampling step, SPADE utilizes agglomerative, single-linkage hierarchical clustering in which the distance between observations is calculated using the absolute value (L1) norm.⁶⁰ After identifying a user-specified number of clusters, SPADE constructs a minimum spanning tree (MST) diagram that connects similar clusters to one another and embeds them in a two-dimensional plot. In SPADE plots, clusters are represented as nodes within the MST whose size corresponds to the number of cells in each cluster, and whose color can be used to represent marker expression. As a widely used tool, SPADE has been implemented in R, C++, and Java and is also available as a graphical user interface (GUI) within Cytobank. Recently, a deterministic implementation of SPADE was developed such that its downsampling and MST construction steps are no longer stochastic; however, this version has not yet received widespread use in the study of cancer.⁶¹

While SPADE was initially developed to cluster and visualize subsets of hematopoietic lineage cells in the healthy immune system, it has since been applied to single-cell cancer data to help parse bulk tumor heterogeneity. In one recent study, investigators applied SPADE to data acquired from blood samples collected from nine patients with secondary acute myeloid leukemia (sAML). After clustering, the authors were able to identify several populations of CD34⁺CD38⁺ AML cells whose intracellular signaling program (specifically, phosphorylated STAT3 and STAT5 expression) responded to thrombopoeitin stimulation differently than healthy controls, revealing a potentially targetable population for therapeutic development.⁶² SPADE has also recently been used to identify a subset of metabolically impaired, tumor-infiltrating CD8⁺ T lymphocytes in clear cell renal cell carcinoma (ccRCC) patient samples analyzed using mass cytometry. In this study, analysis of SPADE plots revealed that a subset of ccRCC CD8⁺ T-cells exhibited a less activated surface phenotype compared to circulating T-cells in ccRCC patients’ peripheral blood, with functional experiments confirming that this resulted from ccRCC T-cells having small, fragmented mitochondria and glucose metabolism-deficiency.⁶³

Another algorithm with similar visualization capabilities to SPADE is FlowSOM, a recently developed clustering approach that also returns its result in the form of an MST. Unlike SPADE, FlowSOM does not require downsampling of its input data, which both significantly reduces its computation time and allows it to analyze a larger number of cells at once.⁶⁴ This is due to the fact that, instead of directly performing hierarchical clustering, FlowSOM first assigns single cells to clusters using an artificial neural network called a self-organizing map (SOM). Self-organizing maps are trained by assigning cells to their most similar node in a discretized grid of the input space, then iteratively adjusting the position of all nodes until similar cells are grouped together in an a priori specified number of clusters.⁶⁴ After clusters are identified, they can then be visualized as an MST and combined into larger meta-clusters in a final agglomerative hierarchical clustering step. While FlowSOM has been applied to studying cancer less than to studying the immune system, one recent study utilized FlowSOM to analyze melanoma cells biopsied from patients both immediately before initiating chemotherapy and after 4 weeks of treatment. The investigators’ analysis revealed one cluster of melanoma cells with a consistent surface marker profile that persisted throughout treatment, suggesting a potential role for this rare subtype in treatment-resistant melanoma.⁶⁵

K-means clustering.

Another commonly-used clustering algorithm is K-means clustering. Like hierarchical clustering, the K-means algorithm requires a user to explicitly specify the numbers of clusters (called K) to be identified within the input data.⁶⁶ Once K is chosen, the algorithm performs a three-step procedure. First, it randomly assigns each observation to one of the K clusters. Second, it computes the mean of each input variable across all data points within each cluster. Third, it reassigns each observation to the cluster whose mean is closest to it, regardless of which cluster that observation was assigned to previously. Thus, the second and third steps of this algorithm can be repeated many times until the means of the K clusters change very little (or not at all), indicating that all observations have been given a stable cluster assignment.

K-means clustering can be used similarly to any of the hierarchical clustering approaches described above, so we avoid going into further detail here. While k-means clustering is commonly used in bioinformatics overall, its tendency to produce spherical clusters has been shown to impair its performance on high-dimensional cytometry datasets, which often contain irregularly-shaped cell subpopulations.⁶⁷ For that reason, variations on k-means clustering such as flowMeans, an algorithm that automatically combines similar clusters detected by k-means clustering, are more commonly used.⁶⁸ Perhaps most importantly, however (and often a source of confusion among novice data scientists), we point out that K-means clustering is different than K-nearest-neighbor classification (and other K-nearest-neighbor algorithms) despite their names sounding similar. Rather, K-nearest-neighbor algorithms—some of which are described below—revolve around identifying a user-specified number of data points (also called K) with the smallest distances to a particular observation and then performing some computation using those data points. While K-nearest neighbor algorithms are useful for a variety of applications, K-means clustering does not involve calculating any point’s K nearest-neighbors.

Graph-based clustering.

In addition to hierarchical and k-means clustering, an increasingly common approach to cell subset detection in high-dimensional cytometry is utilizing graph-based community detection algorithms to identify distinct subpopulations of cells. In graph-based clustering, individual cells are represented as nodes or vertices that are connected to one another along a set of links (called edges) based on their phenotypic similarity to one another. Together, this set of nodes and edges is referred to as a “graph,” an abstract data structure that emphasizes the relationships between data points (and can be visualized two-dimensionally, as in Figure 5). There are many ways to represent a cytometry dataset in graph form, and depending on the kind of graph being constructed, individual cells may have many or few connections to other cells. Regardless of the specific kind of graph used, however, graph representations allow for the application of powerful computational tools to single-cell data in ways that have yielded many unique discoveries.

Figure 5 – Graph architectures can be used to represent cytometry data.

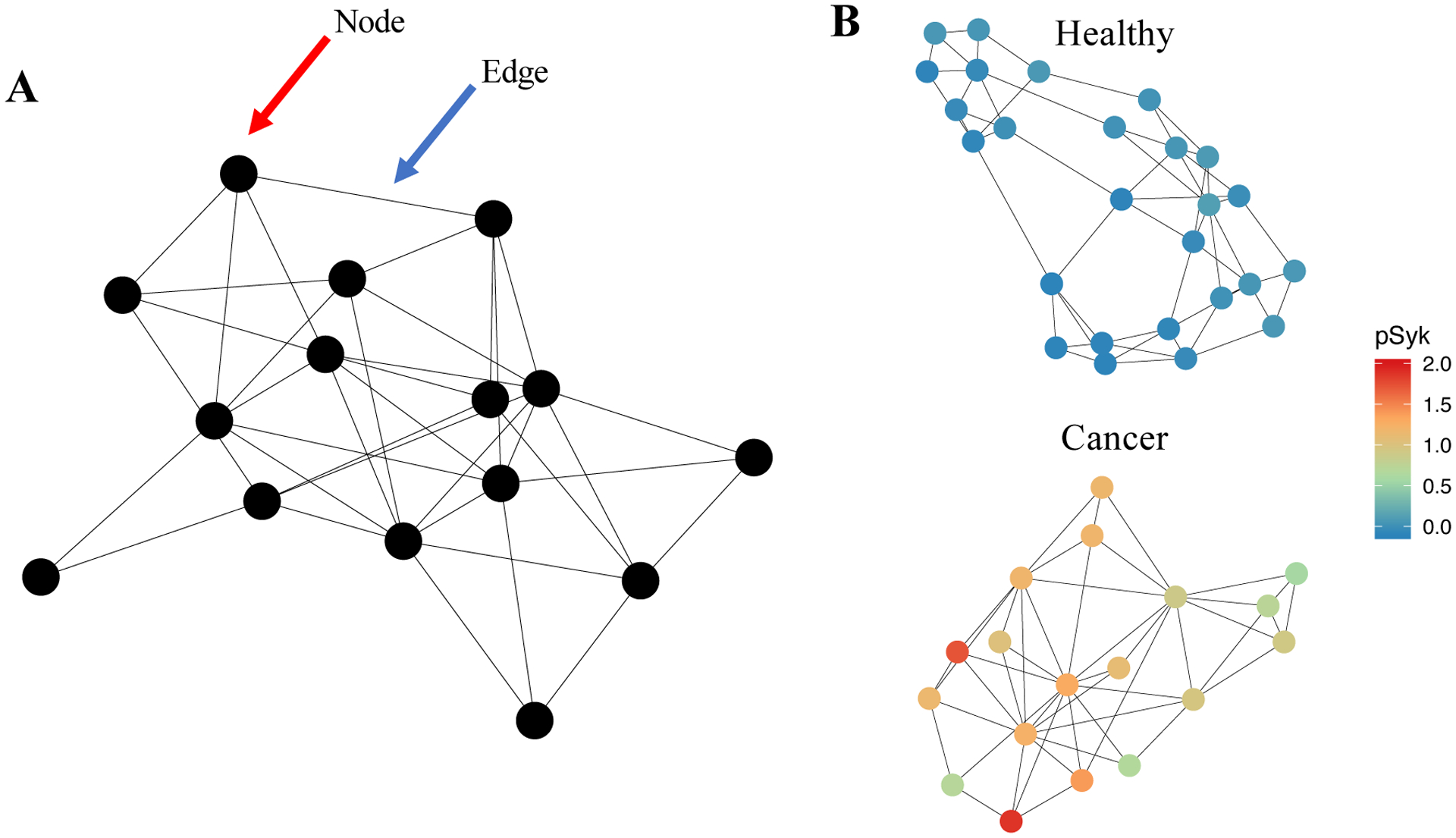
(A) Schematization of a “graph,” a data structure that expresses observations as nodes and the relationships between observations as edges. The red arrow points to a node; the blue arrow points to an edge. (B) Example graphs constructed from cytometry data collected via CyTOF (data taken from Good et al., 2018). This is an example of a graph representing single-cell cytometry data: in it, the nodes represent clusters of single-cell observations and the edges represent relationships between those nodes. In this case, a k-nearest-neighbor graph was built, meaning that each cluster is connected to the k clusters to which it is most similar (using Euclidean distance and k = 3). (B) Clustering was performed by applying PhenoGraph in healthy and leukemic samples. Each cluster’s expression level of phosphylated Syk protein (pSyk), a relapse-predictive feature in pediatric BCPALL, is indicated colorimetrically for each node. This example graph illustrates how biological parameters can be depicted by using a graph-based representation.

An important graph-based clustering algorithm in the study of cancer cells is Louvain clustering, an approach that was first developed to detect interconnected communities in mobile phone networks.⁶⁹ The Louvain algorithm works by repeatedly applying two computational steps. In the first step, the algorithm assigns each node to its own cluster (similar to agglomerative hierarchical clustering). Then, the algorithm combines clusters iteratively until the graph’s overall “modularity”—a measure of the connection density within clusters relative to the connection density between clusters—is locally maximized.⁷⁰ In the second phase, the algorithm constructs a higher-order graph by creating super-nodes out of clusters identified in the first phase. These two phases are repeated until the graph’s modularity can no longer be increased, at which point the final clustering result is returned. Louvain clustering has been implemented in a variety of programming languages and is generally considered both relatively fast and stable relative to many other graph-based algorithms.⁷¹

In the analysis of cytometry data, one variation of Louvain clustering was used to develop the PhenoGraph algorithm, a clustering method specifically developed to study cancer cell heterogeneity.³⁶ In brief, PhenoGraph works by representing the input dataset as a graph in which each cell is connected to each of its k nearest neighbors using Euclidian distance (where k is a user-specified hyperparameter). Using this initial representation, PhenoGraph then builds a second graph in which the similarity between cells is redefined according to their number of shared neighbors using the Jaccard coefficient.⁷² Louvain clustering is then performed on this graph, yielding a clustering result that can detect cell subpopulations as rare as 1/2,000 and that robustly reproduces manual gating.³⁶ Importantly, PhenoGraph accepts only a single user-defined parameter: k, the number of nearest neighbors used to construct the initial graph, and automatically detects the optimal number of clusters present in the dataset without a priori specification.

When it was first presented, PhenoGraph was applied to cytometry data collected from pediatric AML patient bone marrow aspirates. While other clustering methods failed to partition the data into interpretable subpopulations, PhenoGraph clustering revealed that AML cells were distinguishable mainly by their signaling phenotypes (particularly with regard to phosphorylated STAT5 and phosphorylated AKT) despite their high variability in surface phenotype. Since this initial study, PhenoGraph has also been used to characterize rare, progression free survival-associated macrophage and lymphocyte populations in human renal cell carcinoma samples,⁷³ to survey the differences in immune composition between circulating and tumor-infiltrating immune cells in lung adenocarcinoma,⁷⁴ and to identify a novel neutrophil-specific progenitor cell type in human bone marrow that confers pro-leukemic activity when transplanted into immunodeficient mice.⁷⁵ In each of these cases, PhenoGraph was used to identify both small clusters with high-resolution as well as larger “metaclusters” of common cell types shared between tissues and patients.

Density-based clustering.

The final clustering approach that we will discuss is density-based clustering, which partitions high-dimensional data into discrete subpopulations based on local densities. Density-based algorithms are capable of identifying clusters without assuming a particular cluster size or number, and are well-suited for cytometry experiments in which a large number of observations are collected. There are many ways to calculate density estimates in single-cell data, with particular methods performing best for specific applications over others.⁷⁶

One robust density-based algorithm developed specifically for analyzing high-dimensional cytometry data is X-shift.⁷⁷ Using k-nearest-neighbor density estimation, X-shift computes a local density estimate for each cell in the dataset. It then searches for local density maxima among these estimates and labels each of these maxima as a cluster centroid. All remaining data points are then assigned to the nearest cluster along a density-ascending path. After clusters are identified in this way, the final step of the algorithm checks for the presence of local density minima between neighboring centroids—if no clear minima are found, neighboring clusters are merged. Clusters are also merged if they are separated by a Mahalanobis distance of less than 2.0, a value based on the theoretical density-separation cutoff of the normal distribution.⁷⁸ Importantly, the optimal value for the parameter k (signifying the number of nearest neighbors used in local density estimation) is automatically selected by the X-shift algorithm, resulting in an autonomously identified number of clusters. The optimal value of k is selected using line-plus-exponent regression—in other words, k is located at the “switch point” where the number of X-shift clusters begins to increase exponentially. Thus, the switch point is used to set the value of k in order to avoid over fragmenting the input data into an exceedingly larger number of clusters.

Despite the high degree of computational time required to conduct density-based clustering (due to the inherent slowness of exhaustively computing local densities), X-shift’s performance has been validated extensively on flow cytometry datasets of healthy immune cells.⁹ More recently, X-shift has also been applied to cancer immunology. In one recent study, X-shift clustering was used to identify distinct populations of Reed-Sternberg (RS) cells in classical Hodgkin Lymphoma (cHL) patient biopsies.⁷⁹ In addition to demonstrating that some populations of RS cells lose MHC class I expression relative to control lymphoid tissue, X-shift allowed for the identification of multiple differences in cells of the cHL tumor microenvironment, including an expansion of immunosuppressive T helper 1 cells and T-regs. X-shift has also been applied to the dissection of solid tumor cell heterogeneity by identifying a relapse-associated tumor cell subset particularly high in vimentin, HE4, and cMyc expression in 17 high-grade serous ovarian tumor samples.⁸⁰

Together, the clustering methods described above constitute a broad range of strategies for cell subset detection in cancer cytometry data. It is important to note that each of these clustering algorithms is most useful with specific analytical goals in mind. For instance, when fast compute times are important, k-means clustering (and its variants) as well as flowSOM are generally optimal, whereas PhenoGraph, X-shift, and SPADE are significantly slower. By contrast, hierarchical clustering is a useful choice when multiple sets of nested, non-mutually exclusive clusters are desired, and either PhenoGraph or X-shift can be helpful when you’re unsure how many clusters are present in your dataset (due to their ability to automatically detect cluster number). Furthermore, PhenoGraph is particularly useful for detecting especially rare cell subtypes despite requiring a fair amount of computational time and memory resources. And when understanding the phenotypic relationships between clusters is important, both SPADE and flowSOM’s built-in minimum-spanning tree visualization capabilities can make them strong candidates for your analysis. Importantly, we also note that implementation details differ between each of these methods—only flowSOM, SPADE, and X-shift have been implemented with GUIs, so groups unfamiliar with R or Python may find it more difficult to use other tools.

Step 3: Correlative Biology & Predictive modeling

Using a combination of dimensionality reduction, visualization, and clustering tools, it is possible to identify subpopulations of cells with distinct molecular characteristics. But once these clusters are identified, how can we tell which ones (if any) are biologically or clinically important? To answer this question, we can look for associations between cluster characteristics—such as relative abundance, surface marker expression, and intracellular signaling program—and the clinical or experimental conditions of interest within the study. Using statistical techniques, it is possible to identify cell subsets or biological features correlated with (or predictive of) clinical or experimental outcomes. Once these cell populations or features have been identified, they can be further characterized and visualized in turn using the dimensionality reduction and clustering methodologies discussed in previous sections.

While many predictive modeling approaches have been adapted specifically for high-dimensional cytometry data, the majority of them are based on highly-vetted analytical methods originally developed for transcriptome analysis.⁸¹ We discuss some key algorithmic tools including Citrus (cluster identification, characterization, and regression), Statistical Scaffold, and Cox survival analysis below.

Differential Abundance and Differential Expression Analysis.

Most cytometry experiments include samples from two or more categories that investigators hypothesize will be different from each other in a meaningful way. In cancer biology, for instance, an experiment might include bone marrow aspirates collected from both leukemia patients and healthy donors, and investigators might expect to see differentially activated intracellular signaling programs between these two sample types. Alternatively, an experiment might analyze diagnostic samples versus relapse samples, primary tumors versus metastases, samples taken before treatment versus after treatment, or biopsies collected from patients with good prognoses versus poor prognoses. In each of these cases, an important experimental goal is identifying which characteristics represent the most important differences between sample types.

Citrus (cluster identification, characterization, and regression) is an algorithm that was designed specifically to tackle this question.⁸² In its first step, Citrus uses agglomerative hierarchical clustering to group phenotypically similar cells based on marker similarity (using Euclidian distance). For each cluster, Citrus then calculates several features on a per-sample basis—including the proportion of cells in each cluster per sample and the median expression level of each marker within each cluster. These features are used to construct an M × N matrix that represents the N features computed by Citrus across each of the M samples being analyzed. Importantly, Citrus records all clusters identified in the entire clustering hierarchy and uses them for downstream analyses—this means that each cell will be assigned to multiple nested clusters that are all represented in the Citrus feature matrix.

Using this feature matrix, Citrus then trains a supervised model to predict which sample group a sample belongs to based on its cluster features. Specifically, Citrus uses either lasso-regularized multinomial logistic regression or nearest shrunken centroid classification for the predictive step. Multinomial logistic regression is a type of generalized linear model in which input features (in this case, our cluster features) are used to predict the relative probability that a sample belongs to a particular class.⁸³ By contrast, nearest shrunken centroid classification simply assigns each observation to the sample category whose noise-adjusted centroid is closest.⁸⁴ These models produce comparable results and are fitted across a range of “regularization thresholds” that determine how many (or how few) features are included in the final model. Both types of model are validated using 10-fold cross-validation, and the optimal model is ultimately selected based on maximum accuracy. Citrus also provides some built-in visualization of its results, all of which are easily accessible in its Cytobank and R implementations.

By combining clustering, generalized linear modeling, and regularization, Citrus automatically identifies which cytometric features are most closely associated with a particular experimental or clinical outcome. Thus, Citrus performs what is often referred to as feature selection—a process whereby an algorithm identifies a dataset’s most informative variables out of a large group.¹⁷ Because it considers both cluster size and marker expression, Citrus can also be described as performing differential abundance analysis (comparing cluster size between conditions) and differential expression analysis (comparing clusters’ marker expression levels between conditions), both of which are standard bioinformatic tools. Importantly, Citrus requires at least 8 samples for each experimental group being compared in order to maintain sufficient statistical power to differentiate between true differences and normal inter-sample variability (noise).⁸³ This limitation is important to consider when designing experiments—if one’s sample number is limited, Citrus may not provide reproducible results.

Another algorithm that takes a similar approach is Scaffold (single-cell analysis by fixed force- and landmark-directed maps).⁸⁵ Initially developed purely as a visualization tool, Scaffold’s main functionality is to organize cell clusters on a force-directed graph based on their relative similarity to manually-gated reference cell populations.⁸⁶ However, the algorithm was later updated to include the option to apply the significance analysis of microarrays (SAM) permutation-based significance test to the clusters being plotted.⁸⁷ To do so, the updated “Statistical Scaffold” algorithm first calculates the same feature matrix as Citrus. Then, it randomly permutes the sample labels to estimate each feature’s expected difference between sample types solely due to chance. Using this approach, a false-discovery rate for the set of features can be computed, and statistically significant differences can be assessed.⁸⁶ As a differential abundance and expression analysis tool with useful visualization capabilities, Scaffold has been applied to the study of chimeric antigen receptor (CAR) T-cell dynamics in pre-clinical studies of novel CART cell therapies.⁸⁸ However, Scaffold has seen limited use in studying cells outside of the hematopoietic lineage, perhaps due to the often drastic difference between cancer cell phenotypes and those of their native, healthy lineages. Furthermore, due to Scaffold and Citrus’s identical feature matrix calculations, they share similar sample size requirements. In order to maintain sufficient statistical power to detect relevant differences, we recommend a sample size of at least 8 samples per group when using Scaffold as well.

Cox Survival Analysis.

In addition to the analyses mentioned above, many translational studies include the explicit goal of predicting clinical outcomes directly from single-cell data. This is especially true in the study of cancer, in which predicting patient mortality, risk of recurrence, and other adverse outcomes are imminent areas of clinical need. Thus, single-cell studies of clinically annotated human samples may seek to quantify the relationship between cellular features and outcome variables such as patient survival or time to relapse. Importantly, understanding such relationships is becoming increasingly possible due to the emergence of large repositories of clinically annotated datasets such as the National Institute of Health’s Cancer Genome Atlas and Therapeutically Applicable Research to Generate Effective Treatment (TARGET) program.

Statistical modeling for time-to-event outcomes such as mortality or relapse is typically accomplished using Cox regression, a supervised learning tool most commonly used in epidemiology.⁸⁹ Like logistic regression (discussed above), Cox regression is a kind of generalized linear model in which input features are used to predict the “hazard rate” of a particular event happening over time.⁹⁰ Once trained, a Cox model is capable of predicting the relative survival (or event-free survival) probability of a patient with a particular set of input features at any point in time. As generalized linear models, Cox models can be regularized similarly to logistic models, which allows for feature selection of only the most informative predictors. Thus, Cox regression can be a powerful and versatile tool in outcomes prediction when applied to the appropriate dataset.

Conveniently, the Citrus algorithm (discussed at length above) is capable of fitting Cox models to perform survival analyses of multiparameter cytometry data.⁸² Using the same feature matrix computed for logistic regression, Citrus can be specified to train a lasso-regularized Cox model instead of a logistic model.⁹¹ Survival modeling in Citrus is performed using the same procedures as logistic classification, using k-fold cross-validation to build a model using the subset of cluster features most predictive of patient risk. Selected features are reported by Citrus and can be inspected for biological interpretation.

Although Citrus provides a convenient implementation of Cox regression, it has been used infrequently in the analysis of cancer data. This may be the case due to the Citrus workflow’s inability to incorporate other relevant clinical variables—such as patient age, treatment regimen, or tumor genetic subtype—into its survival analyses (see 23). However, the general approach of applying regularized Cox models to cancer cytometry data is easily implemented in a wide variety of available R packages (notably glmnet,⁹² edgeR,⁹³caret,⁹⁴and others).

This strategy was recently used to combine the use of mass cytometry and clinical metadata to predict disease recurrence in a cohort of 60 patient with pediatric B-cell precursor acute lymphoblastic leukemia (BCP-ALL).⁹⁵ In this study, investigators first developed a supervised clustering algorithm (termed a “single-cell developmental classifier”) by using Mahalanobis distance to align leukemic cells with their most similar developmental subpopulation along healthy hematopoietic development (Figure 6). For each healthy-like cluster of leukemic cells, a feature matrix similar to Citrus’s was calculated and used to train an elastic net regularized Cox model to predict patients’ relapse risk with >90% accuracy.⁹⁶ Based on the model’s selected features, investigators were able to identify activated signaling in the mTOR and pre-BCR pathway in specific subpopulations of leukemic cells, thereby identifying potential therapeutic targets for further study in BCP-ALL.

Figure 6 – Schematization of Good et al.’s single-cell developmental classifier.

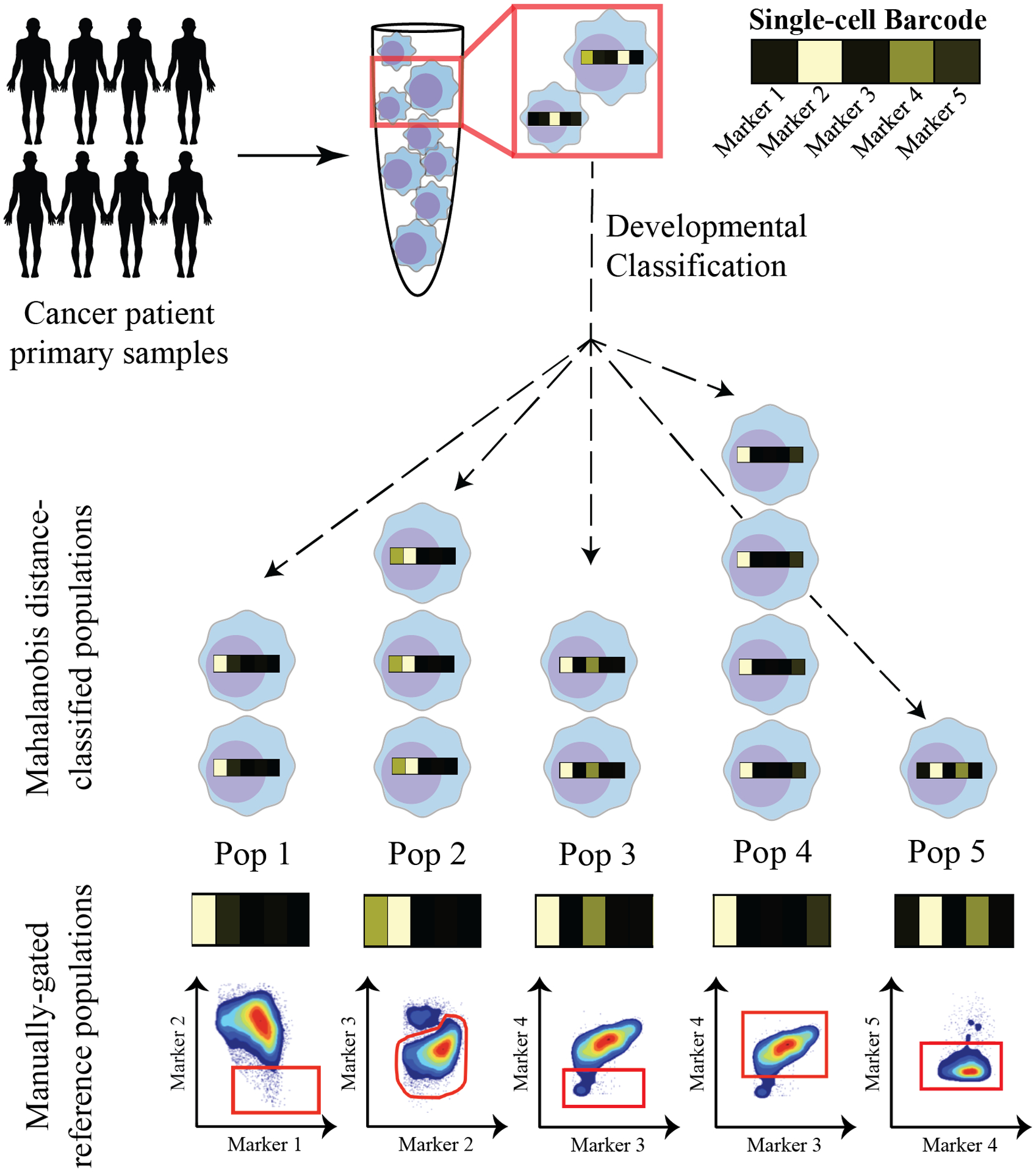
Using this approach, cancer cells are classified into their most analogous healthy cell type in normal lineage development in a series of 2 steps. First, healthy populations across lineage development are manually gated, and a single-cell “barcode” of marker expression values is computed for each manually-gated subpopulation. Second, cancer cells are aligned with their most similar healthy subpopulation based on the Mahalanobis distance between their marker expression profile (or “barcode”) and that of each manually-gated population. Using this method, cancer cells can be classified into readily interpretable, “healthy-like” cell subtypes that each have unique properties.

In sum, each of the tools described above can be used to detect associations between single-cell measurements and clinical or experimental outcomes in annotated samples. Citrus is a convenient tool for a variety of analyses including differential expression analysis, differential abundance analysis, and survival analysis. However, it is limited by both its sample size requirements as well as its inability to model variables outside of its specific feature matrix (such as patient age or gender). Statistical Scaffold is similar to Citrus, but it places a larger emphasis on visualization and thus can be a more useful tool for creating plots to represent your data. Lastly, directly implementing cox, logistic, or any other kind of generalized linear regression can be an incredibly powerful and flexible tool, particularly because regularization approaches such as elastic net can make feature selection relatively easy. However, this approach is less straightforward than applying “off-the-shelf” algorithms like Citrus or Statistical Scaffold and may therefore require a larger amount of data pre-processing and feature extraction, such as Good et al.’s extraction of developmental lineage features from their dataset before model-building. Fortunately, there are numerous open-source tools for most data manipulation tasks, including the “Tidyverse” suite of data analysis tools in R and many other packages for data wrangling, visualization, and modeling.^97,98

Conclusions and Topics For Future Consideration

We have presented a conceptual framework for understanding some of the most commonly used applications of machine learning to cancer cytometry data. Through a combination of dimensionality reduction, visualization, unsupervised clustering, and predictive modeling, it is possible to identify trends in cytometry data that point towards a novel understanding of basic and clinical cancer biology. By allowing high-dimensional data to be visualized in a smaller, more human-readable number of dimensions, dimensionality reduction provides a tool for exploring broad trends in one’s data, detecting batch effects or other technical artifacts, and comparing samples longitudinally across disease progression or treatment. Likewise, clustering analyses allow for the detection of cell subpopulations in a dataset through a variety of different approaches that make unique assumptions about how subpopulations are shaped, sized, and distributed. Finally, differential expression analysis, differential abundance analysis, and predictive modeling techniques can associate the biological measurements in a cytometry dataset with other variables of interest, such as a patient’s risk of relapse or their likelihood to respond to a particular treatment regimen. Thus, the specific goals and capabilities of each of these analytic steps can be used to guide an analysis from its early, exploratory stages to its targeted identification of a clinically- or translationally-important finding. Despite this, many areas for further development remain.

There are dozens of clustering algorithms that have been applied to cytometry data beyond those discussed here. Choosing a clustering approach for one’s own study can be difficult, and the best advice is to try a few different approaches on simple datasets you already understand such as a control dataset. This will allow you to assess the results based on your pre-existing knowledge. Then, you can either increase the complexity of your input data gradually or go straight to your experimental data. Despite the continued development of increasingly sophisticated clustering approaches, an interesting recent trend is the emergence of clustering strategies that explicitly emphasize the interpretability of cluster identity. One approach is the developmental classifier developed by Good et al., which partitions leukemic cells into groups based on prior knowledge about healthy hematopoietic lineage development.⁹⁵ Another approach is that of Marker-Enrichment Modeling (MEM), an algorithm that assigns text labels to pre-identified clusters of cells based on their marker expression profiles relative to user-specified reference populations.⁹⁹ MEM labels are meant to recapitulate historical naming conventions in cytometry in order to emphasize easy interpretation of cluster identity, regardless of the particular clustering method that was used to perform the analysis. Finally, two recently-published algorithms—“GateFinder” and Hypergate—operate in a similar vein by automatically developing multistep, two-dimensional gating strategies for novel cell populations of interest within a dataset.^100–101 Thus, these methods can be used to develop a sorting strategy for cell subsets identified using unsupervised clustering for follow-up experiments and additional characterization.

Regardless of how clusters are identified or annotated, one outstanding limitation of current analysis strategies is their loss of single-cell resolution (due either to clustering or to manual gating) before predictive modeling is performed. Because cells exist in a complex network of biological interaction and functional interdependence, this loss of single-cell information is likely to obscure important relationships between interacting cell types. This is especially true in the study of cancer, where understanding the interplay between individual tumor cells, the stromal microenvironment, and the immune system is generally understood to be of paramount significance. Although several recently developed algorithms are capable of predicting clinical outcomes from cytometry data without the use of clustering, methods that explicitly model potential interactions between cell types are yet to be developed.^102–103

By contrast, current methods that do preserve the single-cell resolution of high-dimensional cytometry datasets are primarily focused on replicating manual gating procedures rather than on modeling clinical or biological outcomes. Such methods—including OpenCyto¹⁰⁴, flowClust,¹⁰⁵ flowDensity,¹⁰⁶ FlowLearn,¹⁰⁷ and DeepCyTOF¹⁰⁸—were developed to reduce the time and resources required for identifying “standard” cell populations as well as to reduce subjectivity in the gating process. Perhaps because cancer cell phenotypes are often much more heterogeneous than those of the immune populations on which these methods were developed, automated gating algorithms have not yet been applied extensively to cancer cytometry data. However, there is growing clinical interest in using automated gating strategies to detect MRD in some subtypes of acute leukemia in humans, which may represent an area of further development of these approaches as they pertain to the study of cancer.¹⁰⁹

Finally, with the progressive availability of large, publicly available multi-omics single-cell datasets, an exciting area for the future of cancer cytometry analysis is the application of deep learning. Because many current studies are often limited by the sparse availability of clinically annotated patient samples, deep learning is likely to overfit the small number of observations in most independent experiments. However, studies have begun to apply deep learning at the single-cell level—an approach that has been particularly effective in the application of convolutional neural networks to computer vision problems in image cytometry^110–111 as well as to batch correction, denoising, and clustering procedures on at least one large, multi-patient dataset.¹¹²

Together, the continued design, refinement, and widespread use of machine learning algorithms in cytometry data analysis hold a great of promise in aiding future developments in our understanding and treatment of cancer. With the application of increasingly powerful and intuitive tools to larger and more diverse datasets, the field of cytometry is likely to provide important biological and clinical insights for decades to come.