Improving Attention Mechanism in Graph Neural Networks via Cardinality Preservation

Abstract

Graph Neural Networks (GNNs) are powerful for the representation learning of graph-structured data. Most of the GNNs use a message-passing scheme, where the embedding of a node is iteratively updated by aggregating the information from its neighbors. To achieve a better expressive capability of node influences, attention mechanism has grown to be popular to assign trainable weights to the nodes in aggregation. Though the attention-based GNNs have achieved remarkable results in various tasks, a clear understanding of their discriminative capacities is missing. In this work, we present a theoretical analysis of the representational properties of the GNN that adopts the attention mechanism as an aggregator. Our analysis determines all cases when those attention-based GNNs can always fail to distinguish certain distinct structures. Those cases appear due to the ignorance of cardinality information in attention-based aggregation. To improve the performance of attention-based GNNs, we propose cardinality preserved attention (CPA) models that can be applied to any kind of attention mechanisms. Our experiments on node and graph classification confirm our theoretical analysis and show the competitive performance of our CPA models. The code is available online: https://github.com/zetayue/CPA.

1. Introduction

Graph, as a kind of data structure in non-Euclidean domain, can represent a set of instances (nodes) and the relationships (edges) between them, thus has a broad application in various fields [Zhou et al., 2018]. Different from regular Euclidean data such as texts and images, graph structured data are irregular so it is not straightforward to apply important operations in deep learning (e.g. convolutions). Consequently, the analysis of graph-structured data remains a challenging and ubiquitous question.

In recent years, Graph Neural Networks (GNNs) have been proposed to learn the representations of graph-structured data and attract a growing interest [Scarselli et al., 2009; Li et al., 2016; Niepert et al., 2016; Kipf and Welling, 2017; Hamilton et al., 2017; Zhang et al., 2018; Ying et al., 2018; Morris et al., 2019; Xu et al., 2019]. GNNs can iteratively update node embeddings by aggregating/passing node features and structural information in the graph. The generated node embeddings can be fed into extra modules and the whole model is trained end-to-end for different tasks.

Though many GNNs have been proposed, it is noted that when updating the embedding of a node v_i by aggregating the embeddings of its neighbor nodes v_j, most of the GNN variants will assign non-parametric weight between v_i and v_j in their aggregators [Kipf and Welling, 2017; Hamilton et al., 2017; Xu et al., 2019]. However, such aggregators (e.g. sum or mean) fail to learn and distinguish the information between a target node and its neighbors during the training. Taking account of different contributions from the nodes in a graph is important in real-world data as not all edges have similar impacts. A natural alternative solution is making the edge weights trainable to have a better expressive capability.

To assign learnable weights in the aggregation, the attention mechanism [Bahdanau et al., 2014; Vaswani et al., 2017] is incorporated in GNNs. Thus the weights can be directly represented by attention coefficients between nodes and give interpretability [Veličković et al., 2018; Thekumparampil et al., 2018]. Though GNNs with the attention-based aggregators achieve promising performance on various tasks empirically, a clear understanding of their discriminative power is missing for the designing of more powerful attention-based GNNs. Recent works [Morris et al., 2019; Xu et al., 2019; Maron et al., 2019] have theoretically analyzed the expressive power of GNNs. However, they are unaware of the attention mechanism in their analysis. So that it is unclear whether using attention mechanism in aggregation will constrain the expressive power of GNNs.

In this work, we make efforts to theoretically analyze the discriminative power of GNNs with attention-based aggregators. Our findings reveal that previous proposed attention-based aggregators fail to distinguish certain distinct structures. By determining all such cases, we reveal the reason for those failures is the ignorance of cardinality information in aggregation. It inspires us to improve the attention mechanism via cardinality preservation. We propose models that can be applied to any kind of attention mechanisms and achieve the goal. In our experiments on node and graph classification, we confirm our theoretical analysis and validate the power of our proposed models. The best-performing one can achieve competitive results comparing to other baselines. Our key contributions are summarized as follows:

• We show that previously proposed attention-based aggregators in message-passing GNNs always fail to distinguish certain distinct structures. We determine all of those cases and demonstrate the reason is the ignorance of the cardinality information in the aggregation.

• We propose Cardinality Preserved Attention (CPA) methods to improve the original attention-based aggregator. With them, we can distinguish all cases that previously always make an attention-based aggregator fail.

• Experiments on node and graph classification validate our theoretical analysis and the power of our CPA models. Comparing to baselines, CPA models can reach state-of-the-art level.

2. Preliminaries

2.1. Notations

Let G = (V, E) be a graph with set of nodes V and set of edges E. The nearest neighbors of node i are defined as $\mathcal{N}(i)=\left\{j\mid d(i,j)=1\right\}$, where d(i, j) is the shortest distance between node i and j. We denote the set of node i and its nearest neighbors as $\tilde{\mathcal{N}}(i)=\mathcal{N}(i)\cup \left\{i\right\}$ For the nodes in $\tilde{\mathcal{N}}(i)$, their feature vectors form a multiset M(i) = (S_i, μ_i), where S_i = {s₁, …, s_n} is the ground set of M(i), and ${\mu }_i:S_i\to \mathbb{N}*$ is the multiplicity function that gives the multiplicity of each s ∈ S_i. The cardinality ∣M∣ of a multiset is the number of elements (with multiplicity) in the multiset.

2.2. Graph Neural Networks

General GNNs

Graph Neural Networks (GNNs) adopt node or edge features and the graph structure as input to learn the representations in graphs for different tasks. In this work, we focus on the GNNs under the massage-passing framework, which updates the node features by aggregating its nearest neighbor node features iteratively. In previous surveys, this type of GNNs is referred as Graph Convolutional Networks in [Wu et al., 2020] or the GNNs with convolutional aggregator in [Zhou et al., 2018]. Under the framework, a learned representation of each node after l layers contains the features and the structural information within l-hop neighborhood. The l-th layer of a GNN can be formulated as:

$$h_i^l={\varphi }^l\left(h_i^{l-1},\left\{h_j^{l-1},\forall j\in \mathcal{N}(i)\right\}\right),$$ (1)

where the superscript l denotes the l-th layer. h_i is the representation of node i, and $h_i^0$ is initialized as X_i. The aggregation function ϕ in Equation (1) propagates information between nodes to update the node features.

In the final layer, since the node representation $h_i^L$ after L iterations contains the L-hop neighborhood information, it can be directly used for local/node-level tasks. While for global/graph-level tasks, the whole graph representation h_G is computed using an extra readout function g:

$$h_G=g\left(\left\{h_i^L,\forall i\in G\right\}\right).$$ (2)

Attention-Based GNNs

In a GNN, when the aggregation function ϕ in Equation (1) adopts attention mechanism, we consider it as an attention-based GNN. The attention-based aggregator in l-th layer can be formulated as follows:

$$e_{ij}^{l-1}=Att\left(h_i^{l-1},h_j^{l-1}\right),$$ (3)

$${\alpha }_{ij}^{l-1}=\text{softmax}\left(e_{ij}^{l-1}\right)=\frac{\text{exp}\left(e_{ij}^{l-1}\right)}{{\sum }_{k\in \tilde{\mathcal{N}}(i)}\text{exp}\left(e_{ik}^{l-1}\right)},$$ (4)

$$h_i^l=f^l\left({\sum }_{j\in \tilde{N}(i)}{\alpha }_{ij}^{l-1}{h}_j^{l-1}\right),$$ (5)

where the superscript l denotes the l-th layer and e_ij is the attention coefficient computed by an attention function Att to measure the relation between node i and node j. α_ij is the attention weight calculated by the softmax function. Equation (5) is a weighted summation that uses all α as weights followed with a nonlinear function f.

2.3. Related Works

Since GNNs have achieved remarkable results in practice, a clear understanding of the power of GNNs is needed to design better models. Recent works [Morris et al., 2019; Xu et al., 2019; Maron et al., 2019] focus on understanding the discriminative power of GNNs by comparing it to the Weisfeiler-Lehman (WL) test [Weisfeiler and Leman, 1968] when deciding the graph isomorphism. It is proved that the massage-passing-based GNNs are at most as powerful as the 1-WL test [Xu et al., 2019]. Inspired by the higher discriminative power of the k-WL test (k > 2) than the 1-WL test, GNNs with a theoretically higher discriminative power than the massage-passing ones have been proposed in [Morris et al., 2019; Maron et al., 2019]. However, the GNNs in those works do not specifically analyze the role of attention mechanism. So it is currently unknown whether the attention mechanism will constrain the discriminative power. Our work focuses on the massage-passing-based GNNs with attention mechanism, which are upper bounded by the 1-WL test.

Another recent work [Knyazev et al., 2019] aims to understand the attention mechanism over nodes in GNNs with experiments in a controlled environment. However, the attention mechanism discussed in the work is used in the pooling layer for the pooling of nodes, while our work investigates the usage of attention mechanism in the aggregation layer for the updating of nodes.

3. Limitation of Attention-Based GNNs

In this section, we theoretically analyze the discriminative power of attention-based GNNs and show their limitations. The discriminative power means how well an attention-based GNN can distinguish different elements (local or global structures). We find that previously proposed attention-based GNNs can fail in certain cases and the discriminative power is limited. Besides, by theoretically finding out all cases that always make an attention-based GNN fail, we reveal that those failures come from the lack of cardinality preservation in attention-based aggregators.

3.1. Discriminative Power of Attention-based GNNs

We assume the node input feature space is countable. For any attention-based GNNs, we give the conditions in Lemma 1 to make them reach the upper bound of discriminative power when distinguishing different elements (local or global structures). In particular, each local structure belongs to a node and is the k-height subtree structure rooted at the node, which is naturally captured in the node feature $h_i^k$ after k iterations in a GNN. The global structure contains the information of all such subtrees in a graph.

Lemma 1. Let $h_i^k$ be a GNN following the neighborhood aggregation scheme with the attention-based aggregator (Equation (5)). For global-level task, an extra readout function (Equation (2)) is used in the final layer $\mathcal{A}$ can reach its upper bound of discriminative power (can distinguish all distinct local structures or be as powerful as the 1-WL test when distinguishing distinct global structures) after sufficient iterations with the following conditions:

• Local-level: Function f and the weighted summation in Equation (5) are injective.

• Global-level: Besides the conditions for local-level, $\mathcal{A}$’s readout function (Equation (2)) is injective.

Proof. Local-level: For the aggregator in the first layer, it will map different 1-height subtree structures to different embeddings from the distinct input multisets of neighborhood node features, since it is injective. Iteratively, the aggregator in the l-th layer can distinguish different l-height subtree structures by mapping them to different embeddings from the distinct input multisets of (l-1)-height subtree features, since it is injective.

Global-level: From Lemma 2 and Theorem 3 in [Xu et al., 2019], we know: when all functions in $\mathcal{A}$ are injective, $\mathcal{A}$ can reach its upper bound of discriminative power, which is the same as the Weisfeiler-Lehman (WL) test [Weisfeiler and Leman, 1968] when deciding the graph isomorphism.

With Lemma 1, we are interested in whether its conditions can always be satisfied, so as to reach the upper bound of discriminative capacity of an attention-based GNN. Since the function f and the global-level readout function can be predetermined to be injective, we focus on the injectivity of the weighted summation function in attention-based aggregator.

3.2. Non-Injectivity of Attention-Based Aggregator

In this part, we aim to answer the following two questions:

Q 1. Can the attention-based GNNs actually reach the upper bound of discriminative power? In other words, can the weighted summation function in an attention-based aggregator be injective?

Q 2. If not, can we determine all of the cases that prevent any kind of weighted summation function being injective?

Given a countable feature space $\mathcal{H}$, a weighted summation function is a mapping $W:\mathcal{H}\to {ℝ}^n$. The exact W is determined by the attention weights α computed from Att in Equation (3). Since Att is affected by stochastic optimization algorithms (e.g. SGD) which introduce stochasticity in W, we have to pay attention that W is not fixed when dealing with the two questions.

In Theorem 1, we answer Q1 with No by giving the cases that make W not to be injective. So that the attention-based GNNs can never meet their upper bound of discriminative power, which is stated in Corollary 1. Moreover, we answer Q2 with Yes in Theorem 1 by pointing out those cases are the only reason to always prevent W being injective. This alleviates the difficulty of summarizing the properties of those cases. Besides, we can specifically propose methods to avoid those cases so as to let W to be injective.

Theorem 1. Assume the input feature space χ is countable. Given a multiset X ⊂ χ and the node feature c of the central node, the weighted summation function h(c, X) in aggregation is defined as h(c, X) = Σ_x∈X α_cxf(x), where $f:\mathcal{X}\to {ℝ}^n$ is a mapping of input feature vector and α_cx is the attention weight between f(c) and f(x) calculated by the attention function Att in Equation (3) and the softmax function in Equation (4). For all f and Att, h(c₁, X₁) = h(c₂, X₂) if and only if c₁ = c₂, X₁ = (S, μ) and X₂ = (S, k · μ) for $k\in \mathbb{N}*$. In other words, h will map different multisets to the same embedding iff the multisets have the same central node feature and the same distribution of node features.

Proof. (Sketch) We prove Theorem 1 in both two directions:

1. If given c₁ = c₂, X₁ = (S, μ) and X₂ = (S, k · μ), we can derive h(c₁, X₁) = h(c₂, X₂) using the formula of the weighted summation function.

2. If given h(c₁, X₁) = h(c₂, X₂) for all f, Att, we denote the multisets X₁ = (S₁, μ₁) and X₂ = (S₂, μ₂). We prove by contradiction that if S₁ ≠ S₂ or c₁ ≠ c₂, the equation h(c₁, X₁) = h(c₂, X₂) for all f, Att is not always true. Thus we have S₁ = S₂ and c₁ = c₂. Then we can derive X₁ = (S, μ) and X₂ = (S, k · μ).

Corollary 1. Let $\mathcal{A}$ be the GNN defined in Lemma 1. $\mathcal{A}$ never reaches its upper bound of discriminative power:

There exists two different subtrees S₁ and S₂ or two graphs G₁ and G₂ that the Weisfeiler-Lehman test decides as non-isomorphic, such that $\mathcal{A}$ always maps the two subtrees/graphs to the same embeddings.

Proof. We provide the cases when $\mathcal{A}$ always maps two subtrees/graphs to the same embeddings:

1. For subtrees, S₁ and S₂ are 1-height subtrees that have the same root node and the same distribution of node features.

2. For graphs, let G₁ be a fully connect graph with n nodes and G₂ be a ring-like graph with n nodes. All nodes in G₁ and G₂ have the same feature x.

We denote {X_i}, i ∈ G₁ as the set of multisets for aggregation in G₁ and {X_i}, j ∈ G₂ as the set of multisets for aggregation in G₂. As G₁ is a fully connect graph, all multisets in G₁ contain 1 central node and n − 1 neighbors. As G₂ is a ring-like graph, all multisets in G₂ contain 1 central node and 2 neighbors. Thus we have

$$X_i=\left(\left\{x\right\},\left\{{\mu }_1(x)=n\right\}\right),\forall i\in G_1,$$

$$X_j=\left(\left\{x\right\},\left\{{\mu }_2(x)=3\right\}\right),\forall j\in G_2,$$

where μ_i(x) is the multiplicity function of the node with feature x in G_i, i ∈ {1, 2}.

From Theorem 1, we know that h(c, X_i) = h(c, X_j), ∀i ∈ G₁, ∀j ∈ G₂. Considering Equation (5), we have $h_i^l=h_i^l,\forall i\in G_1,\forall j\in G_2$ in each iteration l. Besides, as the number of nodes in G₁ and G₂ is equal to n, $\mathcal{A}$ will always map G₁ and G₂ to the same set of multisets of node features {h^l}in each iteration l and finally get the same embedding for the whole graph.

3.3. Only Unpreserved Cardinality Guarantees the Non-Injectivity

With Theorem 1, we are now interested in the properties of all cases that guarantee the non-injectivity of the weighted summation functions W. Since the multisets that all W fail to distinguish share the same distribution of node features, we can say that W ignores the multiplicity information of each identical element in the multisets:

Corollary 2. Let $\mathcal{W}$ be the weighted summation function in any attention-based GNN. $\mathcal{W}$ cannot preserve the cardinality information of the multiset of node features. The lost of cardinality information in $\mathcal{W}$ is the only reason that prevents $\mathcal{W}$ to be injective.

In the next section, we aim to propose improved attention-based models to preserve the cardinality in aggregation.

4. Cardinality Preserved Attention Model

Since the attention-based aggregators do not preserve the cardinality of the multiset, our goal is to propose modifications to any kind of attention mechanism to capture the cardinality information. So that all of the cases that always prevent attention-based aggregator being injective can be avoided.

To achieve our goal, we modify the weighted summation function in Equation (5) to incorporate the cardinality information and do not change the attention function in Equation (3) so as to keep its original expressive power. Two different models named as Additive and Scaled are proposed to modify the Original model in Equation (5):

Model 1. (Additive)

$$h_i^l=f^l\left({\sum }_{j\in \tilde{\mathcal{N}}(i)}{\alpha }_{ij}^{l-1}{h}_j^{l-1}+w^l\odot {\sum }_{j\in \tilde{\mathcal{N}}(i)}{h}_j^{l-1}\right),$$ (6)

Model 2. (Scaled)

$$h_i^l=f^l\left({\psi }^l(|\tilde{\mathcal{N}}(i)|)\odot {\sum }_{j\in \tilde{\mathcal{N}}(i)}{\alpha }_{ij}^{l-1}{h}_j^{l-1}\right),$$ (7)

where w is a non-zero vector $\in {ℝ}^n$, ⊙ denotes the elementwise multiplication, $|\tilde{\mathcal{N}}(i)|$ equals to the cardinality of the multiset $\tilde{\mathcal{N}}(i),\psi :{\mathbb{Z}}^{+}\to {ℝ}^n$ is an injective function that maps the cardinality value to a non-zero vector.

In the Additive model, each element in the multiset will contribute to the term that we added to implicitly preserve the cardinality information. In the Scaled model, the original weighted summation is directly multiplied by a representational vector of the cardinality value. So with these models, distinct multisets with the same distribution will result in different embedding h. Note that both of our models do not change the Att function, such that they can keep the learning power of the original attention mechanism. We summarize the effect of our models in Corollary 3 and illustrate it in Figure 1.

Figure 1:

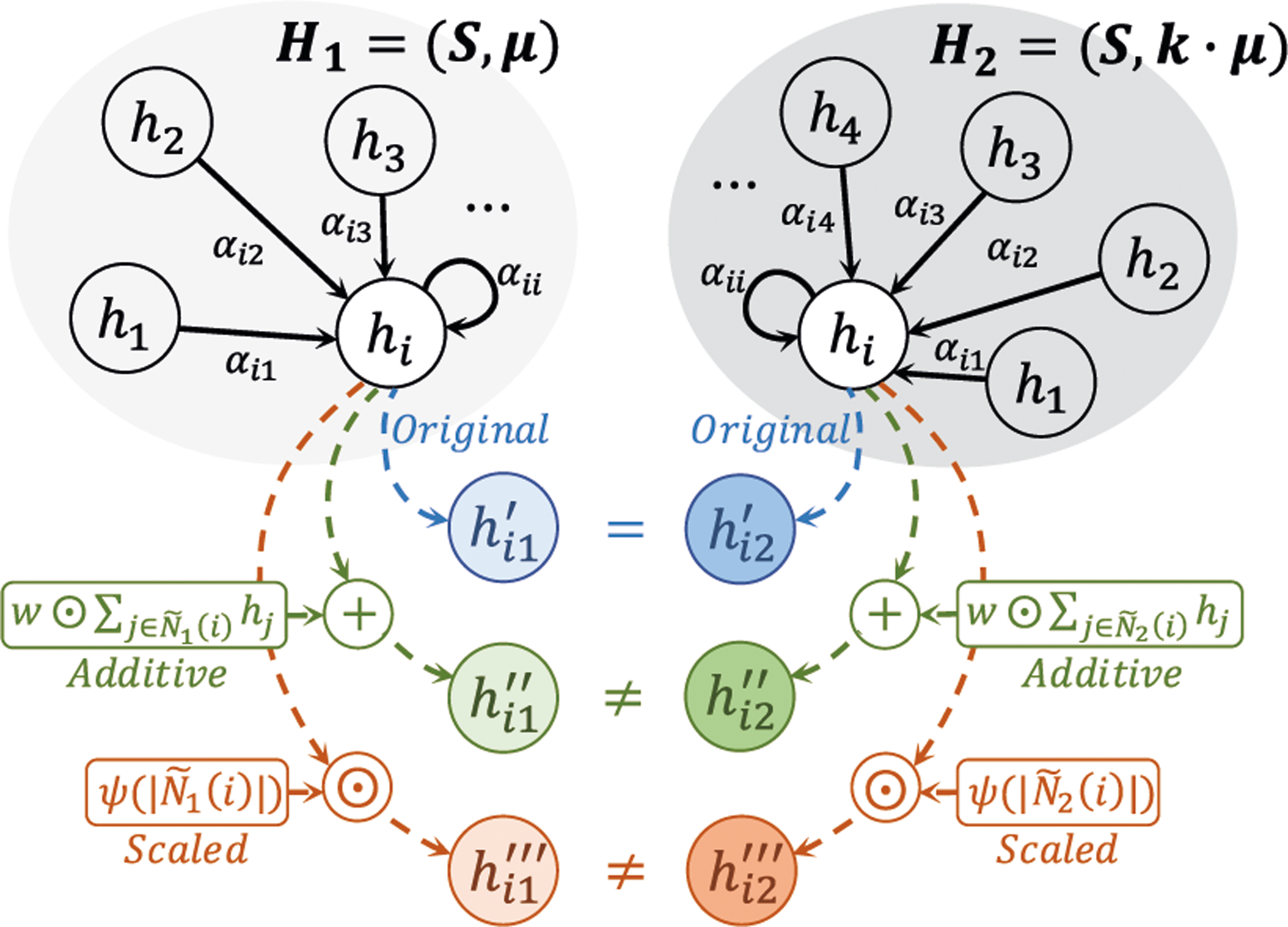
An illustration of different attention-based aggregators on multiset of node features. Given two distinct multisets H₁ and H₂ that have the same central node feature h_i and the same distribution of node features, aggregators will map h_i to h_i1 and h_i2 for H₁ and H₂. The Original model will get $h_{i1}^{\prime }=h_{i2}^{\prime }$ and fail to distinguish H₁ and H₂, while our Additive and Scaled models can always distinguish H₁ and H₂ with $h_{i1}^{\prime \prime }\ne h_{i2}^{\prime \prime }$ and $h_{i1}^{\prime \prime \prime }\ne h_{i2}^{\prime \prime \prime }$.

Corollary 3. Let $\mathcal{T}$ be the original attention-based aggregator in Equation (5) that operates on a multiset $H\subset \mathcal{H}$, where $\mathcal{H}$ is a node feature space mapped from the countable input feature space χ. There exists a $\mathcal{H}$ so that with our proposed Cardinality Preserved Attention (CPA) models in Equation (6) and (7), $\mathcal{T}$ can now distinguish all different multisets in aggregation that it previously always fails to distinguish.

Proof. According to Theorem 1, for any two distinct multisets H₁ and H₂ that $\mathcal{T}$ previously always fail to distinguish (h(c, H₁) = h(c, H₂)), we know H₁ = (S, μ) and $H_2=(S,k\cdot \mu )\subset \mathcal{H}$ for some $k\in \mathbb{N}*$. H₁ and H₂ have the same central node feature c ∈ S in aggregation. We denote $M={\sum }_{h\in H_1}{\alpha }_{ch1}h={\sum }_{h\in H_2}{\alpha }_{ch2}h$, where α_chi is the attention weight that belongs to H_i, and between c and h, h ∈ H_i, i ∈ {1, 2}After applying CPA models, the aggregations in $\mathcal{T}$ can be rewritten as

$$\text{Model\hspace{0.17em}1:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{h}_1\left(c,H_i\right)=M+w\odot {\sum }_{h\in H_i}h,i\in \left\{1,2\right\},$$

$$\text{Model\hspace{0.17em}2:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{h}_2\left(c,H_i\right)=\psi \left(|H_i|\right)\odot M,i\in \left\{1,2\right\}.$$

To prove the existence of $\mathcal{H}$, $\mathcal{H}$ can be defined as following: All h are vectors with positive values.

For Model 1, we have $h_1\left(c,H_1\right)-h_1\left(c,H_2\right)=w\odot \left({\sum }_{h\in H_1}h-{\sum }_{h\in H_2}h\right)$. Since $k\cdot {\sum }_{h\in H_1}h={\sum }_{h\in H_2}h\ne 0,$, we know ${\sum }_{h\in H_1}h-{\sum }_{h\in H_2}h\ne 0,$. Considering w is a non-zero vector, we have h₁(c, H₁) ≠ h₁(c, H₂).

For Model 2, we have h₂(c, H₁)−h₂(c, H₂) = (ψ(∣H₁∣) − ψ(∣H₂∣)) ⊙ M. As α_ch > 0 due to the softmax function, and h ≠ 0 in our definition, we know M ≠ 0 since ψ(∣H₁∣) − ψ(∣H₂∣) ≠ 0, we can get h₂(c, H₁) ≠ h₂(c, H₂).

In conclusion, our CPA models can help $\mathcal{T}$ to distinguish different multisets in aggregation, which it previously always fails to distinguish.

While the original attention-based aggregator is never injective as we mentioned in previous sections, our cardinality preserved attention-based aggregator can be injective with certain learned attention weights to reach its upper bound of discriminative power as stated in Lemma 1. We validate this in our experiments.

For the efficiency of our CPA models compared with the original attention-based aggregator, it is possible that the Model 1 and 2 require more parameters than the original one when our introduced w and $\psi (|\tilde{\mathcal{N}}(i)|)$ are learnable during the training. Thus we further simplify our models by fixing the values in w and $\psi (|\tilde{\mathcal{N}}(i)|)$ and define two CPA variants:

Model 3. (f-Additive)

$$h_i^l=f^l\left({\sum }_{j\in \tilde{\mathcal{N}}(i)}\left({\alpha }_{ij}^{l-1}+1\right)h_j^{l-1}\right),$$ (8)

Model 4. (f-Scaled)

$$h_i^l=f^l\left(|\tilde{\mathcal{N}}(i)|\cdot {\sum }_{j\in \tilde{\mathcal{N}}(i)}{\alpha }_{ij}^{l-1}{h}_j^{l-1}\right).$$ (9)

Model 3 and 4 still preserve the cardinality information while require the same number of parameters as the original model in Equation (5). In practice, we find that the simplified models exhibit similar performance compared with Model 1 and 2 as shown in the experiments.

5. Experiments

In our experiments, we focus on the following questions:

Q 3. Since attention-based GNNs (e.g. GAT) are originally proposed for local-level tasks like node classification, will those models fail or not meet the upper bound of discriminative power when solving certain node classification tasks? If so, can our CPA models improve the original model?

Q 4. For global-level tasks like graph classification, how well can the original attention-based GNNs perform? Can our CPA models improve the original model?

Q 5. How the attention-based GNNs with our CPA models perform compared to baselines?

To answer Question 3, we design a node classification task which is to predict whether or not a node is included in a triangle as one vertex in a graph. To answer Question 4 and 5, we perform experiments on graph classification benchmarks and evaluate the attention-based GNNs with CPA models.

5.1. Experimental Setup

Datasets

In our synthetic task (TRIANGLE-NODE) for predicting whether or not a node is included in a triangle, we generate a graph with 4800 nodes and 32400 edges. 40.58% of the nodes are included in triangles as vertices while 59.42% are not. There are 4000 nodes assigned with feature ‘0’, 400 with feature ‘1’ and 400 with feature ‘2’. The label of each node for prediction is whether or not it is included in a triangle.

In our experiment on graph classification, we use 6 benchmark datasets collected by [Kersting et al., 2020]: 2 social network datasets (REDDIT-BINARY (RE-B), REDDIT-MULTI5K (RE-M5K)) and 4 bioinformatics datasets (MUTAG, PROTEINS, ENZYMES, NCI1).

In all datasets, if the original node features are provided, we use the one-hot encodings of them as input.

Models and Configurations

In our experiments, the Original model is the one that uses the original version of an attention mechanism. We apply each of our 4 CPA models (Additive, Scaled, f-Additive and f-Scaled) to the original attention mechanism for comparison. In the Additive and Scaled models, we take advantage of the approximation capability of multi-layer perceptron (MLP) [Hornik et al., 1989] to model f and ψ. All MLPs have 2 layers with Batch normalization [Ioffe and Szegedy, 2015] and ReLU activation.

For node classification, we use GAT [Veličković et al., 2018] as the Original model. In the GAT variants, we use 2 GNN layers and a hidden dimensionality of 32. The negative input slope of LeakyReLU in the GAT attention mechanism is 0.2. The number of heads in multi-head attention is 1. We use a dropout ratio of 0 and a weight decay value of 0.

For graph classification, we build a GNN (GAT-GC) based on GAT as the Original model: We adopt the attention mechanism in GAT to specify the form of Equation (3). For the readout function, a naive way is to only consider the node embeddings from the last iteration. Although a sufficient number of iterations can help to avoid the cases in Theorem 1 by aggregating more diverse node features, the features from the latter iterations may generalize worse and the GNNs usually have shallow structures [Xu et al., 2019; Zhou et al., 2018]. So the GAT-GC adopts the same function as used in [Xu et al., 2018; Xu et al., 2019; Li et al., 2019], which concatenates graph embeddings from all iterations: $h_G={\Vert }_{k=0}^L\left(\text{Readout}\left(\left\{h_i^k\mid i\in G\right\}\right)\right)$. For the Readout function, we use sum for bioinformatics datasets and mean for social network datasets. In the GAT-GC variants, we use 4 GNN layers. The hidden dimensionality is 32 for bioinformatics datasets and 64 for social network datasets. The negative input slope of LeakyReLU is 0.2. We use a single head in the multi-head attention. The following hyper-parameters are tuned for each dataset: (1) Batch size in {32, 128}; (2) Dropout ratio in f0; 0:5g after dense layer; (3) L₂ regularization from 0 to 0:001.

For all experiments, we perform 10-fold cross-validation and repeat the experiments 10 times for each dataset and each model. Following [Xu et al., 2019], to get a final accuracy for each run, we select the epoch with the best cross-validation accuracy averaged over all 10 folds. The results are reported based on the results averaged across all runs. All models are trained using the Adam optimizer [Kingma and Ba, 2018] and the learning rate is dropped by a factor of 0.5 every 400 epochs for node classifications and every 50 epochs for graph classifications. We use an initial learning rate of 0.01 for the TRIANGLE-NODE and bioinformatics datasets and 0.0025 for the social network datasets. On each dataset, we use the same hyper-parameter configurations in all model variants for a fair comparison.

5.2. Node Classification

For the TRIANGLE-NODE dataset, the proportion P of multisets that hold the properties in Theorem 1 is 29.2%, as shown in Table 1. The classification accuracy of the Original model (GAT) is significantly lower than the CPA models. It supports the claim in Corollary 1: the Original model fails to distinguish all distinct multisets in the dataset and exhibits constrained discriminate power. On the contrary, CPA models can distinguish all different multisets in the graph as suggested in Corollary 3 and indeed significantly improve the accuracy of the Original model as shown in Table 1. This experiment thus well answers Question 3 that we raised.

Table 1:

Testing accuracies (%) of the original GAT and the GAT applied with each of our 4 CPA models on TRIANGLE-NODE dataset for node classification. We highlight the result of the best performed model. The proportion P of multisets that hold the properties in Theorem 1 among all multisets is also reported.

Dataset P(%)	TRIANGLE-NODE 29.2
Original	78.40 ± 7.65
Additive	91.31 ± 1.19
Scaled	91.38 ± 1.23
f-Additive	91.18 ± 1.24
f-Scaled	91.36 ± 1.26

5.3. Graph Classification

Here we aim to answer Question 4 by evaluating the performance of GAT-based GNN (GAT-GC) variants on graph classification benchmarks. Besides, we compare our best-performing CPA model with baselines to answer Question 5.

Social Network Datasets

All graphs in the RE-B and RE-M5K datasets are the graphs stated in Corollary 1 that all attention-based GNNs fail to distinguish: Since those datasets do not contain original node features and we assign all the node features to be the same, we have P = 100.0% in those datasets. Thus all multisets in aggregation will be mapped to the same embedding by the Original GAT-GC. After a mean readout function on all multisets, all graphs are finally mapped to the same embedding. The performance of the Original model is just random guessing of the graph labels as reported in Table 2. While our CPA models can distinguish all different multisets and are confirmed to be significantly better than the Original one.

Table 2:

Testing accuracies (%) of GAT-GC variants (the original one and the ones applied with each of our 4 CPA models) on social network datasets. We highlight the result of the best performed model per dataset. The proportion P of multisets that hold the properties in Theorem 1 among all multisets is also reported.

Datasets P(%)	RE-B 100.0	RE-M5K 100.0
Original	50.00 ± 0.00	20.00 ± 0.00
Additive	93.07 ± 1.82	57.39 ± 2.09
Scaled	92.36 ± 2.27	56.76 ± 2.26
f-Additive	93.05 ± 1.87	56.43 ± 2.38
f-Scaled	92.57 ± 2.06	57.22 ± 2.20

Here we examine a naive approach to incorporate the cardinality information in the Original model by assigning node degrees as input node labels. By doing this way, the node features are diverse and we get P = 0.0%, which means that the cases in Theorem 1 can be all avoided. However, the testing accuracies of Original can only reach 76.65 ± 9.87% on RE-B and 43.71 ± 9.05% on RE-M5K, which are significantly lower than the results of CPA models in Table 2. Thus in practice, our proposed models exhibit good generalization power comparing to the naive approach.

Bioinformatics Datasets

For bioinformatics datasets that contain diverse node labels, we also report the P values in Table 3. The results reveal the existence (P ≥ 29.3%) of the cases in those datasets that can fool the Original model, thus the discriminative power of the Original model is theoretically constrained.

Table 3:

Testing accuracies (%) of GAT-GC variants (the original one and the ones applied with each of our 4 CPA models) on bioinformatics datasets. We highlight the result of the best performed model per dataset. The highlighted results are significantly higher than those from the corresponding Original model under paired t-test at significance level 5%. The proportion P of multisets that hold the properties in Theorem 1 among all multisets is also reported.

Datasets P(%)	MUTAG 56.9	PROTEINS 29.3	ENZYMES 29.4	NCI1 43.3
Original	84.96 ± 7.65	75.64 ± 3.96	58.08 ± 6.82	80.29 ± 1.89
Additive	89.75 ± 6.39	76.61 ± 3.80	58.90 ± 6.96	81.92 ± 1.89
Scaled	89.65 ± 7.47	76.44 ± 3.77	58.35 ± 6.97	82.18 ± 1.67
f-Additive	90.34 ± 6.05	76.60 ± 3.91	59.80 ± 6.18	81.96 ±2.01
f-Scaled	90.44 ± 6.44	76.81 ± 3.77	58.45 ± 6.35	82.28 ± 1.81

To empirically validate this, we compare the training accuracies of GAT-GC variants, since the discriminative power can be directly indicated by the accuracies on training sets. Higher training accuracy indicates a better fitting ability to distinguish different graphs. The training curves of GAT-GC variants are shown in Figure 2. From these curves, we can see even though the Original model has overfitted different datasets, the fitting accuracies that it converges to can never be higher than those of our CPA models. Compared to the WL kernel, CPA models can get training accuracies close to 100% on several datasets, which are comparable with the WL kernel (equal to 100% as shown in [Xu et al., 2019]). These findings validate that the discriminative power of the Original model is limited while our CPA models can approach the upper bound with certain learned weights.

Figure 2:

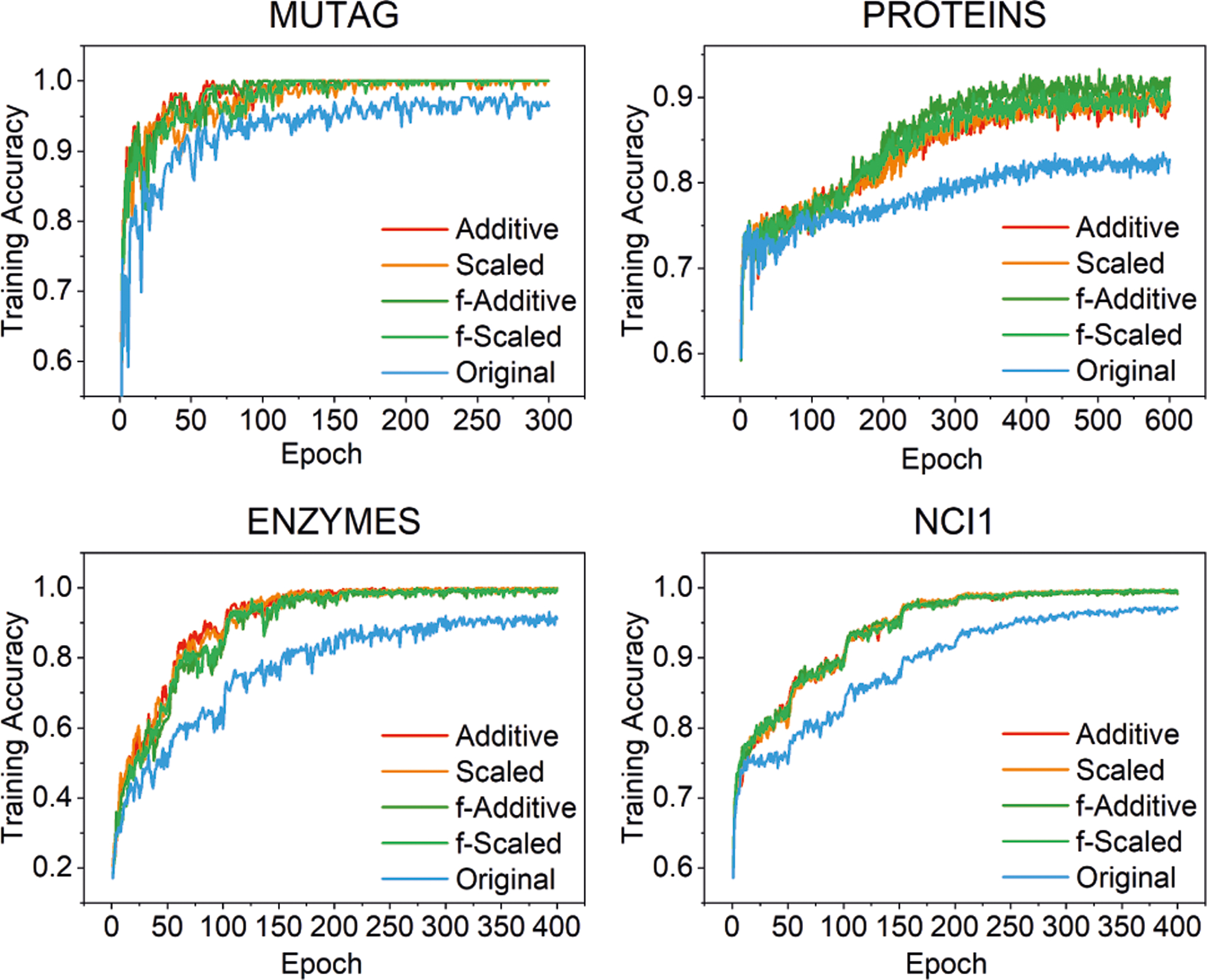
Training curves of GAT-GC variants on bioinfo datasets.

For the performance on testing sets, the testing curves exhibit similar patterns as those shown in Figure 2. The testing accuracies of GAT-GC variants on bioinformatics datasets are reported in Table 3. From those results, we find our proposed CPA models can further improve the testing accuracies of the Original model on all datasets. This indicates that the preservation of cardinality can also benefit the generalization power of the model besides the discriminative power.

Comparison to Baselines

From the previous results in Table 2 and 3, we find the f-Scaled model has the highest average testing accuracy on all datasets. Thus the f-Scaled model is chosen as the best-performing GAT-GC variant to be compared with other baselines. Note that all 4 models (Additive, Scaled, f-Additive and f-Scaled) exhibit very small differences in performance, and fail to be distinguished by paired t-test at significance level 5% on all datasets. The similar performance of the fixed-weight models (f-Additive and f-Scaled) comparing to the full models (Additive and Scaled) demonstrates that the improvements achieved by CPA models are not simply due to the increased capacities given by the additional parameters used in the full models. The preservation of cardinality information in CPA models is the key to the improvements.

We then compare our GAT-GC (f-Scaled) model with several state-of-the-art baselines: WL kernel (WL) [Shervashidze et al., 2011], PATCHY-SAN (PSCN) [Niepert et al., 2016], Deep Graph CNN (DGCNN) [Zhang et al., 2018], Graph Isomorphism Network (GIN) [Xu et al., 2019] and Capsule Graph Neural Network (CapsGNN) [Xinyi and Chen, 2019]. For the baselines, we use the results reported in their original works. If results are not available, we use the best testing results reported in [Xinyi and Chen, 2019; Ivanov and Burnaev, 2018].

In Table 4, the results show that our GAT-GC (f-Scaled) model achieves 4 top 1 and 2 top 2 on all 6 datasets. It should be noted that our model is general enough to adopt any kind of attention mechanism, it is expected that even better performance can be achieved with certain choice of attention mechanism besides the one used in GAT.

Table 4:

Testing accuracies (%) for graph classification. We highlight the result of the best performed model for each dataset. Our GAT-GC (f-Scaled) model achieves the top 2 on all 6 datasets.

	Datasets	MUTAG	PROTEINS	ENZYMES	NCI1	RE-B	RE-M5K
Baselines	WL	82.05 ± 0.36	74.68 ± 0.49	52.22 ± 1.26	82.19 ±0.18	81.10 ± 1.90	49.44 ± 2.36
	PSCN	88.95 ± 4.37	75.00 ±2.51	-	76.34 ± 1.68	86.30 ±1.58	49.10 ±0.70
	DGCNN	85.83 ± 1.66	75.54 ± 0.94	51.00 ±7.29	74.44 ± 0.47	76.02 ± 1.73	48.70 ± 4.54
	GIN	89.40 ± 5.60	76.20 ± 2.80	-	82.70 ± 1.70	92.40 ± 2.50	57.50 ± 1.50
	CapsGNN	86.67 ± 6.88	76.28 ± 3.63	54.67 ± 5.67	78.35 ± 1.55	-	52.88 ± 1.48
	GAT-GC (f-Scaled)	90.44 ± 6.44	76.81 ± 3.77	58.45 ± 6.35	82.28 ± 1.81	92.57 ± 2.06	57.22 ± 2.20

6. Conclusion

In this paper, we theoretically analyze the representational power of GNNs with attention-based aggregators: We determine all cases when those GNNs always fail to distinguish distinct structures. The finding shows that the missing cardinality information in aggregation is the only reason to cause those failures. To improve, we propose cardinality preserved attention (CPA) models to solve this issue. In our experiments, we validate our theoretical analysis that the performances of the original attention-based GNNs are limited. With our models, the original models can be improved. Compared to other baselines, our best-performing model achieves competitive performance. In future work, a challenging problem is to better learn the attention weights so as to guarantee the injectivity of our cardinality preserved attention models after the training. Besides, it would be interesting to analyze different attention mechanisms.