On High-Dimensional Constrained Maximum Likelihood Inference

Abstract

Inference in a high-dimensional situation may involve regularization of a certain form to treat overparameterization, imposing challenges to inference. The common practice of inference uses either a regularized model, as in inference after model selection, or bias-reduction known as “debias.” While the first ignores statistical uncertainty inherent in regularization, the second reduces the bias inbred in regularization at the expense of increased variance. In this article, we propose a constrained maximum likelihood method for hypothesis testing involving unspecific nuisance parameters, with a focus of alleviating the impact of regularization on inference. Particularly, for general composite hypotheses, we unregularize hypothesized parameters whereas regularizing nuisance parameters through a L₀-constraint controlling the degree of sparseness. This approach is analogous to semiparametric likelihood inference in a high-dimensional situation. On this ground, for the Gaussian graphical model and linear regression, we derive conditions under which the asymptotic distribution of the constrained likelihood ratio is established, permitting parameter dimension increasing with the sample size. Interestingly, the corresponding limiting distribution is the chi-square or normal, depending on if the co-dimension of a test is finite or increases with the sample size, leading to asymptotic similar tests. This goes beyond the classical Wilks phenomenon. Numerically, we demonstrate that the proposed method performs well against it competitors in various scenarios. Finally, we apply the proposed method to infer linkages in brain network analysis based on MRI data, to contrast Alzheimer’s disease patients against healthy subjects. Supplementary materials for this article are available online.

1. Introduction

High-dimensional analysis has become increasingly important in modern statistics, where a model’s size may greatly exceed the sample size. For instance, in studying the brain activity, a brain network is often examined, which consists of structurally and functionally interconnected regions at many scales. At the macroscopic level, networks can be studied noninvasively in healthy and disease subjects with functional MRI (fMRI) and other modalities such as MEG and EEG. In such a situation, inferring the structure of a network becomes critically important, which is one kind of high-dimensional inference. Yet, high-dimensional inference remains largely under-studied. In this article, we develop a full likelihood inferential method, particularly for a Gaussian graphical model and high-dimensional linear regression.

In the literature, a great deal of effort has been devoted to estimation. For the linear model, many methods focus on estimation with sparsity-inducing convex and nonconvex regularization such as Lasso, SCAD, MCP, and TLP (Tibshirani 1996; Fan and Li 2001; Zhang 2010; Shen, Pan, and Zhu 2012), among others. For the Gaussian graphical model, methods include the regularized likelihood approach (Rothman et al. 2008; Friedman, Hastie, and Tibshirani 2008; Yuan and Lin 2007; Fan, Feng, and Wu 2009; Shen, Pan, and Zhu 2012) and the nodewise regression approach (Meinshausen and Bühlmann 2006), and their extensions, such as conditional Gaussian graphical (Li, Chun, and Zhao 2012; Yin and Li 2013) and multiple Gaussian graphical models (Zhu, Shen, and Pan 2014; Lin et al. 2017). Despite progress, there is a paucity of inferential methods for high-dimensional models, although some have been recently proposed in Zhang and Zhang (2014), Van de Geer et al. (2014), Javanmard and Montanari (2014), and Janková and Van de Geer (2017), where CI are constructed based on a bias-reduction method called “debias” (Zhang and Zhang 2014). One potential issue of this kind of approach is not asymptotically similar with its null distribution depending on unknown nuisance parameters to be estimated, and most critically the variance is likely to increase after debias, resulting in an increased length of a CI.

In this article, we propose a maximum likelihood method subject to certain constraints for hypothesis testing involving unspecific nuisance parameters, referred to as the constrained maximum likelihood ratio (CMLR) test, which regularizes the degree of sparsity of un-hypothesized parameters in a high-dimensional model, whereas hypothesized parameters are not regularized. This is an analogy of semiparametric inference with respect to the parametric component, which enables to alleviate the inherited bias problem due to regularization. For computation, we employ a surrogate of the L₀-function, a truncated L₁-function, for the constraints. On this ground, we develop the CMLR test, which is asymptotically similar with its null distribution independent of unspecific nuisance parameters. Moreover, we derive the asymptotic distributions of the test in the presence of growing parameter dimensions for the Gaussian graphical model and linear model. Most importantly, the corresponding distribution for the CMLR test statistic converges to the chis-quare distribution when the co-dimension, or the difference in dimensionality between the full and null spaces, is finite, and converges to normal (after proper centering and scaling) when the co-dimension tends to infinity. This occurs in a situation roughly when $\frac{(\left|A^0\right|+|B|)\log p}{n^{1/2}}\to 0$ and $\frac{\sqrt{|B|}(\left|A^0\right|+|B|)}{n}\to 0$, respectively, in the Gaussian graphical model and linear regression, where |B| and |A⁰| are the numbers of the hypothesized parameters and the nonzero unhypothesized parameters. Such a critical assumption is in contrast to a requirement of $\frac{\log p}{n}\to 0$ for sparse feature selection Shen et al. (2013), which has been used in Portnoy (1988) for the maximum likelihood estimation in a different context. Empirically, the asymptotic approximation becomes inadequate when departure from this assumption occurs in a less sparse situation. To our knowledge, our result is the first of this kind, providing a multivariate likelihood test in the presence of high-dimensional nuisance parameters. This is in contrast to a univariate debias test Zhang and Zhang (2014), Van de Geer et al. (2014), Javanmard and Montanari (2014), and Janková and Van de Geer (2017). When specializing the CMLR test to a single parameter in the Gaussian graphical model and linear regression, we show that it has asymptotic power, that is, no less than that of the debias test; see, Theorem 3. This is anticipated since the debias test does not capture all the information contained in the likelihood, whereas the full likelihood takes into account component to component dependencies. This aspect is illustrated by our second numerical example in which a null hypothesis involves a row (column) of offdiagonals of the precision matrix. Of course, a multivariate likelihood test as ours may require stronger conditions than a univariate non-likelihood test, which is analogous to the classical situation of the maximum likelihood versus the method of moments in inference. Throughout this article, we shall focus our attention to the CMLR test as opposed to the corresponding Wald test based on the constrained maximum likelihood, which not asymptotically similar, given that it is rather challenging to invert a high-dimensional Fisher information matrix.

Computationally, we relax the nonconvex minimization using an L₀-surrogate function by solving a sequence of convex relaxations as in Shen, Pan, and Zhu (2012). For each convex relaxation, we employ the alternating direction method of multipliers algorithm Boyd et al. (2011), permitting a treatment of problems of medium to large size. Moreover, we study the operating characteristics of the proposed inference method and compare against the debias methods through numerical examples. In simulations, we demonstrate that the proposed method performs well under various scenarios, and compares favorably against its competitors. Finally, we apply the proposed method to confirm that a reduced level of connectivity is observed in certain brain regions in the default mode network (DMN) but an increased level in others for Alzheimer’s disease (AD) patients as compared to healthy subjects.

The rest of the article is organized as follows. Section 2 proposes a constrained likelihood ratio test, and gives specific conditions under which the asymptotic approximation of the sampling distribution of the test is valid for the Gaussian graphical model and linear regression. Section 3 performs the power analysis for the CMLR test. Section 4 discusses computational strategies for the proposed test. Section 5 performs numerical studies, followed by an application of the tests to detect the structural changes in brain network analysis for AD subjects versus healthy subjects in Section 6. Section 7 is devoted to technical proofs.

2. Constrained Likelihood Ratios

Given an iid sample X₁,...,X_n from a probability distribution with density p_θ, consider a testing problem H₀ : θ_i = 0; i ∈ B versus H_a : θ_i ≠ 0 for some i ∈ B, with unspecific nuisance parameters θ_j for j ∈ B^c, possibly high-dimensional, where $\mathit{\theta }=\left({\theta }_1,\dots ,{\theta }_d\right)\in {ℝ}^d$, and B ⊆ {1,...,d}. Here, we allow the dimension of θ and size of |B| to grow as a function of the sample size n. For a problem of this type, we construct a constrained likelihood ratio with a sparsity constraint on nuisance parameters ${\theta }_{B^c}$. Specifically, define

$${\widehat{\mathit{\theta }}}^{(0)}=\underset{\mathit{\theta }}{\arg \max }{L}_n(\mathit{\theta })\text{subj to:}\sum _{i\notin B}{p}_{\tau }\left(\left|{\theta }_i\right|\right)\le K\text{and}{\mathit{\theta }}_B=0$$ (1)

$${\widehat{\mathit{\theta }}}^{(1)}=\underset{\mathit{\theta }}{\arg \max }{L}_n(\mathit{\theta })\text{subj to:}\sum _{i\notin B}{p}_{\tau }\left(\left|{\theta }_i\right|\right)\le K,$$ (2)

where $L_n(\mathit{\theta })={\sum }_{i=1}^n\log p_{\mathit{\theta }}\left(X_i\right)$ is the log-likelihood, p_τ(x) = min(x/τ, 1) is the truncated L₁-function Shen, Pan, and Zhu (2012) as a surrogate of the L₀-function, and (K, τ) are nonnegative tuning parameters. In this situation, without the sparsity constraint, ${\widehat{\mathit{\theta }}}^{(0)}$ and ${\widehat{\mathit{\theta }}}^{(1)}$ in (1) and (2) are exactly the maximum likelihood estimates under H₀ and H_a, respectively. Now, we define the constrained likelihood ratio as: ${\mathrm{\Lambda }}_n(B)=2\left(L_n\left({\widehat{\mathit{\theta }}}^{(1)}\right)-L_n\left({\widehat{\mathit{\theta }}}^{(0)}\right)\right)$. In what is to follow, we derive the asymptotic distribution of Λ_n(B) in a high-dimensional situation for the Gaussian graphical model and linear regression. On this ground, an asymptotically similar test is derived, whose null distribution is independent of nuisance parameters.

Tuning parameters K and τ in (1) and (2) are estimated using a cross-validation (CV) criterion based on the full model (1). Choosing the same values of (K, τ) in (1) and (2) ensures the nestedness property of Λ_n(B) ≥ 0 because the constrained set in (1) is a subset of that in (2). With K = ∞, the test statistic Λ_n(B) reduces to the classical likelihood ratio test statistic.

2.1. Asymptotic Distribution of Λ_n(B) in Graphical Models

This subsection is devoted to a Gaussian graphical model, where X₁,...,X_n follow from a p-dimensional normal distribution N(0, Ω⁻¹), with Ω a precision matrix, or the inverse of the covariance matrix ∑. In this case, θ = Ω. The log-likelihood is $L_n(\mathit{\theta })=L_n(\mathbf{\Omega })=\frac{n}{2}\log \det (\mathbf{\Omega })-\frac{n}{2}\mathrm{tr}(\mathbf{\Omega }\mathit{S})$, where $\mathit{S}=n^{-1}{\sum }_{i=1}^n{\mathit{X}}_i{\mathit{X}}_i^{\top }$ is the sample covariance matrix, and tr(·) denotes the trace of a matrix.

In the foregoing testing framework, the null and alternative hypotheses can be written as: H₀ : Ω_B = 0 versus H_a : Ω_B ≠ 0 for some prespecified index set B. Then the constrained log-likelihood ratio becomes ${\mathrm{\Lambda }}_n(B)=2(L_n({\widehat{\mathbf{\Omega }}}^{(1)})-L_n({\widehat{\mathbf{\Omega }}}^{(0)}))$, where ${\widehat{\mathbf{\Omega }}}^{(0)}$ and ${\widehat{\mathbf{\Omega }}}^{(1)}$ are the constrained maximum likelihood estimates (CMLE)s based on the null and full spaces of the test.

To establish the asymptotic distribution of Λ_n(B), we first introduce some notations to be used. For any symmetric matrix M, let λ_max(M) and λ_min(M) be the maximum and minimum eigenvalues of M, and ||M||_F be the Frobenius norm of M. Let \ and | · | denote the set difference and the size of a set. For any vector $\mathit{a}\in {ℝ}^m$, let $\Vert \mathit{a}{\Vert }_2=\sqrt{a_1^2+\cdots +a_m^2}$. Denote by ${\overline{\mathbf{\Omega }}}_{A\cup B}^0=\arg {\min }_{\mathbf{\Omega }\succ 0:{\mathbf{\Omega }}_{(A\cup B)}c=0}K\left({\mathbf{\Omega }}^0,\mathbf{\Omega }\right)$ an approximating point in a space $\{\mathbf{\Omega }:\mathbf{\Omega }\succ 0,{\mathbf{\Omega }}_{{(A\cup B)}^c}=0\}$ to the true Ω⁰, where $K({\mathbf{\Omega }}^0,\mathbf{\Omega })=\frac{1}{2}(\mathrm{tr}(\mathbf{\Omega }{\mathbf{\Sigma }}^0)+\log \frac{\det ({\mathbf{\Omega }}^0)}{\det (\mathbf{\Omega })}-p)$ is the Kullback–Leibler information. Let $\Vert {\mathbf{\Omega }}^0-\mathbf{\Omega }\Vert ={\Vert \sqrt{{\mathbf{\Sigma }}^0}\left(\mathbf{\Omega }-{\mathbf{\Omega }}^0\right)\sqrt{{\mathbf{\Sigma }}^0}\Vert }_F$ be the Fisher-norm between Ω⁰ and Ω Shen (1997). Moreover, let $A^0=\{i:{\theta }_i^0\ne 0\}$ be the support of true parameter θ⁰, κ₀ = λ_max(Ω⁰)/λ_min(Ω⁰) be the condition number of Ω⁰, and ${\kappa }_1=\frac{{\overline{\lambda }}^2{}_{\max }}{{\lambda }_{\min }^2({\mathbf{\Omega }}^0)}$, where ${\overline{\lambda }}_{\max }={\max }_{A:|A|\le \left|A^0\right|,A\cap B=\varnothing }{\lambda }_{\max }({\overline{\mathbf{\Omega }}}_{A\cup B}^0)$. Let ${\overline{\lambda }}_{\min }={\min }_{A:|A|\le \left|A^0\right|,A\cap B=\varnothing }{\lambda }_{\min }({\overline{\mathbf{\Omega }}}_{A\cup B}^0)$. Let ${\gamma }_{\min }={\min }_{(i,j)\in A^0}\left|{\omega }_{ij}^0\right|$ be the minimum nonzero offdiagonals of Ω⁰ representing the signal strength. The following technical conditions are made.

Assumption 1 (Degree of separation).

$$\begin{gathered} C_{\min }=\underset{A:A\ne A^0,\left|A\right|=\left|A^0\right|,A\cap B=\varnothing }{\min }\min \left(\frac{{\Vert {\mathbf{\Omega }}^0-{\overline{\mathbf{\Omega }}}_{A\cup B}^0\Vert }^2}{\left|A^0\backslash A\right|},1\right) \\ \ge C_1{\kappa }_1\frac{\left(\left|A^0\right|+\left|B\right|\right)\log p}{n}, \end{gathered}$$ (3)

where C₁ > 0 is a constant.

Assumption 1 requires that the degree of separation C_min exceeds a certain threshold level, roughly $\frac{(\left|A^0\right|+|B|)\log p}{n}$, which measures the level of difficulty of the task of removing zero components of the nuisance (un-hypothesized) parameters of Ω by the constrained likelihood with the L₀-constraint. To better understand (3) of Assumption 1, we consider a sufficient condition of (3) as follows:

Note that $\Vert {\mathbf{\Omega }}^0-{\overline{\mathbf{\Omega }}}_{A\cup B}^0\Vert \ge {\lambda }_{\min }\left({\mathbf{\Sigma }}^0\right){\Vert {\mathbf{\Omega }}^0-{\overline{\mathbf{\Omega }}}_{A\cup B}^0\Vert }_F\ge {\lambda }_{\max }^{-1}\left({\mathbf{\Omega }}^0\right){\gamma }_{\min }\sqrt{\left|A^0\backslash A\right|}$. Consequently, a simpler but stronger condition of (3) in terms of γ_min is

$$\min ({\gamma }_{\min },{\lambda }_{\max }({\mathbf{\Omega }}^0))\ge C_2{\kappa }_0{\overline{\lambda }}_{\max }\sqrt{\frac{(\left|A^0\right|+\left|B\right|)\log p}{n}}$$ (4)

for some constant C₂ > 0.

Assumption 2 (Dimension restriction for Λ_n(B).

Assume that

$$\frac{{\kappa }_0\left(\left|B\right|+\left|A^0\right|\right)\log p}{\sqrt{n}}\to 0,\text{as}n\to \infty .$$

Assumption 2 restricts the size p for an asymptotic approximation of the sampling distribution of the likelihood ratio tests, which is closely related to that in Portnoy (1988) for a different problem. Note that if |A⁰| = O(p) and |B| = O(p) then Assumption 2 roughly requires that $p\log p/\sqrt{n}\to 0$.

Theorem 1 gives the asymptotic distribution of ${\mathrm{\Lambda }}_n(B)$ when |B| is either fixed or grows with n, referred to as Wilks phenomenon and generalized Wilks phenomenon, respectively.

Theorem 1 (Asymptotic sampling distribution of Λ_n(B).

Under Assumptions 1–2, there exists optimal tuning parameters (K, τ) with K |A⁰| and $\tau \le \frac{{\overline{\lambda }}_{\min }\min (\sqrt{C_{\min }},C_{\min }^2)}{12\left|A^0\right|}$ such that under H₀

• (i)
  Wilks phenomenon: If ${\omega }_{ij}^0=0\text{for}(i,j)\in B$ with |B| fixed, then

  $${\mathrm{\Lambda }}_n(B)\stackrel{d}{\to }{\chi }_{\left|B\right|}^2\text{as}n\to \infty .$$
• (ii)
  Generalized Wilks phenomenon: If ${\omega }_{ij}^0=0\text{for}(i,j)\in B$ with |B| → ∞, then

  $${(2|B|)}^{-1/2}\left({\mathrm{\Lambda }}_n(B)-\left|B\right|\right)\stackrel{d}{\to }N(0,1)\text{as}n\to \infty .$$

Concerning Assumptions 1 and 2, we remark that the degree of separation assumption (3) or (4) is necessary for the result of Theorem 1. Without Assumption 1, the result may break down, as suggested by a counter example in Lemma 1 for a parallel condition—Assumption 3 in linear regression in Section 2.2. This is expected because when the constrained likelihood cannot be over-selection consistency when Assumption 1 breaks down in view of the result of Shen, Pan, and Zhu (2012). That means that any under-selected component yields a bias of order $\sqrt{\frac{\log p}{n}}$. As a result, the foregoing results are not generally expected to hold. Moreover, Assumption 2 is intended for joint inference of multiple parameters, for instance, testing zero offdiagonals of one row or column of Ω as in the second simulation example of Section 4. These assumptions, as we believe, are needed for multivariate tests based on a full likelihood although we have not proved so, which appear stronger than those required for a univariate debias test based on a pseudo likelihood Janková and Van de Geer (2017). This is primarily due to the full likelihood approach estimating component to component dependencies in lieu of a marginal approach without them, leading to higher efficiency when possible. This is evident from Corollary 1 that the CMLR gives more precise inference than the debias test under these conditions.

The result of Theorem 1 depends on the optimal tuning parameter K = K⁰ and τ, both of which are unknown in practice. Therefore, K is estimated by cross-validation through tuning, and the exact knowledge of the value K is not necessary, whereas τ is usually set to be a small number, say 10⁻², in practice.

2.2. Asymptotic Distribution of Λ_n(B) in Linear Regression

In linear regression, a random sample ${(Y_i,{\mathit{x}}_i)}_{i=1}^n$ follows

$$Y_i={\mathit{\beta }}^T{\mathit{x}}_i+{ϵ}_i;{ϵ}_i~N(0,{\sigma }^2);i=1,\dots ,n$$ (5)

where β = (β₁,..., β_p)^T and x_i = (x_i1,..., x_ip)^T are p-dimensional vectors of regression coefficients and predictors, and x_i is independent of random error ϵ_i. In (5), it is known priori that β is sparse in that ${\beta }_j=0,j\notin A^0$, and ${\beta }_j\ne 0,j\in A^0$, where $A^0\subseteq \{1,2,\dots ,p\}$.

In this case, θ = (β, σ). Our focus is to test H₀ : β_B = 0 versus H_a = β_B ≠ 0 for some index set B. The log-likelihood is $L_n(\mathit{\theta })=L_n(\mathit{\beta },\sigma )=-\frac{1}{2{\sigma }^2}\Vert Y-X\mathit{\beta }{\Vert }_2^2-n\log (\sqrt{2\pi }\sigma )$, and the constrained log-likelihood ratio is accordingly defined as ${\mathrm{\Lambda }}_n(B)=2(L_n({\widehat{\mathit{\beta }}}^{(1)},{\widehat{\sigma }}^{(1)})-L_n({\widehat{\mathit{\beta }}}^{(0)},{\widehat{\sigma }}^{(0)})),\text{where}{\widehat{\mathit{\beta }}}^{(0)}\text{and}{\widehat{\mathit{\beta }}}^{(1)}$ are the CMLE based on the null and full spaces of the test.

A parallel condition of Assumption 1 is made in Assumption 3.

Assumption 3 (Degree of separation condition, Shen et al. 2013).

$$\underset{A:\left|A\right|\le \left|A^0\right|\text{and}A\ne A^0}{\min }\underset{\mathit{\beta }}{\inf }\frac{{\Vert X{\mathit{\beta }}^0-X_{A\cup B}{\mathit{\beta }}_{A\cup B}\Vert }_2^2}{n\left|A^0\backslash A\right|}\ge C_0{\sigma }^2\frac{\log p}{n}$$ (6)

for some absolute constant C₀ that may depend on the design matrix X.

A parallel result of Theorem 1 is established for linear regression.

Theorem 2 (Sampling distribution of Λ_n(B).

Assume that $\frac{\sqrt{|B|}\left(\left|A^0\right|+|B|\right)}{n}\to 0$. Under Assumptions 3, there exists optimal tuning parameters (K, τ) with K = |A⁰| and $0<\tau \le \sigma \sqrt{\frac{6}{(n+2)p{\lambda }_{\max }\left(X^{\top }X\right)}}$ such that under H₀

• (i)
  Wilks phenomenon: If β_i = 0 for i ∈ B with |B| fixed, then

  $${\mathrm{\Lambda }}_n(B)\stackrel{d}{\to }{\chi }_{\left|B\right|}^2\text{as}n\to \infty .$$
• (ii)
  Generalized Wilks phenomenon: If β_i = 0 for i ∈ B with |B| → ∞, then

  $${(2|B|)}^{-1/2}\left({\mathrm{\Lambda }}_n(B)-\left|B\right|\right)\stackrel{d}{\to }N(0,1)\text{as}n\to \infty .$$

Note of worthy is that the requirement $\frac{\sqrt{|B|}\left(\left|A^0\right|+|B|\right)}{n}\to 0$ in linear regression appears weaker than that $\frac{\left(\left|A^0\right|+|B|\right)\log p}{n^{1/2}}\to 0$ in the Gaussian graphical model. This is primarily because the error for the likelihood ratio approximation in the former is smaller in magnitude.

Next we provide a counter example to show that the result in Theorem 2 breaks down when Assumption 3 is violated in the absence of a strong signal strength. In other words, such an assumption is necessary for such a full likelihood approach to gain the test efficiency, which is in contrast to a pseudo-likelihood approach.

Lemma 1 (A counter example).

In (5), we write y = β₀ + β^⊤ x, where x = (x₁,...,x_p) are independently distributed from N(μ_i, 1) with μ₁ = 0 and μ_j = 1; 2 ≤ j ≤ p, and ϵ is N(0, 1 − n−¹), independent of x. Assume that β₀ = 0 and β = (n^−1/2, 0,...,0), or, y = n^−1/2x₁ + ϵ. Then Assumption 3 is violated. Now consider a hypothesis test of H₀ : β₀ = 0 versus $H_1:{\beta }_0\ne 0.\text{If}\frac{\log p}{n}\to 0$ as n, p → ∞, then ${\mathrm{\Lambda }}_n(B)\stackrel{p}{\to }\infty$ as n, p → ∞, with B = {0}.

3. Power Analysis

This section analyzes the local limiting power function of the CMLR test and compare it with that of the debias test of Janková and Van de Geer (2017) in Gaussian graphical model. To that the null H₀ for fixed index set B for the Gaussian graphical end, we first establish the asymptotic distribution of ${\widehat{\mathit{\theta }}}_B$ under model and linear model. Then, we use those results to carry out a local power analysis for both models.

3.1. Asymptotic Normality

We first introduce some notations before presenting the asymptotic normality results for Gaussian graphical model. Let ${\text{vec}}_B(\mathit{C})={(\sqrt{1+\mathbb{I}(i\ne j)}{c}_{ij})}_{(i,j):(i,j)\text{or}(j,i)\in B}$ is a sub-vector of vec(C) excluding components with indices not in B, $\text{vec}(\mathit{C})={\left(\sqrt{1+\mathbb{I}(i\ne j)}{c}_{ij}\right)}_{i\le j}\in {ℝ}^{\frac{p(p+1)}{2}}$ is a scaled vectorization of a p × p symmetric matrix C (Alizadeh et al. 1998) and $\mathbb{I}(\cdot )$ is the indicator. For the Fisher information, we need the symmetric Kronecker product Alizadeh et al. (1998) for a p × p symmetric matrix C to treat derivatives of the log-likelihood with respect to a matrix. Define the symmetric Kronecker product of $\mathit{C}\mathit{C}{\otimes }_{s}C\in {ℝ}^{\frac{p(p+1)}{2}\times \frac{p(p+1)}{2}}$ as $\left(\mathit{C}{\otimes }_s\mathit{C}\right)\text{vec}(\mathbf{\Delta })=\text{vec}(\mathit{C}\mathbf{\Delta }\mathit{C})$ for any symmetric matrix Δ, and define the Fisher information matrix for the $\frac{p(p+1)}{2}$-dimensional vector $\text{vec}(\mathbf{\Omega })$ as $\mathit{I}={\nabla }^2(-\frac{1}{2}\log \det {\mathbf{\Omega }}^0)=\frac{1}{2}{\mathbf{\Sigma }}^0{\otimes }_s{\mathbf{\Sigma }}^0$, c.f., Lemma 2. Given an index set B, we define a |B| × |B| submatrix I_B,B as ${\mathit{I}}_{B,B}={\left(I_{(i,j),(k,l)}\right)}_{(i,j),(k,l)\in B}$, extracting the corresponding |B| × |B| submatrix from I. Theorem 1 gives the asymptotic distribution of ${\text{vec}}_B({\widehat{\mathbf{\Omega }}}^{(1)})$.

Proposition 1 (Asymptotic distribution of CMLE ${\widehat{\mathbf{\Omega }}}^{(1)}$).

for Gausian graphical model). Under Assumptions 1 and 2, if |B| is fixed, there exists a pair of tuning parameters (K, τ) with K = |A⁰| and $\tau \le \frac{{\overline{\lambda }}_{\min }\min \left(\sqrt{C_{\min }},C_{\min }^2\right)}{12\left|A^0\right|}\text{such that}{\widehat{\mathbf{\Omega }}}^{(1)}$ satisfies

$$\sqrt{n}{\text{vec}}_B\left({\widehat{\mathbf{\Omega }}}^{(1)}-{\mathbf{\Omega }}^0\right)\stackrel{d}{\to }N\left(0,{\left({\mathit{I}}_{A^0\cup B,A^0\cup B}^{-1}\right)}_{B,B}\right),$$ (7)

where ${\left({\mathit{I}}_{A^0\cup B,A^0\cup B}^{-1}\right)}_{B,B}$ extracts a |B| × |B| submatrix from ${\mathit{I}}_{A^0\cup B,A^0\cup B}^{-1}$.

For linear regression, a similar asymptotic result can be derived.

Proposition 2 (Asymptotic distribution of CMLE).

Assume that $X_{A^0\cup B}^{\top }{X}_{A^0\cup B}$ is inevitable. Under Assumptions 3, if |B| is fixed, there exists a pair of tuning parameters (K, τ) with K = |A⁰| and $\tau \le \sigma \sqrt{\frac{6}{(n+2)p{\lambda }_{\max }\left(X^{\top }X\right)}}$ such that ${\widehat{\mathit{\theta }}}_B^{(1)}$ satisfies

$$\sqrt{n}\left({\widehat{\mathit{\beta }}}_B^{(1)}-{\mathit{\beta }}_B^0\right)\stackrel{d}{\to }N\left(0,{\left({\left(n^{-1}{X}_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}\right)}_{B,B}\right),$$ (8)

where M_B,B extracts a |B| × |B| submatrix from a matrix M.

3.2. Local Power Analysis

Consider a local alternative $H_a{\theta }_i^n={\theta }_i^0+{\left({\delta }_n\right)}_i;i\in B$ with ${\left({\delta }_n\right)}_{B^c}=0$, for any ${\theta }_{B^c}$, with ${\Vert {\delta }_n\Vert }_2=\frac{h}{\sqrt{n}}\text{if}|B|$ is fixed, ${\Vert {\delta }_n\Vert }_2=\frac{h|B{|}^{1/4}}{\sqrt{n}}\text{if}|B|\to \infty$, for some constant h. Let ${\mathit{\theta }}^n={\left({\theta }_1^n,\dots ,{\theta }_d^n\right)}^T$. Subsequently, we study the behavior of the local limiting power function for the proposed CMLR test ${\pi }_{LR}\left(h,{\theta }_{B^c}\right)=\lim {\inf }_{n\to \infty }{P}_{H_a}\left({\mathrm{\Lambda }}_n(B)\ge {\chi }_{\alpha ,|B|}^2\right)\text{if}|B|$ is fixed and lim ${\inf }_{n\to \infty }{P}_{H_a}\left({(2|B|)}^{-1/2}{\mathrm{\Lambda }}_n(B)-|B|\right)\ge z_{\alpha })\text{if}|B|\to \infty$. Let the corresponding ${\pi }_{\text{debias}}(h,{\theta }_{B^c})$ of the debias test in Janková and Van de Geer (2017) in the Gaussian graphical model as a result for linear regression is similar.

Theorem 3.

If for any θⁿ = Ωⁿ the Assumptions 1 and 2 for the Gaussian graphical model are met and further assume that |B|^3/2/n → 0, then for any nuisance parameters ${\mathrm{\Omega }}_{B^c}$,

$$\begin{gathered} {\pi }_{LR}\left(h,{\mathrm{\Omega }}_{B^c}\right) \\ \to \{\begin{array}{ll}\mathbb{P}\left({\Vert \mathit{Z}+n^{1/2}{\mathit{J}}_{B,B}^{-1/2}{\mathit{\delta }}_n\Vert }_2^2\ge {\chi }_{\alpha ,\left|B\right|}^2\right)\hfill & \text{when}\left|B\right|\text{is fixed,}\hfill \\ \mathbb{P}\left(Z+\frac{n{\delta }_n^{\top }{\mathit{J}}_{B,B}^{-1}{\delta }_n}{\sqrt{2}\left|B\right|}\ge z_{\alpha }\right)\hfill & \text{when}\left|B\right|\to \infty ,\hfill \end{array} \end{gathered}$$

where α > 0 is the level of significance, Z ∼ N(0, I_{|B| × |B|}) is a multivariate normal random variable, Z ∼ N(0, 1), and J_B,B is the asymptotic variance of ${\text{vec}}_B({\widehat{\mathbf{\Omega }}}^{(1)})$ in (7). In particular, ${\lim }_{h\to \infty }{\pi }_{\text{LR}}(h,{\mathbf{\Omega }}_{B^c})=1$. Moreover, in the one-dimensional situation with |B| = 1, for any h and ${\mathrm{\Omega }}_{B^c}$,

$${\pi }_{\text{LR}}(h,{\mathrm{\Omega }}_{B^c})\ge {\pi }_{\text{debias}}(h,{\mathrm{\Omega }}_{B^c}).$$ (9)

Theorem 3 suggests that the proposed CMLR test has the desirable power properties, which dominates the corresponding debias tests, which is attributed to optimality of the corresponding CMLE and likelihood ratio, as suggested by Theorem 1. Note that the debias test requires Assumption 2.

Next, we compare the asymptotic variance of our estimator to that of Janková and Van de Geer (2017) for the one-dimensional case with |B| = 1. As indicated by Corollary 1, our estimator has asymptotic variance, that is, no larger than that of its debias counterpart.

Corollary 1 (Comparison of asymptotic variances).

Under the assumption of Theorem 1, the asymptotic covariance matrix of ${\left[\sqrt{n}\left({\widehat{\omega }}_{ij}-{\omega }_{ij}^0\right)\right]}_{(i,j)\in B}$ is upper bounded by the matrix ${\left[{\omega }_{i^{\prime }j}^0{\omega }_{i{j}^{\prime }}^0+{\omega }_{j{j}^{\prime }}^0{\omega }_{i{i}^{\prime }}^0\right]}_{(i,j)\in B,\left(i^{\prime },j^{\prime }\right)\in B}$, where ${\widehat{\omega }}_{ij}$ is the ijth element of the $\text{CMLE}\widehat{\mathbf{\Omega }}$. When specializing the above result to the one-dimensional case, it implies that the asymptotic variance of $\sqrt{n}\left({\widehat{\omega }}_{ij}-{\omega }_{ij}^0\right)$ is no larger than ${\left[{\omega }_{ij}^0\right]}^2+{\omega }_{ii}^0{\omega }_{jj}^0$, the asymptotic variance of the regression estimator in Janková and Van de Geer (2017).

A parallel result of Theorem 3 is established for linear regression.

Theorem 4.

If for any θⁿ = βⁿ the Assumptions 1 and 2 for the linear regression model are met. Then

$$\begin{gathered} {\pi }_{LR}\left(h,{\beta }_{B^c}\right) \\ \to \{\begin{array}{ll}\mathbb{P}\left({\Vert \mathit{Z}+n^{1/2}\mathit{A}{\mathit{X}}_B{\mathit{\delta }}_n\Vert }_2^2\ge {\chi }_{\alpha ,\left|B\right|}^2\right)\hfill & \text{if}\left|B\right|\text{is fixed;}\hfill \\ \mathbb{P}\left(Z+\frac{n{\Vert \mathit{A}{\mathit{X}}_B{\delta }_n\Vert }_2^2}{\sqrt{2\mid B\mid }}\ge z_{\alpha }\right)\hfill & \text{if}\left|B\right|\to \infty .\hfill \end{array} \end{gathered}$$ (10)

where $\mathit{A}\in {ℝ}^{n\times |B|}$ with columns being the eigenvalues of ${\mathit{P}}_{A^0\cup B}-{\mathit{P}}_{A^0},Z~N(0,1)$, and Z is a |B| dimensional normal random vector. Hence, for any nuisance parameters ${\beta }_{B^c},{\lim }_{h\to \infty }{\pi }_{\text{LR}}(h,{\beta }_{B^c})=1$.

4. Computation

To compute the CMLEs under the null and full spaces in (1) and (2), we approximately solve constrained nonconvex optimization through difference convex (DC) programming. Particularly, we follow the DC approach of Shen, Pan, and Zhu (2012) to approximate the nonconvex constraint by a sequence of convex constraints based on a difference convex decomposition iteratively. This leads to an iterative method for solving a sequence of relaxed convex problems. The reader may consult Shen, Pan, and Zhu (2012) for convergence of the method.

For (1) and (2), at the mth iteration, we solve

$$\begin{gathered} {\max }_{\mathit{\theta }}{L}_n(\mathit{\theta }) \\ \text{subj to}{\sum }_{i\notin A_1}\left|{\omega }_{ij}\right|\mathbb{I}\left(\left|{\widehat{\omega }}_i^{[m]}\right|\le \tau \right) \\ \le \tau \left(K-{\sum }_{i\notin A_1}\mathbb{I}\left(\left|{\widehat{\omega }}_i^{[m]}\right|>\tau \right)\right),{\mathit{\theta }}_{A_2}=0, \end{gathered}$$ (11)

to yield ${\widehat{\mathit{\theta }}}^{[m+1]}$, where A₁ = B and A₂ = ∅ for (1) and A₁ = A₂ = B for (2). Iteration continues until two adjacent iterates are equal. To solve (11), we employ the alternating direction method of multipliers algorithm (Boyd et al. 2011), which amounts to the following iterative updating scheme

$$\begin{gathered} {\mathit{\theta }}^{[k+1]}=\underset{\mathit{\theta }}{\arg \min }(-L_n(\mathit{\theta })+(\rho /2)· \\ {\Vert \mathit{\theta }-{\mathit{\delta }}^{[k]}+{\mathit{\gamma }}^{[k]}\Vert }_2^2), \end{gathered}$$ (12)

$$\begin{array}{l}{\mathit{\delta }}^{(k+1)}={\mathcal{P}}_{{ℱ}^{[m]}}\left({\mathit{\theta }}^{[k+1]}+{\mathit{\gamma }}^{[k]}\right),\\ {\mathit{\gamma }}^{[k+1]}={\gamma }^{[k]}+{\mathit{\theta }}^{[k+1]}-{\mathit{\delta }}^{[k+1]},\end{array}$$ (13)

where

$$\begin{gathered} {ℱ}^{[m]}=\{\sum _{i\notin A_1}\left|{\theta }_i\right|\mathbb{I}\left(\left|{\theta }_i^{[m]}\right|\le \tau \right) \\ \le \tau \left(K-\sum _{(i,j)\notin A_1}\mathbb{I}\left(\left|{\theta }_i^{[m]}\right|>\tau \right)\right),{\mathit{\theta }}_{A_2}=0\}, \end{gathered}$$

${\mathcal{P}}_{ℱ[m]}(\cdot )$ denotes the projection onto the set ${ℱ}^{[m]}$ and ρ > 0 is fixed or can be adaptively updated using a strategy in Zhu (2017). Note that in both cases, the θ-update (12) can be solved using an analytic formula involving a singular value decomposition for the Gaussian graphical model (see Section 6.5 of Boyd et al. 2011) and solving a linear system for the linear model, while (13) is performed using the L₁-projection algorithm of Liu and Ye (2009) whose complexity is almost linear in a problem’s size. Specifically, consider a generic problem of projection onto a weighted L₁-ball subject to equality constraint:

$${\min }_{x\in {ℝ}^d}\frac{1}{2}\Vert x-y{\Vert }_2^2\text{subj to}{\sum }_{i\notin A}{c}_i\left|x_i\right|\le z\text{and}{x}_i,i\in A,$$

where c_i ≥ 0; i = 1,..., d and A is a subset of {1,...,d}. The solution of this problem is $x_i^{\star }=0\text{if}i\in A;x_i^{\star }=y_i\text{if}{\sum }_{i\notin A}{c}_i\left|y_i\right|\le z;x_i^{\star }=\mathrm{sgn}\left(y_i\right)\max \left(\left|y_i\right|-c_i{\lambda }^{\star },0\right)$ otherwise, where λ^★ is a root of $f(\lambda )={\sum }_{i\notin A}{c}_i\max \left(\left|y_i\right|-c_i\lambda ,0\right)-z$. This root-finding problem is solved efficiently by bisection.

5. Numerical Examples

This section investigates operating characteristics of the proposed CMLR test with regard to the size and power of a test through simulations and compare with several strong competitors in the literature.

For the Gaussian graphical model, we examine three different types of graphs—a chain graph, a hub graph, and a random graph, as displayed in Figure 1. For a given graph $\mathcal{G}=(\mathcal{V},ℰ)$, Ω is generated based on connectivity of the graph, that is, ω_ij ≠ 0 iff there exists a connection between nodes i and j for i ≠ j. Moreover, we set ω_ij = 0.3 if i and j are connected and diagonals equal to 0.3 + c with c chosen so that the smallest eigenvalue of the resulting matrix equals to 0.2. Finally, a random sample of size n = 200 is drawn from N(0, Ω⁻¹).

Figure 1.

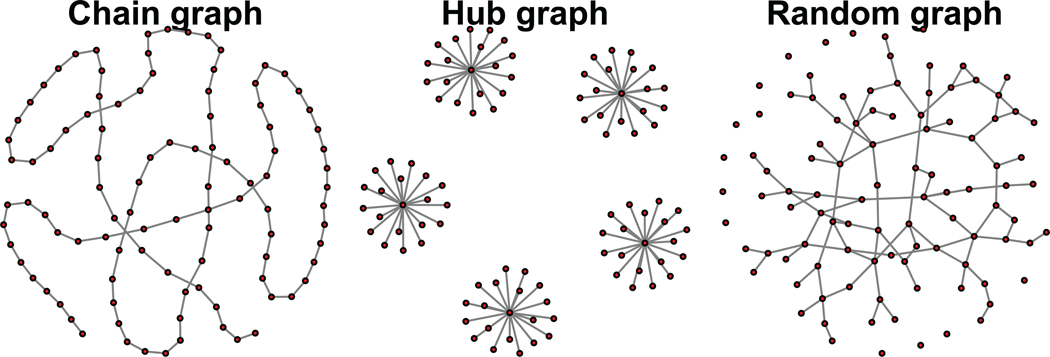
Three types of graphs used in our simulations.

In what follows, we consider two hypothesis testing problems concerning conditional independence of components of a Gaussian random vector X = (X₁,...,X_p). The first concerns null hypothesis $H_0:{\omega }_{i_0{j}_0}=0$ versus its alternative $H_a:{\omega }_{i_0{j}_0}\ne 0;i_0\ne j_0$, for testing conditional independence between $X_{i_0}$ and $X_{j_0}$. The second deals with $H_0:{\omega }_{i_{0}j}=0;1\le j\ne i_0\le p$ versus $H_a:{\omega }_{i_{0}j}\ne 0$ for some j ≠ i₀, for testing conditional independence of component i₀ with the rest. In either case, we apply the proposed CMLR test in Section 2 and compare it with the univariate debias test of Janková and Van de Geer (2017) in terms of the empirical size and power only in the first problem. To our knowledge, no competing methods are available for the second problem in the present situation.

For the size of a test, we calculate its empirical size as the percentage of times rejecting H₀ out of 1000 simulations when H₀ is true. For the power of a test, we consider four different alternatives: $H_a:{\omega }_{ij}={\omega }_{ij}^{(l)}\text{for}(i,j)\ne \left(i_0,j_0\right)\text{and}{\omega }_{i_0{j}_0}^{(l)}=\frac{{\omega }_{i_0{j}_0}l}{4},l=1,\dots ,4$. Under each alternative, we compute the power as the percentage of times rejecting H₀ out of 1000 simulations when H_a is true.

With regard to tuning, we fix τ = 0.001 and propose to use a vanilla cross-validation to choose the optimal tuning parameter K for our test by minimizing a prediction criterion using a 5-fold CV. Specifically, we divide the dataset into five roughly equal parts denoted by ${\mathcal{D}}_1,\dots ,{\mathcal{D}}_5$. Define ${\widehat{\mathbf{\Sigma }}}_l$ and ${\widehat{\mathbf{\Sigma }}}_{-l}$, respectively, as the sample covariance matrices calculated based on samples in ${\mathcal{D}}_l$ and $\left\{{\mathcal{D}}_1,\dots ,{\mathcal{D}}_5\right\}\backslash {\mathcal{D}}_l;l=1,\dots ,5$. Similarly, define ${\widehat{\mathbf{\Omega }}}_{-l}(K)$ to be the precision matrix calculated based on sample covariance matrix ${\widehat{\mathbf{\Sigma }}}_{-l};l=1,\dots ,5$. The 5-fold CV criterion is $\text{CV}(K)=5^{-1}{\sum }_{l=1}^5\left(-\log \det \left({\widehat{\mathbf{\Omega }}}_{-l}(K)\right)+\mathrm{tr}\left[{\widehat{\mathbf{\Sigma }}}_l{\widehat{\mathbf{\Omega }}}_{-l}(K)\right]-p\right)$. Then the optimal tuning parameter is obtained by minimizing CV(K) over a set of grids in the domain of K. Finally, K^★ = arg min _K CV(K) is used to compute the final estimator based on the original data.

For the first testing problem, the nominal size of a test is set to 0.05 for our CMLR test and the univariate debias test of Janková and Van de Geer (2017), denoted as CMLR-chi-square and JG, where the confidence interval in Janková and Van de Geer (2017) is converted to a two-sided test. For each graph type, three different graph sizes p = 50, 100, 200 are examined. As indicated in Table 1, the empirical size of the CMLR test is under or close to the nominal size 0.05. Moreover, as suggested in Table 1, the power of the likelihood ratio test is uniformly higher across all the 12 scenarios with four alternatives and three different dimensions, where the largest improvements are seen for the hub graph, particularly with p = 100, 200 for an amount of improvement of 50% or more. This result is anticipated because the likelihood method is more efficient than a regression approach.

Table 1.

Empirical size and power comparisons of the proposed CMLR test and test of Janková and Van de Geer (2017), denoted by CMLR-chi-square and JG, in the first testing problem for the Gaussian graphical model based on 1000 simulations.

		CMLR-chi-square		JG
Graph	(n, p)	Size	Power	Size	Power
Band	(200,50)	0.054	(0.27, 0.78, 0.98, 1.0)	0.043	(0.24, 0.77, 0.99, 1.0)
	(200,100)	0.055	(0.30, 0.79, 0.98, 1.0)	0.042	(0.24, 0.75, 0.99, 1.0)
	(200,200)	0.048	(0.29, 0.80, 0.99, 1.0)	0.036	(0.23, 0.74, 0.98, 1.0)
Hub	(200,50)	0.019	(0.10, 0.36, 0.74, 0.95)	0.005	(0.06, 0.27, 0.66, 0.92)
	(200,100)	0.028	(0.12, 0.43, 0.81, 0.96)	0.005	(0.02, 0.17, 0.54, 0.86)
	(200,200)	0.031	(0.16, 0.55, 0.86, 0.98)	0.001	(0.02, 0.15, 0.50, 0.86)
Random	(200,50)	0.034	(0.15, 0.51, 0.86, 0.98)	0.025	(0.14, 0.49, 0.83, 0.98)
	(200,100)	0.041	(0.21, 0.68, 0.94, 1.0)	0.018	(0.11, 0.53, 0.92, 0.99)
	(200,200)	0.049	(0.15, 0.47, 0.81, 0.96)	0.034	(0.14, 0.41, 0.78, 0.95)

To study operating characteristics of the constrained likelihood test, we focus on the validity of asymptotic approximations based on the chi-square or normal distribution under H₀. For the first problem, Figure 2 indicates that the chi-square approximation on one degree of freedom is adequate for the likelihood ratio test. Similarly, for the second testing problem involving a column/row of Ω, Figure 3 confirms that the normal approximation is again adequate for the CMLR test. Overall, the asymptotic approximations appear adequate.

Figure 2.

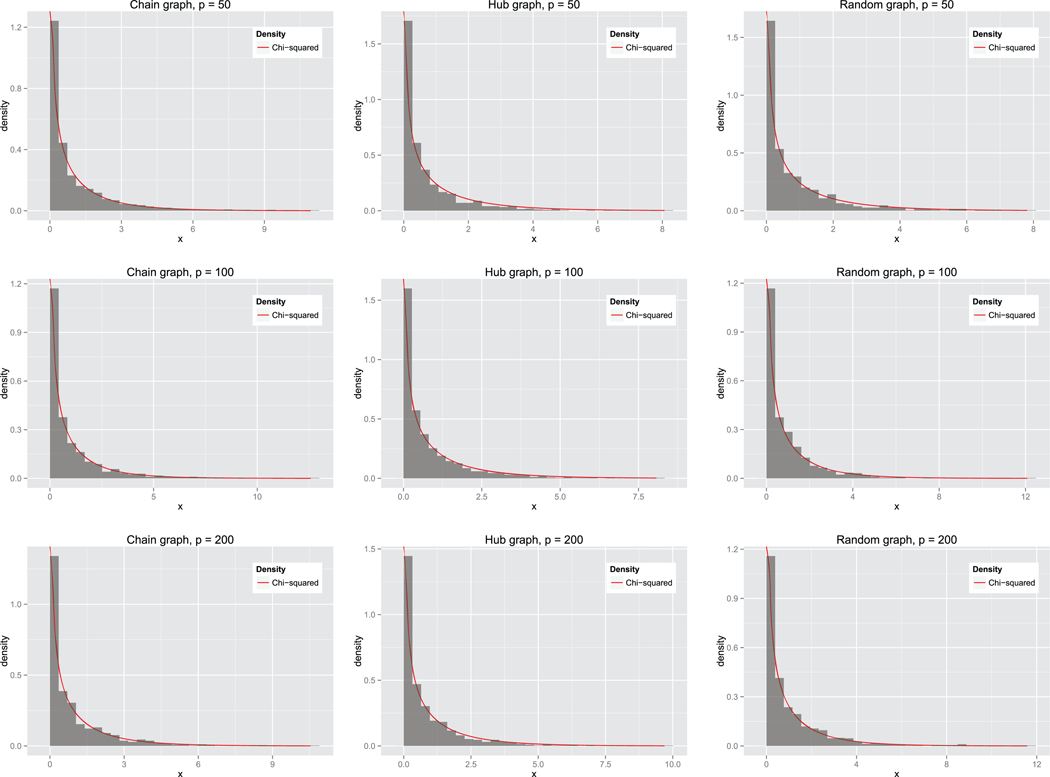
Empirical null distribution of the proposed CMLR test based on the chi-square approximation with n = 200.

Figure 3.

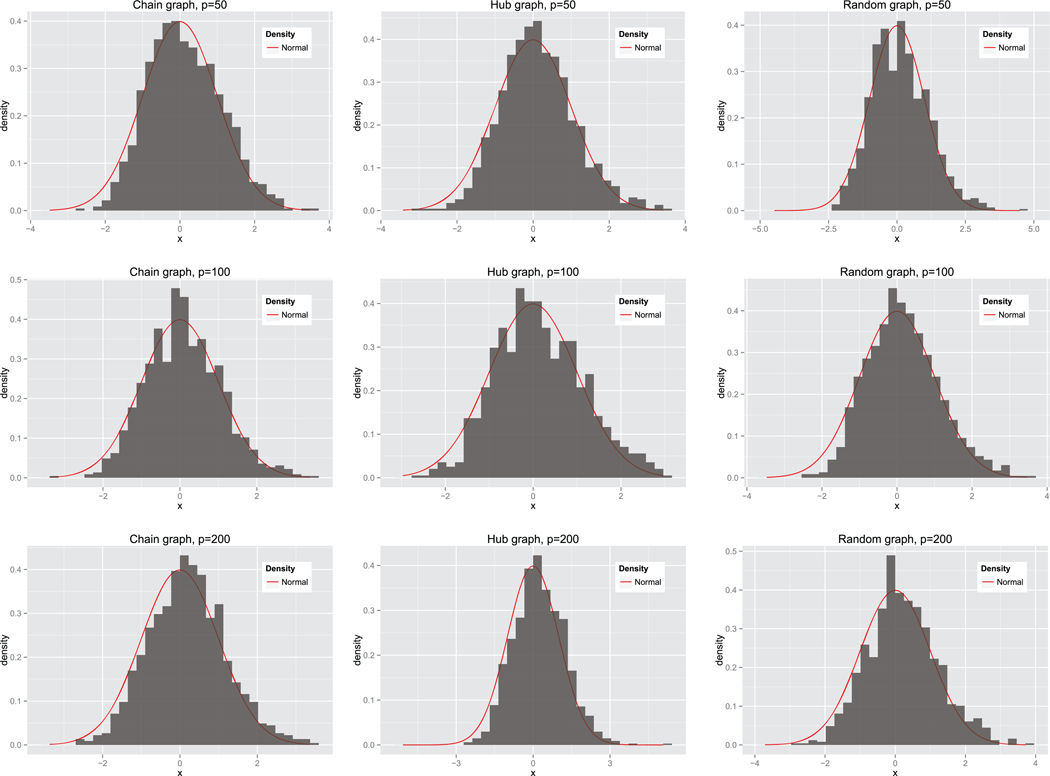
Empirical null distribution of our likelihood ratio test based on the normal approximation for the second testing problem involving a single column/row.

For the linear model, we perform a parallel simulation study to compare the CMLR test with the debiased lasso test (Zhang and Zhang 2014; Van de Geer et al. 2014) and the method of Zhang and Cheng (2017). In (5), we examine (n, p) = (100, 50), (100, 200), (100, 500), (100, 1000), in which predictors x_ij and the error ϵ_i are generated independently from N(0, 1), where ${\beta }^0=\left(1,2,3,{\beta }_B^0,\mathbf{0}\right)$ and ${\Vert {\mathit{\beta }}_B\Vert }_2=l/10$; l = 0, 1,...,4. Now consider a hypothesis test with null hypothesis H₀ : β_B = 0 versus its alternative H_a : β_B ≠ 0, where we let |B| ≠ 1, 5, 10. With regard to size, power, and tuning, we follow the same scheme as in the Gaussian graphical model.

As indicated in Table 2, the empirical size of CMLR-chi-square and CMLR-normal are close to the target size 0.05, while the former does better than the latter for |B| is small and worse for large |B|, which corroborates with the result of Theorem 2. Moreover, the power of CMLR-chi-square is uniformly higher across all the three scenarios with four alternatives compared to the other two competing methods. Interestingly, when |B| is large, the method of Zhang and Cheng (2017) seems to control the size closer to the nominal level than the CMLR test, but the situation is just the opposite when |B| is not large. Additional simulations also suggest that similar results are obtained with additional correlation among covariates, which are not displayed in here.

Table 2.

Empirical size and power comparisons in linear regression as well as estimated tuning parameter $\widehat{K}$ by a 5-fold cross-validation over 1000 simulations.

|B|	n	p	Method	Size	Power	$\widehat{K}$
1	100	50	CMLR-chi-square	0.057	(0.165, 0.489, 0.837, 0.972)	3.36 (1.08)
			CMLR-normal	0.061	(0.17, 0.495, 0.84, 0.972)	NA
			Zhang and Cheng	0.039	(0.109, 0.262, 0.579, 0.788)	NA
			DL	0.033	(0.132, 0.404, 0.724, 0.917)	NA
		200	CMLR-chi-square	0.055	(0.17, 0.524, 0.829, 0.974)	3.191 (0.591)
			CMLR-normal	0.058	(0.176, 0.532, 0.834, 0.975)	NA
			Zhang and Cheng	0.013	(0.042, 0.116, 0.306, 0.476)	NA
			DL	0.052	(0.144, 0.358, 0.694, 0.888)	NA
		500	CMLR-chi-square	0.051	(0.175, 0.509, 0.838, 0.963)	3.159 (0.583)
			CMLR-normal	0.051	(0.179, 0.513, 0.84, 0.963)	NA
			Zhang and Cheng	NA	NA	NA
			DL	NA	NA	NA
		1000	CMLR-chi-square	0.056	(0.165, 0.512, 0.828, 0.962)	3.115 (0.371)
			CMLR-normal	0.058	(0.17, 0.522, 0.83, 0.964)	NA
			Zhang and Cheng	NA	NA	NA
			DL	NA	NA	NA
5	100	50	CMLR-chi-square	0.058	(0.11, 0.328, 0.63, 0.865)	3.33 (0.94)
			CMLR-normal	0.052	(0.109, 0.322, 0.619, 0.862)	NA
			Zhang and Cheng	0.05	(0.063, 0.115, 0.226, 0.346)	NA
			DL	NA	NA	NA
		200	CMLR-chi-square	0.066	(0.114, 0.297, 0.601, 0.878)	3.188 (0.606)
			CMLR-normal	0.063	(0.112, 0.289, 0.592, 0.878)	NA
			Zhang and Cheng	0.037	(0.052, 0.111, 0.153, 0.253)	NA
			DL	NA	NA	NA
		500	CMLR-chi-square	0.064	(0.124, 0.321, 0.625, 0.895)	3.153 (0.56)
			CMLR-normal	0.061	(0.118, 0.315, 0.618, 0.893)	NA
			Zhang and Cheng	NA	NA	NA
			DL	NA	NA	NA
		1000	CMLR-chi-square	0.059	(0.118, 0.304, 0.612, 0.872)	3.11 (0.355)
			CMLR-normal	0.057	(0.112, 0.3, 0.604, 0.869)	NA
			Zhang and Cheng	NA	NA	NA
			DL	NA	NA	NA
10	100	50	CMLR-chi-square	0.068	(0.094, 0.252, 0.528, 0.794)	3.41 (1.20)
			CMLR-normal	0.059	(0.085, 0.233, 0.503, 0.775)	NA
			Zhang and Cheng	0.054	(0.055, 0.085, 0.146, 0.21)	NA
			DL	NA	NA	NA
		200	CMLR-chi-square	0.086	(0.115, 0.253, 0.514, 0.786)	3.193 (0.618)
			CMLR-normal	0.079	(0.104, 0.238, 0.487, 0.767)	NA
			Zhang and Cheng	0.049	(0.055, 0.089, 0.106, 0.152)	NA
			DL	NA	NA	NA
		500	CMLR-chi-square	0.093	(0.123, 0.286, 0.54, 0.773)	3.159 (0.585)
			CMLR-normal	0.078	(0.113, 0.262, 0.516, 0.76)	NA
			Zhang and Cheng	NA	NA	NA
			DL	NA	NA	NA
		1000	CMLR-chi-square	0.073	(0.123, 0.252, 0.526, 0.779)	3.11 (0.355)
			CMLR-normal	0.066	(0.112, 0.23, 0.497, 0.766)	NA
			Zhang and Cheng	NA	NA	NA
			DL	NA	NA	NA

NOTES: Here “CMLR-chi-square,” “CMLR-normal,” “DL,” and “Zhang and Cheng” denote the proposed test based on a chi-square approximation, a normal approximation, the debias method of Zhang and Zhang (2014), and the method of Zhang and Cheng (2017). Note that the nominal size is 0.05, DL is a test converted from a CI, and NA means that a result is not applicable or the code fail to return a result after a code’s runtime exceeds one week.

Concerning sensitivity of the choice of tuning parameters (K, τ) for the proposed method, as illustrated in Figure 4, the choice of τ is much less sensitive than that of K. Moreover, when K ≥ K⁰, both the size and power become less sensitive to a change of K. With regard to the estimated K by cross-validation, the estimator $\widehat{K}$ is close to K⁰ = 3 in the linear regression example, as suggested by Table 2.

Figure 4.

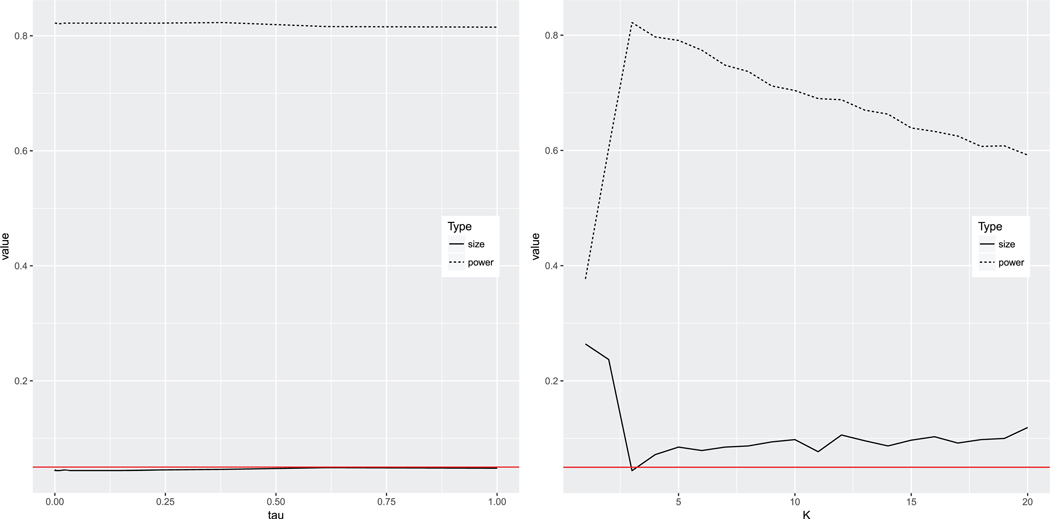
Sensitivity study of power as a function of tuning parameters τ and K, when n = 100, p = 100, and K₀ = 3 in the linear regression problem based on 1000 simulations. Dotted and black lines represent empirical power and sizes of the proposed method, while red lines serve as a reference of the nominal size α = 0.05.

In summary, our simulation results suggest that the proposed method achieves high power compared to its competitors Janková and Van de Geer (2017), Zhang and Zhang (2014), Van de Geer et al. (2014), and Zhang and Cheng (2017). Moreover, the asymptotic approximation seems adequate in all the examples.

6. Brain Network Analysis

Alzheimer’s disease is the most common dementia without cure, while the prevalence is projected to continuously increase with an estimated 11% of the US senior population in 2015 to 16% in 2050, costing over 1.1 trillion in 2050 Alzheimer’s Association (2016). AD is now widely believed to be a disease with disrupted brain networks, and cortical networks based in structural MRI have been constructed to contrast with that of normal/healthy controls (He, Chen, and Evans 2008). Using the ADNI-1 baseline data (adni.loni.usc.edu), we extracted the cortical thicknesses for p = 68 regions of interest (ROIs) based on the Desikan–Killany atlas Desikan et al. (2006). Since previous studies (e.g., Greicius et al. 2004; Montembeault et al. 2015) have identified the DMN to be associated with AD, we will pay particular attention to this subnetwork, which includes 12 ROIs in our dataset. As in He, Chen, and Evans (2008), we first regress the cortical thickness on five covariates (gender, handedness, education, age, and intercranial volume measured at baseline), then use the residuals to estimate precision matrices, for 145 AD patients and 182 normal controls (CNs), respectively. Our approach here differs from previous studies He, Chen, and Evans (2008) and Montembeault et al. (2015) not only in estimating precision matrices, instead of covariance matrices, but also in rigorous inference.

For this data, we consider a hypothesis test of H₀ : ω_ij = 0 versus H_a : ω_ij ≠ 0; 1 ≤ i ≠ j ≤ 12. For each estimated network for the two groups, significant edges under the overall error rate α = 0.05, after Bonferroni correction, are reported for the proposed CMLR test and the debias test of Janková and Van de Geer (2017) or JG. As indicated in Figure 5, the CMLR test yields 28 and 33 signif icant edges for the two groups of CN and AD, which is in contrast to 29 and 28 significant edges by the JG test. In other words, the CMLR test detects slightly more edges than the JG test, which is in agreement of the simulation results in Table 1.

Figure 5.

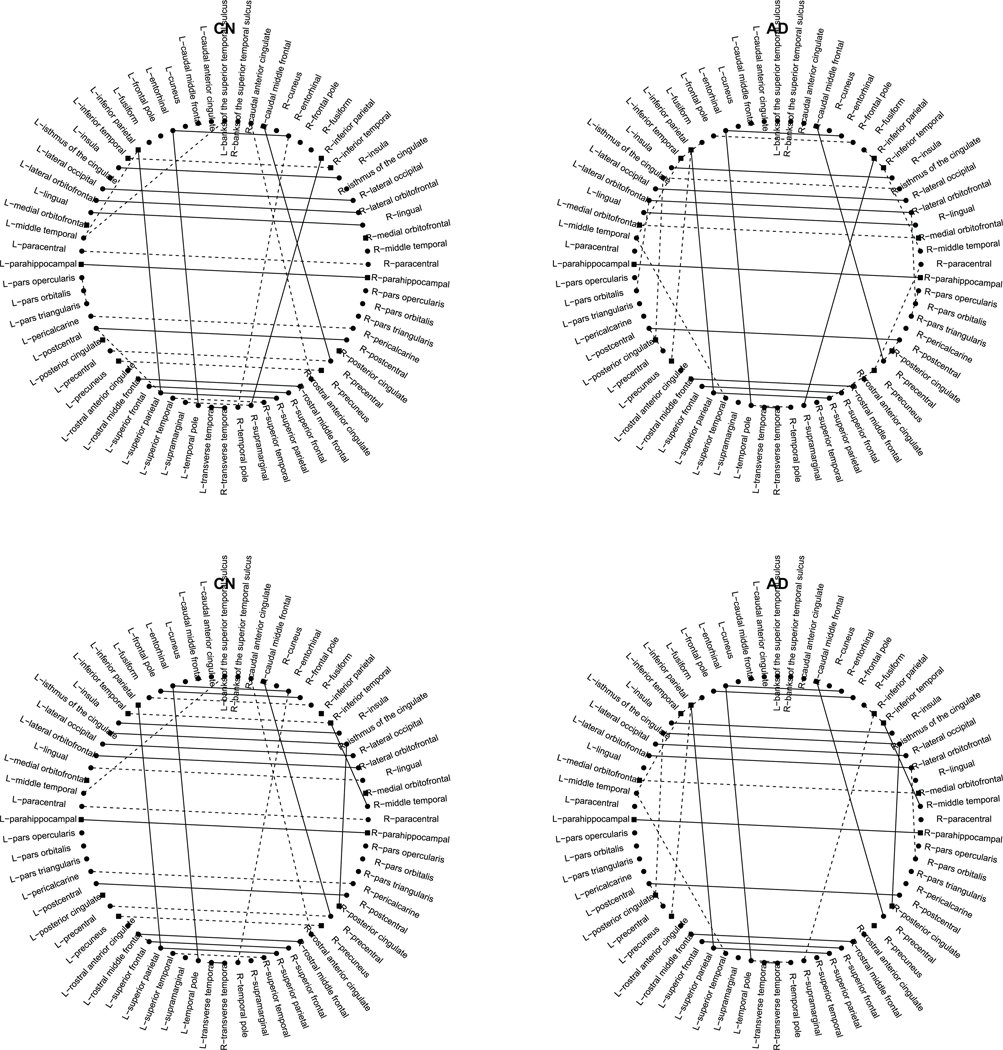
Estimated networks by the proposed method (first row) and the method Janková and Van de Geer (2017) (second row) for the CN (left) and AD (right) groups, where reported edges are significant under a p-value of 0.05 after Bonferroni correction. Nodes with square shape belong to DMN. The solid edges denote those that are shared by the two groups, whereas the dashed edges denote those that are only present within one group.

In what follows, we will focus on scientific interpretations of the statistical findings by the CMLR test. As shown in Montembeault et al. (2015), it is confirmed that for the AD patients, as compared to the normal controls, there seems to be reduced connectivity within DMN, but increased connectivity for some other ROIs, that is, the salience network and the executive network reported in Montembeault et al. (2015). Moreover, it seems that connectivity between the left and right brain within DMN somewhat deteriorates for the AD patients. To further explore the latter point, we then separately test the independence between each node in DMN and the other nodes outside DMN using the proposed CMLR test with the standard normal approximation. Specifically, for node i in DMN, we test H₀ : ω_ij = 0 for all $j\notin \text{DMN}$ versus H_a : ω_ij ≠ 0 for some j ∈ DMN, where DMN denotes the set of 12 nodes in DMN. This amounts to 2 × 12 = 24 tests, with 12 tests for each group. Specifically, it is confirmed that for the group AD, only L-parahippocampal (left side) is independent of all the other nodes outside DMN; in contrast, for the CN group, in addition to L-parahippocampal, three other ROIs in DMN, L-medial prefrontal cortex, R-parahippocampal, and R-precuneus are independent of all the other nodes outside DMN.

Appendix

The following lemmas provide some key results to be used subsequently. Detailed proofs of Lemmas 2–8 are provided in a online Supplementary materials due to space limit. Before proceeding, we introduce some notations. Given an index set $A\subseteq \{(i,j):1\le i\le j\le p\}$, define CMLE ${\widehat{\mathbf{\Omega }}}_A$ as ${\widehat{\mathbf{\Omega }}}_A=\arg {\max }_{\mathbf{\Omega }\succ 0,{\mathbf{\Omega }}_{A}c=0}{L}_n(\mathbf{\Omega })$, with $\succ$ indicating positive definiteness of a matrix. Worthy of note is that ${\widehat{\mathbf{\Omega }}}_A$ becomes the oracle estimator when $A=A^0,\text{where}{A}^0=\{(i,j):i\le j,{\omega }_{ij}^0\ne 0\}$ is the index set including all the indices corresponding to nonzero entries of the true precision matrix ${\mathbf{\Omega }}^0={({\omega }_{ij}^0)}_{p\times p}$

Lemma 2.

For any symmetric matrices C₁ and C₂, $\text{vec}{\left({\mathit{C}}_1\right)}^{\top }\text{vec}\left({\mathit{C}}_2\right)=\text{tr}\left({\mathit{C}}_1{\mathit{C}}_2\right)$. Moreover, for any positive definite matrix $\mathit{C}\succ 0$,

$$\nabla (\log \det \mathit{C})=-\text{vec}({\mathit{C}}^{-1}),$$

$${\nabla }^2(-\log \det {\mathbf{\Omega }}^0)={\mathit{C}}^{-1}{\otimes }_s{\mathit{C}}^{-1},$$ (A.1)

$$\mathit{I}=\frac{1}{2}{\mathbf{\Sigma }}^0{\otimes }_s{\mathbf{\Sigma }}^0,$$ (A.2)

$$\mathrm{var}(\text{vec}(\mathit{X}{\mathit{X}}^{\top }))=4\mathit{I}\text{with}\mathit{X}~N(\mathbf{0},{\mathbf{\Sigma }}^0),$$ (A.3)

$$\text{vec}{(\mathit{C})}^{\top }\mathit{I}\text{vec}(\mathit{C})=\frac{1}{2}\text{tr}({\mathbf{\Sigma }}^0\mathit{C}{\mathbf{\Sigma }}^0\mathit{C}).$$ (A.4)

Lemma 3.

For any symmetric matrix T and ν > 0

$$\mathbb{P}(\left|\text{tr}((\mathit{S}-{\mathbf{\Sigma }}^0)\mathit{T})\right|\ge v)\le 2\exp (-n\frac{v^2}{9\Vert \mathit{T}{\Vert }^2+8v\Vert \mathit{T}\Vert }),$$ (A.5)

where $\Vert \mathit{T}{\Vert }^2=\frac{n}{2}\text{var}(\text{tr}((\mathit{S}-{\mathbf{\Sigma }}^0)\mathit{T}))$. Furthermore, for T₁,...,T_K such that $\Vert {\mathit{T}}_k\Vert \le c_0;k=1,\dots ,K$ with c₀ > 0 and any ν > 0, we have that

$$\begin{gathered} \mathbb{P}\left(\underset{1\le k\le K}{\max }\left|\text{tr}\left(\left(\mathit{S}-{\mathbf{\Sigma }}^0\right){\mathit{T}}_k\right)\right|\ge v\right) \\ \le 2\exp \left(-n\frac{v^2}{9c_0^2+8c_{0}v}+\log K\right), \end{gathered}$$ (A.6)

which implies that ${\max }_{1\le k\le K}\left|\mathrm{tr}\left(\left(\mathit{S}-{\mathbf{\Sigma }}^0\right){\mathit{T}}_k\right)\right|=O_p\left(c_0\sqrt{\frac{\log K}{n}}\right)$. Particularly, for any ν > 0 and any index set B,

$$\begin{gathered} \mathbb{P}\left({\Vert {\text{vec}}_B\left(\mathit{S}-{\mathbf{\Sigma }}^0\right)\Vert }_{\infty }\ge v\right) \\ \le 2\exp \left(-n\frac{v^2\mid }{9{\lambda }_{\max }^2\left({\mathbf{\Sigma }}^0\right)+8v\lambda \max \left({\mathbf{\Sigma }}^0\right)}+\log \left|B\right|\right), \end{gathered}$$ (A.7)

implying that ${\Vert {\text{vec}}_B\left(\mathit{S}-{\mathbf{\Sigma }}^0\right)\Vert }_{\infty }=O_p\left({\lambda }_{\max }\left({\mathbf{\Sigma }}^0\right)\sqrt{\frac{\log |B|}{n}}\right).$

Lemma 4.

(The Kullback–Leibler divergence and Fisher-norm) For a positive definite matrix $\mathbf{\Omega }\in {ℝ}^{p\times p}$, a connection between the Kullback–Leibler divergence K(Ω⁰, Ω) and the Fisher-norm $\Vert {\mathbf{\Omega }}^0-\mathbf{\Omega }\Vert$ can be established:

$$K\left({\mathbf{\Omega }}^0,\mathbf{\Omega }\right)\ge \min \left(\frac{1}{16\sqrt{2}},\frac{\sqrt{K\left({\mathbf{\Omega }}^0,\mathbf{\Omega }\right)}}{2\sqrt{6}}\right)\Vert {\mathbf{\Omega }}^0-\mathbf{\Omega }\Vert ,$$ (A.8)

$$K\left({\mathbf{\Omega }}^0,\mathbf{\Omega }\right)\ge \min \left(\frac{1}{16\sqrt{2}},\frac{\Vert {\mathbf{\Omega }}^0-\mathbf{\Omega }\Vert }{24}\right)\Vert {\mathbf{\Omega }}^0-\mathbf{\Omega }\Vert .$$ (A.9)

Lemma 5.

(Rate of convergence of constrained MLE). Let $\tilde{A}\supseteq A^0$ be an index set. For ${\widehat{\mathbf{\Omega }}}_{\tilde{A}}$, we have that

$$\Vert {\widehat{\mathbf{\Omega }}}_{\tilde{A}}-{\mathbf{\Omega }}^0\Vert \le 12{\Vert {\mathit{I}}_{\tilde{A},\tilde{A}}^{-1/2}\text{vec}\left({\mathbf{\Sigma }}^0-\mathit{S}\right)\Vert }_2.$$ (A.10)

on the event that $\left\{{\Vert I_{\tilde{A},\tilde{A}}^{-1/2}{\text{vec}}_{\tilde{A}}\left({\mathbf{\Sigma }}^0-\mathit{S}\right)\Vert }_2<\frac{1}{8\sqrt{2}}\right\}$. Moreover, if $\frac{|\tilde{A}|\log p}{n}\to 0$, then

$$\Vert {\widehat{\mathbf{\Omega }}}_{\tilde{A}}-{\mathbf{\Omega }}^0\Vert =O_p\left(\sqrt{\frac{\left|\tilde{A}\right|\log p}{n}}\right).$$ (A.11)

Lemma 6.

(Selection consistency). If

$$\begin{gathered} K=\left|A^0\right|,\tau \le \frac{{\overline{\lambda }}_{\min }\min \left(\sqrt{C_{\min }},C_{\min }^{{}_{{}^2}}\right)}{12\left|A^0\right|},\text{then} \\ \max \left(P\left({\widehat{\mathbf{\Omega }}}^{(0)}\ne {\widehat{\mathbf{\Omega }}}_{A^0}\right),P\left({\widehat{\mathbf{\Omega }}}^{(1)}\ne {\widehat{\mathbf{\Omega }}}_{A^0\cup B}\right)\right) \\ \le 2\exp \left(\frac{-n{C}_{\min }}{2560\times 512}+2\log p\right)+\exp \left(\frac{-n}{2560}+\left|A^0\right|\log p\right) \\ +2\exp \left(-n\frac{\min {\left(\sqrt{\frac{\min \left(C_{\min }/512,3/32\right)}{48{\lambda }_{\max }^{{}^2}\left(\left|A^0\right|+\left|B\right|\right)}},{\lambda }_{\max }\left({\mathbf{\Sigma }}^0\right)\right)}^2}{18{\lambda }_{\max }^{{}_{{}^2}}\left({\mathbf{\Sigma }}^0\right)}+2\log p\right) \\ \to 0 \end{gathered}$$ (A.12)

as n → ∞ under Assumptions 1 and 2, where ${\widehat{\mathbf{\Omega }}}^{(0)},{\widehat{\mathbf{\Omega }}}^{(1)}$, and C_min are as defined in (1)–(3).

Lemma 7.

Let ${\mathit{\gamma }}_k=\left({\gamma }_{k1},.,\cdot \cdot {\gamma }_{km}\right)\in {ℝ}^m;k=1,\dots ,n$ be iid random vectors with var(γ₁) = I_m×m. If m is fixed, then

$$n^{-1}{\Vert \sum _{k=1}^n{\mathit{\gamma }}_k\Vert }_2^2\stackrel{d}{\to }{\chi }_m^2,\text{as}n\to \infty .$$ (A.13)

Otherwise, if max (m, m₂m/n, m₃/n, m₃m^3/2/n² → 0), where $m_j={\max }_{1\le i\le m}\mathbb{E}{\gamma }_{1i}^{2j};j=2,3$, then

$$\frac{{\Vert {\sum }_{k=1}^n{\mathit{\gamma }}_k\Vert }_2^2-nm}{n\sqrt{2m}}\stackrel{d}{\to }N(0,1),\text{as}n\to \infty .$$ (A.14)

Lemma 8.

Let X ∼ N(0, Σ⁰) and $\gamma =\text{tr}\left(\mathit{X}{\mathit{X}}^{\top }-{\mathbf{\Sigma }}^0\right)\mathit{T})$ with T a symmetric matrix. Then

$$\mathbb{E}\left({\gamma }^{2m}\right)\le (2m-1)!2^{m-1}{\left(\mathbb{E}\left({\gamma }^2\right)\right)}^m\text{for any integer}m\ge 1.$$ (A.15)

Lemma 9.

(Asymptotic distribution for log-likelihood ratios). The log-likelihood ratio statistic $Lr=2(L_n({\widehat{\mathbf{\Omega }}}_{\tilde{A}})-L_n({\widehat{\mathbf{\Omega }}}_{A^0}))$, where ${\widehat{\mathbf{\Omega }}}_{\tilde{A}}$ is the MLE over index set $\tilde{A}$ with $\tilde{A}\supseteq A^0$. Denote by κ₀ the condition number of Σ⁰. If $\frac{{\kappa }_0|\tilde{A}|\log p}{\sqrt{n}}\to 0$ with p ≥ 2, then,

$$Lr\stackrel{P_0}{\to }{W}_{\left|B\right|},\text{if}\left|B\right|\text{is a constant;}\frac{Lr-\left|B\right|}{\sqrt{2\left|B\right|}}\stackrel{P_0}{\to }Z,\text{if}\left|B\right|\to \infty ,$$

where $B=\tilde{A}\backslash A^0,W_{|B|}$ follows a chi-square distribution χ² on |B| degrees of freedom and Z ∼ N(0, 1), respectively.

Proof of Theorem 1.

By Lemma 6, $\mathbb{P}\left({\widehat{\mathbf{\Omega }}}^{(0)}={\widehat{\mathbf{\Omega }}}_{A^0}\right)\to 1$; $\mathbb{P}\left({\widehat{\mathbf{\Omega }}}^{(1)}={\widehat{\mathbf{\Omega }}}_{A^0\cup B}\right)\to 1$, as n → ∞ under Assumptions 1 and 2. Then, the asymptotic distribution of the likelihood ratio follows immediately from Lemma 9. □

Proof of Proposition 1.

Let $\tilde{A}=A^0\cup B$. By Lemma 6, $\mathbb{P}\left({\widehat{\mathbf{\Omega }}}^{(1)}={\widehat{\mathbf{\Omega }}}_{A^0\cup B}\right)\to 1$, as n → ∞. Asymptotic normality of ${\text{vec}}_B\left({\widehat{\mathbf{\Omega }}}_{A^0\cup B}\right)$ follows from an expansion of the score equation. Specifically, note that

$$\begin{gathered} \sqrt{n}{\text{vec}}_B\left({\widehat{\mathbf{\Omega }}}_{A^0\cup B}-{\mathbf{\Omega }}^0\right)=\frac{\sqrt{n}}{2}{\left[{\mathit{I}}_{\tilde{A},\tilde{A}}^{-1}\right]}_{B,\tilde{A}} \\ \times \left({\text{vec}}_{\tilde{A}}(\mathbf{\Lambda })-{\text{vec}}_A\left(R\left({\widehat{\mathbf{\Delta }}}_{\tilde{A}}\right)\right)\right), \end{gathered}$$

where $R\left({\widehat{\mathbf{\Delta }}}_{\tilde{A}}\right)={\mathbf{\Sigma }}^0{\sum }_{i=2}^{\infty }{(-1)}^i{\left({\widehat{\mathbf{\Delta }}}_A{\mathbf{\Sigma }}^0\right)}^i$. Let $\mathit{J}={\mathit{I}}_{\tilde{A},\tilde{A}}^{-1}$ be as defined in (B.33) of the online supplementary material. Multiplying ${\mathit{J}}_{B,B}^{-1/2}$ on both sides of this identity, we obtain

$$\begin{gathered} \sqrt{n}{\mathit{J}}_{B,B}^{-1/2}{\text{vec}}_B\left({\widehat{\mathbf{\Omega }}}_{A^0\cup B}-{\mathbf{\Omega }}^0\right) \\ =\frac{\sqrt{n}}{2}{\mathit{J}}_{B,B}^{-1/2}{\mathit{J}}_{B,\tilde{A}}\left({\text{vec}}_{\tilde{A}}(\mathbf{\Lambda })-{\text{vec}}_{\tilde{A}}\left(R\left({\widehat{\mathbf{\Delta }}}_{\tilde{A}}\right)\right)\right). \end{gathered}$$ (A.16)

Next, we show that the first term tends to $N\left(\mathbf{0},{\mathit{I}}_{|B|\times |B|}\right)$ in distribution and the second term tends to 0 in probability. For the second term, following similar calculations as in (B.34) of the online supplementary material, we have that ${\Vert {\mathit{J}}_{B,B}^{-1/2}{\mathit{J}}_{B,\tilde{A}}\mathit{x}\Vert }_2^2={\mathit{x}}^{\top }\mathit{J}\mathit{x}-{\mathit{x}}^{\top }{\mathit{I}}_{A^0,A^0}^{-1}\mathit{x}\le {\mathit{x}}^{\top }\mathit{J}\mathit{x}\le {\lambda }_{\min }^{{}_{{}^{-2}}}\left({\mathbf{\Sigma }}^0\right)\Vert \mathit{x}{\Vert }_2^2$ for any $\mathit{x}\in {ℝ}^{|A|}$. This, together with (B.37) of the online supplementary material, implies that

$$\begin{gathered} {\Vert .5\sqrt{n}{\mathit{J}}_{B,B}^{-1/2}{\mathit{J}}_{B,\tilde{A}}{\text{vec}}_{\tilde{A}}\left(R\left({\widehat{\mathbf{\Delta }}}_A\right)\right)\Vert }_2\le .5\sqrt{n}{\Vert {\mathit{J}}^{1/2}{\text{vec}}_{\tilde{A}}\left(R\left({\widehat{\mathbf{\Delta }}}_{\tilde{A}}\right)\right)\Vert }_2 \\ \le .5\sqrt{n}{\lambda }_{\min }^{-1}\left({\mathbf{\Sigma }}^0\right){\Vert R\left({\widehat{\mathbf{\Delta }}}_{\tilde{A}}\right)\Vert }_2\le \sqrt{n}{\kappa }_0{\Vert {\mathbf{\Sigma }}^0{\widehat{\mathbf{\Delta }}}_{\tilde{A}}\Vert }_F^2 \\ =O_p\left(\frac{{\kappa }_0\left|\tilde{A}\right|\log p}{\sqrt{n}}\right)=o_p(1) \end{gathered}$$ (A.17)

under Assumption 2. For the first term, note that

$$\begin{gathered} \mathrm{cov}(\frac{1}{2}{\mathit{J}}_{B,B}^{-1/2}{\mathit{J}}_{B,\tilde{A}}{\text{vec}}_A\left(\mathit{X}{\mathit{X}}^{\top }-{\mathbf{\Sigma }}^0\right), \\ \frac{1}{2}{\mathit{J}}_{B,B}^{-1/2}{\mathit{J}}_{B,\tilde{A}}{\text{vec}}_{\tilde{A}}\left(\mathit{X}{\mathit{X}}^{\top }-{\mathbf{\Sigma }}^0\right)) \\ ={\mathit{J}}_{B,B}^{-1/2}{\mathit{J}}_{B,\tilde{A}}\mathrm{cov}\left(\frac{1}{2}{\text{vec}}_{\tilde{A}}\left(\mathit{X}{\mathit{X}}^{\top }-{\mathbf{\Sigma }}^0\right),\frac{1}{2}{\text{vec}}_{\tilde{A}}\left(\mathit{X}{\mathit{X}}^{\top }-{\mathbf{\Sigma }}^0\right)\right) \\ {\mathit{J}}_{\tilde{A},B}{\mathit{J}}_{B,B}^{-1/2} \\ ={\mathit{J}}_{B,B}^{-1/2}{\mathit{J}}_{B,\tilde{A}}{I}_{\tilde{A},\tilde{A}}{\mathit{J}}_{\tilde{A},B}{\mathit{J}}_{B,B}^{-1/2}=I_{\left|B\right|\times \left|B\right|}. \end{gathered}$$

where the second last equality uses the property of exponential family Brown (1986). Hence, by the central limit theorem, ${\text{vec}}_{\tilde{A}}(\mathbf{\Lambda })\stackrel{d}{\to }N\left(0,{\left[{\mathit{I}}_{\tilde{A},\tilde{A}}^{-1}\right]}_{B,B}\right)$. Finally, by Slutsky’s Theorem, we obtain that $\sqrt{n}{\text{vec}}_B\left({\widehat{\mathbf{\Omega }}}_{A^0\cup B}-{\mathbf{\Omega }}^0\right)\stackrel{d}{\to }N\left(0,{\left[{\mathit{I}}_{\tilde{A},\tilde{A}}^{-1}\right]}_{B,B}\right)$. This completes the proof. □

Proof of Proposition 2.

By Theorem 3 of Shen et al. (2013), $\mathbb{P}\left(\left\{{\widehat{\mathit{\beta }}}^{(1)}={\widehat{\mathit{\beta }}}_{A^0\cup B}^{ls}\right\}\right)\to 1$, as n, p → ∞. Hence, with probability tending to 1,

$$\begin{gathered} {\widehat{\mathit{\beta }}}_B^{(1)}={\text{vec}}_B\left({\left(X_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}{X}_{A^0\cup B}^{\top }Y\right) \\ ={\text{vec}}_B\left({\left(X_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}{X}_{A^0\cup B}^{\top }\left(X_{A^0\cup B}{\mathit{\beta }}_{A^0\cup B}^0+\mathit{ϵ}\right)\right) \\ ={\mathit{\beta }}_B^0+{\text{vec}}_B\left({\left(X_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}{X}_{A^0\cup B}^{\top }\mathit{ϵ}\right). \end{gathered}$$

Simple moment generating function calculations show that when |B| is fixed,

$${\text{vec}}_B\left({\left(X_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}{X}_{A^0\cup B}^{\top }\mathit{ϵ}\right)~N\left(\mathbf{0},{\left[{\left(X_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}\right]}_{B,B}\right).$$

Hence, $\sqrt{n}\left({\widehat{\mathit{\beta }}}_B^{(1)}-{\mathit{\beta }}_B^0\right)\stackrel{d}{\to }N\left(\mathbf{0},{\left[{\left(n^{-1}{X}_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}\right]}_{B,B}\right).$. This completes the proof. □

Proof of Corollary 1.

Let $\tilde{A}=A^0\cup B$. The result follows directly from Theorem 1. Specifically, we bound the asymptotic covariance matrix of ${\left[\sqrt{n}\left({\widehat{\omega }}_{ij}-{\omega }_{ij}^0\right)\right]}_{(i,j)\in B}$ for any B of fixed size. Note that the asymptotic covariance matrix of $\sqrt{n}{\text{vec}}_B\left({\widehat{\mathbf{\Omega }}}_{\tilde{A}}-{\mathbf{\Omega }}^0\right)$ can be bounded: ${\left[{\mathit{I}}_{\tilde{A},\tilde{A}}^{-1}\right]}_{B,B}\underset{\_}{\prec }{\left[{\mathit{I}}^{-1}\right]}_{B,B}=2{\left[{\mathbf{\Omega }}^0{\otimes }_s{\mathbf{\Omega }}^0\right]}_{B,B}$. Moreover, for any $(i,j),\left(i^{\prime },j^{\prime }\right)\in B,2{\left[{\mathbf{\Omega }}^0{\otimes }_s{\mathbf{\Omega }}^0\right]}_{(i,j),\left(i^{\prime },j^{\prime }\right)}$ can be written as

$$\begin{gathered} \frac{\sqrt{1+\mathbb{I}(i\ne j)}\sqrt{1+\mathbb{I}\left(i^{\prime }\ne j^{\prime }\right)}}{2}\text{tr} \\ \times \left(\left({\mathit{e}}_i{\mathit{e}}_j^{\top }+{\mathit{e}}_j{\mathit{e}}_i^{\top }\right){\mathbf{\Omega }}^0\left({\mathit{e}}_{i^{\prime }}{\mathit{e}}_{j^{\prime }}^{\top }+{\mathit{e}}_{j^{\prime }}{\mathit{e}}_{i^{\prime }}^{\top }\right){\mathbf{\Omega }}^0\right) \\ =\sqrt{1+\mathbb{I}(i\ne j)}\sqrt{1+\mathbb{I}\left(i^{\prime }\ne j^{\prime }\right)}\left({\omega }_{i^{\prime }j}^0{\omega }_{i{j}^{\prime }}^0+{\omega }_{jj\prime }^0{\omega }_{i{i}^{\prime }}^0\right). \end{gathered}$$

Using ${\text{vec}}_B(C)={\left(\sqrt{1+\mathbb{I}(i\ne j)}{c}_{ij}\right)}_{(i,j)\in B}$, the asymptotic variance of ${\left[\sqrt{n}\left({\widehat{\omega }}_{ij}-{\omega }_{ij}^0\right)\right]}_{(i,j)\in B}$ is upper bounded by a |B| × |B| matrix ${\left[{\omega }_{i^{\prime }j}^0{\omega }_{i{j}^{\prime }}^0+{\omega }_{j{j}^{\prime }}^0{\omega }_{i{i}^{\prime }}^0\right]}_{(i,j)\in B,\left(i^{\prime },j^{\prime }\right)\in B}$. Particularly, when B = {(i, j)}, this reduces to an upper bound on the asymptotic variance ${\left[{\omega }_{ij}^0\right]}^2+{\omega }_{ii}^0{\omega }_{jj}^0$. This completes the proof. □

Proof of Theorem 2.

By Theorem 3 of Shen et al. (2013), $\mathbb{P}\left(\left\{{\widehat{\mathit{\beta }}}^{(1)}={\widehat{\mathit{\beta }}}_{A^0\cup B}^{ls}\right\}\cap {\widehat{\mathit{\beta }}}^{(0)}={\widehat{\mathit{\beta }}}_{A^0}^{ls}\right)\to 1$, as n, p → ∞, by Assumption 1, where ${\widehat{\mathit{\beta }}}_A^{ls}$ is the least square estimate over A. Hence, in what follows, we focus our attention to event $\left\{{\widehat{\mathit{\beta }}}^{(1)}={\widehat{\mathit{\beta }}}_{A^0\cup B}^{ls}\right\}\cap \left\{{\widehat{\mathit{\beta }}}^{(0)}={\widehat{\mathit{\beta }}}_{A^0}^{ls}\right\}$.

Easily, after profiling out σ, we have ${\mathrm{\Lambda }}_n(B)=n\left(\log \left({\Vert y-X{\widehat{\mathit{\beta }}}^{(0)}\Vert }_2^2\right)-\log \left({\Vert y-X{\widehat{\mathit{\beta }}}^{(1)}\Vert }_2^2\right)\right)$. Then an application of Taylor’s expansion of log(1 − x) yields that

$$\begin{gathered} n\left(\log \left(\Vert y-X\mathit{\beta }{\Vert }_2^2\right)-\log \left({\Vert y-X{\mathit{\beta }}^0\Vert }_2^2\right)\right) \\ =-n\sum _{i=1}^{\infty }\frac{{\left(2{\mathit{ϵ}}^{\top }X\mathit{\delta }-\Vert X\mathit{\delta }{\Vert }_2^2\right)}^i}{i\Vert \mathit{ϵ}{\Vert }_2^{2i}} \end{gathered}$$ (A.18)

where δ = β − β⁰. Moreover, on the event $\left\{{\widehat{\mathit{\beta }}}^{(1)}={\widehat{\mathit{\beta }}}_{A^0\cup B}^{ls}\right\}\cap \left\{{\widehat{\mathit{\beta }}}^{(0)}={\widehat{\mathit{\beta }}}_{A^0}^{ls}\right\}$,

$$\begin{gathered} {\widehat{\mathit{\beta }}}^{(1)}={\mathit{\beta }}^0+{\left(X_{A^0\cup B}^{\top }{X}_{A^0\cup B}\right)}^{-1}{X}_{A^0\cup B}^{\top }\mathit{ϵ}\text{and} \\ {\widehat{\mathit{\beta }}}^{(0)}={\mathit{\beta }}^0+{\left(X_{A^0}^{\top }{X}_{A^0}\right)}^{-1}{X}_{A^0}^{\top }\mathit{ϵ}\text{,} \end{gathered}$$

implying that $X\left({\widehat{\mathit{\beta }}}^{(1)}-{\mathit{\beta }}^0\right)={\mathit{P}}_{A^0\cup B}\mathit{ϵ}$ and $X\left({\widehat{\mathit{\beta }}}^{(0)}-{\mathit{\beta }}^0\right)={\mathit{P}}_{A^0}\mathit{ϵ}$. Consequently, replacing $\mathit{\delta }={\widehat{\mathit{\beta }}}^{(1)}-{\mathit{\beta }}^0$, the right-hand of (A.18) reduces to

$$\begin{gathered} -n\sum _{i=1}^{\infty }\frac{{\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}\right)}^i}{i\Vert \mathit{ϵ}{\Vert }_2^{2i}}=-\frac{n}{\Vert \mathit{ϵ}{\Vert }_2^2} \\ \times \left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}+\sum _{i=2}^{\infty }\frac{{\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}\right)}^i}{i\Vert \mathit{ϵ}{\Vert }_2^{2(i-1)}}\right). \end{gathered}$$

Similarly, replacing δ by ${\widehat{\mathit{\beta }}}^{(1)}-{\mathit{\beta }}^0$, (A.18) becomes $-\frac{n}{\Vert \mathit{ϵ}{\Vert }_2^2}\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0}\mathit{ϵ}+{\sum }_{i=2}^{\infty }\frac{{\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0}\mathit{ϵ}\right)}^i}{i\Vert \mathit{ϵ}{\Vert }_2^{2(i-1)}}\right)$. Taking the difference leads to that ${\mathrm{\Lambda }}_n(B)=\frac{n{ϵ}^{\top }\left({\mathit{P}}_{A^0}{}_{\cup B}-{\mathit{P}}_{A^0}\right)ϵ}{\Vert ϵ{\Vert }_2^2}+R(ϵ)$, where R(ϵ) is

$$\begin{gathered} \sum _{i=2}^{\infty }\frac{{\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}\right)}^i-{\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0}\mathit{ϵ}\right)}^i}{i\Vert \mathit{ϵ}{\Vert }_2^{2(i-1)}} \\ =\sum _{i=2}^{\infty }\frac{{\mathit{ϵ}}^{\top }\left({\mathit{P}}_{A^0\cup B}-{\mathit{P}}_{A^0}\right)\mathit{ϵ}\left({\sum }_{j=0}^{i-1}{\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}\right)}^j{\left({\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0}\mathit{ϵ}\right)}^{i-j-1}\right)}{i\Vert \mathit{ϵ}{\Vert }_2^{2(i-1)}}. \end{gathered}$$

Note that ${\mathit{P}}_{A^0\cup B}-{\mathit{P}}_{A^0}$ is idempotent with the rank |B|. Moreover, ${\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\mathit{ϵ}}\le {\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}$. Thus, R(ϵ) is no greater than

$$\begin{gathered} {\mathit{ϵ}}^{\top }\left({\mathit{P}}_{A^0\cup B}-{\mathit{P}}_{A^0}\right)\mathit{ϵ}\sum _{i=2}^{\infty }{\left(\frac{{\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}}{\Vert \mathit{ϵ}{\Vert }_2^2}\right)}^{i-1} \\ ={\mathit{ϵ}}^{\top }\left({\mathit{P}}_{A^0\cup B}-{\mathit{P}}_{A^0}\right)\mathit{ϵ}\frac{{\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}}{\Vert \mathit{ϵ}{\Vert }_2^2}{\left(1-\frac{{\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}}{\Vert \mathit{ϵ}{\Vert }_2^2}\right)}^{-1} \end{gathered}$$

on the event that $\left\{{\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}<\Vert \mathit{ϵ}{\Vert }_2^2\right\}$. This, together with the facts that $n/\Vert \mathit{ϵ}{\Vert }_2^2\stackrel{\mathbb{P}}{\to }1\text{and}\left|A^0\right|/n\to 0$, implies that ${\mathrm{\Lambda }}_n(B)\stackrel{d}{\to }{\chi }^2(|B|)$ when |B| is fixed, and $\frac{{\mathrm{\Lambda }}_n(B)-|B|}{\sqrt{2|B|}}\stackrel{d}{\to }N(0,1)$ when |B| → ∞ and $\frac{\sqrt{|B|}\left(\left|A^0\right|+|B|\right)}{n}\to 0$, because

$$\begin{gathered} R(\mathit{ϵ})/\sqrt{\left|B\right|}\le \frac{{\mathit{ϵ}}^{\top }\left({\mathit{P}}_{A^0\cup B}-{\mathit{P}}_{A^0}\right)\mathit{ϵ}}{\sqrt{\left|B\right|}}\frac{{\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}}{\Vert \mathit{ϵ}{\Vert }_2^2} \\ \times {\left(1-\frac{{\mathit{ϵ}}^{\top }{\mathit{P}}_{A^0\cup B}\mathit{ϵ}}{\Vert \mathit{ϵ}{\Vert }_2^2}\right)}^{-1}\stackrel{\mathbb{P}}{\to }0 \end{gathered}$$

provided that $\frac{\sqrt{|B|}\left(\left|A^0\right|+|B|\right)}{n}\to 0$ and |B| → ∞. This completes the proof. □