Abstract
Large amounts of missing data could distort item parameter estimation and lead to biased ability estimates in educational assessments. Therefore, missing responses should be handled properly before estimating any parameters. In this study, two Monte Carlo simulation studies were conducted to compare the performance of four methods in handling missing data when estimating ability parameters. The methods were full-information maximum likelihood (FIML), zero replacement, and multiple imputation with chain equations utilizing classification and regression trees (MICE-CART) and random forest imputation (MICE-RFI). For the two imputation methods, missing responses were considered as a valid response category to enhance the accuracy of imputations. Bias, root mean square error, and the correlation between true ability parameters and estimated ability parameters were used to evaluate the accuracy of ability estimates for each method. Results indicated that FIML outperformed the other methods under most conditions. Zero replacement yielded accurate ability estimates when missing proportions were very high. The performances of MICE-CART and MICE-RFI were quite similar but these two methods appeared to be affected differently by the missing data mechanism. As the number of items increased and missing proportions decreased, all the methods performed better. In addition, the information on missing data could improve the performance of MICE-RFI and MICE-CART when the data set is sparse and the missing data mechanism is missing at random.
Keywords: ability estimation, missing data, multiple imputation, CART, random forest
Missing data are a common issue in educational assessments, and it may occur for a variety of reasons (Shi et al., 2019). For example, respondents may forget to answer some items inadvertently or they may not have enough time to answer some items at the end of an examination due to test speededness. It is also possible that respondents may prefer to omit some items just because they are unsure about the right answer. Since the presence of missing data could yield negative consequences such as bias in parameter estimates and decrease in statistical power (Roth, 1994), researchers developed several techniques to handle missing responses. In practice, omitted items are often regarded as wrong answers (i.e., zero replacement), based on the logic that respondents would have answered the item to get a score if they had really known the right answer (De Ayala et al., 2001). In addition to zero replacement, full-information maximum likelihood (FIML) and multiple imputation (MI) methods have also been highly recommended for dealing with missing responses (Schafer & Graham, 2002). Recently, the capabilities of MI have been further improved as MI and recursive partitioning methods were combined within a multivariate imputation by chained equations (MICE) framework (Van Buuren, 2007).
In item response theory (IRT), respondents’ ability levels are estimated based on their responses to a set of items. The presence of missing responses can have a detrimental influence on the parameter estimates when the methods to handle missing data are not suitable (Andreis & Ferrari, 2012). Therefore, previous studies have compared the performance of different methods including FIML, MI, and zero replacement for dealing with missing data within the IRT framework (e.g., Culbertson, 2011; De Ayala et al., 2001; Finch, 2008). Recently, there has been a growing interest in employing data mining methods (e.g., random forest, classification and regression trees) to handle missing data. Previous research showed that data mining methods outperformed traditional methods for handling missing data when estimating item parameters for IRT models (e.g., Andreis & Ferrari, 2012; Edwards & Finch, 2018); however, no studies made a thorough comparison of data mining methods and traditional missing data techniques for ability estimation in the context of IRT.
The purposes of the current study are twofold. First, this study aims to investigate the performance of different methods to handle missing data when estimating IRT ability parameters under several conditions. In the first simulation study, we compared the accuracy of ability estimates when missing responses were handled by FIML, zero replacement, MICE with classification and regression trees (MICE-CART), and MICE with random forest imputation (MICE-RFI). Simulation conditions were sample size, test length, missing data proportion, and missing data mechanism. Depending on the missing data mechanism, missing values themselves can also provide useful information considering that they are related to other observed values or values of missing data themselves. Therefore, the second purpose of the current study was to investigate whether incorporating missing responses into the imputation process with MICE could yield more precise ability estimates. The second simulation study was an extension of the first simulation study where we recoded missing responses as a new response category and used them in the imputation to improve the performance of MICE-CART and MICE-RFI. As for the first simulation study, the accuracy of resulting ability estimates was evaluated under different test lengths, sample sizes, missing data mechanisms, and missing proportions.
Literature Review
Missing Data Mechanisms
Handling missing data properly is an important task when estimating item and person parameters from a sparse response matrix. The decision regarding how missing data should be dealt with depends on several factors, and one of them is the missing data mechanism. Previous studies have already provided comprehensive discussions for the following missing data mechanisms: missing completely at random (MCAR), missing at random (MAR), and not missing at random (NMAR), and interested readers are encouraged to see Rubin (1976) and Graham (2012) for a comprehensive understanding of missing data analysis. To formulate the missing data mechanisms, let Y (I × J) be a response matrix with observed values Yo and missing values Ym, and R (I × J) be the corresponding missing indicator matrix. Each element Rij equals to 1 if the observation value Yij is missing and 0 otherwise. Rubin (1976) used the conditional distribution of R given Y to distinguish three missing data mechanisms. MCAR occurs when missingness is a completely random process, which means that there is no systematic cause for missing data, and the probability of missingness only depends on the probability distribution of R: P(R| Yo, Ym) = P(R). For MAR, the probability that a variable is missing depends on other observed variables in the data and it can be expressed as P(R| Yo, Ym) = P(R| Yo). When data are NMAR, the missingness is due to the variable itself, its covariates with other observed variables, or other unobserved variables in the study.
In practice, when researchers assume that missingness in response data occurs by chance, this condition represents MCAR (Huisman & Molenaar, 2001). If a respondent skips some items due to not knowing the correct answer, this condition may be an example of either MAR or NMAR based on the assumption regarding the underlying missingness mechanism (Finch, 2008). Specifically, the condition is considered as MAR when missing values are related to other measured variables such as a respondent’s responses to other items (Sulis & Porcu, 2017). For example, respondents’ ability levels could be reflected by the number of correct answers if estimated ability levels were partly related to missing responses (De Ayala et al., 2001). De Ayala et al. (2001) argued that highly proficient respondents only omitted items for which they did not know the answer. However, less proficient respondents were unable to distinguish items well and except for skipping unknown items, they might also skip items that they could have answered correctly if they spent enough time on the items. Unlike MAR, NMAR occurs when missing data are directly related to the value of the missing variable itself (Edwards & Finch, 2018). For example, items that respondents are expected to answer incorrectly are more likely to be skipped. In large-scale assessments, both MAR and NMAR are commonly seen. When the missing data mechanism is either MCAR or MAR, both FIML and MI could produce highly accurate parameter estimates (Little & Rubin, 2002). In addition, the zero replacement method assumes unanswered items are unknown to respondents, which might be either MAR or NMAR. Therefore, all these missing data mechanisms (MCAR, MAR, and NMAR) were investigated in the current study.
Methods to Handle Missing Responses
As previously mentioned, omitted items are often regarded as wrong answers (i.e., zero replacement) in large-scale educational assessments. For example, in PISA (Programme for International Student Assessment), TIMSS (Trends in International Mathematics and Science Study), and PIRLS (Progress in International Reading Literacy Study), missing responses are typically scored as incorrect when estimating abilities for students (Martin et al., 2007; Organisation for Economic Co-operation and Development, 2009). This approach assumes that respondents who skip some items on the test do not have adequate proficiency to find the correct answer and thus their missing responses should be considered incorrect. For a dichotomous item, the correct answer would be recoded as 1, the wrong or omitted answers would be recoded as 0 by using the zero-replacement method. However, previous research suggests that when the zero replacement method is used to handle missing data, this could result in highly biased estimates (Finch, 2008; Mislevy & Wu, 1996) because respondents may have to skip some items for different reasons, such as lack of test-taking engagement, anxiety, and test speededness. Therefore, treating missing responses as incorrect could lead to the underestimation of respondents’ true ability levels.
FIML is one of the most commonly used approaches to deal with missing data. It uses the maximum likelihood algorithm with all available data to estimate parameters, instead of replacing or imputing missing values (Eekhout et al., 2015). With FIML, respondents who have missing values in item A would be ignored when estimating item A’s parameters. But, if they respond to item B, their information in item B would still be used for item B’s parameter estimates. FIML could handle the estimation of parameters and their standard errors in a single step, which is more efficient and effective compared with data imputation methods (Graham, 2009). Furthermore, previous research showed that FIML tends to yield unbiased parameter estimates when the type of missingness is either MCAR or MAR (Enders & Bandalos, 2001). Finally, FIML is the default missing data technique in most IRT software programs, making this method convenient to use in practice (Edwards & Finch, 2018).
To date, MI has been widely used for handling missing data (e.g., Leacy et al., 2017; Rezvan et al., 2015). Following a Bayesian approach, MI creates multiple plausible data sets, with missing values replaced by imputed values, and then appropriately combines results from each of the plausible data sets (Sterne et al., 2009). Although several adaptations of MI have been proposed in the literature (e.g., Sulis & Porcu, 2008; Van Buuren & Oudshoorn, 1999), in this study we only discuss MICE-based methods. The MICE framework assumes that data are drawn from a multivariate distribution, and each incomplete variable can be imputed by iteratively sampling from a conditional distribution (Van Buuren & Oudshoorn, 1999). Specifically, let I = (I1, I2, . . ., Ik) be a set of k items where each of the items may be partially observed. When the missing data mechanism is MAR, Ik is imputed from the conditional distribution where t represents a Gibbs sampler iteration counter.
This approach provides greater flexibility in large data sets when there are different data types to impute. In addition, various estimation algorithms can be adopted within the MICE framework, such as MICE-CART and MICE-RFI. CART refers to classification and regression trees. It constructs a predictive model in the form of decision trees, by using a set of predictors and cut points to split the sample into several subgroups (Friedman et al., 2001). The splitting process is repeated several times to produce the most accurate model with the best split and the most homogenous subgroups. In each subgroup (also called leaf), the outcome variable can be either categorical or continuous, and it draws from the conditional distribution for a set of predictors that satisfy cut points (Akande et al., 2017). Van Buuren (2012) mentioned that the CART method shows its strengths when dealing with outliers, nonlinear relationships, and nonnormal distributions. These strengths also make CART a suitable method for data imputation. RFI refers to random forest imputation. Unlike CART that only creates a single decision tree, RFI creates a number of decision trees, which often yields higher variances across samples (Hastie et al., 2009). Therefore, RFI employs bootstrap methods to select a random subset of predictors for the splits on each iteration and aggregates results to identify the most stable predictive model. If there is a collinearity issue due to high correlations among predictors, RFI can address this issue by using highly correlated predictors in different iterations (Hayes et al., 2015).
Previous studies suggest that using either CART or RFI within the MICE framework could get unbiased parameter estimates with appropriate confidence intervals (Doove et al., 2014; Shah et al., 2014). In the context of IRT, MICE-RFI and MICE-CART were found to produce more accurate estimates for item parameters (Edwards & Finch, 2018), but no literature discussed their performance in the context of ability estimation. In this study, we assumed that respondents skipped items because they did not know the correct answers. Under this assumption, the presence of missing responses for a given item can inform the imputation of other items with missing responses. To utilize missing responses in the imputation process, missing responses can be recoded as a separate response category and included as predictors when replacing missing responses with imputed values. In the second simulation study, we applied this strategy to the imputation procedures with MICE-CART and MICE-RFI, which were denoted as MICE-CART2 and MICE-RFI2.
Simulation Study 1
Data Generation
The first Monte Carlo simulation study was conducted using the mirt (Chalmers, 2012) and mice packages (Van Buuren & Groothuis-Oudshoorn, 2010) in R (R Core Team, 2019). Data were generated under the 3PL (three-parameter logistic) IRT model. According to the 3PL model, the probability of a respondent with the ability parameter responding to item i correctly can be expressed as
| (1) |
where is the ability parameter, ai is the discrimination parameter, bi is the difficulty parameter, and ci is the lower asymptote, which is also known as the pseudo-guessing parameter (Birnbaum, 1968). The item parameter distributions were selected based on the simulation guidelines suggested by previous studies (Bulut & Sunbul, 2017; Feinberg & Rubright, 2016). Specifically, the ability parameters follow a normal distribution, θ ~ N(0, 0.7); difficulty parameters follow a uniform distribution, b ~U(−1.5, 1.5); discrimination parameters follow a log-normal distribution, a ~ ln N(0.3, 0.2); and pseudo-guessing parameters follow a beta distribution, c ~ Beta(20, 90). The selected sample sizes were 500, 1,000, and 3,000, respectively. The test length was modified using three conditions: 20, 40, and 60 items. Missing data proportions were 5%, 15%, 30%, and 40%.
The first study generated three types of missing data, MCAR, MAR, and NMAR. For MCAR, the desired proportions of missingness (5%, 15%, 30%, or 40%) were created randomly by replacing original responses with missing responses. For MAR, we divided the respondents into two groups based on the number of correct responses and split the data into two parts based on the mean value. The approach for generating MAR and NMAR was borrowed from previous research (Edwards & Finch, 2018; Enders, 2004; Finch, 2008). For MAR, the first data set including the high-ability group was generated with lower missing proportions and the second one including the low-ability group was generated with higher missing proportions. The average missing proportions were ensured to be equal to the desired missing proportions. For example, under 40% missing data condition, the high-ability group was generated about 30% missing data and the low-ability group was generated around 50% missing data. Finally, the average missing proportions were equal to 40%. These missing data were MAR because the missing values were related to observed variables—the number of correct responses to the nonmissing items. It should be noted that we did not use ability parameters for the MAR condition since missing data related to the latent traits could also be considered as NMAR cases (e.g., Rose et al., 2010; Sulis & Porcu, 2017).
Data generation with NMAR was similar to that of MAR. For NMAR, each examinee’s incorrect responses in the initial data set were assigned a higher probability of being missing while correct responses were assigned a lower probability of being missing. The mean missing proportions of the entire data set were equal to the desired proportions (i.e., 5%, 15%, 30%, or 40%). Again, we use the 40% missing data condition to describe the simulation process. For each item, incorrect responses were generated around 50% missing data, and correct responses were generated around 30% missing data. The average missing proportions were equaled to 40%. This was considered as NMAR because missing responses were related to their true values directly.
Data Analysis
For the MICE-CART and MICE-RFI methods, the current study conducted 20 iterations to impute five data sets in each replication. MICE-RFI grew 10 trees, which was the default number in the mice package. This study selected expected a posteriori (EAP) to estimate ability parameters. EAP is a noniterative technique based on the numerical evaluation of the mean and variance (Bock & Mislevy, 1982). The formula for the EAP estimation can be expressed as
| (2) |
where refers to a Gauss–Hermite quadrature point, refers to the likelihood function of given the response data and refers to the corresponding quadrature weight. EAP for ability estimates could be suitable for all response patterns, including all zero or perfect score patterns. Therefore, several studies adopted this technique for the ability parameter estimation in IRT (e.g., Sakumura & Hirose, 2017; Sinharay, 2016).
The outcomes of interest in this study were the comparisons between true ability parameters (based on the complete data sets) and estimated ability parameters (based on the data sets by using different methods to handle missing values). Bias, root mean square error (RMSE), and Pearson correlation between true ability parameters and estimated ability parameters were used to evaluate the precision of ability estimates for each condition. Bias was computed as
| (3) |
and RMSE was computed as
| (4) |
where represents the estimated ability parameter for respondent j after missing data were handled, represents respondent j’s true ability parameter based on the complete data set, and N represents the sample size. The smaller values of bias and RMSE indicated more accurate ability estimates. The Pearson correlation coefficient was calculated as
| (5) |
where represents the covariance between estimated and true ability parameters, represents the standard deviation of , and represents the standard deviation of . The higher correlations indicated more accurate ability estimates. It should be noted that we used estimated ability parameters based on the complete data sets to represent “true” values rather than ability parameters generated from the normal distribution since the estimation errors include two parts: one from the missing data methods and the other from the ability estimation method—EAP. Using the estimated ability parameters could exclude the estimation error caused by EAP. For all conditions described above, 100 replications were conducted. Since the mean bias value for each condition was close to zero to three decimal places, the results were not presented. The average RMSE and correlation results were reported.
Results of Simulation Study 1
Missing Completely at Random Results
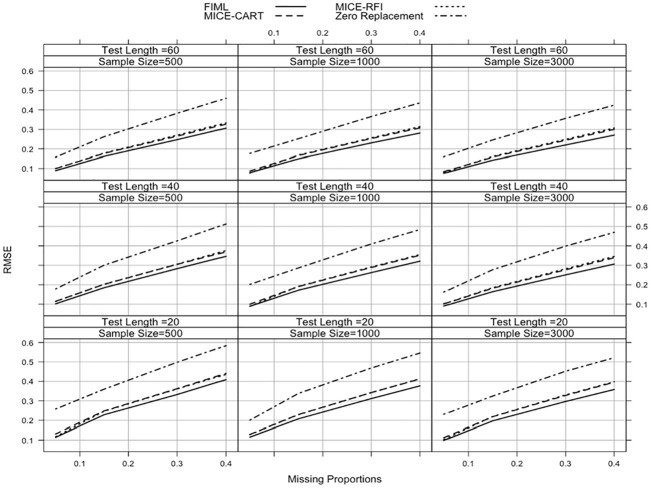
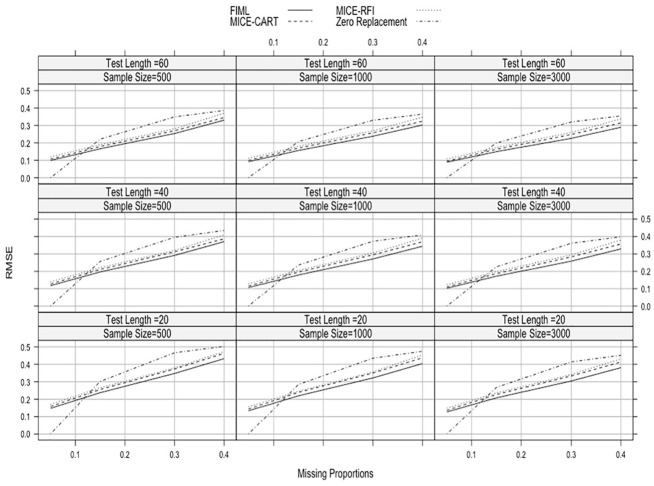
Figure 1 shows the RMSE results of ability estimates for MCAR across different simulation conditions. As the missing proportion increased, RMSE increased for all methods. Zero replacement was the least accurate method with respect to RMSE. It produced the largest RMSE value when the sample size was 500, the test length was 20, and the missing proportion was 40% (RMSE = 0.583). In general, FIML produced much smaller RMSE values, but when the sample size was 1,000, the test length was 60, and the missing proportion was 5%, the performance of MICE-RFI (RMSE = 0.078) was slightly better than FIML (RMSE = 0.079), followed by MICE-CART (RMSE = 0.088) and zero replacement (RMSE = 0.177). Although MICE-CART performed slightly better than MICE-RFI under most conditions, differences in the RMSE results were quite small. However, MICE-RFI always produced lower RMSE values than MICE-CART when the test length was 20, the sample size was 500, regardless of missing proportions. In general, increasing the test length improved the performance of missing data handling methods, but the sample size did not appear to affect RMSE results.
Figure 1.
Average RMSE values across the different simulation conditions when missing data type is MCAR.
Note. RMSE = root mean square error; MCAR = missing completely at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations utilizing classification and regression trees; MICE-RFI = multiple imputation with chain equations utilizing random forest imputation.
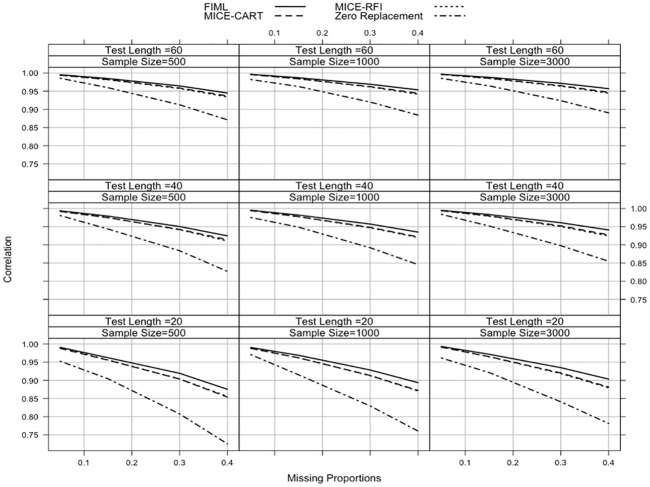
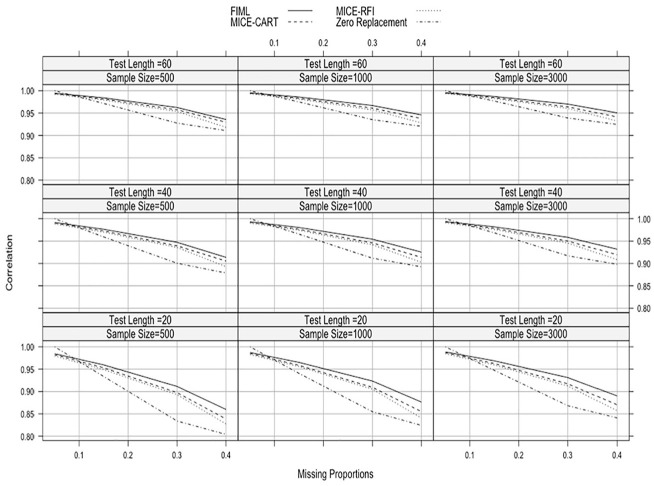
Figure 2 shows the correlation values between true and estimated ability parameters. Similar to the RMSE findings, zero replacement performed the worst across all simulation conditions. It produced the smallest correlation value when the sample size was 500, the test length was 20, and the missing proportion was 40% ( = .725). As the missing proportions increased, correlation values decreased for all methods, regardless of the sample size and test length. Compared with the other methods, FIML performed the best especially under the conditions with higher missing proportions. There was only one exception when the sample size was 1,000, the test length was 60, and the missing proportion was 5%, FIML, MICE-CART, and MICE-RFI yielded very similar correlation values (MICE-RFI: = .997; FIML and MICE-CART: = .996). In general, there were very negligible differences between MICE-CART and MICE-RFI. The sample size had no impact on the correlation results.
Figure 2.
Average correlation values across the different simulation conditions when missing data type is MCAR.
Note. MCAR = missing completely at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations utilizing classification and regression trees; MICE-RFI = multiple imputation with chain equations utilizing random forest imputation.
Missing at Random Results
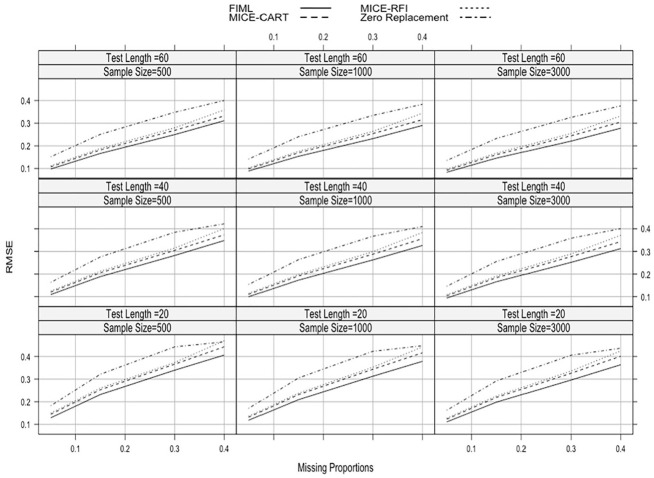
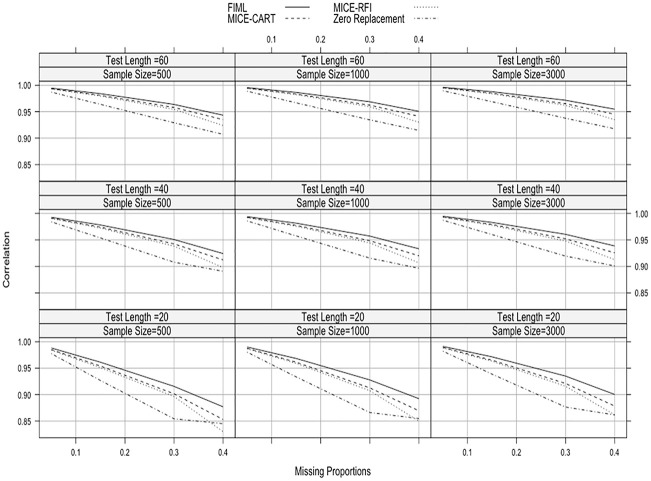
Figures 3 and 4 present the average RMSE and correlation results for MAR. In MAR, the performance gap between zero replacement and the other three methods narrowed down. Even though zero replacement performed the worst under most conditions, it was able to outperform MICE-RFI when the missing proportion was 40%, the test length was 20, and the sample size was either 500 or 1,000. Especially when the sample size was 500, the missing proportion was 40%, the test length was 20, MICE-RFI produced the largest RMSE and the lowest correlation values (RMSE = 0.470, = .830). FIML always yielded small RMSE and large correlation values, followed by MICE-CART. The smallest RMSE and the largest correlation values were obtained when the sample size was 3,000, the missing proportion was 5%, the test length was 60, and the missing data handling technique was FIML (RMSE = 0.083, = .996). Increasing missing proportions and shortening the test length resulted in higher RMSE and lower correlation values; however, sample size had no impact again. When missing proportions increased, the performance difference between MICE-CART and MICE-RFI became more apparent.
Figure 3.
Average RMSE values across the different simulation conditions when missing data type is MAR.
Note. RMSE = root mean square error; MAR = missing at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations utilizing classification and regression trees; MICE-RFI = multiple imputation with chain equations utilizing random forest imputation.
Figure 4.
Average correlation values across the different simulation conditions when missing data type is MAR.
Note. MAR = missing at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations with classification and regression trees; MICE-RFI = multiple imputation with chain equations with random forest imputation.
Not Missing at Random Results
Figures 5 and 6 show the average RMSE and correlation results for NMAR. In NMAR, zero replacement outperformed the other three methods when missing proportions were 5%, regardless of the sample size and test length. Furthermore, it was the only unbiased method since it produced bias and RMSE values of 0 and the correlation result of 1. Under other conditions, FIML always yielded smaller RMSE and larger correlation values, followed by MICE-CART, MICE-RFI, and last by zero replacement. Similarly, only the missing proportion and test length conditions had a noteworthy impact on the accuracy of ability estimates.
Figure 5.
Average RMSE values across the different simulation conditions when missing data type is NMAR.
Note. RMSE = root mean square error; NMAR = not missing at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations utilizing classification and regression trees; MICE-RFI = multiple imputation with chain equations utilizing random forest imputation.
Figure 6.
Average correlation values across the different simulation conditions when missing data type is NMAR.
Note. NMAR = not missing at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations utilizing classification and regression trees; MICE-RFI = multiple imputation with chain equations utilizing random forest imputation.
Simulation Study 2
Data Generation and Analysis
The second Monte Carlo simulation study was designed based on the findings from the first study. The MAR and NMAR conditions in the first simulation study indicated that lower ability respondents were more likely to skip items and items were more likely to be skipped if respondents were not able to answer correctly. Therefore, the assumption of zero replacement was met more properly and its performance in handling missing data was improved substantially. This finding inspired us to improve the performance of the MICE-based methods by using missingness as auxiliary information in the imputation process. Therefore, the second simulation study included two new methods, MICE-CART2 and MICE-RFI2, which considered missing responses as a separate response category. In addition, we removed the sample size conditions, considering sample size had little to no impact on the results in the first simulation study. To test the performances of MICE-CART2 and MICE-RFI2 more properly, we focused only on higher missing proportions, 30%, 40%, and 70%. The missing proportion of 70% was added to create a new condition in which the response data set is highly sparse and thus handing missing data properly would have significant consequences in terms of ability estimation. The three test length conditions were also included in the second simulation study. However, the second simulation study only focused on the MAR and NMAR conditions because missingness in the response data had useful information under these two mechanisms. We adopted the same method as the first simulation study when generating response data with the MAR and NMAR patterns.
For both MICE-CART2 and MICE-RFI2, we followed an iterative process. First, all missing values in dichotomous responses were recoded as a new category “2” except for Item 1 from which the imputation process was initiated. Second, the recoded items were used in the imputation process to replace missing values of Item 1. Next, the missing values (i.e., Category 2) of Item 2 were turned into their original status (not available) and imputed by using Item 1 (now Item 1 had no missing values) and other items on the test. This process was repeated until missing data for all items were imputed. For each condition, this study ran 20 iterations to get five MIs to get the combined results. There were 10 trees to grow for MICE-RFI methods. The second simulation study followed the same data analysis and evaluation criteria as the first study.
Results of Simulation Study 2
Missing at Random Results
Table 1 shows the mean bias, RMSE, and correlation results across different simulation conditions for MAR. As the test length increased, RMSE decreased and the correlation increased for all missing data handling methods. On the contrary, increasing missing proportions resulted in larger RMSE and smaller correlation values. These findings were consistent with the results of the first simulation study. One new finding was that zero replacement outperformed the other missing data handling techniques when missing proportions were 70%. However, FIML generally performed the best whereas zero replacement performed the worst, compared with the other methods. For most conditions, utilizing missing values as a separate response category improved the performance of MICE-RFI, but it had a negative impact on MICE-CART except when the test had 20 items with 40% missing values or data sets were highly sparse (70% missing data). When the missing proportions were 70% and the test had 60 items, MICE-CART produced the largest bias value (Bias = −0.005). Under 70% missing conditions, only FIML and zero-replacement methods retained the mean bias value close to zero to three decimal places, regardless of the test length (either 20, 40, or 60 items). Under sparse data scenarios, MICE-CART2 always produced lower RMSE and higher correlation values, followed by MICE-CART, MICE-RFI2, and MICE-RFI except for the 20-item condition. In this case, MICE-RFI2 outperformed MICE-CART.
Table 1.
Average Bias, RMSE, and Correlation Values for MAR.
| Method | Test length | Missing proportion (%) | Bias | RMSE | Correlation |
|---|---|---|---|---|---|
| FIML | 20 | 30 | 0.000 | 0.339 | .916 |
| MICE-CART | 20 | 30 | 0.000 | 0.366 | .902 |
| MICE-RFI2 | 20 | 30 | 0.000 | 0.367 | .900 |
| MICE-CART2 | 20 | 30 | 0.000 | 0.373 | .897 |
| MICE-RFI | 20 | 30 | 0.000 | 0.373 | .896 |
| Zero replacement | 20 | 30 | 0.000 | 0.443 | .854 |
| FIML | 40 | 30 | 0.000 | 0.282 | .951 |
| MICE-CART | 40 | 30 | 0.000 | 0.304 | .942 |
| MICE-RFI2 | 40 | 30 | 0.000 | 0.311 | .940 |
| MICE-CART2 | 40 | 30 | 0.000 | 0.314 | .938 |
| MICE-RFI | 40 | 30 | 0.000 | 0.314 | .938 |
| Zero replacement | 40 | 30 | 0.000 | 0.384 | .908 |
| FIML | 60 | 30 | 0.000 | 0.250 | .964 |
| MICE-CART | 60 | 30 | 0.000 | 0.268 | .958 |
| MICE-RFI2 | 60 | 30 | 0.000 | 0.278 | .955 |
| MICE-RFI | 60 | 30 | 0.000 | 0.280 | .954 |
| MICE-CART2 | 60 | 30 | 0.000 | 0.283 | .953 |
| Zero replacement | 60 | 30 | 0.000 | 0.348 | .929 |
| FIML | 20 | 40 | 0.000 | 0.406 | .877 |
| MICE-CART2 | 20 | 40 | 0.000 | 0.437 | .857 |
| MICE-CART | 20 | 40 | 0.000 | 0.443 | .853 |
| MICE-RFI2 | 20 | 40 | 0.000 | 0.445 | .850 |
| Zero replacement | 20 | 40 | 0.000 | 0.465 | .845 |
| MICE-RFI | 20 | 40 | 0.000 | 0.470 | .830 |
| FIML | 40 | 40 | 0.000 | 0.348 | .924 |
| MICE-CART | 40 | 40 | 0.000 | 0.373 | .912 |
| MICE-CART2 | 40 | 40 | 0.000 | 0.378 | .910 |
| MICE-RFI2 | 40 | 40 | 0.000 | 0.382 | .908 |
| MICE-RFI | 40 | 40 | 0.000 | 0.401 | .898 |
| Zero replacement | 40 | 40 | 0.000 | 0.422 | .891 |
| FIML | 60 | 40 | 0.000 | 0.311 | .943 |
| MICE-CART | 60 | 40 | 0.000 | 0.332 | .935 |
| MICE-CART2 | 60 | 40 | 0.000 | 0.341 | .931 |
| MICE-RFI2 | 60 | 40 | 0.000 | 0.344 | .930 |
| MICE-RFI | 60 | 40 | 0.000 | 0.358 | .924 |
| Zero replacement | 60 | 40 | 0.000 | 0.400 | .907 |
| Zero Replacement | 20 | 70 | 0.000 | 0.585 | .738 |
| FIML | 20 | 70 | 0.000 | 0.658 | .642 |
| MICE-CART2 | 20 | 70 | 0.000 | 0.681 | .607 |
| MICE-RFI2 | 20 | 70 | 0.000 | 0.691 | .572 |
| MICE-CART | 20 | 70 | 0.000 | 0.705 | .580 |
| MICE-RFI | 20 | 70 | 0.000 | 0.747 | .469 |
| Zero replacement | 40 | 70 | 0.000 | 0.543 | .812 |
| FIML | 40 | 70 | 0.000 | 0.579 | .776 |
| MICE-CART2 | 40 | 70 | 0.000 | 0.604 | .749 |
| MICE-CART | 40 | 70 | −0.004 | 0.622 | .733 |
| MICE-RFI2 | 40 | 70 | −0.001 | 0.631 | .726 |
| MICE-RFI | 40 | 70 | −0.001 | 0.698 | .640 |
| Zero replacement | 60 | 70 | 0.000 | 0.523 | .838 |
| FIML | 60 | 70 | 0.000 | 0.539 | .820 |
| MICE-CART2 | 60 | 70 | −0.001 | 0.559 | .803 |
| MICE-CART | 60 | 70 | −0.005 | 0.568 | .796 |
| MICE-RFI2 | 60 | 70 | −0.001 | 0.585 | .787 |
| MICE-RFI | 60 | 70 | −0.001 | 0.660 | .709 |
Note. RMSE = root mean square error; MAR = missing at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations utilizing classification and regression trees; MICE-RFI = multiple imputation with chain equations utilizing random forest imputation.
Not Missing at Random Results
Mean bias, RMSE, and correlation results across different simulation conditions for NMAR are presented in Table 2. Consistent with previous findings, increasing the number of items and decreasing missing proportions improved the performance of each missing data handling method. FIML outperformed the other missing data handling methods across all conditions, but it yielded a negative bias when the test had 70% missing values and the test length was 60 items (Bias = 0.001). While zero replacement kept the mean bias value close to zero to three decimal places under all conditions, it performed the worst for most conditions except when missing proportions were 70% and the test had 40 or 60 items. Under these two conditions, MICE-RFI2 and MICE-CART2 produced the largest RMSE and the smallest correlation values. In addition, using missing values as a separate category always improved the performance of MICE-RFI but weakened the performance of MICE-CART. When the test had 20 items and 40% missing data, MICE-CART2 produced lower RMSE value (0.456) and higher correlation value ( = .842) than MICE-CART (RMSE = 0.463, = .839). Among these four MICE-based methods, MICE-CART always produced the lowest RMSE and highest correlation values.
Table 2.
Average Bias, RMSE, and Correlation Values for NMAR.
| Method | Test length | Missing proportion (%) | Bias | RMSE | Correlation |
|---|---|---|---|---|---|
| FIML | 20 | 30 | 0.000 | 0.348 | .911 |
| MICE-RFI2 | 20 | 30 | 0.000 | 0.371 | .898 |
| MICE-CART | 20 | 30 | 0.000 | 0.373 | .897 |
| MICE-CART2 | 20 | 30 | 0.000 | 0.375 | .896 |
| MICE-RFI | 20 | 30 | 0.000 | 0.379 | .893 |
| Zero replacement | 20 | 30 | 0.000 | 0.466 | .834 |
| FIML | 40 | 30 | 0.000 | 0.291 | .947 |
| MICE-CART | 40 | 30 | 0.000 | 0.312 | .939 |
| MICE-RFI2 | 40 | 30 | 0.000 | 0.318 | .937 |
| MICE-CART2 | 40 | 30 | 0.000 | 0.319 | .936 |
| MICE-RFI | 40 | 30 | 0.000 | 0.320 | .936 |
| Zero replacement | 40 | 30 | 0.000 | 0.395 | .901 |
| FIML | 60 | 30 | 0.000 | 0.254 | .962 |
| MICE-CART | 60 | 30 | 0.000 | 0.270 | .957 |
| MICE-CART2 | 60 | 30 | 0.000 | 0.281 | .954 |
| MICE-RFI2 | 60 | 30 | 0.000 | 0.281 | .954 |
| MICE-RFI | 60 | 30 | 0.000 | 0.282 | .954 |
| Zero replacement | 60 | 30 | 0.000 | 0.350 | .928 |
| FIML | 20 | 40 | 0.000 | 0.433 | .860 |
| MICE-CART2 | 20 | 40 | 0.000 | 0.456 | .842 |
| MICE-RFI2 | 20 | 40 | 0.000 | 0.460 | .839 |
| MICE-CART | 20 | 40 | 0.000 | 0.463 | .839 |
| MICE-RFI | 20 | 40 | 0.000 | 0.473 | .827 |
| Zero replacement | 20 | 40 | 0.000 | 0.503 | .804 |
| FIML | 40 | 40 | 0.000 | 0.370 | .914 |
| MICE-CART | 40 | 40 | 0.000 | 0.386 | .905 |
| MICE-CART2 | 40 | 40 | 0.000 | 0.393 | .901 |
| MICE-RFI2 | 40 | 40 | 0.000 | 0.401 | .898 |
| MICE-RFI | 40 | 40 | 0.000 | 0.409 | .893 |
| Zero replacement | 40 | 40 | 0.000 | 0.434 | .879 |
| FIML | 60 | 40 | 0.000 | 0.331 | .936 |
| MICE-CART | 60 | 40 | 0.000 | 0.346 | .929 |
| MICE-CART2 | 60 | 40 | 0.000 | 0.352 | .926 |
| MICE-RFI2 | 60 | 40 | 0.000 | 0.364 | .922 |
| MICE-RFI | 60 | 40 | 0.000 | 0.370 | .918 |
| Zero replacement | 60 | 40 | 0.000 | 0.386 | .911 |
| FIML | 20 | 70 | 0.000 | 0.680 | .618 |
| MICE-CART | 20 | 70 | −0.004 | 0.708 | .585 |
| MICE-RFI2 | 20 | 70 | 0.000 | 0.733 | .491 |
| MICE-RFI | 20 | 70 | 0.000 | 0.738 | .487 |
| MICE-CART2 | 20 | 70 | 0.000 | 0.754 | .485 |
| Zero replacement | 20 | 70 | 0.000 | 0.777 | .463 |
| FIML | 40 | 70 | 0.000 | 0.635 | .728 |
| MICE-CART | 40 | 70 | −0.010 | 0.652 | .708 |
| MICE-RFI | 40 | 70 | −0.001 | 0.683 | .660 |
| Zero replacement | 40 | 70 | 0.000 | 0.687 | .665 |
| MICE-RFI2 | 40 | 70 | −0.001 | 0.706 | .634 |
| MICE-CART2 | 40 | 70 | 0.001 | 0.727 | .606 |
| FIML | 60 | 70 | 0.001 | 0.595 | .779 |
| MICE-CART | 60 | 70 | −0.011 | 0.601 | .770 |
| Zero replacement | 60 | 70 | 0.000 | 0.635 | .739 |
| MICE-RFI | 60 | 70 | −0.001 | 0.643 | .727 |
| MICE-RFI2 | 60 | 70 | −0.001 | 0.676 | .698 |
| MICE-CART2 | 60 | 70 | 0.001 | 0.682 | .683 |
Note. RMSE = root mean square error; NMAR = not missing at random; FIML = full-information maximum likelihood; MICE-CART = multiple imputation with chain equations utilizing classification and regression trees; MICE-RFI = multiple imputation with chain equations utilizing random forest imputation.
Discussion
A highly important task in educational assessments utilizing IRT is to obtain accurate item and ability parameter estimates; but the existence of missing responses is inevitable, and it would have a detrimental influence on the accuracy of estimated parameters when missing data are not handled properly (Andreis & Ferrari, 2012). While previous studies focused on the effects of missing data handling methods on item parameter estimates (Edwards & Finch, 2018; Finch, 2008) and ability estimates (Culbertson, 2011), no studies made a thorough comparison of traditional missing data handling methods and data mining methods for ability estimates. In this study, we conducted two Monte Carlo simulation studies to compare the performances of missing data handling methods when estimating ability parameters from dichotomous item responses with missing values. In the first simulation study, we selected four missing data handling methods, namely, zero replacement, FIML, MICE-CART, and MICE-RFI. The first two are commonly used methods in the missing data literature and the latter two are the two new methods utilizing the CART and RFI algorithms within the MICE framework. To evaluate the performances of these methods under different data conditions, missing data mechanisms (MCAR, MAR, and NMAR), missing proportions (5%, 15%, 30%, and 40%), test lengths (20, 40, and 60 items), and sample sizes (500, 1,000, and 3,000) were manipulated. The relative performances of the missing data handling methods were evaluated based on RMSE and correlation values between estimated and true ability parameters.
The first simulation study indicated that the missing data mechanism, the proportion of missing data, and test length could influence the accuracy of ability parameters obtained from a sparse response data set. However, the sample size had almost no impact on the results. This result ties well with previous studies wherein sample size has a negligible effect on ability estimation in IRT (Bulut et al., 2017; de la Torre & Song, 2009). Among the four methods for handling missing data, the zero replacement method performed the worst under most conditions. A similar conclusion was reached by previous research on this method (De Ayala et al., 2001). However, the performance of the zero replacement method appeared to improve under the MAR and NMAR conditions. With MAR and NMAR, it was relatively more reasonable to treat omitted responses as incorrect answers, which yielded more accurate ability estimates especially when the missing proportion was very small.
Another important finding from the first simulation study is that MICE-CART outperformed MICE-RFI under most conditions but the difference between the two methods was negligible. A similar finding was also reported by Edwards and Finch (2018) who compared the performance of MICE-CART and MICE-RFI in estimating IRT item parameters from a sparse response data set. A possible explanation for this finding might be that the CART and random forest (RF) algorithms work quite similarly as recursive partitioning methods. CART builds a prediction model based on a single decision tree, while RF creates multiple decision trees based on bootstrapped samples of data and combines the predictions from all decision trees to build a final prediction model. Furthermore, RF inherits most properties of CART, such as outlier handling and the ability to utilize nonlinear relationships in the data. Therefore, the two algorithms appeared to function very similarly within the MICE framework as they created imputed values for missing responses. However, when dealing with large volumes of data, MICE-CART might be a more desirable method for handling missing responses compared with MICE-RFI, due to its lower computational cost.
To further evaluate the effect of using missing values as auxiliary information in the imputation process, a second simulation study was considered as an extension of the first one. Based on the results of the first simulation study, the second study ignored sample size due to its negligible impact on the accuracy of ability estimates. Also, the second study only focused on the MAR and NMAR conditions that enabled incorporating valuable information from missing values into the imputation process. Findings indicated that utilizing missing values in the imputation process worked well for MICE-RFI but weakened the accuracy of MICE-CART when missing proportions were either 30% or 40%. One possible reason was that under the MAR and NMAR conditions, systematic missingness in the data appeared to provide valuable information for each decision tree created by MICE-RFI2. Consequently, the decision trees in MICE-RFI2 were more informative and they performed better than those in MICE-RFI. In addition, because MICE-CART only created a single decision tree, this approach could possibly consider low rates of missing responses as noise when constructing a decision tree model. This could explain why the performance of MICE-CART2 tends to improve when the missing proportion went up to 70%. When missing proportions were 70%, the new approach improved MICE-based methods under MAR conditions, but it was not suitable for NMAR conditions with large numbers of items, which might be related to their underlying assumptions. MAR assumed that missing values were related to other observed variables, and thus incorporating the missing information from other variables would be meaningful. However, NMAR assumed missing values were only related to themselves, and thus the missing information from other variables might not be as valuable as it was for MAR, especially for highly sparse data. Consequently, adding irrelevant information to the model appeared to be detrimental to the accuracy of ability estimation.
The results of both simulation studies also indicated that using FIML to deal with missing data could result in higher accuracy in the estimation of ability parameters, compared with the zero replacement and MICE methods under most conditions. One possible reason for FIML performing better than the MICE methods was insufficient numbers of repeated imputations. Previous research examined how many imputations could make MI and FIML equivalent, and at least 20 imputations for each data set were recommended (Graham et al., 2007). In this study, we only conducted five imputations for each data set and obtained very similar results for FIML, MICE-CART, and MICE-RFI. Therefore, it is possible that increasing the number of imputations could yield better results for MICE-CART and MICE-RFI. In addition, this study adopted EAP to estimate ability parameters, but previous research indicated that different missing data conditions could influence the performance of EAP in ability estimation (De Ayala et al., 2001). Therefore, the potential interaction between missing data conditions and the ability estimation procedure might have affected the performance of the methods used for handling missing data in the current study.
There are several implications for the current study. In educational assessments with high proportions of missing responses (e.g., formative assessments, low-stakes tests), increasing the number of items could improve the accuracy of respondents’ ability estimates. FIML is recommended to handle missing responses when estimating ability parameters from sparse response data sets due to its convenience and high accuracy in handling missing values. However, if researchers intended to get a complete data set for further analysis, FIML would be inadequate. Instead, MICE-based methods can provide a complete data set with imputed missing values to conduct further data analysis. When the data set is highly response sparse and the missing data mechanism is not clear, FIML and zero-replacement methods can be adopted to handle missing values. However, when the missing values follow the MCAR mechanism and missing proportions are not high, researchers and practitioners should avoid the zero-replacement method. When the response data set includes relatively high missing proportions and researchers attempt to use MICE-RFI, adding missing values in the imputation process could provide more precise results when estimating ability parameters in IRT.
While the current study sought to make a comprehensive comparison of traditional missing data handling methods and data mining imputation methods for ability estimates, there remains room for improvement. First, the current study only discussed CART and RFI as they were readily available in the mice package. Future research should adopt alternative data mining approaches such as stochastic gradient tree boosting and C5.0 (Ramosaj & Pauly, 2017) within the MICE framework and evaluate their performance. Second, the current results were based on the fixed-length assessment scenario in which all test takers responded to the same set of items and test speededness was considered. Other scenarios including computerized adaptive tests and the presence of test speededness should also be investigated in the future. Third, this study only focused on dichotomous items in a unidimensional test scenario. Future studies should examine the performance of the missing data handling methods for ability estimates for polytomous items as well as under a multidimensional test scenario.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: Jiaying Xiao  https://orcid.org/0000-0001-9513-6477
https://orcid.org/0000-0001-9513-6477
References
- Akande O., Li F., Reiter J. (2017). An empirical comparison of multiple imputation methods for categorical data. The American Statistician, 71(2), 162-170. 10.1080/00031305.2016.1277158 [DOI] [Google Scholar]
- Andreis F., Ferrari P. A. (2012). Missing data and parameters estimates in multidimensional item response model. Electronic Journal of Applied Statistical Analysis, 5(3), 431-437. 10.1285/i20705948v5n3p431 [DOI] [Google Scholar]
- Birnbaum A. (1968). Some latent trait models and their use in inferring an examinee’s ability. In Lord F. M., Novick M. R. (Eds.), Statistical theories of mental test scores (pp. 397-479). Addison-Wesley. [Google Scholar]
- Bock R. D., Mislevy R. J. (1982). Adaptive EAP estimation of ability in a microcomputer environment. Applied Psychological Measurement, 6(4), 431-444. 10.1177/014662168200600405 [DOI] [Google Scholar]
- Bulut O., Davison M. L., Rodriguez M. C. (2017). Estimating between-person and within-person subscore reliability with profile analysis. Multivariate Behavioral Research, 52(1), 86-104. 10.1080/00273171.2016.1253452 [DOI] [PubMed] [Google Scholar]
- Bulut O., Sunbul Ö. (2017). Monte Carlo simulation studies in item response theory with the R programming language. Journal of Measurement and Evaluation in Education and Psychology, 8(3), 266-287. 10.21031/epod.305821 [DOI] [Google Scholar]
- Chalmers R. P. (2012). mirt: A multidimensional item response theory package for the R environment. Journal of Statistical Software, 48(6), 1-29. 10.18637/jss.v048.i06 [DOI] [Google Scholar]
- Culbertson M. (2011, April 9-11). Is it wrong? Handling missing responses in IRT [Paper presentation]. Annual meeting of the National Council of Measurement in Education, New Orleans, LA, United States. [Google Scholar]
- De Ayala R. J., Plake B. S., Impara J. C. (2001). The impact of omitted responses on the accuracy of ability estimation in item response theory. Journal of Educational Measurement, 38(3), 213-234. 10.1111/j.1745-3984.2001.tb01124.x [DOI] [Google Scholar]
- de la Torre J., Song H. (2009). Simultaneous estimation of overall and domain abilities: A higher-order IRT model approach. Applied Psychological Measurement, 33(8), 620-639. 10.1177/0146621608326423 [DOI] [Google Scholar]
- Doove L. L., Van Buuren S., Dusseldorp E. (2014). Recursive partitioning for missing data imputation in the presence of interaction effects. Computational Statistics & Data Analysis, 72, 92-104. 10.1016/j.csda.2013.10.025 [DOI] [Google Scholar]
- Edwards J. M., Finch W. H. (2018). Recursive partitioning methods for data imputation in the context of item response theory: A Monte Carlo simulation. Psicológica Journal, 39(1), 88-117. 10.2478/psicolj-2018-0005 [DOI] [Google Scholar]
- Eekhout I., Enders C. K., Twisk J. W., de Boer M. R., de Vet H. C., Heymans M. W. (2015). Analyzing incomplete item scores in longitudinal data by including item score information as auxiliary variables. Structural Equation Modeling, 22(4), 588-602. 10.1080/10705511.2014.937670 [DOI] [Google Scholar]
- Enders C. K. (2004). The impact of missing data on sample reliability estimates: Implications for reliability reporting practices. Educational and Psychological Measurement, 64, 419-436. 10.1177/0013164403261050 [DOI] [Google Scholar]
- Enders C. K., Bandalos D. L. (2001). The relative performance of full information maximum likelihood estimation for missing data in structural equation models. Structural Equation Modeling, 8(3), 430-457. 10.1207/S15328007SEM0803_5 [DOI] [Google Scholar]
- Feinberg R. A., Rubright J. D. (2016). Conducting simulation studies in psychometrics. Educational Measurement: Issues and Practice, 35(2), 36-49. 10.1111/emip.12111 [DOI] [Google Scholar]
- Finch H. (2008). Estimation of item response theory parameters in the presence of missing data. Journal of Educational Measurement, 45(3), 225-245. 10.1111/j.1745-3984.2008.00062.x [DOI] [Google Scholar]
- Friedman J., Hastie T., Tibshirani R. (2001). The elements of statistical learning (Vol. 1, pp. 337-387). Springer. [Google Scholar]
- Graham J. W. (2009). Missing data analysis: Making it work in the real world. Annual Review of Psychology, 60, 549-576. 10.1146/annurev.psych.58.110405.085530 [DOI] [PubMed] [Google Scholar]
- Graham J. W. (2012). Missing data theory. In Missing data (pp. 3-46). Springer. [Google Scholar]
- Graham J. W., Olchowski A. E., Gilreath T. D. (2007). How many imputations are really needed? Some practical clarifications of multiple imputation theory. Prevention Science, 8(3), 206-213. 10.1007/s11121-007-0070-9 [DOI] [PubMed] [Google Scholar]
- Hastie T., Tibshirani R., Friedman J. (2009). The elements of statistical learning: Data mining, inference, and prediction. Springer. [Google Scholar]
- Hayes T., Usami S., Jacobucci R., McArdle J. J. (2015). Using Classification and Regression Trees (CART) and random forests to analyze attrition: Results from two simulations. Psychology and Aging, 30(4), 911-929. 10.1037/pag0000046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huisman M., Molenaar I. W. (2001). Imputation of missing scale data with item response models. In Essays on item response theory (pp. 221-244). Springer. [Google Scholar]
- Leacy F. P., Floyd S., Yates T. A., White I. R. (2017). Analyses of sensitivity to the missing-at-random assumption using multiple imputation with delta adjustment: Application to a tuberculosis/HIV prevalence survey with incomplete HIV-status data. American Journal of Epidemiology, 185(4), 304-315. 10.1093/aje/kww107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little R. J. A., Rubin D. B. (2002). Statistical analysis with missing data (2nd ed.). Wiley. [Google Scholar]
- Martin M. O., Mullis I. V.S., Kennedy A. M. (Eds.). (2007). PIRLS 2006 technical report. TIMSS & PIRLS International Study Center, Boston College. [Google Scholar]
- Mislevy R. J., Wu P. K. (1996, June). Missing responses and IRT ability estimation: Omits, choice, time limits, and adaptive testing (ETS Research Report Series, Vol. 1996, Issue 2). 10.1002/j.2333-8504.1996.tb01708.x [DOI] [Google Scholar]
- Organisation for Economic Co-operation and Development. (2009). Pisa 2006 technical report. https://www.oecd.org/pisa/data/42025182.pdf
- Ramosaj B., Pauly M. (2017). Who wins the Miss Contest for imputation methods? Our vote for Miss BooPF. arXiv. https://arxiv.org/abs/1711.11394
- R Core Team. (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing. [Google Scholar]
- Rezvan P. H., Lee K. J., Simpson J. A. (2015). The rise of multiple imputation: a review of the reporting and implementation of the method in medical research. BMC Medical Research Methodology, 15(1), Article 30. 10.1186/s12874-015-0022-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose N., Von Davier M., Xu X. (2010). Modeling nonignorable missing data with item response theory (IRT) (ETS Research Report Series, Vol. 2010, Issue 1). 10.1002/j.2333-8504.2010.tb02218.x [DOI]
- Roth P. L. (1994). Missing data: A conceptual review for applied psychologists. Personnel Psychology, 47(3), 537-560. 10.1111/j.1744-6570.1994.tb01736.x [DOI] [Google Scholar]
- Rubin D. B. (1976). Inference and missing data. Biometrika, 63(3), 581-592. 10.2307/2335739 [DOI] [Google Scholar]
- Sakumura T., Hirose H. (2017). A bias reduction method for ability estimates in adaptive online IRT testing systems. International Journal of Smart Computing and Artificial Intelligence, 1(1), 59-72. [Google Scholar]
- Schafer J. L., Graham J. W. (2002). Missing data: Our view of the state of the art. Psychological Methods, 7(2), 147-177. 10.1037/1082-989X.7.2.147 [DOI] [PubMed] [Google Scholar]
- Shah A. D., Bartlett J. W., Carpenter J., Nicholas O., Hemingway H. (2014). Comparison of random forest and parametric imputation models for imputing missing data using MICE: A CALIBER study. American Journal of Epidemiology, 179(6), 764-774. 10.1093/aje/kwt312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi D., Lee T., Fairchild A. J., Maydeu-Olivares A. (2019). Fitting ordinal factor analysis models with missing data: A comparison between pairwise deletion and multiple imputation. Educational and Psychological Measurement, 80(1), 41-66. 10.1177/0013164419845039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinharay S. (2016). The choice of the ability estimate with asymptotically correct standardized person-fit statistics. British Journal of Mathematical and Statistical Psychology, 69(2), 175-193. [DOI] [PubMed] [Google Scholar]
- Sterne J. A., White I. R., Carlin J. B., Spratt M., Royston P., Kenward M. G., Wood A.M., Carpenter J. R. (2009). Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ, 338, b2393 10.1136/bmj.b2393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sulis I., Porcu M. (2008, January). Assessing the effectiveness of a stochastic regression imputation method for ordered categorical data (Working Paper 2008/04). https://crenos.unica.it/crenos/sites/default/files/wp/08-04.pdf
- Sulis I., Porcu M. (2017). Handling missing data in item response theory. Assessing the accuracy of a multiple imputation procedure based on latent class analysis. Journal of Classification, 34(2), 327-359. 10.1007/s00357-017-9220-3 [DOI] [Google Scholar]
- Van Buuren S. (2007). Multiple imputation of discrete and continuous data by fully conditional specification. Statistical Methods in Medical Research, 16(3), 219-242. 10.1177/0962280206074463 [DOI] [PubMed] [Google Scholar]
- Van Buuren S. (2012). Flexible imputation of missing data. CRC Press; 10.1201/b1182 [DOI] [Google Scholar]
- Van Buuren S., Groothuis-Oudshoorn K. (2010). mice: Multivariate imputation by chained equations in R. Journal of Statistical Software, 45(3), 1-68. 10.18637/jss.v045.i03 [DOI] [Google Scholar]
- Van Buuren S., Oudshoorn K. (1999). Flexible multivariate imputation by MICE. TNO. [Google Scholar]