The string decomposition problem and its applications to centromere analysis and assembly

Abstract

Motivation

Recent attempts to assemble extra-long tandem repeats (such as centromeres) faced the challenge of translating long error-prone reads from the nucleotide alphabet into the alphabet of repeat units. Human centromeres represent a particularly complex type of high-order repeats (HORs) formed by chromosome-specific monomers. Given a set of all human monomers, translating a read from a centromere into the monomer alphabet is modeled as the String Decomposition Problem. The accurate translation of reads into the monomer alphabet turns the notoriously difficult problem of assembling centromeres from reads (in the nucleotide alphabet) into a more tractable problem of assembling centromeres from translated reads.

Results

We describe a StringDecomposer (SD) algorithm for solving this problem, benchmark it on the set of long error-prone Oxford Nanopore reads generated by the Telomere-to-Telomere consortium and identify a novel (rare) monomer that extends the set of known X-chromosome specific monomers. Our identification of a novel monomer emphasizes the importance of identification of all (even rare) monomers for future centromere assembly efforts and evolutionary studies. To further analyze novel monomers, we applied SD to the set of recently generated long accurate Pacific Biosciences HiFi reads. This analysis revealed that the set of known human monomers and HORs remains incomplete. SD opens a possibility to generate a complete set of human monomers and HORs for using in the ongoing efforts to generate the complete assembly of the human genome.

Availability and implementation

StringDecomposer is publicly available on https://github.com/ablab/stringdecomposer.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Recent advancements in long-read sequencing technologies, such as Pacific Biosciences (PB) and Oxford Nanopore Technologies (ONT), led to a substantial increase in the contiguity of genome assemblies (Koren et al., 2017; Kolmogorov et al., 2019; Ruan and Li, 2020; Shafin et al., 2019) and opened a possibility to resolve extra-long tandem repeats (ETRs), the problem that was viewed as intractable until recently. Assembling ETRs is important since variations in ETR have been linked to cancer and infertility (Barra and Fachinetti, 2018; Black and Giunta, 2018; Ferreira et al., 2015; Giunta and Funabiki, 2017; Miga et al., 2019; Smurova and De Wulf, 2018; Zhu et al., 2018). ETR sequencing is also important for addressing open problems about centromere evolution (Alkan et al., 2007; Henikoff et al., 2015; Lower et al., 2018; Shepelev et al., 2009; Suzuki et al., 2019).

Recent attempts to assemble ETRs (Bzikadze and Pevzner, 2019; Jain et al., 2018; Miga et al., 2019), and recent evolutionary studies of centromeres (Suzuki et al., 2019; Uralsky et al., 2019) revealed the importance of partitioning an ETR (or an error-prone long read sampled from an ETR) into repetitive units forming these repeats. We refer to this problem as the String Decomposition Problem. Although no existing tool explicitly addresses the String Decomposition Problem, Tandem Repeats Finder (TRF) (Benson, 1999), PERCON (Kazakov et al., 2003), Alpha-CENTAURI (Sevim et al., 2016) and the Noise-Cancelling Repeat Finder (NCRF) (Harris et al., 2019) address related problems. Even though these tools can be adapted for string decomposition, they often result in limited accuracy in the case of nested tandem repeats, such as centromeres and rDNA arrays.

Centromeres are the longest tandem repeats in the human genome that are formed by units repeating hundreds or even thousands of times with extensive variations in copy numbers in the human population and limited nucleotide-level variations. Each such unit [referred to as high-order repeat (HOR)] represents a tandem repeat formed by smaller building blocks (referred to as alpha satellites or monomers), thus forming a nested tandem repeat (Fig. 1).

Fig. 1.

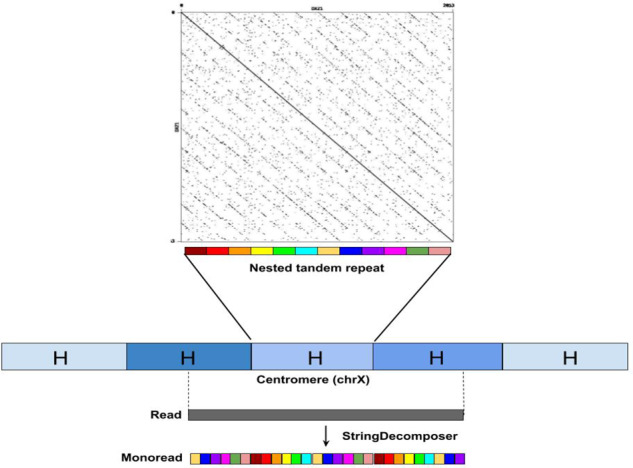
Architecture of cenX. centroFlye assembly of cenX consists of over 1510 HORs that represent units of centromeric ETRs. Five HORs are colored by five shades of blue illustrating HOR variations. Each HORs is a nested tandem repeat formed by various monomers of length $171$ bp. The vast majority of HORs on cenX, referred to as canonical HORs, are formed by 12 monomers (shown by 12 different colors). Figure on top represents the dot plot of a canonical HOR that reveals 12 monomers (also known as alpha satellites). While HORs are 95–100% similar, monomers are only 65–88% similar. In addition to the canonical 12-monomer HORs, there is a small number of non-canonical HORs with varying numbers of monomers. Given a read sampled from a centromere and a set of monomers (referred to as blocks in the String Decomposition Problem), SD translates the read into a monoread written in the monomer alphabet

The alpha satellite repeat family occupies ∼3% of the human genome (Hayden et al., 2013). Each monomer is of length $171$ bp and each HOR is formed by multiple monomers. For example, the vast majority of HORs on the human X centromere (referred to as cenX) consists of 12 monomers. Although different HOR units on cenX are highly similar (95–100% sequence identity), the 12 monomers forming each HOR are rather diverged (50–90% sequence identity). In addition to standard 12-monomer HORs, some units on cenX have non-canonical monomer structure: 35 out of 1510 units are formed by a smaller or larger number of monomers than the canonical 12-monomer unit (Bzikadze and Pevzner, 2019; Suzuki et al., 2019). The tandem repeat structure of human centromeres may be interrupted by retrotransposon insertions (e.g. cenX has a single insertion of a LINE element).

Partitioning of long error-prone reads into units and monomers is critically important for centromere assembly (Bzikadze and Pevzner, 2019; Miga et al., 2019) and evolutionary studies of centromeres (Suzuki et al., 2019). For example, centroFlye (Bzikadze and Pevzner, 2019) requires a translation of each read into a monoread in the monomer alphabet. Unless these monoreads are extremely accurate (e.g. <0.5% error rate), the centroFlye assembly fails. However, the existing tools for analyzing tandem repeats (Benson, 1999; Harris et al., 2019; Sevim et al., 2016) generate monoreads with higher error rates and thus do not provide an adequate solution of the String Decomposition Problem.

Here, we present a simple StringDecomposer (SD) algorithm that takes the set of monomers and a long error-prone read (or a genomic segment) and partitions this read into monomers. The accurate translation of each read into a monomer alphabet opens a possibility to assemble the reads in the monomer alphabet, a more tractable problem than the notoriously difficult problem of assembling ETRs in the nucleotide alphabet. It also opens a possibility to generate the complete set of human HORs, the problem that remains unsolved despite multiple studies in the last four decades (Waye and Willard, 1985). Section 3 demonstrates that SD improves on other tools and describes its applications, such as identification of novel monomers.

2 Materials and methods

String Decomposition Problem. Given a string R (corresponding to a read or an assembly of a centromere) and a set of strings Blocks (each block from Blocks corresponds to an monomer), the goal of the String Decomposition Problem (SD Problem) is to represent R in the alphabet of blocks. We define a chain as an arbitrary concatenation of blocks and an optimal chain for R as a chain that has the highest-scoring global alignment against R among all possible chains. The String Decomposition Problem is to find an optimal chain for R.

Existing approaches to solving the String Decomposition Problem. Although no existing tool explicitly addresses the String Decomposition Problem, Minimap2 (Li, 2018), PERCON (Kazakov et al., 2003), TRF (Benson, 1999), Alpha-CENTAURI (Sevim et al., 2016) and NCRF (Harris et al., 2019) tools address related problems. Suzuki et al. (2019) also developed a custom script implementing a blastn-based string decomposition approach.

Harris et al. (2019) and Mikheenko et al. (2020) demonstrated that the performance of general-purpose sequence aligners such as Minimap2 (Li, 2018) deteriorates in highly repetitive regions, making them not suitable for solving the String Decomposition Problem.

PERCON (Kazakov et al., 2003) is a fast heuristic algorithm for solving a problem similar to the String Decomposition Problem that compares the octanucleotide content of a potential monomer sequence with all known monomers. Unfortunately, PERCON is difficult to benchmark since it was implemented only for Windows OS.

TRF is a de novo tandem repeat finder that does not require specifying either the monomer or its size as an input (Benson, 1999). Given a string containing a tandem repeat formed by unknown monomers, it reports a consensus of these monomers and the location of each monomer in the repeat. Although TRF is able to identify monomers, its output cannot be directly converted into a chain because TRF does not attempt to identify different monomer classes from the input string (and does not accept monomer classes as input). A drawback of this approach is that it often reports a cyclic shift of a consensus monomer and locations of this cyclic shift in the repeat, making it difficult to benchmark TRF against other string decomposition tools (see Supplementary Appendix ‘Benchmarking string decomposition tools’).

The NCRF takes a consensus HOR as an input and partitions an error-prone read into HORs (Harris et al., 2019). It performs well if the entire read is formed by canonical HORs (formed by the same order of monomers as the consensus HOR). However, it generates a suboptimal and somewhat arbitrary partitioning into HORs when a read contains non-canonical HORs or retrotransposons. Since NCRF was not designed for decomposing reads into distinct monomers, it is difficult to benchmark it against monomer-finding tools (see Supplementary Appendix ‘Benchmarking NCRF’).

Alpha-CENTAURI (Sevim et al., 2016) addresses a problem similar to the String Decomposition Problem. It takes a set of long error-prone reads as an input and uses them to generate the most likely set of monomers. It further decomposes each read into such monomers. However, Alpha-CENTAURI does not use additional information about previously inferred HOR structures and has a rather high rate of the incorrectly called monomers in the read decomposition.

Alpha-CENTAURI uses a pre-trained Hidden Markov Model (HMM) for a consensus monomer (consensus of all monomers in the human genome). It aligns this HMM to all reads using the HMMer tool (Eddy, 1998) and clusters the generated alignments in order to identify monomer classes. Since this clustering is imperfect, the accuracy of string decomposition deteriorates as the tool reports spurious abnormal HOR structures (see Supplementary Appendix ‘Benchmarking string decomposition tools’). However, the HMM alignment stage provides an accurate approximation for the starting and ending positions of each monomer. Using the input set of monomers one can identify a monomer with the highest identity for each pair of these starting and ending positions, generate non-overlapping monomer alignments for each read and transform each read into the monomer alphabet as described in the subsection ‘Transformation from the nucleotide alphabet to the block alphabet’. We refer to this approach (based on running HMMer on the consensus HMMs derived by Alpha-CENTAURI) as AC.

String Decomposition Graph. Given a block b and a string R, their standard alignment graph (Compeau and Pevzner, 2018) consists of all vertices (i, j) for $0\le i\le \left|b\right|$, and $0\le j\le \left|R\right|$, where $\left|x\right|$ stands for the length of the string x. A vertex (i, j) is connected to vertices $(i+1,j),\hspace{0.17em}(i,j+1)$ and $(i+1,j+1)$ representing insertions, deletions and matches/mismatches, respectively.

Informally, given a set of t blocks and a string R, their String Decomposition graph (SD graph) consists of t standard alignment graphs that are ‘glued together’ by their 0-th row (Fig. 2). We index vertices in this graph as (b, i, j) using three indices (b represents a block, i represents a position in the block b and j represents a position in string R) except for vertices in the 0-th row that are indexed simply as $(0,j)$ since all blocks share the same ‘glued’ 0-th row. Additionally, we add edges that connect each vertex $(b,|b|,j)$ in the last row (for each block b) with vertex $(0,j)$ in the 0-th row.

Fig. 2.

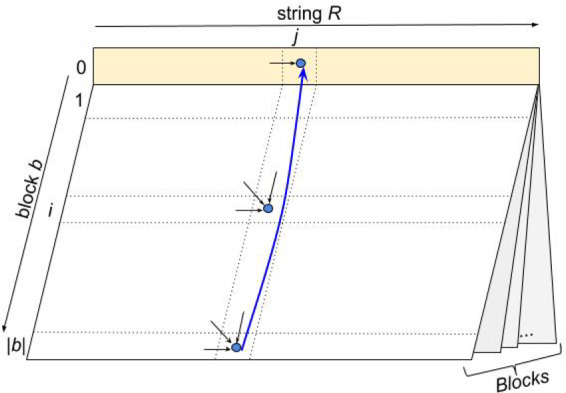
The SD graph represented as a ‘book’ where each page corresponds to an alignment matrix for a single block, and pages are ‘glued’ together by their 0-th row. Arrows represent edges of the String Decomposition Graph. Block-switching edge is colored in blue

Formally, the SD graph is constructed on all vertices (b, i, j), where b is a block, $0\le i\le \left|b\right|$ and $0\le j\le \left|R\right|$ under the assumption that, for each j, all vertices $(b,0,j)$ form a single vertex $(0,j)$. The edge-set of the SD graph consists of the standard alignment edges (as in the standard alignment graph) and the block-switching edges described below. A vertex (b, i, j) is connected to vertices $(b,i+1,j),\hspace{0.17em}(b,i,j+1)$ and $(b,i+1,j+1)$ representing insertions, deletions and matches/mismatches, respectively (as in the standard alignment graph) and said transitions are scored as $-\delta$ for insertions/deletions (indels), $-\sigma$ for mismatches and +1 for matches. Additionally, vertex $(b,|b|,j)$ is connected by a zero-weight block-switching edge to a vertex $(0,j)$ for each block b from the block-set. Each such edge models a transition from the end of an alignment of one block to the start of an alignment of the next block. Although the SD graph has directed cycles, the longest path (i.e. a path with the maximum total weight of its edges) in this graph is well-defined since all directed cycles have negative weights. We refer to the vertex (0, 0) as the source and to each vertex $(b,|b|,|R|)$ as a sink of the SD graph.

The SD algorithm.  Fischetti et al. (1992) described a wrap-around dynamic programming algorithm for solving the String Decomposition Problem in the case of a single block. Matroud et al. (2011) generalized this algorithm for two blocks and further implemented it in the NTRFinder software tool (Matroud et al., 2012). Although NTRFinder can be generalized for multiple blocks, it is not available anymore. SD is a wrap-around dynamic programming algorithm that solves the String Decomposition Problem for an arbitrary number of blocks.

The i-prefix of a block is defined as the string formed by its first i symbols. Given a block b, we define a (b, i)-chain as a chain complemented by the i-prefix of b in the end [note, that multiple (b, i)-chains exist]. A dynamic programming algorithm for solving the SD Problem is based on computing a variable $\text{score}(b,i,j)$ defined as the score of an optimal global alignment between all possible (b, i)-chains and the j-prefix of R. We assume that the alignment is scored using parameters $-\delta$ for indel penalties, $-\sigma$ for mismatch penalty, and + 1 for match premiums. Similarly to the fitting alignment (Gusfield, 1997), i.e. finding a substring of a string v that has the highest-scoring alignment to an entire string w, the variable $\text{score}(b,i,j)$ is initialized as $\text{score}(b,0,j)=0$ for all b and j and $\text{score}(b,i,0)=-i·\delta$ for all i.

To compute $\text{score}(b,i,j)$, the SD algorithm uses dynamic programming to compute the length of a longest path to the vertex (b, i, j) in the SD graph. The solution of the SD Problem is given by the longest path from the source to one of the sinks. A block b that maximizes this score represents the last block in an optimal chain. Other blocks in this chain are inferred by backtracking from the sink $(b,|b|,|R|)$ to the source (0, 0) and are defined by the block-switching edges in the backtracking path.

Each path from the source to a sink in the String Decomposition Graph encodes an alignment of a chain of blocks against the input string R (the score of this alignment is equal to the length of the path). Conversely, each such alignment is encoded by a path in the String Decomposition Graph. Therefore, the solution of the String Decomposition Problem is encoded by a longest path from the source to a sink in the String Decomposition Graph. See Supplementary Appendix ‘Uniqueness of the solution of the String Decomposition Problem’.

The running time and the memory footprint of the longest path algorithm in a directed acyclic graph is linear in the number of edges in this graph. The number of edges in the String Decomposition Graph is $O(|R|·\text{length}(\mathit{\text{Blocks}}))$, where length(Blocks) is the total length of all blocks, but this graph is not acyclic. However, it can be transformed into an equivalent acyclic graph by introducing new vertices $(0,j+1/2)$ and substituting each block-switching edge ending in a vertex $(0,j)$ by a zero-length edge from its start to a new vertex $(0,j+1/2)$ and a zero-length edge from $(0,j+1/2)$ to each vertex from the j + 1 − th column (i.e. (0; j+1) and (b, i, j + 1) for all 0 < i <= | b |). See Supplementary Appendix ‘SD implementation details’.

Transformation from the nucleotide alphabet to the block alphabet. Given a string R and a block-set Blocks, SD generates an optimal chain for R. In the case Blocks represents a monomer-set for a centromere R, we refer to an optimal chain for this centromere as a monocentromere. If Blocks represents a monomer-set for a centromere and R represents a read sampled from this centromere, we refer to an optimal chain for this read as a monoread. We classify a monoread as correct if it represents a substring of the monocentromere, and incorrect, otherwise.

Since errors in reads trigger errors in monoreads, the SD algorithm generates many incorrect monoreads. Another complication is that some regions in centromere are not formed by monomers (e.g. transposon insertions) resulting is a somewhat meaningless translation of such regions into monomers. However, since each monoread typically has very few incorrect monomers, below we classify each monomer in a monoread as either reliable or unreliable. Bzikadze and Pevzner (2019) demonstrated that such classification enables the centromere assembly even though many monoreads are incorrect.

For each block b in an optimal chain for a string R, SD outputs the starting and ending positions of the alignment of this block in R. We denote the substring of R spanning these positions as R(b), construct an alignment between the block b and R(b) and compute the percent identity of this alignment, referred to as ${\text{Identity}}_R(b)$. Additionally, we compute the difference between ${\text{Identity}}_R(b)$ and the percent identity of the second-best aligned monomer to R(b), denoting this difference as IdentityDiff_R(b). We classify a block b as reliable (unreliable) according to the logistic regression model built based on ${\text{Identity}}_R(b)$ and ${\text{IdentityDiff}}_R(b)$ values (see Supplementary Appendix ‘Identification of reliable monomers’). We substitute all unreliable blocks in the string decomposition by the gap symbol ≪?≫, resulting in a translation of the string R into the extended block alphabet that consists of all blocks and the gap symbol (see Supplementary Appendix ‘Processing gaps in the monomer alignments’). The translated sequence is referred to as translation(R). If the string R is a centromeric read Read and blocks represent monomers, we refer to the translation(Read) as a monoread mono(Read).

3 Results

Datasets. We analyzed the rel2 dataset of Oxford Nanopore reads (https://github.com/nanopore-wgs-consortium/CHM13) generated by the Telomere-To-Telomere (T2T) consortium (Miga et al., 2019). The dataset contains 11 069 717 reads (155 Gb total length, 50_x coverage, the N50 read length equal to 70 kb) generated from the CHM13hTERT female haploid cell line. We used the rel2 base-calling with Guppy Flip-Flop 2.3.1.

We benchmarked various approaches to string decomposition using centromeric ONT reads from chromosome X since this centromere (referred to as cenX) was recently assembled, thus providing the ground truth for our benchmarking. This benchmarking utilized 2680 reads (total read length 132.9 Mb) that were recruited to cenX in Bzikadze and Pevzner (2019). In addition to ONT reads, we analyzed 6.9 million accurate PacBio HiFi reads (total length 75.4 Gbp) generated by the T2T consortium (Miga et al., 2019). The length of these reads varies from 2 to 15 bp (57% of HiFi reads have lengths from 10 to 12 bp).

All scripts that were used for analyzing these datasets are available at https://github.com/TanyaDvorkina/sdpaper.

3.1 Benchmarking SD on error-prone reads and cenX assembly

monomers and HOR sequences on cenX. We used the cenX HOR consensus sequence DXZ1* derived in Bzikadze and Pevzner (2019) and decomposed it into 12 monomers ABCDEFGHIJKL using Alpha-CENTAURI (Sevim et al., 2016) (see Supplementary Appendix ‘cenX monomers’).

Reference cenX sequence. We analyzed the cenX v0.7 assembly described in Miga et al. (2019). Out of all 2680 cenX reads 1442 reads were aligned to the reference using TandemMapper (Mikheenko et al., 2020). These reads form the set of mapped reads with total length 121 Mb and with total length of aligned fragments 76 Mb (see Supplementary Appendix ‘Generating accurate read alignments to cenX’).

Since each mapped read is typically aligned over its substring (rather than the entire read), it can be represented as a concatenate of a non-aligned prefix, an aligned substring and a non-aligned suffix. We will find it convenient to trim the non-aligned prefix and suffix in each read, resulting in shorter reads forming a read-set Reads. Each shortened read Read is now aligned to a substring in cenX that we refer to as origin(Read).

Translating X centromere and centromeric ONT reads into the monomer alphabet. Since each read Read in Reads is aligned to a substring origin(Read) in cenX, we can compare the monoread sequence mono(Read) with the accurate monocentromere sequence $\text{mono}\left(\text{origin}\right(\text{Read}))$ representing the ‘ground truth’ with respect to transforming sequences in the monomer alphabet. Using this approach, we benchmarked the SD and AC approaches. We used the SD tool to transform the cenX sequence (3.1 Mb) into the monocentromere mono(cenX) consisting of 18 103 reliable monomers and 36 gap symbols (≪?≫) in the cenX region occupied by the LINE repeat. This conversion is reliable since monomers are rather conserved across cenX (median percent identity 98.8%). Figure 3 presents the distribution of percent identities of 12 cenX monomers and the gap monomers.

Fig. 3.

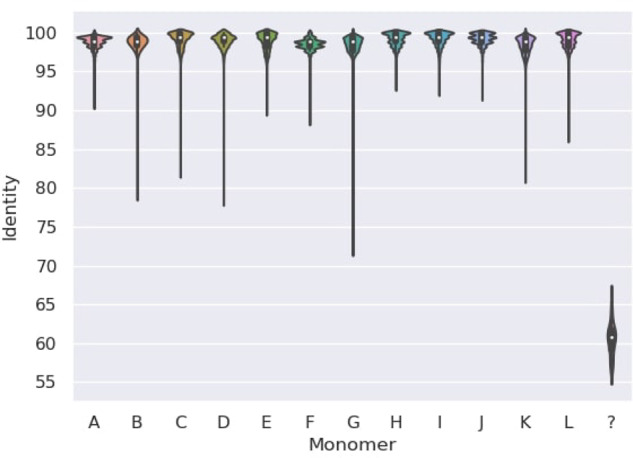
Distribution of percent identities of 12 cenX monomers and the gap monomer ≪?≫. Each violin plot represents the distribution of the percent identity of a particular monomer across cenX. A LINE element at positions 2773652–2779726 is represented by 36 consecutive ≪?≫ symbols in the monocentromere X

Monoread-to-monocentromere alignments. We launched AC and SD to transform each read in Reads into a monoread mono(Read) and aligned it against $\text{mono}\left(\text{origin}\right(\text{Read}))$ using the edit distance scoring (indel and mismatch penalties equal to 1 and match score equal to 0). Each alignment column contains a pair of symbols with the first symbol corresponding to a position in $\text{mono}\left(\text{origin}\right(\text{Read}))$ and the second symbol corresponding to a position in mono(Read). The symbols include 12 monomers, ≪?≫ symbol and the space symbol ≪-≫ representing an indel in the alignment. We classify each column as a match or an error of one of the following types (Supplementary Fig. S3):

• monomer–monomer mismatch (monomer, monomer);

• monomer-gap mismatch (monomer,?);

• monomer-deletion (monomer, -);

• gap-monomer mismatch (?, monomer);

• gap-deletion (?, -);

• monomer-insertion (-, monomer);

• gap-insertion (-,?).

Left panel in Table 1 shows the error statistics for Reads. The monomer-gap mismatches usually occur in corrupted regions of reads, where the identity of the monomer-to-monomer matches flanking these regions usually falls below 80% (see Supplementary Appendix ‘Detailed analysis of errors in string decomposition’).

Table 1.

Summary of errors in the monoread-to-monocentromere alignments computed by the AC (black) and SD (blue) tools for 12 monomers (Left) and for 13 monomers that include 12 known cenX monomers and a novel (K + F) monomer (Right)

Notes: Symbol ≪monomer≫ corresponds to 1 of the 12 cenX monomers or (K + F) monomer, ≪?≫ corresponds to a gap symbol, ≪-≫ corresponds to a space symbol representing an indel in alignment of mono(Read) against $\text{mono}\left(\text{origin}\right(\text{Read}\left)\right)$. A cell (i, j) represents the number of times when a symbol of type i in $\text{mono}\left(\text{origin}\right(\text{Read}))$ was aligned to a symbol of type j in mono(Read). For 12 (13) monomers decomposition, the number of matches is 445 169 (445 206) for SD and 442 783 (442 887) for AC.

Overall, SD resulted in a 3-fold reduction in errors as compared to AC (1457 versus 3816). It may appear that the AC tool is already accurate (0.86% error rate) and a reduction in the error rate (from 0.86% to 0.32%) is a useful but not critically important advance. However, it is important since it provides information about much longer k-monomers in monoreads, thus enabling their assembly into a highly repetitive monocentromere (Bzikadze and Pevzner, 2019; Suzuki et al., 2019). For example, under an (unrealistic) assumption that errors are uniformly distributed, SD provides information about 312-monomers, while AC provides information only about 116-monomers in monoreads ($100/0.32=312$, while $100/0.86=116$). Below we analyze errors made by the AC and SD tools in detail.

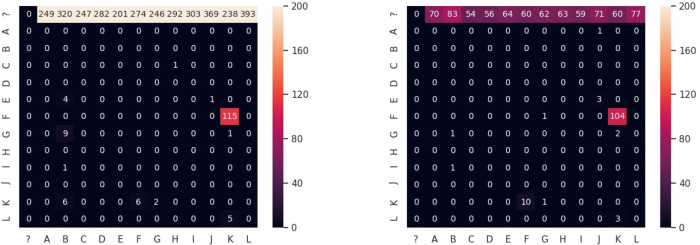
Analyzing monomer–monomer mismatches. Out of 119 monomer–monomer mismatches made by the SD approach 104 mismatches (and 115 out of 139 mismatches made by the AC approach) represent substitutions of the monomer K by the monomer F (Fig. 4). We explored the monoread alignments that substitute F by K and found that all such alignments correspond to the non-standard 16-monomer HOR ABCDEFGHIJ FGHIJKL, where the second occurrence of F is often replaced by K in monoreads. A similar situation can be seen for K into L substitutions (3 and 5 mismatches for the SD and AC approaches, respectively) in alignments of the non-standard 11-monomer HOR ABCDEFGHIJ K.

Fig. 4.

Mismatch substitution matrices for the AC (left) and SD (right) approaches. The (X, Y) cell shows the number of times when symbol X in the monocentromere X (monomer or the gap symbol ≪?≫) was replaced by symbol Y in the monoread

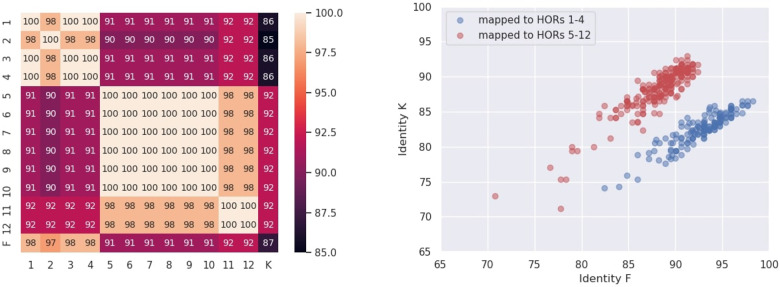
There are six occurrences of the non-standard HOR ABCDEFGHIJ FGHIJKL in the monocentromere X and six occurrences of the non-standard HOR ABCDEFGHIJ KGHIJKL. We refer to regions encoded as F in the former HOR and as K in the latter HOR as FK. We computed pairwise percent identities for nucleotides sequences of each of 12 occurrences of FK in monocentromere and also compared them to monomers F and K (Fig. 5, Left). This analysis reveals two clusters: monomers FK at HORs 1–4 and 5–12 (1–4 and 11–12 were encoded as F, while 5–10 were encoded as K). Since the monomers 1–4 are very close to the monomer F (median percent identity 98%), they likely represent slightly diverged copies of F.

Fig. 5.

Analysis of the non-standard HOR ABCDEFGHIJFGHIJKL. (Left) The heatmap of identities between the occurrences of FK in 12 non-standard HORs ABCDEFGHIJ FGHIJKL and ABCDEFGHIJ KGHIJKL in cenX as well as monomers F and K. (Right) For all 377 occurrences of ABCDEFGHIJ FGHIJKL or ABCDEFGHIJ KGHIJKL in Reads, we computed the identity of 377 alignments of the monomer F (x-axis) and the monomer K (y-axis) against the corresponding substring of the read. Blue (red) circles represent occurrences of monomer F or K aligned to FK from HORs 1–4 (HORs 5–12)

The second cluster, consisting of FK monomers at HORs 5–12, can be divided into subclusters of identical monomers 5–10 and 11–12 (similarity between monomers from these clusters is 98%). Surprisingly, monomers 5–12 FK appear to be equidistant from both monomer F and monomer K with rather low sequence identity 91–92%. Analysis of pairwise alignments between these 8 monomers and monomers F/K reveals that monomers 5–12 likely represent a chimeric monomer formed by the first half of monomer K (first 69–98 positions of K) and the second half of monomer F (last 72–101 positions of F), referred to as K + F (Fig. 6). The monomer K + F has identity $97\%$ with all of eight monomers in the second cluster. The non-standard HOR ABCDEFGHIJ FGHIJKL was found in 272 monoreads generated by the SD approach (a similar HOR ABCDEFGHIJ KGHIJKL was found in 105 monoreads). All $272+105=377$ occurrences of these HORs originated from the non-standard HOR ABCDEFGHIJ FGHIJKL in cenX. We classify these occurrences in two groups: 154 of them correspond to the first cluster (sequences 1–4 in Fig. 5, Right) and $377-154=223$ correspond to the second cluster (sequences 5–12). For each of these 377 occurrences, we extracted the nucleotide sequence that corresponds to FK and aligned them to monomers F and K. Right panel in Figure 5 reveals two clusters of these 377 monomers that correlate well with grouping based on two clusters in Figure 5, Left, confirming that a chimeric monomer K + F is supported by the reads.

Fig. 6.

A 3-way alignment between the monomer F (1st row), monomer FK from the fifth instance of the non-standard HOR ABCDEFGHIJKGHIJKL (second row) and the monomer K (third row). Positions that differ in F and K are colored in red in F and in blue in K. Positions of the monomer FK are colored either in red (if they have the same nucleotide as in F) or in blue (if they have the same nucleotide as in K). Two positions in FK that differ from positions in both F and K are colored in yellow

Emergence of new monomers in the human genome.  Uralsky et al. (2019) recently arrived to similar conclusions by identifying chimeric monomers in reference models of centromeres. We hypothesize a potential mechanism that generated the hybrid monomer K + F. Two cuts were introduced to the canonical 12-monomers ABCDEFGHIJKL roughly in the middle of monomers K and F, resulting in trimmed sequences ABCDEFGHIJK’ and ‘FGHIJKL that were further glued together to form a non-standard 16-monomer ABCDEFGHIJ(K + F)GHIJKL. Our identification of a novel K + F monomer suggests that a set of chromosome-specific monomers may quickly change during evolution by adding and potentially expanding hybrid monomers. It also emphasizes the importance of careful identification of all (even rare) monomers for follow-up centromere assembly efforts.

We decided to recompute the monoread-to-monocentromere alignments with the (K + F) monomer added to the original set of 12 monomers. We used the SD tool to convert each read from Reads and the cenX sequence into the 13-monomer alphabet rather than the 12-monomer alphabet as before. In the new representation of the monocentromere, the non-canonical HORs 5–12 contain monomer K + F instead of F or K. The number of monomer-to-monomer mismatches for both approaches greatly decreased (from 119 to 11 for SD and from 139 to 38 for AC) and the number of other errors hardly changed (Table 1, Right).

Non-standard 11-monomer ABCDEFGHIJ K has only one occurrence within monocentromere X. The monomer K in this 11-monomer has a rather low identity to the monomers K and L (87%). But it has identity $96\%$ to a chimeric monomer K + L constructed from the first part of monomer K and second part of monomer L. For all eight occurrences of non-standard 11-monomer in Reads, the last monomer predicted as K or L has higher identity to K + L ($90$–94%) than to either monomer K ($82$–86%) or to monomer L ($85\%$).

String decomposition in the case when the monomer-set contains highly similar monomers. Distinct monomers forming cenX have rather low similarity with each other (less than 80% for most monomer pairs). However, some other centromeres are formed by more similar monomers that may lead to monomer-to-monomer substitution errors made by string decomposition algorithms. For example, some monomers forming chromosome 8 (Genbank ID M64779.1) are very similar (99% identity).

In order to analyze how string decomposition algorithms perform in the case of very similar monomers, we added a 13-th artificial monomer Z to the original set of 12 monomers. Monomer Z was constructed from monomer A by applying 3, 5, or 8 random nucleotide substitutions at randomly selected positions in the monomer A sequence (the resulting artificial monomers are referred as Z3, Z5 and Z8, respectively). Adding an extra monomer Z to the set of 12 monomers greatly affects only one type of error in Table 1 (monomer–monomer mismatch): in the majority of cases the monomer A is replaced by the monomer Z. After adding the 13-th monomer, the number of monomer–monomer mismatches increased by 235/51/5 for Z3/Z5/Z8 for the SD approach (217/34/8 for the AC approach).

3.2 Automatic HOR extraction from HiFi reads

Recruiting HiFi reads to all human centromeres.  Suzuki et al. (2019) recruited centromeric reads (from a set of error-prone PacBio CLR reads) originating from chromosomes 11, 17 and X (that are dominated by single HORs) and analyzed rare HORs on these chromosomes. Since the accurate HiFi reads (error rate below 1% for most HiFi reads) are better suited for string decomposition and HOR detection than error-prone reads, we attempted to identify HiFi reads that originated from all human centromeres (centromeric reads).

First, we identified all HiFi reads that align to the Flye assembly (Kolmogorov et al., 2019) of the human genome using minimap2 (Li, 2018) and considered reads that have a single high-scoring alignment, covering at least 90% of the read length. Since Flye does not attempt to assemble centromeres, we excluded all mapped reads from further consideration as they are unlikely to be centromeric. Only 17% of all HiFi reads were retained after this filtering step.

At the next step, we applied the first stage of Alpha-CENTAURI to the retained reads using the consensus HMM of all monomers. A read is classified as centromeric if Alpha-CENTAURI aligns the consensus HMM to this read. Only 2% of all HiFi reads were classified as centromeric (123 891 reads with a total length of 1.4 Gbp) and were considered further. Since the remaining 15% of all reads do not contain sequences similar to monomers, they likely represent sequences from other unassembled regions in the human genome or experimental artifacts.

Human monomers.  Sevim et al. (2016) generated a collection of 1868 putative human monomers. Since this monomer collection contains many similar (and even identical) monomers, we clustered similar monomers using single-linkage clustering. Two monomers belong to the same cluster if the edit distance between them doesn’t exceed the threshold MonomerDistance (the default value is 6). This procedure resulted in 965 clusters with the maximum cluster diameter 12 (with respect to the edit distance) and the maximum cluster size 7. We selected a representative monomer in each cluster as a monomer with the smallest maximum edit distance to all other monomers from the cluster. The resulting set of 965 representative monomers (referred to as AllMonomers) reflects the diversity of currently known monomers.

Transforming centromeric HiFi reads into monoreads. We launched the SD tool to transform each selected centromeric read R into a monoread mono(R) using the monomer-set AllMonomers. The analysis of generated monoreads revealed the high identity (95–100%) for the vast majority of monomers against the accurate HiFi reads. However, some monoreads do not encode repetitive patterns. Since such monoreads likely belong to pericentromeric rather than centromeric regions, we only retained 119 807 out of 123 891 monoreads that have at least 36 monomers between leftmost and rightmost monomers with identities $>90\%$, resulting in the set MonoReads of the total length 1288 Mb. We numbered monomers in the decreasing order of their frequencies in monoreads (Supplementary Appendix: ‘Most frequent human monomers’).

Transforming known human HORs into monoHORs.  Alkan et al. (2007) generated a list of 27 known human HOR sequences that contains HORs from all chromosomes, except for chromosomes 13, 14 and 22. We used the SD tool to translate the nucleotide sequence of 26 out of these 27 HORs (except for the HOR D20Z2 that is represented by its partial copy) into a monoHOR by decomposing it into monomers from the set AllMonomers (Fig. 7).

Fig. 7.

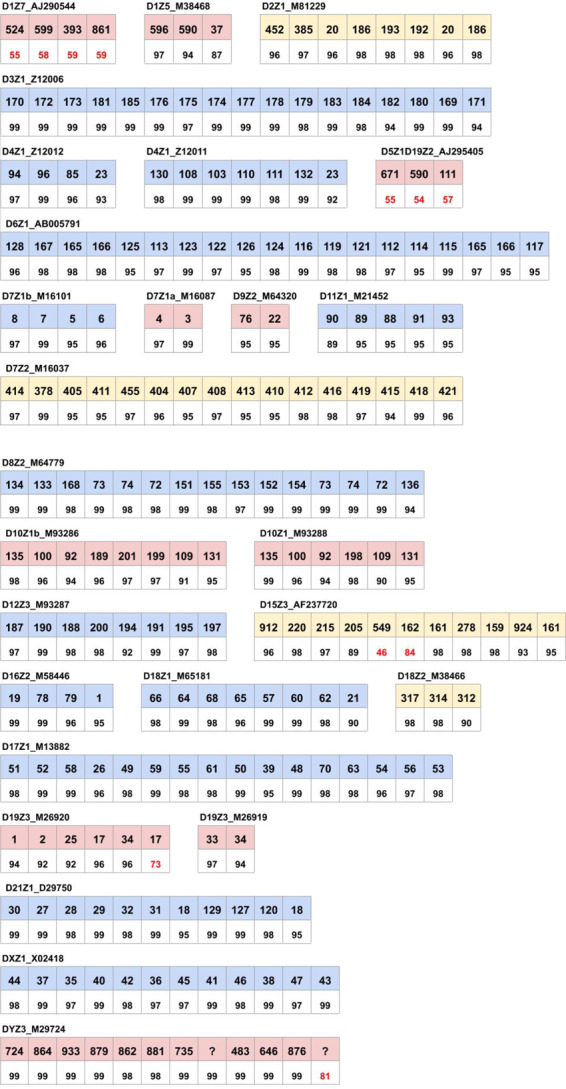
Monomer representation of 27 known canonical HORs. Each row consists of two lines: the sequence of monomers that form a HOR, and their sequence identities to the closest monomer in AllMonomers. Identities below 85% are shown in red. The ≪?≫ symbol reflects monomers that do not appear in any monoread

Only 146 out of 965 monomers participated in this decomposition, indicating that either the set of known human HORs is incomplete or many monomers in AllMonomers are (i) very rare, or (ii) very similar to some of the 146 selected monomers, or (iii) computational artifacts. On the other hand, some monomers in some monoHORs are characterized by a rather low percent identity, indicating that either (i) some human monomers remain unknown, or (ii) some of the known human HORs are incorrect. For example, all five monomers in the HOR D1Z7_AJ290544 on chromosome 1 (formed by monomers 524, 599, 393, 861) have low identities (below 60%), indicating that either the human monomers forming this HOR remain unknown, or that this HOR is incorrect. We classify a monomer in a monoHOR as valid if its identity to the known human monomer exceeds MinHORIdentity (default value $\text{MinHORIdentity}=85\%$).

Inferring putative HORs from monoreads. Although previous centromere studies used various heuristics to derive the most abundant human HORs (Suzuki et al., 2019; Uralsky et al., 2019), a general-purpose algorithm for deriving all HORs (including the rare ones) has not been described yet. Below we describe an algorithm for HOR inference from a set of centromeric reads. For each monoread R and for each k-monomer H in R ($2\le k\le 20$), we calculate the count of the 2k-monomer HH in R (referred to as ${\text{TandemCount}}_R(H)$). We define the Tandem count of a k-monomer H as $\text{TandemCount}(H)=\sum \mathrm{T}{\text{andemCount}}_R(H)$), where the sum is taken over all reads R in the set MonoReads. We rank all k-monomers in the decreasing order of their tandemCounts (the k-monomer with the highest tandemCount is assigned the rank 1) and remove a k-monomer from this list if it either (i) represents a cyclic shift of a k-monomer with a smaller rank or (i) represents a tandem repeat of a k-monomer with smaller rank (see Supplementary Appendix ‘Most frequent putative human HORs’). The resulting set of k-monomers forms a set of putative HORs.

Comparing putative monoHORs with known human monoHORs. Given two monoHORs, we define their overlap as the set of all monomers that these monoHORs share. Two monoHORs are classified as similar if the size of their overlap exceeds $T\%$ (the default value T = 50) of the total number of monomers in each of these monoHORs.

We compared all putative monoHOR (Supplementary Table S3) with all known monoHORs (Fig. 7). No similar putative monoHORs were identified for 10 known monoHORs from chromosomes 1, 5, 7, 9, 10, 19 and Y (shown in red in Fig. 7). Four known monoHORs (D2Z1, D7Z2, D15Z3 and D18Z2) have similar low-frequency putative monoHORs with tandem counts below 1500 (shown in yellow in Fig. 7). For all other known monoHORs, except for D6Z1, D7Z1b, D16Z2 and D18Z1, our method identified identical putative monoHORs.

Suzuki et al. (2019) recently analyzed centromeres in chromosomes 11, 17 and X and used datasets of long error-prone reads (both PBs and ONT reads) to derive 50 putative HORs for these centromeres from multiple individuals (including rare HORs that occurred only in some individuals). In addition to the canonical 12-monomer HOR on chromosome X (ID = 5 in Supplementary Table S2), 5-monomer HOR on chromosome 11 (ID = 6) and 16-monomer HOR on chromosome 17 (ID = 8), our analysis revealed 12 rare HORs (TandemCount of each such HOR exceeds 100) that are similar to these canonical HORs and, thus, have likely originated from chromosomes 11, 17 and X (IDs 68, 82, 131, 142, 149, 150, 152, 162, 172, 178, 184 and 207).

Our approach identified two 15-monomer monoHORs with IDs 68 and 82 that are similar to D17Z1, while Suzuki et al. (2019) only found one such 15-monomer HOR. MonoHOR with ID 68 likely originated from the canonical monoHOR D17Z1 by a deletion of a monomer 70. Similarly, monoHOR with ID 82 likely originated from a deletion of a monomer 63 that is adjacent to the monomer 70 in D17Z1. The rare monoHORs from chromosomes 11, 17 and X, identified by Suzuki et al. (2019) but not by our approach (and vice versa) may reflect the genomic differences between individuals analyzed in Suzuki et al. (2019) and the cell line analyzed by the T2T consortium. Alternatively, some of them may reflect differences in algorithms for inferring putative HORs.

The canonical HOR D8Z2 on chromosome 8 is formed by 15 distinct monomers. However, since some of these monomers are similar they are clustered together in the set AllMonomers. Specifically, monomers 73, 74 and 72 are repeated twice in the monoHOR 31 that corresponds to the canonical D8Z2 (Supplementary Table S3). We refer to the second occurrence of each of these monomers as $73\prime ,\hspace{0.17em}74\prime$ and $72\prime$. The edit distance between monomers 73 and $73\prime$ is 1, the edit distance between monomers 74 and $74\prime$ is 3 and the edit distance between monomers 72 and $72\prime$ is 3. Two substrings of this circular 15-monomer are putative monoHORs 16 and 20 and have a higher tandem counts (5092 and 4937, respectively) than the canonical 15-monomer with tandem count 1357.

Although the known HOR D7Z1b was not found as is, many frequent monoHORs share multiple monomers with D7Z1b. For example, the putative monoHOR 2 (tandem count 67 874) contains all monomers from D7Z1b and two additional monomers 3 and 4. Putative monoHOR 41 (tandem count 1369) differs from D7Z1b by a single substitution of monomer 6 by monomer 3. Both monomers are almost equally distant from the corresponding region of D7Z1b with edit distances 6 and 9 for monomer 6 and monomer 3, respectively.

The canonical HOR D18Z1 on chromosome 18 is highly similar to a putative monoHOR 29 in Supplementary Table S3 (a single substitution of monomer 21 by monomer 163). It turned out that the monomers 163 and 21 are almost equally distant from the corresponding region of D18Z1 (edit distance 11 and 12, respectively).

Figure 8 provides information about matches between known and putative monoHORs and illustrates that the current knowledge of human HORs requires a major update. Since the currently known HORs were largely derived from much shorter Sanger reads, we believe that analysis of long and accurate HiFi reads from the entire human genome provides an opportunity to generate a comprehensive list of all human monomers and HORs.

Fig. 8.

Canonical HORs and similar putative monoHORs. For each out of 13 monoHORs (shown in blue) most frequent putative monoHORs are shown. Numbers on the right represents tandem counts of the corresponding monoHORs

4 Discussion

SD is the first tool designed specifically for decomposing long error-prone reads from ETRs (including nested ETRs such as centromeres) into blocks. We demonstrated that SD accurately transforms long error-prone reads from centromeric regions into monoreads. This transformation remains highly accurate even in the case when the monomer-set contains highly similar monomers with percent identity as high as 98%. We thus project that the SD tool will accelerate the ongoing centromere assembly efforts and will help to close the remaining gaps in the human and other genomes. It also promises to contribute to the discovery of novel emerging (albeit still rare) monomers in the human genome as illustrated by our identification of the emerging K + F and K + L monomers on cenX. Finally, it revealed that the set of currently known human monomers and HORs is incomplete (and likely error-prone) and generated many novel human HORs.