Abstract
Background and objective: One of the main goals of epidemiological studies is to build models capable of forecasting the prevalence of a contagious disease, in order to propose public health policies for combating its propagation. Here, the aim is to evaluate the influence of immune individuals in the processes of contagion and recovery from varicella. This influence is usually neglected.
Methods: An epidemic model based on probabilistic cellular automaton is introduced. By using a genetic algorithm, the values of three parameters of this model are determined from data of prevalence of varicella in Belgium and Italy, in a pre-vaccination period.
Results: This methodology can predict the varicella prevalence (with average relative error of ) in these two European countries. Belgium data can be explained by ignoring the role of immune individuals in the infection propagation; however, Italy data can be explained by considering contagion exclusively mediated by immune individuals.
Conclusions: The role of immune individuals should be accurately delineated in investigations on the dynamics of disease propagation. In addition, the proposed methodology can be adapted for evaluating, for instance, the role of asymptomatic carriers in the novel coronavirus spread.
Keywords: Cellular automaton, Contagious disease, Genetic algorithm, SIR model
1. Introduction
In epidemiological studies based on mathematical models, an accurate estimation of the model parameters is crucial for designing effective control strategies. The role of immune individuals is often neglected in these studies; that is, immune individuals are often disregarded in the transmission and healing processes [1]. The main goal of this work is to examine the validity of this assumption.
Suppose that recovery from an infection confers lifelong immunity. A typical example is varicella (chickenpox), a contagious disease transmitted through social contacts [2]. This disease primarily infects children. Usually, immune adults take care of sick children, without the risk of getting infected again. Also, the meeting of susceptible and infected children is partially promoted by these same immune adults, because children usually go to schools, parks, clubs in the company of them. In this scenario, immune individuals can increase the contagion rate of susceptible individuals and can decrease the convalescence period of infected individuals. Therefore, it is reasonable to conjecture that immune individuals play antagonistic roles in the spread of this infection.
The propagation of contagious diseases, in which immune individuals influence the contagion and recovery rates, was already analytically investigated from a model written as a set of differential equations [3]. Here, an equivalent model formulated in terms of cellular automaton [4] (CA) is proposed to analyze this issue.
Genetic algorithm (GA) is an optimization metaheuristics in which chromosomes, the candidate-solutions for the to-be-solved optimization problem, evolve by applying operators of crossover, elitism, mutation, and selection [5]. It is expected that some of these chromosomes represent near-optimal solutions after some generations. GA has been used for estimating parameters of models based on CA in epidemiological studies [6] and in other contexts [7], [8], [9].
The parameter identification of epidemic models can be considered an inverse problem, which has been solved by employing distinct computational techniques [10], [11], [12]. Here, GA is employed to determine the values of three parameters of the proposed epidemic model based on CA. This parameter identification is performed on data of prevalence of varicella in Belgium and Italy, around the year 2000. The values found for these parameters supports a discussion on the mentioned conjecture.
This manuscript is organized as follow. In Section 2, the epidemic model based on CA and the GA employed in its parameter identification are introduced. In Section 3, the numerical results are presented. In Section 4, the possible relevance of this study is stressed.
2. Methods: CA and GA
CA has been used in works on computational epidemiology [13], [14], [15], [16], [17], [18], [19], [20], [21], [22]. Let a CA be represented by a two-dimensional lattice with n × n cells. To avoid edge effects, the boundary conditions are taken as periodic (that is, the top and bottom edges are connected and the left and right edges are also connected; thus, the lattice has a toroidal shape). Here, each cell of the CA lattice corresponds to an individual of the host population, which may be infected by a pathogen. At each time step t, from each cell, m undirected links start and they end in other cells inside a Moore neighborhood with radius r (thus, m undirected links start from each cell to others pertaining to the square matrix of size centered in such a cell). Let be the probability of a cell contacting any other in the i-th layer, with (the i-th layer is formed by the cells with Moore radius equal to i). For instance, for then is the probability of a cell contacting any of the 8 cells in the layer and is the probability of contacting any of the 16 cells in the layer . All links are rewired at each time step t. Such a time-varying connectivity is used to emulate migratory movements inside the geographical area represented by the two-dimensional lattice. This dynamic random network was called as mainly locally connected graph [23]. In the computer simulations shown in the next section, the topological features of this graph (that is, the values of n, m, and r) remain fixed and the chromosomes of the GA are only composed by genes related to the infection properties. Certainly, other types of complex networks could be employed [24], [25]. They could be used to take into account, for instance, non-isotropic features of the simulated environment [26], [27].
At each time step t, each individual is in one of three states regarding the health status: S (susceptible), I (infected), or R (recovered/immune). The rules of state transition of this SIR model are the following. At the time step t, the transition S → I representing contagion of a S-individual occurs with probability in which VI is the number of I-neighbors at t and k is a positive constant expressing the disease infectivity (observe that and P 1(VI) → 1 for kVI → ∞). If this S-individual was not infected due to direct contact with sick neighbor, the transition S → I can still occur with probability in which VR is the number of R-neighbors and q is a positive constant expressing the disease transmission mediated by R-individuals. At the time step t, the transition I → R representing recovery of an I-individual occurs with the constant probability P 3. If this I-individual remains sick, the transition I → R can still occur with probability in which p is a positive constant expressing cure supported by R-individuals. The transitions I → S and R → S represent death of I and R-individuals, respectively. These transitions occur with the constant probabilities P 5 and P 6, respectively. Note that when I and R-individuals die, they are replaced by S-individuals. Thus, the population size is kept constant and equal to . The states of all individuals are simultaneously updated in the end of each time step. Similar epidemic models based on probabilistic CA were already proposed [23], [28], [29], [30]; however, this is the first one that takes into consideration the role of immune individuals in the spreading of a contagious disease.
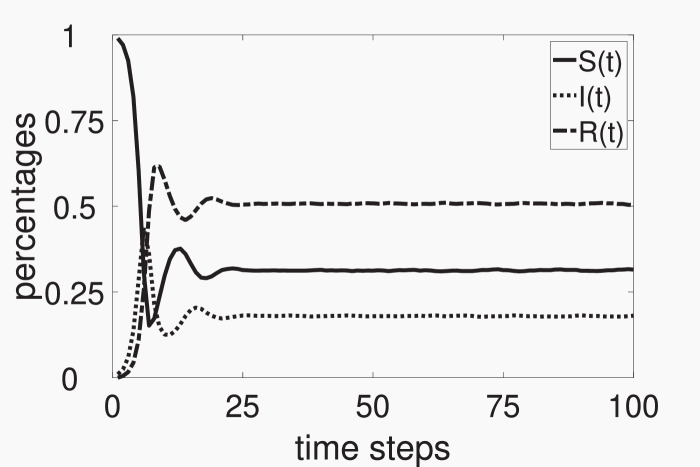
In a computer simulation, after a transient period, the percentages of S, I and R-individuals tend to fluctuate around constant values; that is, the system tends to a stationary solution, as illustrated in Fig. 1 . The percentages of S, I and R-individuals in this steady state are denoted by S*, I*, and . If the steady state is known as disease-free; if I* > 0, as endemic. In a simulation, S* and I* are calculated as the average amounts of S and I-individuals divided by N, obtained in the last w time steps from a total of T time steps. Thus, fluctuations due to the random nature of the CA model are smoothed by this averaging process. On average, the values of S* and I* do not change from one simulation to another; that is, the endemic attractor reached in each simulation does not change. Obviously, w and T must be conveniently chosen; that is, w and T must be chosen in order to compute S* and I* after the system reaching its steady state. In Fig. 1, . Observe that the steady state is attained for t ≃ 30; thus, in this case, would be a suitable choice.
Fig. 1.
Time evolutions of the percentages of S-individuals (solid line), I-individuals (dotted line), and R-individuals (dash-dotted line) from an initial condition with 99% of S-individuals and 1% of I-individuals (and, obviously, 0% of R-individuals), obtained from a numerical simulation of the CA model with and . The systems reaches an endemic steady-state given by and .
The CA parameters to be fitted by the GA are k, q, and p. The values of the other parameters (which are the constant probabilities P 3, P 5, and P 6) are obtained from literature. Thus, each GA chromosome is composed of three genes (the values of k, q, and p). The optimal chromosome contains values of k, q, and p such that, in a simulation with the CA model, then and in which Star and Itar are the targets; that is, the average percentages of S and I-individuals found in the European countries considered in this work.
Three fitness functions, denoted by F 1, F 2, and F 3, are used to evaluate how good a chromosome (a candidate-solution) is. These functions are:
| (1) |
| (2) |
| (3) |
with and 0 < ϵ ≪ 1. If and then LS, LI, ES, and EI are equal to ϵ. In this case, the maximum value is for F 1, 1/(2ϵ) for F 2, and 1/ϵ for F 3. Observe that the better the chromosome, the higher its fitness. In fact, the optimal chromosome maximizes these three functions. Recall that R* is not explicitly considered in these fitness functions because it is not an independent variable.
Each generation of the GA has η chromosomes. In the first generation, these η chromosomes are randomly created. Then, genetic operators are employed for producing new chromosomes as follows [5]:
-
1.
the probability of a chromosome being picked for reproduction is proportional to the value of its fitness. Thus, by using the roulette wheel selection, η chromosomes are picked and η/2 pairs are formed;
-
2.
each pair swaps their genes with probability c per gene in a process called crossover. Thus, a new pair can be conceived;
-
3.
after crossover, a Gaussian mutation is applied for each gene; that is, a new value for each gene is randomly assigned from a Gaussian probability distribution with average as the current value of the gene and standard deviation equal to s. It is imposed that this standard deviation decreases from one generation to another;
-
4.
the new generation is formed by the ξ best evaluated chromosomes (without any modification) of the current generation, which is called elitism, and chromosomes created by crossover and mutation;
-
5.
each chromosome of this new generation is evaluated; that is, from its values of k, q, and p, a computer simulation with the CA model is performed (for T time steps) and the percentages S* and I* are obtained (by considering the last w time steps). Then, the fitness is calculated and the next new generation of η chromosomes is created as described.
Observe that only the long-term behavior of the CA model is taken into account to fit its parameters. The rationale behind this assumption is that varicella was (in fact, still remains, even after vaccination) endemic in many countries. Thus, only data related to S* and I* (and, consequently, )) are usually available and these are the data used here to fit the CA model. If the approach proposed in this work was employed to study the spread of a new pathogen, as the novel coronavirus, then features of the transient behavior of the amounts of S, Iand R-individuals should/could taken into consideration.
The results obtained from numerical simulations by combining CA and GA are presented in the next section.
3. Results
In the CA model, the parameter values of the contact network are (therefore, there are individuals in the host population), (thus, 8 random undirected connections start from each individual), and (recall that r is the radius of the Moore neighborhood where these connections are made). Preliminary tests revealed that these are suitable choices. One time step of the CA model corresponds to one day of real time. The probabilities P 3, P 5, and P 6 are assumed to be the inverse of the mean lifetime related, respectively, to the state transitions I → R, I → S, and R → S. Hence, the probability of recovery from varicella per time step is because the convalescence period is about one week. The death rate by varicella is considered low (about 3 per 100,000 cases); therefore, the values of P 5 and P 6 are taken to be equal in this work. Thus, sick and immune individuals have the same mortality rate. In other words, here, the disease does not increase the chance of dying. By considering that the average life expectancy in Belgium and Italy was about 78 years around the year 2000, then [3].
For Belgium, the target is and [3], [31]; for Italy, and [3], [32]. These numbers represent the normalized amounts of susceptible and infected individuals found in each country.
The initial condition in the CA simulations is 99% of susceptible individuals and 1% of infected individuals, who are homogeneously distributed over the CA lattice. The steady state is achieved after 10–70 time steps. Here, and . Thus, the average values for S* and I* are calculated by taking into account the last 20 time steps of a simulation with 100 time steps. Alternatively, S* and I* could be calculated by running wCA simulations and by averaging the percentages of S and I-individuals at the final time step T obtained in these w simulations.
Each GA generation is composed of chromosomes and only the best one is carried over to the next generation without any alteration; that is, . Mutation starts with and this standard deviation decreases per GA generation. In the crossover, the probability of a pair of chromosomes exchanging their genes is per gene. In the fitness functions, .
The chromosomes of the first generation are randomly created in the interval 0 ≤ k, q, p ≤ 10 from a uniform distribution in the logarithmic scale. This starting point and a time-decreasing standard deviation improved the GA performance. The total number of GA generations is 100; hence, since there are 100 candidate-solutions in each GA generation, the total number of CA simulations is 10000 for each fitness function. The simulations took about 80 hours to run in a workstation with two processors Intel Xeon E5 2620v4 2.1Gh, 64 GB RAM memory, and a graphics processing unit NVIDIA Tesla P100 12GB optimized for parallel computation.
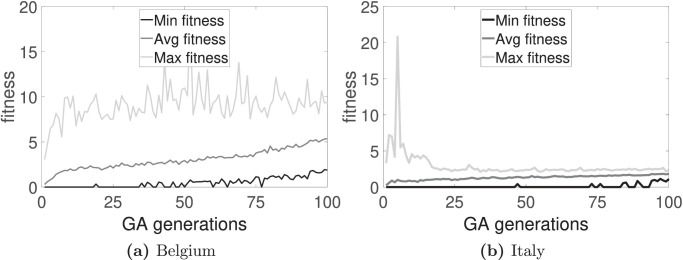
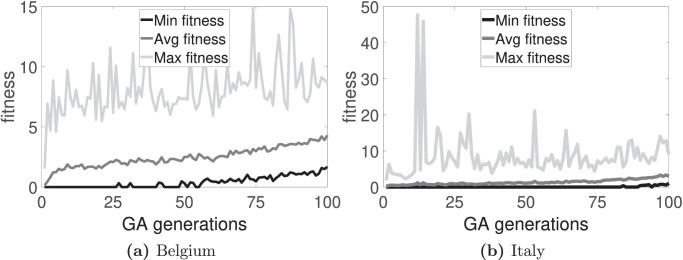
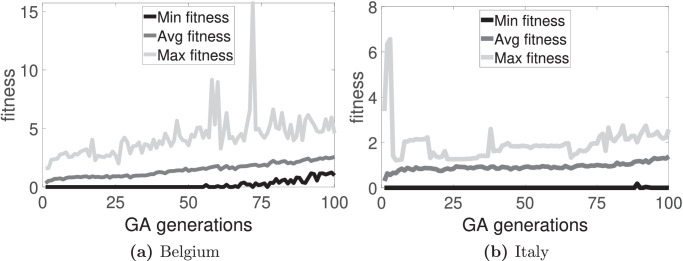
The time evolution of the fitness functions F 1, F 2, and F 3 for the two countries are shown in Fig. 2, Fig. 3, Fig. 4 , respectively. Also, from the best chromosome found for each country and each fitness function, the difference between the target and the steady state reached in the CA model is calculated. Table 1 presents these results. Observe that F 2 gives the best result for Italy data; and F 3, for Belgium data. For Belgium, the average relative error (considering S, I and R-individuals) is about 4% for F 3; for Italy, the average relative error is about 2% for F 2. The three best chromosomes for the three fitness functions for both countries are shown in Table 2 .
Fig. 2.
Time evolution of the fitness by using F1. The minimum, maximum, and average values of F1 are shown for the 100 generations. In each generation, the maximum value corresponds to the best-fit chromosome, the minimum value to the worst-fit chromosome, and the average value is determined by taking into account the 100 chromosomes.
Fig. 3.
Time evolution of the fitness along 100 generations by using F2.
Fig. 4.
Time evolution of the fitness along 100 generations by using F3.
Table 1.
Relative errors for the best chromosome found for each fitness function and each country. For instance, for the relative error is given by with S* obtained from a CA simulation with the best chromosome found by the GA with the fitness function F1. The average relative errors for each fitness function and each country are also shown.
| Target | ||||
|---|---|---|---|---|
| 0.03500 | 0.1143 | 0.1645 | 0.0625 | |
| 0.00022 | 0.0591 | 0.0000 | 0.0636 | |
| 0.96478 | 0.0041 | 0.0060 | 0.0023 | |
| Average error for Belgium | 0.0592 | 0.0568 | 0.0428 | |
| 0.100000 | 0.0186 | 0.0240 | 0.1523 | |
| 0.000033 | 0.1212 | 0.0303 | 0.1212 | |
| 0.899967 | 0.0021 | 0.0027 | 0.0169 | |
| Average error for Italy | 0.0473 | 0.0190 | 0.0968 | |
Table 2.
The three best chromosomes and the corresponding average relative errors found for the three fitness functions and the two countries. The chromosomes in bold are the best ones presented in Table 1.
| Belgium | Fitness function | Chromosome | k | q | p | Average relative error |
|---|---|---|---|---|---|---|
| 1st | 0.317148 | 0 | 2.380381 | 0.0592 | ||
| F1 | 2nd | 0.325249 | 0 | 4.059666 | 0.0772 | |
| 3rd | 0.324976 | 0 | 2.748391 | 0.0784 | ||
| 1st | 0.321887 | 0 | 6.085629 | 0.0568 | ||
| F2 | 2nd | 0.327320 | 0 | 4.603481 | 0.0569 | |
| 3rd | 0.326857 | 0 | 5.351604 | 0.0608 | ||
| 1st | 0.339118 | 0 | 6.312226 | 0.0428 | ||
| F3 | 2nd | 0.328485 | 0 | 6.599133 | 0.0453 | |
| 3rd | 0.337657 | 0 | 6.582061 | 0.0593 |
| Italy | Fitness function | Chromosome | k | q | p | Average relative error |
|---|---|---|---|---|---|---|
| 1st | 0 | 0.066087 | 0.307163 | 0.0473 | ||
| F1 | 2nd | 0 | 0.158563 | 8.702950 | 0.1203 | |
| 3rd | 0 | 0.073670 | 0.290357 | 0.1299 | ||
| 1st | 0 | 0.064927 | 0.299330 | 0.0190 | ||
| F2 | 2nd | 0 | 0.064927 | 0.299330 | 0.0194 | |
| 3rd | 0 | 0.119496 | 1.321768 | 0.0384 | ||
| 1st | 0 | 0.102425 | 0.684363 | 0.0968 | ||
| F3 | 2nd | 0 | 0.051506 | 0.173286 | 0.1698 | |
| 3rd | 0.029681 | 0.030867 | 0.103871 | 0.1901 |
The best chromosome found for Belgium is ; for Italy, . These results are discussed in the next section.
4. Discussion and conclusion
Despite the unknown degree of underreporting, the CA model proposed here can predict (with average relative error of ) the varicella prevalence found in two European countries around the year 2000. For Belgium, k ≃ 0.3, and p ≃ 6. Thus, Belgium data can be explained by ignoring the role of R-individuals in the infection propagation (because ). For Italy, the best chromosome corresponds to q ≃ 0.06, and p ≃ 0.3. Therefore, Italy data can be explained by considering contagion exclusively mediated by R-individuals (because ). Table 2confirms that for Belgium and for Italy compose the best chromosomes for the three fitness functions. Thus, in this work, real-world data can be predicted (with precision of 2–4%) by supposing that disease spread is only due to the direct contact among S and I-individuals (that is, k > 0 and ) or by supposing that disease spread is only due to the direct contact among Sand I-individuals mediated by R-individuals (that is, and q > 0). Certainly, both these ways of disease propagation must simultaneously occur in both countries. However, the epidemic data can be explained by considering either one way or the other way, which is a surprising result. The way with k > 0 and is commonly found in theoretical studies; the way with and q > 0 is the novelty of the proposed CA model. In addition, for Belgium data, the parameter related to recovery mediated by R-individuals is greater than the one for Italy data. In fact, for the first country, p ≃ 6; for the second country, p ≃ 0.3.
In short, the main conclusion is: since R-individuals can take part in the processes of contagion and recovery, their roles should be accurately delineated in studies on dynamics of disease spread. Usually, their presence is assumed to be only beneficial from an epidemiological point of view, because, due to their acquired immunity, they can not directly propagate the infection. However, they can catalyze the meeting among S and I-individuals. This fact should not be neglected in mathematical approaches.
Two particular features of the implemented GA were crucial in the parameter identification: a decreasing mutation rate and the initial generation of chromosomes randomly picked from a uniform distribution in the logarithmic scale. From an expert system perspective, the methodology presented here can be applied to forecast the prevalence of other contagious diseases, as the one caused by the novel coronavirus. In future works, vaccination can also be taken into consideration.
Ethical
This article does not contain any studies with human participants or animals performed by any of the authors.
Declaration of Competing Interest
The authors declare that there is no conflict of interest.
Acknowledgements
LHAM is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under the grant #304081/2018-3. PHTS is partially supported by CNPq under the grants #303743/2016-6 and #402874/2016-1 and by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) under the grants #2017/12671-8 and #2017/50393-0. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - finance code 001.
References
- 1.Anderson R.M., May R.M. Oxford University Press; 1992. Infectious Diseases of Humans: Dynamics and Control. [Google Scholar]
- 2.Heininger U., Seward J.F. Varicella. Lancet. 2006;368(9544):1365–1376. doi: 10.1016/S0140-6736(06)69561-5. [DOI] [PubMed] [Google Scholar]
- 3.Moraes A.L.S., Monteiro L.H.A. On considering the influence of recovered individuals in disease propagations. Commun. Nonlinear Sci. Numer. Simul. 2016;34:224–230. [Google Scholar]
- 4.Wolfram S. Westview Press; 1994. Cellular Automata and Complexity: Collected Papers. [Google Scholar]
- 5.Mitchell M. MIT Press; 1998. An Introduction to Genetic Algorithms. [Google Scholar]
- 6.Gerardi D.O., Monteiro L.H.A. System identification and prediction of dengue fever incidence in rio de janeiro. Math. Probl. Eng. 2011;2011:720304. [Google Scholar]
- 7.Billings S.A., Yang Y. Identification of probabilistic cellular automata. IEEE Trans. Syst. Man Cybern. B. 2003;33(2):225–236. doi: 10.1109/TSMCB.2003.810437. [DOI] [PubMed] [Google Scholar]
- 8.García A.M., Santé I., Boullón M., Crecente R. Calibration of an urban cellular automaton model by using statistical techniques and a genetic algorithm. application to a small urban settlement of NW spain. Int. J. Geogr. Inf. Sci. 2013;27(8):1593–1611. [Google Scholar]
- 9.Mitchell M., Hraber P.T., Crutchfield J.P. Revisiting the edge of chaos: Evolving cellular automata to perform computations. Complex Syst. 1993;7(2):89–130. [Google Scholar]
- 10.Li T., Wang Y., Liu F., Turner I. Novel parameter estimation techniques for a multi-term fractional dynamical epidemic model of dengue fever. Numer. Algorithms. 2019;82(4):1467–1495. [Google Scholar]
- 11.Samsuzzoha M., Singh M., Lucy D. Parameter estimation of influenza epidemic model. Appl. Math. Comput. 2013;220:616–629. [Google Scholar]
- 12.Xiang H.L., Liu B. Solving the inverse problem of an SIS epidemic reaction-diffusion model by optimal control methods. Comput. Math. Appl. 2015;70(5):805–819. [Google Scholar]
- 13.Ahmed E., Agiza H.N., Hassan S.Z. On modeling hepatitis b transmission using cellular automata. J. Stat. Phys. 1998;92(3–4):707–712. [Google Scholar]
- 14.Fuentes M.A., Kuperman M.N. Cellular automata and epidemiological models with spatial dependence. Physica A. 1999;267(3-4):471–486. [Google Scholar]
- 15.Huang C.Y., Sun C.T., Hsieh J.L., Lin H. Simulating SARS: Small-world epidemiological modeling and public health policy assessments. JASSS. 2004;7(4) [Google Scholar]
- 16.Doran J.R., Laffan S.W. Simulating the spatial dynamics of foot and mouth disease outbreaks in feral pigs and livestock in queensland, australia, using a susceptible-infected-recovered cellular automata model. Prev. Vet. Med. 2005;70(1-2):133–152. doi: 10.1016/j.prevetmed.2005.03.002. [DOI] [PubMed] [Google Scholar]
- 17.Mikler A.R., Venkatachalam S., Abbas K. Modeling infectious diseases using global stochastic cellular automata. J. Biol. Syst. 2005;13(4):421–439. [Google Scholar]
- 18.White S.H., del Rey A.M., Sanchez G.R. Modeling epidemics using cellular automata. Appl. Math. Comput. 2007;186(1):193–202. doi: 10.1016/j.amc.2006.06.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sun G.Q., Jin Z., Song L.P., Chakraborty A., Li B.L. Phase transition in spatial epidemics using cellular automata with noise. Ecol. Res. 2011;26(2):333–340. [Google Scholar]
- 20.Holko A., Medrek M., Pastuszak Z., Phusavat K. Epidemiological modeling with a population density map-based cellular automata simulation system. Expert Syst. Appl. 2016;48:1–8. [Google Scholar]
- 21.Cisse B., Yacoubi S.E., Gourbiere S. A cellular automaton model for the transmission of chagas disease in heterogeneous landscape and host community. Appl. Math. Model. 2016;40(2):782–794. [Google Scholar]
- 22.Sharma N., Gupta A.K. Impact of time delay on the dynamics of SEIR epidemic model using cellular automata. Physica A. 2017;471:114–125. [Google Scholar]
- 23.Schimit P.H.T., Monteiro L.H.A. On the basic reproduction number and the topological properties of the contact network: An epidemiological study in mainly locally connected cellular automata. Ecol. Model. 2009;220(7):1034–1042. doi: 10.1016/j.ecolmodel.2009.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ramirez-Ramirez L.L., Gel Y.R., Thompson M., de Villa E., McPherson M. A new surveillance and spatio-temporal visualization tool SIMID: simulation of infectious diseases using random networks and GIS. Comput. Methods Programs Biomed. 2013;110(3):455–470. doi: 10.1016/j.cmpb.2013.01.007. [DOI] [PubMed] [Google Scholar]
- 25.Bouzille G., Poirier C., Campillo-Gimenez B., Aubert M.L., Chabot M., Chazard E., Lavenu A., Cuggia M. Leveraging hospital big data to monitor flu epidemics. Comput. Methods Programs Biomed. 2018;154:153–160. doi: 10.1016/j.cmpb.2017.11.012. [DOI] [PubMed] [Google Scholar]
- 26.Malecki K., Jankowski J., Szkwarkowski M. Modelling the impact of transit media on information spreading in an urban space using cellular automata. Symmetry-Basel. 2019;11(3):428. [Google Scholar]
- 27.He L.Y., Bao J.X., Daccache A., Wang S.F. Optimize the spatial distribution of crop water consumption based on a cellular automata model: A case study of the middle Heihe river basin, china. Sci. Total Environ. 2020;720:137569. doi: 10.1016/j.scitotenv.2020.137569. [DOI] [PubMed] [Google Scholar]
- 28.Schimit P.H.T., Pereira F.H. Disease spreading in complex networks: a numerical study with principal component analysis. Expert Syst. Appl. 2018;97:41–50. doi: 10.1016/j.eswa.2017.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ferraz D.F., Monteiro L.H.A. The impact of imported cases on the persistence of contagious diseases. Ecol. Complex. 2019;40:100788. [Google Scholar]
- 30.Silva H.A.L.R., Monteiro L.H.A. Self-sustained oscillations in epidemic models with infective immigrants. Ecol. Complex. 2014;17:40–45. [Google Scholar]
- 31.Thiry N., Beutels P., Shkedy Z., Vranckx R., Vandermeulen C., Wielen M.V., Damme P.V. The seroepidemiology of primary Varicella-Zoster virus infection in flanders (belgium) Eur. J. Pediatr. 2002;161(11):588–593. doi: 10.1007/s00431-002-1053-2. [DOI] [PubMed] [Google Scholar]
- 32.Gabutti G., Penna C., Rossi M., Salmaso S., Rota M.C., Bella A., Crovari P. The seroepidemiology of varicella in italy. Epidemiol. Infect. 2001;126(3):433–440. doi: 10.1017/s0950268801005398. [DOI] [PMC free article] [PubMed] [Google Scholar]