Hybrid test for publication bias in meta-analysis

Abstract

Publication bias frequently appears in meta-analyses when the included studies’ results (e.g., p-values) influence the studies’ publication processes. Some unfavorable studies may be suppressed from publication, so the meta-analytic results may be biased toward an artificially favorable direction. Many statistical tests have been proposed to detect publication bias in recent two decades. However, they often make dramatically different assumptions about the cause of publication bias; therefore, they are usually powerful only in certain cases that support their particular assumptions, while their powers may be fairly low in many other cases. Although several simulation studies have been carried out to compare different tests’ powers under various situations, it is typically infeasible to justify the exact mechanism of publication bias in a real-world meta-analysis and thus select the corresponding optimal publication bias test. We introduce a hybrid test for publication bias by synthesizing various tests and incorporating their benefits, so that it maintains relatively high powers across various mechanisms of publication bias. The superior performance of the proposed hybrid test is illustrated using simulation studies and three real-world meta-analyses with different effect sizes. It is compared with many existing methods, including the commonly-used regression and rank tests, and the trim-and-fill method.

1. Introduction

Meta-analysis has been a widely-used tool to synthesize and compare the results from multiple studies; however, its validity is often challenged by potential publication bias caused by the underreporting of non-significant results or unfavorable evidence.¹ Publication bias may exaggerate the synthesized results in an artificially favorable direction.² In an effort to assess the quality or certainty in evidence of meta-analytic results, various methods have been proposed to detect publication bias.^3–6 A popular and intuitive method is to examine the asymmetry of the funnel plot, which displays study-specific effect sizes against their standard errors or other precision measures.^7,8 If publication bias does not exist, the studies’ effect sizes should be distributed evenly on both sides of the overall average, so the funnel plot is expected to be approximately symmetric. An asymmetric funnel plot is a sign of the presence of publication bias. Because interpreting the funnel plot may be fairly subjective, quantitative methods have been further introduced to test for or quantify publication bias. These include the widely-used rank test,⁹ the regression test,¹⁰ and the trim-and-fill method.¹¹ Many alternatives, such as various modified regression tests^12,13 and the skewness,¹⁴ are also available and may be preferred in particular situations.

A major limitation of nearly all current methods for publication bias is that they usually have low statistical powers. For example, the trim-and-fill method performs well when its assumption (i.e., the suppression of studies is based on the magnitudes of their effect sizes) is roughly satisfied; otherwise, it is not powerful, especially when the heterogeneity between studies is substantial.¹⁵ Some tests, such as the rank test, may be rather conservative and may not be recommended in many cases.¹⁶ Another important drawback of some publication bias tests (e.g., Egger’s regression) is that their type I error rates may be inflated.¹⁷ This happens when the intrinsic association between the study-specific effect sizes and their sample variances is substantial. For example, for the odds ratio, risk ratio, or risk difference for binary outcomes, its point estimate and sample variance are both based on the four data cells in the 2 × 2 table, so they are dependent even if no publication bias appears.¹³ For continuous outcomes, the standardized mean difference and its sample variance are also mathematically associated, and Egger’s regression test may be still subject to inflated type I error rates.^18–20

In an empirical study of nearly 30,000 meta-analyses, the results produced by different methods have been found to have only low or moderate agreement for detecting publication bias.²¹ No test uniformly outperforms others, so the conclusion about publication bias may not be based on a single method. As different methods are preferred in different situations, an ideal method would be to accurately identify a specific situation for a given meta-analysis and to apply the corresponding preferred publication bias test. However, in practice, it is infeasible to ascertain the conditions in which a specific publication bias test is preferred, especially when the number of studies is small.

This article proposes a hybrid test for publication bias that synthesizes information from a set of different tests. It avoids the unrealistic task of finding the optimal publication bias test. Because it borrows strengths from various tests, its power can be close to that of the optimal test across different situations. This article is organized as follows. Section 2 reviews several existing tests for publication bias. Based on them, Section 3 introduces the hybrid test and the procedure to calculate its p-value. Sections 4 and 5 present numerical results produced by the hybrid test and compare them with those produced by the existing tests via simulation studies and real data analyses. Section 6 provides a brief discussion.

2. Existing tests for publication bias

Consider a meta-analysis consisting of N studies. Let y_i, $s_i^2$, and n_i be the reported effect size, its sample variance, and the total sample size in study i, respectively (i = 1, … , N). If the outcome is binary, n_i00 and n_i01 denote the numbers of subjects without and with the outcome event in study i’s control group, and n_i10 and n_i11 denote those in the treatment group. Also, let n_i0• = n_i00 + n_i01 and n_i1• = n_i10 + n_i11 be the sample sizes in the control and treatment groups, respectively; let n_i•0 = n_i00 + n_i10 and n_i•1 = n_i01 + n_i11 be the total numbers of subjects without and with the event, respectively. We may classify the various existing tests for publication bias into two groups based on the types of outcomes as follows.

2.1. Publication bias tests for generic outcomes

Begg and Mazumdar⁹ proposed to assess the association between the standardized effect size and its standard error. Specifically, each study’s standardized effect size is defined as $y_i^{*}=\left(y_i-\widehat{\theta }\right)/s_i^{*}$, where $\widehat{\theta }={\sum }_{i=1}^N{s}_i^{-2}{y}_i/{\sum }_{i=1}^N{s}_i^{-2}$ is the fixed-effect estimate of the overall effect size θ and $s_i^{*}={\left[s_i^2-{\left({\sum }_{j=1}^N{s}_j^{-2}\right)}^{-1}\right]}^{1/2}$ is the standard error of the numerator $y_i-\widehat{\theta }$. Begg’s rank test uses Kendall’s tau to examine the association between $y_i^{*}$ and $s_i^2$, and it can be applied to all types of outcomes. However, its statistical power may be very low in some cases.¹⁶ We denote this test by T_rank.

Instead of using the rank test to examine the funnel plot’s asymmetry, Egger et al.¹⁰ considered regressing the standard normal deviate, calculated as y_i/s_i, against the inverse of the standard error 1/s_i. The regression intercept is expected to be zero in the absence of publication bias, and Egger’s regression test examines if the intercept is zero. This is equivalent to directly regressing y_i against s_i with weights $1/s_i^2$ and testing if the regression slope is zero; that is,

$$y_i=\alpha +\beta s_i+{ϵ}_i,{ϵ}_i~N\left(0,s_i^2\right).$$ (1)

Denote this test by T_reg. Here, we assume the error terms ϵ_i follow the normal distributions with mean zero and known sample variances $s_i^2$; thus, the true regression model under the null hypothesis of the slope β = 0 yields the fixed-effect meta-analysis model. One may also assume that the error terms have variances $\phi s_i^2$ with the unknown under- or over-dispersion parameter φ > 0. This assumption corresponds to the meta-analysis model with multiplicative heterogeneity,²² which is not often used in practice.

Compared with the multiplicative heterogeneity, the additive heterogeneity assumption is much more popular in meta-analysis. A modified regression test for publication bias can be derived based on this assumption; that is, we can test if the slope is zero in the regression:

$$y_i=\alpha +\beta s_i+{ϵ}_i,{ϵ}_i~N\left(0,s_i^2+{\tau }^2\right),$$ (2)

where the error terms incorporate the additive between-study variance τ². We denote this modified regression test by T_reg-het. When τ² is estimated as zero (i.e., no heterogeneity), this is identical to the original Egger’s regression in Equation (1). In practice, this test can be implemented using the two-step method which was introduced by Thompson and Sharp²² for meta-regression. Specifically, consider the weighted regression with a general predictor x_i as follows:

$$y_i=\alpha +\beta x_i+{ϵ}_i,{ϵ}_i~N\left(0,s_i^2+{\tau }^2\right).$$ (3)

The predictor x_i is the within-study standard error s_i in the modified Egger’s test in Equation (2). First, the heterogeneity variance τ² can be estimated as ${\widehat{\tau }}^2=\text{max}\{0,[Q-(N-2)]/F\}$ based on the method of moments, where $Q={\sum }_{i=1}^N{w}_i{\left(y_i-\widehat{\alpha }-\widehat{\beta }{x}_i\right)}^2,w_i=1/s_i^2$, and $\widehat{\alpha }$ and $\widehat{\beta }$ are the estimates from the regression that does not incorporate the heterogeneity variance as in Equation (1). Also, the denominator F is calculated as

$$F=\sum _{i=1}^N{w}_i-\frac{\sum _{i=1}^N{w}_i^2\sum _{i=1}^N{w}_i{x}_i^2-2\sum _{i=1}^N{w}_i^2{x}_i\sum _{i=1}^N{w}_i{x}_i+\sum _{i=1}^N{w}_i\sum _{i=1}^N{w}_i^2{x}_i^2}{\sum _{i=1}^N{w}_i\sum _{i=1}^N{w}_i{x}_i^2-{\left(\sum _{i=1}^N{w}_i{x}_i\right)}^2}.$$

Then, the ${\widehat{\tau }}^2$ is plugged in Equation (3), and the test T_reg-het can be performed by examining whether the updated estimate of the slope β departs from zero.

Based on the foregoing regressions, Lin and Chu¹⁴ further proposed to quantify publication bias using the skewness of the standardized regression errors ϵ_i/s_i in Equation (1) or ${ϵ}_i/\sqrt{s_i^2+{\tau }^2}$ in Equation (2). The skewness is calculated as $m_3/m_2^{3/2}$, where m₂ and m₃ are the sample second and third central moments of the standardized errors, respectively. If no publication bias appears, the errors should be approximately symmetric around zero; if the magnitude of publication bias increases, the skewness of the errors is away from zero. Thus, the skewness can serve as a test statistic for publication bias. The asymptotic properties of the skewness have been studied, but they may not perform well when the number of studies N is small.¹⁴ The resampling method is an alternative to properly calculate the p-value of the skewness-based test. We denote this test by T_skew if using the standardized errors from the original Egger’s regression in Equation (1) and by T_skew-het if using those from the modified regression in Equation (2) that accounts for the additive heterogeneity.

The predictors in the above regressions are based on the standard errors. Tang and Liu²³ introduced a similar regression test derived from the sample-size-based funnel plot, which presents each study’s total sample size n_i, instead of its standard error s_i, on the vertical axis. Specifically, the study-specific effect size y_i is regressed against $1/\sqrt{n_i}$ with weights n_i; again, we test if the regression slope is zero. The sample size n_i is pre-specified when designing a study and is typically independent of the outcome measure y_i; therefore, the sample-size-based regression test may avoid the problem of the potential intrinsic association between y_i and s_i (e.g., for the standardized mean difference) in standard-error-based regressions, which may lead to inflated type I error rates. We denote this test by T_inv-sqrt-n.

Instead of testing for the association between the effect sizes and certain precision measures, the trim-and-fill method proposed by Duval and Tweedie¹¹ aims to identify potentially suppressed studies. This method assumes that the suppressed studies have the most negative (or positive) effect sizes, which cause the asymmetry of the funnel plot. Three statistics (i.e., R₀, L₀, and Q₀) are available to estimate the number of suppressed studies; among them, the R₀ and L₀ statistics have been recommended based on simulation results and real data analyses.^24,25 This article will use the L₀ statistic, because it is considered more robust to the violation of the trim-and-fill method’s assumption.¹¹ The trim-and-fill method has been attractive because it not only detects but also adjusts for publication bias by incorporating the imputed suppressed studies. However, its performance may be poor in the presence of substantial heterogeneity.¹⁵ We denote the test based on the trim-and-fill method by T_trim-fill.

2.2. Publication bias tests for binary outcomes

The methods in Section 2.1 are designed for generic outcomes. When the outcomes are binary, the reported effect size (typically the odds ratio on a logarithmic scale, estimated as $y_i=\text{log}\frac{n_{i00}{n}_{i11}}{n_{i01}{n}_{i10}}$) and its sample variance ($s_i^2=n_{i00}^{-1}+n_{i01}^{-1}+n_{i10}^{-1}+n_{i11}^{-1}$ for the log odds ratio) within each study both depend on all four data cells in the 2 × 2 table, so they are intrinsically associated, likely leading to inflated type I error rates. Several methods have been specially designed to reduce such inflation when testing for publication bias in meta-analyses with binary outcomes.

Like the regression test by Tang and Liu,²³ the tests proposed by Macaskill et al.¹² and Peters et al.¹³ are also based on the total sample sizes. Specifically, Macaskill et al.¹² suggested to regress the log odds ratio y_i against the sample size n_i with weights n_i•0n_i•1/n_i, and Peters et al.¹³ regressed the log odds ratio y_i against 1/n_i with the same weights n_i•0n_i•1/n_i. We denote these two tests by T_n and T_inv-n accordingly.

Rücker et al.²⁶ considered removing the intrinsic association between the log odds ratio and its sample variance by using the arcsine transformation. They proposed to use the arcsine-transformed effect size ${\Delta }_i=\text{arcsin}\sqrt{\frac{n_{i11}}{n_{i1•}}}-\text{arcsin}\sqrt{\frac{n_{i01}}{n_{i0•}}}$. Its sample variance is approximately ${\Gamma }_i=\frac{1}{4n_{i0•}}+\frac{1}{4n_{i1•}}$ by the delta method, which is free of the event counts n_i01 and n_i11. Consequently, they suggested to replace the y_i and $s_i^2$ in Begg’s rank test and Egger’s regression test with the arcsine-transformed Δ_i and Γ_i. Specifically, the arcsine-based rank test (i.e., the counterpart of Begg’s rank test) examines the correlation between Δ_i and Γ_i. The arcsine-based regression test (i.e., the counterpart of Egger’s regression test) examines if the slope is zero in:

$${\Delta }_i=\alpha +\beta \sqrt{{\Gamma }_i}+{ϵ}_i,{ϵ}_i~N\left(0,{\Gamma }_i\right).$$

Also, the above regression can be modified by incorporating the additive heterogeneity:

$${\Delta }_i=\alpha +\beta \sqrt{{\Gamma }_i}+{ϵ}_i,{ϵ}_i~N\left(0,{\Gamma }_i+{\tau }^2\right),$$

which corresponds to the modified Egger’s regression in Equation (2). We denote these three arcsine-based tests by T_AS-rank, T_AS-reg, and T_AS-reg-het accordingly.

Jin et al.²⁷ also considered a method using the smoothed variance of the log odds ratio to reduce the intrinsic correlation between the log odds ratio and its sample variance. The smoothed variance is calculated as ${\tilde{s}}_i^2={\left(n_{i0•}{\tilde{\pi }}_{00}\right)}^{-1}+{\left(n_{i0•}{\tilde{\pi }}_{01}\right)}^{-1}+{\left(n_{i1•}{\tilde{\pi }}_{10}\right)}^{-1}+{\left(n_{i1•}{\tilde{\pi }}_{11}\right)}^{-1}$, where ${\tilde{\pi }}_{01}=1-{\tilde{\pi }}_{00}=N^{-1}{\sum }_{i=1}^N\frac{n_{i01}}{n_{i0•}}$ and ${\tilde{\pi }}_{11}=1-{\tilde{\pi }}_{10}=N^{-1}{\sum }_{i=1}^N\frac{n_{i11}}{n_{i1•}}$. Replacing the sample variance $s_i^2$ with the smoothed variance ${\tilde{s}}_i^2$, one can test if the slope is zero in:

$$y_i=\alpha +\beta {\tilde{s}}_i+{ϵ}_i,{ϵ}_i~N\left(0,{\tilde{s}}_i^2\right),$$

or in the weighted regression incorporating the additive heterogeneity variance:

$$y_i=\alpha +\beta {\tilde{s}}_i+{ϵ}_i,{ϵ}_i~N\left(0,{\tilde{s}}_i^2+{\tau }^2\right).$$

We denote these two tests by T_smoothed and T_smoothed-het accordingly. The estimates in T_AS-reg-het and T_smoothed-het can be obtained using the same procedure for the regression in Equation (3).

Furthermore, Harbord et al.²⁸ introduced a modified regression test for publication bias based on the score function. The efficient score for the log odds ratio is Z_i = n_i11 − n_i•1n_i1•/n_i and the score variance is $V_i=n_{i0•}{n}_{i1•}{n}_{i•0}{n}_{i•1}/\left[n_i^2\left(n_i-1\right)\right]$. This method tests if the intercept is zero in the regression of $Z_i/\sqrt{V_i}$ against $\sqrt{V_i}$; equivalently, it tests if the slope is zero in the regression of Z_i/V_i against $1/\sqrt{V_i}$ with weights V_i. We denote this test by T_score.

Finally, Schwarzer et al.²⁹ proposed a publication bias test for sparse binary outcomes, where the usual estimate of the odds ratio $\frac{n_{i00}{n}_{i11}}{n_{i01}{n}_{i10}}$ may not be accurate and requires a continuity correction (typically 0.5) if zero counts are present. Conditional on the marginal total counts in the 2 × 2 table, the event count in the treatment group n_i11 in each study follows a non-central hypergeometric distribution with the probability mass function

$$\text{Pr}\left(n_{i11}|n_{i0•},n_{i1•},n_{i•1};{\psi }_i\right)=\frac{\left(\begin{array}{l}{n}_{i1•}\hfill \\ n_{i11}\hfill \end{array}\right)\left(\begin{array}{l}{n}_{i0•}\hfill \\ n_{i01}\hfill \end{array}\right){\psi }_i^{n_{i11}}}{{\sum }_{x\in {\mathcal{U}}_i}\left(\begin{array}{c}{n}_{i1•}\\ x\end{array}\right)\left(\begin{array}{c}{n}_{i0•}\\ n_{i•1}-x\end{array}\right){\psi }_i^x},$$

where ψ_i is the true odds ratio in study i and ${\mathcal{U}}_i=\left\{\text{max}\left(0,n_{i•1}-n_{i0•}\right),\dots ,\text{min}\left(n_{i•1},n_{i1•}\right)\right\}$ is the range of all possible values for n_i11. The expectation and variance of n_i11, E(n_i11;ψ_i) and Var(n_i11;ψ_i), can be calculated based on this probability mass function. Similar to Begg’s rank test, Schwarzer et al.²⁹ considered Kendall’s tau between the standardized cell count $n_{i11}^{*}$ and the variance of the log odds ratio $v_i^{*}$. Using the Mantel–Haenszel odds ratio ${\widehat{\psi }}_{\text{MH}}=\frac{{\sum }_{i=1}^N{n}_{i00}{n}_{i11}/n_i}{{\sum }_{i=1}^N{n}_{i01}{n}_{i10}/n_i}$, the standardized cell count is $n_{i11}^{*}=\frac{n_{i11}-E\left(n_{i11};{\widehat{\psi }}_{\text{MH}}\right)}{{\left[\text{Var}\left(n_{i11};{\widehat{\psi }}_{\text{MH}}\right)\right]}^{1/2}}$ and the variance of the log odds ratio is approximately $v_i^{*}=1/\text{Var}\left(n_{i11};{\widehat{\psi }}_{\text{MH}}\right)$. We denote this test by T_count.

3. Hybrid test for publication bias

3.1. Definition

The various existing publication bias tests in Section 2 are derived under different assumptions and may be powerful only in certain situations. It is infeasible to validate the assumptions and identify the most powerful test for a specific meta-analysis. Due to this difficulty, we propose a hybrid test that can borrow strengths from the various tests.

Consider applying a set of tests $\mathcal{T}$ to detect publication bias in a meta-analysis, and let P_X be the p-value of the test X contained in $\mathcal{T}$. For example, P_reg is the p-value of Egger’s regression test. Then, the test statistic of the hybrid test is calculated as the minimum of the p-values produced by the various tests in $\mathcal{T}$. This idea has been used to test for the differences between high-dimensional mean vectors,^30–32 where the available tests’ powers depend highly on the sparsity of the mean difference vector and the uniformly most powerful test may not exist. Specifically, we define the test statistic of the hybrid test as

$$T_{\text{hybrid}}={}_{X\in \mathcal{T}}^{\text{min}}{}^{P_X.}$$

Note that T_hybrid cannot be directly used as a p-value because it cannot control the type I error rate. We can use the resampling method to obtain the p-value of the hybrid test, denoted by P_hybrid.^33,34 Such a resampling method has been used by Takkouche et al.³⁵ to test for heterogeneity and by Lin and Chu¹⁴ to test for publication bias in meta-analyses. Under the setting of testing for publication bias, the fundamental idea is to: 1) estimate meta-analysis parameters (including the overall effect size and the between-study variance) under the null hypothesis (i.e., no publication bias) via an usual meta-analysis method; 2) resample many meta-analyses under the null to form the test statistic’s empirical null distribution; and 3) calculate the tail probability for the observed test statistic as the p-value. We continue to use the notation in Section 2, and the detailed procedures are described as follows.

3.2. Calculation of the p-value for generic outcomes

For meta-analyses with generic outcomes, the set $\mathcal{T}$ can include any publication bias test reviewed in Section 2.1. Recall that ${\left\{\left(y_i,s_i^2,n_i\right)\right\}}_{i=1}^N$ are the observed effect sizes, their sample variances, and the sample sizes in a meta-analysis with N studies. First, under the null hypothesis of no publication bias, we obtain the estimated overall effect size $\widehat{\theta }$ and the estimated between-study variance ${\widehat{\tau }}^2$ for the N studies. This article uses the random-effects meta-analysis model to estimate the foregoing parameters, because heterogeneity is often expected in meta-analyses.³⁶ The hybrid test statistic is calculated as T_hybrid from these original N studies. Second, we generate a total of B (say, B = 10,000) resampled meta-analyses under the null hypothesis. Specifically, for the bth resampled meta-analysis, we sample N within-study variances from those of the original N studies ${\left\{s_i^2\right\}}_{i=1}^N$ with replacement and denote them by ${\left\{{\left(s_i^{(b)}\right)}^2\right\}}_{i=1}^N$. Such resampling with replacement essentially treats the originally observed data as the whole population, and the resampled data are the new “observed” data; it has been used in many meta-analysis methods.^{33,35,37–39} Also, denote the sample sizes of the corresponding resampled studies by ${\left\{n_i^{(b)}\right\}}_{i=1}^N$. Moreover, the resampled studies’ effect sizes are generated from $y_i^{(b)}~N\left(\widehat{\theta },{\left(s_i^{(b)}\right)}^2+{\widehat{\tau }}^2\right)$. Thus, we can obtain the p-values of all tests in the set $\mathcal{T}$ and calculate the hybrid test statistic $T_{\text{hybrid }}^{(b)}$ for each resampled meta-analysis. Finally, ${\left\{T_{\text{hybrid }}^{(b)}\right\}}_{b=1}^B$ form a null distribution of the hybrid test statistic. Because a smaller value of the hybrid test statistic indicates more significant publication bias, the p-value of the hybrid test is calculated as

$$P_{\text{hybrid }}={(B+1)}^{-1}\sum _{b=1}^B\left[I\left(T_{\text{hybrid }}^{(b)}\le T_{\text{hybrid }}\right)+1\right],$$ (4)

where I(·) is the indicator function. Also, the constant 1 is artificially added to both the numerator and denominator to avoid calculating small p-values as exactly 0. Without such adjustment, a truly small p-value may be calculated as 0 if the number of resampling iterations B is insufficient. In addition, note that only the test T_inv-sqrt-n in Section 2.1 requires the sample sizes n_i; if this test is not in the set $\mathcal{T}$, we do not need to resample the sample sizes in the foregoing procedure.

The theoretical asymptotic properties of some publication bias tests in the set $\mathcal{T}$ may not perform well, especially when the number of studies N is small, and thus p-values based on their theoretical null distributions may be inaccurate. Alternatively, we can also use a similar resampling method to obtain their p-values. It is straightforward to calculate these p-values and thus the hybrid test’s p-value using a double resampling procedure with B(B + 1) resampled meta-analyses, but this is not efficient. In fact, a single loop of resampling with the above B resampled meta-analyses is sufficient for the same purpose.

Specifically, for each test X in the set $\mathcal{T}$, we can calculate its test statistic in the original and B resampled meta-analyses, denoted by T_X and ${\left\{T_X^{(b)}\right\}}_{b=1}^B$, respectively. Then, the resampling-based p-value of the test X in the original meta-analysis can be calculated as $P_X={\left(B+1\right)}^{-1}\left[{\sum }_{b=1}^{B}I\left(|T_X^{(b)}|\ge |T_X|\right)+1\right]$. Note that inequality sign in the indicator function here differs from that in Equation (4) for the hybrid test, because more significant publication bias is indicated by a larger, instead of smaller, absolute value of the test statistic for any test in $\mathcal{T}$. Moreover, we need the p-values of the test X in all B resampled meta-analyses to calculate the corresponding hybrid test statistics $T_{\text{hybrid }}^{(b)}$. In the bth resampled meta-analysis, we can use the other B − 1 resampled meta-analyses to construct the null distribution of the test X, which is formed $T_X^{(c)}(c=1,2,\dots ,B\text{ and }c\ne b)$. Thus, the p-value of the test X in the bth resampled meta-analysis is calculated as $P_X^{(b)}=B^{-1}\left[{\sum }_{c\ne b}I\left(|T_X^{(c)}|\ge |T_X^{(b)}|\right)+1\right]$. Consequently, using these resampling-based p-values, the hybrid test statistics can be obtained in the original and all resampled meta-analyses, and the p-value of the hybrid test can be thus calculated as in Equation (4).

3.3. Calculation of the p-value for binary outcomes

For meta-analyses with binary outcomes, the set $\mathcal{T}$ may include any test in both Sections 2.1 and 2.2. The tests that are specially designed for binary outcomes in Section 2.2 require the four cell counts in the 2 × 2 table in each study. If these tests are in the set $\mathcal{T}$, the above resampling procedure for generic outcomes cannot be directly used, because it does not resample the cell counts in the 2 × 2 tables.

Consider a meta-analysis containing N studies with binary outcomes, and n_i00, n_i01, n_i10, and n_i11 are the four cell counts in study i. Recall that n_i0• and n_i1• are the sample sizes in the control and treatment groups, respectively. The log odds ratios y_i and its within-study variances $s_i^2$ can be estimated using these counts, and a continuity correction (usually 0.5) is applied for studies with zero counts. Such a correction is not needed for the test T_count because this test directly models the event counts in the treatment groups. In addition, we can estimate the event rate in each study as ${\widehat{\pi }}_{i0}=n_{i01}/n_{i0•}$ (after the continuity correction if necessary). To calculate the p-value of the hybrid test for binary outcomes, we propose an alternative resampling procedure based on the cell counts as follows.

First, as in the resampling procedure in Section 3.2, we obtain the estimated overall log odds ratio $\widehat{\theta }$, the estimated between-study variance ${\widehat{\tau }}^2$, and the hybrid test statistic T_hybrid for the original meta-analysis. Second, we generate a total of B resampled meta-analyses under the null hypothesis of no publication bias. Specifically, for the bth resampled meta-analysis, we similarly sample N within-study variances from those of the original N studies with replacement, and denote them by ${\left\{{\left(s_i^{(b)}\right)}^2\right\}}_{i=1}^N$. The corresponding group-specific sample sizes and the control group’s event rate estimates are denoted by ${\left\{\left(n_{i0•}^{(b)},n_{i1•}^{(b)},{\widehat{\pi }}_{i0}^{(b)}\right)\right\}}_{i=1}^N$. The study-specific observed log odds ratios ${\left\{y_i^{(b)}\right\}}_{i=1}^N$ are sampled from $y_i^{(b)}~N\left(\widehat{\theta },{\left(s_i^{(b)}\right)}^2+{\widehat{\tau }}^2\right)$. To obtain the four cell counts $n_{i00}^{(b)}$, $n_{i01}^{(b)}$, $n_{i10}^{(b)}$ and $n_{i11}^{(b)}$ in the 2 × 2 table in each resampled study with the observed effect size $y_i^{(b)}$ and the within-study variance ${\left(s_i^{(b)}\right)}^2$, we can solve the following equations

$$y_i^{(b)}=\text{log}\left[\frac{{\pi }_{i1}^{(b)}/\left(1-{\pi }_{i1}^{(b)}\right)}{{\pi }_{i0}^{(b)}/\left(1-{\pi }_{i0}^{(b)}\right)}\right];$$

$${\left(s_i^{(b)}\right)}^2={\left[n_{i0•}^{(b)}{\pi }_{i0}^{(b)}\left(1-{\pi }_{i0}^{(b)}\right)\right]}^{-1}+{\left[n_{i1•}^{(b)}{\pi }_{i1}^{(b)}\left(1-{\pi }_{i1}^{(b)}\right)\right]}^{-1},$$

with respect to ${\pi }_{i0}^{(b)}$ and ${\pi }_{i1}^{(b)}$. The above two equations can be simplified as a single quadratic equation with respect to ${\pi }_{i0}^{(b)}$. If ${\pi }_{i0}^{(b)}$ has two roots, we select the one closer to ${\widehat{\pi }}_{i0}^{(b)}$. Also, the roots below zero and above one are truncated at zero and one, respectively. Denote the estimated event rates by ${\tilde{\pi }}_{i0}^{(b)}$ and ${\tilde{\pi }}_{i1}^{(b)}$; based on them, the four cell counts in each resampled study are calculated as $n_{i01}^{(b)}=n_{i0•}^{(b)}{\tilde{\pi }}_{i0}^{(b)},n_{i00}^{(b)}=n_{i0•}^{(b)}\left(1-{\tilde{\pi }}_{i0}^{(b)}\right),n_{i11}^{(b)}=n_{i1•}^{(b)}{\tilde{\pi }}_{i1}^{(b)}$ and $n_{i10}^{(b)}=n_{i1•}^{(b)}\left(1-{\tilde{\pi }}_{i1}^{(b)}\right)$, and they are rounded to the corresponding nearest integers. Using the obtained four cell counts in all resampled studies, we calculate the p-value of each publication bias test in the set $\mathcal{T}$ and thus the hybrid test statistic $T_{\text{hybrid }}^{(b)}$. Finally, the hybrid test’s p-value is obtained as in Equation (4).

4. Simulation studies

4.1. Simulation designs

This section presents simulation studies to compare the performance of various tests for publication bias, including the proposed hybrid test, in terms of their type I error rates and statistical powers. We simulated meta-analyses with continuous and binary outcomes under various settings. For simulated meta-analyses with continuous outcomes, we used the standardized mean difference as the effect size, and all seven publication bias tests reviewed in Section 2.1 were applied to each meta-analysis; the hybrid test was based on the p-values of these seven tests. For simulated meta-analyses with binary outcomes, we used the log odds ratio as the effect size, and all sixteen tests reviewed in both Sections 2.1 and 2.2 were applied; the hybrid test was based on the p-values of these sixteen tests. In addition, for the publication bias tests except the hybrid test, their p-values were obtained using their test statistics’ theoretical null distributions and also the resampling method introduced in Sections 3.2 and 3.3. The hybrid test statistic was calculated using both the theoretical and resampling-based p-values of the existing tests included in the set $\mathcal{T}$; its p-value could be only calculated using the resampling method.

Each simulated meta-analysis originally consisted of N = 20 or 50 studies. The within-study total sample size n_i was set to 100, 200, …, 500 for the same number (i.e., N/5) of studies. The treatment allocation ratio was set to 1, which is common in many randomized controlled trials; therefore, the sample sizes in the control and treatment groups were n_i0• = n_i1• = n_i/2 in each simulated study. We generated 500 replications for each simulation setting, and the resampling method was based on B = 200 iterations. The numbers of replications and resampling iterations were not set to be large because the rampling method was relatively time-consuming. The significance level for publication bias was set to 10%, because publication bias tests usually had low statistical powers in many cases.

To evaluate the type I error rates of the various publication bias tests, we generated the study-specific effect sizes and their within-study variances under the null hypothesis of no publication bias. This generation process depended on the types of effect sizes and will be detailed below. To evaluate the tests’ statistical powers, we artificially suppressed certain studies under three scenarios to induce publication bias. Scenario i suppressed studies with the most negative effect sizes, so it met the assumption used by the trim-and-fill method and thus favored this method. Scenario ii suppressed studies with the largest p-values of one-tailed testing (whose alternative hypothesis was that the studies’ true effect sizes were positive). In practice, large studies with many subjects could be still published even if their results were unfavorable. Therefore, similar to scenario ii, we additionally considered scenario iii, in which the suppression was also based on the one-sided p-values but was limited to the studies with the smallest 0.8N sample sizes. The largest 0.2N studies were always included in the meta-analysis, regardless of their effect sizes and p-values. The number of suppressed studies m in all three suppression scenarios was set to 0.2N or 0.4N.

To generate standardized mean differences, we first sampled the study-specific true standard deviations σ_i of the subjects’ outcome measures from U(1,5) in the N studies in a simulated meta-analysis, and this set of σ_i was used for all replications under each simulation setting. The true overall standardized mean difference was set to θ = 0 or 0.8, and the true between-study standard deviation was set to τ = 0 (homogeneity) or 0.2 (heterogeneity). The study-specific true standardized mean differences were generated from θ_i ~ N(θ, τ²) in the N studies. Without loss of generality, the true mean outcome measure in the control group in each study was set to μ_i0 = 0, and that in the treatment group was μ_i1 = μ_i0 + θ_iσ_i.

Consequently, the continuous outcome measures of the subjects in study i were generated as $y_{i0j}~N\left({\mu }_{i0},{\sigma }_i^2\right)$ in the control group (j = 1,2, … , n_i0•) and $y_{i1k}~N\left({\mu }_{i1},{\sigma }_i^2\right)$ in the treatment group (k = 1,2, … , n_i1•). Using these individual data, we calculated the sample means ${\overline{y}}_{i0}=n_{i0•}^{-1}{\sum }_{j=1}^{n_{i0•}}{y}_{ioj}$ and ${\overline{y}}_{i1}=n_{i1•}^{-1}{\sum }_{k=1}^{n_{i1•}}{y}_{i1k}$, and the pooled sample variance $s_{iP}^2=\frac{\left(n_{i0•}-1\right)s_{i0}^2+\left(n_{i1•}-1\right)s_{i1}^2}{n_{i0•}+n_{i1•}-2}$ within each study; here, $s_{i0}^2={\left(n_{i0•}-1\right)}^{-1}{\sum }_{j=1}^{n_{i0•}}{\left(y_{i0j}-{\overline{y}}_{i0}\right)}^2$ and $s_{i1}^2={\left(n_{i1•}-1\right)}^{-1}{\sum }_{k=1}^{n_{i1•}}{\left(y_{i1k}-{\overline{y}}_{i1}\right)}^2$ were the sample variances in the two groups. We used Cohen’s d to estimate the standardized mean difference, because the sample sizes in our simulation studies were relatively large and thus the bias adjustment provided by Hedges’ g was small.^19,40 The point estimate of the standardized mean difference in each study was $y_i=\left({\overline{y}}_{i1}-{\overline{y}}_{i0}\right)/s_{i\text{P}}$ and its within-study variance was approximated as $s_i^2=n_{i0•}^{-1}+n_{i1•}^{-1}+y_i^2/\left[2\left(n_{i0•}+n_{i1•}-2\right)\right]$. The publication bias tests in Section 2.1 and the hybrid test were performed for the simulated data ${\left\{\left(y_i,s_i^2,n_i\right)\right\}}_{i=1}^N$.

To generate log odds ratios, the true event rates p_i0 of the binary outcome in the control groups were sampled from U(0.3,0.7) (common events) or U(0.05,0.1) (relatively rare events) in the N studies in a simulated meta-analysis; each set of p_i0 was used for all replications under each simulation setting. The true overall log odds ratio was set to θ = 0 or 1, and the true between-study standard deviation was set to τ = 0 (homogeneity) or 0.3 (heterogeneity). Thus, we generated the study-specific true log odds ratios from θ_i ~ N(θ, τ²). Therefore, the true event rates in the treatment groups were calculated as $p_{i1}={\left[1+e^{-{\theta }_i}\left(1-p_{i0}\right)/p_{i0}\right]}^{-1}$.

Consequently, the event counts in the control and treatment groups were generated as n_i01 ~ Bin(n_i0•,p_i0) and n_i11 ~ Bin(n_i1•,p_i1), respectively, and thus the counts of subjects without the event were n_i00 = n_i0• − n_i01 and n_i10 = n_i1• − n_i11. Based on these four data cell counts, we calculated the estimated log odds ratio y_i and its within-study variance $s_i^2$ in each study, and performed the publication bias tests.

4.2. Simulation results

Tables 1 and 2 present the type I error rates and statistical powers of the publication bias tests for the simulated meta-analyses of standardized mean differences when N = 20 and 50, respectively. The maximum Monte Carlo standard error of the results was around 2%.

Table 1.

Type I error rates (m = 0) and statistical powers (m > 0) in percentage (%) of various publication bias tests for simulated meta-analyses of standardized mean differences. Each simulated meta-analysis originally contained N = 20 studies before suppressing m “unfavorable” studies under scenario i, ii, or iii.

Test	θ = 0							θ = 0.8
	m = 0	m = 4			m = 8			m = 0	m = 4			m = 8
		i	ii	iii	i	ii	iii		i	ii	iii	i	ii	iii
τ = 0:
Trank	13 (13)	35 (33)	26 (26)	37 (36)	47 (49)	42 (44)	59 (61)	27 (26)	53 (52)	54 (52)	53 (52)	51 (53)	63 (67)	64 (67)
Treg	10 (12)	10 (10)	6 (6)	15 (16)	6 (6)	5 (5)	30 (32)	8 (11)	15 (14)	24 (27)	24 (27)	7 (6)	26 (31)	28 (32)
Treg-het	11 (10)	12 (10)	7 (6)	17 (16)	7 (6)	6 (5)	33 (31)	10 (10)	17 (14)	26 (26)	27 (26)	8 (6)	30 (29)	30 (30)
Tskew	8 (4)	16 (6)	18 (7)	15 (6)	21 (5)	20 (5)	14 (4)	10 (4)	17 (8)	11 (5)	11 (5)	21 (6)	11 (3)	11 (3)
Tskew-het	8 (4)	15 (6)	17 (7)	15 (6)	20 (5)	20 (5)	14 (4)	9 (5)	17 (8)	11 (5)	11 (5)	21 (6)	10 (3)	11 (3)
Tinv-sqrt-n	12 (11)	22 (22)	16 (16)	27 (26)	23 (24)	20 (22)	45 (45)	12 (11)	24 (24)	24 (22)	23 (22)	22 (23)	28 (28)	28 (28)
Ttrim-fill	9 (10)	28 (35)	20 (24)	18 (22)	29 (31)	24 (26)	14 (15)	11 (14)	28 (37)	15 (16)	14 (16)	31 (33)	11 (9)	12 (9)
Thybrid	12 (11)	29 (31)	21 (21)	30 (29)	35 (33)	30 (29)	44 (44)	22 (19)	42 (41)	35 (36)	36 (35)	37 (35)	42 (45)	44 (45)
τ = 0.2:
Trank	10 (8)	21 (17)	15 (13)	24 (19)	26 (26)	21 (22)	45 (43)	30 (24)	37 (32)	56 (52)	58 (54)	32 (32)	62 (62)	68 (70)
Treg	11 (36)	14 (29)	11 (25)	18 (37)	11 (21)	11 (20)	36 (60)	15 (39)	16 (31)	37 (62)	40 (64)	13 (21)	44 (68)	53 (78)
Treg-het	12 (13)	13 (13)	11 (12)	15 (16)	12 (13)	12 (12)	28 (31)	14 (16)	16 (18)	40 (43)	42 (44)	14 (15)	46 (50)	52 (56)
Tskew	10 (7)	17 (11)	17 (10)	19 (9)	20 (7)	19 (8)	19 (8)	10 (6)	18 (11)	12 (7)	14 (7)	22 (9)	15 (5)	14 (6)
Tskew-het	12 (5)	17 (8)	18 (8)	16 (8)	20 (7)	20 (7)	18 (7)	10 (5)	20 (9)	13 (6)	14 (6)	21 (9)	15 (5)	14 (5)
Tinv-sqrt-n	11 (7)	13 (9)	11 (8)	18 (12)	12 (10)	12 (10)	32 (24)	11 (7)	12 (9)	24 (20)	27 (23)	11 (10)	30 (28)	37 (34)
Ttrim-fill	9 (10)	20 (21)	11 (13)	11 (12)	20 (19)	15 (15)	6 (5)	8 (9)	23 (26)	16 (15)	14 (14)	24 (24)	17 (10)	11 (7)
Thybrid	11 (11)	21 (18)	18 (14)	23 (21)	24 (19)	23 (16)	33 (35)	21 (13)	30 (21)	41 (36)	43 (40)	29 (23)	46 (44)	54 (54)

Note: θ, the true overall standardized mean difference; τ, the true between-study standard deviation. The results inside parentheses (except the hybrid test) were based on the tests’ theoretical p-values, and those outside parentheses were based on the resampling method.

Table 2.

Type I error rates (m = 0) and statistical powers (m > 0) in percentage (%) of various publication bias tests for simulated meta-analyses of standardized mean differences. Each simulated meta-analysis originally contained N = 50 studies before suppressing m “unfavorable” studies under scenario i, ii, or iii.

Test	θ = 0							θ = 0.8
	m = 0	m = 10			m = 20			m = 0	m = 10			m = 20
		i	ii	iii	i	ii	iii		i	ii	iii	i	ii	iii
τ = 0:
Trank	14 (13)	64 (63)	46 (46)	63 (63)	89 (89)	80 (79)	97 (97)	61 (59)	95 (95)	95 (94)	94 (94)	93 (92)	98 (98)	99 (98)
Treg	9 (10)	22 (22)	9 (10)	32 (32)	19 (20)	13 (12)	73 (74)	10 (11)	31 (30)	59 (62)	59 (62)	23 (24)	70 (71)	70 (71)
Treg-het	10 (9)	24 (22)	11 (10)	33 (32)	20 (20)	14 (12)	74 (74)	11 (11)	32 (30)	62 (62)	62 (62)	25 (24)	72 (71)	72 (71)
Tskew	9 (7)	41 (32)	44 (33)	26 (20)	51 (39)	51 (38)	22 (15)	9 (7)	42 (35)	12 (8)	11 (8)	54 (42)	14 (10)	13 (10)
Tskew-het	9 (7)	41 (32)	43 (33)	26 (20)	50 (39)	51 (38)	22 (15)	9 (7)	42 (35)	12 (8)	11 (8)	53 (42)	14 (10)	13 (10)
Tinv-sqrt-n	11 (10)	39 (39)	19 (20)	43 (44)	46 (46)	35 (36)	84 (84)	11 (10)	36 (38)	53 (52)	51 (52)	45 (45)	63 (64)	65 (64)
Ttrim-fill	6 (10)	72 (81)	39 (46)	36 (45)	82 (87)	69 (74)	23 (32)	6 (10)	80 (86)	32 (41)	32 (41)	86 (90)	30 (35)	28 (33)
Thybrid	13 (10)	75 (75)	52 (51)	58 (58)	89 (87)	79 (77)	91 (88)	45 (39)	90 (88)	87 (86)	87 (86)	93 (92)	95 (94)	94 (94)
τ = 0.2:
Trank	12 (7)	42 (38)	24 (21)	46 (42)	66 (64)	53 (51)	87 (84)	67 (60)	79 (76)	97 (96)	97 (96)	75 (72)	99 (98)	99 (99)
Treg	10 (34)	13 (32)	14 (29)	29 (52)	15 (25)	10 (18)	71 (88)	17 (43)	27 (43)	72 (91)	76 (92)	23 (35)	84 (94)	91 (97)
Treg-het	10 (11)	14 (14)	13 (15)	23 (24)	14 (15)	11 (12)	57 (61)	18 (19)	25 (25)	77 (77)	78 (80)	22 (22)	84 (87)	90 (91)
Tskew	13 (12)	38 (36)	40 (36)	21 (19)	49 (41)	49 (42)	22 (18)	11 (10)	40 (37)	22 (20)	20 (17)	50 (42)	33 (26)	21 (17)
Tskew-het	12 (9)	42 (35)	43 (36)	23 (16)	50 (41)	49 (40)	21 (15)	12 (8)	42 (35)	24 (19)	22 (16)	51 (43)	35 (26)	23 (17)
Tinv-sqrt-n	11 (6)	13 (10)	13 (10)	28 (22)	15 (13)	11 (10)	70 (58)	11 (7)	16 (12)	50 (42)	55 (48)	15 (14)	59 (56)	72 (67)
Ttrim-fill	8 (9)	52 (56)	21 (24)	12 (15)	58 (62)	44 (47)	4 (6)	7 (9)	66 (72)	35 (38)	26 (30)	69 (72)	39 (43)	16 (17)
Thybrid	10 (10)	56 (47)	40 (27)	40 (31)	67 (64)	58 (51)	75 (70)	48 (20)	74 (67)	91 (74)	92 (79)	74 (73)	94 (86)	97 (90)

Note: θ, the true overall standardized mean difference; τ, the true between-study standard deviation. The results inside parentheses (except the hybrid test) were based on the tests’ theoretical p-values, and those outside parentheses were based on the resampling method.

The resampling-based results were generally similar to those based on the test statistics’ theoretical distributions. However, their differences were large in some situations. For example, when the total number of studies N − m in a meta-analysis was small, the powers of T_skew and T_skew-het based on the resampling method and the theoretical distributions differed by up to 15%, because the theoretical distribution of the skewness was derived under the large-sample setting (in terms of the number of studies), and it did not perform well for meta-analyses with a few studies.¹⁴ When N increased to 50, the differences between the resampling-based and theoretical-distribution-based results became noticeably smaller. Moreover, when substantial heterogeneity was present (τ = 0.2), Egger’s regression test T_reg had seriously inflated type I error rates (up to 36%) if using the test statistic’s theoretical distribution to calculate its p-value. This was because T_reg was based on the fixed-effect setting, and it failed to account for the substantial heterogeneity. However, the resampling method took such heterogeneity into account, so the resampling-based T_reg had well-controlled type I error rates. Because the resampling method may be robust to the violation of the assumptions required for deriving the theoretical null distributions, the following interpretations of the results will focus on those based on the resampling method.

When the true overall standardized mean difference θ was zero, the type I error rates of most tests were controlled fairly well, while those of the rank test T_rank were slightly inflated. The rank test had high powers in many situations; it even outperformed the trim-and-fill method T_trim-fill when N = 20 under scenario i, which favored the assumption of the trim-and-fill method. For example, when m = 4 studies were suppressed under scenario i and τ = 0, the powers of T_rank and T_trim-fill were 35% and 28%, respectively. Benefiting from their relatively high powers, the hybrid test had a power of 29%; although it did not outperform T_rank, it was much powerful than other tests. When N increased to 50 and m = 10 studies were suppressed under scenario i, T_trim-fill became noticeably more powerful than T_rank and it greatly outperformed all other tests. Borrowing strengths from the various tests, the hybrid test had a power of 75%, which was even slightly higher than T_trim-fill. As the heterogeneity standard deviation increased to τ = 0.2, many tests’ powers noticeably decreased, while the hybrid test remained the most powerful.

Under scenario ii based on the studies’ one-sided p-values, T_trim-fill became less powerful compared with scenario i. When N = 50 and τ = 0, T_rank and the skewness-based tests had similar powers of around 45%, and the hybrid test had the highest power of 52%. As τ increased to 0.2, T_skew-het still had a high power of 43%, while the power of T_rank dropped to 24%. Because of the high power of T_skew-het, the hybrid test’s power remained high (40%).

Under scenario iii in which meta-analyses with large sample sizes were not suppressed, the power of T_inv-sqrt-n became more powerful compared with the other two scenarios. This was possibly because the suppression was related to the sample sizes and T_inv-sqrt-n examined the association between the sample sizes and the effect sizes. The regression tests T_reg and T_reg-het also became more powerful, compared with their performance under scenarios i and ii, although they were outperformed by T_rank. The hybrid test did not have the highest power under scenario iii, but its performance was generally close to the most powerful test.

As the true overall standardized mean difference θ increased from 0 to 0.8, the type I error rates of T_rank became seriously inflated (up to 67% when N = 50). Those of the regression tests were also inflated to nearly 20% in the presence of substantial heterogeneity (τ = 0.2). Due to the inflated type I error rates of these tests, the hybrid test’s type I error rate was also inflated, while the inflation was slighter than that of T_rank.

Tables 3 and 4 present the results of the publication bias tests for the simulated meta-analyses of log odds ratios when N = 20 and 50, respectively. The trends of the publication bias tests’ type I error rates and powers were similar to those for meta-analyses of standardized mean differences in Tables 1 and 2 across different scenarios. Generally, type I error rates of most tests were controlled well when the true overall log odds ratio θ was 0 (i.e., the odds ratio was the null value 1). As θ increased from 0 to 1, some tests (including T_rank, T_reg, and T_reg-het) had noticeable inflated type I error rates, especially when the number of studies N was large and the event rate p_i0 was low. Moreover, as the heterogeneity standard deviation increased from 0 to 0.3, type I error rates of many tests tended to be inflated. The tests T_score and T_count had noticeably inflated type I error rates when θ = 0 in the presence of low event rate and high heterogeneity; however, their type I error rates dropped sharply below the nominal level 10% when θ became 1. The type I error rates of T_AS-reg and T_smoothed were also inflated when events were common and heterogeneity was present.

Table 3.

Type I error rates (m = 0) and statistical powers (m > 0) in percentage (%) of various publication bias tests for simulated meta-analyses of log odds ratios. Each simulated meta-analysis originally contained N = 20 studies before suppressing m “unfavorable” studies under scenario i, ii, or iii.

Test	θ = 0							θ = 1
	m = 0	m = 4			m = 8			m = 0	m = 4			m = 8
		i	ii	iii	i	ii	iii		i	ii	iii	i	ii	iii
pi0 ~ U(0.3, 0.7) and τ = 0:
Trank	11 (10)	25 (23)	17 (16)	30 (28)	29 (30)	24 (26)	50 (51)	13 (12)	30 (30)	41 (41)	42 (41)	33 (35)	52 (56)	56 (59)
Treg	12 (9)	14 (12)	9 (8)	22 (20)	10 (8)	7 (6)	41 (39)	12 (13)	19 (17)	40 (40)	42 (41)	14 (12)	49 (47)	55 (53)
Treg-het	12 (8)	15 (12)	10 (8)	23 (20)	11 (8)	9 (6)	43 (37)	14 (12)	21 (17)	42 (38)	44 (40)	16 (12)	52 (47)	57 (52)
Tskew	10 (4)	17 (8)	18 (7)	14 (6)	19 (6)	19 (5)	13 (5)	8 (4)	14 (7)	9 (5)	9 (5)	18 (8)	14 (5)	14 (6)
Tskew-het	10 (4)	17 (7)	18 (7)	14 (6)	19 (6)	19 (5)	13 (5)	8 (5)	14 (7)	8 (5)	9 (5)	18 (8)	13 (5)	14 (6)
Tinv-sqrt-n	12 (10)	24 (23)	15 (15)	29 (28)	26 (26)	23 (23)	51 (50)	11 (12)	21 (23)	33 (37)	35 (37)	24 (28)	42 (43)	44 (45)
Ttrim-fill	8 (12)	30 (36)	18 (22)	18 (23)	31 (32)	27 (28)	13 (14)	9 (12)	37 (41)	25 (27)	25 (26)	40 (40)	24 (18)	21 (14)
Tn	10 (9)	25 (26)	14 (16)	36 (36)	25 (25)	21 (21)	63 (62)	10 (12)	19 (20)	25 (27)	26 (27)	21 (25)	34 (38)	38 (42)
Tinv-n	11 (11)	22 (22)	16 (16)	24 (25)	25 (25)	23 (22)	44 (43)	11 (12)	21 (22)	34 (37)	35 (37)	22 (27)	42 (44)	43 (46)
TAS-rank	13 (11)	23 (23)	15 (14)	30 (27)	27 (25)	23 (21)	54 (50)	11 (11)	22 (22)	35 (34)	36 (34)	25 (24)	43 (43)	46 (48)
TAS-reg	10 (9)	13 (12)	9 (8)	21 (19)	9 (8)	7 (6)	40 (38)	9 (12)	11 (16)	29 (34)	32 (36)	7 (10)	39 (44)	44 (50)
TAS-reg-het	11 (8)	14 (12)	9 (8)	22 (19)	10 (8)	8 (6)	43 (37)	9 (11)	12 (15)	32 (33)	34 (35)	10 (10)	43 (43)	49 (48)
Tsmoothed	12 (11)	14 (13)	10 (8)	21 (21)	9 (9)	8 (6)	42 (40)	11 (15)	15 (18)	31 (34)	33 (36)	11 (13)	35 (37)	41 (43)
Tsmoothed-het	12 (8)	16 (13)	10 (8)	23 (20)	12 (9)	10 (6)	43 (39)	11 (13)	16 (17)	31 (33)	33 (34)	13 (12)	37 (36)	43 (42)
Tscore	12 (10)	24 (23)	15 (15)	29 (28)	26 (26)	22 (23)	51 (50)	8 (10)	18 (20)	29 (34)	29 (34)	21 (25)	39 (46)	40 (46)
Tcount	12 (9)	23 (22)	16 (14)	28 (27)	26 (27)	21 (23)	48 (51)	6 (11)	13 (20)	21 (28)	21 (28)	18 (26)	30 (42)	29 (43)
Thybrid	11 (11)	29 (31)	20 (19)	33 (32)	29 (29)	24 (27)	48 (50)	9 (10)	28 (27)	35 (33)	34 (32)	33 (29)	44 (41)	45 (45)
pi0 ~ U (0.3, 0.7) and τ = 0.3:
Trank	11 (9)	15 (13)	10 (9)	22 (18)	18 (19)	15 (15)	38 (36)	17 (13)	21 (19)	40 (37)	45 (41)	22 (24)	51 (52)	59 (61)
Treg	16 (27)	18 (22)	13 (16)	27 (32)	14 (16)	12 (13)	48 (55)	22 (34)	22 (30)	50 (60)	54 (67)	18 (21)	60 (67)	70 (80)
Treg-het	13 (13)	17 (16)	12 (12)	21 (20)	14 (12)	12 (10)	38 (38)	19 (21)	22 (22)	46 (46)	49 (52)	20 (18)	59 (58)	67 (67)
Tskew	10 (4)	18 (8)	17 (7)	18 (8)	19 (6)	19 (6)	20 (7)	8 (3)	17 (9)	12 (4)	11 (5)	20 (5)	17 (4)	15 (3)
Tskew-het	9 (4)	18 (7)	18 (6)	17 (6)	18 (6)	19 (6)	18 (6)	9 (4)	18 (9)	13 (5)	12 (5)	20 (6)	16 (4)	14 (4)
Tinv-sqrt-n	11 (7)	12 (10)	8 (8)	18 (16)	10 (11)	10 (9)	33 (28)	10 (10)	12 (14)	22 (22)	25 (26)	10 (14)	30 (31)	37 (37)
Ttrim-fill	8 (10)	24 (28)	15 (19)	14 (17)	27 (27)	24 (24)	9 (9)	11 (14)	33 (36)	27 (28)	22 (23)	32 (31)	27 (20)	16 (12)
Tn	9 (10)	12 (11)	9 (9)	23 (24)	12 (13)	9 (11)	43 (43)	8 (11)	9 (12)	17 (20)	24 (25)	11 (13)	27 (30)	35 (36)
Tinv-n	9 (6)	12 (10)	10 (8)	17 (13)	11 (12)	9 (10)	28 (23)	10 (9)	11 (12)	24 (22)	26 (25)	10 (12)	31 (30)	37 (35)
TAS-rank	11 (8)	13 (11)	8 (7)	18 (17)	12 (12)	11 (10)	38 (30)	8 (8)	13 (12)	23 (22)	26 (25)	13 (14)	33 (32)	41 (40)
TAS-reg	16 (27)	15 (20)	11 (16)	24 (31)	12 (14)	10 (10)	44 (53)	8 (26)	10 (17)	23 (37)	28 (44)	8 (14)	34 (46)	44 (61)
TAS-reg-het	14 (13)	15 (13)	11 (10)	19 (18)	13 (11)	11 (8)	35 (35)	11 (13)	10 (13)	25 (28)	28 (32)	9 (12)	36 (39)	44 (48)
Tsmoothed	18 (29)	17 (21)	13 (19)	25 (32)	14 (15)	12 (12)	46 (54)	13 (30)	14 (22)	27 (40)	31 (45)	12 (17)	34 (42)	43 (55)
Tsmoothed-het	15 (13)	15 (14)	11 (11)	18 (18)	13 (12)	12 (9)	36 (35)	12 (14)	14 (15)	27 (29)	28 (31)	12 (13)	33 (35)	40 (42)
Tscore	10 (8)	13 (10)	9 (8)	19 (16)	12 (12)	11 (10)	35 (31)	9 (9)	9 (11)	22 (23)	26 (27)	10 (13)	31 (34)	38 (42)
Tcount	10 (8)	13 (12)	10 (8)	19 (17)	13 (16)	11 (14)	36 (36)	5 (8)	8 (10)	16 (21)	19 (24)	10 (14)	25 (35)	31 (42)
Thybrid	10 (16)	19 (21)	13 (15)	23 (26)	19 (17)	18 (16)	38 (44)	12 (18)	25 (24)	32 (36)	36 (42)	23 (16)	40 (45)	48 (57)
pi0 ~ U (0.05, 0.1) and τ = 0:
Trank	11 (10)	27 (24)	16 (16)	23 (22)	32 (35)	28 (29)	35 (38)	22 (19)	44 (42)	63 (63)	64 (64)	42 (45)	70 (75)	73 (77)
Treg	10 (12)	16 (16)	8 (8)	15 (15)	12 (12)	9 (9)	22 (25)	21 (23)	28 (30)	55 (58)	57 (60)	16 (17)	57 (56)	62 (64)
Treg-het	11 (11)	17 (16)	9 (8)	16 (15)	13 (12)	10 (9)	25 (24)	22 (22)	31 (29)	58 (57)	59 (59)	17 (17)	61 (56)	65 (64)
Tskew	9 (3)	15 (6)	16 (5)	14 (6)	17 (6)	19 (5)	20 (6)	8 (3)	13 (5)	9 (3)	8 (3)	18 (6)	15 (5)	13 (4)
Tskew-het	9 (3)	15 (6)	16 (5)	14 (6)	17 (6)	19 (5)	19 (6)	8 (3)	14 (5)	9 (3)	8 (3)	18 (6)	15 (5)	13 (4)
Tinv-sqrt-n	13 (16)	20 (23)	13 (16)	24 (27)	21 (25)	19 (22)	44 (47)	11 (13)	19 (24)	30 (36)	31 (38)	23 (28)	34 (38)	43 (44)
Ttrim-fill	9 (12)	31 (41)	19 (25)	16 (21)	34 (39)	31 (36)	15 (17)	10 (17)	46 (54)	43 (49)	38 (46)	44 (51)	38 (39)	27 (27)
Tn	8 (9)	13 (17)	9 (13)	23 (28)	16 (20)	14 (18)	49 (54)	8 (9)	14 (19)	20 (25)	25 (29)	17 (21)	26 (29)	36 (40)
Tinv-n	9 (13)	13 (20)	8 (14)	14 (23)	17 (21)	14 (18)	30 (38)	8 (11)	15 (23)	26 (33)	27 (35)	17 (25)	34 (38)	38 (42)
TAS-rank	13 (12)	20 (19)	13 (13)	24 (24)	22 (21)	22 (20)	47 (47)	9 (9)	15 (17)	29 (29)	32 (33)	18 (19)	37 (39)	48 (48)
TAS-reg	9 (13)	6 (12)	3 (7)	11 (17)	4 (6)	3 (5)	22 (33)	3 (10)	2 (11)	9 (26)	12 (32)	1 (6)	12 (33)	22 (47)
TAS-reg-het	9 (11)	9 (12)	4 (7)	13 (16)	5 (6)	4 (5)	28 (31)	5 (9)	5 (10)	16 (25)	19 (30)	2 (6)	20 (32)	35 (45)
Tsmoothed	12 (19)	9 (18)	5 (12)	15 (23)	6 (11)	5 (10)	29 (42)	8 (16)	11 (21)	23 (37)	26 (40)	5 (15)	23 (33)	34 (42)
Tsmoothed-het	12 (16)	11 (17)	6 (11)	17 (21)	7 (11)	6 (9)	33 (39)	9 (14)	12 (19)	25 (34)	29 (37)	9 (14)	26 (32)	36 (41)
Tscore	14 (11)	25 (23)	16 (15)	22 (20)	28 (26)	22 (22)	35 (33)	4 (10)	7 (16)	16 (30)	17 (31)	11 (21)	23 (40)	21 (39)
Tcount	11 (9)	23 (21)	15 (15)	20 (20)	24 (27)	21 (22)	32 (36)	3 (8)	6 (18)	11 (26)	10 (26)	8 (22)	10 (38)	9 (36)
Thybrid	10 (10)	22 (23)	14 (14)	21 (21)	28 (22)	24 (19)	40 (36)	12 (5)	30 (24)	43 (28)	43 (30)	31 (15)	51 (30)	54 (35)
pi0 ~ U (0.05, 0.1) and τ = 0.3:
Trank	14 (12)	15 (12)	13 (10)	12 (11)	22 (23)	19 (21)	17 (19)	12 (8)	24 (21)	38 (33)	39 (34)	26 (26)	44 (46)	43 (44)
Treg	15 (20)	11 (12)	8 (9)	9 (11)	9 (11)	8 (9)	14 (18)	10 (18)	19 (24)	37 (44)	40 (48)	14 (15)	45 (49)	50 (60)
Treg-het	15 (16)	12 (11)	10 (9)	10 (9)	11 (10)	9 (8)	17 (17)	12 (14)	21 (22)	40 (40)	42 (43)	15 (15)	47 (47)	53 (54)
Tskew	7 (3)	13 (8)	14 (7)	16 (8)	18 (5)	17 (5)	26 (7)	9 (3)	17 (8)	16 (6)	17 (7)	22 (6)	16 (4)	16 (5)
Tskew-het	7 (3)	13 (7)	15 (7)	16 (8)	18 (5)	17 (5)	26 (8)	9 (3)	17 (7)	17 (6)	17 (6)	20 (6)	16 (4)	16 (5)
Tinv-sqrt-n	9 (11)	13 (14)	11 (13)	20 (22)	16 (19)	14 (17)	37 (40)	9 (9)	15 (17)	22 (27)	28 (32)	16 (20)	29 (34)	41 (42)
Ttrim-fill	8 (14)	23 (29)	16 (20)	10 (13)	31 (34)	25 (30)	8 (9)	9 (14)	34 (44)	32 (40)	26 (33)	32 (39)	32 (31)	17 (18)
Tn	7 (10)	9 (13)	9 (11)	20 (25)	12 (15)	11 (14)	41 (48)	7 (10)	13 (17)	18 (22)	22 (26)	13 (16)	22 (26)	37 (39)
Tinv-n	5 (10)	8 (11)	7 (11)	11 (15)	11 (16)	8 (13)	21 (28)	6 (9)	10 (17)	16 (24)	20 (27)	12 (19)	24 (30)	33 (36)
TAS-rank	8 (8)	14 (13)	11 (10)	20 (18)	15 (15)	13 (11)	39 (35)	7 (6)	10 (11)	20 (19)	25 (25)	11 (12)	30 (31)	45 (45)
TAS-reg	7 (18)	7 (13)	6 (11)	15 (25)	5 (9)	3 (7)	30 (44)	6 (21)	4 (15)	12 (27)	18 (37)	1 (11)	13 (38)	33 (64)
TAS-reg-het	9 (12)	9 (11)	8 (9)	16 (20)	7 (8)	5 (6)	31 (35)	7 (10)	5 (11)	14 (21)	20 (27)	3 (9)	21 (31)	36 (50)
Tsmoothed	12 (25)	11 (18)	9 (16)	21 (33)	7 (18)	5 (15)	38 (51)	11 (23)	11 (20)	20 (37)	29 (44)	9 (17)	25 (40)	43 (58)
Tsmoothed-het	10 (16)	12 (14)	10 (13)	20 (26)	9 (15)	8 (12)	35 (42)	10 (14)	12 (17)	23 (31)	27 (37)	11 (16)	29 (34)	40 (47)
Tscore	15 (13)	11 (9)	12 (11)	10 (10)	14 (14)	13 (13)	12 (11)	5 (15)	3 (6)	4 (11)	4 (10)	6 (11)	10 (17)	6 (13)
Tcount	16 (13)	10 (9)	11 (11)	11 (11)	14 (15)	12 (14)	14 (15)	4 (13)	2 (6)	3 (9)	2 (9)	3 (11)	6 (18)	3 (14)
Thybrid	11 (9)	16 (13)	15 (11)	19 (17)	18 (13)	15 (11)	29 (29)	8 (7)	20 (15)	26 (18)	29 (22)	22 (9)	32 (18)	38 (30)

Note: θ, the true overall log odds ratio; τ, the true between-study standard deviation; p_i0, the true event rate in the control group. The results inside parentheses (except the hybrid test) were based on the tests’ theoretical p-values, and those outside parentheses were based on the resampling method.

Table 4.

Type I error rates (m = 0) and statistical powers (m > 0) in percentage (%) of various publication bias tests for simulated meta-analyses of log odds ratios. Each simulated meta-analysis originally contained N = 50 studies before suppressing m “unfavorable” studies under scenario i, ii, or iii.

Test	θ = 0							θ = 1
	m = 0	m = 10			m = 20			m = 0	m = 10			m = 20
		i	ii	iii	i	ii	iii		i	ii	iii	i	ii	iii
pi0 ~ U(0.3, 0.7) and τ = 0:
Trank	11 (10)	46 (45)	24 (22)	50 (48)	63 (62)	50 (50)	88 (88)	24 (24)	63 (67)	81 (82)	83 (83)	65 (67)	92 (92)	93 (93)
Treg	12 (10)	34 (26)	12 (9)	41 (36)	27 (20)	19 (14)	82 (78)	16 (17)	42 (39)	80 (82)	83 (83)	32 (31)	89 (88)	92 (92)
Treg-het	12 (10)	34 (26)	12 (9)	41 (36)	28 (20)	20 (14)	83 (77)	17 (17)	43 (39)	82 (82)	84 (83)	34 (31)	90 (88)	92 (92)
Tskew	6 (5)	33 (27)	34 (31)	17 (15)	44 (35)	42 (36)	15 (11)	6 (7)	27 (25)	9 (9)	8 (8)	37 (31)	21 (17)	15 (13)
Tskew-het	6 (5)	33 (27)	34 (31)	17 (15)	44 (35)	42 (36)	14 (11)	6 (7)	26 (25)	10 (9)	9 (8)	37 (31)	21 (17)	15 (13)
Tinv-sqrt-n	11 (10)	43 (42)	20 (20)	48 (48)	55 (56)	41 (43)	88 (88)	8 (12)	36 (47)	64 (70)	64 (71)	42 (50)	78 (80)	82 (83)
Ttrim-fill	8 (13)	77 (85)	39 (48)	40 (50)	86 (90)	75 (81)	25 (35)	9 (15)	84 (89)	57 (66)	54 (61)	87 (91)	50 (59)	30 (37)
Tn	9 (9)	38 (39)	19 (19)	54 (54)	46 (47)	37 (38)	93 (94)	6 (11)	29 (37)	48 (54)	48 (55)	39 (45)	71 (75)	76 (80)
Tinv-n	12 (10)	43 (42)	19 (19)	44 (43)	52 (53)	42 (42)	83 (81)	10 (12)	39 (44)	70 (75)	70 (75)	45 (51)	80 (82)	82 (84)
TAS-rank	11 (9)	41 (40)	19 (17)	46 (43)	56 (54)	44 (42)	88 (87)	9 (12)	47 (52)	70 (73)	69 (74)	53 (57)	84 (83)	87 (87)
TAS-reg	12 (10)	31 (24)	12 (8)	40 (34)	24 (18)	18 (12)	81 (76)	9 (14)	27 (37)	71 (75)	72 (77)	20 (29)	82 (84)	87 (88)
TAS-reg-het	12 (10)	32 (24)	12 (8)	41 (34)	25 (18)	18 (12)	81 (75)	9 (13)	30 (36)	73 (75)	74 (76)	25 (29)	85 (84)	89 (88)
Tsmoothed	13 (11)	33 (27)	13 (10)	41 (36)	26 (21)	19 (14)	82 (77)	9 (13)	23 (30)	62 (68)	61 (69)	20 (25)	73 (74)	78 (80)
Tsmoothed-het	13 (10)	33 (26)	13 (10)	42 (36)	28 (21)	20 (14)	82 (77)	10 (12)	24 (30)	63 (67)	63 (68)	21 (25)	74 (74)	79 (80)
Tscore	12 (11)	44 (43)	20 (20)	48 (48)	54 (54)	41 (42)	88 (88)	4 (11)	24 (40)	51 (71)	52 (72)	33 (47)	74 (83)	77 (85)
Tcount	11 (9)	43 (40)	21 (19)	45 (44)	56 (53)	44 (42)	86 (86)	2 (10)	19 (36)	34 (59)	35 (61)	28 (44)	59 (76)	63 (78)
Thybrid	10 (9)	66 (73)	34 (40)	51 (52)	81 (85)	65 (72)	86 (84)	13 (9)	70 (71)	73 (63)	73 (64)	74 (76)	85 (77)	88 (79)
pi0 ~ U (0.3, 0.7) and τ = 0.3:
Trank	11 (7)	26 (24)	13 (13)	36 (31)	31 (29)	24 (22)	78 (73)	36 (32)	59 (58)	88 (86)	91 (90)	54 (52)	92 (91)	97 (96)
Treg	15 (23)	24 (28)	14 (16)	45 (51)	24 (23)	17 (16)	84 (89)	40 (57)	58 (64)	90 (93)	94 (97)	43 (45)	96 (97)	99 (100)
Treg-het	12 (11)	21 (20)	12 (11)	32 (29)	24 (21)	17 (15)	75 (74)	33 (35)	53 (54)	89 (88)	92 (92)	43 (43)	95 (96)	98 (99)
Tskew	8 (9)	32 (29)	33 (31)	19 (18)	42 (35)	43 (35)	22 (20)	4 (6)	30 (29)	16 (17)	13 (14)	41 (36)	32 (29)	17 (14)
Tskew-het	8 (7)	33 (29)	34 (31)	19 (17)	43 (36)	43 (35)	19 (16)	4 (5)	32 (29)	19 (18)	15 (15)	41 (36)	32 (28)	17 (14)
Tinv-sqrt-n	9 (6)	15 (12)	11 (9)	31 (23)	18 (17)	14 (13)	71 (66)	8 (8)	15 (19)	43 (46)	52 (52)	18 (22)	62 (64)	77 (77)
Ttrim-fill	9 (13)	63 (70)	26 (33)	19 (24)	68 (73)	53 (59)	8 (10)	12 (16)	80 (86)	62 (71)	42 (50)	86 (89)	66 (72)	22 (26)
Tn	9 (9)	15 (14)	13 (13)	42 (41)	17 (18)	13 (14)	78 (78)	8 (11)	14 (19)	34 (40)	44 (49)	18 (23)	52 (55)	72 (74)
Tinv-n	9 (6)	15 (12)	11 (9)	26 (18)	18 (17)	13 (12)	68 (59)	8 (7)	18 (18)	50 (48)	58 (55)	18 (19)	67 (66)	79 (77)
TAS-rank	9 (6)	20 (17)	12 (9)	28 (23)	22 (21)	15 (14)	69 (65)	8 (9)	25 (26)	54 (52)	59 (58)	31 (33)	74 (74)	85 (84)
TAS-reg	15 (24)	19 (23)	14 (16)	39 (45)	19 (18)	13 (13)	77 (83)	9 (25)	21 (32)	54 (72)	65 (81)	17 (30)	73 (83)	88 (93)
TAS-reg-het	10 (10)	17 (16)	12 (12)	26 (24)	18 (15)	13 (11)	69 (68)	8 (12)	20 (26)	58 (64)	67 (73)	20 (28)	78 (80)	89 (91)
Tsmoothed	16 (25)	20 (25)	15 (17)	40 (47)	20 (19)	14 (15)	78 (84)	10 (27)	21 (31)	51 (65)	61 (74)	18 (24)	68 (76)	81 (89)
Tsmoothed-het	11 (10)	18 (16)	12 (12)	26 (24)	19 (16)	13 (12)	68 (67)	8 (12)	19 (23)	50 (57)	57 (64)	18 (21)	67 (70)	79 (80)
Tscore	10 (7)	17 (15)	11 (9)	36 (27)	19 (18)	14 (13)	74 (71)	6 (10)	13 (22)	41 (56)	51 (65)	14 (22)	64 (75)	77 (87)
Tcount	10 (6)	21 (18)	12 (10)	31 (25)	21 (22)	16 (16)	72 (68)	4 (9)	12 (24)	34 (54)	40 (59)	13 (28)	51 (73)	68 (83)
Thybrid	11 (13)	49 (58)	30 (32)	39 (41)	58 (66)	47 (52)	75 (77)	27 (27)	69 (71)	83 (81)	87 (87)	73 (75)	90 (84)	95 (96)
pi0 ~ U (0.05, 0.1) and τ = 0:
Trank	12 (10)	51 (48)	25 (23)	44 (40)	72 (69)	62 (59)	80 (78)	41 (39)	84 (83)	96 (97)	97 (97)	89 (88)	100 (100)	99 (99)
Treg	11 (12)	36 (35)	14 (14)	31 (32)	32 (33)	24 (25)	69 (70)	40 (43)	70 (70)	94 (95)	96 (97)	59 (60)	97 (96)	98 (99)
Treg-het	12 (11)	37 (35)	14 (14)	32 (32)	34 (33)	27 (25)	71 (70)	41 (41)	71 (70)	95 (95)	97 (97)	62 (60)	97 (96)	99 (99)
Tskew	5 (3)	26 (21)	27 (23)	18 (12)	37 (27)	38 (28)	27 (19)	12 (9)	26 (18)	17 (12)	15 (11)	37 (27)	31 (21)	20 (13)
Tskew-het	5 (3)	26 (21)	27 (23)	17 (12)	37 (27)	38 (28)	27 (19)	12 (10)	25 (18)	16 (12)	15 (11)	37 (27)	30 (21)	20 (13)
Tinv-sqrt-n	12 (13)	39 (41)	13 (16)	45 (47)	46 (50)	39 (43)	84 (85)	10 (12)	44 (49)	67 (70)	70 (73)	54 (58)	78 (80)	85 (86)
Ttrim-fill	7 (12)	77 (85)	37 (47)	32 (43)	91 (95)	81 (86)	23 (36)	16 (24)	96 (97)	86 (91)	74 (83)	97 (98)	85 (91)	53 (63)
Tn	8 (12)	25 (32)	10 (13)	45 (50)	32 (39)	27 (34)	85 (89)	7 (11)	33 (40)	49 (55)	53 (59)	41 (49)	66 (70)	77 (80)
Tinv-n	6 (13)	22 (35)	8 (16)	27 (40)	32 (45)	26 (38)	66 (78)	4 (10)	33 (45)	57 (69)	62 (70)	42 (56)	77 (82)	82 (85)
TAS-rank	10 (9)	37 (35)	12 (12)	45 (43)	47 (48)	40 (39)	84 (83)	8 (8)	42 (42)	67 (67)	70 (70)	51 (52)	84 (85)	89 (90)
TAS-reg	8 (12)	15 (21)	4 (6)	24 (34)	12 (19)	9 (14)	66 (75)	3 (11)	14 (31)	45 (63)	52 (70)	8 (30)	55 (80)	74 (90)
TAS-reg-het	9 (10)	18 (21)	5 (6)	29 (33)	15 (19)	11 (14)	69 (75)	4 (9)	21 (31)	53 (63)	60 (70)	16 (30)	72 (80)	84 (90)
Tsmoothed	11 (16)	19 (29)	6 (10)	33 (43)	18 (28)	13 (21)	70 (80)	10 (15)	31 (41)	60 (67)	64 (71)	26 (39)	67 (75)	78 (83)
Tsmoothed-het	11 (14)	24 (29)	7 (10)	35 (42)	21 (28)	16 (21)	74 (79)	10 (13)	33 (41)	62 (67)	67 (70)	32 (38)	71 (74)	80 (83)
Tscore	11 (9)	43 (40)	15 (15)	37 (34)	49 (52)	41 (41)	74 (74)	1 (7)	11 (39)	30 (66)	31 (68)	18 (51)	49 (85)	45 (84)
Tcount	10 (10)	39 (38)	18 (16)	36 (33)	53 (58)	42 (45)	71 (71)	1 (7)	11 (40)	26 (62)	26 (64)	21 (55)	39 (81)	34 (81)
Thybrid	9 (7)	59 (66)	29 (27)	41 (40)	80 (83)	67 (71)	80 (77)	25 (9)	85 (75)	89 (71)	91 (71)	90 (84)	96 (82)	98 (82)
pi0 ~ U (0.05, 0.1) and τ = 0.3:
Trank	20 (15)	25 (25)	14 (12)	20 (18)	43 (40)	34 (32)	51 (47)	18 (15)	53 (51)	73 (71)	77 (75)	58 (54)	89 (89)	89 (88)
Treg	19 (24)	21 (22)	9 (9)	17 (20)	20 (20)	16 (15)	43 (48)	21 (28)	50 (52)	74 (78)	79 (83)	38 (38)	87 (89)	90 (95)
Treg-het	18 (19)	22 (22)	10 (9)	19 (19)	22 (20)	17 (15)	47 (47)	23 (22)	51 (52)	75 (76)	80 (80)	40 (38)	88 (88)	91 (93)
Tskew	7 (5)	34 (26)	39 (31)	19 (16)	46 (34)	47 (36)	31 (24)	8 (7)	34 (26)	26 (21)	19 (16)	46 (33)	35 (26)	23 (17)
Tskew-het	7 (5)	34 (26)	40 (31)	21 (16)	45 (34)	46 (36)	32 (25)	9 (7)	34 (26)	26 (20)	19 (16)	45 (33)	36 (26)	24 (17)
Tinv-sqrt-n	8 (8)	29 (31)	12 (15)	37 (38)	29 (32)	24 (26)	77 (80)	11 (11)	27 (29)	47 (50)	59 (62)	29 (33)	62 (64)	81 (82)
Ttrim-fill	8 (12)	61 (69)	24 (31)	20 (27)	76 (82)	66 (71)	14 (19)	13 (18)	85 (89)	76 (83)	51 (57)	89 (91)	78 (84)	26 (35)
Tn	6 (10)	22 (26)	10 (13)	38 (44)	24 (28)	18 (24)	78 (84)	8 (11)	18 (25)	30 (37)	45 (50)	24 (28)	47 (50)	71 (73)
Tinv-n	5 (7)	20 (27)	9 (15)	21 (32)	22 (30)	18 (26)	54 (64)	7 (11)	15 (26)	32 (44)	44 (52)	20 (27)	54 (62)	71 (75)
TAS-rank	7 (6)	29 (28)	14 (13)	37 (35)	33 (32)	27 (26)	76 (76)	9 (7)	25 (25)	48 (46)	60 (59)	27 (27)	68 (71)	86 (87)
TAS-reg	6 (14)	20 (26)	7 (11)	30 (40)	13 (19)	9 (16)	69 (80)	6 (22)	10 (30)	32 (57)	49 (70)	6 (22)	49 (76)	78 (93)
TAS-reg-het	7 (9)	21 (24)	8 (10)	30 (35)	16 (19)	13 (16)	68 (75)	8 (11)	12 (23)	39 (50)	52 (61)	11 (19)	61 (73)	83 (89)
Tsmoothed	9 (18)	23 (30)	9 (14)	36 (47)	17 (25)	12 (21)	76 (84)	13 (24)	22 (34)	47 (59)	60 (71)	17 (28)	60 (70)	83 (89)
Tsmoothed-het	8 (10)	26 (29)	10 (13)	33 (39)	19 (24)	16 (21)	73 (79)	12 (16)	24 (30)	47 (55)	59 (66)	20 (27)	62 (66)	82 (85)
Tscore	19 (17)	14 (13)	9 (10)	13 (11)	17 (19)	14 (16)	31 (33)	2 (27)	1 (7)	2 (13)	3 (15)	2 (12)	9 (31)	5 (24)
Tcount	19 (15)	15 (15)	9 (10)	13 (12)	20 (22)	15 (17)	33 (36)	1 (24)	1 (6)	1 (14)	2 (14)	4 (16)	6 (32)	4 (24)
Thybrid	13 (12)	47 (50)	24 (22)	34 (33)	64 (66)	55 (56)	68 (66)	15 (7)	66 (55)	67 (46)	68 (51)	74 (66)	82 (56)	85 (65)

Note: θ, the true overall log odds ratio; τ, the true between-study standard deviation; p_i0, the true event rate in the control group. The results inside parentheses (except the hybrid test) were based on the tests’ theoretical p-values, and those outside parentheses were based on the resampling method.

The publication bias tests’ powers for log odds ratios also varied greatly across different simulation settings. The trim-and-fill method T_trim-fill continued to uniformly perform well in scenario i because this suppression scenario favored the method’s assumption. When N = 20, θ = 0, m = 8, p_i0 ~ U(0.3,0.7), and τ = 0, the tests T_rank, T_inv-sqrt-n, T_trim-fill, T_inv-n, and T_AS-rank had similar powers and outperformed other tests under scenario ii. Under scenario iii, T_n was substantially more powerful than all other tests. Such trends continued when N increased to 50 as in Table 4. Moreover, when N = 50, θ = 0, m = 10, and τ = 0.3, the skewness-based tests T_skew and T_skew-het were noticeably more powerful than other tests with well-controlled type I error rates under scenario ii for both rare and common events.

Although the type I error rates and powers of different tests varied across the simulated meta-analyses, the proposed hybrid test maintained high powers; its power was likely close to the highest power among all tests. The type I error rates of the hybrid test was controlled well in most situations; however, they could be inflated due to the serious inflation of type I error rates of other tests. For example, when N = 50, θ = 1, p₀ ~ U(0.05,0.1), and τ = 0, the type I error rates of T_rank and T_reg were inflated to around 40%; they impacted the hybrid test, which also had an inflated type I error rate of 25%.

5. Case studies

This section applies all publication bias tests to three meta-analyses recently published on prestigious medical journals. The first meta-analysis was performed by Plourde et al.⁴¹ to compare the fluoroscopy time in percutaneous coronary intervention between radial and femoral accesses. It contained 19 studies, and the effect size was the mean difference. The second meta-analysis was reported by Paige et al.,⁴² and it investigated 6 studies on the effectiveness of spinal manipulative therapies (other than sham) using the standardized mean differences. The third meta-analysis was performed by Whiting et al.,⁴³ which contained 29 studies on odds ratios of adverse events with cannabinoid vs. placebo.

Figure 1 presents the funnel plots of the three meta-analyses. In the first meta-analysis in Figure 1(a), the large studies with small standard errors seemed fairly symmetric, while the small studies with large standard errors tended to be in the negative direction and favored radial access. In Figure 1(b), the second meta-analysis contained one study that had much smaller standard errors than other five studies. This study had the largest total sample size, and its standardized mean difference was fairly close to zero, while all other studies reported more negative standardized mean differences (favoring spinal manipulative therapies). Consequently, some studies with positive standardized mean differences were likely suppressed from publication. In the third meta-analysis in Figure 1(c), the studies were generally symmetrically distributed, although many smaller studies tended to have larger odds ratios, indicating more adverse events with cannabinoid.

Figure 1.

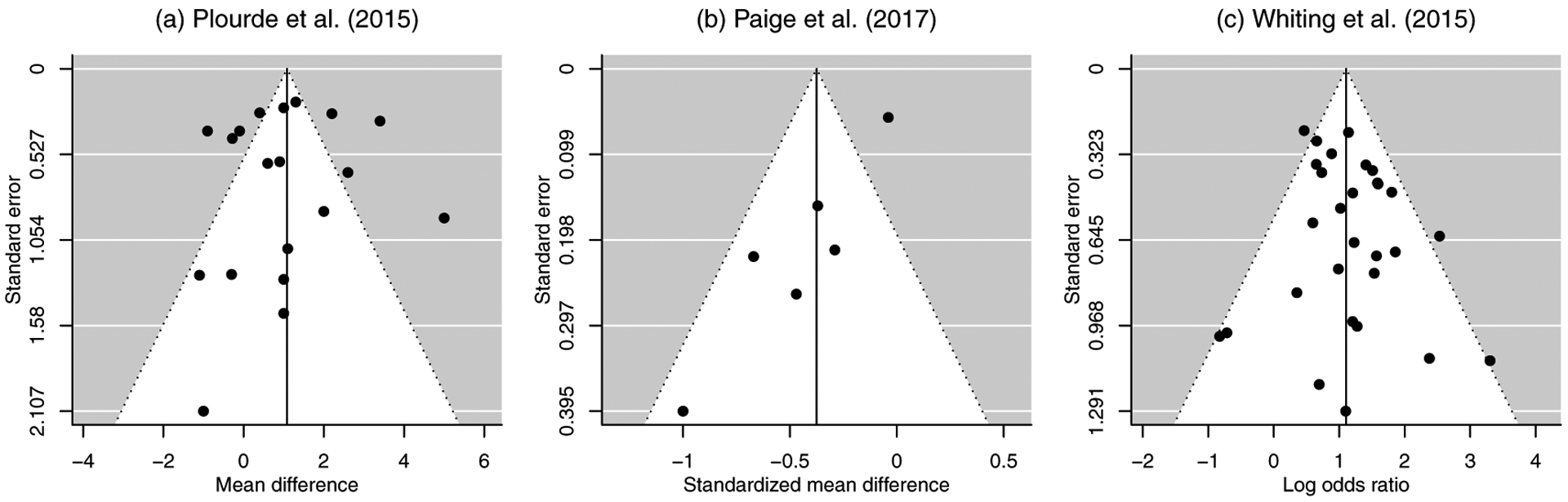
Funnel plots of the three real-world meta-analyses. In each funnel plot, the vertical solid line represents the fixed-effect estimate, and the diagonal dashed lines represent the pseudo 95% confidence limits.

Because the first two meta-analyses had continuous outcomes, only the tests for generic outcomes in Section 2.1 were applied to assess publication bias. For the third meta-analysis, the effect size was the (log) odds ratio, so the tests in both Sections 2.1 and 2.2 were applied. The tests’ p-values were calculated based on the resampling method, because it may control type I error rates better than using the test statistics’ theoretical distributions as shown in Section 4. The number of resampling iterations was set to 10,000 for each meta-analysis. As in the foregoing simulation studies, the significance level for publication bias was set to 0.1.

Table 5 presents the p-values produced by various publication bias tests for each meta-analysis. The trim-and-fill method had p-values of 1 and did not detect any publication bias in all three meta-analyses, possibly because its assumption was violated in the three real datasets. In the first meta-analysis by Plourde et al.,⁴¹ T_skew-het produced the smallest p-value of 0.070, indicating significant publication bias. Also, T_inv-sqrt-n produced a fairly small p-value of 0.116, and T_skew had a p-value of 0.364. All other tests’ p-values were larger than 0.6. Benefiting from T_skew-het and T_inv-sqrt-n, the hybrid test had a relatively small p-value of 0.317, indicating more evidence of publication bias than the commonly used T_rank and T_reg. In the second meta-analysis by Paige et al.,⁴² T_skew and T_skew-het had fairly large p-values over 0.7, while T_reg, T_reg-het, and T_inv-sqrt-n had p-values smaller than 0.1. The p-value of T_rank was also close to the significance level 0.1. Again, benefiting from the three tests that could detect significant publication bias, the hybrid test had a p-value of 0.051 and also implied publication bias. In the third meta-analysis by Whiting et al.,⁴³ only T_n detected significant publication bias with p-value 0.088, and T_reg had a p-value close to the significance level 0.1. Many other tests’ p-values were larger than 0.6. The hybrid test incorporated evidence from all tests and had a relatively small p-value of 0.342.

Table 5.

Various publication bias tests’ p-values for the three real-world meta-analyses.

Test	p-value
	Plourde et al.41	Paige et al.42	Whiting et al.43
Trank	0.936	0.154	0.776
Treg	0.745	0.073	0.160
Treg-het	0.642	0.012	0.357
Tskew	0.364	0.761	0.642
Tskew-het	0.070	0.815	0.682
Tinv-sqrt-n	0.116	0.025	0.483
Ttrim-fill	1.000	1.000	1.000
Tn	NA	NA	0.088
Tinv-n	NA	NA	0.629
TAS-rank	NA	NA	0.658
TAS-reg	NA	NA	0.342
TAS-reg-het	NA	NA	0.586
Tsmoothed	NA	NA	0.413
Tsmoothed-het	NA	NA	0.968
Tscore	NA	NA	0.701
Tcount	NA	NA	0.839
Thybrid	0.317	0.051	0.342

NA: not applicable.

6. Discussion

This article has proposed the hybrid test for publication bias. It is motivated by the fact that various publication bias tests are available, which are powerful only against certain alternative hypotheses about publication bias, while identifying the exact mechanisms that cause publication bias and selecting the optimal test are infeasible in practice. The hybrid test is able to combine the benefits of various tests, so that it likely has satisfactory power across many cases. The simulation studies and three case studies have been used to show the superior performance of the hybrid test.

Although the hybrid test is advantageous for its high power, it may have several limitations. The first limitation is intrinsic for many commonly-used publication bias tests. All tests reviewed in this article and incorporated in the hybrid test were originally motivated by examining the asymmetry of the funnel plot, which is based either on standard error (as in Begg’s rank test T_rank and Egger’s regression test T_reg) or on sample size (as in Tang’s test T_inv-sqrt-n, Macaskill’s test T_n, and Peters’ test T_inv-n). Besides publication bias, the funnel plot’s asymmetry may be also caused by heterogeneity between studies, or by poor quality of small studies, or simply by chance, especially when a meta-analysis contains few studies.^10,44 To ascertain the cause of the funnel plot’s asymmetry, more evidence is required in addition to using these statistical tests. For example, meta-analysts may classify the collected studies into several subgroups based on certain summary characteristics (e.g., age), and assess the funnel plot’s asymmetry within each subgroup. If the overall funnel plot with all studies is asymmetric but the subgroup-specific funnel plots are roughly symmetric, then the asymmetry may be attributed to heterogeneity between subgroups, instead of publication bias. Also, meta-analysts may use the contour-enhanced funnel plot, which incorporates contours depicting the studies’ significance, to aid the interpretation of the asymmetry.^45,46 If the potentially missing studies tend to lie within the area of significant studies in the contour-enhanced funnel plot, then the asymmetry is likely due to factors other than publication bias.

Second, although the hybrid test can incorporate the benefits of various publication bias tests to yield high powers in most cases, it may be contaminated by some included tests that have poor performance as well. For example, in our simulation studies, several tests had highly inflated type I error rates in some cases; influenced by these tests, the hybrid test’s type I error rate was also noticeably inflated. Similarly, when incorporating some tests that had very low powers, the hybrid test was not superiorly powerful; if excluding those tests, the hybrid test’s power could be greatly improved.

In practice, we recommend meta-analysts to select a proper set of tests $\mathcal{T}$ to form the hybrid test by excluding some tests that are evidently inferior in certain cases. The selection of the set $\mathcal{T}$ could be based on the findings and recommendations in the existing meta-analysis literature. For example, Egger’s test T_reg has been found to have seriously inflated type I error rates for odds ratios when heterogeneity is substantial or the true overall odds ratio is away from the null value 1.¹³ As shown in our simulation studies in Section 4, the rank test T_rank may also suffer from the inflation of type I error rates. This issue is essentially caused by the intrinsic association between the observed effect sizes and their sample standard errors; the strength of this association depends on many factors, including the effect size type, the true value of the overall effect size, the study-specific sample size, etc. When the intrinsic association is likely strong, the above tests may be excluded from the set $\mathcal{T}$ for the hybrid test to obtain a relatively conservative conclusion about the existence of publication bias. Similarly, when the assumption of the trim-and-fill method is clearly violated in certain meta-analyses (e.g., the suppression of studies does not depend on their effect size magnitudes), the hybrid test may not incorporate the trim-and-fill method. When the binary outcomes are sparse, T_count may be included in $\mathcal{T}$ as this test is specifically designed for such cases.²⁹

Third, the proposed method is used to test for the presence of publication bias, while it cannot adjust for the bias. Among the methods reviewed in Section 2, only the trim-and-fill method can produce an adjusted overall effect size estimate, although this adjustment may not be accurate if the method’s assumption is violated; the adjusted result is often recommended as a form of sensitivity analysis.^15,47 Besides the trim-and-fill method, several other methods are available to adjust for publication bias, and they are mostly based on certain selection models.^3,48–51 Similar to the dilemma of choosing appropriate tests for publication bias, the performance of the various methods for adjusting for publication bias also depends on their particular model assumptions. In practice, it is difficult to justify these model assumptions and select the optimal method. It might be worthwhile to explore approaches to synthesizing the methods for adjusting for publication bias.

In summary, the proposed hybrid test provides a powerful and convenient way to detect potential publication bias. It does not require meta-analysts to choose a single publication bias test from a large pool of candidates and draw a conclusion based entirely on this single test; it permits them to combine various candidates into synthesized evidence for evaluating publication bias. However, like all statistical methods for dealing with publication bias, the results produced by the hybrid test may not ascertain the absence or presence of publication bias; evidence from other (e.g., clinical) perspectives should be considered to aid the assessment of potential bias.