Summary
In this paper, the problem of social distancing in the spread of infectious diseases in the human network is extended by optimal control and differential game approaches. Hear, SEAIR model on simulation network is used. Total costs for both approaches are formulated as objective functions. SEAIR dynamics for group k that contacts with k individuals including susceptible, exposed, asymptomatically infected, symptomatically infected and improved or safe individuals is modeled. A novel random model including the concept of social distancing and relative risk of infection using Markov process is proposed. For each group, an aggregate investment is derived and computed using adjoint equations and maximum principle. Results show that for each group, investments in the differential game are less than investments in an optimal control approach. Although individuals' participation in investment for social distancing causes to reduce the epidemic cost, the epidemic cost according to the second approach is too much less than the first approach.
Keywords: differential game, infectious diseases, investment, network, optimal control, social distancing
1. INTRODUCTION
Social distancing is changes in behavior that is applied to prevent the transmission of the disease. The dynamics of infectious disease such as influenza, smallpox, aids, etc. depending on the contact network. Social distancing practices can stop or reduce the severity of the epidemic. This distancing is applied to allow individuals to change their behavior in order to reduce the risk of disease. The structure of networks in the prevalence of epidemics such as HIV, 1 , 2 , 3 SARS, 4 , 5 influenza, 6 , 7 , 8 , 9 etc. is important. The basic reproduction number is dependent on the distribution of the contacts that are known as the distribution of degrees. 1 , 10 , 11 Primary work focuses on the effects of small cycles. 12 , 13 , 14 , 15 , 16 Most epidemics such as influenza, HIV, Sars, have expanded. 17 , 18 , 19 It is used network theory to study the dynamics of transmission of infectious diseases in which the nodes represent people, etc. 19 There are two topological and structural properties of the grids which cause the dynamics to spread: Transmissibility 19 , 20 and centrality. 13 , 21 Recovery of infections increases the number of infectious diseases and the mortality rate of the host. 22 , 23 In order to study the best usage of social distancing, we apply control optimal and differential game approaches at a population scale. In game theory, the differential game is a situation of conflict or cooperative where players choose strategies over time.
There are more than one player in the differential game and the payoff to each player depends on the selection paths by all players. Of course, the control problem can be considered as a special case of differential games in which there is only one player. In the differential games, players make their moves over time. In this paper, we find the best investment in social distancing with optimal control and differential game approaches.
Vaccination is considered as one of the most measures to control influenza outbreak. In 2019, Arefin et al 24 investigated two types of vaccines; The traditional trivalent (TIV) flu vaccine and the quadrivalent (QIV) vaccine. They showed that people can choose QIV or TIV vaccine or they select none. Kabir et al 25 presented a model in which a dual social dilemma situation was exhibited. In this model, the treatment behavior changes on a time scale, and the vaccination uptake evolves on a time scale. A model that joins evolutionary game theory with epidemiological dynamics is presented by Tanaka et al. 26 In this model, the policies that encourage vaccination are appraised and in order to suppress the overall social cost of a vaccination program, individual subsidies for vaccinations can be directed to hub agents with priority.
The effect coming from the failure of getting perfect immunity to the individuals who perpetrated vaccination earlier is studied by Alam et al. 27 Their new model slows down the spread of the infectious and also facilitates quicker recovery time. In order to evaluate the performance of vaccination‐subsidizing policies in the face of an epidemic, Kuga et al 28 combined evolutionary game theory and mathematical epidemiology. They investigated how the topology of social networks affects the results. Analyzing the effect of different heterogeneous networks in a population was presented by a two‐layer susceptible‐infected‐recovered/unaware‐aware (SIR‐UA) epidemic model. In this study, the random network topologies are applied to investigate the impact of awareness on the spread of epidemics. 29 The check of this point that a disease transmission network does not necessarily correspond with an information diffusion network was done by Fukuda et al. 30 Evolutionary game theory can be in the context of epidemiology. Two approaches, quasi‐analytical and multi‐agent simulation, can illuminate how an infectious disease diffuses across a social network, which is affected by the public attitude toward vaccination. 31
Vaccination game and social distancing strategies both aim to control an epidemic and minimize its cost. However since in this paper, we assumed that, one is in the lack of vaccine, the concept called “social distancing” is considered and discussed. Therefore in this paper, social distancing is a measure to control an epidemic as long as the vaccine is produced and is available.
In Section 2, the network dynamic of SEAIR model together with the aggregate investment parameter in social distancing are proposed. In Section 2.3, the related novel SEAIR objective functional for the best investment in social distancing is given. In Section 3, the problem for social distancing and its relative risk is solved by using optimal control and differential game approaches. In Section 4, stability is investigated and in Section 5, results and conclusions are given.
2. MODEL
It is shown that in contrast to classical compartment models like SIR, a model that can consider the epidemics of infectious diseases on networks is a model that classifying the population as susceptible (S), exposed (E), asymptomatically infected (A), symptomatically infected (I) and removed (R). Here, we use SEAIR model on networks to obtain the best aggregate investment, which is the average investment of the corresponding population. In order to determine the best aggregate investment strategy with social distancing, we use two different approaches; optimal control and differential game.
2.1. SEAIR model
Consider a Susceptible Exposed Asymptomatically infected Symptomatically infected Recovered (SEAIR) epidemic model with susceptible ( X 1 ), exposed ( X 2 ), asymptomatically infected ( X 3 ), symptomatically infected ( X 4 ), and removed ( X 5 ) states. When an individual is infected with an influenza virus, a short time span between the occurrence of a disease agent and the onset of symptoms, which is called a munition or latency period. This class of individuals who pass through the infected to stricken are called X 2 class. In X 2 class, a significant number of individuals do not reveal the symptoms of illness, but they are capable of transmitting illness. The differential equations describing the SEAIR model are as follows: 19
| (1) |
where the parameters are shown in the Table 1 and are estimated in Table 2.
TABLE 1.
Parameters of the SEAIR model
| Parameters | Description | |
|---|---|---|
|
|
Transmission coefficient between community S k and I j | |
|
|
Transmission coefficient between community S k and A j | |
|
|
Rate of becoming infectious after latency | |
|
|
Rate of becoming asymptomatically infected | |
|
|
Rate of becoming symptomatically infected | |
|
|
Recovery rate of asymptomatically infected | |
|
|
Recovery rate of symptomatically infected |
TABLE 2.
Parameters estimated from the observed data in China 36
| Parameters | Description | |
|---|---|---|
|
|
0.01 | |
|
|
0.188 | |
|
|
0.4 | |
|
|
0.85 | |
|
|
0.15 | |
|
|
0.141 | |
|
|
0.141 |
It is assumed that a safe individual will never be susceptible or infected again, and in this study the births and deaths of natural individuals and migrations will be ignored. In this study, we examine individuals in the network. Each person is marked with one vertex and we show the contact between two individuals with an edge that connects two vertices to each other.
It is assumed that the population is divided into n distinct groups of sizes (k = 1,2,…,n)N k such that each individual is in group k, he (she) will have k contacts per day. Let, the size of the population is N ( N = N 1 + N 2 + … + N n ) thus the probability that an individual has k contacts will be , which is called the degree distributions of the network. It is shown in Empirical studies that many real networks have scale‐free degree distributions with and epidemic threshold is not shown in epidemic model. 18 If and represent the number of susceptible, exposed, asymptomatically infected, symptomatically infected and recovered individuals belonging to group k (where ), then the following system of differential equations is presented as follows,: 20
| (2) |
where and and basic reproduction number . Also,
is constant. Also, for system (2), we consider the following boundary conditions:
2.2. SEAIR model and the aggregate investment in social distancing
We are going to use the aggregate investment (control) in this network model. is defined as the aggregate investment of susceptible individuals in social distancing belonging to the group k. The overbar notation is used to indicate that the aggregate investment is an average investment aggregated over all people in the population. c I is the daily cost of the infection. We first apply the following change to the variable:
As a result, the relative risk for the group k according to is defined as:
| (3) |
m k , is maximum efficiency of social distancing for group k. The maximum efficiency of social distancing will be the maximum number of susceptible people who separate themselves from the population before the cost of this distancing increases than the cost of the disease.
The relative risk graph for the different values of m k is given in Figure 1. In order to work with dimensionless equations, we should take: (let that, ):
hereafter, it will drop the hat‐notation so the dimensionless parameters will be worked. The dynamics of this network model for an epidemic with respect to is as follows:
| (4) |
FIGURE 1.
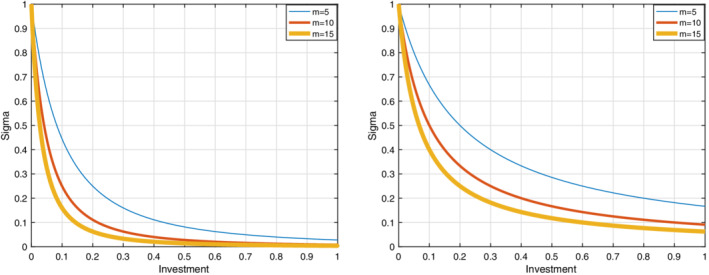
The graphs are related to the relative risk of infection. By increasing the maximum efficiency, the relative risk decreases. The right graph shows the relative risk of infection for each group according to just its investment strategy but the left graph shows the relative risk of infection for each group according to both its investment strategy and others groups investment. The results show that the relative risk of infection in the right graph is less than the relative risk of infection in the left graph [Colour figure can be viewed at wileyonlinelibrary.com]
2.3. Cost functional
Consider the problem of minimizing the performance index J. The whole cost of the epidemic for the community, J, is the sum of the direct costs together with the indirect costs of any economic repercussions from the epidemic. It is considered just considered direct costs of the epidemic (the daily costs from infection, daily investments for social distancing, and the costs for vaccination). Mathematically, 32
| (5) |
where c v is the cost of vaccination per person, and h is the discount rate.
The total cost of the epidemic for group k, J k ,
| (6) |
3. BEST INVESTMENT IN SOCIAL DISTANCING
In order to determine the best strategy of investment in social distancing, we consider two approaches, optimal control approach and differential game approach. The reason for using an optimal control approach in this work is analyzing the solution which is obtained from the differential game approach.
3.1. Optimal control approach
According to optimal control approach, we determine the best investment of each group with regardless of the investment of other groups. The above system is written in the form of the matrix and we have:
As a result, the transmission rate matrix, Q, is as follows:
| (7) |
Considering the The Markov process, as follows:
where P(t) is probabilities that people are in which states and c is the daily investment. The expected present values (V) are calculated (The expected present value is average value one expects after accounting for the probabilities of all future events, and discounting future costs relative to immediate costs) because of the exact time spent and the precise payoff are not predicted. As follows:
| (8) |
where, h is discount rate and . As result, we have for the group k; . In this problem . Let h = 0. 33 As a result,
| (9) |
By solving system (9), we have:
then
| (10) |
Now, we have reduced following system:
| (11) |
will be the expected total cost of the epidemic to group k.
A Nash equilibrium strategy for a population game is a one that is the best response, even when other people are utilizing the same strategy. If Nash equilibrium strategy shows a Nash equilibrium of any subgame of the primary game, it will be a subgame perfect equilibrium. This means that if we consider any smaller game that consisted of the main game, players' behavior would represent a Nash equilibrium of that smaller game. We won solve the problem of ruling out finite‐time blowup of the Hamilton‐Jacobi equation and appointing existence and uniqueness of subgame perfect equilibria. But the analyses support the guess that the strategies calculated are the unique subgame perfect equilibria.The equilibria can be calculated using the general methods of Isaacs. 34 The kernel idea is to use a greedy algorithm, in any step in the game, find the best investment strategy in social distancing that maximizes V S .
We need only study the reduced system
| (12) |
As a result, the best investment in social distancing is as follows:
| (13) |
| (14) |
3.2. Differential game approach
We assume that we have n groups and we want to consider a model which makes a game between groups. We find what the best aggregate investment of the group k with respect to the aggregate investments of other groups is. More precisely, we find the best aggregate investment of each group with respect to the aggregate investments of other groups. The dynamics of this network model for an epidemic with respect to relative risk is as follows:
| (15) |
where
| (16) |
The transmission rate matrix Q, is as follows:
Now, given the adjoint equations evolving according to the Markov process, we have:
where . As a result,
| (17) |
Let h = 0. By solving system (17) we have:
| (18) |
then
| (19) |
Now, we have reduced following system:
| (20) |
Most of the equilibria we calculate are obtained numerically. First, I(t) = I 0 e −t , A(t) = A 0 e −t . Now according to the maximum principle, we have:
| (21) |
As a result, the best investment in social distancing is as follows:
| (22) |
| (23) |
4. STABILITY ANALYSIS IN SEAIR MODEL
We consider SEAIR epidemic model and apply the stability analysis theory. In order to know behavior of the system (9) that is in optimal control, we set in the form of
To investigate the stability, we consider the Jacobian matrix as follows (let, ):
The characteristic equation is,
where,
For the asymptotic stability we use Samuelson conditions 35 and since for different groups the conditions are satisfied, by Samuelson conditions the system (9) in optimal control approach is asymptotically stable.
Now, we investigate the stability in differential game approach and consider the system (17) and have
The Jacobian matrix is as follows: (let, )
thus, the characteristic equation is,
where,
since for different groups the conditions are satisfied, by Samuelson conditions 35 the system (17) in differential game is asymptotically stable.
5. RESULTS AND DISCUSSION
In the lack of vaccine (for the real‐world example see coronaviruses epidemic and the current pandemic of covid‐19) it makes sense that social distancing considers in mathematical simulations. More specifically, the SEAIR model is used on simulation network and the optimal control approach is used to determine the best investment in each group regardless of other groups. The differential game approach shows a Nash equilibrium of any subgame of the primary game. The average investment in social distancing will decrease when the investments that are calculated on average will have fewer values, it will occur when much more people want to make the investment. As a result, if the number of susceptible individuals that they distance in the network increases, their average investment reduce.
According to Figure 1, the results have shown that by increasing the aggregate investment in social distancing, the relative risk decreases. These investments are made by individuals who are susceptible, so there should be an incentive for these individuals to make these investments. Also, this figure shows by increasing the number of susceptible individuals that they are distancing (m), the relative risk decreases. So these individuals want to know what the best investment is that they not to get infected. The two approaches are considered here. In the first approach, which is the optimal control approach, the aggregate investment of each group is obtained regardless of the investment of other groups. In the second approach, which is the game theory approach, the investment of each group in social distancing is obtained with respect to the investment of other groups. Figures 2 and 3 show that social distancing reduces the peak and prolongs the epidemic by comparing two graphs. According to analyses done in the above figures, it can be seen by increasing the number of contacts, the aggregate investment in social distancing increases. These analyses also show that the maximum efficiency of social distancing (m) plays an important role in the best investment. In Figures 4 and 5 observe that as m increases, the investment in social distancing decreases. If the number of infected individuals increases then the best investment, in both approaches is increased too (see Figures 6 and 7). Figures 8 and 9shows that with going on the duration of the epidemic, the optimal investment is reduced. A remarkable point which is seen in above figures is that with regard to the two approaches, the aggregate optimal investments for each group in the second approach are less than the aggregate optimal investments for each group in the first approach. This shows if we want to reduce the investment for each group, we should use the differential game theory approach and divide the individuals into separate groups according to their contacts together and then for each group obtain the best aggregate investment with respect to the aggregate investments for other groups.
FIGURE 2.
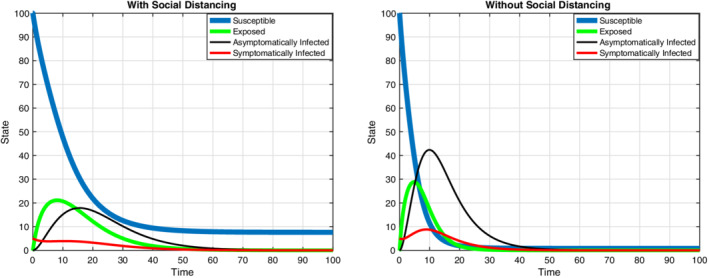
The graphs are related to the states of the system with and without social distancing with optimal control approach, S 0 = 100, m = 60. It is understood that social distancing reduces the peak and prolongs the epidemic by comparing two graphs [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 3.
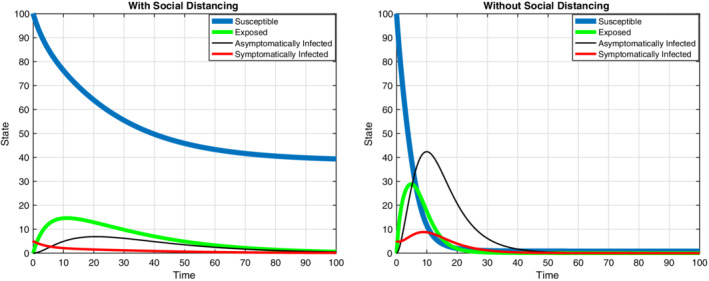
The graphs are related to the states of the system with and without social distancing with differential game approach, S 0 = 100, m = 60. It is understood that social distancing reduces the peak and prolongs the epidemic by comparing two graphs [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 4.
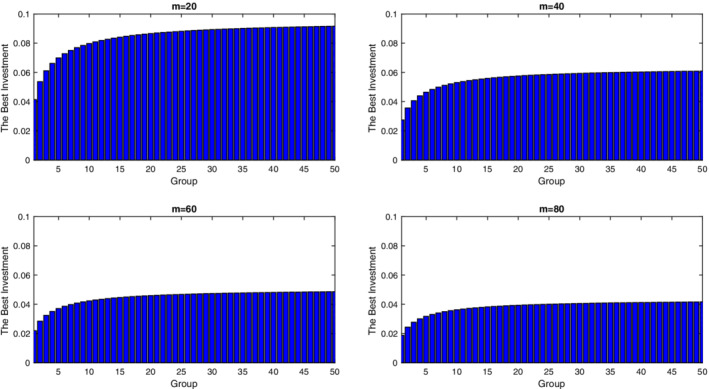
The graphs are related to the best investment for different groups with optimal control approach. According to the graphs, by increasing the maximum efficiency m, the best investment is decreased [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 5.
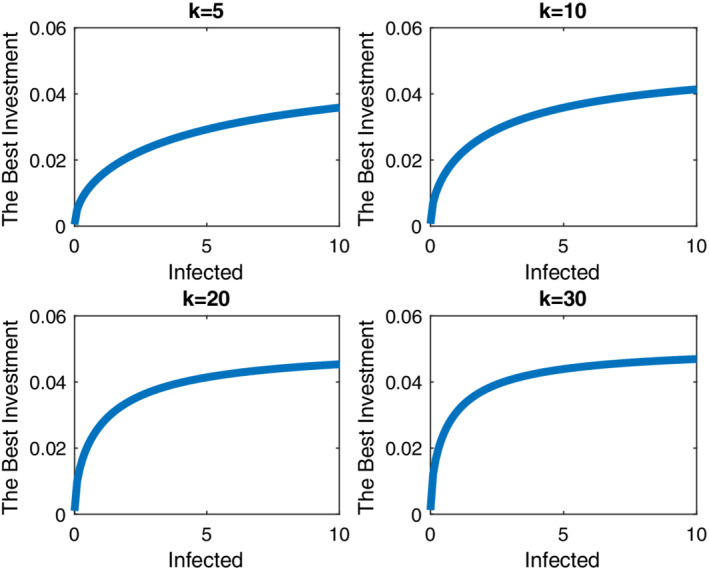
The graphs are related to the best investment with differential game approach for different groups. m = m 1 = m 2 = … = m 1000 = 60. If the number of infected individuals increases then the best investment is increased too [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 6.
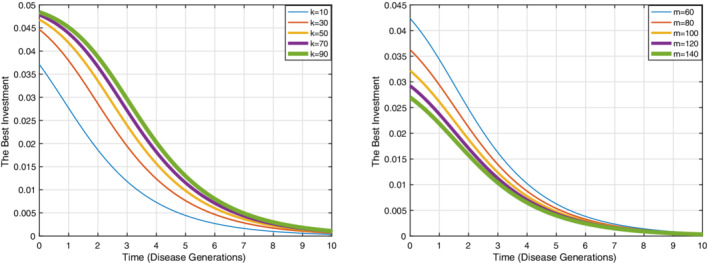
The graphs are related to the best investment in term of time with optimal control approach. The results show that by spending time, the best investment is decreased. The left graph is depicted for different the maximum efficiencies of social distancing. k = 20. The best investment in social distancing is decreased by increasing the maximum efficiencies of social distancing (m). The right graph is depicted for different ( m = 60). By increasing the number of contacts, the best investment in social distancing is increased [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 7.
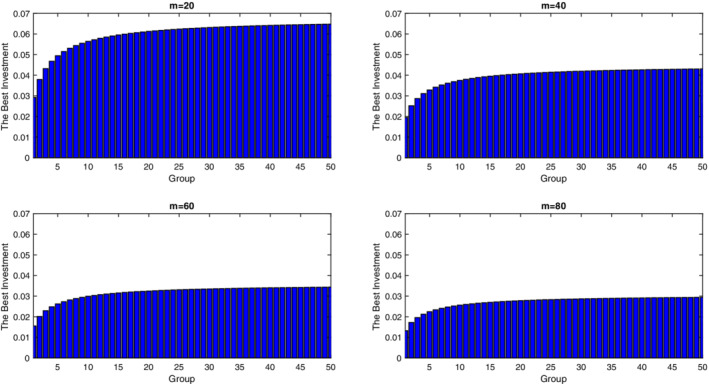
The graphs are related to the best investment with optimal control approach for different groups. m = m 1 = m 2 = … = m 1000 = 60. If the number of infected individuals increases then the best investment is increased too [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 8.
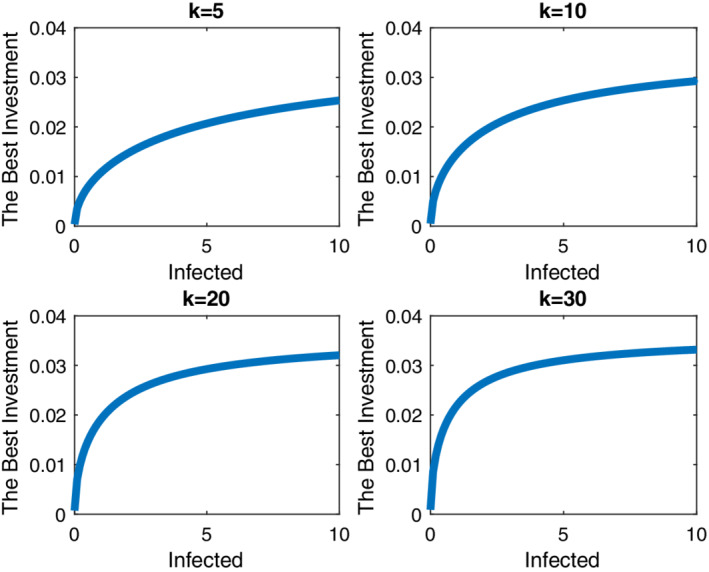
The graphs are related to the best investment with differential game approach for different groups. By increasing the number of infected individuals, the best investment is increased too [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 9.
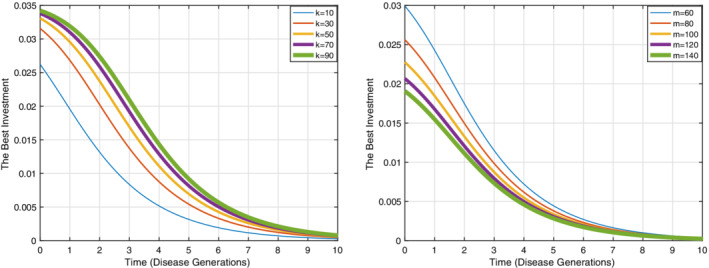
The graphs are related to the best investment in term of time with differential game approach. The results show that by spending time, the best investment is decreased. The left graph is depicted for different the maximum efficiencies of social distancing. k = 20. By increasing m, the best investment in social distancing is decreased. The right graph is depicted for different groups, m = 60. By increasing the number of contacts, the best investment in social distancing is increased [Colour figure can be viewed at wileyonlinelibrary.com]
Epidemic cost and saving in cost per person with both optimal control approach and differential game approach are shown in Figures 10 and 11. The results show that by increasing the basic reproduction number, epidemic cost per person increases. The results show that social distancing is most beneficial on the network with low contacts. If vaccination and other measures are not available then optimal social distancing never recovers more than 14% of the cost of infection.
FIGURE 10.
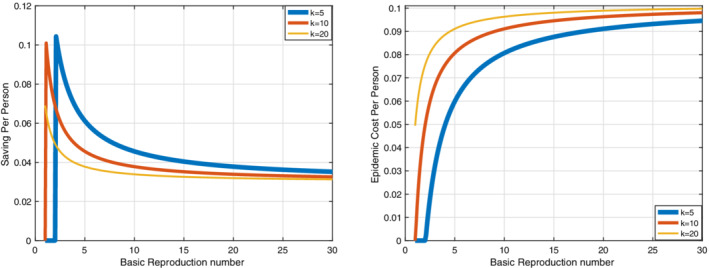
The graphs are related to epidemic cost per person and saving in cost per person with an optimal control approach. By increasing the number of contacts, epidemic cost per person is increased. The results show that for the number of low contacts, there is a peak point in the graph ( k = 1,2,…,10). But the graph is strictly decreasing for the number of more contacts ( k = 11,12,… ). According to (b), by increasing the number of contacts, saving in cost per person is decreased. These graphs are depicted for m = 100 [Colour figure can be viewed at wileyonlinelibrary.com]
FIGURE 11.
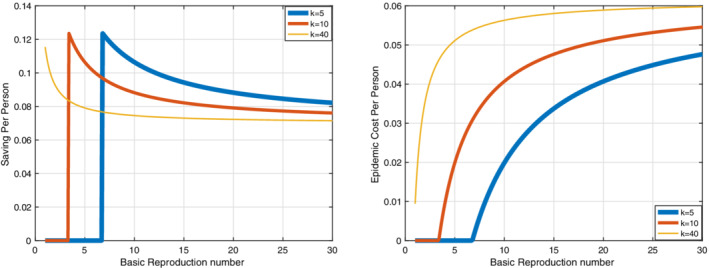
The graphs are related to epidemic cost per person and saving in cost per person with a differential game approach. By increasing the number of contacts, epidemic cost per person is increased. The results show that for the number of low contacts, there is a peak point in the graph ( k = 1, 2,…,35). But the graph is strictly decreasing for the number of more contacts ( k = 35, 36,…). According to (b), by increasing the number of contacts, saving in cost per person is decreased. These graphs are depicted for m = 100 [Colour figure can be viewed at wileyonlinelibrary.com]
In this study, it has been shown that if we deal with a human network and want to control or stop the epidemic, we should impulse individuals to distance. That is, we should motivate individuals in the network to participate in this investment. Two key parameters are considered in this study: the maximum efficiency of social distancing and basic reproduction number. The maximum efficiency of social distancing is the maximum number of susceptible individuals who separate themselves from the population before the cost of social distancing increases from the cost of the disease. By increasing this maximum efficiency, the epidemic cost is reduced. That means that if more individuals are more likely to participate in the distancing, the cost of the epidemic is reduced. Another key parameter is the basic reproduction number. Increasing the basic reproduction number increases the cost of an epidemic. The suggestion in this study is to motivate individuals in the network to participate in distancing. It is shown that the basic reproduction number varies in different groups. This means that social distancing are more beneficial when the basic reproduction number tends to a specific number that must be calculated for each group. In an optimal control approach, for example, for a group with five contacts, social distancing is more beneficial for a basic reproduction number about three. According to this approach, for a group with the number of fourteen contacts, this number is about two. Moreover, in differential game approach, for example, for a group with a contact number of five, social distancing is more useful for basic reproduction number about five, while for a group with the number of fourteen contacts, this number is about six. The results show that for each individual, the best investment strategy in social distancing and epidemic cost in the differential game approach are less than the optimal control approach.
Supporting information
Data S1. Novelty
Dashtbali M, Malek A, Mirzaie M. Optimal control and differential game solutions for social distancing in response to epidemics of infectious diseases on networks. Optim Control Appl Meth. 2020;41:2149–2165. 10.1002/oca.2650
REFERENCES
- 1. Anderson RM, May R. Infectious Diseases of Humans: Dynamics and Control. Oxford, UK: Oxford University; 1991. [Google Scholar]
- 2. Anderson RM. Transmission dynamics of sexually transmitted infections. In: Holmes K, ed. Sexually Transmitted Diseases: McGrawHill; 1999:25‐37. [Google Scholar]
- 3. Morris M. Epidemiology and social networks: Modeling structured diffusion. Sociol Methods Res. 1993;22(1):99‐126. [Google Scholar]
- 4. Lloyd‐Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438:355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Watts S. SARS: a case study in emerging infections. Soc Hist Med. 2005;18:498‐500. [Google Scholar]
- 6. Ferguson NM, Cummings DA, Cauchemez S, Fraser C, Riley S, Meeyai A. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209. [DOI] [PubMed] [Google Scholar]
- 7. Ferguson NM, Cummings DA, Fraser C, Cajka JC, Cooley PC, Burke DS. Strategies for mitigating an influenza pandemic. Nature. 2006;442(7101):448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Halloran ME, Ferguson NM, Eubank S, Longini IM, Cummings DA, Lewis B. Modeling targeted layered containment of an influenza pandemic in the United States. Proc Natl Acad Sci. 2008;105:4639‐4644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Longini IM, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, Cummings DA. Containing pandemic influenza at the source. Science. 2005;309:1083‐1087. [DOI] [PubMed] [Google Scholar]
- 10. Pastor‐Satorras R, Vespignani A. Epidemic spreading in scale‐free networks. Phys Rev Lett. 2001;86:3200. [DOI] [PubMed] [Google Scholar]
- 11. Lloyd AL, May RM. How viruses spread among computers and people. Science. 2001;292:1316‐1317. [DOI] [PubMed] [Google Scholar]
- 12. Smieszek T, Fiebig L, Scholz RW. Models of epidemics: when contact repetition and clustering should be included. Theor Biol Med Model. 2009;6:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Miller C. Spread of infectious disease through clustered populations. J R Soc Interface. 2009;6(41):1121‐1134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. House T, Davies G, Danon L, Keeling MJ. A motif‐based approach to network epidemics. Bull Math Biol. 2009;71:1693‐1706. [DOI] [PubMed] [Google Scholar]
- 15. Eames KT. Modelling disease spread through random and regular contacts in clustered populations. Theor Popul Biol. 2008;73:104‐111. [DOI] [PubMed] [Google Scholar]
- 16. Britton T, Deijfen M, Lageras AN, Lindholm M. Epidemics on random graphs with tunable clustering. J Appl Prob. 2008;45:743‐756. [Google Scholar]
- 17. Tatem AJ, Rogers DJ, Hay S. Global transport networks and infectious disease spread. Adv Parasitol. 2006;62:293‐343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Donner RV, Zou Y, Donges JF, Marwan N, Kurths J. Recurrence networks a novel paradigm for nonlinear time series analysis. New J Phys. 2010;12(3):033025. [Google Scholar]
- 19. Benedictow OJ. The Black Death: The Complete History. Cromwell Press: Boydell and Brewer; 2004:1346‐1353. [Google Scholar]
- 20. Keeling MJ, Eames KT. Networks and epidemic models. J R Soc Interface. 2005;2(14):295‐307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Cohen T, Colijn C, Finklea B, Murray M. Exogenous re‐infection and the dynamics of tuberculosis epidemics: local effects in a network model of transmission. J R Soc Interface. 2007;4(14):523‐531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Schmid Hempel P. Evolutionary Parasitology: The Integrated Study of Infections, Immunology, Ecology, and Genetics. Oxford, UK: Oxford University Press; 2011. [Google Scholar]
- 23. Alizon S, de Roode JC, Michalakis Y. Multiple infections and the evolution of virulence. Ecol Lett. 2013;16(4):556‐567. [DOI] [PubMed] [Google Scholar]
- 24. Arefin MR, Masaki T, Kabir KA, Tanimoto J. Interplay between cost and effectiveness in influenza vaccine uptake: a vaccination game approach. Proc R Soc A. 2019;475(2232):20190608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Kabir KA, Tanimoto J. Modelling and analysing the coexistence of dual dilemmas in the proactive vaccination game and retroactive treatment game in epidemic viral dynamics. Proc R Soc A. 2019;475(2232):20190484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Tanaka M, Tanimoto J. Is subsidizing vaccination with hub agent priority policy really meaningful to suppress disease spreading? J Theor Biol. 2020;486:110059. [DOI] [PubMed] [Google Scholar]
- 27. Alam M, Tanaka M, Tanimoto J. A game theoretic approach to discuss the positive secondary effect of vaccination scheme in an infinite and well‐mixed population. Chaos Solit Fract. 2019;125:201‐213. [Google Scholar]
- 28. Kuga K, Tanimoto J, Jusup M. To vaccinate or not to vaccinate: A comprehensive study of vaccination subsidizing policies with multi‐agent simulations and mean‐field modeling. J Theor Biol. 2019;469:107‐126. [DOI] [PubMed] [Google Scholar]
- 29. Kabir KA, Tanimoto J. Analysis of epidemic outbreaks in two‐layer networks with different structures for information spreading and disease diffusion. Commun Nonlinear Sci Numer Simul. 2019;72:565‐574. [Google Scholar]
- 30. Fukuda E, Tanimoto J, Akimoto M. Influence of breaking the symmetry between disease transmission and information propagation networks on stepwise decisions concerning vaccination. Chaos Solit Fract. 2015;80:47‐55. [Google Scholar]
- 31. Tanimoto J. Evolutionary Games with Sociophysics: Analysis of Traffic Flow and Epidemics. Switzerland: Springer; 2019:1. [Google Scholar]
- 32. Reluga TC. Game theory of social distancing in response to an epidemic. PLoS Comput Biol. 2010;6(5):e1000793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Reluga TC, Medlock J, Galvani AP. The discounted reproductive number for epidemiology. Math Biosci Eng. 2009;6:377‐393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Isaacs R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization. New York: John Wiley and Sons: Courier Corporation; 1999. [Google Scholar]
- 35. Brauer F, Castillo‐Chavez C, Castillo‐Chavez C. Mathematical Models in Population Biology and Epidemiology. Vol 2. New York, NY: Springer; 2012. [Google Scholar]
- 36. Jin Z, Zhang J, Song LP, Sun GQ, Kan J, Zhu H. Modelling and analysis of influenza A (H1N1) on networks. BMC Public Health. 2011;11(1):S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Novelty


