Analysis of the vibrational and sound spectrum of over 100,000 protein structures and application in sonification

Abstract

We report a high-throughput method that enables us to automatically compute the vibrational spectra of more than 100,000 proteins available in the Protein Data Bank to date, in a consistent manner. Using this new algorithm we report a comprehensive database of the normal mode frequencies of all known protein structures, which has not been available before. We then use the resulting frequency spectra of the proteins to generate audible sound by overlaying the molecular vibrations and translating them to the audible frequency range using the music theoretic concept of transpositional equivalence. The method, implemented as a Max audio device for use in a digital audio workstation (DAW), provides unparalleled insights into the rich vibrational signatures of protein structures, and offers a new way for creative expression by using it as a new type of musical instrument. This musical instrument is fully defined by the vibrational feature of almost all known protein structures, making it fundamentally different from all the traditional instruments that are limited by the material properties of a few types of conventional engineering materials, such as wood, metals or polymers.

Introduction

Most conventional music instruments are made of natural materials with complex microstructures such as wood, bamboo, horsehair and silk [1–3], whose characteristics are responsible for the unique sound features, or the timbre, of each instrument [4–6]. Indeed, musical instruments rely on the natural vibrations and resonances of built structures and the used engineering materials. This is the basis for the construction of instruments like the piano, guitar or violin. In most cases, the basis to sound generation is the vibration of an object like a string that is connected to a resonance structure to amplify and shape the nature of the sound. In attempts to reproduce the sound of natural instruments synthetically, other sound synthesis methods have been developed to enable to produce complex sounds using computers, either using samples, wavetables (or similar), or physical modeling. A direct method is to use sampling, by which the sound of instruments, typically played at different pitches and with different expressions, is recorded as an audio file and played back through a computer [7–11]. These various methods essentially aim to create a spectrum of overlapping waves either to mimic the sounds of natural instruments or to generate new sounds that do not naturally exist.

Proteins represent the most abundant molecular building blocks of virtually all living matter, and their structure, dynamics and interactions are critical for understanding their assembly [12–17]. An area of particular concern is the linking of structure to functional properties, and the utilization of proteins as building blocks for new designer materials [15, 18]. Here, we explore a distinct avenue of exploration of protein mechanics through the combination of high-throughput computing and sound, facilitating the exploitation of natural proteins not as the basis for new materials but as the basis for new methods of sound generation.

Here we propose an alternative approach, to base sound synthesis on the natural vibrational frequencies of protein structures, but using a computer algorithm to convert these inaudible vibrations into a space that the human ear can process. The natural vibrational frequencies represent the mechanisms by which proteins, which make up most of the living world including human cells, tissues, and materials like tendon or bone, freely move and vibrate at the nanoscale [12–16, 19–21]. By making these natural vibrations of the proteins audible, they can then used to creatively express sound and generate music that is based on the complex vibrational spectrum offered by these protein structures [22, 23]. This offers an avenue to sonify the characteristic overlays of natural frequencies, and to use them as a playable musical instrument [24].

Indeed, protein molecules constitute the basic biopolymers that can be generally found in many different forms in the body of living creatures. A protein molecule is usually composed of one or several polypeptide chains that wind together to form a certain folded three-dimensional (3D) protein structure. The forming of the protein structure is usually a spontaneous self-folding process, driven by the interaction inside or between the building blocks of the polypeptide chains, known as amino acids. There are only 20 standard amino acids in eukaryotes and they all have an identical backbone defined by three atoms (N-C-C) that are covalently bonded, along with a side chain specific to each amino acid that is covalently bonded to the center carbon atom.

Because of the different chemistry of the side chain, some amino acids are charged, some are hydrophobic and some are hydrophilic. These features, combined with the generally existing van der Waals interaction and the hydrogen bonding between atoms, causing different interactions of the amino acid to other amino acids. It is generally agreed that a polypeptide chain can start with any randomly bended conformation but will always end up with a unique folded structure after equilibration, and the resulting 3D structure is fully determined by the amino acid sequence, as the name of amino acids along the chain from its head to its tail. Therefore, a protein with a folded 3D structure is at the equilibrium of many atomic interactions. Many of these interactions are weak, making protein structures not as stable as covalently bonded material systems, such as diamond or graphene, and thus their structures are easily excited by external force and vibrate [17].

From a theoretical standpoint, there is no intrinsic difference between the various vibrations that come from a protein or from the wood material used to build a violin [7–11, 25]. In all cases, the overlaid spectrum of frequencies account for the characteristic sound the system produces. We are thus inspired to extract the vibrational feature of different protein structures and use them to generate audible sounds with different character that is directly generated based on the frequencies of natural vibrations.

Results

We first describe the results of the computational algorithm to extract the natural frequencies of all proteins in the protein database, and then proceed to the description of sonifying them and implementing them in a playable instrument.

We developed an efficient way to extract the vibrational feature of a protein is normal mode analysis (NMA), which provides the normal modes of the most general motion of a protein structure. Any possible vibration deformation of a protein can be expressed as a superposition of its normal modes. The modes are normal in the sense that each mode is orthogonal to all the other modes, suggesting that the mode cannot be expressed by other modes, that is to say that an excitation of one mode will never cause motion of a different mode. NMA for a protein structure can be performed by computing the eigenvector and eigenvalue of the hessian matrix, which is a square matrix composed of second-order partial derivatives of the potential energy function, which is defined by the 3D structure of the fully atomic model and the energy functions (known as the force field) for all the atomic interactions.

It is rather computationally expensive to use only computational power to solve the folded 3D structure of a given protein since a regular functional protein with thousands of atoms can adopt so many configurations. Hence, it is impossible to calculate the structure of a very large number of proteins based on existing computing power. However, experimental measurements have shown more advantages in solving the folded 3D structure of many functional proteins. At the time of writing this paper, there were 130,754 high-resolution protein structures that could be obtained from the Protein Data Bank [12]. Those structures are typically obtained by X-ray crystallography, nuclear magnetic resonance spectroscopy, or more recently cryo-electron microscopy and cover a very broad variety of structurally and functionally diverse protein molecules.

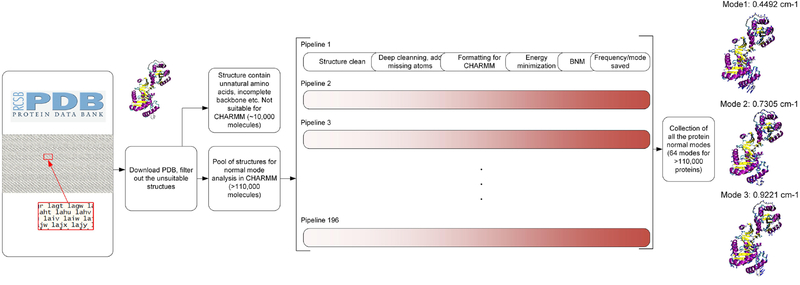
We build a full database of all the first 70 normal modes of each of the 110,511 natural protein structures composed of only standard amino acids, taken from the full list of 130,754 structures that are currently available in the Protein Data Bank (PDB, [12]). We use a custom bash script that allows integrating multiple open source software with the CHARMM c37b1 program [26] to automatically download, clean and analyze each of the protein molecular structure in parallel. We equally distribute the total workload to 196 pipelines within our compute cluster, with each of them responsible for analyzing a group of molecular structures. The protein structure are downloaded from the Protein Data Bank and is first cleaned using the Visual Molecular Dynamics (VMD) and Multiscale Modeling Tools (MMTSB) toolset to remove redundant inorganic particles and only leave the polypeptide chains [27, 28]. For protein structures that are composed of multiple chains, we separate them into individual files and perform a deeper cleaning by using a program for predicting side-chain conformations for a given protein backbone (SCWRL4), which helps us to complete missing atoms of protein side-chains with high reliability [29]. The overall workflow is summarized in Figure 1.

Figure 1.

Overview of the method to obtain, filter, clean and run massive in-parallel NMA for computing the normal modes of almost all known protein structures (>110,000) in the protein databank. The result is summarized as a database of the 64 normal modes and corresponding natural frequencies of all the protein structures. For example, modes 1 to 3 for the protein structure 1g0t.

After these formatting and cleaning stages, the protein structures are moved to CHARMM [26] for energy minimization and then normal mode analysis. The analysis is performed using the CHARMM19 all-atom energy function and an implicit Gaussian model for the water solvent [13, 30]. The implicit solvent is necessary to reduce the noise of normal mode analysis that would otherwise be introduced by the dynamics of water molecules. It also facilitates a more rapid structural organization towards the equilibrium geometry due to the lack of viscosity imposed by explicit water. The use of this solvation potential has been shown to be an efficient and reliable approach to take into account solvent effects of large molecular structures and is particularly suitable for structure prediction applications [14, 15, 31].

Before the normal mode analysis, we perform 10,000 steps of energy minimization with a steepest descent algorithm and another 10,000 steps of energy minimization with an adopted basis Newton-Raphson algorithm [32], which has been used widely for the optimization of the energy of biomolecules in the CHARMM package [26]. The energy minimization is necessary to relax the protein structure to remove unnatural coordinates that can be introduced during the cleaning process. We do not perform extra dynamical simulation after the energy minimization because the protein structures available in PDB are experimentally measured, suggesting that they are already in a well equilibrated state. It is also noted that without dynamical simulations that include a random seed for velocity distribution, the structures and normal modes are highly reproducible as they are identical for repeating runs.

We use the Block Normal Mode (BNM) method [33, 34] in CHARMM for the normal mode analysis of each of the protein structures. BNM projects the full atomic hessian matrix into a subspace spanned by the eigenvectors of blocks, as each block is defined by an amino acid. This approximation reduces the size of the eigenvalue problem dramatically from (3N)² to (6n)², where N is the total number of atoms, and n is the total number of amino acids. We save the first 70 modes with lowest frequencies, ordered from lower to higher frequency, of each protein molecule.

The first 6 modes always have zero eigenvalues and zero frequency because they correspond to the rigid-body movement and rotation of the molecule. The higher order modes 7 and onwards, i.e., the last 64 normal modes amongst the 70 generated, describe the molecular deformation. For the purpose of sound creation, we hence only use the frequency value of the last 64 modes out of these 70 ones. These frequency values are denoted in sequence as f₀, f₁, f₂, … f₆₃, which represent the vibrational spectrum of each protein structure. Moreover, without special note, mode N always frequency refers to the Nth none-zero frequency in our paper.

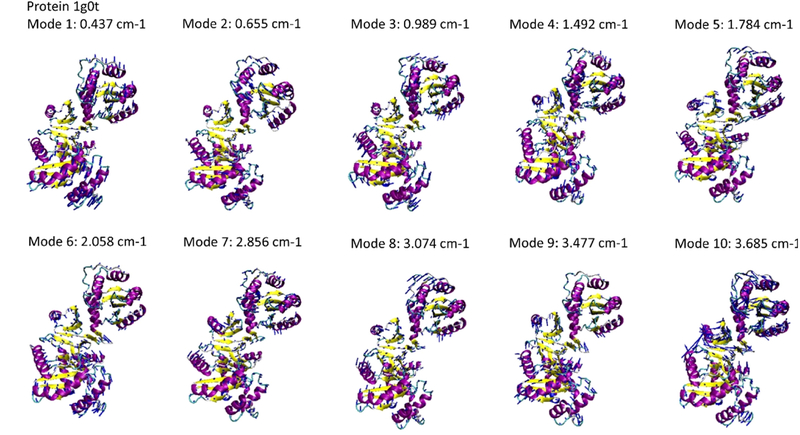
We built a database that summarizes the full atomic vibration modes of all 110,511 protein structures, as well as the corresponding frequencies, as shown in Fig. 2 for the protein structure 1g0t for example. The information is helpful in understanding all decoupled deformation modes of a protein in a freely dynamical vibration process, as well as the frequencies for dynamic deformations. The format of the data file (attached as Supporting Information) that contains the vibrational spectrum of all proteins analyzed is

Figure 2.

The vibration modes 1 to 10 (after rigid body motion modes) and corresponding natural frequencies computed for the protein structure 1g0t. Each of the vibration modes is given by the collective displacement of alpha carbon atoms of the amino acids within the protein structure, visualized by blue arrow pointing from each alpha carbon atoms.

[PROTEIN ID], [PROTEIN ID IN PDB] [f_0/f_0] [f_1/f_0] [f_2/f_0] [f_3/f_0]…;

An example file looks like this:

1, 2bjy 1.00 1.008378436 1.030715836 1.042870685 1.05679907 1.197504816…;

2, 1mfr 1.00 1.004021038 1.008026787 1.009678011 1.013072195 1.345060086…;

3, 1jre 1.00 1.008745375 1.031036908 1.062318442 1.087392594 1.199064306…;

4, 1ji4 1.00 1.003761123 1.017001498 1.062119683 1.0803596 1.256459652…;

5, 1qgh 1.00 1.031281534 1.038941382 1.067944837 1.091459499 1.213160872…;

6, 1l8h 1.00 1.003180136 1.024905972 1.091780571 1.110586185 1.250007645…;

7, 1jxv 1.00 1.017980002 1.06477999 1.094991285 1.119377427 1.1889582…;

8, 1gl6 1.00 1.009662722 1.082759991 1.091428921 1.142830933 1.166131548…;

9, 1hzd 1.00 1.025563404 1.03620463 1.108292817 1.129330642 1.226722319…;

10, 1a0c 1.00 1.013072195 1.078479039 1.105632511 1.186573097 1.201082469…;

11, 1fwu 1.00 1.056248662 1.06667584 1.104730453 1.150643672 1.214812097…;

…

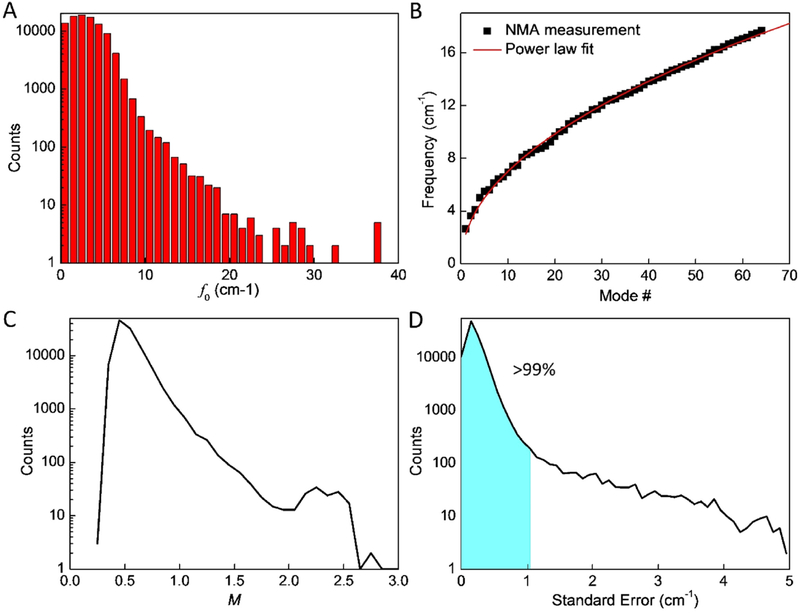
To better understand these natural frequencies, we analyze and statistically investigate the dataset. The results are summarized in Fig. 3. Figures 3A shows that f₀ varies a lot for different protein structures, suggesting that their vibrational spectrum is sensitive to protein structures even though they are made of similar sets of amino acids as their elementary chemical building blocks. It is further shown that the histogram of f₀ follows a log-normal distribution and most protein structures have a rather low base frequency f₀, as f₀< 5 cm⁻¹ accounts for >90% protein structures, as shown in Fig. 3A. These frequencies are much lower than covalent bonds, as 3,700–3,100 cm⁻¹ for the vibration of O-H bonds in water molecules because of the much weaker interactions and large molecular weight [35]. Moreover, we find that for each protein structure, its frequency spectrum f0..63 follows a power law as

$$f_{i\_fit}=b{i}^M.$$ (1)

Figure 3.

Statistical and analysis results of the database of the natural frequency of protein structures. A) The histogram of the distribution of the base frequency f₀. B) The natural frequencies of the vibration mode 1 to 64 of the protein structure 101m and the result as fitted to the power law as given by Eq. (1) as f_i= 2.26i^0.491. C) The histogram of the distribution of the power factor M. D) The histogram of the distribution of the standard error between the NMA measurements and the results fitted by the power law, it is noticed that >99% of the results has σ_SE<1 cm⁻¹.

This equation yields the natural frequency f_{i_fit} for the (i+1) mode (i starts from 0) where b=f₀ for the value of base frequency, M is the power of the function that defines the increment trend of the natural frequencies for larger modes. The agreement between the collection of frequencies and the fitting function is shown in Fig. 3B for the protein structure 101m, for example. We use Eq. (1) to fit the frequencies computed for all the protein structures and summarize the histogram of their M value as given in Fig. 3C. It is shown that >98% protein structures have M<1, suggesting that for most structures the increasing speed of their natural frequency decreases for higher modes, suggesting a higher frequency value may correspond to a larger number of different modes than the lower frequency. We also quantitatively compute the standard error of the fitted value for each protein structure by

$${\sigma }_{SE}=\sqrt{\frac{\sum _{i=0}^{63}{\left(f_i-f_{i\_fit}\right)}^2}{62}}.$$ (2)

We use 62 instead of 64 here as the degree of freedom by considering the two fitting parameters in Eq. (1) are used for computing f_{i_fit}. The histogram of δ_SE is given in Fig. 3D, showing that the 64 frequencies can be fitted by Eq. (1) for [b, M], and the frequencies of over 99% of the protein structure are interpreted correctly with a small standard error δ_SE < 1 cm⁻¹.

To translate the vibrational frequencies into audible sound, we use the concept transpositional equivalence, playing or writing music in a way that makes it sound higher or lower in pitch while retaining the relationships between tones or chords played. This transposition method ensures that the relative values of the vibrational frequencies within each amino acid and amongst different amino acids are retained. We rescale the lowest frequency to a frequency that reflects the frequencies associated with conventional musical tones, and build the spectrum of higher order frequencies on top of them to reflect the characteristic nature of each protein. This method, described in more detail in the next paragraph, is implemented in a Max audio processing tool that can be used as an interactive synthesizer to produce varying sounds derived from the vibrational spectrum [36]. Max is a visual programming language for music and used here to implement a method to realize the sound of all proteins analyzed using our method [36]. We use a MIDI input device as an interactive means to control the parameters of the instrument, especially the relative contributions of the various vibrational modes.

In our translation from protein vibrations to audible sound, we use the set of natural frequencies of each protein. We normalize the ratios = f_i / f₀ starting from 1.0(=f₀ / f₀) to higher values (f₁ / f₀, f₂ / f₀ …) as higher modes are considered. Thereafter, importantly, the base frequency is scaled based on the particular musical note played (e.g., for a C3 corresponds to f_C=130.813 Hz). We select 130.813 Hz here to ensure that most speakers can be used to play the lowest frequencies. The total sound is overlaid by all sound waves with the same energy at higher frequencies, each computed based on the frequency ratio f_C, f_C f₁ / f₀, f_C f₂ /f₀… The device generates sound from multiple vibrational frequencies of each protein. The use of an audible base frequency and overlaying higher frequencies based on the particular spectrum of each protein allows us to translate the frequencies into audible space, and also, to maintain the characteristic sound spectrum associated with each protein.

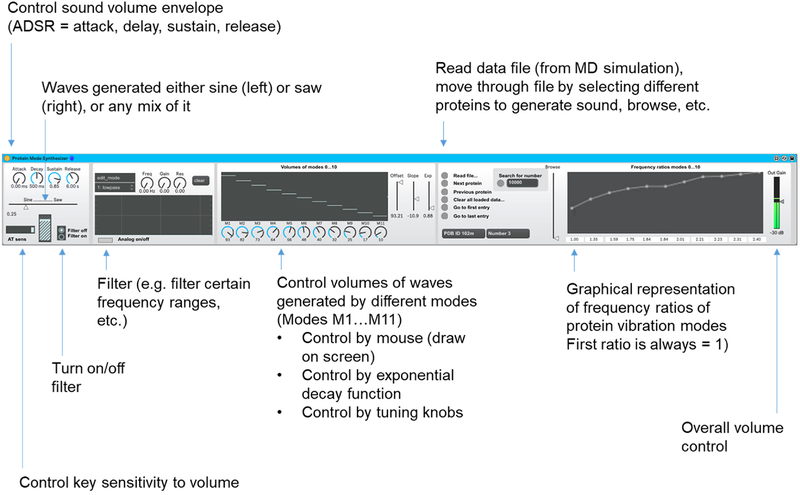
We develop a sonification method to convert the normal frequencies into music by using the Max device. We describe the features of the Max device (shown in Fig. 4) from left to right and explain the underlying sound generation principles. The device generates sound from up to 11 vibrational frequencies of each protein (this could be easily extended by modifying the device, but for demonstrating purposes it is limited to those first frequencies). The frequencies f_i are normalized by the first normal mode f₀, resulting in a set of frequency ratios starting from 1.0(=f₀ / f₀) to higher values as higher modes are considered. The base frequency is computed based on the MIDI note played, and it is overlaid by waves at higher frequencies, computed based on the frequency ratio. The Max device offers Attack-Decay-Sustain-Release (ADSR) control, and allows for a continuous mix between sine and saw wave forms, aftertouch (AT) sensitivity (AT is the capability in a keyboard or similar device such as ROLI BLOCKS by which sound can be changed interactively after the player presses a key, thereby allowing variations of sound while a key is held). The device also includes a variety of filter options to offer additional ways to control the nature of the produced sound (implemented in the left part of the device).

Figure 4.

Image of the Max device, with labels added to explain the various features. The synthesizer includes control of Attack, Delay, Sustain, and Release (ADSR), and uses either sine or saw waves (or a mixture of both) as a basis for sound generation. The Aftertouch (AT) sensitivity can be chosen. A set of filters is implemented (lowpass, highpass, bandpass, etc.). Various ways are implemented to control the volumes of the different modes, from M1…M11. One way to control them is by directly choosing their relative volume with the knobs at the bottom. Another way is to draw the characteristic volumes with a computer input device, such as a mouse (directly in the black window). A third way is to change the three knobs (offset, slope, exp). These implement mathematical functions that set the relative volume of all modes together. The volumes of each of the modes N are set as V(N; off, slop, exp) = min (max(off +slop · N^exp)). This enables the player to interactive change the participation of the various modes in the generation sound and dramatically change the character of the instrument. The device allows to load data files and scan through various protein structures (read file, next protein, previous protein…) and it displays the frequency ratios for all 11 modes used in sound generation.

The device implements three alternative ways to control the relative volume of the vibrations corresponding to the mode, depicted in the center of the device, and visualized using the sliders in the center allows to control the volumes of the modes. The first method of control is that 1) the volumes can be drawn in into the graph, using a mouse. The second method is 2) the use of the knobs below the graph, so that they can also be controlled via automation (knobs M1…M11). A third way of control exists 3) by moving the sliders Offset, Slope, and Exponential, which apply a power law function of different strengths to the frequencies (V(N; off, slop, exp) = min(max(off + slop · N^exp)).). This can be used as a mechanism to interactively and effectively make the sound more pure, focusing on the natural frequency f₀ or gradually increasing the contributions of the higher modes, reflecting the characteristic nature of the particular protein.

The next section in the device allows loading different data files. The standard data file included with this paper is the data that describes all protein structures analyzed. The device allows loading the file and browsing through all protein structures loaded (including specific functions: next, previous, first, last, and search for a certain PROTEIN ID). The browser slide bar allows to quickly browse through all proteins loaded and explore all sounds. The graph to the right depicts all frequency ratios f_i / f₀ (the first ratio is always 1.0). We implemented this setup in Ableton Live 10.0.2, a software music sequencer and digital audio workstation (DAW) [37] for recording and rendering sound.

We illustrate the sound exploration capabilities in a couple of examples (all audio examples are summarized in Table 1, files attached as Supplementary Information. Sample audio files A1…A7 are attached to this paper for download in MP3 format. The Max device will be shared upon request. In the first example, we demonstrate the sound of a C3 tone for the first 32 protein structures, to illustrate the sound they produce. A1 showcases this sound for an exponential decay of the volumes of modes, so that the first mode is most prominent and the higher modes successfully softer. A2 showcases this sound for identical volume of the modes. A3 illustrates the same data for same volume for the first two modes, as an illustration. Now we utilize a couple of proteins and illustrate the distinct sound character that can be achieved based on them. A4 uses PDB ID 101m to generate sound. Playing a continuous C2 tone for several bars, we systematically change the participation of higher and lower modes, resulting in significant variations. The frequency ratios in this case range up to 2.82 for the 11^th mode. In the next example displayed in A5, we use protein PDB ID 4yz2 and the play a C1 tone for several bars. As in the previous example, we systematically change the participation of higher and lower modes, resulting in significant variation. Since the frequency ratio is much greater in this case, ranging up to 84.31, the sound characteristic is vastly different. Next we illustrate a similar exercise for protein PDB ID 5oyi, leading to yet another distinct sound, as shown in A6. Finally, A7 illustrates a simple composition created using three copies of the protein synthesizer playing three distinct melodies, along with a TR-808 drum loop for texture.

Table 1:

Summary of all audio files.

Audiofile (all in MP3 format)	Description
A1	The sound of a C3 note for the first 32 protein structures: power law decay of the volumes of modes
A2	The sound of a C3 note for the first 32 protein structures: identical volume of the modes
A3	The sound of a C3 note for the first 32 protein structures: same volume for the first two modes
A4	Sound generated based on PDB ID 101m, playing a C2 note for several bars
A5	Sound generated based on PDB ID 4yz2, playing a Cl note for several bars
A6	Sound generated based on PDB ID 5oyi, playing a Cl note for several bars
A7	A simple composition created using three copies of the protein synthesizer (each playing a distinct melody or chord progressions), along with a drum loop generated with a Roland TR-808 for texture

Discussion and conclusions

In this paper, we reported a systematic nanomechanical analysis of the vibrational spectrum of over 100,000 protein structures. Using a Max audio device, we generated a software synthesizer that uses the frequency spectrum to generate sound, which can be used to compose new music. This study exemplifies the use of mechanical principles, combined with computer methods, to extract audible frequencies. In addition to understanding the nature of vibrations of protein structures and the use as a new form of an electronic instrument, this method offers novel avenues for STEM outreach.

An interesting insight is the interplay of universality and diversity. The elementary building blocks of proteins – e.g., amino acids and secondary structure types – are limited. However, the structures that are built from these, using hierarchical principles of organization, are complex and responsible for proteins to being capable to act in so many functional roles (e.g. enzyme, structural material, molecular switch, etc.). Since the spectrum of the protein vibrations are defined by a protein’s entire structure including tertiary, quaternary and higher order structures, the resulting spectra and audible sounds are distinct across the protein molecules. Moreover, the type of amino acids and secondary structures largely define the interactions at a local scale, which involves a small amount of mass and thus responsible for high frequency vibrations, while the low frequency vibrations are largely defined by the large-scale pattern of the sequence and the higher order folded structure. Our study confirms this hypothesis and shows that indeed, at a wide spreading of normal frequencies can be obtained for different protein structures. Besides being capable of creating many different sounds, the quality of the proposed synthesis method can be evaluated by its consistency, in that it that the resulting sound is defined uniquely by the particular folded structure of protein, which in turn is identified based on its most fundamental chemical interactions between atoms. The method of sound generation reported here may also find applications as a method to use sound in resonance with biological tissues or for sensing or sorting of molecules.

In terms of fundamental engineering impacts, we highlight three major points:

1. We developed a novel high-throughput method that enables us to automatically compute the vibrational spectra of all proteins available in the Protein Data Bank, in a consistent manner.

2. Based on this method, we computed a large database of normal frequencies of all known protein structures. This dataset has not been available before and by itself, could find numerous uses and applications for further engineering and scientific analysis.

3. By using the resulting frequencies of the protein to generate audible sound by overlaying the molecular vibrations in various patterns, we give access to understand the vibrations of proteins using a new paradigm. It may be useful to understand the effect mutations have on vibrations, or how different classes of proteins (enzyme vs. fibrous, etc.) behave differently from a nanomechanical perspective. For example, the assembly of many proteins is mediated by the nanomechanical motions of the molecules, which can be altered based on mutations, leading to disease. The way of analyzing this type of mechanical behavior using a new method can offer new understanding.

The limitations of the results reported here include general limitations of the force field used, as opposed to using more accurate quantum mechanical methods such as density functional theory. Future work could also consider a broader spectrum of vibrational modes and explore the effect of the assembly of proteins into higher-order materials and how it changes the vibrational properties. Other future work could include a systematic analysis of the differences between different simulation approaches form quantum to coarse-grained levels and how it affects the results.

Proteins are the most abundant building blocks of all living things, and their motion, structure and failure in the context of both normal physiological function and disease is a foundational question that transcends many academic disciplines. In this paper we focused on developing a model for the vibrational spectrum, an elementary nanomechanical property. This concept is broadly important as at the nano-level of observation, all things always move, reflecting the fact that they are tiny objects excited by thermal energy and set in motion to undergo large deformations, which we exploit here to extract new musical compositions as one way to represent nature’s concept of hierarchy as a paradigm to create function from universal building blocks.

More broadly, the translation from various hierarchical systems into one another poses a powerful paradigm to understand the emergence of properties in materials, sound, and related systems, and offers new design methods for such systems.