Estimation of Equipotent Doses for Anti‐Inflammatory Effects of Prednisolone and AZD9567, an Oral Selective Nonsteroidal Glucocorticoid Receptor Modulator

Abstract

AZD9567 is a potent and selective nonsteroidal oral glucocorticoid receptor modulator. It is developed as an anti‐inflammatory drug with improved safety profile compared with steroids like prednisolone. Throughout the clinical development of AZD9567, dose selection and data interpretation require a method for determining doses with the same anti‐inflammatory effect as prednisolone. Equipotent doses of AZD9567 and prednisolone were defined by the same average inhibition of TNFα release, a biomarker of anti‐inflammatory effect, measured in a lipopolysaccharide‐stimulated whole blood ex vivo assay. Based on pharmacokinetic‐pharmacodynamic models, TNFα dose‐response relationships for AZD9567 and prednisolone were established. A comparison of the dose‐response curves enabled estimation of an equipotency relationship. Specifically, 20 mg prednisolone was estimated to be equipotent to 40 mg AZD9567 (95% confidence interval: 29–54 mg). Static concentration‐response analyses showed that the relative potencies for inhibition of TNFα release of AZD9567 and prednisolone were well aligned with several other pro‐inflammatory cytokines.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ AZD9567 is a potent and selective oral nonsteroidal glucocorticoid receptor modulator designed to have similar anti‐inflammatory effect as steroids like prednisolone, with an improved safety profile. The dose selection strategy for design of future clinical studies requires a method for determining doses of AZD9567 and prednisolone with similar anti‐inflammatory effect.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ How to estimate equipotent doses of AZD9567 and prednisolone (i.e., doses with similar anti‐inflammatory effect), based on pharmacokinetic/pharmacodynamic (PK/PD) modeling of the ex vivo biomarker TNFα.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ The key outcome is an equipotent dose relationship between AZD9567 and prednisolone. In addition, models were developed to describe the PK and PD (effect on TNFα) of the two compounds in healthy volunteers receiving single or repeated oral dosing.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ The derived equipotency relationship enables prediction of the therapeutic dose and comparisons of effects on safety biomarkers on a dose‐equivalent scale for both compounds, which can guide dose selection in the future clinical development program for AZD9567.

AZD9567 is a potent and selective nonsteroidal oral glucocorticoid receptor modulator developed for the treatment of inflammatory diseases. ¹ It has been designed to deliver similar efficacy as oral steroids like prednisolone, but with reduced side‐effects. Oral steroids are associated with several side‐effects, including hyperglycemia, ² , ³ , ⁴ weight gain, ⁴ and osteoporosis, ⁵ where AZD9567 has the potential for safety differentiation. AZD9567 has a different binding mode to the glucocorticoid receptor from prednisolone. In preclinical studies, AZD9567 displays better separation of effects on inflammation and glucose metabolism as compared with prednisolone. ¹ , ⁶ Clinical data supporting the differentiation was recently published. ⁷ In these first two studies in humans, AZD9567 showed a promising separation between anti‐inflammatory and dysglycemic effects as compared with prednisolone.

Given the well‐established clinical efficacy of prednisolone and its wide use, dose selection and data interpretation throughout the future clinical development of AZD9567 requires a strategy for estimating equipotent doses of AZD9567 and prednisolone with the same anti‐inflammatory effect. To begin with, it is important to estimate an equipotent dose to 20 mg prednisolone, a dose commonly used short term in clinical practice. Treatment duration is, however, limited by side effects. In addition, prednisolone 20 mg is a moderate dose that falls within the American College of Rheumatology recommendations for treatment of active disease. Moderate doses have been shown to be just as effective as higher doses in active early rheumatoid arthritis (RA), ⁸ a potential indication for AZD9567. Considering the range of doses and dose titration used in different indications, it is furthermore desirable to derive an equipotency relationship for a range as wide as possible.

Equipotent doses of AZD9567 and prednisolone were defined by the same average inhibition of TNFα release, a biomarker of anti‐inflammatory effect, measured in a lipopolysaccharide (LPS)‐stimulated whole blood ex vivo assay. ⁹ TNFα is a central mediator of inflammation and is strongly suppressed in a dose‐dependent manner by glucocorticoids along with additional pro‐inflammatory cytokines. ¹⁰ Several studies have used TNFα as the major efficacy biomarker and it is widely accepted as the biomarker of choice for evaluating efficacy of anti‐inflammatory treatment. Specifically, TNFα is one of the drivers of RA. ¹¹

A model‐based approach was used to estimate the equipotency relationship between AZD9567 and prednisolone. The models were developed using data from the first two clinical trials of AZD9567 in humans, evaluating its safety, pharmacokinetics (PK), and comparing effects on ex vivo biomarkers of anti‐inflammatory effect, hypothalamic pituitary adrenal axis activity, and glucose control with those of prednisolone. In addition to TNFα, the inhibitory effect on several other pro‐inflammatory cytokines were assessed ex vivo in blood.

METHODS

Modeling strategy

The following approach was taken to estimate the equipotency relationship between AZD9567 and prednisolone. First, two separate population PK models were developed, one for each compound. Then, with the fixed PK models as inputs, one common population pharmacodynamic (PD) model for TNFα was developed for both compounds. Finally, the full PK/PD model was used for simulations of dose‐response curves, which, in turn, were compared to determine the equipotent doses of AZD9567 and prednisolone. By carefully considering the uncertainty of the two dose‐responses simultaneously, the uncertainty of the predicted equipotent doses could also be estimated. Additional considerations regarding the strategy for establishing equipotent doses are provided in the Supplementary Methods .

Prior to the detailed PK/PD modeling performed for TNFα, a more straightforward static concentration‐effect analysis was performed for TNFα and five additional cytokines measured in the ex vivo LPS‐stimulated whole blood assay. This was done to investigate whether similar anti‐inflammatory properties for AZD9567 and prednisolone prevail in a spectrum of pro‐inflammatory cytokines, thereby challenging the choice of TNFα as the biomarker for the equipotency estimation.

Clinical studies

Models were developed using data from a single ascending dose (SAD) study ¹² and a multiple ascending dose (MAD) study. ¹³ A detailed description of these studies has previously been published. ⁷ The SAD study was a randomized, placebo‐controlled, single‐blind study in healthy volunteers. A total of nine cohorts with eight participants in each (six active and two placebo) were evaluated. Eight of the nine cohorts were assigned to active AZD9567 and one cohort were assigned to active prednisolone. The doses of AZD9567 were 2, 10, 20, 40, 80, 100, 125, and 155 mg. The dose of prednisolone was 60 mg. The MAD study was a randomized, active‐controlled, single‐blind study. A total of six cohorts were evaluated, one in prediabetic obese subjects and the rest in healthy volunteers. The doses of AZD9567 were 10, 20, 40, 80, and 125 mg (7 participants per dose). The doses of prednisolone were 5, 20, and 40 mg (at least 13 participants per dose). Additional considerations regarding the clinical studies are provided in the Supplementary Methods .

The data used for the PK/PD modeling and the static concentration‐effect modeling were measurements of plasma concentration of the respective compound and concentrations of the cytokines TNFα, interferon‐γ, interleukin‐6, interleukin‐8, and macrophage inflammatory protein‐1α and ‐1β, as released in response to an ex vivo whole blood LPS‐stimulation. ⁹ A subset of the prednisolone PK samples was analyzed for both total concentrations and the fraction unbound. To ensure that a large range of prednisolone concentrations were covered, some samples were spiked with known prednisolone concentrations. The spiked samples were not used for measuring cytokine concentrations. The lower limit of quantification of the PK bioanalysis methods was 5 nM for AZD9567 and 2 nM for prednisolone. There were no below the limit of quantification data for TNFα or the other cytokines. For all analyses, data from the SAD and MAD studies were pooled.

PK/PD modeling

Nonlinear mixed effects PK/PD modeling was done sequentially, fixing both fixed and random effects of the PK models before fitting the PD model. The PD model contained both common and compound‐specific parameters and was fitted for both compounds simultaneously. All models were estimated with NONMEM version 7.3.0 using the first order conditional estimation method. ¹⁴ Visual predictive checks (VPCs) were computed using Perl‐speaks‐NONMEM. ¹⁵ Visualization of model diagnostics was done in R version 3.5.1 ¹⁶ using the nonmem2R package. ¹⁷ Some data were excluded from the analysis, including prediabetic obese subjects from the first MAD cohort and PK data below the lower limit of quantification. The details and rationale for data exclusions and selection of the final models are provided in Supplementary Methods .

AZD9567 PK model

A two‐compartment model with first order absorption and lag time was used to describe the PK of total concentrations of AZD9567:

$$\frac{\mathrm{d}{A}_{\mathrm{a}}\left(t\right)}{\mathrm{d}t}=F\times \text{Input}\left(t\right)‐k_{\mathrm{a}}\times A_{\mathrm{a}}\left(t\right),$$

$$\frac{\mathrm{d}{C}_{\mathrm{c}}\left(t\right)}{\mathrm{d}t}=\frac{k_{\mathrm{a}}\times A_{\mathrm{a}}\left(t\right)}{V_{\mathrm{c}}}‐\frac{\mathit{CL}}{V_{\mathrm{c}}}\times C_{\mathrm{c}}\left(t\right)‐\frac{Q}{V_{\mathrm{c}}}\times C_{\mathrm{c}}\left(t\right)+\frac{Q}{V_{\mathrm{c}}}\times C_{\mathrm{p}}\left(t\right),$$

$$\frac{\mathrm{d}{C}_{\mathrm{p}}\left(t\right)}{\mathrm{d}t}=\frac{Q}{V_{\mathrm{p}}}\times C_{\mathrm{c}}\left(t\right)‐\frac{Q}{V_{\mathrm{p}}}\times C_{\mathrm{p}}\left(t\right),$$

where $A_{\mathrm{a}}\left(t\right)$ is the drug amount in the absorption compartment, $C_{\mathrm{c}}\left(t\right)$ and $C_{\mathrm{p}}\left(t\right)$ are the drug concentrations in the central (including plasma) and peripheral compartments, $F$ the relative bioavailability, $k_{\mathrm{a}}$ the absorption rate, $\mathit{CL}$ the clearance, $Q$ the intercompartment clearance, and $V_{\mathrm{c}}$ and $V_{\mathrm{p}}$ the central and peripheral volumes of distribution. Lognormal interindividual variability was assumed for clearance, relative bioavailability, and peripheral volume. The residual error was modeled as lognormally distributed (additive normal error on log‐transformed data). Initial modeling suggested that the relative bioavailability, $F$, was decreasing with increasing doses. Because of this, dose was used in a continuous covariate model for $F$:

$$F=1‐s\times \text{Dose},$$

where $s$ is a parameter describing the decrease in $F$ per mg dose AZD9567. Other, more complex, covariate models for the dose‐dependent change in $F$ were also evaluated but did not perform better than the linear model. The dose was also used in a covariate model for the absorption rate $k_{\mathrm{a}}$:

$$k_{\mathrm{a}}=\left(\lambda +\left(1‐\lambda \right)e^{‐\alpha \times \text{Dose}}\right)k_{\mathrm{a}0},$$

where $\lambda$ and $\alpha$ are parameters of the model and $k_{\mathrm{a}0}$ is a parameter describing the absorption rate in the limit of zero dose. Lognormal interoccasion variability was used for doses on days 1 and 5, for the lag time, $t_{\text{lag}}$, and $k_{\mathrm{a}\mathrm{0}}$. No interoccasion variability was used for doses on days 2, 3, and 4, because only trough samples were taken.

Prednisolone PK model

Because of the known nonlinear plasma protein binding, PK modeling for prednisolone was performed based on free concentrations. Total prednisolone plasma concentrations were first converted into unbound concentrations, and PK modeling was subsequently performed on the converted data. Conversion of total to unbound prednisolone concentrations was handled by a separate model, explained in detail in Supplementary Methods .

A two‐compartment model with a transit compartment approximation ¹⁸ was used to describe the PK of unbound prednisolone:

$$\frac{\mathrm{d}{C}_{\mathrm{c}}\left(t\right)}{\mathrm{d}t}=\frac{r_{\mathrm{a}}\left(t\right)}{V_{\mathrm{c}}}‐\frac{\mathit{CL}}{V_{\mathrm{c}}}\times C_{\mathrm{c}}\left(t\right)‐\frac{Q}{V_{\mathrm{c}}}\times C_{\mathrm{c}}\left(t\right)+\frac{Q}{V_{\mathrm{c}}}\times C_{\mathrm{p}}\left(t\right),$$

$$\frac{\mathrm{d}{C}_{\mathrm{p}}\left(t\right)}{\mathrm{d}t}=\frac{Q}{V_{\mathrm{p}}}\times C_{\mathrm{c}}\left(t\right)‐\frac{Q}{V_{\mathrm{p}}}\times C_{\mathrm{p}}\left(t\right).$$

Here, $C_{\mathrm{c}}\left(t\right)$ and $C_{\mathrm{p}}\left(t\right)$ are the drug concentrations in the central (including plasma) and peripheral compartments, $\mathit{CL}$ the clearance, $Q$ the intercompartment clearance, and $V_{\mathrm{c}}$ and $V_{\mathrm{p}}$ the central and peripheral volumes of distribution. The term $r_{\mathrm{a}}\left(t\right)$ is the rate of absorption defined by the transit compartment approximation:

$$r_{\mathrm{a}}\left(t\right)=F\times \text{Dose}\times k_{\text{tr}}\times e^{\left(n\times \ln \left(k_{\text{tr}}\times t_{\mathrm{d}}\right)‐k_{\text{tr}}\times t_{\mathrm{d}}‐\ln \left(\sqrt{2\pi }\right)‐\left(n+\frac{1}{2}\right)\times \ln \left(n\right)+n\right)},$$

where $F$ is the relative bioavailability, $n$ the number of transit compartments, $t_{\mathrm{d}}$ the time since last dose, and $k_{\text{tr}}=\left(n+1\right)/t_{\mathrm{m}}$ where $t_{\mathrm{m}}$ is the mean transit time. Lognormal interindividual variability was assumed for clearance, relative bioavailability, mean transit time, and number of transit compartments. The residual error was modeled as lognormally distributed (additive normal error on log‐transformed data). Additional considerations regarding the prednisolone PK model are provided in the Supplementary Methods .

TNFα PK/PD model

The observed inhibition of TNFα typically reached its maximum later than the timepoint of maximal plasma concentrations of the drugs, which suggests that there is a delayed response. Based on this observation, different models exhibiting an indirect response were explored. The preferred model was a standard I_max‐model in which the driving drug concentration was a weighted sum of the plasma concentration and the concentration in a transduction delay compartment. This model was considered mechanistically plausible for the whole blood assay of cytokine release following the LPS challenge because it addresses the equilibration of the PK and PD process, which dynamically impacts on accumulation of TNFα release during incubation of the blood sample. The concentrations driving the PD model were total concentrations for AZD9567 and unbound concentrations for prednisolone.

The weighted plasma‐transduction‐compartment PD model is defined in the following way. A transduction compartment with a time‐dependent concentration $C_{\mathrm{t}}\left(t\right)$ was introduced and described by the following differential equation:

$$\frac{\mathrm{d}{C}_{\mathrm{t}}\left(t\right)}{\mathrm{d}t}=k_{\mathrm{t}}\left(C_{\mathrm{c}}\left(t\right)‐C_{\mathrm{t}}\left(t\right)\right),$$

where the parameter $k_{\mathrm{t}}$ determines the rate of equilibration. The concentrations in the central and transduction compartments are combined to form a weighted concentration:

$$C_{\mathrm{w}}\left(t\right)=w\times C_{\mathrm{c}}\left(t\right)+\left(1‐w\right)\times C_{\mathrm{t}}\left(t\right).$$

The weighting parameter $w$ was estimated from data, and thus the model had the ability to revert into a direct response model or into a transduction delay model, or to adopt an intermediate setting. The ex vivo TNFα concentration, $E\left(t\right)$, is modeled by an I_max‐model driven by the weighted concentration, $C_{\mathrm{w}}\left(t\right)$,

$$E\left(t\right)=E_0\left(1‐{\mathrm{I}}_{max}\left(\frac{C_{\mathrm{w}}^{\gamma }\left(t\right)}{C_{\mathrm{w}}^{\gamma }\left(t\right)+{\text{IC}}_{50}^{\gamma }}\right)\right),$$

where $E_0$, ${\mathrm{I}}_{max}$, $I{C}_{50}$, and $\gamma$, are the TNFα release baseline, the maximal possible inhibition, the concentration of drug in the weighted plasma‐transduction compartment producing a half‐maximal inhibition, and the sigmoidicity parameter, respectively. The parameter ${\mathrm{I}}_{max}$ was fixed to 1 for both AZD9567 and prednisolone. Lognormal interindividual variability was assumed for $E_0$ and for the half‐maximal inhibitory concentration ${\text{IC}}_{50}$ of each compound. The residual error was modeled as lognormally distributed (additive normal error on log‐transformed data). Additional considerations regarding the TNFα PK/PD model are provided in the Supplementary Methods .

Dose‐response

Dose‐response curves for each compound were determined by simulating the PK/PD model in R version 3.5.1 using the mrgsolve package. ¹⁹ The response was defined as the average inhibition of TNFα over 24 hours following 5 consecutive daily doses,

$$R=\frac{1}{24}\underset{t=4\times 24}{\overset{t=5\times 24}{\int }}\left(1‐\frac{E\left(t\right)}{E_0}\right)\mathrm{d}t=\frac{1}{24}\underset{t=4\times 24}{\overset{t=5\times 24}{\int }}{\mathrm{I}}_{max}\left(\frac{C_{\mathrm{w}}^{\gamma }\left(t\right)}{C_{\mathrm{w}}^{\gamma }\left(t\right)+I{C}_{50}^{\gamma }}\right)\mathrm{d}t.$$

This expression is independent of $E_0$, which means that the uncertainty of the $E_0$ estimate is not affecting the dose‐response uncertainty or, in turn, the uncertainty of the equipotency relationship. Confidence intervals for the dose‐response curves were obtained by repeated simulations with parameter samples drawn according to the estimated covariance matrix for the parameter standard errors.

Equipotent dose relationship

Equipotent doses of AZD9567 and prednisolone were defined as doses resulting in the same average inhibition of TNFα. Pairs of equipotent doses were identified using the simulated dose‐response curves. Confidence intervals for the equipotent dose relationship were determined by simultaneously accounting for the uncertainty in the dose‐response of each compound. The details of that procedure are described in Supplementary Methods .

Concentration‐effect analysis

Nonlinear mixed effects I_max‐models were used to describe the static relationship between observed total AZD9567 and prednisolone plasma concentrations and release of the six pro‐inflammatory cytokines,

$$E=E_0\left(1‐{\mathrm{I}}_{max}\left(\frac{C^{\gamma }}{C^{\gamma }+I{C}_{50}^{\gamma }}\right)\right).$$

Here, $E_0$, ${\mathrm{I}}_{max}$, $C$, ${\text{IC}}_{50}$, and $\gamma$, are the cytokine release baseline, the maximal possible inhibition, the concentration of drug in plasma, the concentration of drug in plasma producing a half‐maximal inhibition, and the sigmoidicity parameter, respectively. Lognormal interindividual variability was assumed for $E_0$. The residual error was modeled as lognormally distributed (additive normal error on log‐transformed data). All models were estimated with NONMEM version 7.3.0 using the first order conditional estimation method. ¹⁴

RESULTS

AZD9567 PK model

A two‐compartment model with first‐order absorption and a lag time described the PK of AZD9567. Parameter estimates are shown in Table 1 and a VPC is shown in Figure 1a . Additional model diagnostics are shown in Figure S1 . The first phase had the largest contribution to the area under the concentration curve (AUC; 88%) and was associated with a half‐life of 4.4 hours. Because the PK was not dose‐proportional, the oral dose was used in a linear covariate model for the relative bioavailability. We estimate that the relative bioavailability decreases by ~ 1% unit for every additional 4 mg AZD9567 dosed. Dose‐dependency was also required for the absorption rate constant to adequately capture the absorption phase, which occurs more rapidly for lower doses. This effect can be seen in the insets of Figure 1a where the time of maximal concentration increases with dose.

Table 1.

PK/PD model parameters

Model	Parameter	Symbol	Unit	Value	RSE (%)	IIV (%)	RSE IIV (%)
PK AZD9567	Lag time	$t_{\text{lag}}$	h	0.183	2	12a	14a
	Absorption rate constant	$k_{\mathrm{a}0}$	h−1	38.2	32	72a	8a
	Relative bioavailability	$F$		1b		20	9
	Central volume of distribution	$V_{\mathrm{c}}$	L	26.8	4
	Intercompartment clearance	$Q$	L h−1	0.500	8
	Peripheral volume of distribution	$V_{\mathrm{p}}$	L	392	13	108	17
	Clearance	$\text{CL}$	L h−1	3.70	6	27	9
	Covariate model (dose on $F$)	$s$	mg−1	0.00253	12
	Covariate model (dose on $k_{\mathrm{a}}$)	$\mathrm{\lambda }$		0.103	32
	Covariate model (dose on $k_{\mathrm{a}}$)	$\alpha$	mg−1	0.0592	19
	Residual error	$\sigma$	%	10.9	5
PK prednisolone	No. of transit compartments	$n$		8.11	12	61	15
	Mean transit time	$t_{\mathrm{m}}$	h	0.772	7	41	10
	Relative bioavailability	$F$		1b		17	15
	Central volume of distribution	$V_{\mathrm{c}}$	L	352	5
	Inter‐compartment clearance	$Q$	L h−1	5.81	50
	Peripheral volume of distribution	$V_{\mathrm{p}}$	L	23.6	32
	Clearance	$\text{CL}$	L h−1	110	3	12	12
	Residual error	$\sigma$	%	35.5	7
PK/PD TNFα	Baseline TNFα	$E_0$	ng/L	28.6 × 103	4	36	8
	Transduction rate constant	$k_{\mathrm{t}}$	h−1	0.308	12
	Weighting parameter	$w$		0.216	12
	Maximal inhibition, AZD9567	${\mathrm{I}}_{max}$		1b
	Concentration for half‐maximal effect, total AZD9567	${\text{IC}}_{50}$	nM	765	10	46	16
	Concentration for half‐maximal effect, unbound AZD9567	${\text{IC}}_{50}$	nM	4.87c
	Sigmoidicity parameter, AZD9567	$\gamma$		1.40	7
	Maximal inhibition, prednisolone	${\mathrm{I}}_{max}$		1b
	Concentration for half‐maximal effect, unbound prednisolone	${\text{IC}}_{50}$	nM	17.0	10	16	33
	Sigmoidicity parameter, prednisolone	$\gamma$		1.33	7
	Residual error	$\sigma$	%	44.5	5

Reporting of percent IIV, IOV, and residual error was done using the approximation $100\sqrt{{·}^2}$.

IIV, interindividual variability; IOV, interoccasion variability; PD, pharmacodynamic; PK, pharmacokinetic; RSE, relative standard error.

^aThe IIV and RSE IIV columns are used for IOV for t _lag and k _a0.

^bFixed, not estimated.

^cDerived from the estimate of IC₅₀ for total AZD9567 concentrations using an unbound fraction of 0.637%.

Figure 1.

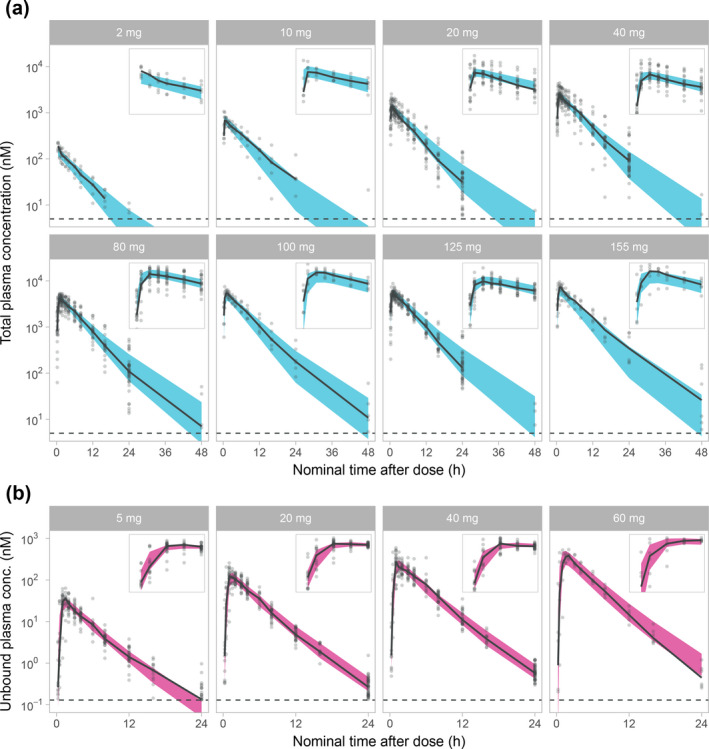
Visual predictive checks on a logarithmic scale, stratified on dose for the AZD9567 pharmacokinetic (PK) model (a) and the prednisolone PK model (b). Plots are showing the 95% confidence interval for the model median (blue for AZD9567, red for prednisolone), observed individual data (gray dots) and their median (solid black line), and the lower limit of quantification (dashed black line). Insets are showing a magnification of the first 4 hours after dose. The y‐scale of the insets are different but always show a 10‐fold range for AZD9567 and a 1,000‐fold range for prednisolone.

Prednisolone PK model

Due to nonlinear plasma protein binding of prednisolone, a static model was first developed to convert total plasma concentrations into unbound concentrations. The parameter estimates of this model are shown in Table S1 and diagnostic plots are provided in Figure S2 . This model showed that the unbound fraction increases from 6% in the limit of low concentrations to 38% in the high limit. The original total prednisolone concentrations have previously been reported. ⁷ A two‐compartment model with a transit compartment approximation for the absorption described the PK of unbound prednisolone. Parameter estimates are shown in Table 1 and a VPC is shown in Figure 1b . Additional model diagnostics are shown in Figure S3 . The first phase had the largest contribution to AUC (66%) and was associated with a half‐life of 1.9 hours.

Concentration‐effect relationships for cytokines

AZD9567 and prednisolone inhibited the release of the cytokines in the ex vivo LPS‐stimulation assay in a concentration‐dependent manner. Figure 2 shows a comparison of ${\text{IC}}_{50}$ estimates from a concentration‐effect model based on total concentrations of the two compounds, which demonstrates that the relative potency of AZD9567 and prednisolone is consistent between TNFα and the other cytokines.

Figure 2.

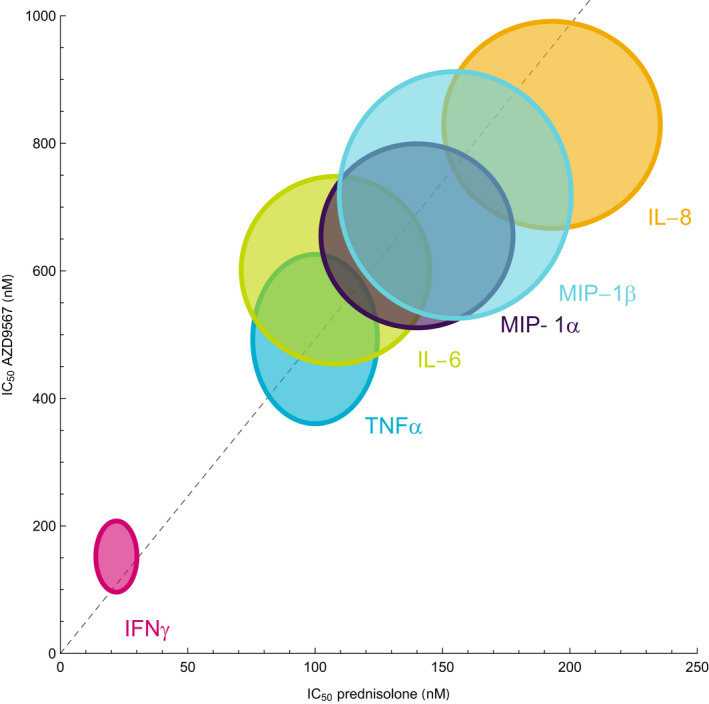
The total concentration AZD9567 producing half‐maximal inhibition of cytokine release (IC₅₀) plotted against the corresponding total concentration prednisolone ${\text{IC}}_{50}$. Uncertainties of the ${\text{IC}}_{50}$ pairs are shown as 95% confidence regions around the point estimates. A reference line (dashed) is defined by the axes origin and the pair of ${\text{IC}}_{50}$ point estimates for TNFα inhibition. The ${\text{IC}}_{50}$ estimates for the other cytokines line up along the reference line, showing that the relative potency is similar across the set of cytokines. IFN‐ γ, interferon‐γ; IL, interleukin; MIP, macrophage inflammatory protein.

TNFα PK/PD model

TNFα inhibition was modeled by an inhibitory I_max‐model with sigmoidicity parameter. Parameter estimates are shown in Table 1 and a VPC is shown in Figure 3 . Additional model diagnostics are shown in Figure S4 . The estimate of the weighting parameter (the plasma proportion) was 22%, favoring the transduction compartment as the main PD driver. The ${\text{IC}}_{50}$ was estimated to 765 nM (95% confidence interval (CI): 610–920 nM) for total AZD9567 and to 17.0 nM (95% CI: 13.5–20.4 nM) for unbound prednisolone. Given an unbound fraction of 0.637% (data on file, AstraZeneca), the ${\text{IC}}_{50}$ estimate of 765 nM for total AZD9567 corresponds to 4.87 nM for unbound AZD9567. Attempts were made to simultaneously fit the final PK and PD models, but without successful convergence.

Figure 3.

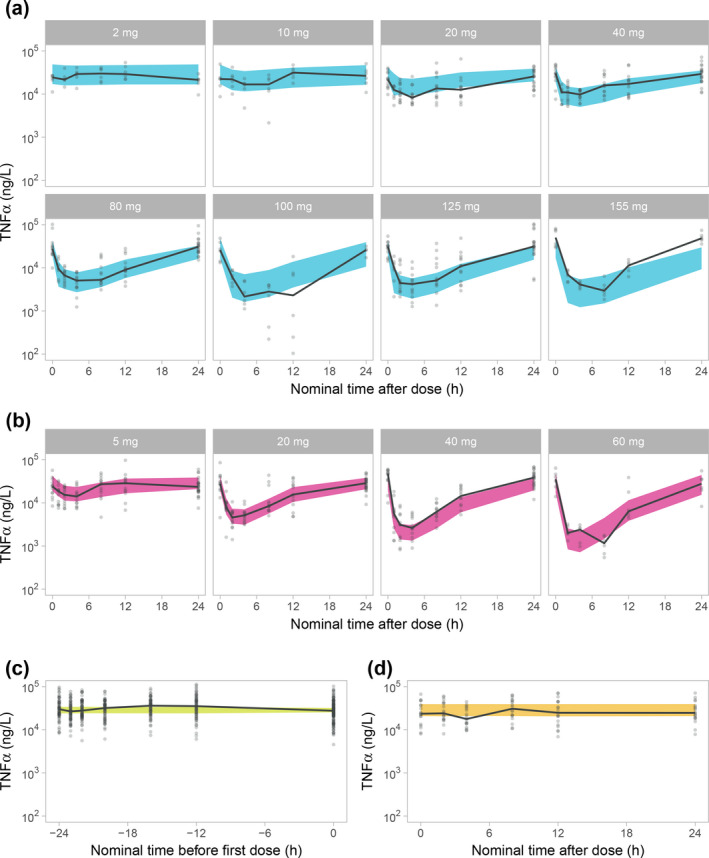
Visual predictive checks on a logarithmic scale for the TNFα pharmacokinetic/pharmacodynamic model for AZD9567 (a), prednisolone (b), baseline (c), and placebo (d). a and b are stratified on dose. Plots are showing the 95% confidence interval for the model median (blue for AZD9567, red for prednisolone, green for baseline, and yellow for placebo), observed individual data (gray dots) and their median (solid black line).

Simulated PK and PD profiles

PK and PD profiles from the PK/PD model were simulated following 5 consecutive daily doses of 40 mg AZD9567 and the commonly used 20 mg prednisolone (Figure 4 ). These doses were estimated to be equipotent (i.e., the average TNFα inhibition on day 5 is the same). Relative to the estimated ${\text{IC}}_{50}$, prednisolone reaches higher concentrations in all compartments compared with AZD9567, but is cleared faster. The TNFα inhibition profile is flatter during the dosing interval for AZD9567 compared with prednisolone. Overall, the PK and PD profiles are similar for the two compounds.

Figure 4.

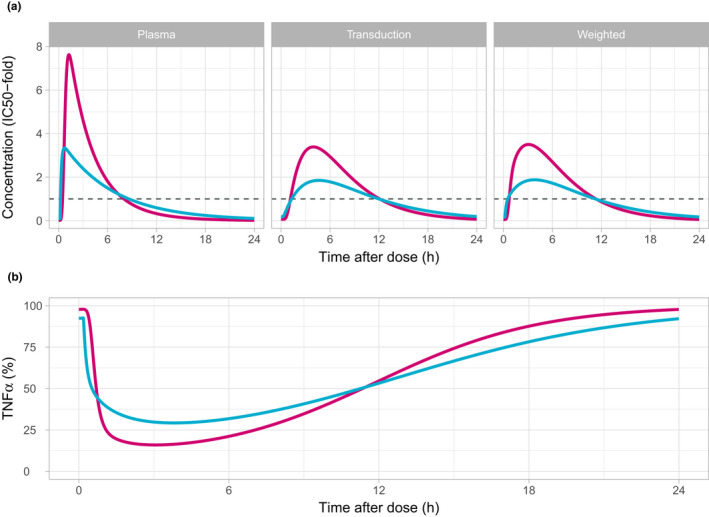
Simulation on a linear scale of the pharmacokinetic (a) and TNFα (expressed as percent of baseline) (b) profiles in a typical individual following the fifth dose of once daily dosing of either 40 mg AZD9567 (blue) or 20 mg prednisolone (red). Drug concentrations in the plasma, transduction, and weighted transduction compartment are scaled with the respective half‐maximal inhibitory concentration (${\text{IC}}_{50}$) to facilitate a comparison between the two compounds. The estimated ${\text{IC}}_{50}$ is shown as reference (dashed line). The transduction compartment concentration profile has a delayed maximum compared to the plasma concentration. The weighted concentration always lies in between the plasma and transduction compartment concentration. The main difference compared with the transduction compartment is a more rapid increase just after dosing. Ex vivo TNFα is shown relative to the estimated baseline. The onset of effect on TNFα is slightly faster for AZD9567 due to its somewhat more rapid absorption, but prednisolone reaches its maximal level of inhibition faster than AZD9567. Prednisolone also achieves a higher maximal reduction of TNFα, but AZD9567 compensates by a slower return toward the baseline.

Dose‐response relationships

The dose‐response relationships for AZD9567 and prednisolone are shown in Figure 5 for the range of doses given in the SAD and MAD studies. The steepness of the dose‐response gradually decreases with increasing doses, and a TNFα inhibition of 60–75% is achieved at the highest studied doses. This may seem to contradict a maximal possible TNFα inhibition of 100% and plasma concentrations that are ~ 10 times the ${\text{IC}}_{50}$ or more for both compounds at the highest doses. However, the exposure is not sufficiently high to achieve a full or near full TNFα inhibition over the whole day, which would be needed to approach a 100% average response.

Figure 5.

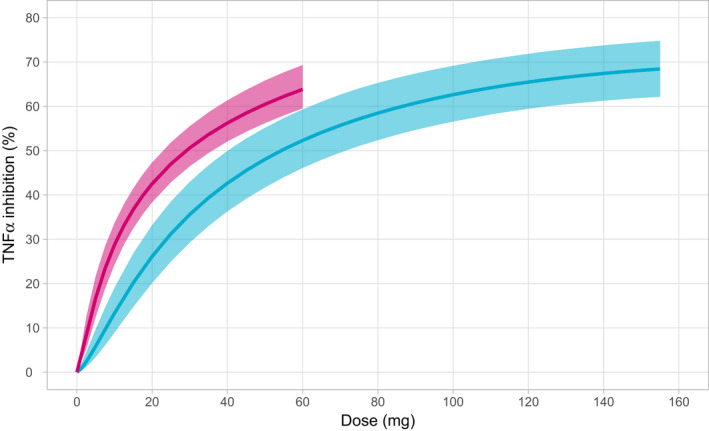
Dose‐response curves with 95% confidence intervals for AZD9567 (blue) and prednisolone (red). Response is defined as the average TNFα inhibition over 24 hours following 5 consecutive daily doses.

Equipotency relationship

The simulated dose‐response relationships for the two compounds were used to estimate equipotent doses. Given a dose of prednisolone, the resulting TNFα inhibition was determined, and the dose of AZD9567 achieving the same level of inhibition was estimated. A CI was derived by simultaneously accounting for the uncertainty of both dose‐responses. When performed over the whole range of studied doses, comparisons of the dose‐response curves defined the full equipotency relationship (Figure 6 ). For example, it was estimated that a dose of 40 mg AZD9567 (95% CI: 29–54 mg) was equipotent to 20 mg prednisolone, with both doses resulting in an average TNFα inhibition of 43%. Table S2 shows estimates of equipotent AZD9567 doses for all prednisolone doses given in the SAD and MAD studies (5, 20, 40, and 60 mg). The relationship is nonlinear and there is no simple formula such as a factor that relates the equipotent doses.

Figure 6.

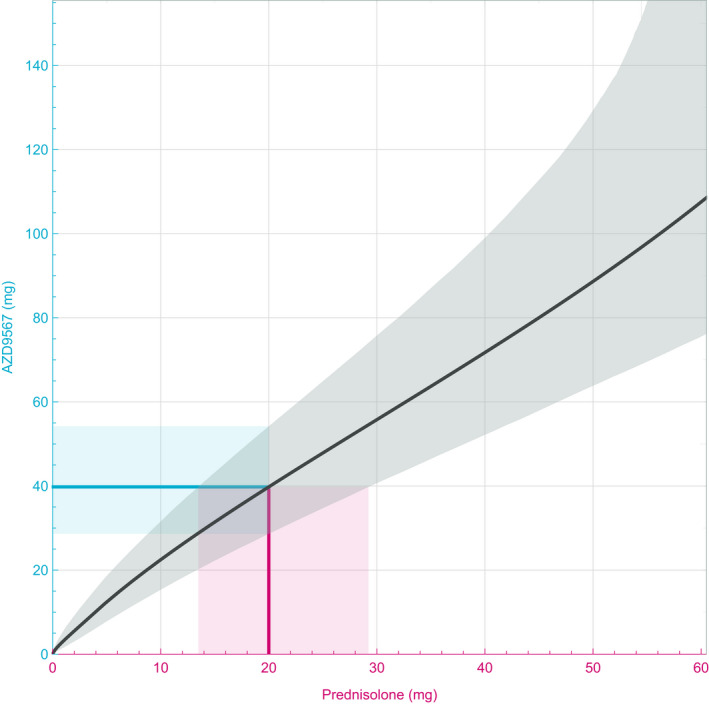
The point estimate (black) and the 95% confidence interval (gray) of the equipotency relationship between AZD9567 and prednisolone. Illustration of a dose‐to‐dose translation shows that 20 mg prednisolone (red line) is equipotent to 40 mg AZD9567 (blue line), with a 95% confidence interval (CI) of 29–54 mg (blue shaded region). Similarly, 40 mg AZD9567 is equipotent to 20 mg prednisolone, with a 95% CI of 14–29 mg (red shaded region).

To understand the impact of PK uncertainty on the equipotency relationship, CIs were re‐computed with uncertainty of PK parameters set to zero (Table S2 ). At lower doses of 5 to 20 mg prednisolone, the impact of PK uncertainty is marginal. At higher prednisolone doses of 40 to 60 mg, there is a small impact on the CI (CI decreased between 2 and 4 mg). Thus, the largest contributor to the uncertainty in the equipotency relationship is the PD response.

DISCUSSION

A model‐based approach was used to estimate an equipotency relationship between AZD9567 and prednisolone. This relationship serves two important purposes. First, the equipotency relationship is critical for evaluating the differentiation vs. prednisolone on a set of key biological functions where sustained treatment causes debilitating side‐effects, in areas such as bone turnover and glycemic control. For meaningful assessment of differentiation, it is necessary to compare AZD9567 and prednisolone at doses with equal anti‐inflammatory effect. ²⁰ For instance, a side‐effect related biomarker dose‐response for AZD9567 could be translated onto a prednisolone‐equivalent dose scale, for a direct comparison with the corresponding dose‐response for prednisolone. Another approach is to translate both AZD9567 and prednisolone doses into predicted average TNFα inhibition and use that as a common scale for comparisons. The latter strategy was used to jointly analyze the dose‐response for the change from baseline in plasma glucose AUC after an oral glucose tolerance test (see Figure S2B in the supplement of ref. 7). Second, the equipotency relationship is useful for prediction of therapeutic doses and can be used to guide dose selection in future clinical studies with prednisolone as an active comparator. Specifically, 40 mg AZD9567 is estimated to match 20 mg prednisolone, and these doses were selected for a head‐to‐head comparison in a Ph2a study in patients with RA. ²¹ The equipotency relationship is currently used in the planning of future studies in the clinical development program.

In addition to the value for the future development of AZD9567, we believe that the methodology to derive the equipotency relationship has general value and application in drug development. The principles of constructing the equipotency relationship, including the CI, is applicable to any scenario where two dose‐responses are to be compared with respect to relative potency. A related approach based on the analytical solution to logistic concentration‐effect models has previously been used for cross‐species comparison of neurotoxicity. ²² More theoretical perspectives of dose‐response comparisons, acknowledging different possible applications, have also been laid out. ²³ However, to the best of the authors’ knowledge, a PK/PD model‐derived dose‐dose plot comparing two compounds has not been presented before.

Both PK and PD models for AZD9567 and prednisolone described the integrated data well. The unbound fraction of prednisolone was estimated to increase from 6% in the limit of low concentrations to 38% in the high limit. This is lower but still comparable with the low and high limits of 9% and 53% defined by a literature average of the prednisolone plasma protein binding parameters. ²⁴ , ²⁵ , ²⁶ , ²⁷ The half‐life of unbound prednisolone was in line with previous studies. ²⁸ , ²⁹ , ³⁰ , ³¹ Estimates of apparent clearance and volume of distribution are at the upper end of reported values, which is consistent with the relatively lower estimate of the unbound fraction. AZD9567 and prednisolone had similar PK profiles and delays in ex vivo TNFα inhibition, resulting in similar profiles of TNFα inhibition. The ${\text{IC}}_{50}$ estimate of 765 nM for total AZD9567 corresponds to 4.87 nM for unbound AZD9567. Compared with the estimated ${\text{IC}}_{50}$ of 17.0 nM for unbound prednisolone, AZD9567 is thus a ~ 3.5‐fold more potent inhibitor of TNFα release. The still roughly twofold higher doses of AZD9567 required for equipotency is explained by the low fraction unbound, which implies a more than fivefold higher unbound clearance for AZD9567.

The use of a weighted plasma‐transduction compartment driving the I_max‐model is a novel idea that is mechanistically plausible given the experimental procedure. When fresh blood is drawn it is immediately collected in a tube containing LPS, which triggers a dynamic process of cytokine release during incubation of the sample. After incubation, samples are analyzed for the accumulated TNFα content. In parallel with the LPS‐induced cytokine release, there is also a counteracting process by which the drug inhibits the release. Because the glucocorticoid receptor is an intracellular receptor, a modulator or agonist would first have to relocate from the plasma into the cytosol of a glucocorticoid receptor‐expressing cell before it can engage with the target. This would regulate gene transcription through a series of downstream events and eventually inhibit the release of TNFα. Hence, there are several dynamic processes at play, with potentially overlapping timescales, that simultaneously impacts on the amount and timing of cytokine release. It is, therefore, reasonable to assume that the accumulation of TNFα is influenced by the complete history of drug concentration at the target and by the history of downstream effects following target engagement. In addition to cellular responses, prednisolone is known to have a delayed effect on circulating lymphocyte numbers through cell trafficking mechanisms, ³² which may impact on the amount of TNFα being released. The weighted transduction delay model captures the essence of these ideas by forming an average, or effective concentration, that is used to drive the I_max‐model. A more realistic PD model from a mechanistic point of view would consider the details of the dynamic processes determining TNFα release and aim to mathematically integrate the accumulated TNFα in the blood sample. Several sophisticated mechanistic models of in vivo TNFα dynamics has been developed, ³³ , ³⁴ even including the dynamics of LPS. ³⁵ These models typically require rich data sets to inform the parameter estimation and their application to our scenario would require time series data from the process occurring in the blood sample during incubation. The weighted concentration model is a model of reasonable complexity that still has some capability to address the underlying mechanisms of the TNFα measurements while being identifiable from the current SAD and MAD data.

In addition to the PK/PD model of TNFα, a static concentration‐effect analysis was performed on a set of pro‐inflammatory cytokines. Although the potency for inhibiting release was found to be different for each cytokine, the relative potency between AZD9567 and prednisolone was similar across the set of cytokines. This indicates that the AZD9567 mechanism of action for an anti‐inflammatory effect is similar as that of prednisolone. It also suggests that the equipotency relationship is robust with respect to the choice of cytokine on which it is based. However, it remains to be shown that the effect of AZD9567 on the pro‐inflammatory cytokines translates into clinical efficacy.

A limitation in the outcome of our model‐based approach is the size of the estimated uncertainty of the equipotency relationship, which grows rapidly for higher doses. It should be noted that the uncertainties of the doses‐response curves—from which the equipotency relationship is derived—is not behaving the same way. Except for very low doses, the dose‐response uncertainties essentially remain constant throughout the dose range. The driver of the growing uncertainty of the equipotency relationship is instead the shape of the dose‐response curves. As they flatten out, every percent unit increase in TNFα inhibition requires an increasing amount of dose. The weaker the dose‐response becomes, the more sensitive the equipotent dose becomes to the dose‐response uncertainties. Estimating a PD model for both compounds simultaneously helps to reduce the uncertainty of the equipotency prediction because correlations of parameter standard errors can be utilized. Unfortunately, it was not possible to estimate PK and PD models simultaneously, which may have further reduced the uncertainty of the prediction. On the other hand, we showed that the uncertainty originating from the PK parameters is limited.

Because of the relatively small sample size in the two clinical studies performed in young healthy volunteers, the PK/PD modeling did not include a covariate analysis to investigate the influence of subject demographics. Specifically, all subjects in the SAD study were men and in the MAD study only four women were exposed to AZD9567, preventing conclusions on sex‐specific effects on PK/PD. An important extension of the current understanding of the PK/PD relationship will be the covariate information from the patient population in the Ph2a study. ²¹ Moreover, as TNFα is measured in this study, the validity of the translation of a biomarker effect to a clinical effect can be assessed. By integrating information on PK, TNFα inhibition, and clinical effect (DAS28 ³⁶ ) a future model could potentially extend the equipotency relationship to include clinical efficacy.

In conclusion, an equipotency relationship between AZD9567 and prednisolone was obtained by a model‐based integrated evaluation of PK and PD from two clinical studies in healthy volunteers. The derived equipotency relationship enables comparisons of effects on safety biomarkers and guides dose selection in the future clinical development of AZD9567.

Funding

The clinical studies upon which these analyses are based were funded by AstraZeneca.

Conflict of Interest

J.A., M.W.S., U.E., T.H.M., S.P., and J.L. are employees of AstraZeneca and may own stock or stock options.

Authors Contributions

J.A., M.W.S., U.E., T.H.M., S.P., and J.L. wrote the manuscript. U.E., T.H.M., S.P., and J.L. designed the research. J.A., M.W.S., and J.L. performed the research. J.A., M.W.S., and J.L. analyzed the data.

Supporting information

Fig S1

Fig S2

Fig S3

Fig S4

Supplementary Material

Table S1

Table S2