Helicity-dependent photocurrents in the chiral Weyl semimetal RhSi

The CPGE spectrum and optical conductivity in RhSi are measured and discussed, comparing to theoretical predictions.

Abstract

Weyl semimetals are crystals in which electron bands cross at isolated points in momentum space. Associated with each crossing point (or Weyl node) is a topological invariant known as the Berry monopole charge. The circular photogalvanic effect (CPGE), whereby circular polarized light generates a helicity-dependent photocurrent, is a notable example of a macroscopic property that emerges directly from the topology of the Weyl semimetal band structure. Recently, it was predicted that the amplitude of the CPGE associated with optical transitions near a Weyl node is proportional to its monopole charge. In chiral Weyl systems, nodes of opposite charge are nondegenerate, opening a window of wavelengths where the CPGE resulting from uncompensated Berry charge can emerge. Here, we report measurements of CPGE in the chiral Weyl semimetal RhSi, revealing a CPGE response in an energy window that closes at 0.65 eV, in agreement with the predictions of density functional theory.

INTRODUCTION

Soon after Dirac discovered his celebrated equation describing a relativistic electron, Weyl pointed out (1) that a massless particle could have a simpler description because the particle’s helicity or handedness is constant, independent of reference frame. Although these Weyl fermions were ruled out as fundamental Standard Model particles after the discovery of neutrino masses, an analog appears in certain semimetals in which nondegenerate bands cross in momentum space (2). These crossing points (or Weyl nodes) act as monopoles of Berry curvature, and a theorem by Nielsen and Ninomiya (3) requires the total monopole charge in the Brillouin zone to be zero. As a result of this constraint, Weyl nodes cannot be gapped independently and are thus topologically protected.

In recent years, the existence of Weyl nodes and the Fermi arc surface states predicted to accompany them (4) has been conclusively demonstrated by angle-resolved photoemission (5–9). With their existence thus verified, an important goal of future research is to identify the role of Weyl topology in shaping responses to external perturbations. A key step toward this goal is to distinguish topologically derived responses from those primarily determined by symmetry. The issue arises because topology and symmetry are inextricably linked in Weyl semimetals, as the existence of Weyl nodes requires either inversion or time-reversal symmetry to be broken.

Photogalvanic effects, wherein photocurrents proportional to the light intensity appear in the absence of an applied bias, are examples of responses allowed by symmetry in Weyl semimetals that break inversion. In the circular photogalvanic effect (CPGE), the direction of the current reverses on changing the photon polarization between left and right circular (10). The CPGE has been used effectively to probe broken symmetry states in a variety of condensed matter systems (11–14).

The first hint that topology can shape the CPGE amplitude (15) arose in the context of the crossing of nondegenerate bands at the surface of three-dimensional (3D) topological insulators such as Bi₂Se₃. Figure 1A illustrates how helicity-dependent photocurrent can arise in such a system as a result of the correlation of the direction of an electron’s momentum with that of its spin (or pseudospin). A photon with definite helicity induces a transition that flips the direction of spin and, through spin-momentum locking, creates a particle-hole pair that carries a net current. Hosur (15) showed that the current associated with photoexcitation of an electron-hole pair at momentum k was proportional to the Berry curvature, Ω(k). However, in this 2D system, the net CPGE current vanishes on integration over k in the presence of n-fold rotational symmetry (for n ≥ 3). Nonzero CPGE requires lowering the symmetry by applying in-plane strain or a magnetic field or inducing photoexcitation at oblique incidence (16).

Fig. 1. Photocurrents from Weyl semimetals and experimental apparatus.

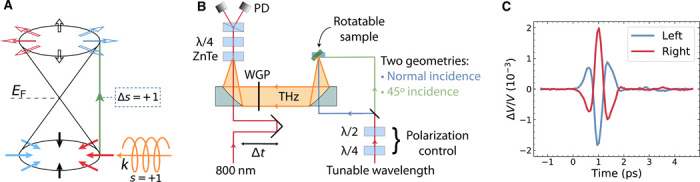
(A) Helical radiation preferentially excites one side of a Weyl cone centered at the Fermi energy, generating a current parallel to the optical wave vector. (B) Schematic of the experimental geometry. Variable wavelength pump light is incident on the sample at either normal or 45^° incidence. Terahertz (THz) radiation is collected and focused onto a ZnTe crystal for electro-optic sampling. PD, photodiode; WP, Wollaston prism; WGP wire grid polarizer. (C) Individual terahertz pulses measured from left and right circularly polarized 2000-nm pump light at 45^° angle of incidence. Their difference is the photon helicity–dependent CPGE signal.

Recently, de Juan et al. (17) showed that, in contrast to the 2D case, rotational symmetry does not cause CPGE to vanish for the 3D band crossings that define Weyl semimetals. Instead, the CPGE current from a single Weyl node in the clean, noninteracting limit is proportional to its quantized topological charge and fundamental constants e and h. In an ideal system, this result is independent of material-specific properties and the frequency of the excitation light over a band of wavelengths. The rate of current generation by circularly polarized light is described by the equation

$$\frac{\mathrm{d}{j}_i}{\mathrm{d}t}=i\mathrm{\pi }\frac{e^3}{h^2}C{\widehat{\mathrm{\beta }}}_{\mathit{ij}}{[\mathbf{E}(\mathrm{\omega })\times {\mathbf{E}}^{*}(\mathrm{\omega })]}_j$$ (1)

where $\text{Tr}{\widehat{\mathrm{\beta }}}_{\mathit{ij}}=1$ and C is the monopole charge (or Chern number) (17).

Although each Weyl node contributes a quantum of CPGE, this direct signature of topological charge is hidden in systems that retain mirror symmetry, which requires that nodes of opposite charge be degenerate in energy. This leads to an exact cancellation of the CPGE current for pairs of perfectly symmetric Weyl nodes. Despite this, nonzero CPGE is seen in mirror symmetric Weyl semimetals such as TaAs (18–23) as a consequence of departures from symmetric dispersion that occur in real systems, for example, curvature or tilting of the Dirac cones (24). However, in such systems, the CPGE amplitude is not a topological property uniquely related to the Berry monopole charge.

The properties of chiral Weyl semimetals, in which all mirror symmetries are broken, are qualitatively different from mirror-preserving materials such as TaAs (17, 25). In chiral structures, isolated Weyl nodes can occur at time-reversal invariant momenta. As a result, they can be separated by wave vectors on the order of the full Brillouin zone, allowing for a richer structure of Fermi arc surface states (26–28). Of more direct relevance to the CPGE, in chiral Weyl semimetals, nodes with opposite topological charge need not be degenerate in energy. Thus, it is possible for one node to lie near the Fermi energy, E_F, while its oppositely charged partner is below. Transitions near the node below E_F are Pauli blocked at sufficiently low photon energy, and a quantized CPGE (QCPGE) arising from the Weyl node near E_F will emerge. This prediction (17, 25) motivates measurements of CPGE as a function of photon energy to search for an energy window in which overall Berry charge neutrality is frustrated by Pauli blocking, even if the precise quantization suggested by Eq. 1 is modified by disorder or interaction effects.

Chiral semimetals can host multiple band crossings with monopole charges C larger than 1. Despite higher multiplicity and band curvature in these multifold fermion systems, it was shown theoretically that approximate CPGE quantization continues to hold, with corrections at low energy when spin-orbit interaction is included (27, 29, 30). Furthermore, the magnitude of the CPGE is enhanced for multifold compared to Weyl fermions because of the greater topological charge.

RhSi is a structurally chiral material proposed as an ideal candidate to exhibit a QCPGE. The prediction of multifold fermion dispersion and exotic Fermi arcs (27, 28) was confirmed recently by angle-resolved photoemission spectroscopy measurements in this compound and in isostructural materials (31–33). The QPGE is predicted to have an especially simple form in this family of compounds because in their cubic space group, P2₁3 (#198), the dimensionless anisotropy tensor ${\widehat{\mathrm{\beta }}}_{\mathit{ij}}$ reduces to the unit tensor multiplied by a scalar β = ¹/₃. Furthermore, band theory predicts a large energy splitting between the two nodes of opposite charge, such that the regime of Pauli blocking extends to a photon energy of approximately 0.65 eV, well into the near-infrared range (29).

RESULTS

A schematic of the apparatus for photogeneration and detection of CPGE current in the photon energy range from 0.48 to 1.1 eV is shown in Fig. 1B. The component of photogalvanic current parallel to the surface of the RhSi crystal radiates an electromagnetic pulse into free space that is focused onto a ZnTe crystal for time-resolved electro-optic sampling. This all-optical technique avoids artifacts from asymmetric electrical contacts and laser-induced heating and enables precise determination the direction of the current through measurement polarization of the pulse in the far field. Figure 1C shows typical pulses measured with an excitation photon energy of 0.60 eV. The reversal of polarity between left and right circular excitation is the defining property of the CPGE.

Before examining the CPGE spectrum, we first tested that the CPGE and linear PGE (LPGE) currents obey the polarization properties consistent with the space group symmetry of RhSi. Because ${\widehat{\mathrm{\beta }}}_{\mathit{ij}}$ is predicted to be diagonal, the CPGE current should obey the relation, j ∝ β(E × E^*), and therefore be directed parallel to the wave vector of light, independent of the crystal orientation. The direction of the LPGE current, on the other hand, depends on both the light polarization and the crystal axes. For our measurements, in which the sample was rotated by an angle ϕ about the normal to the [111] surface, the direction of the LPGE surface current, θ, is predicted to rotate three times as fast (see the Supplementary Materials).

Figure 2A shows a typical measurement of the direction of the current, obtained by using a linear polarizer in the far field to resolve the two orthogonal components of the electric field. Figure 2B shows the direction of the LPGE current as a function of ϕ for normal incidence, confirming the relation θ = 3ϕ. In contrast, the CPGE signal is below measurement noise level at normal incidence, consistent with the prediction that it flows directly into the bulk of the crystal, with zero surface component. At 45^° incidence (Fig. 2C), the LPGE current exhibits the same θ = 3ϕ dependence, and CPGE current is now observed, with direction independent of ϕ. This latter result is consistent with the expectation that the CPGE current is parallel to the wave vector of the excitation light, because in this case, the surface current direction is locked to the plane of incidence (see Fig. 2D), independent of crystal orientation.

Fig. 2. Symmetry of CPGE and LPGE responses in RhSi.

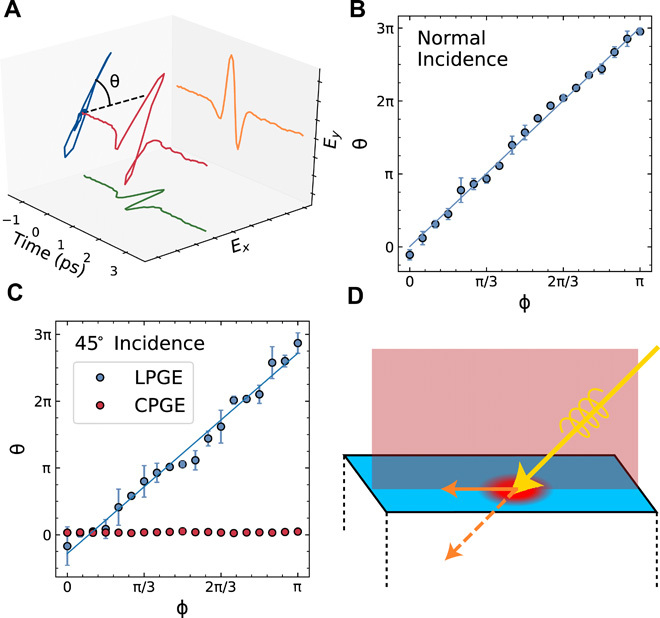
(A) Measurement of the terahertz polarization. Orange and green curves show the vertical and horizontal components of the pulse as a function of time. The reconstructed terahertz pulse (red curve) is then projected onto a plane, showing the direction of linear polarization, θ. (B) Dependence of the angle of LPGE terahertz polarization, θ, on angle of rotation of [111] face about the surface normal, ϕ, with pump at normal incidence. The relation θ = 3ϕ predicted by the space group P2₁3 symmetry is confirmed. The CPGE signal is below measurement noise level in this geometry. (C) Same as (B) except for 45^∘ incidence. LPGE polarization again varies as =3ϕ. CPGE is horizontally polarized independent of the crystal orientation, confirming that the CPGE current is parallel to the pump wave vector. (D) Schematic showing that the resulting in-plane CPGE current is fixed by the plane of incidence of the pump light. The CPGE current at normal incidence is normal to the surface of the sample and thus does not radiate into free space.

Having confirmed that the polarization selection rules are consistent with crystal symmetry, we turn to the dependence of the CPGE amplitude on photon energy ℏω in the range from 0.5 to 1.1 eV. We note first that this amplitude is proportional to the βτ product, where τ is the momentum lifetime of photexcited carriers, rather than β itself. The reason is that the dynamics are in the quasi–steady state regime of Eq. 1, in which τ is shorter than the ∼100-fs duration of the excitation pulse. This conclusion follows from the observation that the terahertz emission waveform follows the envelope of the laser pulse, rather than persisting for an observable momentum lifetime. The quasi–steady state regime is consistent with τ = 8 fs for equilibrium carriers as determined from transport measurements (see the Supplementary Materials). The τ of photoinjected “hot” carriers can be expected to be at least as short as that of the equilibrium ones.

Figure 3 shows the dependence of βτ on pump photon energy. Converting the measured terahertz emission to surface current and ultimately an absolute determination of βτ requires accounting for multiple wavelength-dependent factors involving the photoexcitation source, the linear optical response of RhSi at the pump laser and terahertz wavelengths, and the spectral function of the terahertz detection optics. Propagation of systematic and statistical errors through these multiple factors suggests an order-of-magnitude uncertainty in the absolute surface current (see the Supplementary Materials for a detailed discussion of these factors).

Fig. 3. CPGE spectrum.

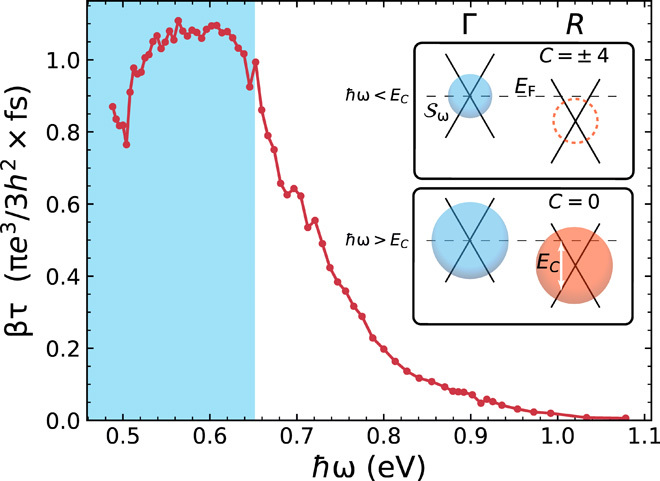
CPGE amplitude βτ in units of $\frac{\mathrm{\pi }{e}^3}{3h^2}\times$ fs as a function of photon energy, showing abrupt quenching above 0.65 eV. The inset contains a schematic showing the surface 𝒮_ω in k-space defined by the available optical transitions at photon energy ℏω. For ℏω < E_C, 𝒮_ω encloses a single node and has integrated Berry flux C = ±4. Above E_C, it encloses two topological nodes of opposite chirality and C = 0. The blue shaded region in the main plot indicates the region where 𝒮_ω encloses only a single node.

The notable feature of the CPGE spectrum is the rapid decrease in βτ that occurs when ℏω exceeds 0.65 eV. Above this energy, βτ decays from its peak value by a factor of ∼200 as ℏω reaches 1.1 eV. This spectral feature cannot be accounted for by the aforementioned wavelength-dependent conversion factors, as they vary smoothly through this energy range.

DISCUSSION

The photon energy at which the CPGE response decreases agrees with theoretical predictions (29, 30) based on a crossover in effective Berry monopole charge as a function of ℏω. The inset in Fig. 3 illustrates this crossover, showing the evolution of the surface 𝒮_ω in k-space defined by the available optical transitions at energy ℏω. The CPGE is proportional to the integrated flux of the Berry curvature through 𝒮_ω (17), referred to as C. For sufficiently small ℏω, 𝒮_ω is a single surface enclosing the Γ point, and the total Berry flux is equal to the topological charge at Γ, which is 4. For ℏω > E_C, a surface surrounding the R point appears such that 𝒮_ω now encloses two nodes of opposite chirality, driving the net Berry flux and, consequently, the CPGE, to zero.

Although our observation of the predicted cutoff in the CPGE spectrum is suggestive of an interpretation in terms of band structure topology, this tentative assignment comes with several caveats. First, the photon energy dependence of the hot-carrier lifetime will be reflected in the CPGE response, which, as previously mentioned, is proportional to the βτ product. Although we cannot measure τ(ω) directly as it is below our ∼100-fs time resolution, we believe that it is unlikely to decrease sufficiently rapidly with energy to account for the ∼100-fold decrease in the CPGE response that begins when ℏω exceeds 0.65 eV. This would require that τ decrease from its cold-carrier value of 8 to ∼0.08 fs. Converting τ to mean-free path l using the Fermi velocity v_F ≈ 4.3 × 10⁷ cm/s derived from density functional theory band structure (27) yields l ≈ 3.5 nm, or about seven lattice constants, for electrons at the Fermi surface. Thus, l would have to decrease to less than 0.1 lattice constant to account for the entire decrease in CPGE current as the photon energy is increased. Nevertheless, it is certainly possible that the energy dependence of τ contributes to the observed CPGE photocurrent spectrum.

A further consideration for the interpretation of the CPGE spectrum is the possibility that optical transitions, other than those originating from the Γ and R points, contribute to photon absorption in the infrared range. To examine this possibility, we measured the linear optical conductivity, σ₁(ω), throughout the spectral range of our photocurrent spectroscopy. Figure 4 (A and B) shows the normal incidence reflectivity measured at room temperature and the corresponding σ₁(ω) obtained by Kramers-Kronig analysis, respectively. Shown in Fig. 4B as well is the predicted contribution from interband transitions near the Weyl nodes (34), where the spectrum is smoothed, assuming disorder and thermal broadening to be ∼0.1 eV. From the comparison, we see that σ₁(ω) does indeed show contributions beyond those expected from interband transitions near the Weyl nodes: a Drude component at low energy and a peak near 0.8 eV that may be associated with the transitions near the M point (27). The spectra suggest that only ∼¹/₃ of the absorbed photons generate transitions near the Γ, and thus, β is expected to be modified considerably from the universal value predicted for an idealized chiral Weyl system.

Fig. 4. Reflectivity and optical conductivity.

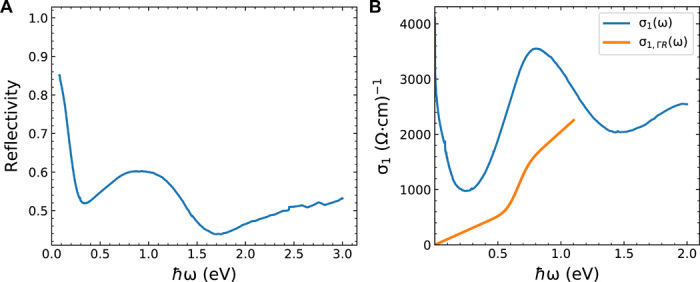
(A) Measured reflectivity of RhSi. (B) Optical conductivity determined by reflectivity measurements and Kramers-Kronig analysis (blue curve). The Drude peak is used to infer that the scattering time has value τ = 8.6 fs. The orange curve represents the optical conductivity from the Γ and R nodes alone (34).

Our room temperature measurements of linear conductivity have been confirmed by a recent study of the temperature, T, dependence performed on samples from the same growth as used in our experiments (35). On the basis of the T dependence at low photon energies, it was possible to resolve the intraband (Drude) and interband contributions and determine that σ₁(ω) is dominated by the interband contribution above a photon energy of ∼0.3 eV. From this, we conclude that the cutoff at 0.65 eV is not related to a crossover from intraband to interband absorption. In addition, it was confirmed that σ₁(ω, T) increases throughout the spectral range where we observe the rapid decrease in the CPGE amplitude. Overall, we believe that the linear conductivity data support the hypothesis that the CPGE spectral cutoff can be understood as the onset of transitions whose contribution to the total photocurrent is opposite in sign.

Last, we believe that regardless of the underlying mechanism, our observation of CPGE photocurrents in a chiral semimetal will stimulate new research directions into the interaction of topological systems with light. For example, the CPGE photocurrent generated by light at normal incidence flows directly into the bulk of crystal but decays exponentially with increasing depth. This is an unusual example of a longitudinal current created by a transverse light field. Conservation laws suggest that this CPGE will cause charge and pseudospin to accumulate, which would then couple to longitudinal excitations of the medium such as plasmons and phonons. Thus, it may be possible to control the amplitude and phase of these collective modes through the polarization state of incident photons, which would be especially exciting when applied to chiral metals that become superconductors at low temperature.

MATERIALS AND METHODS

Crystal growth and structure refinement

Single crystals of RhSi were grown from a melt using the vertical Bridgman crystal growth technique. The crystal growth was performed with an off-stoichiometric composition containing slightly excess Si. First, a polycrystalline ingot was prepared using the arc melt technique with a stoichiometric mixture of Rh and Si metal pieces of 99.99% purity. Then, the crushed powder was filled in a custom-designed sharp-edged alumina tube and lastly sealed inside a tantalum tube with argon atmosphere. The temperature profile for the crystal growth was controlled with a thermocouple attached at the bottom of the tantalum ampoule containing the sample. The sample was heated to 1500^°C and then slowly cooled to cold zone with a rate of 0.8 mm/hour. Single crystals with average dimensions of ∼15-mm length and ∼6-mm diameter were obtained. A picture of the grown crystal is shown in the inset of fig. S1. The crystals were analyzed with a white-beam backscattering Laue x-ray diffraction technique at room temperature. The samples show very sharp spots that can be indexed by a single pattern, revealing excellent quality of the grown crystals without any twinning or domains. A Laue diffraction pattern of the oriented RhSi single crystal superposed with a theoretically simulated pattern is presented in fig. S1. The structural parameters were determined using a Rigaku AFC7 four-circle diffractometer with a Saturn 724+ charge-coupled device detector applying graphite-monochromatized Mo-Kα radiation. The crystal structure was refined to be cubic P2₁3 (#198) with a lattice parameter, a = 4.6858(9) Å.

Terahertz emission spectrometer

The photoexcitation source was an optical parametric amplifier pumped by an amplified Ti:Sapphire laser, producing wavelength-tunable pulses from 1150 to 2600 nm (0.48 to 1.1 eV) and duration τ_pulse ≈ 100 fs. The terahertz emission was collected and collimated by off-axis parabolic mirrors and then focused onto a ZnTe crystal for electro-optic sampling. A linear polarizer placed in the collimated beam was used to measure the vertical and horizontal components of the terahertz electric field.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/29/eaba0509/DC1