Reconfigurable Floquet elastodynamic topological insulator based on synthetic angular momentum bias

Spatiotemporally modulated array of piezoelectric patches implements a Floquet topological insulator for elastic waves.

Abstract

Originating with the discovery of the quantum Hall effect (QHE) in condensed matter physics, topological order has been receiving increased attention also for classical wave phenomena. Topological protection enables efficient and robust signal transport; mechanical topological insulators (TIs), in particular, are easy to fabricate and exhibit interfacial wave transport with minimal dissipation, even in the presence of sharp edges, defects, or disorder. Here, we report the experimental demonstration of a phononic crystal Floquet TI (FTI). Hexagonal arrays of circular piezoelectric disks bonded to a PLA substrate, shunted through negative electrical capacitance, and manipulated by external integrated circuits, provide the required spatiotemporal modulation scheme to break time-reversal symmetry and impart a synthetic angular momentum bias that can induce strong topological protection on the lattice edges. Our proposed reconfigurable FTI may find applications for robust acoustic emitters and mechanical logic circuits, with distinct advantages over electronic equivalents in harsh operating conditions.

INTRODUCTION

Topologically ordered states, such as those induced by two-dimensional quantum Hall and quantum spin Hall effects, and three-dimensional topological insulators (TIs) have received notable attention in the past few years. Topological states of matter were first described in electronic materials using Fermi-Dirac statistics (1–3), then in bosonic systems such as photonic crystals and classical waves in electromagnetic materials (4–10), and, more recently, for mechanical waves in phononic systems (11–16). The most intriguing property of these topological states is their unusual ability to guide waves along any desired trajectories, with minimal back-reflection from sharp edges over broad frequency ranges (13, 17).

In recent years, TIs have been developed to control phonons (elastic waves in solids) in the form of static (zero-frequency floppy modes) (11, 18–20) and dynamical edge states (14, 21). Phononic systems benefit from much smaller wavelengths and stronger boson-boson interactions as compared with photonic systems operating at similar frequencies (22). Specifically, mechanical TIs can be classified into two broad groups. The first actively breaks time-reversal symmetry to realize chiral edge states analogous to the quantum Hall effect (QHE) (15, 16, 22), while the other one passively breaks inversion symmetry to realize helical edge states analogous to the quantum spin Hall effect (13, 14, 17). However, only breaking time-reversal symmetry guarantees complete immunity to backscattering, regardless of the nature of the defect (23). In mechanical systems, breaking time-reversal symmetry has been accomplished via Lorentz forces (24), gyroscopes (25), rotating frames (22, 26), and Coriolis forces (15, 27, 28). Nonetheless, experimental realizations of these complex methods are challenging and further complicated by loss and noise mechanisms associated with moving media. One possible scenario for overcoming these issues is to instead use time-varying properties to synthesize a momentum bias (29, 30). Recently, Fleury et al. (23)proposed a nonreciprocal acoustic metamaterial analog of a Floquet TI (FTI), where the material properties are modulated in time and space in a time-harmonic rotating manner. While FTIs were originally introduced in quantum and photonic systems (31–33), and later shown in sonic systems by using strongly coupled ring resonators (34), experimental demonstrations of FTIs that break time-reversal symmetry based on time modulation have never been studied, to the best of our knowledge, neither in phononics nor in other wave platforms. In photonics, the required time modulation would make impractical to use electro-optical modulation. Phononic systems, while they can somewhat relax the requirements on modulation speeds, require large actuations to notably alter the material properties in time. Compared with the previously demonstrated FTIs that obey time-reversal symmetry, the proposed time modulation scheme synthesizes an effective on-site rotation of each unit cell, without the requirement of phase uniformity across the lattice, imparting a gauge bias to the lattice that breaks reciprocity and induces topological order. This is particularly intriguing for applications that require isolation and one-way signal flows. In addition, the presented platform naturally offers programmability, which enables the possibility of guiding waves in various paths with minimal loss. These two features, exploited in the case of a single unit cell element to realize circulators for radio waves (35), represent a stepping stone toward practical implementations of reconfigurable broadband nonreciprocal TIs for mechanical waves.

Here, we report the first design and fabrication of a phononic FTI exhibiting protected edge states. We use piezoelectric patches connected to a negative capacitance circuit and a programmable switch to markedly change in time the local effective elasticity modulus of the coupled system. Topologically protected wave propagation from the source to the receiver (at an arbitrary location) in the proposed structure can then be controlled in real time, which implements a fully reconfigurable device in which topological order can be imparted on demand. Our implementation, inspired by the theoretical design by Fleury et al. (23), addresses several challenges in the practical implementation and characterization of time-modulated FTIs, including, e.g., the existence of multiple polarizations and resonant modes.

The property of TIs to guide waves with minimal loss around sharp edges and the dynamic reconfigurability of the proposed structure open the possibility of using them as a platform to design robust acoustic-based devices. These devices can be used to design multiplexers and demultiplexers in communication-based devices, where the edge state pathway can be reconfigured and routed in real time. These mechanical devices are cheaper, lighter, and consume less battery. In addition, they can be used in hazardous situations or harsh environment.

The realized system consists of a graphene-like lattice (hexagonal honeycomb) formed by a periodic array of shunted piezoelectric disks bonded to a thin polylactic acid (PLA) plate. These hexagonal lattices support Dirac points, whose inherent time-reversal symmetry can be broken by the synthetic angular momentum imparted in each unit cell by the rotating spatiotemporal modulation of the lattice Young’s modulus. In turn, this creates a bandgap supporting topologically protected edge states. The time modulation is implemented by external circuits with a time-modulated negative capacitance connected to the piezoelectric (PZT) disks.

RESULTS

Topological crystal with broken time-reversal symmetry

Fig. 1A shows a schematic of the proposed phononic metamaterial, composed of hexagonal unit cells (shown in Fig. 1B) formed by 0.5-mm-thick circular piezoelectric disks of diameter d₁ = 7 mm and capacitance C_p = 1.5 nF, attached to an elastic PLA plate of thickness h₀ = 0.5 mm. Each piezoelectric disk can be viewed as an elastic resonator bonded to the top surface of the host material. Figure 1D depicts the band structure for the unmodulated unit cell (red dashed lines), documenting a twofold degeneracy at the edge of the unit cell (i.e., K-point), where two distinct Lamb modes (36) meet at f ≈ 84.5 kHz. Note S1 provides a full discussion on the generation of these dispersion curves and their associated mode shapes.

Fig. 1. Time-reversal symmetry breaking in a phononic crystal.

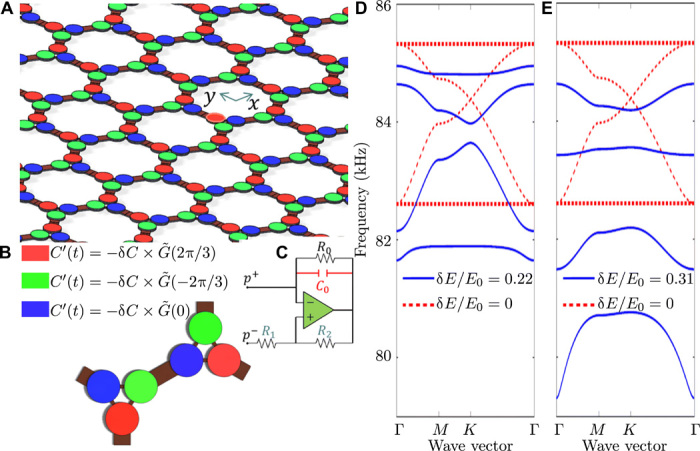
(A) Schematic of the time-dependent phononic crystal formed by hexagonal unit cells with PLA (h₀ = 0.5 mm thick) as the host layer and attached circular piezoelectric (PZT) patches with thickness of h₁ = 0.5 mm (d₁ = 7 mm in diameter). (B) The elastic modulus of each PZT patch is periodically modulated in time in a rotating manner (with uniform handedness throughout the lattice) through connections to external circuits. (C) The shunted circuits, composed of two resistors (R₁ and R₂ in blue), one capacitor (C₀ in red), and an operational amplifier, provide a negative capacitance C′ = −(R₂C₀)/R1, which is altered in time by a switch that turns on/off at the frequency f₀ = ω₀/2π with the function $\tilde{G}(\mathrm{\varphi })=\text{sgn}(\text{cos}({\mathrm{\omega }}_{0}t)+\mathrm{\varphi }))-1$. The resistor (R₀) parallel to the capacitor prevents saturation of the capacitor. (D) Comparison between the band structures along the irreducible Brillouin zone perimeters in the absence (red dashed curves with a Dirac point at ≈84.5 kHz) and in the presence (blue solid curves with modulation at f₀ = 50 kHz, δC = 2.5 nF, and δE/E₀ = 0.22) of modulation. (E) Comparison between the band structures along the irreducible Brillouin zone perimeters in the absence (red dashed curves with a Dirac point at ≈84.5 kHz) and in the presence (blue solid curves with optimal modulation at f₀ = 50 kHz, δC = 2 nF, and δE/E₀ = 0.31) of modulation. The time modulation has the effect of folding the band structure along the frequency axis and lifting the degeneracy at the K and Γ points, opening a complete bandgap with topological protection. Note S1 provides the complete band structure of the proposed system, showing folded frequencies in the vertical direction.

The next step in realizing an analog of QHE in this system requires breaking time-reversal symmetry and opening a topological bandgap at the Dirac point. This is achieved by connecting negative capacitance circuits to each PZT disk while modulating these circuits by a periodic on-site potential $\mathrm{\Delta }C=-\mathrm{\delta }C\times \tilde{G}(\mathrm{\varphi })$ with strength δC and frequency f₀ = ω₀/2π, where $\tilde{G}(\mathrm{\varphi })=\text{sgn}(\text{cos}({\mathrm{\omega }}_{0}t+\mathrm{\varphi }))-1$ is the modulation function. The phase ϕ in $\tilde{G}$ depends on the considered PZT in a way such that the modulation imparts an effective spin onto each trimer. The negative capacitance obtained by the circuit depicted in Fig. 1D results in substantial changes in the effective Young’s modulus of the connected PZT disk (37–39). The circuit is composed of two resistors (R₁ = 10 ohms and R₂ = 20 ohms), one capacitor (C₀ = 1 nF), and an operational amplifier, providing a negative capacitance of C′ = −(R₂C₀)/R₁ = −2 nF (for the optimal case) when connected to the PZT in series. Last, periodic on-off operation of the switch connecting the circuit to the PZT disk induces an effective modulus variation between E_m = 55 GPa (for the optimal case) and E₀ = 80 GPa, with a period of T₀ = 2π/ω₀. Note S2 provides full details on calculating the modulated modulus of elasticity.

Figure 1D plots the band structure of the described unit cell undergoing time modulation (blue curves, δC = 2.5 nF and f₀ = 50 kHz), which documents lifting of the degeneracy at both the Γ and K points. Note that, by further increasing the modulation strength (with f₀ being unchanged), the bandgap opens until we reach a maximum bandgap with flat bands. Figure 1E displays the band structure corresponding to this optimal case for δC = 2 nF. Further increases in the modulation strength are detrimental to gap opening width because of pinching of the bands at the Γ point. Note that the band structures in Fig. 1(E and F) are plotted for the frequency range of interest (79 to 86 kHz); hence, folded bands along the frequency axis are not visible. Note S1 provides the complete band structure including all folded bands. Because of time-reversal symmetry breaking, the opened bandgap supports a topological nature with nonvanishing Chern number. As discussed in (23), a semi-analytical approach based on the stroboscopic effective Hamiltonian can be developed to characterize the system in terms of topological invariants. We show in note S3 that the topological invariant calculated from arbitrary harmonics of Floquet state in this periodically modulated system is equivalent to the one from the static eigenstates of the effective stroboscopic Hamiltonian. Last, the harmonic function U(k, t) with l = 0 is obtained from first-principle simulation and used to find the corresponding Chern numbers to be {1,0,0, − 1} for right-handed modulation (see note S2 for more details).

Emergence of topologically protected edge waves

A unique property of nonreciprocal TIs is the presence of one-way edge modes at the interface between domains with opposite topological invariants. According to the bulk-edge correspondence principle, the number of edge states at a given interface is the sum of Chern numbers of all the bulk modes below the bandgap (40). To realize the edge states of the system, a finite 1 × 7 super cell is considered. Figure 2A illustrates the band diagram for this strip with uniform modulation handedness (see Fig. 2B), periodically repeated in the x direction with the modulation strength and frequency of δC = 2 nF and f₀ = 50 kHz, respectively. The figure reveals the existence of one pair of edge modes within each bandgap. Since these topologically protected edge modes are in the bandgap, they cannot scatter into the bulk of the structure and propagate only along the edges in one direction. Figure 2B shows the displacement field of the strip at 83 kHz (marked with a green star), documenting an edge mode localized at the top boundary.

Fig. 2. Numerical computation of topologically protected edges states.

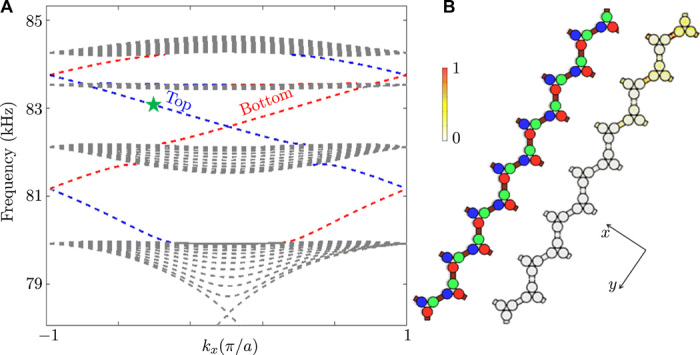
(A) Quasi-band structure of a super cell composed of 1 × 7 arrays of unit cells, periodically repeated in the x direction and analyzed using Floquet boundary conditions. Gray areas depict bulk bands, and blue dashed lines depict the edge modes. (B) Schematic of the super cell and the corresponding wave distribution at frequency f = 83 kHz (marked with a green star), showing wave localization at the top edge. All displacements are normalized by the maximum deformation of the cell.

Experimental observation of topological edge modes

A set of experiments validate the performance of the proposed FTI. Figure 3A depicts the experimental setup formed by bonding 150 piezoelectric disks to a three-dimensional printed PLA host material. Each piezoelectric disk connects to an external circuit with a programmable controller to provide space and time stiffness modulation (see note S4 for full details on the experimental setup). The experimentally measured frequency response of the system is depicted in Fig. 3B for the range 86 to 90 kHz, showing the transfer function between the input and the two points marked with pink and green stars in Fig. 3C. We observe two clear bandgaps over which the transfer function is close to zero for the point (pink star) within the bulk, while for the point on the edge (green star), two edge modes support transmission close to unity, ensuring efficient transport for the fabricated structure. Figure 3C exhibits the experimentally measured root mean square (RMS) wavefield resulting from excitation at 89.5 kHz. Because of the imperfections in the experimental setup and stiffness of connected wires, this frequency is slightly above the one predicted using numerical modeling. The provided figure confirms the presence of QHE-like edge modes at the free interface.

Fig. 3. Experimentally measured edge states.

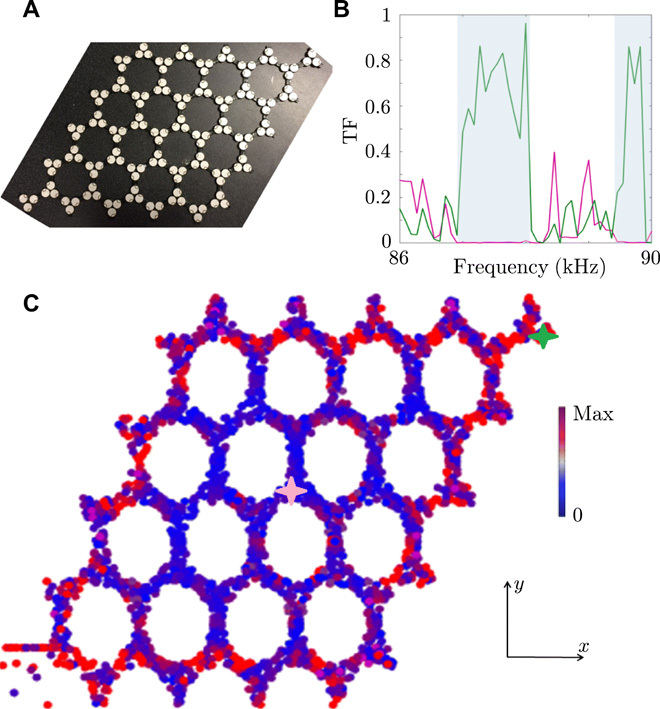
(A) Fabricated TI configured to exhibit an edge mode on free surfaces for a uniform right-handed synthetic angular momentum imparted by the spatiotemporal modulation. Each PZT is connected to an external circuit. (B) Experimentally measured transfer function (TF) at the two points marked with pink and green stars. The light blue areas show the topological bandgap. (C) Experimentally measured RMS displacement field excited by a source with frequency 89.5 kHz, documenting wave propagation along the free edges without backscattering. All displacements have been normalized to the amplitude of the input wave.

To study wave propagation at the interface of two domains with opposite Chern numbers and show real-time reconfigurability, we change the topological features of our sample by modifying the modulation pattern. Since the two sides of the interface have opposite Chern numbers, there will be a total of two chiral edge states flowing in the same direction at the interface. In Fig. 4A, we divide the sample into two regions: One subdomain experiences a right-handed synthetic angular momentum modulation, and the other subdomain experiences a left-handed one; therefore, they share a topologically protected domain wall where localized waves can propagate one way and without scattering into the bulk. Figure 4A reports the RMS response of the system at 89.5 kHz for a horizontal interface, exhibiting wave propagation from a source on the right side to a receiver on the left side of the structure. As another example, Fig. 4D shows the response of the system at the same frequency for a different modulation scheme, forming a triangular domain wall. As shown, waves travel from the source on the right side to reach the receiver at the top of the structure, with minimal scattering at the sharp edge. To observe propagation of the wave at the interfaces, return wave propagation at the edges is prevented in this case by sticking absorbing patches on the perimeter. Note S4 shows snapshots in time of the propagating modes during the transient excitation for the experiments in Fig. 4 at various instances of time from the start of the excitation, showing the time evolution from the transient response to steady state.

Fig. 4. Experimentally measured domain wall states.

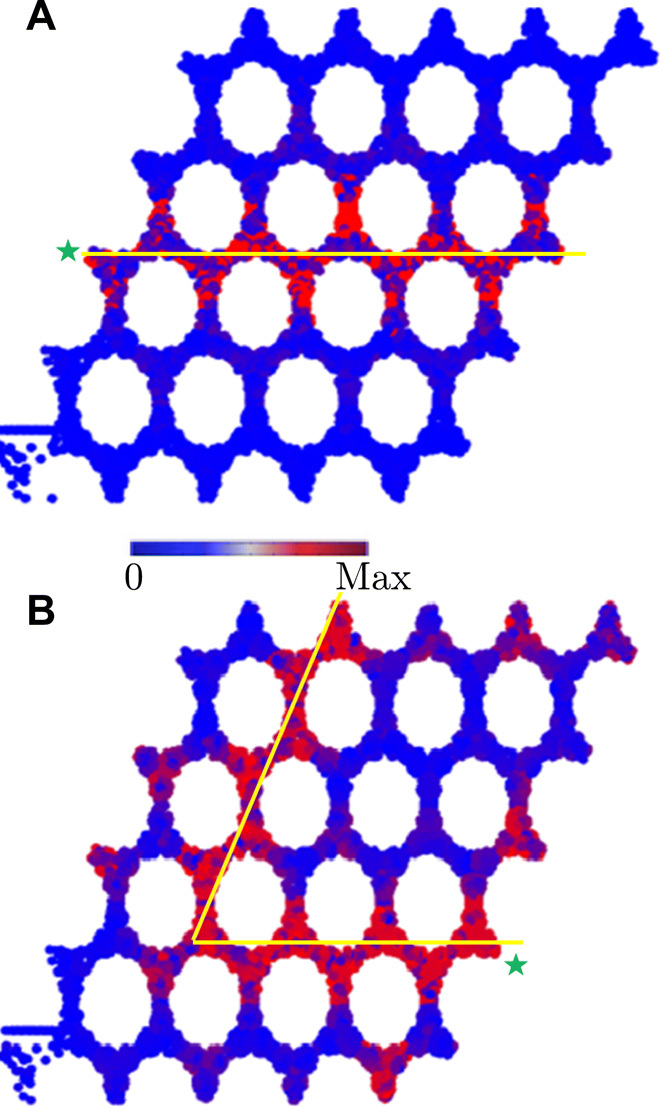
Experimentally measured RMS displacement field of the system excited by a source (marked with a green star) with frequency 89.5 kHz, documenting immune to backscattering wave propagation along (A) a horizontal domain wall and (B) a triangular-shaped domain wall, created by modulating different regions of the lattice with oppositely handed synthetic angular momentum. All displacements have been normalized to the amplitude of the input wave. For these interfaces, modulation of unit cells on one side of the yellow line is right handed, and on the other side is left handed.

DISCUSSION

In summary, this article reports the first experimental implementation of a nonreciprocal FTI based on synthetic angular momentum bias, implemented using spatiotemporal modulation in elastodynamics. A unit cell composed of a PLA host layer bonded to six time-modulated piezoelectric disks is biased by a synthetic angular momentum imparted by a rotating phase of the modulation signal, which breaks time-reversal symmetry. The time modulation of the PZT disks is implemented using external circuits with effective negative capacitance. Numerical simulations document a topologically protected bandgap with edge states connecting the bulk modes. Experimental measurements nicely confirm these predictions by demonstrating topologically protected, backscattering immune wave propagation along edges and interfaces. The modulation network is directly amenable to provide reconfigurability: By simply controlling the capacitance of the circuits, reconfigurable domain walls have also been experimentally demonstrated. The fabricated metamaterial represent an advantageous platform to realize acoustic multiplexers, demultiplexers, and mechanical logic elements in engineered systems.

MATERIALS AND METHODS

The fabricated composite structure is realized from a 0.5-mm-thick PLA layer with 150 glued (using 3M DP270 epoxy adhesive) piezoelectric disks. Each of these piezoelectric disks has a diameter of 7 mm and a thickness of 0.5 mm (PZT4). For each circuit attached to a PZT disk, negative capacitance C′ = − 2 nF is obtained using R₁ = 10 ohms and R₂ = 20 ohms, C₀ = 1 nF, and R₀ = 1 megohms. On/off switching of the circuits is accomplished using three output channels of a general-purpose data acquisition system (National Instruments cDAQ-9174 with a digital output module). A LabVIEW script then generates three output signals with the desired delay. A Polytec PSV-400 scanning laser Doppler vibrometer measures the resulting out-of-plane wavefield velocity, repeating each measurement 10 times (to reduce the influence of noise). A bonded input PZT disk (PZT4) produces an incident wave in response to a 150-mV (peak-to-peak) burst sinusoidal signal, using a function generator (Agilent 33220A) coupled to a voltage amplifier (B&K1040L). Proper triggering of the laser measurements allows full reconstruction of the out-of-plane velocity field. To show edge propagation only along the domain wall, absorbing patches have been used near the source and around the sample in Fig. 4.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/29/eaba8656/DC1