The causal influence of brain size on human intelligence: Evidence from within-family phenotypic associations and GWAS modeling

Abstract

There exists a moderate correlation between MRI-measured brain size and the general factor of IQ performance (g), but the question of whether the association reflects a theoretically important causal relationship or spurious confounding remains somewhat open. Previous small studies (n < 100) looking for the persistence of this correlation within families failed to find a tendency for the sibling with the larger brain to obtain a higher test score. We studied the within-family relationship between brain volume and intelligence in the much larger sample provided by the Human Connectome Project (n = 1,022) and found a highly significant correlation (disattenuated ρ = 0.18, p < .001). We replicated this result in the Minnesota Center for Twin and Family Research (n = 2,698), finding a highly significant within-family correlation between head circumference and intelligence (disattenuated ρ = 0.19, p < .001). We also employed novel methods of causal inference relying on summary statistics from genome-wide association studies (GWAS) of head size (n ≈ 10,000) and measures of cognition (257,000 < n < 767,000). Using bivariate LD Score regression, we found a genetic correlation between intracranial volume (ICV) and years of education (EduYears) of 0.41 (p < .001). Using the Latent Causal Variable method, we found a genetic causality proportion of 0.72 (p < .001); thus the genetic correlation arises from an asymmetric pattern, extending to sub-significant loci, of genetic variants associated with ICV also being associated with EduYears but many genetic variants associated with EduYears not being associated with ICV. This is the pattern of genetic results expected from a causal effect of brain size on intelligence. These findings give reason to take up the hypothesis that the dramatic increase in brain volume over the course of human evolution has been the result of natural selection favoring general intelligence.

0. General Introduction

People with bigger brains tend to be smarter. Furthermore, overall brain size is the only proxy for neural complexity that can be reliably obtained from fossils across a wide range of species and times, specifically from skull endocasts (Jerison, 1973). For these reasons overall brain size is perhaps the anatomical correlate of g that most interests researchers contemplating the long-term evolution of human intelligence (Burkart, Schubiger, & van Schaik, 2017). Among all such correlates, none that can be simply measured shows a consistently replicated correlation with IQ exceeding the ∼0.25 shown by brain size (Chabris, 2007; Pietschnig, Penke, Wicherts, Zeiler, & Voracek, 2015; Haier, 2017; Gignac & Bates, 2017). Furthermore, since brain volume has tripled during the most recent 3 million years of our evolutionary history (Holloway, 2008; Herculano-Houzel, 2016), the study of its relationship with g promises to shed light on the nature of the selective advantage that has propelled this remarkable change.

There continues to be some doubt, however, about whether it is justified to interpret this correlation in terms of brain size affecting intelligence (Nisbett et al., 2012). One powerful method of testing whether a correlation is the result of spurious confounding by other variables affecting the two focal traits is to see whether the correlation persists within reared-together sibling pairs (Jensen & Sinha, 1993; Turkheimer & Waldron, 2000; McGue, Osler, & Christensen, 2010; Beauchamp, Cesarini, Johannesson, Lindqvist, & Apicella, 2011; Lee, 2012). If the correlation does persist, then it cannot be attributable to aspects of the environment affecting both physical and mental development that are fixed for all siblings. Two previous studies taking this approach, each with a sample size of about 35 sibling pairs, failed to find a significant correlation (Schoenemann, Budinger, Sarich, & Wang, 2000; Gignac, Vernon, & Wickett, 2003).

We reexamined this empirical issue in a Human Connectome Project (HCP) (Van Essen et al., 2012; Van Essen et al., 2013) sample of 1,022 young adults, each of whom is a twin or ordinary sibling of another sample member. We also tested the significance of the within-family correlation between head circumference and IQ in an independent Minnesota Center for Twin and Family Research (MCTFR) (Miller et al., 2012) sample of 11-year-old children and 17-year-old adolescents (865 MZ and 484 DZ twin pairs); external measurements of the head provide a noisy proxy of underlying brain volume.

The presence or absence of a within-family association between brain size and intelligence is probably the most intuitively compelling observational data that can be brought to bear on the issue of a causal influence of the former trait on the latter. There are alternative explanations of the population correlation between these two traits, however, that cannot be eliminated by the finding of a significant within-family association. These are listed in Table 1.

Table 1:

Strengths and limitations of methods for causal inference.

	Ruled out by . . .
	WF	LDSC	LCV
Confounding by shared environment	Yes	Yes	No
Confounding by non-shared environment	No	Yes	No
Cross-assortative mating	Yes	No	No
Genetic pleiotropy	No	No	Yes
Reverse causation	No	No	Yes

Each row corresponds to an alternative explanation of the correlation between brain size and intelligence other than the former being a cause of the latter. “Yes” indicates that a positive result obtained with the method given in the column provides evidence against that alternative explanation. A simple yes- or-no answer is always given for the sake of simplicity; consult the text for more nuance. WF, within-family phenotypic association; LDSC, bivariate LD Score regression; LCV, Latent Causal Variable.

To weaken these alternatives to the hypothesis of a causal effect of brain size on intelligence, we turned to recently developed methods for interpreting data from genome-wide association studies (GWAS) (Gondro, van der Werf, & Hayes, 2013; Chabris, Lee, Cesarini, Benjamin, & Laibson, 2015; Lee, Vattikuti, & Chow, 2016). The first of these is bivariate LD Score regression, a method for estimating genetic correlations from GWAS data (Bulik-Sullivan et al., 2015a). Each trait can be regarded as the sum of a genetic and environmental term; if we imagine taking away the environmental part of each trait and calculating the correlation between whatever remains, we are left with a quantity called the genetic correlation (r_g) by quantitative geneticists (Lynch & Walsh, 1998). (The remaining genetic term is called the “breeding” or “additive genetic” value. This corresponds to the “A” in the ACE model of behavioral genetics.) Care must be taken to ensure that the estimate of the genetic correlation is not itself biased by environmental confounders affecting both traits, and bivariate LD Score regression contains a powerful safeguard against such confounding (Bulik-Sullivan et al., 2015a; Lee, McGue, Iacono, & Chow, 2018). An estimated genetic correlation that is significant and unbiased rules out the possibility of the total correlation being entirely the result of environmental confounders that can assume different values even within the same sibship. It is also consistent with a causal effect of one trait on the other, since genetic influences on the upstream trait must be propagated to the downstream one (Duffy & Martin, 1994; Minica, Dolan, Boomsma, de Geus, & Neale, 2018).

A significant genetic correlation is also consistent, however, with some of the alternative explanations in Table 1. One of these is a kind of genetic confounding known as pleiotropy: the same or correlated polymorphic sites in the genome affecting both traits without either trait affecting the other. Another possibility, perhaps an obvious one, is reverse causation: perhaps it is really the exercise of intelligence that affects brain size, through some form of plasticity.

The method that we employed to address these possibilities that can be understood in the following intuitive manner; see Fig. 1 for an illustration of the logic. Suppose that the variable X is brain size and Y is a measurement of intelligence. If X → Y is the case, then any genetic polymorphisms affecting X must also affect Y. Conversely, there may be many polymorphisms affecting Y through some non-X mechanism and therefore showing no effect on X (Pickrell et al., 2016; Visscher & Yang, 2016; O’Connor & Price, 2018). These predictions also hold, mutatis mutandis, if Y → X is the case. In contrast, genetic pleiotropy should lead to a rejection of both causal directions. We used the Latent Causal Variable (LCV) method to determine which of these three possibilities—one causal direction, the other causal direction, non-directed pleiotropy—offers the best approximation of the pattern inherent in GWAS summary statistics of head size and cognition.

Figure 1:

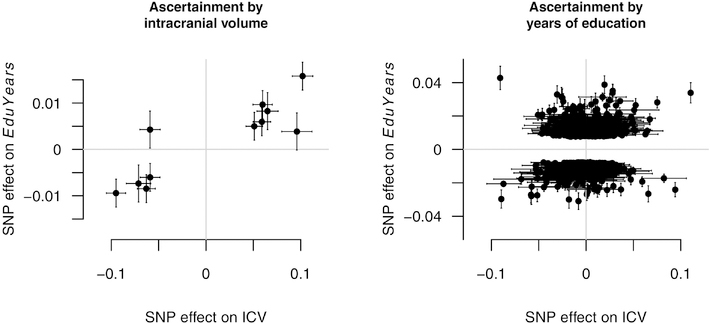
The nature of the causal relationship between brain volume and years of education inferred from the asymmetry of GWAS results. Each data point represents the effects of a single-nucleotide polymorphism (SNP) on intracranial volume (ICV) and years of education (EduYears) respectively, as estimated in genome-wide association studies (GWAS) of these two traits. The left panel displays 11 SNPs reaching genome-wide significance in the latest GWAS of ICV (Adams et al., 2016), whereas the right panel displays 1,044 SNPs reaching genome-wide significance in the latest EduYears GWAS (Lee et al., 2018) that are also found in the publicly available summary statistics of the ICV GWAS (Hibar et al., 2015). Both traits have been standardized. The error bars represent plus/minus 1 SE. In the right panel, ICV errors larger than 0.03 (about 5 percent of all SNPs) have been omitted for clarity.

1. Study 1: Within-Family Association Between IQ and Measures of Brain Size

1.1. Introduction

The common environment shared by all siblings growing up in the same home may conceivably affect both brain size and intelligence, accounting for the correlation between these two traits. A powerful means of ruling out this source of confounding is the calculation of the within-family association: does the sibling with the larger brain also tend to have the higher IQ?

It may be worthwhile to review the two earlier studies that have examined this question. Other studies have obtained relevant data, mostly from twins, but have not analyzed their data in this particular way.

Schoenemann et al. (2000) studied 36 pairs of sisters, administering a number of cognitive tests (including Raven’s Progressive Matrices and a vocabulary test) and acquiring the volumes of many different brain regions. The large number of cognitive and brain measures led to many correlations, but it probably suffices to report that they found a within-family correlation between total brain volume and the first principal component of their test battery equaling −0.05. This was despite a nominally significant between-family correlation (i.e., the correlation between sibship average brain volume and test score) of 0.45.

Gignac et al. (2003), performing additional analyses of data first presented by Wickett, Vernon, and Lee (2000), studied 32 pairs of brothers. They found a non-significant within-family correlation of 0.16 between total brain volume and IQ as assessed by the Multidimensional Aptitude Battery. The estimate of the between-family correlation, 0.31, was not significant either.

We cannot find any serious fault in either of these studies, other than that their samples of sibling pairs were far too small to draw any definitive conclusions. For example, in the case of a sample size equaling 36 and an estimated correlation −0.05, the upper endpoint of the 95% CI is 0.28. Clearly, even with results favoring the two-sided null hypothesis as closely as one might stipulate, a study of this size is incapable of ruling out theoretically significant values of the within-family correlation. In the current study, we were able to estimate the within-family correlation between MRI-measured brain volume and intelligence with more than 10 times as many families and thereby bring much greater statistical power to ruling out confounding by shared environment as the exclusive contributor to the population correction.

A significant within-family association would also rule out another source of confounding that does not easily fit into the framework of the General Introduction. The definition of the genetic correlation (Lynch & Walsh, 1998) includes contributions from cross-assortative mating, the tendency of individuals with a certain attribute to prefer mates with a certain other attribute (Jensen & Sinha, 1993; Redden & Allison, 2006; Keller et al., 2013). An example is the tendency of individuals with higher IQs to prefer mates who are taller. After many generations of such cross-assortative mating, a given genome tending to carry IQ-increasing alleles will also tend to carry height-increasing alleles at distinct sites, an example of long-distance linkage disequilibrium (LD). This mechanism does appear to contribute to the actual height-IQ genetic correlation (Keller et al., 2013).

It does not seem plausible that people find brain size per se to be attractive in potential partners, as opposed to the possible effects of brain size on psychological traits. This intuition can be given rigorous support by the finding of a significant within-family correlation between brain size and IQ (Jensen & Sinha, 1993; Beauchamp et al., 2011). Whereas under cross-assortative mating a given parent may tend to carry alleles increasing both traits, Mendelian independent assortment means that there will be no tendency for an offspring inheriting the allele increasing trait 1 at a site heterozygous in the parent to also inherit the allele increasing trait 2 at an unlinked site.

1.2. Methods

1.2.1. Human Connectome Project

Data from the Human Connectome Project (HCP) (Van Essen et al., 2013) was used as the primary analysis sample. Here, we included only families with at least two siblings. Some descriptive statistics of the HCP sample are given in the first column of Table S1; about 75 percent of the families in the HCP dataset are white. Details relating to participant selection and MRI acquisition have been reported (Van Essen et al., 2012). We chose to use total brain volume as the independent variable in our primary analysis.

We found that the mean and variance of total brain volume in the HCP differs substantially between the two sexes (Table S1). Males have both larger brains on average (d = 1.67) and greater variability (VR = 1.31). These differences are consistent with those observed in a recent study of a larger sample (Ritchie et al., 2018). For this reason we decided to standardize brain volume separately in each sex and use the resulting Z-score as the independent variable. We employed this standardization procedure in every robustness check.

Family “types” in the HCP are quite heterogeneous. For example, one family may consist of two MZ twins and their younger sibling. We included any family regardless of composition, so long as it contained at least two offspring with the same listed mother and father. In Table 2, the “MZ” subsample consisted solely of MZ twins. If an individual happens to be an MZ twin whose co-twin is absent from the dataset, that individual was not included in the MZ subsample. The “DZ” subsample was constructed similarly. The “non-twin” subsample consisted of all families that did not qualify for either the MZ or DZ subsample; for example, one such family might consists of two siblings—an MZ twin whose co-twin is missing and his older sibling. Thus, by construction, the three HCP subsamples listed in Table 2 below the total sample were non-overlapping.

Table 2:

Within-family associations between brain/head size and IQ.

Dataset	Families	Measure	β ± SE	ρ	p-value
HCP
All sibs	381	Brain volume	0.142 ± 0.040	0.18	4 × 10−4
MZ	138	Brain volume	0.175 ± 0.168	0.22	0.30
DZ	79	Brain volume	0.055 ± 0.109	0.07	0.61
Non-twins	161	Brain volume	0.162 ± 0.064	0.21	0.01
MCTFR
All sibs	1,349	Head circumference	0.172 ± 0.031	0.19	3 × 10−8
MZ 11 yr	642	Head circumference	0.150 ± 0.049	0.17	0.002
DZ 11 yr	363	Head circumference	0.219 ± 0.053	0.24	5 × 10−5
MZ 17 yr	223	Head circumference	−0.050 ± 0.086	−0.06	0.56
DZ 17 yr	121	Head circumference	0.209 ± 0.104	0.23	0.05

β is the estimated partial regression coefficient of brain/head size in a model predicting IQ with family fixed effects. Both size and IQ were standardized. “All sibs” means all families in the dataset, regardless of type (e.g., zygosity). Within each dataset, the rows beneath “All sibs” correspond to subsamples of the total sample. ρ, the partial regression coefficient (β) divided by the square root of the IQ test’s internal-consistency reliability.

We selected two of the tests administered to the HCP subjects as our measures of general intelligence (g). The first is called the Penn Progressive Matrices in the HCP Data Dictionary. This is an abbreviated 24-item version of Raven’s Standard Progressive Matrices; it is labeled “Non-Verbal IQ” in Table S1. The second is the NIH Toolbox Picture Vocabulary Test (age-adjusted scale score); it is labeled “Verbal IQ” in Table S1. The correlation between these two tests in the HCP data is 0.45, consistent with the g loadings of roughly 0.7 reported for these two types of test in the literature (Jensen, 2001; Johnson, Bouchard, Krueger, McGue, & Gottesman, 2004; Gignac, 2015). To construct our main dependent variable, we standardized each of these two tests separately, added the standardized scores, and finally standardized the sum. We found that this sum exhibits a sex difference of ∼0.3 favoring males. We applied another standardization, this time within each sex separately, to produce our final measure of g.

1.2.2. Minnesota Center for Twin and Family Research

The data are derived from the Minnesota Center for Twin and Family Research (MCTFR), including monozygotic (MZ) and same-sex dizygotic (DZ) twin pairs born in Minnesota. Some descriptive statistics of this sample are given in the final two columns of Table S1. Twin births from 1972 to 1984 were identified from Minnesota state birth records. Contact information was found for 91 percent of the families of these twins. Twins and their families were invited to a day-long assessment in a laboratory located in Minneapolis when the twins were approximately 11 or 17 years of age. Among invited families, 17 percent refused to participate. Over 95 percent of participating families were white. This sample is much simpler in structure than the HCP, in that each family for our purposes consists of two twins (either MZ or DZ).

Head circumference (HC) was measured with a metal tape run around the head immediately above the eyebrows and ears. Males and females had nearly identical means at age 11, but at age 17 males had a roughly 1-SD larger HC (Table S1). The female mean HC at age 11 was 98 percent of the female mean at age 17, and the male mean at age 11 was 95 percent of the male mean at age 17. Males and females did not show a substantial difference in variance at either age. We standardized HC within each combination of sex and age cohort.

Full-Scale IQ, Performance IQ (called “Non-Verbal IQ” in Table S1), and Verbal IQ were measured using abbreviated versions of the Wechsler Adult Intelligence Scale-Revised (WAIS-R) for the 17-year-old twins and the Wechsler Intelligence Scale for Children-Revised (WISC-R) for 11-year-old twins. The short forms consisted of two Verbal subtests (Information, Vocabulary) and two Performance subtests (Block Design, Picture Arrangement). We found the correlation between Verbal and Performance among the 11-year-old twins to be about 0.47, which seems somewhat low; given the loadings on g of the WAIS-R subtests calculated by Gignac (2005), we might expect the correlation to exceed 0.65. Among the 17-year-old twins, the correlation is only 0.28. We do not have an explanation for the small magnitude of this estimated correlation, although it should be kept in mind that its standard error is relatively large. We converted IQ from its conventional scale (M = 100, SD = 15) to the standardized scale with mean zero and unit variance.

Our dataset largely overlaps with that of Silventoinen, Iacono, Krueger, and McGue (2012), who reported a significant positive genetic correlation between head circumference and IQ. Here we calculated not the genetic correlation but rather the within-family correlation. It should be understood that these two quantities do not necessarily provide the same information (Beauchamp et al., 2011). For instance, positive correlations between genomic sites affecting two distinct traits as a result of cross-assortative mating contribute to the genetic correlation, but not to the within-family correlation (Table 1).

1.2.3. Data analysis

We introduced dummies for family membership to estimate the within-family association between our measures of brain size and intelligence. All members of a given family were required to share the same mother and father. In the case of two siblings per family, the procedure that we followed—i.e., the regression of intelligence on brain size with family-membership dummies as covariates—is equivalent to the regression of the sibling difference in intelligence on the sibling difference in brain size. In our case the use of dummies is more efficient because many HCP families have more than two siblings.

We included the first three powers of mean-centered age as covariates whenever appropriate. There are no opposite-sex twins in any of our cohorts; in twin-only analyses, we dropped the age covariates. As a robustness check, we re-estimated the regression models with the first three powers of standardized height and weight as additional covariates. See the Supplemental Material for justification of these procedures.

The partial regression coefficients of brain/head size in the prediction of IQ are given in the “β ± SE” column of Table 2. Since both independent and dependent variables were standardized, these coefficients should be somewhat comparable to correlations reported in previous studies.

A correlation of 0.45 between the two indicators of g in the HCP leads to an estimated internal-consistency reliability of the IQ composite equaling 0.62; reliabilities exceeding 0.9 are possible with a higher-quality battery of tests (Brunner, Nagy, & Wilhelm, 2012). Because psychometric quality appears to have a substantial impact on reported estimates of the correlation between brain size and intelligence (Gignac & Bates, 2017), it may be advisable to apply the disattenuation procedure of classical test theory (Lord & Novick, 1968; McDonald, 1999). We corrected the coefficients for unreliability of the IQ measure using the formula β/√ω_h, where β is the coefficient to be disattenuated and ω_h is McDonald’s hierarchical coefficient omega (Zinbarg, Yovel, Revelle, & McDonald, 2006). In the case of a non-standardized dependent variable, one need not correct regression coefficients for unreliability of the dependent variable because zero-mean noise does not change the conditional expectation of the dependent variable given the independent variable. However, in our case of a standardized dependent variable where both true scores and errors contribute to the variance, such a correction is justified.

The IQ battery used in the MCTFR has excellent norming data. The g loadings of the WAIS-R subtests calculated by Gignac (2005) on the basis of these data suggest that the internal-consistency reliability of the abbreviated Full-Scale IQ in the MCTFR is 0.82, according to the formula for McDonald’s coefficient omega. For reasons that are unclear, the correlation between Verbal and Performance observed in the MCTFR does not seem consistent with such high reliability. We nevertheless used a conservative value of 0.82 in calculating the disattenuated associations; the assumption of a lower value would lead to larger apparent effects.

A correction for unreliability using McDonald’s hierarchical coefficient omega assumes that it is the common factor, g, rather than group or test-specific factors, that is responsible for the correlation with brain size. Previous results already make this assumption a reasonable one (MacLullich et al., 2002; Kievit et al., 2012; Gignac & Bates, 2017). To confirm it in our own data, we looked at the within-family correlation between brain/head size and each subtest in our IQ composites.

The equality of the within-family coefficient across sibship types (MZ, DZ, non-twin full sibling) is not only compatible with a causal relationship between brain volume and intelligence but in fact is predicted by such a relationship in the absence of confounding by genetic pleiotropy or non-shared environment (McGue et al., 2010; Frisell, Öberg, Kuja-Halkola, & Sjölander, 2012). That is, if brain size affecting intelligence is the only reason for the correlation between these variables, then any given difference between siblings in brain size—even if induced environmentally (which is the only possibility in an MZ pair)—is expected to produce the same difference between them in g. To test whether the equality of the relationship holds across sibship types, we re-estimated the regression model with family fixed effects in the non-overlapping samples of MZ twins only, DZ twins only, and non-twin siblings only. We then tested whether any difference between estimates is significantly different from zero.

1.3. Results

1.3.1. Human Connectome Project

The overall correlation between MRI-measured brain volume and IQ is 0.26 (0.33 upon correction for unreliability), in line with previous research (Pietschnig et al., 2015; Haier, 2017; Gignac & Bates, 2017). In the case of brain volume, the MZ and DZ intraclass correlations are 0.96 (CI95%: 0.94, 0.97) and 0.74 (CI95%: 0.62, 0.82) respectively; IQ, 0.74 (CI95%: 0.65, 0.80) and 0.57 (CI95% CI: 0.39, 0.70). Both MZ correlations are larger than their DZ counterparts, as expected in the case of a heritable trait.

The results of the within-family analysis are given in Table 2. In a model controlling for family background, the partial regression coefficient of brain volume is 0.142 standardized units of IQ per standardized unit of brain volume (CI95%: 0.062, 0.222; p < .001). A correction for unreliability brings this to 0.18. The upper endpoint of the CI95% becomes 0.28 upon disattenuation, and this may be consistent with the equality of the within-family and population correlations. It should be kept in mind, however, that the exact upper endpoint bounding the disattenuated correlation is uncertain as a result of quantities such as the internal-consistency reliability being estimated rather than known.

As can be seen in Table S2, the within-family correlation is also significant when the dependent variable is either the vocabulary or matrix-reasoning component of the IQ composite (both p < .05). This supports the correlation being with the general factor g rather than any test-specific factor.

No difference between subsample coefficients in the HCP is significant (Table 2), although the statistical power to find any difference is poor. If a given difference between siblings in brain volume were truly associated with the same difference in IQ, regardless of how the siblings are related, this would be powerful evidence for our postulated causal relation.

A number of robustness checks affirmed the conclusions above. Upon excluding the non-whites and re-estimating the regression model with the same specification, we obtained a very similar result (β = 0.130, p < .005). We also re-estimated the regression model with the first three powers of standardized height and weight as additional covariates (Table S3). The result is nearly unchanged (β = 0.124, p < .005).

1.3.2. Minnesota Center for Twin and Family Research

As can be seen in Table 2, we found a significant within-family correlation between HC and IQ (p < 10⁻⁷). This replicates two earlier studies (Jensen & Johnson, 1994; Jensen, 1994) and improves upon them, in that one of these studies was small (143 pairs) and the other only examined children no older than 7 years. In the age-17 cohort, the DZ within-family coefficient is almost significantly larger than the MZ (p = .055). If this were a reliable difference, it would provide evidence for the presence of confounding in addition to our hypothesized causal relation, perhaps attributable to pleiotropic influences on HC and IQ (Silventoinen et al., 2012). Our inclination, however, is to treat this difference as a chance fluctuation. By contrast, in the age-11 cohort, the MZ within-family correlation between HC and IQ is very significant (p < .005) and not distinguishable in magnitude from the DZ within-family correlation.

Overall, then, the body of results in Table 2 is roughly consistent with the hypothesis of brain size (measured by its proxy HC) affecting intelligence. The disattenuated coefficient of 0.19 is again consistent with the equality of the within-family and population correlations. It happens that our sample individual-level correlation is 0.15.

Table S2 shows that the within-family correlations of HC with both Verbal and Performance IQ are also significant (p < .001), supporting a correlation of head size with g rather than any group or test-specific factor.

Upon inclusion of the first three powers of standardized and weight as covariates, the coefficient of HC becomes slightly smaller but remains highly significant (β = 0.148, p < 10⁻⁴).

1.4. Discussion

In two datasets we found positive and very robustly significant estimates of the within-family association between brain size and intelligence. Regardless of how brain size was measured, the type of IQ test, the composition of the sample, and choice of covariates, we did not discern any meaningful difference in the within-family association. These results provide strong evidence against the population correlation between brain size and intelligence being entirely the result of cross-assortative mating, confounding by the common environment shared by children in the same home, or some combination of these two mechanisms. Note that there remain theoretically viable alternative explanations of the population correlation (Table 1), and it is the purpose of Study 2 to address these.

The more specific finding of a significant within-MZ correlation would further bolster the case for brain size affecting IQ. Additionally, the within-MZ coefficient must be equal to the other within-family coefficients to affirm that pleiotropic genetic confounding and non-shared environment make no contribution. As can be seen in Table 2, the evidence for these propositions is tentative. This must be regarded as a limitation of Study 1. It is evident that there is some value in collecting samples of twins and siblings even larger than those we have relied upon here. Such samples would be able to estimate the overall within-family correlation much more precisely. Our disattenuated estimate of 0.18 on the basis of the HCP data qualifies as a relatively small effect size according to the guidelines of Gignac and Szodorai (2016), but the confidence interval extends upward to values that would qualify as typical. The reduction of this uncertainty may be worthwhile. Note that since many within-family correlations are smaller than their population counterparts, the guidelines of Gignac and Szodorai (2016) should be considered conservative.

2. Study 2: Causal Inference Based on GWAS Data

2.1. Introduction

The calculations of the within-family correlation between IQ and brain/head size in Study 1 required phenotypic data only. In Study 2 we tested the causal status of the relationship by using recently developed methods for interpreting data from genome-wide association studies (GWAS), which are capable of ruling out the additional alternative explanations of reverse causation, a non-directed genetic overlap (pleiotropy), and confounding by non-shared environment (Table 1).

There have been many twin studies reporting a positive genetic correlation between brain size and IQ (Pennington et al., 2000; Posthuma et al., 2002; van Leeuwen et al., 2009; Betjemann et al., 2010; Silventoinen et al., 2012). There is nevertheless great value in estimates based on the alternative data source provided by GWAS, especially since the GWAS-based technique of bivariate LD Score regression deals with confounding in a manner that appears quite different from the twin method and its equal-environment assumption. Recall that a significant and unbiased estimate of the genetic correlation rules out environmental confounding, whether by shared or non-shared factors, as the sole explanation of the phenotypic correlation.

A genetic correlation by itself is consistent with both reverse causation and pleiotropic confounding. We therefore turned to another method, also based on GWAS data, that bears on the issue of causality. If genetic variation affecting X is propagated to Y in the simple causal chain G → X → Y, then any parts of G identified in GWAS of X must also show concordant effects on Y. Furthermore, the effects of these GWAS-identified single-nucleotide polymorphisms (SNPs) on Y must be proportional to their effects on X. In contrast, there may be many SNPs affecting Y through some non-X mechanism, and GWAS of Y should therefore detect many SNPs with no discernible effects on X. To follow this logic, it may be helpful to consult Fig. 1.

Actual empirical results are not likely to conform exactly to these simple predictions even under the most favorable conditions. It is easy to imagine that there are parts of the brain, perhaps subcortical, whose sizes could hypothetically be altered in a manner increasing the brain’s overall volume without affecting higher cognition (Jerison, 1973; Jung & Haier, 2007). The portion of the brain serving as the substrate of cognition would then act effectively as a confounder, its size sending causal arrows to both overall brain size and intelligence. Nevertheless, we attempted to determine the extent to which the predictions from the simple G → X → Y model are borne out by GWAS data.

2.2. Methods

2.2.1. Bivariate LD Score regression

Here we present estimates of relevant genetic correlations between measures of head size and cognition, updated from previous GWAS reports to reflect increases in sample size (Okbay et al., 2016; Hagenaars et al., 2016; Sniekers et al., 2017). We used bivariate LD Score regression (Bulik-Sullivan et al., 2015b; Bulik-Sullivan et al., 2015a; Lee et al., 2018), as implemented in the LCV software tool (O’Connor & Price, 2018). If there is a tendency for a SNP with a relatively large effect on one trait to also show a relatively large effect of the same sign on the other, then this method will return a positive estimate of the genetic correlation. An attractive feature of LD Score regression is that its means of controlling the influence of confounding variables extends not just to the evidence of association at individual SNPs but also to its genome-wide estimates of genetic correlations; ideally, the regression intercepts absorb all confounding, including the effects of environmental variables correlated with genetic variation that happen to affect both traits. The Supplemental Material discusses this point in more detail.

Whereas a positive result obtained by LD Score regression does provide evidence against environmental confounding, such a result does not bear on environmental mediators of genetic influence, including mediators conveying a causal influence in the direction opposite of what we are hypothesizing. For example, there may be genetic influences on intelligence or intellectual curiosity that lead to more educational attainment, which may then increase brain size through a plasticity-based mechanism. Such possibilities can be addressed not by LD Score regression itself but rather the LCV method, which will be described shortly in 2.2.2.

We obtained the GWAS summary statistics of EduYears, IQ, and infant head circumference from the websites of the consortia that conducted these GWAS (Taal et al., 2012; Okbay et al., 2016; Lee et al., 2018). The GWAS summary statistics of adult intracranial volume can be obtained by contacting the ENIGMA Consortium (Hibar et al., 2015). We ran bivariate LD Score regression, as implemented in the LCV software (downloaded July 3, 2018) (O’Connor & Price, 2018). We used all recommended default settings. One recommendation is to remove all SNPs in the MHC region, but to our knowledge the LCV developers do not provide a definition of this region. We adopted the definition used by the DEPICT bioinformatics tool of all SNPs on chromosome 6 between positions 25,000,000 and 35,000,000 (Pers et al., 2015).

As measures of intelligence, we examined both years of education (EduYears) and IQ. We designated EduYears as our primary measure because the attainable GWAS sample size for EduYears is currently larger than that for IQ. Previous studies have found a high genetic correlation (∼0.7) between IQ and EduYears, and the top SNPs identified in the respective GWAS of these traits show very strong concordance. Our two measures of brain size are adult intracranial volume (ICV) (Hibar et al., 2015) and infant head circumference (HC) (Taal et al., 2012). ICV is an excellent proxy for brain volume with the advantage that it does not decline sharply with age (Davis & Wright, 1977); thus, any correlation with intelligence cannot be explained by the effects of neural atrophy on cognitive decline. According to bivariate LD Score regression, adult ICV and infant HC show a genetic correlation of 0.75 (Adams et al., 2016).

The samples for IQ and EduYears consist of the cohorts studied in the largest published GWAS of EduYears at the time of writing with the exception of 23andMe (Lee et al., 2018). The EduYears sample size is ∼760,000, reflecting a net increase of ∼465,000 since the last reported calculation of the ICV-EduYears genetic correlation. The sample size for IQ is ∼260,000. The sample sizes for adult ICV and infant HC, 11,373 and 10,678 respectively, are unchanged since their GWAS were published. There has been a more recent and larger GWAS of ICV (Adams et al., 2016), but its full summary statistics are not publicly available.

It is possible to estimate the genetic correlations between measures of brain size and cognition using twin data, of the kind that we employed in Study 1, rather than GWAS summary statistics. Our HCP dataset contains too few twins, however, to produce a reliable estimate of the genetic correlation. As we stated earlier, the twins in the MCTFR have already been used to estimate the genetic correlation between IQ and HC (Silventoinen et al., 2012).

Another method for estimating genetic correlations is the genomic relatedness restricted maximum-likelihood (GREML) method (Lee, Yang, Goddard, Visscher, & Wray, 2012), which has been used in many applications, including a study showing that both twin analyses and GREML produce similarly large estimates of the genetic correlations between different mental tests (Trzaskowski et al., 2013). We discuss the data requirements and assumptions of LD Score regression and GREML respectively in the Supplemental Material.

2.2.2. Latent Causal Variable

The most recent GWAS of intracranial volume reported seven genome-wide significant SNPs in its Table 1 (Adams et al., 2016). We included the four additional SNPs in Supplementary Table S9 of this paper that were found to reach genome-wide significance upon a meta-analysis of both adult intracranial volume and infant head circumference. These are the 11 SNPs plotted in the left panel of our Fig. 1. One of these SNPs, rs138074335, has changed its identifier and is not present in the summary statistics of Lee et al. (2018). We took its association statistics from the summary file of Okbay et al. (2016).

Eleven genome-wide significant SNPs does not provide enough power to make use of the testing framework proposed by Pickrell et al. (2016) for the data plotted in Fig. 1. We therefore turned to LCV, a recently developed method that overcomes the limitation of insufficient significant SNPs by using genome-wide summary statistics and additionally addresses the problem of the candidate causal variable X being a proxy affected by residual genetic variation (O’Connor & Price, 2018). The Supplemental Material contains an extensive discussion of the LCV method, providing intuitive explanations on top of those here in the main text and comparing it in great depth with a distinct class of methods (Mendelian randomization) for drawing causal inferences from GWAS data. The output of LCVis the genetic causality proportion (GCP), which ranges in possible value from −1 to +1. A value of zero means that the genetic correlation is entirely attributable to undirected pleiotropy; a value of +1 means that all genetic variation affecting X is propagated to Y in a perfect causal chain; a value of −1 means that it is actually Y affecting X. The developers suggest |GCP| > 0.6 as a cutoff for considering the relationship between the two traits to approximate a causal one reasonably well.

To be clear, Fig. 1 does not depict the results of our main analysis relying on LCV. It depicts the data that would be used in the method of Pickrell et al. (2016), which has been generalized and made more robust by LCV. Fig. 1 is nevertheless useful for illustrating the intuition behind the LCV method and suggesting the pattern in the genome-wide summary statistics that drives our positive results.

The LD Score regression slope Z-statistic of ICV is roughly 4, which falls short of the threshold of 7 recommended by the LCV developers. The Supplemental Material explains the rationale behind this recommendation. Therefore, as a robustness check, we meta-analyzed ICV and HC with PLINK 1.9 (Chang et al., 2015) and used the resulting ICV + HC trait with an effectively twofold sample size as the candidate causal variable in LCV. Recall that the genetic correlation between ICV and HC is high; both measures of brain size are in turn genetically correlated with IQ (Sniekers et al., 2017; Savage et al., 2018).

2.3. Results

2.3.1. Genetic correlations between head size and measures of cognition estimated by bivariate LD Score regression

As can be seen in Table 3, IQ shows a significant genetic correlation with adult ICV (r_g = 0.29, SE = 0.11), as does EduYears (r_g = 0.41, SE = 0.08). These estimates are fully consistent with previous DNA-level studies, one of which used largely overlapping data to study IQ (Savage et al., 2018). The estimates are also consistent with previous twin studies. To give just one example, the HC-IQ genetic correlations based on the MCTFR (one of the datasets in Study 1) are 0.32 in the 11-year-old boys (CI95%: 0.14, 0.50), 0.28 in the 11-year-old girls (CI95%: 013, 0.46), 0.25 in the 17-year-old boys (CI95%: 0.10, 0.42), and 0.17 in the 17-year-old girls (CI95%: 0.04, 0.30) (Silventoinen et al., 2012).

Table 3:

Genetic correlations and genetic causality proportions.

Traits	rg ± SE	GCP ± SE
Intracranial volume
IQ	0.291 ± 0.107	0.746 ± 0.146
EduYears	0.411 ± 0.077	0.721 ± 0.174
ICV + HC
IQ	0.306 ± 0.083	0.495 ± 0.137
EduYears	0.353 ± 0.064	0.450 ± 0.136

r_g, the genetic correlation estimated by bivariate LD Score regression between the measures of head size (Taal et al., 2012; Hibar et al., 2015) and cognition (Lee et al., 2018); GCP, the genetic causality proportion, which ranges between zero (genetic variation acts purely as a confounder X ← G → Y ) and one (joint genetic influences act purely through the causal chain G → X → Y ); ICV + HC, GWAS meta-analysis of adult intracranial volume and infant head circumference.

2.3.2. Causal inference from asymmetry of GWAS results

The effects of the top SNPs identified in GWAS of ICV and EduYears respectively are displayed in Fig. 1. Note that we use the term “effect” loosely, because the SNPs plotted in Fig. 1 may not be causal themselves but in LD with the actual causal sites (Lee & Chow, 2013). The left panel displays the 11 genome-wide significant SNPs identified in the largest GWAS of ICV (Adams et al., 2016). Since we can be highly confident that these SNPs are associated with brain size, a causal effect of brain size on intelligence implies the tight clustering of the data points around a straight line. The right panel displays the 1,044 genome-wide significant SNPs identified in the largest GWAS of EduYears (Lee et al., 2018) that are also contained in the ICV summary statistics. We can be highly confident that these SNPs are associated with EduYears, but the complement of the subset acting through brain size should show no association with ICV.

Ten of the 11 SNPs associated with ICV show concordant effects on EduYears (signtest one-sided p < .01). Of the 10 concordant SNPs, the associations of 9 with EduYears are nominally significant (all p < .05). In contrast, only 592 of the 1,044 SNPs as-certained through the GWAS of EduYears show concordant associations with ICV (57 percent, sign-test one-sided p < 10⁻⁵). The Spearman correlation between effect sizes is 0.83 when ascertainment is by ICV, whereas it is only 0.17 when ascertainment is by EduYears. Qualitatively, then, this pattern is consistent with a causal effect of brain size on intelligence.

To determine whether the pattern evident in Fig. 1 extents to the entire genome, including sub-significant SNPs, we applied LCV to the complete GWAS summary statistics of our traits. The results can be found in Table 3. When the candidate causal variable is ICV, the estimated values of GCP exceeding 0.7 are very significantly different from zero (both p < 10⁻⁴ on the assumption of a normal sampling distribution). The LCV developers consider GCP > 0.6 to be indicative of a good approximation to a causal relationship between the two variables. In fact, for neither EduYears nor IQ can we reject the hypothesis GCP = 1 (both p > 0.15).

In our setting, the LCV model is consistent with an appealing interpretation. Suppose that only a portion of the brain affects intelligence. Upon standardization of all breeding (additive genetic) values, the breeding value of the intelligence-supporting part of the brain has an effect on the ICV breeding value equaling 0.884 and an effect on the EduYears breeding value equaling 0.467. These two path coefficients reproduce the values of r_g and GCP given in Table 3 for ICV and EduYears. Thus it may be reasonable to treat a measure like ICV as the actual causal variable affecting intelligence—despite the likely existence of brain regions unrelated to higher cognition function (Jerison, 1973; Jung & Haier, 2007)—because genetic influences uniquely affecting such regions are comparatively slight.

As a robustness check, we meta-analyzed adult ICV and infant HC and used the resulting GWAS summary statistics as input to the LCV method. This use of ICV + HC as the outcome variable led to GCP estimates between 0.45 and 0.50 (Table 3). An effect of the intelligence-supporting portion of the brain on ICV + HC equaling 0.753 and on EduYears equaling 0.472 reproduces the relevant values of r_g and GCP, although the interpretation of the variable ICV + HC is admittedly unclear.

A potential limitation of Study 2 is that the relevant intercepts in bivariate LD Score regression may not adequately reflect the degree of confounding in the GWAS if the cohorts were sampled from different latitudes in Europe along a cline in average intelligence; the Supplemental Material further discusses this possibility. As another robustness check, we reran the LCV software with the GWAS summary statistics of EduYears taken this time, not from Lee et al. (2018), but from a single large cohort (the UK Biobank) analyzed with a linear mixed model to address confounding and other biases (Loh, Kichaev, Gazal, Schoech, & Price, 2018). We obtained very similar results (r_g = 0.43, SE = 0.08; GCP = 0.78, SE = 0.15), indicating that confounding is indeed unlikely to be seriously biasing our inferences.

2.4. Discussion

Applying bivariate LD Score regression to GWAS summary statistics, we found significant genetic correlations between measures of head size and cognition whose magnitudes agree well with those obtained in twin studies. This agreement across methods suggests that each provides a reasonably accurate estimate of this key quantity and thus can be relied upon to rule out confounding by non-heritable environmental factors as the sole contributor to the total phenotypic correlation.

A nonzero genetic correlation by itself is silent about whether the relationship between the two traits is causal and the direction of the causal influence. To make the further causal inference, we turned to the LCV method, which generalizes the logic illustrated in Fig. 1: if G → X → Y is the case, then those parts of G identified in GWAS of X must show concordant and proportional associations in GWAS of Y, whereas the top signals in GWAS of Y may often affect Y through non-X mechanisms and thus show no association with X. We obtained estimates of the genetic causality proportion exceeding 0.7, which can be interpreted as ICV being an effective proxy for those parts of the brain where size affects intelligence. We obtained a smaller estimate when meta-analyzing ICV and HC as a robustness check, which perhaps implies that HC measured in infancy is a noisier proxy for the sizes of the relevant brain regions. Further precision will come with increasing the GWAS sample size for three-dimensional measures of brain size, which certainly seems likely to occur; there are currently plans to acquire high-quality imaging data of many different organs in the UK Biobank.

The novelty of the LCV method should be kept in mind. Other ingenious methods in statistical genetics have often disclosed non-obvious intricacies only years after their introduction (Speed, Hemani, Johnson, & Balding, 2012; Lee & Chow, 2014; Lee et al., 2018; Berg et al., 2018), although it is notable how robust these methods remain even after they have become better understood. The Supplemental Material summarizes at some length the simulation studies conducted by the LCV developers, but it is hard to know whether a given set of simulations covers all plausible states of nature. This is an issue worth following as research unfolds. Right now, what we can say is that the LCV method is a generalization of the notions associated with Fig. 1 and thus appears to rest on a solid basis (Pickrell et al., 2016; Visscher & Yang, 2016).

3. General Discussion

Altogether, the results of Studies 1 and 2 provide a compelling case for brain volume (or the volumes of certain brain regions) affecting intelligence within the human species. Study 1 found that the sibling with a larger MRI-measured brain volume (or externally measured head circumference) tends to have the higher level of g. Study 2 found that SNPs in the human genome that are associated with intracranial volume also tend to be associated with both years of education and IQ; furthermore, whereas the effect of a SNP on intracranial volume is strongly predictive of its effect on intelligence, there appear to be many SNPs associated with intelligence that have no appreciable effect on intracranial volume.

We now discuss the relevance of these empirical findings to the notion of brain size affecting intelligence.

3.1. Significant within-family correlation is evidence against confounding by shared environment and cross-assortative mating

A detailed consideration of the within-family correlation leads to many theoretical arcana, but the basic notion is simple and compelling: if there is a significant within-family correlation, then the correlation observed in the population at large cannot be wholly ascribed to confounding variables that assume the same value for siblings growing up together. Despite the abundance and variety of the existing evidence, the failure to observe a significant correlation between MRI-measured brain volume and IQ in the few within-family studies reporting this estimate has been perhaps the weightiest point against accepting a nontrivial causal relationship between these two variables (Nisbett et al., 2012).

Here we have examined the within-family correlation in a sample consisting of more than 10 times as many families as those used in either of the two previous studies and obtained a significant result. We supplemented this finding with a calculation of the within-family correlation between IQ and head circumference, which is a noisier proxy for brain volume but is available to us in a much larger sample of twin pairs. We found this correlation to be significant as well.

3.2. Significant genetic correlation estimated by bivariate LD Score regression is evidence against exclusive confounding by non-shared environment

A within-family correlation might still be attributed to environmental confounders that can vary even within the same household (Frisell et al., 2012). We ruled out this kind of confounding as the sole explanation of the correlation between brain size and intelligence by replicating the genetic correlation between head size and two distinct measures of cognition. For this purpose we used bivariate LD Score regression, a powerful method that guards against environmental confounders affecting the two traits whose genetic correlation is to be calculated.

The sensitivity of this method to cross-assortative mating and other evolutionary forces inducing long-range LD between a site affecting trait 1 and a distant site affecting trait 2 is an interesting question that we did not consider here (although for the sake of simplicity Table 1 states that a positive result from bivariate LD Score regression does not provide evidence against this possibility). A within-family correlation between two highly polygenic traits, however, is very unlikely to be the result of long-range LD.

3.3. Significant LCV estimate is evidence against genetic pleiotropy and reverse causation

After ruling out the ascription of the entire correlation between brain size and intelligence to the combination of family background, non-shared environment, and cross-assortative mating, we are still left with the possibility of pleiotropic confounding—the same genetic polymorphisms affecting the two traits, without one trait affecting the other. We acknowledge that pleiotropy must, strictly speaking, be favored a priori as the explanation of the correlation over a directed causal relationship, if for no other reason than the plausible existence of brain regions that do not subserve higher cognitive functions (Jerison, 1973; Jung & Haier, 2007).

On the other hand, there is good reason to think that overall brain size acting as a cause of intelligence could prove to be an extremely useful approximation. Nearly 80 percent of the human brain by volume is taken up by the cerebral cortex (Swanson, 1995), the seat of memory, attention, thought, and language. Furthermore, there are strong individual-level correlations (both genetic and overall phenotypic) between the volumes of different regions within our own species (Rentería et al., 2014). The means available to nature of adjusting one brain region often act on functionally distinct regions as well. If overall brain size is as good a proxy for the sizes of the cognition-supporting regions as suggested by these considerations, then we are well justified in testing the (near) validity of strong hypotheses that fix measures of overall size as causally upstream of intelligence.

Examples of such strong hypotheses include the equality of the within-family regression coefficient across sibship types and a perfectly linear relationship between GWAS effect sizes upon ascertainment of SNPs whose associations with the measure of brain size reach genome-wide statistical significance. Although the first hypothesis was not clearly borne out in the sibling analysis of Study 1, both the data plotted in Fig. 1 and the results of applying the LCV method do support the approximate validity of the second hypothesis. Furthermore, they provide a nearly definitive refutation of reverse causation. The right panel of Fig. 1 seems to reveal hundreds of SNPs with significant effects on EduYears having no effect on intracranial volume, and the formal LCV results back up this impression by providing overwhelming statistical evidence against GCP = −1 (perfect causal chain) and the developer-recommended cutoff of GCP = −0.6 (reasonable approximation of causal chain). This conclusion agrees with that of van Leeuwen et al. (2009), who argued against reverse causation on the grounds that the high heritability of brain volume is evidence against the propagation of environmental influences on intelligence to brain volume.

3.4. Limitations

We have pointed to limitations of each study in its own Discussion section. Here we mention a limitation common to both studies—the low reliability with which g was often measured (Gignac & Bates, 2017).

In Study 1’s HCP dataset, we chose only two subtests as indicators of g for reasons of content validity and consequently suffered from an internal-consistency reliability of roughly 0.6. Similarly, the largest cohort contributing to the GWAS meta-analysis of IQ in Study 2 was assessed with an IQ test containing only a dozen items (Lee et al., 2018); the hierarchical coefficient omega of this test may well be less than 0.6. The relatively low reliability of the HCP test probably led to a diminution of the within-family correlation, although we tried to account for this with corrections based on classical test theory. It is tempting to think that the genetic correlation is not susceptible to unreliability because the greater error variance is simply part of the environmental term wiped away in the definition of this quantity. But care must be taken with such reasoning in genetic studies of behavioral traits (Chabris et al., 2013). Psychometric errors of measurement may in fact represent stable and heritable attributes that are not affected by brain size, and thus even the estimates in Table 3 may increase with greater reliability. Highly reliable measurements of psychological traits are typically difficult to obtain in large studies where any given research goal is incidental, but their acquisition should remain a priority of differential psychologists involved in such projects.

3.5. Wider implications of brain size affecting intelligence in humans

We think that alternative explanations of the correlation between brain size and intelligence have been sufficiently weakened to justify some tentative remarks about what deeper meaning a causal relationship might hold.

We can imagine a brain becoming larger by either increasing the sizes of its neurons or adding more of them. The number of neurons is probably the more promising focus of theoretical and empirical inquiry, for reasons that we now explain.

It is a well-known paradox that humans are certainly the most cognitively advanced species but nevertheless show a smaller average brain size, by weight or volume, than elephants and whales. One attempt at a resolution of this paradox invoked the encephalization quotient (EQ), a measure of brain mass normalized essentially by body mass (Jerison, 1973). Many researchers found EQ appealing because it served well to distinguish humans from other species, but this measure turns not to provide an acceptable rank order of other species (Deaner, Isler, Burkart, & van Schaik, 2007; MacLean et al., 2014); for example, monkeys are more encephalized than the undoubtedly intelligent great apes (Deaner, van Schaik, & Johnson, 2006). Furthermore, the notion of an EQ may not be applicable to individual differences within the human species, for both birds and mammals exhibit within-species brain-body scaling that is weaker and more variable than in other vertebrates (Tsuboi et al., 2018).

The more likely resolution of this paradox is that whereas average neuron size increases along with average neuron number in most taxa, this relationship has been abolished in primates, where neuron size remains fairly constant across a wide range of neuron number (Herculano-Houzel, Manger, & Kaas, 2014). Some large-bodied representatives of non-primate taxa thus have more voluminous brains than humans merely because their neurons are larger. The relevance of a neuron’s size to its function is unclear; the number of synapses per neuron, a critical computational attribute, varies very weakly with neuron size across species (Wang, Ambrosini, & Wittenberg, 2016). When the average number of cortical neurons is the measure of size, then humans are by far the top-ranked species (Herculano-Houzel, Catania, Manger, & Kaas, 2015), followed in an intuitive order by other species (Herculano-Houzel, 2016). It therefore seems reasonable to infer that our intraspecific variation in neuron number is causally antecedent to g. This inference is compatible with the implication of genes and pathways associated with the regulation of neurogenesis in the GWAS of EduYears (Okbay et al., 2016; Lee et al., 2018), and it may be possible to add to the coherence of these findings by partitioning the genetic covariance between brain size and intelligence between subsets of the genome with different functional annotations (Lu et al., 2017; Ni, Moser, Schizophrenia Working Group of the Psychiatric Genomics Consortium, Wray, & Lee, 2018).

By positing that neuron number is a cause of g because the human brain has evolved more neurons than that of any other species, we have relied on the assumption that the average level of g in our lineage has increased over the last several million years as a result of evolution by natural selection (Burkart et al., 2017; Lee & Chabris, 2017). Genetic data may soon show whether this assumption is empirically well founded.

• Among offspring of the same parents, the sibling with the greater MRI-measured brain volume (or externally measured head circumference) tends to have the higher IQ.

• GWAS summary statistics show that genetic influences on head size and cognition overlap substantially.

• According to the Latent Causal Variable method, the genetic overlap between intracranial volume and years of education (or IQ) is largely consistent with a causal effect of the former on the latter.