Asymptotic properties of principal component analysis and shrinkage-bias adjustment under the generalized spiked population model

Abstract

With the development of high-throughput technologies, principal component analysis (PCA) in the high-dimensional regime is of great interest. Most of the existing theoretical and methodological results for high-dimensional PCA are based on the spiked population model in which all the population eigenvalues are equal except for a few large ones. Due to the presence of local correlation among features, however, this assumption may not be satisfied in many real-world datasets. To address this issue, we investigate the asymptotic behavior of PCA under the generalized spiked population model. Based on our theoretical results, we propose a series of methods for the consistent estimation of population eigenvalues, angles between the sample and population eigenvectors, correlation coefficients between the sample and population principal component (PC) scores, and the shrinkage bias adjustment for the predicted PC scores. Using numerical experiments and real data examples from the genetics literature, we show that our methods can greatly reduce bias and improve prediction accuracy.

1. Introduction

Principal component analysis (PCA) is a very popular tool for analyzing high-dimensional biomedical data, where the number p of features is often substantially larger than the number n of observations. PCA is widely used to adjust for population stratification in genome-wide association studies [21] and to identify overall expression patterns in transcriptome analysis [23]. However, the asymptotic properties of PCA in high-dimensional data are profoundly different from the properties in low-dimensional (p finite, n → ∞) settings. In high-dimensional settings, the sample eigenvalues and eigenvectors are not consistent estimators of the population eigenvalues and eigenvectors [12, 20], and the predicted principal component (PC) scores based on the sample eigenvectors can be systematically biased toward zero [14].

There has been extensive effort to investigate the asymptotic behavior of PCA in high-dimensional settings. To provide a statistical framework for PCA in these settings, Johnston introduced a spiked population model, which assumes that all the eigenvalues are equal except for finitely many large ones called the spikes. A spiked population covariance matrix is basically a finite-rank perturbation of a scalar multiple of the identity matrix. A typical example of a spiked population with two spikes is shown in Figure 1a. This two-spike eigenvalue structure arises if the population consists of three sub-populations, and the features are largely independent with equal variances. Under this model, convergence of sample eigenvalues, eigenvectors and PC scores have been extensively studied [4, 11, 14, 20].

Figure 1:

Eigenvalue structures for SP and GSP models.

In many biomedical data, however, the assumption of the equality of non-spiked eigenvalues can be violated due to the presence of local correlation among features. In genome-wide association studies, for example, the genetic variants are locally correlated due to linkage disequilibrium. In gene-expression data, since genes in the same pathway are often expressed together, their expression measurements are often correlated. These local correlations can cause substantial differences in non-spiked eigenvalues. To illustrate this phenomenon, we obtained eigenvalues with an autoregressive within-group correlation structure rather than the independent structure of the previous example. Figure 1b shows that the equality assumption is clearly violated. Thus, if methods developed under the equality assumption are applied to these types of data, we will obtain biased results.

The generalized spiked population model [3] has been proposed to address this problem. The condition that the non-spikes have to be equal is removed in this generalization. In this model, the set of population eigenvalues consists of finitely many large eigenvalues called the generalized spikes, which are well separated from infinitely many small eigenvalues. Although the generalized spiked population model has a great potential to provide more accurate inference in high-dimensional biomedical data, only limited literature is available on the asymptotic properties of PCA under this model and their application to real data. Bai and Yao [3] and Ding [8] provided results regarding convergence of eigenvalues and eigenvectors. However, their work remained largely theoretical. Moreover, to the best of our knowledge, no method has been developed for estimating the correlations between the sample and population PC scores, and adjusting biases in the predicted PC scores under the generalized spiked population model.

In this paper, we systematically investigate the asymptotic behavior of PCA under the generalized spiked population model, and develop methods to estimate the population eigenvalues and adjust for the bias in the predicted PC scores. We first propose two different approaches to consistently estimate the population eigenvalues, the angles between the sample and population eigenvectors, and the correlation coefficients between the sample and population PC scores. We compare these two methods and show the asymptotic equivalence of the estimators across them. Finally, we propose a method to reduce the bias in the predicted PC scores based on the estimated population eigenvalues.

The paper is organized as follows. We begin in Section 2 by providing the definition of the generalized spiked population model and present existing theoretical results. We develop our methods to consistently estimate the population spikes in Section 3. In Section 4, we construct consistent estimators of the angles between the sample and population eigenvectors, and the correlation coefficients between the sample and population PC scores. We also propose the bias-reduction technique for the predicted PC scores. Section 5 presents the algorithm [9] to estimate the population limiting spectral distribution and the non-spiked eigenvalues. In Section 6, we present results from simulation studies and an example from the Hapmap project to demonstrate the improved performance of our method over the existing one. Finally, we conclude the paper with a discussion.

2. Generalized spiked population model

In order to formally define generalized spiked population model, we require the concept of spectral distribution. In the random matrix literature, it is natural to associate a probability measure to the set of eigenvalues as the dimension p goes to infinity. More explicitly, if a Hermitian matrix Σ_p has eigenvalues λ₁,…, λ_p, we can define the empirical spectral distribution (ESD) of Σ_p to be H_p based on the probability measure

$$d{H}_p(x)=\frac{1}{p}\sum _{i=1}^p{\delta }_{{\lambda }_i}(x),$$

where δ_λi (x) is unity when x = λ_i, and otherwise zero. Now, for a sequence (Σ_p) of covariance matrices, if the corresponding sequence (H_p) of ESDs converge weakly to a non-random probability distribution H as p → ∞ to, then we define H as the limiting spectral distribution (LSD) of the sequence (Σ_p).

The generalized spiked population model [3] is defined as follows. Suppose that H_p is the ESD corresponding to the population covariance matrix Σ_p and that it converges weakly to a non-random probability distribution H. Let Γ_H be the support of H and d(x, A) = inf_y∈A |x – y| be the distance metric from a point x to a set A. Then the set of eigenvalues of Σ_p comprises of two subsets of eigenvalues α₁ ≥ ⋯ ≥ α_m and β_p,1 ≥ ⋯ ≥ β_p,p−m, as follows:

1. there exists δ > 0 such that d(α_i, Γ_H) > δ for all i ∈ {1,…, m}; α₁,…, α_m are called the generalized spikes.

2. max_{1≤i≤p−m}d(β_p,i, Γ_H) = ϵ_p → 0;β_p,1,…,β_p,p−m are called the non-spikes.

It is obvious from the definition that the generalized spikes are measure zero points of the population LSD. For Johnstone’s spiked population model [11], the population LSD is H = δ_{1} indicating Γ_H = {1}. From the definition above, all eigenvalues larger than 1 are spikes. Hence, Johnstone’s spiked population model is a special case of the generalized spiked population model.

Suppose that the population covariance matrix Σ_p has eigenvalues λ₁ ≥ ⋯ ≥ λ_p, and the sample covariance matrix S_p = X^⊺X/n has eigenvalues d₁ ≥ ⋯ > d_p, where X is an n × p data matrix. Let Σ_p = EΛ_pE^⊺ and S _p = UD_pU^⊺ be the spectral decompositions of Σ_p and S _p, respectively. Further, we will assume the following throughout the paper.

1. p → ∞, n → ∞, p/n → γ< ∞.

2. $X=Y{\mathrm{\Lambda }}_p^{1/2}{E}^{\top }$, where Y is an n × p random matrix with iid elements such that E(Y_ij) = 0, E(|Y_ij|²) = 1, E(|Y_ij|⁴) < ∞.

3. The population eigenvalues follow the generalized spiked population (GSP) model with m generalized spikes. Let H_p be the population ESD, H be the population LSD, and Γ_H be the support of H. Moreover, the sequence (∥Σ_p∥) of spectral norms is bounded.

4. The generalized spikes are larger than sup Γ_H.

Even though we will develop our estimation methods based on the asymptotic regime where p/n → γ < ∞, we will discuss the applicability of our methods when p is greatly larger than n in Section 4.6.

In this paper, we will derive and discuss asymptotic properties of different functions of eigenvalues and angles between the sample and population eigenvectors, both of which are rotation-invariant, i.e., if we rotate X by some p×p orthogonal matrix P, the eigenvalues (both sample and population) and angles between the sample and population eigenvectors will remain the same. The new population covariance matrix ${\tilde{\Sigma }}_p=P^{\top }{\Sigma }_{p}P$ will have the same eigenvalues as Σ_p, and the new sample covariance matrix ${\tilde{S}}_p=P^{\top }{S}_{p}P$ will also have the same eigenvalues as S_p. The angles between the eigenvectors of ${\tilde{S}}_p$ and ${\tilde{\Sigma }}_p$ will be the same as the angles between the eigenvectors of S _p and Σ_p, both given by the elements of the matrix E^⊺ U. Therefore, without loss of generality, by using P = E, we can assume the population covariance matrix to be diagonal.

From the Marčenko-Pastur theorem [16], the sample ESD F_p converges weakly to a non-random probability distribution F with support Γ_F. For α ∉ Γ_H, α ≠ 0 and x > 0, we define the following two functions:

$$\psi (\alpha )=\alpha +\gamma \alpha \int \frac{\lambda dH(\lambda )}{\alpha -\lambda },f_F(x)=x/\left\{1+\gamma \int \frac{\tau dF(\tau )}{x-\tau }\right\}.$$ (1)

The following result by Bai and Yao [3] provides the almost sure limits of the sample eigenvalues corresponding to the population generalized spikes.

Result 1. Suppose assumptions (A)-(D) hold. Let λ_k be a generalized spike of multiplicity 1 and the corresponding sample eigenvalue is d_k. Moreover, let ψ′ denote the first derivative of the function ψ. Then,

1. If ψ′(λ_k) > 0, then the sample eigenvalue d_k converges almost surely to ψ(λ_k), i.e., $\left|d_k-\psi \left({\lambda }_k\right)\right|\stackrel{a.s.}{\to }0$.

2. If ψ′(λ_k) ≤ 0, then let (u_k, v_k) ⊂ (sup Γ_H, ∞) be the maximal interval on which ψ′ > 0. The sample eigenvalue d_k converges almost surely to ψ (w) is a boundary of [u_k, v_k] that is nearest to λ_k.

Given that ψ’(α) is a strictly increasing function for α > sup Γ_H, if a generalized spike λ_k is large enough such that ψ’(α) > 0, according to Result 1 the corresponding sample eigenvalue will converge almost surely to ψ(λ_k). However if the generalized spike lies close enough, i.e., ψ’(λ_k) ≤ 0, to the set of non-spikes, then the convergence of the corresponding sample eigenvalue is given by the second part of the result. We will denote a generalized spike λ_k as a “distant spike” if ψ’(λ_k) > 0; otherwise we will call it a “close spike”.

3. Consistent estimation of the generalized spikes

The following theorem provides two different consistent estimators of the distant spikes.

Theorem 1. Let λ_k be a distant spike of multiplicity 1 and the corresponding sample eigenvalue is d_k. If the assumptions (A)-(D) hold, then

$$\left|{\psi }^{-1}\left(d_k\right)-{\lambda }_k\right|\stackrel{p}{\to }0,$$

where ψ⁻¹ is the left inverse of ψ. Also, $\left|f_F\left(d_k\right)-{\lambda }_k\right|\stackrel{p}{\to }0$.

This theorem shows that for any distant spike λ_k we have two consistent estimators ψ⁻¹(d_k) and f_F(d_k). Notice that the function f_F depends only on the sample LSD which can be approximated by the sample ESD. Thus, f_F(d_k) can be approximated directly using the sample eigenvalues. More explicitly, f_F(d_k) can be closely approximated as

$$f_F\left(d_k\right)\approx d_k/\left\{1+\frac{\gamma }{p-m}\sum _{i=m+1}^p\frac{d_i}{d_k-d_i}\right\}.$$

In contrast, the ψ function depends on the population LSD which is unknown. We can estimate the ψ function using the algorithm described in Section 5 and then find the inverse function ψ⁻¹ using a Newton-Raphson type algorithm.

4. Consistent estimators of the asymptotic shrinkage in predicting the PC scores

In this section, we investigate the convergence of sample eigenvectors, PC scores, and shrinkage factors in predicting the PC scores. Let e_i and E_i be the ith sample and population eigenvectors, respectively. In addition to assumptions (A)-(D), we further assume that the distant spikes are of multiplicity 1. This assumption is to restrict the dimension of the corresponding eigenspaces to 1, as otherwise the angle between sample and population eigenvectors, or shrinkage in predicted PC scores cannot be well defined.

4.1. Angle between sample and population eigenvectors

We first present the following theorem on the convergence of the quadratic forms of the sample eigenvectors.

Theorem 2. Let λ_k be a distant spike of multiplicity 1, and the assumptions (A)-(D) hold. Consider the quadratic form ${\widehat{\eta }}_k=s_1^{\top }{e}_k{e}_k^{\top }{s}_2$, where s₁ and s₂ are non-random vectors with uniformly bounded norm for all p. Then

$$\left|{\widehat{\eta }}_k-{\eta }_k\right|\stackrel{a.s.}{\to }0,$$

where ${\eta }_k={\lambda }_k{\psi }^{\prime }\left({\lambda }_k\right)s_1^{\top }{E}_k{E}_k^{\top }{s}_2/\psi \left({\lambda }_k\right)$.

Mestre [19] showed similar asymptotic properties of the quadratic forms under the assumption that the number of spikes increases with the dimension. Theorem 2 shows the convergence of the angle between sample and population eigenvectors. Suppose s₁ = s₂ = E_k. Then

$${\widehat{\eta }}_k=E_k^{\top }{e}_k{e}_k^{\top }{E}_k={\langle e_k,E_k\rangle }^2,{\eta }_k={\lambda }_k{\psi }^{\prime }\left({\lambda }_k\right)/\psi \left({\lambda }_k\right).$$

Combining them, we can show

$$\left|{\langle e_k,E_k\rangle }^2-{\lambda }_k{\psi }^{\prime }\left({\lambda }_k\right)/\psi \left({\lambda }_k\right)\right|\stackrel{a.s.}{\to }0.$$

Therefore, {λ_kψ’(λ_k)/ψ(λ_k)}^1/2 is a consistent estimator of the cosine of the angle, i.e., the absolute value of the inner product, between the kth sample and population eigenvectors. In order to obtain this estimator, we first need to estimate the ψ function using the algorithm described in Section 5.

The following result by [8] provides another consistent estimator for the angle between the kth sample and population eigenvectors. The proof of the asymptotic equivalence of these two estimators is given in the Appendix.

Result 2. Let λ_k be a distant spike of multiplicity 1, and d_k be the corresponding sample eigenvalue. Assume that (A)-(D) hold. Define,

$$g_F(x)={\left\{1+\gamma f_F(x)\int \frac{\tau }{{(x-\tau )}^2}dF(\tau )\right\}}^{-1}.$$

Then $\left|{\langle e_k,E_k\rangle }^2-g_F\left(d_k\right)\right|\stackrel{p}{\to }0$.

Hence g_F (d_k)^1/2 also works as a consistent estimator of |〈e_k, E_k〉|. Since the function g_F depends only on sample LSD, it can be approximated directly using sample eigenvalues. More explicitly, if there are m spikes in the population, the function g_F can be closely approximated as

$$g_F\left(d_k\right)\approx {\left\{1+\frac{\gamma f_F\left(d_k\right)}{p-m}\sum _{i=m+1}^p\frac{d_i}{{\left(d_k-d_i\right)}^2}\right\}}^{-1}.$$

The above equation can be used to estimate the angle between the sample and population eigenvectors.

4.2. Correlation between sample and population PC scores

The sample and population PC scores are the projections of the data on the sample and population eigenvectors, respectively. The correlation between them can be perceived as a measure of accuracy of the PCA. The squared correlation can also be interpreted as the proportion of variance in the population PC scores that can be explained by corresponding sample PC scores. The following theorem provides the consistent estimators of the correlation between the sample and population PC scores corresponding to a distant spike.

Theorem 3. Suppose λ_k is a distant spike of multiplicity 1, d_k is the corresponding sample eigenvalue, and the assumptions (A)-(D) hold. Let the normalized kth population PC score be P_k = XE_k/(nλ_k)^1/2 and the normalized kth sample PC score be p_k = Xe_k/(nd_k)^1/2. Then

$$\left|{\langle P_k,p_k\rangle }^2-{\psi }^{\prime }\left({\lambda }_k\right)\right|\stackrel{p}{\to }0$$

and

$$\left|{\langle P_k,p_k\rangle }^2-d_k{g}_F\left(d_k\right)/f_F\left(d_k\right)\right|\stackrel{p}{\to }0,$$

where the function g_F is as defined in Result 2.

Since P_k and p_k are normalized random vectors, the absolute value of the inner product 〈P_k, p_k〉 is identical to the absolute value of their correlation coefficient. Since correlation is scale invariant, this is also the correlation between kth sample and population PC scores. Therefore we can consider both ψ’(λ_k)^1/2 and {d_kg_F(d_k)/f_F(d_k)}^1/2 to be consistent estimators of the correlation between the kth sample and population PC scores.

4.3. Asymptotic shrinkage factor

Suppose λ_k is a distant spike. Let the kth sample PC score for the jth observation x_j be $p_{kj}=x_j^{\top }{e}_k$, and the kth predicted PC score for a new observation x_new be $q_k=x_{new}^{\top }{e}_k$. Then the quantity ${\rho }_k={\text{lim}}_{p\to \infty }{\left\{\text{E}\left(q_k^2\right)/\text{E}\left(p_{kj}^2\right)\right\}}^{1/2}$ describes the asymptotic shrinkage in the kth predicted PC score for a new observation. As both p_kj and q_k are centered, i.e., E(p_kj) = E(q_k) = 0, ρ_k represents the limiting ratio of the standard deviations of the predicted PC scores and the sample PC scores. Therefore, if we can estimate p_k, then the shrinkage bias in the kth predicted PC scores can be easily adjusted by rescaling the predicted scores by the factor ${\rho }_k^{-1}$. The following theorem provides the consistent estimator of the asymptotic shrinkage factor p_k.

Theorem 4. Suppose λ_k is a distant spike of multiplicity 1, d_k is the corresponding sample eigenvalue, and the assumptions (A)-(D) hold. Let p_kj and q_k be as defined above. Then

$$\left|\sqrt{\text{E}\left(q_k^2\right)/\text{E}\left(p_{kj}^2\right)}-{\lambda }_k/d_k\right|\stackrel{p}{\to }0.$$

This is a surprising result in which the asymptotic shrinkage factor is expressed as a simple ratio of the population and sample eigenvalues. Recall that we already constructed the consistent estimators for population eigenvalues in the previous sections. Using these results, the asymptotic shrinkage factor ρ_k can be consistently estimated by ${\widehat{\lambda }}_k/d_k$, where ${\widehat{\lambda }}_k$ is any consistent estimator of λ_k.

4.4. Comparison of the two different estimators

For each of the quantities discussed above, we proposed two asymptotically equivalent estimators. In terms of practical applications, they have their own advantages and disadvantages. One of them can be approximated directly based only on the sample eigenvalues, while the other one requires to estimate the LSD of the population eigenvalues to obtain the ψ function. For ease of discourse, we will call the former “d-estimator” and the later “λ-estimator”.

If the number of spikes is known, estimating the d-estimator is computationally more efficient than estimating the λ-estimator as it does not involve estimating the population LSD. However, by estimating the population LSD the λ-estimation procedure can verify whether an estimated eigenvalue is actually a distant spike by checking if ψ’ > 0. Thus it can be used to estimate the number of distant spikes when it is unknown; see Section 5. In contrast, the d-estimation procedure provides no information on the population LSD and thus cannot distinguish among distant spikes, close spikes and non-spikes.

To summarize, when the number of spikes is known or we only want to estimate few of the largest eigenvalues which are known to be distant spikes, then the d-estimation procedure has the advantage of a faster computation, while the λ-estimation procedure is more useful when the number of spikes is unknown or the distribution of the non-spikes is of interest.

4.5. Comparison of the Generalized Spiked Population (GSP) model and the Spiked Population (SP) model

As mentioned before, the SP model [11] is a special case of the GSP model. It is easy to verify that when the population eigenvalues follow the SP model, our consistent estimators for the spiked eigenvalues, the angles between the eigenvectors, the correlation coefficients between the PC scores and the shrinkage factors conform to the consistent estimators derived by [4, 14, 20]. For an SP model where all the non-spikes are equal to 1, the LSD H is a degenerate distribution at 1, and

$$\psi (\alpha )=\alpha \{1+\gamma /(\alpha -1)\},{\psi }^{\prime }(\alpha )=1-\gamma /{(\alpha -1)}^2.$$

Now, ψ’(α) > 0 if and only if α > 1 + γ^1/2. If α > 1 + γ^1/2 and d is the corresponding sample eigenvalue, then the consistent estimator of α is given by ψ⁻¹ (d), and

$$\frac{\alpha {\psi }^{\prime }(\alpha )}{\psi (\alpha )}=\frac{1-\gamma /{(\alpha -1)}^2}{1+\gamma /(\alpha -1)},\frac{\alpha }{\psi (\alpha )}=\frac{\alpha -1}{\alpha +\gamma -1},$$

which show that all our results match with the results from [14].

It is of interest to investigate how closely methods developed under the SP model can approximate the consistent estimators for the distant spikes when the population eigenvalues actually follow a GSP model. Suppose the population eigenvalues λ₁ ≥ ⋯ ≥ λ_p follow the GSP model with m distant spikes. The sample eigenvalues are d₁ ≥ ⋯ ≥ d_p. Let λ_k be a distant spike with multiplicity 1, and the corresponding sample eigenvalue is d_k. Then according to Result 1, d_k → ψ(λ_k) almost surely. From the definition of ψ,

$$\psi \left({\lambda }_k\right)={\lambda }_k\left\{1+\gamma \int \frac{\lambda }{{\lambda }_k-\lambda }dH(\lambda )\right\}={\lambda }_k+\gamma \int \frac{\lambda }{1-\lambda /{\lambda }_k}dH(\lambda ).$$

If H is almost degenerate, i.e., the non-spikes are nearly identical, then

$$\psi \left({\lambda }_k\right)\approx {\lambda }_k+\frac{\gamma \overline{\lambda }}{1-\overline{\lambda }/{\lambda }_k},$$ (2)

where $\overline{\lambda }=\int \lambda dH(\lambda )$ is the mean of the population LSD which can be closely approximated by the mean of the non­spikes. By contrast, if the spike λ_k is very large compared to all the non-spikes such that λ/λ_k ≈ 0 for any λ ∈ Γ_H, then

$$\psi \left({\lambda }_k\right)\approx {\lambda }_k+\gamma \overline{\lambda }.$$

Now, suppose that instead of using the GSP assumption, we use the SP assumption to estimate the distant spikes. We assume that under the SP model, the population covariance matrix is scaled by a factor ζ and the population eigenvalues are β₁ ≥⋯≥ β_m > ζ = ⋯ = ζ. If β_k is the population eigenvalue corresponding to d_k, then d_k → ψ(β_k) almost surely, where

$$\psi \left({\beta }_k\right)={\beta }_k\left(1+\gamma \frac{\zeta }{{\beta }_k-\zeta }\right)={\beta }_k+\frac{\gamma \zeta }{1-\zeta /{\beta }_k}.$$

Here ζ is estimated as the mean of the non-spikes as they are all assumed to be equal to ζ. Notice that this expression is approximately equal to the expression in (2) with β_k = λ_k and $\zeta =\overline{\lambda }$. Therefore, the asymptotic limit of d_k under both the GSP and the SP model are approximately equal when the non-spikes are nearly identical. In contrast, when the spike β_k is very large compared to all the non-spikes such that ζ/β_k ≈ 0, then ψ(β_k) ≈ β_k + γζ. In this case also, the asymptotic limit of d_k under both the GSP and the SP model are approximately equal with β_k = λ_k and $\zeta =\overline{\lambda }$. Therefore, if a generalized spike is very far away from the support of the population LSD, then the estimate of the spike based on an SP model will closely approximate the estimate based on a GSP model. However, the SP model will provide potentially biased estimates if the non-spikes are not similar and the ratio between the largest non-spike and the spike of interest is substantially larger than zero.

4.6. Comparison with ultra high-dimensional regime-based results when p/n is large

Our methods are developed under the high-dimensional regime p/n → γ < ∞, and do not theoretically warrant them to be applied in ultra-high dimensional (UHD) regime where p/n → ∞. However, often times in real-world applications, we only have data with large p and large n, but the relative rate of their asymptotic divergence is unknown. Therefore, we do not know whether the true asymptotic regime is high-dimensional (p/n → γ < ∞) or ultra high-dimensional (p/n → ∞).

Suppose that the true asymptotic regime is high-dimensional with γ finite but large compared to n, and the eigenvalues follow the GSP model. In such situations, we can either correctly assume the high-dimensional regime and apply the results discussed in this paper, or we can falsely assume the ultra high-dimensional asymptotic regime and employ the theoretical results derived under this regime [15]. In this section, we will investigate whether it is prudent to assume the UHD regime in such situations. In other words, we will try to answer how large γ can be considered to be diverging to infinity for practical applications.

We first show that for large enough γ, the theoretical results based on the UHD regime become nearly identical to the results under the correctly assumed GSP (under high-dimensional regime) model. The UHD-based results presented in [15] require weaker conditions for the non-spiked eigenvalues than those for the spiked population model. Instead of assuming that the non-spiked eigenvalues are the same, Lee et al. [15] assumes certain conditions on the moments of the non-spiked eigenvalues. Since the population LSD has a finite support and all of its central moments are finite, the condition on their moments, i.e., Condition 2 in [15] is satisfied with an additional assumption that n³/ p² = o(1). Without loss of generality, we assume that the mean of the non-spikes is unity. Then, under the UHD regime,

$$d/\lambda \stackrel{p}{\to }\gamma /\lambda +1\text{ when }\lambda \ge O(\gamma ),d/\gamma \stackrel{p}{\to }1\text{ when }\lambda =o(\gamma ),$$ (3)

where λ and d are a spiked population eigenvalue and its corresponding sample eigenvalue, respectively. Here λ ≥ O(γ) means λ/γ is bounded away from zero, and λ = o(γ) means λ/γ → 0. Lee et al. [15] also showed the convergence of sample eigenvectors and PC scores.

Alternatively, under the GSP model, d → ψ(λ) when λ is a distance spike. From Theorem 1, a distant spike λ must satisfy

$$1-\gamma \int \frac{x^2}{{(\lambda -x)}^2}dH(x)>0,$$

where H is the population LSD. Since f_λ(x) = x²(λ − x)⁻² is a continuous function for λ > sup Γ_H and x ∈ Γ_H, where Γ_H is the support of H, there exists x* ∈ (inf Γ_H, sup Γ_H) such that ∫x²(λ − x)⁻² dH(x) = x^*2 (λ – x*)⁻². Then

$$1-\gamma x^{*2}/{\left(\lambda -x^{*}\right)}^2>0,$$

which implies $\lambda >x^{*}+x^{*}\sqrt{\gamma }$. Thus, for any $\lambda >x^{*}+x^{*}\sqrt{\gamma },d/\lambda -\psi (\lambda )/\lambda$ converges to zero.

Now, under the true asymptotic regime (high-dimensional) λ and γ are both finite and non-zero, and thus λ = O(γ). However, under the falsely assumed UHD regime, one can further assume λ ≥ O(γ) or λ = o(γ) depending on whether λ is large or small compared to γ. If one assumes λ ≥ O(γ), then the difference between the convergence of d/λ from the two models is

$$\psi (\lambda )/\lambda -\gamma /\lambda -1=\frac{\gamma }{\lambda }\left\{\int \frac{x}{1-x/\lambda }dH(x)-1\right\}.$$ (4)

Since γ/λ = O(1) and ∫ x (1 – x/λ)⁻¹dH(x) − 1 = O(1/λ) as the mean of the non-spikes is unity, (4) becomes almost identical to zero when λ is sufficiently large.

Now, suppose one assumes λ = ο(γ). Let λ ≃ a + bγ^k for some finite a, b and k ∈ [1/2,1). Then, the difference between our result and the UHD result is

$$\left|\psi (\lambda )/\gamma -1\right|=\left|\lambda /\gamma +\lambda \int \frac{x}{\lambda -x}dH(x)-1\right|=O\left({\gamma }^{k-1}\right).$$ (5)

Thus, in this case also (5) becomes almost identical to zero when γ is sufficiently large. We can also show the similar results for eigenvectors and PC scores.

Although both GSP and UHD eventually provide nearly identical results when γ is sufficiently large, the GSP model can provide substantially better estimates. The difference can be large when λ is small compare to γ, i.e., k < 1, since the difference in (5) is of the order O(γ^k−1). The difference will be at least as large as $O(1/\sqrt{\gamma })$ in such cases. In simulation studies, we show this numerically.

One important thing to note here is that the results under the ultra high-dimensional regime do not provide any consistent estimators for the spiked eigenvalues, albeit there still can be methods to estimate shrinkage. When the spike λ = ο(γ), the limiting behavior of the corresponding sample eigenvalue does not depend on λ, and when λ ≥ O(γ), $d/\lambda \stackrel{p}{\to }\gamma /\lambda +1$ does not imply d − γ to be a consistent estimator of λ because λ itself is divergent.

In the simulation studies and real data applications, we further evaluated the performance of d − γ as an estimator. Lee et al. [15] also provided an estimator of the asymptotic shrinkage which we have evaluated in the simulation studies. A recent paper by Cai et al. [7] provided limiting laws for spiked eigenvalues and corresponding eigenvectors when the spikes are divergent, under more general assumptions than the ultra high-dimensional assumptions of [15]. In terms of eigenvalue estimation, this model will still have the problem of the spikes not being estimable. However, it can be an interesting future research direction to find estimators of the shrinkage under this model.

5. Estimation of the population LSD

The λ-estimators rely on ψ, that is a function of the unknown population LSD H. To use the λ-estimators, it is thus required to estimate H. Using the Stieltjes transformation and the Marčenko-Pastur theorem, El Karoui [9] developed a general algorithm to estimate the population LSD from the sample ESD, F_p. We propose to use El Karoui’s method to estimate the population LSD H and then use it to estimate ψ.

5.1. El Karoui’s algorithm

Suppose $v_{F_p}$ is the Stieltjes transformation of the set of eigenvalues in the sample covariance matrix in which

$$v_{F_p}(z)=\frac{1}{n}\sum _{i=1}^n\frac{1}{d_i-z}$$

for any $z\in {ℂ}^{+},{ℂ}^{+}=\{x\in ℂ: \text{lm} (x)>0\}$. According to the Marčenko-Pastur theorem [16], when assumptions (A)-(D) hold, $v_{F_p}$ converges point-wise almost surely to a non-random limit v_F, which uniquely satisfies the following equation:

$$v_F(z)=-{\left\{z-\gamma \int \frac{\lambda }{1+\lambda v_F(z)}dH(\lambda )\right\}}^{-1}.$$

El Karoui’s method first calculates $v_{F_p}$ for a grid of values z₁,…, z_J, and then finds

$$\widehat{H}={\text{arg}}_H\text{min}L\left[{\left\{\frac{1}{v_{F_p}\left(z_j\right)}+z_j-\frac{p}{n}\int \frac{\lambda }{1+\lambda v_{F_p}\left(z_j\right)}dH(\lambda )\right\}}_{j=1}^J\right],$$

where L is any pre-defined convex loss function. In order to approximate the integral inside the loss function, the algorithm discretizes H as

$$dH(\lambda )\simeq \sum _{k=1}^K{w}_k{\delta }_{t_k}(\lambda ),$$

where ${\delta }_{t_k}(\lambda )=1$ if λ = t_k and 0 otherwise, w₁ + ⋯ + w_K = 1 with w_k > 0 for all k ∈ {1,…, K}, and t₁,…, t_K is a grid of points on the support of H. This is basically approximating H by a discrete distribution with support t₁,…, t_K. Then the integral is approximated by

$$\int \frac{\lambda }{1+\lambda v_F(z)}dH(\lambda )\simeq \sum _{k=1}^K{w}_k\frac{t_k}{1+t_k{v}_{F_p}\left(z_j\right)},$$

and the minimization problem transforms into

$$\widehat{H}={\text{arg}}_H\text{min}L\left[{\left\{\frac{1}{v_{F_p}\left(z_j\right)}+z_j-\frac{p}{n}\sum _{k=1}^K{w}_k\frac{t_k}{1+t_k{v}_{F_p}\left(z_j\right)}\right\}}_{j=1}^J\right].$$ (6)

El Karoui [9] has shown the weak convergence of $\widehat{H}$ to H, i.e., $\widehat{H}\to H$.

Some examples of the convex loss function L are

1. L_∞(e₁,…, e_J) = max_j·max{|Re(e_j)|, |Im(e_j)|};

2. L₁(e₁,…,e_J) = |e₁| + ⋯ + |e_j|;

3. L₂(e_l,…, e_J) = |e₁|² + ⋯ + |e_J|².

For the convex loss functions described above, the estimation of H in (6) reduces to a convex optimization problem [6]. El Karoui also provided a translation of this problem into a linear programing (LP) problem when the L_∞ loss function is used. Further details can be found in [9].

5.2. Implementing El Karoui’s algorithm when the number of spikes is known

Since the generalized spikes fall outside the support of the population LSD, El Karoui’s algorithm cannot be directly applied to estimate the spikes. Furthermore, Bai and Silverstein [2] showed that the probability of a sample eigenvalue falling outside the support of the sample LSD will go to zero as p increases, which implies that the sample eigenvalues corresponding to the population generalized spikes will be measure zero points in the sample LSD. Since the spikes behave like measure zero points (or outliers) when we are concerned about estimating the population LSD, we can exclude the sample eigenvalues corresponding to the population generalized spikes while calculating $v_{F_p}$ and that will lead to a more robust estimation of H. Therefore, we will apply El Karoui’s algorithm in the following way:

1. Suppose the population covariance matrix possesses m generalized spikes. We exclude the top m sample eigenvalues while calculating $v_{F_p}$, viz.

   $$v_{F_p}(z)=\frac{1}{n-m}\sum _{i=1}^n\frac{1}{d_i-z}.$$

2. Apply El Karoui’s algorithm to obtain $\widehat{H}$. Additionally, if it is reasonable to assume that the true population LSD is a continuous or piecewise continuous distribution function, suitable kernel smoothing algorithm can be used on $\widehat{H}$ to obtain a more continuous approximation of H.

3. The quantiles of $\widehat{H}$ can be considered as the estimators of the non-spikes.

4. Suppose ${\widehat{\lambda }}_{m+1},\dots ,{\widehat{\lambda }}_p$ are the estimated non-spikes. Then the ψ function is estimated by

   $$\widehat{\psi }(\alpha )=\alpha +\frac{\gamma \alpha }{p-m}\sum _{i=m+1}^p\frac{{\widehat{\lambda }}_i}{\alpha -{\widehat{\lambda }}_i}.$$

Due to the weak convergence $\widehat{H}\to H$, $\widehat{\psi }$ will also converge to ψ point-wise. Thus, all the estimates provided in Section 3 and 4 will still be consistent if we replace ψ with $\widehat{\psi }$.

A computationally challenging part in El Karoui’s algorithm is solving the LP problem, for which there are many fast algorithms available that can solve it in polynomial (in K, the grid size of w₁,…, w_K) computation time. An important property of El Karoui’s algorithm is that the complexity of the LP step does not depend on p, which is especially useful for estimating the LSDs of large covariance matrices. In our implementation, we used the lpSolve R package [5] to solve the LP problem.

5.3. Estimating the number of spikes

Our application of El Karoui’s algorithm to the GSP model depends on the number of spikes m, which is usually unknown. If we have some knowledge of the underlying structure of the data, we can use it to estimate m roughly. Suppose we know that the data are coming from a mixture of K subpopulations, and within each subpopulation the observations are iid $\mathcal{N}\left({\mu }_k,\Sigma \right)$, where μ_k represents the mean for the kth subpopulation, and Σ is the common within-group population covariance matrix. Then, as the spikes represent the between-group differences, the number of spikes should be the same as the rank of the between-group covariance matrix which is K − 1. However in real data, it is often hard to accurately assess the number of such homogeneous subpopulations. In those cases, we can use the following algorithm to estimate m.

1. Start with a reasonable finite upper bound m_max of the number of spikes. The upper bound can be selected based on prior information on the subpopulations, or by examining the sample eigenvalues. Set m = m_max.

2. Use El Karoui’s algorithm to estimate the population LSD and the non-spikes. Suppose the estimated non­spikes are ${\widehat{\lambda }}_{m+1}\ge \cdots \ge {\widehat{\lambda }}_p$, and the ψ function is estimated by

   $$\widehat{\psi }(\alpha )=\alpha +\frac{\gamma \alpha }{p-m}\sum _{i=m+1}^p\frac{{\widehat{\lambda }}_i}{\alpha -{\widehat{\lambda }}_i}.$$
3. Find S_ψ > λ_m+1 using the Newton-Raphson algorithm such that

   $${\widehat{\psi }}^{\prime }\left(S_{\psi }\right)=1-\frac{\gamma }{p-m}\sum _{i=m+1}^p{\left(\frac{{\widehat{\lambda }}_i}{S_{\psi }-{\widehat{\lambda }}_i}\right)}^2=0.$$

4. Since any distant spike must be larger than S_ψ, and $\widehat{\psi }$, ${\widehat{\psi }}^{\prime }$ are both continuous and strictly increasing functions on (S_ψ, ∞), the equation $\widehat{\psi }(\lambda )-d_k=0$ has a root in (S_ψ, ∞) if and only if $\widehat{\psi }\left(S_{\psi }\right)-d_k<0$. Therefore, find the smallest index i* ∈ {1,…, m} such that $d_{i^{*}}\le \widehat{\psi }\left(S_{\psi }\right)$. If all d₁,…, d_m are larger than $\widehat{\psi }\left(S_{\psi }\right)$, then stop and select m as the number of distant spikes. Otherwise, set m = i^* − 1 and repeat step (II)-(IV).

Note that the close spikes occur so close to the support of the population LSD that they cannot be distinguished separately from the non-spikes when the number of spikes is unknown.

The selection of m_max is subjective. It can be selected based on the prior knowledge on the number of subpopulations or by investigating the sample eigenvalues. In real data applications, we are usually interested in only a few large eigenvalues. In such situations, m_max can also be selected to be slightly larger than the number of eigenvalues we are interested in. As seen from our simulation studies, this spike selection algorithm can overestimate the number of spikes if the upper bound m_max is too large or underestimate the number of spikes if there are close spikes present; see the Online Supplement. However, as long as m_max is small compared to n and p, the estimation of the true population distant spikes will still remain consistent.

6. Simulation studies and real data example

6.1. Simulation studies: Compare GSP and SP-based methods

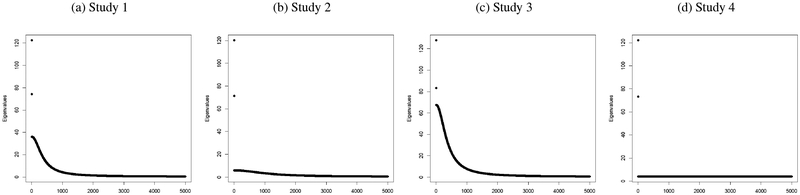
In this section we will present simulation studies of four different scenarios to compare the performances of the proposed GSP-based methods and the existing SP-based method proposed by Lee et al. [14]. For each study, we simulated a training dataset with n = 500 individuals and p = 5000 features. The data were generated from three subpopulations with sample sizes 100, 150 and 250. For each subpopulation we first selected a mean vector μ_i by drawing its elements randomly with replacement from {−0.3,0,0.3}. Then samples in the ith subpopulation were drawn from ${\mathcal{N}}_p\left({\mu }_i,V\right)$ where V is the AR(1) covariance matrix with variance σ² and autocorrelation ρ. The (σ²,ρ) pairs used for the four studies were (4,0.8), (1,0.7), (7.5,0.8) and (4,0). The population eigenvalue plots for all the studies are shown in Figure 2.

Figure 2:

Eigenvalue structures in simulation studies comparing GSP-based and SP-based methods.

We also generated test datasets for each study with the same settings as the training datasets. Then we applied our GSP-based methods and the existing SP-based method to estimate the population spikes, the angles between the sample and population eigenvectors, the correlations between the sample and population PC scores and the asymptotic shrinkage factors. For all of the studies, we used the upper bound m_max = 5 to estimate the number of distant spikes using the algorithm described in Section 5.3. We simulated each study 200 times to calculate the empirical biases and standard errors of the estimates. The results are presented in Table 1.

Table 1:

Simulation results for GSP-based and SP-based methods for estimating the population eigenvalues, cosine of the angles between sample and population eigenvectors, correlations between sample and population PC scores, and the asymptotic shrinkage factors. Each cell has empirical bias (%) with coefficients of variations (%) in parentheses.

Settings		Method	Eigenvalue		Angle		Correlation		Shrinkage
No.			1	2	1	2	1	2	1	2
1	n = 500 p = 5000 σ2 = 4 ρ = 0.8	SP	5.27 (2.37)	18.27 (3.11)	6.52 (0.32)	34.07 (0.60)	3.83 (0.03)	23.33 (0.08)	5.32 (0.60)	17.88 (1.06)
		λ-GSP	0.43 (2.67)	0.95 (5.27)	0.53 (0.77)	3.28 (6.26)	0.33 (0.31)	2.79 (4.69)	0.47 (0.92)	0.58 (3.31)
		d-GSP	0.47 (2.67)	0.69 (5.45)	0.47 (0.77)	2.48 (6.70)	0.24 (0.31)	2.11 (5.07)	0.51 (0.92)	0.31 (3.51)
2	n = 500 p = 5000 σ2 = 1 ρ = 0.7	SP	0.10 (0.90)	0.46 (1.27)	0.16 (0.04)	0.44 (0.08)	0.08 (0.001)	0.24 (0.003)	0.18 (0.08)	0.39 (0.16)
		λ-GSP	−0.04 (0.90)	0.04 (1.28)	0.01 (0.04)	0.004 (0.10)	0.01 (0.03)	0.01 (0.01)	0.03 (0.08)	−0.03 (0.18)
		d-GSP	−0.004 (0.90)	0.10 (1.28)	0.03 (0.04)	0.03 (0.10)	0.004 (0.03)	0.01 (0.01)	0.07 (0.08)	0.03 (0.18)
3	n = 500 p = 5000 σ2 = 7.5 ρ = 0.8	SP	25.68 (2.54)	—	64.06 (0.52)	—	46.50 (0.07)	—	26.41 (0.90)	—
		λ-GSP	2.92 (5.7)	—	12.62 (11.90)	—	10.95 (10.13)	—	3.47 (4.20)	—
		d-GSP	2.45 (5.74)	—	12.25 (10.52)	—	10.87 (8.58)	—	3.00 (4.24)	—
4	n = 500 p = 5000 σ2 = 4 ρ = 0	SP	0.05 (1.58)	−0.26 (2.35)	0.06 (0.23)	−0.06 (0.53)	0.03 (0.02)	0.05 (0.08)	0.07 (0.43)	−0.22 (0.90)
		λ-GSP	0.03 (1.58)	−0.35 (2.35)	0.02 (0.24)	−0.18 (0.54)	0.01 (0.02)	−0.02 (0.09)	0.04 (0.43)	−0.31 (0.91)
		d-GSP	0.16 (1.58)	−0.12 (2.35)	0.10 (0.23)	−0.03 (0.53)	0.01 (0.02)	0.02 (0.09)	0.18 (0.42)	−0.08 (0.90)

It is clear from Table 1 that for Studies 1, 2 and 3, our methods reduced the bias in all the estimates while having similar standard errors as the existing method. The positive empirical biases in all the SP estimates suggest that the SP method tends to overestimate all the quantities. In Study 4, since the underlying population satisfied the SP assumption, all methods provided very similar and almost unbiased estimates (< 1%). The results also verify that the λ-estimates and d-estimates are asymptotically equivalent. The performances of the λ-estimates and the d-estimates are nearly identical in all the simulation studies.

In Study 1, the ratio of the largest non-spike with the two spikes are 0.29 and 0.48, which are substantially larger than zero. Thus according to the discussion in Section 4, the SP model does not closely approximate the GSP model. The results support this assertion as the SP model-based estimates are highly biased whereas the estimates based on our methods have very little empirical bias. In Study 2, the largest non-spike is very small compared to the smallest spike (ratio 0.08). Thus the estimates based on the SP model closely approximate the estimates based on the GSP model, and we find very little empirical bias (< 1%) in all of the SP model-based estimates. In Study 3, even though there were two spikes present, only the largest population eigenvalue was a distant spike. So we presented only the estimates corresponding to the largest population eigenvalue. Since the ratio of the largest non-spike and the largest spike is substantially larger than zero (0.53) in this study, we observe very high empirical bias in the SP model-based estimates. However, our methods provided negligible empirical biases even in the presence of a close spike. We also presented the estimated number of distant spikes in each of the simulation studies in the Online Supplement. Note that in some cases, our algorithm over-estimates the number of distant spikes. However, as the over-estimation is only finite, the estimates of the distant spikes still remain consistent.

6.2. Simulation studies: Compare GSP and UHD-based methods

In Section 4.6, we compared the asymptotic results under the UHD regime and the results based on the high­dimensional GSP model when p is greatly larger than n, but p/n is large but finite. We theoretically established that the results from the two regimes become almost identical when p/n = γ is sufficiently large. However, given large but finite γ in the data, the difference can be substantial when the spike is smaller compared to γ.

In this section, we will assess that result by numerically comparing the GSP and UHD-based estimates for different values of γ. We considered five different scenarios where the largest population eigenvalue $\lambda \in \left\{\gamma ,0.6\gamma ,60+0.1\gamma ,6\sqrt{\gamma },4{\gamma }^{2/3}\right\}$. For the first three scenarios, under the UHD regime, λ/γ can be assumed to be bounded away from zero, and for the last two, λ/γ → 0 as γ →∞. To compare the performances as γ increases, we selected six different values for γ, viz. γ ∈ {100,200,500,1000,2500,5000}. For each combination of γ and λ, we simulated 200 datasets, each with n = 200 samples from a population with only one spike λ, and the non-spikes generated from the AR(1) covariance structure with (σ², ρ) = (1,0.9).

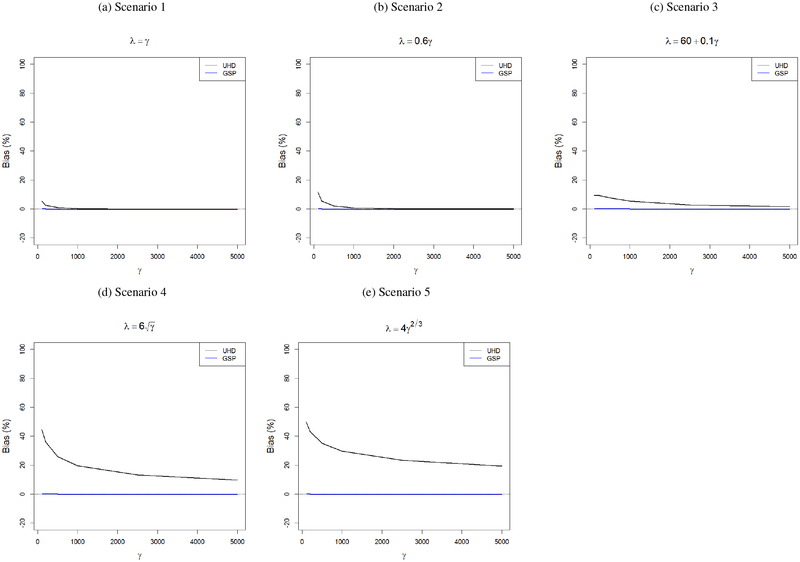
First, we compare the convergence results of the largest sample eigenvalue d from Theorem 1 and (3). For this purpose, we assume the population eigenvalues and the rate of increment of λ are known, and we compare the relative errors ϵ_GSP = {d − ψ(λ)}/d and ϵ_UHD = (d − λ − γ)/d or (d − γ)/d depending on whether λ/γ is assumed to be bounded away from zero or not. Figure 3 shows that for all combinations of (γ, λ), the GSP-based convergence result (Theorem 1) has very negligible relative errors. In contrast, the UHD-based convergence result (3) has substantially large relative errors even for γ as large as 5000 in Scenarios 3, 4 and 5. For Scenarios 1 and 2, since λ increases at a faster rate with γ than in other scenarios, the relative errors based on the two results converge much faster. However, for relatively smaller values of γ (100, 200, 500), the differences are substantial even though γ is large compared to n = 200. This suggests that we need γ to be large in an absolute sense, and not only in a relative sense compared to n in order to assume γ → ∞ and apply UHD-based results.

Figure 3:

Relative errors (%) in the convergence results of the largest sample eigenvalue derived under GSP and UHD regimes. The population eigenvalues and the rate of increment of the largest population eigenvalue are assumed to be known.

Next, we compare the estimates of the spike λ using GSP-based and UHD-based methods assuming the population eigenvalues and the rate of increment of the population spike λ to be unknown. Among the GSP-based methods, we only used the d-GSP method for this purpose due to the computational burden associated with applying the λ-GSP method on such a large number of simulated datasets. One thing to note here is that the UHD results do not provide any consistent estimators for λ, as it is assumed to be divergent when λ ≥ O(γ), and the asymptotic properties of the sample eigenvalues do not depend on λ when λ/γ → 0. Thus, in order to compare these methods, we estimate λ by λ = d − γ when considering the UHD regime.

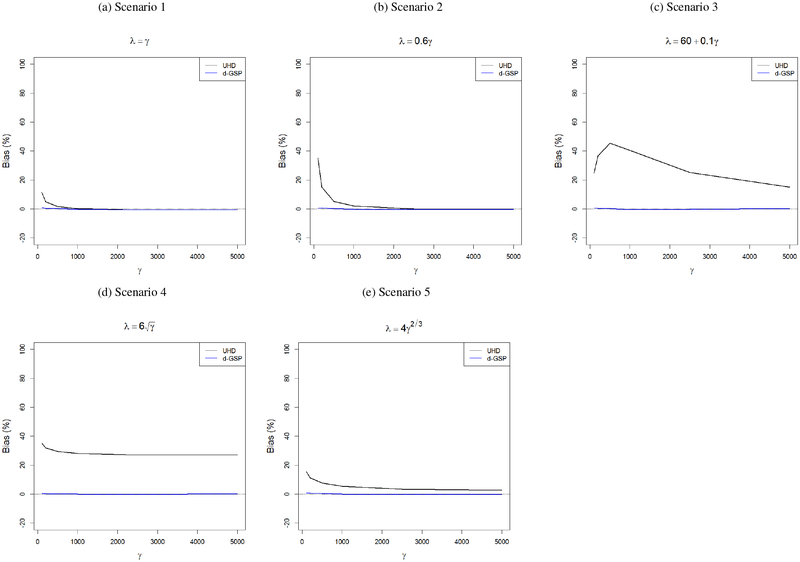
From Figure 4 we can see that our proposed d-GSP method provides almost negligible biases for all combinations of (γ, λ), whereas the UHD-based estimates have substantial biases even for γ as large as 5000 in Scenarios 3, 4 and 5. For Scenarios 1 and 2, both methods provide almost unbiased estimates when γ ≥ 1000 and γ ≥ 2000, respectively. Further, we compare the estimated shrinkage factors based on these two methods in the Online Supplement. They also show very similar patterns as the estimated spikes.

Figure 4:

Empirical biases (%) in estimating the largest population eigenvalue for GSP-based and UHD-based methods. The population eigenvalues and the rate of increment of the largest population eigenvalue are assumed to be unknown.

6.3. Application on Hapmap III data

For this demonstration, we used genetic data from the Hapmap Phase III project (http://hapmap.ncbi.nlm.nih.gov/). Our sample consisted of unrelated individuals sampled from two different populations: a) Utah residents with Northern and Western European ancestry (CEU) and b) Toscans in Italy (TSI). We only included genomic markers that are on chromosome 1–22, have less than 5% missing values, and those with minor allele frequency more than 0.05. We also excluded two samples (both from CEU) with outlier PC scores (more than six standard deviations away from the mean PC score corresponding to at least one distant spike). We then mean-centered and variance-standardized the data for each marker. The final sample consisted of 198 individuals (110 from CEU and 88 from TSI). Total number of markers selected across chromosome 1–22 was 1,389,511.

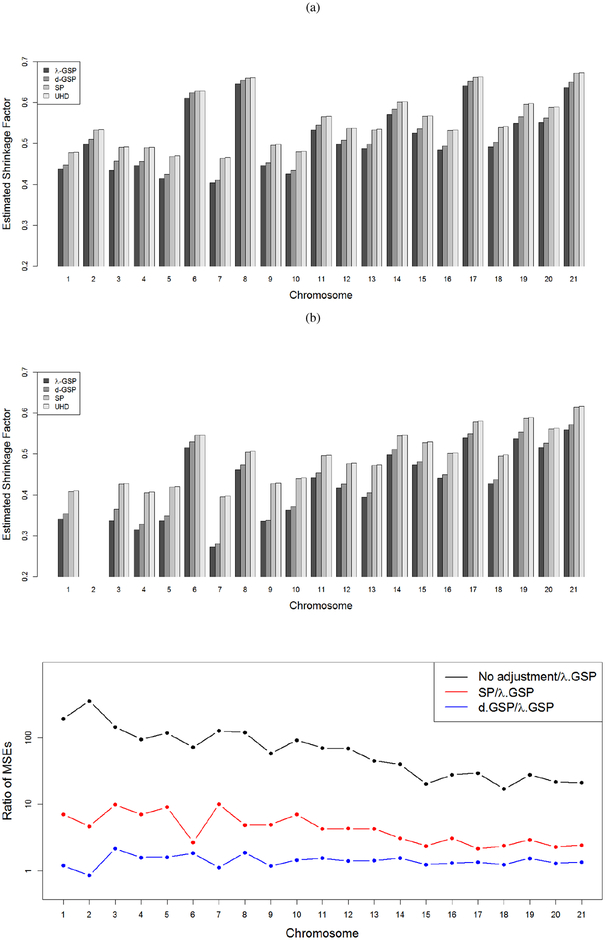
To evaluate the performance of the proposed methods with different p, we performed PCA on each chromosome separately. The number of markers varied from 19,331 (chromosome 21) to 116,582 (chromosome 2). The distribution of the number of markers across different chromosomes are presented in the Online Supplement. We first estimated the number of distant spikes using the algorithm described in Section 5.3. We found no distant spike in chromosome 22 and only one distant spike in chromosome 2. Then we applied our GSP-based methods, the existing SP-based method [14] and the UHD-based method [15] to estimate the asymptotic shrinkage factors corresponding to the distant spikes. Figure 5a, 5b compares the estimated asymptotic shrinkage factors for the first two PCs across different chromosomes. The plots show that for all the chromosomes, λ-GSP and d-GSP methods provided almost equal estimates while the SP and UHD estimates are larger than both the GSP estimates. This suggests that the SP method would over-estimate the shrinkage factors when the population eigenvalues deviate from the assumption that the non-spiked eigenvalues are the same. Moreover, the UHD method over-estimated the shrinkage factors even for p/n nearly as large as 600 (chromosome 2).

Figure 5:

Estimated shrinkage factors for (a) PC1 and (b) PC2 across chromosomes 1–21 based on three different methods. (c) Comparison of the mean squared errors (MSE) of the unadjusted and adjusted PC scores based on the d-GSP and SP methods with the adjusted PC scores based on the λ-GSP method. The ratios of the MSEs are presented for chromosome 1–21 using the threshold ϵ = 1. The y-axis is presented in a logarithmic scale.

To investigate whether the proposed shrinkage-bias adjustment can improve the prediction accuracy, we performed a leave-one-out cross-validation. In each iteration we removed one individual (test sample) and performed PCA on the remaining individuals (training samples) to predict the PC score of the test sample. For each predicted PC score, we adjusted the shrinkage-bias using the GSP-based, SP-based and UHD-based shrinkage factor estimates.

One important issue with this cross-validation is that the exclusion of one individual can substantially change the PC-coordinates, in which the PC score plots from the training sample-based and complete sample-based PCA can be substantially different. To circumvent this problem, in each iteration we first rescaled the PC scores based on their corresponding sample eigenvalues to make the PCs comparable. In addition, we obtained the mean squared difference of the training sample PCl-2 scores with and without the exclusion of the test sample (for chromosome 2, only PCl is used), and excluded the test sample from the prediction error estimation if the mean squared difference was above a threshold ϵ. We used four different values 0.5,1,5 and 10 for the threshold parameter ϵ, and for each value of ϵ we calculated the mean squared errors (MSE) of the unadjusted and adjusted predicted PC scores of the test samples. The sample sizes of the test samples that were finally included in the prediction error estimation for different values of ϵ are shown in the Online Supplement.

Figure 5 shows the estimated MSEs for ϵ = 1. It is clear that both the λ-GSP and d-GSP methods have much smaller MSEs than the SP method. The UHD-based method had almost identical MSEs as the SP-based method for all the chromosomes, hence we omitted the UHD-based results in this plot. As expected, the unadjusted predicted PC scores have substantially larger MSE than all the proposed adjustments. The plots are very similar for the other values of ϵ, and they can be found in the Online Supplement.

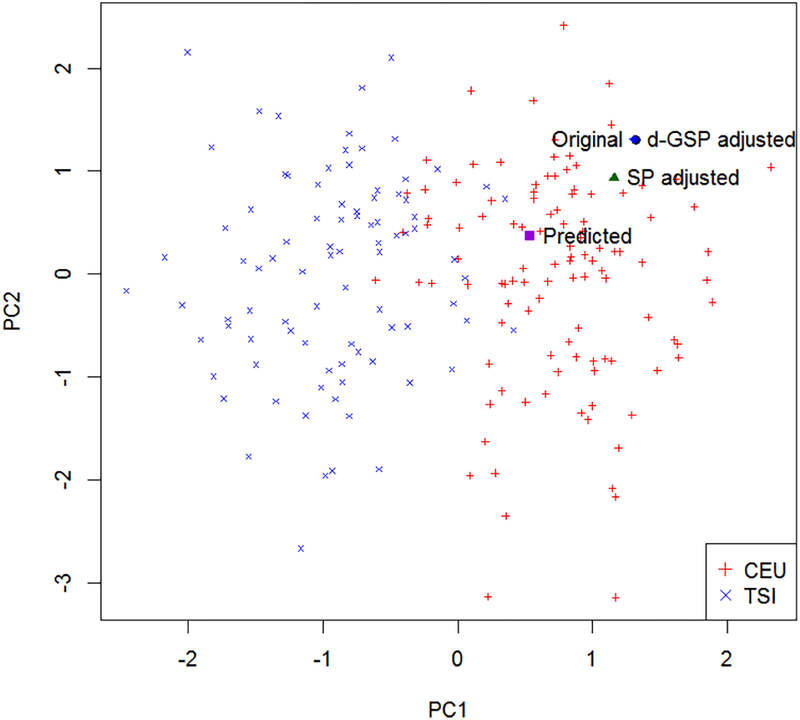
Figure 6 illustrates the shrinkage-bias adjustment for the PC1 and PC2 scores of an individual based on the markers on chromosome 7. The plot clearly shows that the bias-adjusted PC score based on the SP model is still biased towards zero, whereas the bias-adjusted PC score based on the GSP model is very close to the original sample PC score. We only showed the d-GSP adjusted score in the plot as the d-GSP and λ-GSP adjusted scores were almost equal.

Figure 6:

PCl vs PC2 plot of the Hapmap III CEU and TSI samples based on chromosome 7. The predicted PC scores for the illustrative individual, and its bias-adjusted PC scores are also presented. Since the d-GSP and the λ-GSP adjusted scores are nearly the same, the λ-GSP adjusted scores are not presented.

7. Conclusions and discussion

In this paper, we investigated the asymptotic properties of PCA under the Generalized Spiked Population model and derived estimators of the population eigenvalues, the angles between the sample and population eigenvectors, and the correlation coefficients between the sample and population PC scores. We also proposed methods to adjust the shrinkage bias in the predicted PC scores. Further, theoretically and using simulation studies, we compared our results with the results developed under the ultra-high dimensional regime [15], and showed that our methods provide more accurate results under the high-dimensional regime even when p is greatly larger than n. Since the proposed methods do not require the equality of the non-spiked eigenvalues, they can be widely used in high-dimensional biomedical data analysis. We implemented all our algorithms in the R package hdpca.

We note that Mestre [18, 19] proposed an asymptotic setting similar to the generalized spiked population model but with a different assumption on the number of spikes in which the number of spikes increases with the dimension. Under this assumption, he provided asymptotic properties of sample eigenvalues and eigenvectors. However, in many biomedical data, the number of spikes is usually finite as the spikes represent the difference between finitely many underlying subpopulations. Therefore we believe that the generalized spiked population model is more appropriate in such cases.

In some special cases, even though the features exhibit strong local correlation, one can use the spiked population model based methods after some suitable data manipulation. In genome-wide association studies, SNP pruning [1] can be used to remove locally correlated SNPs to satisfy the spiked population model. For example, Lee et al. [14] reported good performance of the spiked population model-based methods with the SNP-pruned Hapmap III dataset. This approach, however, can lead to a considerable loss of information; the SNP-pruning in Hapmap III data removed nearly 90% of the SNPs. Since the proposed approach does not require this additional step, it can use most of the information present in the data.

Appendix

Proof of Theorem 1. The first part of the proof follows directly from Result 1 along with the fact that on the domain of the distant spikes, the ψ function is strictly increasing, and hence is left invertible. Since ψ”(α) > 0 for any α > sup Γ_H, ψ’(α) is a strictly increasing function for α > sup Γ_H. Let S_ψ > sup Γ_H be a solution for ψ’(α) = 0. Then for any α > sup Γ_H, ψ’(α) > 0 if and only if α > S_ψ. Therefore the interval (S_ψ, ∞) is the domain of the distance spikes, and ψ is a strictly increasing function on this interval. The second part follows from Lemma B. □

Proof of Theorem 2. The proof closely follows the proof of Theorem 2 in [18]. However, contrary to [18], we do not assume that the population LSD contains the generalized spikes. Thus, some of the derivation steps and results are substantially different from [18]. We start the derivation by first noting that the quadratic forms ${\widehat{\eta }}_k$ can be expressed as contour integrals of a special class of Stieltjes transforms of the sample covariance matrix. Let us define, for all $z\in {ℂ}^{+}$,

$${\widehat{m}}_p(z)=s_1^{\top }{\left(S_p-z{I}_p\right)}^{-1}{s}_2=\sum _{j=1}^p{s}_1^{\top }{e}_j{e}_j^{\top }{s}_2/\left(d_j-z\right),$$

where s₁ and s₂ are non-random vectors with uniformly bounded norms. Girko [10] and Mestre [17] showed that under the assumption that the population LSD contains the generalized spikes, one has, for all $z\in {ℂ}^{+}$,

$$\left|{\widehat{m}}_p(z)-m_p(z)\right|\stackrel{a.s.}{\to }0,$$ (A.1)

Where

$$m_p(z)=s_1^{\top }{\left\{w(z){\mathrm{\Sigma }}_p-z{I}_p\right\}}^{-1}{s}_2=\sum _{j=1}^p\frac{s_1^{\top }{E}_j{E}_j^{\top }{s}_2}{w(z){\lambda }_j-z}.$$

The function w(z) is defined as w(z) = 1 − γ – γzb_F(z), where b_F(z) = ∫ (τ − z)⁻¹dF(τ) is the Stieltjes transform of the sample LSD. It is easy to check, by the same arguments provided in [17], that the result still holds when the generalized spikes are considered lying outside the support of the population LSD.

The functions ${\widehat{m}}_p$, m_p and b_F can be extended to ${ℂ}^{-}=\{z\in ℂ: \text{lm} (z)<0\}$ by defining ${\widehat{m}}_p(z)={\widehat{m}}_p^{*}\left(z^{*}\right),m_p(z)=m_p^{*}\left(z^{*}\right)$ and $z\in {ℂ}^{-}$, where z* is the complex conjugate of z.

With this definition, $\left|{\widehat{m}}_p(z)-m_p(z)\right|\stackrel{a.s.}{\to }0$ even when $z\in {ℂ}^{-}$. Now ${\widehat{\eta }}_k$ can be expressed as an integral of ${\widehat{m}}_p$, viz.

$${\widehat{\eta }}_k=\frac{1}{2\pi i}{\oint }_{\partial {\widehat{ℝ}}_y^{-}\left(k\right)}{\widehat{m}}_p(z)dz,$$

where $i=\sqrt{-1},y>0$ and $\partial {\widehat{ℝ}}_y^{-}(k)$ is the negatively (clockwise) oriented boundary of the rectangle

$${\widehat{ℝ}}_y(k)=\left\{z\in ℂ:{\widehat{a}}_1\le Re (z)\le {\widehat{a}}_2,| \text{lm} (z)|\le y\right\}.$$

The values of ${\widehat{a}}_1$ and ${\widehat{a}}_2$ can be arbitrarily chosen provided that ${\widehat{ℝ}}_y(k)$ contains only the sample eigenvalue d_k and no other sample eigenvalue. Then the following lemma gives the almost sure limit of ${\widehat{\eta }}_k$.

Lemma A.

$$\left|\frac{1}{2\pi i}{\oint }_{\partial {\widehat{ℝ}}_y^{-}(k)}{\widehat{m}}_p(z)dz-\frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}(k)}{m}_p(z)dz\right|\stackrel{a.s.}{\to }0,$$

where y > 0 and $\partial {ℝ}_y^{-}(k)$ is the negatively (clockwise) oriented boundary of the rectangle

$${ℝ}_y(k)=\left\{z\in ℂ:a_1\le Re (z)\le a_2, lm (z)|\le y\right\}.$$

The constants a₁ and a₂ can be arbitrarily chosen so that ψ(λ_k) ∈ [a₁, a₂] and [a₁, a₂] ⊂ ψ(S_ψ, ∞), where S_ψ > sup Γ_H, ψ′(S_ψ) = 0. Here, ψ(S_ψ, ∞) denotes the image of the interval (S_ψ, ∞) under ψ.

Lemma A implies

$$\left|{\widehat{\eta }}_k-\sum _{j=1}^p\left\{\frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}\left(k\right)}\frac{dz}{w(z){\lambda }_j-z}\right\}{s}_1^{\top }{E}_j{E}_j^{\top }{s}_2\right|\stackrel{a.s.}{\to }0.$$ (A.2)

Now we need to evaluate the integral in (A.2) in order to get the almost sure limit of the random variable ${\widehat{\eta }}_k$. First, we extend the ψ function to ${ℝ}_y(k)$ as follows. For all $z\in {ℝ}_y(k)$,

$$\psi (z)=z\left\{1+\gamma \int \frac{\lambda }{z-\lambda }dH(\lambda )\right\}.$$

According to [16], for all $z\in {ℂ}^{+}$, b_F(z) = b is the unique solution to the equation

$$b=\int \frac{1}{\lambda (1-\gamma -\gamma zb)-z}dH(\lambda )$$ (A.3)

in the set $\left\{b\in ℂ:\gamma b-(1-\gamma )/z\in {ℂ}^{+}\right\}$. It is easy to see that b_F also satisfies (A.3) when $z\in {ℂ}^{-}$. Now we formally define the f_F function introduced in (1). For all $z\in ℂ\backslash ℝ$, set

$$f_F(z)=\frac{z}{w(z)}=\frac{z}{1-\gamma -\gamma z{b}_F(z)}.$$ (A.4)

Then b_F can be expressed in terms of f_F as

$$b_F(z)=\frac{(1-\gamma )f_F(z)-z}{\gamma z{f}_F(z)}.$$

By replacing b with {(1 – γ)f − z}γzf in (A.3), we get

$$f\left\{1+\gamma \int \frac{\lambda }{f-\lambda }dH(\lambda )\right\}=z.$$ (A.5)

It is easy to see that b_F is a solution to (A.3) if and only if f_F is a solution to (A.5). Therefore, for all $z\in {ℂ}^{+}$ (similarly for $z\in {ℂ}^{-}$, f_F(z) = f is the unique solution to (A.5) on ${ℂ}^{+}$ (respectively, ${ℂ}^{-}$). This implies ψ{f_F(z)}=for all $z\in {ℝ}_y(k)\backslash \left[a_1,a_2\right]$.

Now we focus on the case when $z\in ℝ\backslash \left\{0\right\}$. According to [22], we can extend b_F to $ℝ\backslash \left\{0\right\}$ by defining $b_F\left(z\right)={\text{lim}}_{y\to 0^{+}}{b}_F(z+iy)$ for any $z\in ℝ\backslash \left\{0\right\}$. The definition of f_F can also be extended in a similar fashion. In Lemma B we have shown that f_F is the inverse function of ψ on (S_ψ, ∞), and there exists M_f > sup Γ_F for which f(S_ψ, ∞) = (M_f, ∞). Thus, [a₁, a₂] ⊂ ψ(S_ψ, ∞) implies ψ{f_F(z)} = z for all $z\in {ℝ}_y(k)$. Furthermore, the function ψ is continuous and differentiable on ${ℝ}_y(k)$, and the derivative is given by

$${\psi }^{\prime }(z)=1-\gamma \int {\left(\frac{\lambda }{z-\lambda }\right)}^{2}dH(\lambda ).$$

Then the integral in (A.2) can be expressed in terms of ψ and f_F as follows:

$$\begin{gathered} \frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}(k)}\frac{dz}{w(z){\lambda }_j-z}=\frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}\left(k\right)}\frac{dz}{\frac{z}{f_F(z)}{\lambda }_j-z} \\ =\frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}(k)}\frac{1}{{\lambda }_j-f_F(z)}\times \frac{f_F(z)}{\psi \left\{f_F(z)\right\}}dz. \end{gathered}$$ (A.6)

The integrand in the final expression is holomorphic on ${ℝ}_y^{-}(k)$ when j ≠ k and possesses a simple pole ψ(λ_k) when j = k. Therefore, when j ≠ k the integral in (A.6) is zero. When j = k, applying the residue theorem on the final integral, we get

$$\begin{gathered} \frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}(k)}\frac{dz}{w(z){\lambda }_k-z}=\underset{z\to \psi \left({\lambda }_k\right)}{\text{lim}}\frac{\psi \left({\lambda }_k\right)-z}{{\lambda }_k-f_F(z)}\times \frac{f_F(z)}{\psi \left\{f_F(z)\right\}} \\ =\underset{z\to \psi (k)}{\text{lim}}\frac{\psi \left({\lambda }_k\right)-\psi \left\{f_F(z)\right\}}{{\lambda }_k-f_F(z)}\times \frac{f_F(z)}{\psi \left\{f_F(z)\right\}}=\frac{{\lambda }_k{\psi }^{\prime }\left({\lambda }_k\right)}{\psi \left({\lambda }_k\right)}. \end{gathered}$$

This implies

$$\frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}(k)}\frac{dz}{w(z){\lambda }_j-z}=\{\begin{array}{ll}{\lambda }_k{\psi }^{\prime }\left({\lambda }_k\right)/\psi \left({\lambda }_k\right)\hfill & \text{ if }j=k,\hfill \\ 0\hfill & \text{ if }j\ne k,\hfill \end{array}$$

and the proof of Theorem 2 is complete. □

Proof of Lemma A. First, we show that ${\widehat{a}}_1$, ${\widehat{a}}_2$, a₁, a₂ can be chosen satisfying ${\widehat{a}}_1\to a_1$ and ${\widehat{a}}_2\to a_2$. This is possible due to the fact that $d_k\stackrel{a.s.}{\to }\psi \left({\lambda }_k\right)$ and ψ(λ_k) ⊂ ψ(β_ψ, ∞) = (M_f, ∞), where M_f > sup Γ_F. Therefore, we can choose a neighborhood [a₁, a₂] around ψ(λ_k) so that [a₁, a₂] ⊂ (M_f, ∞). Moreover, as M_f is bounded away from the support of the sample LSD F and $d_k\stackrel{a.s.}{\to }\psi \left({\lambda }_k\right)$, we can select a neighborhood [${\widehat{a}}_1$, ${\widehat{a}}_2$] around d_k which does not contain any other eigenvalue for which ${\widehat{a}}_1\to a_1$, ${\widehat{a}}_2\to a_2$. Then

$$\left|\frac{1}{2\pi i}{\oint }_{\partial {\widehat{ℝ}}_y^{-}(k)}{\widehat{m}}_p(z)dz-\frac{1}{2\pi i}{\oint }_{\partial {ℝ}_y^{-}(k)}{m}_p(z)dz\right|\le \frac{1}{2\pi }\left\{\underset{z\in \partial {\widehat{ℝ}}_y^{-}(k)\cup \partial {ℝ}_y^{+}(k)}{\text{sup}}\left|{\widehat{m}}_p(z)\right|\right\}\left(\left|{\widehat{a}}_1-a_1\right|+\left|{\widehat{a}}_2-a_2\right|\right)+\frac{1}{2\pi }{\oint }_{\partial {ℝ}_y^{-}(k)}\left|{\widehat{m}}_p(z)dz-m_p(z)\right|\times \left|dz\right|.$$ (A.7)

From the Cauchy-Schwarz inequality, we can obtain the following upper bound for ${\widehat{m}}_p$.:

$$\left|{\widehat{m}}_p(z)\right|\le \Vert s_1\Vert \times \Vert s_2\Vert /d\left(z,{\mathrm{\Gamma }}_{F_p}\right).$$

Here, $d\left(z,{\mathrm{\Gamma }}_{F_p}\right)={\text{inf}}_{y\in {\mathrm{\Gamma }}_{F_p}}\left|z-y\right|$. Since F_p → F point-wise and [a₁, a₂] is bounded away from Γ_F, $d\left(z,{\mathrm{\Gamma }}_{F_p}\right)$ is bounded away from zero with probability 1 for large enough p and n. Therefore $\left|{\widehat{m}}_p(z)\right|$ is finite for $z\in {ℝ}_y(k)$ with probability 1 for large enough p and n. Moreover, since $\left[{\widehat{a}}_1,{\widehat{a}}_2\right]\to \left[a_1,a_2\right]$, the interval $\left[{\widehat{a}}_1,{\widehat{a}}_2\right]$ will eventually be bounded away from Γ_F. Thus, eventually the upper bound for $\left|{\widehat{m}}_p(z)\right|$ will also be finite for $z\in {\widehat{ℝ}}_y(k)$. Therefore, the first term on the right-hand side of (A.7) will go to zero as ${\widehat{a}}_1\to a_1$, ${\widehat{a}}_2\to a_2$.

Now, as ${\widehat{m}}_p(z)$ and m_p(z) are holomorphic functions on the compact set $\partial {ℝ}_y^{-}(k)$, we have

$$\underset{z\in \partial {ℝ}_y^{-}(k)}{\text{sup}}\left|{\widehat{m}}_p(z)-m_p(z)\right|<\infty .$$

Also from (A.1), $\left|{\widehat{m}}_p(z)-m_p(z)\right|\stackrel{a.s.}{\to }0$ point-wise for all $z\in ℂ\backslash ℝ$. Therefore, by Lebesgue’s Dominated Convergence Theorem, the second term on the right-hand side of (A.7) also converges to zero almost surely. This completes the proof of Lemma A. □

We can show the asymptotic equivalence of the limits derived in Theorem 2 and Result 2 as a direct application of the following lemma.

Lemma B. Suppose assumptions (A)-(D) hold. If λ_k is a distant spike with multiplicity 1, and d_k is the corresponding sample eigenvalue, then

$$f_F\left(d_k\right)\stackrel{p}{\to }{\lambda }_k,\frac{d_k{g}_F\left(d_k\right)}{f_F\left(d_k\right)}\stackrel{p}{\to }{\psi }^{\prime }\left({\lambda }_k\right).$$

Proof. We have already established in the proof of Theorem 2 that for all $z\in {ℂ}^{+}$ (similarly for $z\in {ℂ}^{-}$), f_F (z) = f is the unique solution to (A.5) on ${ℂ}^{+}$ (respectively, ${ℂ}^{-}$). When z is restricted to $ℂ\backslash ℝ$, using (A.4) and the fact that b_F (z) = ∫ (τ − z)⁻¹dF(τ), we can write

$$f_F(z)=z\left\{1+\gamma \int \frac{\tau }{z-\tau }dF(\tau )\right\}.$$

Now suppose $z=x\in ℝ\backslash \left\{0\right\}$. Then both Eqs. (A.3) and (A.5) will have multiple roots, both real and complex valued depending on x and H. If we look at (A.5) closely, we can see for real-valued x, it can be represented as ψ{f (x)} = x, where the ψ function is as defined in (1). As we have seen in the proof of Theorem 1, ψ is strictly increasing in the interval (S_ψ, ∞), where S_ψ > sup Γ_H and ψ’(S_ψ) = 0. Therefore, any real-valued solution f of ψ{f (x)} = x in (S_ψ, ∞) has to be the inverse of ψ, which is unique due to the strict monotonicity of ψ on (S_ψ, ∞). Now suppose Γ_F is the support of the sample LSD F. We will show that there exists M_f > sup Γ_F such that for any x > M_f, the function f_F is real-valued and it is a solution to (A.5) in the interval (S_ψ, ∞). Thus it is also the unique such solution and the inverse of the ψ function in (S_ψ, ∞).

Let $x\in ℝ,x>$ sup Γ_F and $z=x+iy\in {ℂ}^{+}$. Now, as $z\in {ℂ}^{+}$, f_F(z) is the unique solution to (A.5) in ${ℂ}^{+}$. Therefore, if we express f_F(z) as u(z) + iv(z), then v(z) > 0. Also, the imaginary part of (A.5) can be written as

$$v(z)\left[1-\gamma \int \frac{{\lambda }^2}{{\{u(z)-\lambda \}}^2+v{(z)}^2}dH(\lambda )\right]=y.$$

Both v(z) and y being positive implies that

$$1-\gamma \int \frac{{\lambda }^2}{{\{u(z)-\lambda \}}^2+v{(z)}^2}dH(\lambda )>0.$$ (A.8)

Due to the continuity of f_F on the set $\left\{z\in {ℂ}^{+}:z=x+iy,x>\text{sup}{\Gamma }_F\right\}$,

$$f_F(x)=\underset{y\to 0^{+}}{\text{lim}}\frac{x+iy}{1+\gamma \int \tau {(x+iy-\tau )}^{-1}dF(\tau )}=\frac{x}{1+\gamma \int \tau {(x-\tau )}^{-1}dF(\tau )},$$

which is real-valued. Thus u(z) → f_F(x) and v(z) → 0 as y ↓ 0. Therefore as y ↓ 0, the inequality (A.8) becomes

$$1-\gamma \int \frac{{\lambda }^2}{{\left\{f_F(x)-\lambda \right\}}^2}dH(\lambda )>0,$$

which implies ψ’{f_F(x)} > 0.

We can see that f_F(x) attains zero at sup Γ_F and it is strictly and unboundedly increasing for x > sup Γ_F. This ensures the existence of a threshold M_F > sup Γ_F such that the function f_F maps the interval (M_F, ∞) to (S_ψ, ∞). Therefore, f_F and ψ are both strictly increasing, continuous and bijective mappings between the intervals (M_F, ∞) and (S_ψ, ∞). Since f_F(z) is the unique solution to (A.5) in ${ℂ}^{+}$ when $z\in {ℂ}^{+}$, f_F is also a solution to (A.5) in (S_ψ, ∞) when x > M_F due to the continuity of the left-hand side of (A.5) on the set $\left\{f\in {ℂ}^{+}:f=u+iv,u>S_{\psi }\right\}$, which further implies that f_F is the inverse function of ψ on (S_ψ, ∞).

The first part of Lemma B is proved as a corollary to Result 1 as ψ⁻¹ = f_F on the domain of distant spikes, i.e., (S_ψ, ∞). For the second part, we first need to derive the expression of ${f^{\prime }}_F$, and then derive the expression of ψ’ in terms of f_F and F, viz.

$$f_F^{\prime }(x)=f(x)\left\{1+\gamma v_F(x)\right\}/x;v_F(x)=\int \frac{\tau }{{(x-\tau )}^2}dF(\tau ).$$

For a distant spike λ_k, using the expression of ${f^{\prime }}_F$, we get

$$\frac{{\lambda }_k{\psi }^{\prime }\left({\lambda }_k\right)}{\psi \left({\lambda }_k\right)}=\frac{{\lambda }_k}{\psi \left({\lambda }_k\right)f_F^{\prime }\left\{\psi \left({\lambda }_k\right)\right\}}=\frac{1}{1+\gamma f_F\left\{\psi \left({\lambda }_k\right)\right\}\int \tau {\left\{\psi \left({\lambda }_k\right)-\tau \right\}}^{-2}dF(\tau )}=g_F\left\{\psi \left({\lambda }_k\right)\right\}.$$

As ψ(λ_k) > M_f, g_F is continuous at ψ(λ). Since $d_k\stackrel{p}{\to }\psi \left({\lambda }_k\right)$,

$$g_F\left(d_k\right)\stackrel{p}{\to }{g}_F\left\{\psi \left({\lambda }_k\right)\right\}={\lambda }_k{\psi }^{\prime }\left({\lambda }_k\right)/\psi \left({\lambda }_k\right),d_k{g}_F\left(d_k\right)/f_F\left(d_k\right)\stackrel{p}{\to }{\psi }^{\prime }\left({\lambda }_k\right).$$

This concludes the proof of Lemma B. □

Proof of Theorem 3. We have

$${\langle P_k,p_k\rangle }^2=\frac{1}{n^2{\lambda }_k{d}_k}{\langle X{E}_k,X{e}_k\rangle }^2=\frac{1}{{\lambda }_k{d}_k}{\left(E_k^{\top }{X}^{\top }X{e}_k/n\right)}^2=\frac{1}{{\lambda }_k{d}_k}{\left\{E_k^{\top }\left(\sum _{i=1}^p{d}_i{e}_i{e}_i^{\top }\right)e_k\right\}}^2=\frac{d_k}{{\lambda }_k}{\langle e_k,E_k\rangle }^2.$$

Using the limits derived in Theorem 2 and Result 1, we deduce that

$$\left|\frac{d_k}{{\lambda }_k}{\langle e_k,E_k\rangle }^2-{\psi }^{\prime }\left({\lambda }_k\right)\right|\stackrel{p}{\to }0.$$

Using Lemma B, we conclude that

$$\left|\frac{d_k}{{\lambda }_k}{\langle e_k,E_k\rangle }^2-\frac{d_k{g}_F\left(d_k\right)}{f_F\left(d_k\right)}\right|\stackrel{p}{\to }0.$$

Proof of Theorem 4. We show that the denominator $\text{E}\left(p_{kj}^2\right)$ converges to ψ(λ_k) and the numerator $\text{E}\left(q_k^2\right)$ converges to ${\lambda }_k^2/\psi \left({\lambda }_k\right)$. The proof will be complete using the fact that $d_k\stackrel{p}{\to }\psi \left({\lambda }_k\right)$. For the denominator, we have

$$\begin{gathered} \text{E}\left(p_{kj}^2\right)=\frac{1}{n}\text{E}\left(\sum _{i=1}^n{p}_{ki}^2\right)=\frac{1}{n}\text{E}\left\{\sum _{i=1}^n{\left(x_i^{\top }{e}_k\right)}^2\right\}=\text{E}\left(e_k^{\top }{X}^{\top }X{e}_k/n\right) \\ =\text{E}\left\{e_k^{\top }\left(\sum _{i=1}^p{d}_i{e}_i{e}_i^{\top }\right)e_k\right\}=\text{E}\left(d_k\right)\to \psi \left({\lambda }_k\right). \end{gathered}$$

For the numerator, we have

$$\text{E}\left(q_k^2\right)=\text{E}\left\{{\left(x_{new}^{\top }{e}_k\right)}^2\right\}=\text{E}\left\{\text{E}{\left(x_{new}^{\top }{e}_k\right)}^2|e_k\right\}=\text{E}\left\{var\left(x_{new}^{\top }{e}_k\right)|e_k\right\}=\text{E}\left(e_k^{\top }{\Sigma }_p{e}_k\right).$$

Now, using the notations in the proof of Theorem 2 and Lemma B, we have b_F(z) = ∫ (τ − z)⁻¹dF(τ) as the Stieltjes transform of the sample LSD and the function f_F defined as f_F(z) = z{1 − γ − γzb_F(z)}⁻¹. Therefore,

$$b_F(z)=\frac{(1-\gamma )f_F(z)-z}{\gamma z{f}_F(z)}.$$

The functions b_F and f_F can be extended to the real axis by defining the extensions as shown in the proof of Lemma B. Thus, for the sample eigenvalue d_k corresponding to the distant spike λ_k we have

$$b_F\left(d_k\right)=\frac{(1-\gamma )f_F\left(d_k\right)-d_k}{\gamma d_k{f}_F\left(d_k\right)}.$$

According to Theorem 4 in [13], the limit of $e_k^{\top }{\Sigma }_p{e}_k$ is given by d_k{1 − γ − γd_kb_F(d_k)}⁻². Replacing the expression of b_F (d_k) in this limit, we get

$$\left|e_k^{\top }{\Sigma }_p{e}_k-f_F^2\left(d_k\right)/d_k\right|\stackrel{p}{\to }0.$$

Using Result 1 and Lemma B, we have $f_F^2\left(d_k\right)/d_k\stackrel{p}{\to }{\lambda }_k^2/\psi \left({\lambda }_k\right)$. Therefore, the limit of the numerator is given by

$$\text{E}\left(q_k^2\right)=\text{E}\left(e_k^{\top }{\Sigma }_p{e}_k\right)\to {\lambda }_k^2/\psi \left({\lambda }_k\right).$$

This completes the proof of Theorem 4. □