Techno-economic assessment of solar energy coupling with large-scale desalination plant: The case of Morocco

Abstract

This paper examines the cost competitiveness of an extra-large-scale (275,000 m³/d) solar-powered desalination, taking as a case study the Chtouka Ait Baha plant in Morocco. It assesses the conditions at which solar Photovoltaics (PV) and Concentrated Solar Power (CSP) would be competitive with a grid (mainly fossil) driven desalination plant for the reference year and by 2030. The paper considers also a scenario where battery storage complements PV power generation. To conduct the analysis, a simple model of water cost calculation is built. Second, the cost related to energy consumption is calculated for different power supply options to evaluate the impact of energy provision cost on the final cost of water. The first main result of this paper is that desalinated water can be obtained at an acceptable cost of around 1 $/m³. The second one is that PV without storage remains the cheapest power supply option today and by 2030. Storage based solution appears less competitive today but can be more attractive in a framework of increasing electricity grid prices and higher flexibility requirements in the future. The paper gives recommendations regarding the implication of different technology choices in the framework of the future Moroccan energy system.

1. Introduction

Having access to safe drinking water is one of the human basic rights that are still unequally distributed on earth. Still 3 out of 10 persons lack access to drinking water services in the World [1]. These “left behind” people are a prioritized target of the 2030 Agenda for sustainable development which aims at achieving global access to water and sanitation for all human, especially in the highly water stressed countries [2]. In particular, the Middle East and North Africa (MENA) region figures on the top of the very highly stressed zones in the world, due to water supply and demand imbalance [3]. Driven by the joint effect of increased urbanization, population growth, industrialization and climate change, this gap may further increase in the coming decades. It is expected that unmet water as percentage of total demand in the region will increase from 31% in the period 2020–2030 to 51% in 2040–2050 [4]. Bridging the water gap in the MENA region would have an average annual cost estimated to reach more than US$ 100 billion during 2040–2050 [4]. This cost largely varies across the countries and is influenced by the climate change projection scenario that is considered (wet, dry). The distribution of adaptation costs would appear to be very skewed as >57% of the total cost needs would be covered by three countries, namely Iraq (27%), Saudi Arabia (19%) and Morocco (11%) [4].

To overcome present and future water shortage challenges in the MENA region, many alternatives can be experienced such as water productivity upgrade (especially in agriculture), water demand management and water supply diversification. Besides traditional water supply sources such as lakes, rivers or groundwater reservoirs, seawater and brackish water desalination can be a valuable option in many countries to diversify the water mix. Desalination is a water treatment technique that consists in removing salts from water. Two main techniques are commonly used to desalt water. Historically, distillation was the leading process in the desalination market but in the recent decade membrane based processes largely overcame distillation covering now >65% of current installed capacity [5]. Up to 2015, >92 million m³/d of commissioned desalination capacity in the world (supplied by >18,000 plants) covered a part of water needs for around 300 million people [5]. Between 2010 and 2016, global installed capacity of desalination units grew at almost 9% per year [5]. Though its long history and its upward trajectory in terms of installed capacity, desalination supplies only 1% of drinking water in the World [6]. Indeed, the high energy requirements to power a desalination unit increases the final cost of desalinated water, which may negatively affect the economic attractiveness of desalination projects. The type (electrical or thermal) and amount of specific energy consumption vary according to the considered desalination technique. For example sea water membrane separation process requires between 3 and 5 kWh/m³ whereas for distillation processes, both thermal (60–70 kWh/m³) and electrical energy (1.5–2 kWh/m³) are required [7]. Aside from the amount of energy consumed, the price of the purchased energy to power the desalination unit has also a significant impact on the final cost of desalinated water. The calculation of the cost of water depends on several factors and assumptions which makes the fair comparison of results a hard task. However, a comprehensive survey gives interesting ranges of the estimated cost of water reported in the literature [8]. For large sea water RO plants with a capacity ranging between 100,000 m³/d and 320,000 m³/d, the reported cost of water varies between 0.45 $/m³ and 0.66 $/m³, whereas for medium plants with a capacity between 15,000 m³/d and 60,000 m³/d, the cost of water ranges between 0.48 $/m³ and 1.62 $/m³. For small plants of 1000 m³/d to 4800 m³/d, the cost of water ranges between 0.7 $/m³ and 1.72 $/m³. For Electrodialysis plants, the cost of water ranges between 0.6 $/m³ and 1.05 $/m³ [8]. Regarding distillation techniques, the cost of water for multistage flash distillation plants with a production capacity between 23,000 m³/d and 52,800 m³/d varies between 0.52 $/m³ and 1.75 $/m³. For Multi-effect distillation plants with a capacity higher than 90,000 m³/d, the cost of water ranges between 0.52 $/m³ and 1.01 $/m³. However, for lower capacities (12,000 m³/d to 55,000 m³/d), the reported cost is higher ranging between 0.95 $/m³ and 1.95 $/m³. Contrarily to previous desalination techniques that rely on large capacities, Vapor Compressor usually have small capacities and higher costs. For example, the reported cost of water ranges between 2 $/m³ and 2.6 $/m³ for a capacity around 1000 m³/d [8].

Available information reveals that 99% of total desalinated water around the world is powered by fossil energies which are harmful to the environment [9]. The use of renewable energy sources (RES) such as solar, wind, wave, geothermal can therefore bring new opportunities for a sustainable growth of large-scale cost effective renewable powered desalination systems. A variety of coupling options exists between renewable energy sources and desalination techniques [[10], [11], [12], [13]]. These coupling options are shown to be technologically and economically feasible but have today various levels of technological maturity from basic research to the application stage [10]. Among all renewable driven desalination plants, solar energy is the dominant power source. Between 1974 and 2009, 70% of the 131 RES desalination plants installed in the World were powered by solar and only 20% by wind. Almost one third of RES powered desalination plants are Reverse Osmosis (RO) units powered by photovoltaics (PV), making this configuration (PV/RO) the most dominating option currently, especially for small scale installations [7]. A large part of the literature has investigated the potential of small scale RO systems driven by PV in different locations such as Greece, Italy, Spain, Saudi Arabia or Egypt either as part of theoretical studies or pilot experiments [14]. For example, based on a techno-economic feasibility study of a 20 m³/d RO plant in Abu Dhabi, it was found that a fully solar driven unit without batteries with a cost of water of 7.34 $/m³ would be competitive compared with a fully diesel powered unit (7.64 $/m³) [15]. In general, when solar resources are abundant, PV-RO is found to be more competitive than diesel powered units [16,17]. However one limit of PV-RO design is the intermittency of solar PV generation that can be smoothed using storage device to allow a 24 h steady state operation mode of the PV-RO desalination unit [18]. Introducing lead-acid batteries to a PV system is found to be the most cost competitive solution to power a RO unit compared to a diesel generator or a diesel/wind power supply [19]. Similar conclusions are drawn in [20] with a 30% cost reduction when batteries are integrated to remote PV-RO systems. However, batteries have limited lifetime which could be even reduced further in hot climate, requiring regular replacement and thus increasing the overall desalination operation cost.

Concentrated Solar Power (CSP) is being more and more considered for powering desalination units. The literature remains however much less abundant as CSP technology for large-scale solar developments has only started to gain interest in the last decade. A roadmap for short medium and long term large scale CSP powered desalination in the MENA region [21] revealed that a potential of 146 billion m³ per year by 2050 could be expected for the whole MENA region among which 400 million m³ per year only for Morocco. Egypt, Saudi Arabia, Libya, Syria and Yemen are expected to dominate the CSP desalination market in the coming decades [22]. However, despite this huge potential, electricity from CSP is still high which limits the large development of this solar technology. Conducting a technical and economic feasibility of distillation process integration to a 100MW_elec CSP plant in Namibia, [23] concluded that water and electricity cogeneration could be an interesting option in the country, but is still less attractive than a grid powered RO design. In the case of a CSP+ distillation plant, the cost of desalinated water ranges between 2.6 $/m³ and 3.6 $/m³ depending on the brine temperature (respectively 75 °C and 60 °C). The high capital cost of central CSP receiver plants, and the cost of inland seawater pumping would be the main limiting factors affecting the economics of such a design. As CSP electricity generation is still high, the introduction of high feed-in tariffs for CSP generation makes large solar fields with large thermal storage systems becoming economically interesting compared to conventional designs. To breakeven with conventional distillation cogeneration and for a 24,000 m³/d capacity plant, feed-in tariffs for CSP generation would have to reach 0.27 $/kWh and 0.34 $/kWh respectively for Jordan and Israel, whereas for RO-CSP systems, they would be at a minimum of 0.26 $/kWh and 0.35 $/kWh respectively [24]. The use of CSP powered desalination plants with heat storage would provide an opportunity to the large-scale deployment of CSP technologies while supplying sustainable fresh water in arid areas (Chile, Namibia, Australia, and MENA region). Compared to a PV+ battery system which generally needs high investment because of expensive storage requirements, cogeneration of desalinated water and electricity using CSP allows the use of a relative cheap thermal energy [25]. Even if critical factors such as the CSP plant location (desert or coast) and design may prevent this development, future cost reduction in CSP technologies and the wish to encourage sustainability of industrial processes could boost large-scale CSP powered desalination plants. Several countries have already made the choice to develop this technology and it is particularly the case of Morocco which already installed 580 MW of CSP plants by 2018.

An increasing number of renewable powered desalination units have started to be developed, especially during the last few years (Spain, Abu Dhabi, Tunisia, Algeria, Australia, Israel, South Africa and Morocco). Though most of these recent desalination projects have small (<1000 m³/d) or medium capacities (1000–10,000 m³/d), the trend is to move to large (10,000–50,000 m³/d) and extra-large scale plants (>50,000 m³/d). It is worth mentioning for example several desalination plants in operation in Australia [26], e.g. Port Augusta (8000 m³/d) power by CSP tower power plant or Perth (274,000 m³/d) and Sydney (250,000 m³/d) both powered by wind farms and grid. One recent large-scale project including solar power launched in the World is the Chtouka Ait Baha plant (Souss Massa region) in Morocco. The plant of a capacity of 275,000 m³/d (extendible to 400,000 m³/d before 2030) [27] is expected to contribute to achieve the Moroccan desalination objectives of 768,000 m³/d [28] and even 1.4 Mm³/d according to another source [29].

Based on the Chtouka Ait Baha specifications as a case study, this paper examines the cost competitiveness of an extra-large scale (275,000 m³/d) solar powered desalination. It provides an analysis of the conditions for which solar Photovoltaics (PV) and Concentrated Solar Power (CSP) would be competitive with a grid (mainly fossil) driven seawater reverse osmosis (SWRO) desalination plant. The paper considers also a scenario where battery storage complements PV power generation. The objectives of this paper are threefold. First it analyses the economics of large-scale solar RO plants under present cost assumptions and by 2030. Second, it provides estimates of solar electricity production cost in the country and assesses the economics of Lead-acid battery storage in the Moroccan context. Third, it discusses the implication of solar technology choice for desalination purpose in the framework of the Moroccan energy policy. The paper is organized as follows: In Section 2, the main Chtouka Ait Baha plant characteristics are described and an overview of the methodology adopted in this paper is given. In Section 3, results are presented and discussed. Section 4 provides a prospective analysis on the evolution of the cost of water by 2030. Main conclusions of this study are summarized in Section 5.

2. Methodology

Desalination in Morocco constitutes a market segment with high potential for solar electricity deployment. In order to evaluate this potential rigorously, representative data of solar irradiation, desalinated water capacity and associated electricity needs are required. In this work, localization and specifications of the Chtouka Ait Baha desalination plant (technology and capacity) are chosen to conduct the study. In order to fully assess the competitiveness of solar driven desalination, two steps are followed. First, a simple model that assesses the final cost of desalinated water is computed. Second, the cost related to energy consumption is calculated for different power supply options to assess the impact of energy provision on the final cost of water. This section briefly describes the Chtouka Ait Baha project, introduces the cost of water model (detailed in the Appendix A), gives an overview of the methodology used to calculate the cost of solar electricity and the cost of storage, and finally displays the four main scenarios of power supply retained in this paper.

2.1. The Chtouka Ait Baha project

The Chtouka Ait Baha seawater desalination plant is based on RO technology and is designed for a production capacity of 275,000 m³ m³/d from which 150,000 m³/d are dedicated to fresh water needs and 125,000 m³/d to irrigation (area of 13,000 ha) [30]. Aman El Baraka, which is the Moroccan subsidiary of the project concession company Abengoa, will build, operate and maintain the desalination plant over a period of 20 years. First construction works started in July 2018. The plant will be located at 300 m from Agadir coast at an altitude of 44 m. The project gathers together different local and foreign partners: Ministry of Economy and Finance, Ministry of Agriculture, Maritime Fisheries, Rural Development and Water and Forests, national energy and water utility (ONEE), Spanish companies (Abengoa SA Company, Abengoa Water International Company, SEDA, SA) and the Moroccan BMCE bank, who all signed a convention agreement in 2017. The project cost is about $M 440 of which $M 220 are dedicated to the freshwater production. ONEE is expected to devote additional investments of $M 66 for the construction of 44 km of pipelines, a 35,000 m³ drinking water tank, the installation of 3 high voltage power lines over 55 km from the Tiznit source station which is already connected to the Noor Ouarzazate solar complex and the construction of 2 pumping stations and 2 loading tanks [27]. The specifications of the Chtouka Ait Baha project that have been used as input data for this work are the following (Table 1 ):

Table 1.

Specifications taken from the Chtouka Ait Baha project.

Desalination technology	RO
Daily water production (m3/d)	275,000
Annual availability rate (%)	95
Amortization time (years)	20

2.2. Cost of water model

A simplified model is used to determine the daily production and the water cost of a reverse osmosis (RO) desalination plant powered by any energy source. Due to the relatively quick dynamic of such a system, simulation over a given day is calculated as a succession of steady states, hour per hour. For the purpose of this study, RO is supposed to be operated 24 h a day. When solar resource is not available or insufficient, energy storage (electricity or heat for CSP) or the grid takes over.

Developed with Microsoft Excel™, it includes the following calculation modules:

• ▪RO module: it comprises two user modes: sizing of the RO unit for a required desalting capacity and determining the operating point of the previously sized unit when available power varies. Calculations are based on the method described in FILMTEC™ Reverse Osmosis Membranes Technical Manual [31,32].
• ▪Cost module: usual cost functions for RO are used for CAPEX and OPEX calculations. Coupled with the performance module, it provides a detailed calculation of CAPEX, OPEX and finally the LCOW. Data for this module are taken from different sources [6,[33], [34], [35], [36], [37], [38]]. This module gives water cost breakdown.

Validation of the RO model has been carried out using experimental results from literature and a benchmark with different professional tools (DEEP, IAEA, WAVE) available shows that performance and cost are predicted with a deviation better than 10%.

In most reviewed paper on desalination literature, the cost of desalinated water is computed using the “amortization factor” or “annualized life cycle cost method [[39], [40], [41]]. This calculation method is generally known as Simplified Cost of Water (SCOW) (Eq. (1)) and is based on initial capital costs annualization using an amortization factor [42] (Eq. (2)):

$$\mathit{SCOW}=\frac{I_0\times \alpha +C}{M_w}$$ (1)

$$\alpha =\frac{i{\left(1+i\right)}^n}{{\left(1+i\right)}^{-n}-1}$$ (2)

• I₀: Investment expenditures in $,

• C: Annual operation cost in $,

• M_w: Annual produced quantity of water in m³,

• i: Discounting rate,

• n: Economic lifetime in year,

• α: The amortization rate.

Investment costs (CAPEX) include four major types of expenditure: specific capital cost (pre-treatment, desalination system, post-treatment and other auxiliary equipment), water distribution and storage equipment and finally other capital costs: permitting, land, construction, design and engineering [42,43]. Operating costs (OPEX) include spare parts such as membrane replacement, maintenance cost, chemicals, insurance and labor, and energy cost. The cost of desalinated water is very sensitive to assumptions, input data and methodologies, which challenges the suitable perception of water cost across studies and experiments [43], calling for a clear understanding of desalination cost determinants. Such a clarification, in the case of Morocco, will be one of the major aims of this paper. Therefore, a significant part of the paper is devoted to a thorough description and assessment of both the costs of energy and capital (including technological aspects).

It should be reminded that the calculation of operation costs (OPEX) in the model excludes the cost of energy since it is the principal parameter of the study. Indeed, as the paper mainly focused on the impact of different power supply options on the competitivity of a large scale desalination plant, the specific consumption of the SWRO (kWh/m³) is first calculated, then the power required (kW) and finally the corresponding energy (kWh) over a given period (a year) are computed. Since the plant operates at full capacity 24 h a day, 365 days a year (95% of availability factor), these values are fixed. Depending on the power supply option considered, the only cost that changes is the one related to energy consumption. The energy consumption includes the energy consumption of the reverse osmosis unit (high-pressure pumps and booster downstream of the DREs) but also that of the seawater supply pumps, taking into account the pressure losses in the pipes and in the seawater pre-treatment. The back pressures of the brine and freshwater discharges produced (thus including post-treatment) are also taken into account.

2.3. Solar power economics

As mentioned previously, CAPEX and OPEX (excluding energy) are derived from the cost of water model and are fixed whatever the power supply considered. What varies across all power options is related to the cost of electricity consumption which is obtained by multiplying the quantity of electricity consumed (kWh) by the cost of electricity.

Even if criticized by some authors, the Levelized Cost of Electricity (LCOE) is a commonly used metric to assess the economic feasibility of an electricity production project [44]. It corresponds to the present value of the project costs (in $) per unit of electricity generated (in kWh) over the plant lifecycle [45,46] (Eq. (3)).

$$\mathit{LCOE}=\frac{I_0+\sum _{t=1}^{t=n}\frac{A_t}{{\left(1+i\right)}^t}}{\sum _{t=1}^{t=n}\frac{{M_{\mathit{elec},}}_t}{{\left(1+i\right)}^t}}$$ (3)

• I₀: Investment expenditures in $,

• A_t: Annual operation cost in $ in year t,

• M_elec,t: Annual electricity output in kWh in year t,

• i: Discounting rate,

• n: Economic lifetime in year,

• t: Year of lifetime.

For PV systems, CAPEX includes the cost of modules with the balance of systems (mounting structure, electrical connections, power electronics, tracking systems, etc.) as well as the land cost. OPEX include insurance costs and maintenance, regular cleaning and performance monitoring of the device's costs. For CSP plants, CAPEX includes the solar field (mirrors and receivers), the thermal storage and the power block. OPEX include thermal storage and solar field maintenance (including mirror's periodic cleaning).

Today, PV is the leading solar technology in terms of installed capacity and is the most cost competitive one. Driven by continuous technological improvements and large-scale deployment, PV LCOE has dropped in average from 0.36 $/kWh to 0.10 $/kWh between 2010 and 2017, following the IRENA database statistics [47,48]. In the same period, average CSP LCOE has decreased at a slower rate from 0.33 $/kWh to 0.22 $/kWh. Long term forecasts and roadmaps suggest a further decrease in the cost of solar technologies [49,50]. By 2030, expected LCOE for solar technologies would reach 0.03 $/kWh for PV and 0.05 $/kWh for CSP systems [51]. These values correspond to the 2030 “aggressive cost targets” of the U.S. Department of Energy (DOE).

When PV systems include storage devices, the cost of stored electricity can be calculated using the Levelized Cost of Storage (LCOS) metric (Eq. (4)) which is derived from the LCOE method. The LCOS is defined as the total lifetime cost of the investment in electricity storage technology divided by its cumulative delivered electricity [52]. CAPEX is added to the annual cost of storage A _t discounted over the lifetime of the project. This sum is then divided by the discounted sum of annual electricity output W _outt. A _t is composed of operation expenditures OPEX, reinvestments in storage components CAPEX _ret,and the cost of electricity supply determined by the price of electricity c _el times the amount of electricity delivered to the battery W _in (Eq. (5)).

$$\mathit{LCOS}=\frac{I_0+\sum _{t=1}^{t=n}\frac{A_t}{{\left(1+i\right)}^t}}{\sum _{t=1}^{t=n}\frac{{W_{\mathit{out}}}_t}{{\left(1+i\right)}^t}}$$ (4)

• I₀: Investment expenditures in $,

• A_t: Annual cost of storage in $ in year t,

• W_outt: Annual electricity output in kWh in year t,

• i: Discounting rate,

• n: Economic lifetime in year,

• t: Year of lifetime

$$A_t=\mathit{OPE}{X}_t+\mathit{CAPE}{X_{\mathit{re}}}_t+c_{\mathit{el}}\times W_{\mathit{in}}$$ (5)

• A_t: Annual cost of storage in $ in year t,

• CAPEX_ret: Reinvestment in storage system components in year t,

• c_el: Price of electricity supply,

• W_in: Annual electricity input.

Several studies assessed the LCOS of different energy storage technologies [53,54]. For example, [55] found a LCOS for lead-acid batteries of 0.17 $/kWh whereas the LCOS for li-ion batteries is found to vary between 0.2 $/kWh and 0.3 $/kWh by Lazard [56]. These costs are expected to decrease strongly in the next decade due to technological developments and decreasing CAPEX. By 2030, the LCOS of Li-ion batteries at 365 cycles per year would vary between 0.09 $/kWh and 0.23 $/kWh whereas the LCOS for lead acid batteries is expected to range between 0.11 $/kWh 0.15 $/kWh [52].

2.4. Power supply cases

Four case studies of power supply have been considered in this work. Case 1 supposes that the desalination plant is powered by the national grid. Case 2 assumes that the desalination energy requirements are satisfied jointly by the grid and by a nearly located PV power plant. Case 3 considers that the desalination plant is powered by the grid, the nearly located PV power plant and lead-acid batteries. Case 4 assumes that the desalination plant is powered by the grid and an inland CSP plant located in the desert. More details of each case are given below:

• ▪Case 1 is based on a fully “Grid “power supply. The plant is powered by the national grid and purchases its electricity at present utility tariffs which are hourly dependent and taken from the ONEE website [57].
• ▪In Case 2, part of the grid power supply is replaced by solar electricity coming from a PV plant located on the same site as the desalination plant. To design the PV plant, the chosen area of solar panels (m²) is selected so as the maximum solar electricity production equals the nominal maximum power of the desalination plant. The PV plant design is based on the day of the year where solar irradiation is the maximum over the year. Under this design, there is no excess PV production in the year and the grid is supposed to complement solar electricity supply whenever needed.
• ▪In Case 3, Lead-acid batteries are introduced for peak shaving. As the Moroccan load curve shows a high peak load during evening hours (5 pm to 10 pm in the winter and 6 pm to 11 pm in the summer), using batteries can increase the desalination plant self-consumption and contribute to maintaining grid stability. Moreover, electricity tariffs are the highest during this period of the day. Batteries are designed only to power the plant during these peak hours. To determine the additional area of solar panels required to feed the batteries, the marginal area needed to supply the five peak hours consumption is added to the PV panel area calculated in case 2. Cost data of batteries are taken from the relevant literature.
• ▪In Case 4, a future unit of the Noor CSP Complex (including thermal storage) is supposed to be entirely dedicated to the power the desalination unit. It is assumed that the CSP unit powers the RO plant from 10 am to 10 pm (12 h of operation) in average, whereas the grid powers the desalination plant for the remaining hours of the day. In this case, the cost of CSP power generation is based on present CSP LCOE in Morocco.

All cases are compared through the sum of all variable charges related to the different power supply sources used to power the desalination plant. For each case, an average cost (variable) of electricity is deduced and used as an input to calculate the final cost of desalinated water depending of the power configuration adopted. (Table 2 ).

Table 2.

Alternative cases of power supply covered in this study.

Case number	Name
Case 1	Grid
Case 2	PV + Grid
Case 3	PV + Storage + Grid
Case 4	CSP + Storage + Grid

3. Results

3.1. Breakdown of the cost of water

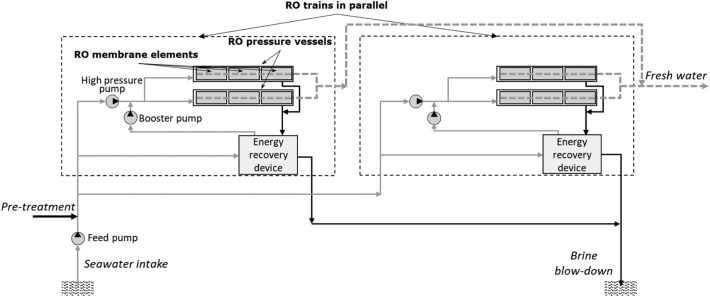
The modelling approach developed aims at analysing the interrelations between the cost of desalinated water and the cost of energy in a large-scale desalination with 95% availability. In order to evaluate rigorously the impact of the technology on the desalinated water cost, it is mandatory to have an accurate description of the technical choices made for building the desalination plant. As these details are not public, technical characteristics of a virtual desalination plant that could fulfil the global production specification of the Chtouka Ait Baha plant has been determined and sized (Table 3 ) using the model described in detail in Appendix A.

Table 3.

Calculated technical characteristic of the virtual “Chtouka Ait Baha like” RO plant.

Calculated energy needs
Total nominal power (kWe)	45,740
Annual energy consumption (GWh/y)	380
Specific energy consumption (kWh/m3)	4.0

Calculated technical details of RO plant
Number of trains	16
Number of pressure vessels/train	150
Number of membrane elements/pressure vessel	7
Total number of membrane elementsa	16,800
Energy recovery devicesb	220
Feed pressure (bar)	64
Conversion rate	43.5%

^aThe standard membrane surface for each membrane element is 37,15 m².

^bThe energy recovery device based on pressure exchanger is based on ERI PX300 model.

These technical components and their dimensioning have been used to determine the CAPEX for building the desalination plant and its OPEX, excluding energy consumption cost, that is studied in the next section. Calculated data are gathered in Table 4 .

Table 4.

Inputs for LCOW calculation - Estimation of CAPEX and OPEX based on the model output and on data from literature [[33], [34], [35], [36], [37], [38],42].

CAPEX	Value ($/(m3/d))
RO modules (trains, pressure vessels and membrane elements)	70
Other equipment (pumps, pre-treatment (filtration and chemicals), energy recovery devices, power electronics etc.)	450
Sea water intake/brine reject	100
Site preparation - Construction	400
Other costs (engineering, shipping, legal costs)	140
Total CAPEX (including 5% for contingency)	1220

OPEX	Value ($/m3)
Membrane replacement (20%/y)	0.03
Chemicals	0.08
Maintenance & spare parts (2% total CAPEX/y)	0.07
Brine disposal and other externalities	0.04
Insurance (0,5% total CAPEX/y)	0.02
Labor	0.05
Electricity	See next section
Total OPEX excluding electricity	0.29

To calculate the contribution of CAPEX ($/m³) to the LCOW, the amortization rate α is calculated and found to be 0.087 using Eq. (2), and assuming a discounting rate of 6%, an amortization time of 20 years and 95% plant availability (A). Using Eq. (6) below, the CAPEX contribution in ($/m³) is calculated to reach 0.31 $/m³. Excluding the cost of energy, the contribution of OPEX to the LCOW is estimated to be 0.29 $/m³.

$$CAPEX=\frac{\mathit{Total}\left(\mathit{daily}\right)\mathit{CAPEX}\times \alpha }{A\times 365}$$ (6)

• Total (daily) CAPEX: Total CAPEX expressed in a daily base in $/(m³/d),

• α: Amortization rate,

• A: Plant availability in %.

Thus, the CAPEX+OPEX cost (without energy) of the optimized plant appears to be 0.60 $/m³. The fixed costs (capital and most part of the operation costs) represent about half of the water production costs. This implies that it is very important to use the desalination plant continuously over the year, if it is kept in mind that there is always a strong demand for water. This result is the base of all the following computations where the desalination plant is supposed to run all the yearlong. Besides, knowing that energy needs are about 4 kWh per m³, and that the public cost of electricity is close to 0.1 $/kWh (in order of magnitude), it can be concluded first of all that the cost of energy is a very important parameter (representing roughly half of the cost) and second of all, that the production cost of water will be about 1 $/m³, which is a very competitive/interesting result, in line with the range found in the literature. Such a good result is obtained because of two mains causes: the high performance of the reference technology (which is fully up to date) and the high rate of average sun irradiation in Morocco.

As the final cost of desalinated water depends heavily on the cost of electricity, the following part of the paper will focus on this item. Several solar based power supply configurations considered in this paper and respective costs are calculated and discussed in the following section.

3.2. The cost of power supply

This section mainly focuses on the cost of electricity generation from the four different power supply options retained in this paper.

3.2.1. Case 1: Grid power supply

In Morocco, electricity tariffs are administrated and regulated by the government to protect the economic competitiveness of local industries and the purchasing power of low-income households. Under the current pricing scheme, subsidies and associated electricity tariffs depend on the consumer category (urban/rural household, energy-intensive industries…) and the daily time slot of electricity consumption [57]. For the medium voltage (case of the desalination plant), subsidies and associated electricity tariffs depend on the season (summer, winter) and the hour considered: i.e. peak, full, and off-peak. As displayed in Table 5 , the off-peak tariff is 0.73 times the full hour tariff whereas the peak tariff is 1.36 times higher than “the full hours” tariff. In addition to variable electricity tariffs, an annual power charge of 56 $/kVA/y1 is applied (tariffs include a 14% added value tax applied for electricity products).

Table 5.

Electricity pricing for medium voltage industries [57].

.	Peak hour	Full hour	Off peak
Winter	5 pm–10 pm	7 am-5 pm	10 pm–7 pm
Summer	6 pm–11 pm	7 am-6 pm	11 pm–7 pm
Electricity price ($/kWh)	0.15	0.11	0.08

Based on the above pricing and since the electricity consumed by the desalination plant is supposed to be “flat” (i.e. identical at each hour at a level of 43 MWh), the average electricity cost is assumed to be around 0.11 $/kWh (corresponding to the ONEE “full hours” tariff). The average electricity cost is simply obtained by dividing the sum of hourly grid charges in M$ (hourly consumption * hourly tariff) with annual desalination consumption (kWh).

3.2.2. Case 2: PV + Grid power supply

Considering that the city of Agadir (near Chtouka Ait Baha) benefits from excellent solar irradiation and that the cost of solar PV modules decreases continuously, it is worth investigating the economic feasibility of a PV + Grid configuration to power the desalination plant. To estimate the average yearly energy production of a PV system connected to the electricity grid in Agadir, the PVGIS online tool was used for input solar irradiation hourly data. The calculations consider solar irradiation, and type of PV module. The modules are supposed to be mounted on a free-standing rack, without any tracking system. As it is proved to be the most cost-effective solution for solar power generation in Morocco [58], polycrystalline silicon technology is considered. In PVGIS, the optimum slope and orientation that maximizes the yearly energy production based on typical meteorological year data (2014) are automatically generated. Table 6 displays input data for the PV plant design. As the module efficiency depends on irradiation and temperature, an average efficiency module value is selected. The performance ratio takes into account all system loss. As polycrystalline silicon is a very robust technology, it is assumed that availability is also included in the performance ratio. The typical meteorological year (TMY) database from PVGIS displays annual representative solar data for the chosen location based on selected data over a long period (2007–2016). This annual data set is used to calculate PV electricity production based on irradiation data.

Table 6.

PV plant data design.

PV configuration		Source
PV technology	Crystalline silicon	PVGIS-CMSAFa
Optimized slope	31°	PVGIS-CMSAF
Optimized azimuth	11°	PVGIS-CMSAF
Module efficiency	15.2%	[58]
(Latitude, longitude)	(30.421, −9.583)	PVGIS-CMSAF
Yearly GHI (kWh/m2/year)	2128	PVGIS-CMSAF (TMY)
Performance ratio	81%	[58]

^ahttps://re.jrc.ec.europa.eu/pvg_tools/en/tools.html.

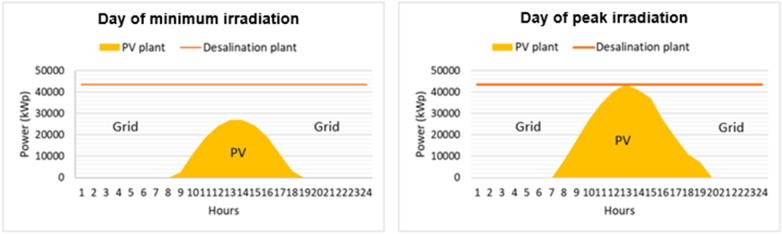
According to the download TMY for Agadir location, the yearly solar irradiation reaches 2128 kWh/m²/y which corresponds to 262 kWh/m²/y of PV electricity output (2128×0.15×0.81). To size the PV system a first reference case is considered. It supposes that all the PV output is self-consumed by the desalination plant (no excess PV production during the year). The area of PV modules is determined such as the maximum PV power (0.13 kW/m²) during the solar peak hour (29 April at noon) equals the nominal power of the desalination plant (43 MW). The required area is about 323,200 m² (43/0.13) which implies a surface ratio of 7.48 m²/kWp. This represent less than a square km, with the current densities of panels in solar farms in the Maghreb. Even if this surface is not negligible, it is no difficulty to find it near Agadir. Under this design, all the desalination load is satisfied by PV on the solar peak hour, whereas for the remaining hours of the year, depending on the PV output, the desalination electricity requirements are partially or fully met by the grid (e.g. at night). Fig. 1 displays an example of the respective contributions of PV and grid power supply to satisfy the desalination plant power consumption on representative days of high and low irradiance days.

Fig. 1.

PV and Grid respective power supply to satisfy the RO unit electricity needs for two representative days of low (left) and high solar irradiance (right).

With this first hypothesis, the ratio between annual electricity consumed from PV and total desalination electricity needs is around 22%. This ratio is quite low, which shows that this case appears not to be far from the case 1, with a “marginal” addition of solar energy. The ratio of PV consumption/PV production is exactly 100% as all the PV production is used.

To assess the cost of PV production, PV LCOE is computed based on Eqs. (3), (7) [59], (8) and input data displayed in Table 7 . Indeed, the annual electricity output M_elec is calculated by integrating the instantaneous PV production of Eq. (7) over one year, corrected with Eq. (8) to take into account ageing. M_elec is then introduced into Eq. (3) to obtain the LCOE over the entire lifetime of the PV farm. Doing so all contributions to electricity cost such as maintenance or amortization are included.

$$P{V_{\mathit{output}}}_t=\mathit{GH}{I}_t\times P{V}_{\mathit{eff}}\times \mathit{PR}\times A$$ (7)

• PV_outputt: Electricity output in time t,

• GHI_t: Global horizontal irradiance in t in kWh/m²,

• PV_eff: Efficiency of polycrystalline silicon modules in %,

• PR: Performance ratio in %,

• A: Total solar panels area (m²).

Table 7.

Input data for PV LCOE calculation.

Component	Value	Source
CAPEX ($/kWp)	1130	[60]
OPEX (% CAPEX)	1.5%	[61]
Output degradation factor	0.9%/y	[58]
Lifetime	25 years	[58]
Discount rate	6%	[62]

Ageing can be modelled very simply by Eq.(8) as following:

$$E_t=E_o\times {\left(1-d\right)}^t$$ (8)

• E_t: The annual energy output during the year t in kWh,

• E_o:The annual energy output during first-year operation in kWh,

• d: The degradation rate (%) of PV systems over the specified period,

• t: Years

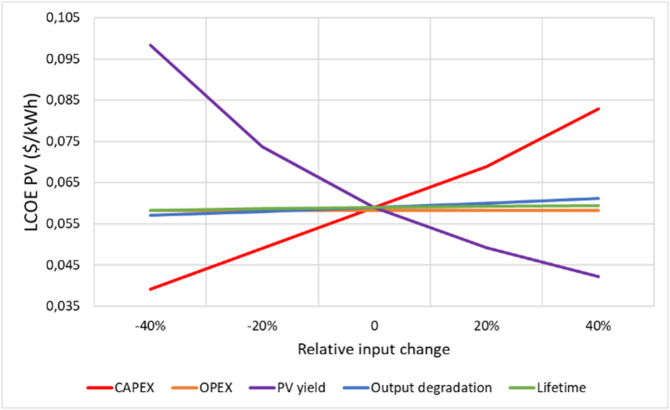
The calculated PV LCOE is found to reach 0.06 $/kWh. In order to capture the change in LCOE caused by relative percentage change in input parameters, a sensitivity diagram was constructed (Fig. 2 ). A variation of ±40% on the reference value of CAPEX, OPEX, PV yield, output degradation and lifetime (as displayed in Table 7) has been conducted. Among the technical parameters, the PV yield is the most important factor that influences the LCOE. The lower the PV yield, the higher the LCOE. CAPEX is also a determining factor in the LCOE calculation. The higher the CAPEX, the higher the LCOE. This result reveals the importance of CAPEX cost reductions and technological improvements to achieve lower LCOE. Output degradation, lifetime and OPEX variation seem to have a very limited impact on the LCOE within a variation range of −40% + 40% compared to the reference value.

Fig. 2.

PV LCOE sensitivity diagram as a function of various engineering parameters.

The chosen value of the discount rate is also a determining factor that influences the value of the calculated LCOE. The reference discount rate used in this study is assumed to be 6%, which is a relevant level for a strategic investment largely driven by the national administration. For a minimum discount rate of 4% (close to a fully public rate), the LCOE would decrease by 20% whereas for a discount rate of 10% (more private rate), the LCOE would increase by almost 40%.

The calculated PV LCOE (0.06 $/kWh) represents 55% of the average electricity price of the first case of this study, namely the fully Grid power supply option. In case 2, using PV by a share of 22% would drop the average cost of electricity from 0.11 $/kWh in the case of a 100% Grid option to 0.096 $/kWh (−13%) in the present case of hybrid PV + Grid power supply. This comes from a cost of solar energy which is half of the average cost of the national grid in average.

It is worth noting that the cost of PV electricity (0.06 $/kWh) is low compared to the values classically found in the literature [47]. Such a value is possible because of the high solar irradiation in Morocco, with advanced hardware. In this study, local PV production competes with electricity of the national grid, the price of which, even if subsidized, includes significant transport costs. The first conclusion that can be drawn is that there is an economical interest in linking the desalination plant to a solar farm. In addition, this case 2, as described above, offers the best yield from each solar panel, because all the production is used. The drawback is that the share of solar electricity remains low (22%). In fact, this case does not represent the minimum cost without storage.

If part of the solar production is curtailed, the share of solar electricity available to power the desalination plant could significantly increase. However, this configuration would lead to an additional charge to be “paid” for this larger share of solar PV production, as part of the production has to be curtailed and wasted. Fig. 3 displays the impact of doubling and tripling the reference PV surface on the average electricity cost (which is the weighted cost due to PV and grid electricity).

Fig. 3.

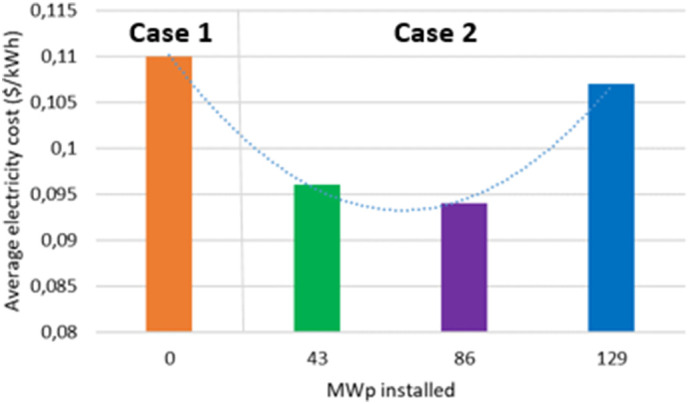
Impact of PV installed capacity on the average electricity cost ($/kWh). Case 1 is based on a 100% grid power supply. In case 2, the PV surface is varied from 43 MWp (reference case) to 129 MWp (tripling of the reference PV surface).

The least cost option appears to be close to the one where the PV surface is doubled compared to the reference case. In addition, the minimum seems to be rather flat and it can be considered to be close to the optimum. Consequently, in the following and for economical comparisons, the retained PV surface for case 2 is the one resulting in the installation of 646,400 m² of PV panels. As the PV area is doubled, more solar electricity is produced. Therefore, the PV electricity contribution to power the desalination plant illustrated by the ratio PV electricity consumption/desalination total electricity demand also increases. Doubling the PV surface results in an increase in this ratio from 22% to 35%. However, the ratio of PV consumption/PV production decreases from 100% to 78% since the surplus PV production is curtailed and wasted (no storage considered, nor selling to the national grid). When tripling the initial PV surface, the contribution of PV electricity to the desalination electricity demand increases to 39%, and the ratio of PV consumption/PV production decreases further to 58% (same hypothesis). Table 8 summarizes the results of this sensitivity analysis.

Table 8.

Summary of results in the hybrid PV + Grid case.

PV plant size	Max PV power = 1*Desal power	Max PV power = 2*Desal power	Max PV power = 3*Desal power
MWp installed	43	86	129
PV surface (m2)	323,200	646,400	969,600
PV electricity/desalination electricity demand	22%	35%	39%
PV consumption/PV production	100%	78%	58%
Average electricity price ($/kWh)	0.096	0.094	0.107

One of the main results is that the use of PV (without storage) allows to decrease the total cost of electricity by around 15% (0.094 $/kWh instead of 0.11 $/kWh).

A remaining question, with the important share of curtailed electricity quoted above, would be to implement a module of power electronics and sell power to the national grid. However, selling the peak production to the grid, in a future where Morocco plans to rely more and more on solar energy (with a significant share of PV) does not look a sustainable option: the future value of PV in peak production hours could decrease rapidly over time. Another relevant option for avoiding wasting PV electricity is to consider the storage of surplus electricity. This option is studied in case 3.

3.2.3. Case 3: PV + Storage + Grid power supply

This case supposes the introduction of lead-acid batteries (lower CAPEX than Li-ion; heavier, but without consequences for the purpose of this paper) to meet the desalination load during the evening peak hours when electricity tariffs are the highest in Morocco and when there is no sun in winter. Starting from the case 2 (where no excess PV is produced with the installation of 43 MWp), an additional area of PV panels is introduced to power the five evening hours demand of the desalination unit. Batteries are designed for behind-the-meter peak shaving especially when peak demand occurs in the evening as for Morocco. Excess PV electricity produced by these additional PV panels during sunny hours is stored in the batteries and then reused to power the desalination plant using an efficiency ratio of around 77% (see hereafter). During off-peak and full load hours, the grid completes the PV output. Based on available data and in order to give global estimates on the effect of introducing batteries on the desalination electricity cost, the design of batteries is based on a simple approach that considers a typical spring day (15 April 2014) for the calculation even if the resulting size of batteries is not expected to be the exact optimal one (as for PV sizing). In winter days, solar irradiance is the lowest and the energy produced by PV panels is low, so batteries are not (fully) charged in this period of the year. In summer days, energy produced by the PV plant is the highest resulting in excess energy production that need to be (partially) stored in batteries. During the summer, days are longer and solar irradiation is higher so there is paradoxically not a strong need to charge batteries. As an intermediate solution, choosing a day of spring (mid-season) appears as a reasonable option to dimension the batteries in order to assess the profitability of introducing batteries to power the desalination. Table 9 summarizes basic parameters considered in this case 3.

Table 9.

Battery parameters retained in this study.

Battery parameters	Value	Source
Battery degradation	1%	[63]
Battery lifetime (years)	10	[52]
Depth of discharge	50%	[52]
Roundtrip efficiency	77%	[52]
Discount rate	6%	[62]

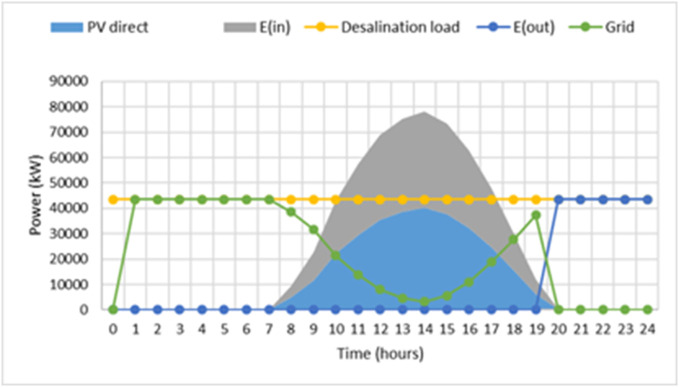
As the hourly consumption of the desalination plant is identical throughout the year, and based on the reference spring day, the daily electricity that needs to flow out from the batteries E(out) is 215 MWh (43×5). Considering a roundtrip efficiency of 77%, excess PV production that flows in the batteries needs to be 1.3 times higher (215×1.3), reaching 269 MWh. Considering a depth of discharge of 50% for limiting battery degradation, the size of batteries needs then to be doubled, reaching 538 MWh (269×2). Using the bisection method and considering the daily PV surplus (including efficiency losses), it is found that 300,000 m² additional PV panels are required to satisfy the desalination plant consumption during the 5 additional peak hours (Fig. 4 ). PV direct corresponds to the PV energy produced. E(in) is the surplus energy that flows in the battery and E(out) is the energy that flows out of the battery. It is worth noting that the additional PV surface obtained (based on mid-season) is found to be close to the one calculated previously as the PV surface that lowers the average annual cost of electricity without any storage.

Fig. 4.

Consumption from batteries, PV and the Grid for the mid-season (reference).

Results of direct and surplus PV generation are displayed in Table 10 based on simulation on the mid-season.

Table 10.

Direct and surplus PV production.

PV production	(GWh/y)
Direct PV production	85
Excess PV production E(in)	80
Excess PV production out of storage E(out)	79

The cost of direct and excess PV production is based on the PV LCOE, whereas the cost of electricity stored in batteries and used to power the desalination plant during peak hours is based on the LCOS which is computed on the base of Eq. (5) and input data displayed in Table 11 .

Table 11.

Input data for LCOS calculation.

CAPEX	Value	Source
Storage unit ($/kWh)	280	[52]
Discharging unit ($/kW)	80	[52]

OPEX	Value	Source
Discharging power (% CAPEX)	2	[52]

The calculation of the LCOS is based on different days (representing various seasons) for battery sizing. The lowest LCOS is obtained when designing batteries on the mid-season (15th April). The calculated LCOS is found to be equal to 0.3 $/kWh (<0.5 $/kWh found in [56]). The average electricity cost is found to reach 0.135 $/kWh. This cost is calculated as the sum of (PV consumption×LCOE PV), (Grid consumption × hourly tariff), and (consumption from batteries ×LCOS), divided by the total desalination demand. This result, even if it is not the exact minimum, shows clearly that for a quasi-similar surface of PV, introducing batteries rises the average cost of electricity by almost 50%. This result suggests that for large scale RO, batteries may not be a relevant option for lowering the cost of power supply. However, this statement might change when taking into account the remuneration for the service batteries provide to the system, but this analysis is out of the scope of this study.

The results advocate for future research, based on detailed data, for assessing if there will be room (and when) for batteries, especially for allowing to reduce the net evening demand for electricity (“net” meaning that the apparent load of the desalination plant could be decreased when using the batteries; the question is certainly difficult, because the evening peak demand occurs in winter, when the solar production is the lowest). This question is in fact a broader one, because it addresses the value of storage for the Moroccan grid.

3.2.4. Case 4: CSP + Storage + Grid power supply

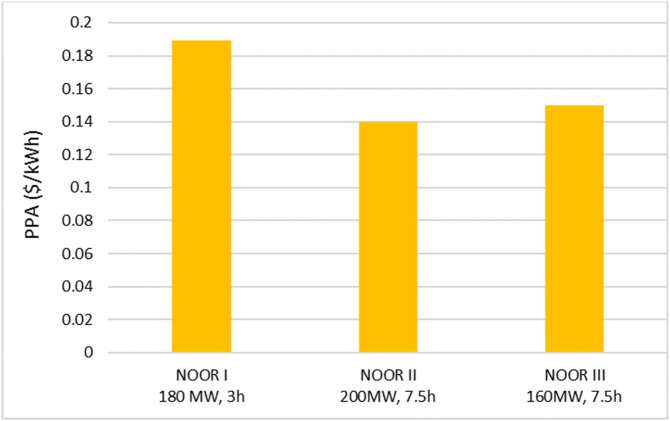
Since its new energy strategy in 2009, Morocco has gained experience in CSP project development. The first CSP plant Noor I (160 MW, 3 h of molten salt storage) was operational in 2016 and produced 402 GWh in 2017 [64]. Noor II (200 MW, 7 h of storage) and Noor III (160 MW, 7.5 h of storage) are expected to be operational soon. Fig. 5 shows the expected reduction of the Purchasing Power Agreement (PPA) of these three power plants in Morocco [65], which is considered as an indicator of the LCOE of CSP plants. CSP PPAs follow a downward trajectory dropping from almost 0.2 $/kWh for Noor I to 0.13 $/kWh for Noor II (both based on parabolic trough which is a commercially proven and the dominant technology in the market with a 90% market share in 2018). The LCOE of Noor III (tower technology) is estimated to reach 0.15 $/kWh which is slightly higher than Noor II because tower technology is less commercially developed than parabolic trough. However, as tower technology allows operation at higher temperatures and pressures (increasing operational efficiency), significant scale economies are expected from wider tower development in the coming years. As a general trend, the LCOE of both CSP technologies are expected to fall down in the coming years.

Fig. 5.

PPA ($/kWh) of NOOR CSP power plants in Morocco [65].

Along with the development of CSP power plants, this case considers that instead of using batteries for peak shaving, an inland CSP plant located in Ouarzazate will be dedicated to meet the desalination plant for 12 h of operation. The power plant, with its heat storage capacity, is supposed to operate from 7 am to 10 pm, during “full hours” and “peak hours”, where electricity tariffs are the highest and to take advantage of CSP storage during evening peak hours. It is thus considered that for 15 h, the desalination plant electricity requirements are met by solar production coming from the inland desert. In this case 4, the reasonable assumption that the cost of this solar electricity would be equal to Noor III LCOE (0.15 $/kWh) is made. For this cost of electricity generation, a rough estimation of the cost of electricity transmission from Ouarzazate to Agadir (300 km) is conducted based on technical data for the French Flamanville line project2 [66,67] and data on transmission line cost published by ETSAP [68]. Table 12 summarizes input data used in the estimation of the cost of transmission. A discount rate of 6% and a lifetime of 25 years are supposed for the calculation.

Table 12.

Input data to calculate the cost of the transmission line (1€ = 1.11$).

Component	Unit	Value	Source	Comment
Transmission line	($/MW/km)	1170	[[66], [67], [68]]	Average value (Flamanville, ETSAP)
Pylons	($/MW/km)	160	[66,67]
Land use	($/MW/km)	330	[66,67]
Substations	($/MW)	19,000	[[66], [67], [68]]	Average value

Supposing that the transmission line capacity is 100 MW for a tension of 220 kV (this capacity represents more than the double of the desalination capacity, because for long distance few projects would imply too high costs). It is assumed that the remaining capacity is used – at cost – for linking the Ouarzazate production complex to the coastal grid near Agadir, and that 2 substations are required. The breakdown of the cost of the transmission line is given as follows:

• ▪Cost of the line (M$): 35
• ▪Cost of pylons (M$): 5
• ▪Cost of land use (M$): 10
• ▪Cost of substations (M$): 4

The total cost of the transmission line is therefore roughly estimated at 54 M$ which corresponds to 1,8 k $/MW-km. Assuming an annual production factor of around 50%, the transported energy is estimated to reach 440 GWh (100×8760×0.5). Transmission losses are fixed at 5%. The obtained cost is around 0.01 $/kWh. The total cost of producing and transporting electricity from Ouarzazate to Agadir is therefore fixed to 0.16 $/kWh (0.15 + 0.01).

Based on the estimated cost of CSP generation (including electricity transport) and the ONEE tariffs, the average cost of electricity in the case of a CSP + Storage + Grid power supply option reaches 0.13 $/kWh. This cost is calculated as the sum of CSP consumption × CSP LCOE (including transport) and grid consumption × hourly tariff divided by the desalination total consumption.

3.2.5. Review of results on electricity cost

Based on all the above cases, it is now possible to compare the different possibilities of supplying the desalination plant with solar electricity, in order to assess the relevance of the different power supply options, in the Moroccan context. Table 13 summarizes the average electricity cost in each of the cases covered in this study. The lower cost option is achieved when PV is combined to the grid without using batteries (around 86 MWp of installed PV), whereas “PV + Storage + Grid” is found to be the less cost competitive option compared to all the power supply options considered. When comparing solutions with storage, CSP + Storage + Grid is slightly more competitive than PV + Storage + Grid. But introducing storage whatever the solar technology adopted, is less competitive than a grid-based solution or only a PV+ Grid solution.

Table 13.

Annual electricity charge and average electricity cost of different power supply options.

Power supply	Grid ONEE tariffs	PV + Grid (Max PV power = Desal power)	PV + Grid (Max PV power = 2*Desal power)	PV + Storage + Grid	CSP + Storage + Grid
Average electricity tariff ($/kWh)	0.110	0.096	0.094	0.135	0.130

As all the studied cases rely on the grid to fully or partially satisfy the desalination load. A variation of the average grid electricity tariffs would impact the average cost of electricity to the desalination plant. As it is well known that electricity tariffs in Morocco are below the cost of electricity generation, it may be expected that if electricity prices were cost reflective, the competitiveness between all cases would change. The estimation of the recovery cost of electricity in Morocco will be the subject of a forthcoming paper3 but the result is important in the framework of this work. In particular, the decision of building a desalination plant such as Chtouka Ait Baha relies to the Moroccan administration. Thus, this body will have to examine the global economic balance of the different electric supplies also in term of impact on the national budget by considering the “real” cost of electricity production and distribution, which is higher than the present tariffs. All the preceding results are based on a cost of electricity derived from the existing tariffs. All the costs are then based on market prices and the spirit of this assessment is to choose the lower cost electricity mix for a private firm investing in the desalination plant. This can be discussed since energy decision largely refers to the choice of the government. Indeed, the Moroccan government is the major decision maker, the main ruler and main investor (even if investments are done by private firms, but the capital of which is largely state owned) is the state itself. Indeed, the ONEE tariffs do not take fully account of the real cost of electricity production, as they can be viewed from the state (because of the presence of subsidies, and because of external costs). For instance, if these “hidden” costs are high, a decision based on a myopic analysis could favour an electric mix which implies important losses for the government (subsidies) or the collectivity (external costs).

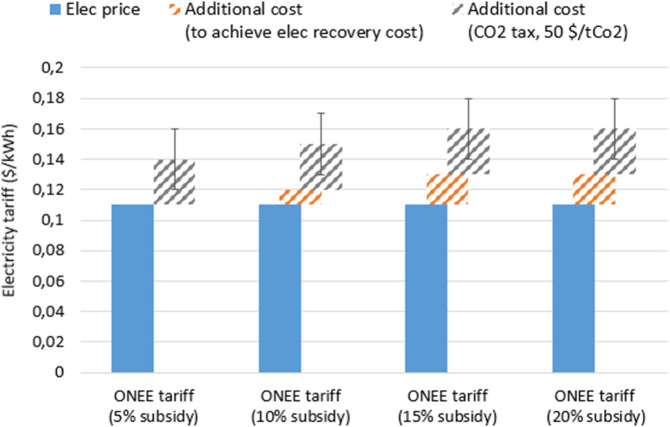
Because of a limited public data access, the estimation of the recovery cost of electricity in Morocco is a difficult task. Though, the World Bank recent report on MENA utilities performance revealed that the ratio of total energy sales out of total costs for ONEE is around 87% in 2013 [69]. This ratio is considered as a financial indicator of utilities performance. The ratio is constructed as revenues related to energy consumption and service ($) / (OPEX + depreciation of fixed assets+ other depreciation and provisions – net interest). In the absence of detailed data, a reasonable assumption is to consider that electricity subsidies vary between 5% and 20% of the generation cost, which supposes that the average electricity tariff would range between 0.11 $/kWh and 0.13 $/kWh without considering any additional cost for CO₂ emissions. If a carbon tax of 50 $/tCO₂ is applied to the 21 MtCO₂ generated in 2016 (data applied to 2016 because of data availability) by the power sector to generate the 31 TWh of electricity generation in Morocco (2016 data) [70], an additional cost of 0.03 $/kWh would lead to higher tariffs, varying between 0.14 $/kWh and 0.16 $/kWh. Fig. 6 displays the variation of the electricity price based for three different subsidy rates: 5%, 10%, 15% and 20% and taking into account the CO₂ tax. As shown, electricity prices could increase from 0.14 $/kWh up to 0.16 $/kWh depending on the taken hypothesis on the rate of electricity subsidies and on the value of the CO₂ tax.

Fig. 6.

Variation of electricity cost under different subsidies with a 50 $/tCO₂ tax on fossil generation. (Here it is not considered that the supply to national grid could be more decarbonized in the future, because it is assumed that this trend will occur much slower than the start of the desalination plant.)

With electricity subsidies varying between 5% and 20% and a 50 $/tCO₂ tax, the cost of electricity would range between 0.14 $/kWh and 0.16 $/kWh resulting in a cost of water between 1.16 $/kWh and 1.24 $/kWh in the case of a 100% Grid power supply. These costs could be interpreted as the cost of desalinated water from the “public” point of view as compared to the previous costs calculated from a private firm standpoint (not a very significant different option). Because of a high incertitude on the real increase rate for which ONEE tariffs would be cost reflective (real subsidies, future carbon tax), Fig. 7 represents the expected increase on the average cost of electricity for different power supply to the desalination plant with an increase in ONEE tariffs between of 10% and 40%.

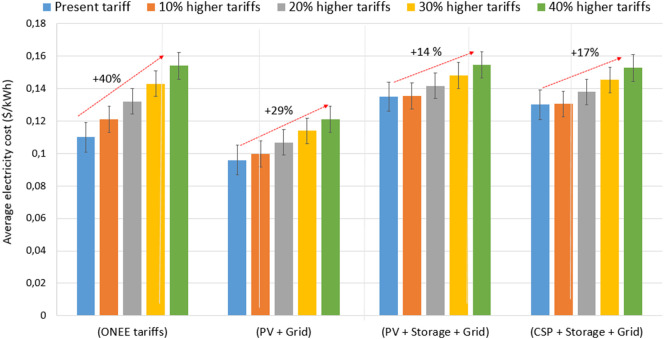
Fig. 7.

Impact of the increase in grid tariffs (+10%, +20%, +30% and +40% from current ONEE tariffs) on the average cost of electricity in all cases considered in this study.

The relative sensitivity to the grid price increase differs across the cases. For a 40% increase in the grid average electricity price, the average cost of electricity of the four power supply options ranges between +14% to +40%. Obviously the most affected option is the one that relies the most on the grid which the 100% grid power supply option. An increase of 40% of grid electricity prices would rise the average cost of electricity for the PV + Grid option by 29%. However, both cases with storage are less sensitive to the variation in electricity prices resulting in an increase of 14% and 17% in case of PV + Storage + Grid and CSP + Storage + Grid respectively. It is worth nothing that if grid electricity prices increase by 40%, the cost of electricity from a 100% grid power supply, PV + Storage + Grid and CSP + Storage + Grid would be almost equal (around 0.15 $/kWh) which reveals that the use of solar technologies for desalination is all the more relevant in a context of rising electricity prices which is a very realistic scenario in the Moroccan context. Even if the PV + Grid alternative is more sensitive to the two storage-based solutions, it remains the least cost option even with an increase of 40% in grid electricity prices. Compared to the three other power supply alternatives, the PV + Grid option results in an average cost of electricity of 0.12 $/kWh which is 20% lower than the average cost of all other alternatives (0.15 $/kWh). As stated above, the remuneration from demand curtailment due to storage is not taken into account but if considered, it will probably increase the attractiveness of storage-based solution compared to battery-less power supply alternative especially in the context of increasing electricity tariffs. As stated above, even if electricity remains subsidized in Morocco, the level of cost to be taken by the public authorities has to take account both the subsidy costs and the external costs.

3.3. The impact of electricity cost on the cost of water: illustration for farmers

Based on the average electricity tariffs for each of the power supply options calculated previously, Fig. 8 displays the total cost of water, distinguishing between the energy cost related part and the non-energy cost part. Results reveal that the cost of desalinated water would range between 0.98 $/m³ (PV + Grid) and 1.14 $/m³ (PV + Storage + Grid) with the share of electricity cost in the total cost of water varying between 39% and 47% respectively.

Fig. 8.

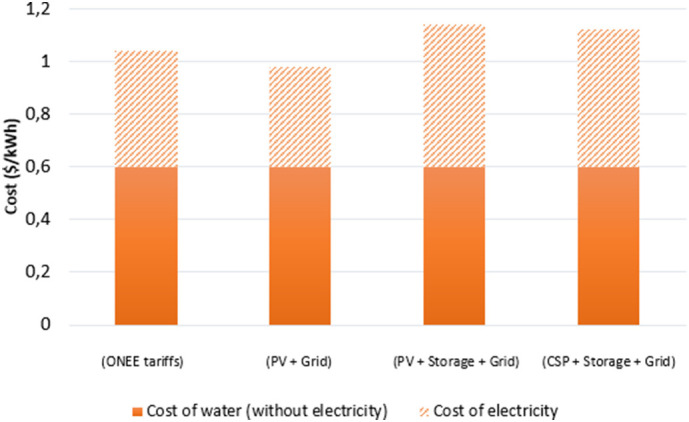
Cost of water ($/m³) for different power supply options (without value added tax).

To summarize, it has been shown that for all the power supply options considered in this paper, the cost of electricity ranges between 0.094 $/kWh and 0.135 $/kWh which results in a cost of water ranging between 0.98 $/m³ and 1.14 $/m³.

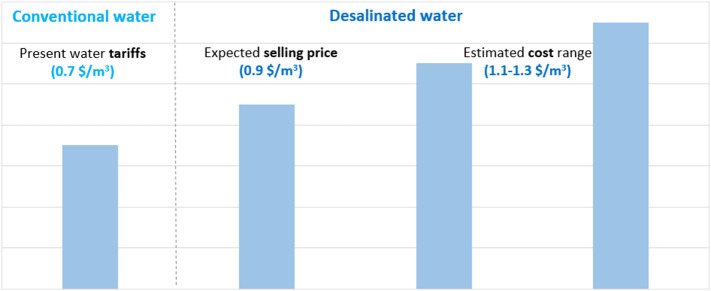
It is interesting to compare the cost of water from desalination with the current prices of water in the region. The example of the impact of desalination for farmers can be a good illustration especially that the Souss region is known for its high agricultural output. For farmers, the selling tariff of desalinated water fixed by Oman El Baraka fell from 1.8 $/m³ to 1.2 $/m³ before it was finally fixed at 0.6 $/m³/y plus an additional subscription fee of 1100 $/ha/y. Each farmer has to commit to a 3600 m³/ha/y (396 m³/ha/y during six irrigation campaigns)4 . For example, a farmer who owns 50 ha will commit to 180, 000m³/y (3,600×50) and will pay 0.3 $/m³/y ((1100×50)/180,000) of fixed subscription fee plus a variable fee of 0.6 $/m³. Per year, the farmer will thus pay 0.9 $/m³ (0.6 + 0.3). If this cost of water is supposed to already include the value added tax of 14% [71] applied to water and energy products, then the cost of desalinated water would range between 1.11 $/m³ and 1.3 $/m³ depending on the power supply considered. The selling price of desalinated water as proposed by Oman El Baraka would represent only 70% to 81% of the estimated cost range of desalinated water according to the power supply considered in this paper. This result suggests that the difference between the cost of desalinated water and the price at which it is intended to be sold would probably be compensated by public subsidies varying between 20% and 30% of the estimated cost of desalinated water.

In addition, it is interesting to compare the estimated cost range and the expected selling price of desalinated water to the present water tariffs as applied by the local distributor of water. To be coherent with the previous paragraphs, the same farmer is considered. Water tariffs according to RAMSA5 (for industrial clients because there is no specific tariff for agricultural clients) include a fix tariff of 1.2 $/month (including the 14% value added tax rate) and a variable tariff of 0.7 $/m³ (including the 14% value added tax rate). For a farmer who needs the same water consumption as previously mentioned (180,000 m³/y), the total cost of water consumed will be around 0.7 $/m³ ((1.2×12)/180,000) plus a variable tariff of 0.7 $/m³. Thus, for a farmer, the expected selling price of desalinated water is almost 30% higher than the cost of water based on present RAMSA tariffs, whereas the estimated cost range of desalinated water based on the different power supply options covered in this paper are 60% higher to 86% higher than the cost of water based on present RAMSA tariffs. Fig. 9 displays graphically the cost and selling price of desalinated water compared to the present selling prices of water.

Fig. 9.

Cost and selling price of desalinated water compared to present RAMSA tariffs.

As noticed earlier the cost of water from desalination is higher than present water tariffs which may be unfavourable to the promotion of desalination as a future technique to cope with the increasing water pressure in Morocco. However, as water is increasingly becoming a scarce resource in the country, one may expect that water tariffs will increase in the coming years (market signal price for scarcity and incentive to water conservation). Water supply diversification using desalination (even it appears costly today) can therefore contribute to avoid future water shortage that could hamper the socio-economic development of a whole country.

4. Discussion and prospective analysis

Detailed results from the previous section, describing a large set of solar electricity production technologies, reveal that the cost of electricity can significantly impact the cost of desalinated water:

• ▪Under present conditions, solar use for large scale desalination projects is already competitive for solar PV without storage, compared to grid-only powered alternative. In this case, only part of the supply comes from solar (about one third). Larger use of PV supply would increase the total cost of water under the assumptions retained in this paper.
• ▪Moreover, the introduction of batteries (with PV and the grid) is found to lead to higher costs of water (+43% compared to battery-less PV option). The extreme design which would be based on PV only + very large batteries set has not been studied. But, as its cost would lie much above the results obtained in the paper, it appears somewhat out of the scope.
• ▪The use of CSP (with storage and the grid) appears also not yet competitive compared to PV only option and to the grid alternative. Even if the PV + Storage + Grid option results in a slightly higher cost of water, this difference with the CSP based alternative(s) is not significant. This indicates that the choice between both these technologies with their respective storage solution for future desalination applications is not much evident based on present costs and assumptions.

From the “private” point of view, it is of the first interest to examine how cost competitiveness between all the power supply options would change by 2030. To conduct this prospective analysis, three scenarios are considered. Business As Usual (“BAU”) scenario is related to the present costs used in this study. The scenario “High” refers to the aggressive target costs of PV and CSP by 2030 published recently by the NREL, and to the target cost in reference [51] and reference [52] for lead-acid storage (average value). The “Mid” scenario considers that only one third cost reduction by 2030 is achieved. For CSP costs in 2030, a value of 0.01 $/kWh (as calculated previously) is added to the target cost of electricity generation to account for electricity transport as previously done in this paper. Table 14 summaries cost assumptions used in this prospective analysis. Regarding the electricity cost of the grid, BAU scenario supposes no relative change in prices by 2030 whereas “Mid” and “High” assume an increase of 1.5%/y and 3%/y respectively.

Table 14.

Scenario projection of the cost of solar electricity generation and grid electricity tariffs by 2030.

Average electricity price (% increase/year until 2030)
BAU	Mid (1.5%/y)	High (3%/y)
0.11	0.13	0.15

LCOE PV
BAU	Mid (−30%)	High (−50%)
0.06	0.04	0.03

LCOE CSP
BAU	Mid (−33%)	High (−66%)
0.15	0.10	0.05

LCOS (lead – acid)
BAU	Mid (−28%)	High (−56%)
0.3	0.22	0.13

As this paper focuses mainly on the impact of different electricity costs on the relative costs of desalinated water, it is assumed that by 2030, the CAPEX and OPEX (without electricity) would remain at the same level. The only component of the cost of water that is assumed to vary is therefore the cost of electricity consumption, based on different assumptions on the increase in electricity prices and on the pace of solar and storage technologies cost reduction by 2030. In the case of storage, Lead acid batteries are taken as the reference storage technology but the reduction of the cost of storage could be reach by other storage technologies (Li-ion…).

Many combinations of cost reduction assumptions can be computed for the different technologies compared in this paper. Some cases are however not plausible, as for example an increase in electricity tariffs with a strong cost reduction of solar technologies. Future electricity prices depend on the future electricity mix. With a strong cost reduction of solar technologies and their increase proportion in the mix, the price of electricity is not expected to increase by a large amount. For this reason, a reasonable assumption has to be retained for the two prospective scenarios:

• ▪Scenario 1: supposes moderate increase of the grid electricity prices (Mid) and high achievements of cost reduction targets by 2030 for solar technologies and batteries (High)
• ▪Scenario 2: supposes high increase of the grid electricity tariffs (High) but no further cost reduction for solar technologies and batteries (BAU).

As displayed in Fig. 10 , the main trend in the Scenario 1 is the contrary effects of technological progress and an increase in the electricity tariffs, leading to a globally stable desalinated water production cost. But the rank of the technology's changes. Under this scenario, the most competitive solution remains the PV + Grid alternative, the cost evolution of which is rather flat from the base year up to 2030. However, beside this “flat” evolution, there are two different trends for the other technologies. The first is the logical increase in the cost of water for a 100% Grid based solution that gives by 2030 the highest cost of water (14% increase compared to the lowest cost provided by PV + Grid in 2030). The second trend is the decreasing evolution of the cost of water in the case of CSP + Storage + Grid and PV + Storage + Grid alternatives. The two storage-based solutions, owing to the assumed decrease of the costs of solar technologies and storage, achieve grid parity by 2023 and 2024 respectively. In addition, these two solutions lead to the same cost of water (parity) a little before 2030.

Fig. 10.

Cost of water in scenario 1 for each power supply option by 2030.

The Scenario 2 in some way is closed to the analysis from the “public” point of view here above, because the main drivers of the evolution in electricity tariffs take into account the real production cost of the electricity and the CO₂ externalities. The scenario supposes in fact a high increase in electricity tariffs but no further cost reduction of the other technologies. As displayed in Fig. 11 , the cost of water increases by 2030 for all solutions compared to the reference level as all alternatives are grid-dependent. The least cost option is always PV + Grid whereas the power alternative with the highest cost of water is PV + Storage + Grid. Under the assumptions of this scenario, CSP + Storage + Grid achieves full grid parity by 2030.

Fig. 11.

Cost of water in scenario 1 for each power supply option by 2030.

Table 15 summarizes the changes in the cost competitiveness of the different power supply alternatives studied in this paper from the reference year up to 2030. It shows that PV+ Grid is still the cheapest power supply alternative for which the lower cost of water is achieved on the full period of time.

Table 15.

Change in the ranking of the power supply alternatives by 2030, (1 is the best cost option, 4 is the most expensive option).

Time period	Grid	PV + Grid	PV + Storage + Grid	CSP + Storage + Grid
Scenario 1
<2023	2	1	4	3
2023–2024	3	1	4	2
2024–2028	4	1	3	2
>2028	4	1	2/3	2/3
Scenario 2
<2030	2	1	4	3
>2030	3	1	4	2

It is worth nothing that the cost competitiveness between PV + Storage + Grid and CSP + Storage + Grid appears to be not too discriminant which suggests for a more comprehensive multi-criteria analysis to clearly discriminate between those power supply options.

Practically, in terms of decisions by the Moroccan State, these results are clearly in favour of a policy aiming to develop a first programme of RO desalination with an increasing share of electricity from a local PV source (the bulk of supply coming from the national grid). This share is easy to adapt, whereas it does not exceed one third to half of the total, taking account the technology and regulation evolutions. The parallel development of centralized CSP appears also a reasonable source of diversification and could supply, in a second programme, competitive electricity to future desalination plants, taking advantage of their increasing size and scale effects (CSP plants and electric lines) that are more important than the expected improvement of the local PV fields. When referring to the two programmes, it is not proposed to rely only on PV+ Grid in the first one (namely in the 20ies) and to shift (in the 30ies) to CSP. Clearly, after a delay of one decade the costs of the two technologies will be in the same range. The system costs of PV will begin to increase significantly with its share in total electricity production. Thus, a new generation of systems, based on CSP, will have the great advantage to allow to diversify the behaviour of both electric plants, when adding a (very) significant capacity of storage. In order to prepare this situation, it appears important that Morocco continues its efforts to develop this technology, in order to be fully ready, at a large scale, in about 10 years. But, once more, the results of this paper suggest strongly to begin the development of “low carbon” desalination with PV.

However, it is more difficult today to precisely assess how the trends exposed in this paper could practically be developed because of the sars-cov-2 pandemic the World is experiencing today. It could cause many delays before such large scale plants become operational. In addition, under the current situation, it is plausible that energy subsidies in Morocco would still be maintained at least for the next two years or more to support the revival of national industries that stopped their activities during the lockdown period. However, in a context of higher uncertainties, a diversification of electric mix as long as an increase of domestic (non-fossil) electric production could offer an interesting way of robustness.

Aside from this specific economic context that may cause many disruption in the desalination market (in the short and medium term), large scale desalination plants powered by solar energy suffer from inherent challenging issues that lead by the past to the give up of solar powered desalination units. For example, a first obstacle can be related to the reliability of contractors and project partners. For example, the Al Khafji plant (Saudi Arabia) which is the first large scale solar SWRO plant of a capacity of 60,000 m3/d and powered by a PV plant of 20 MW, experienced a delay because initially only one contractor (Abengoa which almost went bankrupt in 2015) had to do everything (Desalination unit + PV plant). This is not the case for the Chtouka Ait Baha plant where several partners are engaged in the project under a public private partnership. In addition, the desalination unit and the power supply unit are not built by the same operator.

A second limiting factor of large-scale solar powered desalination plants is related to logistics considerations, among which the spatial distribution of solar energy and saline water (generally inland versus along the coast) and grid interconnection policy and infrastructure constitute the main factors. In addition, as large scale desalination plants have high energy demands, the required area can be a significant issue (land availability and conflict with other land usage) especially if both solar and desalination plants are located along the coast. Another limitation of large scale solar powered desalination unit is related to their optimal operation that requires accurate solar production forecasting models.

5. Conclusion

In this paper, the economic competitiveness of large scale solar powered Reverse Osmosis desalination plant has been investigated taking as a case study the Chtouka Ait Baha desalination (275,000 m³/d) plant in Morocco. The bulk of the paper consists in the assessment of desalinated water cost for different power supply alternatives (using PV, CSP, batteries technologies and the Grid). This analysis allows to compare the cost of desalinated water for these four power supply alternatives for the reference year (2017) and by 2030.

Based on a global water cost model, this paper demonstrates at first that desalination, with the last up to date technologies, is affordable at an acceptable cost of around 1 $/m³ (range of 0.98 $/m³ and 1.14 $/m³ depending on the power supply option). In addition, the results show that the selling price of desalinated water as proposed by Oman El Baraka (0.9 $/m³, VAT included) would represent only 70% to 81% of the estimated cost range of desalinated water according to the power supply considered in this paper. This result suggests that the difference between the cost of desalinated water and the price at which desalinated water is expected to be sold would probably be compensated by public subsidies varying between 20% and 30% of the estimated cost of desalinated water. When assessing the impact of the cost of electricity supply on the cost of desalinate water, this paper demonstrates that solar energy is a competitive way to feed large scale reverse osmosis plant today. PV without storage appears today the most competitive solution. Electricity storage is not yet fully competitive (in this paper, storage services to the national grid are not considered). CSP appears today to be more costly, partly because of the need in the Moroccan context, to build a high voltage electric line to transport electricity from the desert. The results of the prospective analysis towards 2030 shows potential benefits of CSP + Storage + Grid and PV + Storage + Grid alternatives even if the most competitive solution remains PV + Grid.

This study not only illustrates the difficulty to determine the best option to supply a large-scale desalination plant somewhere in Africa, but also points out some promising technical combinations. Indeed, one of the main results of this paper is that both PV and CSP technologies may be part of the game of RO desalination in a quite short future. In fact, PV + Grid appears regularly the best solution. From a “public point of view”, CSP appears not to be much more expensive. Moreover, the capacity of CSP to store heat at low cost offers an important source of flexibility to this technique, which allows too deeply decrease the share of electricity from the grid in the total consumption, if needed. In addition, with a large deployment of desalination plants, it becomes possible to build high power electric lines with lower costs, to transport electricity from the inland desert to coastal territories where the demand for water is peaking. Beyond the optimal technological choice, the results of this paper advocate for the necessary upstream integration of energy requirements from the water sector in the future energy planning schemes in Morocco. To conclude, and based on the results of this study, a first programme of desalination plants based on PV + Grid should be launched, while a second programme based on CSP should be prepared.

However, this study faces some limitations. One limit is related to the only decision criterion selected to assess the competitiveness of the retained power supply options that is the minimum cost of water. Beyond this metric, a discriminatory criterion could be the reliance on the grid or the global CO₂ emissions resulting from each alternative. A multi-criteria analysis with a cost/advantage approach taking into account technical, economic (including job creation or local industry potential), and environmental aspects would provide a more complete picture of the attractiveness of each power supply option for the whole system including. Indeed, environmental externalities include for example brine rejection that harms small marine organisms, especially in regions that highly rely on fishing activities. It is also worth noting that this analysis is based on a simplified approach with approximations especially for solar PV sizing. Optimizing PV design could allow getting more precise storage requirement specifications and evaluate more accurately the weight of storage in the average electricity cost. In addition, future works could also consider different feed-in tariffs schemes for solar electricity surplus sold to the national grid.

Finally, Morocco will have to cope with the consequences of the sars-cov-2 epidemic. The impact on the economy will certainly be hard, in the range of −5% in GDP, or more. This situation may require several years to be fully stabilized and overcome. The assumptions on costs retained in this study will probably remain robust, but one could expect important changes or delay in economic growth of agriculture and demand for electricity, inducing major inflexions in the Moroccan water and energy policies.

Credit author statement

Maryème Kettani: Writing- Reviewing and Editing, Writing- Original draft preparation, Data curation, Investigation, Conceptualization, Visualization, Supervision.

Philippe Bandelier: Software, Methodology, Formal analysis, Validation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. RO model

A simplified model is used to determine the daily production and the water cost of a reverse osmosis (RO) desalination plant powered by any energy source. Due to the relatively quick dynamic of such a system, simulation over a given day is calculated as a succession of steady states, hour per hour. For the purpose of this study, RO is supposed to be operated 24 h a day. When solar resource is not available or insufficient, energy storage (electricity or heat for CSP) or the grid takes over.

Fig. a shows RO desalination system. One pass RO unit is considered, without brine recirculation. It comprises a number of trains in parallel. Each train is composed of a number of pressure vessels in parallel containing membrane elements in series. Seawater pumps feed the trains after pre-treatment (filtration and addition of chemicals). Their number is to choose (one or several trains per pump). High pressure pumps feed the vessels. Each train includes a high-pressure pump and a set of energy recovery devices to recover high pressure from the brine.

A sea water pumping system and pre-treatment facility are supposed to be common for the whole desalination plant.

Fig. a.

RO desalination system with membrane elements, pressure vessels and trains.

Before simulating the operation of RO plant over a day, a preliminary step is required to size the RO system. To this effect, two options are implemented in the model: sizing or operating the RO plant.

Developed with Microsoft Excel™, it includes the following calculation modules:

• •RO module: this is the most important and complex module because it controls or uses all the others. It comprises two user modes: sizing of the RO unit for a required desalting capacity and determination of the operating point of the previously sized unit when available power varies. To size the RO system, a membrane element is selected from the supplier's catalogue. Their characteristics are entered: surface, permeability, salt rejection, etc. A default reference is proposed6 and related characteristics are the default values in the calculations.

Seawater characteristics are also required (temperature, salinity, flow factor). Calculations are based on the method described in FILMTEC™ Reverse Osmosis Membranes Technical Manual [31]. The basic equation to calculate the separation of water and salt is:

$$Q=N_E.S_E.\overline{A}.\mathit{TCF}.\mathit{FF}.\left\{\left(P_f-\frac{\overline{∆P_{\mathit{fc}}}}{2}.P_p-{\pi }_f.\left[\frac{\overline{C_{\mathit{fc}}}}{C_f}.p_f-\left(1-\overline{R}\right)\right]\right\}\right)$$

([31])

• $\overline{A}$: membrane permeability, m³.m⁻².s⁻¹.Pa⁻¹.

• C_f: feed concentration, kg.kg⁻¹.

• $\overline{C_{\mathit{fc}}}$: average concentration-side concentration, kg.kg⁻¹.

• FF: average flow factor due to membrane fouling, −.

• N_E: number of membrane elements per pressure vessel, −.

• p_f: polarization factor, −.

• P_f: feed pressure, Pa.

• P_p: permeate pressure, Pa.

• Q: permeate flow rate, m³.s⁻¹.

• $\overline{R}:$ average salt rejection, −.

• S_E: surface of one membrane element, m².

• TCF: temperature correction factor, −.

• $\overline{∆P_{\mathit{fc}}}$: average pressure drop on concentrate-side, Pa.

• π_f: feed osmotic pressure, Pa.

References [31,32] give more details about the calculation method and the determination of different factors.

The module is used to size the RO system. For a given desalination capacity, it returns the number of standard membrane elements per pressure vessel, the number of pressure vessels per train and the number of RO trains. The number of required energy recovery devices (ERD) is determined according to a selected unit capacity in a proposed pressure exchanger's catalogue. Operating conditions - feed pressure and flow rate, conversion ratio - are chosen to minimize either specific energy consumption or water cost.

The calculation of OPEX in the model excludes the cost of energy since it is the principal parameter of the study. First, the specific consumption of the SWRO (kWh/m³) is calculated, then the power required (kW) and finally the corresponding energy (kWh) over a given period (a year) are computed. Since the plant operates at full capacity 24 h a day, 365 days a year (95% of availability factor), these values are fixed. The different electricity cost scenarios combined with this required energy give the contribution of the energy cost to the water price.

The energy consumption includes the energy consumption of the reverse osmosis unit (high-pressure pumps and booster downstream of the ERDs) but also that of the seawater supply pumps, taking into account the pressure losses in the pipes and in the seawater pre-treatment. The back pressures of the brine and freshwater discharges produced (thus including post-treatment) are also taken into account.

• ▪Cost module: usual cost functions for RO are used for CAPEX and OPEX calculations. They are taken from different sources [6,[33], [34], [35], [36], [37], [38]]. Coupled with the performance module, it provides a detailed calculation of CAPEX, OPEX and finally the Levelized Cost Of Water (LCOW). The effective daily operation time is taken into account as it has a strong effect on the contribution of CAPEX to the water cost via the capital amortization. This module gives water cost breakdown.

Validation of the RO model has been carried out using experimental results from literature [[72], [73], [74], [75], [76]]. A benchmark with different professional tools available shows that performance and cost are predicted with a deviation better than 10%. Tools are DEEP v5.13 code updated by IAEA in 2014, WAVE 1.64 edited by Dow Chemical in 2018 (update of ROSA 9.1 merged with others water processing simulation tools) and GWI online desalination cost estimator.