Gini coefficients as a single value metric to define chemical probe selectivity

Abstract

Selectivity is a key requirement of high-quality chemical probes and lead medicines, however methods to quantify and compare the selectivity of small molecules have not been standardized across the field. Herein, we discuss the origins and use of a comprehensive, single value term to quantify selectivity, the Gini coefficient. Case studies presented include compounds that target protein kinases, small molecules that bind RNA structures, and small molecule chimeras that bind to and degrade target RNA. With an increasing number of transcriptome- and proteome-wide studies, we submit that reporting Gini coefficients as a quantitative descriptor of selectivity should be used broadly.

Graphical Abstract

The development of chemical probes and lead medicines has historically benefitted from various ligand-metrics to help optimize compounds and establish features that ideal probes should display.¹ Fundamental features of high-quality chemical probes include: (i) physicochemical properties that confer solubility and metabolic stability in cellulis and in vivo; (ii) demonstrated target engagement; (iii) demonstrated potency for modulating phenotype; and (iv) selectivity. [We direct the reader to two notable reviews on this topic for additional information.^{2, 3}] Selectivity can be a challenge to quantify, and yet it is one of the most critical features of a chemical probe. Current metrics of selectivity include comparison of IC₅₀s for inhibition of related targets, ratio of K_is, occupancy of the desired vs. related targets, in vitro binding affinity, etc. Herein, we describe the Gini coefficient as a standardized metric of selectivity. We explore its historical development, the calculation of this metric, its limitations, and its implementation with respect to kinase inhibitors, RNA-targeted small molecules, and small molecule chimeras that bind and facilitate cleavage of the target RNA through nuclease recruitment.

History of the Gini Coefficient

The Gini coefficient was first described in 1912 by Corrado Gini as a quantitative metric generated from Lorenz curves⁴ to describe the statistical distribution of wealth amongst a country’s residents, i.e. the wealth inequality amongst the members of a population.⁵ A population where wealth is evenly distributed translates to a Gini coefficient of 0, whereas a population in which a single member possesses all wealth is assigned a Gini coefficient of 1. As the Gini coefficient does not have an economic-specific meaning, it has been broadly applied in fields such as sociology,^6–8 agriculture,⁹ ecology,¹⁰ engineering,¹¹ and the natural sciences.^12–17 In the natural sciences, the Gini coefficient has been applied to study the selectivity of small molecule inhibitors, if in the economic definition: i) “population” is replaced by a panel of biomolecules, whether proteins or nucleic acids; and ii) “wealth” is changed to the percent inhibition of a biomolecule’s activity. The estimated “wealth inequality” therefore translates to the selectivity of an inhibitor against a panel of biomolecules. Thus, a Gini coefficient of 0 indicates a non-selective inhibitor/modulator, while a coefficient of 1 describes an exquisitely selective compound.

Indeed, in 2007, Piotr Graczyk introduced the Gini coefficient as a single value to quantify the selectivity of kinase inhibitors.¹⁸ Below, we summarize how Gini coefficients are calculated (Supplemental Figure S1 and Supplemental Dataset 1). For a detailed discussion of how the calculation is completed, we direct the reader to Graczyk’s original report. In brief, a Gini coefficient is calculated by measuring the percentage by which each target is inhibited by a small molecule at a single concentration. The targets are then rank ordered from least to most potently inhibited, and a cumulative fraction of each target is calculated. For example, if 20 targets were evaluated, the least potently inhibited target would have a cumulative fraction of 0.05 (1/20), while the second would have a value of 0.1 (0.05 + 0.05), the third 0.15, and so on and so forth.

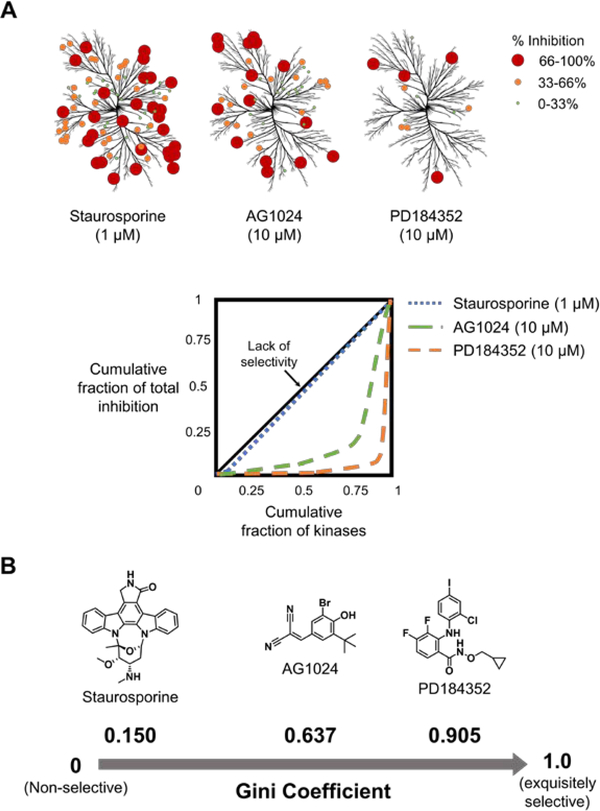
The percent inhibition for each target is then summed to afford the “total cumulative effect”. The fraction of total inhibition is calculated for each target by dividing its percent inhibition by the total cumulative effect. The cumulative inhibition fraction is then calculated for each compound and the targets are positioned in rank order, akin to the cumulative fraction of each target described above. The cumulative fraction of inhibition is plotted as a function of cumulative fraction of targets, similar to a Lorenz curve⁴ (Figure 1A). The Gini coefficient is calculated by the formula G = 1 − 2 × B, where B is the area under the resulting curve, calculated by using the trapezium method (Figure 1A).¹⁸

Figure 1.

Gini coefficients to quantify the selectivity of kinase inhibitors. A) Kinase inhibition maps for Staurosporine, AG1024, and PD18432 and the corresponding Lorenz curves used to calculate their Gini coefficients. Data were taken from Graczyk (100 μM ATP concentration).¹⁹ B) Gini coefficients for each kinase inhibitor calculated from Lorenz curves.¹⁹

In the case that a small molecule equally inhibits all targets (Gini coefficient = 0), a diagonal line is obtained (black line in Figure 1A). As selectivity increases, the curvature of the Lorenz curve increases. That is, the curve will initially increase slowly followed by a sharp rise for the latter half (green and orange dotted lines in Figure 1A). The sharper the curvature of this line the more selective the compound is. In general, a compound is considered selective if its Gini coefficient > 0.75.¹⁹

Inaugural Application of Gini Coefficients to Biological Systems: General Features and Considerations

Graczyk’s implementation of Gini coefficients used available data for the inhibition of 85 kinases by 40 different inhibitors evaluated at a single concentration.¹⁸ His study verified that non-selective inhibitors have Gini coefficients close to 0, and as selectivity increases the Gini coefficient approaches 1 (Figure 1B). For example, Staurosporine (a known non-selective kinase inhibitor)²⁰ has a Gini coefficient of 0.150 (blue dotted line; Figure 1A), while AG1024 (a moderately selective kinase inhibitor)²¹ and PD184352 (a selective inhibitor of MAPKK1)²² have Gini coefficients of 0.637 and 0.905, respectively (green and orange lines, respectively; Figure 1A).¹⁸ These studies also revealed that the size of the dataset analyzed, i.e., the number of kinases, does not significantly affect the average Gini coefficient, indicating that a subset of randomly chosen kinases could be used as a proxy or estimate for the entire kinome. A sufficient number of kinases (i.e. ~50 in this case), however, should be used in the panel to mitigate errors that occur when the Gini coefficient is calculated using too small of a subset of kinases (i.e., 10 targets in this example).¹⁸ The targets that are included in the panel do indeed influence the value of the Gini coefficient, and thus the subset of kinases used must be selected carefully to include known or suspected off-targets.

Since Gini coefficients are calculated at a single concentration, several factors must be carefully considered to ensure the accuracy and precision of Gini coefficients. For example, precision is increased when the compound is profiled at a concentration where strong inhibition is observed (maximum inhibition between 91 – 99%), corresponding to 10 – 100 times the IC₅₀.¹⁸ In the simplest case, the Gini coefficients of two compounds assayed at the same concentration can be compared directly, provided their most potent IC₅₀ against a target in the panel is similar and their maximal observed percent inhibition is similar (AG1024 and PD184352, for example; Figure 1A). If these two criteria are not met, then the concentrations of inhibitors should be adjusted accordingly, so the ratios of maximum potency/concentration for each compound are equal. For example, in Figure 1, Staurosporine (1 μM) is compared to AG1024 and PD184352 (10 μM),¹⁸ demonstrating that the data analyzed to calculate the Gini coefficient may be from inhibitor concentrations that are the same or different (Figure 1A). Interestingly, for a set of five inhibitors with similar maximum percent inhibition and IC₅₀s, although the concentration affected the value of the Gini coefficient, it did not affect the selectivity ranking of the compounds,¹⁸ indicating that Gini coefficients can predict relative selectivity across a range of concentrations. Although this observation is likely a general feature of Gini coefficients, independent of the system studied, it should be verified experimentally.

In addition to the Gini coefficient, other metrics have been used to assess the selectivity of small molecule kinase inhibitors. For example, the standard selectivity score (S(x) where x represents a user-defined threshold of kinase activity inhibition upon compound treatment) has also been applied to kinase profiling studies.²³ The main disadvantage of this metric is the need to establish a threshold for the enzymatic activity of inhibited protein kinases. Variations in the value of the applied threshold have been reported to affect the final value of the selectivity score.²⁴ Similarly, the partition index (PI) has also been used to define selectivity.²⁵ This metric, however, uses K_d, K_i, or IC₅₀ values obtained from dose-dependent studies that are not cost effective for large panels.²⁴ As in the case of PIs, selectivity entropy (Ssel) also employs K_d, K_i, or IC₅₀ values.²⁶ This results in increased costs for kinase inhibitor profiling projects, a disadvantage in academic settings. Comparison studies among these traditional selectivity metrics have been reported²⁴ and produce selectivity rankings of kinase inhibitors in good agreement across all three methods.

Since each selectivity metric has its own limitations, none has been clearly established as a standard for assessing small molecule selectivity. At present, measuring selectivity needs to be treated with care, while considering the goal of the research project as well as the resources available. Due to the low costs of acquiring percentage kinase inhibition data, the Gini coefficient allows for robust ranking of the overall selectivity of kinase inhibitors, offering an attractive alternative for academic labs to measure chemical probe selectivity in a reproducible manner.

Expanding Gini Coefficients Across the Biological Sciences

The biological sciences have benefitted from the versatility of the Gini coefficient, which allowed analysis of the extent of the statistical distribution of the property/parameter under investigation. For example, Weidlich et al.¹⁵ applied the Gini coefficient to assess the chemical diversity of random and publicly available compound sets. By representing the structural features of the molecules within the databases as binary fingerprints, the authors generated a simple quantitative measure of how chemically diverse one compound set is compared to another. In another example, Jiang et al.²⁷ implemented the Gini coefficient within a computational method termed GiniClust, which detects rare cell types within a large population of cells with high sensitivity. By applying GiniClust to publicly available single-cell RNA-seq datasets, the normalized gene expression data identified rare clusters of cells within heterogeneous mouse embryonic stem cell, glioblastoma primary tumor, mouse somatosensory cortex, and hippocampus CA1 region cell populations. Similarly, the Gini coefficient was used to measure the extent of expression variation of a gene of interest within a dataset.¹³ This allowed for the identification of higher quality “housekeeping” genes to be applied in the normalization of gene expression profiling studies. Therefore, repurposing the Gini coefficient for different biological applications is straightforward and can broadly be applied to various datasets.

Expanding Gini Coefficients to Assess the Selectivity of Small Molecules Interacting with RNA in cellulis

The Gini coefficient has proven a useful metric for proteins, particularly kinase inhibitors,^28–30 and likely will be equally useful for chemical probes targeting other biomolecules. RNA has become an increasingly important drug target, as it causes or contributes to a wide variety of diseases including cancer,^{31, 32} microsatellite/repeat expansion disorders,³³ and dementia via RNAs that encode toxic proteins,^{34, 35} amongst others. Indeed, a number of small molecules interacting with RNA (SMIRNAs) have been developed to recognize the three dimensional (3D) folds within these disease-causing RNAs and ameliorate their dysfunction in cells and in vivo.^36–38 As targeting RNA with small molecules is an emerging field, it will be important not only to demonstrate direct target engagement in cells,³⁷ but also to define and compare the selectivity of these compounds. Thus, we hypothesize that Gini coefficients will be key in the comprehensive characterization of SMIRNAs.

Beginning with the traditional definition of the Gini coefficient from social sciences, transcriptome-wide SMIRNA selectivity can be assessed if: i) “population” is represented by a randomly chosen panel or all RNA targets that can be detected in disease-relevant cells; and ii) “wealth” is changed to the alteration of expression levels within the RNA target population upon SMIRNA treatment at a previously validated concentration and time period. We recommend that SMIRNA selectivity should be measured at a concentration that affects a target RNA and triggers an RNA-centric phenotypic change. This modulation of RNA target abundance and phenotypic change must be linked to direct target engagement. Selectivity data for SMIRNAs in cellulis can be easily generated through RT-qPCR profiling, microarrays, or high throughput RNA sequencing (RNA-seq). Typically, the resulting data are visualized with volcano plots (Figure 2A) or with plots comparing expression levels in treated and untreated cells (Figures 2B–C). Fortuitously, such datasets can be used as input to calculate Gini coefficients by employing either the fold-change directly provided by RT-qPCR or microarray measurements or by converting the fold-change to percentage inhibition (a step-by-step guide is provided in Supplemental Figure 1 and Supplemental Dataset 1).

Figure 2.

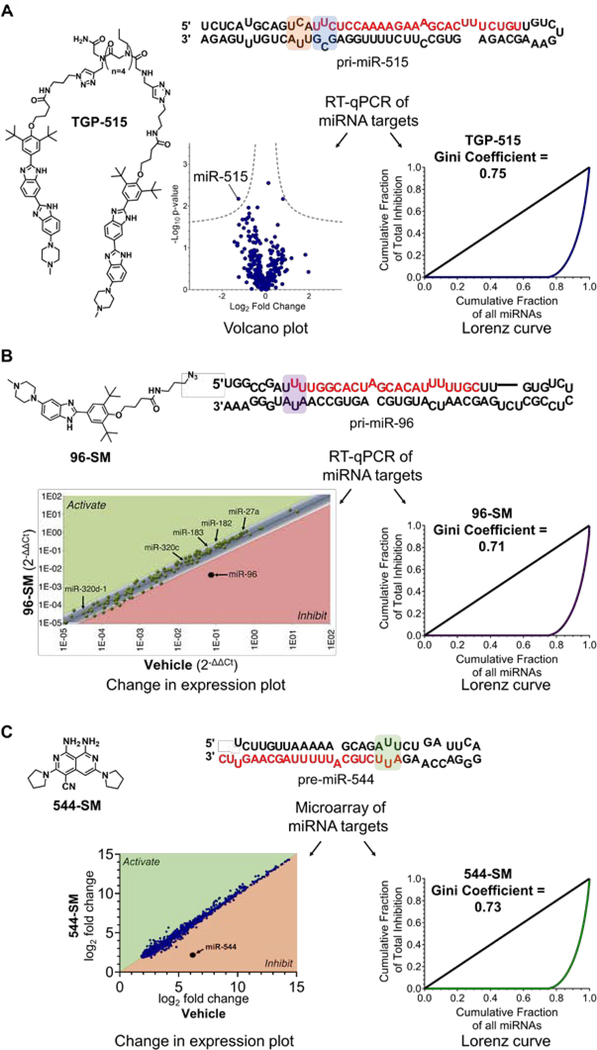
Application of Gini coefficients to quantify the cellular selectivity of SMIRNAs. A) Selectivity of TGP-515 (1 μM, the IC₅₀) in MCF-7 cells generated from RT-qPCR profiling data as shown by the Volcano plot (left panel) and the Lorenz curve (right panel). TGP-515 binds to adjacent loops (highlighted in orange and blue) near the Drosha processing site of pri-miR-515. B) Selectivity of 96-SM (40 μM, the IC₅₀) in MCF-7 cells via change in expression plot (left panel) and Lorenz curve (right panel) generated from RT-qPCR profiling data. 96-SM binds to an internal loop in the Drosha processing site of pri-miR-96 (highlighted in purple). C) Selectivity of 544-SM (0.02 μM, the IC₈₀) in MDA-MB-231 triple negative breast cancer cells via change in expression plot (left panel) and Lorenz curve (right panel) generated from microarray profiling data. 544-SM binds to an internal loop in the Dicer processing site of pre-miR-544 (highlighted in green).

Below, we discuss the application of Gini coefficients to small molecules targeting structured motifs in microRNA (miRNA) precursors to inhibit biogenesis of the mature miRNA.^39–41 Briefly, miRNAs regulate gene expression by binding to complementary regions in the 3’ untranslated regions (UTRs) of messenger (m)RNAs, inducing cleavage or translational repression.^42–44 Their biogenesis requires two steps: (i) processing of the primary transcript (pri-miRNA) in the nucleus by Drosha⁴⁵ and (ii) subsequent processing of the resultant precursor (pre-miRNA) in the cytoplasm by Dicer.^{46, 47} It has been shown in various iterations that small molecule binding to these functional processing sites can inhibit production, and hence function, of the mature miRNA, de-repressing its downstream protein targets.

In our previous studies of small molecules targeting miRNA precursors, we assessed selectivity by measuring the compound’s effect on the levels of all expressed mature miRNAs typically by RT-qPCR^{39, 48} but also in one instance by microarray.⁴⁹ Using these previously reported data, we calculated Gini coefficients for these compounds, all of which are ~0.7.^{39, 48, 49} In the first example, we studied the selectivity of a designed, dimeric small molecule that simultaneously binds the 3D structure present in the Drosha processing site of pri-miR-515 and a neighboring structured element.⁴⁸

Named Targaprimir-515 (TGP-515; Figure 2A), this dimeric compound inhibits pri-miR-515 biogenesis with an IC₅₀ of ~1 μM.⁴⁸ Analysis of the effect of TGP-515 on miR-515 levels vs. the entire miRNome in MCF-7 breast adenocarcinoma cells, upon 24 h treatment, afforded the volcano plot highlighted in Figure 2A, where miRNAs that are significantly affected upon compound treatment fall outside of the dotted lines which represent -log₁₀ of the P-value (in this case P = 0.01). The data generated by the RT-qPCR profiling experiment was then used to calculate a Gini coefficient, which is equal to 0.75 (Supplemental Figure 1), indicating that TGP-515 is indeed selective (Figure 2A). Therefore, a Gini coefficient can be generated from RT-qPCR profiling data and can be presented alongside a volcano plot to quantitatively express the selectivity of chemical probes targeting RNA.

We have also designed two traditional small molecules that inhibit two other miRNAs: (i) 96-SM (Figure 2B) binds the Drosha site in oncogenic pri-miR-96, inhibiting its biogenesis, de-repressing the pro-apoptotic transcription factor Forkhead box protein O1 (FOXO1), and inducing apoptosis of breast adenocarcinoma cells;³⁹ and (ii) 544-SM (Figure 2C) that binds the Dicer site of the hypoxia-inducible oncogenic pre-miR-544, inhibits its biogenesis, boosts levels of its downstream target mammalian target of rapamycin (mTOR), and induces apoptosis of MDA-MB-231 triple negative breast cancer cells (TNBC).⁴⁹ The Gini coefficients for 96-SM, determined from fold-change data generated from RT-qPCR profiling of the miRNome, and 544-SM, calculated from microarray analysis of the miRNome, are 0.71 and 0.73, respectively (Figure 2B–C). Interestingly, for all three studies presented, the Gini coefficients for the SMIRNAs were similar to oligonucleotide-based antagomiRs for the corresponding target (range: 0.62 – 0.72; also measured at their IC₅₀s).

Collectively, these studies show that Gini coefficients can be applied to small molecules that target RNA and importantly, that SMIRNAs that recognize structure can indeed be selective. The highlighted examples also show that Gini coefficients offer a more quantitative estimate to express and compare selectivity of chemical probes targeting RNA, which can be difficult to grasp from volcano plots and change in expression plot representations alone (Figure 2). Further, these studies will enable the optimization of SMIRNAs,⁵⁰ balancing potency and selectivity, to provide higher quality chemical probes capable of targeting the transcriptome with reduced off-target effects.

Gini Coefficients to Quantify Selectivity of SMIRNAs that Recruit Endogenous Nucleases, Ribonuclease Targeting Chimeras (RIBOTACs)

Emerging modalities with novel modes of action hold the promise to change the landscape of modulating biological targets for therapeutic benefit.^{51, 52} For example, proteolysis targeting chimeras (PROTACs)⁵³ and ribonuclease targeting chimeras (RIBOTACs)^54,55 are recently developed small molecule strategies to hijack cellular machineries to promote targeted degradation of protein and RNA targets, respectively. Their modular nature, comprising a protein- or RNA-binding small molecule and an enzyme recruiting module, is well-suited to convert a simple binding compound into a degrader, which generally exhibit superior potency and selectivity.^{55, 56}

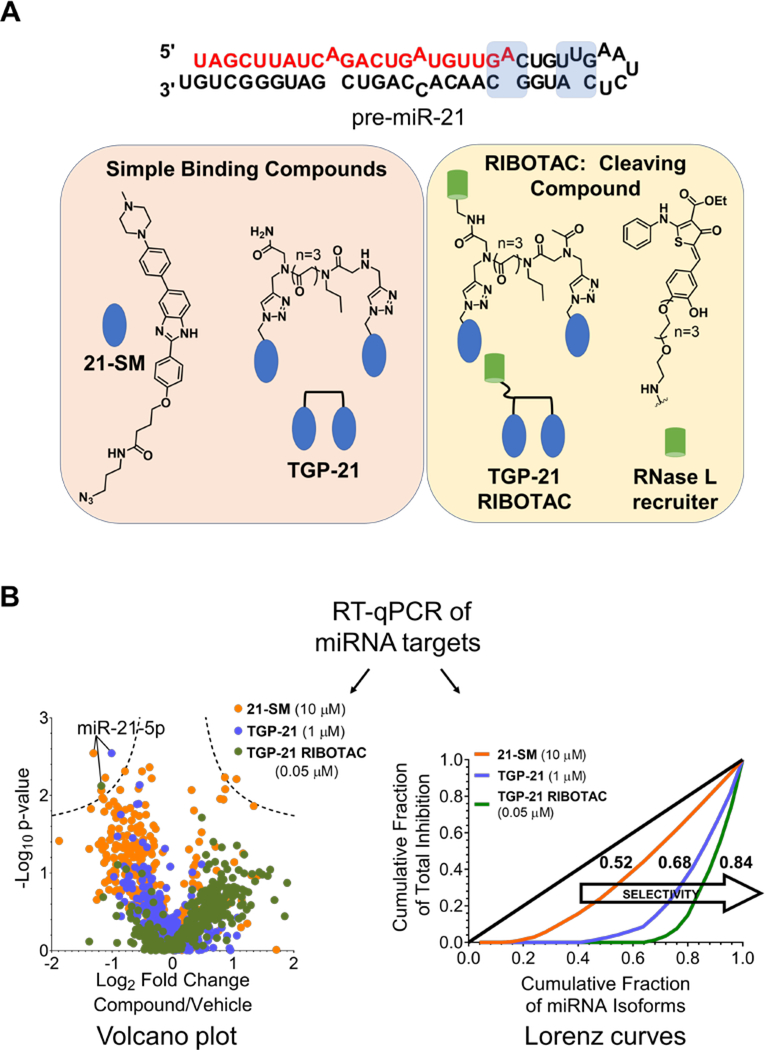
Indeed, Gini coefficients can be used to evaluate and compare the selectivity of small molecules with different modes of action, for example traditional small molecules, dimeric compounds that bind two sites in an RNA target simultaneously, and nuclease recruiting RIBOTACs, i.e., an enzymatic cleavage mechanism. Costales et al.⁵⁶ recently reported such a comparison in the targeted degradation of oncogenic miR-21 by recruiting endogenous RNase L. Three compounds were profiled at their IC₅₀s for reducing mature miR-21 levels: monomeric compound 21-SM (10 μM), dimeric derivative TGP-21 (1 μM), and TGP-21 RIBOTAC (0.05 μM) (Figure 3A). MiRNome-wide profiling upon compound treatment of MDA-MB-231 TNBC cells via RT-qPCR generated the volcano plot shown in Figure 3B; here miRNAs that are significantly affected fall outside of the dotted lines which represent -log₁₀ of the P-value (in this case P = 0.01). With the volcano plots alone, it was difficult to quantitatively estimate the difference in selectivity between TGP-21 and monomeric 21-SM. Thus, the same data sets were used to calculate Gini coefficients, which clearly indicated that TGP-21 exhibited higher selectivity (Gini coefficient = 0.68) than monomeric 21-SM (Gini coefficient = 0.52) (Figure 3B). Indeed, various reports have shown that dimerization improves both potency and selectivity compared to the monomeric components from which they are derived.^{57, 58}

Figure 3.

Comparing the selectivity of a traditional small molecule, 21-SM, a dimeric compound with improved potency, TGP-21, and the nuclease recruiting TGP-21 RIBOTAC with Gini coefficients. A) Structure of the pre-miR-21 hairpin, where compound binding sites are highlighted in blue. Chemical structures of SMIRNA chemical probes 21-SM and TGP-21 and nuclease recruiting chemical probe TGP-21 RIBOTAC. B) RT-qPCR profiling data of chemical probes 21-SM (10 μM), TGP-21 (1 μM) and TGP-21 RIBOTAC (0.05 μM) in MDA-MB-231 cells shown as a Volcano plot. Gini coefficients and Lorenz curves calculated from the profiling data indicate selectivity for miR-21 increases in the following order: 21-SM < TGP-21 < TGP-21 RIBOTAC.

Converting the simple binding compound TGP-21 into nuclease recruiting TGP-21 RIBOTAC further increased selectivity at an ~20-fold lower dose, yielding a Gini coefficient of 0.84 (Figure 3B). The increased potency of TGP-21 RIBOTAC can, at least in part, be attributed to its substoichiometric and catalytic nature. Further, the enhanced selectivity of the TGP-21 RIBOTAC can be traced to the combined selectivity of the dimeric RNA-binding component, TGP-21, and inherent substrate specificity of the nuclease RNase L.^{54, 55} Collectively, Gini coefficients can quantitatively express the selectivity of SMIRNAs and RIBOTACs and therefore compare biological selectivity between chemical probes with different modes of action. Moreover, this analysis demonstrated the conversion of SMIRNAs to RIBOTACs is a robust and straightforward method to generate more potent and selective chemical probes targeting disease-causing RNAs in cells.

Discussion

Drug discovery campaigns and chemical probe development have been driven by the integration of various parameters that have guided the prioritization, optimization and further advancement of lead molecules identified in target- and/or phenotypic-based screens into potent, selective and safe clinical candidates. Overall, these metrics improved the decision making process to pursue the most promising chemical probes for further phenotypic profiling⁵⁹ in physiologically relevant models,⁶⁰ in vivo, and ultimately success in clinical trials.

An important parameter in the drug discovery process is the assessment of selectivity of the small molecule leads across diverse biological targets in vitro and in vivo. Steering biological target selectivity⁶¹ via the incorporation of Gini coefficients can standardize the representation and comparison of hit compounds’ selectivity and simplify lead discovery and development campaigns, allowing for faster identification of the most promising and selective chemical probes. For example, the development of selective kinase inhibitors is challenging as they share an ATP binding site across more than 500 family members. Despite this obvious hurdle, the development of kinase inhibitors into clinically approved entities has greatly expanded in recent decades. Besides technological advancements, one key factor has been the availability of in vitro kinase profiling studies, which facilitated ranking compounds according to their Gini coefficient.³⁰ These data guided the optimization towards candidates with enhanced selectivity suitable for testing in vivo^{29, 62} and further in clinical trials. Alternatively, it provided a rational approach to repurpose kinase inhibitors towards new disease indications⁶³ and design of kinase inhibitors with rationally controlled polypharmacology.⁶⁴

Kinase profiling studies are routinely implemented in the early stages of drug discovery efforts to investigate selectivity.⁶⁵ Indeed, Gini coefficients were applied in the profiling of fragments to enable their development into lead-like kinase inhibitors.^{66, 67} The public availability of these selectivity metrics allowed the development of safer medicines exhibiting favorable selectivity profiles. Interestingly, PD184352 (Gini coefficient = 0.905) was the first highly selective mitogen-activated protein kinase kinase (MEK) targeted derivative which entered clinical trials. PD184352 exhibits no considerable off-target effects, which combined with its favorable safety profile, allows for continuous dosing. Although there is no record of the implementation of the Gini coefficient in the optimization of PD184352, the exquisite selectivity of this compound was later quantified due to data availability of numerous massive kinase profiling studies.^{68, 69}

Another consequence of assessing selectivity of kinase inhibitors is the development of chemogenomic sets of chemical probes for kinases, such as Published Kinase Inhibitor Set (PKIS)^{70, 71} and kinase chemogenomic set (KCGS).^{19, 72} Ideally, these sets encompass highly potent and selective chemical probes with kinase-annotated inhibitor activity in vitro and in cellulis, which can be used in an open-source fashion to validate the contribution of a particular kinase or kinase isoform in disease-relevant phenotypic assays.

Herein, we highlighted the potential of using a single Gini coefficient selectivity metric to quantitatively evaluate transcriptome-wide selectivity of SMIRNAs and RIBOTACs in cells. Considering the technological advancements and the high-throughput capabilities of RNA sequencing,⁷³ we encourage the medicinal chemistry and chemical biology communities to incorporate Gini coefficients broadly in their selectivity studies. Considering the impact of the Gini coefficient and other selectivity metrics in developing selective kinase inhibitors, we similarly envision an increase in the quality of chemical probes targeting disease-causing RNAs when Gini coefficients are adopted as a standard metric of selectivity. Indeed, reporting selectivity data as Gini coefficients will allow a more reliable and reproducible measure of small molecule chemical probe selectivity across research groups. Upon rigorous assessment of target engagement of newly developed RNA-targeted chemical probes, both in vitro and in cellulis, selectivity can be benchmarked against already established SMIRNAs or RIBOTACs.

Since the concentration, time of exposure, cell lines used, and readout all play crucial roles in the assessment of selectivity, these parameters need to be carefully selected to allow for robust quantification of selectivity via Gini coefficients, and subsequent comparison among a group of compounds. The concentration of chemical probe used should be ≥IC₅₀ value, where the cellular phenotype in a disease-relevant cell population is significantly affected. Of key importance is the number of RNA targets in the panel in which selectivity is assessed, as well as the cell line in which selectivity is measured. These parameters should be identical when comparing Gini coefficients between different chemical probes and research groups. Since the Gini coefficient is largely population independent, it is likely possible to use RT-qPCR or microarray data obtained for only a subset of the transcriptome to calculate Gini coefficients (see discussion about the size of kinase panels above). Here, the incorporation of jackknifing or bootstrapping resampling procedures can further add statistical rigor through standard error, variance, confidence intervals, percentiles, etc., of the calculated Gini coefficient value.⁷⁴ These are evaluated by either sampling various subsets from the already available database in the case of jackknifing or by replacing subsets from the initial database with randomly generated sample sets in the case of bootstrapping.

Incorporation of the Gini coefficient in small molecule profiling studies will further aid the chemical biology community in exploring the selectivity of novel chemical probes targeting disease-causing RNAs and will allow for selectivity to be standardized amongst academic labs. Calculating the Gini coefficient for chemical probes targeting RNA at various concentrations, over extended time periods, and in different cell lines will help assess the broad selectivity of these compounds across cell lines and tissues. Such selectivity investigations will be crucial to mitigate potential off-target effects when optimized compounds are advanced to clinical evaluation. In addition, reporting Gini coefficients of different chemical probes within the community will better guide the medicinal chemistry optimization towards more selective leads.

The RNA target selectivity of a chemical probe evaluated by the Gini coefficient is target agnostic, i.e. not expressed relative to a particular RNA target. It rather expresses the extent of inhibition selectivity across the entire RNA target population in cells. Such studies can be integrated with analysis of statistical confidence associated with changes in expression levels of individual RNA targets which can be expressed on volcano plots. We encourage the community to include both volcano plots and Gini coefficient representations in reporting selectivity of chemical probes targeting RNA. Volcano plots will indicate the RNA target(s) significantly affected by the treatment with the chemical probe under investigation while Lorenz curves and Gini coefficients will express the extent of selectivity across the entire RNA population considered.

There are fundamental differences between the kinase inhibition studies performed in vitro and the inhibition of RNA targets by chemical probes in cells. In the former case, profiling is performed in isolation and does not recapitulate the complexity of the cellular milieu. One potential caveat of measuring inhibition of RNA targets in cells is that changes in gene expression may be due to direct and/or indirect effects. For example, direct effects, including off-target effects, result from the occupancy of the engaged RNA target(s) and its subsequent inhibition. Indirect effects arise from the downstream effects of deactivating the RNA target, which might trigger compensatory mechanisms. Consequently, the fold change in expression of RNA targets provided by RT-qPCR or microarray upon treatment with a chemical probe is the sum of such direct and indirect effects. Therefore, we emphasize the importance of combining selectivity assessment of chemical probes in cells with rigorous target engagement studies,⁷⁵ to better define and understand cellular occupancy, selectivity, and downstream consequences in cells.

As highlighted in the previous sections, chemical biology studies will immediately benefit from comparisons to benchmark selectivity between small molecules⁷⁶ and emerging modalities,⁷⁷ such as PROTACs and RIBOTACs. Although Gini coefficients have not yet been applied to PROTACs, we imagine that the selectivity of such probes can be measured using whole-proteome quantitative mass spectrometry (MS)-based techniques, which have greatly improved in terms of multiplexing, sensitivity and proteome-coverage. Here, abundance in the proteome can be evaluated and selectivity of different PROTAC probes⁷⁸ could easily be assessed. Notably, direct and indirect effects of the proteasomal degradation mediated by PROTAC probes have been reported in the literature,⁷⁹ which will play an important role in the safety evaluation of novel modalities before their integration in full-fledged drug discovery programs.

As highlighted in this Perspective, Gini coefficients can be generated using different input data and can be integrated with bioinformatic approaches.^{17, 27, 80} As Gini coefficients become more widely used, it will also be important to consider potential disadvantages of using this metric. Studies of kinase inhibitor selectivity do not rely on a threshold value, such as K_i, K_d or IC₅₀, but instead uses the calculated percent inhibition of targets, which can be highly dependent on experimental conditions such as the concentration of probe or ATP, etc.²⁴ Target panel size and composition are also important factors to consider to ensure an unbiased assessment of selectivity.²⁴ The limitations of the Gini coefficient in the case of chemical probes targeting RNA will be uncovered as the metric is incorporated more broadly. Furthermore, it is important to not rely solely on selectivity measurements in the development of novel chemical probes, but also to perform a variety of target validation and engagement experiments to confirm the probe’s mechanism of action in cells.³⁷ For example, it is possible for two compounds to have the same Gini coefficient in vitro, but differ in the physiological response they produce in cells, providing a rationale to advance one compound over the other.

Conclusions

Targeting proteins with small molecule chemical probes⁸¹ has revealed valuable lessons about the importance of rigorous assessment of selectivity in vitro and in vivo to confirm mechanistic hypotheses.⁸² We envision that quantifying selectivity with Gini coefficients in translational chemical biology⁸³ will become an important feature in the generation of higher quality chemical probes,^{2, 84} leading to a better understanding of the causality between small molecules and modulated biological targets. RNA has emerged as an important biological target to consider for both drug development and when assessing off-target effects of advanced clinical candidates. Determination of transcriptome-wide selectivity, via Gini coefficients, will provide selectivity data in a timely and cost-effective manner, providing a rationale for further optimization by eliminating off-target effects of novel chemical probes. To maximize the impact of chemical biology tools in drug discovery,⁸⁵ quantifying protein and RNA selectivity of chemical probes via robust and easy to grasp metrics will be essential to drive innovation towards the generation of transformative medicines with improved clinical success.