Abstract
When the electrostatic environment surrounding binding partners changes between unbound and bound states, the net uptake or release of a proton is possible by either binding partner. This process is pH-dependent in that the free energy required to uptake or release the proton varies with pH. This pH-dependence is typically not considered in conventional free energy methods where the use of fixed protonation states is the norm. In the present paper, we apply a simple two-step approach to calculate the pH-dependent binding free energy of a model cucubit[7]uril host/guest system. Using λ-dynamics with an enhanced sampling protocol, adaptive landscape flattening, pKa shifts and reference binding free energies upon complexation were determined. This information enables the construction of pH-dependent binding profiles which accurately capture the pKa shifts and reproduce binding free energies at the different pH conditions that were observed experimentally. Our calculations illustrate a general framework for computing pH-dependent binding free energies, but also point to some issues in modeling the molecular charge distributions within this series of molecules with CGENFF. However, by introducing some minor charge modifications to the CGenFF force field we saw significant improvement in accuracy of the calculated pKa shifts.
Graphical Abstract
Introduction
Chemical properties of small molecule guests noncovalently encapsulated by macrocyclic hosts, such as cucurbiturils, octa-acids, and cyclodextrins, may change due to an altered microenvironment and isolation of the guest molecule away from solvent.1-7 For example, encapsulation may reduce the likelihood of guest molecule aggregation and nonspecific adsorption, it enhances thermal and photostability, and prevents bi-molecular interactions such as oxidation.8, 9 In the pharmaceutical industry, it is estimated that about 40% of drugs currently on the market and 60% of compounds in research and development suffer from poor water solubility.10, 11 Formulation of hydrophobic drug molecules with macrocyclic hosts can provide desirable enhancements in solubility. Additionally, 60-80% of all orally administered drugs are either weak acids or bases, in which the protonation state can be altered by changes in the electrostatic environments in the cell or receptor.12-16 When protonation state changes are observed as a result of binding, the binding free energy is said to be pH-dependent, because the observed binding free energy will change in response to the surrounding pH.16 Different macrocyclic hosts feature different electrostatic interior environments, thus, an appropriate guest’s acid-base equilibrium can be tuned or shifted based on the macrocyclic container selected to encapsulate the guest.17
The Cucurbit[n]urils (CBn) family of macrocyles has been studied extensively due to its dramatic effect on the acid-base equilibria of encapsulated guests.17 CBn are water-soluble macrocyclic containers consisting of n glycoluril molecules that have a rigid hydrophobic cavity, are barrel-shaped, and have two highly negative portals lined by carbonyl groups (Figure 1).18, 19 Based on these properties, CBns display a high selectivity and affinity for guest molecules with complementary polarity, size, and shape.20 Due to its unique structural characteristics, CBn interacts with its guests through ion-dipole as well as hydrophobic interactions.21 Based on their remarkable binding properties and the reversible nature of the host-guest formation, applications have been realized in fields including sensing, catalysis, materials, and drug delivery.22-29 Compared to the other CBns, the modest water solubility of Cucurbit[7]uril (CB7) (~5 mM in pure water)7, makes it an ideal host to study various physicochemical aspects of its guests, such as binding thermodynamics.17
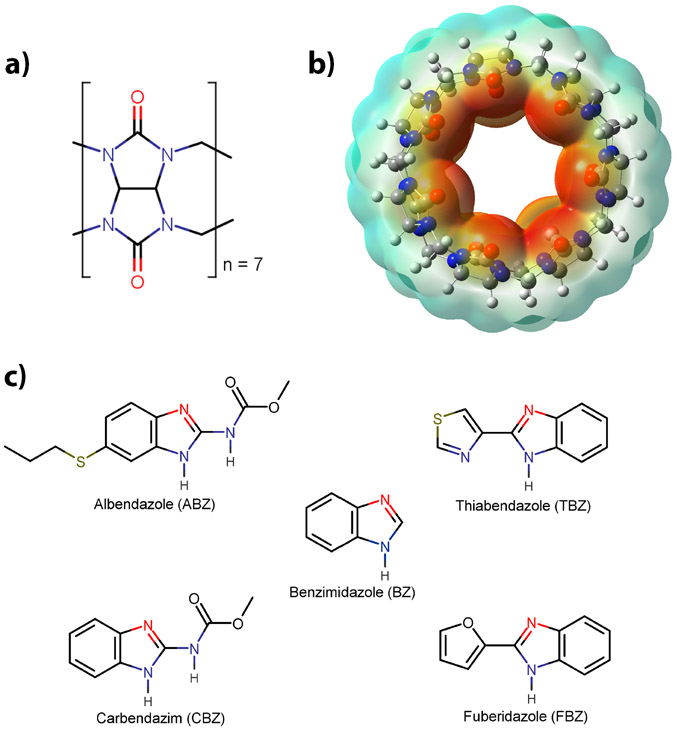
Figure 1.
a) Structure of a glycoluril unit; b) cucurbit[7]uril (CB7), where the electrostatic surface is shown; and c) The ligand set consisting of benzimidazole and its derivatives. The site of protonation within the benzimidazole core is shown in red for all derivatives.
Recently, computational free energy methods such as thermodynamic integration (TI)30-32 and free energy perturbation (FEP)33-35 have been used to calculate binding free energies, however, they typically utilize fixed protonation states for the bound and free forms of the binding partners (ligands, proteins, etc…). The use of fixed protonation states is a limiting assumption that may lead to errors due to coupling between ligand and proton binding and it is therefore important to assign the correct pKa and protonation state to obtain accurate binding free energies.16 Methods have been developed, such as various flavors of constant pH molecular dynamics (CpHMD)36-38, which allow the protonation state of multiple titratable groups to fluctuate as changes occur in their respective electrostatic environments. For CpHMD simulations utilizing λ-dynamics, the protonation state of a titrating residue is described by a continuous variable lambda (λ), where the dynamics of λ and the system are coupled. The success of these λ-dynamics based CpHMD methods has been shown for pH dependent systems involving, protein folding39, 40, aggregation41, chaperon activity42, and the effect of electrostatics on protein stability43. Additionally, the successful predictions of pKa values of titratable groups within proteins44-46 and nucleic acids47-49 as well as pH dependent conformational changes have also been demonstrated50. Therefore, based on previous successes, we sought to apply a simple two-step approach to predict the pH dependent binding free energy for a model host/guest system, between a set of benzimidazole derivatives and CB7. In the first step, a pKa is determined for each guest molecule in the presence of CB7, based on the difference in relative stability of the protonated forms of the benzimidazole derivatives in a free and bound state. Next, binding free energies of the unprotonated benzimidazole derivatives is computed and used along with the pKa information obtained in the first step to predict the binding energy as a function of pH.51 Recently, a similar two-step approach was successfully applied by Shen and coworkers to study the allosteric modulation of inhibitor selectivity for an important drug target related to Alzheimer’s disease, β-secretase.52
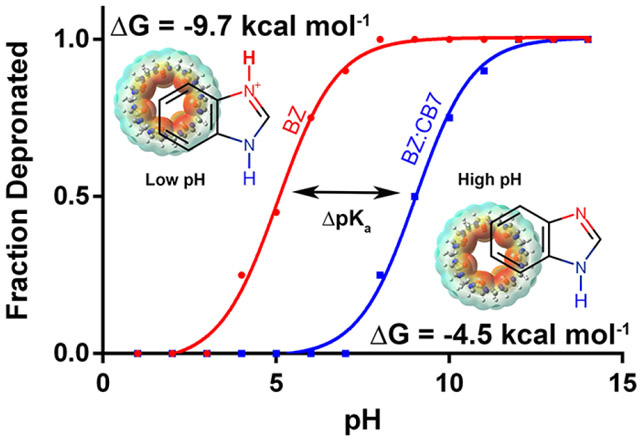
This host/guest system has been studied previously by B. R. Brooks and coworkers, where they utilized an enveloping distribution method53, 54 enhanced with Hamiltonian replica exchange55, 56 to compute pKa shifts and used a virtual bond algorithm (VBA)57 to determine absolute binding free energy.58 Their computed pKa values and binding free energies obtained for CB7:benzimidazole (BZ) were overestimated (pKa=12.7, ΔGbind=−17.5 kcal mol−1) due to overstabilization of the protonated state BZH+. This overstabilization was attributed to the use of overpolarized partial charges of the host and protonated BZ molecule when parametrized with the CGenFF59 force field. However, using the same force field parameters (BZ is a known molecule within the force field), our two-step approach more accurately reproduced experimental values for both the pKa shift as well as the binding free energy of BZ. Furthermore, our approach was successfully extended to the rest of the BZ derivatives (Figure 1) studied by the Nau and coworkers1. This accounted for pH dependent binding free energy changes originating from altering the structure of BZ, by the addition of small pendent groups such as amido or furan moieties. We use a different approach that employs simulations with adaptive landscape flattening (ALF)60, where sampling is iteratively optimized by flattening free energy barriers. By reducing the free energy barriers on either side of the thermodynamic cycle, trapping of individual states is avoided and sampling is more evenly distributed across all unprotonated and protonated states. This allows us to increase the accuracy of our pKa and binding free energy predictions with little to no loss of efficiency.
Theory
Based on the binding polynomial formalism developed by Wyman61 and Tanford62 a general description for ligand association can be used to represent the binding of a titratable ligand to a receptor,
| (1) |
where the ligand and receptor:ligand complex may contain different protonated forms of the titratable ligand and/or receptor. Since CB7 itself does not titrate within a typical biological pH range and the ligand has a single titratable site, equation (1) can be rewritten as;
| (2) |
where concentrations are reported rather than activities, assuming ideal dilute solution behavior. Based on a thermodynamic cycle used to describe proton-linked binding of the ligand to CB7 (shown in the SI; Figure S1) and acid dissociation constants for the free and bound forms equation (2) can be rewritten in terms of the overall change in free energy of binding ΔG (pH).
| (3) |
The pH dependence of the binding affinity can be obtained from the pKa of the free and bound ligand and the unprotonated binding free energy (ΔGref).
Utilizing λ-dynamics63, 64 with enhanced sampling (ALF)60, free energies differences (ΔG) between the unprotonated and protonated ligands were calculated in bound and unbound states. From the resulting free energy change (ΔΔG) one can convert these quantities to relative ΔpKa using the relationship between ΔG and the equilibrium constant Ka.
| (4) |
| (5) |
| (6) |
| (7) |
The free energy difference between the fixed bias (this is the difference in bias between the unprotonated and protonated forms) on either side of the thermodynamic cycle was used to calculate ΔpKa upon host/guest complexation (SI; Figure S1). A detailed explanation of the fixed and variable biases can be found here.60, 65 In brief, the fixed bias adjusts the energetic end points of all states to have similar free energies, which optimizes sampling during our simulations. Additionally, the fixed bias can be used as an indicator for how stable, relative to the reference, a certain species is (protonated or unprotonated) within a free and bound state. The ΔpKa calculated based on equation (7) is then added to the reference pKa value (experimentally determined, from equation 3) to obtain a pKa for each ligand in a bound state ( from equation 3).
Computational Methods
The CB7 structure used in this study was obtained from a crystal structure (PDB ID: 6F7W)66 describing a host-guest complex with dimethyllysine within a sugar binding protein. Benzimidazole (BZ) and its derivatives (protonated and unprotonated) were constructed and geometrically optimized using the Gaussian g0967 software at the 6-31G* level utilizing density functional theory B3LYP68. Figure 1 shows the five ligands that make up the guest component as well as the structure of CB7, which is the host component of the system. The resulting optimized ligand structures were rigidly docked into the cavity of the CB7 structure using Autodock Vina version 1.5.669 with an exhaustiveness value set to 20. This docking procedure produced 5-20 poses for each ligand where the top ranked poses among the different ligands were similar in position and interaction. The resulting complex structures (Figure 2) were used as the initial structures for the λ-dynamics simulations utilizing a newly developed method for accelerating alchemical sampling called Adaptive Landscape Flattening (ALF)60. In this approach, iterative runs of λ-dynamics (MD) simulations are performed, which allows for the construction of free energy profiles in λ-space that can be flattened by the addition of fixed and variable biases. A three-state model, incorporating proton tautomerization (shown in SI, Figure S5), was used to describe the protonation states of the guest molecules used in this study. For example, BZ was modeled in an unprotonated form by two separate states (State 1:N1—H or State 2:N2—H), where the protonated form was model by a single state(State 3:both N1—H and N2—H). For all the guest molecules, the protonated form is symmetric with respect to both charge and atom type for the N1 and N2 atoms within the benzimidazole core. The convpdb.pl tool from the MMTSB toolset70 was used to solvate the host/guest complex in a cubic box of explicit TIP3P water71, with enough space to provide a 12 Å buffer between the edge of the box and the host molecule. This produced final box dimensions of 38.2 x 38.2 x 38.2 Å3. An appropriate number of counter ions (Na+ and Cl−) were added to neutralize the charge and achieve an ionic strength of 150mM NaCl. The entire system was then energy minimized for 400 steps utilizing a steepest decent method, followed by 500 steps of adopted basis Newton-Raphson minimization to remove any steric clashes.
Figure 2.
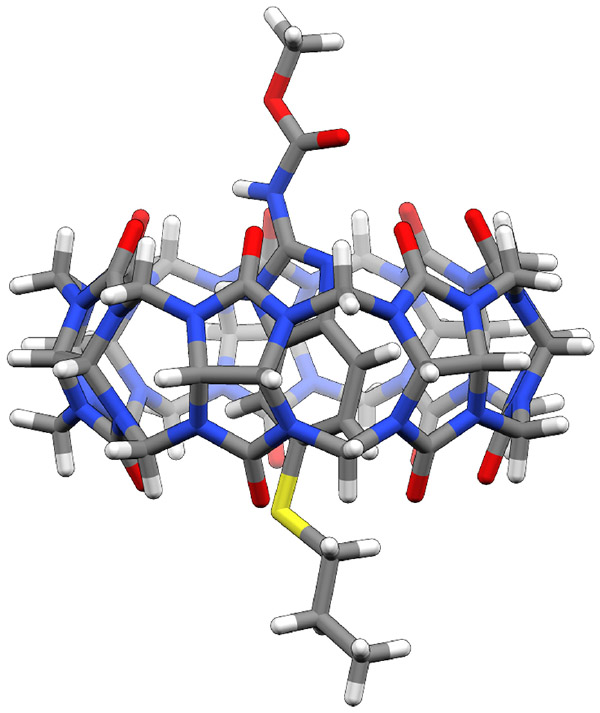
The structure of CB7 and Albendazole (ABZ) complex generated from docking
Simulations were carried out in three phases. During the first phase, 100-150 iterations of 200 picoseconds of λ-dynamics were performed, where in the initial iteration all biases equal 0, which allows for a gradual refinement of the fixed and variable biases. The first 100 picoseconds of simulation time were treated as equilibration and were discarded from the bias refinement. Results from the previous 10 iterations are combined using WHAM72 to obtain an estimate of the λ-space free energy landscape. In the second and third phases, the same fitting procedure was used, however with fewer iterations (phase 2 = 10 and phase 3 = 5) and longer simulation times of 1 and 5 nanoseconds, respectively. Results from the last 5 iterations are combined in WHAM72 and new biases are obtained. Finally, 5 independent production simulations were performed of 50 ns each with the optimized biasing potential. This allowed for determination of statistical uncertainties, i.e. the square root of the sum of squared standard deviations from either side of the thermodynamic cycle. New biasing potentials were calculated from the 50 ns production runs and used to determine the pKa shifts because these fixed biases correspond to the free energy differences between the tautomeric states at each site. Using this approach, free energies were obtained for the molecule of interest within a solvated environment for both free and complexed forms.
Simulations were carried out with CPT dynamics using domain decomposition (DOMDEC73) on graphics processing units (GPUs) within the CHARMM74, 75 molecular simulation package, development version 44a1. A friction coefficient of 10 ps−1 was applied to all atoms to maintain a constant temperature. The Leapfrog Verlet integrator was used with a integration time step of 2 fs in conjunction with a c = 5.565 (implicit constraint coefficient)76. All hydrogen bond lengths were constrained using the SHAKE77 algorithm. Electrostatic and van der Waals interactions were truncated with force switching (fswitch and vfswitch, respectively) between 10 and 12 Å. Furthermore, a soft-core Lennard Jones potential was employed for all free energy calculations to modulate the van der Waals interactions with respect to λ.60 Linear scaling by λ was applied to all guest molecule non-bonded energy terms. Bonds, angles, dihedrals, and improper intramolecular energies were not scaled by λ to maintain physically reasonable geometries at intermediate λ values. Both CB7 and the ligand set were parameterized using the CGenFF59 forcefield within the ParamChem78, 79 program. In order to explore the effects of a different charging scheme, RESP80-82 charges were used along with CGenFF59 parameters to test the charge dependency on the computed free energy (SI; Figure S4 and Table S1).
The underlying physics behind λ-dynamics have been discussed in detail elsewhere.63, 65, 76 In brief, the λ-dynamics framework employs the BLOCK facility in CHARMM which partitions your molecular system into blocks and allows for the use of coefficients that scale the interaction energies between these blocks. Environment atoms, including CB7, counter ions, and TIP3P water, were loaded to the first block while the protonation states of the guest molecules were loaded into subsequent blocks (4 in total). A holonomic constraint was used on λ (between 0 and 1; 0 < λ < 1) to maintain physically relevant endpoints during our simulations where λ is transformed into another variable θ. This work used the λNexp functional form for defining λ as a function of θ (see implicit constraint coefficient above c=5.5). Each θ was assigned a fictitious mass of 5 amu·Å2 and was propagated dynamically by the equations of motion, then converted back to λ values used for energy evaluation. λ was saved every 10 steps to compute the relative free energies. Populations were determined by counting the amount of time each state was sampled based on a threshold of λ ≥ 0.99, this was used to approximate physical end states (λ = 1).60, 83 NOE restraints using a flat-bottom potential with a force constant of 25 kcal/mol·Å2 applied at separations greater than 1.0 Å were imposed on the heavy atoms (two separate carbon atoms) connecting the pendant groups off the benzimidazole core.
Binding free energies were calculated for the unprotonated guest molecules using a dual-topology approach within the λ-dynamics framework. This approach differs from traditional CpHMD due to the use of whole ligand topologies that describe the alchemical state at a single site. Additionally, a thermodynamic cycle (SI; Figure S2) was used that describes the host/guest binding process for this study.
Results and Discussion
Inspired by a recent SAMPL384 challenge, a community wide blind competition to predict the binding affinities of various host-guest system, we sought to apply a two-step approach to predict the binding affinities of a host guest system for which the protonation state of the ligand was likely to change upon binding. Figure 1 shows the structure of the host (CB7) and the ligands (BZ, ABZ, CBZ, FBZ, and TBZ) used within this study. Previous studies have used the CB7:BZ complex as a model system to study the pH-dependency of binding and, thus, was chosen for this work’s benchmarking efforts.16, 58
Experimentally determined pKa and binding constants have been obtained by the Nau group utilizing UV titrations where they showed pKa shifts ranging from 2.5 to 4 pH units for BZ and its derivatives upon complexation with CB7.1 Furthermore, they saw enhancements in photostability and solubilities of BZ and its derivatives upon encapsulation.1 Additionally, binding constants were determined under basic conditions where the unprotonated species should dominate in both the free and bound forms. Experimentally determined pKa shifts and binding affinities are shown in Tables 1 and 2, respectively.
Table 1.
Experimental pKa shifts of benzimidazole and its derivatives upon complexation with CB7. pKa results were taken from ref.1
| Ligand | pKaFree | pKaComplex | ΔpKa |
|---|---|---|---|
| BZ | 5.5 | 9.0 | 3.5 |
| ABZ | 3.5 | 6.1 | 4.0 |
| CBZ | 4.5 | 7.0 | 3.8 |
| FBZ | 4.8 | 8.6 | 2.6 |
| TBZ | 4.6 | 8.6 | 2.5 |
Table 2.
Experimental binding free energies of benzimidazole and its derivatives upon complexation with CB7.1 refers to the unprotonated binding free energy while was calculated based on equation (3) for the protonated ligands at pH 7.0
| Ligand | ||
|---|---|---|
| BZ | −4.4 | −7.1 |
| ABZ | −6.6 | −6.7 |
| CBZ | −6.0 | −6.4 |
| FBZ | −2.3 | −4.5 |
| TBZ | −3.0 | −5.2 |
pKa Determination
In this study, we estimated the pKa shift of BZ and its derivatives induced by CB7 binding from λ-dynamics63 with enhanced sampling (ALF)60 simulations. We compare the relative stability of the protonated form both in the presence and absence of CB7. Experimental binding constants and pKa values suggest that the protonated form should be more energetically favored when bound to CB7 than when it is free in solution. This expected trend was observed. Table 3 shows the computed pKa values obtained after host/guest complexation using CGenFF59 parameters and partial charges. From the data generated using CGenFF-derived partial charges it is apparent that at neutral pH (7.0), BZ and its derivatives would be protonated except for ABZ, which is slightly more acidic in nature. The value of pKaCGenFF for BZ was found to be 9.4, which is a shift of more than 3.5 pK units from its reference value of 5.5. This indicates that the preferred protonation state of BZ depends on the surrounding environment. For example, at a neutral pH (7.0) BZ would be deprotonated in its free solvated form and would switch to a protonated state upon binding to CB7. This, in turn, increases the hydrogen bonding potential of BZ to interact with the carbonyl oxygen atoms located at the portal of CB7. Therefore, the induced shift in pKa has a stabilizing effect when BZ binds to CB7. The statistical uncertainty associated with the computed pKa was generally small for the sample size (n=5), but was larger for ABZ and CBZ. These ligands differ structurally from BZ due to the presence of an amido group positioned off the head group of the BZ core. The slow relaxation of the torsional degrees of freedom of the amido group yielded larger statistical fluctuations in the findings, which resulted in a higher standard deviation among the trials for those two derivatives. A possible approach to address this slow rotational degree of freedom is to allow dihedrals to scale by λ during the simulations thus, allowing free rotation along the dihedral that connects the amido group to the BZ core when that derivative is in the off state (λ<0.2, not interacting with the environment atoms). However, this concept has not been explored and most likely will be addressed in a subsequent study.
Table 3.
A comparison between the experimental pKa1 after complexation and those computed using the CGenFF parameters and charges.
| Ligand | pKaComplex | pKaCGenFF |
|---|---|---|
| BZ | 9.0 | 9.4±0.2 |
| ABZ | 6.1 | 6.1±0.5 |
| CBZ | 7.0 | 7.8±0.8 |
| FBZ* | 8.6 | 10.4±0.2 |
| TBZ* | 8.6 | 10.0±0.3 |
| MUE | 0.9 | |
| Pearson (R) | 0.9 | |
| Spearman | 0.8 |
Note a modified charging scheme was used for FBZ and TBZ (see discussion below).
Modified CGenFF Partial Charges
Derivatives FBZ and TBZ produced the largest deviation from the experimental results and can be explained based on an apparent improper charge assignment to their protonated forms FBZ+ and TBZ+. During the partial charge assignment utilizing ParamChem78, 79 FBZ+ and TBZ+ were erroneously assigned a neutral charge whereas they should have been assigned a +1 charge. No manipulation of the mol2 file, e.g. explicitly defining bonds or changing SYBYL atom types resulted in a proper assignment of the +1 state for either one of these derivatives. Interestingly in the stream file generated by ParaChem78, 79 for FBZ+ and TBZ+, both nitrogen atoms had large negative charges of −1.025e−. This high negative charge appears to be unphysical when compared to the charges obtained for the protonated forms of BZ+, ABZ+, and CBZ+, where the correct charge state (+1) and more reasonable nitrogen partial charge (−0.457 to −0.471) were observed. Simulations performed with the original CGenFF59 charge scheme for FBZ+ and TBZ+ produced unphysical pKa values shifted higher than 14. Therefore, we modified the partial charges for FBZ+ and TBZ+ by calculating the change in charge (Δq) between BZ:BZ+ and CBZ:CBZ+ and then applied an averaged Δq to the neutral form of FBZ and TBZ to generate the partial charges used for their protonated forms (the modified charges are included in the SI, Figure S6 and S7). The remaining unbalanced charge was then evenly distributed among the atoms present within the furan and thiazole moieties. Due to the fact that the Δq for BZ:BZ+ and CBZ:CBZ+ were similar in both magnitude and direction (AVG std < 0.02), and that their structures varied at the same position, we assumed Δq would be similar for the FBZ:FBZ+ and TBZ:TBZ+ constructs. This modified CGenFF charge scheme seems to have better reproduced pKa similar to those observed experimentally for FBZ and TBZ (experiment=8.6, computed≈10.0), however they are still elevated by ~1.4 pH units. This elevated pKa could be partially due to improper charge assignments within the imidazole core or due to the empirical approach of charge modification and redistribution described above. Nevertheless, the modified CGenFF charge, when compared to experimentally determined pKa values, performed better (lower MUE) than the original CGenFF charges. The better performance of the modified CGenFF charges indicates that charge optimization procedures might be required for accurate pKa determination.
Reference Binding Free Energy
Reference binding free energies (Table 4) (ΔGCompuuted) were computed for the unprotonated benzimidazole derivatives. To remain consistent with the pKa calculations, we performed simulations utilizing a dual-topology approach and CGenFF59 force field parameters and charges (modified for FBZ and TBZ as noted above) for the benzimidazole ligands. This resulted in high Pearson (0.9) and Spearman values (0.7) indicating good agreement with the experimentally determined binding free energies and their relative ranking, respectively. The largest error was obtained for derivative ABZ, where the calculated binding free energy deviated significantly from the experimental result by 2.3 kcal/mol. This deviation was due to frequent shuttling of the propylthio group in and out of the hydrophobic cavity of CB7, which resulted in pushing the benzimidazole core and amido head group out of the binding pocket. The observed movement is consistent with NMR experiments that showed upfield shifts for the propylthio moiety, which suggests partial or temporary inclusion inside CB7.1 Within the simulations, this change in position significantly decreased the likelihood of forming a second hydrogen bond, originating from the amido head group, with the portal of CB7. Therefore, binding energies obtained for this group mirrored BZ where only one hydrogen bond, originating from the benzimidazole core, was possible.
Table 4.
A comparison between the experimental binding free energy1 for the unprotonated benzimidazole derivatives and those predicted using the CGenFF force field
| Ligand | ΔGCGenFF | |
|---|---|---|
| BZ | −4.4 | −4.4±0.0 |
| ABZ | −6.6 | −4.3±0.5 |
| CBZ | −6.0 | −5.7±0.5 |
| FBZ | −2.3 | −0.3±0.7 |
| TBZ | −3.0 | −0.8±0.5 |
| MUE | 1.4 | |
| Pearson (R) | 0.9 | |
| Spearman | 0.7 |
Predicting the pH Dependent Free Energy Profile
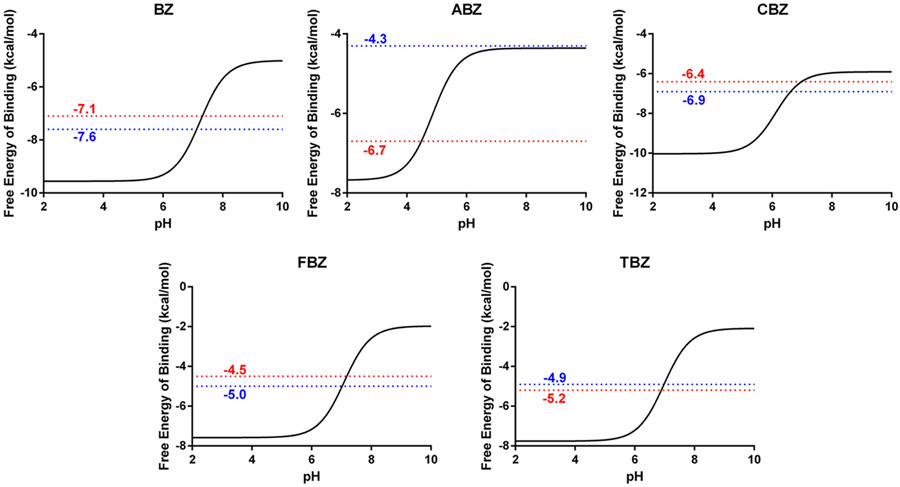
Combining the pKa results obtained in the first step with the binding free energies determined for the unprotonated guests, in the second step using equation (3), we were able to predict the binding free energy of the guest molecules as a function of pH. Equation (3) provides a method for computing this pH dependence by applying a correction term to the reference binding free energy. This correction term changes with pH and thus can be used to construct a full pH dependent binding profile for each of the guest molecules. These profiles are shown in Figure 3. Examining the binding profiles within a biologically relevant pH region (5-9), a range of more than 3 kcal/mol was observed for all guest molecules. This observation indicates that if typical assumptions (fixed protonation states based on reference pKa values) were applied here, it would have resulted in major deviations in the binding free energies obtained (excepting high and low pH environments where binding free energies fluctuations are small). For example, if this assumption were made for the BZ:CB7 complex it would have resulted in a deviation in the binding free energy of 2.7 kcal/mol (Table 4 and 5). Similar deviations were also observed for the other guest molecules and ranged from 0 to 4.7 kcal/mol. For FBZ and TBZ, the calculated reference binding free energies were significantly decreased from the experimentally determined ones. This should have resulted in a decrease in accuracy for the predicted pH dependent binding free energies, however, this was not observed. Instead, the depressed reference binding free energy was compensated for by overestimating the pKa in a bound state, producing errors of opposite sign for each calculation. This indicates some cancellation of error within this two-step approach. However, this contrasts with the results obtained for ABZ, where a depressed reference binding free energy was not compensated for by an increase in the calculated pKa.
Figure 3.
pH dependent binding free energies for each benzimidazole derivative as labeled. The red line represents the experimentally derived binding free energies for the protonated guest molecules while the blue line represents the predicted binding free energy utilizing our two-step computational approach.
Table 5.
A comparison between the experimental binding free energy for the protonated benzimidazole derivatives. was obtained from equation (3) using the experimental pKa and binding free energies. was obtained from equation (3) using the pKa and binding free energies computed using the CGenFF force field. Free energies are shown in kcal mol−1
| Ligand | ||
|---|---|---|
| BZ | −7.1 | −7.6±0.2 |
| ABZ | −6.7 | −4.3±0.7 |
| CBZ | −6.4 | −6.9±0.9 |
| FBZ | −4.5 | −5.0±0.7 |
| TBZ | −5.2 | −4.9±0.6 |
| MUE | 0.8 | |
| Pearson (R) | 0.5 | |
| Spearman | 0.3 |
Conclusion
In this study we sought to apply a simple two-step approach to predict the pH dependent binding free energy for a model host/guest system. In the first step, pKas were accurately reproduced for a variety of benzimidazole derivatives when in complex with CB7. The pKas were determined utilizing CGenFF59 partial charges (modified charges for FBZ+ and TBZ+) and parameters which produced results highly correlated with experiments with Pearson and Spearman values of 0.9 and 0.8, respectively. This was a substantial enhancement in accuracy over a previous study58 that used a different method and the same host/guest system. Charge modifications to the CGenFF59 force field were required for derivatives FBZ+ and TBZ+, which resulted in a significant improvement in accuracy of their calculated pKas. These findings suggest that the charging model in ParamChem78, 79/CGenFF59 for this type of moiety is insufficient. Furthermore, the calculated pKas were very sensitive to the partial charge scheme employed. This conclusion is supported by work presented in the SI, where changing the partial charge scheme to RESP significantly altered the calculated pKa’s. These findings are in basic agreement with earlier studies from B. Brooks and co-workers58, that also used fully explicit solvent simulation models, but are inconsistent with mixed implicit/explicit solvent models from McCammon and coworkers16 earlier studies. Additionally, six other simpler charging schemes were tested (not shown in the present study) which resulted in significant changes to the calculated pKa’s (difference of more than 2 pK units). Therefore, based on our method, the accuracy of the calculated pKa is dependent on the partial charge scheme employed. Taken together, these studies suggest that care must be exercised in combining charging schemes and force fields, and solvent models, in arbitrary ways.
In the second step, binding free energies were obtained for the unprotonated guest molecules utilizing a dual-topology approach and CGenFF59 partial charges and parameters. The results obtained were accurate and highly correlated to the experimental values (Pearson = 0.9 and Spearman = 0.7). Combining the pKa results with the binding free energies obtained with the CGenFF59 force field, a full description of the pH dependent binding behavior was obtained, and a range of more than 3 kcal/mol was observed for all guest molecules within a biologically relevant pH range. This observation indicates that if fixed protonation states were used errors of up to 3 kcal/mol are possible. With high accuracy, utilizing an explicit water model, this two-step approach successfully accounts for changes in the binding free energy during complex formation that are pH dependent.
Supplementary Material
Acknowledgments
This research was supported by NIH Grants GM103695, GM037554, GM107233, and GM130587.
Footnotes
Supporting information
Thermodynamic cycles used to determine pKas and relative binding free energies. Flattened free energy barriers. Table and Graphical comparison between experimentally determined and computed pKa values using two separate charging methods, CGenFF and RESP. Three-state model used to describe the benzimidazole derivatives. Modified CGenFF charges for FBZ+ and TBZ+.
The authors declare no competing financial interest.
References:
- 1.Koner AL; Ghosh I; Saleh NI; Nau WM Supramolecular Encapsulation of Benzimidazole-derived Drugs by Cucurbit[7]uril. Can. J. Chem 2011, 89, 139–147. [Google Scholar]
- 2.Kim JS; Quang DT Calixarene-Derived Fluorescent Probes. Chem. Rev 2007, 107, 3780–3799. [DOI] [PubMed] [Google Scholar]
- 3.Lagona J; Mukhopadhyay P; Chakrabarti S; Isaacs L The Cucurbit[n]uril Family. Angew. Chem. Int. Ed 2005, 44, 4844–4870. [DOI] [PubMed] [Google Scholar]
- 4.Lee JW; Samal S; Selvapalam N; Kim HJ; Kim K Cucurbituril Homologues and Derivatives: New Opportunities in Supramolecular Chemistry. Acc. Chem. Res 2003, 36, 621–630. [DOI] [PubMed] [Google Scholar]
- 5.Wu J; Isaacs L Cucurbit[7]uril Complexation Drives Thermal Trans-cis-Azobenzene Isomerization and Enables Colorimetric Amine Detection. Chem. Eur. J 2009, 15, 11675–11680. [DOI] [PubMed] [Google Scholar]
- 6.Shaikh M; Dutta Choudhury S; Mohanty J; Bhasikuttan AC; Nau WM; Pal H Modulation of Excited-State Proton Transfer of 2-(2′ - Hydroxyphenyl)benzimidazole in a Macrocyclic Cucurbit[7]uril Host Cavity: Dual Emission Behavior and pKa Shift. Chem. Eur. J 2009, 15, 12362–12370. [DOI] [PubMed] [Google Scholar]
- 7.Koner AL; Nau WM Cucurbituril Encapsulation of Fluorescent Dyes. Supramol. Chem 2007, 19, 55–66. [Google Scholar]
- 8.González-Béjar M; Montes-Navajas P; García H; Scaiano JC Methylene Blue Encapsulation in Cucurbit[7]uril: Laser Flash Photolysis and Near-IR Luminescence Studies of the Interaction with Oxygen. Langmuir 2009, 25, 10490–10494. [DOI] [PubMed] [Google Scholar]
- 9.Mohanty J; Nau WM Refractive Index Effects on The Oscillator Strength and Radiative Decay Rate of 2,3-diazabicyclo[2.2.2]oct-2-ene. Photoch. Photobio. Sci 2004, 3, 1026–1031. [DOI] [PubMed] [Google Scholar]
- 10.Larrañeta E; Stewart S; Ervine M; Al-Kasasbeh R; Donnelly RF Hydrogels for Hydrophobic Drug Delivery. Classification, Synthesis and Applications. J. Funct. Biomater 2018, 9, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fahr A; Liu X Drug Delivery Strategies for Poorly Water-soluble Drugs. Expert Opin. Drug Deliv 2007, 4, 403–416. [DOI] [PubMed] [Google Scholar]
- 12.Manallack DT The Acid-base Profile of a Contemporary Set of Drugs: Implications for Drug Discovery. SAR. QSAR. Environ. Res 2009, 20, 611–655. [DOI] [PubMed] [Google Scholar]
- 13.Leeson PD; St-Gallay SA; Wenlock MC Impact of Ion Class and Time on Oral Drug Molecular Properties. MedChemComm 2011, 2, 91–105. [Google Scholar]
- 14.Meanwell NA Improving Drug Candidates by Design: A Focus on Physicochemical Properties As a Means of Improving Compound Disposition and Safety. Chem. Res. Toxicol 2011, 24, 1420–1456. [DOI] [PubMed] [Google Scholar]
- 15.Manallack DT; Prankerd RJ; Yuriev E; Oprea TI; Chalmers DK The Significance of Acid/Base Properties in Drug Discovery. Chem. Soc. Rev 2013, 42, 485–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kim MO; Blachly PG; Kaus JW; McCammon JA Protocols Utilizing Constant pH Molecular Dynamics to Compute pH-Dependent Binding Free Energies. J. Phys. Chem. B 2015, 119, 861–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Barooah N; Sundararajan M; Mohanty J; Bhasikuttan AC Synergistic Effect of Intramolecular Charge Transfer toward Supramolecular pKa Shift in Cucurbit[7]uril Encapsulated Coumarin Dyes. J. Phys. Chem. B 2014, 118, 7136–7146. [DOI] [PubMed] [Google Scholar]
- 18.Barrow SJ; Kasera S; Rowland MJ; del Barrio J; Scherman OA Cucurbituril-Based Molecular Recognition. Chem. Rev 2015, 115, 12320–12406. [DOI] [PubMed] [Google Scholar]
- 19.Assaf KI; Nau WM Cucurbiturils: From Synthesis to High-affinity Binding and Catalysis. Chem. Soc. Rev 2015, 44, 394–418. [DOI] [PubMed] [Google Scholar]
- 20.Basílio N; Gago S; Parola AJ; Pina F Contrasting pKa Shifts in Cucurbit[7]uril Host-Guest Complexes Governed by an Interplay of Hydrophobic Effects and Electrostatic Interactions. ACS Omega 2017, 2, 70–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Márquez C; Hudgins RR; Nau WM, Mechanism of Host-Guest Complexation by Cucurbituril. J. Am. Chem. Soc 2004, 126 (18), 5806–5816. [DOI] [PubMed] [Google Scholar]
- 22.Ghale G; Nau WM Dynamically Analyte-Responsive Macrocyclic Host–Fluorophore Systems. Acc. Chem. Res 2014, 47, 2150–2159. [DOI] [PubMed] [Google Scholar]
- 23.Pemberton BC; Raghunathan R; Volla S; Sivaguru J, From Containers to Catalysts: Supramolecular Catalysis Within Cucurbiturils. Chem. Eur. J 2012, 18, 12178–12190. [DOI] [PubMed] [Google Scholar]
- 24.Joseph R; Nkrumah A; Clark RJ; Masson E Stabilization of Cucurbituril/Guest Assemblies via Long-Range Coulombic and CH· · ·O Interactions. J. Am. Chem. Soc 2014, 136, 6602–6607. [DOI] [PubMed] [Google Scholar]
- 25.Pessêgo M; Basilio N; Moreira JA; García-Río L Cucurbit[7]uril: Surfactant Host–Guest Complexes in Equilibrium with Micellar Aggregates. ChemPhysChem 2011, 12, 1342–1350. [DOI] [PubMed] [Google Scholar]
- 26.Basilio N; García-Río L; Moreira JA; Pessêgo M Supramolecular Catalysis by Cucurbit[7]uril and Cyclodextrins: Similarity and Differences. J. Org. Chem 2010, 75, 848–855. [DOI] [PubMed] [Google Scholar]
- 27.Zheng L; Sonzini S; Ambarwati M; Rosta E; Scherman OA; Herrmann A Turning Cucurbit[8]uril into a Supramolecular Nanoreactor for Asymmetric Catalysis. Angew. Chem. Int. Ed 2015, 54, 13007–13011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Basílio N; Pischel U Drug Delivery by Controlling a Supramolecular Host–Guest Assembly with a Reversible Photoswitch. Chem. Eur. J 2016, 22, 15208–15211. [DOI] [PubMed] [Google Scholar]
- 29.Carvalho CP; Uzunova VD; Da Silva JP; Nau WM; Pischel U A Photoinduced pH Jump Applied to Drug Release From Cucurbit[7]uril. Chem. Comm 2011, 47, 8793–8795. [DOI] [PubMed] [Google Scholar]
- 30.Khavrutskii IV; Wallqvist A Improved Binding Free Energy Predictions from Single-Reference Thermodynamic Integration Augmented with Hamiltonian Replica Exchange. J. Chem. Theory. Comput 2011, 7, 3001–3011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lee H-C; Hsu W-C; Liu A-L; Hsu C-J; Sun Y-C Using Thermodynamic Integration MD Simulation to Compute Relative Protein–ligand Binding Free Energy of a GSK3β Kinase Inhibitor and Its Analogs. J. Mol. Graph. Model 2014, 51, 37–49. [DOI] [PubMed] [Google Scholar]
- 32.Bhati AP; Wan S; Wright DW; Coveney PV, Rapid, Accurate, Precise, and Reliable Relative Free Energy Prediction Using Ensemble Based Thermodynamic Integration. J. Chem. Theory. Comput 2017, 13, 210–222. [DOI] [PubMed] [Google Scholar]
- 33.Jiang W; Roux B Free Energy Perturbation Hamiltonian Replica-Exchange Molecular Dynamics (FEP/H-REMD) for Absolute Ligand Binding Free Energy Calculations. J. Chem. Theory. Comput 2010, 6, 2559–2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fratev F; Sirimulla S An Improved Free Energy Perturbation FEP+ Sampling Protocol for Flexible Ligand-Binding Domains. Sci. Rep 2019, 9, 16829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang L; Wu Y; Deng Y; Kim B; Pierce L; Krilov G; Lupyan D; Robinson S; Dahlgren MK, et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- 36.Huang Y; Chen W; Wallace JA; Shen J All-Atom Continuous Constant pH Molecular Dynamics With Particle Mesh Ewald and Titratable Water. J. Chem. Theory. Comput 2016, 12, 5411–5421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Khandogin J; Brooks CL III. Constant pH Molecular Dynamics with Proton Tautomerism. Biophys. J 2005, 89, 141–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Goh GB; Hulbert BS; Zhou H; Brooks CL III. Constant pH Molecular Dynamics of Proteins in Explicit Solvent with Proton Tautomerism. Proteins 2014, 82, 1319–1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Khandogin J; Chen J; Brooks CL III. Exploring Atomistic Details of pH-dependent Peptide Folding. Proc. Natl. Acad. Sci. U. S. A 2006, 103, 18546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Khandogin J; Raleigh DP; Brooks CL III. Folding Intermediate in The Villin Headpiece Domain Arises from Disruption of a N-Terminal Hydrogen-Bonded Network. J. Am. Chem. Soc 2007, 129, 3056–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Khandogin J; Brooks CL III. Linking Folding with Aggregation in Alzheimer β-amyloid Peptides. Proc. Natl. Acad. Sci. U. S. A 2007, 104, 16880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang BW; Brunetti L; Brooks CL III. Probing pH-Dependent Dissociation of HdeA Dimers. J. Am. Chem. Soc 2011, 133, 19393–19398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shen JK Uncovering Specific Electrostatic Interactions in the Denatured States of Proteins. Biophys. J 2010, 99, 924–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Swails JM; Roitberg AE Enhancing Conformation and Protonation State Sampling of Hen Egg White Lysozyme Using pH Replica Exchange Molecular Dynamics. J. Chem. Theory. Comput 2012, 8, 4393–4404. [DOI] [PubMed] [Google Scholar]
- 45.Meng Y; Roitberg AE Constant pH Replica Exchange Molecular Dynamics in Biomolecules Using a Discrete Protonation Model. J. Chem. Theory. Comput 2010, 6, 1401–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Williams SL; de Oliveira CAF; McCammon JA Coupling Constant pH Molecular Dynamics with Accelerated Molecular Dynamics. J. Chem. Theory. Comput 2010, 6, 560–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Goh GB; Knight JL; Brooks CL III. Toward Accurate Prediction of the Protonation Equilibrium of Nucleic Acids. J. Phys. Chem. Lett 2013, 4, 760–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Goh GB; Knight JL; Brooks CL III. Constant pH Molecular Dynamics Simulations of Nucleic Acids in Explicit Solvent. J. Chem. Theory. Comput 2012, 8, 36–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Goh GB; Knight JL; Brooks CL III. pH-dependent Dynamics of Complex RNA Macromolecules. J. Chem. Theory. Comput 2013, 9, 935–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Laricheva EN; Arora K; Knight JL; Brooks CL III. Deconstructing Activation Events in Rhodopsin. J. Am. Chem. Soc 2013, 135, 10906–10909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Law SM; Zhang BW; Brooks CL III. pH-sensitive Residues in the p19 RNA Silencing Suppressor Protein from Carnation Italian Ringspot Virus Affect siRNA Binding Stability. Protein Sci. 2013, 22, 595–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Harris RC; Tsai C-C; Ellis CR; Shen J, Proton-Coupled Conformational Allostery Modulates the Inhibitor Selectivity for β-Secretase. J. Phys. Chem. Lett 2017, 8, 4832–4837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Christ CD; Gunsteren WF Enveloping Distribution Sampling: A Method to Calculate Free Energy Differences from a Single Simulation. J. Chem. Phys 2007, 126, 184110. [DOI] [PubMed] [Google Scholar]
- 54.Christ CD; Gunsteren WF Multiple Free Energies from a Single Simulation: Extending Enveloping Distribution Sampling to Nonoverlapping Phase-space Distributions. J. Chem. Phys 2008, 128, 174112. [DOI] [PubMed] [Google Scholar]
- 55.Sugita Y; Kitao A; Okamoto Y Multidimensional Replica-exchange Method for Free-energy Calculations. J. Chem. Phys 2000, 113, 6042–6051. [Google Scholar]
- 56.Fukunishi H; Watanabe O; Takada S On the Hamiltonian Replica Exchange Method for Efficient Sampling of Biomolecular Systems: Application to Protein Structure Prediction. J. Chem. Phys 2002, 116, 9058–9067. [Google Scholar]
- 57.Boresch S; Tettinger F; Leitgeb M; Karplus M Absolute Binding Free Energies: A Quantitative Approach for Their Calculation. J. Phys. Chem. B 2003, 107, 9535–9551. [Google Scholar]
- 58.Lee J; Miller BT; Brooks BR Computational Scheme for pH-dependent Binding Free Energy Calculation with Explicit Solvent. Protein Sci. 2016, 25, 231–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P, et al. CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with The CHARMM All-atom Additive Biological Force Fields. J. Comput. Chem 2010, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hayes RL; Armacost KA; Vilseck JZ; Brooks CL III. Adaptive Landscape Flattening Accelerates Sampling of Alchemical Space in Multisite λ Dynamics. J. Phys. Chem. B 2017, 121, 3626–3635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.W. J. Jr. Linked Functions and Reciprocal Effects in Hemoglobin: A Second Look. Adv. Protein Chem 1964, 19, 223–286. [DOI] [PubMed] [Google Scholar]
- 62.Tanford C Protein Denaturation. C. Theoretical Models for The Mechanism of Denaturation. Adv. Protein Chem 1970, 24, 1–95. [PubMed] [Google Scholar]
- 63.Knight JL; Brooks CL III. Lambda-dynamics Free Energy Simulation Methods. J. Comput. Chem 2009, 30, 1692–1700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kong X III, Brooks CL III. λ-dynamics: A New Approach to Free Energy Calculations. J. Chem. Phys 1996, 105, 2414–2423. [Google Scholar]
- 65.Knight JL; Brooks CL III. Multi-Site λ-dynamics for Simulated Structure-Activity Relationship Studies. J. Chem. Theory. Comput 2011, 7, 2728–2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Guagnini F; Antonik PM; Rennie ML; O'Byrne P; Khan AR; Pinalli R; Dalcanale E; Crowley PB Cucurbit[7]uril-Dimethyllysine Recognition in a Model Protein. Angew. Chem. Int. Ed 2018, 57, 7126–7130. [DOI] [PubMed] [Google Scholar]
- 67.Frisch MJT,GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Mennucci B; et al. Gaussian 09, Gaussian Inc; : Wallingford CT, 2009. [Google Scholar]
- 68.Lee C; Yang W; Parr RG Development of The Colle-Salvetti Correlation-energy Formula Into a Functional of The Electron Density. Phys. Rev. B 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
- 69.Trott O; Olson AJ AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem 2010, 31, 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Feig M; Karanicolas J; Brooks CL III. MMTSB Tool Set: enhanced Sampling and Multiscale Modeling Methods for Applications in Structural Biology. J. Mol. Graphics Modell 2004, 22, 377–395. [DOI] [PubMed] [Google Scholar]
- 71.Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- 72.Kumar S; Rosenberg JM; Bouzida D; Swendsen RH; Kollman PA The Weighted Histogram Analysis Method for Free-energy Calculations on Biomolecules. I. The Method. J. Comput. Chem 1992, 13, 1011–1021. [Google Scholar]
- 73.Hynninen A-P; Crowley MF New Faster CHARMM Molecular Dynamics engine. J. Comput. Chem 2014, 35 (5), 406–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Brooks B; Bruccoleri R; Olafson B; States D; Swaminathan S; Karplus M, CHARMM: A Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J. Comput. Chem 2004, 4, 187–217. [Google Scholar]
- 75.Brooks BR; Brooks CL III; Mackerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C, et al. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Knight JL; Brooks CL III. Applying Efficient Implicit Nongeometric Constraints in Alchemical Free Energy Simulations. J. Comput. Chem 2011, 32 (16), 3423–3432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Gunsteren WF; Berendsen HJC Algorithms for Macromolecular Dynamics and Constraint Dynamics. Mol. Phys 1977, 34, 1311–1327. [Google Scholar]
- 78.Vanommeslaeghe K; MacKerell AD Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. J. Chem. Inf. Model 2012, 52, 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Vanommeslaeghe K; Raman EP; MacKerell AD Automation of The CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model 2012, 52, 3155–3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Bayly CI; Cieplak P; Cornell W; Kollman PA A Well-behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem 1993, 97, 10269–10280. [Google Scholar]
- 81.Cornell WD; Cieplak P; Bayly CI; Kollman PA Application of RESP Charges to Calculate Conformational Energies, Hydrogen Bond Energies, and Free Energies of Solvation. J. Am. Chem. Soc 1993, 115, 9620–9631. [Google Scholar]
- 82.Cieplak P; Cornell WD; Bayly C; Kollman PA Application of The Multimolecule and Multiconformational RESP Methodology to Biopolymers: Charge Derivation for DNA, RNA, and Proteins. J. Comput. Chem 1995, 16, 1357–1377. [Google Scholar]
- 83.Armacost KA; Goh GB; Brooks CL III. Biasing Potential Replica Exchange Multisite λ-Dynamics for Efficient Free Energy Calculations. J. Chem. Theory Comput 2015, 11 (3), 1267–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Skillman AG SAMPL3: Blinded Prediction of Host–Guest Binding Affinities, Hydration Free Energies, and Trypsin Inhibitors. J. Comput. Aided Mol. Des 2012, 26, 473–474 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.