Eco-evolutionary control of pathogens

Significance

Vaccinations and therapies targeting evolving pathogens aim to curb the pathogen and to steer it toward a controlled evolutionary state. Control is leveraged against the pathogen’s intrinsic evolutionary forces, which in turn, can drive an escape from control. Here, we analyze a simple model of control, in which a host produces antibodies that bind the pathogen. We show that the leverages of host (or external intervention) and pathogen are often highly imbalanced: an error threshold separates parameter regions of efficient control from regions of compromised control, where the pathogen retains the upper hand. Because control efficiency can be predicted from few measurable fitness parameters, our results establish a proof of principle how control theory can guide interventions against evolving pathogens.

Abstract

Control can alter the eco-evolutionary dynamics of a target pathogen in two ways, by changing its population size and by directed evolution of new functions. Here, we develop a payoff model of eco-evolutionary control based on strategies of evolution, regulation, and computational forecasting. We apply this model to pathogen control by molecular antibody–antigen binding with a tunable dosage of antibodies. By analytical solution, we obtain optimal dosage protocols and establish a phase diagram with an error threshold delineating parameter regimes of successful and compromised control. The solution identifies few independently measurable fitness parameters that predict the outcome of control. Our analysis shows how optimal control strategies depend on mutation rate and population size of the pathogen, and how monitoring and computational forecasting affect protocols and efficiency of control. We argue that these results carry over to more general systems and are elements of an emerging eco-evolutionary control theory.

Control of human pathogens is a central goal of medicine. Important examples are antimicrobial and antiviral therapies and vaccinations; similarly, cancer therapies aim to control tumor cell populations. Biological hosts, notably the human immune system, face related issues of pathogen control. In most cases, control targets pathogen populations with fast-paced replication and evolution. Its goal is to alter these dynamics: to prevent or elicit an evolutionary process of the pathogen or to curb the pathogen population by reducing its ecological niche. Pathogen control has seen spectacular successes (e.g., in the eradication of smallpox and in HIV combination therapies) (1). However, control is often compromised by escape evolution of the pathogen, highlighting the importance to factor pathogen evolution into control protocols (2, 3). Promising evolutionary avenues include adaptive pathogen control and cancer therapy (4–6), vaccination, drug development and immunotherapy strategies based on evolutionary predictions (7–10), and controlled evolution of immune antibodies (11–13). However, we need quantitative relations between leverage and cost of control in order to generate optimization criteria and protocols that are comparable across systems. These are central elements of an eco-evolutionary control theory.

Because population dynamics and evolution are stochastic processes, any eco-evolutionary control operates on the likelihood of future states. Successful control turns a likely process into an unlikely one (e.g., the evolution of antibiotic resistance) or vice versa (e.g., the evolution of a broadly neutralizing antibody). In a broader scientific context, directing a stochastic process toward a future objective is a classic subject of control theory (14, 15). There is a well-established conceptual and computational framework to optimize control protocols, given complete knowledge of the dynamical rules and the ability to forecast likely future outcomes. However, the swords of eco-evolutionary control are blunter, and establishing an appropriate control theory faces new challenges. First, the control of an evolving population is based, at best, on limited dynamical information and forecasting capabilities. Here, we compare three modes of control update dynamics: by Darwinian evolution of a biotic host system, by regulation (which requires sensing of the current pathogen state as input), and by computation (which requires sensing and forecasting). For human interventions, optimizing control is inextricably linked to predictive evolutionary analysis, which is a topic of high current interest but far from a comprehensive understanding (16). Second, control theory has to factor in the underlying biological mechanism of control. Host–pathogen interactions are often based on biomolecular interactions, such as drug–target or antibody–antigen binding (17). The form of these interactions imposes specific constraints on control forces and their leverage on the pathogen system, which are discussed below. Third, developing an appropriate dynamical model of control update and pathogen response calls for a merger of control theory with ecological dynamics and population genetics. These questions are the topic of the present paper.

In the first part, we develop dynamical principles of eco-evolutionary control. The evolution and population dynamics of the pathogen are governed by intrinsic forces, including fitness and entropy of pathogen traits, and by the additional selective force imposed by control. We derive general minimum-leverage relations that specify the strength of control needed to alter the evolution of the pathogen toward the host’s control objective. The control force has a payoff function in the host system, which includes the pathogen load and the cost of control, and is updated in response to the pathogen. For control by evolution or regulation, host and pathogen follow similar dynamical rules. The fixed points of the coupled dynamics, which are relevant for long-term control, are coevolutionary (Nash) equilibrium points. Through control by computation, however, a host can globally maximize its integrated payoff over an extended control period, often trading an initial dip for a later gain. We show that computational control defines a class of dynamical fixed points, called computational equilibria, which differ from Nash equilibria and reflect the added value of computation.

The second part focuses on applications to biomolecular control of pathogens. We analyze a minimal model of control, in which the host produces antibodies that bind to the pathogen. This model captures two complementary control modes, which are associated with different host–pathogen interactions. For ecological control, bound antibodies impede pathogen growth. The control objective is to reduce the pathogen’s carrying capacity; a deleterious collateral is the evolution of resistance. For evolutionary control, bound antibodies reduce pathogenicity. The control objective is the adaptive evolution of an antibody binding site (epitope) in the pathogen population; a collateral is the concurrent increase of the carrying capacity. We develop an analytical solution of the minimal model for ecological and evolutionary control. The solution includes maximum-payoff stationary and time-dependent protocols for antibody dosage, and it maps efficiency phase diagrams that delineate parameter regimes of efficient and compromised control.

The control theory of the minimal model has a number of key characteristics we argue to be general features of biomolecular control. First, control phase diagrams contain an error threshold, marking a switch in molecular antibody–antigen recognition and a rapid change of control efficiency. Second, control by computation shows striking differences to evolutionary and regulatory host protocols: computational equilibrium points can reach higher payoff than Nash equilibria and in turn, be outcompeted by protocols with intermittent time dependence. Third, protocols and success of control depend on the pathogen’s mutation rate and population size, highlighting how control depends on the underlying population genetics and ecology. We discuss implications of these results for biomedical applications: how information processing impacts mode and efficiency of control and how measurements of core pathogen and host data can be used to predict control outcomes.

Eco-evolutionary Control Theory

Eco-evolutionary Dynamics of Pathogens.

Consider a population of pathogens with a quantitative, heritable trait $G$ that is a target of host–pathogen interactions, including control. Selection on the trait is described by a fitness landscape $f_p\left(G,\zeta \right)$; this function depends on a time-dependent control protocol $\zeta \left(t\right)$ generated by a host system. The eco-evolutionary process of the pathogen population has three components, which are detailed in Methods and SI Appendix.

First, common mutations with individually small trait effects $\mathrm{\Delta }G$ produce a heritable trait distribution $\rho \left(G,t\right)$ that is acted upon by selection. As described by [17] in Methods, this Darwinian process generates a trait distribution peaked at its mean $\mathrm{\Gamma }\left(t\right)$, which evolves by diffusion in a free fitness landscape ${\psi }_p\left(\mathrm{\Gamma },\zeta \right)$. This landscape generates an evolutionary force given by its gradient,

$${\partial }_{\mathrm{\Gamma }}{\psi }_p\left(\mathrm{\Gamma },\zeta \right)=2N_p^e\left(\mathrm{\Gamma }\right)\hspace{0.17em}{\partial }_{\mathrm{\Gamma }}{\overline{f}}_p\left(\mathrm{\Gamma },\zeta \right)+{\partial }_{\mathrm{\Gamma }}{S}_p\left(\mathrm{\Gamma }\right).$$ [1]

The selective force component is generated by the mean population fitness ${\overline{f}}_p\left(\mathrm{\Gamma },\zeta \right)$; below, we will approximate ${\overline{f}}_p\left(\mathrm{\Gamma },\zeta \right)\simeq f_p\left(\mathrm{\Gamma },\zeta \right)$, which is appropriate for a peaked trait distribution. The mutational component is generated by the entropy $S_p\left(\mathrm{\Gamma }\right)$, defined as the log density of sequence states with trait value $\mathrm{\Gamma }$. This force measures changes in mutational target, which impede evolution by gain of function (${\partial }_{\mathrm{\Gamma }}{S}_{p}d\mathrm{\Gamma }<0$) but facilitate loss of function (${\partial }_{\mathrm{\Gamma }}{S}_{p}d\mathrm{\Gamma }>0$). The effective population size $N_p^e\left(\mathrm{\Gamma }\right)$, which equals the coalescence time of the evolutionary process, enters the trait’s heritable variation and its Darwinian response to selection and control (18, 19) (Methods).

Second, mutations of large effect $\mathrm{\Delta }G$ shift the trait from an initial value ${\mathrm{\Gamma }}_1$ to a value ${\mathrm{\Gamma }}_2={\mathrm{\Gamma }}_1+\mathrm{\Delta }G$; the substitution process involves a mean trait $\mathrm{\Gamma }\left(t\right)=\left(1-x\left(t\right)\right)\hspace{0.17em}{\mathrm{\Gamma }}_1+x\left(t\right)\hspace{0.17em}{\mathrm{\Gamma }}_2$ and a free fitness ${\psi }_p\left(t\right)=\left(1-x\left(t\right)\right)\hspace{0.17em}{\psi }_p\left({\mathrm{\Gamma }}_1,\zeta \left(t\right)\right)+x\left(t\right)\hspace{0.17em}{\psi }_p\left({\mathrm{\Gamma }}_2,\zeta \left(t\right)\right)$ that depend on the frequency $x\left(t\right)$ of the mutant allele. While small-effect mutations generate evolutionary trajectories toward a local fitness maximum, large-effect mutations can cross fitness valleys and bridge between different local maxima and their basins of attraction. Large-effect trait shifts can also be generated by pairs of a deleterious and a compensatory mutation. The relative weight of diffusive and large-effect trait evolution will prove to be an important determinant of eco-evolutionary control.

Third, the pathogen population dynamics follows a minimal ecological model, which is given by [18] in Methods. This model describes a stochastic birth–death process with basic reproductive rate ${\overline{f}}_p\left(\mathrm{\Gamma },\zeta \right)$ in an ecological niche of constraint $c$. Given a static or slowly varying reproductive rate, these dynamics generate population size fluctuations around a carrying capacity $\overline{N}\left(\mathrm{\Gamma },\zeta \right)\simeq {\overline{f}}_p\left(\mathrm{\Gamma },\zeta \right)/c$.

In an individual pathogen population, the controlled evolutionary dynamics defines a control path $\left(\mathit{\Gamma },\mathit{\zeta }\right)$ that tracks the evolving trait $\mathrm{\Gamma }\left(t\right)$ and the underlying control protocol $\zeta \left(t\right)$. We define the evolutionary flux over a time interval $\left(t_1,t_2\right)$,

$${\mathrm{\Theta }}_p\left(\mathit{\Gamma },\mathit{\zeta }\right)={\int }_{t_1}^{t_2}{\partial }_{\mathrm{\Gamma }}\hspace{0.17em}{\psi }_p\left(\mathrm{\Gamma }\left(t\right),\zeta \left(t\right)\right)\hspace{0.17em}\dot{\mathrm{\Gamma }}\left(t\right)\hspace{0.17em}dt,$$ [2]

which sums the entropy increments and the scaled fitness increments generated by trait changes along the path $\left(\mathit{\Gamma },\mathit{\zeta }\right)$. The flux ${\mathrm{\Theta }}_p\left(\mathit{\Gamma },\mathit{\zeta }\right)$ is an important building block of eco-evolutionary control theory: it characterizes the likelihood of the evolutionary path $\mathit{\Gamma }$ given the control protocol $\mathit{\zeta }$. This is shown in SI Appendix, building on previous results in stochastic thermodynamics and evolutionary statistics (20, 21). Pathogen evolution often involves large flux amplitudes (${\mathrm{\Theta }}_p\gg 1$), which can be generated by strong selection or sufficiently complex evolutionary traits. In this case, we obtain a deterministic criterion: observable evolutionary paths have a nonnegative flux,

$${\mathrm{\Theta }}_p\left(\mathit{\Gamma },\mathit{\zeta }\right)\ge 0;$$ [3]

that is, the evolution of the pathogen acts to increase its instantaneous free fitness ${\psi }_p$. Importantly, this relation holds not only for the full process but for any subperiod $\left(t_1,t_2\right)$, as long as flux amplitudes remain large. Pathogen evolution is often counteracted by control acting to decrease ${\psi }_p$.

Minimum-Leverage Relations for Pathogen Evolution.

Eco-evolutionary control is exerted by altering selection: the controlled system is governed by a free fitness landscape ${\psi }_p\left(\mathrm{\Gamma },\zeta \right)={\psi }_b\left(\mathrm{\Gamma }\right)+f_c\left(\mathrm{\Gamma },\zeta \right)$, which contains a background component ${\psi }_b\left(\mathrm{\Gamma }\right)$ and a host-dependent control component $f_c\left(\mathrm{\Gamma },\zeta \right)$. We now use the flux inequality [3] to determine lower bounds on $f_c\left(\mathrm{\Gamma },\zeta \right)$ (i.e., a minimum leverage of the controlling onto the controlled system required for successful control).

A control protocol $\mathit{\zeta }$ can elicit a trait value ${\mathrm{\Gamma }}_e$ from an initial value ${\mathrm{\Gamma }}_0$, if there is a trait path $\mathit{\Gamma }$ from ${\mathrm{\Gamma }}_0$ to ${\mathrm{\Gamma }}_e$ that fulfils the flux condition [3] for any segment covered in an arbitrary subperiod $\left(t_1,t_2\right)$. That is, the trait $\mathrm{\Gamma }\left(t\right)$ moves uphill in the local free fitness gradient given by [1] (20). This amounts to the local minimum-leverage condition

$$2N_p^e\left(\mathrm{\Gamma }\right)\hspace{0.17em}{\partial }_{\mathrm{\Gamma }}{f}_c\left(\mathrm{\Gamma },\zeta \right)>-2N_p^e\left(\mathrm{\Gamma }\right)\hspace{0.17em}{\partial }_{\mathrm{\Gamma }}{f}_b\left(\mathrm{\Gamma }\right)-{\partial }_{\mathrm{\Gamma }}{S}_p\left(\mathrm{\Gamma }\right),$$ [4]

which compares the control force with the evolutionary forces in the absence of control. In particular, the control force must bridge fitness valleys of the background landscape $f_b\left(\mathrm{\Gamma }\right)$, which often requires high transient control amplitudes. Control must also overcome bottlenecks of the pathogen entropy landscape $S_p\left(\mathrm{\Gamma }\right)$, which arise for evolution by gain of function. The deterministic minimum-leverage condition [4] is valid up to small fitness troughs that can be crossed by common mutations at low effective population size.

If the population states ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_e$ are linked by large-effect mutations and if the control amplitude $\zeta$ changes slowly over typical substitution periods, the minimum-leverage relation [4] takes the simpler form

$${\psi }_p\left({\mathrm{\Gamma }}_e,\zeta \right)>{\psi }_p\left({\mathrm{\Gamma }}_0,\zeta \right),$$ [5]

which relates the free fitness values at the end points of the evolutionary path $\mathit{\Gamma }$ (SI Appendix) (20, 22). In the case of a constant $N_p^e$, this inequality further reduces to ${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b>0$; that is, the control leverage ${\mathrm{\Theta }}_c=2N_p^e\left[f_c\left({\mathrm{\Gamma }}_e,\zeta \right)-f_c\left({\mathrm{\Gamma }}_0,\zeta \right)\right]$ has to exceed the drop in free fitness of the uncontrolled system, $-{\mathrm{\Theta }}_b={\psi }_b\left({\mathrm{\Gamma }}_0\right)-{\psi }_b\left({\mathrm{\Gamma }}_e\right)$. The end point minimum-leverage condition applies whenever large-effect substitutions are frequent on timescales relevant for the control task (i.e., for sufficiently large populations and sufficiently long control periods). A case in point is the maintenance of a controlled pathogen state ${\mathrm{\Gamma }}_e$ by stationary control. The condition [5] says that escape mutations from ${\mathrm{\Gamma }}_e$ to ${\mathrm{\Gamma }}_0$ are suppressed by negative selection. In large populations, this condition is often necessary for successful control. However, as shown by an example given below, it can be undercut in small populations when escape mutations are rare.

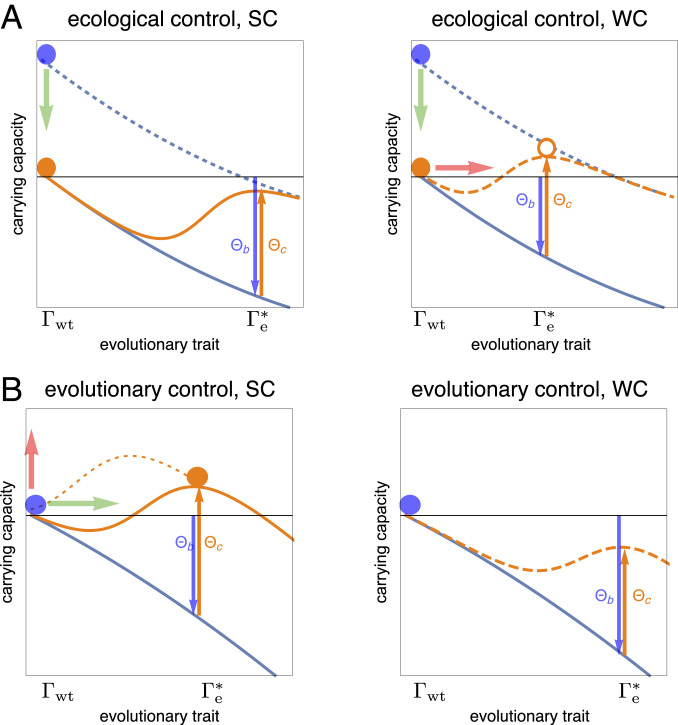
Fig. 1 illustrates the minimum-leverage relation for a minimal model of control with a time-independent amplitude $\zeta$. The pathogen free fitness landscape ${\psi }_p\left(\mathrm{\Gamma },\zeta \right)$ has two local maxima, the wild type ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ and the optimal evolved state ${\mathrm{\Gamma }}_e^{*}\left(\zeta \right)$, which are assumed to be linked by large-effect mutations. We consider two complementary control scenarios: ecological control aimed at reducing the pathogen load ${\overline{N}}_p$ while maintaining the wild-type trait ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ against the evolution of a resistant state ${\mathrm{\Gamma }}_e^{*}$ (Fig. 1A) and evolutionary control aimed at maintaining an evolved equilibrium ${\mathrm{\Gamma }}_e^{*}$ against reversal to ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ (Fig. 1B). In both cases, the minimum-leverage relation [5] is seen to delineate a strong control (SC) regime, where the control objective is achieved, and a weak control (WC) regime, where the objective is missed. These regimes and their dependence on the control amplitude $\zeta$ will be further discussed below.

Fig. 1.

Modes and leverage of eco-evolutionary control. A pathogen population with mean trait $\mathrm{\Gamma }$ under control with amplitude $\zeta$ lives in a free fitness landscape ${\psi }_p\left(\mathrm{\Gamma },\zeta \right)$ (orange lines), which is the sum of a background component ${\psi }_b\left(\mathrm{\Gamma }\right)$ (blue lines) and a control landscape $f_c\left(\mathrm{\Gamma },\zeta \right)$. An evolutionary path from the wild type ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ to an optimal evolved state ${\mathrm{\Gamma }}_e*$ involves the control leverage ${\mathrm{\Theta }}_c=2N_p^e\left[f_c\left({\mathrm{\Gamma }}_e*,\zeta \right)-f_c\left({\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}},\zeta \right)\right]$ (orange arrows) and a change in background free fitness, ${\mathrm{\Theta }}_b={\psi }_b\left({\mathrm{\Gamma }}_e*\right)-{\psi }_b\left({\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}\right)$ (blue arrows). (A) Ecological control, starting from an uncontrolled wild-type pathogen (blue dots), has the objective of reducing the pathogen’s carrying capacity (green arrows)—here by antibody binding—and the collateral effect of resistance evolution (red arrows). SC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b<0$) suppresses the evolution of resistance and generates a stable wild type (orange dot; i.e., the reverse path from ${\mathrm{\Gamma }}_e*$ to ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ fulfils the minimum-leverage condition [5]). WC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b>0$) triggers the evolution of resistance (orange circle). (B) Evolutionary control has the objective of eliciting a new pathogen trait (green arrow) and the collateral of increasing its carrying capacity (red arrow). Dynamical control elicits the evolved trait along a path of positively selected trait increments, which requires elevated transient control amplitudes (dotted orange line). SC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b>0$) generates a stable evolved trait (orange dot; i.e., the path from ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ to ${\mathrm{\Gamma }}_e*$ fulfils the minimum-leverage condition [5]). WC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b<0$) cannot elicit an evolved state (or triggers a reversal to the wild type).

The inequalities [4 and 5] specify the minimum leverage that a controlling host system must exert on the controlled pathogen system in order to elicit a feature that would not evolve spontaneously and to maintain this feature against reverse evolution toward the wild type. These relations are formally related to the maximum-work theorem of thermodynamics, which specifies the minimum-work uptake (or maximum-work release) associated with a given free energy change of a thermodynamic system. Unlike in thermodynamics, however, the minimum-leverage relations say nothing about cost and benefit of control for the controlling system. This requires explicit modeling of the host’s control dynamics and of the host–pathogen interactions, to which we now turn.

Control by Darwinian Evolution or Regulation.

How can pathogen evolution under control be optimized for the controlling host system? To address this question, we have to specify a host payoff function and the resulting dynamics of the control amplitude $\zeta \left(t\right)$. Eq. 19 in Methods specifies a stochastic update rule: $\zeta \left(t\right)$ changes by small increments (i.e., by diffusion) in the payoff landscape ${\psi }_h\left(\mathrm{\Gamma },\zeta \right)$. This local rule, which is analogous to the evolution of the pathogen trait by common mutations, depends only on the payoff gradient ${\partial }_{\zeta }{\psi }_h\left(\mathrm{\Gamma }\left(t\right),\zeta \left(t\right)\right)$ at the instantaneous point of the control path $\left(\mathit{\Gamma },\mathit{\zeta }\right)$. It can be realized by Darwinian evolution in a host population, where the control amplitude is a quantitative trait peaked at its population mean value $\zeta \left(t\right)$ (12). In this case, the payoff function takes again the form of a free fitness; i.e., ${\partial }_{\zeta }{\psi }_h\left(\mathrm{\Gamma },\zeta \right)=2\hspace{0.17em}{N}_h^e\left(\zeta \right)\hspace{0.17em}{\partial }_{\zeta }{\overline{f}}_h\left(\mathrm{\Gamma },\zeta \right)+{\partial }_{\zeta }{S}_h\left(\zeta \right)$, where ${\overline{f}}_h\left(\mathrm{\Gamma },\zeta \right)$ is the mean population fitness, $S_h\left(\zeta \right)$ is an entropy generated by the molecular encoding of the control amplitude, and $N_h^e\left(\zeta \right)$ is an effective population size (Methods).

Control by local update rules can readily lead to a local maximum of the host’s payoff ${\psi }_h\left(\mathrm{\Gamma },\zeta \right)$. In contrast, so-called greedy protocols globally maximize the instantaneous payoff, as described by [20] in Methods. In a complex payoff landscape, this involves bridging payoff valleys and requires large host populations that harbor large-effect control amplitude changes in their standing variation. Otherwise, evolutionary update of the control amplitude becomes mutation limited and often prohibitively slow. In appropriate host systems, as in the example given below, global payoff maximization can be implemented more rapidly by regulation. Given a recurrent pathogen, a trained regulatory network can sense the instantaneous pathogen load and generate an approximately optimal control amplitude as output. Because regulation is faster than the eco-evolutionary pathogen dynamics, it produces a greedy maximization of the instantaneous host payoff. These dynamics can again be modeled as a stochastic or deterministic process in the payoff landscape ${\psi }_h\left(\mathrm{\Gamma },\zeta \right)$ (Methods).

Given a control path $\left(\mathit{\Gamma },\mathit{\zeta }\right)$, we define the host flux

$${\mathrm{\Theta }}_h\left(\mathit{\Gamma },\mathit{\zeta }\right)={\int }_{t_1}^{t_2}{\partial }_{\zeta }\hspace{0.17em}{\psi }_h\left(\mathrm{\Gamma }\left(t\right),\zeta \left(t\right)\right)\hspace{0.17em}\dot{\zeta }\left(t\right)\hspace{0.17em}dt,$$ [6]

in analogy to the pathogen flux given by [2]. Under a joint stochastic process of pathogen evolution and (gradient or greedy) instantaneous control, these fluxes take symmetric roles. The total flux ${\mathrm{\Theta }}_p+{\mathrm{\Theta }}_h$ is related to the probability of the path $\left(\mathit{\Gamma },\mathit{\zeta }\right)$ (SI Appendix). In the deterministic limit, instantaneous-update protocols have a nonnegative flux,

$${\mathrm{\Theta }}_h\left(\mathit{\Gamma },\mathit{\zeta }\right)\ge 0;$$ [7]

that is, control acts to increase the instantaneous host payoff ${\psi }_h$. These dynamics are often counteracted by pathogen evolution acting to decrease ${\psi }_h$.

A stable fixed point $\left({\mathrm{\Gamma }}^{†},{\zeta }^{†}\right)$ of deterministic pathogen evolution and instantaneous-update control satisfies the conditions

$$\left({\mathrm{\Gamma }}^{†},{\zeta }^{†}\right)=\arg \underset{\mathrm{\Gamma }}{max}{\psi }_p\left(\mathrm{\Gamma },{\zeta }^{†}\right)=\arg \underset{\zeta }{max}{\psi }_h\left({\mathrm{\Gamma }}^{†},\zeta \right),$$ [8]

where the maxima are to be taken over all trait values and control amplitudes accessible over the relevant period. These conditions define a Nash equilibrium of an evolutionary game with payoff functions ${\psi }_p$ and ${\psi }_h$ (23). In the strong-selection limit ($N_p^e,N_h^e\gg 1$), they reduce to conditional maximization of the fitness functions $f_p$ and $f_h$. In other words, control by Darwinian evolution or regulation leads to optimization problems familiar from other coevolutionary and ecological systems.

Control by Computation.

A more ambitious goal, and the subject of control theory, is to optimize protocols toward an objective defined over an extended period of the dynamics, including the future. Here, we use a scoring function of the form

$$\mathrm{\Omega }\left(\mathit{\Gamma },\mathit{\zeta }\right)=\mathrm{\Psi }\left(\mathit{\Gamma },\mathit{\zeta }\right)-\lambda T_{\delta }\left(\mathit{\Gamma },\mathit{\zeta }\right).$$ [9]

The first term is the time integral of the host payoff function, $\mathrm{\Psi }\left(\mathit{\Gamma },\mathit{\zeta }\right)=\int {\psi }_h\left(t\right)\hspace{0.17em}dt$. For computational control of human pathogens, this function may include survival, life quality, and public health components. The second term penalizes the duration of controlled adaptation, $T_{\delta }\left(\mathit{\Gamma },\mathit{\zeta }\right)$, defined as the time needed to reach a payoff maximum ${\psi }_h^{*}$ by a margin $\delta$, with a coefficient $\lambda \ge 0$. This term weighs in the speed of the control dynamics toward a given objective, which is often crucial in biomedical applications but comes at the price of a reduced payoff score $\mathrm{\Psi }$. Maximizing $\mathrm{\Omega }$ requires computation preempting the future evolution of the pathogen. This problem can be cast in the form of a so-called Hamilton–Jacobi–Bellman (HJB) equation for the optimal score with given boundary conditions. In Methods, we solve the HJB equation analytically for deterministic control with scoring functions of the form [9]. Computational protocols often steer through payoff valleys, trading transient periods with ${\mathrm{\Theta }}_h<0$ and a concurrent decline of ${\psi }_h$ for a later gain. Such protocols violate the flux condition [7]; hence, they cannot be realized by any instantaneous-update rule in the payoff landscape ${\psi }_h\left(\mathrm{\Gamma },\zeta \right)$. As discussed below, this does not exclude more complex evolutionary or regulatory circuits programming investments for future payoff gains.

A stationary state $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$ that maximizes $\mathrm{\Omega }$ satisfies the conditions

$$\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)=\arg \underset{\mathrm{\Gamma }}{max}{\psi }_p\left(\mathrm{\Gamma },{\zeta }^{*}\right)=\arg \underset{\zeta }{max}{\psi }_h\left({\mathrm{\Gamma }}^{*}\left(\zeta \right),\zeta \right);$$ [10]

that is, it is evolutionarily stable against pathogen escape mutations and maximizes ${\psi }_h$ by preempting pathogen response before it happens. We refer to $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$ as a computational equilibrium point. As we will show below, the optimality condition [10] can lead to different fixed points than the Nash equilibrium condition [8]. Specifically, computational control can reach higher stationary payoff ${\psi }_h^{*}$, but the control amplitude ${\zeta }^{*}$ has to be maintained by computation against a payoff gradient. Explicitly time-dependent computational control, including the protocols of adaptive trait formation and metastable control discussed below, can reach high payoff faster than evolutionary or regulatory protocols and maintain a higher average payoff than any stationary protocol.

Pathogen Control by Antibodies

Antibody–Antigen Interactions.

We now focus on a specific control scenario, in which a host exerts control by producing antibodies that bind to a pathogen (also referred to as antigen in this context). The probability that the pathogen is bound,

$$P_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\left(G,\zeta \right)=\frac{1}{1+{\zeta }^{-1}\exp \left(ϵG\right)},$$ [11]

depends on the pathogen trait $G$ (with wild-type value $G_{\mathrm{w}\mathrm{t}}=0$) and the antibody density or dosage $\zeta$ (measured in units of the dissociation constant or half-maximal inhibitory concentration [IC50] of the wild-type pathogen). We consider two cases, which cover the control modes illustrated in Fig. 1. For ecological control ($ϵ=+1$), $G$ is a resistance trait (the log of the dissociation constant; i.e., a population with evolved resistance [${\mathrm{\Gamma }}_e^{*}>0$] has reduced binding). For evolutionary control ($ϵ=-1$), $G$ is the epitope affinity (the log of the association constant); this mode is to elicit an evolved population (${\mathrm{\Gamma }}_e^{*}>0$) with increased binding.

Pathogen Fitness and Host Payoff Landscapes.

We assume that host and pathogen live in coupled landscapes of the form

$$\begin{array}{ll}\hfill f_p\left(\mathrm{\Gamma },\zeta \right)& =f_{p,0}-c_p\mathrm{\Gamma }-ϵq_{ph}\hspace{0.17em}{P}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\left(\mathrm{\Gamma },\zeta \right),\hfill \\ \hfill {\psi }_h\left(\mathrm{\Gamma },\zeta \right)& ={\psi }_{h,0}-c_h\zeta -q_{hp}{L}_p\left(\mathrm{\Gamma },\zeta \right).\hfill \end{array}$$ [12]

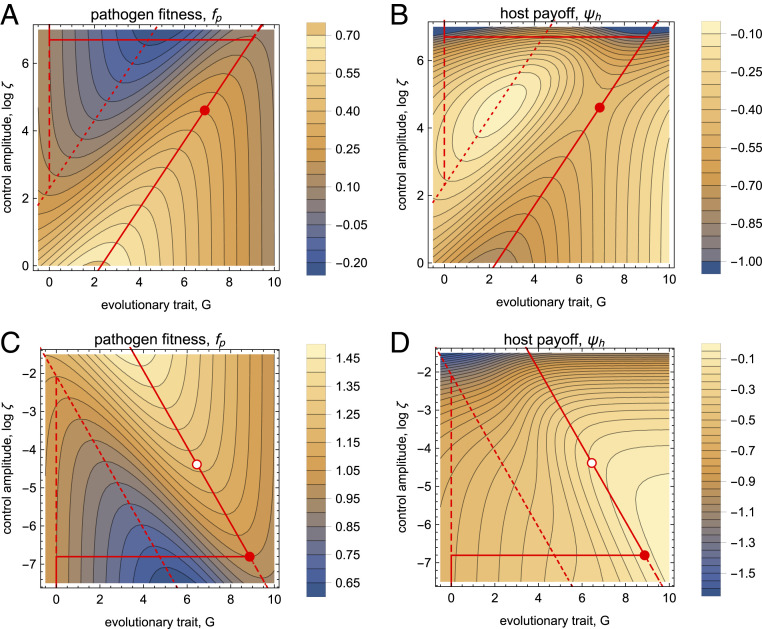
The pathogen has a background fitness $f_{p,0}$ in the uncontrolled wild type, a background cost $c_p>0$ per unit of the trait (the linear form is taken for simplicity), and a binding-dependent control term $f_c=-ϵq_{ph}\hspace{0.17em}{P}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}$ with a selection coefficient $q_{ph}>0$. The host has a background payoff ${\psi }_{h,0}$ in the absence of control and pathogens, a production cost $c_h$ per unit of antibody, and an interaction term depending on the pathogen load $L_p\left(\mathrm{\Gamma },\zeta \right)$ with a selection coefficient $q_{hp}>0$. In the case of ecological control, the load is generated by the full pathogen population, $L_p\left(\mathrm{\Gamma },\zeta \right)=f_p\left(\mathrm{\Gamma },\zeta \right)$, where the pathogen is assumed to be at its carrying capacity $\overline{N}=f_p/c$ given by [18] and measured in units of $c$. In the case of evolutionary control, we use a load function $L_p\left(\mathrm{\Gamma },\zeta \right)=\left(1-P_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\left(\mathrm{\Gamma },\zeta \right)\right)f_p\left(\mathrm{\Gamma },\zeta \right)$, assuming that bound pathogens lose their pathogenicity. Fig. 2 shows the landscapes of [12] for ecological and evolutionary control. In both cases, the pathogen has two local fitness maxima (solid and dashed lines) with a rank order depending on the antibody dosage.

Fig. 2.

Fitness and payoff landscapes of pathogen control. (A and B) Ecological control and (C and D) evolutionary control. Pathogen fitness $f_p$ (A and C) and host payoff ${\psi }_h$ (B and D) are shown as functions of the log control amplitude (antibody dosage), $\log \zeta$, and the pathogen trait, $G$. Specific control loci: pathogen fitness minimum (dotted), pathogen fitness maxima (stable: solid; metastable: dashed; stability switch: horizontal lines), computational equilibrium control $\left(\log \zeta *,G*\right)$ (dots), Nash equilibrium of evolutionary control, $\left(\log {\zeta }^{†},G^{†}\right)$ (circles). Model parameters: $f_{p,0}=1,q_{ph}=1/q_{ph}=0.9,c_p=0.09,c_h=0.001$ (ecological control); $f_{p,0}=1,q_{ph}=0.9,q_{hp}=5/9,c_p=0.09,c_h=5$ (evolutionary control).

Optimal Stationary Control.

We now focus on pathogens that can be contained by sustained treatment but cannot be eradicated by a short-time protocol (this is, currently, an appropriate assumption for HIV and some cancers). First, we compute the maximum-payoff stationary control protocol, as given by the computational equilibrium condition [10], which is relevant for long-term treatment. Given a large pathogen population under stationary control, the trait evolves to a dosage-dependent fitness maximum, ${\mathrm{\Gamma }}^{*}\left(\zeta \right)=\arg \underset{\mathrm{\Gamma }}{max}{\psi }_p\left(\mathrm{\Gamma },\zeta \right)\simeq \arg \underset{\mathrm{\Gamma }}{max}{f}_p\left(\mathrm{\Gamma },\zeta \right)$, with a negligible contribution of the entropy. In the landscapes of [12], the resulting optimal control $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$ can be computed analytically ([27–30] in Methods). In the case of ecological control, we find two control regimes, SC and WC, as shown schematically in Fig. 1. These regimes are separated by a transition at

$$c_h^{•}=q_{ph}{q}_{hp}\hspace{0.17em}\exp \left(1-\frac{q_{ph}}{c_p}\right).$$ [13]

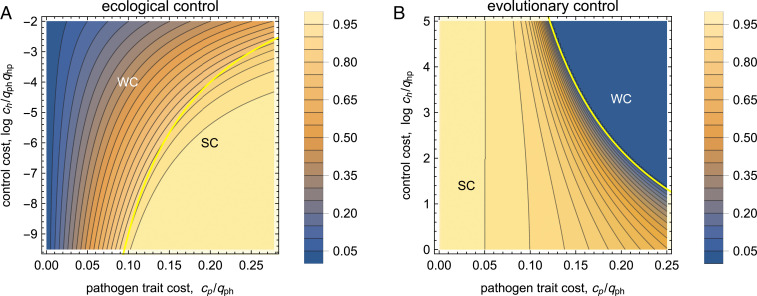
In the SC regime ($c_h<c_h^{•}$), the optimal protocol keeps the pathogen in its wild type, maintaining antibody–antigen binding and suppressing the evolution of resistance. In the WC regime ($c_h>c_h^{•}$), control is compromised by evolved pathogen resistance (this case is shown in Fig. 2A). At the transition, the resistance trait switches from ${\mathrm{\Gamma }}^{*}=0$ (SC) to ${\mathrm{\Gamma }}^{*}=q_{ph}/c_p-1$ (WC), akin to the order parameter of a first-order phase transition, while ${\psi }_h$, $f_p$, and ${\zeta }^{*}$ remain continuous (SI Appendix, Fig. S1). Antibody–antigen binding switches from $P_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\sim 1$ (SC) to $P_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\ll 1$ (WC); that is, the transition can be interpreted as an error threshold of molecular recognition (24). To map the phase diagram of optimal stationary control, we define the control efficiency ${\eta }^{*}=\left({\psi }_h\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)-{\psi }_{h,0}\right)/\delta {\psi }_{max}$ as the payoff gain relative to its maximum, $\delta {\psi }_{max}=q_{ph}{q}_{hp}$, which is reached for perfect control at no cost. Fig. 3A shows the efficiency as a function of the cost parameters $\left(c_p,c_h\right)$. The error threshold $c_h^{•}\left(c_p\right)$ (yellow line) marks a rapid decline from ${\eta }^{*}\sim 1$ in the SC regime to ${\eta }^{*}\ll 1$ in most of the WC regime.

Fig. 3.

Phase diagrams of stationary control. (A) Ecological control and (B) evolutionary control. The control efficiency $\eta *$ is shown as a function of the (scaled) cost parameters $c_p$ and $c_h$. A yellow line marks the error threshold $c_h^{•}\left(c_p\right)$ between WC and SC.

For stationary evolutionary control, we find a similar emergence of two control regimes with an error threshold

$$c_h^{•}=q_{hp}\hspace{0.17em}\frac{c_p}{q_{ph}}\left(1-\frac{c_p}{q_{ph}}\right)\hspace{0.17em}\exp \left(\frac{q_{ph}}{c_p}-1\right).$$ [14]

In the SC regime ($c_h<c_h^{•}$), control maintains an evolved trait ${\mathrm{\Gamma }}^{*}>{\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ with antibody–antigen binding beneficial to host and pathogen. In the WC regime ($c_h>c_h^{•}$), control is too weak to maintain the evolved trait, and the pathogen reverts to the unbound wild type. At the transition, ${\mathrm{\Gamma }}^{*}$ and ${\zeta }^{*}$ switch, while $f_p$ and ${\psi }_h$ remain continuous (SI Appendix, Fig. S1). Fig. 3B shows the control efficiency ${\eta }^{*}=\left({\psi }_h\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)-{\psi }_{h,0}\right)/\left(q_{hp}{f}_{p,0}\right)$ as a function of the cost parameters $\left(c_p,c_h\right)$. In this case, ${\eta }^{*}$ is a decreasing function of both parameters (i.e., host and pathogen cost impede evolutionary control). The error threshold $c_h^{•}\left(c_p\right)$ marks the transition between ${\eta }^{*}>0$ (SC) and ${\eta }^{*}=0$ (WC).

Instantaneous-Update Control.

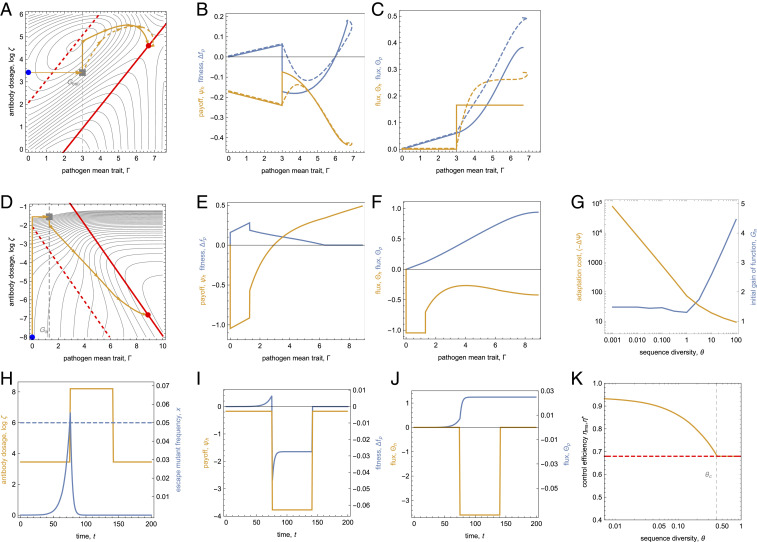
Next, we consider the dynamical accessibility of the computational equilibrium point. In the case of ecological control, $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$ is a stable fixed point of deterministic pathogen evolution and instantaneous dosage update, which satisfies the Nash equilibrium condition [8] (Methods). Hence, this point can be reached by a control dynamics based on host evolution or regulation; examples of such control paths are shown in Fig. 4A. In the SC regime, the pathogen wild type is stable (${\mathrm{\Gamma }}^{*}={\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$); the conditional host payoff landscape ${\psi }_h\left({\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}},\zeta \right)$ has a single peak ${\zeta }^{*}$ that can be reached by local or greedy instantaneous-update protocols. In the WC regime, control paths start with a large-effect escape mutation of the pathogen (orange arrow), which is followed by a coupled dynamics of common pathogen mutations and antibody dosage changes. A control path with local stochastic update gets localized to $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$; deterministic paths with local or greedy update converge to the same point. Host payoff and pathogen fitness evolve in a nonmonotonic way along these control paths (Fig. 4B), reflecting the mutually deleterious effects of host and pathogen in the landscapes of [12]. The host and pathogen fluxes, however, are positive throughout in accordance with the flux conditions [3, 4, and 7] (Fig. 4C). In this case, computational update generates control paths with a similar convergence to the fixed point $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$; evolutionary, regulatory, and computational protocols have only transient differences in their time-dependent efficiency (SI Appendix, Fig. S2). We conclude that the ecological control equilibrium can be dynamically reached and maintained in a robust way.

Fig. 4.

Control dynamics. (A–C) Ecological control by instantaneous-update protocols. (A) Control paths $\left(\mathbf{\Gamma },\mathit{\zeta }\right)$ generated by local deterministic (dashed orange) and greedy (solid orange) control dynamics. These paths start with a pathogen escape mutation (gray square) and converge to the optimal stationary protocol $\left(\mathrm{\Gamma }*,\zeta *\right)$ (red dot), which is a computational and a Nash equilibrium. (B) Time-dependent pathogen fitness, $f_p\left(t\right)$, and host payoff, ${\psi }_h\left(t\right)$, of these control paths. (C) Pathogen flux, ${\mathrm{\Theta }}_p\left(t\right)$, and host flux, ${\mathrm{\Theta }}_h\left(t\right)$. Both fluxes are monotonically increasing functions of the path coordinate $\mathrm{\Gamma }\left(t\right)$. (D–G) Evolutionary control for adaptive trait formation. (D) Deterministic computational control path in the SC regime (orange line). This path maximizes the score $\mathrm{\Omega }\left(\mathit{\Gamma },\mathit{\zeta }\right)$ for given values of the speed parameter and of the pathogen sequence diversity (here $\lambda =0$, $\theta =1$) (SI Appendix, Fig. S3). The initiation phase ($\mathrm{\Gamma }\le G_{\mathrm{i}\mathrm{n}}$) with a gain-of-function mutation (gray square) is followed by a breeding phase ($\mathrm{\Gamma }>G_{\mathrm{i}\mathrm{n}}$); the path converges to the optimal stationary protocol (red dot), which is a computational but not a Nash equilibrium. (E) Pathogen fitness, $f_p\left(t\right)$, and host payoff, ${\psi }_h\left(t\right)$, along the computational control path. (F) Fluxes ${\mathrm{\Theta }}_p\left(t\right)$ and ${\mathrm{\Theta }}_h\left(t\right)$ as functions of the path coordinate $\mathrm{\Gamma }\left(t\right)$. This path has negative increments of the host flux ($\partial \mathrm{\Theta }/\partial \mathrm{\Gamma }<0$) at the start and in the final segment. (G) Cost of adaptation, $\left(-\mathrm{\Delta }\mathrm{\Omega }\right)$ (orange), and initial gain-of-function trait, $G_{in}$ (blue), of the maximum-score computational protocol as a function of the pathogen diversity, $\theta$ for $\lambda =0$. (H–K) Metastable ecological control. (H) Time-dependent protocol $\zeta \left(t\right)$ with baseline dosage ${\zeta }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$, boost dosage ${\zeta }_{\mathrm{r}\mathrm{e}\mathrm{s}}$, and boost duration $T_{\mathrm{r}\mathrm{e}\mathrm{s}}$ (orange); pathogen escape mutant frequency $x\left(t\right)$ (blue) using a detection threshold $x\left(t\right)>0.05$ to initiate rescue boost (dashed line). (I) Pathogen mean fitness, ${\overline{f}}_p\left(t\right)$, and host payoff, ${\psi }_h\left(t\right)$. (J) Fluxes, ${\mathrm{\Theta }}_p\left(t\right)$ and ${\mathrm{\Theta }}_h\left(t\right)$. (K) Efficiency of maximum-score metastable protocols, ${\eta }_{\mathrm{m}\mathrm{s}}$ (orange), as a function of the pathogen diversity, $\theta$, together with the efficiency of the optimal stationary protocol, $\eta *$ (red dashed). For $\theta <{\theta }_c$, metastable control outperforms stationary control. Parameters: ${ϵ}_0=1$, others as in Fig. 2.

Computational Control of Adaptive Trait Formation.

In contrast, the optimal stationary (computational equilibrium) protocol $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$ for evolutionary control in the SC regime is not a Nash equilibrium of deterministic pathogen evolution and instantaneous dosage update. Hence, it cannot be reached or maintained by an evolutionary or regulatory host system. Time-dependent computational protocols maximizing the score $\mathrm{\Omega }\left(\mathit{\Gamma },\mathit{\zeta }\right)$ in the fitness and payoff landscapes [12] can be evaluated analytically (Fig. 4D and Methods). These protocols have two phases. Starting from a wild-type pathogen, we apply a high initial dosage ${\zeta }_{in}$ to trigger an intermediate-effect gain-of-function mutation of the pathogen that establishes antibody binding at a trait value $G_{in}$ (orange arrow). This initial-phase protocol flattens the pathogen fitness valley for trait formation but generates a drop in host payoff (Fig. 4E). In a second “breeding” phase, small-effect trait and dosage changes increase host payoff and steer the control path toward the stationary point $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$. The pathogen evolutionary flux is positive throughout this process, following the conditions [3 and 4]. The host flux has negative increments in the initial phase and final phase, which violate the condition [3] and mark strong deviations of the computational protocol from evolutionary or regulatory protocols (Fig. 4F). These instantaneous-update protocols converge to a Nash equilibrium point $\left({\mathrm{\Gamma }}^{†},{\zeta }^{†}\right)$ or to the WC fixed point $\left({\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}},0\right)$, both of which have smaller payoff than the computational equilibrium protocol $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$ (SI Appendix, Fig. S2).

Computational protocols of adaptive trait formation maximize the score $\mathrm{\Omega }$ by jointly tuning payoff and duration of the initial and the breeding phase. The optimal protocol depends on the speed scoring parameter $\lambda$; protocols with large $\lambda$ steer the pathogen along paths of near-maximal speed of trait evolution (SI Appendix, Fig. S3). Importantly, the optimal protocol also depends on the pathogen population size, which affects the mutational supply in the adaptive process (SI Appendix, Fig. S3). To map these effects, we evaluate the score of a time-dependent path relative to the optimal stationary protocol, $\mathrm{\Delta }\mathrm{\Omega }=\mathrm{\Delta }\mathrm{\Psi }-\lambda T_{\delta }$ with $\mathrm{\Delta }\mathrm{\Psi }=\int \left[{\psi }_h\left(\mathrm{\Gamma }\left(t\right),\zeta \left(t\right)\right)-{\psi }_h^{*}\right]\hspace{0.17em}dt$; we call $\left(-\mathrm{\Delta }\mathrm{\Psi }\right)$ the cost of adaptation. In Methods, we solve an extended HJB equation for $\mathrm{\Delta }\mathrm{\Omega }$ with a maximum-likelihood approximation for the initial phase, which uniquely relates the gain-of-function amplitude $G_{in}$ to the initial dosage ${\zeta }_{in}$. These protocols have a scoring function of the form

$$\mathrm{\Delta }\mathrm{\Omega }=\frac{1}{\theta }\hspace{0.17em}\omega \left(\theta ,G_{in}{/ϵ}_0\right),$$ [15]

which depends on the sequence diversity of the pathogen trait, $\theta =2\hspace{0.17em}\mu N_e$, and on the gain-of function trait measured in units of the mutational scale ${ϵ}_0$ (Methods). In small populations ($\theta \lesssim 1$), the maximum-score protocol has $G_{in}{/ϵ}_0\sim 1$; larger values of $G_{in}$ are suppressed by an exponentially longer waiting time for a gain-of-function mutation. In large populations ($\theta \gtrsim 1$), the maximum-score protocol has $G_{in}{/ϵ}_0\sim \log \theta$. This amplitude is set by a simple rule: the optimal $G_{in}$ is the largest adaptive gain-of-function amplitude likely to be seeded from standing variation of the initial pathogen population (Methods). That is, the optimal protocol of adaptive trait formation eliminates the bottleneck of waiting for de novo gain-of-function mutations by circumnavigating the pathogen fitness valley (SI Appendix, Fig. S4). Larger values of $G_{in}$ are still suppressed by waiting time; smaller ones require an excess control cost $c_h{\zeta }_{in}$ and additional breeding time. In both regimes, the cost of adaptation decreases, and $G_{in}$ monotonically increases with increasing $\theta$ (Fig. 4G). We conclude that in small pathogen populations, adaptive trait formation requires higher control effort and is more costly.

Metastable Computational Control.

Strikingly, optimal computational protocols can be time-dependent even for long-term control with the stationary objective of maximizing the host payoff integral $\mathrm{\Omega }=\mathrm{\Psi }$ (we set $\lambda =0$ here). As an example, consider ecological control in the WC regime. The control protocols discussed above, which lead to the equilibrium point $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$, apply to sufficiently large pathogen populations that evolve resistance by frequent escape mutations (Fig. 4A). In smaller populations, such mutations become rare, and the pathogen will stay in a metastable state (here, the wild type) over extended periods. Computational control can reinforce metastability by deepening the pathogen fitness valley for escape mutations; we refer to such protocols as metastable control. Provided we can detect escape mutants at low frequency, we can keep the bulk pathogen population permanently in the metastable state by a two-state protocol (Fig. 4H). As long as no escape mutant is detected, we apply a baseline antibody dosage ${\zeta }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$ to jointly curb pathogen load and escape rates. After an escape mutant is detected above a threshold frequency $x_0$, we apply a rescue boost of higher dosage ${\zeta }_{\mathrm{r}\mathrm{e}\mathrm{s}}$ over a period $T_{\mathrm{r}\mathrm{e}\mathrm{s}}$ to drive that mutant to loss. Metastable control shows intermittent drops in host payoff (Fig. 4I) and flux (Fig. 4J), which mark strong deviations from instantaneous-update protocols.

For metastable control over a long period $T$, the average score relative to the optimal stationary state per unit of time, $\mathrm{\Delta }\omega =\mathrm{\Delta }\mathrm{\Omega }/T$, can be written in the form

$$\mathrm{\Delta }\omega =\mathrm{\Delta }{\omega }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}-\theta \hspace{0.17em}{c}_{\mathrm{r}\mathrm{e}\mathrm{s}},$$ [16]

where $\mathrm{\Delta }{\omega }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$ refers to the baseline protocol and $c_{\mathrm{r}\mathrm{e}\mathrm{s}}>0$ is proportional to the average payoff cost per rescue. This expression governs the joint optimization of baseline and boost protocols (Eq. 37 in Methods and SI Appendix, Fig. S4). For $\mathrm{\Delta }{\omega }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}>0$ and $\theta <{\theta }_c=\mathrm{\Delta }{\omega }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}/c_{\mathrm{r}\mathrm{e}\mathrm{s}}$ (i.e., at sufficiently low mutation rates or in sufficiently small populations), metastable control outperforms stationary control. This is shown in Fig. 4K, which compares the efficiency of maximum-score metastable and stationary protocols, ${\eta }_{\mathrm{m}\mathrm{s}}$ and ${\eta }^{*}$, as functions of $\theta$.

For evolutionary control in the WC regime, a similar protocol can stabilize a metastable evolved trait ${\mathrm{\Gamma }}_e$ against reversal to the wild type. Alternative protocols exploiting metastable pathogen states include temporarily suspending control (25) or switching to a secondary defense against escape mutants. All of these time-dependent protocols depend on $\theta$ in a similar way, indicating that metastable control becomes more effective in small pathogen populations.

Discussion

In this paper, we solve the optimization problem for a minimal model of pathogen control operating on realistic biomolecular host–pathogen interactions. Specific features of host and pathogen biology enter the eco-evolutionary control theory of this system at several stages. In particular, control mechanisms are based on physiological effects of host–pathogen interactions—here, antibody–antigen binding—and the objective functions of control, Eq. 12, account for the fitness and payoff effects of these interactions. As we have shown, these biological features strongly impact the eco-evolutionary control dynamics and the efficiency of optimized protocols.

A salient feature of eco-evolutionary control is the emergence of high- and low-efficiency parameter regimes separated by an error threshold of molecular recognition (Fig. 3). This behavior can be traced to the nonlinearities in the Hill function of antibody–antigen binding, Eq. 11. First, binding-mediated control has a diminishing-return leverage, which is bounded by the pathogen selection coefficient $q_{ph}$. Second, the control cost depends exponentially on the chemical potential $\left(\log \zeta \right)$, which determines the evolved pathogen state ${\mathrm{\Gamma }}_e$ (Fig. 2). Hence, the minimum-leverage control [5] has a moderate cost in the SC regime but is too expensive or mechanistically impossible in the WC regime. Because such nonlinearities are a generic feature of biomolecular interactions, we expect error thresholds to emerge also in more complex models of pathogen control.

In biomedical applications of pathogen control, it is crucial to predict the likely efficiency of control prior to any intervention. Our results show that few independently measurable cost parameters can inform such estimates. The pathogen cost parameters ($c_p$ and $q_{ph}$ in the minimal model) are routinely measured in dosage–response assays (26). The control cost parameter $c_h$ can, for example, be estimated as the metabolic production cost per unit of antibody (27, 28). The arguably most case-specific parameter is the pathogen cost to the host. This parameter can be measured by fitness assays in microbial systems but is more complex to assess for human hosts.

Optimal control protocols and their efficiency also depend on mutation rate and population size of the pathogen. Eqs. 15 and 16 describe opposing effects: adaptive formation of pathogen traits becomes less costly in large populations; maintenance of traits by metastable control is more efficient in small populations. These effects reflect differences between control strategies. Evolutionary control aimed at eliciting a pathogen trait has to circumnavigate valleys of the pathogen’s fitness and entropy landscape in order to catalyze its adaptive dynamics. In contrast, metastable control has to broaden fitness valleys surrounding a metastable state in order to suppress pathogen adaptation by escape mutations. In both cases, we can compute optimized control paths by combining probabilistic, discrete jumps across fitness valleys with continuous dynamics on smooth flanks in between. These navigation principles and their computational implementation are expected to extend to strong-selection control in more complex landscapes.

An equally important issue for control by humans and by natural hosts is optimizing the control dynamics in tune with the monitoring and computation capabilities of the host system (29). Instantaneous-update dynamics following local payoff gradients can often be realized efficiently by Darwinian evolution in the host (i.e., by variation of and selection on antibody levels). Protocols based on regulation can, in principle, circumnavigate payoff valleys and implement an approximate maximization of the instantaneous host payoff. However, signaling and regulatory networks require prior training by learning or by evolution, and they generate an additional cost to the host. Optimization of control toward future objectives depends, to various degree, on computation. The minimal model displays the relative efficiency of these control modes. For ecological control, the computational equilibrium point (i.e., the stationary state of maximal host payoff) is also a Nash equilibrium and can be reached by instantaneous-update protocols; for evolutionary control, this point can only be reached by computation. In more complex systems, the success of human computational control is limited by the ability to predict pathogen evolution. An example is vaccine selection for human influenza based on predictive analysis, where current methods have a prediction and control horizon of about one year (8, 16). For biotic, nonhuman host systems, it remains a fascinating question how far evolutionary and regulatory mechanisms can emulate control by computation.

A case in point is metastable control, which realizes the time-independent objective of maintaining a controlled pathogen state by a time-dependent protocol responding to recurrent pathogen attacks. In the control theory literature, this class of protocols is known as closed loop control (14). Here, we have solved a minimal model of metastable control, which maintains a metastable pathogen state against escape mutations by a two-state protocol of baseline control and rescue boosts. We find that metastable control can outperform the computational equilibrium protocol $\left({\mathrm{\Gamma }}^{*},{\zeta }^{*}\right)$ under two conditions: there is a metastable point of high host payoff (undercutting the quasistatic minimum-leverage relation [5]), and escape mutants have a substantial intrinsic cost (generating positive selection for the metastable state during rescue boosts). In the minimal model, an optimized resource allocation between baseline and rescue protocols can only be achieved by computation. We can compare this model with the adaptive immune system of vertebrates, which controls multiple pathogens by a complex pattern of resource allocation (30). From the perspective of control theory, the immune system mounts a bilayer baseline protocol of naive and memory B cells; control boosts involving the evolution of target-specific high-affinity antibodies (affinity maturation) respond to acute infections by specific antigens (akin to escape mutations in the minimal model). Remarkably, affinity maturation continues for several weeks after an infection, which is an investment toward future infections by similar antigens. Together, adaptive immunity may be regarded as an instance of metastable control by nested circuits of evolution (of antibody–antigen affinities) and regulation (of antibody levels).

In summary, this paper establishes a conceptual framework and infers navigation principles for eco-evolutionary control based on a minimal model of host–pathogen interactions with stationary control objectives. Several complexities of biomedical control problems are not captured by the minimal model. For example, the human immune system has a complex antibody repertoire, and pathogens often have multiple antigenic binding sites (microbial and viral epitopes, cancer neoantigens). This generates multiple antibody–antigen interactions (i.e., multiple potential control channels with independent control amplitudes, leverage, and cost parameters). Conversely, pathogens with a high mutation rate often have multiple channels of escape mutations from a given antibody (31). Consequently, the fitness and payoff landscapes of host and pathogen live in a multidimensional parameter space; an appropriate control dynamics is to navigate this space toward high-efficiency protocols. An important example is the competitive selective dynamics of broadly neutralizing and specific antibodies for HIV (11, 13). Another layer of complexity arises for pathogens embedded in microbiota, which are multispecies systems with a tightly connected ecology. The control of a given pathogen can perturb the entire microbiota, generating cross-resistance of multiple pathogens and complex collateral effects for the host (32). Gearing up eco-evolutionary control theory to these systems is an important avenue for future work.

Methods

Stochastic Pathogen Dynamics.

We consider a population of pathogens with a quantitative trait $G$, which has a peaked trait distribution $\rho \left(G\right)$ characterized by its mean $\mathrm{\Gamma }$ and variance $\mathrm{\Delta }$. We describe the evolution of the trait and the concurrent population dynamics in an ecological niche by coupled stochastic equations for the mean $\mathrm{\Gamma }$ and the population size $N$,

$$\dot{\mathrm{\Gamma }}=D\hspace{0.17em}\frac{\partial {\psi }_p\left(\mathrm{\Gamma },t\right)}{\partial \mathrm{\Gamma }}+{\chi }_{\mathrm{\Gamma }}\left(t\right),$$ [17]

$$\dot{N}=f\left(\mathrm{\Gamma },t\right)N-c{N}^2+{\chi }_N\left(t\right),$$ [18]

with white noise ${\chi }_{\mathrm{\Gamma }}\left(t\right),{\chi }_N\left(t\right)$ of mean 0 and variance $⟨{\chi }_{\mathrm{\Gamma }}\left(t\right){\chi }_{\mathrm{\Gamma }}\left(t^{\prime }\right)⟩=D\hspace{0.17em}\delta \left(t-t^{\prime }\right)$, $⟨{\chi }_N\left(t\right){\chi }_N\left(t^{\prime }\right)⟩=N\hspace{0.17em}\delta \left(t-t^{\prime }\right)$. By [1], the trait dynamics of Eq. 17 depend on the entropy landscape $S\left(\mathrm{\Gamma }\right)$, which is defined as the log density of states with trait value $\mathrm{\Gamma }$, and the fitness seascape $f\left(\mathrm{\Gamma },t\right)$, which is often explicitly time dependent. The trait diffusion constant, $D={Uϵ}_0^2$, is set by the total rate $U$ and the mean square trait effect ${ϵ}_0^2$ of mutations at genomic loci encoding the trait (19, 33). The trait response to selection, $\mathrm{\Delta }=2D{N}_e$, is also proportional to the effective population size $N_e$, which equals the coalescence time of the evolutionary process (18, 19). This quantity depends on the population size dynamics in a model-dependent way, often generating an inhomogeneous response to selection, $\mathrm{\Delta }\left(\mathrm{\Gamma }\right)=2D{N}_e\left(\mathrm{\Gamma }\right)$. The population dynamics of [18] depend on the fitness $f\left(\mathrm{\Gamma },t\right)$, which sets the basic reproductive rate, and the constraint parameter $c$ of the ecological niche. Given a static or slowly varying fitness function, these dynamics generate population size fluctuations around a carrying capacity $\overline{N}\left(\mathrm{\Gamma },t\right)\simeq f\left(\mathrm{\Gamma },t\right)/c$. Details of this stochastic calculus are given in SI Appendix.

Instantaneous-Update Control Dynamics.

The diffusive update rule for the control amplitude takes the form

$$\dot{\zeta }={\mathrm{\Delta }}_h\frac{\partial f_h\left(\mathrm{\Gamma },\zeta \right)}{\partial \zeta }+{\chi }_{\zeta },$$ [19]

with white noise of mean 0 and variance $⟨{\chi }_{\zeta }\left(t\right){\chi }_{\zeta }\left(t^{\prime }\right)⟩=D_{\zeta }\hspace{0.17em}\delta \left(t-t^{\prime }\right)$, similar to the stochastic trait dynamics given by [17]. Greedy update is defined by

$${\zeta }_{max}\left(t\right)=\arg \underset{\zeta }{max}{f}_h\left(\mathrm{\Gamma }\left(t\right),\zeta \right)+{\chi }_{\zeta }.$$ [20]

The deterministic limit of these dynamics ($D_{\zeta }=0$) is used in Fig. 4A; stochastic control paths are shown in SI Appendix, Fig. S2.

Computational Control Dynamics.

Given deterministic pathogen evolution and landscapes ${\psi }_p\left(\mathrm{\Gamma },\zeta \right),{\psi }_h\left(\mathrm{\Gamma },\zeta \right)$ without explicit time dependence, maximum-score control paths based on common mutations can be computed from a reduced payoff function,

$$\mathrm{\Delta }{\psi }_{\lambda }\left(\mathrm{\Gamma },\zeta \right)\equiv {\psi }_h\left(\mathrm{\Gamma },\zeta \right)-{\psi }_h*-\lambda H_{\delta }\left({\psi }_h*-{\psi }_h\left(\mathrm{\Gamma },\zeta \right)\right).$$ [21]

Here, ${\psi }_h*$ is the payoff at the computational equilibrium, Eq. 10, and we define $H_{\delta }\left(x\right)=1$ for $x>\delta$ and $H_{\delta }\left(x\right)=0$ otherwise. The optimal control amplitude as a function of the trait is given by

$$\zeta *\left(\mathrm{\Gamma }\right)=\arg \underset{\zeta }{max}\frac{\mathrm{\Delta }{\psi }_{\lambda }\left(\mathrm{\Gamma },\zeta \right)}{V_p\left(\mathrm{\Gamma },\zeta \right)},$$ [22]

where $V_{\mathrm{\Gamma }}\left(\mathrm{\Gamma },\zeta \right)=D\hspace{0.17em}\partial {\psi }_p\left(\mathrm{\Gamma },\zeta \right)/\partial \mathrm{\Gamma }$ is the deterministic evolutionary speed in [17]. The maximum payoff $\mathrm{\Delta }{\psi }_{\lambda }*\left(\mathrm{\Gamma }\right)=\underset{\zeta }{max}\mathrm{\Delta }{\psi }_{\lambda }\left(\mathrm{\Gamma },\zeta \right)$ gives the reduced score, relative to the optimal stationary protocol, of the optimal control path linking an initial trait value $G$ with the equilibrium value $\mathrm{\Gamma }*$,

$$J\left(G\right)={\int }_G^{\mathrm{\Gamma }*}\frac{\mathrm{\Delta }{\psi }_{\lambda }*\left(\mathrm{\Gamma }\right)}{V_p\left(\mathrm{\Gamma },\zeta \right)}\hspace{0.17em}d\mathrm{\Gamma }.$$ [23]

These results are derived in SI Appendix.

Pathogen Equilibrium States.

In the parameter regime of interest, the pathogen fitness landscape of [12] has two local fitness maxima. 1) The wild type $\mathrm{\Gamma }=0$ (vertical lines in Fig. 2) is assumed to be a boundary (i.e., the trait evolution generates only values $\mathrm{\Gamma }\ge 0$). 2) The evolved state ${\mathrm{\Gamma }}_e\left(\zeta \right)$ (inclined lines in Fig. 2) exists in the regime $c_p/q_{ph}<1/4$, which provides a bound to the pathogen cost. Maximization of $f_p\left(G,\zeta \right)$ with respect to $G$ determines two characteristics of the evolved state. First, the trait value ${\mathrm{\Gamma }}_e$ is shifted by an amount $r_e\equiv {\mathrm{\Gamma }}_e\left(\zeta \right)-G_{1/2}\left(\zeta \right)=\log \left(q_{ph}/c_p\right)$ with respect to the half-binding point $G_{1/2}\left(\zeta \right)$ (i.e., the trait value that has the IC50 value $\zeta$). Second, the error $q_e$, which is defined as $q_e=P_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}$ for ecological control $\left(ϵ=+1\right)$ and as $q_e=1-P_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}$ for evolutionary control $\left(ϵ=-1\right)$, is given by

$$q_e=\exp \left(-r_e\right)=\frac{c_p}{q_{ph}};$$ [24]

here, we have used the exponential asymptotic form of the binding probability (11). These characteristics determine the trait of the evolved state

$${\mathrm{\Gamma }}_e\left(\zeta \right)=ϵ\log \zeta +\log \frac{q_{ph}}{c_p}$$ [25]

and the resulting fitness $f_{p,e}\left(\zeta \right)=f_p\left({\mathrm{\Gamma }}_e\left(\zeta \right),\zeta \right)$. The fitness ranking (i.e., the evolutionary stability) of the evolved state and the wild type depends on the control amplitude $\zeta$ (stable/metastable pathogen states are shown as solid/dashed line segments in Fig. 2). The rank switch, which marks the loss of the evolved trait, occurs at a value ${\zeta }_l$ determined by the condition $f_{p,e}\left({\zeta }_l\right)=f_p\left({\zeta }_l,0\right)$ (horizontal lines in Fig. 2). This determines the cross-over point

$$\left({\mathrm{\Gamma }}_l,{\zeta }_l^{ϵ}\right)\hspace{0.17em}=\left(\frac{q_{ph}}{c_p}-1,\frac{c_p}{q_{ph}}\exp \left(\frac{q_{ph}}{c_p}-1\right)\right).$$ [26]

Computational Control Equilibria.

We compute the point of optimal stationary control, $\left(\mathrm{\Gamma }*,\zeta *\right)$, by evaluating the host payoff with the pathogen at its conditional stable equilibrium, $f_h\left(\mathrm{\Gamma }*\left(\zeta \right),\zeta \right)$, and maximizing this function with respect to $\zeta$. For ecological control in the SC regime, the pathogen is in the wild type ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}=0$; in the WC regime, the pathogen is in the evolved state ${\mathrm{\Gamma }}_e\left(\zeta \right)$ given by [25]. We obtain the equilibrium point

$$\left(\mathrm{\Gamma }*,\zeta *\right)=\left\{\begin{array}{cc}\left(0,\frac{c_p}{q_{ph}}\exp \left(\frac{q_{ph}}{c_p}-1\right)\right)\hspace{1em}\hfill & \left(\text{SC},c_h<c_h^{•}\right),\hfill \\ \left(\log \frac{q_{ph}{q}_{hp}}{c_h},\frac{q_{hp}{c}_p}{c_h}\right)\hspace{1em}\hfill & \left(\text{WC},c_h>c_h^{•}\right);\hfill \end{array}\right.$$ [27]

this determines the pathogen fitness $f_p*=f_p\left(\mathrm{\Gamma }*,\zeta *\right)$, the host payoff ${\psi }_h*={\psi }_h\left(\mathrm{\Gamma }*,\zeta *\right)$, and the control efficiency

$$\eta *=\left\{\begin{array}{cc}1-\frac{c_p{c}_h}{q_{ph}^2{q}_{hp}}\exp \left(\frac{q_{ph}}{c_p}-1\right)\hspace{1em}\hfill & \left(\text{SC},c_h<c_h^{•}\right),\hfill \\ \frac{c_p}{q_{ph}}\hspace{0.17em}\log \frac{q_{ph}{q}_{hp}}{c_h}\hspace{1em}\hfill & \left(\text{WC},c_h>c_h^{•}\right)\hfill \end{array}\right.$$ [28]

(Fig. 3 and SI Appendix, Fig. S1). The transition between the SC and WC control regimes is determined by the condition ${\mathrm{\Gamma }}_e={\mathrm{\Gamma }}_l$, from which we obtain the transition line $c_h^{•}\left(c_p,q_{ph},q_{hp}\right)$, Eq. 13.

For evolutionary control, the pathogen has an evolved pathogen trait ${\mathrm{\Gamma }}_e\left(\zeta \right)$ in the SC regime and a wild-type trait ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}=0$ in the WC regime. We obtain the equilibrium point

$$\left(\mathrm{\Gamma }*,\zeta *\right)=\left\{\begin{array}{cc}\left(\frac{q_{ph}}{c_p}-1,\frac{q_{ph}}{c_p}\exp \left(1-\frac{q_{ph}}{c_p}\right)\right)\hspace{1em}\hfill & \left(\text{SC},c_h<c_h^{•}\right),\hfill \\ \left(\mathrm{0,0}\right)\hspace{1em}\hfill & \left(\text{WC},c_h>c_h^{•}\right).\hfill \end{array}\right.$$ [29]

The optimal SC control is now at $\left(\mathrm{\Gamma }*={\mathrm{\Gamma }}_l,\zeta *={\zeta }_l\right)$, as given by [26], where the pathogen has the maximum stable ${\mathrm{\Gamma }}_e$ value. This point has the pathogen load $L_p*=q_e{f}_p*$ with $q_e=\left(1-P_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\right)$ given by [24], the host payoff $f_h*$, and the control efficiency

$$\eta *=\left\{\begin{array}{cc}1-\frac{c_p}{q_{ph}}-\frac{c_h{q}_{ph}}{c_p{q}_{hp}}\exp \left(1-\frac{q_{ph}}{c_p}\right)\hspace{1em}\hfill & \left(\text{SC},c_h<c_h^{•}\right),\hfill \\ 0\hspace{1em}\hfill & \left(\text{WC},c_h>c_h^{•}\right)\hfill \end{array}\right.$$ [30]

(Fig. 3 and SI Appendix, Fig. S1). The transition between the SC and WC control regimes is determined by the condition ${\eta }_{\mathrm{S}\mathrm{C}}*=0$, from which we obtain the transition line $c_h^{•}\left(c_p,q_{ph},q_{hp}\right)$, Eq. 14.

Dosage Protocols for Adaptive Trait Formation.

In the protocols described above, an initial-phase dosage $\zeta$ elicits a gain-of-function mutation to a trait value $G$, which is the starting point for the subsequent breeding phase. The extended HJB equation for these two-phase protocols determines the relative score

$$\mathrm{\Delta }\mathrm{\Omega }\left(G,\zeta \right)=\mathrm{\Delta }{\mathrm{\Omega }}_{in}\left(G,\zeta \right)+J_{\mathrm{b}\mathrm{r}}\left(G\right)$$ [31]

with an initial-phase component $\mathrm{\Delta }{\mathrm{\Omega }}_{\mathrm{i}\mathrm{n}}\left(G,\zeta \right)$ and a breeding-phase component $J_{\mathrm{b}\mathrm{r}}\left(G\right)$ given by [23]. To compute $\mathrm{\Delta }{\mathrm{\Omega }}_{in}\left(G,\zeta \right)$, we assume that trait-changing mutations have an exponential rate distribution, $u\left(G\right)\sim \mu \exp \left(-G{/ϵ}_0\right)$. The selective effects of these mutations are given by the pathogen fitness landscape, Eq. 12. Prior to the start of control, all mutants with $G>0$ evolve under negative selection of strength $s_0\left(G\right)=f_p\left(G,0\right)-f_{p,0}<0$. Under control, gain-of-function mutants have a positive selection coefficient against the wild type, $s\left(G,\zeta \right)=f_p\left(G,\zeta \right)-f_{p,0}>0$, leading to an adaptive fixation rate

$$v\left(G,\zeta \right)=2N_{e}u\left(G\right)\hspace{0.17em}s\left(G,\zeta \right)=\theta \exp \left(-G{/ϵ}_0\right)\hspace{0.17em}s\left(G,\zeta \right).$$ [32]

Because $s$ and $s_0$ are of similar magnitude, the number of mutants with trait amplitude $G$ that are present at the start of control and destined for fixation under the initial-phase protocol follows a Poisson distribution with expectation value close to $2N_{e}u\left(G\right)$. Hence, the expected time to high frequency of such mutants is

$$T_{in}\left(G,\zeta \right)=\frac{1-\exp \left[-2N_{e}u\left(G\right)\right]}{s\left(G,\zeta \right)}+\frac{\exp \left[-2N_{e}u\left(G\right)\right]}{v\left(G,\zeta \right)}.$$ [33]

The two terms on the right-hand side describe the contributions of standing variation at the start of control and of de novo mutations originating under control, respectively. The resulting initial-phase score reads

$$\mathrm{\Delta }{\mathrm{\Omega }}_{in}\left(G,\zeta \right)=\left(-q_{hp}-c_h\zeta -{\psi }_h*-\lambda \right)\hspace{0.17em}{T}_{in}\left(G,\zeta \right).$$ [34]

We evaluate the diversity $\theta =2N_e\mu$ in the initial phase with $N_e={\overline{N}}_0\equiv f_0/c$. Combining Eqs. 31–34 displays the scaling form of the score, Eq. 15, where the scaling function $\omega$ describes the cross-over in prevalence between de novo mutations ($\theta \lesssim 1$) and standing variation ($\theta \gtrsim 1$) driving the initial gain-of-function evolution. The breeding phase has a related cross-over from periodic selection ($\theta \lesssim 1$) to clonal interference ($\theta \gtrsim 1$) (34), which sets the effective population size in that phase (SI Appendix). Using Eqs. 23 and 34 together with a maximum-likelihood approximation for the gain-of-function amplitude,

$$G*\left(\zeta \right)=\arg \underset{G}{min}{T}_{in}\left(G,\zeta \right),$$ [35]

the HJB Eq. 31 determines the global maximum-score protocol (SI Appendix, Fig. S4). This protocol has a gain-of-function dynamics

$$\left(G_{in},{\zeta }_{in}\right)=\arg \underset{\zeta }{max}\mathrm{\Omega }\left(G*\left(\zeta \right),\zeta \right)$$ [36]

and a breeding phase described by [22] (Fig. 4 D–G and SI Appendix, Figs. S2 and S3).

Dosage Protocols for Metastable Control.

For the two-state protocol, we evaluate the relative score per unit of time as a function of the escape amplitude $G$ and baseline dosage $\zeta$ for $\lambda =0$,

$$\mathrm{\Delta }\omega \left(G,\zeta \right)=\mathrm{\Delta }{\omega }_{base}\left(\zeta \right)+v\left(G,\zeta \right)\hspace{0.17em}\mathrm{\Delta }{J}_{res}\left(G,\zeta \right).$$ [37]

Here, $v\left(G,\zeta \right)$ denotes the $\theta$-dependent establishment rate of escape mutations given by [32], $\mathrm{\Delta }{\omega }_{base}\left(\zeta \right)={\psi }_h\left(0,\zeta \right)-{\psi }_h*$ is the baseline score per unit of time, and $\mathrm{\Delta }{J}_{res}\left(G\right)=J_{res}\left(G\right)-T_{res}\left(G\right)\mathrm{\Delta }{\omega }_{base}\left(\zeta \right)$ is the negative excess payoff per rescue boost. The optimal score per rescue, $J_{res}\left(G\right)$, is computed in a simple approximation: we apply a constant dosage ${\zeta }_{res}\left(G\right)=\exp \left(G+2r_e\right)$, which generates positive selection of strength $s_{res}\left(G\right)\approx c_p{G}_{res}$ of the wild type against the escape mutant. The boost dosage is maintained over a period

$$T_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(G\right)=a\hspace{0.17em}\frac{\log \left(2N_e{x}_{\mathrm{e}\mathrm{s}\mathrm{c}}{s}_{res}\left(G\right)\right)}{s_{res}\left(G\right)},$$ [38]

which is proportional to the expected time to loss of the mutant ($x_{\mathrm{e}\mathrm{s}\mathrm{c}}$ is the detection threshold frequency; the constant $a$ determines the expected failure rate of rescue). The resulting rescue score is

$$J_{res}\left(G\right)=\left[{\psi }_h\left(0,{\zeta }_{res}\left(G\right)\right)-{\psi }_h*\right]\hspace{0.17em}{T}_{res}\left(G\right).$$ [39]

Using again a maximum-likelihood approximation for escape mutations,

$$G*\left(\zeta \right)=\arg \underset{G}{max}v\left(G,\zeta \right),$$ [40]

we obtain the optimal metastable protocol by maximization of $\mathrm{\Delta }\omega$, Eq. 37 (SI Appendix, Fig. S4). This protocol has a baseline dosage

$${\zeta }_{base}=\arg \underset{\zeta }{max}\mathrm{\Delta }\omega \left(G*\left(\zeta \right),\zeta \right),$$ [41]

which determines the escape trait $G_{\mathrm{e}\mathrm{s}\mathrm{c}}=G*\left({\zeta }_{base}\right)$ and the rescue dosage ${\zeta }_{res}=\exp \left(G_{res}+2r_e\right)$ (Fig. 4 H–J). The maximum score per unit of time, $j=\underset{\zeta }{max}\mathrm{\Delta }\omega \left(G*\left(\zeta \right),\zeta \right)$, sets the long-term efficiency gain of metastable control, ${\eta }_{ms}-\eta *=j/\left(q_{ph}{q}_{hp}\right)$ (Fig. 4K).

Data Availability.

Analysis notebooks are available at Open Science Framework (OSF), https://osf.io/6nakg/.