Temporal encoding of bacterial identity and traits in growth dynamics

Significance

Microbiology has traditionally been defined by the study of the phenotypic traits of microorganisms. While some traits can be easily explained with a direct genetic basis, most are a result of complex interactions between the organism and its environment. We demonstrate that phenotypes with a sufficiently high information content can distinguish strains and predict traits such as antibiotic response. This has implications for how clinicians can better identify and treat bacterial infections. In particular, our results highlight that both phenotype-based and sequence-based approaches contribute valuable information and can be used alongside one another in practice.

Abstract

In biology, it is often critical to determine the identity of an organism and phenotypic traits of interest. Whole-genome sequencing can be useful for this but has limited power for trait prediction. However, we can take advantage of the inherent information content of phenotypes to bypass these limitations. We demonstrate, in clinical and environmental bacterial isolates, that growth dynamics in standardized conditions can differentiate between genotypes, even among strains from the same species. We find that for pairs of isolates, there is little correlation between genetic distance, according to phylogenetic analysis, and phenotypic distance, as determined by growth dynamics. This absence of correlation underscores the challenge in using genomics to infer phenotypes and vice versa. Bypassing this complexity, we show that growth dynamics alone can robustly predict antibiotic responses. These findings are a foundation for a method to identify traits not easily traced to a genetic mechanism.

In microbiology, the main approach to identify bacteria has been through the characterization of observable phenotypes (1). However, advances in sequencing technology have shifted the focus to genetic information (2). In general, mapping from a piece of DNA to the corresponding product (RNA or protein) is definitive, as dictated by the central dogma. To this end, genome-wide association studies have been instrumental in identifying genes responsible for observed phenotypic traits (2–4). For example, studies have enumerated genes encoding β-lactamase, an enzyme that degrades β-lactam antibiotics (3). These have become a genetic signature for identifying resistance to β-lactam antibiotics (4).

However, how a gene and its product affect the behavior of an organism is typically difficult to predict (2, 5). This challenge is, in part, due to the sheer magnitude of interactions between genes, their products, and environmental factors that collectively define the operation of an organism (6–9). While the genetic sequences of β-lactamases are well documented, how this enzyme affects an organism depends on other factors (5). For instance, even in the presence of the β-lactamase gene, expression can be too low for single-cell antibiotic tolerance. However, a population can still survive with a sufficiently high initial cell density (5, 10). Simultaneously, phenotypic resistance can arise in the absence of a clear and unequivocal genetic basis. It has been shown for some antibiotics, like those that target the ribosome, that antibiotic tolerance can be cell density dependent, as with the inoculum effect (11–13). This complexity limits the general utilization of genetics for trait prediction (14).

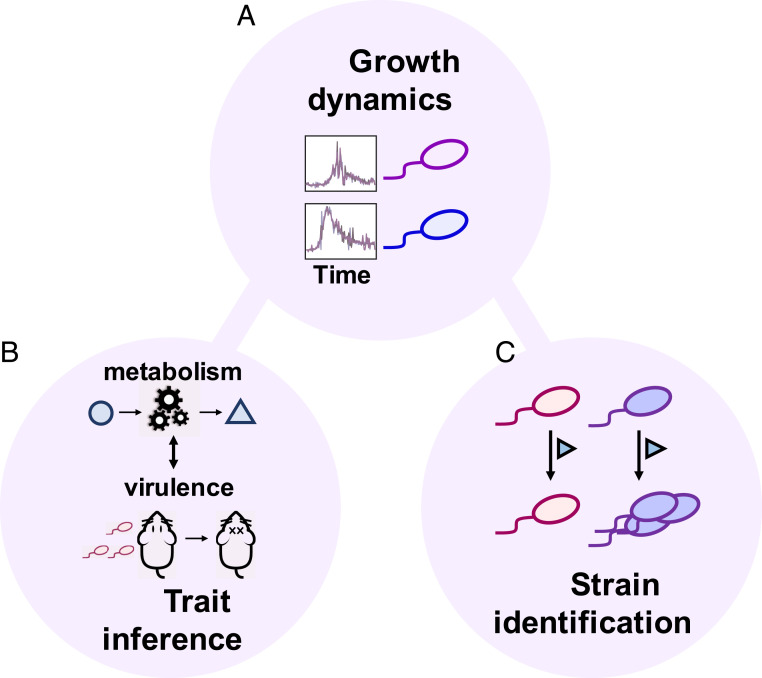
Conversely, it remains impossible to deduce the complete genomic information of an organism solely based on its phenotypic traits. However, for many applications, the ability to differentiate between organisms of interest is sufficient (Fig. 1) (15). Consider two bacterial strains in the same environment; we define a strain as an organism with a unique genetic sequence. Typically, these strains would exhibit two different phenotypes (e.g., growth rate, nutrient utilization) (16–20). For instance, pathogenic and commensal strains of Escherichia coli can be differentiated by the carbon sources they utilize (21–23).

Fig. 1.

Growth dynamics reflect the complex interplay between microbes and their environments and encode rich information. (A) The interactions between cells and their environment are complex and manifest in temporal growth dynamics. Such a complex phenotype contains information on microbial organisms from genetic identity to key characteristics. In the same environment, two genetically different strains are expected to generate different growth dynamics. (B and C) The information encoded in the growth dynamics can be used for trait inference or strain identification.

Alternatively, a single strain growing in two different environments generally exhibits two distinct phenotypes (24). Yet these phenotypes are intrinsically linked as both arise from the same genotype. With a sufficiently strong relationship, it is possible to use one to infer the other. This intuition underlies several ad hoc applications with phenotypic signatures linked to traits of interest (19–22, 25). In Klebsiella pneumoniae, changes in d-arabinose metabolism have been linked to hypervirulence (20). Additionally, studies have identified instances where resistance to bacteriophages, viruses that infect bacteria, is correlated with antibiotic resistance (26, 27).

The interactions between cells and their environment are complex, changing over time and across environmental conditions. Previous work has shown that these interactions can manifest in temporal growth dynamics, which quantify changes in cell growth over time (28–30). For example, Tan et al. demonstrated that growth signatures can differentiate laboratory strains as well as the same strain under different environmental conditions (28). We take advantage of this property to use growth dynamics for both strain identification and antibiotic resistance prediction. The fundamental requirement for this strategy is for the phenotype to be adequately complex, such that there exists a sufficiently unique mapping with the underlying genotype or another phenotype.

Results

We utilized a library of bacterial isolates collected from patients across the Duke University Hospital and North Carolina Community Hospital systems (Methods). This library consists of 244 fully sequenced clinical isolates, which corresponds to 203 unique strains based on whole-genome sequencing (WGS) and 41 unique sequence types according to multilocus sequence typing (SI Appendix, section 3.1) (31). We chose this library for its two main properties: 1) its composition, as it contains a few genera within Enterobacteriaceae, mainly E. coli, and 2) its characterization, which includes WGS and the antibiotic resistance profile spanning numerous antibiotic classes (32). The first point is crucial for evaluating the feasibility of strain-level identification, even when the strains of interest are closely related. The second point becomes useful for evaluating the mapping between growth and other traits.

Determining Identity from Growth Dynamics.

We first examined whether temporal growth dynamics contain sufficient information for strain-level discrimination. To do this, we used the time derivative of the growth curve as the input to train a support vector machine (SVM) model (Methods). Specifically, we took the derivative of 99 time point growth curves, resulting in 98 features representing the change in cell density over time. SVM is a supervised learning algorithm which maximizes the margin (distance) between support vectors, data points closest to a separating hyperplane (boundary), and this boundary. This trait allows SVM to develop accurate models for small datasets (33). For our multiclass classification problem, we applied a one-versus-all approach where each model consisted of n classifiers (corresponding to n strains). Each classifier is an independent SVM model that discriminates between one strain and all others. The classifier corresponding to the maximum margin, the largest-valued margin of n classifiers, is the predicted class. A larger value implies a greater confidence in the prediction being correct: The farther a sample is from the boundary, the less likely noise could push it to either side. Accordingly, we used the maximum margin as a metric to estimate the confidence of predictions (SI Appendix, section 1.5).

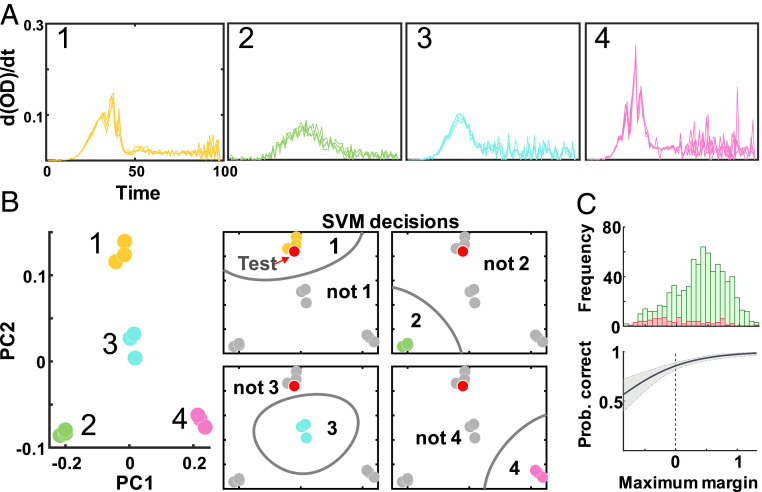
As an initial proof of concept, we generated a dataset consisting of technical replicates. We measured the growth dynamic of 203 strains grown under a rich media condition (lysogeny broth [LB] with 10,000× dilution) for ∼16 h (99 time points in 10 min increments) (Fig. 2). The use of technical replicates allowed the minimization of variabilities due to other factors, like those associated with each starter culture. In these technical replicates, the growth rates would still fluctuate due to the bacteria–environment interaction in different wells; it is these fluctuations that we use for strain identification. In Fig. 3, we provide an example of the training process using SVM with four random strains. Here, we applied principal component analysis to examine the features in a two-dimensional (2D) space. Like this 2D example, SVM optimizes the separating hyperplanes in our true model, albeit in a 98-dimensional space. Using a single-nucleotide polymorphism (SNP)-based approach to strain definition (Methods), we saw an average classification accuracy of 91.50% (SI Appendix, section 1.1). This accuracy drastically surpassed what we expected with random chance (0.49%). In addition to the SNP-based approach, which utilizes SNPs to measure the genetic distance between isolates, we also demonstrate the general applicability of this method to changing strain definitions. To this end, we utilize a multilocus sequence typing (MLST)-based approach which uses a core set of genes to evaluate genetic distance. With a MLST-based approach to strain definition, we saw an average classification accuracy of 97.56%. In SI Appendix, we explore how this strain-level prediction is affected by changing the input features (SI Appendix, section 1.1).

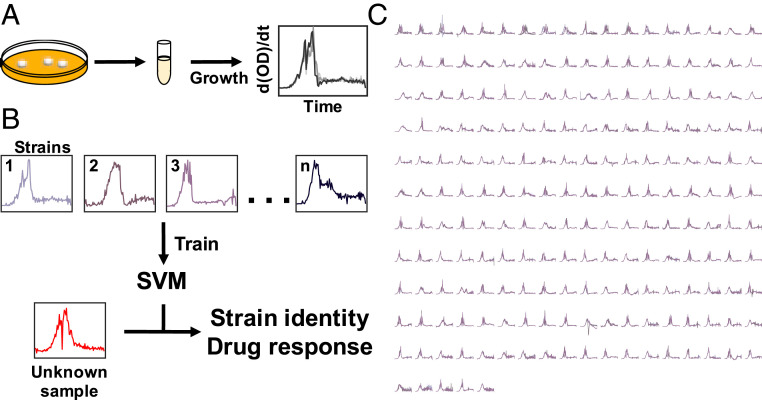
Fig. 2.

Workflow for growth-based predictions. (A) Experimental procedure. From individual colonies, isolates were grown overnight. These cultures were diluted into 96-well plates and grown under standardized conditions to generate growth dynamics. (B) Model development. The training dataset consists of antibiotic susceptibility profiles and strain identity. Growth dynamics train SVM models; these models predict either strain identity or antibiotic resistance. For an unknown sample, growth is the input for the trained models to predict identity and resistance profile. (C) Phenotypic profiles of clinical isolates. Growth dynamics (time derivative of growth curves) for the 10,000× condition.

Fig. 3.

Development of prediction confidence. (A) Four-strain example. Growth dynamics are the time derivative of smoothed growth curves (10,000× condition). (B) SVM output. We examine SVM predictions in 2D through principal component analysis as an example for visualization purposes. The Left illustrates the training set. In this four-class example (1, 2, 3, 4), the test point (red) is predicted as 1. (C) Maximum margin: CI estimate. We examine the distribution of maximum margins for correctly classified (green) and misclassified (red) samples in the test set (10,000×). Logistic regression predicts the probability of the prediction being correct; the shaded region indicates the 95% CI.

To demonstrate the generality of these findings to a higher degree of experimental variability, we generated a secondary dataset containing growth dynamics for the same clinical isolate library with both biological and technical replicates (Methods). With an average classification accuracy of 82.56% (SNP-based strain definition), we show the robustness of the predictive power. In fact, biological replicates not previously seen by the model could also be predicted with a high degree of accuracy (SI Appendix, section 1.7); this was consistently shown using both a SNP- and MLST-based approach to strain definition. This approach would ideally be how this method would be used in long-term applications. This general capability allows us to distinguish organisms beyond the species level, using phenotypes, in a scalable manner.

A critical requirement for this approach to work is that the data are of sufficient temporal resolution and reproducibility. In SI Appendix, we examine the impact of changing the temporal resolution of growth dynamics on predictive power and observe that in general, increasing temporal resolution leads to an increase in classification accuracy (SI Appendix, Fig. S1.1). Importantly, the variability between replicates should be less than the difference between strains. To illustrate this point, we analyzed a set of recently published growth curves for the Keio collection, an E. coli single-gene knockout library (SI Appendix, section 1.3) (34). Using the time derivative of the growth curves as the features, we achieved an accuracy of 12.69% for 3,866 strains. In this model, the predicted class label was based on the highest-valued 10 margins (k = 10). Here, k represents the number of highest-valued margins we consider. For each test sample, the output of the SVM model was 3,866 margins, each corresponding to the distance from the separating boundary to this sample (per class). For k = 10, if the class corresponding to one of the highest-valued 10 margins was the same as the true class, then the prediction was considered to be correct. The accuracy for this library was much lower than that from our own dataset, likely due to two technical issues: 1) low temporal resolution (49 time points over 18 h) and 2) fewer replicates under higher experimental variability. Despite these caveats, the accuracy far exceeded random chance (0.26% for k = 10) on a library consisting of over 3,000 strains differing in genetic sequence by a single gene, underscoring the rich information content in growth dynamics.

Given the high accuracy in distinguishing different strains solely based on growth dynamics, we wondered if a correlation exists between genetic and phenotypic distances. To date, there is no consensus in the literature about whether this correlation exists (35–40). Plata et al. describe a correlation between phenotypic similarity in terms of carbon utilization and genetic distance, especially at lower genetic distances (particularly at the species level) (36). One of the main limitations of this work, however, lies in the utilization of 16S rRNA sequences to quantify genetic distance. While a common approach to examining bacterial phylogeny, it has a limited taxonomic resolution, which constrains the ability to measure genetic distance. In contrast, Galardini et al. report no correlation between phenotypic and phylogenetic distances for a library of about 700 E. coli strains grown under 214 conditions (35). Although this analysis uses WGS to calculate genetic distance, responses to the growth conditions used to define the phenotypic distance are controlled by a small subset of genes. As a result, the correlation becomes highly dependent on the evolutionary rate of genes regulating the chosen phenotypes relative to the other genes of E. coli.

Previous work examining the correlation between phenotypic and genetic distances is additionally limited by their approach to measuring phenotypic profiles. Specifically, they use metrics to calculate phenotypic distances that limit the dynamic range of the phenotype (35, 36). For example, Plata et al. define the phenotypic profile with a binary metric for growth; this results in much of the information stored within the phenotype being discarded. To avoid the confounding factors that limit the interpretability of previous work, we use 1) WGS to define genetic distances and 2) temporal growth dynamics to define phenotypic distances. The first ensures the high-resolution measure of genetic distances. The second allows the utilization of a phenotype that is regulated by a diverse set of genes and is crucial to enhancing the dynamic range of phenotypic diversity.

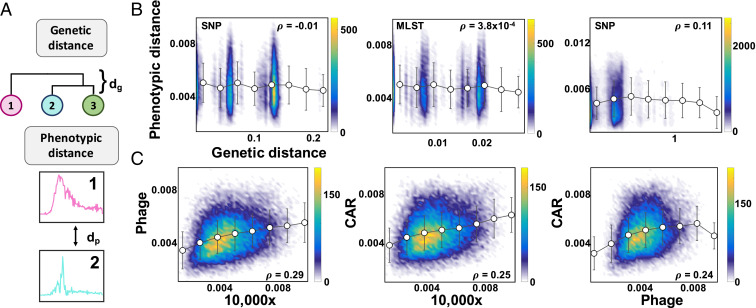
Here, we computed the phenotypic distances between two strains as the Euclidean distance between the time derivative of the growth curves (Methods). The genetic distance between them was the pairwise distance used to construct the phylogenic tree. This is defined according to the Tamura–Nei model, in which the number of base substitutions between sequences reflect estimates of evolutionary divergence (Methods) (41). This metric is generally used in phylogeny to generate a tree in which branch length and structure describe the evolutionary history of a set of organisms. With these metrics, there was no statistically significant correlation between the genetic distance, as determined by phylogenetic analysis (SNP-based definition), and the phenotypic distance, defined as the distance between the average growth dynamics under the 10,000× condition (Fig. 4 A and B). Similarly, there was no statistically significant correlation when the genetic distance was defined by MLST (SI Appendix, Table S2.1).

Fig. 4.

Correlation between genetic and phenotypic landscape. (A) Distance metrics. Genetic distance is defined by phylogeny, and phenotypic distance is the Euclidean distance between pairs of curves representing the time derivative of the growth curve. (B) Correlation between genetic and phenotypic distances. Each point in the density plot is defined as the distance comparison (x axis is genetic distance, and y axis is phenotypic distance) of a pair of isolates. As the color goes from blue to yellow, the number of isolates at a particular point on the plot increases. No significant correlation exists between genetic and phenotypic distances. The Left corresponds to the 10,000× condition for the clinical isolates using a SNP approach to strain definition (P value = 0.59). The Center corresponds to the 10,000× condition for the clinical isolates using a MLST definition of strain identity (P value = 0.49). The Right corresponds to environmental isolates, taxonomic order Bacillales, using a SNP approach to strain definition (P value = 2.7 × 10⁻⁷). (C) Correlation between phenotypic distances. Each point in the density plot is defined as the phenotypic distance comparison (between growth dynamics of growth conditions) of a pair of isolates. As the color goes from blue to yellow, the number of isolates at a particular point on the plot increases. Here, CAR refers to the carbenicillin growth condition. A significant correlation exists between pairs of phenotypes for the clinical isolates.

One reason for the lack of correlation may have been the limited genetic diversity of our clinical isolates. To test this notion, we constructed a library of 607 environmental isolates collected around the Duke University campus, which were more genetically diverse (Methods). The isolates in this library spanned over 17 taxonomic orders. For 143 unique strains grown under a rich media condition, tryptic soy broth (10,000× dilution), we achieved a classification accuracy of 82.75% on a validation set. This was significantly better than chance, 0.70%. By changing the features from the time derivative of growth curves to growth rate, we enhanced this accuracy to 90.68%. This indicated that distinct strain libraries may benefit from different data processing pipelines. Despite an increase in experimental variability (batch and platform controls), we maintained high predictive power. As with the clinical isolates, we saw no correlation between phenotypic and genetic distances for the environmental isolates (Fig. 4B and SI Appendix, Fig. S2.3 and Table S2.3).

With a lack of correlation between phenotypic and genetic distances, we were interested in whether one phenotype could predict a second phenotype. To start, we examined the correlation between pairs of phenotypes. To this end, we used phage and antibiotic treatments for two reasons: 1) their ability to perturb growth dynamics and 2) a previously described relationship between resistances to phage and antibiotics (26, 27). We used $\lambda$ phage, a well-studied temperate phage that targets E. coli. Despite this general ability, the infection and coexistence parameters can differ between strains, resulting in growth variation (42, 43). Similarly, we used a sublethal concentration of carbenicillin, to which organisms could exhibit unique response parameters (5). Specifically, resistance to antibiotics has been shown to be mediated by modulations in bacterial metabolism, which can lead to changes in growth dynamics (44, 45). As with the 10,000× condition, the growth dynamics in each condition were able to distinguish different strains with high accuracy. In particular, the phage and carbenicillin conditions resulted in an average classification accuracy of 92.12 and 91.01%, respectively. Like the 10,000× condition, there was no correlation between genetic and phenotypic distances for either condition (SI Appendix, section 2.2). In contrast, the correlation between growth dynamics of a pair of conditions was statistically significant (Fig. 4C and SI Appendix, section 2.2). This correlation occurred likely because these traits were intrinsically related by genotype.

Growth Predicts Antibiotic Resistance.

Given the strong correlation between growth dynamics under different conditions, we reasoned that they can serve as the basis to predict a more distant, but still related, phenotype: antibiotic resistance. This was implied with previous work, which showed that phenotypic drug sensitivity profiles cluster based on common mechanisms of action (46). For the 244 clinical isolates, we had the corresponding resistance profiles to four antibiotics from the clinical microbiology laboratory. The antibiotics were ampicillin–sulbactam (SAM), trimethoprim–sulfamethoxazole (SXT), gentamicin (GM), and ciprofloxacin (CIP). For a direct comparison to sequence-based approaches, we used the WGS of these isolates to predict antibiotic resistance with three sources of antibiotic resistance genes: 1) a compiled database of resistance mechanisms from the literature, 2) a curated amino acid sequence database, the Comprehensive Antibiotic Resistance Database (CARD), and 3) a curated database of nucleotide sequences, ResFinder (SI Appendix, section 3.2) (47, 48).

We defined the true resistance phenotype as that from clinical antimicrobial susceptibility tests; isolates were classified as resistant if they presented either an intermediate or resistant phenotype, according to the minimum inhibitory concentration (32). This acted as the label for an SVM model (1 = resistance, 0 = sensitive) where the input was growth dynamics for a set of growth conditions. We tested all combinations of growth conditions as the input (Methods; 10,000× dilution, 100× dilution, phage, and carbenicillin), and the results of these predictions are visualized (Fig. 5 and SI Appendix, Fig. S1.2 and section 1.2). To predict antibiotic resistance, previous work has used specific genetic signatures and growth under the corresponding antibiotic (4). In contrast, we show in Fig. 5 that growth dynamics in the absence of the corresponding antibiotic can similarly predict resistance. Due to the characteristics of the clinical isolate library, one caveat is that genetically similar isolates could be present in both the training and test datasets for this prediction. While in this work this may inflate the reported predictive accuracy, this is an expected feature of clinical isolates should this approach be applied in practice.

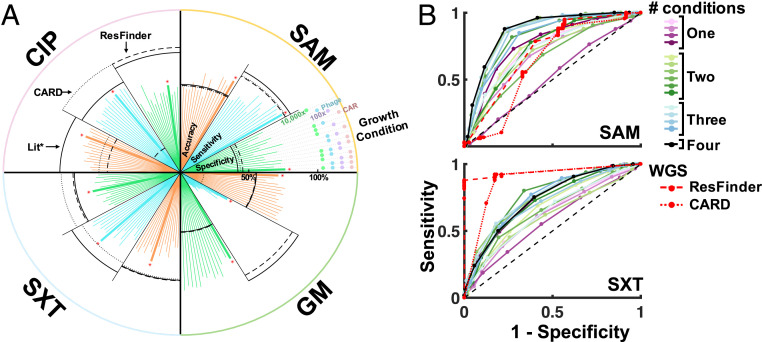
Fig. 5.

Antibiotic resistance prediction. (A) Growth dynamics can predict antibiotic resistance. We predict antibiotic resistance profiles for four antibiotics. Each line going outward from the center represents the strength of the mapping for one of three metrics: accuracy, sensitivity, or specificity. Each quarter of the circle represents the predictions for one of four antibiotics. The black lines within each slice correspond to WGS-based predictions using three databases: 1) the literature, 2) CARD, and (3) ResFinder. The black asterisk refers to literature. The red asterisks highlight the condition at which the best prediction occurs based on the highest value for the average of accuracy, sensitivity, and specificity. (B) Evaluation of resistance prediction. We compare ROC curves for the phenotype-based predictions and genotype-based predictions (red).

In Fig. 5A, we illustrate the differences between antibiotic resistance predictions using growth dynamics and WGS-based methods. Specifically, the accuracy of predictions for SAM resistance was on par with WGS, while WGS performed better in the case of SXT. This is additionally demonstrated by the receiver operating characteristic (ROC) curves (Fig. 5B). A ROC curve shows the false positive rate vs. the true positive rate and is used to evaluate different models. Here, the red curves (WGS-based methods) were closer to the ideal theoretical ROC curve [passes through point (0, 1)] for SXT relative to the phenotype-based ROC curves. In contrast, the reverse was true of SAM. For CIP, the results were mixed, with WGS having improved performance only when using a set of simple genetic markers (49, 50). Similarly, the results for GM were inconclusive due to generally poor accuracy for both methods. Taken as a whole, this result highlights that both phenotype-based predictions and sequence-based ones contribute valuable information and can be used alongside one another. Additionally, this result is a demonstration of predicting antibiotic resistance using a secondary phenotype without requiring growth in the corresponding antibiotic.

The main limitation with sequence-based approaches is that the effect of a gene on an organism is difficult to predict (14). The presence of a gene conferring resistance does not necessarily mean phenotypic resistance and vice versa (8, 13). This lack of a direct connection was especially apparent for SAM and GM, where WGS predictions had a significantly higher sensitivity than specificity. Sensitivity is defined as the proportion of positive (resistant) isolates that are correctly predicted, while specificity is defined as the proportion of negative (sensitive) isolates that are correctly predicted. In this context, a higher sensitivity than specificity implied the presence of sensitive isolates predicted as resistant. This may have occurred due to the presence of genes known to confer resistance not providing phenotypic resistance.

In contrast, resistance to CIP is mediated by specific mutations in the targets, DNA gyrase and topoisomerase (50). Since these are crucial to cell division, they are relatively conserved, making mutations highly likely to correspond to a resistant phenotype, resulting in high specificity and sensitivity. As for GM, one reason the predictions with growth dynamics were not accurate may have been due to the imbalanced dataset; only 15% of the 244 clinical isolates were resistant. While the phenotype-based predictions were not necessarily better than the sequence-based benchmark for all antibiotics, the growth conditions were not optimized for this prediction and can be significantly improved upon in future iterations. The use of growth conditions that maximize the information from the resulting growth dynamics could potentially improve the predictive accuracy. This was shown with the increased accuracy of SAM resistance prediction when using the carbenicillin growth condition in the predictor (SI Appendix, Table S1.5).

Discussion

For a given environment, a genotype is typically uniquely mapped to a particular phenotype (1). However, knowing the genotype does not necessarily enable phenotype prediction due to the complex mapping between the two (5, 14). One explanation for this complexity is that genotype to phenotype maps of different systems can have unique properties (14). For complex gene networks, changes in genotype can result in a similar phenotype (51). However, in RNA folding, even minor changes in the genotype can result in vastly different structures and functions (14). The challenge in developing this mapping is, in part, reflected by the lack of correlation between genetic and phenotypic distances, which we and others have observed (35, 38). Previous work has indicated contradictory findings of the existence of this correlation (35, 36). As a result, we took two measures to address limitations associated with these studies. The first was to utilize growth as the phenotype, which is a high-level trait and a fundamental feature of organisms. The second was to increase the dynamic range of phenotypic distance by using the temporal domain of growth.

There are several explanations that could underlie this apparent lack of correlation between genetic and phenotypic distances (35, 38, 40). Most pertinently, genetic variants are often neutral. Another explanation may be an incomplete view of the genetic information (a lack of annotated information on plasmids, which can affect growth). By definition, genomic sequences have a much higher dimension (∼4 million bases) than the growth data (∼100 data points). While the variations in the growth curves directly reflect phenotypic variation, many of the variations in the genomic sequence do not. There are likely elements of the genetic sequence that should be weighted more heavily in the distance calculation than others. Due to the inability to apply this weighting in an unbiased manner, however, many of the genetic variations may act as noise. Based on our findings, the concept of a genotype to phenotype correlation may be more nuanced than previously appreciated, with the results dependent on the approach to quantifying phenotypic and genetic distances.

There are several implications for the lack of correlation between the genetic and phenotypic landscapes. A major one is that it casts doubts on the attempt to directly use WGS to predict phenotypic traits, especially for those with a complex genetic basis (52). Some have commented on approaches to bypass this complexity (53). Burga and Lehner described intermediate phenotypes, like gene expression, as an alternative to genetics for phenotype prediction (53). These can be useful for developing a mapping since they capture both genetic and nongenetic factors. However, for certain applications, our results show that an explicit mapping is unnecessary. In particular, we show that growth dynamics contain sufficient information to distinguish different strains, even beyond the species level. Intuitively, this is expected, as single-gene mutations have been shown to affect growth (34). However, the ability to distinguish hundreds of closely related strains has not been previously explored. In contrast to the lack of correlation between genetic and phenotypic distances, we saw statistically significant correlations between phenotypic distances of different growth conditions. This correlation was unexpected but implies that at an organism level, seemingly unrelated phenotypes can be linked. We show this by using growth dynamics to predict related phenotypes of practical relevance. While we focus on antibiotic resistance, we envision that such phenotype–phenotype mappings can be established for other traits of interest, especially those that are more difficult to quantify like biofilm formation and virulence.

This work has implications for how clinicians identify and treat bacterial infections. In particular, we demonstrated the ability to differentiate clinically relevant bacteria with a resolution beyond that of standard methods of bacterial identification. Additionally, we described a method to bypass the current combinatorial problem of antibiotic resistance detection. Rather than testing all possible antibiotics with multiple concentrations for a pathogen of interest, the prediction of antibiotic resistance with growth phenotypes can be used to narrow down treatment options.

In contrast to other efforts to map phenotypes, the fundamental innovation of our strategy is the use of the temporal features of growth dynamics. The intuition here is that the temporal domain incorporates the feedback between microbial growth and environmental factors (29). This information is lost, however, when studies discretize growth dynamics with metrics like the area under the curve or maximum value (20, 24, 37, 39). For example, the Biolog system generates a metric summarizing the growth of microbes for each condition in a panel of metabolites (54). Like our work, this system has identified unique growth signatures of individual strains (55). Doing so, however, requires a screen of about 1,200 growth conditions (55). This is difficult to scale up, especially for the differentiation of a large set of strains. In contrast, we show that temporal growth dynamics can increase the information content of individual growth conditions, simplifying experiments by requiring fewer conditions. As a result, it is more compact and can be more readily scaled up and standardized. The importance of these dynamics has been suggested, but it is unclear whether this is generally applicable (28). To this end, our work demonstrates the broad scope of temporal growth dynamics to encode information.

Methods

Strains, Media, and Growth Conditions.

Clinical isolates.

We used a library of clinical isolates collected from two sources. The first source consists of 185 isolates within a few genera in the family Enterobacteriaceae (e.g., Klebsiella, Citrobacter, and Escherichia) isolated from blood samples at the Duke University hospital (supplied by Vance Fowler and Joshua Thaden), and the second consists of 59 multidrug-resistant E. coli isolates collected from patients at North Carolina community hospitals (supplied by Deverick Anderson) (32). The raw WGS data for all isolates utilized in this paper have been deposited in National Center for Biotechnology Information (NCBI). Those for the first source were stored under either Bioproject PRJNA290784 or PRJNA259658 (isolates are labeled as GN0xxxx). Those for the second source were deposited at the DNA Data Bank of Japan (DDBJ)/European Molecular Biology Laboratory (EMBL)/GenBank Sequence Read Archive 423 (SRA) under accession numbers DRX055674 to DRX05573.

To generate the primary dataset consisting of technical replicates, we follow the following protocol. For each isolate, a frozen stock was plated on LB agar (Miller’s) plates, and individual colonies were randomly selected to inoculate growth media for experiments. Three milliliters of LB (Miller’s) were used to prepare overnight cultures, which were shaken at 37 °C for 12 h. The optical density (OD) (absorbance at 600 nm) for the overnight culture was taken on a plate reader (Victor3, Perkin-Elmer or infinite M200 Pro, Tecan) to ensure a consistent initial cell number. To calculate the initial cell number, we assumed that 1 OD₆₀₀ = 8 × 10⁸ cells/mL This overnight culture (for each isolate) was used to inoculate 4 wells in a 96-well plate (to generate four technical replicates). For the growth curves, measurements for each well were taken every 10 min with periodic shaking (5 s orbital) at 30 °C for a total of 99 measurements under one of four growth conditions. Each well was covered with 50 μL of mineral oil. The four conditions were 1) LB (Miller’s) with an initial cell density of 2 × 10⁴ cells/well, 2) LB (Miller’s) and $\lambda$ bacteriophage (multiplicity of infection = 1) with an initial cell density of 2 × 10⁴ cells/well, 3) LB (Miller’s) with an initial cell density of 2 × 10⁶ cells/well, and 4) LB (Miller’s) to a concentration of 5 μg/mL. Carbenicillin had an initial cell density of 2 × 10⁴ cells/well. In the main text (Results section), we describe these conditions as 10,000× dilution, phage, 100× dilution, and carbenicillin, respectively. To prepare the phage condition, we propagated $\lambda$ bacteriophage by transfecting $\lambda$ DNA from New England Biolabs (NEB) (catalog #N3011s) into chemically competent JM101 E. coli cells from Agilent technologies (catalog #200234). The transformed E. coli were plated, and phage stocks were collected and titered.

To generate a secondary dataset on a subset of the clinical isolates consisting of both biological and technical replicates in a higher-throughput manner, we followed the following protocol. For biological replicate experiments, frozen stocks were plated on LB agar plates, and three distinct colonies were selected to inoculate growth media. Overnight cultures were prepared in 1 mL of LB broth in 96-well deep-well microplates (VWR), which were shaken at 37 °C for 16 h at 1,000 rpm. The OD (absorbance at 600 nm) for the overnight culture was taken on a plate reader (Tecan Spark multimode microplate reader). To ensure a consistent initial cell number, cultures were diluted to 1 OD₆₀₀ (assumed to be equivalent to 8 × 10⁸ cells/mL) and further diluted 1:8 (1 × 10⁸ cells/mL). Cultures were then finally diluted 10-fold in 100 µL of fresh LB in a 384-well deep-well plate (Thermo Scientific) using a MANTIS liquid handler for an initial cell density of 1 × 10⁶ cells/well. Each of the three overnight cultures (biological replicates each from a distinct colony) were used to inoculate four wells (to generate four technical replicates). The spatial position of all wells for each experiment was randomized across the plate to minimize plate effects. To minimize evaporation, the plate was loaded with the lid into the Tecan Spark microplate reader equipped with a lid lifter, and the chamber temperature was maintained at 30 °C. OD₆₀₀ readings were taken every 10 min with periodic shaking (5 s orbital) for 24 h.

Environmental isolates.

A library consisting of 607 environmental isolates was collected across the Duke University campus as part of an undergraduate program: The Blue Devil Resistome Project (a Bass Connections project). The raw WGS data of all isolates utilized in this paper are publicly available at NCBI under accession number PRJNA543692. These have also been deposited in the China National GeneBank DataBase (CNGBdb) (https://db.cngb.org/) with accession number CNP0000455. For this isolate library, we used tryptic soy rather than LB because that was the media the isolates were originally isolated from the environment on. For each isolate, one frozen stock was plated on tryptic soy agar plates, and individual colonies were randomly selected to inoculate growth media for experiments. Three milliliters of tryptic soy broth were used to prepare overnight cultures, which were shaken at either 30 °C or 37 °C for at least 16 h (until sufficient growth for subsequent experiments). The OD (absorbance at 600 nm) for the overnight culture was taken on a plate reader (Victor3, Perkin-Elmer, or infinite M200 Pro, Tecan) to ensure a consistent initial cell number. For all isolates, measurements were taken every 10 min with periodic shaking (5 s orbital) in replicates of 12 under a single growth condition at 30 °C for a total of 99 measurements. Here, we had two sets of biological replicates, each of which had six technical replicates. Each well was covered with 50 μL of mineral oil. The growth condition used here was tryptic soy broth with an initial cell density of 2 × 10⁴ cells/well. In the main text (Results section), we describe this growth condition as 10,000× dilution. Additionally, the replicates (per isolate) were processed in batches of six such that six replicates were conducted, with a different colony, on one plate reader on 1 d and the second set of six were conducted on a different platform (plate reader) on a different day. This allowed us to include both technical and biological replicates in this protocol. The purpose of this protocol design was to introduce both batch and platform variability into the dataset. Of the 607 sequenced isolates in this library, we collected growth curves for 522 isolates, which, based on WGS, were composed of 143 unique strains.

Processing Plate Reader Data.

Each 96-well plate included three or four blanks containing only media (LB [Miller’s] or tryptic soy broth). Similarly, each 384-well plate included 96 blanks containing only media (LB [Miller’s]). We averaged these wells and subtracted the result from all time courses, then zeroed all negative OD₆₀₀ values. To convert these blanked growth curves into the time derivative, we filtered noise with a median filter of size 3 and then took the derivative between consecutive time points. Unless specified otherwise, in the main text (Results section), we used a weighted growth rate metric $\left(\frac{dc}{dt}\right)$ rather than growth rate $\left(\frac{d\text{ln}\left(c\right)}{dt}\right)$ where c refers to cell concentration and t represents time. This metric uses cell density as a weighting factor such that higher OD₆₀₀ values are weighted more heavily than lower values. The intuition behind this approach is that instrument noise is higher at lower cell densities and lower at higher cell densities. To convert the blanked growth curves into growth rate, we filtered noise with a moving average filter of size 5 and took the numerical gradient of the log of the smoothed growth curves. We compare in SI Appendix the result of using the growth rate, time derivative of the growth curves, and other data processing methods.

Model development.

Clinical isolates: Prediction of genetic identity and antibiotic resistance.

For the clinical isolates, we applied a fourfold cross-validation procedure to optimize model parameters based on the prediction accuracy of the training set. To do this, we split the replicates for each unique strain into the test set (one replicate) and training set (three replicates) and ran the SVM model on a set of hyperparameters. We rotated through the replicates such that each was used as the test set once. The average of the test set across these four folds is used to optimize the model hyperparameters and is reported in the main text (Results section). In SI Appendix, we compare these results to those from a holdout-based dataset splitting approach. Additional details can be found in SI Appendix, sections 1.1 and 1.2.

Due to the small size of the isolate library, we modified the method for splitting a dataset for training to examine the potential for predicting antibiotic resistance. In this approach, we used all replicates for all isolates except one isolate for training and used the four replicates from the left-out isolate as the test set. This was repeated for all isolates, and the predictions are reported in terms of accuracy $\left(\frac{\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{true}\hspace{0.17em}\text{positive}\hspace{0.17em}\text{samples}}{\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{samples}}\right)$, true positive rate or sensitivity $\left(\frac{\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{true}\hspace{0.17em}\text{positive}\hspace{0.17em}\text{samples}}{\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{positive}\hspace{0.17em}\text{samples}}\right)$, and true negative rate or specificity $\left(\frac{\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{true}\hspace{0.17em}\text{negative}\hspace{0.17em}\text{samples}}{\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{negative}\hspace{0.17em}\text{samples}}\right)$, such that the predictions for all isolates were combined. For 244 isolates with four replicates per isolate, the total number of samples used to calculate each of the described metrics was 976.

Environmental isolates: Prediction of genetic identity.

For the environmental isolates, we applied a threefold cross-validation procedure with holdout to optimize model parameters based on the prediction accuracy of the training set. To do this, we split the replicates for each unique strain into the validation set (three replicates), test set (three replicate), and training set (six replicates) and ran the SVM model on a set of hyperparameters. To train the model, we rotated through the replicates (except those in the validation set) such that each fold (consisting of three replicates) was used as the test set once. The average accuracy of the test sets across the three folds was used to optimize the model hyperparameters. Using the optimized model parameters, we predicted the accuracy of the validation set, which is reported in the main text (Results section). Additional details can be found in SI Appendix, section 1.4.

Keio collection (published data): Prediction of genetic identity.

For the published data of the Keio collection, we applied a threefold cross-validation procedure to optimize model parameters based on the prediction accuracy of the training set. To do this, we split the replicates for each unique strain into the test set (one replicate) and training set (two replicates) and ran the SVM model on a set of hyperparameters. We rotated through the replicates such that each was used as the test set once. The average accuracy of the test set across these three folds was used to optimize the model hyperparameters and was reported in the main text. Additional details can be found in SI Appendix, section 1.3.

Calculation of Phenotypic Distance.

We took the mean of all replicates (12 for environmental isolates and 4 for clinical isolates) of the time derivative of the growth curves. The final phenotypic distance between a pair of strains was defined as the Euclidean distance between their mean growth dynamics. In the main text (Results section), we used the time derivative of the growth curves from the 10,000× dilution growth condition. SI Appendix includes additional analysis where the phenotypic distance between pairs of strains was based on all possible combinations of growth conditions as well as using the growth rate as the phenotype (SI Appendix, section 2.2).

Processing of Whole-Genome Sequences.

SNP phylogeny: Clinical isolates.

SNPs were identified from genome assemblies or raw reads following the Nucleic Acid Structure Predictor (NASP) pipeline using E. coli strain EC958 (GenBank accession no. HG941718.1) as a reference (SI Appendix, Fig. S3.2) (56). Duplicated regions of the reference genome, including repeat regions and multiple gene copies, were determined by aligning the reference sequence to itself using NUCmer version 3.23 (57). SNPs that fell within these duplicate regions were excluded from further analysis to avoid false SNP calls due to ambiguous read alignment. Each query genome assembly was aligned to the reference with NUCmer version 3.23. Raw reads were adapter trimmed with Trimmomatic (58). Trimmed reads were aligned against a FASTA-formatted reference using Burrows-Wheeler Aligner Maximal Exact Matches (BWA-MEM) binary alignment map files created with Samtools version 1.2. SNPs were detected with GenomeAnalysisTK version 3.4, and the best SNPs in all genomes compared to the reference were concatenated in a matrix (59–61). A maximum-likelihood tree was inferred on the matrix with MEGA7 using the Tamura–Nei model (SI Appendix, SI Appendix 3.1) (41).

SNP phylogeny: Environmental isolates.

The genomic DNA of the environmental isolates were sequenced on the MGISEQ-2000 (BGI) platform to obtain about 100× clean data for each sample, and paired-end libraries with an insert size of 200 to 400 base pairs were constructed. We filtered out poor-quality reads with SOAPnuke (https://github.com/BGI-flexlab/SOAPnuke) and fastp (62). We assembled the clean reads with SPAdes version 3.13.0 and used MetaPhlan2 to identify the species of the isolates based on marker genes (63, 64). For the isolates unclassified by MetaPhlan2, MASH was used to find the closest species by distance estimation against NCBI RefSeq genomes, and the species was assigned when the top two hits were identical (65). Since the isolates were highly diverse, we grouped them by order (SI Appendix, Table S3.1). Phylogenetic analysis of each order was performed based on whole-genome SNPs following the NASP pipeline, and the reference was chosen according to SI Appendix, Table S3.1 (56). Duplicated regions of the reference genome, including repeat regions and multiple gene copies, were determined by aligning the reference sequence to itself using the NUCmer version 3.23. SNPs that fell within these duplicate regions were excluded from further analysis to avoid false SNP calls due to ambiguous read alignment. Each query genome assembly was aligned to the reference with NUCmer version 3.23. The best SNPs in all genomes, relative to the reference, were concatenated in a matrix. The pairwise distance analysis was inferred on the matrix with MEGA7 using the Tamura–Nei model (41, 66).

MLST phylogeny: Clinical isolates.

For MLST, we uploaded the assembled fasta files to MLST 2.0 on the Center for Genomic Epidemiology website (https://cge.cbs.dtu.dk/services/MLST/) and chose Escherichia coli #1 as the MLST configuration (31). The pairwise distance analysis was inferred with MEGA X using the Tamura–Nei model (41, 66).

Antibiotic resistance analysis.

We compiled a database with the sequences of resistance genes for four different antibiotic classes, including 477 genes for SAM, a β-lactam and β-lactamase inhibitor combination therapy; 272 genes for SXT, a sulfonamide and methoprim combination therapy; 166 genes for GM, an aminoglycoside; and 97 genes for CIP, a fluoroquinolone (SI Appendix, section 3.2). The whole-genome sequences of the clinical isolates were aligned against the database using Blast+(Nucleotide-Nucleotide BLAST 2.6.0+). The parameters for BLAST search were ≥95% gene identity and 50% sequence length of the resistance gene. The similarity between the antibiotic resistance gene in the database and the corresponding sequence in the genome, which means the percentage of alignment length (subtracting gaps and mismatches), was determined. BLAST results with expected values better than 10⁻²⁰ were considered to be significant (67). Additionally, we used two curated databases, CARD and ResFinder, to predict antimicrobial resistance using only perfect hits (47, 48). The first is a gene nucleotide sequence database, and the second is a gene product amino acid sequence database.

Correlation between Phenotypic and Phylogenetic Distance.

To examine the correlation between phylogenetic and phenotypic distance, we use the Mantel test, as implemented by Glerean et al. in the MATLAB package bramila_mantel (68). Both the phylogenetic distance and the phenotypic distance (per growth condition) are represented by a square distance matrix. To assess the statistical significance between these matrices, the bramila_mantel package uses the Mantel test by correlating the upper triangular matrix of the two and reports the Spearman coefficient (SI Appendix, section 2.2). The corresponding P values are obtained through a permutation test (5,000 iterations) which interpolates the density function from the permutations.

Data Availability.

The raw WGS data of the environmental isolate library described in this paper are publicly available at NCBI (accession no. PRJNA543692). The relevant data (plate reader experiments) and code that support the findings of this study are available in a Github repository (https://github.com/youlab/strain_prediction_CZ) (69).