Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Aug 23;15(10):5635–5641. doi: 10.1021/acs.jctc.9b00586

Applicability of Tail Corrections in the Molecular Simulations of Porous Materials

Kevin Maik Jablonka 1, Daniele Ongari 1, Berend Smit 1,*
PMCID: PMC7445744  PMID: 31442035

Abstract

graphic file with name ct9b00586_0006.jpg

Molecular simulations with periodic boundary conditions require the definition of a certain cutoff radius, rc, beyond which pairwise dispersion interactions are neglected. For the simulation of homogeneous phases the use of tail corrections is well-established, which can remedy this truncation of the potential. These corrections are built under the assumption that beyond rc the radial distribution function, g(r), is equal to one. In this work we shed some light on the discussion of whether tail corrections should be used in the modeling of heterogeneous systems. We show that for the adsorption of gases in a diverse set of nanoporous crystalline materials (zeolites, covalent organic frameworks, and metal–organic frameworks), tail corrections are a convenient choice to make the adsorption results less sensitive to the details of the truncation.

1. Introduction

Microporous materials are characterized by nanosized pores and large internal surface areas. These features have been exploited to separate1 and store gas molecules2 because of the attractive interactions between the molecules and the atoms of the frameworks. Further gas-related applications include catalysis3,4 and sensing.5

Metal–organic frameworks (MOFs), covalent organic frameworks (COFs),6 and zeolites7 are three classes of microporous materials that also have the quality of being crystalline, i.e., their unit cells repeat periodically, and the bulk materials can be typically represented by just a few hundreds of atoms. Tens of thousands of these microporous crystals have been reported in the literature,8−10 and many more have been generated in silico as potentially synthesizable structures.11−13 Finding the best material for any application related to the adsorption of some specific molecules, or understanding their property–performance relations, appears to be an increasingly vast combinatorial problem.14,15 Molecular simulations are a valuable tool to screen these materials, but they rely on accurate modeling of the gas–framework interaction and the methods of statistical thermodynamics to predict the thermodynamics properties that are used to identify promising materials among numerous candidates.16

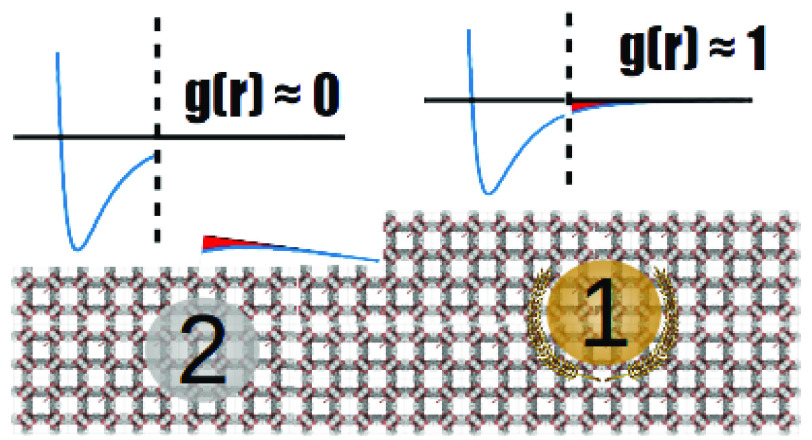
It is common in the modeling of gas adsorption in crystalline microporous materials to keep the geometry of the framework fixed17,18 and to model the adsorbate–gas and gas–gas interactions by dispersion interactions (e.g., Lennard-Jones or Buckingham potential) combined with Coulombic interactions between partial charges.19 When a reliable protocol is found for the modeling, it is important to provide a detailed description of this protocol,20 ideally in a findable, accessible, interoperable, and reusable (FAIR) way,21,22 including the parameters used for the dispersion interactions and their mixing rules and the charge-derivation method; this is referred to as the “force field” used in the model. Other important details should be included to fully describe the force field. These are the cutoff distance for the dispersion interactions, which is used to avoid computing the interaction between atoms that are so far apart that their interactions can be ignored; the truncation method (the choice of setting to zero the potential beyond the cutoff, shifting the entire potential to have a zero value at the cutoff distance, or the usage of a switching potential); and finally, whether tail corrections are applied or not. On this last point we focus our attention, to highlight the influence of tail corrections on the results and convergence behavior (with respect to the cutoff radius) in typical gas adsorption calculations. In this way, we address a question that is still debated in the literature: should tail correction be used for simulations of microporous crystals?23−25

In periodic simulations, one would like to avoid a particle interacting twice with the same portion of the space, and therefore, one typically imposes that the size of the simulation box is bigger than two times the cutoff radius.26 Consequently, in the case of microporous materials, one has to replicate the number of unit cells until this criterion is met, with a significant increase of the computational time for each replication due to the larger number of particles and therefore pairwise distances to compute. Thus, it is advisable to choose an adequate cutoff radius, which is a compromise between the desire to avoid large simulation boxes while preventing the neglect of significant interactions. For a long time, a cutoff radius not greater than 6–8 Å (i.e., around 2.5 times the typical Lennard-Jones σ) was normally employed,27 whereas in most of the recent simulations common cutoffs are in the range of 12–18 Å,28 thanks to faster computers.

For homogeneous systems, like liquids, it is usually assumed that one can correct for contributions above the cutoff using tail corrections, which are based on the assumption that the radial distribution function g(r) ≈ 1 for r ≥ rc.26 This means that one assumes that beyond the cutoff, particles are randomly displaced, and one can analytically compute their overall dispersion interactions with the bead. For example, the correction that applies to the popular Lennard-Jones 12–6 potential energy is29

1. 1

and similar expressions exist for the pressure and chemical potential. Even though there are special long-range correction schemes for surfaces30−32 and other geometries,33 tail corrections of the general form of eq 1 are still the most widely used ones.

It has been shown that these tail corrections can have a pronounced effect on the computed thermodynamics properties, such as the critical temperature of homogeneous particles.27,34 For heterogeneous systems, such as microporous crystals, however, the radial distribution function does not necessarily converge to one at rc, and therefore, the validity of the tail-correction approximation is matter of debate: Siperstein found that tail corrections might be applicable,23 whereas other authors24,25 state that they should not be used in microporous frameworks. This controversy motivated this work. To address the question of whether the use of tail corrections for adsorption in porous media is advisable, we consider the simple case of methane adsorption in microporous materials, where methane is modeled as a single bead particle interacting with a 12–6 Lennard-Jones potential, where Coulomb interactions can be neglected because they are small for methane adsorption. Here, we systematically study for a large set of structures (including MOFs, COFs, and zeolites) the effect of these tail corrections on commonly computed properties (e.g., the Henry coefficient, gas uptake at different pressures, and deliverable capacity).

2. Methods

2.1. Structure Selection

The simulations shown in this study were performed on a selection of 40 microporous crystals: 10 COFs from the revised CoRE-COF database, which Ongari et al. released as the CURATED-COFs database;10,35 10 zeolites from the IZA database;8 10 MOFs from the CoRE-MOF database;9 and 10 other common MOFs, chosen because of their popularity in computational studies.

We characterized all materials in these databases considering the following properties as descriptors of our pore–property space: accessible surface area, density, largest free sphere, number of channels, number of pockets, pocket surface area, and largest included sphere. These properties were calculated using the Zeo++ code,36 using a probe diameter of 1.86 Å and atomic diameters corresponding to the Lennard-Jones σ parameter of the force field. To rationally choose a diverse set of porous structures for our investigation, the first 30 frameworks were selected from their databases based on k-nearest neighbor clustering (with k = 10) in pore-property space, as implemented in our structure-comp python package.37 After knn clustering in property space, the samples closest to the k centroids are selected for the study, which ensures that we do not miss any cluster that may exist in the hyperspace of geometrical properties.

2.2. Monte Carlo Simulations

We used the AiiDA package38 to design a reproducible workflow for the Monte Carlo (MC) simulations, which were performed using the RASPA39 code. In our workflow, we performed all the simulations at 298 K, considering a single-bead methane particle (with methane–methane interactions described by the TraPPE united-atom model).40

Simulations, with and without the tail corrections, were run at different cutoffs, in the range of 6–30 Å. All relative errors shown in the following are computed relative to the values at a cutoff radius of 24 Å. The absolute values of all properties are shown in the Supporting Information and indicate that most simulations are well-converged for cutoff radii above 20 Å. We performed 300 000 Widom insertions41 to calculate the Henry coefficients KH at infinite dilution. Grand-canonical Monte Carlo (GCMC) simulations were used to evaluate the uptake at 5.8, 35, and 65 bar. We used the Peng–Robinson equation of state to convert the pressure to the corresponding fugacity.42 We used 15 000 cycles for equilibration and 15 000 for production. We found the number of MC cycles sufficient to give small error bars compared to the error due to the truncation of the potential (compare the absolute values in the Supporting Information). NVT ensemble simulations with a single methane bead were employed to calculate the radial distribution function inside the frameworks, considering rc = 20 Å.

To model the interaction with the frameworks, we used the DREIDING force field,43 where, for the missing elements (Cd, Cu, Mg, Sr, Ti, and Zr), we added the Lennard-Jones parameters from the UFF force field.44 We applied Lorentz–Berthelot mixing rules to compute the interaction parameters. For all simulations shown in the main text we blocked inaccessible pores.45,46 Given that some structures from our selection have nonpermeable pores, as determined using the Zeo++ code,47,48 we also performed simulations without pore blocking and discuss them in the Supporting Information.

3. Results and Discussion

3.1. Error Bounds

In the following, we discuss the error in the potential energy that comes from truncating the pairwise potential. This error is directly related to the radial distribution function for the adsorbed particles in the microporous material. For a pairwise potential of the form

3.1. 2

the average potential energy in the canonical ensemble, ⟨U⟩, can be written as a double integral over the product of the pair–correlation function, g(2), given as the ensemble average over pair–correlations of positions

3.1. 3

and the pairwise energy term u(|ri – rj|):49

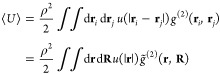3.1. 4

Here, ρ = N/V is the number density of particles, and we changed the variables to center-of-mass R = (ri + rj)/2 and relative coordinates r = ri – rj. Note that the more popular radial distribution function, g(r), is obtained by integrating the pair-correlation function, g̃(2)(r, R), over the center-of-mass positions R and the spherical angles ϕ and θ

3.1. 5

The error in the potential energy due to the truncation, εtrunc., that one introduces by neglecting the interactions beyond a cutoff, i.e., for |r| > rc, is

3.1. 6

We can rearrange the equation using the mean-value theorem. To do so, we assume that both the potential u(|r|) and the pair–correlation function g̃(2)(r, R) are continuous over the range of integration, and we introduce a new upper boundary of integration, p, to approximate the indefinite integral with a definite integral. This new upper boundary of integration, p, is large enough such that u(|p|) = 0 (i.e., |p| → ∞). Finally, we define a value ξ ∈ [rc, p] for the relative distances, and we rewrite the error as

3.1. 7

The tail corrections are based on the assumption that g̃(2)(r, R) = 1 for r ≥ rc; hence, the error εt.c. on the potential energy can be written as

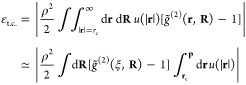3.1. 8

Comparing eq 8 with eq 7, we see that the error using tail correction is in general smaller than for the simple truncation if ∫dRg̃(2)(ξ, R) > 0.5, ∀ ξ. In terms of the radial distribution function, this corresponds to g(r) > 0.5 ∀ r > rc; if this is the case, one can be confident that the use of homogeneous tail corrections, instead of simple truncation, is the more accurate choice. We will show in the following sections that this is the case for all the microporous materials that we selected for this study and that have permeable pores, as well as for the simulations of Macedonia and Maginn,25 who were the first to question the applicability of tail corrections in porous systems.

3.2. Proof of Concept on a Simplified Model

As a numeric example of the behavior of tail corrections in crystalline materials, we first start recalling the simple case of a Lennard-Jones fluid with the well-known pair potential

3.2. 9

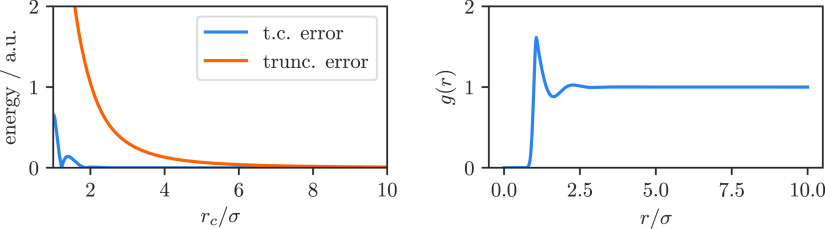
for which we can use a parametrization of the radial distribution function from Matteolia et al.34Figure 1 illustrates that the tail correction gives us an estimate of the energy that is less sensitive to the cutoff radius, i.e., we have εtrunc. > εt.c. for the physical sensible region of rc > σ.

Figure 1.

Figure 1

Open in a new tab

Error for truncated potential (trunc. error) and truncation with tail correction (t. c. error) for a Lennard-Jones fluid.

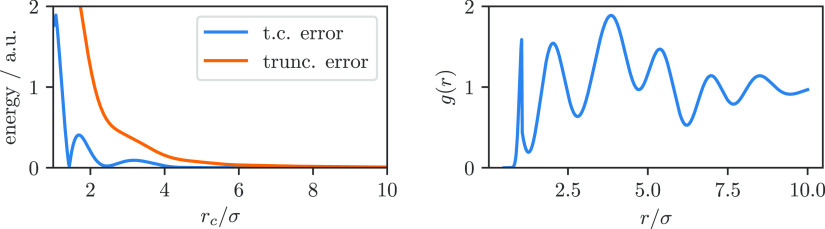
We can now perturb the radial distribution function from Matteolia et al. to imitate the behavior in a crystal, i.e. by using a smaller exponential decay and adding additional oscillations (see the Supporting Information) as shown in Figure 2. Note that similar approximations have already been used in the literature to describe porous materials, e.g., aluminum oxide.50,51

Figure 2.

Figure 2

Open in a new tab

Error for truncated potential (trunc. error) and truncation with tail correction (t. c. error) for a perturbed Lennard-Jones fluid.

In ref (25), Macedonia and Maginn make the case that for the tail correction to be exact g(r) must converge to one for sufficiently large r. Here, we take a slightly different point of view in the sense that we show that the errors related to different values of the cutoff radius are smaller if we use a tail correction rather than simple truncation for which different groups use different values of the cutoff radius. For periodic systems, where g(r1, r2) = g(r1 + Ri, r2 + Ri) ∀ Ri, and where the Ri form a Bravais lattice,52 one might intuitively expect some error compensation due to the oscillatory nature of g(r), and still, it is not clear a priori to what extent this is the case in porous materials. However, we could show in this perturbed model that, even when the periodicity is broken, one can still find that the simulations with tail corrections are less sensitive to the cutoff radius of the truncation (see Figure 2).

3.3. Framework-CH4 Radial Distribution Functions

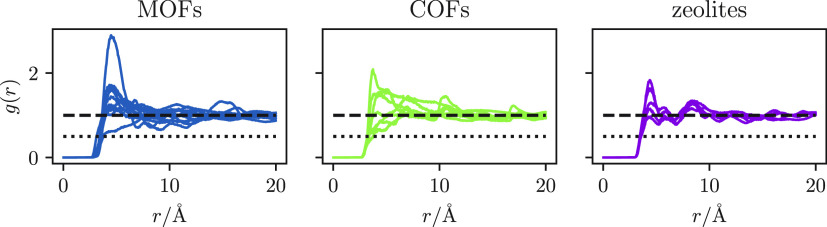
In Figure 3 we show the framework-CH4 radial distribution functions in the limit of infinite dilution (i.e., one particle per unit cell) for all the microporous materials in our set that have pores that are accessible to our methane bead.

Figure 3.

Figure 3

Open in a new tab

CH4-framework radial distribution functions. Dashed lines indicate g(r) = 1; dotted lines indicate g(r) = 0.5.

We observe that, within 20 Å, most of the radial distribution functions do not converge to g(r) ≈ 1. Additionally, we also observe for all the structures with accessible pores that g(r) > 0.5 (we discuss the cases with nonaccessible cases in the Supporting Information), which is the threshold we derived by comparing eq 8 with eq 7 and indicates that the use of tail corrections should be a more appropriate choice, if compared to simple truncation.

3.4. Convergence of Henry Coefficient at Different Pressures

For the Henry coefficient, KH, we can write

3.4. 10

with
3.4. 11

These expressions show that the Henry coefficients depend exponentially on the tail correction,23 and therefore, they are a useful probe to study the influence of the tail correction on simulation results.

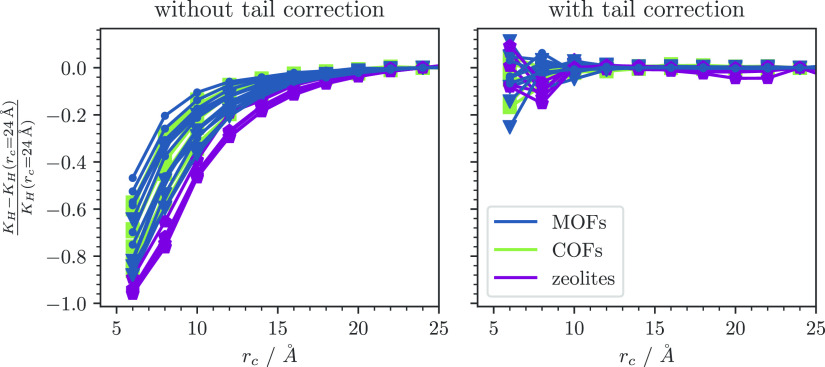
For all structures, we find that KH – KH,converged is smaller with tail corrections than without (cf. Figure 4), especially at cutoff radii around 12 Å, which are commonly used in current molecular simulations. We also find that the converged results of simulations with and without tail corrections are identical within the error of the simulations (cf. details in the Supporting Information). In the Supporting Information we also demonstrate that the more desirable convergence behavior with respect to the cutoff can also be found for the more complex cases of adsorption of water and longer alkanes.

Figure 4.

Figure 4

Open in a new tab

Convergence of the Henry coefficient KH as a function of the cutoff distance with and without tail corrections. We show the relative error due to the large spread of Henry coefficients and give the absolute values in the Supporting Information.

3.5. Convergence of Methane Loading at Different Pressures

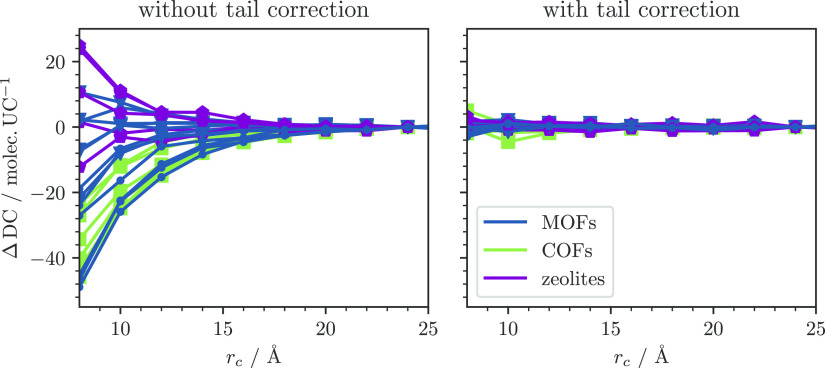
To further illustrate the applicability of tail corrections, we compared real-case adsorption simulations of methane to assess the effect of tail corrections at different cutoff radii. The actual application property for gas storage, the deliverable capacity DC, is defined as the difference between the amount of methane stored at storage pressure and the methane that remains at depletion pressure, DC65 bar,5.8 bar = θ65 bar – θ5.8 bar, where we have chosen the depletion pressure set by the Advanced Research Projects Agency-Energy (ARPA-E) of the US Department of Energy that is part of the design target to make adsorbed natural gas storage competitive with compressed natural gas storage.53,54

Also for this property we find that simulations with tail corrections generally show a more desirable convergence behavior with respect to the cutoff than simulations without tail corrections (cf. Figure 5).

Figure 5.

Figure 5

Open in a new tab

Convergence of deliverable capacities DC65 bar,5.8 bar as a function of the cutoff distance with and without tail corrections. ΔDC = DC(rc) – DC(rc = 24 Å).

Notably, in the case of deliverable capacity, the error coming from the truncation (without tail corrections) can lead to both an overestimation or underestimation, while, when considering the total uptake at a certain pressure, the truncation leads to weaker interactions and always lower values (see the Supporting Information).

Because it is common for high-throughput screenings for methane deliverable capacity to employ cutoffs around 12 Å, the findings from Figure 5 indicate the use of tail correction might be a preferable choice for these studies. Indeed, the deliverable capacity is, in all the cases, less sensitive to the choice of the cutoff. In contrast, simulations with truncated potentials lead to nonsystematic deviations of around 10% from the cutoff-converged results.

4. Conclusions

In this work we investigated, for microporous frameworks, the influence of tail corrections on the convergence behavior of gas adsorption properties with respect to the truncation radius of the pairwise dispersion potential. We found that for most of the systems, the strict condition g(r) > 0.5 ∀ r > rc holds, and homogeneous tail corrections give results that are far less sensitive to the details of the truncation of the potential (e.g., the cutoff radius) and therefore are the preferable choice. These findings are proven to be valid for a test set of diverse structures, including zeolites, metal–organic frameworks, and covalent organic frameworks.

Given that there is no commonly agreed cutoff for the potential, we recommend the use of tail corrections when modeling gas adsorption in microporous materials in order to allow for a more consistent direct comparison of the results from different simulation studies.

Acknowledgments

The research of D.O. and B.S. was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 666983, MaGic). K.M.J. acknowledges his scholarships from the Alfred-Werner fund of the Swiss chemical society and the German Academic Scholarship Foundation.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.9b00586.

  • Additional sampling and simulation information and the converged properties for simulations with and without tail corrections (PDF)

The authors declare no competing financial interest.

Notes

The AiiDA workchain and database are available on the Materials Cloud Archive (https://archive.materialscloud.org/2019.0024), and the results can be interactively explored in the Materials Cloud Discover section (https://www.materialscloud.org/discover/tc-applicability).

Supplementary Material

ct9b00586_si_001.pdf (6.6MB, pdf)

References

  1. Li J.-R.; Kuppler R. J.; Zhou H.-C. Selective Gas Adsorption and Separation in Metal–Organic Frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. 10.1039/b802426j. [DOI] [PubMed] [Google Scholar]
  2. Morris R. E.; Wheatley P. S. Gas Storage in Nanoporous Materials. Angew. Chem., Int. Ed. 2008, 47, 4966–4981. 10.1002/anie.200703934. [DOI] [PubMed] [Google Scholar]
  3. Lee J.; Farha O. K.; Roberts J.; Scheidt K. A.; Nguyen S. T.; Hupp J. T. Metal–Organic Framework Materials as Catalysts. Chem. Soc. Rev. 2009, 38, 1450–1459. 10.1039/b807080f. [DOI] [PubMed] [Google Scholar]
  4. Weckhuysen B. M.; Yu J. Recent Advances in Zeolite Chemistry and Catalysis. Chem. Soc. Rev. 2015, 44, 7022–7024. 10.1039/C5CS90100F. [DOI] [PubMed] [Google Scholar]
  5. Kreno L. E.; Leong K.; Farha O. K.; Allendorf M.; Van Duyne R. P.; Hupp J. T. Metal–Organic Framework Materials as Chemical Sensors. Chem. Rev. 2012, 112, 1105–1125. 10.1021/cr200324t. [DOI] [PubMed] [Google Scholar]
  6. Feng X.; Ding X.; Jiang D. Covalent Organic Frameworks. Chem. Soc. Rev. 2012, 41, 6010–6022. 10.1039/c2cs35157a. [DOI] [PubMed] [Google Scholar]
  7. Li Y.; Yu J. New Stories of Zeolite Structures: Their Descriptions, Determinations, Predictions, and Evaluations. Chem. Rev. 2014, 114, 7268–7316. 10.1021/cr500010r. [DOI] [PubMed] [Google Scholar]
  8. Baerlocher C.; McCusker L. Database of Zeolite Structures. 2016; http://www.iza-structure.org/databases/ (accessed March 15, 2019).
  9. Nazarian D.; Camp J. S.; Chung Y. G.; Snurr R. Q.; Sholl D. S. Large-Scale Refinement of Metal-Organic Framework Structures Using Density Functional Theory. Chem. Mater. 2017, 29, 2521–2528. 10.1021/acs.chemmater.6b04226. [DOI] [Google Scholar]
  10. Tong M.; Lan Y.; Yang Q.; Zhong C. Exploring the Structure-Property Relationships of Covalent Organic Frameworks for Noble Gas Separations. Chem. Eng. Sci. 2017, 168, 456–464. 10.1016/j.ces.2017.05.004. [DOI] [Google Scholar]
  11. Wilmer C. E.; Leaf M.; Lee C. Y.; Farha O. K.; Hauser B. G.; Hupp J. T.; Snurr R. Q. Large-Scale Screening of Hypothetical Metal–Organic Frameworks. Nat. Chem. 2012, 4, 83–89. 10.1038/nchem.1192. [DOI] [PubMed] [Google Scholar]
  12. Martin R. L.; Simon C. M.; Smit B.; Haranczyk M. In Silico Design of Porous Polymer Networks: High-Throughput Screening for Methane Storage Materials. J. Am. Chem. Soc. 2014, 136, 5006–5022. 10.1021/ja4123939. [DOI] [PubMed] [Google Scholar]
  13. Mercado R.; Fu R.-S.; Yakutovich A. V.; Talirz L.; Haranczyk M.; Smit B. In Silico Design of 2D and 3D Covalent Organic Frameworks for Methane Storage Applications. Chem. Mater. 2018, 30, 5069–5086. 10.1021/acs.chemmater.8b01425. [DOI] [Google Scholar]
  14. Kirkpatrick P.; Ellis C. Chemical Space. Nature 2004, 432, 823–823. 10.1038/432823a. [DOI] [Google Scholar]
  15. Yaghi O. M.; O’Keeffe M.; Ockwig N. W.; Chae H. K.; Eddaoudi M.; Kim J. Reticular Synthesis and the Design of New Materials. Nature 2003, 423, 705–714. 10.1038/nature01650. [DOI] [PubMed] [Google Scholar]
  16. Colón Y. J.; Snurr R. Q. High-Throughput Computational Screening of Metal–Organic Frameworks. Chem. Soc. Rev. 2014, 43, 5735–5749. 10.1039/C4CS00070F. [DOI] [PubMed] [Google Scholar]
  17. Smit B.; Maesen T. L. M. Molecular Simulations of Zeolites: Adsorption, Diffusion, and Shape Selectivity. Chem. Rev. 2008, 108, 4125–4184. 10.1021/cr8002642. [DOI] [PubMed] [Google Scholar]
  18. Coudert F.-X.; Fuchs A. H. Computational Characterization and Prediction of Metal–Organic Framework Properties. Coord. Chem. Rev. 2016, 307, 211–236. 10.1016/j.ccr.2015.08.001. [DOI] [Google Scholar]
  19. Ongari D.; Boyd P. G.; Kadioglu O.; Mace A. K.; Keskin S.; Smit B. Evaluating Charge Equilibration Methods To Generate Electrostatic Fields in Nanoporous Materials. J. Chem. Theory Comput. 2019, 15, 382–401. 10.1021/acs.jctc.8b00669. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Coudert F.-X. Reproducible Research in Computational Chemistry of Materials. Chem. Mater. 2017, 29, 2615–2617. 10.1021/acs.chemmater.7b00799. [DOI] [Google Scholar]
  21. Wilkinson M. D.; Dumontier M.; Aalbersberg I. J.; Appleton G.; Axton M.; Baak A.; Blomberg N.; Boiten J.-W.; da Silva Santos L. B.; Bourne P. E.; Bouwman J.; Brookes A. J.; Clark T.; Crosas M.; Dillo I.; Dumon O.; Edmunds S.; Evelo C. T.; Finkers R.; Gonzalez-Beltran A.; Gray A. J. G.; Groth P.; Goble C.; Grethe J. S.; Heringa J.; ’t Hoen P. A. C.; Hooft R.; Kuhn T.; Kok R.; Kok J.; Lusher S. J.; Martone M. E.; Mons A.; Packer A. L.; Persson B.; Rocca-Serra P.; Roos M.; van Schaik R.; Sansone S.-A.; Schultes E.; Sengstag T.; Slater T.; Strawn G.; Swertz M. A.; Thompson M.; van der Lei J.; van Mulligen E.; Velterop J.; Waagmeester A.; Wittenburg P.; Wolstencroft K.; Zhao J.; Mons B. The FAIR Guiding Principles for Scientific Data Management and Stewardship. Sci. Sci. Data 2016, 3, 160018. 10.1038/sdata.2016.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pizzi G.. In Handbook of Materials Modeling; Andreoni W., Yip S., Eds.; Springer International Publishing: Cham, 2018; pp 1–24. [Google Scholar]
  23. Siperstein F.; Myers A. L.; Talu O. Long Range Corrections for Computer Simulations of Adsorption. Mol. Phys. 2002, 100, 2025–2030. 10.1080/00268970110109916. [DOI] [Google Scholar]
  24. Dubbeldam D.; Torres-Knoop A.; Walton K. S. On the Inner Workings of Monte Carlo Codes. Mol. Simul. 2013, 39, 1253–1292. 10.1080/08927022.2013.819102. [DOI] [Google Scholar]
  25. Macedonia M. D.; Maginn E. J. A Biased Grand Canonical Monte Carlo Method for Simulating Adsorption Using All-Atom and Branched United Atom Models. Mol. Phys. 1999, 96, 1375–1390. 10.1080/00268979909483082. [DOI] [Google Scholar]
  26. Allen M. P.; Tildesley D. J.. Computer Simulation of Liquids, reprinted ed.; Clarendon Press: Oxford, 2009. [Google Scholar]
  27. Smit B. Phase Diagrams of Lennard-Jones Fluids. J. Chem. Phys. 1992, 96, 8639–8640. 10.1063/1.462271. [DOI] [Google Scholar]
  28. Glover T. G. Gas Adsorption in Metal-Organic Frameworks: Fundamentals and Applications, 1st ed.; CRC Press: Boca Raton, FL, 2018. [Google Scholar]
  29. Frenkel D.; Smit B. In Understanding Molecular Simulation, 2nd ed.; Frenkel D., Smit B., Eds.; Academic Press: San Diego, 2002; pp 23–61. [Google Scholar]
  30. de Gregorio R.; Benet J.; Katcho N. A.; Blas F. J.; MacDowell L. G. Semi-Infinite Boundary Conditions for the Simulation of Interfaces: The Ar/CO2(s) Model Revisited. J. Chem. Phys. 2012, 136, 104703. 10.1063/1.3692608. [DOI] [PubMed] [Google Scholar]
  31. Werth S.; Rutkai G.; Vrabec J.; Horsch M.; Hasse H. Long-Range Correction for Multi-Site Lennard-Jones Models and Planar Interfaces. Mol. Phys. 2014, 112, 2227–2234. 10.1080/00268976.2013.861086. [DOI] [Google Scholar]
  32. Shen V. K.; Mountain R. D.; Errington J. R. Comparative Study of the Effect of Tail Corrections on Surface Tension Determined by Molecular Simulation. J. Phys. Chem. B 2007, 111, 6198–6207. 10.1021/jp070374f. [DOI] [PubMed] [Google Scholar]
  33. Wilding N. B.; Schoen M. Absence of Simulation Evidence for Critical Depletion in Slit Pores. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1999, 60, 1081–1083. 10.1103/PhysRevE.60.1081. [DOI] [PubMed] [Google Scholar]
  34. Matteoli E.; Mansoori G. A. A Simple Expression for Radial Distribution Functions of Pure Fluids and Mixtures. J. Chem. Phys. 1995, 103, 4672–4677. 10.1063/1.470654. [DOI] [Google Scholar]
  35. Ongari D.; Yakutovich A. V.; Talirz L.; Smit B.. Building a consistent and reproducible database for adsorption evaluation in Covalent-Organic Frameworks. 2019; https://archive.materialscloud.org/2019.0034/v1. [DOI] [PMC free article] [PubMed]
  36. Willems T. F.; Rycroft C. H.; Kazi M.; Meza J. C.; Haranczyk M. Algorithms and Tools for High-Throughput Geometry-Based Analysis of Crystalline Porous Materials. Microporous Mesoporous Mater. 2012, 149, 134–141. 10.1016/j.micromeso.2011.08.020. [DOI] [Google Scholar]
  37. Jablonka K. M.; Ongari D.; Smit B. structure comp; 2019; https://github.com/kjappelbaum/structure_comp. [DOI] [PMC free article] [PubMed]
  38. Pizzi G.; Cepellotti A.; Sabatini R.; Marzari N.; Kozinsky B. AiiDA: Automated Interactive Infrastructure and Database for Computational Science. Comput. Mater. Sci. 2016, 111, 218–230. 10.1016/j.commatsci.2015.09.013. [DOI] [Google Scholar]
  39. Dubbeldam D.; Calero S.; Ellis D. E.; Snurr R. Q. RASPA: Molecular Simulation Software for Adsorption and Diffusion in Flexible Nanoporous Materials. Mol. Simul. 2016, 42, 81–101. 10.1080/08927022.2015.1010082. [DOI] [Google Scholar]
  40. Martin M. G.; Siepmann J. I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. 10.1021/jp972543+. [DOI] [Google Scholar]
  41. Widom B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. 10.1063/1.1734110. [DOI] [Google Scholar]
  42. Peng D.-Y.; Robinson D. B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. 10.1021/i160057a011. [DOI] [Google Scholar]
  43. Mayo S. L.; Olafson B. D.; Goddard W. A. DREIDING: A Generic Force Field for Molecular Simulations. J. Phys. Chem. 1990, 94, 8897–8909. 10.1021/j100389a010. [DOI] [Google Scholar]
  44. Rappe A. K.; Casewit C. J.; Colwell K. S.; Goddard W. A.; Skiff W. M. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. 10.1021/ja00051a040. [DOI] [Google Scholar]
  45. Bates S. P.; van Well W. J. M.; van Santen R. A.; Smit B. Energetics of n - Alkanes in Zeolites: A Configurational-Bias Monte Carlo Investigation into Pore Size Dependence. J. Am. Chem. Soc. 1996, 118, 6753–6759. 10.1021/ja953856q. [DOI] [Google Scholar]
  46. Gómez-Alvarez P.; Ruiz-Salvador A. R.; Hamad S.; Calero S. Importance of ´ Blocking Inaccessible Voids on Modeling Zeolite Adsorption: Revisited. J. Phys. Chem. C 2017, 121, 4462–4470. 10.1021/acs.jpcc.7b00031. [DOI] [Google Scholar]
  47. Haranczyk M.; Sethian J. A. Automatic Structure Analysis in High-Throughput Characterization of Porous Materials. J. Chem. Theory Comput. 2010, 6, 3472–3480. 10.1021/ct100433z. [DOI] [PubMed] [Google Scholar]
  48. Ongari D.; Boyd P. G.; Barthel S.; Witman M.; Haranczyk M.; Smit B. Accurate Characterization of the Pore Volume in Microporous Crystalline Materials. Langmuir 2017, 33, 14529–14538. 10.1021/acs.langmuir.7b01682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Tuckerman M. E.Statistical Mechanics: Theory and Molecular Simulation; Oxford University Press: Oxford, 2010. [Google Scholar]
  50. Cherkas N. L.; Cherkas S. L. Smeared Lattice Model as a Framework for Order to Disorder Transitions in 2D Systems. Crystals 2018, 8, 290. 10.3390/cryst8070290. [DOI] [Google Scholar]
  51. Behnke J. F.; Sands T. Bimodal Spatial Distribution of Pores in Anodically Oxidized Aluminum Thin Films. J. Appl. Phys. 2000, 88, 6875–6880. 10.1063/1.1321780. [DOI] [Google Scholar]
  52. McCarley J. S.; Ashcroft N. W. Correlation Functions in Classical Solids. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1997, 55, 4990–5003. 10.1103/PhysRevE.55.4990. [DOI] [Google Scholar]
  53. Simon C. M.; Kim J.; Gomez-Gualdron D. A.; Camp J. S.; Chung Y. G.; Martin R. L.; Mercado R.; Deem M. W.; Gunter D.; Haranczyk M.; Sholl D. S.; Snurr R. Q.; Smit B. The Materials Genome in Action: Identifying the Performance Limits for Methane Storage. Energy Environ. Sci. 2015, 8, 1190–1199. 10.1039/C4EE03515A. [DOI] [Google Scholar]
  54. U.S. Department of Energy/ARPA-E. MOVE: Methane Opportunities for Vehicular Energy. 2012; http://arpa-e.energy.gov/?q=arpa-e-programs/move (accessed May, 10 2019).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct9b00586_si_001.pdf (6.6MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES