Evaluating β-amyloidosis progression in Alzheimer’s disease with Mueller polarimetry

Abstract

We applied the wide-field Mueller imaging polarimetry for the screening of formalin-fixed paraffin-embedded samples of mouse brain tissue at different stages of brain β-amyloidosis in Alzheimer’s disease (AD). The accumulation of amyloid-beta (Aβ) deposits throughout the brain tissue is one of the key pathological hallmarks observed with the AD progression. We demonstrate that the presence of Aβ plaques influences the properties of backscattered polarized light, in particular, its degree of depolarization. By means of statistical analysis, we demonstrate that the high-order statistical moments of depolarization distributions, acquired with the multi-spectral Mueller imaging polarimetry, can be used as sensitive markers of the growing presence of Aβ plaques. The introduced label-free polarimetric approach has a potential to facilitate the current practice of the histopathology screening in terms of diagnosis accuracy, time and cost efficiency.

1. Introduction

Due to the ongoing aging of the population, dementia has become one of the major social and financial burdens in the modern world [1,2]. In 2015, the total number of people with dementia worldwide was estimated at 46M and was predicted to raise up to 115.4M by the year 2050 [2]. The Alzheimer’s disease (AD) is the most frequent cause of dementia [2]; therefore, there is a growing demand for the improving of diagnosis and treatment of AD.

The major hallmarks of the AD are the accumulation of extracellular senile plaques composed of amyloid-beta (Aβ) and intracellular neurofibrillary tangles composed of hyperphosphorylated tau protein accompanied by neuronal cell losses throughout grey matter and hippocampi [3]. Clinical diagnostics of AD is performed with the use of computed tomography (CT), magnetic resonance imaging (MRI), positron emission tomography (PET), and single-photon emission computed tomography (SPECT) [1]. However, these techniques are restricted by the spatial resolution of minimum 100-200 µm [4,5], which limits their accuracy. Therefore, in order to assess a detailed structure of brain tissue, there is a need for the histological analysis, which currently is the only technique that provides definite diagnosis of AD (post mortem). Standard routine procedure of histological analysis implies laborious sample preparation, which includes fixation of the brain in 4% formalin for 1–3 weeks (depending on the brain size), sectioning and processing of the fixed tissue, dehydration, embedding in paraffin, thin sectioning of the obtained formalin-fixed paraffin-embedded (FFPE) tissue block with a microtome, mounting the acquired thin brain slices on a glass slide, staining, and finally microscopic investigation of the thin tissue sections. This protocol is very costly and time-consuming, depends strongly on the pathologist skills and provides only qualitative information. Thus, there is a need for a new label-free and less labor-intensive technique, which in the future could be enhanced with machine learning algorithms to improve the diagnosis accuracy.

Among the cutting-edge research, a number of techniques based on optical microscopy have shown promising results in label-free visualization of senile plaques in thin slices of fixed brain tissue. The examples are optical coherence microscopy (OCM) [6], polarization-sensitive optical coherence microscopy (PS-OCM) [7], diffraction phase microscopy (DPM) [8], multiphoton microscopy [9], cryo-micro-optical sectioning tomography (cryo-MOST) [10], stimulated Raman scattering (SRS) microscopy [11]. It has been shown that the structural changes, in particular, Aβ plaques are mostly observed in the grey matter and hippocampi, whereas the changes in the white matter are minor [8]. Moreover, it has been demonstrated that the brain tissue with AD exhibits higher inhomogeneity of refractive index, higher scattering coefficient, higher birefringence due to parallel alignment of fibrils in Aβ plaques and higher anisotropy of scattering [7,8]. Though the abovementioned techniques allow label-free imaging of brain tissue with sub-micron resolution, they require sectioning the FFPE tissue block into thin slices. In the current study, we examine the bulk mouse brain tissue in the FFPE block (without cutting it in thin sections) by using optical wide-field imaging Mueller polarimetric technique.

The use of imaging and characterization techniques based on polarization of light in biomedical research has been growing during the past several years [12]. In particular, imaging Mueller matrix (MM) polarimetry is a powerful approach, which has shown very promising results in functional characterization of various types of tissues. The technique is based on measuring the 4 × 4 MM of a sample. All elements of MM are real numbers, MM contains full information on polarimetric properties of the sample in the absence of non-linear effects. In the recently published studies, MM polarimetry has been applied to differentiating the polycrystalline structure of healthy and pathologically altered tissues of myocardium [13], characterization of rectum wall tissue, vaginal wall during genital prolapse, brain tissue [14], detection of healthy and pre-cancerous regions of uterine cervix tissue [15–17], blood films characterization for cancer diagnosis [18], detection of cancer of colorectal tissue [19,20] and characterization of other tissues [21,22]. Other polarization-based techniques, such as Stokes polarimetry based on circularly polarized illumination [23,24], Jones-matrix tomography [25,26], Stokes correlometry [27] were also widely used for the characterization of various tissues.

In this study, we used MM polarimetry to investigate the possibility of express screening of brain tissue in FFPE blocks with progressing structural malformations caused by AD. The aim of this study was the proof of concept of possibility to develop a fast label-free cost-effective express screening technique for pathology analysis and quantitative scoring of FFPE brain tissue blocks with AD based on the wide-field imaging MM polarimetry operating in the visible spectrum range. To enhance the diagnostic accuracy of MM polarimetry, we applied statistical analysis of polarimetric parameters. This approach was also used in previous studies [13,14,18,20,28].

2. Method and materials

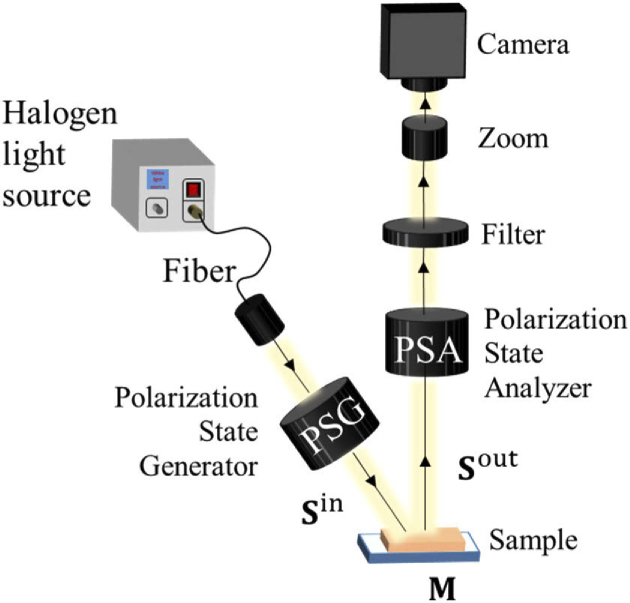
The multi-wavelength liquid-crystal-based imaging MM system operating in backscattering geometry [29,30] was developed in the LPICM, Ecole polytechnique, France. The schematic of the setup is shown in Fig. 1. The polarization of the light emitted by the halogen light source is modulated by the Polarization State Generator (PSG), which consists of a linear polarizer and two electrically driven liquid crystals. The polarization state of incident light beam is changed due to the interaction with a sample. Light, backscattered from a sample, passes through the polarization state analyzer (PSA), which consists of the same optical components as PSG, but assembled in a reversed order. A spectral wheel with 6 bandpass filters (20 nm bandwidth centered at 450–550 nm with a 50 nm step) is placed in front of the CCD camera. During the measurements, four different polarization states of light are sequentially generated by PSG. For each polarization state of the illuminating beam, the PSA, modulated sequentially to one of the same four polarization states, transmits the backscattered light, thus, forming 16 different intensity images on the CCD camera. These 16 raw intensity images are processed using the calibration data of the system obtained prior to measurements to get a MM of a sample. The light incidence angle is about 15° from normal; the CCD camera is placed at normal to the sample measurement plane. The measured samples were covered with index matching liquid (refractive oil) in order to flatten the top surface and reduce the artifacts associated with specular reflection. The elements of MM were normalized by m11, representing dimensionless quantities varying from -1 to 1. The interpretation of the MM of mouse brain samples was performed using Lu-Chipman decomposition algorithm [31] that represents any physically realizable MM as a product of three matrices of basic optical elements, namely, diattenuator, retarder and depolarizer.

Fig. 1.

Schematic presentation of the custom-built MM imaging polarimeter [29,30]. Further details are given in the text.

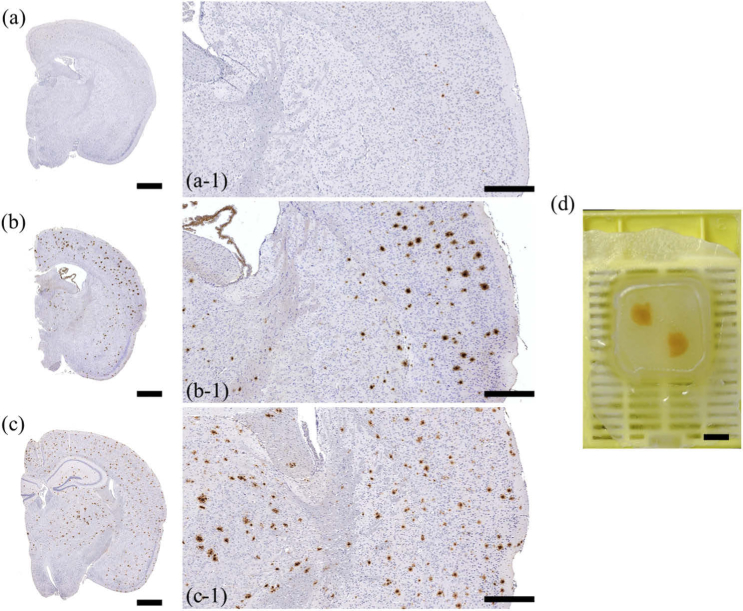
In the current study, we investigated 21 FFPE mouse brain tissue specimens. All protocols involving the breeding and use of animals were approved by the Norwegian Food Safety (Mattilsynet). All study procedures were performed in accordance with the European Communities Council Directive of September 22, 2010 (2010/63/EU). The brain hemispheres were excised from sacrificed APP-transgenic mice (APPPS-21, APPtg) [32] at different ages: 50, 75, 100, 125, 150, 175, and 200 days (3 samples per each AD stage). The stage of the β-amyloidosis correlates with the age of animals. The animals start with Aβ deposition at an age of 45 days. Figures 2(a, a-1), 2(b, b-1), 2(c, c-1) show histological images of the brain cuts of mice of different age, obtained with the help of immunohistochemistry (IHC) techniques [33–36] and a conventional optical microscope. Figures 2(a, a-1) show the histology images of a 50-days old mouse, while Figs. 2(b, b-1) and 2(c, c-1) show the histology images of a 125-days old and 200-days old mice, respectively. Figures 2(a-1), 2(b-1), 2(c-1) show magnified images from Figs. 2(a), 2(b), 2(c). Aβ plaques are observed in Figs. 2(b, b-1) and 2(c, c-1) as dark brown spots throughout the brain tissue due to IHC staining. The increased amount of Aβ plaques correlates with a more advanced AD stage. Each of the FFPE blocks contains two mouse brain hemispheres [see a photograph of a FFPE block in Fig. 2(d)].

Fig. 2.

Images of mouse brain specimens: (a, a-1) Histological images of the brain slices of a 50-day-old, (b, b-1) a 125-day-old, and (c, c-1) a 200-day-old mouse with AD. Panels (a-1, b-1, c-1) show magnified images in (a, b, c). (d) A photograph of a FFPE block. Scale bars: (a, b, c) 1 mm, (a-1, b-1, c-1) 500 µm, (d) 5 mm.

3. Mueller matrix imaging of brain tissue with AD

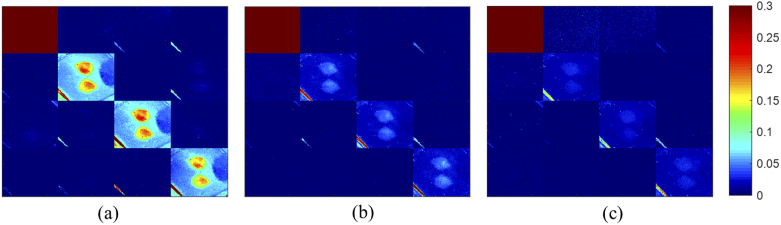
The MM images of one FFPE brain sample of a 75-days old mouse obtained with the wide-field MM polarimeter at 450, 500, and 550 nm central wavelength are shown in Figs. 3(a)–3(d). For all FFPE brain samples screened in the current study, the corresponding MM demonstrated similar structure as shown in Fig. 3. As it was shown in Fig. 2(d), each FFPE tissue block contained the brain tissue and surrounding paraffin. For the analysis of the obtained MMs of FFPE blocks, the regions containing brain tissue were selected from the images based on the spatial distribution of non-normalized m11 element (total intensity image) taken at 450 nm. The selection was performed using polynomial region of interest (ROI) selection toolbox in MATLAB. The ROIs selected at 450 nm were transformed to the MM results taken at other wavelengths with consideration of the slight shifts in spatial coordinates, imposed by the wavelength difference.

Fig. 3.

4 × 4 MM images of a FFPE mouse brain sample (75-days old) obtained at (a) 450 nm, (b) 500 nm, (c) 550 nm. Field of view: 12 mm × 14.5 mm (251 × 301 pixels). Refer to Supplement 1 ^{(4.3MB, pdf)} for high resolution images of m22, m33, m44 (Fig. S1-S3).

As one can see in Fig. 3, the only non-zero elements of the MM are located at the main diagonal of the matrices. The values of off-diagonal elements did not exceed 0.02. The diagonal structure of MM was observed for all brain samples measured at 450-550 nm. The diagonal MM is an indicator that the sample acts as a partial depolarizer (for an ideal depolarizer, all MM elements are equal to 0 except of m11) and does not possess any significant retardance or diattenuation. Therefore, all examined samples of paraffin-embedded brain behave as partial depolarizers. Thus, only the diagonal elements, m22, m33, and m44, which characterize the degree of depolarization of linearly (0°-90°, ±45° frames) and circularly polarized light, respectively, contain relevant information for the quantitative analysis. Refer to Supplement 1 ^{(4.3MB, pdf)} for high resolution images of m22, m33, m44 (Figs. S1-S3).

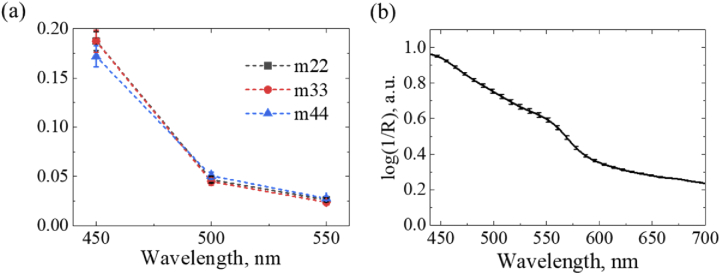
The results presented in Fig. 3 show that the values of diagonal elements of MM decrease at each pixel of the image and the contrast between the brain tissue and paraffin in m22, m33, and m44 images drops with the increase of the wavelength of incident light. A plot of wavelength dependence of values of m22, m33, and m44 averaged over selected ROI of brain tissue is presented in Fig. 4(a). The observed decrease in the averaged values of m22, m33, and m44 [see Fig. 4(a)] correlates well with the absorbance of the FFPE brain tissue, which was measured with a hyperspectral camera (SPECIM, Finland). Figure 4(b) shows the calculated absorbance spectrum of the FFPE brain tissue. Here, the absorbance spectrum is presented in terms of log(1/R), where R is reflectance of the brain tissue, which was selected from the reflectance cube of the whole tissue block using ROI selection and then averaged over the selected brain area. The reflectance cube of the tissue block was calculated as a ratio between the acquired hyperspectral reflection cubes of the tissue block and a reference sample (spectralon).

Fig. 4.

(a) Averaged values of discrete components of m22, m33 and m44 elements of the mouse brain sample (75-days old); (b) Absorbance spectrum of the same sample measured with a hyperspectral camera (SPECIM, Finland).

The decrease in absorbance with the increase of the wavelength of incident illumination [see Fig. 4(b)] enhances the penetration depth, which leads to the growing number of scattering events. Thus, higher depolarization values were observed at 500 and 550 nm [37]. Therefore, due to higher preservation of the polarization of backscattered light, the results obtained at the wavelength 450 nm were chosen for the further analysis.

According to results presented in Fig. 4(a), the values of m22 and m33 are larger than m44 value (m22 = m33 > m44) at 450 nm by approximately 8%. It means that the incident circularly polarized light is more depolarized by the sample compared to the incident linearly polarized light. This is a typical response for biological tissues that exhibit Rayleigh scattering rather than Mie scattering when measured in backscattering configuration [37–39]. At longer wavelengths, m22 ≈ m33 ≈ m44, which means that the sample exhibits scattering in the Rayleigh–Mie transition regime and acts as an isotropic depolarizer [39].

4. Statistical analysis

As discussed in the previous section, m22, m33, m44 elements and total depolarization obtained at 450 nm central wavelength were identified as the most relevant elements for the analysis. The parameter of total depolarization of tissue is calculated as [40]:

$$\mathrm{\Delta }=1-\frac{|m22|+|m33|+|m44|}{3}.$$ (1)

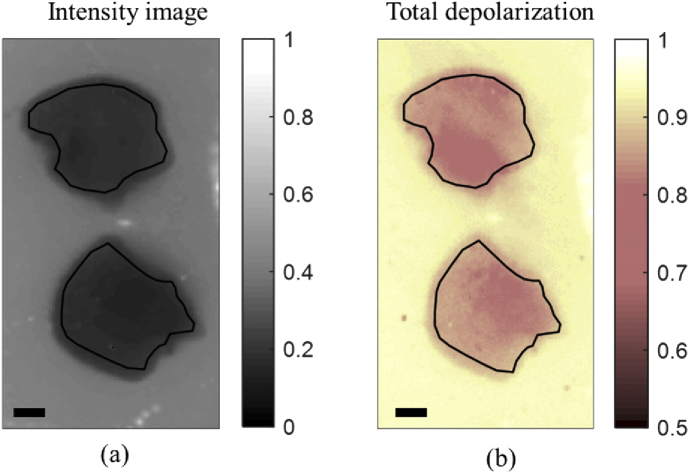
The spatial distribution of total depolarization were analyzed for the ROI contained brain tissue only (see Fig. 5).

Fig. 5.

(a) Unpolarized total intensity image at 450 nm (m11 element) with black line contours showing the selected ROI. (b) Map of total depolarization with the black ROI contours transferred from (a). The total depolarization data inside the selected ROI were used for the statistical analysis. Scale bar: 1 mm.

Statistical moments from 1^st to 4^th order (mean value (Z₁), standard deviation (Z₂), skewness (Z₃), kurtosis (Z₄)) of the distributions of total depolarization (Δ), and diagonal elements of MM within the selected brain tissue zones were calculated for 21 samples using the following equations [28]:

$$Z_1=\frac{1}{N}{\sum }_{j=1}^N{\mathrm{\Delta }}_j;$$ (2)

$$Z_2=\sqrt{\frac{1}{N-1}{\sum }_{j=1}^N{({\mathrm{\Delta }}_j-Z_1)}^2};$$ (3)

$$Z_3=\frac{1}{Z_2^3}\frac{1}{N}{\sum }_{j=1}^N{({\mathrm{\Delta }}_j-Z_1)}^3;$$ (4)

$$Z_4=\frac{1}{Z_2^4}\frac{1}{N}{\sum }_{j=1}^N{({\mathrm{\Delta }}_j-Z_1)}^4$$ (5)

Here, N is the total number of pixels in each analyzed ROI image, while index j stands for pixel number.

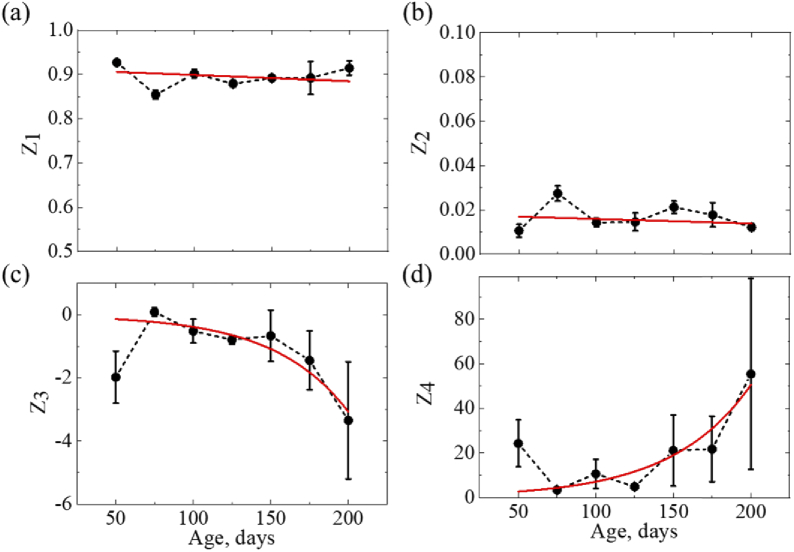
The obtained statistical moments were averaged over the corresponding age group. Figure 6 shows the averaged values of the obtained 1^st to 4^th statistical moments of the distributions of total depolarization of screened mouse brain samples plotted versus the animal’s age. Error bars represent standard deviation of statistical moments.

Fig. 6.

Statistical moments of the 1^st - 4^th orders characterizing the spatial distributions of total depolarization of FFPE mouse brain with AD (50 to 200 days) measured at 450 nm: (a) mean, (b) standard deviation, (c) skewness, (d) kurtosis. Red solid lines show fitting functions: linear in (a, b), exponential in (c, d).

The obtained results have shown that the 1^st and 2^nd order statistical moments of depolarization are not sensitive to the AD progression, whereas statistical moments of the higher orders show exponential changes with the progression of the disease (see Fig. 6). The negative value of the 3^rd statistical moment designates that the distribution is negatively skewed (the tail is extended towards lower values), indicating that both mean and median values are less than the mode in the analyzed data set. The 4^th statistical moment characterizes the strength of the outliers of the distribution [41].

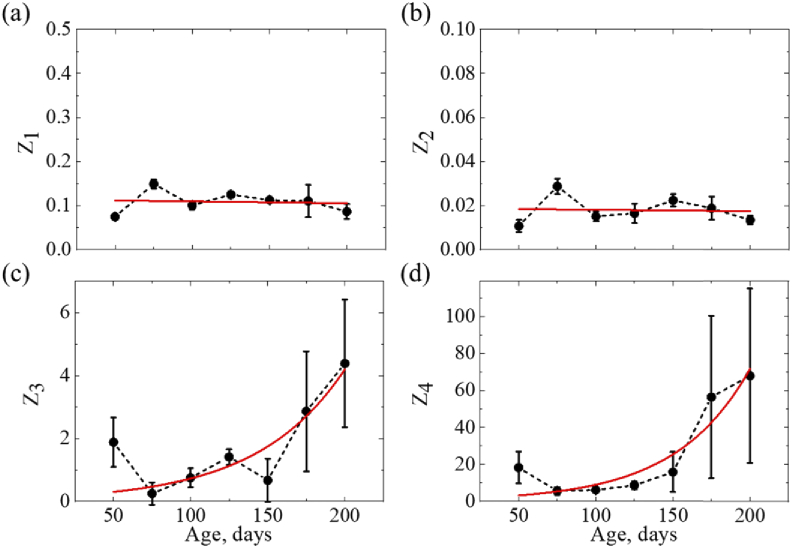
Figure 7 shows the results of statistical analysis of the spatial distributions of m22 element, which represents the degree of residual polarization of the incident linearly polarized light backscattered by the medium and contributes to the total depolarization parameter [see Eq. (1)]. The statistical analysis of m22 coefficient has shown similar dependencies of statistical moments. According to the obtained results, the statistical moments of the 1^st and 2^nd orders of the spatial distributions of degree of residual linear polarization do not exhibit noticeable changes, whereas the high-order statistical moments reveal exponential changes with the AD progression (see Fig. 7). The 3^rd statistical moment of m22 [see Fig. 7(c)] is positive, which indicates that the distribution is skewed towards higher values. This is consistent with the 3^rd statistical moment of total depolarization distribution [see Fig. 6(c)], due to the relation between m22 and total depolarization parameter [see Eq. (1)].

Fig. 7.

Statistical moments of the 1^st- 4^thorders characterizing the spatial distributions of m22 element of MM measured from FFPE mouse brain with AD (50 to 200 days) at 450 nm: (a) mean, (b) standard deviation, (c) skewness, (d) kurtosis. Red, solid lines show fitting functions: linear in (a, b), exponential in (c, d).

As it was demonstrated in previous studies [8], due to the accumulation of Aβ plaques, the AD-affected brain exhibits higher scattering coefficient (µ_s) and larger size of scattering particles. The latter results in higher anisotropy of scattering (g) compared to normal tissues. While with the AD progression, both µ_s and g grow, their changes compensate each other in terms of variations of the reduced scattering coefficient ${\mathrm{\mu }}_{\text{s}}\mathrm{\prime }={\mathrm{\mu }}_s(1-\text{g})$ [42]. Thus, as ${\mathrm{\mu }}_{\text{s}}\mathrm{\prime }$ of the bulk brain tissue remains nearly unchanged [8], the impact of structural alterations, associated with accumulation of Aβ plaques, is not clearly observed by 1^st and 2^nd statistical moments of spatial distributions of total depolarization, as well as by m22 [see Figs. 6(a), 6(b), 7(a), 7(b)]. In addition, the lack of changes in the values of 1^st and 2^nd statistical moments is arguably conditioned by the large variability of optical properties of different brain areas that are affected differently by the Aβ plaques deposition [8].

The exponential changes in the 3^rd statistical moment indicate that the distributions of total depolarization and depolarization of linearly polarized light (linear (horizontal) depolarization, Δ_LH= 1 - |m22| [43]) become more skewed towards lower values with the later AD stage. The exponential grow of the 4^th statistical moment indicates that with the AD progression, the distributions of total and linear depolarization have more strength in the outliers or become “heavy-tailed”. The changes in high-order statistical moments are conditioned by the structural malformations of the AD brain tissue, tending to enhance the effective scattering cross-section in the tissue due to increase in the size of scattering particles [8], which, in turn, influences the scattering phase function. Therefore, with the AD progression, the scattering of light becomes anisotropic (Mie-like scattering), and the angular dependence of scattering is enhanced [42,44]. Moreover, the increase of the spatial inhomogeneity of AD-affected brain tissue contributes to the irregularity of the scattering phase function. The angular non-uniformity of the scattering phase function leads to the higher extremity of deviations of resultant photon trajectories in the tissue. Due to the different number of scattering events associated with different pathlengths of photons in the tissue, the degree of polarization of emerging photons is reduced to the different extent [44]. These phenomena make the distributions of depolarization irregular showing lower symmetry with respect to the central peak (i.e. higher absolute value of skewness) and lead to the greater extremity of deviations of values of total and linear depolarization with respect to the mean value (i.e. higher kurtosis). The observed behavior of high-order statistical moments could be used as a marker of the β-amyloidosis severity.

5. Summary and conclusions

We demonstrate the possibility to perform screening for amyloid deposits of mouse brain tissue embedded in FFPE block at different stages of AD using wide-field multi-spectral MM imaging polarimetry. In the current study, the MM images of 21 FFPE samples of mouse brain tissue at different stages of AD were acquired at 450-550 nm wavelengths. By analyzing the obtained multispectral MM images and corresponding imaging results acquired with a hyperspectral camera, we have identified that the wavelength range around 450 nm is the most sensitive to the brain tissue structure. Moreover, the particular elements of MM, which contain valuable information on the structural alterations in the tissue, were identified and analyzed. With the help of statistical analysis of the obtained results, we have found exponential dependencies of the high-order statistical moments of total and linear depolarization from the growing structural alterations associated with AD progression, namely, accumulation of Aβ plaques. This effect is conditioned by the increase of the anisotropy of light scattering due to increase of the size of the scattering cross-section in tissue. The obtained dependencies demonstrate that high-order statistical moments of total and linear depolarization could be used as sensitive markers of the growing presence of Aβ plaques. The introduced label-free, contact-free approach shows of a potential to improve the existing practice of protein aggregate screening in AD diagnostics in terms of time and cost efficiency by using FFPE blocks for the analysis without the need to slice and stain the tissue. The method could also be useful for screening of optic active aggregated proteins (e.g. prion protein) in other diseases that are highly infectious, such as Creutzfeldt-Jakob disease.

Funding

Horizon 2020 Framework Programme10.13039/100010661 (Marie Skłodowska-Curie grant No.713606, 643417); Cost Actions (CA16118); the ATTRACT project funded by the EC under Grant Agreement (777222); Academy of Finland10.13039/501100002341 (314369, 325097, 326204); INFOTECH strategic funding; Deutsche Forschungsgemeinschaft10.13039/501100001659 (DFG PA930/12); Latvian Council of Science FLPP (lzp-2018/1-0275); Nasjonalforeningen for Folkehelsen10.13039/501100013263 (16154); HelseSØ (2016062, 2019054, 2019055); Norges Forskningsråd10.13039/501100005416 (251290 FRIMED2, 260786 PROP-AD); MEPhI Academic Excellence Project (02.a03.21.0005); Russian Science Foundation10.13039/501100006769 (19-72-30012); Tomsk State University10.13039/501100008566 (D.I. Mendeleev Fund Program).

Disclosures

The authors declare no conflicts of interest.

Supplementary Material

See Supplement 1 ^{(4.3MB, pdf)} for supporting content.