Abstract
A typical challenge in air pollution epidemiology is to perform detailed exposure assessment for individuals for which health data are available. To address this problem, in the last few years, substantial research efforts have been placed in developing statistical methods or machine learning techniques to generate estimates of air pollution at fine spatial and temporal scales (daily, usually) with complete coverage. However, it is not clear how much the predicted exposures yielded by the various methods differ, and which method generates more reliable estimates. In this paper, we aim to address this gap by evaluating a variety of exposure modeling approaches, comparing their predictive performance. Using PM2.5 in year 2011 over the continental U.S. as a case study, we generate national maps of ambient PM2.5 concentration using: (i) ordinary least squares and inverse distance weighting; (ii) kriging; (iii) statistical downscaling models, that is, spatial statistical models that use the information contained in air quality model outputs; (iv) land use regression, that is, linear regression modeling approaches that leverage the information in Geographical Information System (GIS) covariates; and (v) machine learning methods, such as neural networks, random forests and support vector regression. We examine the various methods’ predictive performance via cross-validation using Root Mean Squared Error, Mean Absolute Deviation, Pearson correlation, and Mean Spatial Pearson Correlation. Additionally, we evaluated whether factors such as, season, urbanicty, and levels of PM2.5 concentration (low, medium or high) affected the performance of the different methods. Overall, statistical methods that explicitly modeled the spatial correlation, e.g. universal kriging and the downscaler model, outperform all the other exposure assessment approaches regardless of season, urbanicity and PM2.5 concentration level. We posit that the better predictive performance of spatial statistical models over machine learning methods is due to the fact that they explicitly account for spatial dependence, thus borrowing information from neighboring observations. In light of our findings, we suggest that future exposure assessment methods for regional PM2.5 incorporate information from neighboring sites when deriving predictions at unsampled locations or attempt to account for spatial dependence.
1. INTRODUCTION
Accurate exposure assessment plays an essential role in the success of any environmental health study. Past air pollution epidemiological studies regularly utilize ambient air quality measurements from large monitoring networks to estimate population and individual exposures. However, measurements from these networks are spatially sparse, temporally incomplete, and preferentially located in areas with dense population and high pollution levels. There is increasing interest in developing methods to retrospectively estimate air pollution levels at fine spatial scales and with complete spatial-temporal coverage to minimize exposure measurement error (Alexeeff et al., 2015), support more spatially-resolved health effect analyses (Kloog et al., 2012; Hao et al., 2016), and perform impact assessments in low- and middle-income settings (Shaddick et al., 2018). Advances in Geographical Information Systems (GIS), remote sensing, and numerical model simulations have further contributed to a proliferation of modeling approaches to estimate air pollution over the past decade.
This paper aims to address an important gap in the current literature: the fact, that when models to estimate ambient air pollution exposure are being developed, they are typically only compared to simpler models within the same modeling paradigms. Examples include comparisons between regression models with different predictors, especially in land use regression models (Tang et al., 2013; Wang et al, 2016); between geostatistical models with different spatial dependence structures (Reich et al., 2011); or between different machine learning algorithms (Singh et al., 2013; Reid et al., 2015). There has been very limited cross-paradigm comparisons (Adam-Poupart et al., 2014; Yu et al., 2018), likely due to the analytic effort and expertise required to carry out the different approaches. In particular, there is a lack of comparison between machine learning and advanced geostatistical approaches. As exposure modeling becomes increasingly complex and computationally demanding, there is a pressing need to better understand the advantages and limitations associated with different modeling approaches. However, synthesis of results from existing studies is challenging due to the use of different data sources and inconsistent criteria for evaluating model performance.
Our objective is to critically evaluate different exposure modeling approaches via a case study of estimating regional daily ambient fine particulate matter of aerodynamic diameter less than 2.5μg/m3 (PM2.5) across the contiguous United States. We consider major classes of approaches that can provide complete spatial and temporal coverage using monitoring measurements, meteorology, land use variables, and numerical model simulations. These approaches include ordinary least squares, universal kriging (Cressie, 1993), statistical downscaling (Berrocal et al, 2010), and machine learning methods, including random forest (Hu et al., 2017), support vector machine (Liu et al., 2017), and neural networks (Di et al., 2016). Air quality estimates from these approaches have already been used in health effect and health impact analyses (Chang et al., 2011; Strickland et al., 2016; Di et al., 2017). Our evaluation focuses specifically on a model’s spatiotemporal predictive ability.
A related issue that has hindered cross-comparison is the limited availability of data and analytic code from exposure modeling studies. This is in contrast to efforts in other fields, such as genetics, genomics and neuroimaging, where established publicly available and well-documented datasets are available for methods development and comparison (Mailman et al., 2007; Leinonen et al., 2010; Van Essen et al., 2013). Sophisticated exposure estimates often require considerable efforts in data processing and parameter tuning to maximize performance. A notable example is the air pollution modeling framework for 2-week averages from the MESA Air study (Keller et al., 2015) where an R package has been made available (Lindstrom et al., 2012). Hence, another contribution of this study is the documentation of all data and analytic code. We also only considered methods that can be readily implemented using packages from the statistical R software (R Core Team 2018). This will ensure better reproducibility, allow for future evaluation of other methods, and facilitate adaptation of these methods by other groups.
2. DATA SOURCES
2.1. PM2.5 Monitoring data
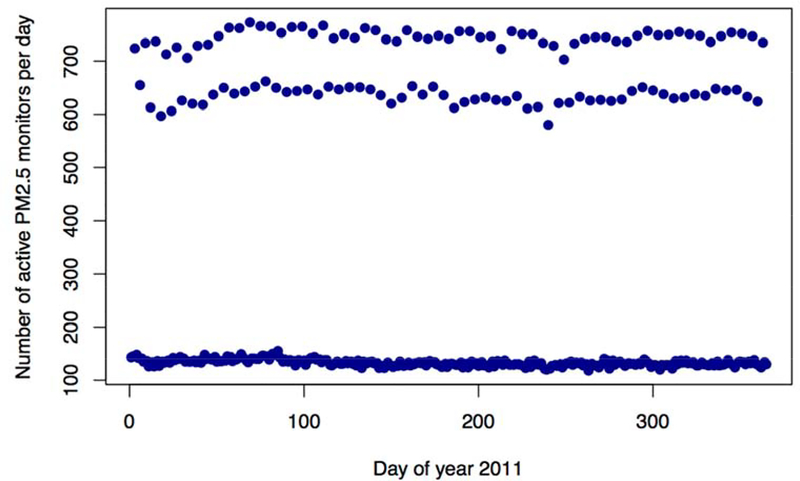
For year 2011, daily PM2.5 measurements were obtained from the Air Quality System (AQS) database of the US Environmental Protection Agency (EPA). A total of 829 monitors are available in the contiguous United States. Monitors typically take measurements every 1, 3 or 6 days, with only approximately 15% of monitors sampling daily in 2011. Figure A1 in the Appendix shows the number of active monitors each day: most days have less than 200 measurements across the contiguous US.
2.2. Computer model output
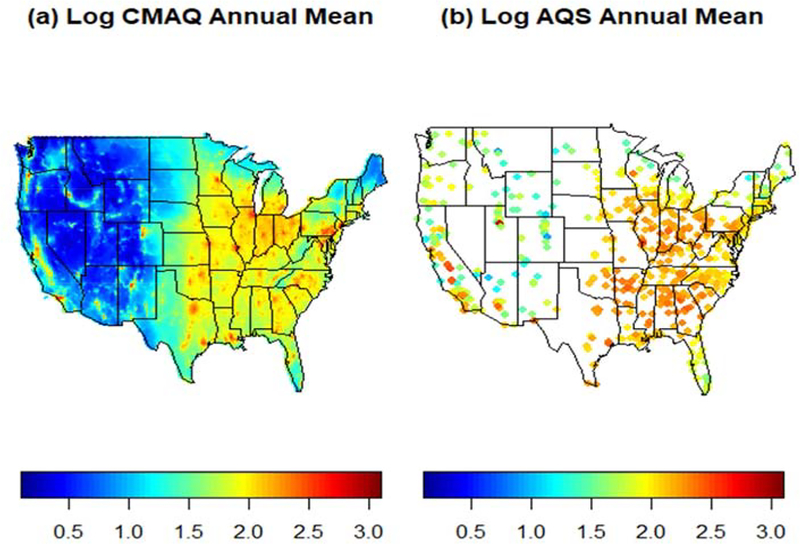
Computer models for air quality use information on emission sources to simulate the fate and transport of air pollutants by taking into account complex atmospheric chemistry and physics. There is increasing use of computer model outputs to estimate air pollution levels at locations without monitoring data (Berrocal et al., 2010). We obtained output of hourly PM2.5 concentrations yielded by runs of the Community Multiscale Air Quality model (CMAQ; Byun and Schere, 2006) version 4.7 performed by the EPA at 12km spatial resolution across the contiguous US for year 2011 using 13 vertical layers that span up to the top of the troposphere. We aggregated the layer 1 (about 19m from the ground) hourly output to generate CMAQ output of daily average PM2.5 concentration. At this horizontal spatial resolution, the study area is covered by a grid of 299 by 459 cells, with about half of those cells over the contiguous US. Each PM2.5 monitor was linked to the CMAQ grid cell that contains it. Figure 2 compares annual average PM2.5 concentrations obtained from CMAQ simulations and AQS measurements, on the log scale. As the figure shows, the CMAQ output captures the overall spatial pattern in the annual log PM2.5 concentration as measured by the monitors, with some estimation inaccuracies particularly along the West Coast. Figure A2 in the Appendix, presents output of daily average PM2.5 concentration as estimated by CMAQ and as observed at monitoring sites for two days in 2011. Additionally, assessment of the reliability and accuracy of CMAQ as compared to the observed PM2.5 concentrations are provided in Tables 4 through 7.
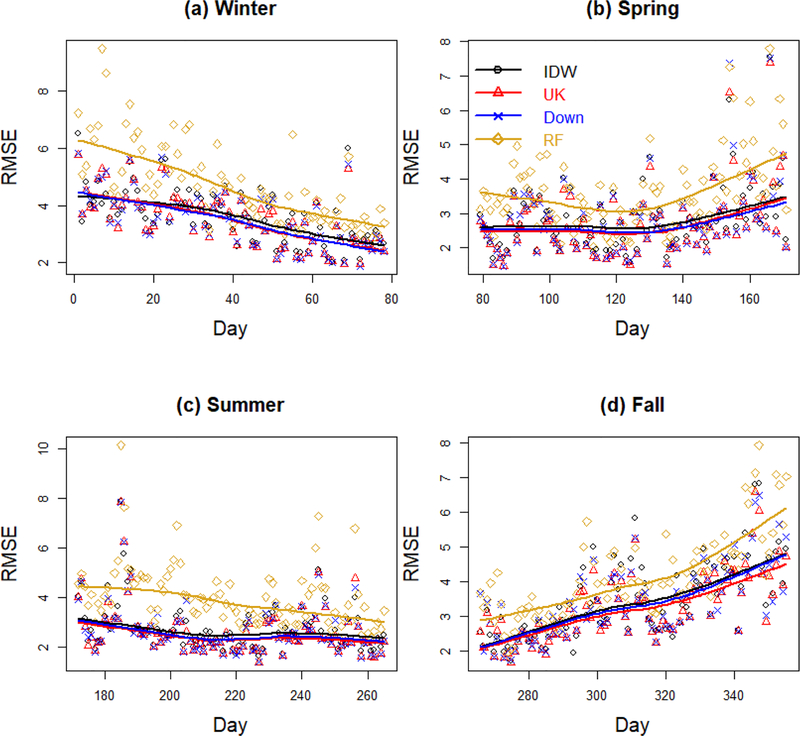
Figure 2. Daily cross-validation RMSE over year 2011 stratified by season.
Daily root mean squared error (“RMSE”) for PM2.5 concentration predictions in μg/m3 stratified by season. Results are displayed for four representative methods: Inverse Distance Weighting (“IDW”), Universal Kriging with CMAQ as only predictor (“UK”), the Downscaler model (“Down”) and Random Forest (“RF”). In each panel, the lines are loess smoothers.
Table 4. Overall performance of exposure assessment methods.
Assessment of the various statistical and machine learning methods over space and time by averaging: Root Mean Squared Error (“RMSE”), Mean Absolute Deviation (“MAD”), correlation between predicted and observed values (“Corr”), and empirical coverage of the predictive 95% intervals. Both RMSE and MAD are in units of μg/m3. The methods considered are: raw CMAQ output, ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”).
| Method | RMSE | MAD | Corr | Coverage |
|---|---|---|---|---|
| CMAQ | 7.19 | 4.68 | 0.51 | -- |
| OLS (CMAQ) | 4.80 | 3.09 | 0.65 | 0.62 |
| OLS (Covs) | 4.63 | 2.97 | 0.67 | 0.79 |
| OLS (CMAQ + Covs) | 4.22 | 2.63 | 0.74 | 0.83 |
| IDW | 3.22 | 1.82 | 0.85 | -- |
| UK (CMAQ) | 3.08 | 1.70 | 0.87 | 0.95 |
| UK (Covs) | 3.25 | 1.79 | 0.85 | 0.93 |
| UK (CMAQ + Covs) | 3.15 | 1.76 | 0.86 | 0.93 |
| Downscaler (CMAQ) | 3.10 | 1.70 | 0.87 | 0.94 |
| RF (CMAQ + Covs) | 4.23 | 2.74 | 0.73 | 0.96 |
| SVR (CMAQ + Covs) | 3.83 | 2.22 | 0.79 | -- |
| NN (CMAQ + Covs) | 3.90 | 2.49 | 0.78 | -- |
Table 7. Overall performance of exposure assessment methods by level of observed PM concentration.
Correlation coefficient between PM2.5 concentration predictions and observed PM2.5 concentration in μg/m3 stratified by PM2.5 concentration level. Groupings are based on: whether PM2.5 is less than 6 μg/m3, 6–12 μg/m3 and greater than or equal to 12 μg/m3 (12 μg/m3 is the EPA standard). The methods considered are: raw CMAQ output, ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”). The last line reports the mean and standard deviation, in parenthesis, for the observed PM2.5 concentration within each category (low, medium or high).
| Method | Low | Med | High |
|---|---|---|---|
| CMAQ | 0.37 | 0.26 | 0.21 |
| OLS (CMAQ) | 0.33 | 0.33 | 0.31 |
| OLS (Covs) | 0.40 | 0.43 | 0.42 |
| OLS (CMAQ+Covs) | 0.32 | 0.36 | 0.36 |
| IDW | 0.41 | 0.56 | 0.66 |
| UK (CMAQ) | 0.50 | 0.62 | 0.65 |
| UK (Covs) | 0.49 | 0.61 | 0.64 |
| UK (CMAQ+Covs) | 0.45 | 0.55 | 0.64 |
| Downscaler (CMAQ) | 0.49 | 0.62 | 0.65 |
| RF (CMAQ + Covs) | 0.37 | 0.42 | 0.42 |
| SVM (CMAQ + Covs) | 0.37 | 0.55 | 0.46 |
| NN (CMAQ + Covs) | 0.37 | 0.44 | 0.54 |
| PM2.5 | 4.14 (1.21) | 8.66 (1.71) | 17.48 (5.81) |
2.3. Meteorological and land use data
Daily average meteorological fields were obtained from the North American Land Data Assimilation System (NLDAS) and the North American Regional Reanalysis (NARR). Meteorological variables include temperature at 2m, 30m, 150–180mb above ground, downward longwave and shortwave radiation flux, relative humidity at 2m, boundary layer height, visibility, dew-point temperature, potential evaporation, convective available potential energy, pressure at 2m, 10m, and 30m, and U- and V-wind speed at 10m. All these variables are known to influence the transport and chemistry of fine particle matters, are readily available and have been incorporated in previous studies estimating PM2.5 concentration using machine learning methods and leveraging remote sensing data (Hu et al., 2017).
We also obtained the following land use variables: elevation from the US Geological Survey, major roadway lengths and percentage of forest cover from the National Land Cover database, population density from the U.S. 2010 Census Bureau at the census tract level, percentage of impervious surface from Landsat, and PM2.5 primary emission sources from the 2011 US EPA National Emissions Inventory Facility Emissions report. Although all the above mentioned variables were available at different spatial resolution (point level, in some cases, grids, etc.), they were re-gridded to the CMAQ 12km grid. Specifically, for predictors with finer spatial resolutions than CMAQ (e.g. elevation), we used the average of cell values that intersect with the CMAQ cell. For predictors with coarser spatial resolution than CMAQ (e.g. meteorology), the value of the nearest grid cell centroid was used.
3. METHODS
In this section we describe all the methods we used to obtain daily estimates of PM2.5 concentration across the contiguous US. We start by first describing the variable selection procedure we implemented to identify the predictors we leveraged to generate estimates of PM2.5 concentration during year 2011, and then move onto describing each of the exposure assessment methods considered for comparison in the manuscript.
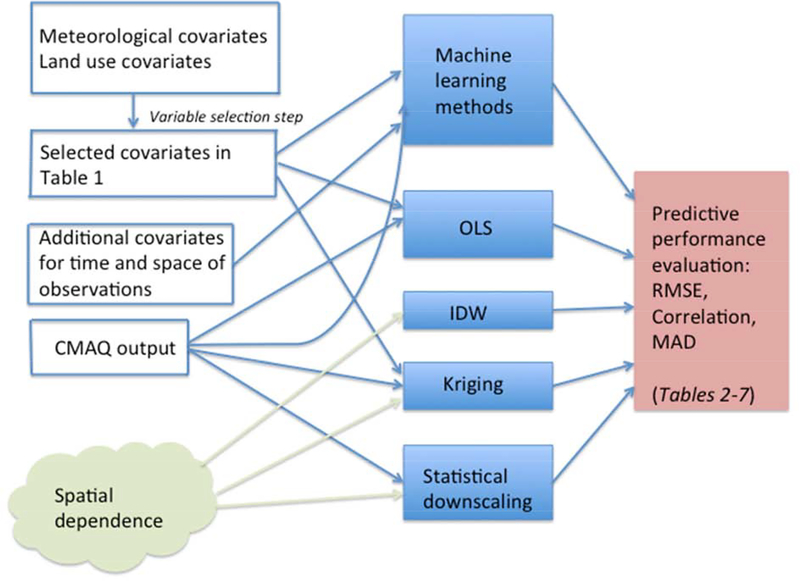
The last subsection describes the various metrics used to compare the predictive performance of the various exposure assessment methods. A schematic diagram summarizing all the methods is available in the Appendix (Figure A3).
3.1. Variable selection
It is well established that meteorological variables and land use characteristic are good predictors of PM2.5 concentration (Hoek et al., 2008). To identify which predictors should be used in the exposure models considered in our subsequent model comparisons, we first performed variable selection via cross validation and best subset regression (Kutner et al., 2005). Best subset regression is a variable selection method that compares all the regression models containing a given number of predictors and determines the best fitting model, e.g. the “best set of predictors”, based on some validation criteria. In our case, we used the criteria cross-validation root mean square error.
Hence, we randomly split the monitors into 5 folds, performed best subset regression using data from the other 4 folds and predicted PM2.5 concentration at the hold-out fold. For each hold-out set, we computed the root mean square error (RMSE), comparing the predicted values with the held-out PM2.5 observations. We averaged the RMSEs across the five folds and selected the model which yielded the best predictive performance. This identified a model with 11 predictors: including an additional predictor only improved prediction by less than 0.1%. After having determined the number of predictors to include in the model, we identified the set of 11 predictors again via best subset regression. In this second step, best subset regression was performed on the full data using all meteorological variables and land use covariates.
We implemented subset regressions as a two-step procedure by first identifying the number of needed predictors and then determining the selected covariates, simply because we did not use all the data and different training datasets could identify a different number and set of predictors. Even though using a cross-validation strategy forced us to adopt a two-stage procedure for variable selection, this approach reduces the chance of overfitting.
The 11 selected predictors are shown in Table 1. The set consisted mostly of meteorological variables, likely due to our interest in estimating daily PM2.5 concentrations.
Table 1. Set of eleven predictors selected via best subset regression.
In parentheses it is indicated the original database from which each predictor was obtained: North American Land Data Assimilation System (NLDAS) and North American Regional Reanalysis (NARR).
| Percentage of Impervious Surface (Landsat) | Potential Evaporation (NLDAS) |
| Downward Longwave Radiation Flux (NLDAS) | Convective Available Potential Energy (NLDAS) |
| Relative Humidity (NLDAS) | V-Wind at 10m (NLDAS) |
| Pressure (NLDAS) | Dew-point Temperature (NARR) |
| Visibility (NARR) | Boundary Layer Height (NARR) |
| Temperature 150–180mb above ground (NARR) |
3.2. Exposure assessment: Statistical methods
Let Yt(s) be the monitor measurement of PM2.5 at spatial location s and day t. Each observation is associated with land-use covariates and meteorological variables at s, Xt(s), and the CMAQ output at the grid cell that contains s, Zt(s). We assume monitoring data are available at n sites s1,…, sn and for days t=1,…,T. The distance (in km) between location si and sj is denoted dij. The objective of all methods is to make a prediction of PM2.5 concentration at a location s0 that does not have a monitor, with prediction uncertainty quantified through
3.2.1. Ordinary least squares
Predictions of PM2.5 concentrations using Ordinary Least Squares are obtained by fitting a linear regression model separately every day for daily with log PM2.5 concentration at the training sites as outcome variable and different sets of predictors :
Only the corresponding daily log CMAQ output at the grid cells that contain the training sites;
The covariates selected by best subset regressions for the same day and at the grid cells that contain the training sites;
Both the log CMAQ output and the selected covariates.
Predictions are backtransformed onto the original scale, and the prediction variance is the usual prediction variance under linear regression.
3.2.2. Inverse distance weighting
Inverse distance weighting (IDW) does not use the covariates and simply uses a weighted average of nearby observations as the prediction. The intuition behind IDW is that the weights for observations near the prediction location should be higher than the weights for observations far from the prediction location. The weight assigned to the observation at location si for prediction at location s0 decays as the distance d0i between s0 and si increases,
| (1) |
where the rate of decay is controlled by ϕ > 0, which we select using cross validation.
The IDW prediction is
| (2) |
The weights W0i are standardized to sum to one so that predictions are unbiased. Because no statistical model is assumed, there is no natural variance estimate, vt(s).
3.3. Exposure assessment: Geostatistical methods
In geostatistics, the problem of generating predictions of a continuous spatial process at unsampled locations is typically handled via Kriging. As with IDW, in Kriging the prediction is a linear combination of the observations Yt(s1),…, Yt(sn) with weights λ = (λ1,⋯,λn), that is, . The weight vector λ is in turn determined by finding the set of λ’s that yield the Best Linear Unbiased Predictor (BLUP), i.e.
The expression for the weights depends on the assumptions made on Yt(s), such as whether the process is second-order stationary (i.e., the covariance depends only on the separation between points) and whether its mean varies spatially and depends on covariates. For computational tractability, we assume a stationary covariance function (Cressie, 1993). In addition, given that we are generating predictions of PM2.5 concentration across the entire United States it is safe to assume that the mean concentration varies spatially as function of covariates. Thus, we will generate our predictions using Universal Kriging (Cressie, 1993) that includes covariates in the mean function.
3.3.1. Universal Kriging
In Universal Kriging we assume that, for each day t, Yt(s) is a Gaussian process with a predetermined covariance function and a mean E[Yt(s)] = μt(s), linear function of spatially-varying covariates. In our implementation-we assume that the spatial covariance does not change in time and the correlation between PM2.5 concentration at two sites decays exponentially with distance. Note that in Universal Kriging, the spatial covariance function represents the spatial dependence in the process, e.g. in PM2.5 concentration, after having accounted for the effect of the covariates. With covariates varying in space and time, it is very likely that all the temporal variability in PM2.5 concentration is captured by CMAQ and/or the meteorological and land-use covariates, thus making it very plausible that the residual spatial dependence does not vary in time. We compare different scenarios for μt(s):
μt(s) depends only on the CMAQ output Zt(s), i.e.
| (3) |
μt(s) depends only on meteorological and land-use covariates Xt(s), i.e.
| (4) |
μt(s) depends on both the CMAQ output Zt(s) and the meteorological and land-use covariates Xt(s), i.e.
| (5) |
To implement the universal Kriging models, we use a two-stage procedure and use the gstat and geoR (Ribeiro Jr and Diggle, 2018), packages in R (R Core Team, 2018). Specifically, we first estimate the spatial covariance parameters via weighted least squares (WLS) using the gstat package, fitting an exponential semi-variogram to the empirical semi-variogram of the time-averaged residuals of the linear regressions implied by (3), (4), and (5), respectively.
Using the spatial covariance parameters estimated via WLS as initial values, we used the geoR package (Ribeiro Jr and Diggle, 2018) and maximum likelihood to iteratively estimate the regression parameters βt, γ0,t and γ1,t and the covariance parameters. Using such estimates, we then generate predictions of Yt(s0) via Universal Kriging separately for each day. Because the data are assumed to be Gaussian, Kriging predictions are accompanied by predictions variance estimates .
3.4. Exposure assessment: Downscaler
The downscaler model generates predictions of air pollution concentration at any location s by exploiting the relationship between the observed concentration measured at a monitor and the estimated air pollution concentration generated by an air quality model, CMAQ. The simplest downscaler model (Berrocal et al., 2010) relates the observed log concentration at location s on day t, Yt(s), to the CMAQ output, Zt(s), at the grid cell that contains location s via a linear regression model with spatially and temporally-varying coefficients. We adopt the following version of the downscaler model
| (6) |
where β0,t(s) is a spatially and temporally-varying intercept term, while γ1,t, indicates a slope term, constant in space but varying in time.
As on a given day t, we postulate that sites located nearby have a similar intercept term, to account for spatial dependence, we model β0,t(s) as a stationary spatial processes with an exponential correlation function, i.e.:
| (7) |
In (7), and ϕ0 represent, respectively, the spatial variability in β0,t(s) and the rate at which the spatial correlation vanishes.
The downscaler model in (6) is fit within a Bayesian framework (Gelman et al., 2013); thus, its specification is completed once prior distributions for all the model parameters are provided. Specifically, we assume that, for each day t, the spatially varying intercept β0,t(s), admits a constant mean β0,t, which is interpreted as the overall additive calibration of the CMAQ output. In contrast, β1,t represents the overall multiplicative calibration term for CMAQ. The two global calibration parameters (β0,t, β1,t)′ are assumed to be independent in time and follow a bivariate normal distribution with mean (0, 1)′ and with a diagonal, covariance matrix with large prior variances. The two variance parameters, τ2, and representing, respectively, the non-spatial and spatial variability in PM2.5 concentration, are provided with vague Inverse Gamma priors, while a Uniform prior on the interval (0.0001 km, 0.1 km) is placed on the decay parameters ϕ0.
Inference on model parameters is carried out through the posterior distribution, which is approximated using an MCMC algorithm (Gelman et al., 2013) we ran for 10,000 iterations, with the first 5,000 discarded for burn-in. For the case study discussed in the paper, we make a slight modification to the downscaler model, allowing the spatial dependence parameters and the non-spatial variance τ2 to vary with time. With this modification we can implement the downscaler model using the spBayes (Finley et al., 2015) package in R.
Predictions of air pollution concentrations on day t at an unsampled location s0 and uncertainty estimates for the predictions are obtained using the posterior predictive distribution of Yt(s0) given the observed data. Specifically: we take as predicted concentration, the median of the posterior predictive distribution, while we characterize uncertainty in the prediction via the 95% equal-tailed predictive interval. Finally, we use the sample variance of the predicted values to quantify the variance in the predictions.
3.5. Exposure assessment: Machine learning methods
The spatial regression models in Sections 3.3 and 3.4 represent the data-generating process of PM2.5 concentration with a small number of interpretable parameters. In contrast, machine learning algorithms have countless uninterpretable parameters and are thus essentially black-box prediction machines. However, these algorithms are flexible, general and have often outstanding predictive performance. Below we briefly describe the machine learning algorithms used in our comparison; for a detailed description see James et al. (2013).
For application of machine learning methods we do not explicitly model spatial correlation, although spatial coordinates and spatial covariates are used as predictors in these regression models. Since we do not model spatial correlation we denote the observed PM2.5 concentration and covariates relative to observation i=1,…,n (n is the combined sample size over space and time) as Yi and Xi, respectively. The p=15 covariates in Xi are: longitude, latitude, day of year, the covariates in Table 1 and CMAQ model output.
3.5.1. Random forests
A random forest (Breiman, 2001) is an ensemble of regression trees (Morgan and Sonquist, 1963). A regression tree is grown via recursive partitioning of the covariate space called ``leaves”, and then fitting separate linear models within each leaf. For each partition, m input variables are selected at random as candidates for splitting. Randomizing over the covariates decreases the correlation between trees and improves the prediction accuracy of the ensemble. The intuition is that interactions are likely present when considering the entire covariate space, but when considering small subregions of the covariate space linear models likely fit well within each subregion.
To construct a random forest for PM2.5 concentration, many regression trees are grown with the prediction being a weighted average of the predictions over the trees.
Unlike most machine learning methods, it is possible to quantify the uncertainty in the prediction vt(s) using the sample variance of the trees predictions. Random forest is a desirable data mining method because it is easily understood and it is computationally efficient for very large samples. The number of trees used for prediction is selected by out-of-bag error (Hastie et al., 2001), a cross validation technique where the observations that are not selected in a tree are then used to estimate the error. For our case study, we implemented random forest using the R package randomForest (Liaw and Wiener, 2002). We used the default values m = p/3 at each split. Based on out-of-bag error 500 trees are used as the final predictive model.
3.5.2. Support vector regression (SVR)
Support vector machines (Cortes and Vapnik, 1995) are most well known as a classification tool, but they can also be used for regression. In SVR a hyperplane is optimized to be within a certain threshold of the selected data, called the support vectors, and the hyperplane is used for regression prediction. The predicted PM2.5 concentration for an observation with covariates X0 is
where αi and are the support vectors and is the radial basis kernel function. The support vectors αi and are estimated as the solution to the convex optimization
| (8) |
so that for all i, and . The constant C is the box constraint that defines the trade off between penalty for observations further than ϵ away from the hyperplane and smoothness in the prediction hyperplane.
The calculation of the optimum solution to (8) is computationally expensive in large datasets and there is no straightforward method to estimate prediction variances. We implement support vector regression using the R package e1071 (Dimitriadou et al., 2006) and the function svm.
3.5.3. Neural networks
Neural networks have successfully been used to predict air pollution levels (Di et al., 2016). They are attractive because they can handle massive data and can model nonlinearity and interactions. We use a multilayer perceptron network (Rumelhart et al., 1986) that consists of an input layer, several hidden layers and an output layer. For an observation with covariates X0=(X01, …, X0p) the
| (9) |
where L1 and L2 are the number of neurons in each layer, f is the activation function, and and are the bias and weights estimated to minimize mean squared error in the training data.
Fitting a neural network requires tuning the number of hidden layers, the numbers of neurons in each layer, and the activation function. Increasing the size of the network provides more flexibility but also may lead to overfitting. Therefore, we also tune the number of epochs, drop-out rate, learning rate, and minibatch size (Goodfellow et al., 2016). The model is fit using keras (Chollet et al., 2015) in R. We tried relu and sigmoid activation functions and networks with 1 to 3 hidden layers, with 500 to 2000 neurons in the the first layer, and a reduced number of neurons in each of the next layers. Further tuning with the following possible combinations were considered: number of epochs ranging from 50 to 200, drop-out rate ranging from 0.1 to 0.5, learning rate ranging from 0.0005 to 0.01, and minibatch size ranging from 128 to 1024. Based on five-fold cross-validation, the final selected model has 2 hidden layers with 2000 and 100 neurons for the first and second layer, respectively, relu activation function f(x) = max{0, x}, 200 epochs, 0.4 drop-out rate, 0.003 learning rate and 1024 minibatch size.
3.6. Predictive performance assessment
We compare the predictive performance across methods described in Section 3.2 through 3.5 via five-fold cross validation by randomly sampling, without replacement, 20% of the sites to be in the test set in each of the five folds. Within each fold, we train each of the models on the data from the remaining 80% of the sites and we generate predictions at the test sites.
We evaluate the accuracy of the predictions yielded by the various methods in different ways: we assess them in a spatio-temporal sense by computing daily Root Mean Squared Errors (RMSEs) and daily Pearson correlations between the predicted and the observed PM2.5 concentrations, and we report their summary statistics over time. Note that the mean daily Pearson correlation averaged over time is also referred to as Mean Spatial Pearson Correlation, following Chen et al. (2018).
We also assess the exposure assessment methods overall, averaging different predictive performance statistics over space and time. Specifically, we average across days and sites: Root Mean Squared Error (RMSE); Mean Absolute Deviation (MAD), that is, the absolute difference between the predicted PM2.5 concentration and the observed PM2.5 concentration; Pearson’s correlation between predicted and observed PM2.5 concentrations; and coverage of the 95% prediction intervals. The latter is obtained by counting how many of the values in the test set fall in their corresponding prediction interval. A coverage equal or close to the nominal level (e.g. 95% for a 95% prediction interval) is best. As baseline comparison, we derive the same predictive performance measures also for the raw CMAQ output.
4. RESULTS
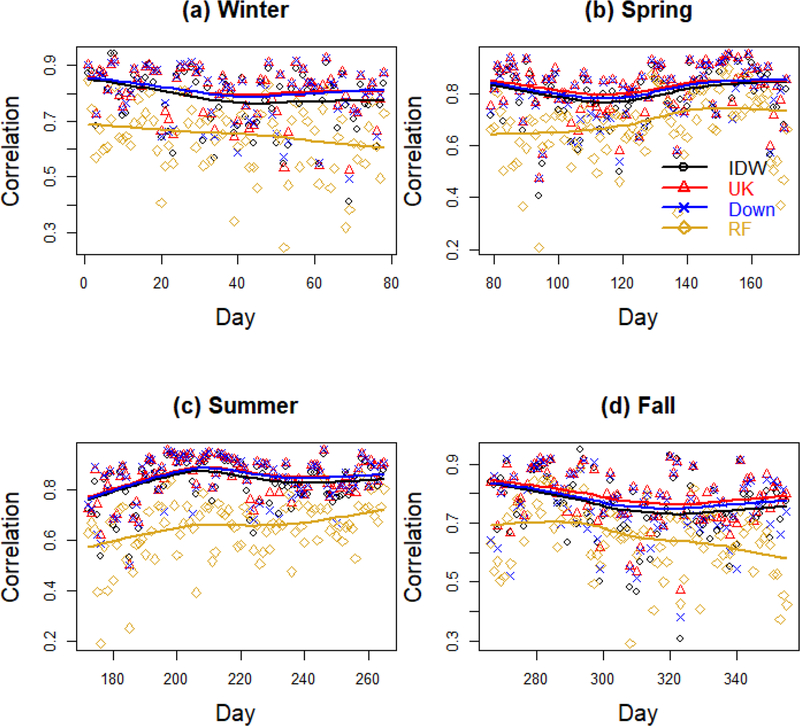
Figures 2 and 3 present spatio-temporal predictive assessment for four exposure assessment methods, representative of statistical methods (Inverse Distance Weighting), geostatistical methods (Universal Kriging), downscaling (Downscaler) and machine learning (Random Forests). In particular, Figure 2 shows daily RMSEs while Figure 3 presents daily Pearson correlations between predicted and observed PM2.5 concentrations, both stratified by season. As both figures show, for any exposure assessment method, the accuracy of the predictions varies over time with Spring and Summer being characterized by smaller RMSEs and higher correlation. Additionally while the quality of the predictions is almost constant across Summer and most of Spring, it worsens during Fall and it improves as Winter comes to an end. Finally, while the daily predictive performances of Universal Kriging and the Downscaler are very similar, predictions yielded by Random Forest have typically larger daily RMSEs and lower correlation with the observed PM2.5 levels over any day of 2011.
Figure 3. Daily cross-validation Pearson correlation over year 2011 stratified by season.
Daily Pearson correlation coefficient between predicted and observed PM2.5 concentration in μg/m3 stratified by season. Results are displayed for four representative methods: Inverse Distance Weighting (“IDW”), Universal Kriging with CMAQ as only predictor (“UK”), the Downscaler model (“Down”) and Random Forest (“RF”). In each panel, the lines are loess smoothers.
Summary statistics of the daily RMSEs and Pearson correlation coefficients for all exposure assessment methods, including CMAQ are presented in Tables 2 and 3, respectively. Confirming what already observed in Figures 2 and 3, when summarized across the entire year 2011, Universal Kriging with only CMAQ as predictor has the lowest mean daily RMSE over time and the highest mean daily Pearson correlation, also called Spatial Pearson Correlation Coefficient. Universal Kriging with only CMAQ as predictor is closely followed by the Downscaler model and Universal Kriging with CMAQ and other meteorological and land-use predictors. Inverse Distance Weighting performs similarly to the Downscaler model in terms of daily correlation, but has a slightly worse performance in terms of daily RMSE. Somewhat worse is the performance of the machine learning methods, particularly Support Vector Machine and Neural Network, whose MSPC and mean daily RMSE are, respectively about 11% lower and 25% higher than those of Univeral Kriging.
Table 2. Daily cross-validation results: summary statistics for RMSE.
Mean, standard deviation, and other quantile summaries of daily root mean squared error (“RMSE”) for PM2.5 concentration predictions in μg/m3. The methods considered are ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”).
| Summary Statistic | Mean | SD | Min | Q1 | Median | Q3 | Max |
|---|---|---|---|---|---|---|---|
| OLS (CMAQ) | 4.71 | 1.68 | 2.00 | 3.53 | 4.32 | 5.28 | 12.15 |
| OLS (Covs) | 4.57 | 1.53 | 1.80 | 3.48 | 4.28 | 5.39 | 10.15 |
| OLS (CMAQ+Covs) | 4.15 | 1.42 | 1.64 | 3.18 | 3.85 | 4.76 | 9.34 |
| IDW | 3.25 | 1.14 | 1.58 | 2.42 | 2.94 | 3.89 | 7.87 |
| UK (CMAQ) | 3.09 | 1.12 | 1.38 | 2.27 | 2.81 | 3.69 | 7.85 |
| UK (Covs) | 3.27 | 1.44 | 1.45 | 2.39 | 2.99 | 3.79 | 18.52 |
| UK (CMAQ+Covs) | 3.19 | 1.17 | 1.39 | 2.36 | 2.87 | 3.78 | 7.81 |
| Downscaler(CMAQ) | 3.15 | 1.19 | 1.39 | 2.31 | 2.88 | 3.73 | 8.63 |
| RF (CMAQ + Covs) | 4.21 | 1.46 | 1.95 | 3.23 | 3.86 | 4.80 | 10.76 |
| SVM (CMAQ + Covs) | 3.87 | 1.53 | 1.60 | 2.82 | 3.53 | 4.46 | 10.31 |
| NN (CMAQ + covs) | 3.89 | 1.37 | 1.65 | 3.00 | 3.55 | 4.46 | 10.96 |
Table 3. Daily cross-validation results: summary statistics for Pearson correlation.
Mean (or Mean Spatial Pearson Correlation – MSPC), standard deviation, and other quantile summaries of daily Pearson correlations between PM2.5 concentration predictions in μg/m3 and observed values. The methods considered are ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”).
| Summary Statistic | Mean or MSPC | SD | Min | Q1 | Median | Q3 | Max |
|---|---|---|---|---|---|---|---|
| OLS (CMAQ) | 0.51 | 0.16 | −0.16 | 0.42 | 0.53 | 0.62 | 0.82 |
| OLS (Covs) | 0.55 | 0.15 | −0.07 | 0.45 | 0.56 | 0.66 | 0.92 |
| OLS (CMAQ+Covs) | 0.64 | 0.12 | 0.13 | 0.57 | 0.65 | 0.73 | 0.92 |
| IDW | 0.79 | 0.11 | 0.31 | 0.72 | 0.81 | 0.87 | 0.95 |
| UK (CMAQ) | 0.81 | 0.09 | 0.47 | 0.75 | 0.83 | 0.88 | 0.96 |
| UK (Covs) | 0.79 | 0.11 | 0.13 | 0.74 | 0.81 | 0.87 | 0.96 |
| UK (CMAQ+Covs) | 0.80 | 0.10 | 0.43 | 0.74 | 0.81 | 0.87 | 0.96 |
| Downscaler(CMAQ) | 0.80 | 0.11 | 0.25 | 0.73 | 0.82 | 0.88 | 0.96 |
| RF (CMAQ + Covs) | 0.65 | 0.12 | 0.19 | 0.58 | 0.66 | 0.73 | 0.90 |
| SVM (CMAQ + Covs) | 0.72 | 0.10 | 0.31 | 0.67 | 0.74 | 0.80 | 0.91 |
| NN (CMAQ + covs) | 0.71 | 0.11 | 0.29 | 0.66 | 0.73 | 0.80 | 0.94 |
Table 4 presents various predictive performance statistics, averaged over space and time, using all sites, while Tables 5, 6 and 7 focus on stratified analyses and present Pearson correlation between the predicted PM2.5 concentration and the observed concentration for specific subsets of sites (Tables 5 and 6) or subsets of days and sites (Table 7). It is clear that in each case, using the raw CMAQ output as an estimate of PM2.5 concentration is not very useful.
Table 5. Overall performance of exposure assessment methods by number of nearby stations.
Correlation coefficient between PM2.5 concentration predictions and observed PM2.5 concentration in μg/m3 stratified by the number of active monitoring sites within 50 miles of the prediction site for each day. The methods considered are: raw CMAQ output, ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”).
| Active nearby stations | <5 | 5–9 | 10–19 | ≥ 20 |
|---|---|---|---|---|
| CMAQ | 0.50 | 0.56 | 0.59 | 0.59 |
| OLS (CMAQ) | 0.60 | 0.69 | 0.73 | 0.77 |
| OLS (Covs) | 0.70 | 0.80 | 0.81 | 0.85 |
| OLS (CMAQ+Covs) | 0.64 | 0.74 | 0.75 | 0.79 |
| IDW | 0.82 | 0.91 | 0.92 | 0.90 |
| UK (CMAQ) | 0.84 | 0.92 | 0.92 | 0.92 |
| UK (Covs) | 0.83 | 0.91 | 0.92 | 0.92 |
| UK (CMAQ+Covs) | 0.81 | 0.91 | 0.91 | 0.91 |
| Downscaler(CMAQ) | 0.83 | 0.92 | 0.93 | 0.92 |
| RF (CMAQ + Covs) | 0.69 | 0.78 | 0.81 | 0.84 |
| SVM (CMAQ + Covs) | 0.74 | 0.86 | 0.87 | 0.87 |
| NN (CMAQ + covs) | 0.74 | 0.83 | 0.85 | 0.86 |
Table 6. Overall performance of exposure assessment methods by urbanization.
Correlation coefficient between PM2.5 concentration predictions and observed PM2.5 concentration in μg/m3 stratified by urbanization. The methods considered are: raw CMAQ output, ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”). The last line reports the mean and standard deviation, in parenthesis, for the observed PM2.5 concentration at urban versus nonurban monitoring sites.
| Method | Urban | Non-Urban |
|---|---|---|
| CMAQ | 0.54 | 0.50 |
| OLS (CMAQ) | 0.66 | 0.60 |
| OLS (Covs) | 0.75 | 0.69 |
| OLS (CMAQ+Covs) | 0.68 | 0.63 |
| IDW | 0.87 | 0.77 |
| UK (CMAQ) | 0.88 | 0.80 |
| UK (Covs) | 0.87 | 0.80 |
| UK (CMAQ+Covs) | 0.86 | 0.79 |
| Downscaler (CMAQ) | 0.88 | 0.80 |
| RF (CMAQ + Covs) | 0.74 | 0.67 |
| SVM (CMAQ + Covs) | 0.80 | 0.74 |
| NN (CMAQ + Covs) | 0.79 | 0.73 |
| PM2.5 | 10.16 (6.21) | 9.03 (6.01) |
In Table 4, predictions obtained via a linear regression model fit separately to PM2.5 concentration each day serves as a baseline for comparison, and it yields an RMSE of 4.22 μg/m3 and a correlation of 0.74 when both CMAQ and the selected covariates listed in Table 1 are included in the model. Machine learning methods yield predictions that are substantially improved over those obtained via least squares, by accounting for potential non-linear and interaction effects of the covariates. Of the machine learning algorithms, Support Vector Regression has the smallest RMSE (3.83 μg/m3) and the highest correlation (0.79). All of the statistical methods that explicitly model the spatial correlation in the data have smaller RMSE and higher correlation than the machine learning methods. Inverse distance weighting which generates prediction by simply taking a local average of the available monitoring data has an RMSE of 3.22 μg/m3. The best method in terms of RMSE is Universal Kriging (UK) when only CMAQ is used as a covariate. The spatial downscaler model yields a comparable RMSE (3.10 μg/m3 vs 3.08 μg/m3) and same correlation (0.87).
Table 5 examines whether the quality of the predictions is improved based on the number of nearby monitoring sites with data available on the day of the prediction. The table presents predictive performance results stratified by the number of monitoring stations within a 50 miles radius of the prediction location with same-day PM2.5 measurements. As with overall predictions, the geostatistical methods have the highest correlation between predicted PM2.5 concentrations and observed PM2.5 levels for all numbers of active training sites. The Appendix includes analogous tables stratified by distance to nearest monitoring location, longitude, and season, while this section presents results stratified by urbanization (Table 6) and PM2.5 concentration magnitude (Table 7).
The ranking of the prediction methods remains similar across all of these strata, with Universal Kriging with CMAQ as only covariate yielding the best results. In addition, for all the spatial statistical methods generate predictions with accurate uncertainty quantification: the 95% prediction intervals constructed using spatial statistical methods have coverage at or near the nominal 95% level.
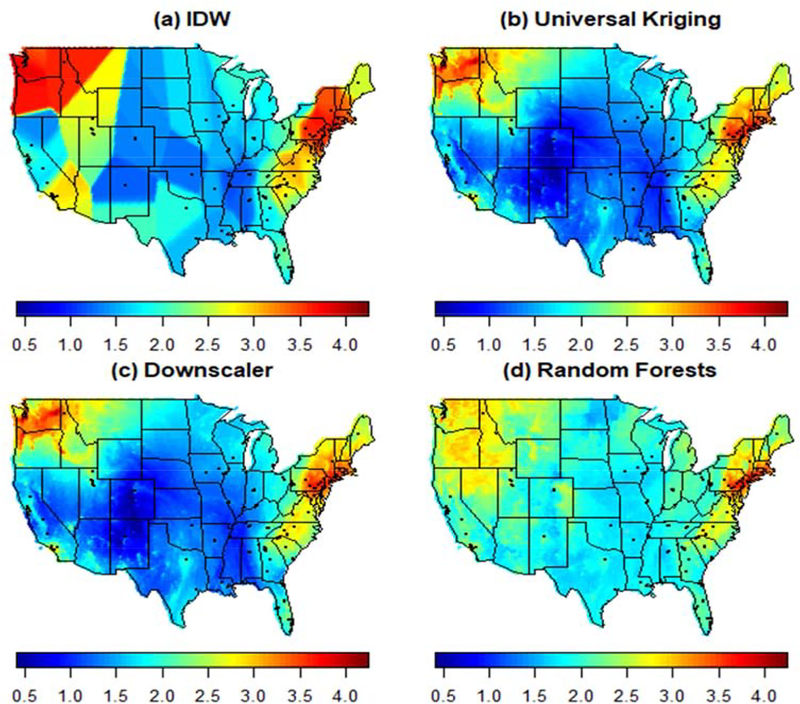
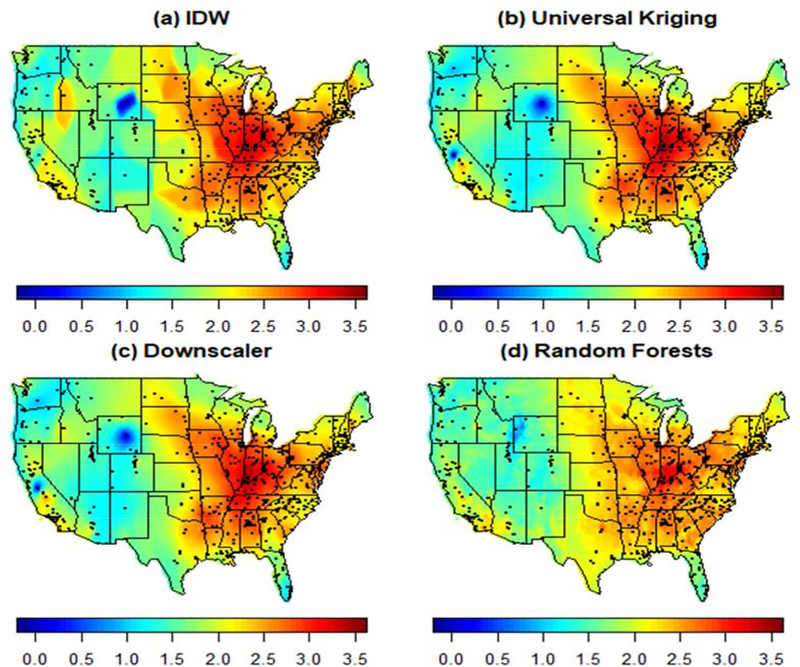
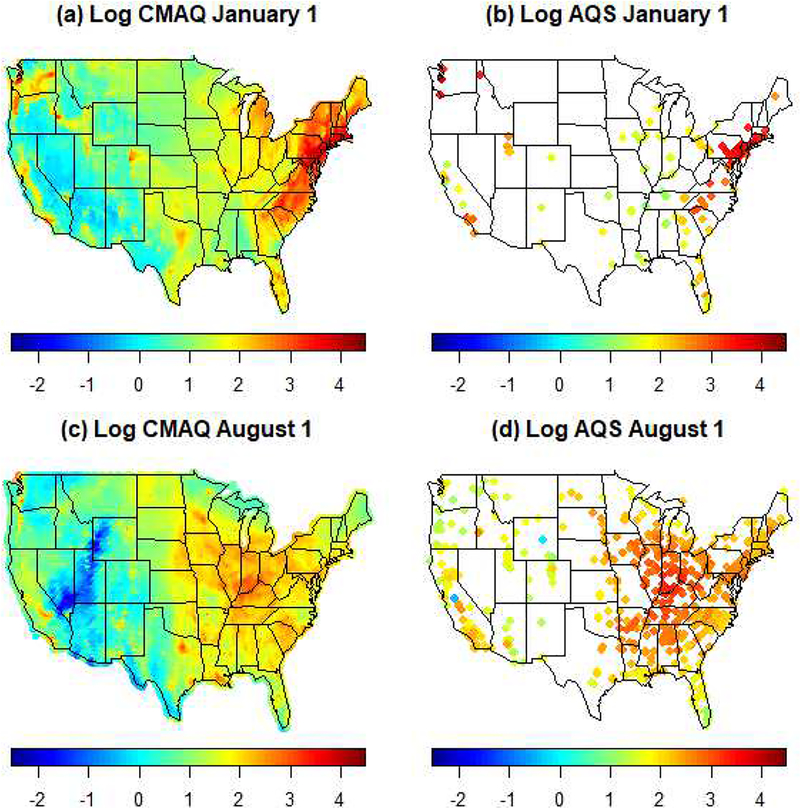
Spatial predictions of log PM2.5 over the entire contiguous United States can be seen in Figures 4 and 5 for January 1, 2011 and August 1, 2011, respectively. As the figures indicate, PM2.5 concentration tends to be higher in the winter (January 1) than in the summer (August 1), with areas in the North East and the North West, especially along the coasts, having higher PM2.5 levels. In contrast, on August 1, it is the interior region in the Eastern United States that experienced higher levels of PM2.5 compared to the rest of the country.
Figure 4.
Predicted log PM2.5 concentration for January 1, 2011 using Inverse Distance Weighting (“IDW”), Universal Kriging with CMAQ as only predictor, the Downscaler model and Random Forest. Points displayed in the map represent active monitors.
Figure 5.
Predicted log PM2.5 concentration for August 1, 2011 using Inverse Distance Weighting (“IDW”), Universal Kriging with CMAQ as only predictor, the Downscaler model and Random Forest. Points displayed in the map represent active monitors.
The predictive surfaces of PM2.5 concentration yielded by Universal Kriging and the downscaler model present similar spatial gradients on both days. In both cases, the surfaces are generally smooth, but present fine spatial variation particularly in areas where more monitoring data is available. Although geographical space is utilized as another independent variable in Random Forest (through the use of latitude and longitude as covariates), the spatial maps of PM2.5 concentration yielded by Random Forest are typically smooth and tend to display similar patterns to those observed in the predictive surfaces generated by the spatial statistical methods (UK and the downscaler). However, Random Forest’s predictive surfaces generally have less variability than the predictive surfaces obtained using spatial statistics methods, and tend to generate predictive distributions that do not have long tails as the predicted PM2.5 values. As a result, predictions tend to shrink closer to the mean. Finally, while the IDW method seems to yield a spatial surface that is closer to that obtained using the other methods on August 1, the predictive surface is overly smooth and does not show fine-scale spatial variability. In particular, since IDW generates predictions using only the information available from nearby monitors on each day, on days where few observations are available the predictions tend to be the same across large subregions. This leads to maps with a blocky appearance, and sudden, unrealistic, sharp changes in regions where more monitoring data is available. As such, predictive PM2.5 maps generated via IDW are not recommended as maps capturing the spatial distribution of PM2.5 concentration in the contiguous United States.
5. DISCUSSION
In this paper, we present a review of commonly used statistical and machine learning methods for air pollution exposure assessment with the goal of improving our understanding of the fundamental differences among these methods. The contribution of this paper is to provide a rigorous comparison of these exposure modeling methods and make analytic code available to the broader scientific community to implement these techniques through a GitHub repository (https://github.com/yawenguan/DataFusion). In our case study on PM2.5 concentration in the contiguous United States, we have found that the downscaler model and Universal Kriging yield better predictive performance than machine learning algorithms, potentially due to the fact that these methods explicitly account for the spatial dependence in PM2.5 concentration. This may hold true for other environmental exposure (e.g. ozone, or other pollutants of primary origin) where spatial dependence is not negligible. We believe that this is an important finding given the ever increasing utilization of predicted ambient exposures in air pollution epidemiological as well as environmental justice studies, and the widespread application of Artificial Intelligence (AI) in all realm of science.
Machine learning algorithms are attractive methods for analyzing large data sets due to their computational speed and easy implementation for massive data, partly driven by the recent availability of highly optimized computing software. In this review paper, we have chosen Random Forest, Support Vector Regression and Neural Network for comparison, because these methods have already been used for exposure modeling (Hu et al., 2017; Liu et al., 2017; Reid et al., 2015) and software within R is readily available.
In our case study, we have found that the machine learning methods yield worse predictive performance than the statistical methods that account for spatial dependence. An explanation for this finding can be due to the number of variables used in our case study, which is smaller than the number of variables typically used in applications of these methods. Another reason for the underperformance of machine learning techniques might be due to the fact that these methods do not account explicitly for spatial dependence, which we have shown to be important for exposure modeling. The better performance by spatial statistical models in the first case is likely due to the borrowing of strength from neighboring observations. This also indicates that to improve the predictive performance of machine learning methods, algorithms that leverage values from neighboring sites for prediction, such as it is done in convolution neural net, might be useful for this application.
We note also that in this paper we have focused on estimation of regional PM2.5 concentration, as our interest was in generating maps of PM2.5 concentration across the contiguous United States. As such, we have not included among the predictors indicators of traffic or measure of traffic volumes, which have been found to be important predictors of air pollution in urban environments in previous studies. As spatial statistical studies of traffic-related pollutants and PM2.5 concentration in near-road urban environments have shown that in such settings, the spatial dependence in air pollutants level decays rather quickly and it is mostly explained by wind speed and wind direction (e.g. being downwind vs upwind; Gilani et al, 2016, 2019), it is plausible that in that context, a comparison of spatial statistical models and machine learning methods will yield opposite results from what we have obtained here.
Figure 1.
Annual mean log PM2.5 concentration for year 2011 in log μg/m3 as estimated by CMAQ output versus AQS monitor data.
Highlights.
We evaluate exposure assessment methods for ambient PM2.5 over the US in 2011.
Evaluation across-paradigm and code for methods presented in the paper provided.
Air quality model output (CMAQ), meteorological and land-use covariates are used.
Assessment of spatio-temporal estimation ability, overall and for different strata.
Statistical methods that account for spatial dependence outperform any other method.
6. ACKNOWLEDGMENTS
The authors thank Drs. Xuefie Hu and Yang Liu for providing the land use and meteorology data, and James Mulholland and Niru Senthilkumar for providing the CMAQ and air quality data. This material was based upon work partially supported by the National Science Foundation under Grant DMS-1638521 to the Statistical and Applied Mathematical Sciences Institute. BJR is also supported by NIH R01ES027892, DOI-JFSP 14-1-04-9 and KAUST 3800.2; VJB is supported by NIH P30ES017885. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Institutes of Health and the National Science Foundation, U.S.
Funding sources: National Science Foundation Grant DMS-1638521, National Institutes of Health (NIH) Grant R01ES027892, National Institutes of Health (NIH) Grant P30ES017885, Department of Interior Grant DOI-JFSP 14-1-04-9 and King Abdullah University of Science and Technology Grant 3800.2.
7. APPENDIX
This Appendix presents maps with spatial predictions of log PM2.5 concentrations in μg/m3 over the entire contiguous United States on January 1, 2011 and August 1, 2011, respectively, as well maps of the observed and CMAQ output for the same day. In addition, it presents a comparison of the various methods for PM2.5 concentration estimation, similar to those discussed in Section 4.
Specifically, Table A1 provides a simplified view on characteristics of the various methods compared in this case study with respect to computational speed, prediction accuracy, implementation difficulty and whether prediction uncertainty can be obtained for the various statistical and machine learning methods. We note that the computational speed varies across machines and it depends heavily on the software and code optimization. Hence, the computational speed here only serves as a rough guideline of the computational complexity and the comparisons are made based on the authors’ experience.
Additional tables compare the quality of the predictions by the various methods with stratification by distance to nearest monitoring location (Table A2), longitude (Table A3), and season (Table A4).
Table A1. Assessment of computational speed, difficulty, and accuracy of exposure assessment methods.
The table reports whether for our data analysis the methods were executed in less than a few hours on a standard PC (“Fast”), whether they ranked near the best cross-validation error (“Accurate”), whether they were fit with standard software without many tuning parameters (“Easy”) and whether predictions were paired with measures of uncertainty (“Uncertainty”).
| Method | Fast | Accurate | Easy | Uncertainty |
|---|---|---|---|---|
| OLS | ✓ | ✕ | ✓ | ✓ |
| IDW | ✓ | ✓ | ✓ | ✕ |
| Universal Kriging | ✓ | ✓ | ✓ | ✓ |
| Downscaler | ✕ | ✓ | ✕ | ✓ |
| Random forests | ✓ | ✓ | ✓ | ✓ |
| Support vector regression | ✓ | ✕ | ✓ | ✕ |
| Neural networks | ✓ | ✕ | ✕ | ✕ |
Table A2. Overall performance of exposure assessment methods stratified by distance to closest other ACTIVE monitoring station on each day.
Correlation coefficient between PM2.5 concentration predictions and observed PM2.5 concentration in μg/m3 stratified by distance to closest other ACTIVE monitoring station on each day. The methods consdered are: raw CMAQ output, ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”). The last line in the table reports the mean and standard deviation, in parenthesis, of PM2.5 concentration observed at monitoring sites within each substratum.
| Method | Closest Station < 50 Miles | Closest Station ≥50 Miles |
|---|---|---|
| CMAQ | 0.53 | 0.50 |
| OLS (CMAQ) | 0.66 | 0.58 |
| OLS (Covs) | 0.75 | 0.65 |
| OLS (CMAQ+Covs) | 0.69 | 0.57 |
| IDW | 0.88 | 0.72 |
| UK (CMAQ) | 0.89 | 0.77 |
| UK (Covs) | 0.88 | 0.76 |
| UK (CMAQ+Covs) | 0.88 | 0.71 |
| Downscaler (CMAQ) | 0.89 | 0.76 |
| RF (CMAQ + Covs) | 0.75 | 0.64 |
| SVM (CMAQ + Covs) | 0.81 | 0.68 |
| NN (CMAQ + Covs) | 0.80 | 0.70 |
| PM2.5 | 10.07 (6.12) | 9.36 (6.56) |
Table A3. Cross-validation results by East/West location in the US identified by the vertical line longitude=−100.
Correlation coefficient between PM2.5 concentration predictions and observed PM2.5 concentration in μg/m3 stratified by East/West location. The methods considered are: raw CMAQ output, ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”). The last line in the table provides the mean and standard deviation (in parenthesis) for PM2.5 concentration observed at monitoring sites within each category.
| Method | West | East |
|---|---|---|
| CMAQ | 0.41 | 0.53 |
| OLS (CMAQ) | 0.40 | 0.65 |
| OLS (Covs) | 0.61 | 0.74 |
| OLS (CMAQ+Covs) | 0.56 | 0.67 |
| IDW | 0.79 | 0.85 |
| UK (CMAQ) | 0.79 | 0.87 |
| UK (Covs) | 0.78 | 0.86 |
| UK (CMAQ+Covs) | 0.78 | 0.85 |
| Downscaler (CMAQ) | 0.79 | 0.87 |
| RF (CMAQ + Covs) | 0.64 | 0.73 |
| SVM (CMAQ + Covs) | 0.71 | 0.79 |
| NN (CMAQ + Covs) | 0.71 | 0.78 |
| PM2.5 | 8.87 (7.69) | 9.97 (6.19) |
Table A4. Cross-validation results by season.
Correlation coefficient between PM2.5 concentration predictions and observed PM2.5 concentration in μg/m3 stratified by season. The methods considered are: raw CMAQ output, ordinary least squares (“OLS”), inverse distance weighting (“IDW”), universal Kriging(“UK”), downscaler, random forests (“RF”), support vector regression (“SVR”) and Neural networks (“NN”). Methods use either CMAQ and/or other geographic covariates (“Covs”). The last line in the table provides the mean and standard deviation, in parenthesis, for monitored PM2.5 concentration during each season.
| Method | Winter | Spring | Summer | Fall |
|---|---|---|---|---|
| CMAQ | 0.57 | 0.60 | 0.57 | 0.48 |
| OLS (CMAQ) | 0.71 | 0.69 | 0.61 | 0.56 |
| OLS (Covs) | 0.80 | 0.75 | 0.70 | 0.69 |
| OLS (CMAQ+Covs) | 0.75 | 0.67 | 0.63 | 0.63 |
| IDW | 0.89 | 0.89 | 0.81 | 0.83 |
| UK (CMAQ) | 0.90 | 0.90 | 0.83 | 0.84 |
| UK (Covs) | 0.90 | 0.89 | 0.82 | 0.84 |
| UK (CMAQ+Covs) | 0.90 | 0.89 | 0.79 | 0.83 |
| Downscaler (CMAQ) | 0.90 | 0.90 | 0.82 | 0.84 |
| RF (CMAQ + Covs) | 0.80 | 0.73 | 0.69 | 0.70 |
| SVM (CMAQ + Covs) | 0.83 | 0.81 | 0.77 | 0;.75 |
| NN (CMAQ + Covs) | 0.84 | 0.81 | 0.71 | 0.76 |
| PM2.5 | 10.59 (7.05) | 9.47 (5.81) | 10.82 (5.93) | 9.01 (5.74) |
Figure A1. Number of active monitors per day over year 2011.
Figure A2.
Average daily log PM2.5 concentration 2011 in log μg/m3 as estimated by CMAQ output versus AQS monitor data on January 1 and August 1, 2011, respectively.
Figure A3.
Schematic representation of the data and methods applied and considered in the study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
The authors declare they have no actual or potential competing financial interests
REFERENCES
- Adam-Poupart A, Brand A, Fournier M, Jerrett M and Smargiassi A (2014). Spatiotemporal modeling of ozone levels in Quebec (Canada): a comparison of kriging, land-use regression (LUR), and combined Bayesian maximum entropy–lur approaches. Environmental Health Perspectives, 122, 970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexeeff SE, Schwartz J, Kloog I, Chudnovsky A, Koutrakis P and Coull BA (2015). Consequences of kriging and land use regression for pm2. 5 predictions in epidemiologic analyses: insights into spatial variability using high-resolution satellite data. Journal of Exposure Science and Environmental Epidemiology, 25, 138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berrocal VJ, Gelfand AE and Holland DM (2010). A spatio-temporal downscaler for output from numerical models. Journal of Agricultural, Biological, and Environmental Statistics, 15,176–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L (2001) Random forests. Machine Learning, 45, 5–32. URL: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- Byun D and Schere K (2006). Review of the governing equations, computational algorithms, and other components of the models-3 community multiscale air quality (cmaq) modeling system. Applied Mechanical Reviews, 59, 51–77. URL: https://CRAN.R-project.org/doc/Rnews/. [Google Scholar]
- Chang HH, Reich BJ and Miranda ML (2011). Time-to-event analysis of fine particle air pollution and preterm birth: results from North Carolina, 2001–2005. American Journal of Epidemiology, 175, 91–98. [DOI] [PubMed] [Google Scholar]
- Chen S, Yuval, and Broday DM. (2018). A new modeling approach for assessing the contribution of industrial and traffic emissions to ambient NOx concentrations. Atmospheric Environment, 173, 173–184. [Google Scholar]
- Chollet F (2015) Keras. https://keras.io. [Google Scholar]
- Cortes C and Vapnik V (1995). Support-vector networks. Machine learning, 20, 273–297. [Google Scholar]
- Cressie N (1993). Statistics for spatial data Wiley series in probability and mathematical statistics: Applied probability and statistics. J. Wiley; URL: https://books.google.com/books?id=4SdRAAAAMAAJ. [Google Scholar]
- Di Q, Dai L, Wang Y, Zanobetti A, Choirat C, Schwartz JD and Dominici F (2017). Association of short-term exposure to air pollution with mortality in older adults. JAMA, 318, 2446–2456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Q, Kloog I, Koutrakis P, Lyapustin A, Wang Y and Schwartz J (2016). Assessing PM2.5 exposures with high spatiotemporal resolution across the continental united states. Environmental Science & Technology, 50, 4712–4721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimitriadou E, Hornik K, Leisch F, Meyer D, Weingessel A and Leisch MF (2006). The e1071 package. Misc Functions of Department of Statistics (e1071), TU Wien. [Google Scholar]
- Finley AO, Banerjee S and Gelfand AE (2015). spBayes for large univariate and multivariate point-referenced spatio-temporal data models. Journal of Statistical Software, 63, 1–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Carlin J, Stern H, Dunson D, Vehtari A and Rubin D (2013) Bayesian Data Analysis, Third Edition Chapman & Hall/CRC Texts in Statistical Science. Taylor & Francis; URL: https://books.google.com/books?id=ZXL6AQAAQBAJ. [Google Scholar]
- Gilani O, Berrocal VJ, and Batterman S (2016). Non-stationary spatio-temporal modeling of traffic-related pollutants in near-road environments. Spatial and spatio-temporal epidemiology, 18, 24–37. [DOI] [PubMed] [Google Scholar]
- Gilani O, Berrocal VJ, and Batterman S (2019). Nonstationary spatiotemporal Bayesian data fusion for pollutants in the near-road environment. Environmetrics. DOI: 10.1002/env.2581. [DOI] [Google Scholar]
- Goodfellow I, Bengio Y and Courville A (2016). Deep Learning. MIT Press; http://www.deeplearningbook.org. [Google Scholar]
- Hao H, Chang HH, Holmes HA, Mulholland JA, Klein M, Darrow LA and Strickland MJ (2016). Air pollution and preterm birth in the US state of Georgia (2002–2006): Associations with concentrations of 11 ambient air pollutants estimated by combining Community Multiscale Air quality model (CMAQ) simulations with stationary monitor measurements. Environmental Health Perspectives, 124, 875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R and Friedman J (2001). The Elements of Statistical Learning. Springer Series in Statistics. New York, NY, USA: Springer New York Inc. [Google Scholar]
- Hoek G, Beelen R, de Hoogh K, Vienneau D, Gulliver J, Fischer P and Briggs D (2008). A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmospheric Environment, 42, 7561–7578. [Google Scholar]
- Hu X, Belle JH, Meng X, Wildani A, Waller LA, Strickland MJ and Liu Y (2017). Estimating PM2.5 concentrations in the conterminous United States using the Random Forest approach. Environmental Science & Technology, 51, 6936–6944. [DOI] [PubMed] [Google Scholar]
- James G, Witten D, Hastie T and Tibshirani R (2013). An introduction to statistical learning, Vol. 112 Springer, New York. [Google Scholar]
- Keller JP, Olives C, Kim S-Y, Sheppard L, Sampson PD, Szpiro AA, Oron AP, Lindström J, Vedal S and Kaufman JD (2015). A unified spatiotemporal modeling approach for predicting concentrations of multiple air pollutants in the Multi-Ethnic Study of Atherosclerosis and air pollution. Environmental Health Perspectives, 123, 301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kloog I, Coull BA, Zanobetti A, Koutrakis P and Schwartz JD (2012). Acute and chronic effects of particles on hospital admissions in New England. PloS ONE, 7, e34664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutner MH, Nachtsheim CJ, Neter J, Li W (2005). Applied Linear Statistical Models. McGraw-Hill international edition McGraw-Hill Irwin: URL:https://books.google.com/books?id=0xqCAAAACAAJ. [Google Scholar]
- Leinonen R, Sugawara H, Shumway M and Collaboration INSD (2010). The sequence read archive. Nucleic Acids Research, 39, D19–D21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liaw A and Wiener M (2002). Classification and regression by randomforest. R News, 2, 18–22. URL: https://CRAN.R-project.org/doc/Rnews/. [Google Scholar]
- Lindström J, Szpiro A, Sampson P, Bergen S and Oron A (2012). Spatiotemporal: Spatiotemporal model estimation. R Package version 1. [Google Scholar]
- Liu B-C, Binaykia A, Chang P-C, Tiwari MK and Tsao C-C (2017). Urban air quality forecasting based on multi-dimensional collaborative Support Vector Regression (SVR): A case study of Beijing-Tianjin-Shijiazhuang. PloS ONE, 12, e0179763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mailman MD, Feolo M, Jin Y, Kimura M, Tryka K, Bagoutdinov R, Hao L, Kiang A, Paschall J, Phan L, Popova N, Pretel S, Ziyabari L, Lee M, Shao Y, Wang ZY, Sirotkin K, Ward M, Kholodov M, Zbicz K, Beck J, Kimelman M, Shevelev S, Preuss D, Yaschenko E, Graeff A, Ostell J and Sherry ST (2007). The NCBDI dbGaP database of genotypes and phenotypes. Nature Genetics, 39, 1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan J and Sonquist J (1963). Problems in the analysis of survey data and a proposal. Journal of the American Statistical Association, 58, 415–434. [Google Scholar]
- R Core Team (2018). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: URL: https://www.R-project.org/. [Google Scholar]
- Reich BJ, Eidsvik J, Guindani M, Nail AJ and Schmidt AM (2011). A class of covariate dependent spatiotemporal covariance functions. The Annals of Applied Statistics, 5, 2265–2287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid CE, Jerrett M, Petersen ML, Pfister GG, Morefield PE, Tager IB, Raffuse SM and Balmes JR (2015). Spatiotemporal prediction of fine particulate matter during the 2008 Northern California wildfires using machine learning. Environmental Science & Technology, 49, 3887–3896. [DOI] [PubMed] [Google Scholar]
- Ribeiro PJ Jr and Diggle PJ (2018). geoR: Analysis of Geostatistical Data. URL: https://CRAN.Rproject.org/package=geoR. R package version 1.7–5.2.1. [Google Scholar]
- Rumelhart DE, Hinton GE and Williams RJ (1986). Learning internal representations by error propagation In Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1: Foundations (eds. Rumelhart DEand Mcclelland JL), 318–362. Cambridge, MA: MIT Press. [Google Scholar]
- Shaddick G, Thomas M, Amini H, Broday DM, Cohen A, Frostad J, Green A, Gumy S, Liu Y, Martin RV et al. (2018). Data integration for the assessment of population exposure to ambient air pollution for global burden of disease assessment. Environmental Science & Technology. DOI: 10.1021/acs.est.8b02864. [DOI] [PubMed] [Google Scholar]
- Singh KP, Gupta S and Rai P (2013). Identifying pollution sources and predicting urban air quality using ensemble learning methods. Atmospheric Environment, 80, 426–437. [Google Scholar]
- Strickland MJ, Hao H, Hu X, Chang HH, Darrow LA and Liu Y (2016). Pediatric emergency visits and short-term changes in PM2.5 concentrations in the US State of Georgia. Environmental Health Perspectives, 124, 690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang R, Blangiardo M and Gulliver J (2013). Using building heights and street configuration to enhance intraurban pm10, nox, and no2 land use regression models. Environmental Science & Technology, 47, 11643–11650. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, and WU-Minn HCP Consortium (2013). The human connectome project: an overview. Neuroimage, 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M, Sampson PD, Hu J, Kleeman M, Keller JP, Olives C, Szpiro AA, Vedal S and Kaufman JD (2016). Combining land-use regression and chemical transport modeling in a spatiotemporal geostatistical model for ozone and PM2.5. Environmental Science & Technology, 50, 5111–5118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Russell A, Mulholland J, Odman T, Hu Y, Chang HH and Kumar N (2018). Cross-comparison and evaluation of air pollution field estimation methods. Atmospheric Environment, 179, 49–60. [Google Scholar]