In Vivo Estimates of Liver Metabolic Flux Assessed by ¹³C-Propionate and ¹³C-Lactate Are Impacted by Tracer Recycling and Equilibrium Assumptions

SUMMARY

Isotope-based assessment of metabolic flux is achieved through a judicious balance of measurements and assumptions. Recent publications debate the validity of key assumptions used to model stable isotope labeling of liver metabolism in vivo. Here, we examine the controversy surrounding estimates of liver citric acid cycle and gluconeogenesis fluxes using a flexible modeling platform that enables rigorous testing of standard assumptions. Fasted C57BL/6J mice are infused with [¹³C₃]lactate or [¹³C₃]propionate isotopes, and hepatic fluxes are regressed using models with gradually increasing complexity and relaxed assumptions. We confirm that liver pyruvate cycling fluxes are incongruent between different ¹³C tracers in models with conventional assumptions. When models are expanded to include more labeling measurements and fewer constraining assumptions, however, liver pyruvate cycling is significant, and inconsistencies in hepatic flux estimates using [¹³C₃]lactate and [¹³C₃]propionate isotopes emanate, in part, from peripheral tracer recycling and incomplete isotope equilibration within the citric acid cycle.

Graphical Abstract

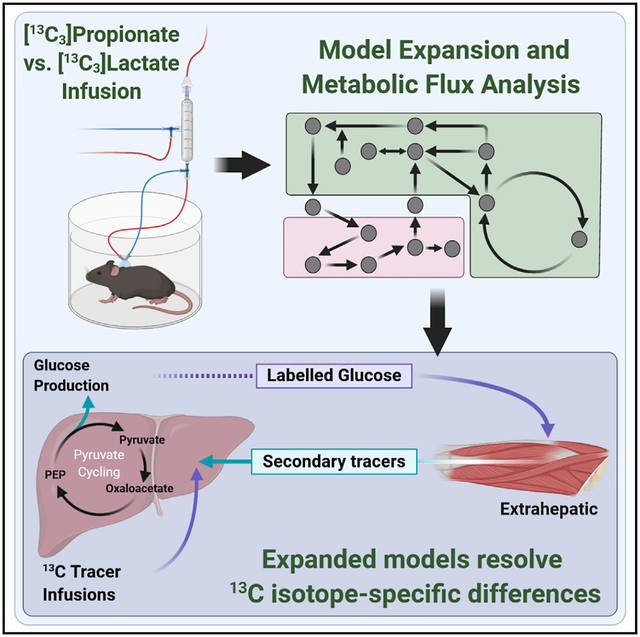
In Brief

Prior studies of in vivo liver metabolism using ¹³C tracers have produced divergent estimates of Krebs cycle and anaplerotic fluxes. Hasenour et al. present findings that are critical for interpreting experiments with two widely used metabolic tracers and introduce modeling strategies to improve isotope-based determination of liver metabolic fluxes.

INTRODUCTION

Hepatic gluconeogenesis and the mitochondrial citric acid cycle (CAC) act in concert to supply the body with glucose when the dietary supply is reduced (e.g., during fasting). Many reactions in these pathways are catalyzed by regulatory enzymes that have been proposed as drug targets for treating insulin resistance, type 2 diabetes, and fatty liver disease. There has been a long-running debate regarding the nature of liver metabolic adaptations that occur during progression of these obesity-related conditions. Some groups hypothesize that impairments in mitochondrial metabolism are responsible for accumulation of toxic lipid species that cause insulin resistance and tissue damage in the liver. Others hypothesize that hepatic lipid overload causes elevations in CAC and anaplerotic fluxes that drive excess gluconeogenesis and accumulation of toxic free radicals. Because metabolic flux alterations cannot be assessed in vivo without isotope tracers, the two competing hypotheses cannot be completely resolved without accurate methods to model and interpret data from in vivo isotope labeling experiments (ILEs).

An ILE introduces a stable or radioactive tracer (e.g., containing heavy isotopes such as ¹³C or ¹⁴C) to a live biological system. After the tracer has been sufficiently metabolized through the target biochemical pathways of interest, the isotope enrichment of downstream metabolites is determined experimentally. Because different pathways rearrange the labeled atoms in unique ways, it is often possible to calculate metabolic flux rates from the relative abundance of different isotopically labeled species (i.e., isotopomers) comprising those metabolites. Various approaches have been taken to estimate hepatic pathway fluxes from in vivo ILEs. Least-squares regression approaches have been developed to estimate fluxes from metabolite mass isotopomer distributions (MIDs). Other approaches relate positional isotopomer abundances to pathway fluxes through distilled mathematical equations.

Regardless of the approach, assumptions are implemented to limit the complexity of model-based flux analysis. It is often assumed that primary isotopes equilibrate completely in the liver; also, the release, circulation, and reuptake of enriched products of liver metabolism are assumed to have a negligible effect on liver metabolic flux estimates. A challenge to these assumptions was illustrated in the classic debate over in vivo estimates of the parameter y, which represents the ratio of liver anaplerosis to citrate synthase flux. In the academic exchange, studies that used isotopic acetate or lactate yielded very different flux ratios. This incompatibility was partially reconciled by evidence showing that, in contrast to lactate, the extensive extrahepatic metabolism of isotopic acetate generated metabolites that artifactually lowered y values (Beylot et al., 1995; Katz et al., 1993; Landau, 1991; Landau et al., 1993; Schumann et al., 1991).

The aforementioned studies underscore the importance of secondary sites of isotope metabolism and generation. We previously developed a modeling platform for in vivo liver metabolic flux analysis (MFA) that has been optimized for application to the conscious mouse (Hasenour et al., 2015; Figure 1A). Mice are infused with ²H and/or ¹³C isotopes, metabolites are analyzed by gas chromatography-mass spectrometry (GC-MS), and fluxes are estimated by least-squares regression of MID measurements using the Isotopomer Network Compartmental Analysis (INCA) software (Young, 2014). One advantage of INCA is that users can adjust the mathematical model to rapidly test the effects of specific reactions or modeling assumptions on the best-fit solution (Figure 1B). Nevertheless, our MFA platform shares some common challenges with other contemporary in vivo flux analysis approaches. Specifically, stable isotopes delivered in mass quantities may perturb the intrinsic metabolism of the pathways they are intended to assess. Primary isotopes or their enriched products may also be metabolized in non-target tissues in vivo, and metabolites enriched from their breakdown or exchange may circulate to the liver and further affect flux estimates.

Figure 1. Metabolic Flux Analysis (MFA) Determines Fluxes through Model-Based Regression of Isotope Labeling Measurements.

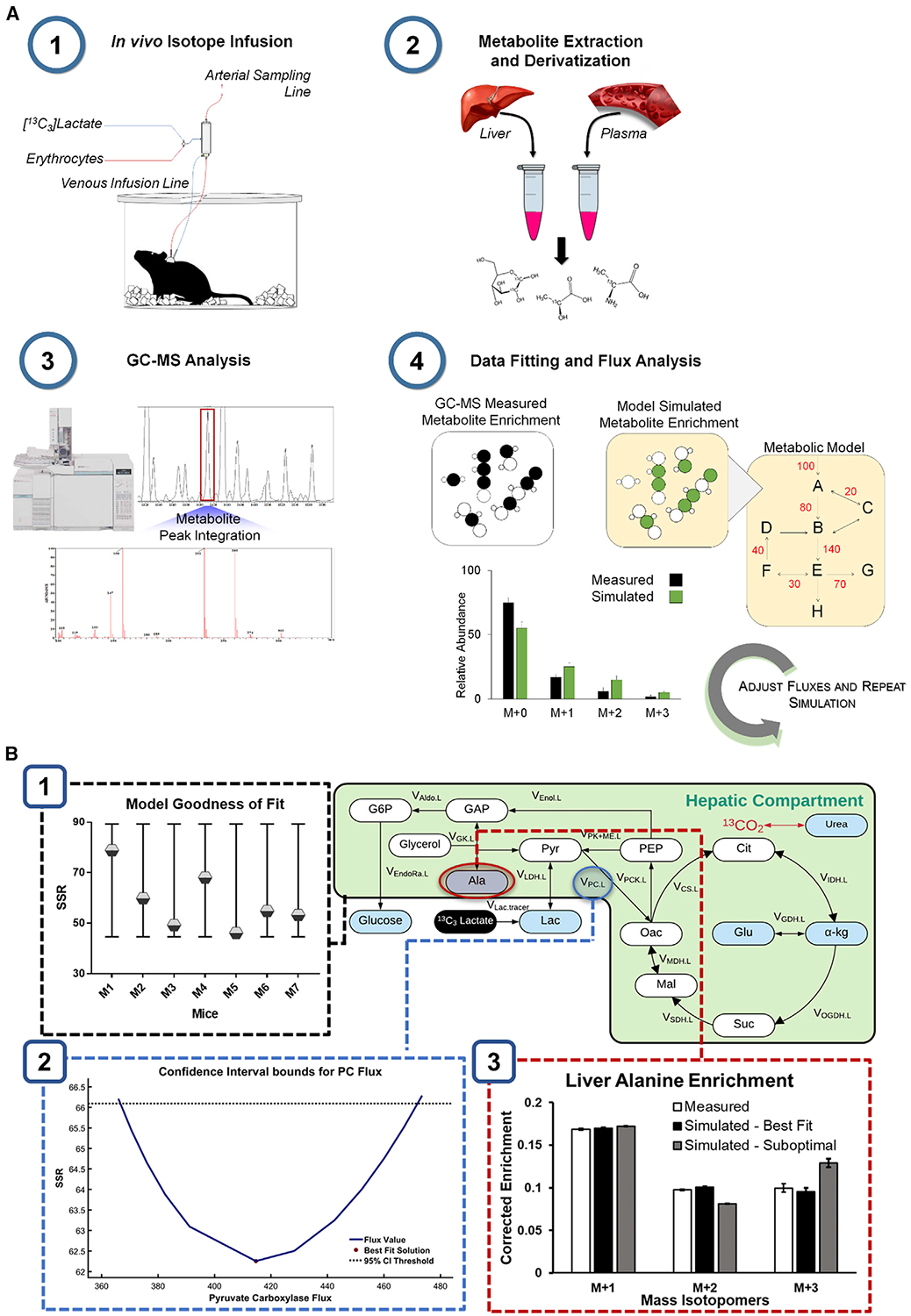
(A) MFA workflow. (1) Stable isotopes and replacement erythrocytes are infused intravenously into catheterized mice to enrich liver and plasma metabolites. (2) Plasma and liver tissue harvested at the end of the infusion are extracted and derivatized for GC-MS analysis. (3) Chromatographic peaks corresponding to the metabolites of interest are integrated and processed to obtain mass isotopomer distributions (MIDs). (4) The best-fit solution for all fluxes included in the metabolic model is obtained by minimizing the sum of squared residuals (SSR) between experimentally determined and model-simulated MIDs.

(B) Verification of the best-fit solution. (1) The best-fit solution for each mouse is accepted when the minimized SSR is within the expected range of a chi-square cumulative distribution function. (2) Flux uncertainties are assessed by determining the sensitivity of the minimized SSR to variations in each flux value. For example, the points of intersection with the dotted line indicate the boundaries of the 95% confidence interval (CI) of the estimated pyruvate carboxylase (PC) flux.

(3) Varying the flux values away from the optimal solution increases the measurement residuals, as shown in the suboptimal case.

Here we applied INCA to model the formation and effects of secondary tracers on liver flux analysis in vivo. These effects were tested in models that treat the liver as a single compartment or as a central hub in a multi-compartment network that accommodates the Cori cycle. Fluxes were regressed in models constrained by more common assumptions (base models) or expanded to rigorously account for incomplete isotope equilibration and additional metabolite measurements (expanded models). Using the aforementioned models, we assessed differences in the utility of [¹³C₃]propionate (¹³C₃Prop) and [¹³C₃] lactate (¹³C₃Lac) as tracers for regressing liver metabolic fluxes, with or without ²H isotopes, in overnight-fasted C57BL/6J mice.

RESULTS

Secondary Tracer Effects Influence Estimates of Liver Pyruvate Cycling

We previously described a base model of in vivo liver metabolism that was applied to regress hepatic CAC and gluconeogenic fluxes from MID measurements of plasma glucose obtained from conscious, unrestrained mice (Hasenour et al., 2015). The model consists of a biochemical network with hydrogen and carbon atom transitions defined for each reaction (Table S1). The model assumes full equilibration of four-carbon (4C) intermediates in the CAC and no re-entry of labeled CO₂ or other secondary tracers. We used the best-fit solutions obtained from our prior studies of four long-term fasted mice infused with ¹³C₃Prop/²H tracers to simulate the predicted MIDs of liver lactate (Lac261) and alanine (Ala260) fragment ions (Figure 2A). The simulated MIDs qualitatively resembled the measured enrichments of liver lactate and alanine, confirming that the base model is capable of accurately predicting isotope enrichments in other liver-derived metabolites in addition to glucose.

Figure 2. The Base Model Shows Evidence of Secondary Tracer Effects and Provides Different Estimates of Hepatic Fluxes for ¹³C₃Lac/²H and ¹³C₃Prop/²H Tracers.

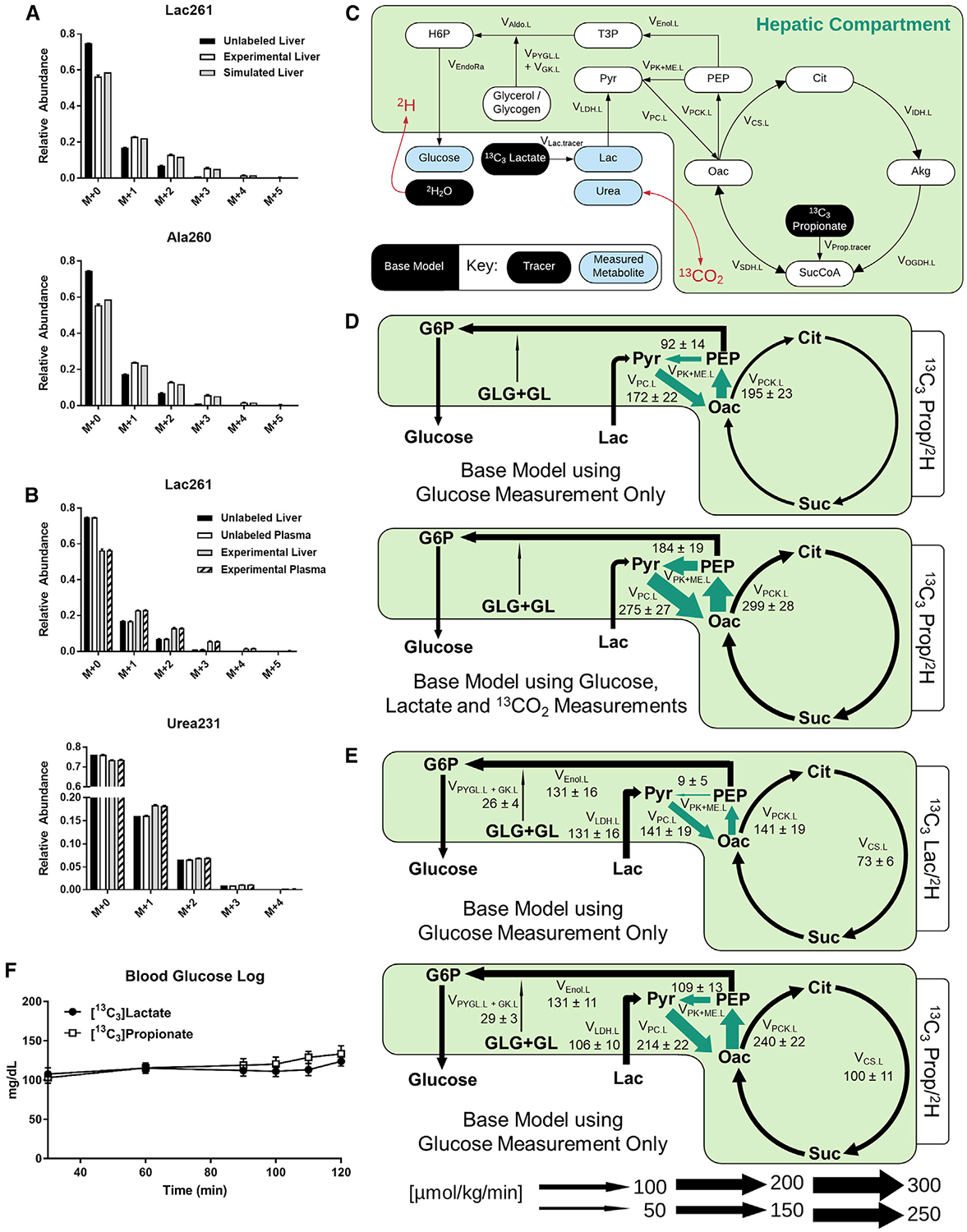
(A) Model-simulated and empirically measured (means ± SEM, n = 4) liver metabolite MIDs for lactate (mass-to-charge ratio [m/z] 261) and alanine (m/z 260).

(B) MIDs of plasma and liver lactate (m/z 261) and urea (m/z 231) obtained at isotopic steady state from long-term fasted C57BL/6J mice infused with ¹³C₃Prop/²H isotopes contrasted with MIDs from unlabeled control samples (means ± SEM, n = 4).

(C) Network map of the base model showing infusion of ¹³C₃Lac or ¹³C₃Prop with ²H₂O. Plasma urea was used as a proxy measurement for CO₂ enrichment.

(D) Flux estimates obtained from the base model using plasma glucose enrichments alone contrasted with those that included ¹³CO₂ and plasma lactate measurements in the flux regression. Arrows highlighted in green represent significant changes between flux estimates obtained from the base model using the two measurement sets. Fluxes are expressed as means ± SEM (n = 4, *p ≤ 0.05).

(E) Flux estimates obtained from the base model using plasma glucose enrichments alone in mice infused with ¹³C₃Lac/²H or ¹³C₃Prop/²H isotopes. Arrows highlighted in green show significant flux changes between the ¹³C₃Lac/²H and ¹³C₃Prop/²H isotope studies using the base model. Fluxes are expressed as means ± SEM (n = 6–7, *p ≤ 0.05).

(F) Blood glucose log (milligrams per deciliter) during infusion of ¹³C₃Lac/²H or ¹³C₃Prop/²H isotopes in 19- to 20-h-fasted C57BL/6J mice (means ± SEM, n = 6–7).

The assumption that secondary tracer effects are minimal is a pragmatic first approximation because analyzing sources of secondary tracers and deriving equations that account for those measurements ad hoc may be impractical in some cases. However, upon further investigation, we found that plasma lactate and urea (an indicator of circulating bicarbonate) were enriched significantly above the natural isotopic background following 120 min of ¹³C₃Prop/²H infusion (Figure 2B). Inclusion of these measured lactate and CO₂ enrichments in the model regressions (Figure 2C) increased pyruvate cycling flux estimates (V_PC.L, V_PCK.L, and V_PK+ME.L[see MFA Model Terminology in the STAR Methods]) in the liver (Figures 2D and S1A), similar to the effect of ¹⁴CO₂ recycling in prior studies using [3-¹⁴C]lactate in humans (Magnusson et al., 1991). In summary, these findings indicate that recycling of labeled lactate and CO₂ to the liver from the plasma is significant and that it likely affects in vivo estimates of liver pyruvate cycling obtained with ¹³C tracers when applying the assumptions implicit to our base model.

Incongruent Hepatic Flux Estimates Are Obtained with Base Models of ¹³C₃Lac/²H and ¹³C₃Prop/²H Tracers

Adjustments were made to the base model of liver metabolism to accommodate a study with infusion of ¹³C₃Lac/²H or ¹³C₃Prop/²H isotopes (Table S1). The infusion rate for each ¹³C isotope was analogous to previous studies (Hasenour et al., 2015; Perry et al., 2016). All mice were long term fasted to induce a gluconeogenic state of the liver. No differences in glucose-producing fluxes or blood glucose concentrations were observed ¹³C₃Lac/²H and ¹³C₃Prop/²H tracer infusions (Figures 2E, 2F, S1B, and S2A). Nevertheless, pyruvate cycle fluxes (V_PC.L, V_PCK.L, and V_PK+ME.L) estimated from ¹³C₃Prop/²H infusions were higher than those estimated with an analogous model of ¹³C₃Lac/²H infusion (Figures 2E, S1B, and S2A; Table S2). Thus, best-fit pyruvate cycle fluxes obtained from base models were incongruent between ¹³C₃Lac/²H and ¹³C₃Prop/²H labeling studies.

A similar disparity has been observed in perfused livers (Satapati et al., 2015) and in vivo (Perry et al., 2016). Others have proposed that these discrepancies may result from incomplete randomization of ¹³C atoms derived from ¹³C-lactate because of its lesser interconversion with symmetric 4C intermediates in the CAC. This is purported to occur for ¹³C tracers that enter the CAC downstream of fumarate (e.g., lactate or alanine) rather than those that enter upstream of succinate (e.g., propionate) (Satapati et al., 2015). Thus, we next examined the effects of incomplete isotope randomization on estimated flux ratios in our base models.

¹³C₃Lac Infusion without ²H Tracers Enables Rigorous Testing of Base Model Assumptions

Because of the aforementioned uncertainties related to (1) the extent of reversibility of 4C reactions of the CAC and (2) the influence of secondary tracer recycling on liver flux estimates, we designed a study to specifically address these assumptions by infusing mice with ¹³C₃Lac only (Figures 1A and 3A), without interference from ²H tracers. Our measurement set was expanded to include additional plasma and liver metabolites not typically considered in prior in vivo flux analyses: lactate and alanine from both liver and plasma and glutamate, alpha-ketoglutarate, aspartate, and urea extracted from liver tissue.

Figure 3. Testing the Assumptions of Secondary Tracer Effects and Fumarate/Oxaloacetate Equilibration in a ¹³C₃Lac Infusion Study.

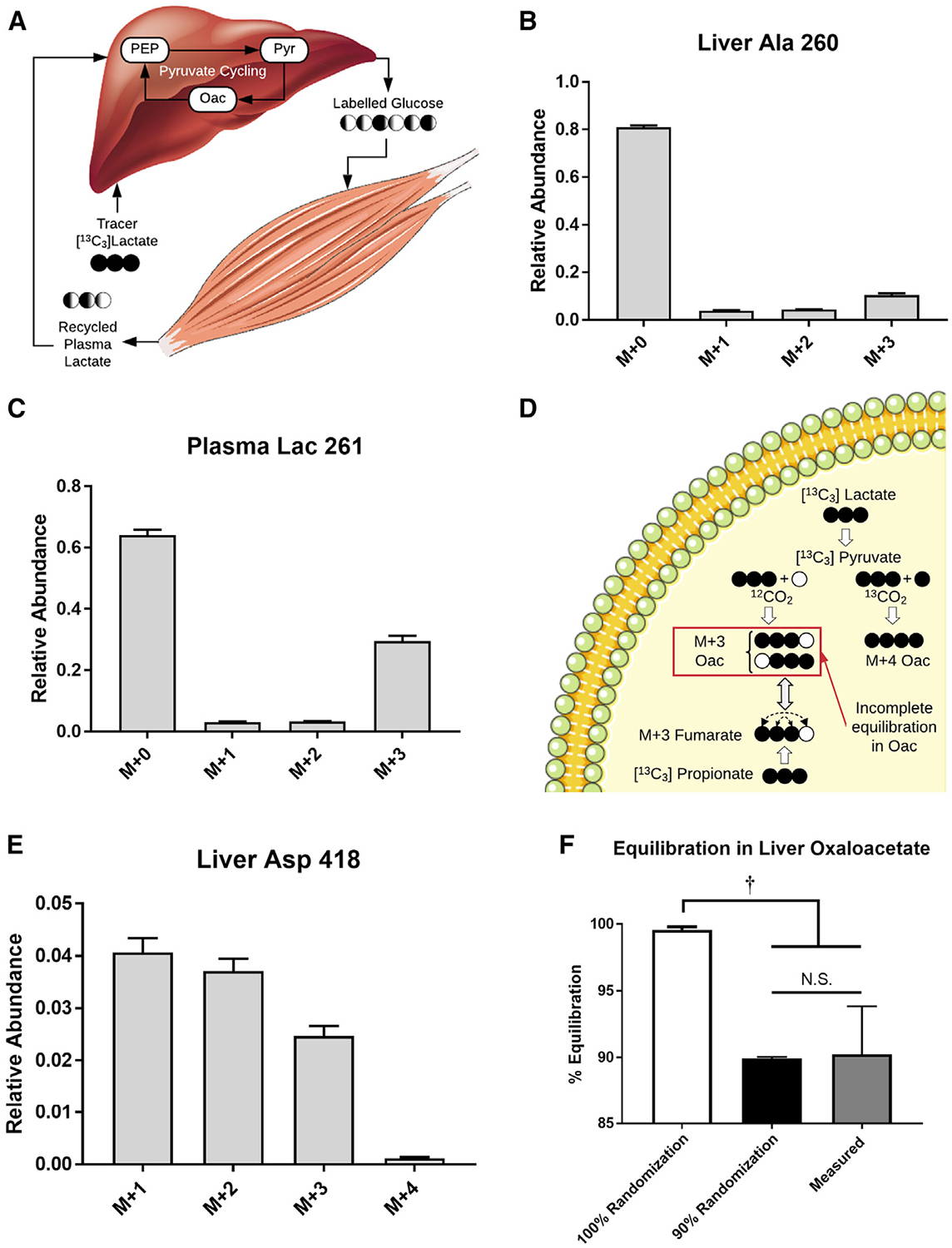
(A) Hepatic production of labeled glucose from ¹³C₃Lac can be metabolized by the muscle to produce recycled lactate that can contribute to secondary tracer effects (Cori cycling).

(B) MID of liver alanine (m/z 260) obtained at the end of the ¹³C₃Lac infusion. Data are corrected for natural isotope abundance and presented as means ± SEM (n = 7).

(C) MID of plasma lactate (m/z 261) obtained at the end of the ¹³C₃Lac infusion. Data are corrected for natural isotope abundance and presented as means ± SEM (n = 7).

(D) CAC isotopomers formed directly from ¹³C₃Lac or ¹³C₃Prop tracers. Carboxylation of M+3 pyruvate with ¹²CO₂ produces M+3 oxaloacetate (Oac) labeled at carbon positions 1–3 (i.e., Oac₁₁₁₀). Reversible exchange between Oac and fumarate results in randomization of Oac₁₁₁₀ and Oac₀₁₁₁ isotopomers because of the rotational symmetry of fumarate. The extent of equilibration between Oac₁₁₁₀ and Oac₀₁₁₁ depends on the rate of Oac-fumarate interconversion relative to the rate of lactate anaplerosis. In contrast, anaplerotic flux from propionate must traverse the symmetric fumarate pool prior to exiting the CAC. In the presence of ¹³CO₂ recycling, carboxylation of M+3 pyruvate with ¹³CO₂ produces M+4 Oac.

(E) The M+4 isotopomer is detected in the MID of liver aspartate (m/z 418), indicative of ¹³CO₂ recycling. Data are corrected for natural isotope abundance and presented as means ± SEM (n = 7).

(F) Equilibration of M+3 Oac isotopomers derived from ¹³C₃Lac. Percent equilibration was assessed using the measured MIDs of Asp418 and Asp390 ions as described in STAR Methods. This empirical estimate was compared with theoretical values obtained from model-simulated MIDs predicted under assumptions of 100% or 90% randomization of Oac produced in the PC reaction. Data are presented as means ± SEM (n = 7); †p ≤ 0.05.

Infusion of ¹³C₃Lac significantly increased the enrichment of circulating and hepatic metabolites (Figure S3). We observed significant M+1 and M+2 enrichments of liver alanine (Figure 3B) and plasma lactate (Figure 3C) after correcting the MIDs for natural background abundance of stable isotopes. The presence of these mass isotopomers reflects contributions from liver pyruvate cycling and extrahepatic Cori cycling. The abundance of recycled M+1 and M+2 isotopomers relative to the uncycled M+3 isotopomer is higher in liver alanine than in plasma lactate, indicating that intrahepatic pyruvate cycling occurs after lactate is extracted from plasma. The presence of M+1 and M+2 isotopomers in plasma lactate also provides some evidence that tracer recycling occurs outside of the liver, and the contribution from Cori cycling should be considered when making quantitative estimates of liver pyruvate cycle fluxes.

Next we examined measurements of liver oxaloacetate labeling to assess the randomization of M+3 species that traverse the 4C reactions of the CAC (Figure 3D). The measured M+3 and M+4 abundances of the Asp418 fragment ion (Figure 3E), which is biosynthetically derived from oxaloacetate, and the M+3 abundance of Asp390 (Figure S3A), which is derived from carbons 2–4 of oxaloacetate, were used to calculate the fractional abundances of the Oac₁₁₁₀ and Oac₀₁₁₁ isotopomers (STAR Methods). After accounting for ¹³CO₂ recycling, randomization in the oxaloacetate pool was determined to be ~90% with ¹³C₃Lac as a tracer (Figure 3F). A similar calculation can be performed with predicted Ala and Asp MIDs simulated from the base model of liver metabolism; a model that accounts for ¹³CO₂ recycling and assumes 90%, but not 100%, randomization leads to results comparable with those derived from the empirically measured MIDs (Figure 3F). These results suggest that in vivo estimates of hepatic metabolism would benefit from relaxing common assumptions regarding secondary tracer recycling and equilibration of 4C intermediates in the CAC.

Model Expansion to Account for Extrahepatic Metabolism Significantly Alters Pyruvate Cycle and CAC Fluxes

To relax several constraining assumptions of the base model and accommodate a broader set of plasma and tissue measurements, we constructed an expanded model that explicitly accounts for Cori cycling between hepatic and extrahepatic compartments (Figure 4A; Table S3). Liver pyruvate was allowed to reversibly exchange with liver lactate/alanine and glutamate was allowed to reversibly exchange with α-ketoglutarate. Importantly, the triose phosphate isomerase (TPI) and fumarate hydratase (FH) reactions were no longer assumed to fully equilibrate; instead, the reaction reversibilities were treated as adjustable parameters and determined by model regression of plasma and tissue MIDs. When the expanded model was regressed to data from ¹³C₃Lac infusions, the best-fit flux estimates indicated that the FH reaction was ~92% equilibrated, matching closely values determined empirically from analysis of oxaloacetate isotopomer ratios (Figure 3F). Because mice were fasted to deplete liver glycogen prior to isotope infusions, the regressed estimates of glucose production from glycogen were typically ~1%. Thus, flux from glycogen to G6P in liver (V_PYGL.L) was treated as inactive in the subsequent analyses to improve model reproducibility.

Figure 4. Expansion of the Base Model in Mice Infused with ¹³C₃Lac Only.

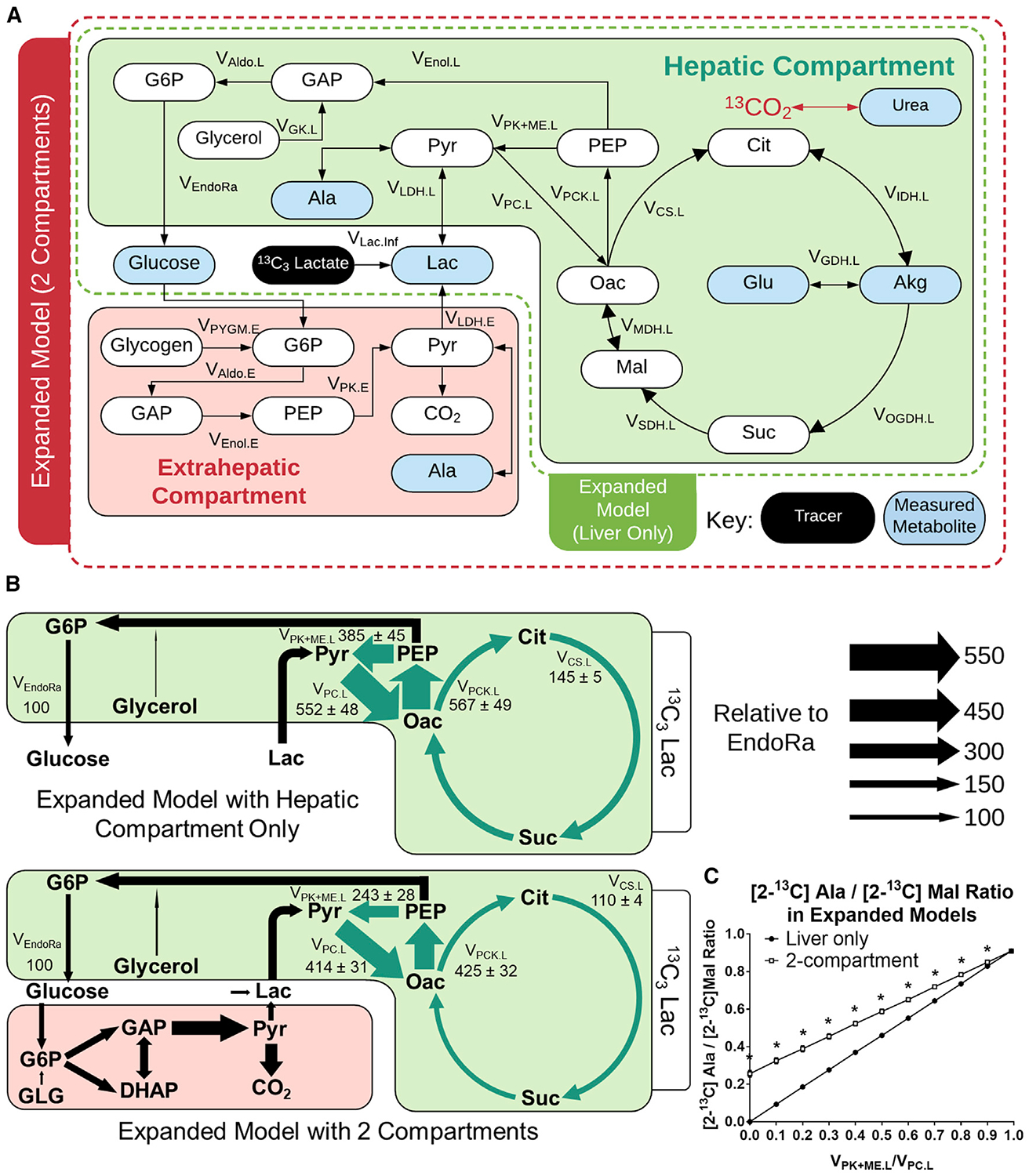
(A) Network diagram showing the expanded model with an extrahepatic compartment to facilitate descriptions of Cori cycling in ¹³C₃Lac tracer experiments. A broader set of plasma and tissue measurements was used to constrain the model (Table S3).

(B) Comparison of expanded model flux results with one compartment (liver only) or two compartments, showing relative flux estimates in 19- to 20-h-fasted C57BL/6J mice infused with ¹³C₃Lac. Fluxes are normalized to total glucose production (V_EndoRa = 100). Fluxes highlighted in green show significant changes between the two models. Data are presented as means ± SEM (n = 7); p ≤ 0.05.

(C) [2-¹³C]alanine/[2-¹³C]malate ratio predicted for varying liver V_PK+ME.L/V_PC.L ratios in a simulated study using [3-¹³C]lactate. Simulations were performed using the best-fit solutions obtained from a liver-only or two-compartment expanded model regressed to fit the ¹³C₃Lac measurements. Data are presented as means ± SEM (n = 7); *p ≤ 0.01, determined using unpaired t test without assuming consistent SD.

We compared best-fit solutions obtained from one-compartment (i.e., liver only) or two-compartment versions of the expanded model when regressed with plasma and liver MIDs obtained from ¹³C₃Lac infusions (Figures 4B and S4). Model expansion did not adversely affect flux precision as the confidence intervals for most fluxes were well constrained in both models (Figures S5A and S5B). Liver glucose production and net lactate uptake fluxes were not significantly different between the two models. Gluconeogenesis from phosphoenolpyruvate (PEP) accounted for the majority of endogenous glucose production (V_EndoRa), with a smaller fraction emanating from glycerol, and total liver cataplerotic/anaplerotic flux (V_PCK.L) was ~4-fold higher than the rate of citrate synthase (V_CS.L) in both models (Figures 4B and S4). In contrast, allowing return of lactate through the Cori cycle reduced liver pyruvate cycling (V_PK+ME.L, V_PC.L, and V_PCK.L) and CAC (V_CS.L) fluxes in the two-compartment model relative to the liver-only model (Figure 4B). Nevertheless, liver pyruvate cycling remained substantial in both models, with ~57% of total anaplerosis returned to pyruvate (V_PK+ME.L) in the two-compartment model compared with ~68% in the liver-only model (Figure 4B).

Pyruvate decarboxylation by the pyruvate dehydrogenase (PDH) complex is generally assumed to be low under long-term-fasted conditions. Although less precise, fluxes regressed using one- or two-compartment expanded models with an active PDH reaction were consistent with low levels of pyruvate decarboxylation (V_PDH.L was ~5% the rate of total pyruvate flux into the CAC) (Figure S6). Estimates of liver glutamate anaplerosis were particularly sensitive to changing model assumptions about PDH activity because increased glutamate entry effectively offset reductions in V_CS.L so that estimates of V_MDH.L were unchanged when PDH was active (Figures S4 and S6). Other liver fluxes were not significantly altered by inclusion of PDH in the reaction network. Importantly, the effects of Cori cycling to reduce pyruvate cycle and CAC fluxes were replicated in models with an active PDH complex (_VPDH.L) (Figure S6). In summary, estimates of liver pyruvate cycling and CAC-associated fluxes were sensitive to changing model assumptions regarding secondary tracer recycling and equilibration in the CAC. On the other hand, glucose-producing fluxes were robust to changes in these same model assumptions.

Finally, we examined whether an alternative approach for assessing liver pyruvate cycling would be similarly affected by assumptions related to secondary tracer recycling. Perry et al. (2016) previously described a method for estimating liver pyruvate cycling that relies on the measured ratio of [2-¹³C]alanine to [2-¹³C]malate enrichments following infusion with [3-¹³C]lactate. We simulated steady-state ¹³C enrichments at the C2 positions of malate and alanine derived from [3-¹³C]lactate based on best-fit flux solutions obtained from the one- or two-compartment expanded model. Both models simulated [2-¹³C] Ala/[2-¹³C]Mal ratios that varied linearly with the liver V_PK+ME/V_PC ratio, but the two-compartment model predicted higher isotopomer ratios compared with the liver-only model (Figure 4C). The divergence between the models was most substantial at the lower range of V_PK+ME/V_PC flux, where the two-compartment model predicted a non-zero [2-¹³C]Ala/[2-¹³C]Mal ratio even in the absence of liver pyruvate cycling because of contributions from extrahepatic sources of [2-¹³C]Ala. This incongruity provides evidence that secondary tracer effects are also embedded in liver flux estimates obtained from other stable isotope approaches because these estimates do not differentiate between pyruvate cycling within the liver or in an extrahepatic compartment.

Expanded Two-Compartment Models Provide Consistent Hepatic Flux Estimates Using ¹³C₃Prop/²H and ¹³C₃Lac/²H Tracers In Vivo

Plasma and liver tissues extracted from mice in prior ¹³C₃Prop/²H and ¹³C₃Lac/²H studies (assessed with base models in Figure 2D and 2E) were re-analyzed to yield a set of metabolite MIDs similar to those in Figure S3. Expanded models for exchange of ¹³C/¹²C and ²H/¹H atoms were constructed to accommodate measurements from ¹³C₃Lac/²H and ¹³C₃Prop/²H experiments (Figure 5A; Table S4). These models were similar to the expanded ¹³C-only model in Figure 4A with the following modifications: (1) hydrogen atom transitions were included, (2) reactions to account for infusion of ²H and ¹³C₃Prop tracers were added, (3) glycogenolysis was assumed to be active, and (4) glutamate anaplerosis was assumed to be inactive. The latter assumption was necessary because glutamate MID measurements were not attainable from samples collected in ¹³C₃Lac/²H and ¹³C₃Prop/²H experiments, making the flux from the unenriched anaplerotic source of glutamate (V_Glu.source) unidentifiable. Hepatic flux estimates obtained from ¹³C₃Lac/²H and ¹³C₃Prop/²H infusions were similar when regressed with expanded models: V_EndoRa and V_Enol.L were comparable (Figures 5B and S7), and pyruvate cycle and CAC fluxes were not significantly different (Table S2). Thus, expanded models that allow secondary tracer recycling and data-driven estimation of in vivo reaction reversibility provide congruent liver flux estimates with ¹³C₃Prop/²H or ¹³C₃Lac/²H.

Figure 5. Comparison of ¹³C₃Lac/²H and ¹³C₃Prop/²H Isotopes for Hepatic Flux Estimation Using Expanded Models of Metabolism.

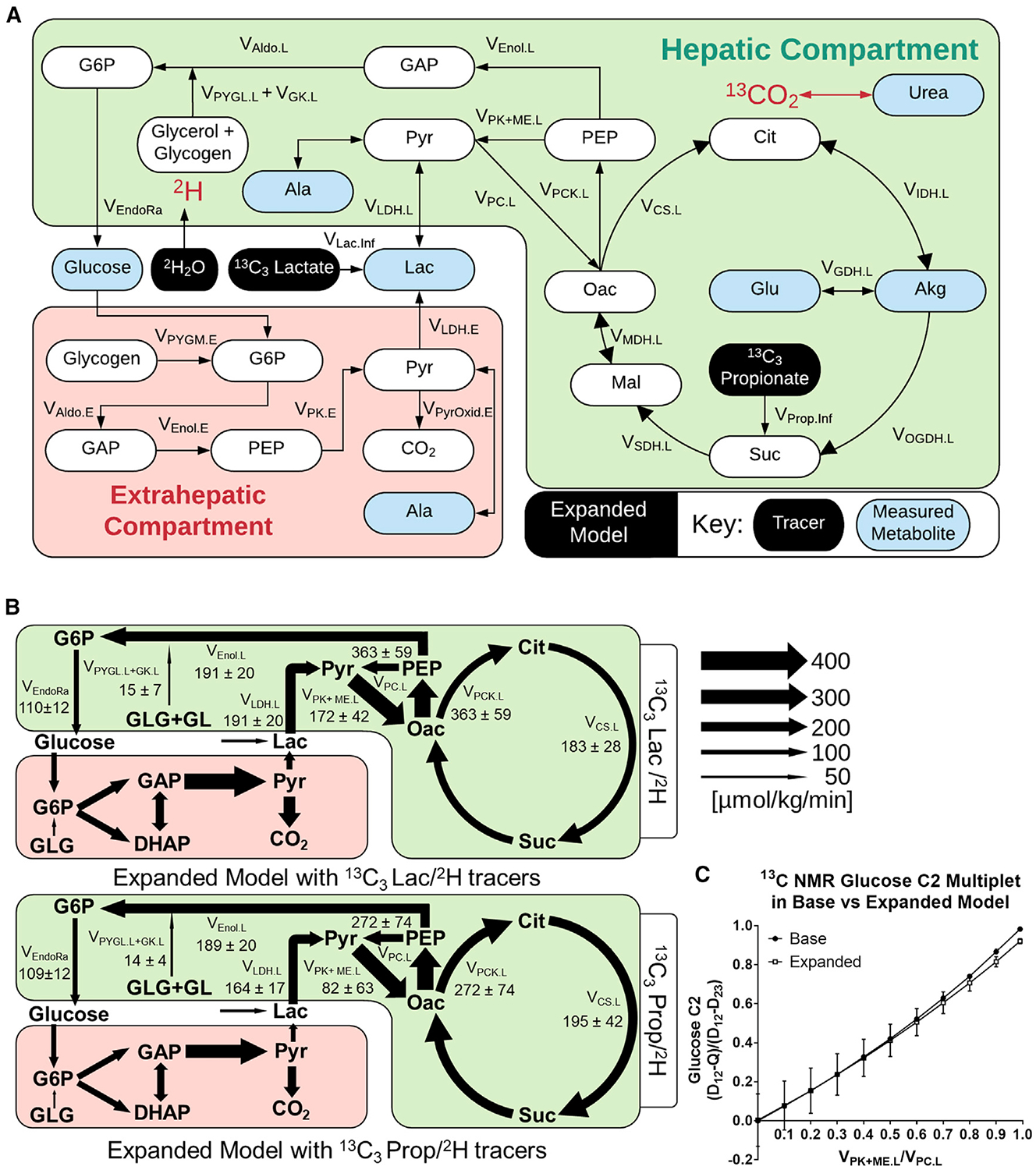
(A) Network map showing the expanded model with ¹³C₃Prop/²H or ¹³C₃Lac/²H isotopes and highlighting measured metabolites.

(B) Comparison of two-compartment expanded models regressed to ¹³C₃Prop/²H or ¹³C₃Lac/²H labeling measurements. Absolute flux estimates are shown for 19- to 20-h-fasted C57BL/6J mice. Data are presented as means ± SEM (micromoles per kilogram per minute, n = 5).

(C) Glucose-C2 ¹³C-NMR (D12-Q)/(D12-D23) multiplet ratio predicted for varying liver V_PK+ME.L/V_PC.L ratios using different models of the ¹³C₃Prop tracer experiment. Simulations were performed using the best-fit solutions obtained from the base model (Figure 2D) or two-compartment expanded model (Figure 5B) regressed to ¹³C₃Prop/²H measurements. Data are presented as means ± SEM (n = 4 for the base model, n = 7 for the expanded model).

To investigate the effects of model expansion, we compared flux estimates from expanded versus base models using the same tracer datasets. There were no significant differences between fluxes estimated by the expanded and base ¹³C₃Prop/²H models. However, the expanded ¹³C₃Lac/²H model showed a significant elevation in hepatic pyruvate cycling (V_PK+ME.L, V_PC.L, and V_PCK.L) and CAC (V_CS.L) fluxes compared with the base ¹³C₃Lac/²H model (Table S2). Thus, model expansion had a more pronounced effect on flux estimates obtained from ¹³C₃Lac/²H studies than ¹³C₃Prop/²H studies.

Finally, we used our expanded model of ¹³C₃Prop/²H experiments to assess a ¹³C NMR approach for estimating liver metabolic fluxes using this same combination of tracers. Jin et al. (2005) previously described a method for estimating liver pyruvate cycling that relies on the measured ratio of (D12-Q)/(D12-D23) multiplets obtained from the C2 resonance of plasma glucose. We adapted our base and expanded models to simulate these multiplet signals (Deja et al., 2020) using best-fit flux solutions obtained from our ¹³C₃Prop/²H infusions. Both models simulated C2 multiplet ratios that varied roughly in proportion to liver V_PK+ME/V_PC flux, with only slight divergence at higher levels of pyruvate cycling flux (Figure 5C). The agreement between the two models can be explained by the approximately offsetting effects of ¹³CO₂ recycling and Cori cycling on the simulated C2 multiplet ratio. ¹³CO₂ recycling tends to elevate the quartet (Q) signal, whereas Cori cycling tends to decrease it, thus making the (D12-Q)/(D12-D23) ratio insensitive to model expansion. This empirical finding is not a theoretically generalizable result, however, and may depend on the tracer infusion rate, the physiological state of the animals, as well as other methodological parameters.

DISCUSSION

Isotope-based flux analysis is the gold standard for measurements of in vivo metabolism and has provided important insights into whole-body fuel utilization, cancer metabolism, insulin resistance, and fatty liver disease (Faubert et al., 2017; Hasenour et al., 2020; Hui et al., 2017; Perry et al., 2015; Satapati et al., 2015; Sunny et al., 2011). Thus, use of MFA to model and interpret data from in vivo ILEs is only expected to increase. During an effort to improve the robustness of our own MFA platform for assessing in vivo liver metabolism, we noted isotope-specific inconsistencies similar to previous observations that have given rise to a contentious debate in the literature (Befroy et al., 2014, 2015; Satapati et al., 2015). Studies with ¹³C-propionate administered to humans with fatty liver or high-fat-fed mice have reported dramatic elevations in liver CAC and anaplerotic fluxes compared with controls (Satapati et al., 2012; Sunny et al., 2011). In contrast, studies with ¹³C-acetate have reported no increases in CAC or anaplerotic fluxes in patients with fatty liver (Petersen et al., 2016). However, the mathematical model used to estimate fluxes in the latter study neglected liver pyruvate kinase (PK) activity and, therefore, did not account for the possibility of liver pyruvate cycling, which is needed to explain the labeling patterns typically observed with ¹³C NMR analysis of plasma samples obtained from ¹³C-propionate tracer studies (Burgess et al., 2015).

The omission of PK flux in models of liver metabolism is supported by arguments that “futile” pyruvate cycling is not energetically feasible, that inhibition of PK by glucagon during fasting should prevent pyruvate cycling, and that some experiments with ¹³C-lactate tracers indicate that liver pyruvate cycling is negligible (Befroy et al., 2015). One explanation for the divergent results of prior studies is that elevated rates of liver anaplerosis and pyruvate cycling reported in some cases may have been an artifact of ¹³C-propionate administration (Perry et al., 2016). However, large estimates of hepatic PK flux have been reported under fasted conditions across species with radioactive and stable isotopes (Beylot et al., 1995; Jones et al., 1997; Katz et al., 1993; Magnusson et al., 1991). One might expect liver flux analysis in perfusion or in vitro to clarify discrepancies in PK flux estimates. However, removal of the liver from the physiological milieu can rapidly alter PK activity (Large et al., 1997; Riou et al., 1985). Liver PK activity is also responsive to endocrine hormone regulation. This has been shown using [3-¹³C]lactate to assess metabolic fluxes in perfused livers from 48-h-fasted rats in the presence or absence of glucagon (Large et al., 1997). V_PK was ~50% the rate of V_PCK in control livers, which was reduced to ~20% during perfusion of glucagon (Large et al., 1997). The aforementioned work is one publication among several to yield sizeable estimates for the ratios of V_PK+ME/V_PCK and V_PK+ME/V_CS in the liver (Katz et al., 1993; Large and Beylot, 1999; Magnusson et al., 1991); it is noteworthy that no research in these cited publications used isotopic propionate to estimate liver fluxes.

Because of the significance of pyruvate cycling in the interpretation of ILEs and the importance of PK in regulating liver glycolysis and gluconeogenesis, we sought to examine the incongruent findings of prior studies by testing specific modeling assumptions and assessing different combinations of isotope tracers and measurements that have been used previously to estimate liver metabolic fluxes in vivo. We confirmed that assumptions about extrahepatic tracer recycling and equilibration of 4C CAC intermediates can significantly alter estimates of pyruvate cycle fluxes. These assumptions may be sensitive to hormonal and nutritional status and to whether the primary tracer enters “upstream” or “downstream” of Oac. It is noteworthy that multi-compartment models with expanded metabolite labeling measurements and fewer simplifying assumptions still indicated significant liver pyruvate cycling.

Previous work suggests that extrahepatic tissues may not process isotopic propionate and lactate equivalently (Landau et al., 1993). This has been shown in the perfused heart, where the provision of propionate can influence oxidative metabolism (Purmal et al., 2014). Nevertheless, liver flux estimates using both isotopes achieved reasonable agreement when broader in vivo physiology was modeled. Liver V_PK+ME flux was reduced but not eliminated by in vivo operation of the Cori cycle in models that accounted for extrahepatic metabolism. Total anaplerosis was consistently observed to be higher than the rate of citrate synthase, regardless of the isotope used in the study. Estimates of the V_PCK/V_CS ratio reported here are within the range observed previously across modeling platforms and species using various isotopes (Befroy et al., 2014; Beylot et al., 1995; Burgess et al., 2005; Jin et al., 2005; Katz et al., 1993; Large and Beylot, 1999; Magnusson et al., 1991; Satapati et al., 2012). These observations perhaps help to resolve some of the recent concerns expressed by others regarding the incompatibility of ¹³C-labeled propionate or lactate for measurement of hepatic fluxes. Our results also underscore the importance of model design and optimal isotope selection for accuracy and precision of MFA (Metallo et al., 2009).

No differences in plasma glucose concentration, endogenous glucose production, or gluconeogenesis were observed in mice infused with ¹³C₃Prop or ¹³C₃Lac, consistent with other recently published data (Hasenour et al., 2015; Satapati et al., 2015). The substrate actions of propionate on hepatic metabolism, however, are unclear. Others have reported that propionate increases glucose production and plasma glucose concentrations in rats (Befroy et al., 2014). Conversely, administration of propionate with lactate in perfused liver has been shown to inhibit glucose production (Blair et al., 1973). Similar limitations may also be important for use of ¹³C₃Lac because circulating lactate acts as a major carbon shuttle between and within numerous tissues in the body (Hui et al., 2017), and recycled lactate significantly contributes to gluconeogenesis during fasting (Wang et al., 2020). In fact, infusion of [U-¹³C₆]glucose and generation of enriched lactate from extrahepatic tissues may serve as an experimental tracer strategy for estimating endogenous glucose production and gluconeogenesis (Antoniewicz et al., 2006; Cappel et al., 2019). In consideration of these data, we developed expanded models where liver and extrahepatic metabolism were treated as separate compartments bridged by a plasma compartment, and plasma lactate was allowed to equilibrate with extrahepatic pyruvate/alanine.

Affirmative claims regarding the ability of these expanded models to resolve specific peripheral fluxes should be viewed with caution because the extrahepatic compartment was not designed to encompass the gamut of metabolism present outside of the liver. For example, gluconeogenic fluxes from extrahepatic tissues (e.g., kidney) were assumed to have a marginal influence on plasma glucose enrichment. This assumption was validated in part by the acceptable agreement between plasma glucose and liver metabolite enrichments obtained when both were regressed simultaneously using expanded models. It is also plausible that other enriched plasma metabolites not measured here could influence flux solutions. Although the liver displays some functional heterogeneity, liver metabolites were modeled as steady-state components of a single gluconeogenic compartment. This is a limited but reasonable assumption for hepatocytes but not likely to be true for nonparenchymal cells of the liver, which could not be separated from tissue extracts. It is important to also consider that our results are specific to a discrete set of well-controlled in vivo conditions; the experimental strategy and results presented here should not necessarily be extrapolated to other designs (e.g., involving significant variations in nutrient load). A carotid artery catheter was surgically implanted to avoid mouse handling during plasma sample collection. It is not known whether other sampling procedures might affect the endocrine state of the mouse and interfere with flux estimates.

Model-based regression approaches are needed to account for the complexities of in vivo stable isotope experiments and to rigorously test assumptions used in the calculation of metabolic fluxes. The availability of flexible modeling tools (e.g., INCA [Young, 2014], Metran [Yoo et al., 2008], and 13CFLUX2 [Weitzel et al., 2013]) now make this increasingly possible. Comprehensive isotopomer modeling and integrative flux analysis methodologies have the potential to reconcile apparently divergent results and identify flux estimates that are sensitive to methodological differences or, conversely, robust to a variety of study designs and assumptions. The INCA software is generalizable to tracers with any combination of labeled atoms, and we can readily construct models that take differences in tracers or administration routes into account. Furthermore, INCA can model transient labeling experiments that result from a step input of labeled tracer (Young, 2014). As a result, we expect that the findings of the current study are applicable to a wide range of experimental systems used in metabolism research, and the models can be adapted to other possible study designs.

Here we demonstrate the significance of secondary tracer effects and incomplete isotope equilibration on flux estimates obtained from in vivo ILEs, which can affect a variety of flux modeling approaches. When we expanded our base model by adding several liver-specific metabolite measurements while relaxing assumptions related to isotopic equilibrium and tracer recycling, our results indicated that significant liver pyruvate cycling persisted under fasting conditions. Furthermore, we did not find evidence that exogenous propionate administration had a significant effect on glucose-producing or pyruvate cycling fluxes. Although estimates of liver pyruvate cycling were influenced by Cori cycle activity, accounting for extrahepatic metabolism in an expanded multi-compartment MFA model did not abolish liver pyruvate cycle flux. One potential way to further examine the role and importance of pyruvate cycling in the liver would be to utilize liver-specific, genetic, or pharmacological inhibition of the PK enzyme.

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jamey Young (j.d.young@vanderbilt.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The dataset supporting each metabolic flux model has been uploaded to Mendeley Data and is accessible at https://dx.doi.org/10.17632/c3kvmfsmdk.2

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All animal experiments were performed in accordance with institutional guidelines and approved protocol at Vanderbilt University Animal Care and Use Committee. C57BL/6J mice were purchased from Jackson Laboratories (Bar Harbor, ME) and studied at ~10–11wks of age. Male mice were studied to limit any potential variation caused by estrus cycles and for a closer base of comparison to previous studies. Mice were provided free access to a standard chow diet (LabDiet 5001, PMI Nutrition International) and water and maintained on a 12:12h light-dark cycle in a temperature (23°C) and humidity stable environment.

METHOD DETAILS

In vivo Procedures in the Mouse

Indwelling catheters were surgically implanted in the jugular vein and carotid artery ~1wk prior to experimentation for infusing and sampling, respectively, as previously described (Ayala et al., 2006). In vivo studies were performed identically to those described in detail elsewhere in long-term (~19–20hr) fasted mice (Hasenour et al., 2015). Briefly, mice received an intravenous primed, continuous infusion of [6,6-²H₂]glucose (440μmol/kg + 4.4μmol/kg/min), bolus of ²H₂O to enrich body water to 4.5% (abbreviated collectively as ²H), and a primed, continuous infusion of ¹³C₃Prop (1.1mmol/kg + 0.055mmol/kg/min) or ¹³C₃Lac (0.160mmol/kg + 0.040mmol/kg/min) (Cambridge Isotope Laboratories, Tewksbury MA). Isotopes were delivered over a 4hr time course, as previously described. A separate cohort of overnight fasted mice was infused with a primed, continuous infusion of ¹³C₃Lac (0.160mmol/kg + 0.040mmol/kg/min, respectively) for 120min in the absence of ²H isotopes for relative liver flux estimation. Mice were sacrificed through cervical dislocation and liver tissue was rapidly excised and freeze-clamped in liquid nitrogen at the close of the study; plasma samples and tissues obtained at the end of the study were stored at −8°C prior to analysis.

Metabolite Extraction, Derivatization, and GC-MS

Plasma glucose was extracted and derivatized according to protocols developed elsewhere (Antoniewicz et al., 2011). Following acetone or a biphasic methanol/water/chloroform extraction, polar plasma (~10–50μL) and liver (~30–50mg) metabolites were converted to their methoxamine tert-butylsylil derivatives (TBDMS) using MBTSTFA+1% TBDMCS (ThermoFisher Scientific, Waltham MA). Glucose and other metabolite derivatives were injected in an Agilent 7890A gas chromatograph equipped with an HP-5ms capillary column and 5975C mass spectrometer in scan mode for analysis of isotopic enrichment. Metabolites were identified through comparison to a library of known standards, and the accuracy of MID measurements was validated through an assessment of unenriched control samples. Post hoc simulations for metabolite MIDs were performed following best-fit flux regression for each mouse.

Metabolic Flux Analysis (MFA)

All metabolic models were constructed using the Isotopomer Network Compartmental Analysis (INCA) software package (accessible at http://mfa.vueinnovations.com/mfa; Young, 2014); metabolic networks and carbon/hydrogen atom transitions for each modeled reaction are summarized in Tables S1, S3, and S4. Flux models were constructed from classical biochemical reactions with consideration to those published previously (Antoniewicz et al., 2006; Jones et al., 1997; Magnusson et al., 1991). Unless otherwise noted, assumptions used for flux analysis were the same as those provided in a previous publication (Hasenour et al., 2015). MIDs for glucose, plasma and liver polar metabolites were introduced into INCA for flux regression. After constraining citrate synthase flux (V_CS.L) to an arbitrary value of 100, relative fluxes were estimated by minimizing the sum of squared residuals (SSRs) between simulated and experimentally derived MIDs. Measurement uncertainties were estimated based on the root-mean square error of unenriched control samples and/or the standard error of measurement of technical GC-MS replicates. Best-fit flux estimates were obtained from least-squares regression starting from at least 25 random initial values. Goodness of fit was assessed by a chi-square test, and 95% flux confidence intervals were calculated by evaluating the sensitivity of SSRs to variations in flux values (Antoniewicz et al., 2006). In studies where both ¹³C/²H isotopes were infused, relative fluxes were converted to absolute fluxes using the known [6,6-²H₂]glucose infusion rate and mouse weights. For mice infused with ¹³C/²H isotopes, glucose-producing flux from glycerol (V_GK.L) was summed with glycogen (V_PYGL.L) and presented in hexose units (V_PYGL+GK.L).

MIDs and NMR positional enrichments were simulated in INCA using the best-fit flux solutions obtained from in vivo labeling experiments. Where appropriate, urea and lactate enrichments obtained during the isotopic steady state were included in the liver flux regressions. An increase in the ¹³C enrichment of the CO₂ pool in vivo is anticipated to some extent, given the introduction of propionate or lactate isotopes into the CAC. A modeling approach was taken to accommodate the reintroduction of locally synthesized ¹³CO₂ in the liver in a previous publication (Hasenour et al., 2015). Here, ¹³CO₂/bicarbonate enrichment was assumed to equilibrate with the carbonyl carbon of urea (retained by the urea-TBMDS m/z 231 ion), since carbamoyl phosphate is formed from HCO₃⁻ in hepatic mitochondria. As such, the Urea231 enrichment was used as a proxy for ¹³CO₂, similar to that applied elsewhere (Magnusson et al., 1991). The MIDs of additional metabolites (e.g., Lac261 ion as a measure of lactate enrichment) were included in specific flux regressions as described in Results (Table S5). Unless otherwise noted, a two-tailed t test was used to test for differences with significance at p ≤ 0.05.

MFA Model Terminology

13C3Lac	[13C3]Lactate
13C3Prop	Sodium [13C3]Propionate
AcCoA	Acetyl-CoA
Akg	α-Ketoglutarate
Ala	Alanine
BPG	1,3-Bisphosphoglycerate
CAC	Citric acid cycle
Cit	Citrate
CO2	Carbon dioxide
DHAP	Dihydroxyacetone Phosphate
FH	Fumarate hydratase
Fum	Fumarate
G6P	Glucose-6-phosphate
GAP	Glyceraldehyde-3-phosphate
GL	Glycerol
GLG	Glycogen
Glu	Glutamate
Glu.source	Unenriched anaplerotic source of glutamate
H6P	Hexose-6-phosphate
ILE	Isotope labeling experiments
Lac	Lactate
Lac.source	Unenriched anaplerotic source lactate
Mal	Malate
MID	mass isotopomer distribution
NMR	Nuclear magnetic resonance
Oac	Oxaloacetate
PEP	Phosphoenolpyruvate
PropCoA	Propionyl-CoA
Pyr	Pyruvate
Suc	Succinate
SucCoA	Succinyl-CoA
T3P	Triose-3-phosphate
TPI	Triose phosphate isomerase
VALT	Flux between Pyr and Ala
VAldo	Flux between H6P and T3P or F1,6BP, GAP, and DHAP
VCS	Flux from Oac and AcCoA to Cit
VEndoRa	Endogenous glucose production
VEnol	Flux from PEP to BPG
VFH	Flux between Mal and Fum
VGAPDH	Flux between T3P or GAP and PEP
VGDH	Flux between Glu and αKG
VGK	Flux from glycerol to T3P or DHAP
VGlu.source	Flux from unenriched anaplerotic source of glutamate
VGPI	Glucose Phosphate Isomerase
VGlc.inf	[6,6-2H2]glucose infusion
VHK	Flux from Glc to G6P
VIDH	Flux circuit between Cit and αKG
VLac.inf	[13C3]lactate infusion
VLac.source	Flux from unenriched anaplerotic source of lactate
VLacTransport	Lac transport from the plasma into the liver
VLDH	Flux from Lactate to Pyruvate
VMDH	Flux between Oac and Mal
VOGDH	Flux from αKG to SucCoA
VPC	Flux from Pyr to Oac
VPCC	Flux from PropCoA to SucCoA
VPCK	Flux from Oac to PEP
VPDH	Flux from Pyr to AcCoA
VPK+ME	Contribution of pyruvate kinase (PK) and malic enzyme (ME) to Pyr
VProp.inf	[13C3]propionate infusion
VPYGL	Flux from glycogen to G6P in liver
VPYGL+GK	Combined flux from glycogen (VPYGL) and glycerol (0.5VGK) to endogenous glucose production in hexose units
VPYGM	Flux from glycogen to G6P in muscle
VPyrOxid	Metabolism of Pyr to CO2
VSCS	Flux from SucCoA to Suc
VSDH	Flux from Suc to Fum
VTPI	Flux between DHAP and GAP
VTracer	13C3Lac or 13C3Prop tracer flux into the liver

Correction of Liver Oxaloacetate Isotopomers to Account for ¹³CO₂ Recycling

In the absence of ¹³CO₂ recycling, the fully labeled M+4 isotopomer Oac₁₁₁₁ should exhibit negligible abundance and only the M+3 oxaloacetate isotopomers Oac₁₁₁₀ and Oac₀₁₁₁ should be formed from ¹³C₃Lac infusion. Yet, after correcting the aspartate MID for natural isotopic background, significant M+4 enrichment was detected (Figure 3E), which stems from carboxylation of M+3 pyruvate with recycled ¹³CO₂ (Figure 3D). Because ¹³CO₂ can lead to production of M+3 oxaloacetate isotopomers other than Oac₁₁₁₀ and Oac₀₁₁₁, the measured MIDs of alanine (a proxy for liver pyruvate) and urea (a proxy for liver CO₂) were used to mathematically correct the M+3 oxaloacetate isotopomers to account for contributions from ¹³CO₂ recycling:

$$Oa{c}_{1234}^{cor}(M+3)=Oa{c}_{1234}(M+3)+\frac{V_{PC}}{V_{\Sigma Ana}}\cdot {}^{13}C{O}_2\cdot \left[Py{r}_{123}(M+3)-Py{r}_{123}(M+2)\right]$$

$$Oa{c}_{234}^{cor}(M+3)=Oa{c}_{234}(M+3)-\frac{V_{PC}}{V_{\Sigma Ana}}\cdot {}^{13}C{O}_2\cdot Py{r}_{23}(M+2),$$

where

$$Oa{c}_{1234}(M+3)=M+3\text{ abundance of Asp}418\text{ fragment ion }(\text{derived from carbons }1-4\text{ of oxaloacetate})$$

$$Oa{c}_{234}(M+3)=M+3\text{ abundance of Asp}390\text{ fragment ion }(\text{derived from carbons }2-4\text{ of oxaloacetate})$$

$$Oa{c}_{1234}^{cor}(M+3)=M+3\text{ abundance of Asp}418\text{ after correction for }{}^{13}{\text{CO}}_2\text{ recycling}$$

$$Oa{c}_{234}^{cor}(M+3)=M+3\text{ abundance of Asp}390\text{ after correction for }{}^{13}{\text{CO}}_2\text{ recycling}$$

$$Py{r}_{123}(M+3)=M+3\text{ abundance of Ala}260\text{ fragment ion }(\text{derived from carbons }1-3\text{ of pyruvate})$$

$$Py{r}_{123}(M+2)=M+2\text{ abundance of Ala}260$$

$$Py{r}_{123}(M+2)=M+2\text{ abundance of Ala}232\text{ fragment ion }(\text{derived from carbons }2-3\text{ of pyruvate})$$

$${}^{13}C{O}_2=M+1\text{ abundance of Urea}231\text{ fragment ion }({\text{derived from liver CO}}_2),$$

and the ratio of pyruvate carboxylase flux (V_PC) to total anaplerosis (V_ΣAna) is determined by:

$$\frac{V_{PC}}{V_{\Sigma Ana}}=\frac{Oa{c}_{1234}(M+4)}{Py{r}_{123}(M+3)\cdot {}^{13}C{O}_2}.$$

All MIDs were corrected for natural stable isotope abundance prior to applying the above equations.

Calculation of Percent Equilibration in the 4C reactions of the CAC

If oxaloacetate fully equilibrates with rotationally symmetric CAC intermediates (i.e., fumarate and succinate) through reversible exchange, an equal abundance of the M+3 oxaloacetate isotopomers Oac₁₁₁₀ and Oac₀₁₁₁ would be expected (Figure 3D). However, incomplete equilibration would cause the abundance of Oac₁₁₁₀ (formed directly from pyruvate carboxylation) to exceed the abundance of Oac₀₁₁₁ (formed from reversible exchange with fumarate). Once the corrected oxaloacetate M+3 abundances were calculated as described above, the abundances of Oac₁₁₁₀ and Oac₀₁₁₁ positional isotopomers formed from ¹³C₃Lac were determined as follows:

$$Oa{c}_{0111}=Oa{c}_{234}^{cor}(M+3)$$

$$Oa{c}_{1110}=Oa{c}_{1234}^{cor}(M+3)-Oa{c}_{234}^{cor}(M+3).$$

These abundances were then used to assess the percentage isotope equilibration using the equation:

$$\%\mathit{\text{Equilibration}}=\left(1-\frac{Oa{c}_{1110}-Oa{c}_{0111}}{Oa{c}_{1110}+Oa{c}_{0111}}\right)\times 100\%$$

QUANTIFICATION AND STATISTICAL ANALYSIS

All data were analyzed using an unpaired Student’s t test without assuming a consistent standard deviation between groups. Biological replicates and significance values for each analysis are noted in each figure caption.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Methoxamine (MOX) Reagent	Thermo Fisher Scientific	Cat#TS-45950
MTBSTFA + 1 % TBDMCS Silylation Reagent	Thermo Fisher Scientific	Cat#TS-48927
Sodium Propionate (13C3, 99%)	Cambridge Isotope Laboratories	Cat#CLM-1865-PK
Sodium L-Lactate (13C3, 98%) 20% W/W in H2O	Cambridge Isotope Laboratories	Cat#CLM-1579-MPT-PK
D-Glucose (6,6,-D2, 99%)	Cambridge Isotope Laboratories	Cat#DLM-349–1
Deuterium Oxide (D, 99.9%)	Cambridge Isotope Laboratories	Cat#DLM-4–100
Deposited Data
MID enrichment data	This paper; Mendeley Data	https://dx.doi.org/10.17632/c3kvmfsmdk.2
Experimental Models: Organisms/Strains
Mouse: C57BL/6J	The Jackson Laboratory	https://www.jax.org/strain/000664; RRID: IMSR_JAX:000664
Software and Algorithms
Prism 7	GraphPad	https://www.graphpad.com
MATLAB 9.1	Mathworks	https://www.mathworks.com
Microsoft Excel 2015	Microsoft	https://www.microsoft.com/en-us/
INCA (Isotopomer Network Compartmental Analysis)	Young (2014)	https://academic.oup.com/bioinformatics/article-lookup/doi/10.1093/bioinformatics/btu015

Highlights.

• Secondary tracers and incomplete equilibration influence in vivo flux estimates

• Liver pyruvate cycle flux is affected by assumptions vis-à-vis Cori cycle activity

• Expanded models resolve ¹³C tracer-specific differences in hepatic fluxes

• ¹³C lactate and propionate tracers indicate significant liver pyruvate cycling