Mathematical Model Shows How Sleep May Affect Amyloid-β Fibrillization

Abstract

Deposition of amyloid-β (Aβ) fibers in the extracellular matrix of the brain is a ubiquitous feature associated with several neurodegenerative disorders, especially Alzheimer’s disease (AD). Although many of the biological aspects that contribute to the formation of Aβ plaques are well addressed at the intra- and intercellular levels in short timescales, an understanding of how Aβ fibrillization usually starts to dominate at a longer timescale despite the presence of mechanisms dedicated to Aβ clearance is still lacking. Furthermore, no existing mathematical model integrates the impact of diurnal neural activity as emanated from circadian regulation to predict disease progression due to a disruption in the sleep-wake cycle. In this study, we develop a minimal model of Aβ fibrillization to investigate the onset of AD over a long timescale. Our results suggest that the diseased state is a manifestation of a phase change of the system from soluble Aβ (sAβ) to fibrillar Aβ (fAβ) domination upon surpassing a threshold in the production rate of sAβ. By incorporating the circadian rhythm into our model, we reveal that fAβ accumulation is crucially dependent on the regulation of the sleep-wake cycle, thereby indicating the importance of good sleep hygiene in averting AD onset. We also discuss potential intervention schemes to reduce fAβ accumulation in the brain by modification of the critical sAβ production rate.

Significance

This work provides a minimal theoretical model for explaining the fibrillization of Aβ and its aggregation to plaques in the brain from a couple of years to a few decades. According to the model, an imbalance between the production and clearance of Aβ leads to the change of the homeostatic state of the brain from soluble Aβ dominance to Aβ plaque dominance. Recent medical reports demonstrate that sleep disturbance is a common symptom occurring a few years before patients are diagnosed with Alzheimer’s disease. Considering that general neural activity is affected by sleep, a disturbance in sleep cycle may lead to higher Aβ production. If the altered production rate is higher than a critical value, fibrillization occurs and results in Aβ plaque formation in the long term.

Introduction

Amyloid-β (Aβ) accumulation is a common pathological characteristic of several neurodegenerative and neuroinflammatory disorders, especially Alzheimer’s disease (AD) (1,2). The clinical symptoms and cellular dysfunction that contribute to pathological burden in AD are generally considered to be the outcome of neurodegenerative effects of the formation of Aβ plaques in the extracellular space (3) and neurofibrillary tangles of τ protein in neurons (4). Regulation of Aβ levels in the interstitial fluid (ISF) is mediated by circadian rhythm (5), which also modulates the neuro-immune-endocrine system through several complex biochemical mechanisms (6, 7, 8). Thus, it might be possible that the circadian rhythm and the emergence of neurodegenerative disorders have a bidirectional modulatory relationship with each other. For example, the sleep-wake cycle, which affects and is affected by the circadian rhythm, is known to be altered several years before the onset of AD (9,10), and prolonged neuroinflammation may also contribute to worsen the sleep hygiene.

It is often debated whether alteration in the sleep rhythm is a causal player in AD or only correlates with it (9, 10, 11). There exists a positive correlation between the circadian gene expression and the number of hypothalamic neurons in the suprachiasmatic nucleus (SCN), which acts as a master regulator of circadian rhythm (12,13). An intriguing fact in this regard is that a significant loss of neurons is found in the SCN of the mammals debilitated with AD (14), which may suggest why the sleep-wake cycle is disrupted in a broad range of neuroinflammatory disorders. Moreover, a disturbance in sleep hygiene is found to correlate with Aβ deposition in the brain (15).

Aβ is produced by neurons upon synaptic activity and released into the ISF (16,17), thereby having an interplay with neural activity. As the SCN controls diurnal neural activity through circadian rhythm, the secretion of Aβ into the ISF follows a similar diurnal rhythm in normal circumstances. This implies that a disturbance in the sleep-wake cycle or unchecked deprivation in sleep may result in higher Aβ production through higher neural activity and may also lead to Aβ neurotoxicity and oxidative stress to neurons. As a consequence, a disrupted central circadian rhythm results in altered hippocampal Aβ rhythm and causes accumulation of amyloid plaques. Aβ plaques that contribute to neurotoxicity disturb the neural function in the SCN and impair the regulation of circadian neural activity throughout the brain (12). This acts as a positive feedback loop, resulting in more Aβ accumulation in the SCN, more neurotoxicity to the SCN, less regulation of the global brain diurnal rhythm, and Aβ secretion as well as subsequent fibrillization.

Because there are a plethora of factors that can contribute to neuroinflammation and neurodegeneration as we age, it is practically impossible to take all the details in shorter timescales (e.g., milliseconds in case of neuronal firing rate) and draw a broad unified picture of the disease development over an extremely long timescale, i.e., in years. Thus, it will be intriguing to design a mean-field approach with which one can, starting from the key components of the underlying system, understand the transition into the diseased state characterized by Aβ fibrillization long before the pathophysiological symptoms occur and neuroinflammatory response starts. We propose a minimal model and show that the onset of AD is driven by a phase change from the soluble form of Aβ to its fibrillar form. The proposed model has the advantage of simplicity compared with the recent mathematical models (18, 19, 20, 21). A few other in silico studies explained how the Aβ fibers form in the brain using an agent-based model (22) or numerically solving the partial differential equations (21,23). Although many aspects of the disease are explained and understood from these models, we still lack a simple explanation of how different factors affect the brain in the course of AD.

In this work, we employ a minimal mathematical model based on ordinary differential equations (ODEs) to investigate Aβ fibrillization in the brain, and its dependence on associated factors such as Aβ production by neurons and their clearance by microglia or efflux through the cerebrospinal fluid (CSF). Our results suggest that the accumulation of fibrillar Aβ can be viewed as a shift in the scaling law between the concentration of fibrillar Aβ and soluble Aβ production rate due to neuronal activity. Our work also predicts that even a twofold increase in Aβ production may trigger a phase change from soluble Aβ to fibrillar Aβ. This ODE-based model suggests that AD can be seen as the outcome of perturbations in brain homeostasis. We believe that such a minimal model could also pave a way for new potential treatments or prevention strategies.

Methods

We base the mathematical model on major mechanisms regulating the fibrillization process, namely fibrillar Aβ (fAβ) formation from soluble Aβ (sAβ), Aβ production by neurons, and their clearance by glial cells or efflux through the CSF.

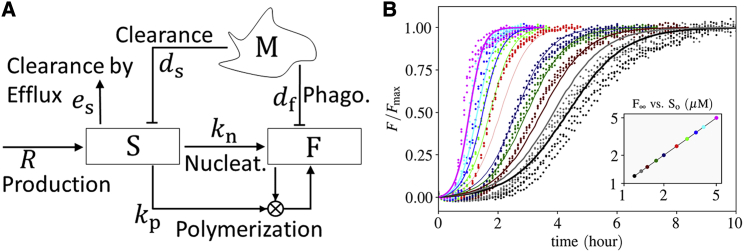
The interaction network of the fibrillization of Aβ in AD is depicted in Fig. 1 A. The changes in the number and activity of astrocytes, neurons, and microglia are ignored. The cycling time of microglia is much faster (a few days) than the timescale of Aβ accumulation (a few years). Thus, we assume that the number of activated microglia reaches its carrying capacity through a fast logistic growth due to proliferation in the presence of sAβ and fAβ. We assume that the number of neurons does not vary significantly over the course of the onset of Aβ fibrillization (24,25), such that the production rate of Aβ, R, remains stable for a long period of time. With the aforementioned assumptions, the equation for the rates of change in Aβ concentrations in the ODE-based model, depicted in Fig. 1 A, can be obtained as

$$\dot{S}=R-k_{\text{p}}SF-k_{\text{n}}{S}^2-\underset{{\lambda }_{\text{s}}}{\underbrace{\left(d_{\text{s}}M+e_{\text{s}}\right)}}S,$$ (1)

$$\dot{F}=k_{\text{p}}SF+k_{\text{n}}{S}^2-\underset{{\lambda }_{\text{f}}}{\underbrace{d_{\text{f}}M}}F,$$ (2)

where S and F are the concentration of Aβ oligomers in soluble (S $\equiv$ [sAβ]) and fibrillar form (F $\equiv$ [fAβ]), respectively. λ_s = d_sM + e_s and λ_f = d_fM, where M represents the number density of microglia. Overdots denote time derivative ($\dot{X}\equiv$ dX/dt). R is the rate of sAβ production over a day due to neural synaptic activity. Although the production rate has a circadian pattern, its day average is used as an approximation. k_n and k_p are the Aβ nucleation and polymerization rate constants, respectively. The parameter values are provided in Table 1.

Figure 1.

Model. (A) Signaling network of Aβ fibrillization. sAβ (S) is produced by the mean rate R and cleared by efflux through the CSF. S transforms to fAβ (F) by nucleation and polymerization. Microglia (M) clear S and F through macropinocytosis and phagocytosis, respectively. The blocking arrows from microglia (M) to S and F represent that microglia clear S and F by macropinocytosis and phagocytosis, respectively. (B) Estimation of the nucleation and polymerization rate constants according to the ThT experiments conducted by Cohen et al. (44). The points and lines correspond to the experimental data and the model, respectively. The colors in the main plot correspond to the marker colors in the inset. A reduced model is used for the estimation, in which only an initial concentration for sAβ (S_o) and the nucleation k_n and polymerization rate constant k_p are taken into account, i.e., Eqs. 1 and 2 reduce to $\dot{S}$ = −k_pSF − k_nS² and F = S_o − S. The parameters are estimated through the differential evolution algorithm (68) with logarithmic weight 1/logS_o on the cost function to weigh lower concentrations more because the physiological concentrations are orders of magnitude lower than the experimental concentrations. k_n = 2.2 × 10⁻¹μM⁻¹ ⋅ day⁻¹ and k_p 2.1 × 10¹μM⁻¹ ⋅ day⁻¹. The proposed minimal model is able to catch the fibrillization behavior quite well. To see this figure in color, go online.

Table 1.

Model Parameters and their Estimated Values

Symbol	Description	Estimated Value	Unit	Reference
S	concentration of Aβ oligomers in soluble form	variable	micromolar	N/A
F	concentration of Aβ oligomers in fiber form	variable	micromolar	N/A
R	mean rate of sAβ secretion by neurons	variable	μM day−1	(50)
a	normalized amplitude of circadian rhythm in sAβ production	25%	N/A	(50,63, 64, 65)
τ	period of circadian rhythm	∼1	day	N/A
M	number density of microglia, Nmgl/Vbrain, assuming that microglia/neuron ratio is unity	∼ 6.7 × 107	mL−1	(66,67)
kp	rate constant of Aβ fiber growth	2.1 × 101	μM−1 day−1	(44)a
kn	rate constant of Aβ fiber nucleation	2.2 × 10−1	μM−1 day−1	(44)a
ds	rate of sAβ clearance by microglia	5.3 × 10−9	day−1 mL	(31,34,35)
es	rate of sAβ efflux through the CSF	1.9	day−1	(29,30)
df	clearance of fAβ by microglia	∼ds/30	day−1 mL	(36)

It is noted that for all the analysis in this work, the parameters are taken from this table unless otherwise specified. N/A, not applicable.

^aEstimation of k_n and k_p has been done using the differential evolution method (see Fig. 1B; (68)).

The biological observations and associated modeling assumptions are explained as follows.

sAβ efflux

In addition to CSF, it has been found that meningeal lymphatics plays an important role in the clearance of the brain waste including sAβ (26, 27, 28). For simplicity, we merge the meningeal lymphatics to CSF in the model. Indeed, both the meningeal lymphatics and CSF are a medium for Aβ clearance, and the efflux of sAβ through them is independent of the existence of microglia and is driven by diffusion. The efflux rate of sAβ in the CSF, e_s, has been reported to be around 7.6–8.3% per hour (29,30) (i.e., e_s = 1.9 ± 0.4 day⁻¹).

Aβ clearance by microglia

fAβ is cleared by microglia through phagocytosis, whereas its soluble form (sAβ) is cleared through macropinocytosis (31,32), a process mediated by cellular internalization. Macropinocytosis is linearly dependent on the concentration of the entities that are internalized by the cell. Thus, the rate of sAβ clearance does not saturate because of such a mechanism. In contrast, fAβ ligates a receptor on microglia, and its phagocytosis is better represented by a saturable rate obeying the Michaelis-Menten kinetics (33). Nevertheless, the clearance or decay rates of sAβ and fAβ are modeled similarly, assuming that the number of microglia receptors is much greater than the number of Aβ. Although this assumption holds true until the onset of AD with low concentrations of fAβ, it may be invalid at the late stages of AD with high concentrations of fAβ. The concentrations of sAβ, S $\equiv$ [sAβ], and fAβ, F $\equiv$ [fAβ], decrease in time by the rates d_sM and d_fM.

It was observed that the intracellular concentration of sAβ depends linearly on the concentration of sAβ in the tissue (as a result of macropinocytosis) (31). Furthermore, the intracellular concentration of sAβ decays exponentially. With this, the clearance rate of sAβ by microglia is estimated as 0.22 h⁻¹ N_mglV_mgl/V_brain, assuming a 100% uptake by microglia, with N_mgl, V_mgl, and V_brain being the total number of microglial cells, the volume of microglial cell, and the total volume of the brain, respectively. A lower transparency level of microglial membrane to Aβ does not change the behavior of the system. This property can be incorporated into the clearance rates d_s and d_f, meaning that they can speak for both uptake of Aβ and their chemical clearance in the cytoplasm. Microglia have a plethora of shapes and sizes according to their activation states (34,35), making the estimation for V_mgl challenging. Here, it is assumed that V_mgl is on the order of 1000 μm³, leading to d_s = 0.22 × 10⁻⁹ h⁻¹ mL. It is roughly estimated that d_f is 30 times smaller than d_s (36). With the estimated values, microglial clearance composes 20% of the whole clearance, whereas the efflux has a greater share of 80%. These proportions are valid only for the estimated physiological values, whereas they vary in the whole range of 0–100% in our analysis (cf. Figs. 3, S1, and S3). Note that R_c depends on the ratio d_sM/e_s, as well as on d_s/d_f and k_n/k_p.

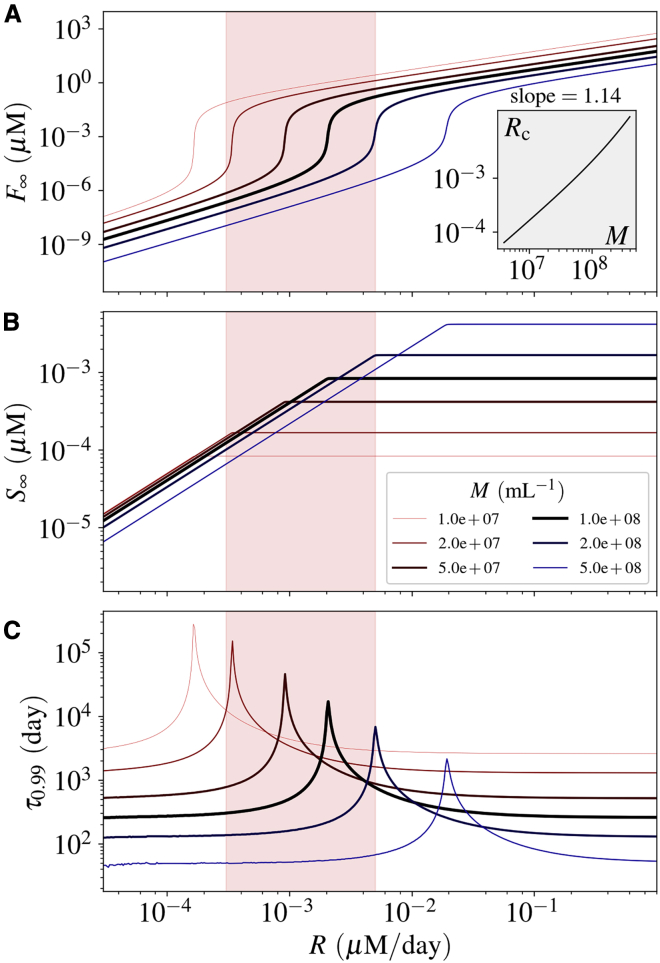
Figure 3.

Effect of the number of microglia (M) on the fibrillization of Aβ. Similar to Fig. 2, (A) and (B) show the concentrations and (C) shows the settling time. The inset diagram shows the relation between the critical production rate R_c and the microglial cell density M. The estimated physiological production rate is shown by a red-highlighted vertical band in each diagram. See Figs. S1–S3 for the impact of other parameters. To see this figure in color, go online.

Fibrillization process

Shortly after the introduction of amyloid cascade hypothesis (37), the fibrillization of Aβ has been investigated extensively by many scientists (38). According to the seminal model for amyloid fibrillization proposed by Lomakin et al. (39), the accumulation of Aβ is driven through two distinct pathways, the initial nucleation and the secondary nucleation by adjoining of sAβ to amyloid fibers (39). Although the amyloid aggregation is still an active field of research, there is a consensus that such a phenomenon occurs through these two mechanisms. The secondary nucleation has been understood as the leading mechanism for amyloid plaque formation in AD (40, 41, 42).

We take the simplest form of amyloid aggregation, considering a primary and secondary nucleation, referred to as nucleation and polymerization, respectively. In the primary nucleation, sAβ comes together and forms small fibers with the nucleation rate constant k_n. In the secondary nucleation, sAβ adjoins the fibers with polymerization rate constant k_p. The required energy for Aβ nucleation is one order of magnitude higher than for their polymerization (43), implying that the polymerization rate is much greater than the nucleation rate (k_p ≫ k_n). To calibrate the model parameters with the experimental results, the recent thioflavin T (ThT) fluorescence experiments of amyloid aggregations (44), upon which many kinetic models of polymer aggregation are being validated (45, 46, 47) have been used. The estimated values for k_n and k_p are tabulated in Fig. 1 B and Table 1.

The large difference between the values of k_p and k_n and the scaling of Aβ nucleation with S² because of its self-interaction are essential in determining an abrupt phase change from soluble to fibrillar Aβ. Such a fibrillization dynamics is in qualitative agreement with the complex kinetic models for amyloid fibrillization (39,46, 47, 48, 49).

Results and Discussion

The emergence of a soluble and a fibrillar phase with distinct scaling laws

We assume that a healthy brain in its initial state does not have any fAβ and is characterized by sAβ production due to neuronal activity. Formation of sAβ by neurons sets Aβ dynamics in the system and initiates the interplay between several biological processes as discussed above. Because the “diseased” state of the brain in AD is marked by a high concentration of fAβ, it becomes primarily important to understand how the dynamics of the system may result in fAβ formation in the extracellular matrix and how it would depend on the production rate of sAβ, R. To perceive this, we first calculate the steady state of our model system and depict its dependence on R (Fig. 2). Considering that the system starts with zero concentration of fAβ, the steady-state solutions (S_∞ $\equiv$ [sAβ]_{t → ∞} − S_c and F_∞ $\equiv$ [fAβ]_{t → ∞}) of Eqs. 1 and 2 read

$$S_{\infty }=\alpha -\beta F_{\infty }$$ (3)

and

$$F_{\infty }=\frac{2\alpha +\delta -\alpha \gamma /\beta \pm \sqrt{\Delta }}{2\left(\beta -\gamma \right)},$$ (4)

where α = R/λ_s, β = λ_f/λ_s, γ = k_p/k_n, δ = λ_s/k_n, and Δ = (αγ/β)² + δ² + 4αδ − 2δαγ/β.

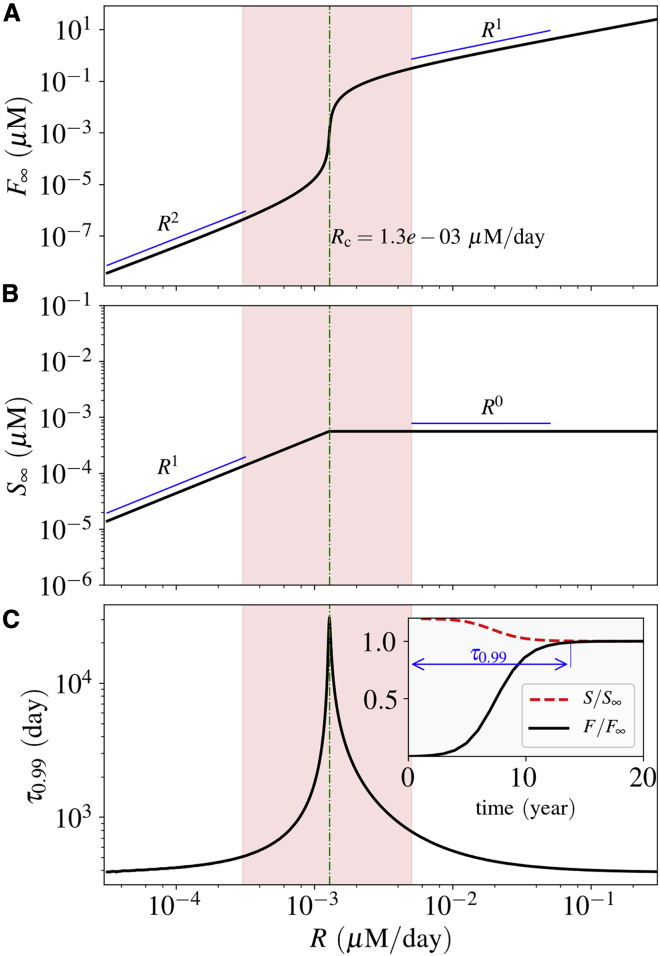
Figure 2.

Steady-state solution and settling time. (A) and (B) show the steady-state solutions for the concentration of fAβ and sAβ, respectively. The critical Aβ production rate R_c is shown in the diagram. (C) shows the corresponding settling time, as defined in the inset. It increases abruptly as the production rate gets closer to the critical rate R_c. The inset diagram shows the normalized concentrations in time for the case R = 1.5 × 10⁻³μM ⋅ day⁻¹ = 1.15 R_c. The estimated physiological production rate is shown by a red-highlighted vertical band in each diagram. To see this figure in color, go online.

We note that Eq. 4 has only one positive solution for the biologically plausible parameter values listed in Table 1. The steady-state solutions of the system variables, F_∞ and S_∞, are depicted in Fig. 2. We observe that there is a critical Aβ production rate (R_c) at which the scaling relation of these steady-state solutions with respect to R changes (see Fig. 2 A for F_∞ and Fig. 2 B for S_∞). Mathematically, R_c is the point at which Δ takes its minimal value with respect to α (R_c = λ_sδβ(γ − 2β)/γ²). Below R_c, F_∞ scales as the second power of R, reflecting that nucleation is the leading mechanism of fibrillization. Above R_c, the scaling of F_∞ changes to the first power of R, implying that polymerization (i.e., adjoining of single oligomers to amyloid fibers) is the leading mechanism. S_∞ scales with respect to R with an exponent of unity below R_c and zero above it. It means that the system of ODEs predicts a saturation point for sAβ. The system has two distinct phases, one phase dominated by soluble Aβ and another dominated by Aβ in fiber form. As depicted in Fig. 2 A, the fAβ concentration between the two phases differs by many orders of magnitude, which suggests a clear distinction between the “diseased” state as compared with the “healthy” one.

The time that the system variable F takes to reach 99% of its steady-state value is defined as the settling time τ_0.99, as depicted in the inset diagram of Fig. 2 C. The settling time is a measure of how fast the system reaches its steady state.

We note that the shortest settling time is around 1 year, whereas it exceeds 100 years as the system moves toward the critical value of the Aβ production rate R_c (see Fig. 2 C). As can be seen from Fig. 2 C, τ_0.99 varies sharply at the close proximity to R_c, whereas it retains lower values on either side of R_c and away from it.

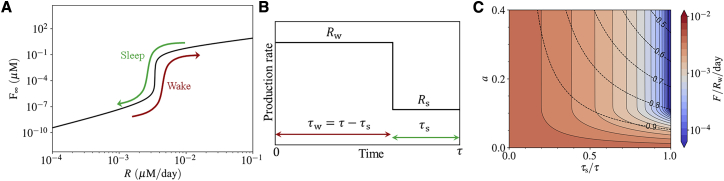
We next estimate the biologically plausible range of R in the case of humans. It has been shown that Aβ levels in the human brain fluctuate with a diurnal rhythm, whose mesors are around 2.3 × 10⁻⁴ μM for Aβ42 and 2.6 × 10⁻³ μM for Aβ40, with normalized amplitudes of 10–20% (50). The production rate of sAβ has been reported to be around 6–8% per hour in the CSF (29,30), implying the physiologically plausible range of R ≈ 3 × 10⁻⁴–5 × 10⁻³ μM/day (shown by the red-highlighted vertical band in Fig. 2). Please note that R_c belongs to this range based on the values tabulated in Table 1.

Transformation into fibrillar phase depends critically on the system parameters

As the alteration of the phase of Aβ from soluble to fibrillar crucially depends on the critical sAβ production rate R_c, it is intriguing to explore the various means to shift the value of R_c to unravel the impact of the distinct underlying biological processes that give rise to the fibrillar phase dominated by fAβ. It may also uncover potential medical intervention strategies for the prevention or delay of AD onset. To elucidate this, we have studied how a modification in each of the system parameters, listed in Table 1, affects R_c.

As expected, R_c is dependent on the parameters of the model. It scales inversely with k_p (Fig. S2), and linearly with e_s (Fig. S3) and d_f (Fig. S1). Here, as an example, we investigate the effect of M in more details. The effect of M in the fibrillization process is important because it is directly related to the immune system. Physical and chemical properties of the system, namely e_s, k_n, and k_p, are not easily controlled by external stimuli. However, biological properties such as M are more accessible and might be regulated by drugs or Aβ antibodies (51).

We observe that R_c scales superlinearly with M as depicted in the inset of Fig. 3 A. The steady-state solutions of the system variables (F_∞ and S_∞) are also shown for several values of M in Fig. 3. Whereas F_∞ decreases as we increase M (Fig. 3 A), S_∞ shows a complex trend (Fig. 3 B). For a characteristic R which is beyond R_c-values for all the microglial densities in consideration, S_∞ attains a larger value for a higher microglial density (Fig. 3 B). Furthermore, as can be seen from Fig. 3 C, the settling time (τ_0.99) decreases as R_c (or M) increases. In general, the results suggest that an efficient clearance of sAβ by microglia and an enhanced sAβ efflux through CSF diminish the risk of developing AD, whereas a high rate of Aβ fiber growth or higher rate of sAβ production makes an individual prone to AD. Among these factors, the microglial clearance is more controllable by the conventional intervention schemes.

Time-dependent parametric perturbations can induce accumulation of Aβ fibers: role of clearance processes and astrocytes

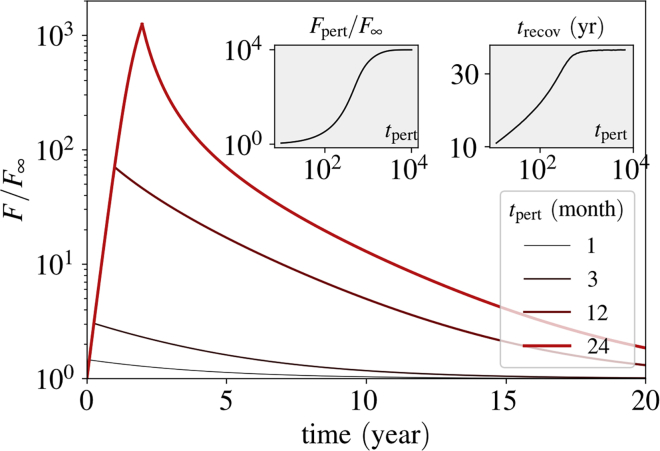
The physiological processes that have been taken into consideration in the model might encounter a plethora of biological perturbations, which may reflect as alteration in the system parameters in a time-dependent manner. Such systemic perturbations can arise from inflammatory conditions or even from a new sleeping habit. Any of our model parameters can get altered for a certain duration because of such a change in the microenvironment of the brain. Because the settling time and the steady-state concentration of fAβ are both dependent on the critical sAβ production rate R_c, any time-dependent or persistent perturbation in the system parameters resulting in even a slight change of R_c may have a significant impact on the amount of fAβ. Whether the system would evolve to a phase dominated by fAβ and how rapidly the system would recover from the effect of such a transient modification in a system parameter crucially depend on the change in R_c due to the parametric perturbation. If R exceeds the modified R_c, the fibrillar phase starts to dominate, resulting in a rapid production of fAβ. The recovery time t_recov, which is defined as the time required for the system variable F to settle to 99% of its original steady-state value (before parametric perturbation), may be relatively longer if the system faces a strong or a long perturbation.

As an example, we have reduced the microglia density, M, to one-tenth (1/10) of its original value for several periods of perturbation t_pert and analyzed how the concentration of fAβ evolves as a result of this parametric perturbation both during and after t_pert (Fig. 4). The time of recovery, t_recov, lengthens as we increase t_pert. Furthermore, we note that the concentration of fAβ at the end of the perturbation period increases considerably with t_pert, as depicted in the left inset of Fig. 4. This suggests that the risk of developing AD can be much higher when the microglial density drops even for a year.

Figure 4.

Impact of a perturbation in M on fibrillization. During the perturbation time, t_pert, the number of microglia M is reduced 10-fold. F is depleted relative to its steady-state value before perturbation. The inset diagram on the left side shows the concentration of fAβ at the end of the perturbation period, F_pert. The inset diagram on the right side shows the recovery time, t_recov, as a function of the perturbation period. The perturbation time in the inset diagrams is plotted in the units of days. R = 1.2 × 10⁻³ = 0.92 R_c. To see this figure in color, go online.

Disturbed sleep can be a key factor in the emergence of AD

Because the production and clearance of Aβ both are regulated by the circadian rhythm, it is crucial to consider the impact of a disrupted sleep-wake cycle on Aβ accumulation. Here, it is assumed that the circadian rhythm is directly related to the sleep-wake cycle and affects the neural Aβ production. The circadian rhythm of the other model parameters is neglected, knowing that the most influential parameter in the model system is the production rate R.

Although the model omits an explicit consideration of circadian rhythm in the production rate, it still allows us to gain insight into a more realistic setting that includes a circadian rhythm of Aβ production. Moreover, a simplistic idea of taking the average of the sAβ production rate to predict the final phase of the system (soluble or fibrillar) does not work in cases in which the sAβ production rate oscillates daily around R_c because of variations of neural activity in wake and sleep states (Fig. 5 A). Under these circumstances, even a small alteration in the sAβ production rate may result in a significant change in the settling time close to R_c, thereby making the final phase of the system closely dependent on the sleep-wake cycle.

Figure 5.

Impact of the circadian rhythm on the fibrillization process. (A) During the sleep-wake cycle, the system can pass through the critical production rate. In such cases, the circadian cycle of Aβ production alleviates a persistent fibrillization. (B) The production rate shown in the course of the circadian time period, τ (approximately a day). It is represented by a periodic rectangular function, with the wake production rate R_w and the sleep production rate R_s during the wake and sleep periods, τ_w and τ_s. (C) The estimated daily fAβ accumulation over the wake production rate R_w is shown as a function of the normalized circadian amplitude a = (R_w − R_s)/(R_w + R_s) and sleep period τ_s, for the case R_w = 1.6 × 10⁻³ (μM/day). The dashed contour lines show the mean daily production rate R = (R_wτ_w + R_sτ_s)/τ over the wake production rate R_w. To see this figure in color, go online.

This regulatory aspect is essential because the production rate of sAβ is estimated to lie in a physiological plausible range (the red-highlighted vertical bands in Fig. 2) that includes its critical value R_c. We assume that the diurnal rhythm of overall neural activity results in a diurnal pattern in the production rate of sAβ, which is represented by a rectangular periodic function $\tilde{R}$ for mathematical simplicity (Fig. 5 B). $\tilde{R}$ fluctuates between the wake (w) and sleep (s) courses, each with a specific sAβ production rate R_w and R_s and a duration of τ_w and τ_s, respectively. We define the normalized circadian amplitude as a = (R_w − R_s)/(R_w + R_s).

Because both the settling time and the steady-state value of fAβ concentration depend on the production rate of sAβ, the mean accumulation of fAβ is determined by a and τ_s, especially when the production rate is in a close neighborhood of R_c. The daily accumulation of fAβ is estimated as $F_{\infty }^{\text{w}}{\tau }_{\text{w}}/{\tau }_{0.99}^{\text{w}}+F_{\infty }^{\text{s}}{\tau }_{\text{s}}/{\tau }_{0.99}^{\text{s}}$ and depicted in Fig. 5 C. The settling time to reach the steady-state value F_∞ varies widely for different $\tilde{R}$ around the critical point R_c. As can be seen from Fig. 5 C, accumulation of fAβ per day is significantly reduced by having proper relaxation of the overall neural activity; for instance, through sleeping.

The circadian amplitude a plays a pivotal role in this regard. With sufficiently large a, the switch between the two states becomes prominent, and τ_s turns into the controlling factor of the amyloid plaque clearance. The longer τ_s is, the faster the plaques dissolve. All this is possible because the settling time is long in the proximity of R_c. The clearance rate of fAβ remains constant in the whole sleep-wake cycle. If the settling time were not longer than or comparable to the clearance timescale, the system would not find the time to get rid of the produced fAβ. The amyloid plaques would then form quickly regardless of the sleeping phase time.

Good sleep hygiene can be an important protective factor to curtail the accumulation of Aβ in its fibrillar form, thereby averting the onset of AD. Sleep hygiene refers to different aspects such as deepness of sleep, sleep duration, and its timing and regularity. Although the model only refers explicitly to sleep duration, it can be expected that the other aspects are also helpful in keeping the system below R_c and ensuring more pronounced clearance of fAβ. For instance, a deeper sleep results in more relaxation of neurons, and consequently, less amyloid production. Moreover, regular sleep provides less opportunity for the accumulation of amyloid plaques, leading to lower fAβ concentration. These aspects may only be addressed by a more complicated model that includes a more rigorous relation between sleep and neural relaxation and also takes the spatial characteristics of the brain into account.

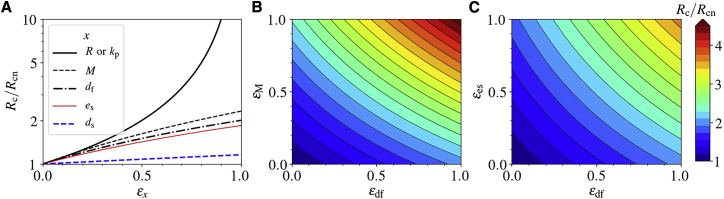
Potential intervention strategies to prevent or delay fibrillization by elevating R_c

We next consider several potential intervention schemes reducing fAβ accumulation in the brain to prevent/treat AD by elevating the critical sAβ production rate R_c. In a neuropathological milieu, different drugs may affect different parameters of the model. The impact of a drug on the parameter x can be modeled as either (1 − ε_x)x for a drug that decreases the value of a parameter (inhibitory drug), where ε_x ∈ [0, 1], or (1 + ε_x)x for a drug that enhances the value of a parameter (stimulatory drug), where ε_x ≥ 0, ε_x being the efficacy of the drug on parameter x. Hence, to lift R_c, the potential strategies should have an inhibitory effect for the parameters R and k_p (i.e., R → (1 − ε_R)R and k_p → (1 − ε_kp)k_p), whereas the rest of the system parameters are to be under a stimulatory treatment (i.e., M → (1 + ε_M)M, e_s → (1 + ε_es)e_s, etc.). Here, we assume a permanent intervention scheme with a constant function with respect to time.

First, we consider a “monotherapy” that alters only one parameter in the system. Defining R_cn as the nominal value of R_c without treatment, Fig. 6 A shows the variation of R_c/R_cn for several treatment methods corresponding to the efficacy parameters in the range ε_x ∈ [0, 1]. As can be seen from Fig. 6 A, a reduction in R or k_p has the strongest impact on R_c because R_c ≈ R_cn(1 − ε_x)⁻¹ for both x = R and x = k_p. According to Fig. 6 A, the change in R_c is more sensitive to the production rate R than to any other parameter.

Figure 6.

Intervention strategies. The critical production rate R_c, normalized to its nominal value R_cn, as a function of drug efficacies. The treatment strategy is increasing the value of R_c as much as it exceeds the actual production rate R. This happens when a drug decreases the parameters R or k_p or increases any other parameter. ε_x is the efficacy of a drug applying to parameter x. (A) R_c/R_cn for single therapies. (B) and (C) R_c/R_cn for two different combination therapies. To see this figure in color, go online.

The simultaneous incorporation of two or more such schemes in a “combination therapy” may significantly enhance R_c. We note that the impact resulting from inhibition of R and that of k_p on R_c are too strong to be achieved with the “combination therapy” with any two of the other parameters. Fig. 6, B and C show changes of R_c due to stimulatory effect on the parameter pairs d_f-M and d_f-e_s, respectively. As expected, the “combination therapy” averts AD by increasing R_c remarkably in a nonlinear manner. For instance, whereas a stimulatory “monotherapy” either on M or d_f with ε_x = 1 hardly increases R_c by twofold, a combination of both of these results in around 4.5-fold enhancement of R_c (see Fig. 6 B), pointing toward the efficacy of such an approach. Moreover, a “combination therapy” on two parameters that do not each play a significant role may have higher impact than a “monotherapy” on a more influential parameter. For example, a combination of stimulatory therapy on d_f and e_s compensates their individual lower impact on increasing R_c as compared with the “monotherapy” on M (compare Fig. 6, A and C). Our simple model thus offers key insight into several options to prevent and treat neuroinflammatory conditions in the context of fAβ accumulation in the brain.

Conclusions

We have developed a minimal ODE-based model of Aβ fibrillization to understand the initiation of AD, based on the amyloid cascade hypothesis (2,37,52). Our theoretical framework is based on the balance between Aβ production by neurons and their clearance by microglia or physical discharge through the CSF. The model suggests that an imbalance between the production and clearance of Aβ may lead to the formation of fibrillar amyloid plaques (fAβ), which sediment in the brain. Once formed, fAβ plaques are not only more persistent against clearance by microglia but also trigger the close-by soluble Aβ oligomers (sAβ) for a fast fibrillization. Therefore, the homeostatic state of the brain shifts toward the dominance of fAβ over sAβ, a process associated with the development of AD in the long run.

Our model predicts two distinct phases for the system, one dominated by sAβ oligomers and the other dominated by fAβ plaques. It is argued that if the system finds itself in the latter phase, the amyloid plaques gradually form, leading to the onset of AD. The two phases are separated by a critical Aβ production rate, R_c. The phase change occurs when the production rate R is greater than R_c. If the physiological value of R is very close to R_c, a perturbation in the production or the clearance of Aβ may trigger the phase change in the system and initiate fibrillization. A return from the fibrillar phase might take years according to our results, implying that the system may not be able to find its original “healthy” homeostatic state again.

The production of Aβ is related to the synaptic activity of neurons (16,17). We have studied how the lack in relaxation of the neural activity facilitates the onset of Aβ fibrillization. Various physiological conditions, such as neuroinflammation, trauma, and even disturbances in sleep may affect the neural activity and indirectly lead to the accumulation of Aβ (10). For instance, flu infection has been recently shown to have an influence on the activation of microglia and neural impairment on mice long after disease recovery (53), indicating that an acute infection may lead to a long-term neuroinflammation that in turn changes the brain homeostatic state and neural activity. Our results suggest that short-term perturbations in the system parameters may result in an abrupt increase in Aβ levels that can persist for years after perturbation. Specifically, we used our model to reveal how sleep might play a key role in preventing the development of AD by reducing the production of Aβ oligomers. These results are in accordance with the observation that AD patients had sleep disturbance problems years before they showed symptoms of AD (9,10). Our model results can also provide an explanation for the connection between the loss of neurons in the SCN and the disturbance of the circadian neural activity (12).

Because a reduction of R_c could initiate progressive fibrillization of Aβ, the onset of AD could be hindered by the treatment strategies that increase the value of R_c. Such an analysis guides us toward new therapeutic or prevention strategies. Efflux of sAβ through CSF and clearance by microglia and astrocytes are the primary ways by which the system can get rid of Aβ. Both of these ways could be modulated by drugs, diseases, and injuries. For example, the efficiency of microglia in fAβ clearance through phagocytosis may be regulated by drugs (54,55). These effects could be translated into higher fAβ decay rate. However, one treatment strategy could be more effective than another if the system has a stronger response to it, which is described by the scaling of R_c with respect to different parameters. The model shows that R_c scales superlinearly with the number of microglia, linearly with their efficiency in clearing Aβ for either the soluble or fibrillar form, and linearly with the efflux rate of sAβ in CSF. It implies that triggering microglial proliferation is more effective in increasing R_c than stimulating their efficiency in phagocytosis. This does not mean that such a treatment strategy will work because the neuroinflammatory aspects of the system have been ignored in the model. Whether more abundant microglia may lead to stronger neuroinflammation is a question we should be cautious of.

According to the model, the direct regulation of sAβ production or polymerization rate of fAβ would be very effective in the prevention of fibrillization and AD onset. First, the impact of apolipoprotein E4 allele (ApoE4) on the disease progression is as important as the production rate of Aβ because ApoE4 directly affects the polymerization rate (56, 57, 58). It implies that blocking ApoE4 protein should be one of the most influential intervention strategies for the individuals who carry it. Second, because further reduction of the polymerization rate may require the recruitment of astrocytes or changing the chemical properties of the brain parenchyma, one should be careful of the side effects of such a therapy and cautiously check whether they might overweigh the treatment benefits. Because changing R_c is difficult, the regulation of Aβ production seems to be the best solution with the least side effects on the system. The production of Aβ is directly related to the expression of synaptic amyloid precursor protein, which gives rise to Aβ if cleaved abnormally (59). In addition, amyloid precursor protein cleavage products alter synaptic plasticity and activity (60,61), meaning that Aβ production is not only affected by neural activity but also affects itself. If such a relation is known, the production of Aβ can be regulated by neural stimulation, which brings about broad new therapeutic schemes focusing on electrical stimulation of neurons to regulate Aβ production for AD prevention.

It must be noted that the model presented here is an approximation of the underlying process. The real physiology of AD is much more complex. Thus, our results should be interpreted in a qualitative rather than a quantitative perspective. In a physiological setting, the scaling of sAβ and fAβ with respect to R, as well as the scaling relations for the other parameters, might be different. For example, at high concentrations of fAβ, microglia might reach their limit of Aβ-clearance, then following a Michaelis-Menten dynamics, which would result in an unlimited increase of fAβ. In addition, our ODE model cannot address spatial accumulation of amyloid plaques, which is an important aspect of AD. Nevertheless, the presented generic model provides a mechanistic understanding of the onset of Aβ fibrillization and insights for therapeutic interventions.

Compared with the other recent mathematical models of AD (18, 19, 20, 21), this model is able to explain global features of the onset of the disease because it combines the physics of fibrillization and the biology of immune system and neural activity to explain how their interplay regulates the production and clearance of Aβ. This comes at the price of loss of complexity of some processes at each of the timescales spanned by the current model. Thanks to the simplicity of the model, we have provided a systematic investigation of the effect of essential parameters in AD. Without such a minimal model, it would not have been feasible to investigate the whole parameter space and draw a broad picture of the disease.

All in all, as Karran et al. reviewed in 2011 (62), the complexity of the disease has not been understood completely, such that many clinical trials focusing on reducing the production of Aβ failed because the disease had already shifted to a new phase, in which many other pathological and neuroinflammatory factors entered. In this regard, it is difficult to directly relate the model results to clinical trials. Nevertheless, the model predicts which treatment strategies could be more effective essentially before the onset of the disease. For instance, we can safely argue that targeting less amyloid production at the first place is equally effective as avoiding ApoE4 but far more beneficial than the clearance through antibodies because of the scaling laws we have obtained from the model.

Author Contributions

M.H. and M.M.-H. designed the research. M.H. developed the mathematical model. M.H., S.K., G.M., and T.M. did the analysis and investigation. M.M.-H. supervised the research. All authors contributed in discussions and wrote the manuscript.

Editor: Arthur Sherman.