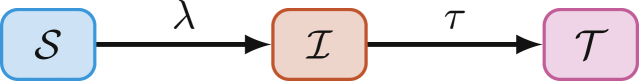Abstract
Background
Epidemic models of sexually transmitted infections (STIs) are often used to characterize the contribution of risk groups to overall transmission by projecting the transmission population attributable fraction (tPAF) of unmet prevention and treatment needs within risk groups. However, evidence suggests that STI risk is dynamic over an individual’s sexual life course, which manifests as turnover between risk groups. We sought to examine the mechanisms by which turnover influences modelled projections of the tPAF of high risk groups.
Methods
We developed a unifying, data-guided framework to simulate risk group turnover in deterministic, compartmental transmission models. We applied the framework to an illustrative model of an STI and examined the mechanisms by which risk group turnover influenced equilibrium prevalence across risk groups. We then fit a model with and without turnover to the same risk-stratified STI prevalence targets and compared the inferred level of risk heterogeneity and tPAF of the highest risk group projected by the two models.
Results
The influence of turnover on group-specific prevalence was mediated by three main phenomena: movement of previously high risk individuals with the infection into lower risk groups; changes to herd effect in the highest risk group; and changes in the number of partnerships where transmission can occur. Faster turnover led to a smaller ratio of STI prevalence between the highest and lowest risk groups. Compared to the fitted model without turnover, the fitted model with turnover inferred greater risk heterogeneity and consistently projected a larger tPAF of the highest risk group over time.
Implications
If turnover is not captured in epidemic models, the projected contribution of high risk groups, and thus, the potential impact of prioritizing interventions to address their needs, could be underestimated. To aid the next generation of tPAF models, data collection efforts to parameterize risk group turnover should be prioritized.
Keywords: Mathematical modelling, Transmission, Risk heterogeneity, Turnover, Sexually transmitted infection, Population attributable fraction
Abbreviations: STI, sexually transmitted infection; HIV, human immunodeficiency virus; tPAF, transmission population attributable fraction
Graphical abstract
Highlights
-
•
A new framework for parameterizing turnover in risk groups is developed.
-
•
Mechanisms by which turnover influences sexually transmitted infection (STI), prevalence in risk groups are examined.
-
•
Turnover reduces the ratio of equilibrium STI prevalence in high vs low risk groups.
-
•
Inferred risk heterogeneity is higher when fitting transmission models with turnover.
-
•
Ignoring turnover in risk could underestimate the transmission population attributable fraction (tPAF), of high risk groups to the overall epidemic.
1. Introduction
Heterogeneity in transmission risk is a consistent characteristic of epidemics of sexually transmitted infections (STI) (Anderson & May 1991). This heterogeneity is often demarcated by identifying specific populations whose risks of acquisition and onward transmission of STI are the highest, such that their specific unmet prevention and treatment needs can sustain local epidemics of STI (Yorke et al., 1978). Disproportionate risk can be conferred in several ways at the individual-level (higher number of sexual partners), partnership-level (reduced condom use within specific partnership types), or structural-level (stigma as a barrier to accessing prevention and treatment services) (Baral et al., 2013). The contribution of high risk groups to the overall epidemic can then be used as an indicator in the appraisal of STI epidemics, helping to guide intervention priorities (Mishra et al., 2016; Shubber et al., 2014).
Traditionally, contribution to an epidemic was quantified using either: the classic population attributable fraction (PAF) via the relative risk of incident infections within a risk group versus the rest of the population and the relative size of the risk group (Hanley, 2001); or the distribution of new infections across subsets of a population (Case et al., 2012; Mishra et al., 2014). So when small risk groups experience disproportionately higher rate of incident infections – e.g. 5 percent of a population acquire 30 percent of STI infections – contribution is interpreted as 5 percent of the population contributing to 30 percent of all infections (Prüss-Ustün et al., 2013). However, the classic PAF does not account for chains of (indirect) transmission, and has been shown to underestimate the contribution of some higher-risk groups to cumulative STI infections, especially over time (Mishra et al., 2014). Thus, transmission models are increasingly being used to quantify contribution by accounting for indirect transmission and projecting the transmission population attributable fraction (tPAF). The tPAF is calculated by simulating counterfactual scenarios where transmission between specific subgroups is stopped, and the relative difference in cumulative infections in the total population over various time-periods is measured (Mishra et al., 2014; Mukandavire et al., 2018). Transmission can be stopped by setting susceptibility and/or infectiousness to zero in the model (Mishra et al., 2014). The tPAF is then interpreted as the fraction of all new infections that stem, directly and indirectly, from a failure to prevent acquisition and/or to provide effective treatment in a particular risk group (Maheu-Giroux et al., 2017; Mishra et al., 2016; Mukandavire et al., 2018).
There is limited evidence on how model structure might influence the tPAF of higher risk groups (Maheu-Giroux et al., 2017; Mishra et al., 2016; Mukandavire et al., 2018), especially movement of individuals between risk groups, an epidemiologic phenomenon that is well-described in the context of sexual behaviour (Watts et al., 2010). Such movement is often referred to in the STI epidemiology literature as turnover (Watts et al., 2010). For example, turnover may reflect entry into or retirement from formal sex work, or other periods associated with higher STI susceptibility and onward transmission due to more partners and/or vulnerabilities (Marston & King, 2006; Watts et al., 2010). Risk group turnover has been shown to influence the predicted equilibrium prevalence of an STI (Stigum et al., 1994; Zhang et al., 2012); the fraction of transmissions occurring during acute HIV infection (Zhang et al., 2012); the basic reproductive number (Henry & Koopman, 2015); and the coverage of antiretroviral therapy required to achieve HIV epidemic control (Henry & Koopman, 2015). Yet how, and the extent to which, turnover influences tPAF has yet to be examined.
There is variability in how turnover has been previously implemented (Boily et al., 2015; Eaton & Hallett, 2014; Koopman et al., 1997; Stigum et al., 1994), in large part because of four main assumptions or epidemiologic constraints surrounding movement between risk groups. For example, in the context of turnover, the relative size of specific populations in the model may be constrained to remain constant over time (Eaton & Hallett, 2014; Koopman et al., 1997; Stigum et al., 1994), such as the proportion of individuals who sell sex. Second, some individuals may enter into high risk groups at an early age, and subsequently settle into lower risk groups; thus the distribution of risks among individuals entering into the transmission model may be assumed to be different from the distribution of risks among individuals already in the transmission model (Eaton & Hallett, 2014). Third, turnover may be constrained to reflect the average duration of time spent within a given risk group (Boily et al., 2015), such as duration engaged in formal sex work (Watts et al., 2010). Finally, turnover could reflect data on how sexual behaviour changes following exit from a given risk group (Boily et al., 2015). Most prior models used some combination of these constraints, based on their specific data or research question, but to date there is no unified approach to modelling turnover.
In this study, we explored the mechanisms by which turnover may influence the tPAF of a high risk group using an illustrative STI model with treatment-induced immunity and without STI-attributable mortality. First, we developed a unified approach to implementing turnover based on epidemiologic constraints. We then sought the following objectives: 1) understand the mechanisms by which turnover influences group-specific STI prevalence and ratios of prevalence between risk groups; 2) examine how inclusion/exclusion of turnover in a model influences the level of risk heterogeneity inferred during model fitting; and 3) examine how inclusion/exclusion of turnover in a model influences the projected tPAF of the highest risk group after model fitting to a particular setting.
2. Methods
We developed a new, unified framework for implementing turnover. We then simulated a deterministic compartmental model of an illustrative STI, with turnover as per the framework, to conduct out experiments.
2.1. A unified framework for implementing turnover
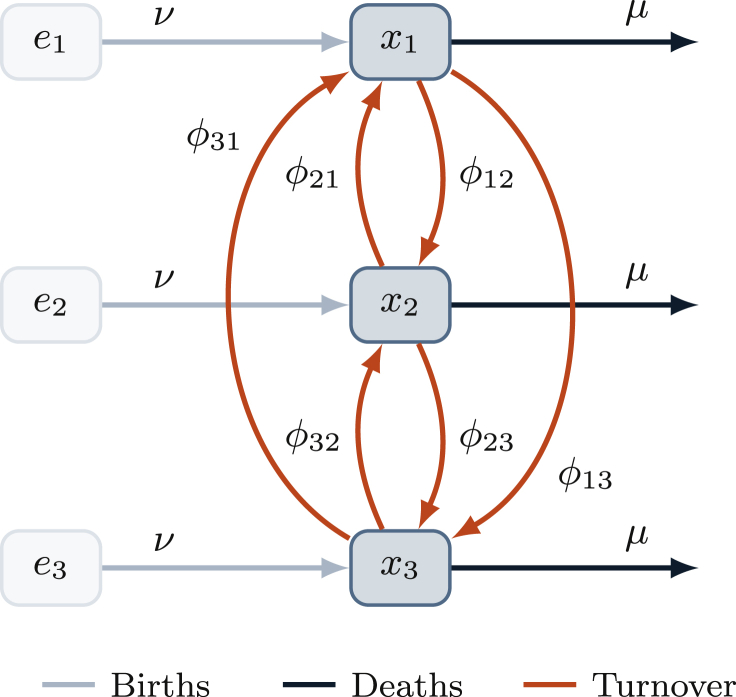
We developed a framework for implementing turnover, as depicted in Fig. 1 and detailed in Appendix A. In the framework, the simulated population is divided into G risk groups. The number of individuals in group is denoted , and the relative size of each group is denoted , where N is the total population size. Individuals enter the population at a rate ν and exit at a rate μ per year. The distribution of risk groups at entry into the model is denoted , which may be different from . The total number of individuals entering group i per year is therefore given by . Turnover rates are collected in a matrix φ, where is the proportion of individuals in group i who move from group i into group j each year. The framework is independent of the disease model, and thus transition rates φ do not depend on health states.
Fig. 1.
System of risk groups and turnover between them.
: number of individuals in risk group i; : number of individuals available to enter risk group i; ν: rate of population entry; μ: rate of population exit; : rate of turnover from group i to group j.
The framework assumes that: 1) the relative sizes of risk groups are known and should remain constant over time; and 2) the rates of population entry ν and exit μ are known, but that they may vary over time. An approach to estimate ν and μ is detailed in Appendix A.2.1. The framework then provides a method to estimate the values of the parameters and φ, representing G and total unknowns. In the framework, and φ are collected in the vector , where . To uniquely determine the elements of , a set of linear constraints are constructed. Each constraint k takes the form , where is a constant and is a vector with the same length as . The values of are then obtained by solving:
| (1) |
using existing algorithms for solving linear systems (LAPACK, 1992).
The framework defines four types of constraints, which are based on assumptions, that can used to solve for the values of and φ via . The frameworks is flexible with respect to selecting and combining these constraints, guided by the availability of data. However, exactly non-redundant constraints must be specified to produce a unique solution, such that exactly one value of satisfies all constraints. Table 1 summarizes the four types of constraints, with their underlying assumptions, and the types of data that can be used in each case. Additional details, including constraint equations, examples, and considerations for combining constraints, are in Appendix A.2.2.
Table 1.
Summary of constraint types for defining risk group turnover.
| Constraint | Assumption | Parameters | Types of data sources for parameterization |
|---|---|---|---|
| 1. Constant group size | the relative population sizes of groups are known or assumed, and assumed to not change over time | demographic health surveys (The DHS Program, 2019), key population mapping and enumeration (Abdul-Quader et al., 2014) | |
| 2. Specified elements | the relative numbers of people entering into each group upon entry into the model or after leaving another group are known or assumed | , | demographic health surveys (The DHS Program, 2019), key population surveys (Baral et al., 2014) |
| 3. Group duration | the average durations of individuals in each group are known or assumed | cohort studies of sexual behaviour over time (Fergus et al., 2007), key population surveys (Watts et al., 2010; Baral et al., 2014) | |
| 4. Turnover rate ratios | ratios between different rates of turnover are known or assumed | demographic health surveys (The DHS Program, 2019), key population surveys (Baral et al., 2014) |
: rate of turnover from group i to group j; : proportion of individuals in risk group i; : proportion of individuals entering into risk group i; : average duration spent in risk group i.
2.2. Transmission model
We developed a deterministic, compartmental model of an illustrative sexually transmitted infection with 3 risk groups. We did not simulate a specific pathogen, but rather constructed a biological system that included susceptible, infectious, and treated (or recovered/immune) health states. The transmission model therefore was mechanistically representative of sexually transmitted infections like HIV, where effective antiretroviral treatment represents a health state where individuals are no longer susceptible nor infectious (Maartens et al., 2014), or hepatitis B virus, where a large proportion of individuals who clear their acute infection develop life-long protective immunity (Ganem & Prince, 2004).
The model is represented by a set of coupled ordinary differential equations (Appendix B.1) and includes three health states: susceptible , infectious , and treated (Fig. 2), and levels of risk: high H (smallest), medium M, and low L (largest).
Fig. 2.
Modelled health states: : susceptible; : infected; : treated; and transitions: : force of infection; treatment.
Risk strata are defined by different number of partners per year, so that individuals in risk group i are assumed to form partnerships at a rate per year. The probability of partnership formation between individuals in group i and individuals in risk group k is assumed to be proportionate to the total number of available partnerships within each group Garnett and Anderson (1994):
| (2) |
The biological probability of transmission is defined as β per partnership. Individuals transition from the susceptible to infectious health state via a force of infection per year, per susceptible in risk group i:
| (3) |
Individuals are assumed to transition from the infectious to treated health state at a rate τ per year, reflecting diagnosis and treatment. The treatment rate does not vary by risk group. Individuals in the treated health state are neither infectious nor susceptible, and individuals cannot become re-infected.
2.2.1. Implementing turnover within the transmission model
As described in Section 2.1, individuals enter the model at a rate ν, exit the model at a rate μ, and transition from risk group i to group j at a rate . The turnover rates φ and distribution of individuals entering the model by risk group were computed using the methods outlined in Appendix A.2.2, based on the following three assumptions. First, we assumed that the proportion of individuals entering each risk group was equal to the proportion of individuals across risk groups in the model . Second, we assumed that the average duration of time spent in each risk group was known. Third, we assumed that the absolute number of individuals moving between two risk groups in either direction was balanced, meaning that if 10 individuals moved from group i to group j, then another 10 individuals moved from group j to group i. These three assumptions were selected because they reflect the common assumptions underlying turnover in prior models (Henry & Koopman, 2015; Zhang et al., 2012) and also to avoid any dominant direction of turnover. That is, we wanted to study the influence of movement between risk groups in general, as compared to no movement, and at various rates of movement, rather than movement predominantly from some groups to some other groups. The system of equations formulated from the above assumptions and constraints is given in Appendix B.2. To satisfy all three assumptions, there was only one possible value for each element in φ and . That is, by specifying these three assumptions, we generated a unique set of φ and .
Under the above three assumptions, we still needed to specify the particular values of the parameters , , ν, and μ. Such parameter values could be derived from data as described in Appendix A.2.2. However, in all our experiments, we used the illustrative values summarized in Table 2. After resolving the system of equations Eq. (1) using these values, was equal to (assumed), and φ was:
| (4) |
Table 2.
Default model parameters for experiments.
| Symbol | Description | Default value |
|---|---|---|
| transmission probability per partnership | 0.03 | |
| rate of treatment initiation among infected | 0.1 | |
| initial population size | 1000 | |
| proportion of system individuals by risk group | [0.05, 0.20, 0.75] | |
| proportion of entering individuals risk by risk group | [0.05, 0.20, 0.75] | |
| average duration spent in each risk group | [5, 15, 25] | |
| C | number of partners per year by individuals in each risk group | [25, 5, 1] |
| rate of population entry | 0.05 | |
| rate of population exit | 0.03 |
All rates have units year−1; durations are in years; parameters stratified by risk group are written [high, medium, low] risk.
We then simulated epidemics using φ above and the parameters shown in Table 2. The transmission model was initialized with individuals who were distributed across risk groups according to . We seeded the epidemic with one infectious individual in each risk group at in an otherwise fully susceptible population. We numerically solved the system of ordinary differential equations (Appendix B.1) in Python using Euler’s method with a time step of years. Code for all aspects of the project is available at: https://github.com/mishra-lab/turnover.
2.3. Experiments
We designed three experiments to examine the influence of turnover on simulated epidemics. We analyzed all outcomes at equilibrium, defined as steady state at years with change in incidence per year.
2.3.1. Experiment 1: mechanisms by which turnover influences equilibrium prevalence
We designed Experiment 1 to explore the mechanisms by which turnover influences the equilibrium STI prevalence of infection, and the ratio of prevalence between risk groups (prevalence ratios). We defined prevalence as . Similar to previous studies (Henry & Koopman, 2015; Zhang et al., 2012), we varied the rates of turnover using a single parameter. However, because our model had risk groups, multiplying a set of base rates φ by a scalar factor would change the relative population sizes of risk groups . Instead of a scalar factor, we controlled the rates of turnover using the duration of time spent in the high risk group , because of the practical interpretation of in the context of STI transmission, such as the duration in formal sex work (Watts et al., 2010). A shorter yielded faster rates of turnover among all groups. The duration of time spent in the medium risk group was then defined as a value between and the maximum duration which scaled with following: , with . The duration of time in the low risk group similarly scaled with , but due to existing constraints, specification of and ensured only one possible value of . Thus, each value of yielded a unique set of turnover rates φ whose elements all scaled inversely with the duration in the high risk group .
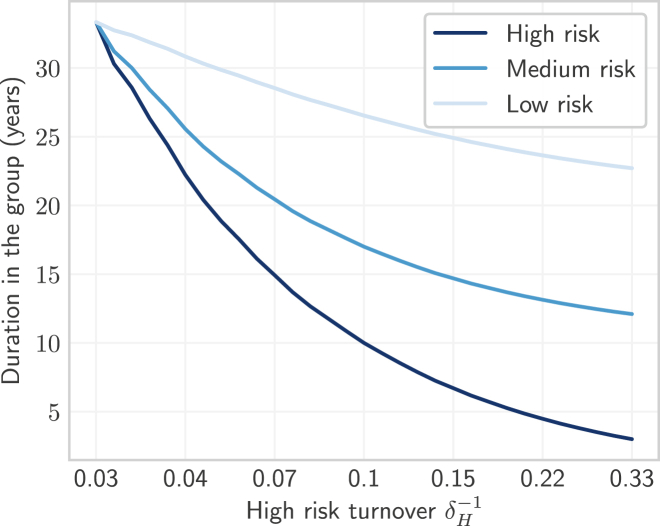
We varied across a range of 33 to 3 years, reflecting a range from the full duration of simulated sexual activity years, through an average reported duration in sex work as low as 3 years (Watts et al., 2010). The resulting duration of time spent in each group versus turnover in the high risk group is shown in Fig. 3.
Fig. 3.
Average duration of time spent in each risk group versus turnover.
Turnover rate (log scale) is a function of the duration of time spent in the high risk group , where shorter time spent in the high risk group yields faster turnover. No turnover is indicated by , due to population exit rate .
For each set of turnover rates, we plotted the equilibrium prevalence in each risk group, and the prevalence ratios between high/low, high/medium, and medium/low risk groups. In order to understand the mechanisms by which turnover influenced prevalence and prevalence ratios (Objective 1), we additionally plotted the absolute number of individuals gained/lost per year in each health state and risk group, due to each of the following five processes:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
where represents any health state, and all five processes sum to the net rate of change described in Eq. (B.1b). Since the influence of turnover on prevalence was only mediated by processes 1 and 2 (processes 3–5 were defined as constant rates which did not change with turnover), our analysis focused on processes 1 and 2. Finally, to further understand trends in incident infections versus turnover (process 2), we factored equation Eq. (3) for incidence into constant and non-constant factors, and plotted the non-constant factors versus turnover.
2.3.2. Experiment 2: inferred risk heterogeneity with vs without turnover
We designed Experiment 2 to examine how the inclusion versus exclusion of turnover influences the inference of transmission model parameters related to risk heterogeneity, specifically the numbers of partners per year across risk groups. The ratio of partner numbers is one way to measure of how different the two risk groups are with respect to acquisition and transmission risks. Indeed, ratios of partner numbers are often used when parameterizing risk heterogeneity in STI transmission models (Mishra et al., 2012).
First, we fit the transmission model with turnover and without turnover, to equilibrium infection prevalence across risk groups. Specifically, we held all other parameters at their default values and fit the numbers of partners per year in each risk group to reproduce the following: 20% infection prevalence among the high risk group, 8.75% among the medium risk group, 3% among the low risk group, and 5% overall. To identify the set of parameters (i.e. partner numbers C in each risk group) that best reproduced the fitting targets, we minimized the negative log-likelihood of group-specific and overall prevalence. Sample sizes of 500, 2000, 7500, and 10,000 were assumed to generate binomial distributions for the high, medium, low, and overall prevalence targets respectively, reflecting typical sample sizes in nationally representative demographic and health surveys (The DHS Program, 2019), multiplied by the relative sizes of risk groups in the model . The minimization was performed using the SLSQP method (Kraft, 1988) from the SciPy Python minimize package. To address Objective 2, we compared the fitted (posterior) ratio of partners per year in the model with turnover versus the model without turnover.
2.3.3. Experiment 3: influence of turnover on the tPAF of the high risk group
We designed Experiment 3 to examine how the tPAF of the high risk group varies when projected by a model with versus without turnover (Objective 3). We calculated the tPAF of risk group i by comparing the relative difference in cumulative incidence between a base scenario, and a counterfactual where transmission from group i is turned off, starting at the fitted equilibrium. That is, in the counterfactual scenario, infected individuals in the high risk group could not transmit the infection. The tPAF was calculated over different time-horizons (1–50 years) as (Mishra et al., 2014):
| (6) |
where is the time corresponding to equilibrium, is the rate of new infections at time t in the base scenario, and is the rate of new infections at time t in the counterfactual scenario. We then compared the tPAF generated from the fitted model with turnover to the tPAF generated from the fitted model without turnover.
3. Results
3.1. Experiment 1: mechanisms by which turnover influences equilibrium prevalence
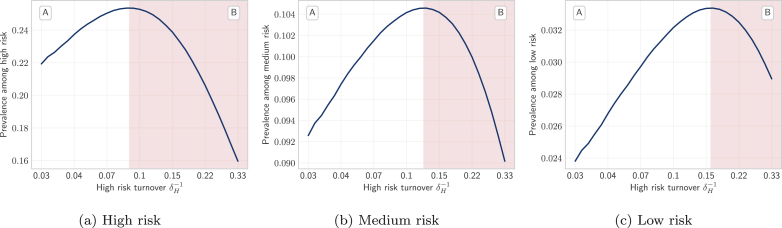
Fig. 4 shows the trends in equilibrium STI prevalence among the high (a), medium (b), and low (c) risk groups, at different rates of turnover which are depicted on the x-axis, based on duration of time spent in the high risk group. Fig. 4 reveals an inverted U-shaped relationship between STI prevalence and turnover in all three risk groups. That is, equilibrium STI prevalence was higher in systems with slow turnover versus those with no turnover (Fig. 4, region A). Equilibrium STI prevalence then peaked at slightly faster turnover before declining in systems with even faster turnover (region B in Fig. 4). Comparison of group-specific prevalence in Fig. 4 shows that the threshold turnover rate at which group-specific prevalence peaked varied by risk group: prevalence in the high risk group peaked at the lower turnover threshold (Fig. 4a), while prevalence in low risk group peaked at a higher turnover threshold (Fig. 4c). To explain the inverted U-shape and different turnover thresholds by group, we examined the processes contributing to prevalence, first in the smallest high risk group, and then in the largest low risk group. Prevalence in the medium risk group is then driven by a combination of these processes; as such, we don’t detail the processes in the context of the medium risk group.
Fig. 4.
Relationship between equilibrium STI prevalence in high, medium, and low risk groups versus turnover rate. Regions A and B denote where equilibrium prevalence is increasing and decreasing with different rates of turnover, respectively.
Turnover rate (log scale) is a function of the duration of time spent in the high risk group , where shorter time spent in the high risk group yields faster turnover. No turnover is indicated by , due to population exit rate .
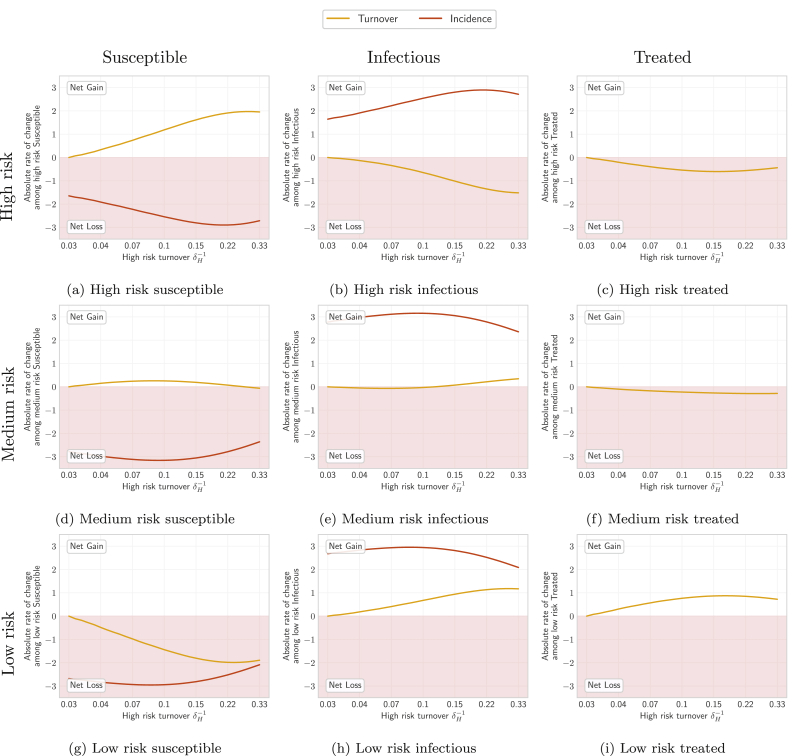
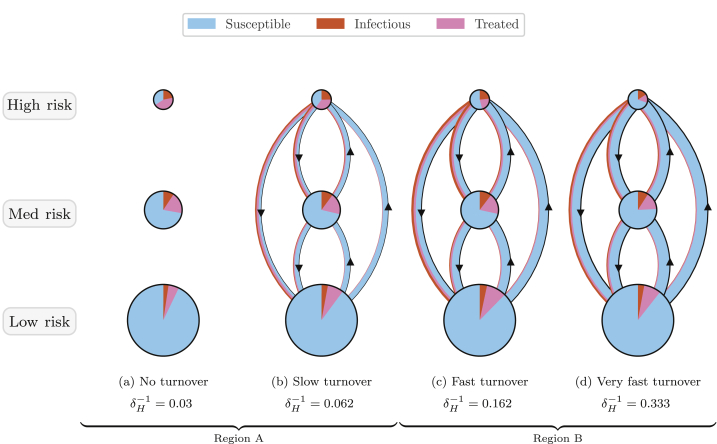
Fig. 5 shows the yearly gain/loss of individuals via turnover, and gain/loss via incident infections, in each health state and risk group, at equilibrium under different rates of turnover. Fig. 6 also illustrates the distribution of health states in each risk group and among individuals moving between risk groups under four different rates of turnover.
Fig. 5.
Absolute rates of change at equilibrium (number of individuals gained/lost per year) among individuals in each health state and risk group, due to: loss/gain via turnover (yellow), and loss/gain via incident infections (red). Based on Eq. (B.1). See Figure C2 for all processes.
Turnover rate (log scale) is a function of the duration of time spent in the high risk group , where shorter time spent in the high risk group yields faster turnover. No turnover is indicated by , due to population exit rate .
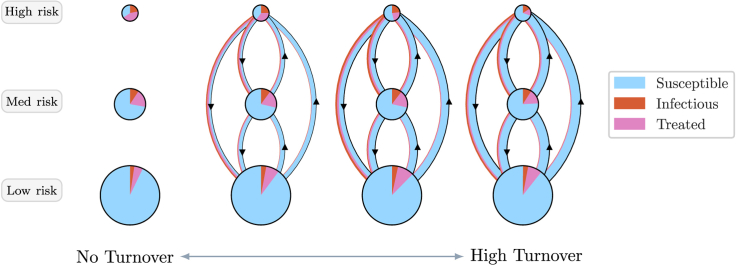
Fig. 6.
Depiction of health states of individuals in each risk group and of individuals moving between risk groups, obtained from models at equilibrium under four overall rates of turnover.
Circle sizes are proportional to risk group sizes. Circle slices and arrow widths are also proportional to the proportion of health states within risk groups and among individuals moving between risk groups, respectively. However, circle sizes and arrow widths do not have comparable scales. Appendix Fig. C1 illustrates proportions of health states versus turnover in full.
3.1.1. Influence of turnover on equilibrium prevalence in the high risk group
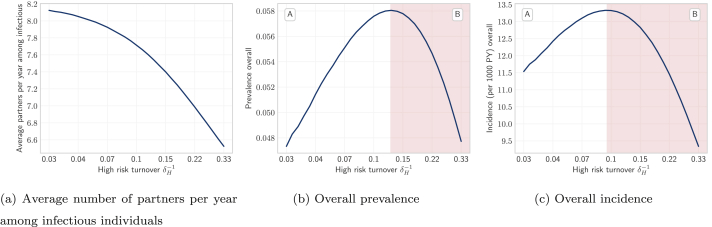
As shown in Fig. 6, at all four rates of turnover the proportion of individuals who were in the infectious state (STI prevalence) was largest in the high risk group. As infectious individuals left the high risk group via turnover, they were largely replaced by susceptible individuals from lower risk groups (Fig. 6b and 5a vs 5b, yellow). The pattern of net outflow of infectious individuals from the high risk group via turnover persisted across the range of turnover rates (Fig. 5b, yellow). This net outflow of infectious individuals via turnover acted to reduce STI prevalence in the high risk group (phenomenon 1). Treated individuals were similarly replaced largely by susceptible individuals (Fig. 6b and 5a vs 5c, yellow). The net replacement of both infectious and treated individuals with susceptible individuals in the high risk group acted to reduce herd effect in that group. Reduced herd effect then contributed to a rise in the number of incident infections in the high risk group, as the system moved from no turnover to slow turnover (Fig. 5b, red; phenomenon 2). Incidence was further influenced by a third phenomenon as systems moved from no turnover to higher rates of turnover: the net movement of infectious individuals from high to low risk (Fig. 6b) reduced the average number of partners per year made available by individuals in the infectious state (Fig. 7a). As shown in Appendix B.4, modelled incidence in all risk groups was proportional to the average number of partners per year among infectious individuals (Fig. 7a), and overall prevalence (Fig. 7b). Thus, as the average number of partners per year among infectious individuals fell with faster turnover, incidence decreased (Fig. 7c, region B; phenomenon 3).
Fig. 7.
Overall incidence and the non-constant factors of incidence versus turnover. The product of factors (a) and (b) is proportional to (c) overall incidence. See Appendix B.4 for proof.
Turnover rate (log scale) is a function of the duration of time spent in the high risk group , where shorter time spent in the high risk group yields faster turnover. No turnover is indicated by , due to population exit rate .
Therefore, the inverted U-shaped relationship between turnover rate and equilibrium STI prevalence in the high risk group was mediated by the combination of the above three phenomena. When systems moved from no turnover to slow turnover, reduction in herd effect (phenomenon 2) predominated, leading to increasing equilibrium prevalence with turnover (Fig. 4a, region A). When systems were modelled under faster and faster turnover, outflow of infectious individuals from the group via turnover (phenomenon 1) and reduction in the average number of partners per year among infectious individuals (phenomenon 3) predominated, leading to lower equilibrium prevalence at faster rates of turnover (Fig. 4a, region B).
3.1.2. Influence of turnover on equilibrium prevalence in the low risk group
As shown in Fig. 6, at equilibrium, the low risk group was composed mainly of susceptible individuals. Moving from a system no turnover to one with slow turnover lead to a net inflow of infectious and treated individuals (Fig. 5h and i, yellow), and a net removal of susceptible individuals (Fig. 5g, yellow). The net inflow of infectious individuals (Fig. 5h, yellow) contributed to higher equilibrium prevalence in the low risk group when the system moved from no turnover to slow turnover (phenomenon 1). The inflow of infectious and treated individuals only slightly reduced the already large proportion who were susceptible in the low risk group. Thus, there was little increase in herd effect within the low risk group as turnover increased (phenomenon 2). However, incident infections still rose in the low risk group as the system moved from no turnover to slow turnover (Fig. 5h, red) due to higher incidence in the total population (Fig. 7c) which was largely driven by reduced herd effect in the high risk group (see Section 3.1.1; phenomenon 2). Under faster rates of turnover, incident infections declined in the low risk group (Fig. 5h, red) due to lower incidence in the total population (Fig. 7c) which was driven by decreasing number of partners per year among infectious individuals (Fig. 7a; phenomenon 3), as described in Section 3.1.1.
Therefore, as in the high risk group, the inverted U-shaped relationship between turnover rate and equilibrium STI prevalence in the low risk group was mediated by the combination of the above three phenomena. Moving from no turnover to slow turnover, the net inflow of infectious individuals (phenomenon 1) and reduced herd effect in the high risk group (phenomenon 2) predominated, leading to higher equilibrium prevalence (Fig. 4c, region A). At higher rates of turnover, a decreasing overall incidence due to a reduction in the number of partners among infectious individuals (phenomenon 3) predominated, leading to declining equilibrium prevalence (Fig. 4c, region B).
In sum, there were three phenomena that drove shifts in equilibrium STI prevalence across risk groups at variable rates of turnover: 1) net flows of infectious individuals from high risk groups into low risk groups; 2) changes to herd effect, especially within the high risk group; and 3) changes to the number of partnerships available with infectious individuals. The effects of these phenomena on the medium risk group were a mixture of the effects on the high and low risk groups, as illustrated in Fig. 5d–f, leading to the unique profile shown in Fig. 4b.
3.1.3. Influence of turnover on STI prevalence ratio between high and low risk groups
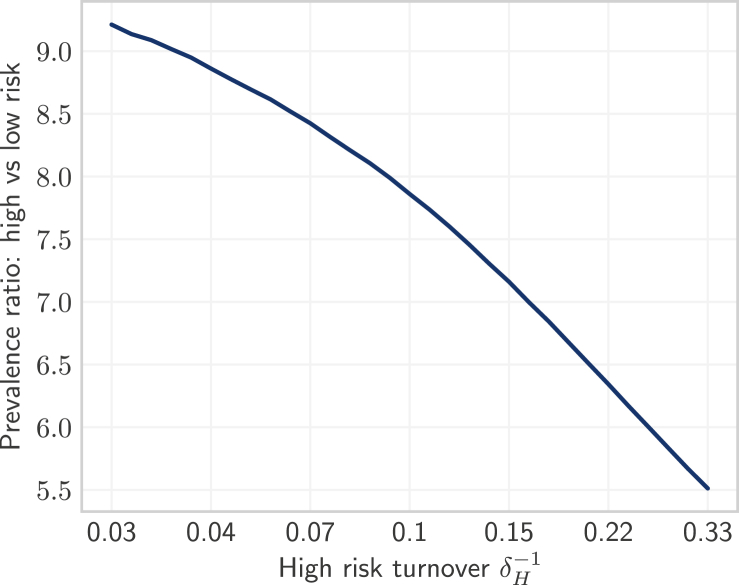
As discussed in Sections 3.1.1, 3.1.2, turnover caused a net outflow of infectious individuals from the high risk group (Fig. 5b, yellow) and a net inflow of infectious individuals into the low risk group (Fig. 5h, yellow). In contrast, the influence of turnover on the rate of incident infections followed a more similar pattern in both the high and low risk groups (Fig. 5b and h, red). Therefore, differences in the influence of turnover on prevalence between risk groups were driven by net movement of infectious individuals from high to low risk, causing prevalence in the high and low risk groups to come closer together with faster turnover. As shown in Fig. 8, the ratio of equilibrium STI prevalence in the high versus low risk groups was thus reduced under faster turnover rates. For example, the prevalence ratio between high and low risk groups was: 6.7 in the model under high turnover ( years) versus 9.2 in the model without turnover ( years) (Table 3). Finally, the propensity for equilibrium STI prevalence to decrease in the high risk group and for prevalence to increase in the low risk group with faster turnover (due to net movement of infectious individuals from high to low risk) also explains why prevalence peaked at slower turnover in the high risk group (Fig. 4a) and faster turnover in the low risk group (Fig. 4c).
Fig. 8.
Equilibrium prevalence ratios between high and low risk groups under different rates of turnover.
Turnover rate (log scale) is a function of the duration of time spent in the high risk group , where shorter time spent in the high risk group yields faster turnover. No turnover is indicated by , due to population exit rate .
Table 3.
Equilibrium partnership formation rates and prevalence among the high and low risk groups predicted by the models with and without turnover, before and after model fitting.
| Context | Number of Partners |
Prevalence |
||||
|---|---|---|---|---|---|---|
| High | Low | High/Low | High | Low | High/Low | |
| Turnover | 25.0 | 1.0 | 25.0 | 21.6% | 3.2% | 6.7 |
| No Turnover | 25.0 | 1.0 | 25.0 | 21.9% | 2.4% | 9.2 |
| Turnover [fit] | 24.3 | 1.0 | 23.9 | 20.0% | 3.0% | 6.7 |
| No Turnover [fit] | 23.5 | 1.5 | 15.2 | 20.0% | 3.0% | 6.7 |
3.2. Experiment 2: inferred risk heterogeneity with versus without turnover
After model fitting, our two STI transmission models (one with turnover and one without turnover) reproduced the target equilibrium STI prevalence values of 20%, 8.75%, 3%, and 5% in the high, medium, low risk groups, and total population, respectively (Table 3; Figure C7). When fitting the model with turnover to these group-specific prevalence targets, the fitted numbers of partners per year (the only non-fixed parameter) had to compensate for the reduction in STI prevalence ratio between high and low risk groups (Fig. 8). As a result, the ratio of fitted partner numbers between high and low risk groups () had to be higher in the model with turnover compared to the model without turnover: 23.9 vs 15.2 (Table 3). That is, the inferred level of risk heterogeneity was higher in the model with turnover than in the model without turnover.
3.3. Experiment 3: influence of turnover on the tPAF of the high risk group
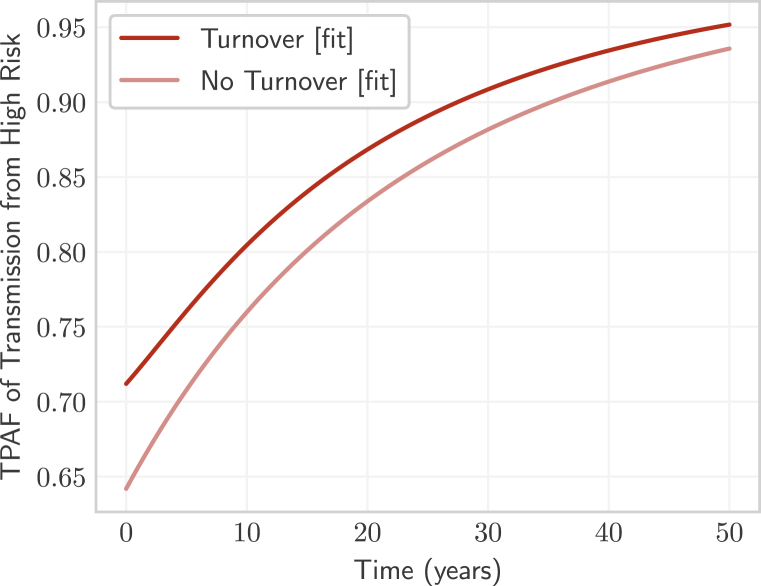
Finally, we compared the tPAF of the high risk group projected by the fitted model with turnover and the fitted model without turnover (Fig. 9). The tPAF projected by both models increased over longer and longer time horizons, indicating that unmet prevention and treatment needs of the high risk group were central to epidemic persistence in both fitted models. The model with turnover projected a larger tPAF at all time-horizons compared with the tPAF projected by the model without turnover. The larger tPAF projected by the model with turnover stemmed from more risk heterogeneity (Table 3) which led to more onward transmission from the unmet prevention and treatment needs of the high risk group.
Fig. 9.
Transmission population attributable fraction (tPAF) of the high risk group in models with and without turnover, after fitting the number of partners per year to group-specific prevalence.
4. Discussion
Using a mechanistic modelling analysis, we found that turnover could be important when projecting the tPAF of high risk groups to the overall epidemic. Mechanistic insights include disentangling three key phenomena by which turnover alters equilibrium STI prevalence within risk groups, and thereby the level of inferred risk heterogeneity between groups via model fitting. Methodological contributions include a framework for modelling turnover which uses a flexible combination of data-driven constraints. Taken together, our explanatory insights and framework have mechanistic, public health, and methodological relevance for the parameterization and use of epidemic models to project intervention priorities for high risk groups.
Influence of turnover on prevalence. Building on prior work by Stigum et al. (1994); Zhang et al. (2012); Henry and Koopman (2015) which similarly found an inverted U-shaped relationship between turnover and overall equilibrium STI prevalence, we identified three key phenomena that generated this relationship. These turnover-driven phenomena were: 1) a net flow of infectious individuals from higher risk groups to lower risk groups; 2) reduced herd effect in the higher risk groups due to net gain of susceptible individuals; and 3) reduced incidence overall due to fewer partner numbers among infectious individuals. The above three phenomena contributed to the pattern of declining prevalence ratio between the highest and lowest risk groups for increasing rates of turnover. A decline in prevalence ratio due to turnover implies a reduction in risk heterogeneity. Since risk heterogeneity is associated with epidemic emergence and persistence (May & Anderson, 1988) – i.e. the basic reproductive number – our findings are thus consistent with Henry and Koopman (2015), who demonstrated that turnover reduces the basic reproductive number by reducing heterogeneity. Indeed, epidemiological and transmission modelling studies have shown that prevalence ratios are an important marker of risk heterogeneity, and in turn the impact of interventions focused on high risk groups (Baral et al., 2012; Mishra et al., 2012).
Implications for interventions. Our comparison of fitted models with and without turnover showed that if turnover exists in a given setting but is ignored in a model, the inferred heterogeneity in risk would be lower than in reality, while reproducing the same STI prevalence in each risk group. As a result, the projected tPAF of high risk groups could be systematically underestimated by models that ignore turnover. Although we examined a single parameter to capture risk (number of partners per year), the findings would hold for any combination of factors that alter the risk per susceptible individual (force of infection), including biological transmission probabilities and rates of partner change (Anderson & May 1991). The public health implications of models ignoring turnover, and thereby underestimating risk heterogeneity and the tPAF of high risk groups, is that resources could potentially be misguided away from high risk groups, For example, epidemic models which fail to include or accurately capture turnover may underestimate the importance of addressing the unmet needs of key populations at disproportionate risk of HIV and other STIs, such as gay men and other men who have sex with men, transgender women, people who use drugs, and sex workers. That is, epidemic models without turnover may underestimate the potential impact of prioritizing, allocating, and tailoring interventions for key populations: interventions such as enhanced and prioritized screening and testing, early diagnoses and treatment, condom use programmes, and reductions in structural barriers to safer sex (World Health Organization, 2016). In many HIV epidemic models of regions with high HIV prevalence, such as in Southern Africa, key populations have historically been subsumed into the overall modelled population; which meant, by design, less risk heterogeneity (Cori et al., 2014; Eaton et al., 2012; Mishra et al., 2016). Our findings suggest that even when key populations are included, it is important to further capture within-person changes in risks over time (such as duration in sex work). Underestimating risk heterogeneity could also underestimate the resources required to achieve local epidemic control, as suggested by Henry and Koopman (2015); Hontelez et al. (2013). Important next steps surrounding the potential bias in tPAF projections attributable to inclusion/exclusion of turnover include quantifying the magnitude of bias, and characterizing the epidemiologic conditions under which the bias would be meaningfully large in the context of public health programmes.
Turnover framework. We developed a unified framework to parameterize risk group turnover using available epidemiologic data and/or assumptions. There are four potential benefits of using the framework to model turnover. First, the framework defines how specific epidemiologic data and assumptions could be used as constraints to help define rates of turnover. Second, the framework allows flexibility in which constraints can be chosen and combined, so that the constraints best reflect locally available data and/or plausible assumptions. In fact, the framework can adequately reproduce several prior implementations of turnover in various epidemic models (Eaton & Hallett, 2014; Henry & Koopman, 2015; Stigum et al., 1994). Third, this flexible approach also allows the framework to scale to any number of risk groups. Finally, the framework avoids the need for a burn-in period to establish a demographic steady-state before introducing infection, which was required in some previous models (Boily et al., 2015).
As noted above, one benefit of the unified framework for modelling turnover is clarifying data priorities for parameterizing turnover. Absolute or relative population size estimates across risk groups may be obtained from population-based sexual behaviour surveys (The DHS Program, 2019), and from mapping and enumeration of marginalized persons such as sex workers (Abdul-Quader et al., 2014). The proportion of individuals who enter into each risk group may be available through sexual behaviour surveys: for example, among individuals who became sexually active for the first time in the past year, the proportion who also engaged in multiple partnerships within the past year. The average duration of time spent within each risk group, such as the duration in sex work, may be drawn from cross-sectional survey questions such as “for how many years have you been a sex worker?” albeit with the recognition that such data are censured (Watts et al., 2010). Longitudinal, or cohort studies that track self-reported sexual behaviour over time can also provide estimates of duration of time spent within a given risk strata (Fergus et al., 2007), or provide direct estimates of transition rates between risk strata.
Limitations. Our framework for modelling turnover was developed specifically to answer mechanistic questions about the tPAF; as such, there are two key limitations of the framework in its current form. First, the framework did not stratify the population by sex or age. In the context of real-world STI epidemics, the relative size of risk groups may differ by both sex and age, such as the often smaller number of females and/or males who sell sex, versus the larger number of males who pay for sex (clients of female or male sex workers). Second, the framework does not account for infection-attributable mortality, such as HIV-attributable mortality. However, modelling studies have shown that HIV-attributable mortality can reduce the relative size of higher risk groups who bear a disproportionate burden of HIV, which in turn can cause an HIV epidemic to decline (Boily & Mâsse, 1997). As such, many models of HIV transmission that include very small ( of the population) high risk groups, such as female sex workers, often do not constrain the relative size of the sub-group populations to be stable over time (Pickles et al., 2013). By ignoring infection-attributable mortality, the proposed framework would similarly allow risk groups to change relative size in response to disproportionate infection-attributable mortality. Future modifications of the proposed framework include methods to optionally re-balance infection-attributable mortality, and relevant age-sex stratifications so that the framework can be applied more broadly to pathogen-specific epidemics.
Our analyses of turnover and tPAF also have several limitations. First, we did not capture the possibility that some individuals may become re-susceptible to infection after treatment – an important feature of many STIs such as syphilis and gonorrhoea (Fenton et al., 2008). As shown by Fenton et al. (2008) and Pourbohloul et al. (2003), the re-supply of susceptible individuals following STI treatment could fuel an epidemic, and so the influence of turnover on STI prevalence and tPAF may be different. In fact, the herd effect underpinning phenomenon 2 relies on the existence of a treated/immune group, since only net replacement of treated (versus infectious) individuals with susceptible individuals via turnover can increase prevalence in the high risk group as observed. However, our findings may also be relevant to non-STI pathogens when risk heterogeneity is present, many of which have natural or treatment-induced immunity. Second, we mainly examined how turnover influences STI prevalence and tPAF of the highest risk group. Future work could explore the mechanisms underlying the influence of turnover on STI prevalence and tPAF of other risk groups. Third, our analyses were restricted to equilibrium STI prevalence. The influence of turnover on prevalence and tPAF may vary within different phases of an epidemic – growth, mature, declining (Wasserheit & Aral, 1996). Finally, our analyses reflected an illustrative STI epidemic in a population with illustrative risk strata. Important next steps in the examination of the extent to which turnover influences the tPAF include pathogen- and population-specific modelling – such as the comparisons of model structures by Hontelez et al. (2013); Johnson and Geffen (2016) – and at different epidemic phases.
Conclusion. In conclusion, turnover may influence prevalence of infection, and thus influence inference on risk heterogeneity when fitting risk-stratified epidemic models. If models do not capture turnover, the projected contribution of high risk groups, and thus, the potential impact of prioritizing interventions to meet their needs, could be underestimated. To aid the next generation of epidemic models used to estimate the tPAF of high risk groups – including key populations – data collection efforts to parameterize risk group turnover should be prioritized.
Funding
The study was supported by the National Institutes of Health, Grant number: NR016650; the Center for AIDS Research, Johns Hopkins University through the National Institutes of Health, Grant number: P30AI094189.
Contributions
JK and SM conceptualized the study and drafted the manuscript; JK designed the experiments with input from LW, HM, and SM. JK developed the unified framework and conducted the modelling, experiments, and analyses; conducted the literature review, and drafted the first version of the manuscript. LW, HM, SB, and SS led substantial structural revisions to the manuscript, including assessment of epidemiological constraints and assumptions; and provided critical discussion surrounding implications of findings. All authors contributed to interpretation of the results and manuscript revision.
Declaration of competing interest
Declarations of interest: none.
Acknowledgements
We would like to thank Kristy Yiu (Unity Health Toronto) for logistical support, the Siyaphambili research team for helpful discussions, and Carly Comins (Johns Hopkins University) for facilitating the modelling discussions with the wider study team. SM is supported by an Ontario HIV Treatment Network and Canadian Institutes of Health Research New Investigator Award.
Handling editor. Dr Y. Shao
Footnotes
On behalf of the Siyaphambili study team.
Peer review under responsibility of KeAi Communications Co., Ltd.
Supplementary Appendix to this article can be found online at https://doi.org/10.1016/j.idm.2020.07.004.
Appendix.
References
- Abdul-Quader A.S., Baughman A.L., Hladik W. Vol. 9. 2014. pp. 107–114. (Estimating the size of key populations: Current status and future possibilities). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., May R.M. 1991. Infectious diseases of humans: Dynamics and control. Infectious diseases of humans: Dynamics and control. [Google Scholar]
- Baral S., Beyrer C., Muessig K., Poteat T., Wirtz A.L., Decker M.R.…Kerrigan D. Burden of HIV among female sex workers in low-income and middle-income countries: A systematic review and meta-analysis. The Lancet Infectious Diseases. 2012;12:538–549. doi: 10.1016/S1473-3099(12)70066-X. [DOI] [PubMed] [Google Scholar]
- Baral S., Ketende S., Green J.L., Chen P.A.A., Grosso A., Sithole B., Ntshangase C., Yam E., Kerrigan D., Kennedy C.E., Adams D. Reconceptualizing the HIV epidemiology and prevention needs of female sex workers (FSW) in Swaziland. PloS One. 2014;9 doi: 10.1371/journal.pone.0115465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baral S., Logie C.H., Grosso A., Wirtz A.L., Beyrer C. Modified social ecological model: A tool to guide the assessment of the risks and risk contexts of HIV epidemics. BMC Public Health. 2013;13:482. doi: 10.1186/1471-2458-13-482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boily M.C., Mâsse B. Mathematical models of disease transmission: A precious tool for the study of sexually transmitted diseases. Canadian Journal of Public Health. 1997;88:255–265. doi: 10.1007/bf03404793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boily M.C., Pickles M., Alary M., Baral S., Blanchard J., Moses S., Vickerman P., Mishra S. What really is a concentrated HIV epidemic and what does it mean for west and central Africa? Insights from mathematical modeling. Journal of Acquired Immune Deficiency Syndromes. 2015;68:S74–S82. doi: 10.1097/QAI.0000000000000437. [DOI] [PubMed] [Google Scholar]
- Case K., Ghys P., Gouws E., Eaton J., Borquez A., Stover J., Cuchi P., Abu-Raddad L., Garnett G., Hallett T. Understanding the modes of transmission model of new HIV infection and its use in prevention planning. Bulletin of the World Health Organization. 2012;90:831–838. doi: 10.2471/blt.12.102574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cori A., Ayles H., Beyers N., Schaap A., Floyd S., Sabapathy K.…Fraser C. Hptn 071 (PopART): A cluster-randomized trial of the population impact of an HIV combination prevention intervention including universal testing and treatment: Mathematical model. PloS One. 2014;9 doi: 10.1371/journal.pone.0084511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eaton J.W., Hallett T.B. Why the proportion of transmission during early-stage HIV infection does not predict the long-term impact of treatment on HIV incidence. Proceedings of the National Academy of Sciences. 2014;111:16202–16207. doi: 10.1073/pnas.1323007111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eaton J.W., Johnson L.F., Salomon J.A., Bärnighausen T., Bendavid E., Bershteyn A.…Hallett T.B. HIV treatment as prevention: Systematic comparison of mathematical models of the potential impact of antiretroviral therapy on HIV incidence in South Africa. PLoS Medicine. 2012;9 doi: 10.1371/journal.pmed.1001245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenton K.A., Breban R., Vardavas R., Okano J.T., Martin T., Aral S., Blower S. Infectious syphilis in high-income settings in the 21st century. The Lancet Infectious Diseases. 2008;8:244–253. doi: 10.1016/S1473-3099(08)70065-3. [DOI] [PubMed] [Google Scholar]
- Fergus S., Zimmerman M.A., Caldwell C.H. Growth trajectories of sexual risk behavior in adolescence and young adulthood. American Journal of Public Health. 2007;97:1096–1101. doi: 10.2105/AJPH.2005.074609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganem D., Prince A.M. Hepatitis B virus infection —natural history and clinical consequences. New England Journal of Medicine. 2004;350:1118–1129. doi: 10.1056/NEJMra031087. [DOI] [PubMed] [Google Scholar]
- Garnett G.P., Anderson R.M. Balancing sexual partnership in an age and activity stratified model of HIV transmission in heterosexual populations. Mathematical Medicine and Biology. 1994;11:161–192. doi: 10.1093/imammb/11.3.161. [DOI] [PubMed] [Google Scholar]
- Hanley J.A. A heuristic approach to the formulas for population attributable fraction. Journal of Epidemiology & Community Health. 2001;55:508–514. doi: 10.1136/jech.55.7.508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry C.J., Koopman J.S. Strong influence of behavioral dynamics on the ability of testing and treating HIV to stop transmission. Scientific Reports. 2015;5:9467. doi: 10.1038/srep09467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hontelez J.A.C., Lurie M.N., Bärnighausen T., Bakker R., Baltussen R., Tanser F.…de Vlas S.J. Elimination of HIV in South Africa through expanded access to antiretroviral therapy: A model comparison study. PLoS Medicine. 2013;10 doi: 10.1371/journal.pmed.1001534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson L.F., Geffen N. A Comparison of two mathematical modeling frameworks for evaluating sexually transmitted infection epidemiology. Sexually Transmitted Diseases. 2016;43:139–146. doi: 10.1097/OLQ.0000000000000412. [DOI] [PubMed] [Google Scholar]
- Koopman J.S., Jacquez J.A., Welch G.W., Simon C.P., Foxman B., Pollock S.M.…Lange K. The role of early HIV infection in the spread of HIV through populations. Journal of Acquired Immune Deficiency Syndromes. 1997;14:249–258. doi: 10.1097/00042560-199703010-00009. [DOI] [PubMed] [Google Scholar]
- Kraft D. DLR German Aerospace Center — Institute for Flight Mechanics; Koln, Germany: 1988. A software package for sequential quadratic programming. Technical Report DFVLR-FB 88-28. [Google Scholar]
- LAPACK Lapack: Linear algebra PACKage. 1992. http://www.netlib.org/lapack URL:
- Maartens G., Celum C., Lewin S.R. HIV infection: Epidemiology, pathogenesis, treatment, and prevention. The Lancet. 2014;384:258–271. doi: 10.1016/S0140-6736(14)60164-1. [DOI] [PubMed] [Google Scholar]
- Maheu-Giroux M., Vesga J.F., Diabaté S., Alary M., Baral S., Diouf D., Abo K., Boily M.C. Changing dynamics of HIV transmission in côte d’Ivoire: Modeling who acquired and transmitted infections and estimating the impact of past HIV interventions (1976-2015) Journal of Acquired Immune Deficiency Syndromes. 2017;75:517–527. doi: 10.1097/QAI.0000000000001434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marston C., King E. Factors that shape young people’s sexual behaviour: A systematic review. Lancet. 2006;368:1581–1586. doi: 10.1016/S0140-6736(06)69662-1. [DOI] [PubMed] [Google Scholar]
- May R.M., Anderson R.M. 1988. The transmission dynamics of human immunodeficiency virus (HIV) [DOI] [PubMed] [Google Scholar]
- Mishra S., Boily M.C., Schwartz S., Beyrer C., Blanchard J.F., Moses S., Castor D., Phaswana-Mafuya N., Vickerman P., Drame F., Alary M., Baral S.D. Data and methods to characterize the role of sex work and to inform sex work programs in generalized HIV epidemics: Evidence to challenge assumptions. Annals of Epidemiology. 2016;26:557–569. doi: 10.1016/j.annepidem.2016.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra S., Pickles M., Blanchard J.F., Moses S., Boily M.C. Distinguishing sources of HIV transmission from the distribution of newly acquired HIV infections: Why is it important for HIV prevention planning? Sexually Transmitted Infections. 2014;90:19–25. doi: 10.1136/sextrans-2013-051250. [DOI] [PubMed] [Google Scholar]
- Mishra S., Steen R., Gerbase A., Lo Y.R., Boily M.C. Impact of high-risk sex and focused interventions in heterosexual HIV epidemics: A systematic review of mathematical models. PloS One. 2012;7 doi: 10.1371/journal.pone.0050691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukandavire C., Walker J., Schwartz S., Boily M.C., Danon L., Lyons C., Diouf D., Liestman B., Diouf N.L., Drame F., Coly K., Muhire R.S.M., Thiam S., Diallo P.A.N., Kane C.T., Ndour C., Volz E., Mishra S., Baral S., Vickerman P. Estimating the contribution of key populations towards the spread of HIV in Dakar, Senegal. Journal of the International AIDS Society. 2018;21 doi: 10.1002/jia2.25126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickles M., Boily M.C., Vickerman P., Lowndes C.M., Moses S., Blanchard J.F., Deering K.N., Bradley J., Ramesh B.M., Washington R., Adhikary R., Mainkar M., Paranjape R.S., Alary M. Assessment of the population-level effectiveness of the avahan HIV-prevention programme in South India: A preplanned, causal-pathway-based modelling analysis. The Lancet Global Health. 2013;1:e289–e299. doi: 10.1016/S2214-109X(13)70083-4. [DOI] [PubMed] [Google Scholar]
- Pourbohloul B., Rekart M.L., Brunham R.C. Impact of mass treatment on syphilis transmission: A mathematical modeling approach. Sexually Transmitted Diseases. 2003;30:297–305. doi: 10.1097/00007435-200304000-00005. [DOI] [PubMed] [Google Scholar]
- Prüss-Ustün A., Wolf J., Driscoll T., Degenhardt L., Neira M., Calleja J.M.G. HIV due to female sex work: Regional and global estimates. PloS One. 2013;8 doi: 10.1371/journal.pone.0063476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shubber Z., Mishra S., Vesga J.F., Boily M.C. The HIV modes of transmission model: A systematic review of its findings and adherence to guidelines. Journal of the International AIDS Society. 2014;17:18928. doi: 10.7448/IAS.17.1.18928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stigum H., Falck W., Magnus P. The core group revisited: The effect of partner mixing and migration on the spread of gonorrhea, chlamydia, and HIV. Mathematical Biosciences. 1994;120:1–23. doi: 10.1016/0025-5564(94)90036-1. [DOI] [PubMed] [Google Scholar]
- The DHS Program 2019. https://www.dhsprogram.com Data. URL:
- Wasserheit J.N., Aral S.O. The dynamic topology of sexually transmitted disease epidemics: Implications for prevention strategies. Journal of Infectious Diseases. 1996;174:S201–S213. doi: 10.1109/ICPDS.2016.7756727. [DOI] [PubMed] [Google Scholar]
- Watts C., Zimmerman C., Foss A.M., Hossain M., Cox A., Vickerman P. Remodelling core group theory: The role of sustaining populations in HIV transmission. Sexually Transmitted Infections. 2010;86:iii85–iii92. doi: 10.1136/sti.2010.044602. [DOI] [PubMed] [Google Scholar]
- World Health Organization . WHO Guidelines; 2016. Consolidated guidelines on HIV prevention, diagnosis, treatment and care for key populations. [PubMed] [Google Scholar]
- Yorke J.A., Hethcote H.W., Nold A. Dynamics and control of the transmission of gonorrhea. Sexually Transmitted Diseases. 1978;5:51–56. doi: 10.1097/00007435-197804000-00003. [DOI] [PubMed] [Google Scholar]
- Zhang X., Zhong L., Romero-Severson E., Alam S.J., Henry C.J., Volz E.M., Koopman J.S. Episodic HIV risk behavior can greatly amplify HIV prevalence and the fraction of transmissions from acute HIV infection. Statistical Communications in Infectious Diseases. 2012;4 doi: 10.1515/1948-4690.1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.